Open Access Article
Open Access ArticleActivation in the rate of oxygen release of Sr0.8Ca0.2FeO3−δ through removal of secondary surface species with thermal treatment in a CO2-free atmosphere†
Giancarlo
Luongo
,
Alexander H.
Bork
 ,
Paula M.
Abdala
,
Paula M.
Abdala
 ,
Yi-Hsuan
Wu
,
Yi-Hsuan
Wu
 ,
Evgenia
Kountoupi
,
Felix
Donat
,
Evgenia
Kountoupi
,
Felix
Donat
 * and
Christoph R.
Müller
* and
Christoph R.
Müller
 *
*
Laboratory of Energy Science and Engineering, Department of Mechanical and Process Engineering, ETH Zurich, Leonhardstrasse 21, 8092 Zürich, Switzerland. E-mail: donatf@ethz.ch; muelchri@ethz.ch
First published on 27th February 2023
Abstract
We elucidate the underlying cause of a commonly observed increase in the rate of oxygen release of an oxygen carrier with redox cycling (here specifically for the perovskite Sr0.8Ca0.2FeO3−δ) in chemical looping applications. This phenomenon is often referred to as activation. To this end we probe the evolution of the structure and surface elemental composition of the oxygen carrier with redox cycling by both textural and morphological characterization techniques (N2 physisorption, microscopy, X-ray powder diffraction and X-ray absorption spectroscopy). We observe no appreciable changes in the surface area, pore volume and morphology of the sample during the activation period. X-ray powder diffraction and X-ray absorption spectroscopy analysis (at the Fe and Sr K-edges) of the material before and after redox cycles do not show significant differences, implying that the bulk (average and local) structure of the perovskite is largely unaltered upon cycling. The analysis of the surface of the perovskite via X-ray photoelectron and in situ Raman spectroscopy indicates the presence of surface carbonate species in the as-synthesized sample (due to its exposure to air). Yet, such surface carbonates are absent in the activated material, pointing to the removal of carbonates during cycling (in a CO2-free atmosphere) as the underlying cause behind activation. Importantly, after activation and a re-exposure to CO2, surface carbonates re-form and yield a deactivation of the perovskite oxygen carrier, which is often overlooked when using such materials at relatively low temperature (≤500 °C) in chemical looping.
1. Introduction
Perovskite-based oxides find application in many areas, including solid oxide fuel cells,1,2 catalysis,3,4 gas separation membranes,5,6 photoelectrochemical water splitting,7,8 and as oxygen carriers for chemical looping applications.3,9,10 Perovskite oxides have the general formula ABO3−δ, where the A cation is a rare or alkaline earth metal, the B cation is a transition metal oxide and delta δ refers to the oxygen non-stoichiometry.3 Perovskites possess high mixed ionic and electronic conductivity, as well as high rates of oxygen exchange with molecular oxygen in the gas phase.11,12 Chemical looping applications exploit the reversible release and uptake of oxygen from perovskites according to eqn (1):9 | (1) |
At a given temperature, T, some perovskites release gaseous oxygen in a N2 atmosphere (or in other low oxygen partial pressure, pO2, environments) and can be re-oxidized in air (high pO2). Perovskites can accommodate a wide variety of A- and B-site cations, which allows for the tuning of their chemical and physical properties (e.g. temperature and quantity of oxygen release, enthalpy of reaction, and melting temperature).9,13 Specifically, strontium and iron-based perovskites were identified as promising oxygen carriers for low temperature chemical looping applications (400–600 °C).9,11,14 Several works studied the effect of the substitution of Sr- and/or Fe-with different cations in SrFeO3−δ (e.g. La or Ca for the A-site, or Co, Ni or Cu for the B-site) on its thermodynamic properties (e.g. the equilibrium oxygen partial pressure, enthalpy of reaction or oxygen storage capacity), which largely determine the suitability of an oxygen carrier for a given chemical looping application.9,12 We investigated in a previous work the effect of Ca A- or Co B-site substitution on the performance of these materials (i.e. Sr1−xCaxFeO3−δ and SrFe1−xCoxO3−δ) for chemical looping air separation (CLAS). When assessing the redox cyclic stability of both unsubstituted and substituted samples, we observed that the amount of oxygen released at 500 °C increased with the number of redox cycles, indicating that the material “activated” during redox cycling.14
A cycle number-dependent activation of oxygen carriers in chemical looping applications is not specific to the SrFeO3−δ family, and has indeed been reported for many other oxides, including natural minerals such as ilmenite and supported Fe- or Cu-based oxides.15–17 Most of these studies have investigated the material behavior at high temperatures (>800 °C).18–20 For example, for ilmenite, a type of oxygen carrier that has been used for chemical looping-based combustion processes, it was found that long heat treatments (e.g. 950 °C for 24 h in air) enhance its redox activity.21–23 With redox cycling, ilmenite was found to activate further24,25 and there is a clear correlation between the degree of reduction and the extent of activation in each redox cycle.26 The activation of ilmenite is accompanied by the formation of surface cracks and an increase in porosity, from ∼1% up to ∼40%,27 but also the segregation of iron oxide from the Fe–Ti–O mixed phases and the lowering of the oxygen storage capacity (OSC).28 Other routes of activation of oxygen carriers such as ilmenite include their doping, e.g. by K using K2CO3 as the precursor.29–33 For Fe–O-based oxygen carriers, the interactions of Fe with the support material (often Al2O3) and the re-distribution of Fe within the material have been put forward to explain their activation, but also its deactivation, during redox cycling.34–38
Concerning perovskite-based oxygen carriers for chemical looping application at lower temperatures (≤500 °C), the phenomenon of activation has not been studied and hence the underlying cause is currently unknown. However, in other research areas, e.g. electrochemistry in the context of the oxygen reduction reaction (ORR) and the oxygen evolution reaction (OER), the activation and deactivation of perovskites have indeed been studied thoroughly. Different from chemical looping, here activation and deactivation refer to an increase and decrease, respectively, of the oxygen exchange rates and the catalytic activity of perovskites, without changes in the bulk phase.39–42 For example, for the electrocatalyst (La, Sr)(Mn, Fe, Co)O3−δ it was found that a decrease in the rate of oxygen exchange was accompanied by the segregation of the A-site cation Sr from the perovskite structure and the formation of secondary phases on the surface, identified as SrOx or SrCO3.39,43–48 It was also shown that the deactivation could be reversed by thermal treatment at T > 800 °C.39,40
Hence, the aim of this work is to elucidate the prevailing activation mechanism of Sr1−xCaxFeO3−δ perovskites in low-temperature chemical looping applications. To this end, we perform a detailed (bulk) structural and morphological characterization of the material during activation. This is complemented by measurements of the material's surface and changes thereof using X-ray photoelectron spectroscopy (XPS) and in situ Raman spectroscopy. Our findings show that CO2 (often present as impurity in both oxidizing and reducing gas streams) impair the performance of Sr-containing oxygen carriers through the formation of surface carbonates. Exposure to CO2-free streams gradually removes these surface carbonates, leading in turn to an activation of the material. These findings are of relevance for both the design of oxygen carrier materials and their operation in low-temperature chemical looping process schemes.
2. Experimental
2.1 Synthesis of the oxygen carrier
The perovskites were synthesized via a sol–gel method by dissolving stoichiometric amounts of nitrate precursors, i.e. Sr(NO3)2 (Sigma Aldrich, ACS reagent, 99.9%), Fe(NO3)3·9H2O (Sigma Aldrich, ACS reagent, ≥ 98%) and Ca(NO3)2·4H2O (Sigma Aldrich, 99%) in deionized water together with citric acid (3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 molar ratio of citric acid to metal ions) and ethylene glycol (1.2
1 molar ratio of citric acid to metal ions) and ethylene glycol (1.2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 molar ratio of ethylene glycol to citric acid). The solution was held at 80 °C until a gel formed and subsequently dried at 130 °C for 10 h. The powder was crushed and first calcined in air at 500 °C for 7 h (heating rate 3 °C min−1) and then at 1000 °C for 10 h (heating rate 5 °C min−1).
1 molar ratio of ethylene glycol to citric acid). The solution was held at 80 °C until a gel formed and subsequently dried at 130 °C for 10 h. The powder was crushed and first calcined in air at 500 °C for 7 h (heating rate 3 °C min−1) and then at 1000 °C for 10 h (heating rate 5 °C min−1).
2.2 Characterization of the oxygen carrier
 | (2) |
To estimate the atomic composition, the atomic sensitivity factors (ASF) of Scofield were used.52 In the case of the Sr 3d spectrum, where different peaks originate from the same element due to orbital splitting, the following constraints were used: the difference in binding energy between the Sr 3d5/2 and Sr 3d3/2 components was 1.7 eV and the ratio between the peak areas of Sr 3d5/2 and Sr 3d3/2 was fixed at 1.5.39
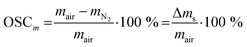 | (3) |
The change in oxygen non-stoichiometry Δδ, used to evaluate the relaxation time of the reaction, was calculated according to eqn (4):
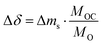 | (4) |
3. Results and discussion
3.1 Activation in the rate of the oxygen release from Sr1−xCaxFeO3−δ
The oxygen release and uptake of Sr0.8Ca0.2FeO3−δ over ten redox cycles in a TGA at 500 °C is shown in Fig. 1a. Considering the first cycle, after 40 min of reduction in N2 the OSCm was 1.60 wt%. After a subsequent oxidation for 20 min in air, the mass had regained the initial value. In the following redox cycles, an increased mass loss was observed at the end of each consecutive reduction step, reaching an OSCm of 2.15 wt% after the 10th reduction step. This is consistent with our previous results showing an increase in the rate of oxygen release, and hence the amount of oxygen released within a given time with increasing cycle number.14 The observed rates of the oxygen release and uptake can be quantified by fitting the change in the oxygen non-stoichiometry Δδ (eqn (4)) with an exponential first-order decay function,54 as defined in eqn (5) and (6) for the reduction and oxidation steps, respectively: | (5) |
 | (6) |
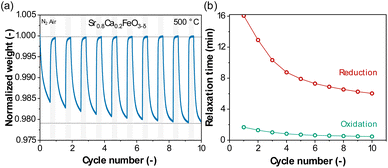 | ||
| Fig. 1 (a) Normalized weight upon redox cycling (40 min reduction in N2 and 20 min oxidation in compressed air) collected in the TGA at 500 °C for Sr0.8Ca0.2FeO3−δ; (b) relaxation times of the reduction and oxidation steps, obtained by fitting the temporal change of the normalized sample weight with an exponential decay function, as defined in eqn (5) and (6). | ||
Here, a and b are two fitting parameters, which could be interpreted, respectively, as the asymptotic value of the oxygen non-stoichiometry of the reduction reaction and the beginning of the oxidation reaction, only had the reaction time t approached infinity; since the reaction times were short in our cycling experiments and the reduction reaction incomplete, a and b were always different. τRED and τOX are the fitted relaxation times for the reduction and oxidation reactions (e.g. for the reduction step, after time t = τRED, Δδ becomes 0.63 × a, meaning that the reaction has reached 63% of the fitted asymptotic value of the oxygen non-stoichiometry). In other words, a short relaxation time τ means that the asymptotic value of the oxygen non-stoichiometry for a given combination T and pO2 is reached faster and the OSCm is greater (in a given time) as opposed to a long relaxation time. Fig. S1† exemplary shows a fitting of the change in oxygen non-stoichiometry Δδ during reduction and oxidation in the first cycle of Fig. 1a using eqn (5) and (6). Fig. 1b plots the obtained relaxation times τRED and τOX over ten cycles, showing a clear decrease in τRED and τOX with cycle number. It is noteworthy that an activation occurred for both the reduction and oxidation steps, as evident by the decreasing values of the relaxation times for increasing cycle number, yet the degree of activation was significantly more pronounced in the reduction step. All fitted parameters (a, b, τRED and τOX) and goodness of fit (R2) values obtained when calculating the relaxation times in Fig. 1b and 2 are provided in the ESI,† Table S1.
To elucidate the cause of the increase in the rate of oxygen release, first it is critical to examine under what operating conditions the phenomenon is observed and exclude any experimental artifacts. To this end, we investigated the influence of different sample compositions and operating conditions (i.e. atmosphere, particle size, flow rate, sample weight, temperature, and crucible type) on the activation behavior.
Fig. S2† shows the TGA curves obtained over ten redox cycles using SrFeO3−δ, Sr0.9Ca0.1FeO3−δ and Sr0.75Ca0.25FeO3−δ as the oxygen carriers.
We can observe an increase in the rate of oxygen release with increasing cycle number for all samples. Note that we studied only phase pure Sr1−xCaxFeO3−δ perovskites, hence the value of x is limited to x ≤ 0.25, as reported in previous work.14 Fig. S3† summarizes the effects of total flowrates, sample masses, particle size distributions, reducing atmospheres (by using also 5% H2/N2) and crucible sizes (a shallow 30 μL instead of a 70 μL crucible) on the activation behavior of Sr0.8Ca0.2FeO3−δ.
From these control experiments, we observed that each operating parameter affected the cyclic activation of Sr0.8Ca0.2FeO3−δ to some degree (Fig. S3†), yet the phenomenon of activation was always observed. Hence, in the following a fixed set of experimental conditions was used (i.e. flow rate 200 mL min−1, sample weight 30 mg, particle size 25–53 μm, 70 μL crucible).
In order to understand whether the activation of the perovskite is a temporary or long-lasting effect, we carried out “aging” experiments, in which the sample was cooled down after activation in the TGA and stored at ambient conditions in a closed vial for a fixed period of time. Fig. 3a summarizes the relaxation times as a function of the cycle number determined from cycling experiments (30 redox cycles each) for the as-synthesized sample and the same sample (redox-cycled) stored in the laboratory at ambient conditions for 1 week, another 2 weeks, another 2 h, and finally another 2 weeks again; the results of the individual redox cycling experiments are provided in Fig. S4.† From the first cycle to the thirtieth cycle we observed the expected activation behavior of the as-synthesized material described by a decrease in the relaxation time. After 1 week of storage in the laboratory, the sample displayed a longer relaxation time in the first cycle, i.e. the thirty-first cycle compared to the thirtieth cycle, which indicates that the sample deactivated during its storage at ambient conditions. From the subsequent storage and redox cycling experiments, we observed that a longer storage time (2 weeks compared to 2 h) resulted in a higher degree of deactivation (i.e. longer relaxation times). Hence, there was a direct correlation between the storage time and the degree of deactivation.
Since the perovskite deactivated in ambient conditions, we investigated whether the deactivation may be ascribed to humidity (H2O) or CO2 present in ambient air. For this purpose, we exposed the sample to dry CO2 (1%, 5%, 10% CO2/air) or H2O (synthetic, CO2-free, air with ∼90% relative humidity) in the TGA (at 500 °C or 25 °C) for 20 min, between two sets of five redox cycles (Fig. 2). A slight, continuous weight gain was observed when exposing the sample to 2% H2O at ambient temperature (Fig. 2d), which most likely can be ascribed to adsorbed water. Such weight increase was not observed at 500 °C (Fig. 2b). Fig. 3b summarizes the relaxation times of the reduction reaction before and after the exposure to CO2 or H2O at 500 °C. The exposure to CO2 resulted in a significantly increased relaxation time in the second set of the redox cycles, while the exposure to H2O had no noticeable effect.
A similar observation was made after exposure to CO2 at 25 °C, but there was no apparent effect on the rate of oxygen release after exposure to H2O at 25 °C.
Therefore, we can conclude that the presence of CO2 was the main cause of deactivation of the perovskite, while the effect of activation occurred through redox cycling in the absence of CO2.
We note that the activation through redox cycling at 500 °C was gradual and incomplete after each of the 30 cycle experiments, i.e. the relaxation time was still decreasing after each of the 30 cycles as can be seen in Fig. 3a.
Fig. S5† shows TGA experiments carried out at 450 °C, 475 °C, 500 °C, 550 °C, 575 °C and 600 °C, with the corresponding relaxation times of the reduction steps as a function of cycle number summarized in Fig. 3c. The highest OSC of Sr0.8Ca0.2FeO3−δ was achieved when operating at 500 °C and 550 °C (2.15 wt% and 2.08 wt%, respectively).14 With increasing temperature, the rate of oxygen release increased, as evident by decreased relaxation times.
At the lowest temperature investigated, i.e. 450 °C, the relaxation time was 24 min and remained constant with cycle number, meaning that activation did not occur at this temperature, or at least was not observed within the time of reduction; this is discussed below in Section 3.4. At 475 °C, activation was observed, and the relaxation time gradually decreased from 20 min in the first reduction step to 16 min in the 10th cycle. Increasing the reduction temperature further, we observed that the relaxation time stabilized after 6 cycles at 550 °C, 4 cycles at 575 °C and after 2 cycles at 600 °C. This suggests that the change of the material (in the structure or the surface, see the following sections) due to the presence of CO2 occurred faster at higher temperatures, and that temperatures ≥475 °C were needed to activate the sample. In the following section, we investigated whether the observed activation/deactivation was related to structural changes in the bulk or the surface of the oxygen carrier.
3.2 Bulk perovskite structure and changes upon redox cycling
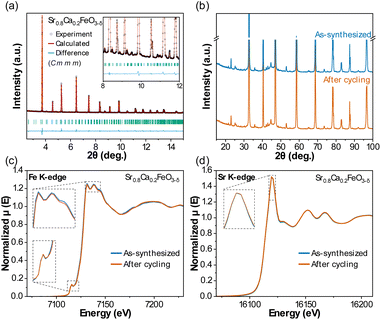
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) was used to describe the structure of Sr0.8Ca0.2FeO3−δ. However, our XRD measurements (using both synchrotron radiation and laboratory XRD at room temperature) revealed reflections that cannot be explained with a cubic structural model. We thus revised the crystal structure of this material by describing it with the orthorhombic Cmmm space group based on a previously reported structure,57 and obtained the unit cell parameters a = 10.9324(1) Å, b = 7.7042(5) Å and c = 5.4810(2) Å. The XRD patterns of Sr0.8Ca0.2FeO3−δ collected in our laboratory before and after 30 redox cycles in the TGA are shown in Fig. 4b. The difference in the calculated cell parameters between the sample before and after cycling (Fig. S7†) is <0.05%, and we thus conclude that no appreciable changes occurred in the bulk structure of the material.
m) was used to describe the structure of Sr0.8Ca0.2FeO3−δ. However, our XRD measurements (using both synchrotron radiation and laboratory XRD at room temperature) revealed reflections that cannot be explained with a cubic structural model. We thus revised the crystal structure of this material by describing it with the orthorhombic Cmmm space group based on a previously reported structure,57 and obtained the unit cell parameters a = 10.9324(1) Å, b = 7.7042(5) Å and c = 5.4810(2) Å. The XRD patterns of Sr0.8Ca0.2FeO3−δ collected in our laboratory before and after 30 redox cycles in the TGA are shown in Fig. 4b. The difference in the calculated cell parameters between the sample before and after cycling (Fig. S7†) is <0.05%, and we thus conclude that no appreciable changes occurred in the bulk structure of the material.
To determine whether changes in the oxidation state and/or local structure of Fe or Sr in the perovskite occurred during redox cycling in the oxidized state (i.e. comparing the as-synthesized Sr0.8Ca0.2FeO3−δ and the material after ten cycles), we applied X-ray absorption near edge structure (XANES) analysis of Sr0.8Ca0.2FeO3−δ as a fingerprint technique. Note that these measurements were performed ex situ, and hence the samples were exposed to ambient conditions prior to the measurements. The Fe K-edge XANES in Fig. 4c shows features typical for a Fe-containing perovskite, with a white line at 7130 eV due to the dipole-allowed transitions from Fe 1s to 4p (with two additional peaks at 7132 eV and 7138 eV), and a pre-edge peak due to the quadrupolar transitions from Fe 1s to 3d at ∼7115 eV, corresponding to a valence state of Fe between Fe3+ and Fe4+ (Fig. S8†).58 The Sr K-edge XANES in Fig. 3d shows a sharp white line at ∼16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 112 eV, in line with previous XANES reports on Sr-based perovskite in the oxidized state and corresponding to a valence state of Sr2+.59 A comparison of the spectra collected for the as-synthesized and redox cycled materials confirms that the local structure of the perovskite did not change appreciably during redox cycling.
112 eV, in line with previous XANES reports on Sr-based perovskite in the oxidized state and corresponding to a valence state of Sr2+.59 A comparison of the spectra collected for the as-synthesized and redox cycled materials confirms that the local structure of the perovskite did not change appreciably during redox cycling.
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group, yielding the unit cell parameters a = b = c = 3.897(1) Å (Fig. S9†). The evolution of the most relevant diffraction peaks in the 2θ range 31–33° was followed under redox conditions (500 °C, reduction in N2 and oxidation in compressed air), and the XRD data collected in the reduction steps of the first, fifth and tenth cycle are plotted in Fig. 5a–c, respectively. The respective contour plots (intensity vs. time and 2θ angle) are shown in Fig. 5d–f. By inspecting the evolution of the intensity and the position of the peaks in each cycle, we identify three regions. (I) A transition within the perovskite phase in which the 2θ position of the cubic perovskite peak, indexed as (110), shifts towards lower angles due to lattice expansion, as iron was reduced and oxygen vacancies were generated within the perovskite lattice.60 (II) The appearance of three new peaks due to the formation of a brownmillerite phase, with the general formula ABO2.5 and an orthorhombic crystal structure (Ibm2), indexed as (020), (411) and (002).14 The phase transition from perovskite to brownmillerite involves a decrease in the symmetry of the lattice and the ordering of oxygen vacancies.57 In this second stage, there is also a simultaneous shift of the position of the perovskite peak (110) towards lower diffraction angles, but at a slower rate compared to region (I). (III) The presence of only the brownmillerite phase without any further notable structural changes with time, indicating that most of the oxygen had been released from the oxygen carrier.
m space group, yielding the unit cell parameters a = b = c = 3.897(1) Å (Fig. S9†). The evolution of the most relevant diffraction peaks in the 2θ range 31–33° was followed under redox conditions (500 °C, reduction in N2 and oxidation in compressed air), and the XRD data collected in the reduction steps of the first, fifth and tenth cycle are plotted in Fig. 5a–c, respectively. The respective contour plots (intensity vs. time and 2θ angle) are shown in Fig. 5d–f. By inspecting the evolution of the intensity and the position of the peaks in each cycle, we identify three regions. (I) A transition within the perovskite phase in which the 2θ position of the cubic perovskite peak, indexed as (110), shifts towards lower angles due to lattice expansion, as iron was reduced and oxygen vacancies were generated within the perovskite lattice.60 (II) The appearance of three new peaks due to the formation of a brownmillerite phase, with the general formula ABO2.5 and an orthorhombic crystal structure (Ibm2), indexed as (020), (411) and (002).14 The phase transition from perovskite to brownmillerite involves a decrease in the symmetry of the lattice and the ordering of oxygen vacancies.57 In this second stage, there is also a simultaneous shift of the position of the perovskite peak (110) towards lower diffraction angles, but at a slower rate compared to region (I). (III) The presence of only the brownmillerite phase without any further notable structural changes with time, indicating that most of the oxygen had been released from the oxygen carrier.
For a quantitative assessment of the phase transition during oxygen release, we fitted the observed peaks to analyze the evolution of their integrated intensities and positions. The integrated intensity of the peaks is proportional to the phase quantity, and the position of the peaks relates to the lattice parameters.50Fig. 5g and h show the results of the peak fitting for the first cycle, the fifth cycle and the tenth cycle. The evolution of the lattice parameter of the cubic perovskite phase, calculated based on the (110) peak position, is reported in Fig. S10.† Comparing the three representative cycles in Fig. 5g and h, the total duration of the phase transition from the perovskite to the brownmillerite phase during the reduction step (i.e. from t = 0 to the beginning of region (III)) decreased with cycle number (∼15 min in the first cycle, ∼12 min in the fifth cycle, and ∼10 min in the tenth cycle). The decrease in the total reduction time points to an activation during cycling and is in line with the results of the TGA experiments (e.g.Fig. 1a). The duration of region (I) was between 3 and 4 min in cycles one, five and ten (Fig. 5g and h). Thus, within the time resolution of our laboratory base XRD (∼65 s per scan), no appreciable changes of the duration of region (I) with cycle number were found. On the other hand, we observed a relevant change in the duration of region (II), which decreased with increasing cycle number (∼11 min in the first cycle, ∼8 min in the fifth cycle, and ∼6 min in the tenth cycle). In region (II), the rate of the shift of the position of the perovskite peak and the phase transition from the perovskite to the brownmillerite phase increased with cycle number (Fig. S11†).
Subsequently, the structural evolution of the oxygen carrier as probed by in situ XRD was correlated with the amount of oxygen released through two separate sets of experiments: The reduction of the as-synthesized oxygen carrier in the TGA at 500 °C in N2 was terminated at different times and the sample was cooled rapidly such that further oxygen release was prohibited (Fig. S12a†). The partially reduced oxygen carrier samples were then analyzed by XRD at room temperature (Fig. S12b and S12c†). Here, after only 1 min of reduction (point 2), when the oxygen released by the oxygen carrier was 0.32 wt%, the brownmillerite peaks were already visible. This indicates that the amount of oxygen released within region (I) (Fig. 5g and h) was relatively low (<0.3 wt%) and that most of the oxygen release occurred while the oxygen carrier transitioned from the perovskite to brownmillerite phase, i.e. in region (II). The XRD pattern of activated Sr0.8Ca0.2FeO3−δ (treatment in synthetic air for 2 h at 600 °C) after 1 min of reduction (point 2*, 0.42 wt% oxygen release) showed a larger fraction of the brownmillerite phase than point 2, confirming that the rate of phase evolution and oxygen release were directly correlated in region (II).
In the second set of experiments, we correlated the structural transition of Sr0.8Ca0.2FeO3−δ from the perovskite to brownmillerite phase with pO2 at 500 °C under equilibrium conditions (Fig. S13a†). From TGA measurements performed under identical conditions (i.e. 500 °C and varying ratios of N2/air to obtain different pO2, Fig. S13b†), we derived the maximum weight fraction of oxygen that can be released from the oxygen carrier without transitioning to the brownmillerite phase. As can be seen from Fig. S13a,† the brownmillerite phase is thermodynamically not favored for pO2 ≥ 0.04 bar at 500 °C. For pO2 = 0.04 bar, Fig. S13b† indicates that maximal ∼0.31 wt% of oxygen can be released from the oxygen carrier while avoiding the formation of a brownmillerite phase. Compared with pO2 = 0.21 bar, the perovskite peak (110) shifted by 0.083° at pO2 = 0.04 bar, corresponding to a change in the cell parameter of Δa = 0.0108 Å. This value is consistent with the evolution of the cell parameter during region (I), Δa = 0.01012 Å in Fig. S10,† and confirms that only a relatively small fraction of oxygen is released by Sr0.8Ca0.2FeO3−δ at 500 °C before the transition to a brownmillerite occurs, and that the effect of activation of the oxygen carrier is most significant when the brownmillerite phase has been formed.
In summary, the analysis of the in situ XRD measurements showed a marked increase in the rate of phase transition during reduction (region (II)) upon cycling, consistent with the activation phenomenon observed in the TGA. We also observed that in each cycle the phase transition from the perovskite to brownmillerite phase was preceded by a reduction within the perovskite structure (region (I)), which occurred at a similar rate in all cycles (within the time resolution of the in situ XRD measurements that was ∼65 s per scan, and possibly affected by the slow gas displacement in the reaction chamber when switching from air to N2). The amount of oxygen released within region (I) was relatively small (∼0.3 wt%) and the principal reaction pathway during reduction appeared to remain unchanged with cycling, as no other intermediate phases that might have contributed to the activation of the perovskite were observed within the narrow 2θ range investigated. We note that a full range XRD pattern with a higher time-resolution would be required (e.g. using synchrotron-based XRD) to confirm that no phases other than perovskite and brownmillerite are formed during oxygen release. The following section focuses on the analysis of possible changes in the surface area, pore volume and morphology of Sr0.8Ca0.2FeO3−δ with cycle number since previous studies have argued that changes of these properties are the primary cause for the activation of oxygen carriers.24–27
3.3 Surface area, pore volume and morphology of Sr0.8Ca0.2FeO3−δ before and after redox cycling
The morphology of the as-synthesized perovskite (sieved to 53–106 μm) and after ten redox cycles was studied through N2 sorption. For the as-synthesized sample, the BET surface area and the total pore volume were 2 m2 g−1 and 0.01 cm3 g−1, respectively; after ten redox cycles, these values did not change (i.e. 2 m2 g−1 and 0.01 cm3 g−1, respectively). Equally, also the distributions of the pore volume, shown in Fig. S14a,† measured before and after cycling did not show significant differences. The morphology before and after redox cycling was also studied by means of HR-SEM measurements of dense pellets of Sr0.8Ca0.2FeO3−δ, Fig. S14b.† The images of the as-synthesized pellets before and after redox cycling show no discernable changes in the morphology, and we observed a very similar grain size before (55 ± 5 nm) and after cycling (57 ± 4 nm), assuming spherical grains and by averaging more than 20 grains before and after cycling.Hence, the analysis of the textural properties of the sample, i.e. surface area, pore volume and morphology, did not show any significant changes over redox cycling that would explain the observed activation. Different from most other studies on oxygen carrier activation in chemical looping, relatively small particles were used in our investigation, such that morphological changes such as surface cracks might have been observed had larger particles (say, >500 μm) been used.
3.4 The role of the surface elemental composition in the oxygen exchange rate
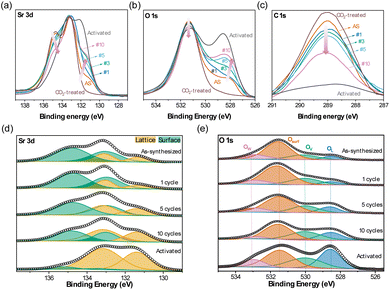
XPS measurements were used to probe the elemental composition at and close to the surface of the following oxidized samples: as-synthesized, after a representative number of cycles (viz. after 1, 3, 5 or 10 redox cycles performed in the TGA at 500 °C), after exposure to 50% CO2 at 500 °C in the TGA, and after activation without exposure to ambient air. In the latter case, the oxygen carrier was activated in a quartz tube reactor at 700 °C under N2, then oxidized in synthetic air, followed by cooling to room temperature. The reactor was then flushed with N2 and transferred to a glovebox, where the oxygen carrier sample was placed in a custom-made air-tight cell for the XPS measurement. Note that for the other samples the XPS data were collected within 24 h after the TGA measurement to mitigate changes to the sample due to CO2 in ambient air (see Fig. 3a). When comparing the Sr 3d spectra with cycle number in Fig. 6a, a clear trend was observed, i.e. an increase in the shoulder feature at ∼131.2 eV and a decrease in the intensity of the secondary peak at ∼134.3 eV with cycle number; the features at 131.2 eV and 134.3 eV correspond to surface- and lattice-Sr, respectively.39,46,48,61–63 Similarly, the O 1s spectra (Fig. 6b) showed a change in the distribution of oxygen species with cycle number, specifically, the intensity of the feature at ∼528.8 eV (lattice oxygen64,65) increased with cycle number, while the intensity of the feature at ∼531.3 eV (surface oxygen species64–66) decreased. Lastly, the C 1s spectra displayed two peaks at ∼284.6 eV and at ∼289.1 eV (Fig. 6c, note that we highlight only the region 287 to 291 eV); the first peak (not shown in Fig. 6c) was due to the C used for the calibration of the spectra, while the latter can be assigned to carbonate species on the surface of the sample.64–67 We observed a reduced intensity of the peak at 289.1 eV due to carbonates with increasing cycle number, but the peak was still seen after ten redox cycles at 500 °C, suggesting that not all carbonates were removed or that a small amount of CO2 was adsorbed as carbonates on the sample during sample transfer to the sealed vial. For the activated sample that was not exposed to ambient air, there was no significant peak due to carbonates.Next, we fitted the relevant XPS spectra to yield a more quantitative interpretation of the changes occurring during redox cycling. Fig. 6d shows the fittings of the Sr 3d spectra, for which two distinct binding environments of Sr were observed, i.e. a low-energy component at ∼131.2 eV, referred to as lattice-Sr (Sr bound in the lattice of the perovskite structure), and a high-energy component at ∼134.2 eV, referred to as surface-Sr, in line with previous works.39,40 Surface-Sr comprises surface-bound Sr, i.e. secondary phases in the termination layer of the perovskite (e.g. SrOx, carbonates, hydroxides).39,46,48 In the as-synthesized sample, a large fraction (∼70%) of the Sr signal was ascribed to the surface-Sr species. Upon activation, the ratio of low-to high-energy Sr changed: the amount of surface-Sr species (potentially SrOx or carbonates as indicated by the C 1s spectra) decreased, while the amount of lattice-Sr (e.g. Sr in the bulk perovskite structure) increased; in the activated sample hardly any surface-Sr species were seen, suggesting also that the surface had less defects. A similar observation was made by Tripković et al. when studying the reversible activation/deactivation of La0.6Sr0.4FeO3, used as an electrode material in solid oxide cells.39 They noted that the deactivation of the sample was not due to a change in the absolute amount of Sr on the surface, but due to changes in the ratio of Sr in the perovskite structure (lattice-Sr) to strontium in secondary phases (surface-Sr). Specifically, it was also observed that the ratio lattice-Sr to surface Sr species increased due to Sr segregation upon thermal activation (1000 °C in air).
Turning to the fitting of the O 1s region (Fig. 6e), four types of oxygen where used for its convolution: lattice oxygen species (OL) at ∼528.8 eV, oxygen species located in the vicinity of oxygen vacancies (OV) at ∼530.3 eV, surface oxygen species (e.g. hydroxyl OH− and/or carbonate CO32−, Osurf or Ocarb) at ∼531.3 eV, and adsorbed water (Ow) at ∼533 eV.6,64–66 Upon redox cycling, the area below and the intensity of the deconvolution peak due to lattice oxygen species OL increased, while the area below and the intensity of the deconvolution peak ascribed to surface oxygen species Osurf decreased (Fig. 6b and e). The area below and the intensity of the deconvolution peak ascribed to oxygen vacancies OV remained unchanged. For the activated sample, the contribution of lattice oxygen was increased significantly.
The Fe XPS spectra displayed two main peaks, at ∼711.1 eV and ∼724.5 eV, corresponding to Fe 2p3/2 and Fe 2p1/2, respectively, and a minor satellite peak at ∼716.2 eV. The peak at ∼711.1 eV was deconvoluted in Fe2+ 2p3/2 (∼710.1 eV) and Fe3+ 2p3/2 (∼712.3 eV), and the peak at ∼724.5 eV was deconvoluted in Fe2+ 2p1/2 (∼723.8 eV) and Fe3+ 2p3/2 (∼726.3 eV).39,46 A change in the relative intensity of the peaks ascribed to Fe2+ and Fe3+ was observed upon redox cycling, with a decrease in the ratio Fe2+/Fe3+ with cycle number (Fig. S15a†). A summary of the peak positions and intensity of the analyzed spectra is provided in Table S2.† Analysis of the elemental atomic composition of the region close to the surface by XPS (Fig. S15b†) shows an enrichment of Fe at the surface of the perovskite after ten redox cycles. It is noteworthy that the relative concentration of Fe at the surface of the perovskite remained largely unchanged in the first five cycles, and it increased only after ten cycles once the material was activated by a large degree. This observation suggests that the effect of activation, which is most significant in the first few redox cycles, is not linked to a change of the relative atomic concentration of Fe at the surface.
Yet, the decrease in both surface oxygen Osurf and surface-Sr species in combination with a decrease in intensity of carbonates (C 1s spectra) suggest a decrease in the extent of secondary Sr-phases (presumably carbonate species) on the surface of the perovskite upon redox cycling.
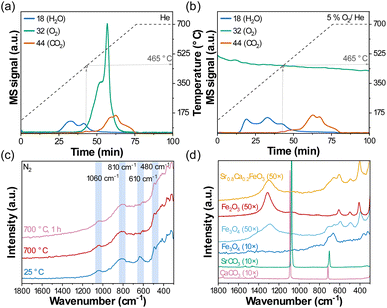
Further evidence for the removal of surface carbonates during activation is provided through temperature programmed desorption (TPD) experiments in which the gas released during the heating up of Sr0.8Ca0.2FeO3−δ in He was measured by a mass spectrometer (MS) (Fig. 7a). We observed the presence of CO2 (m/z 44) in the off-gas at temperatures ≥ 465 °C that most likely originates from the decomposition of surface carbonate species. The decomposition onset temperature of 465 °C explains why Sr0.8Ca0.2FeO3−δ was not activated in the TGA experiment at 450 °C (Fig. S5a†).
The MS data also shows that oxygen release started at lower temperatures, i.e. at ∼400 °C, consistent with our previous results.14 The release of oxygen did not affect the onset of the decomposition of surface carbonate species, as shown in a second control experiment: When using 5% O2/He instead of pure He in the TPD experiment (Fig. 7d), CO2 was detected again at around ∼465 °C, while no oxygen was released by the perovskite because of the high pO2. This result implies that the activation of the oxygen carrier, or the decomposition of the surface carbonate species, occurs also in a high pO2 environment and not only under reducing conditions (i.e. in N2 or He). This observation was confirmed through additional cycling experiments in the TGA at 500 °C, in which the sample was cycled once, then exposed to N2, synthetic air (O2/N2) or compressed air (containing small quantities of CO2) for 10 h, followed by another nine redox cycles (Fig. S6†). We observed that the material activated when exposed to both N2 and O2/N2 for 10 h, such that the activation during the following redox cycles was less relevant when compared to Fig. 1. Note that the extent of activation was more significant during the treatment for 10 h in N2 than in O2/N2. Only little activation was observed when using compressed air (contains ∼400 ppm of CO2), which emphasizes the detrimental impact of CO2 even in low concentrations on the rate and extent of oxygen release.
Carbonate species (e.g. monodentate or bidentate carbonate, or bicarbonate) adsorbed to the surface of a material can also be probed using Raman spectroscopy.67,68Fig. 7c plots the results of an in situ Raman spectroscopy experiment when heating up Sr0.8Ca0.2FeO3−δ to 700 °C in N2 at 10 °C min−1. The Raman spectra collected at 25 °C of the as-synthesized sample showed Raman bands at ∼1060 cm−1, ∼810 cm−1, ∼610 cm−1 and ∼480 cm−1. At 700 °C, the bands at ∼1060 cm−1 and ∼480 cm−1 remained unchanged, while the band at ∼610 cm−1 disappeared. The band at ∼1060 cm−1 is similar to the strongest peak of the reference SrCO3 (Fig. 7b; symmetric stretching vibration ν1 (ref. 69)) but appears to be stable at 700 °C and thus is unlikely to contribute to the activation or deactivation of the perovskite that is taking place at much lower temperature. In fact, TGA measurements in Fig. S16† show that bulk SrCO3 does not decompose below ∼760 °C in N2. Since the band at ∼610 cm−1 disappeared when heating Sr0.8Ca0.2FeO3−δ to 700 °C (Fig. 7c), it is unlikely that it originated from carbonate species as they have not been reported to give Raman bands in this region.70 In Fig. 7d, Raman spectroscopy measurements of iron oxide references (Fe3O4 and Fe2O3 at room temperature) using a higher optical magnification (50× instead of 10×, which reduces the spot size of the laser to ∼0.7 μm) indicate that the band at ∼610 cm−1 (and also the one at ∼480 cm−1) originates from iron oxide. Indeed, the measurement of a magnified region of Sr0.8Ca0.2FeO3−δ (50× at 25 °C, Fig. 7d and S17†) showed great similarity with Fe2O3, suggesting also that the oxygen carrier was initially not entirely composed of a single perovskite phase, but contained isolated clusters of iron oxide. Indeed, the data shown in Fig. S18† demonstrate that such iron oxide clusters disappeared after only one redox cycle, suggesting they were incorporated into the perovskite structure.71 Upon exposure to CO2 in the reaction cell at 500 °C, which led to a deactivation of the sample (Fig. 3), iron oxide clusters did not seem to reappear, confirming that the activation phenomenon is not linked to the presence and disappearance of small iron oxide clusters (Fig. S19†).
To summarize, the XPS and TPD measurements revealed the presence of surface carbonates on the as-synthesized materials that were effectively removed at temperatures > 475 °C, as also seen from the TGA results in Fig. 3c.
The formation of surface carbonate species was also reported by Yang et al. when studying SrFe0.9Ti0.1O3−δ in the context of the electrochemical abatement of organic pollutants in water.
It was argued that the catalytic activity of the material decreased with increasing surface carbonate formation.72 It was found that SrCO3 formed when exposing SrFe0.9Ti0.1O3−δ to pure CO2 at T > 600 °C.72 Furthermore, Østergaard et al. studied Ce-doped SrFeO3 and observed a decrease in its catalytic activity due to the formation of “surface SrCO3” when the sample was exposed to an aqueous environment, likely due to the presence of CO2 in water.73 Additionally, they demonstrated that the deactivation could effectively be reversed by a thermal treatment in air at 530 °C that removes SrCO3. It is conceivable that the formed “surface” carbonate species (such as small clusters, highly defective or amorphous surface structures) require a lower temperature for decomposition than their “bulk” counterpart. This interpretation is supported by XRD measurements, as the formation of crystalline (bulk) carbonate species such as SrCO3 was not observed. We also note that the presence of Ca in the oxygen carrier, which is known to readily form CaCO3 in the presence of CO2, did not influence the activation (or deactivation) behavior of the Sr-based oxygen carriers (see e.g. Fig. S2† in which the cyclic performances of different oxygen carrier compositions are compared). Hence, we speculate that the carbonates that are linked to material activation are strontium carbonate structures that originate from Sr segregation at the oxygen carrier's surface.74 Such surface defects are known to reduce the rate of ionic transport significantly, which may explain the lowered rate of oxygen transfer from the surface of the oxygen carrier to the bulk gas phase.75,76 Raman spectroscopy measurements, however, were inconclusive in providing further insight on the nature of these carbonate structures, requiring further designated studies.
Importantly, our findings may explain why the activation phenomenon of Sr-based perovskites has been overlooked in other chemical looping studies, including theoretical works.12,77 Often much higher operating temperatures were used (T > 600 °C78–80) such that the material activated already upon heating before the cycling experiment started,81,82 and during the cycling experiment no stable surface carbonate species were formed. Further, when using high purity gases that do not contain CO2 (laboratory experiments as opposed to practical industrial testing) such activation behavior would be absent.83–86 From a practical point of view, it is exactly such CO2 impurities in reducing and oxidizing gases that may be problematic when using Sr-based perovskites for chemical looping and other applications at low temperatures (i.e. ≤500 °C), because the rate of oxygen transfer to and from the perovskite (and therefore its practical OSC) is reduced substantially.
4. Conclusions
In this work, we provide fundamental material insight to explain the activation phenomenon (i.e. the increasing rate of oxygen release) of Sr0.8Ca0.2FeO3−δ-based oxygen carries upon redox cycling. To this end, we first carried out a systematic thermogravimetric analysis to study the influence of different operating conditions on the activation phenomenon (particle size, sample mass, flow rate, reducing gas, volume of the crucible) to exclude effects due to varying experimental conditions. An increase in the rate of oxygen release with redox cycling was observed at temperatures between 475 °C and 600 °C, and also for different perovskite compositions Sr1−xCaxFeO3−δ (0 ≤ x ≤ 0.25). From a structural point of view, XRD and XAS measurements did not show any apparent changes in the bulk (average or local) structure of the perovskite before and after activation. In situ XRD measurements showed that a significant increase in the rate of phase transition from perovskite to brownmillerite occurred upon activation. By combining TGA and in situ XRD measurements, we find that ∼85% of the oxygen is released during the phase transition from perovskite to brownmillerite, which combines well the observed increase in the rate of phase transition and increase in rate of oxygen release with activation. From a textural point of view, no significant changes in surface area, pore volume and morphology of Sr0.8Ca0.2FeO3−δ were observed when comparing the material before and after activation. Additionally, “aging” experiments revealed that the activation is only temporary, and that deactivation occurs upon exposure to CO2 (but not H2O), even in low concentrations contained in air (≪1%) and at ambient conditions.XPS measurements combined with TPD measurements revealed the formation of surface carbonate species upon exposure to CO2, which were abundant in the as-synthesized/deactivated sample, and likely originate from Sr segregation at the oxygen carrier's surface. Importantly, we show that such surface carbonate species are effectively removed upon treatment in a CO2-free atmosphere above 465 °C.
Our experiments have shown that relatively low concentrations of CO2 (≪1%) in the atmosphere lead to the formation of surface carbonate species that hinder the efficient oxygen transfer to and from the oxygen carrier, rendering the material almost impractical at the process level. Thus, means of CO2 removal upstream of the chemical looping process would have to be implemented. It is therefore important for future research activities to investigate novel formulations or modifications of Sr-based oxygen carriers that can tolerate small quantities of CO2 in the reducing and oxidizing gases.75
Author contributions
Giancarlo Luongo: data curation, formal analysis, validation, writing – original draft, Alexander H. Bork: conceptualization, writing – review & editing, Paula M. Abdala: conceptualization, writing – review & editing, Yi-Hsuan Wu: formal analysis, Evgenia Kountoupi: formal analysis, Felix Donat: conceptualization, writing – review & editing, funding acquisition, Christoph Müller: conceptualization, supervision, writing – review & editing, funding acquisition.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors would like to acknowledge the Swiss Office of Energy (BFE, SI/501590-01) for financial support. This publication was created as part of NCCR Catalysis (grant number 180544), a National Centre of Competence in Research funded by the Swiss National Science Foundation. We acknowledge Swiss Federal Laboratories for Materials Science and Technology (EMPA) for access to the XPS facility. Dr Agnieszka Kierzkowska (ETH Zürich) is acknowledged for assisting with the SEM measurements. The SNBL and ESRF are acknowledged for the provision of beamtime and Drs Wouter van Beek, Dragos Stoian, and Agnieszka Paul-Poulain for assistance during XAS and XRD measurements. Angelo Bellia and Maximilian Krödel, Dr Denis Kuznetsov, Annelies Landuyt, David Niedbalka, and Alexander Oing are acknowledged for their support in the BET measurements, XPS analysis, microscopy measurements, TPD measurements, and discussions, respectively.References
- M. B. Hanif, M. Motola, S. Rauf, C. J. Li and C. X. Li, Chem. Eng. J., 2022, 428, 132603 CrossRef.
- X. Mao, Z. Li, M. Li, X. Xu, C. Yan, Z. Zhu and A. Du, J. Am. Chem. Soc., 2021, 143(25), 9507–9514 CrossRef CAS PubMed.
- X. Zhu, Q. Imtiaz, F. Donat, C. R. Müller and F. Li, Energy Environ. Sci., 2020, 13, 772–804 RSC.
- Y. Gao, X. Wang, J. Liu, C. Huang, K. Zhao, Z. Zhao, X. Wang and F. Li, Sci. Adv., 2020, 6(17), 9339 CrossRef PubMed.
- Y. Zhu, D. Liu, H. Jing, F. Zhang, X. Zhang, S. Hu, L. Zhang, J. Wang, L. Zhang, W. Zhang and B. Pang, Sci. Adv., 2022, 8(15), 4072 CrossRef PubMed.
- C. Sun, J. A. Alonso and J. Bian, Adv. Energy Mater., 2021, 11(2), 2000459 CrossRef CAS.
- Z. Wang, H. Huang, G. Li, X. Yan, Z. Yu, K. Wang and Y. Wu, Appl. Phys. Rev., 2021, 8(2), 021320 CAS.
- H. Chen, M. Zhang, T. Tran-Phu, R. Bo, L. Shi, I. Di Bernardo, J. Bing, J. Pan, S. Singh, J. Lipton-Duffin and T. Wu, Adv. Funct. Mater., 2021, 31(4), 2008245 CrossRef CAS.
- X. Zhu, K. Li, L. Neal and F. Li, ACS Catal., 2018, 8(9), 8213–8236 CrossRef CAS.
- G. Luongo, F. Donat, A. H. Bork, E. Willinger, A. Landuyt and C. R. Müller, Adv. Energy Mater., 2022, 2200405 CrossRef CAS.
- B. Bulfin, J. Vieten, D. E. Starr, A. Azarpira, C. Zachäus, M. Hävecker, K. Skorupska, M. Schmücker, M. Roeb and C. Sattler, J. Mater. Chem. A, 2017, 5(17), 7912–7919 RSC.
- J. Vieten, B. Bulfin, P. Huck, M. Horton, D. Guban, L. Zhu, Y. Lu, K. A. Persson, M. Roeb and C. Sattler, Energy Environ. Sci., 2019, 12(4), 1369–1384 RSC.
- M. Kubicek, A. H. Bork and J. L. Rupp, J. Mater. Chem. A, 2017, 5(24), 11983–12000 RSC.
- G. Luongo, F. Donat and C. R. Müller, Phys. Chem. Chem. Phys., 2020, 22(17), 9272–9282 RSC.
- D. Hosseini, F. Donat, S. M. Kim, L. Bernard, A. M. Kierzkowska and C. R. Müller, ACS Appl. Energy Mater., 2018, 1(3), 1294–1303 CrossRef CAS.
- J. Chen, L. Duan, F. Donat, C. R. Mueller, E. J. Anthony and M. Fan, Chem. Eng. J., 2018, 351, 1038–1046 CrossRef CAS.
- J. Ma, X. Tian, H. Zhao, S. Bhattacharya, S. Rajendran and C. Zheng, Energy Fuels, 2017, 31(2), 1896–1903 CrossRef CAS.
- L. Chen, G. Wei and K. Liu, Fuel Process. Technol., 2022, 228, 107139 CrossRef CAS.
- A. Abad, J. Adanez, A. Cuadrat, F. Garcia-Labiano, P. Gayan and F. Luis, Chem. Eng. Sci., 2011, 66(4), 689–702 CrossRef CAS.
- T. Mattisson, S. Sundqvist, P. Moldenhauer, H. Leion and A. Lyngfelt, Int. J. Greenhouse Gas Control, 2019, 87, 238–245 CrossRef CAS.
- H. Leion, T. Mattisson and A. Lyngfelt, Int. J. Greenhouse Gas Control, 2008, 2(2), 180–193 CrossRef CAS.
- M. Johansson, T. Mattisson and A. Lyngfelt, Ind. Eng. Chem. Res., 2004, 43(22), 6978–6987 CrossRef CAS.
- D. Yamaguchi, L. Tang and K. Chiang, Chem. Eng. J., 2017, 322, 632–645 CrossRef CAS.
- G. L. Schwebel, H. Leion and W. Krumm, Chem. Eng. Res. Des., 2012, 90(9), 1351–1360 CrossRef CAS.
- Z. Yu, Y. Yang, S. Yang, Q. Zhang, J. Zhao, Y. Fang, X. Hao and G. Guan, Carbon Resour. Convers., 2019, 2(1), 23–34 CrossRef CAS.
- J. Adánez, A. Cuadrat, A. Abad, P. Gayán, L. F. de Diego and F. Garcia-Labiano, Energy Fuels, 2010, 24(2), 1402–1413 CrossRef.
- A. Cuadrat, A. Abad, J. Adánez, L. F. De Diego, F. García-Labiano and P. Gayán, Fuel Process. Technol., 2012, 94(1), 101–112 CrossRef CAS.
- P. Knutsson and C. Linderholm, Appl. Energy, 2015, 157, 368–373 CrossRef CAS.
- L. Chen, J. Bao, L. Kong, M. Combs, H. S. Nikolic, Z. Fan and K. Liu, Appl. Energy, 2017, 197, 40–51 CrossRef CAS.
- J. Bao, Z. Li, H. Sun and N. Cai, Ind. Eng. Chem. Res., 2013, 52(42), 14817–14827 CrossRef CAS.
- J. Bao, Z. Li and N. Cai, Ind. Eng. Chem. Res., 2013, 52(18), 6119–6128 CrossRef CAS.
- Y. Ku, H. C. Wu, P. C. Chiu, Y. H. Tseng and Y. L. Kuo, Appl. Energy, 2014, 113, 1909–1915 CrossRef CAS.
- N. Khakpoor, E. Mostafavi, N. Mahinpey and H. De la Hoz Siegler, Energy, 2019, 169, 329–337 CrossRef CAS.
- W. C. Cho, C. G. Kim, S. U. Jeong, C. S. Park, K. S. Kang, D. Y. Lee and S. D. Kim, Ind. Eng. Chem. Res., 2015, 54(12), 3091–3100 CrossRef CAS.
- Z. Ma, S. Zhang and Y. Lu, Energy Fuels, 2020, 34(12), 16350–16355 CrossRef CAS.
- Z. Ma, S. Zhang and R. Xiao, Energy Convers. Manage., 2019, 188, 429–437 CrossRef CAS.
- Z. Ma, R. Xiao and L. Chen, Energy Convers. Manage., 2018, 168, 288–295 CrossRef CAS.
- Y. Saito, F. Kosaka, N. Kikuchi, H. Hatano and J. Otomo, Ind. Eng. Chem. Res., 2018, 57(16), 5529–5538 CrossRef CAS.
- Đ. Tripković, J. Wang, R. Küngas, M. B. Mogensen, B. Yildiz and P. V. Hendriksen, Chem. Mater., 2022, 34(4), 1722–1736 CrossRef.
- Đ. Tripkovic, R. Küngas, M. B. Mogensen and P. V. Hendriksen, J. Mater. Chem. A, 2019, 7, 11782–11791 RSC.
- J. Suntivich, H. A. Gasteiger, N. Yabuuchi, H. Nakanishi, J. B. Goodenough and Y. Shao-Horn, Nat. Chem., 2011, 3, 546–550 CrossRef CAS PubMed.
- N. Tsvetkov, Q. Lu, L. Sun, E. J. Crumlin and B. Yildiz, Nat. Mater., 2016, 15, 1010–1016 CrossRef CAS PubMed.
- Y. Chen, W. Jung, Z. Cai, J. J. Kim, H. L. Tuller and B. Yildiz, Energy Environ. Sci., 2012, 5, 7979–7988 RSC.
- M. Kubicek, G. M. Rupp, S. Huber, A. Penn, A. K. Opitz, J. Bernardi, M. Stöger-Pollach, H. Hutter and J. Fleig, Phys. Chem. Chem. Phys., 2014, 16(6), 2715–2726 RSC.
- W. Lee, J. W. Han, Y. Chen, Z. Cai and B. Yildiz, J. Am. Chem. Soc., 2013, 135, 7909–7925 CrossRef CAS PubMed.
- Z. Cai, M. Kubicek, J. Fleig and B. Yildiz, Chem. Mater., 2012, 24, 1116–1127 CrossRef CAS.
- G. M. Rupp, A. K. Opitz, A. Nenning, A. Limbeck and J. Fleig, Nat. Mater., 2017, 16, 640–645 CrossRef CAS PubMed.
- D. Kim, R. Bliem, F. Hess, J.-J. Gallet and B. Yildiz, J. Am. Chem. Soc., 2020, 142, 3548–3563 CrossRef CAS PubMed.
- J. Rodríguez-Carvajal and T. Roisne, International Union for Crystallography, Newletter N, vol. 20, 1998 Search PubMed.
- B. D. Cullity, Elements of X-ray Diffraction, Addison-Wesley Publishing, 1956 Search PubMed.
- D. A. Shirley, Phys. Rev. B: Solid State, 1972, 5(12), 4709 CrossRef.
- J. H. Scofield, J. Electron Spectrosc. Relat. Phenom., 1976, 8(2), 129–137 CrossRef CAS.
- B. Ravel and M. Newville, J. Synchrotron Radiat., 2005, 12, 537–554 CrossRef CAS PubMed.
- I. A. Starkov, S. F. Bychkov, S. A. Chizhik and A. P. Nemudry, Chem. Mater., 2014, 26(6), 2113–2120 CrossRef CAS.
- E. J. Popczun, S. Natesakhawat, C. M. Marin, T. D. Nguyen-Phan, Y. Zhou, D. Alfonso and J. W. Lekse, J. Mater. Chem. A, 2020, 8(5), 2602–2612 RSC.
- J. Dou, E. Krzystowczyk, X. Wang, A. R. Richard, T. Robbins and F. Li, J. Phys.: Energy, 2020, 2(2), 25007 CAS.
- J. P. Hodges, S. Short, J. D. Jorgensen, X. Xiong, B. Dabrowski, S. M. Mini and C. W. Kimball, J. Solid State Chem., 2000, 151(2), 190–209 CrossRef CAS.
- O. Haas, U. F. Vogt, C. Soltmann, A. Braun, W. S. Yoon, X. Q. Yang and T. Graule, Mater. Res. Bull., 2009, 44(6), 1397–1404 CrossRef CAS.
- K. Tamai, S. Hosokawa, K. Kato, H. Asakura, K. Teramura and T. Tanaka, Phys. Chem. Chem. Phys., 2020, 22(42), 24181–24190 RSC.
- D. D. Taylor, N. J. Schreiber, B. D. Levitas, W. Xu, P. S. Whitfield and E. E. Rodriguez, Chem. Mater., 2016, 28(11), 3951–3960 CrossRef CAS.
- E. J. Crumlin, E. Mutoro, Z. Liu, M. E. Grass, M. D. Biegalski, Y. L. Lee, D. Morgan, H. M. Christen, H. Bluhm and Y. Shao-Horn, Energy Environ. Sci., 2012, 5(3), 6081–6088 RSC.
- E. J. Crumlin, E. Mutoro, W. T. Hong, M. D. Biegalski, H. M. Christen, Z. Liu, H. Bluhm and Y. Shao-Horn, J. Phys. Chem. C, 2013, 117(31), 16087–16094 CrossRef CAS.
- Y. Li, W. Zhang, T. Wu, Y. Zheng, J. Chen, B. Yu, J. Zhu and M. Liu, Adv. Energy Mater., 2018, 8(29), 1801893 CrossRef.
- Y. Gao, X. Wang, J. Liu, C. Huang, K. Zhao, Z. Zhao and F. Li, Sci. Adv., 2020, 6(17), 1597–1617 Search PubMed.
- D. Chen, D. He, J. Lu, L. Zhong, F. Liu, J. Liu, J. Yu, G. Wan, S. He and Y. Luo, Appl. Catal., B, 2017, 218, 249–259 CrossRef CAS.
- S. Song, W. Xu, J. Zheng, L. Luo, M. H. Engelhard, M. E. Bowden, B. Liu, C. M. Wang and J. G. Zhang, Nano Lett., 2017, 17(3), 1417–1424 CrossRef CAS PubMed.
- H. An, L. Wu, L. D. Mandemaker, S. Yang, J. de Ruiter, J. H. Wijten, J. C. Janssens, T. Hartman, W. van der Stam and B. M. Weckhuysen, Angew. Chem., Int. Ed., 2021, 60(30), 16576–16584 CrossRef CAS PubMed.
- Y. Dai, M. Xu, Q. Wang, R. Huang, Y. Jin, B. Bian, C. Tumurbaatar, B. Ishtsog, T. Bold and Y. Yang, Appl. Catal., B, 2020, 277, 119271 CrossRef CAS.
- W. Kaabar, S. Bott and R. Devonshire, Spectrochim. Acta, Part A, 2011, 78(1), 136–141 CrossRef CAS PubMed.
- G. Socrates, Infrared and Raman Characteristic Group Frequencies: Tables and Charts, John Wiley & Sons, 2004 Search PubMed.
- Y. Yang, Y. Li, Y. Jiang, M. Zheng, T. Hong, X. Wu and C. Xia, Electrochim. Acta, 2018, 284, 159–167 CrossRef CAS.
- F. Donat and C. R. Müller, Appl. Catal., B, 2020, 278, 119328 CrossRef CAS.
- M. B. Østergaard, A. B. Strunck, V. Boffa and M. K. Jørgensen, Catalysts, 2022, 12(3), 265 CrossRef.
- M. T. Dunstan, F. Donat, A. H. Bork, C. P. Grey and C. R. Müller, Chem. Rev., 2021, 121(20), 12681–12745 CrossRef CAS PubMed.
- B. Koo, K. Kim, J. K. Kim, H. Kwon, J. W. Han and W. Jung, Joule, 2018, 2(8), 1476–1499 CrossRef CAS.
- J. Irvine, J. L. Rupp, G. Liu, X. Xu, S. Haile, X. Qian, A. Snyder, R. Freer, D. Ekren, S. Skinner and O. Celikbilek, J. Phys.: Energy, 2021, 3(3), 031502 CAS.
- X. Wang, Y. Gao, E. Krzystowczyk, S. Iftikhar, J. Dou, R. Cai, H. Wang, C. Ruan, S. Ye and F. Li, Energy Environ. Sci., 2022, 15(4), 1512–1528 RSC.
- Z. Rui, J. Ding, Y. Li and Y. S. Lin, Fuel, 2010, 89(7), 1429–1434 CrossRef CAS.
- Q. Yin, J. Kniep and Y. S. Lin, Chem. Eng. Sci., 2008, 63(8), 2211–2218 CrossRef CAS.
- R. Cai, J. Dou, E. Krzystowczyk, A. Richard and F. Li, Chem. Eng. J., 2022, 429, 132370 CrossRef CAS.
- X. Wang, E. Krzystowczyk, J. Dou and F. Li, Chem. Mater., 2021, 33(7), 2446–2456 CrossRef CAS.
- E. J. Popczun, T. Jia, S. Natesakhawat, W. Xu, C. M. Marin, Y. Duan and J. W. Lekse, J. Alloys Compd., 2022, 896, 162783 CrossRef CAS.
- H. Ikeda, A. Tsuchida, J. Morita and N. Miura, Ind. Eng. Chem. Res., 2016, 55(22), 6501–6505 CrossRef CAS.
- T. Masunaga, J. Izumi and N. Miura, J. Ceram. Soc. Jpn., 2010, 118(1382), 952–954 CrossRef CAS.
- G. E. Wilson, I. D. Seymour, A. Cavallaro, S. J. Skinner and A. Aguadero, J. Electrochem. Soc., 2022, 169(4), 044509 CrossRef.
- Y. Yoshiyama, S. Hosokawa, H. Asakura, K. Teramura and T. Tanaka, J. Phys. Chem. C, 2022, 126(9), 4415–4422 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2ta09102j |
| This journal is © The Royal Society of Chemistry 2023 |