A high voltage aqueous proton battery using an optimized operation of a MoO₃ positive electrode

Abstract

Aqueous proton batteries have attracted increasing attention owing to their potential of high safety standard, high rate capability, and long cyclability. While some inorganic negative electrode materials for proton batteries have recently been found, inorganic positive electrode materials have rarely been reported. In this work, we investigate the proton insertion–extraction mechanism of MoO₃ using operando X-ray diffraction and density functional theory calculation to optimize its operating conditions as a positive electrode. It is found that the phase transition between MoO₃ and phase-I H_xMoO₃ can reversibly be utilized by preventing irreversible phase transition from phase-I to phase-III involving the change of proton accommodation from the intralayer to interlayer sites. A MoO₃ electrode using the phase transition between MoO₃ and phase-I shows an average reduction potential of 0.44 V vs. SHE with a maximum reversible capacity of 100 mA h g⁻¹. A MoO₃|50 wt% H₂SO₄ aq.|H_xMoO₃ full-cell exhibits a maximum discharge capacity of 73 mA h g⁻¹ and maintains nominal discharge voltage above 0.47 V, which is the highest voltage among aqueous proton batteries composed of insertion-type oxide active materials.

---

1. Introduction

Aqueous proton batteries with two insertion-type electrodes, where protons go back and forth between these electrodes during charging and discharging, are attractive candidates for post-lithium-ion batteries.¹ These battery systems potentially satisfy high safety standards owing to aqueous electrolyte solutions and have high rate capabilities because of protons' high mobility. In addition, the protons' small ionic radius possibly contributes to the high cyclabilities of insertion-type active materials. However, aqueous proton batteries have not been commercialized due to the lack of active materials for practical applications. Acid electrolyte solutions are generally used for aqueous proton batteries to ensure high proton conductance and prevent the insertion of other cations. Therefore, active materials for aqueous proton batteries are required to have not only the ability of reversible proton insertion/extraction but also stability in acidic electrolyte solutions. Examples of electrode materials for proton batteries are organic materials² and cyanide complexes^1,3 but they are relatively bulky, which is unfavorable for high energy density of the cells. Promising compact materials are oxides, and some insertion-type oxide negative electrode materials, such as MoO₃,⁴ WO₃,⁵ and TiO₂,⁶ have been reported. However, insertion-type oxides as a positive electrode material, which is needed to establish aqueous proton batteries composed of insertion-type active materials for both electrodes, have rarely been found.

In this study, we focused on MoO₃ as a positive electrode material for aqueous proton batteries. MoO₃ has long been studied as a hydrogen insertion material.^7,8 Besides pristine MoO₃ (space group Pbnm, number 62), four stable phases are reported as the proton-inserted product H_xMoO₃: phase-I (0.23 < x < 0.40; Cmcm, 63), phase-II (0.85 < x < 1.04; C2/m, 12), phase-III (1.55 < x < 1.72; C2/m), and phase-IV (x = 2.0; space group unknown, monoclinic).^7,8 In addition, phase-IIa (0.6 < x < 0.8; C2/m) has also been reported as a metastable phase.⁹ Although the space group symmetry changes by reduction and oxidation, the layered structure framework of MoO₃ is retained. Recently, MoO₃ has been recognized as a negative electrode material for aqueous proton batteries, which has a relatively high reversible capacity of ca. 220 mA h g⁻¹ in sulfuric and phosphoric acid electrolytes.^10,11 In addition, W. Xu et al. have very recently found that H_xMoO₃ can also be utilized as a positive electrode material though its operating potential was relatively low (ca. 0.3 V vs. standard hydrogen electrode (SHE)).¹² MoO₃ shows two reversible redox reactions at around 0.3 and −0.1 V vs. SHE and also shows an irreversible reduction reaction around 0.5 V vs. SHE (Fig. S1†). On the other hand, the phase transition behavior during the reduction–oxidation processes is not fully understood due to ex situ characterization used in most of the previous research.^11,13

In this study, we conducted operando X-ray diffraction (XRD) measurements and density functional theory (DFT) calculations to investigate the reduction–oxidation mechanism of MoO₃ both experimentally and theoretically. We clarify the phase transition process of MoO₃ during reduction–oxidation, including irreversible phase transition from phase-I to phase-III in the first reduction by exploring the thermodynamically stable sites for proton insertion in phase-I and phase-III (or phase-II). Furthermore, we show that the reduction reaction around 0.5 V vs. SHE could reversibly utilize by optimizing the cut-off potential and successfully construct an aqueous proton battery composed of insertion-type oxide active materials with an average discharge potential of 0.47 V.

2. Experimental methods

2.1. Electrochemical measurements and characterization

MoO₃ composite electrodes were composed of MoO₃ (Kanto Chemical) : carbon black (Li-250, Denka) : polyvinylidene difluoride (KF polymer L#9305, Kuraray) = 85 : 10 : 5 wt%. The electrode slurry in an N-methyl pyrrolidone (Kanto Chemical) solvent was coated on a graphite sheet current collector (Panasonic, thickness: 25 μm) and dried at 80 °C for 12 h in a constant temperature oven (DX302, Yamato).

Operando XRD measurements were carried out using an electrochemical three-electrode cell (Fig. S2(a)†), an electrochemical measurement system (SP-50, Bio-Logic), and an XRD system (SmartLab, Rigaku) using Mo Kα radiation at 60 kV and 150 mA. The electrochemical three-electrode cell consisted of the MoO₃ composite electrode as the working electrode, a commercial Ag|AgCl|saturated KCl aq. electrode (RE-1CP, BAS) as the reference electrode, a Pt mesh as the counter electrode, and 50 wt% (ca. 7.1 mol dm⁻³) H₂SO₄ aq. as the electrolyte solution. The XRD patterns of the MoO₃ electrode were recorded from the backside of the electrode through the graphite sheet current collector (Fig. S2(a)†). The geometrical area of the working electrode was defined as 1.77 cm² with a fluororubber o-ring.

The reduction–oxidation measurements of MoO₃ half-cells were conducted using an electrochemical three-electrode cell (Fig. S2(b)†) composed of the same components as those of the operando XRD cell and a multichannel charge–discharge system (HJ1001SM8A, Hokuto Denko). The geometrical area of the working electrode was defined as 0.50 cm² with a fluororubber gasket. The charge–discharge measurements of MoO₃|50 wt% H₂SO₄ aq.|H_xMoO₃ full-cells were performed using an electrochemical three-electrode cell with the commercial Ag|AgCl|saturated KCl aq. reference electrode (Fig. S2(c)†) and a multichannel charge–discharge system (EF-7100p, Electrofield). The geometrical areas of the positive and negative electrodes were defined as 0.50 cm² with a fluororubber gasket, and the loading masses of the positive and negative electrodes were set to the same value. Before the full-cell construction, the positive and negative electrodes were electrochemically preconditioned with the half cells. The positive electrode was reduced and oxidized in the potential range from 0.1 to 0.5 V at 100 mA g⁻¹ for 30 cycles, and the cycle was terminated in the reduced state. The negative electrode was reduced and oxidized in the potential range from −0.3 to 0.0 V at 100 mA g⁻¹ for 3 cycles, and the cycle was terminated in the oxidized state.

All the electrochemical measurements were performed at 25 ± 2 °C, and the electrodes were exposed to a 5 min open-circuit period between charge and discharge.

The electrodes as-prepared and taken out from the cells were characterized using field emission scanning electron microscopy (FE-SEM) (SU8230, Hitachi High-Tech) and energy dispersive X-ray spectroscopy (EDS) (XFlash FlatQUAD 5060F, BRUKER).

2.2. DFT calculations

DFT calculations were performed using the plane-wave basis projector augmented wave (PAW) method as implemented in the Vienna ab initio simulation package (VASP) 6.1.^14,15 The generalized gradient approximation (GGA) parameterized by Perdew, Burke, and Ernzerhof¹⁶ and the Hubbard U extension¹⁷ with an effective U of 4.38 eV for the Mo-4d orbital were used as the exchange–correlation functional. The cut-off energy was set at 520 eV. A gamma-centered 8 × 2 × 8 k-point mesh was used for the unit cell, and the number of divisions were adjusted for supercells by their size. The total energy converged to 10⁻⁶ eV per atom. Atomic positions and lattice constants were relaxed until the total energy converged to 10⁻⁵ eV per atom.

Proton inserted models were constructed as follows: protons were attached to O atoms. The OH units were directed to adjacent O atoms to form hydrogen bonds. The O–H distances were set to be one third of the O–O distances. All symmetry-independent configurations were employed as initial structures. Atom positions were randomly displaced by 0.01 Å to break the symmetry before the structural relaxation. Notes that are specific to individual models will be described in the Results and discussion section. Pymatgen¹⁸ and enumlib^19–21 packages were used to construct the structural models.

3. Results and discussion

3.1. Operando XRD

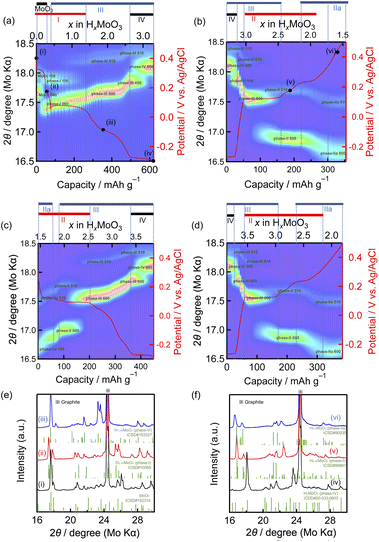
Operando XRD measurement of the MoO₃ electrode during reduction–oxidation was carried out in the potential range between 0.50 and −0.30 V at a current density of 100 mA g⁻¹ to investigate the phase transition behavior between MoO₃ and the fully protonated phase-IV. Fig. 1(a)–(d) show the operando XRD patterns during the first and second reduction–oxidation processes, while Fig. 1(e) and (f) show the full XRD profiles of selected states, showing that the states (i), (ii), (iii), (iv), (v) and (vi) correspond to MoO₃, phase-I, phase-III, phase-IV, phase-II, and phase-IIa, respectively. In the first reduction, MoO₃ shows three phase-transitions from MoO₃ to phase-IV via phase-I and III (Fig. 1(a), (e) and (f)). First, a MoO₃/phase-I biphasic reaction is observed on the potential plateau at around 0.35 V evidenced by the gradual decrease of MoO₃ 060 (17.7°) diffraction intensity and concurrent increase of phase-I 060 (17.4°) diffraction. Second, a phase-I/phase-III biphasic reaction occurs on the plateau at around 0.05 V indicated by gradual decrease of the phase-I 150 (17.9°) diffraction and concurrent increase of the phase-III 510 (18.2°) diffraction. Finally, the phase-III/phase-IV biphasic reaction on the plateau at around −0.27 V is shown by the gradual decrease of the phase-III 600 (17.8°) diffraction and concurrent increase of the phase-IV 600 (18.1°) diffraction. Monophasic reactions of phase-I and phase-III are also observed after the MoO₃/phase-I and phase-I/phase-III biphasic reactions, respectively, evidenced by the continuous shifts of the diffraction peaks, such as phase-I 060 and phase-III 600. During the first oxidation, while the phase-III/phase-IV biphasic reaction is observed on the plateau at around −0.27 V, phase transitions in higher potential regions are totally different from those in the first reduction process, as shown in Fig. 1(b). After the phase-III monophasic reaction between −0.27 V and 0.05 V, the phase-III/phase-II biphasic reaction on the plateau at around 0.05 V is shown by the gradual decrease of the phase-III 600 (17.5°) diffraction and concurrent increase of the phase-II 600 (17.0°) diffraction. Then, the phase-II/phase-IIa biphasic reaction is suggested by the gradual decrease/increase of the phase-II 42-2 (26.3°)/phase-IIa 51-2 (27.8°) diffractions (Fig. S3†). In the second reduction, the change was reverse to that observed during the first oxidation, and H_xMoO₃ shows reversible phase transitions between phase-IIa and phase-IV afterward, as shown in Fig. 1(c) and (d). These results indicate that the phase transition from phase-I to phase-III is an irreversible process.

Fig. 1 Operando XRD patterns of the MoO₃ electrode during reduction–oxidation in the potential range from −0.30 to 0.50 V at 100 mA g⁻¹; contour plots of (a) the 1st reduction, (b) the 1st oxidation, (c) the 2nd reduction, and (d) the 2nd oxidation; (e and f) line plots with reference patterns.

Next, we performed operando XRD to investigate the reversibility of MoO₃/phase-I biphasic and phase-I monophasic reactions for their possible use as high-potential electrode reactions, when there is no phase-III formation with the operating potential range at above 0.10 V. Fig. 2(a)–(d) show the operando XRD patterns during the first and second reduction–oxidation processes. Gradual decrease/increase of the MoO₃ 060 (17.7°)/phase-I 060 (17.4°) diffractions and continuous shifts of the phase-I 060 diffraction are observed in both the first reduction and oxidation though the appearance of the MoO₃ 060 diffraction does not completely proceed in the fully oxidized state (Fig. 2(a) and (b)). In the second cycle, we decreased the reduction–oxidation rate to 10 mA g⁻¹, a tenth of the rate in the first cycle, to reduce kinetic factors to the reversibility. Phase-I 060 diffraction shifts to a higher diffraction angle and proton content, x in H_xMoO₃, becomes higher at the end of the reduction (Fig. 2(c)) compared to the first cycle, indicating that the proton insertion proceeded further with the decrease in the reduction current. In addition, the phase transition from phase-I to MoO₃ proceeds more than that in the first high-rate cycle, as evidenced by the higher intensity of MoO₃ 060 diffraction and lower proton content x in H_xMoO₃ after the second oxidation (Fig. 2(d)). These results clearly show that the phase-I monophasic reaction and the MoO₃/phase-I biphasic reaction are essentially reversible while the phase transition from phase-I to MoO₃ is kinetically limited. To the best of our knowledge, this is the first study to report the reversibility of these high-potential reactions.

Fig. 2 Operando XRD patterns of the MoO₃ electrode during reduction–oxidation in the potential range from 0.10 to 0.50 V; contour plots of (a) the 1st reduction and (b) the 1st oxidation at 100 mA g⁻¹ and (c) the 2nd reduction and (d) the 2nd oxidation at 10 mA g⁻¹. (e) A schematic of the phase transitions of the MoO₃ electrode.

The phase transition of MoO₃ during reduction–oxidation is summarized in Fig. 2(e). The reduction below 0.10 V causes an irreversible phase transition from phase-I to phase-III. Then the reversible phase transitions between phase-IIa and phase-IV, via phase-II and phase-III, are involved in the subsequent cycles when the voltage range is set at −0.3 to 0.5 V. The reversibility of the phase transition between phase-IIa and phase-IV is consistent with the charge–discharge performances of MoO₃ as the negative electrode.^4,22 On the other hand, MoO₃/phase-I biphasic and phase-I monophasic reactions mostly reversibly occur when the voltage range is set at 0.1 to 0.5 V.

The appearance of phase-IV in the fully reduced state and that of phase-II and phase-III in the reverse oxidation process observed in this study agree with previously reported ex situ XRD studies.^8,11 R. Schöllhorn et al. have reported based on their ex situ XRD measurement that the reduction of MoO₃ in the range of 0.5 < x < 1.67 in H_xMoO₃, corresponding to the plateau at 0.05 V in this study, yielded a mixture of phases-I, II, and III, which is probably caused by the decomposition of metastable phases I and III to phase-II in the course of ex situ measurement. We speculate that phase transition from phase I to III is kinetically more favourable than that from phase I to II.

Fig. 1(a) and (b) show that our MoO₃ electrode has a redox plateau at around 0.3 and −0.1 V, which have not been observed in other studies,^4,10 resulting in a relatively high reversible capacity of ca. 300 mA h g⁻¹ at a 100 mA g⁻¹ rate. This redox plateau disappears when the charge–discharge rate is increased to 1 or 2 A g⁻¹ (Fig. S4†), explaining why this process was not observed in previous studies with high testing rates. A high cut-off oxidation potential of 0.50 V in this study may also induce this process. We deduce that this process is attributed to some surface reactions on MoO₃, because no structural changes are observed in operando XRD (Fig. 1(a) and (b)). Further study is needed to identify it. The low rates used in this study would also lead to the hydrogen evolution reaction and composition ambiguity of phases II, IIa, III and IV.

3.2. DFT calculations

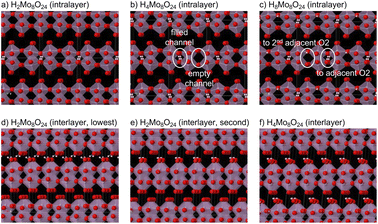
DFT calculations were carried out to obtain theoretical insights into the proton accommodation sites in H_xMoO₃ and the irreversible phase transition from phase-I to phase-III. For clarifying the proton accommodation sites, the crystal structure of MoO₃ is schematically illustrated in Fig. S5.† MoO₃ has an orthorhombic structure of the Pbnm (62) space group with one Mo site and three O sites. Mo atoms are coordinated by six O atoms forming MoO₆ octahedra. MoO₆ octahedra share their edges to form corrugated chains along the c-axis and share their corners along the a-axis. The edge- and corner-sharing MoO₆ octahedra form MoO₃ layers with intralayer channels, and the MoO₃ layers are stacked along the b-axis with van der Waals gaps. There are two potential sites for inserted protons. One is an O2 site, a bridging site between two corner-sharing MoO₆ octahedra, and protons are accommodated in the intralayer channels (intralayer site). The other is an O3 site, a terminal site on the surface of MoO₃ layers, and protons are accommodated in the interlayer gaps (interlayer site). The O1 site, which is shared by edge-sharing MoO₆ octahedra, is hardly accessible for protons. Calculated structural parameters are summarized in Table S1.† The calculated lattice constants a and c are in good agreement with the experimental values with an error of ca. 1%, whereas the lattice constant b is overestimated by ca. 12%. The overestimation of b is probably due to the use of the conventional GGA exchange–correlation functional, in which van der Waals interaction is not properly considered.

First, preferable proton accommodation sites in MoO₃ were investigated using a 2 × 1 × 2 supercell with an additional proton (H₁Mo₁₆O₄₈ supercell). A proton was attached to an O site toward one of its adjacent O atoms within 3.1 Å. All symmetry-independent configurations were employed as initial structures, and the structures converged into several groups after the structural relaxation. The lowest energy group has a proton attached to an O2 site toward an adjacent O2 site. The calculation results show that two Mo atoms sharing the OH unit are a pair of Mo⁵⁺ and Mo⁶⁺ ions. The second group has a proton attached to an O3 site toward an adjacent O3 site in the next MoO₃ layer, and it is higher in energy by 0.32 eV than the lowest energy group. Structures having a proton attached on an O1 site show 0.58 eV higher energy than the lowest energy group, or the proton was migrated to an adjacent O2 site during the structural relaxation. These results suggest that the protons are preferably accommodated within the MoO₃ layers and attached to the O2 sites, and this is consistent with the formation of phase-I in the early stage of the first reduction.

Second, preferable proton configurations in the intralayer sites were investigated using a 2 × 1 × 1 supercell of H_nMo₈O₂₄ (n = 2 and 4). The MoO₃ framework of phase-I with a space group of Cmcm was used as the initial structure, and protons were attached to O2 sites toward their adjacent O2 sites within 3.1 Å. The lowest energy structure of H₄Mo₈O₂₄ consists of MoO₃ layers having alternate filled and empty channels as illustrated in Fig. 3(b). The lowest energy structure of H₂Mo₈O₂₄ consists of a MoO₃ layer with alternate filled and empty channels, and another MoO₃ layer with empty channels only (Fig. 3(a)). This structure has slightly higher energy by 0.02 eV per proton than a mixture of H₄Mo₈O₂₄ and MoO₃. Structures with protons in different channels have 0.12 eV per proton or higher energy than the lowest energy structures in both compositions. These calculation results suggest that the inserted protons are not randomly distributed at the intralayer sites and that the protons tend to be aligned in the channels. This is consistent with a previous report.¹¹ Although structures with less-than-half filled channels were not examined in this study due to a huge number of proton configurations for larger supercells, structures with multiple empty channels between the filled channels are plausible at lower proton contents than H_0.5MoO₃, suggesting wide proton solubility in phase-I. To investigate the accommodation sites for further proton insertion, a 2 × 1 × 1 supercell of H₈Mo₈O₂₄ was examined. In the lowest energy structure, all protons are attached to O2 sites. Half of the protons are directed to the adjacent O2 sites, whereas the other half are directed to the second adjacent O2 sites (Fig. 3(c)). This suggests that the proton insertion behavior into the intralayer sites significantly changes over the composition of H_0.5MoO₃.

Fig. 3 Schematic views of the lowest energy structure models for (a) H₂Mo₈O₂₄ with intralayer protons, (b) H₄Mo₈O₂₄ with intralayer protons, (c) H₈Mo₈O₂₄ with intralayer protons, (d) H₂Mo₈O₂₄ with interlayer protons, (e) H₂Mo₈O₂₄ with interlayer protons of the second lowest energy, and (f) H₄Mo₈O₂₄ with interlayer protons. Purple polyhedra, red spheres, and white spheres denote MoO₆ octahedra, O atoms, and protons, respectively.

Next, preferable proton configurations in the interlayer sites was investigated using a 1 × 1 × 2 supercell of H_nMo₈O₂₄ (n = 2, 4). We have our interest in comparison of the proton accommodation sites between the intralayer and interlayer sites and getting insights into the irreversible phase transition from phase-I to phase-III, and thus the proton compositions examined in this study were much less than the actually reported compositions of phase-III (1.55 < x < 1.72 in H_xMoO₃). To reduce the number of configurations, the MoO₃ framework of the Cmcm space group, which is a common supergroup of the space groups of MoO₃ (Pbnm) and phase-III (C2/m), was used as the initial structure, and protons were attached to O3 sites toward their adjacent O3 sites of the next MoO₃ layer within 3.1 Å. For H₄Mo₈O₂₄, configurations were restricted to two protons in each gap with inter-proton distances more than 1.8 Å to further reduce the configurations. This restriction excludes structures having a proton facing another proton and those having multiple protons attached to a single O3 site. In the lowest energy structure of H₂Mo₈O₂₄, two protons are attached to different O3 sites forming a chain of hydrogen bonds (Fig. 3(d)). The second lowest energy structure has two protons attached to a single O3 site (Fig. 3(e)). The energy difference between these two structures is 0.002 eV per proton, which is negligible in consideration of computation accuracy. Their energies are also close to that of the lowest energy structure with intralayer protons. The lowest energy structure of H₄Mo₈O₂₄ has OH₂ units at two O3 sites (Fig. 3(f)), even though such configurations are excluded in the initial structures of H₄Mo₈O₂₄. This structure is lower in energy by 0.09 eV per proton than the lowest energy structure of H₄Mo₈O₂₄ with intralayer protons. However, it is still difficult to conclude that the protons are accommodated in the interlayer sites more preferably than in the intralayer sites at H_0.5MoO₃. This is because the conventional GGA exchange–correlation functional does not properly take van der Waals interaction into account, which could overestimate the energies of MoO₃ and H_xMoO₃ with intralayer protons (while having no hydrogen bonds between the MoO₃ layers). As the local structure of the intralayer protons considerably changes in the H₈Mo₈O₂₄ model, the interlayer protons would become stable at x > 0.5 in H_xMoO₃. Singly attached interlayer protons seem rather unstable at H₄Mo₈O₂₄ because all relaxed structures have at least one OH₂ unit. The hydrogen bonds toward the next MoO₃ layers cooperatively result in a monoclinic distortion. The OH₂ units at the interlayer sites have been experimentally observed from inelastic neutron scattering spectra for highly reduced H_xMoO₃.¹³

Even though protons often moved to other sites during the structural relaxation, none of the protons moved between the intralayer and interlayer sites. This implies a high potential barrier between the intralayer and interlayer sites. Hence, the phase transition between phase-I and phase-III (or other phases with interlayer protons) would occur by phase boundary migration, not by rearrangement of protons in the bulk. To transform phase-III (or phase-II) into phase-I, it is necessary to remove all the protons from the interlayer sites and to reinsert them into the intralayer sites. This would require similar potential to form the MoO₃ phase from phase-III. This is a probable reason why phase-I was never observed during the oxidation processes of phase-III.

3.3. Charge–discharge properties as a positive electrode for proton batteries

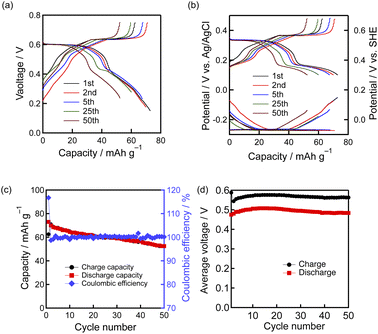
Since the MoO₃/phase-I biphasic and phase-I monophasic reactions occur at relatively high potential (ca. 0.5 V vs. SHE), they can be used as a positive electrode material for proton batteries. Therefore, repeated reduction–oxidation processes were conducted with MoO₃ half-cells in the potential range from 0.10 to 0.50 V to investigate the cyclability as a positive electrode material. Fig. 4(a) and (b) show the reduction–oxidation curves, reduction–oxidation capacities, and coulombic efficiencies of the MoO₃ electrode at 100 mA g⁻¹. The first reduction and oxidation capacities are ca. 80 and 60 mA h g⁻¹. The irreversible capacity in the first cycle comes from the incomplete phase transition from phase-I to MoO₃ as shown in operando XRD (Fig. 2). In the subsequent cycles, the reduction–oxidation capacities increase as the cycle number increases and reach a maximum value of ca. 100 mA h g⁻¹ in the 37th cycle with an average reduction voltage of ca. 0.24 V (0.44 V vs. SHE). The reason for the capacity increase is described in the next paragraph. When the reduction cut-off voltage was set at 0.05 V, the average electrode potential of 0.24 V (0.44 V vs. SHE) decreased to 0.11 V (0.31 V vs. SHE) (Fig. S6†) due to the irreversible phase transition from phase-I to phase-III in the first reduction. While the use of the reduction–oxidation process between phase-IIa, phase-II, and phase-III has recently been reported,¹² preventing the phase transition from phase-I to phase-III can lead to higher operating potential in aqueous proton batteries.

Fig. 4 Reduction–oxidation properties of the MoO₃ electrode at 100 mA g⁻¹ in the potential range from 0.10 to 0.50 V; (a) reduction–oxidation curves; (b) reduction–oxidation capacities and coulombic efficiency; (c) dQ/dV plots. (d) Ex situ XRD patterns of the MoO₃ electrodes after the 1st and 30th oxidation steps.

Fig. 4(c) shows the dQ/dV plots in the first and 37th cycles. The redox peaks at ca. 0.35 and 0.15 V, which are attributed to the MoO₃/phase-I biphasic and phase-I monophasic reactions, are observed in both the first and 37th cycles, showing that the phase transition behavior is basically unchanged. On the other hand, the capacities in the high overpotential regions clearly increase (shown as blue arrows in Fig. 4(c)), which suggests that the promotion of MoO₃ formation during oxidation and proton insertion during reduction causes the capacity increase. The higher intensity of MoO₃ diffraction after the 30th oxidation than that after the first oxidation in the ex situ XRD patterns (Fig. 4(d)) supports the facilitation of MoO₃ formation during oxidation in the reduction–oxidation cycles. The ex situ FE-SEM/EDS images of the MoO₃ electrodes (Fig. S7†) show almost no morphological change after the first reduction, which indicates that the MoO₃/phase-I biphasic reaction is an insertion reaction rather than a conversion reaction. In contrast, there are some cracks in MoO₃ particles after the 30th oxidation, which are probably caused by the repeated anisotropic volume changes during the reduction–oxidation cycles. Phase transition from MoO₃ to phase-I causes ca. 1.5% and 1.1% increase in the lattice constants b and c, respectively, and ca. 1.7% decrease in the lattice constant a. We speculate that the particle cracking facilitates the phase-transition and proton diffusion, resulting in capacity increase, and thus the optimization of the morphology can improve the reduction–oxidation properties. Fig. S8† shows the reduction–oxidation curves of the MoO₃ electrode at different current densities. The oxidation capacity at 1 A g⁻¹ is ca. 50% of that at 100 mA g⁻¹, which shows that the rate capability is not so limited despite the sluggish phase transition from phase-I to MoO₃.

3.4. Charge–discharge properties of the MoO₃|H₂SO₄ aq.|H_xMoO₃ full-cell

Finally, we constructed a MoO₃|H₂SO₄ aq.|H_xMoO₃ full-cell, to demonstrate the operation of an aqueous proton battery composed of two insertion-type oxide materials. We utilized the phase-III monophasic and phase-III/phase-IV biphasic regions in the potential range from −0.3 to 0 V for the negative electrode reactions. Fig. 5(a)–(d) show the charge–discharge curves, charge–discharge capacities, and average charge–discharge voltages of the MoO₃|H₂SO₄ aq.|H_xMoO₃ full-cell at 200 mA g⁻¹ based on the mass of MoO₃ on one side of the electrode. The loading masses of MoO₃ in the positive and negative electrodes were set to the same value as described in the Experimental section. The charge–discharge potential curves of the positive and negative electrodes (Fig. 5(b)) indicate that the designed reactions reversibly occur in the full-cell with the main voltage plateau of 0.6 V (Fig. 5(a)). We therefore conclude that a rocking-chair-type proton battery composed of insertion-type oxide active materials is successfully established. The highest discharge capacity is 73 mA h g⁻¹ in the first cycle, and the capacity retention rate in the 50th cycle is ca. 70%. The optimization of the material morphology,²³ positive–negative mass ratio, cell fabrication process and cut-off voltage could improve the slight capacity decrease during cycling. The cell keeps the coulombic efficiency over 98% until the 50th cycle. The average discharge voltage and the energy density based on the total mass of the active materials are 0.48 V and 17 W h kg⁻¹, respectively, in the 1st cycle, which are higher than those of the full cell using the conventional positive electrode reaction, 0.33 V and 15 W h kg⁻¹ (Fig. S9 and Table S2†).

Fig. 5 Charge–discharge properties of the MoO₃|50 wt% H₂SO₄|H_xMoO₃ full-cell at 200 mA g⁻¹; (a) cell voltage; (b) potentials of positive and negative electrodes; (c) charge/discharge capacities and coulombic efficiency; (d) average charge/discharge voltages. The capacities were calculated based on the mass of MoO₃ on one side of the electrode.

4. Conclusions

The proton insertion–extraction mechanism of MoO₃ was investigated using operando XRD and DFT calculation. The operating potential of the MoO₃ electrode as a positive electrode for aqueous proton batteries was optimized based on the obtained results, and the MoO₃|H₂SO₄ aq.|H_xMoO₃ full-cell was successfully constructed.

The phase transition behavior of the MoO₃ electrode between MoO₃ and fully protonated phases (phase-IV) was clarified by operando XRD, including irreversible phase transition from phase-I to phase-III. It was also shown by operando XRD that phase transition from MoO₃ to phase-I could almost reversibly be utilized by preventing the irreversible phase transition from phase-I to phase-III below 0.3 V vs. SHE. DFT calculation suggested that the stable proton accommodation site changed from the intralayer site to the interlayer site at higher proton contents than H_0.5MoO₃ and implied a high potential barrier between the intralayer and interlayer sites. From these results, it was strongly suggested that the irreversibility of the phase transition from phase-I to phase-III originated from the change of the proton accommodation site from intralayer to interlayer.

The MoO₃ electrode using phase transition between MoO₃ and phase-I showed a maximum reversible capacity of 100 mA h g⁻¹ and an average reduction potential of 0.44 V vs. SHE. The MoO₃|50 wt% H₂SO₄ aq.|H_xMoO₃ full-cell exhibited an average discharge voltage of 0.47 V, which is the highest among reported aqueous proton batteries (composed of insertion-type oxide active materials) and maintains a maximum discharge capacity of 73 mA h g⁻¹.

Considering that commercially available MoO₃ powder with micrometer-order size was used in this study and phase transition from phase-I to MoO₃ was kinetically sluggish, it is strongly expected that the charge–discharge characteristics can be improved by controlling the particle morphology.

Author contributions

A. I.: investigation (experiments), methodology (operando XRD), and writing – original draft, Y. K.: investigation (DFT calculations) and writing – original draft, T. N.: investigation (experiments), and H. A.: project administration, conceptualization, and writing – review & editing.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

FE-SEM and EDS measurements were supported by Prof. Masaaki Hirayama, Prof. Naoki Matsui, Prof. Kota Suzuki, and Prof. Ryoji Kanno (Tokyo Institute of Technology). Electrochemical measurements were technically supported by Ms Yuko Narita and Mr Teruya Hiramatsu (Tokyo Institute of Technology). Some of the DFT calculations were performed on the Numerical Materials Simulator at the National Institute for Materials Science.

References

1. J. Li, H. Yan, C. Xu, Y. Liu, X. Zhang, M. Xia, L. Zhang and J. Shu, Nano Energy, 2021, 89, 106400.
2. X. Wang, J. Zhou and W. Tang, Energy Storage Mater., 2021, 36, 1–9.
3. X. Wu, J. J. Hong, W. Shin, L. Ma, T. Liu, X. Bi, Y. Yuan, Y. Qi, T. W. Surta, W. Huang, J. Neuefeind, T. Wu, P. A. Greaney, J. Lu and X. Ji, Nat. Energy, 2019, 4, 123–130.
4. X. Wang, Y. Xie, K. Tang, C. Wang and C. Yan, Angew. Chem., Int. Ed., 2018, 57, 11569–11573.
5. J. B. Mitchell, N. R. Geise, A. R. Paterson, N. C. Osti, Y. Sun, S. Fleischmann, R. Zhang, L. A. Madsen, M. F. Toney, D.-e. Jiang, A. I. Kolesnikov, E. Mamontov and V. Augustyn, ACS Energy Lett., 2019, 4, 2805–2812.
6. N. Makivić, J.-Y. Cho, K. D. Harris, J.-M. Tarascon, B. Limoges and V. Balland, Chem. Mater., 2021, 33, 3436–3448.
7. J. Birtill and P. Dickens, Mater. Res. Bull., 1978, 13, 311–316.
8. R. Schöllhorn, Angew. Chem., Int. Ed., 1980, 19, 983–1003.
9. S. Adams, J. Solid State Chem., 2000, 149, 75–87.
10. L. Yan, J. Huang, Z. Guo, X. Dong, Z. Wang and Y. Wang, ACS Energy Lett., 2020, 5, 685–691.
11. H. Jiang, W. Shin, L. Ma, J. J. Hong, Z. Wei, Y. Liu, S. Zhang, X. Wu, Y. Xu, Q. Guo, M. A. Subramanian, W. F. Stickle, T. Wu, J. Lu and X. Ji, Adv. Energy Mater., 2020, 10, 2000968.
12. W. Xu, K. Zhao, X. Liao, C. Sun, K. He, Y. Yuan, W. Ren, J. Li, T. Li, C. Yang, H. Cheng, Q. Sun, I. Manke, X. Lu and J. Lu, J. Am. Chem. Soc., 2022, 144, 17407–17415.
13. P. Dickens, J. Birtill and C. Wright, J. Solid State Chem., 1979, 28, 185–193.
14. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169.
15. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758.
16. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
17. S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. Humphreys and A. P. Sutton, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505.
18. S. P. Ong, W. D. Richards, A. Jain, G. Hautier, M. Kocher, S. Cholia, D. Gunter, V. L. Chevrier, K. A. Persson and G. Ceder, Comput. Mater. Sci., 2013, 68, 314–319.
19. G. L. Hart and R. W. Forcade, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 224115.
20. G. L. Hart and R. W. Forcade, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 014120.
21. G. L. Hart, L. J. Nelson and R. W. Forcade, Comput. Mater. Sci., 2012, 59, 101–107.
22. H. Guo, D. Goonetilleke, N. Sharma, W. Ren, Z. Su, A. Rawal and C. Zhao, Cell Rep., 2020, 1, 100225.
23. W. Liu, Z. Zhang, J. Shi, Y. Zheng, Y. Wu, X. Fu, N. Liu, J. Sua and Y. Gaoa, J. Mater. Chem. A, 2022, 10, 4043–4052.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2ta08581j

---