Crumpled graphene oxide for enhanced room temperature gas sensing: understanding the critical roles of surface morphology and functionalization†
Kelsey
Haddad
a,
Ahmed
Abokifa
 b,
Siyuan
An
b,
Siyuan
An
 a,
Junseok
Lee
a,
Junseok
Lee
 d,
Baranidharan
Raman
c,
Pratim
Biswas
d,
Baranidharan
Raman
c,
Pratim
Biswas
 a and
John D.
Fortner
a and
John D.
Fortner
 *d
*d
aDepartment of Energy, Environmental and Chemical Engineering, Center for Aerosol Science and Engineering, Washington University in St. Louis, St. Louis, MO 63130, USA
bDepartment of Civil, Materials and Environmental Engineering, The University of Illinois at Chicago, Chicago, IL 60607, USA
cDepartment of Biomedical Engineering, Washington University in St. Louis, St. Louis, MO 63130, USA
dDepartment of Chemical and Environmental Engineering, Yale University, New Haven, CT 06520, USA. E-mail: john.fortner@yale.edu; Tel: +1-203-436-9066
First published on 1st December 2022
Abstract
This work fundamentally explores graphene oxide morphology and functionality with regard to room temperature gas sensing performance. Highly-oxidized, crumpled graphene oxide (HO-CGO) was synthesized using a scalable, aerosol-based process. To minimize sample-to-sample synthesis variability, CGO and flat graphene oxide materials were thermally reduced allowing for a serial library of graphene oxide materials with comparable shape and surface chemistries. Room temperature sensitivity to ethanol was then systematically evaluated as a function of curing temperature, time (i.e., degree of thermal reduction), and morphology. HO-CGO showed the strongest response after one hour of reduction at a relatively mild temperature (220 °C), which removed most of the oxygen functionality. In contrast, flat graphene oxide sheets at the same C/O ratios showed no response. Density functional theory (DFT) and ab initio molecular dynamics (AIMD) simulations of ethanol interactions with these material surfaces were employed to develop a mechanistic understanding of the observed enhanced (CGO) sensing response. Adsorption energy calculations revealed that point defects have the most favorable adsorption energy for ethanol, followed by oxygen functionalities, and pristine graphene, respectively. In addition, AIMD on a simulated crumpled structure of graphene oxide indicate that ethanol molecules prefer to adsorb at/in the geometrical valleys of the CGO structure. Enhanced gas sensing performance of CGO is proposed to be a function of structural valleys, which act as both stable sites for oxygen defects and preferential binding sites for the ethanol molecules, whose adsorption occurs through physisorption, with a substantial contribution (∼50%) derived from dispersive forces. This work directly demonstrates the benefits of the crumpled structure of CGO, with concave morphological regions, compared to other carbon-based materials, and informs its processing and material incorporation into functional room temperature gas sensing devices.
1 Introduction
Historically, work on gas sensing has focused on single-species gas sensors.1 Accordingly, traditional approaches to the design and synthesis of sensing materials have focused on lock-and-key type mechanisms.2,3 However, single analyte sensors can often suffer from poor selectivity, exhibiting cross-sensitivity to a number of different gases. Further, a tradeoff exists between the selectivity and the post-response recovery of the active material, as selectivity tends to be a function of strong binding via specific interactions, whereas rapid post-response recovery tends to be a function of weak interactions, typical of non-specific forces, such as van der Waals forces. To manage this tradeoff, gas sensor arrays allowing for analyte differentiation, have gained attention.4 For successful application, such complex devices should be rationally designed, which requires a mechanistic understanding of how different sensor materials interact with (potential) analytes. Such mechanistic understanding can be gained by systematically studying how specific sensor materials interact with different classes of target compounds. For scalability, libraries of sensing materials should be easy to synthesize and modify. Towards this, carbon-based nanomaterials are strong candidates for such arrays due to high sensitivity, large surface area, and ease of tailoring.5 However, predicting complex, combitorial analyte–sensor response(s) for carbon materials, which are key for rational design and scale-up, remains challenging.6Pioneering work on gas sensing with carbon-based, nanoscale materials began with the demonstration of semiconducting single-walled carbon nanotubes (SWNTs) as highly sensitive, room temperature gas sensors for NO2 and NH3.7 Further studies revealed that SWNT defect sites played an important role in sensing response.8–10 Specifically, a relatively small amount of chemical functionalization through oxidation (around 2%) significantly affects sensitivity and selectivity of the sensors for several gases.8 Surface area enhancements provided further gains in conductivity and allowed for room-temperature detection limit(s) down to individual gas molecules.11,12 As with carbon nanotubes, further exploration revealed that the sensing response of pristine graphene also depends on the type and geometry of defects.13
Sensing devices made of carbon nanotubes and pristine graphene sheets are currently limited by relatively high production cost, complex fabrication routes, and limited durability/robustness.14 Further, the application of SWNTs for sensor arrays is largely restricted by the difficulty of controlling the synthesis of semiconducting SWNTs, as samples typically consist of mixtures of both metallic and semiconducting SWNTs, which remain difficult to separate.2 Such realities result in fabrication complexity, low sensor yields, and poor reproducibility.15 In addition to synthesis constraints, device fabrication using SWNTs or graphene typically require relatively complex processes, including patterning and top-down synthesis techniques, increasing device cost(s) and response variability.14
Based on the demonstrated role of defects and functional groups observed for carbon nanotubes and graphene sensors, related research has evolved towards the use of chemically modified graphene (CMG). One interesting class of CMG is reduced graphene oxide (RGO), which is inexpensive, easy to produce, while containing a diverse range of reactive oxygen functional groups that can be modified to balance conductivity with active surface sites.16 RGO sensor response depends on molecular adsorption to both low-energy adsorption sites, such as sp2-bonded carbon, and higher-energy adsorption sites, such as defects and functional groups.17 The reduction process and the distribution of functional groups play key roles in the sensing performance of RGO.17–22
While RGO can potentially overcome fabrication challenges posed by graphene, RGO sheets tend to aggregate, decreasing the surface area exposed to target gases and significantly decreasing performance in comparison to monolayer graphene or graphene oxide (GO).22 As an alternative to RGO sheets, nanostructured carbon materials, including porous and foam-like structures, have been recently explored;14,22–24 however, surfactant-free and simple fabrication of hierarchical graphene structures is still complex. Crumpled graphene oxide (CGO) materials possess a low tendency for aggregation while maintaining high specific surface area and exceptional electronic properties similar to those of flat graphene sheets. Hence, CGO provides a potentially unique material solution which can be incorporated into thin films and integrated in scalable and reproducible sensors.25,26 Additionally, synthesizing CGO via a furnace aerosol reactor (FuAR) is a scalable and well-studied process.25,27 In contrast to other 3D synthesis methods, this continuous process does not require catalysts, vacuum conditions, or high temperatures. The FuAR process is appealing for synthesizing libraries of materials for gas sensor arrays as the morphology (size and degree of crumpling) and functionalization can be easily tuned by varying parameters such as the concentration of GO in the aerosol droplet, the furnace temperature, and residence time.27–29 In addition, highly stable crumpled particles resist aggregation and compression, limiting the impact of the processing history on material performance.25 Unlike carbon nanotubes, these materials feature inherent oxygen functionality that can be easily and efficiently controlled by varying the synthesis temperature.30–32 Moreover, the crumpled ridges of the CGO sheets can be considered as line defects, which can enhance adsorption for sensing applications. Crumpled graphene oxide, in contrast to 2D flat analogues, has been applied for gas sensing in only a few studies.33–35 Chen et al. focused on the role of the enhanced surface area of crumpled graphene-based nanosheets in gas sensing performance, but did not explore the roles of point defects, line defects, or functional groups.33
In this work, we fundamentally explore the role of functional groups and morphology on the gas-phase sensing response of CGO for ethanol, as a model, polar organic analyte. Specifically, we compare the performance of CGO structures to the performance of flat GO sheets to determine the effect of shape on the ethanol sensing response. We employ both experimental observations and theoretical calculations to elucidate interactions of ethanol with sensor materials – determining binding affinities and charge transfer mechanisms at defect sites, along ridges, and on functional groups. Results provide key insights toward a mechanistic understanding of the combined interactions between functional groups, defects, and morphology, which is necessary to realize the high potential for the application of crumpled graphene oxide materials in gas sensor arrays.
2 Methods
2.1 Preparation of graphene oxide
Graphene oxide (GO) was prepared via modified Hummers' method.36 First, 50 mL of concentrated sulfuric acid (H2SO4, 96.4% purity) was added to 2 grams of graphite powder. The mixture was cooled to 0 °C in an ice bath. After the mixture was allowed to return to room temperature, six grams of potassium permanganate (KMnO4) were added. The suspension was then heated to 50 °C and stirred for 2 hours. The elevated temperature in this step, as compared to the temperature in previous studies conducted by our group, improved the graphene oxide oxidation efficiency.37 The initial synthesis of a highly oxidized graphite oxide powder allowed for the subsequent synthesis of highly oxidized crumpled graphene oxide (HO-CGO), which will be discussed in later sections. The mixture was again cooled to 0 °C in an ice bath and diluted with 350 mL of DI water. An aqueous hydrogen peroxide solution (H2O2, 30%) was added to the diluted mixture with stirring until the gas was no longer seen to be evolving. The suspension was then rinsed with DI water and vacuum filtered. After the graphite oxide was allowed to dry for 24 hours, the powder was redispersed in DI water and sonicated with a probe sonicator for 3 hours to exfoliate the stacked sheets into single sheets of graphene oxide. The suspension was centrifuged at 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 rpm for 3 hours, and the supernatant, the final graphene oxide solution, was decanted.
000 rpm for 3 hours, and the supernatant, the final graphene oxide solution, was decanted.
2.2 Graphene oxide modification: crumpling and reduction
The single sheets were then crumpled in a furnace aerosol reactor (Lindber/Blue M 1100 °C Tube Furnace), shown in Fig. 1a schematic. GO coupons were fed into the reactor as a 300 ppm aqueous solution via a Collison nebulizer (BGI Incorporated). The six jet nebulizer was operated at 14 psi, resulting in a flow rate of 12.4 L min−1 and roughly 3 μm droplets.27 Droplets were delivered by N2 carrier gas into the furnace via a ceramic tube with an inner diameter of 25 mm and a length of 1 m. The residence time of the particles in the heated zone, set at 400 °C, was ∼1.6 seconds.2.3 Characterization of graphene oxide
The morphology and size of the flat GO and the crumpled GO (CGO) samples were characterized using transmission electron microscopy (TEM, Tecnai™ Spirit, FEI Co.), field emission scanning electron microscopy (SEM, Nova NanoSEM 230, FEI Co.), and atomic force microscopy (AFM, Veeco Nanoman). The TEM samples were prepared by drop-casting aqueous GO solution onto a carbon film on 300 mesh copper grids (electron microscopy sciences, CF300-Cu). AFM of the thin films was performed with a scan size of 30 μm (fully covering the area between interdigitated electrodes), at a rate of 0.1000 Hz. Information on the electrical bond and functionality of the surface was obtained with X-ray photoelectron spectroscopy (XPS, PHI 5000 Versa Probe II, monochromatic Al Kα X-ray source at 1486.6 eV). The peaks were fit using a mixed fit of 80% Gaussian and 20% Lorentzian characters in the PHI Multipak software. Calibration was carried out by aligning the C1s peak (C–C) with its reference line at 284.8 eV (associated with graphitic carbon), and a Shirley background subtraction was performed. For the fitting, the full width at half maximum (FWHM) values was fixed at 1.2 eV for all peaks and the positions of each deconvolution peak were maintained within 0.2 eV of the assigned position. Three measurements were made on each sample at different locations. Finally, the defect structure was examined via Raman spectroscopy (Renishaw InVia Reflex confocal Raman spectrometer). The Raman spectra were collected using a 514.5 nm laser excitation at 10% power, focused on the sample using a 50× objective.2.4 Graphene oxide sensor fabrication
Sensor fabrication was performed by drop-casting 60 μL of 100 ppm aqueous GO/CGO solution onto interdigitated electrodes. The electrodes were fabricated on Si (100) substrate (380 μm thickness, n-type, University Wafers) with a 100 nm layer of SiO2 grown via plasma-enhanced chemical vapor deposition (PECVD, Nanofab, Oxford Instruments). Interdigitated electrode patterns with 40 interdigitated fingers at 20 μm spacing were patterned using a laser writer (DWL66+ laser lithography system, Heidelberg Instruments) followed by thermal evaporation and deposition of a 10 nm chromium adhesion layer and a 70 nm gold layer. The as-deposited films were then dried overnight in a vacuum oven at room temperature. To remove any remaining bulk and interstitial water, the films were heated for 1 hour at 60 °C. To eliminate the device-to-device variability associated with the drop-casting procedure, the as-deposited films were then incrementally reduced via low-temperature thermal reduction by incrementally heating them in a 220 °C ± 1 °C, vacuum oven at 0.08 MPa (DZF-6020 Vacuum Oven, MTI Corporation) for 4 minutes, 1 hour, 4 hours, and 24 hours.38 Fabricated sensor(s) photo is shown in Fig. S1.†2.5 Gas-sensing measurements
Gas sensing measurements were performed on a previously described system.39 The sensors were preconditioned by flowing dry, filtered air at 750 sccm (standard cubic centimeter per minute) for one hour prior to the pulsed testing. Each pulsed test consisted of five cycles alternating between five minutes of dry, filtered air with ethanol at different concentrations (gas) followed by five minutes of dry, filtered room air (degas). Throughout the cycling process, the air flow was maintained at 750 sccm. Five different concentrations were tested: 20, 40, 50, 100, and 200 ppm.2.6 Computational methods
For the adsorption calculations, an ethanol molecule was allowed to adsorb on one side of the slab and dipole corrections were employed to produce accurate adsorption energies. During geometry optimization, all atoms were allowed to relax using the conjugate gradient algorithm until the Hellmann–Feynman forces on each ion were smaller than 0.01 eV Å−1, with an overall energy convergence criterion of 10−5 eV per cell. For Brillouin zone integration, k-meshes were generated automatically using the Monkhorst–Pack (MP) method with a (5 × 5 × 1) k-point mesh. Because noncovalent interactions were expected to play an important role in adsorption, the empirical van der Waals corrections, as prescribed by Grimme (DFT-D3) with Becke–Jonson (BJ) damping, were considered in all calculations.45
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps) were generated for the adsorbate–adsorbent system.
000 steps) were generated for the adsorbate–adsorbent system.
3 Results and discussion
3.1 Material synthesis and characterization
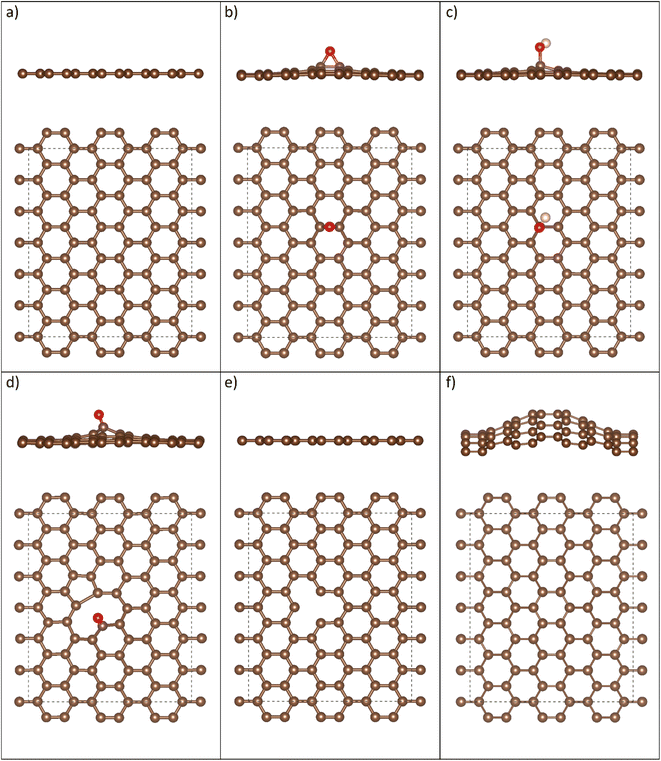
As-synthesized GO and CGO samples were characterized by AFM and TEM to compare morphology and structure. Fig. 1b–e shows representative morphologies observed for flat graphene oxide sheets and corresponding 3D structure after being crumpled in the furnace aerosol reactor (FuAR). Smaller in diameter than their flat counterparts, CGO particles have distinct ridges that effectively create peaks and valleys. The size distribution of the crumpled graphene oxide was analyzed by measuring the diameter of over 100 particles in TEM images, using ImageJ software. The average particle size was roughly 500 nm, with over 80% of the particles in the range of 300–700 nm (Fig. S2†). XPS analysis was employed to determine the oxidation state of as-synthesized material and for different synthesis phases. GO starting material was highly oxidized, with a C/O ratio of 1.4 ± 0.07. The starting ratio is much lower than what is typically observed for GO synthesized by the modified Hummers' method due to the increased temperature (35 °C → 50 °C) employed in this work to enhance bulk oxidation processes.30 Two factors control the morphology of CGO particles synthesized in a FuAR. The first, Fa, is the capillary/crumpling force generated through the evaporation of the aqueous droplet:27,46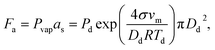 | (1) |
| Fc = AC1/δDDp−1/δDd3/δD | (2) |
 , C in the mass concentration (kg m−3), δ is the force scaling exponent for a self-avoiding sheet (0.25), D is the characteristic fractal dimension of GO (2.54), and Dp is the mobility diameter (nm). At 400 °C, Fa is greater than Fc and the sheets are crumpled. Previous studies show that, at this temperature, some of the oxygen-containing functional groups remain, resulting in a C/O ratio of 3.2 ± 0.1.30,31 Unlike the forces required for crumpling, the reduction of the graphene oxide sheets is dependent on reaction kinetics, and therefore, on the amount of time the material is exposed to a given temperature and also the oxidation state of the starting material. By leveraging the kinetics of the reduction process and starting with a highly oxidized form of GO, we are able to synthesize a highly oxidized crumpled graphene oxide (HO-CGO), in contrast to previously synthesized CGO. The C/O ratio of the HO-CGO synthesized at 400 °C was 2.0, which is more typical of GO synthesized by the traditional modified Hummers' method.47
, C in the mass concentration (kg m−3), δ is the force scaling exponent for a self-avoiding sheet (0.25), D is the characteristic fractal dimension of GO (2.54), and Dp is the mobility diameter (nm). At 400 °C, Fa is greater than Fc and the sheets are crumpled. Previous studies show that, at this temperature, some of the oxygen-containing functional groups remain, resulting in a C/O ratio of 3.2 ± 0.1.30,31 Unlike the forces required for crumpling, the reduction of the graphene oxide sheets is dependent on reaction kinetics, and therefore, on the amount of time the material is exposed to a given temperature and also the oxidation state of the starting material. By leveraging the kinetics of the reduction process and starting with a highly oxidized form of GO, we are able to synthesize a highly oxidized crumpled graphene oxide (HO-CGO), in contrast to previously synthesized CGO. The C/O ratio of the HO-CGO synthesized at 400 °C was 2.0, which is more typical of GO synthesized by the traditional modified Hummers' method.47
3.2 Sensor fabrication and characterization
The GO and (HO-)CGO solutions were drop-cast onto sensing substrates, maintaining the same mass loading between the two samples. The morphologies of the as-deposited CGO films are shown in Fig. 3. In addition to imaging surface morphology, the surface area and roughness of each 30 μm × 30 μm analysis area were intermittently characterized throughout the reduction process by AFM (Fig. S3†). Initially, the CGO films had a roughness (Rq) of 181 nm and a surface area of 1143 μm2. Following reduction for 20 hours, CGO films had a surface roughness of 171 nm and a surface area of 1077 μm2. Visual inspection of the AFM images of the surface also showed that the CGO materials maintain their crumpled morphology, i.e. not reverting to a flat or rippled structure following prolonged reduction. The GO film had a roughness (Rq) of 75 nm and a surface area of 955 μm2. The AFM images of the GO thin films reveal a layered, slightly wrinkled graphene oxide structure. In addition, the calculated surface area difference percentage representing the difference between the three-dimensional surface area and its two-dimensional footprint, was 4.89% for GO and 24.75% for CGO, as to be expected for a 3D porous structure. For the same mass-loading over the same area, we can see that the surface area of the films and the access of the surface to analyte vapors is significantly improved with CGO.CGO is both compression- and aggregation-resistant, and can be readily dispersed in both apolar and polar solvents.25 One of the key requirements for solution-based printing/manufacturing is the successful (stable) dispersion of nanoparticles to avoid aggregation. Compared to flat reduced graphene oxide sheets, CGO offers the potential to simplify sensor fabrication through low cost, simple printing techniques.48 These printing techniques can be used on flexible substrates, which offer improved portability and sturdiness. In addition, in a previous study using a similar annealing technique for thermal reduction, portions of the flat graphene oxide films delaminated from the surface.38 Thermal reduction of GO sheets is suggested to cause delamination through the rapid evaporation of intercalated water and/or the evolution of gas(es) during the reduction process. In contrast, CGO thin films did not show any delamination from the surface in these experiments. The inherent structure of the CGO thin films, with spacing and pores for the gases and water to escape through, likely aids in preventing such processes.49
Sensing performance is a function not only of access to binding sites, but also of the number of available binding sites. As mentioned, oxygen-containing functional groups and defects on the surface are thought to act as preferential binding sites for target analyte(s). Therefore, we measured not only the surface area but also the oxygen-containing functional groups on the surface and the defect structure, using XPS and Raman spectroscopy, respectively. As can be seen from the XPS spectrum scan of the C1s peak in Fig. S4,† the starting materials for both the HO-CGO and GO, have two peaks, which is indicative of oxygen-containing functional groups on the surface. For both CGO and GO, after 1 hour of reduction at 220 °C, the second peak was reduced to a shoulder of the C–C peak. The same trend can be seen in the C/O ratio. After 1 hour of reduction, the GO and CGO have the same C/O ratio of 3.2. As shown in Fig. 4a, the C1s peak was deconvoluted to determine the percent area of functional groups on the surface. In accordance with previous work, the five most common oxygen functionalities were identified and fit: C–C (284.8 eV), C–OH (286.2 eV), C–O–C (287.1 eV), C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O (287.7 eV), and COOH (288.8 eV).47,50 The C–C area ratio for CGO started at 54% and gradually increased to roughly 70%. Remaining oxygen-containing functional groups on the surface after reduction at 220 °C are primarily attributed to hydroxide groups.
O (287.7 eV), and COOH (288.8 eV).47,50 The C–C area ratio for CGO started at 54% and gradually increased to roughly 70%. Remaining oxygen-containing functional groups on the surface after reduction at 220 °C are primarily attributed to hydroxide groups.
To probe surface defects, Raman spectroscopy was intermittently employed on films throughout the reduction process. The Raman spectra, taken for different processing temperatures, shown in Fig. 4b (CGO) and Fig. S5† (GO), are scaled to the height of the G-peak for comparison. Initially, spectra scans of both HO-CGO and GO show similar structures, with a prominent D-peak around 1355 cm−1 and a broad G-peak in the range of 1580–1615 cm−1.51 The G-peak for GO gradually shifts down with increased thermal reduction (Fig. 4c), indicating restoration of a hexagonal network of carbon atoms with defects.52 In addition, the D-peak intensity gradually increased with reduction (Fig. S5†), which suggests the formation of small but numerous regions of aromatic carbons. HO-CGO did not show a change in the intensity of the D-peak, rather the more prominent trend was the formation of a shoulder on the G-peak of the CGO films. This type of G-peak splitting has been observed to be a function of curvature-induced strain in both carbon nanotubes and graphene sheets.53,54 For both GO and the HO-CGO, physically and chemically induced defects exist. As shown in the AFM images, the graphene oxide thin films have large wrinkles whereas each individual crumpled graphene oxide particle has wrinkles as well as ridges and valleys, all of which can be considered as extended/line defects.55 Indeed, in both spectra, a 2D band with two peaks is seen (Fig. S5†), which is indicative of physical, but not chemical, defects.55 The failure of the CGO D-peak to follow a trend similar to the established change in the GO peak following thermal reduction indicates that the defect structure of the material is driven primarily by physical and not chemical defects. In addition, the FWHMs of the D- and G-peaks are broad, which was previously observed for few-layer wrinkled graphene.55 The FWHMs of the CGO films were consistently larger than those of their GO counterparts, as shown in Fig. 4d, which again can be explained by the physical inhomogeneity of the crumpled samples, due to inconsistent morphology of line defects. Overall, Raman spectra demonstrate that both the GO and CGO films remain highly disordered (carbon environment) upon reduction, even following the removal of oxygen-containing functional groups. A more detailed study of the role of crumpling on Raman spectroscopy should be performed on single crumpled sheets to elucidate the differences between the chemical and physical defect structure response(s).
3.3 Sensing response
The response of the CGO sensor to ethanol is shown in Fig. 5. Initially, the sensor (HO-CGO) has a relatively high baseline resistance of 92 MΩ and shows a very weak response to ethanol at elevated concentrations (>100 ppm). After thermal reduction for four minutes at 220 °C, the sensor begins to show improved performance. A response, although somewhat noisy, can now be seen in the lower concentration range. There is a decrease in the baseline resistance of the material, which is consistent with the XPS results which indicated carbon reduction and partial restoration of the sp2 structure. However, there is only a small change in the functionalization of the material compared to the dried sensor. As previously discussed, the Raman spectra of the CGO sensor showed no change in the D-band intensity or the G-band intensity in this first reduction step. In contrast, following the reduction of the material for 1 hour at 220 °C, the sensor exhibits excellent sensing response, showing clear response in the lowest concentration range explored (Fig. 5d). For this system, CGO material has reduced surface oxidation (Fig. 4), with a C/O ratio of 3.2 ± 0.29. For comparison, flat graphene oxide films which also have a C/O ratio of 3.2 ± 0.18, exhibit no sensing response. The large difference in response suggests morphology plays a critical role in sensing performance.After an additional 3 hours of reduction, the baseline resistance of the sensor continues to decrease (Fig. 5e); however, few additional functional groups are removed from the surface, which maintains a relatively constant C/O ratio of 3.2 ± 0.44 (Fig. 4). The decrease in resistance can be attributed to the restructuring of the defective surface, which improves electrical conductivity, as observed by others.38 Although there is still a response at lower concentrations, the magnitude of the response is ca. 50% less than the response observed in Fig. 5c, after being normalized for the change in baseline. Finally, when sensors were thermally reduced for 24 hours (Fig. 5f), there was additional decrease in the baseline resistance of material. This decrease was much smaller than observed in previous reduction steps, despite the much longer reduction time, suggesting the limit(s) of restructuring and return of the sp2 structure of the crumpled material was approached (under stated conditions). Again, the sensing response was diminished but still observed, with a response measured at 50 ppm.
3.4 Theoretical calculation insights
| Eads = ΔEtot = −[Eslab+mol − (Eslab + Emol)], | (3) |
| Structure | E ads (eV) | ΔEdisp (eV) |
|---|---|---|
| Defective graphene | 0.511 | 0.255 |
| GO–hydroxyl | 0.505 | 0.304 |
| GO–carbonyl | 0.485 | 0.301 |
| GO–epoxide | 0.361 | 0.271 |
| Pristine graphene | 0.223 | 0.221 |
Fig. 6 depicts the stable adsorption configurations of ethanol on the pG, dG, and GO sheets. The relaxed structures show that the adsorption of ethanol induces minor deformations in graphene oxide and defective graphene, while no changes are observed in the structure of pristine graphene after adsorption. For GO with a carbonyl group, the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond elongates by 0.5%, while for the epoxide group the C–O–C bond elongates by 0.7%. For GO with a hydroxyl group, the O–H bond elongates by 1.5%, while the C–O bond shrinks by 1.8%. For defective graphene, ethanol adsorption pushes one of the under-coordinated carbon atoms out of plane by 0.651 Å. Moreover, a close-range electrostatic interaction appears to take place between ethanol's hydrogen and the oxygen atoms of GO with a carbonyl group (bond distance 1.855 Å) and an epoxide group (bond distance 2.042 Å), while for GO with a hydroxyl group, a similar interaction takes place between GO's hydrogen and ethanol's oxygen (bond distance = 1.818 Å). The results suggest that point defects in defective graphene and functional groups on GO serve as favorable binding sites for the adsorption of polar VOCs.
O bond elongates by 0.5%, while for the epoxide group the C–O–C bond elongates by 0.7%. For GO with a hydroxyl group, the O–H bond elongates by 1.5%, while the C–O bond shrinks by 1.8%. For defective graphene, ethanol adsorption pushes one of the under-coordinated carbon atoms out of plane by 0.651 Å. Moreover, a close-range electrostatic interaction appears to take place between ethanol's hydrogen and the oxygen atoms of GO with a carbonyl group (bond distance 1.855 Å) and an epoxide group (bond distance 2.042 Å), while for GO with a hydroxyl group, a similar interaction takes place between GO's hydrogen and ethanol's oxygen (bond distance = 1.818 Å). The results suggest that point defects in defective graphene and functional groups on GO serve as favorable binding sites for the adsorption of polar VOCs.
Long-range van der Waals (vdW) interactions are considered in our calculations based on the empirical dispersion corrections proposed by Grimme (D3) in conjunction with the Becke–Jonson (BJ) damping technique. In this method, the total corrected energy of the system, Etot, is the summation of the conventional DFT energy, EDFT, and an additional energy term that accounts for dispersive interactions, Edisp.56 Hence, by using a formula similar to the one employed for calculating the adsorption energy, the contribution of dispersive interactions between the surface and the adsorbate molecule can be evaluated as
| Eads = ΔEtot = ΔEDFT − ΔEdisp | (4) |
Calculated values of the dispersion energy for the adsorption of ethanol on pG, dG, and GO are given in Table 1. For all the studied systems, the contribution of dispersive interactions to the adsorption energy is substantial (≥50%). The contribution of dispersive interactions is inversely proportional to the overall adsorption energy, with defective graphene features having the highest adsorption energy and the lowest contribution from dispersive forces (49.86%). In contrast, pristine graphene has almost 100% contribution from dispersive forces. The contribution of dispersive forces to Etot indicates that the enhanced binding strength for defective graphene comes from the strong electrostatic interactions between functional groups or defects and ethanol. However, for pristine graphene, the adsorption is driven almost exclusively by vdW interactions.
3.5 Sensing mechanism
Two key factors in sensing performance of the CGO thin films are increased access to preferential binding sites and/or an increased number of potential (favorable) binding sites. When considering adsorption sites, a defective surface (attributed to either oxygen-containing functional groups or point defects) creates a more favorable adsorption environment than pristine sheets. Consequently, the as-deposited CGO thin films, with the largest number of oxygen-containing functional groups, were expected to have an enhanced performance. However, the best response for ethanol was observed after the films were reduced for one hour. The difference between the theoretical and experimental results can be explained by a balance between favorable electronic properties and favorable binding sites, as the additional oxygen moieties act not only as preferential binding sites but also as electron-withdrawing groups, resulting in a relatively noisy sensor signal and thus decreased sensor performance. Upon carbon reduction, partial sp2 character of the material is restored and, while a sensing response is still observed, sensitivity is significantly decreased. During the reduction of graphene oxide, topological defects and vacancies are created, albeit with kinetic considerations as reduction for longer periods allows for diffusion and coalescence of the defects to restructure into more stable configurations.57 The increase in the conductivity after four minutes of reduction, despite little to no change observed in the surface functionalization, indicates that structural changes do occur. Based on the theoretical results, which show the most favorable adsorption at point defects, the strong sensing performance observed for the CGO thin films reduced for one hour is attributed to binding at such vacancies. Using a tight-binding molecular dynamics (TBMD) simulation, two neighboring single vacancies have been previously shown to form a double vacancy (C2), also called a 5-8-5 defect, and further work showed these defects are more stable on curved surfaces.57,58 The curved ridges and valleys of the CGO particles can act as a collection site for such defects, as the material being reduced effectively minimizes the defect energy. Of note, this also shows that the most reduced form of the material may not necessarily have the best performance, and thus the synthesis process must be optimized to determine the best response for different VOCs. For a molecule with stronger binding affinity or charge transfer potential, the favorable electronic properties may not be necessary to see a robust response. The role of reduction time on the sensing performance for different classes of compounds should be explored moving forward, as this may offer the opportunity to use the same material, processed for different amounts of time, in an array-type configuration.The AIMD simulations further underscore the role of CGO morphology with regard to sensing performance. Experimental results demonstrate that CGO thin films have relatively larger surface area compared to their flat counterparts, which increases the overall potential number of interactions between the surface and the target analytes. Additionally, AIMD simulations highlight how the valleys of the crumpled structure are especially important for physisorption processes driven by vdW forces, for which DFT calculations showed contributions between 45 and 99% of the adsorption energy for ethanol. Further, these valleys likely contain stable point defects that act as preferential binding sites for ethanol molecules. Thus when compared to other engineered carbon nanomaterial counterparts such as fullerenes and carbon nanotubes, whose convex (exposed) surfaces offer comparatively reduced interaction(s) with similar, target analytes, the CGO sensing advantage becomes clear.
4 Conclusions
In this work, highly-oxidized CGO synthesis was demonstrated using a oxidized GO starting material, rather than relying on the furnace temperature during synthesis to control surface derivatization. GO functionalization and morphology were explored to determine their role(s) in gas sensing performance. While theoretical calculations indicate that oxygen-containing functional groups act as favorable binding sites for ethanol, a large number of oxygen-containing functional groups limit the application of the material as a chemiresistive gas sensor due to diminished electronic properties (compared to ethanol sensing signal). In contrast, point defects were shown to be thermodynamically stable adsorption sites for ethanol molecules that do not have the same deleterious effects with regard to electronic structure (compared with oxygen functionality). In addition, the morphology of the material was shown to be a critical variable. Valley topology, inherent to CGO, enhances the surface area and analyte vdW interactions, while likely stabilizing point defects. Based on these results, the role of both functional groups and morphology are clearly intertwined and should be further explored in conjunction for other classes volatile organic compounds.In addition to surface tunability, CGO is an attractive material with regard to scale-up synthesis and ease of incorporation into sensing devices. Aggregation-resistance, conferred by the crumpled morphology, enables wet chemical deposition and processing strategies for thin films. In contrast, application of isolated and/or single sheet flat graphene oxide typically requires advanced processing due to aggregation tendencies (i.e. stacking), increasing fabrication costs and variability between devices. It is also notable that the reduction process used in this work is below back-end-of-line thermal budgets for semiconductor manufacturing.38 When taken together, new mechanistic insight (and approach) in this work will inform rational design and application of CGO for a range of possible sensing devices.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the US National Science Foundation’s CAREER Award (CBET 1454656). The authors also thank McDonnell Academy Global Energy and Environment Partnership (MAGEEP), Washington University in St. Louis for Haddad's funding support. Electron microscopy work was performed at the Nano Research Facility (NRF) at Washington University in St. Louis, a member of the National Nanotechnology Infrastructure Network (NNIN), supported by the National Science Foundation under Grant No. ECS-0335765.References
- R. A. Potyrailo, Chem. Rev., 2016, 116, 11877–11923 CrossRef CAS PubMed.
- U. Tisch and H. Haick, MRS Bull., 2010, 35, 797–803 CrossRef CAS.
- J. J. Lavigne and E. V. Anslyn, Angew. Chem., Int. Ed., 2001, 40, 3118–3130 CrossRef CAS PubMed.
- E. H. Oh, H. S. Song and T. H. Park, Enzyme Microb. Technol., 2011, 48, 427–437 CrossRef CAS PubMed.
- F. Yin, W. Yue, Y. Li, S. Gao, C. Zhang, H. Kan, H. Niu, W. Wang and Y. Guo, Carbon, 2021, 180, 274–297 CrossRef CAS.
- T. Wang, D. Huang, Z. Yang, S. Xu, G. He, X. Li, N. Hu, G. Yin, D. He and L. Zhang, Nano-Micro Lett., 2016, 8, 95–119 CrossRef PubMed.
- J. Kong, N. R. Franklin, C. Zhou, M. G. Chapline, S. Peng, K. Cho and H. Dai, Science, 2000, 287, 622 CrossRef CAS PubMed.
- J. A. Robinson, E. S. Snow, Ş. C. Bădescu, T. L. Reinecke and F. K. Perkins, Nano Lett., 2006, 6, 1747–1751 CrossRef CAS PubMed.
- N. Govind, J. Andzelm and A. Maiti, IEEE Sens. J., 2008, 8, 837–841 CAS.
- A. Salehi-Khojin, F. Khalili-Araghi, M. A. Kuroda, K. Y. Lin, J.-P. Leburton and R. I. Masel, ACS Nano, 2011, 5, 153–158 CrossRef CAS PubMed.
- F. Schedin, A. K. Geim, S. V. Morozov, E. W. Hill, P. Blake, M. I. Katsnelson and K. S. Novoselov, Nat. Mater., 2007, 6, 652–655 CrossRef CAS PubMed.
- J. Cooper, M. Myers, E. Chow, L. Hubble, J. Cairney, B. Pejcic, K.-H. Müller, L. Wieczorek and B. Raguse, J. Nanopart. Res., 2013, 16, 1–13 Search PubMed.
- A. Salehi-Khojin, D. Estrada, K. Y. Lin, M.-H. Bae, F. Xiong, E. Pop and R. I. Masel, Adv. Mater., 2012, 24, 53–57 CrossRef CAS.
- F. Yavari, Z. Chen, A. V. Thomas, W. Ren, H.-M. Cheng and N. Koratkar, Sci. Rep., 2011, 1, 166 CrossRef PubMed.
- C. Li, D. Zhang, X. Liu, S. Han, T. Tang, J. Han and C. Zhou, Appl. Phys. Lett., 2003, 82, 1613 CrossRef CAS.
- S. J. Rowley-Neale, E. P. Randviir, A. S. Abo Dena and C. E. Banks, Appl. Mater. Today, 2018, 10, 218–226 CrossRef.
- J. T. Robinson, F. K. Perkins, E. S. Snow, Z. Wei and P. E. Sheehan, Nano Lett., 2008, 8, 3137–3140 CrossRef CAS PubMed.
- D. Zhang, J. Liu, H. Chang, A. Liu and B. Xia, RSC Adv., 2015, 5, 18666–18672 RSC.
- W. Yuan, A. Liu, L. Huang, C. Li and G. Shi, Adv. Mater., 2013, 25, 766–771 CrossRef CAS.
- S. Cui, H. Pu, E. C. Mattson, Z. Wen, J. Chang, Y. Hou, C. J. Hirschmugl and J. Chen, Anal. Chem., 2014, 86, 7516–7522 CrossRef CAS.
- Y. R. Choi, Y.-G. Yoon, K. S. Choi, J. H. Kang, Y.-S. Shim, Y. H. Kim, H. J. Chang, J.-H. Lee, C. R. Park, S. Y. Kim and H. W. Jang, Carbon, 2015, 91, 178–187 CrossRef CAS.
- L. Guo, H.-B. Jiang, R.-Q. Shao, Y.-L. Zhang, S.-Y. Xie, J.-N. Wang, X.-B. Li, F. Jiang, Q.-D. Chen, T. Zhang and H.-B. Sun, Carbon, 2012, 50, 1667–1673 CrossRef CAS.
- T. H. Han, Y.-K. Huang, A. T. L. Tan, V. P. Dravid and J. Huang, J. Am. Chem. Soc., 2011, 133, 15264–15267 CrossRef CAS PubMed.
- Z. Chen, J. Wang, N. Cao, Y. Wang, H. Li, N. F. d. Rooij, A. Umar, Y. Feng, P. J. French and G. Zhou, ACS Appl. Nano Mater., 2021, 4, 13234–13245 CrossRef CAS.
- J. Luo, H. D. Jang, T. Sun, L. Xiao, Z. He, A. P. Katsoulidis, M. G. Kanatzidis, J. M. Gibson and J. Huang, ACS Nano, 2011, 5, 8943–8949 CrossRef CAS.
- S. W. Cranford and M. J. Buehler, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 205451 CrossRef.
- W.-N. Wang, Y. Jiang and P. Biswas, J. Phys. Chem. Lett., 2012, 3, 3228–3233 CrossRef CAS PubMed.
- W.-N. Wang and X. He, Aerosols: Science and Engineering, 2022, p. 43 Search PubMed.
- P. Biswas and G. Yablonsky, Aerosols: Science and Engineering, Walter de Gruyter GmbH & Co KG, 2022 Search PubMed.
- Y. Jiang, R. Raliya, J. D. Fortner and P. Biswas, Environ. Sci. Technol., 2016, 50, 6964–6973 CrossRef CAS PubMed.
- Y. Jiang, W.-N. Wang, P. Biswas and J. D. Fortner, ACS Appl. Mater. Interfaces, 2014, 6, 11766–11774 CrossRef CAS.
- S. An, Q. Zeng, W. Li and J. Fortner, J. Colloid Interface Sci., 2021, 588, 725–736 CrossRef CAS PubMed.
- Z. Chen, J. Wang, A. Umar, Y. Wang, H. Li and G. Zhou, ACS Appl. Mater. Interfaces, 2017, 9, 11819–11827 CrossRef CAS.
- R. Kim, J. S. Jang, D. H. Kim, J. Y. Kang, H. J. Cho, Y. J. Jeong and I. D. Kim, Adv. Funct. Mater., 2019, 29, 1903128 CrossRef.
- Z. Yang, H. Zou, Y. Zhang, F. Liu, J. Wang, S. Lv, L. Jiang, C. Wang, X. Yan and P. Sun, Adv. Funct. Mater., 2022, 32, 2108959 CrossRef CAS.
- W. S. Hummers and R. E. Offeman, J. Am. Chem. Soc., 1958, 80, 1339 CrossRef CAS.
- D. C. Marcano, D. V. Kosynkin, J. M. Berlin, A. Sinitskii, Z. Sun, A. Slesarev, L. B. Alemany, W. Lu and J. M. Tour, ACS Nano, 2010, 4, 4806–4814 CrossRef CAS PubMed.
- C. D. Zangmeister, Chem. Mater., 2010, 22, 5625–5629 CrossRef CAS.
- A. A. Abokifa, K. Haddad, J. Fortner, C. S. Lo and P. Biswas, J. Mater. Chem. A, 2018, 6, 2053–2066 RSC.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953 CrossRef.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS PubMed.
- S. Kavadiya, R. Raliya, M. Schrock and P. Biswas, J. Nanopart. Res., 2017, 19, 43 CrossRef.
- A. Ganguly, S. Sharma, P. Papakonstantinou and J. Hamilton, J. Phys. Chem. C, 2011, 115, 17009–17019 CrossRef CAS.
- S. Khan, L. Lorenzelli and R. S. Dahiya, IEEE Sens. J., 2015, 15, 3164–3185 Search PubMed.
- S. Stankovich, D. A. Dikin, R. D. Piner, K. A. Kohlhaas, A. Kleinhammes, Y. Jia, Y. Wu, S. T. Nguyen and R. S. Ruoff, Carbon, 2007, 45, 1558–1565 CrossRef CAS.
- S. Yumitori, J. Mater. Sci., 2000, 35, 139–146 CrossRef CAS.
- A. C. Ferrari and J. Robertson, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 61, 14095 CrossRef CAS.
- I. K. Moon, J. Lee, R. S. Ruoff and H. Lee, Nat. Commun., 2010, 1, 73 CrossRef PubMed.
- T. M. G. Mohiuddin, A. Lombardo, R. R. Nair, A. Bonetti, G. Savini, R. Jalil, N. Bonini, D. M. Basko, C. Galiotis, N. Marzari, K. S. Novoselov, A. K. Geim and A. C. Ferrari, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 205433 CrossRef.
- S. D. M. Brown, A. Jorio, P. Corio, M. S. Dresselhaus, G. Dresselhaus, R. Saito and K. Kneipp, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 155414 CrossRef.
- A. Kaniyoor and S. Ramaprabhu, AIP Adv., 2012, 2, 032183 CrossRef.
- J. Klimeš and A. Michaelides, J. Chem. Phys., 2012, 137, 120901 CrossRef PubMed.
- G.-D. Lee, C. Wang, E. Yoon, N.-M. Hwang, D.-Y. Kim and K. Ho, Phys. Rev. Lett., 2005, 95, 205501 CrossRef PubMed.
- K. N. Kudin, B. Ozbas, H. C. Schniepp, R. K. Prud'homme, I. A. Aksay and R. Car, Nano Lett., 2008, 8, 36–41 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2ta06883d |
| This journal is © The Royal Society of Chemistry 2023 |