Effects of crowding on the diffusivity of membrane adhered particles
Paige
Liu
 and
Peter J.
Beltramo
and
Peter J.
Beltramo
 *
*
Department of Chemical Engineering, University of Massachusetts Amherst, Amherst, MA 01003, USA. E-mail: pbeltramo@umass.edu
First published on 28th September 2023
Abstract
The lateral diffusion of cell membrane inclusions, such as integral membrane proteins and bound receptors, drives critical biological processes, including the formation of complexes, cell–cell signaling, and membrane trafficking. These diffusive processes are complicated by how concentrated, or “crowded”, the inclusions are, which can occupy between 30–50% of the area fraction of the membrane. In this work, we elucidate the effects of increasing concentration of model membrane inclusions in a free-standing artificial cell membrane on inclusion diffusivity and the apparent viscosity of the membrane. By multiple particle tracking of fluorescent microparticles covalently tethered to the bilayer, we show the transition from expected Brownian dynamics, which accurately measure the membrane viscosity, to subdiffusive behavior with decreased diffusion coefficient as the particle area fraction increases from 1% to around 30%, approaching physiological levels of crowding. At high crowding, the onset of non-Gaussian behavior is observed. Using hydrodynamic models relating the 2D diffusion coefficient to the viscosity of a membrane, we determine the apparent viscosity of the bilayer from the particle diffusivity and show an increase in the apparent membrane viscosity with increasing particle area fraction. However, the scaling of this increase is in contrast with the behavior of monolayer inclusion diffusion and bulk suspension rheology. These results demonstrate that physiological levels of model membrane crowding nontrivially alter the dynamics and apparent viscosity of the system, which has implications for understanding membrane protein interactions and particle-membrane transport processes.
1 Introduction
Biological membranes have a critical function in nature, acting as the outer boundary of a cell, as well as the barrier that compartmentalizes organelles. The membrane backbone is the phospholipid bilayer, a pseudo two-dimensional interface which is flexible, tensionable, and fluid in nature to allow for the lateral diffusion of membrane components, including peripheral and integral membrane proteins, which can comprise up to 50% by mass (or area) of the membrane.1–3 The mobility of these inclusions is critical to many of the structure, signaling, and transport functions of the cellular membrane.4 For example, the reduced lateral diffusivity of different receptors allows for them to cross-link in order to form a signaling complex.5 Concentrated quantities of intrinsically disordered peripheral membrane proteins cause steric pressure on the membrane, allowing membrane fission to occur more readily.6,7 Membrane undulations, tension and bending rigidity both impact the behavior of and are affected by the presence of ion channels, as has been shown theoretically,3 by molecular dynamics simulations,8 and experimentally.9The crowded nature of biological cell membranes induces complex anomalous dynamics of proteins and inclusion molecules, with subdiffusion observed in experiments on living cells, experimental artificial bilayer studies, and simulations of the cell membrane. For example, fluorescence correlation spectroscopy (FCS) was used to study the diffusion of Golgi resident membrane proteins in HeLa cells, finding lower than expected diffusion coefficients and subdiffusion.10 Manzo and Garcia-Parajo11 showed, with a combination of simulations and single particle tracking measurements of the diffusion of transmembrane proteins, subdiffusion arising from temporal or spatial heterogeneity within the plasma membrane. In addition to protein inclusion crowding being a source of anomalous dynamics, bilayer interactions with the cytoskeletal environment also influence the dynamics within cell membranes. For example, clathrin interacts with specific lipids and proteins to form a clathrin coated pit to initialize endocytosis,12 and remodeling of the cortical actin network causes non-Gaussian dynamics of acetylcholine receptors.13 A combination of macromolecular crowding and transient compartmentalization/binding to the actin cytoskeleton causes anomalous dynamics of the Kv2.1 potassium ion channel.14,15 It would be of value to divorce the effects of protein crowding from native cell environments, which have complicating factors such as the cytoskeleton and immobile barriers to diffusion, in order to elucidate the effect of crowding in a simplified model membrane system.
Simulations have revealed several contributing factors underlying these anomalous membrane dynamics. For example, it was shown that, depending on protein size, subdiffusive dynamics arise as membrane crowding increases.16 Non-Gaussian behavior was observed in coarse grained and stochastic modeling of protein crowding in a DPPC lipid bilayer and attributed to spatiotemporal heterogeneity in lipid diffusion.17 Specific lipid–protein interactions also can contribute to subdiffusive translational and rotational dynamics of proteins, such as the interaction between pleckstrin homology domains and phosphatidyl–inositol phosphate lipids revealed by multiscale molecular dynamics simulations.18,19
A number of different model membrane systems have been leveraged to investigate the dynamics of membrane inclusions in order to understand the fundamental underpinnings of these biological processes, from the dilute to crowded regime. Peters and Cherry20 measured bacteriorhodopsin and lipid diffusion simultaneously in multilamellar vesicles, which was one of the first experiments to show that steric effects due to crowding were likely to alter membrane dynamics. Studies using supported lipid bilayers (SLBs) have indicated a decrease in the diffusivity of membrane inclusions with increasing crowding as well as the observation of anomalous diffusion.21–23 However, it remains unclear how crowding would impact the diffusivity of membrane inclusions in free-standing model membranes, where interactions between the substrate and the lipid bilayer would not affect inclusion diffusivity. Such systems also confer the advantage of being able to manipulate the bending rigidity and tension of the membrane. Studies in this regard have been done measuring changes in the diffusion coefficient of proteins against their concentration in GUVs, with the highest protein concentration measured to be ≈103 proteins per μm2 (less than 10% by area).24 However, physiological levels of inclusion crowding (30–50% by area), either using membrane proteins or model inclusion systems, have not been investigated in the context of a free-standing model membrane.
In the dilute limit, the diffusion of peptides and proteins reconstituted in black lipid membranes (BLMs)25 and giant unilamellar vesicles (GUVs)26 was found to be well-represented by the hydrodynamic continuum theory developed by Saffman and Delbrück,27 which gives ΛT, the translational drag coefficient, as
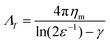 | (1) |
Colloidal particles strongly adhered to lipid bilayers via avidin coated particles binding to biotinylated lipids have been used in conjunction with eqn (1) in order to measure the viscosity of lipid bilayers in the dilute limit. Hormel et al.28 used dicolloidal probes with two 200 nm diameter lobes to measure simultaneous translational and rotational diffusion, demonstrating an increase in membrane viscosity with increasing concentrations of the vesicle tracking protein Sar1p. Later, the same group used 3 μm by 1 μm polystyrene ellipsoids to show consistent measurement of membrane viscosity between tracking membrane-anchored particles and phase-separated lipid domains.29 Collectively, these results show the utility of using avidin–biotin linkages between microparticles and membranes in order to accurately determine membrane viscosity in the dilute limit, but the impact on increasing colloidal particle area fraction on the dynamics and apparent viscosity of the membrane has not been explored.
The crowding of colloidal particles on free-standing, flexible, interface such as a phospholipid bilayer is also an interesting problem from a hydrodynamic and thin film mechanics standpoint. The rheology of bulk particle suspensions has been thoroughly investigated both in experimental and theoretical terms and has been well characterized with respect to changes in the particle volume fraction. A dilute suspension of particles is known to have a viscosity which scales against the particle volume fraction, ϕ, according to the Einstein relation 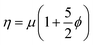 .30 As random close packing is approached, the effective viscosity of the suspension scales as 1 − (ϕ/ϕm)−2, where ϕm is the volume fraction for random close packing.31 However, an analogous scaling is not well developed for colloidal crowding at a static or flexible two-dimensional interface. At a fluid interface, inter-particle forces are complicated by the hydrodynamic contribution of the surrounding fluid,32 therefore it has been an on going challenge to determine what is dictating changes in 2D fluidity with crowding.33
.30 As random close packing is approached, the effective viscosity of the suspension scales as 1 − (ϕ/ϕm)−2, where ϕm is the volume fraction for random close packing.31 However, an analogous scaling is not well developed for colloidal crowding at a static or flexible two-dimensional interface. At a fluid interface, inter-particle forces are complicated by the hydrodynamic contribution of the surrounding fluid,32 therefore it has been an on going challenge to determine what is dictating changes in 2D fluidity with crowding.33
In a lipid monolayer system, 2D crowding was studied by controlling the area fraction of solid domains diffusing within a continuous fluid phase.34 The surface viscosity of the continuous phase was found to scale with the increasing area fraction of the solid domains in a power law relationship, and this scaling was found to be consistent with that of 3D suspensions. Investigating these scaling effects on a flexible interface where the material properties (bending rigidity, tension) of the interface can be controlled, such as in a lipid bilayer membrane, in order to understand dynamic biological processes is the goal of this and future work.
In this study, we use neutravidin functionalized microspheres tethered to a biotinylated lipid bilayer to probe the effects of increasing particle concentration on the apparent rheology of the bilayer–particle system. Particle dynamics are monitored on a large area model biomembrane (LAMB), a planar, free-standing membrane platform, affording ease of imaging for particle tracking and crowding studies. 1,2-dioleoyl-sn-glycero-3-phosphocholine (DOPC) is used as the basis for the model bilayer since it has been used in several studies of bilayer viscosity, allowing the validation of membrane viscosity in the dilute limit. We then show the impact of increasing particle crowding on membrane dynamics, revealing decreases in diffusion coefficient and subdiffusion. Finally, we relate these changes in diffusivity to changes in the apparent viscosity of the 2D system, demonstrating scaling behavior which contrasts that of bulk suspensions and monolayer interfaces.
2 Methods
2.1 Materials
The lipids DOPC and 1,2-dioleoyl-sn-glycerol-3-phosphoethanolamine-N-(cap biotinyl) (DOPE-cb) were obtained from Avanti Polar Lipids (Alabaster, AL). HPLC-grade chloroform, n-hexadecane, otadecyltrichlorosilane (OTS), sodium chloride (NaCl), sodium bicarbonate (NaHCO3), and calcium chloride (CaCl2) were purchased from Thermo Fisher Scientific (Waltham, MA). Before use, the hexadecane is filtered twice through a 0.2 μm aluminum oxide mesh (Sigma Aldrich). Fluorescent and non-fluorescent neutravidin functionalized 1 μm diameter microspheres were from Molecular Probes (Eugene, OR). All aqueous solutions were prepared using ultrapure water filtered using a reverse osmosis system from Millipore (Billerica, MA) and filtered using a 0.2 μm pore filter. The glass microfluidic “bikewheel” chip was custom fabricated by Micronit (Enschede, the Netherlands), and the sample holder was 3D printed using VeroWhite from Stratasys (Eden Prairie, MN). The chip has channels leading to a “bikewheel” with 24 spokes leading into an open aperture which is 0.9 mm in diameter and is installed in an aluminum holder leading to a capillary tube. To commission the microfluidic chip for making a bilayer, the chip is cleaned in a concentrated solution of NaOH in ethanol, then functionalized in a solution of OTS in hexadecane to make the surface slightly hydrophobic.2.2 Bilayer fabrication
Bilayers are formed on the LAMB platform as previously described.35–39 Briefly, DOPC and DOPE-cb are diluted in chloroform to form stock solutions. These stock solutions are then combined in a 7 mL scintillation vial according to a target molar composition, typically 99 to 1 DOPC to DOPE-cb. The combined solution is then dried under nitrogen to remove excess chloroform then fully dried overnight under vacuum at ≤20 millibar. The dried lipids are then resuspended in hexadecane at a concentration of 2.5 mg mL−1, and the resulting lipid–oil mixture is sonicated for at least 2 hours before use in an experiment.To form the bilayer, the microfluidic chip is first loaded with the lipid–oil mixture. The chip is then loaded into a sample holder with chambers for aqueous buffer and a temperature control system to keep the sample at 25 °C. The capillary is connected to a pressure control system (ElveFlow), which is used to control the drainage of the lipid–oil film formed in the center of the aperture and the area of the subsequent bilayer. The pressure on the chip is first increased quickly to form a thick film across the aperture, then the pressure is slowly decreased to allow the film to thin. When the film has thinned sufficiently, a lipid bilayer nucleates and then populates an area that is kept constant at around 0.5 mm2 using the pressure control system.
2.3 Particle addition and imaging
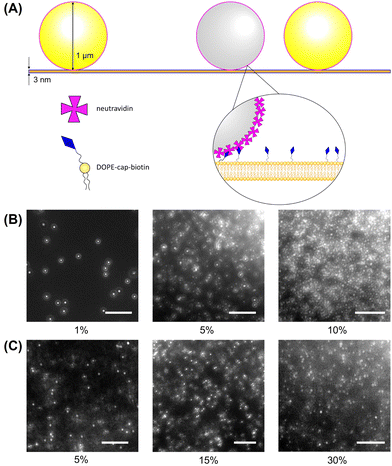
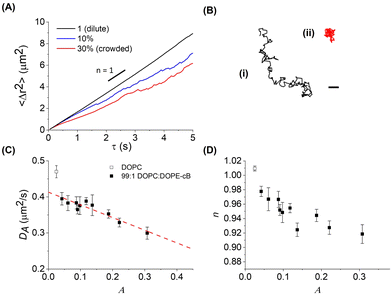
Fluorescent 1 μm diameter neutravidin functionalized latex particles, which strongly adhere to the biotinylated lipids in the bilayer, are used as probes to measure membrane fluidity (Fig. 1A). Particle crowding is controlled by the amount of particles added and allowed to settle on the bilayer, or by changing bilayer area. At higher fluorescent particle concentrations, it becomes difficult to resolve individual particles (Fig. 1B). To reduce the amount of fluorescent noise and overcome this limitation, fluorescent particles are combined with unlabeled particles which have the same surface functionalization and diameter at a 1:19 number ratio. This allows for high area fractions to be imaged without a loss in individual particle resolution (Fig. 1C). The particles are diluted from their stock suspensions and then added to the bilayer by pipetting them in 2 μL aliquots into the top chamber of the sample cell. After allowing 15–30 minutes for the particles to settle, fluorescence images of the bilayer–particle system are taken at 20 FPS under 40× zoom (Nikon Ti-2e). In a given experiment, multiple videos are taken to be analyzed, with at least 200 particles in focus for each video.2.4 Particle tracking and analysis
Particle location and tracking was done using a brightness weighted centroid algorithm.40 After initially filtering by intensity, the particle count from the particle tracking software was used to estimate a particle area fraction, A, by:| A = m × Ap | (2) |
After the particle tracks were further filtered by size and eccentricity, the mean squared displacements (MSDs) of the individual particle tracks were calculated. The individual MSDs were then averaged together to obtain an ensemble MSD. The ensemble MSD can be used to fit an anomalous diffusion descriptor, which is defined by a power law according to:
| 〈Δr2〉 = 4Dtn | (3) |
As expanded upon below, a decreasing diffusion coefficient and the appearance of subdiffusive dynamics are observed with increasing particle area fraction. We note that erroneous identification of subdiffusion has been observed in single-particle tracking experiments.41 However, robust criteria for verifying the presence of either subdiffusive, diffusive, or superdiffusive dynamics have been developed by analysis of the power spectral density of the trajectories.42 We have applied these criteria to our trajectories to validate that the observation of subdiffusion is independent of any remnant static or dynamic localization errors. Related machine learning models are also under development in order to both identify different modes of diffusion and extract further insight into the observed dynamics.43
3 Results and discussion
3.1 Determination of dilute membrane viscosity
In order to assess how the fluidity of the bilayer changes with crowding, we first use experiments in the dilute regime to benchmark measurements of membrane viscosity determined using different hydrodynamic models against literature values. We start by evaluating the efficacy of the Saffman–Delbrück model within our system.27 At dilute area fractions (A ≈ 0.01), we observe that particle trajectories on a 99/1 DOPC/DOPE-cb bilayer are unhindered, and their MSDs fit a classical Brownian model, in which the exponent of the lag time is n = 1 (Fig. 2A). The diffusion coefficient at low concentrations was found to be 0.39 μm2 s−1. Comparatively, the diffusion coefficient for a 1 μm2 s−1 latex particle in a bulk aqueous solution at the same temperature would be 0.49 μm2 s−1. As a control, we measured the diffusion of particles that had settled on the surface of a DOPC membrane with no biotinylated lipids and found that their diffusion coefficient was close to the expected diffusion coefficient of these particles in bulk, so the reduced diffusion coefficient with biotin–streptavidin linkages present indicates adhesion to the membrane. Based on an estimated inclusion radius of 100 nm, a membrane thickness of 3 nm measured in previous experiments,37 and an expected membrane viscosity of nPa s m, we expect the dimensionless parameter ε to be order 1 (see eqn (1)). In this range, the Saffman–Delbrück model is no longer strictly valid, but if applied, yields ηm = 2.2 nPa s m.
nPa s m, we expect the dimensionless parameter ε to be order 1 (see eqn (1)). In this range, the Saffman–Delbrück model is no longer strictly valid, but if applied, yields ηm = 2.2 nPa s m.
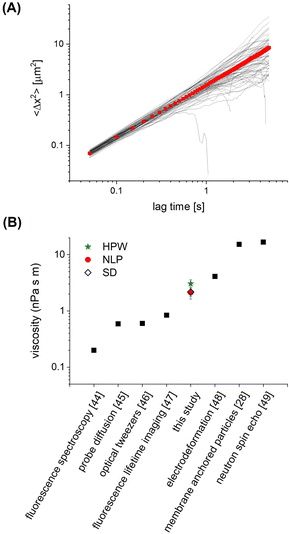 | ||
| Fig. 2 (A) Ensemble MSD (red) and individual particle tracks (grey) for dilute (A = 0.01) 1 μm diameter particles on a 99/1 DOPC/DOPE-cb bilayer. (B) The membrane viscosity calculated from the diffusion coefficient using different models compares well to the range of viscosity values found in literature for DOPC. Example viscosities shown are measured using fluorescence spectroscopy,44 probe diffusion,45 optical tweezers,46 fluorescence lifetime imaging,47 electrodeformation,48 membrane anchored particles,28 and neutron spin echo.49 | ||
Extended approaches have been developed to account for larger values of ε. By accounting for the flow field around a membrane inclusion, Hughes, Pailthorpe, and White (HPW) extended the asymptotic solutions of the SD model for arbitrary values of ε, in which the translational drag on the inclusion scales by ft ∝ ηmhε.50 Petrov et al. developed empirical solutions to the HPW hydrodynamic model which have been validated for 10−3 < ε < 103:51
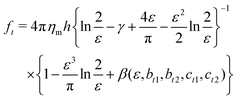 | (4) |
We additionally consider the size and protrusion effects of our probe particle against the membrane hydrodynamic length scale, lm = ηm/η, intrinsic to the SD and HPW models. From our initial dilute viscosity result, we find lm ≈ 17a. At this length scale, in which lm is not grossly greater than a, dissipation of momentum caused by the inclusion in the bulk fluid should be considered. The effect of locally induced curvature on the effective mobility of a membrane inclusion was incorporated into a model developed by Naji, Levine, and Pincus (NLP):52
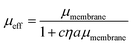 | (5) |
We validate our approach by comparing to DOPC viscosity measurements previously reported in the literature. Despite the varied assumptions and considerations in each model, all result in values for the DOPC membrane viscosity that are well within the range of DOPC bilayer viscosities reported in literature (Fig. 2B),28,44–49 with the caveat that these literature values span two orders of magnitude. Our results are most closely aligned with the viscosity of 4.11 nPa s m measured by electrodeformation of a giant unilamellar vesicle.48 Since the NLP model relaxes the inherent assumptions of the simpler models to more closely accommodate the nature of this experimental system, it will be used in the analysis of crowded membrane dynamics that follows. We note that the choice of inclusion radius in the range of 50–150 nm for our 500 nm radius particle alters the membrane viscosity by 25–30%, still well within the range determined via other methods. More important than the exact value of membrane viscosity, however, is the dependence of viscosity with crowding, which does not appreciably change with choice of inclusion radius. This is discussed in Section 3.3. In Section 3.2, we further analyze the dynamics and statistics of microparticle diffusion with increased crowding without any assumptions.
3.2 2D particle crowding effects
Over a series of experiments, particle concentrations ranging from dilute coverage (A < 0.01) to coverage approaching physiological levels of crowding (A ≈ 0.3) on a DOPC bilayer with 1 mol% biotinylated lipids were measured. As a control, experiments in the dilute regime were performed on lipid bilayers without biotinylated lipids. As the particle area fraction increases, particle diffusion becomes attenuated, as shown in Fig. 3(A) and (B). Fitting this data to eqn (3) reveals that particle tethering causes a significant decrease in diffusion coefficient, from 0.48 to 0.39 μm2 s−1, in the dilute regime. This indicates that the particles, which have over an order of magnitude smaller diffusion coefficient than the lipids (Dlipid ∼ 10 μm2 s−1) are in effect immobilizing the lipids and restricting their diffusion to the tethered region, which in turn attenuates the diffusion of the microparticle (Fig. 3C). As the particle concentration increases, the diffusion coefficient decreases to around 0.3 μm2 s−1 at high crowding (30% area fraction, Fig. 3C), with a concurrent decrease in n (Fig. 3D). The source of this subdiffusion may be due to a number of factors, which we discuss through the rest of this section.It is most straightforward to explain the decrease in diffusivity by steric effects, which are represented in the Boltzmann lattice model:
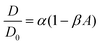 | (6) |
In bulk suspensions, it has been shown that DSS/D0 = 1 − β3Dϕ, where DSS is the short time self-diffusion coefficient, ϕ is the volume fraction of particles, and β3D is the equivalent scaling coefficient for a bulk system. Using diffusing wave spectroscopy, β3D was measured to be approximately 1.86.53 This β3D was determined to be independent of particle size53,54 and slightly lower than the theoretically predicted value of 5/2.30 From these results, it is apparent that in moving from bulk suspensions to monolayers to bilayers, the α term remains constant while β steadily decreases. In going from 3D to 2D diffusion, steric effects have a reduced impact, while when moving from monolayers to bilayers, the ability of the free-standing membrane to be flexible likely further attenuates steric interactions. We expect the particle size dependence of the particle diffusivity scaling observed in monolayers to also manifest in particles tethered to bilayers and are interested in exploring this facet in the future.
The decrease in diffusion coefficient coincides with a decrease of the exponent of the power law descriptor, n, from 1 to 0.9 at higher particle area fractions, indicating subdiffusion of particles caused by interparticle crowding (Fig. 3D). Similar anomalous diffusion behavior has been reported on SLB systems as well as in simulations.21,22,55,56 Interestingly, measurements of particle trajectories on supported bilayer systems find evidence of subdiffusion even when the membrane inclusions are dilute. We postulate that this may arise from additional interactions between the inclusion, the membrane, and the SLB substrate whereas the model membrane in this work is free-standing, causing subdiffusion to only appear at higher area fractions.
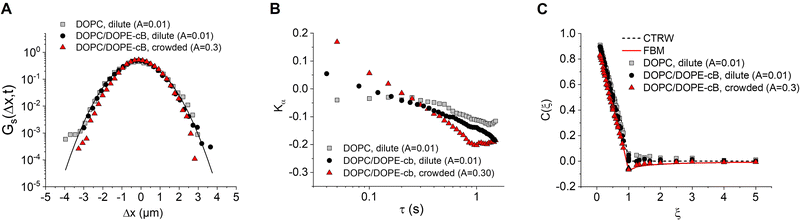
In order to understand the underlying mechanism of the observed subdiffusion, we analyze the onset of non-Gaussian behavior as crowding increases. As a first check, we compare the Van Hove self correlation function of untethered dilute particles (A = 0.01, DOPC, dilute), tethered dilute particles (A = 0.01, DOPC/DOPE-cB, dilute), and tethered crowded particles (A = 0.30, DOPC/DOPE-cB, crowded) at 800 ms lag times. The Van Hove function gives the probability that particle j will move in the vicinity r within time t:
| Gs(Δr,t) = 〈δ(r − Δrj)〉 | (7) |
If the particle displacement is expected to be Gaussian, the Van Hove function can be written as:
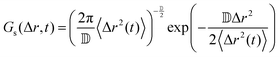 | (8) |
![[Doublestruck D]](https://www.rsc.org/images/entities/char_e167.gif) is the number of dimensions. We see that the displacement of dilute particles at 800 ms follows Gaussian behavior, but the displacements of the particles in the crowded, tethered system have a narrower distribution (Fig. 4A). Complementary to the Van Hove correlation, the excess kurtosis can be calculated as a measure of deviation from Gaussianity of the particle movement:
is the number of dimensions. We see that the displacement of dilute particles at 800 ms follows Gaussian behavior, but the displacements of the particles in the crowded, tethered system have a narrower distribution (Fig. 4A). Complementary to the Van Hove correlation, the excess kurtosis can be calculated as a measure of deviation from Gaussianity of the particle movement: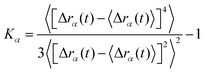 | (9) |
We find that in the three cases, the excess kurtosis becomes negative at a lag time of around 1, indicating platykurtotic behavior (Fig. 4B). The test statistic ZKα is used to determine whether or not the deviation of Kα from 0 is signficant. It is defined as ZKα = Kα/σKα, where:
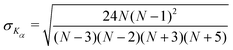 | (10) |
From this, we find that cutoff for a significantly non-zero value of Kα is −0.1. For our data, this shows that the diffusion of untethered particles remains Gaussian, as expected, but the deviation from Gaussianity for particles both in the dilute and crowded ranges is observed.
Lastly, we consider models that might be used to describe the onset of non-Gaussian, subdiffusive behavior with 2D crowding. Anomalous diffusion models have been developed to describe diffusive dynamics in the crowded cell environment. Three such models commonly applied to cell dynamics are the continuous time random walk (CTRW), the obstructed diffusion model (OD), and the fractional Langevin equation (FLE). CTRW is characterized by random jump lengths following a power law distribution and has been used to describe motion in systems such as colloidal tracers moving in an actin network.57 In contrast, FLE and its subcase, fractional Brownian motion (FBM), are self-similar processes which have been used to describe such systems as the anomalous diffusion of lipids in a cholesterol doped environment, the diffusion of membrane-binding protein domains, and subdiffusion in the cytoplasm.19,58,59 It should be noted that recent work has suggested that none of these models completely describe anomalous diffusion with respect to crowding, and a hybrid model may need to developed for a complete description.17 To see how our data fits these models, we test for the onset of anti-persistence in the particle motion as crowding increases with the velocity autocorrelation function (VACF):59
 | (11) |
We additionally consider the possibility that the lipids themselves become immobilized as biotinylated lipids in the bilayer tether to a large, slower moving particle. Therefore, the decrease in the diffusion coefficient may not simply arise out of crowding but may also be due to particle–bilayer interactions reducing phospholipid mobility within the bilayer. This idea is supported by computational studies which show that membrane proteins form a complex with the lipids surrounding them and that the lipids in this complex diffuse more slowly relative to lipids outside the immediate vicinity of the protein.60 While this phenomenon has not been studied extensively in lipid–particle systems, viscosities that are higher than would be expected in literature have been measured in a similar system utilizing a two-particle complex as a probe to measure membrane viscosity, which indicates deformation of the membrane and/or immobilization of lipids surrounding those directly adhered to a probe may be affecting the overall membrane viscosity.28 However, such an effect should impact all experiments, regardless of area fraction.
3.3 Scaling of effective viscosity with crowding
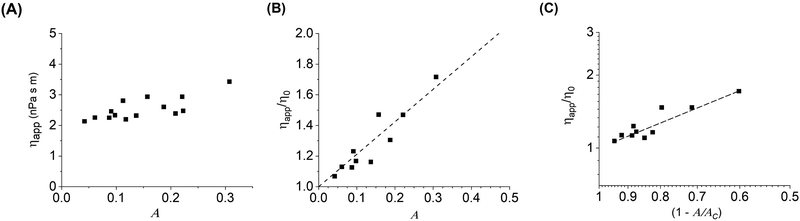
The inclusion crowding and decrease in diffusion coefficient affect the apparent rheology of the membrane–particle system. The bilayer viscosity for the different diffusion coefficients measured with increasing particle coverage is calculated using the NLP model (Fig. 5(A) and (B)). The viscosity of the bilayer increases significantly with increasing particle area fraction, going from 2 to 3.5 nPa s m.As mentioned earlier, in a bulk 3D suspension of hard spheres in a viscous fluid, it has been shown that the suspension viscosity scales quadratically with volume fraction.31 Analogous behavior was also observed in a monolayer system of highly viscous domains diffusing in a continuous low viscosity matrix, where the viscosity of the entire monolayer system increased as a power law,34ηs/ηso = [1 − A/Ac]−2.07, where ηs is the measured shear viscosity of the system, ηso is the shear viscosity of the continuous lipid matrix, and Ac is the critical inclusion area fraction analogous to the sphere volume fraction at random close packing ϕc. Thus, the viscosity in both bulk colloidal suspensions and phospholipid monolayers scales, within experimental error, with a power law exponent of 2.
Fig. 5C tests this behavior for spheres diffusing on a 2D membrane. We find a linear scaling between the particle area fraction and their diffusion coefficient of 1.07, which is around a factor of 2 lower than the scaling observed in the bulk suspension and monolayer systems. It is possible that particles tethered to membranes are interacting with each other less strongly than in the other systems, causing ηapp to increase more slowly with increasing concentration and is consistent with the decrease in diffusion coefficient. In addition, differences in the intrinsic viscosities of the different systems may be a factor in the scaling differences. In the 2D monolayer system, the continuous phase viscosity, ηso, was determined to be 0.16 μPa s m, which is three orders of magnitude larger than the viscosity measured in the dilute case for DOPC and indeed much larger than bilayer viscosities reported in literature. Although we have examined a wide range of area fractions and have approximated biological levels of crowding, we are interesting in pursuing these results to higher concentrations, which are more readily accessible in the monolayer and bulk suspension case, in order to probe the limits of the observed scaling and any deviations. In addition, synthetic techniques to control microparticle surface chemistry and strength of interaction with bilayer membranes,61 or the addition of depletant molecules to the aqueous phase62 may be applied in the future to manipulate particle–particle interactions and particle–bilayer interactions to study their effects on membrane dynamics.
4 Conclusions
Neutravidin coated particles strongly bound to biotinylated lipids in a bilayer were used as probes to interrogate changes in diffusion dynamics and apparent membrane viscosity as the particle crowding increased. While the membrane viscosity determined using the NLP hydrodynamic model agreed with alternative approaches in the dilute regime, the flexible nature of the bilayer interface contributes to important contrasts to monolayer and bulk systems in crowded environments. As the particles became highly crowded, subdiffusion and non-Gaussian dynamics were observed. Both the scaling in diffusion coefficient and membrane viscosity point towards a decrease in steric effects in the bilayer system. This may have important biological ramifications and explain how membranes are able to maintain their fluidity despite being decorated with high concentrations of integral and peripheral membrane proteins. Careful manipulation of both the membrane biophysical properties through lipid chemistry and inclusion size in the future is expected to further elucidate the nontrivial interplay between lipids and the dynamics of membrane-bound objects.Author contributions
PJB conceptualized and acquired funding for the study. PL and PJB designed the experiments. PL performed the experiments and analyzed the data. PL and PJB discussed the findings and wrote the manuscript.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
The authors would like to thank the University of Massachusetts Institute for Applied Life Sciences Advanced Digital Design and Fabrication facility as well as Gary Czupkiewicz for help with the fabrication of sample cells used in this work. Funding for this research was provided by the National Science Foundation under award no. CBET-1942581.Notes and references
- F. Höfling and T. Franosch, Rep. Prog. Phys., 2013, 76, 046602 CrossRef PubMed
.
- B. Alberts, A. Johnson, J. Lewis, M. Raff and K. Roberts, 2007.
- M. Lindén, P. Sens and R. Phillips, PLoS Comput. Biol., 2012, 8(3), e1002431 CrossRef
.
- M. Löwe, M. Kalacheva, A. J. Boersma and A. Kedrov, FEBS J., 2020, 287, 5039–5067 CrossRef PubMed
.
- R. Irannejad and M. von Zastrow, Curr. Opin. Cell Biol., 2014, 27, 109–116 CrossRef CAS PubMed
.
- W. T. Snead, C. C. Hayden, A. K. Gadok, C. Zhao, E. M. Lafer, P. Rangamani and J. C. Stachowiak, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, E3258–E3267 CrossRef CAS PubMed
.
- W. T. Snead and J. C. Stachowiak, J. Mol. Biol., 2018, 430, 2293 CrossRef CAS
.
- A. L. Duncan, T. Reddy, H. Koldsø, J. Hélie, P. W. Fowler, M. Chavent and M. S. Sansom, Sci. Rep., 2017, 7, 1–15 CrossRef CAS PubMed
.
- E. Perozo, A. Kloda, D. M. Cortes and B. Martinac, Nat. Struct. Biol., 2002, 9, 696–703 CrossRef CAS PubMed
.
- M. Weiss, H. Hashimoto and T. Nilsson, Biophys. J., 2003, 84, 4043–4052 CrossRef CAS PubMed
.
- C. Manzo and M. F. Garcia-Parajo, Rep. Prog. Phys., 2015, 5(1), 011021 Search PubMed
.
- A. V. Weigel, M. M. Tamkun and D. Krapf, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, E4591–E4600 CrossRef CAS PubMed
.
- W. He, H. Song, Y. Su, L. Geng, B. J. Ackerson, H. B. Peng and P. Tong, Nat. Commun., 2016, 7, 1–8 Search PubMed
.
- A. V. Weigel, B. Simon, M. M. Tamkun and D. Krapf, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 6438–6443 CrossRef CAS PubMed
.
- S. Sadegh, J. L. Higgins, P. C. Mannion, M. M. Tamkun and D. Krapf, Phys. Rev. X, 2017, 7, 011031 Search PubMed
.
- M. Javanainen, H. Martinez-Seara, R. Metzler and I. Vattulainen, J. Phys. Chem. Lett., 2017, 8, 4308–4313 CrossRef CAS
.
- J. H. Jeon, M. Javanainen, H. Martinez-Seara, R. Metzler and I. Vattulainen, Phys. Rev. X, 2016, 6, 021006 Search PubMed
.
- E. Yamamoto, A. C. Kalli, T. Akimoto, K. Yasuoka and M. S. Sansom, Sci. Rep., 2015, 5, 1–12 Search PubMed
.
- E. Yamamoto, T. Akimoto, A. C. Kalli, K. Yasuoka and M. S. Sansom, Sci. Adv., 2017, 3(1), e1601871 CrossRef PubMed
.
- R. Peters and R. J. Cherry, Proc. Natl. Acad. Sci. U. S. A., 1982, 79(14), 4317–4321 CrossRef CAS PubMed
.
- H. L. Coker, M. R. Cheetham, D. R. Kattnig, Y. J. Wang, S. Garcia-Manyes and M. I. Wallace, Biophys. J., 2019, 116, 1085–1094 CrossRef CAS PubMed
.
- M. R. Horton, F. Höfling, J. O. Rädler and T. Franosch, Soft Matter, 2010, 6, 2648–2656 RSC
.
- J. R. Houser, D. J. Busch, D. R. Bell, B. Li, P. Ren and J. C. Stachowiak, Soft Matter, 2016, 12, 2127–2134 RSC
.
- S. Ramadurai, A. Holt, V. Krasnikov, G. V. D. Bogaart, J. A. Killian and B. Poolman, J. Am. Chem. Soc., 2009, 131, 12650–12656 CrossRef CAS PubMed
.
- C. C. Lee and N. O. Petersen, Biophys. J., 2003, 84, 1756–1764 CrossRef CAS PubMed
.
- K. Weiß, A. Neef, Q. Van, S. Kramer, I. Gregor and J. Enderlein, Biophys. J., 2013, 105, 455–462 CrossRef PubMed
.
- P. Saffman and M. Delbruck, Proc. Natl. Acad. Sci. U. S. A., 1975, 72, 3111–3113 CrossRef CAS PubMed
.
- T. T. Hormel, S. Q. Kurihara, M. K. Brennan, M. C. Wozniak and R. Parthasarathy, Phys. Rev. Lett., 2014, 112, 1–5 CrossRef PubMed
.
- P. E. Jahl and R. Parthasarathy, Biophys. J., 2021, 120, 5513–5520 CrossRef CAS PubMed
.
-
W. B. Russel, D. A. Saville and W. R. Schowalter, Colloidal Dispersions, Cambridge University Press, 1989 Search PubMed
.
- J. F. Brady, J. Chem. Phys., 1993, 99, 567–581 CrossRef CAS
.
-
P. Kralchevsky and K. Nagayama, Particles at Fluid Interfaces and Membranes, Elsevier Science, 1st edn, 2001 Search PubMed
.
- Y. Peng, W. Chen, T. M. Fischer, D. A. Weitz and P. Tong, J. Fluid Mech., 2009, 618, 243–261 CrossRef CAS
.
- A. K. Sachan, S. Q. Choi, K. H. Kim, Q. Tang, L. Hwang, K. Y. Lee, T. M. Squires and J. A. Zasadzinski, Soft Matter, 2017, 13, 1481–1492 RSC
.
- P. J. Beltramo, R. V. Hooghten and J. Vermant, Soft Matter, 2016, 12, 4324–4331 RSC
.
- P. J. Beltramo, L. Scheidegger and J. Vermant, Langmuir, 2018, 34, 5880–5888 CrossRef CAS PubMed
.
- P. Liu, O. Zabala-Ferrera and P. J. Beltramo, Biophys. J., 2021, 120, 1755–1764 CrossRef CAS PubMed
.
- L. Scheidegger, L. Stricker, P. J. Beltramo and J. Vermant, J. Phys. Chem. B, 2022, 126, 5842–5854 CrossRef CAS PubMed
.
- O. Zabala-Ferrera, P. Liu and P. J. Beltramo, Membranes, 2023, 13, 129 CrossRef CAS PubMed
.
- J. C. Crocker and D. G. Grier, J. Colloid Interface Sci., 1996, 179, 298–310 CrossRef CAS
.
- D. S. Martin, M. B. Forstner and J. A. Käs, Biophys. J., 2002, 83, 2109–2117 CrossRef CAS PubMed
.
- V. Sposini, D. Krapf, E. Marinari, R. Sunyer, F. Ritort, F. Taheri, C. Selhuber-Unkel, R. Benelli, M. Weiss, R. Metzler and G. Oshanin, Commun. Phys., 2022, 5, 1–10 CrossRef
.
- H. Seckler and R. Metzler, Nat. Commun., 2022, 13, 1–13 Search PubMed
.
- Y. Nojima and K. Iwata, J. Phys. Chem. B, 2014, 118, 8631–8641 CrossRef CAS PubMed
.
- C. Herold, P. Schwille and E. P. Petrov, Phys. Rev. Lett., 2010, 104(14), 148102 CrossRef CAS PubMed
.
- G. J. Amador, D. van Dijk, R. Kieffer, M.-E. Aubin-Tam and D. Tam, Proc. Natl. Acad. Sci. U. S. A., 2021, 118(21), e2100156118 CrossRef CAS PubMed
.
- Y. Wu, M. Stefl, A. Olzynska, M. Hof, G. Yahioglu, P. Yip, D. R. Casey, O. Ces, J. Humpolickova and M. K. Kuimova, Molecular rheometry: direct determination of viscosity in Lo and Ld lipid phases via fluorescence lifetime imaging, Phys. Chem. Chem. Phys., 2013, 15, 14986–14993 RSC
.
- H. A. Faizi, R. Dimova and P. M. Vlahovska, Biophys. J., 2022, 121, 910–918 CrossRef CAS PubMed
.
- S. Chakraborty, M. Doktorova, T. R. Molugu, F. A. Heberle, H. L. Scott, B. Dzikovski, M. Nagao, L.-R. Stingaciu, R. F. Standaert, F. N. Barrera, J. Katsaras, G. Khelashvili, M. F. Brown and R. Ashkar, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 21896–21905 CrossRef CAS PubMed
.
- B. D. Hughes, B. A. Pailthorpe and L. R. White, J. Fluid Mech., 1981, 110, 349–372 CrossRef CAS
.
- E. P. Petrov, R. Petrosyan and P. Schwille, Soft Matter, 2012, 8, 7552–7555 RSC
.
- A. Naji, A. J. Levine and P. A. Pincus, Biophys. J., 2007, 93, 49–51 CrossRef PubMed
.
- X. Qiu, X. L. Wu, J. Z. Xue, D. J. Pine, D. A. Weitz and P. M. Chaikin, Phys. Rev. Lett., 1990, 65, 516–519 CrossRef CAS PubMed
.
- W. van Megen, S. M. Underwood, R. H. Ottewill, N. J. S. Williams and P. N. Pusey, Faraday Discuss. Chem. Soc., 1987, 83, 47–57 RSC
.
- F. Hofling and T. Franosch, Rep. Prog. Phys., 2013, 76, 50 CrossRef
.
- M. J. Saxton, Biophys. J., 1994, 66, 394–401 CrossRef CAS PubMed
.
- I. Y. Wong, M. L. Gardel, D. R. Reichman, E. R. Weeks, M. T. Valentine, A. R. Bausch and D. A. Weitz, Phys. Rev. Lett., 2004, 92, 30–33 CrossRef
.
- J. Hyung Jeon, H. M. Seara Monne, M. Javanainen and R. Metzler, Phys. Rev. Lett., 2012, 109, 188103 CrossRef PubMed
.
- K. Speckner and M. Weiss, Entropy, 2021, 23, 892 CrossRef PubMed
.
- P. S. Niemelä, M. S. Miettinen, L. Monticelli, H. Hammaren, P. Bjelkmar, T. Murtola, E. Lindahl and I. Vattulainen, J. Am. Chem. Soc., 2010, 132, 7574–7575 CrossRef
.
- C. V. D. Wel, N. Bossert, Q. J. Mank, M. G. Winter, D. Heinrich and D. J. Kraft, Langmuir, 2017, 33, 9803–9810 CrossRef PubMed
.
- H. T. Spanke, J. Agudo-Canalejo, D. Tran, R. W. Style and E. R. Dufresne, Phys. Rev. Res., 2022, 4, 023080 CrossRef CAS
.
| This journal is © The Royal Society of Chemistry 2023 |

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
: