A geometric probabilistic approach to random packing of hard disks in a plane

Abstract

In this paper, the random packing fraction of hard disks in a plane is analyzed, following a geometric probabilistic approach. First, the random close packing (RCP) of equally sized disks is modelled. Subsequently, following the same methodology, a simple, statistical geometric model is proposed for the random loose packing (RLP) of monodisperse disks. This very basic derivation of RLP leads to a packing value (≈0.66) that is in very good agreement with values that have been obtained previously for 2D disk packings. The present geometrical model also enables a closed-form expression for the contact (coordination) number as a function of the packing density at different states of compaction. These predictions are thoroughly compared with empirical and simulation results, among others the Rényi parking model, yielding good agreement.

---

1. Introduction

The packing of hard disks is of interest in mathematics and physics. In the mathematical branch it is generally known as “circles packing”. In physics the packing of spheres in a plane, which is equivalent to that of circles in a plane, is studied as an introduction to 3-dimensional (3D) problems. Furthermore, the packing of disks and spheres in a plane has been used to model the structure of monolayer films, the adsorption on substrates, and the organization of cells.^1–3

For ordered/regular packings in the 2-dimensional (2D) Euclidean plane, Lagrange proved in 1773 that the highest-density lattice packing of circles is the hexagonal arrangement, in which the centers of the circles are arranged in a triangular lattice, and each circle is surrounded by 6 other circles (Fig. 1a), packing fraction φ_tri = π/2√3 ≈ 0.907. This packing was proved to be the densest disk packing in the plane, so optimal among all packings, not just lattice packings, by Thue in 1910,^4,5 although some consider Thue's proof flawed.² Fejes Tóth published rigorous proof that this triangular packing has optimal packing indeed.^2,6 In Fig. 1(b) also the honeycomb hexagonal lattice is shown, which can be seen as a union of two offset triangular lattices, with packing fraction φ_hon = π/3√3 ≈ 0.605.

Fig. 1 Hexagonal disk lattices, (a) triangular and (b) honeycomb.

Randomly, or jammed, close packed disks in 2D were first studied 60 years ago,⁷ where a random packing fraction of 0.89 φ_tri (≈0.807) was measured. Later, experimental, modelling and simulation studies yielded φ_rcp ≈ 0.82–0.89.^7–26 Higher packing fractions, φ_rcp ≈ 0.88–0.89, were found by Shahinpoor¹⁶ and Zaccone,²⁶ the latter's result leading to scientific debate.²⁶ Random loose packing (RLP) fraction studies have resulted in φ_rlp ≈ 0.66–0.84.^{3,12,19,24,27–30} The lowest of these packing fraction values was reported recently.^29,30

In this paper, the random close packing (RCP) and random loose packing fraction (RLP) of hard disks are analyzed, following a geometric probabilistic approach. Statistical geometry (or integral geometry) can be traced back to the three problems formulated in the 18th century by George-Louis Leclerc, better known as Comte de Buffon. These three mathematical games of chances were the clean tile problem, the needle problem and the grid problem.^31,32

Here, in Section 2 first a geometric probabilistic model for the RCP is presented, an approach also followed in ref. 10. Next, in Section 3 a new model is put forward for RLP. Subsequently, in Section 4 the statistical models are used to obtain closed-form expressions between packing fraction and number of contacts (coordination number). In Section 5 the classic Rényi probability theory of car parking^33–35 is applied to assess and confirm the obtained RCP and RLP contact numbers. The conclusions are collected in Section 6.

For convenience, in this paper the diameter of the congruent disks (circles) is set to unity, so that the disk area is π/4 and the circumference is π.

2. Random close packing

The packing of RCP has been studied experimentally, numerically and using analytical, relatively simple, models based on statistical geometry.^3,7–26 In ref. 3, a packing fraction of 0.824 for maximum random jammed (MRJ) disks was numerically generated, whereby the MRJ state can be thought of as the “most random” state of packing.

For RCP, the method used is very similar to that reported in ref. 10 and 20, which considered a unit cell formed by 4 disks, the centers of the 4 disks forming a parallelogram, α being the angle between neighbor disks (Fig. 2), the enclosed disk area A_d being π/4. For RCP, with α = π/3, locally a triangular domain is obtained, considered as the densest possible packing configuration, and with α = π/2 a square lattice, with φ_sq = π/4 (≈0.785).

Fig. 2 Schematic representation of the RCP unit.

The area of the parallelogram reads

A_t = sin α (1)

And the packing fraction φ follows as

Assuming a uniform probability density for the angle α between π/3 and π/2, the RCP density follows from eqn (1) and (2) as

yielding φ_rcp ≈ 0.824.

This value is in accordance with the majority of measured and modeled results.^{1,3,7–15,17–25} This confirms that the statistical approach of the considered unit, with α uniformly distributed from π/3 to π/2, is a representative of RCP. For α = π/3 and α = π/2, the ordered triangular and the square lattice domains, respectively, are obtained locally, and all other α values account for the disordered random nature.

An alternative and even more straightforward approach is based on the area pertaining to the mean angle α.²⁰ Using the arithmetic mean of α = π/3 and α = π/2, [small alpha, Greek, macron] = 5π/12, eqn (1) yields Ā_t = 0.483, and hence eqn (2)φ_rcp ≈ 0.813. Also, this value is close to the aforesaid values.

3. Random loose packing

By introducing order³ or friction,^29,30,36,37 a jammed random packing can be generated with lower packing fractions (and coordination numbers). Also, unjammed or glass-like packings have a lower packing fraction. This lower random packing limit was explored in ref. 12, 19, 24, and 27–30. Recently, from numerical simulations, Pica Ciamarra and Coniglio²⁹ estimated φ_rlp = 0.675, Jin et al.³⁰ estimated φ_rlp = 0.67, and Atkinson et al.³ mapped φ_rlp = 0.66 as the lowest jammed packing fraction.

As ansatz for a statistical approach of RLP, a unit cell of a quadrangle formed by 4 disks is proposed (Fig. 3), the assembly forming a trilateral trapezoid (or isosceles trapezoid). The assembly is governed by the angle α, π/2 ≤ α ≤ 2π/3. From elementary geometric considerations, it follows that

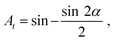and that the disk area A_d of the 4 disks in the quadrangle is again π/4.

Fig. 3 Schematic representation of the RLP unit.

When α is 2π/3, the presented RLP unit allows for a local honeycomb domain, and for α being π/2, a square lattice, similar to the presented RCP unit (Fig. 2). Assuming a uniform probability density for the angle α between π/2 and 2π/3, the RLP density follows from eqn (2) and (4) as

yielding φ_rlp ≈ 0.662. This value is in the range of computer modeled values, viz. 0.66–0.675.^3,29,30

For completeness, also the RLP fraction is computed based on the arithmetic mean of α = π/2 and α = 2π/3, [small alpha, Greek, macron] = 7π/12, i.e. again following the approach by Williams.²⁰Eqn (4) yields Ā_t ≈ 1.216, and hence from eqn (2) it follows that φ_rlp ≈ 0.646.

In other words, whichever method followed, a uniform probability density for the angle α or a mean angle [small alpha, Greek, macron], the presented simple derivation produces an RLP packing value that is slightly different from those that have been obtained previously.

4. Contact number

The presented approach, in the previous sections, for RCP and RLP also allows correlating the packing fraction to the number of contact points (or coordination number) Z.

4.1 Present model

The coordination number Z can vary when the mean angle is lower or higher than the geometrically averaged ones determined in the previous sections. This can be the case when the state of MRJ packing has not yet been attained, when friction is introduced, ordering takes place, etc.

For the RCP model, with

a mean coordination Z = 4.8 for mean [small alpha, Greek, macron] = 5π/12 is obtained. Alexander³⁸ demonstrated a minimum of Z = 4 for frictionless spheres. Assuming maximum disorder (and excluding local order), Bideau et al. confirmed experimentally and numerically that in such case the maximum coordination number is 4,¹⁸ which may be lower when friction is at play. Also from packing studies it followed that random or MRJ packings are isostatic, so Z = 4 (2d), with d the dimension, for disks.^3,22,23 The present model is not able to reproduce this value, according to the model Z = 4 corresponds to the square lattice, with packing fraction φ_sq = π/4 (≈0.79).

For all configurations π/3 ≤ α ≤ π/2, so 4 ≤ Z ≤ 6, φ can be expressed algebraically in Z by combining eqn (1), (3) and (6), yielding

This relation is included in Fig. 4 for Z ranging from 4 to 6, and hence φ from π/4 to π/2√3.

Fig. 4 Phase diagram of 2D disk packings, mean number of contacts Z versus packing fraction φ. Frictional I: ζ = 0.5, Z₀ = 2.35, Z_c = 3 and φ_c = 0.660, frictionless I: ζ = 0.5, Z₀ = 3.55, Z_c = 4 and φ_c = 0.842, frictional II: ζ = 0.5, Z₀ = 2.35, Z_c = 3, and φ_c = φ_hon = π/3√3 ≈ 0.605, frictionless II: ζ = 0.5, Z₀ = 5.74, Z_c = 4, and φ_c = φ_sq = π/4 ≈ 0.785.

For the RLP model, using mean [small alpha, Greek, macron] = 7π/12, eqn (6) yields as mean coordination number Z = 24/7 ≈ 3.43. This value is in line with Williams²⁷ and Uhler and Schilling²⁸ who found values of 3.2 and 3.333–3.416, respectively, by geometric probability calculations. From numerical simulations Hinrichsen et al.¹⁹ assessed Z = 3.02. Note that Z = 3 (d + 1) is the “loosest packing condition of Hilbert”.³⁸ Atkinson et al.³ reported a tendency towards a kagomé (or trihexagonal) ordering (φ_trh = π√3/8 ≈ 0.68) near their RLP packing fraction (φ_rlp = 0.66), having Z = 4.

Coordination number and packing fraction can also be related in closed-form in the range 3 ≤ Z ≤ 4. By combining eqn (1), (4) and (6), it follows:

which is also set out in Fig. 4, for Z ranging from 3 to 4, and hence φ from π/3√3 to π/4.

4.2 Empirical data and other models

In Fig. 4 also the experimental values of ref. 9 taken from “Table I” and “Fig. 10” are included. The outlying packing fractions 0.090, 0.092, 0.098 and 0.385 of “Table I”⁹ are omitted. The depicted values in Fig. 4 are tabulated in Tables 1 and 2 (Appendix).

The scatter of the experimental points of “Table I”⁹ is considerable, but the positive relation between coordination number and packing density becomes obvious. Quickenden and Tan⁹ observed local ordering (crystallization), which became more pronounced with higher packing fractions. The points/line from “Fig. 10”⁹ furthermore illustrates the sharp decrease in coordination number (from sixfold to fourfold) in a relatively small packing fraction change, which is captured in eqn (7) and (8).

By developing a “jamming phase diagram” based on numerical simulations, in ref. 22 and 23 for disks in 2D and spheres in 3D a fit of the form:

Z − Z_c = Z₀(φ − φ_c)^ζ (9)

was derived, where ζ is independent of potential, polydispersity, and dimensionality d. For 2d, ζ ≈ ½, Z_c = 4 (2d) and φ_c = 0.842. For the 3D packing of spheres, the same ζ was fitted. The fact that ζ is independent of potential is intriguing because it suggests that ζ depends only on the geometry of the packing. The fact that ζ is also independent of dimensionality suggests that there is a property of the packing that is independent of dimension d.^22,23

For frictionless monodisperse disks, Z₀ was not given and is therefore extracted from “Fig. 9”,²² see Table 3 (Appendix), yielding Z_c = 4, φ_c = 0.842 and Z₀ = 3.55. As verification, the same procedure is followed for the spheres given in “Fig. 9”,²² taking Z_c = 6 and φ_c = 0.639,^22,23 and the provided value Z₀ = 7.7 could be reproduced.

In Fig. 4, eqn (9) is set out for Z₀ = 3.55, Z_c = 4 and φ_c = 0.842, φ ranging from 0.842 to φ_tri (frictionless I). One can see that the equation yields Z ≈ 4.9 for φ_tri (instead of 6). This is not surprising as eqn (9) was derived for (φ, Z) in the vicinity of (φ_c, Z_c). If Z₀ was 7.5, the value of 3D, the right endpoint of the curve would be (φ, Z) = (0.907, 6) instead of (0.907, 4.9).

To examine (φ, Z) for RLP of disks, the paper by Silbert³⁸ is instrumental. In ref. 38, (φ, Z) of both frictional and frictionless spheres was simulated. In Tables 4 and 5 (Appendix), the extracted values for frictionless and frictional spheres packings, respectively, are listed, taken from “Fig. 9”, they are shown in Fig. 5.

Fig. 5 Number of contacts Z versus packing fraction φ for packing of spheres (3D). Eqn (9) frictional: ζ = 0.5, Z₀ = 7.7, Z_c = 4 and φ_c = 0.56, eqn (9) frictionless: ζ = 0.5, Z₀ = 7.7, Z_c = 6 and φ_c = 0.639.

Also here it appears that eqn (9) is applicable for both packings, again with ζ = ½ and Z₀ = 7.7 for both packing configurations. Note that in ref. 22 and 23, the same ζ and Z₀ were proposed for the 3D frictionless sphere packing, which values seem to be applicable to frictional spheres as well. For frictionless spheres, it appears also that the values Z_c = 6 and φ_c = 0.639 are identical as in ref. 22 and 23. In Fig. 5, eqn (9) is set out with these values, and also for Z_c = 4 and φ_c = 0.560 for frictional spheres. The isostatic condition requires that for frictional spheres the critical Z_c = d + 1, and for frictionless spheres Z_c = 2d.³⁷ One can see that with aforesaid values, eqn (9) follows that numerical data of ref. 38 very well, both for frictional and frictionless spheres. So again, eqn (9) is consistent with a broad set of data.

Eqn (9) is apparently applicable to both frictional and frictionless spheres, so all (φ, Z), even with the same ζ, and this also holds for frictionless disks. It is therefore plausible to propose that eqn (9) is also applicable to frictional disks, so in the lower (φ, Z) range of Fig. 4, again with ζ = 0.5, Z_c = 3 (= d + 1) and φ_c = 0.66 (frictional I). By invoking Z₀ = 2.35, eqn (9) has as the right endpoint (φ, Z) = (0.842, 4), which is the left endpoint of the frictionless disk packing curve (Fig. 4).

The frictionless and frictional sphere curves of ref. 38 are concave and have a discontinuity at Z = 2d (Fig. 5), which is also the case for eqn (7) and (8). Only the packing fraction values at Z = 3, 4 and 6 are not equal. To illustrate the similarity of eqn (7)–(9), In Fig. 4, eqn (9) is set out for ζ = 0.5, Z₀ = 2.35, Z_c = 3, and φ_c = φ_hon = π/3√3 ≈ 0.605, and for ζ = 0.5, Z₀ = 5.74, Z_c = 4, and φ_c = φ_sq = π/4 ≈ 0.785 (frictional II and frictionless II, respectively). Note that for φ = π/3√3, π/4 and π/2√3, these equations yield Z = 3, 4 and 6, respectively. From Fig. 4, it follows that eqn (7) and (8), based on the simple geometric model, are following eqn (9) quite closely. This latter correlation has its foundation in the results of thermodynamic modelling.

All data in Fig. 4 feature an increase of Z with packing fraction φ, as expected. But following the presented models and refs. 22, 23, and 38, Z(φ) is a concave function in 2D and 3D. Also, the experiments by ref. 9 suggest a concave-shaped relation. For refs. 22, 23, and 38, this concave trend follows from the exponent ζ ≈ ½, which is smaller than unity.

In Fig. 4, also (Z, φ) is included as computed by Jin et al.³⁰ pertaining to φ_RCP = 0.804 (“n = 3”), listed in Table 6 (Appendix). The data shows a convex Z(φ) relation, so a power ζ > 1. Also, the model by Zaccone et al.²⁶ and Anzivino et al.³⁹ yields a convex equation. This can be attributed to their assumption that Z is proportional to the product of φ and the semi-empirical Carnahan-Starling (CS) expression. For d = 2, this CS expression reads (1 − 0.436φ)/(1 − φ)².²⁶

In all, the phase diagram of the 2D disk packing shows that eqn (7) and (8) are able to correlate reported measured and simulated (Z, φ) quite well, especially considering the simplicity of the presented model.

5. Parking problem approach

Rényi's^33,34 classic parking problem (or 1D sequential interval packing problem) concerns the probabilistic properties of the following random process: consider an interval of length x (x ≥ 0), with x eventually tending to infinity, and sequentially and randomly pack disjoint unit in x as long as the remaining space permits placing any new unit segment. At each step of the packing process, the position of the newly placed interval is chosen uniformly from the available space.

The expected value of the covered part is denoted by M(x), so the ratio M(x)/x is the expected filling density of the “parking process”. The interval x is the street curb, and the packed unit segments are the parked cars. The placing of disks on a center disk can be modelled using this parking model (Fig. 6). The circumference of the center disk corresponds to 6 units (disks) and can be seen as a circular street curb. After parking the first unit on a center sphere, a closed interval of length x = 5 is remaining in which the remaining units (disks) are randomly placed on the center sphere.

Fig. 6 Schematic representation of randomly placing (“parking”) spheres on a center sphere. After placing the first sphere (closed line) there is a place left for the parking of a maximum 5 other spheres (“cars”), i.e., the “street interval” length x = 5. The dotted line sphere represents the first randomly placed sphere.

Weiner³⁵ presented the following lower and upper limits for M(x) for x > 4:

0.7432x − 0.2568 ≤ M(x) ≤ 0.75x − 0.25, (10)

yielding 3.46 ≤ M(5) ≤ 3.5.

These values are compatible with the approximate solution provided by Rényi^33,34 for large x:

M(x) ≈ Cx − (1 − C), (11)

with C ≈ 0.748, yielding M(5) ≈ 3.49. C is the Rényi parking constant which is the asymptotic mean filling density M(x)/x for x → ∞. To summarize, the parking approach to the RCP disk packing yields Z ≈ 4.48, which is not far from the value 4.8 derived here.

The parking problem approach can also be applied to the RLP of disks. To allow for obtaining a lower parking density, each unit (disk) that is placed on the center disk is considered to have extra excluded space in which another unit cannot be parked. With the estimated Z ≈ 3.35 for RLP, the space taken by one unit can be estimated.

After parking the first unit, in the remaining interval x, 2.35 units can be parked. The following equation³⁴

is exact for 3 ≤ x < 4, and with M(x) = 2.35, it follows that x = 3.5. The total interval length x is hence 4.5 units, i.e. the circumference of the center disk can accommodate 4.5 loosely placed disks. In other words, where in the case of a random close packing, the circumference can accommodate 6 disks, in random loose packing, it is about 75% of this value. So, in RCP, each disk occupies π/6 (or 3π/18) of the center disk's circumference of π, as the disk diameter is unity (Fig. 5). For RLP, on the other hand, the excluded space of each disk effectively is about 4π/18 of this circumference.

6. Conclusions

This paper addresses the ancient problem of random packing of hard disks/circles in a plane, of interest in mathematics, science and engineering, following a geometric probabilistic approach.

Simple models for RCP and RLP units are constructed (Fig. 2 and 3), which assume that each state can be visited with equal probability. They result in packing fractions and contact numbers φ_rcp = 3 ln(3)/4 ≈ 0.824 and Z = 4.8 for RCP, and φ_rlo ≈ 0.662 and Z = 24/7 ≈ 3.43 for RLP. Both Z-values are higher than the minimum Z required by isostatisticy, Z = 4 (2d) and Z = 3 (d + 1), respectively. The derived packing fraction values are commonly observed, in other probabilistic studies, more sophisticated computer simulations, and experimental studies.

The derived mean contact number of RCP, Z = 4.8, is also very close to the number that is obtained here by applying the classic Rényi parking theory, viz. Z ≈ 4.5. Applying the Rényi parking solution to Z ≈ 3.35 for RLP reveals that the disks occupy 4π/18 of the center disk's circumference of π on which they are placed, whereas it is π/6 for RCP (resulting in aforesaid Z = 4.8).

It also appears that the present approach allows for a phase diagram of average contact number versus 2D disks packing fraction (Fig. 4), based on closed-form expression eqn (7) and (8). Also, these equations produce results that are only slightly different from eqn (9) provided by ref. 22 and 23 both for packed disks in 2D and for spheres in 3D.

In line with the geometric probabilistic approach^10,11,31 and Rényi's parking model,^33,34 a uniform distribution of the disks is invoked here. In other words, there is no preference for α (Fig. 2 and 3) nor where a car/sphere is placed (Fig. 6). In future work, it would be interesting to study the effect of non-uniform distributions (e.g. by perturbing the uniform distribution) on the packing fraction and mean contact number.

Conflicts of interest

There are no conflicts to declare.

Appendix

Tables 1–6

Table 1 Packing fraction φ versus coordination number Z, taken from “Fig. 10” of Quickenden and Tan⁹

Φ	Z	Φ	Z	φ	Z
0.630	2.999	0.841	5.992	0.878	5.999
0.830	3.988	0.848	5.992	0.899	5.999
0.840	5.004	0.871	5.999	0.910	5.999

---

Table 2 Packing fraction φ versus coordination number Z, taken from “Table I” of Quickenden and Tan⁹

Φ	Z	Φ	Z	φ	Z
0.832	4.31	0.876	4.70	0.909	5.43
0.63	2.81	0.906	5.10	0.792	3.49
0.869	4.03	0.844	5.37	0.819	4.36
0.863	4.45	0.873	5.25	0.858	4.45
0.823	4.42	0.888	5.43	0.838	5.18
0.825	4.65	0.891	5.55	0.869	5.44

---

Table 3 Z ₀ computed from packing fraction φ and coordination number Z, extracted from the disks (2D) line shown in “Fig. 9” of O’Hern et al.,²² using eqn (9) and ζ = ½, Z_c = 4, and φ_c = 0.824

log(φ − φc)	Φ	log(Z − Zc)	Z	Z 0
−4.793	0.842	−1.847	4.01	3.5
−4.203	0.842	−1.559	4.03	3.5
−3.600	0.842	−1.249	4.06	3.6
−3.001	0.843	−0.950	4.11	3.6
−2.398	0.846	−0.651	4.22	3.5
−1.795	0.858	−0.342	4.46	3.6

---

Table 4 Packing fraction φ and coordination number Z, extracted from the frictional spheres (3D) as shown in “Fig. 9” of Silbert³⁸

Φ	Z	Φ	Z	φ	Z
0.563	4.34	0.595	5.46	0.626	6.01
0.571	4.74	0.602	5.61	0.633	6.10
0.579	5.02	0.610	5.73	0.641	6.21
0.588	5.27	0.617	5.86	0.648	6.31

---

Table 5 Packing fraction φ and coordination number Z, extracted from the frictionless spheres (3D) as shown in “Fig. 9” of Silbert³⁸

φ	Z	Φ	Z	φ	Z
0.639	6.04	0.642	6.39	0.647	6.69
0.640	6.15	0.643	6.51	0.648	6.79
0.641	6.27	0.645	6.59	0.650	6.84

---

Table 6 Packing fraction φ versus coordination number Z, taken from “Fig. 2 (n = 3)” of Jin et al.³⁰

φ	Z	Φ	Z	φ	Z
0.655	3.298	0.831	4.197	0.889	5.098
0.683	3.402	0.839	4.298	0.895	5.195
0.709	3.499	0.848	4.398	0.895	5.296
0.732	3.599	0.859	4.499	0.899	5.397
0.757	3.703	0.865	4.596	0.902	5.497
0.772	3.799	0.869	4.696	0.904	5.594
0.796	3.896	0.876	4.797	0.903	5.698
0.806	3.997	0.880	4.897	0.906	5.795
0.817	4.101	0.885	4.998

---

Acknowledgements

Dr Lucas Gerin from CMAP, École Polytechnique, Palaiseau (France) is acknowledged for providing and explaining.³⁵ Dr Anna Kaja is thanked for retrieving the graphical data of ref. 9 and 30, see Tables 2 and 6, and Mr Yan Luo for extracting the data of ref. 22 and 38 shown in Tables 3–5.

References

1. H. H. Kausch, D. G. Fesko and N. W. Tschoegl, The random packing of circles in a plane, J. Colloid Interface Sci., 1971, 37, 603–611.
2. J. H. Conway and N. J. A. Sloane ( 1999), Sphere Packings, Lattices, and Groups, Springer Verlag, New York.
3. S. Atkinson, F. H. Stillinger and S. Torquato, Existence of isostatic, maximally random jammed monodisperse hard-disk packings, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 18436–18441.
4. A. Thue, Über die dichteste Zusammenstellung von kongruenten Kreisen in einer Ebene, Norske Vid. Selsk. Skr., 1910, 1, 1–9 (in German).
5. A. Thue ( 1977), Selected Mathematical Papers, Universitetsforlaget, Oslo.
6. L. Fejes Tóth, Über die dichteste Kugellagerung, Math. Z., 1940, 48, 676–684 (in German).
7. F. H. Stillinger, E. A. Dimarzio and R. L. Kornegay, Systematic approach to explanation of the rigid disk phase transition, J. Chem. Phys., 1964, 40, 1564–1576.
8. W. M. Visscher and M. Bolsterli, Random packing of equal and unequal spheres in two and three dimensions, Nature, 1972, 239, 504–507.
9. T. I. Quickenden and G. Tan, Random packing in two dimensions and the structure of monolayers, J. Colloid and Interface Sci., 1974, 48, 382–393.
10. A. Gamba, Random packing of equal spheres, Nature, 1975, 256, 521–522.
11. D. N. Sutherland, Random packing of circles in a plane, J. Colloid and Interface Sci., 1977, 60, 96–102.
12. M. Shahinpoor, Statistical mechanical considerations on the the random packing of granular materials, Powder Technol., 1980, 25, 163–176.
13. K. I. Kanatani, An entropy model for shear deformation of granular materials, Lett. Appl. Eng. Sci., 1980, 18, 989–998.
14. M. Sugiyama, A new approach to hard sphere system in equilibrium III, Prog. Theor. Phys., 1980, 63, 1848–1853.
15. M. Rubinstein and D. R. Nelson, Order and deterministic chaos in hard-disk arrays, Phys. Rev. B: Condens. Matter Mater. Phys., 1982, 26, 6254–6275.
16. M. Shahinpoor, A model for crystallization of monomolecular layers on contracting surfaces, J. Colloid Interface Sci., 1982, 85, 227–234.
17. J. G. Berryman, Random close packing of hard spheres and disks, Phys. Rev. A, 1983, 27, 1053–1061.
18. D. Bideau, A. Gervois, L. Oger and J. P. Troadec, Geometrical properties of disordered packings of hard disks, J. Phys., 1986, 47, 1697–1707.
19. E. L. Hinrichsen, J. Feder and T. Jøssang, Random packing of disks in two dimensions, Phys. Rev. E, 1990, 41, 4199–4209.
20. D. E. G. Williams, Packing fraction of a disk assembly randomly close packed on a plane, Phys. Rev. E, 1998, 57, 7344–7345.
21. T. Odagaki and A. Hoshiko, Random jammed packing of binary disks, J. Phys. Soc. Jpn., 2002, 71, 2350–2351.
22. C. S. O’Hern, S. A. Langer, A. J. Liu and S. R. Nagel, Random packings of frictionless particles, Phys. Rev. Lett., 2002, 88, 075507.
23. C. S. O’Hern, L. E. Silbert, A. J. Liu and S. R. Nagel, Jamming at zero temperature and zero applied stress: The epitome of disorder, Phys. Rev. E, 2003, 68, 011306.
24. S. Meyer, C. M. Song, Y. L. Jin, K. Wang and H. A. Makse, Jamming in two-dimensional packings, Physica A, 2010, 389, 5137–5144.
25. R. Blumenfeld, Disorder criterion and explicit solution for the disc random packing fraction, Phys. Rev. Lett., 2021, 127, 118002.
26. A. Zaccone, Explicit analytical solution for random close packing in d = 2 and d = 3, Phys. Rev. Lett., 2022, 128, 028002; A. Zaccone, Explicit analytical solution for random close packing in d = 2 and d = 3, Phys. Rev. Lett., 2022, 129, 039901(E) See also discussion arXiv:2201.07629, arXiv:2201.10951, arXiv:2201.10550, arXiv:2201.12784, arXiv:2204.13901, arXiv:2205.00720, arXiv:2201.06129, arXiv:2202. 05078.
27. D. E. G. Williams, Stability in 2D random packing, J. Phys. C: Solid State Phys., 1985, 18, L181–L184.
28. W. Uhler and R. Schilling, A local description of stable 2D random packings, J. Phys. C: Solid State Phys., 1985, 18, L979–L983.
29. M. Pica Ciamarra and A. Coniglio, Random very loose packing, Phys. Rev. Lett., 2008, 101, 128001.
30. Y. Jin, J. G. Puckett and H. A. Makse, Statistical theory of correlation in random packings of hard particles, Phys. Rev. E, 2014, 89, 052207.
31. A. M. Mathai ( 1999), An introduction to geometrical probability: distributional aspects with applications, Gordon and Breach, Amsterdam.
32. Buffon's needle problem is best known; a needle is dropped on a floor made of parallel strips, each the same width. In the case where the needle length l is not greater than the width t of the strips, the probability that the needle will lie across a line between two strips is 2l/πt.
33. A. Rényi, On a one-dimensional problem concerning random space filling, Publ. Math. Inst. Hung. Acad. Sci., 1958, 3, 109–127 (in Hungarian).
34. A. Rényi, On a one-dimensional problem concerning random space filling, Sel. Transl. Math. Stat. Probab., 1963, 4, 203–218.
35. H. Weiner, Elementary treatment of the parking problem, Sankhyā, Indian J. Stat., Ser. A, 1969, 31, 483–486.
36. H. Ikeda, E. Brito, M. Wyart and F. Zamponi, Jamming with tunable roughness, Phys. Rev. Lett., 2020, 124, 208001.
37. S. Alexander, Amorphous solids: their structure, lattice dynamics and elasticity, Phys. Rep., 1998, 296, 65–236.
38. L. E. Silbert, Jamming of frictional spheres and random loose packing, Soft Matter, 2010, 6, 2918–2924.
39. C. Anzivino, M. Casiulis, T. Zhang, A. S. Moussa, S. Martiniani and A. Zaccone, Estimating random close packing in polydisperse and bidisperse hard spheres via an equilibrium model of crowding, J. Chem. Phys., 2023, 158, 044901.

---

Footnote

† This article is dedicated to my late study friend ir. M.E. (Marc) van der Ree (26 December 1961 – 16 April 2000).

---