Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Fluid–solid transitions in photonic crystals of soft, thermoresponsive microgels†
M.
Hildebrandt
a,
D.
Pham Thuy
a,
J.
Kippenberger
a,
T. L.
Wigger
 a,
J. E.
Houston
a,
J. E.
Houston
 b,
A.
Scotti
b,
A.
Scotti
 c and
M.
Karg
c and
M.
Karg
 *a
*a
aInstitut für Physikalische Chemie I: Kolloide und Nanooptik, Heinrich-Heine-Universität Düsseldorf, Universitätsstraße 1, D-40225 Düsseldorf, Germany. E-mail: karg@hhu.de
bEuropean Spallation Source ERIC, Box 176, SE-221 00 Lund, Sweden
cInstitute of Physical Chemistry, RWTH Aachen University, Landoltweg 2, 52056 Aachen, Germany
First published on 4th September 2023
Abstract
Microgels are often discussed as well-suited model system for soft colloids. In contrast to rigid spheres, the microgel volume and, coupled to this, the volume fraction in dispersion can be manipulated by external stimuli. This behavior is particularly interesting at high packings where phase transitions can be induced by external triggers such as temperature in the case of thermoresponsive microgels. A challenge, however, is the determination of the real volume occupied by these deformable, soft objects and consequently, to determine the boundaries of the phase transitions. Here we propose core–shell microgels with a rigid silica core and a crosslinked, thermoresponsive poly-N-isopropylacrylamide (PNIPAM) shell with a carefully chosen shell-to-core size ratio as ideal model colloids to study fluid–solid transitions that are inducible by millikelvin changes in temperature. Specifically, we identify the temperature ranges where crystallization and melting occur using absorbance spectroscopy in a range of concentrations. Slow annealing from the fluid to the crystalline state leads to photonic crystals with Bragg peaks in the visible wavelength range and very narrow linewidths. Small-angle X-ray scattering is then used to confirm the structure of the fluid phase as well as the long-range order, crystal structure and microgel volume fraction in the solid phase. Thanks to the scattering contrasts and volume ratio of the cores with respect to the shells, the scattering data do allow for form factor analysis revealing osmotic deswelling at volume fractions approaching and also exceeding the hard sphere packing limit.
1. Introduction
Microgels and nanogels are composed of chemically and/or physically crosslinked polymer chains and are swollen by large amounts of solvent under good and typically even bad solvent conditions.1,2 With this large solvent content and their soft polymeric network structure the physical properties of microgels are complex, featuring characteristics that are common for colloids, surfactants and macromolecules.3–8 Depending on the polymer composition, microgels can react to different external stimuli like temperature, pH or ionic strength.9–11 The most prominent examples of temperature responsive microgels are based on poly-N-isopropylacrylamide (PNIPAM). PNIPAM microgels undergo a pronounced volume phase transition (VPT) at a transition temperature of 32 °C or higher depending on the crosslinker density.12–14 This behavior is related to the lower critical solution temperature (LCST) of PNIPAM in water.15,16 The precipitation of PNIPAM at temperatures above the LCST is also the basis for the rather straightforward synthesis of related microgels by (seeded) precipitation polymerization.17,18 The resulting microgels typically possess an inhomogeneous internal network structure resembling a gradient in crosslinking and consequently a polymer density that is decreasing in the outer periphery of the microgels. This gradient is the result of the faster consumption of the crosslinker during the precipitation polymerization and leads to a higher crosslinked core and a loose outer shell that also contains dangling chains.19–21 This structure was also found for the polymeric shell of core–shell microgels that contain rigid nanoparticle cores such as gold22 and silica.23 In recent years the structural evolution of microgels in dense packings, either in 2-dimensional confinement or 3-dimensional samples in bulk dispersion, has attracted significant interest.1,24,25 Despite their softness, microgels can (self-) assemble into highly ordered structures and, for example, crystalline phases similar to hard spheres were observed.5,12,13,26–31 In contrast to rigid colloids, responsive microgels allow for external control of the microgel volume fraction due to their VPT behavior, i.e. for a given number concentration, N, for example temperature can be used to alter the volume fraction and thereby induce phase transitions.28,32 This behavior renders microgels particularly interesting for fundamental studies on crystallization, crystal melting and jamming. Surprisingly, little is known about the minimal temperature change needed to induce the fluid/solid and solid/fluid transitions.28,30,33 A challenge related to structural investigations at high volume fractions is the deswelling and faceting that alters the form factor of the microgels in dependence of their concentration.34–41 This behavior in combination with the inhomogeneous internal network structure and the high solvent contents hamper the determination of the volume fraction. The easier accessible quantity is the generalized volume fraction that considers the microgel volume in the dilute, non-interacting state.32,42In situ studies on phase transitions consequently require knowledge of the form as well as structure factor in dense packings that typically requires deuteration strategies and complex contrast variation using X-ray and neutron scattering.20,35In this work, we use silica-PNIPAM core–shell (CS) microgels to study fluid–solid transitions in dense packings. Our aims are (i) to determine transition temperatures where fluid–solid transitions occur, (ii) to study the structure and long-range order of both phases and (iii) to determine the microgel size and volume fraction in the concentration range where osmotic deswelling is expected to alter the microgel form factor. To do so, we use a combination of absorbance spectroscopy and synchrotron SAXS measurements for samples of various concentrations in the regime of dense packing. Importantly, the shell-to-core size ratio of the CS microgels was chosen to provide contrast for both, the shell and the core in SAXS investigations. This allows for the direct determination of structure as well as form factors at high volume fractions from single, individual scattering profiles. In the solid regime, we use Bragg peak analysis to study the crystal structure and domain size. Therefore, this work provides not only an ideal, new model system to tackle fundamental challenges related to studying and understanding phase transitions but also provides a direct link between the optical properties and the structure and long-range order of the CS microgel assemblies. This comparison is well justified because of the rather larger probed volumes in non-microfocus SAXS and standard optical spectroscopy giving access to the ensemble behavior rather than only local phenomena.
2. Experimental section
Chemicals
L-Arginine (PanReacAppliChem, ≥99%), cyclohexane (Fisher Scientific, analytical reagent grade), tetraethyl orthosilicate (TEOS, Sigma Aldrich, 98%), 3-(trimethoxysilyl)propyl methacrylate (MPS, Sigma Aldrich, 98%), N,N-methylenebis(acrylamide) (BIS, Sigma-Aldrich, 99%), potassium persulfate (PPS, Sigma-Aldrich, 99,0%) and heavy water (D2O, Sigma Aldrich, 99.9%) were used as received without further purification.N-Isopropylacrylamide (NIPAM, TCI, >98%) was recrystallized from cyclohexane prior to use. Water was always used in ultra-high purity provided by a Milli-Q system (Merck Millipore) with a resistivity of 18.2 MΩ cm.
Synthesis of silica cores
Silicon dioxide seed particles were synthesized by an interphase-mediated condensation reaction,43 where 82 mg (0.47 mmol) of L-arginine were dissolved in 78 mL of water in an 100 mL Erlenmeyer flask and an organic phase was added by the addition of 4.05 mL of cyclohexane. The reaction mixture was equilibrated for 30 minutes at 60 °C in an oil bath and stirred only gently in order to prevent the aqueous and organic phase from mixing. Afterwards, 4.95 mL (22.2 mmol) of TEOS were added to the organic phase and the reaction was allowed to proceed for 72 h. The resulting silica particles were then surface-functionalized with MPS to increase the hydrophobicity as needed for the later precipitation polymerization. To do so, the aqueous phase was used without any purification and 9 mL of cyclohexane were added to the dispersion. After equilibration for 30 minutes at 60 °C, 90 μL of MPS were added to the organic phase. After stirring for 24 h, the aqueous phase was separated and the mass content of the dispersion was determined. The obtained MPS-functionalized seeds were used without further purification.Synthesis of CS microgels
CS microgels were synthesized by free-radical precipitation polymerization using 4000 mg (35.4 mmol) NIPAM monomer, 817 mg (5.3 mmol) of BIS as crosslinking comonomer and 122 mg MPS-functionalized seeds dispersed in 600 mL of water. The reaction medium was degassed with nitrogen for 45 minutes at a temperature of 70 °C. Then, 50 mg (0.19 mmol) of PPS dissolved in 1 mL of water were added in one shot to initiate the polymerization. The reaction was conducted for 6 h. The CS microgels were purified and concentrated by three centrifugation and redispersion (water) steps at 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 rcf for 3 h followed by dialysis against pure water for at least seven days with multiple water exchanges.
000 rcf for 3 h followed by dialysis against pure water for at least seven days with multiple water exchanges.
Sample preparation
CS microgel dispersions with defined mass contents used for absorbance spectroscopy and SAXS measurements were prepared by freeze-drying the respective amount of a stock dispersion with known mass content and redispersion of the microgels in the respective volume of D2O or H2O. CS microgel dispersions with only low mass contents were prepared by dilution of a stock dispersion. Dense samples at high concentrations were prepared in 0.2 mm × 4.00 mm × 10 mm rectangular, flat-wall capillaries (VitroTubes). The respective CS microgel dispersions were sucked into the capillaries by applying a small reduced pressure from one side of the capillary. Afterwards, the capillaries were flame-sealed with a hydrogen torch. After sample preparation, the samples were annealed using a temperature cycle. First, the samples were heated from 20 °C to 50 °C with a rate of 1.5 °C h−1. Then the temperature was kept constant at 50 °C for 1 h. Finally, the samples were cooled back to 20 °C with a rate of 1.5 °C h−1. These samples were used for SAXS and temperature-dependent absorbance spectroscopy. For SAXS measurements above 20 °C, we prepared CS microgel dispersions in 1 mm round capillaries (WJM Glas) and sealed with epoxy glue. The mass content of dilute CS microgel dispersions prepared for form factor measurements was adjusted to yield a volume fraction of around 0.03, in both swollen and collapsed state. A sample list is given in Table S1 in the ESI.†SAXS
Synchrotron SAXS experiments were performed on the CoSAXS beamline at the MAX IV synchrotron in Lund (Sweden). The instrument was equipped with an Eiger2 4M detector exhibiting a sensitive area of 155.1 × 162.2 mm2 with total pixel sizes of 75 × 75 μm2. SAXS measurements were recorded with acquisition times of 10 ms. The energy of the X-ray beam was 12.4 keV and the sample-to-detector distance was set to 6.85 m resulting in an effective q-range from 0.015 nm−1 to 0.5 nm−1 for the measurements performed at 20 °C. For the experiments performed at 40 °C the sample-to-detector distance was set to 11.04 m resulting in an effective q-range from 0.01 nm−1 to 0.5 nm−1. Due to limited available beamtime and limitations in precisely controlling the sample temperature with our unusual sample geometry, experiments could only be performed at 20 and 40 °C. Detector images were radially averaged using a mask accounting for the inactive section of the detector boundaries and the beamstop. The resulting SAXS profiles were background corrected for D2O.In addition, SAXS measurements on selected samples were performed on a Xeuss 2.0 (XENOCS) equipped with a Pilatus3R 300K detector exhibiting a sensitive area of 83.8 × 106.5 mm2 with total pixel sizes of 172 × 172 μm2. The sample-to-detector distance was set to 1.2 m and the energy of the X-ray beam was 8.048 keV leading to an effective q-range of 0.03 nm−1 to 2 nm−1. All measurements were performed in order to extract scattering intensities in absolute units with 1 mm glassy carbon as reference. Here we note that only the SAXS profiles based on measurements performed with the Xeuss 2.0 and using glassy carbon as reference exhibit absolute units. All data from synchrotron SAXS measurements of CS microgels in dense packings are reported in arbitrary units as the data analysis focusing on the form and structure factor does not require absolute scaling. Scattering profiles were recorded with acquisition times of 3600 s. The resulting SAXS profiles were corrected for the respective solvent as background. Samples were measured in round capillaries with a diameter of 1 mm and a wall thickness of 0.01 mm (WJM Glas). The concentration used for the CS microgels was 10 wt%, while silica particles were investigated in dilute state.
Radial averaged scattering profiles were analyzed with the SasView software.44 The 2D SAXS patterns were simulated with the software Scatter by Förster and Apostol.45
Absorbance spectroscopy
UV-Vis-NIR absorbance spectroscopy was performed on a SPECORD S600 (Analytik Jena) equipped with a temperature-controlled sample changer. We want to note that we measured the exact same samples by absorbance spectroscopy as by synchrotron SAXS.Angle-dependent reflectance spectroscopy
Reflectance spectroscopy was performed with a home-built setup consisting of a tungsten-lamp as light source and the Flame VIS-NIR Spectrometer (Ocean Insight) as detector. Both, detector and the light source were equipped with visible-NIR fibers to ensure free movement of the detector and light source in a goniometer-like fashion. The sample holder and fiber guides were 3D printed using a Prusa MK3 FDM printer. Measurements were performed in reflectance with the incident angle matching the angle of detection.Dynamic light scattering
Temperature-dependent dynamic light scattering (DLS) measurements were performed with the Zetasizer Nano S (Malvern Panalytical) equipped with a laser of 633 nm wavelength and scattered light was detected in an angle of 173°. Measurements were conducted between 17 °C and 60 °C with steps of 0.2 °C. Three measurements with acquisition times of 60 s each were performed at each temperature step. The measurements were recorded in semi-macro cuvettes (polymethylmethacrylate, VWR) with CS microgel mass contents of 0.05 wt% in water. The hydrodynamic radii (z-average) were determined by cumulant analysis provided by the instrument software.Angle-dependent DLS measurements were done on a 3D LS Spectrometer (LS Instruments, Switzerland) operated in 2D mode (pseudo cross-correlation) equipped with a HeNe laser (632.8 nm) as light source while the scattered light was detected with two avalanche photodetectors. A CS microgel dispersion, filtered through a 5 μm syringe filter (PTFE, Carl Roth) with a mass content of 0.01 wt% was prepared in a cylindrical glass cuvette (10 × 75 mm, borosilicate, Fisher scientific). Beforehand, the glass cuvette was treated with 2 vol% Hellmanex solution, followed by cleaning in an acetone fountain. Finally, samples were placed in a temperature-controlled decalin bath (JULABO CF31, PT100 close to sample position) and measured in angles between 30° and 140° in 5° steps with acquisition times of 60 s. The recorded data was analyzed by the CONTIN algorithm46 as implemented in AfterALV v.1.0e (Dullware).
Electrophoretic mobility determination
The temperature-dependent electrophoretic mobility of the CS microgels dispersed in water was determined using a Litesizer 500 from Anton Paar.Transmission electron microscopy
Transmission electron microscopy (TEM) was performed with a JEOL JEM-2100Plus TEM in bright-field mode. The acceleration voltage was set to 80 kV. Aqueous CS microgel dispersions were drop-casted on carbon-coated copper grids (200 mesh, Electron Microscopy Science) and dried for several hours at room temperature before investigation. TEM images were exported with the GMS 3 software from Gatan and the particle size was determined using ImageJ.473. Results and discussion
Characterization in the dilute regime
We synthesized CS microgels that feature spherical silica nanoparticle cores and crosslinked PNIPAM shells. Fig. 1 summarizes the basic characterization in the dilute (non-interacting) regime. A schematic illustration of the microgel structure and the most relevant dimensions for this work are shown in Fig. 1(a). The SAXS profile in Fig. 1(b) reveals the form factors measured at 20 °C and 40 °C with contributions from the core in the high q range and contributions from the shell in the mid to low q range. Form factor analysis on the basis of a CS model with a homogeneous core and a shell with an exponentially decaying density profile (red line) provided a core radius of Rcore = 18 ± 2 nm and a total radius of the CS microgels of 138 ± 14 nm at 20 °C. More details on the form factor analysis including the application of other models can be found in the ESI† (Table S3 and Fig. S1). Due to the thermoresponsive behavior of PNIPAM based microgels, the CS microgels collapse above the volume phase transition temperature (VPTT). This is also reflected by the scattering profile recorded at 40 °C, i.e. well above the VPTT. In this state a simple CS model with homogeneous core and shell can be used to describe experimental scattering data. The respective fit to the data yields a total radius of 90 ± 8 nm. For more details on the fitting parameters see Table S2 in the ESI.†Temperature-dependent DLS measurements reveal the typical VPT behavior of the PNIPAM shell in aqueous dispersion (Fig. 1(c)). In the swollen state (20 °C) the CS microgels possess a hydrodynamic radius of Rh = 147 ± 3 nm. The radius continuously decreases with increasing temperature reaching a value of 97 ± 1 nm at 50 °C. The VPTT is approximately 35.0 °C. We want to note that we used 15 mol% of BIS in the synthesis (nominal) which explains the slightly higher temperature of the VPT as compared to ‘classical’ PNIPAM microgels. This is in agreement with findings from previous studies on comparable systems.22,48 Since the precision of the hydrodynamic dimensions in the swollen and collapsed state is of utmost importance for the further analysis in this work, we used angle-dependent DLS in addition to the fixed angle results. The good agreement between both sets of measurements can be seen in Fig. S2 in the ESI.† In addition, we recorded the temperature-dependent electrophoretic mobility of the CS microgels under dilute conditions (Fig. S3, ESI†) revealing the expected behavior with rather low mobilities (−1.23 μm cm V−1 s−1, 20 °C) in the swollen state, followed by a decrease when the particles undergo the VPT (−2.23 μm cm V−1 s−1, 40 °C). Here, the negative electrophoretic mobility is related to the initiator PPS, introducing negative charges and a decrease in negative mobility is associated to an increase in charge density of the microgels.
Fig. 1(d) shows a representative TEM image of the CS microgels where the cores and shells can be clearly distinguished due to their difference in contrast. The image supports that each microgel contains a single nanoparticle core with an average radius of Rcore = 17.5 ± 1.6 nm. SAXS measurements of the bare silica cores (Fig. S4, ESI†) are in good agreement with the results from TEM leading to an average radius of 17.8 ± 1.8 nm. A histogram from size analysis of a large number of microgels along with additional TEM images is provided in the ESI† (Fig. S5). We found that less than 1% of the microgels feature more than one or no core. As expected, the microgel shells significantly shrink due to the sample preparation and the high vacuum conditions during TEM investigation. This is illustrated by the red circle in Fig. 1(d) that highlights the swollen state dimensions determined by DLS.
Fluid–solid transitions in dense packings
Similar to hard spheres, microgels including our CS microgels are expected to crystallize at large enough packing fractions. Due to the total size of our CS microgels approaching visible wavelength scale total dimensions, absorbance spectroscopy is a convenient tool to monitor the phase behavior.30,48Fig. 2(a) shows Vis-NIR absorbance spectra of samples with 5.4 to 10.9 wt% CS microgels obtained directly after sample preparation (dashed lines) and after the SAXS investigation in the solid regime (solid lines) which is addressed later in this work. Prior to the SAXS investigation of the solid regime, the samples were annealed at 50 °C followed by slow cooling to 20 °C. More details on the annealing procedure and the parameters that we have identified for the best annealing conditions can be found in the ESI† (Fig. S6). The annealing process reduces the linewidths of the narrow Bragg peaks, enhances their maximum intensity indicating a reduction in incoherent scattering. At the same time, only small spectral shifts are observed. For the lowest concentration (5.4 wt%) a Bragg peak is only observed prior to annealing. This can be attributed to a liquid-crystal coexistence phase and potentially local concentration differences right after sample preparation. During the annealing, the crystallites melt and the resulting fluid homogenizes resulting in a fluid phase that even remains after slow cooling to room temperature where the volume fraction is significantly increased. This behavior indicates that the volume fraction of this particular sample in the swollen state is close to the threshold volume fraction where crystallization occurs. In Fig. S7 in the ESI,† additional absorbance spectra recorded at different points in time can be found while Fig. S8 (ESI†) shows results from angle-dependent reflectance measurements. The reflectance data show the expected blue shift of the Bragg peak for increasing angle of incidence (with respect to the normal).What happens during the heating and cooling cycles in our annealing protocol can be nicely followed by absorbance spectroscopy. It is notable that the sample volume probed in Vis-NIR spectroscopy is much larger than the volumes probed by microscopy33 or microfocus SAXS28 and, therefore, our approach provides a more representative ensemble picture of the phase behavior of the CS microgels. Detailed information about the temperature cycling can be found in the ESI† (Fig. S9). Fig. 2(b) shows as an example the spectra recorded during the heating in 0.3 °C steps starting at 20 °C for the sample with 7.3 wt% CS microgels. During the first approximately 10 °C of heating the Bragg peak remains nearly unchanged in position, intensity and full width at half maximum (FWHM). When approaching a temperature of 30 °C and higher (inset in Fig. 2(b)), we can see a decrease of the Bragg peak accompanied by a blue shift and broadening. These changes are related to a significant shrinking of the PNIPAM shell that reduces the microgel volume fraction ϕ. This is related to the VPT of the microgels (see Fig. 1(c)). At temperatures of 31.7 °C and higher, the Bragg peak cannot be observed anymore indicating that only a fluid phase is left. To follow this phase transition more closely, Fig. 2(c) shows the evolution of the Bragg peak absorbance with temperature for a heating (red symbols) and cooling (blue symbols) series. The data for both, the heating and cooling cycle, almost perfectly overlap with very little hysteresis and slightly smaller inflection points for the cooling cycle (30.7 °C in contrast to 31.6 °C for the heating cycle). Surprisingly, the temperature window where the solid–fluid (fluid–solid) transition occurs is very narrow as indicated by the green vertical bar. Within approximately 2 °C the crystals completely melt during the heating cycle and reversibly recrystallize during the cooling cycle. In addition, a change in temperature of a few millikelvin is enough for the dispersion of CS microgels to undergo the change from a partially crystalline (green transition area) to a completely fluid phase. It is important to note that data shown were not normalized or anyhow modified. We simply take in account the maximum absorbance values at the respective position of the Bragg peak with only the incoherent background scattering being subtracted. This background subtraction is the reason why the plotted intensities remain nearly unchanged for temperatures outside the green-colored area. Following only the development of the coherent signal reveals the very sharp and reversible phase transition. The same heating/cooling study was also performed for the samples containing 9.1 and 10.9 wt% CS microgels. The respective data can be found in the ESI† (Fig. S10 and Table S4). In addition, we performed time-dependent Vis-NIR absorbance spectroscopy in the temperature range of the phase transition between the fluid and solid state, to verify that the samples reached equilibrium at the time of the measurement. As presented in Fig. S11 in the ESI,† the intensity of the Bragg peak changes within the first 100 s, after reaching the target temperature and from this point on stays constant. Therefore, not only the CS microgels show a fast response towards temperature,49 but also the phase behavior exhibits a rather fast response towards temperature changes (∼100 s), and the suspension quickly reaches equilibrium when temperature steps are sufficiently small. Here, we conclude that the samples are at equilibrium when spectra are recorded after 720 s equilibration time.
Similar to our previous works on gold-PNIPAM CS microgels,22,50 we can use the SAXS scattering contribution of the nanoparticle cores (here: silica) to determine the microgel number concentration, N. A detailed explanation for the data treatment and calculations is given in the ESI† (Fig. S12–S14 and Tables S5–S8). Having access to N allows us to determine the generalized volume fraction ζ that is based on the hydrodynamic microgel volume in the dilute, non-interacting regime available from our DLS data. Fig. S15 in the ESI† shows the evolution of ζ with temperature. We can now use the transition temperatures determined from the spectroscopic data, listed in Table S4 of the ESI,† to determine the values of ζ where the solid–fluid (fluid–solid) transitions occur. Fig. 2(d) shows the respective results for the heating and cooling cycles as a function of mass content of the samples. The data for the three different concentrations scatter around the average value of ![[small zeta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c7.gif) transition = 0.45 ± 0.05 (black line in Fig. 2(d)) without a clear trend. The hysteresis between cooling (blue symbols) and heating (red symbols) is the largest for the sample at a concentration of 7.3 wt% and almost not observable for 9.1 and 10.9 wt%. Here, the 2 °C interval, where the CS microgels undergo the phase separation corresponds to an approximate change in ζ of around 0.05 ± 0.01. As the transition temperatures are close to the VPT, we propose that the microgels are nearly in the collapsed state and thereby can be hardly collapsed further. We want to note that the volume fractions are well below the random close packing and, therefore, the generalized volume fraction can correspond to the real packing fraction.38,51 Our mean value of 0.45 is slightly smaller than the freezing volume fraction of hard spheres (0.494).52 We attribute this small deviation to an electrostatic contribution due to the anionic radical initiator used in the precipitation polymerization rendering the CS microgels charged.
transition = 0.45 ± 0.05 (black line in Fig. 2(d)) without a clear trend. The hysteresis between cooling (blue symbols) and heating (red symbols) is the largest for the sample at a concentration of 7.3 wt% and almost not observable for 9.1 and 10.9 wt%. Here, the 2 °C interval, where the CS microgels undergo the phase separation corresponds to an approximate change in ζ of around 0.05 ± 0.01. As the transition temperatures are close to the VPT, we propose that the microgels are nearly in the collapsed state and thereby can be hardly collapsed further. We want to note that the volume fractions are well below the random close packing and, therefore, the generalized volume fraction can correspond to the real packing fraction.38,51 Our mean value of 0.45 is slightly smaller than the freezing volume fraction of hard spheres (0.494).52 We attribute this small deviation to an electrostatic contribution due to the anionic radical initiator used in the precipitation polymerization rendering the CS microgels charged.
Structure in the fluid regime
We performed synchrotron SAXS measurements on the dense samples at 40 °C, i.e. where the PNIPAM shells are collapsed. According to the analysis from absorbance spectroscopy, all samples should be in a fluid-like state at this temperature (see Fig. S10 in the ESI†) as Bragg peaks were not observed. Fig. 3(a) shows a 2D detector image of a 9.1 wt% CS microgel dispersion recorded at 40 °C. A distinct fluid structure factor contribution, as well as some oscillations related to the form factor are visible in the isotropic scattering pattern. Additional detector images recorded from samples with different mass contents are provided in the ESI† (Fig. S16). The results agree very well to the observation from absorbance spectroscopy. The radially averaged scattering profile is shown in Fig. 3(b) (black circles). The profile shows a pronounced structure factor contribution in the range of low q (<0.05 nm−1). The mid to high q regime is dominated by the form factor of the CS microgels (see also Fig. 1(b)). Scattering profiles for samples with 5.4 to 12 wt% CS microgel content are shown in Fig. S17 in the ESI.† The data reveal the expected changes in the structure factor, i.e. a shift of the first structure factor maximum to larger q for increasing concentration. At the same time the form factor contribution remains unchanged. This implies that the microgel do not change due to osmotic deswelling in the collapsed state, at least in the range of concentrations studied. Consequently, the structure factor can be calculated directly from the scattering intensities of the dense samples (Iconc(q)) using the known form factor (S(q) = Iconc(q)/P(q)). Due to a small structure factor contribution in the experimental scattering profile of the dilute CS microgel dispersion (1.25 wt%) recorded at 40 °C (see Fig. S18, ESI†), we did not use the experimental data in the range of low q (<0.025 nm−1) for this calculation. In the latter case, the theoretical form factor as shown by the fit in Fig. 1(b) was used. Fig. 3(b) shows the resulting structure factor (green circles) for the 9.1 wt% sample. The vertical dashed line highlights the value in q separating the range in q where the form factor fit was used for the calculation (q < 0.025 nm−1) and the range where the experimental data (1.25 wt%) were used (q > 0.025 nm−1). More details on this data treatment are provided in the ESI† (Fig. S19). The Percus–Yevick53 (PY) hard sphere structure factor fit describes the determined structure factor almost perfectly.Fig. 3(c) compares the extracted structure factors for the samples in the range of 5.4 to 12 wt% with increasing concentration from bottom to top. All data can be nicely fitted by the PY structure factor model. We also observe the expected shift of the first structure factor maximum to larger q for increasing concentration. At the same time, we observe a reduction in structure factor peak width. Results from the structure factor analysis are summarized in Table S9 in the ESI.† The effective hard sphere volume fraction increases from 0.32 for 5.4 wt% to 0.46 for 12 wt%. At the same time, the effective hard sphere radius decreases from 142 to 124 nm – values that are significantly larger than the value of the hydrodynamic radius in the collapsed state (40 °C) as determined from DLS. The significant deviation between Rh and the effective hard sphere radius obtained from the fit of the data with the PY model indicates a pronounced influence of electrostatic interactions between the CS microgels, which are not considered in the classical hard sphere model. Therefore, the extracted values for the hard sphere volume fractions and for the effective hard sphere radii do not reflect the real packing fraction and size of the CS microgels. For a more realistic description a more complex model would be required, ideally together with support from theoretical calculations or computer simulations. However, the focus of the present work is rather on the fluid–solid transition than on the role of electrostatic interactions. The latter will be carefully addressed in a follow-up work. Noteworthy, when the CS microgels undergo the VPT, the effective charge density also increases, as reflected by the electrophoretic mobility (Fig. S3, ESI†). This enhances the influence of electrostatics in the phase behavior of the microgels.
We attribute the decrease in hard sphere radius to an increasing electrostatic screening as the microgel and consequently the counterion concentration increases. Fig. S20 in the ESI† shows only the low q region of the structure factors and reveals the good match between PY structure factor fit and experimental data towards q = 0 nm−1. This underlines the hard sphere-like behavior of the CS microgels in the collapsed state. In swollen state experimental structure factors of microgels were shown to deviate from the hard sphere approximation which was related to the soft character of the interaction potential.54
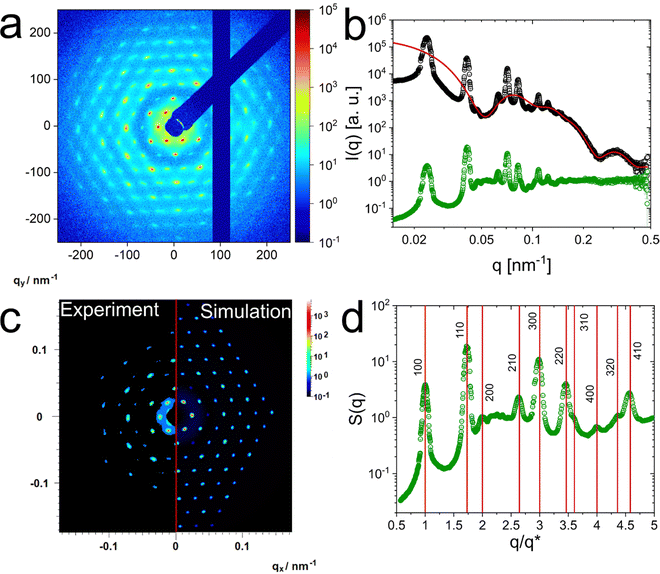
Structure in the solid regime (crystalline)
The absorbance spectra of Fig. 2(a) indicate that the crystallinity is significantly improved by the applied temperature annealing protocol. To verify this and to determine the crystal structure, we used synchrotron SAXS. Fig. 4(a) shows the 2D detector image recorded for the 9.1 wt% sample at 20 °C, as a representative example. Pronounced and sharp Bragg peaks of at least 10 orders of diffraction are observed. Furthermore, the six-fold symmetry of the diffraction pattern is clearly visible indicating the alignment of hexagonal close-packed planes parallel to the capillary wall.28 Apparently, SAXS studies on microgels and CS microgels in dense packings are scarce and from reported 2D diffraction patterns typically only up to four orders of diffraction are observed.28,50,55 Although not directly comparable due to the different experimental smearing and detector resolution, analysis of colloidal crystals of microgels by small-angle neutron scattering (SANS) revealed diffraction with Bragg peaks of four diffraction orders.48 The long-range order and superior crystallinity of our system can also be observed for the 7.3 and 10.9 wt% sample as shown in the ESI† (Fig. S21) Here, the combination of the presented SAXS pattern and the Vis-NIR spectra recorded from the same samples (Fig. 2(a)) allow for a direct correlation between the order of the assemblies and the obtained spectra. Previous works on colloidal crystals in microgel suspensions made use of optical spectroscopy to follow and/or identify crystallization but could not provide a direct link between optical properties and crystal structure as well as degree of order. Notably, the synchrotron SAXS (non-microfocus) and Vis-NIR spectroscopy applied here, both illuminate a relatively large volume. Therefore, the scattering data and optical spectra provide a representative ensemble picture of the crystalline assemblies of the CS microgels. Fig. 4(b) shows the radially averaged data (black circles) corresponding to the detector image shown in Fig. 4(a). The structure factor with pronounced and well distinguishable Bragg peaks is clearly visible in the mid to low q region (q < 0.15 nm−1). In addition, the form factor minima related to the core (q ≈ 0.23 nm−1) and the microgel shell (q < 0.1 nm−1) are clearly visible. Due to the distinct intensity minima, we can model the form factor even in the densely packed state where analysis is typically difficult/not possible due to changes in the microgel size and shape (osmotic deswelling and faceting)41,56,57 and the superposition with the structure factor. The red line in Fig. 4(b) corresponds to our modeled form factor. Here, the CS structure of our microgels simplifies the modeling process, because the core contribution is well resolved and isolated from the shell as well as structure factor contribution. Consequently, also the particle number density, N, can be precisely determined through the form factor contribution of the core. The contribution of the shell can be modeled based on the distinct form factor minimum at q ≈ 0.05 nm−1. With the resulting form factor, P(q), in the concentrated regime, we can calculate the structure factor by dividing the measured scattering intensity by P(q) similar as has been presented before in the fluid regime.The extracted structure factor is shown in Fig. 4(b) (green circles). In the high q region S(q) approaches the expected value of 1. This underlines that the modelled form factor describes the high q region precisely. In the limit of low q, S(q) approaches very low values close to zero. Extrapolation to q = 0 nm−1 reveals a value S(0) = 0.03.
The large number of Bragg peaks allows us to simulate theoretical scattering patterns in direct comparison to the recorded 2D detector images. Fig. 4(c) shows the good agreement with a hcp lattice. The Bragg peaks from simulation do not only match the experimental data in terms of peak positions and intensities but also the azimuthal and radial peak widths match closely. Detailed information on the simulation parameters and additional simulations performed on the 7.3 and 10.9 wt% samples are presented in Table S10 and Fig. S22 in the ESI.†
To further support the hcp structure, the agreement between measured peak positions and theoretical ones for a hcp lattice is also seen in Fig. 4(d). Here, the experimental structure factor is plotted with a normalized q axis. Normalization was done based on the position of the first structure factor maximum, q*. The vertical, red lines correspond to the calculated positions for a hcp lattice:
 | (1) |
A similar analysis for samples in a range of concentrations from 5.4 to 10.9 wt% is presented in Fig. 5(a). Here the q axis is again normalized by q*. Only in case of the 5.4 wt% sample that revealed a mostly fluid character after long temperature annealing, the data were normalized by the second structure factor maximum (110 plane). The first structure factor maximum located at q ≈ 0.02 nm−1 is mostly attributed to a fluid like structure factor while the second one at q ≈ 0.03 nm−1 exhibits a small width and more distinctive shape and therefore is considered as a Bragg peak. We relate the Bragg peak to small residual crystallites. In Fig. S24 (ESI†) we show a fit of the fluid-like structure factor. From this, we conclude that the volume fraction of the CS microgels in the 5.4 wt% dispersion is very close to the freezing concentration. As Fig. 2(c) indicates, only small change in temperature are required to induce the start of the crystallization or, vice-versa, melting.
For all samples with mass contents above 5.4 wt%, we find a nearly perfect agreement between the experimental and the theoretical positions of the Bragg peaks assigned to the hcp crystal structure. In Fig. 5(b), we show the linear relation of the Bragg peak position, qhkl, and the d-spacing between lattice planes for hcp structures. The slopes of the linear fits provide the respective lattice constants, a, according to:
 | (2) |
Table S11 in the ESI† lists the determined values of a. In addition, the lattice constant is accessible from the simulations of the 2D detector images like shown in Fig. 4(c) as well from the positions of the Bragg peaks from absorbance spectroscopy, λdiff:
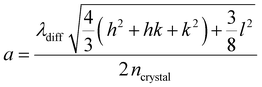 | (3) |
For the hcp crystal structure, we assign the Bragg peak from the absorbance spectra to the 002 lattice. Fig. S25 in the ESI† shows the good agreement of the lattice constants, a, as obtained from analysis of SAXS data and absorbance spectra. The lattice constant decreases from 322 nm (7.3 wt% sample) to 284 nm (10.9 wt% sample). We can now calculate the volume fraction of the crystalline samples, ϕcrystal, based on the unit cell dimensions:
 | (4) |
Fig. 5(c) compares the determined volume fractions based on the hydrodynamic radius in the dilute state, i.e. the generalized volume fraction, ζ (blue circles and black line) and using radii that we determined from the form factor analysis of the SAXS data directly in the densely packed state. The latter values allow us to rescale the hydrodynamic radius, Rh, using the obtained radii from SAXS in the dilute (RSAXS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) dil.) and concentrated state (RSAXS):
dil.) and concentrated state (RSAXS):
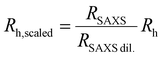 | (5) |
We see a good agreement between the volume fractions calculated based on Rh with the number concentration N (black line) and the volume fraction calculated with Rh and the unit cell dimensions (blue circles) shown in Fig. 5(c). The red lines indicate the standard deviation of the calculated ζ based on the number concentration. The values of ζ obtained from the unit cell dimensions lie within the respective standard deviation. This underlines the reliability of the extraction of ζ via the number concentration obtained from the scattering of the core in SAXS.
The calculated values of the effective volume fractions are presented in Fig. 5(c) as green symbols. The calculation is either based on the particle number concentration from SAXS measurements (filled, green symbols) or based on the lattice constants as obtained from SAXS measurements on crystalline samples (open, green circles). The data follow the same trend with slightly smaller volume fractions obtained from the crystal structure analysis. Again, the difference lies within the standard deviation with exception for the 5.4 wt% sample, where the lattice constant is related to small crystallites not representing the average bulk volume fraction of the dispersion. When reaching the threshold of crystallization (Fig. 2(d)) we observe a significant deviation of the volume fraction from the generalized volume fraction. This is most pronounced for the 9.1 and 10.9 wt% samples where the volume fraction approaches values of approximately 0.52 which is far away from the closed packed volume fraction of 0.74 for hard spheres. This is in agreement to the values reported by Scotti based on comprehensive analysis of microgels in dense packing using SANS.51
In addition, we show the respective volume fractions based only on RSAXS without any normalization to the hydrodynamic radius Rh in the ESI† (Fig. S26). Due to the smaller total size of the CS microgels as observed by SAXS, the determined volume fractions are significantly smaller although still following the trend seen in Fig. 5(c).
To analyze the domain sizes of the crystalline samples, we use the Williamson–Hall analysis64 that is based on the azimuthal and radial widths of the Bragg peaks as shown in Fig. S27 in the ESI.† This analysis revealed very low strains below 1% for our colloidal crystals and coherently scattering domain sizes between 3 and 4 μm (Fig. 5(d)). These values are in good agreement with the slightly smaller domain sizes from analysis of the 2D detector images using Scatter. Based on the total size of our CS microgels we estimate that these domain volumes contain approximately 2000 microgels per single domain.
Osmotic deswelling in the solid regime (crystalline)
As reported in the literature, the concentration of counterions, which determines the osmotic stress of the suspension, grows with increasing microgel concentration for ionic microgels37,38,65 and also for microgels that are often considered neutral but typically carry some charges from the ionic initiator.36,66 As a consequence, when the bulk modulus of the microgels is lower than the external osmotic pressure the microgels start to deswell, even when they are not in direct contact.36,39,51,67 In our case, the CS microgels carry chargeable groups that are only attributed to the used anionic radical initiator. The electrophoretic mobility measured at 20 °C and dilute conditions is −1.23 μm cm V−1 s−1. Thus, our microgels can be considered as weakly charged in the swollen state. Due to the unique contrast situation of our CS microgels for SAXS, we can extract the form factor even in the regime of dense packings, i.e. where S(q) ≠ 1. The measured SAXS profiles (symbols) and the modeled form factors (solid lines) are presented in Fig. 6(a). The high q region can be very reliably described with the form factor model due to the contribution of the core. Since the rigid cores do not change in size, shape and its size polydispersity remains constant, the form factor contribution of the cores does not change. This is highlighted by the vertical solid line that marks the position of the form factor minimum due to the core contribution. In the mid and, in particular, low q region where the structure factor contribution is strong, the fit and experimental data seem to deviate. This however is only caused by the absence of the structure factor in the model. The first minimum of the form factor contribution of the shell is still well-resolved and not hampered by the structure factor. Therefore, we get very good agreement between fit and data around the minimum (approximately 0.05 nm−1). The parameters used for the form factor modeling are listed in Table S12 in the ESI.† As the grey arrow indicates, the minimum associated to the microgel shell shifts towards lower q with decreasing concentration. This means that the particle size decreases with increasing concentration. In other words, the microgel shells shrink as the particle number density increases.Fig. 6(b) shows radial polymer density profiles as the result from the form factor analysis. The respective polymer volume fractions are extracted from a radial density profile of the scattering length density shown in Fig. S28 in the ESI.† Here we also present the constant integrals of the radial density profiles. The rigid silica cores have a mean radius of 18 nm. Consequently, in Fig. 6(b) the polymer volume fraction is zero for r < 18 nm. Within the shell region (r > 18 nm) the polymer volume fraction decreases from very similar values of 0.31, independently on the mass content of the samples, to zero, following the exponential decay of the SLD in the corresponding form factor model. With an increase in mass content, we can detect a decrease of RSAXS from 138 nm to 116 nm and a more pronounced decline in the exponential decay, indicating a deswelling process. The fact that we can accurately determine interparticle-distances, based on the lattice constant of the crystalline structure formed by the CS microgels, reveals that deswelling occurs far before interparticle contact. This again indicates the presence of a pronounced electrostatic influence on the microgel behavior, even when the particles are in the swollen state, exhibiting rather low electrophoretic mobilities. The influence of electrostatics on potential deswelling of microgels (here in the dilute state) was also shown by Bergman et al. where changes in the ionic strength of the dispersion resulted in a deswelling of charged microgels.11 Reconsidering the phase behavior of the CS microgels at 40 °C in addition to the deswelling, we conclude that the microgels must exhibit a pronounced electrostatic contribution. Therefore, the deswelling of the CS microgels, most likely, is a result of the overlapping between the individual ion-clouds exhibited by the microgels, increasing osmotic pressure, forcing the microgels to deswell. As we could not detect an increase in the polydispersity of the CS microgels for the deswelling process, in combination with the electrostatic contribution and due to the dense packing of the CS microgels inside of the colloidal crystal we conclude that the microgels undergo an isotropic osmotic deswelling.41,51,68 This leads to the decrease in radius and the more pronounced decline of the polymer volume fraction as described above. From literature it is known that the internal microgel architecture including the nominal crosslinker content dictates whether isotropic deswelling or faceting of the microgels is observed.13 For microgels with high nominal crosslinker contents (≥5 mol% BIS), like in our case, it is known that isotropic deswelling occurs before faceting.20,51 A similar behavior was found for hollow microgels that showed isotropic osmotic deswelling when the particle concentration in the dispersion was increased. In this case it was attributed that deswelling is favored over faceting due to the presence of the cavity inside the microgel which allows for rearrangement of the polymer chains within the microgel.56,69 Ultra low crosslinked microgels, expressing pronounced soft behavior, show faceting when they are dispersed in a crowded environment, rather than undergoing isotropic deswelling before microgels make contacts.51,70
4. Conclusion
Core–shell microgels with polymeric shells that are significantly larger than the incompressible core are ideal candidates to study fluid–solid transitions by small-angle scattering without the need of selective deuteration and contrast variation.20,35,51 We have shown that SAXS is particularly powerful given that the core as well as the shell provide sufficient contrast with respect to the solvent environment. In our case this was realized by silica-PNIPAM core–shell microgels with shell-to-core size ratios on the order of 8 (swollen state). The form factor contribution of the silica cores in the range of large q is well separated from the scattering of the shell and also from structure factor contributions in dense packings. Due to the overall microgel dimensions approaching the wavelength of visible light, crystallization of the microgels can be easily followed optically due to the photonic properties. We used absorbance spectroscopy as an efficient and easily available method to study solid–fluid/fluid–solid transitions induced by heating/cooling of the samples. Analysis of the data revealed very narrow temperature windows where the phase transitions occur with almost no hysteresis between heating and cooling within a change in volume fraction of about 0.05. The freezing point is registered at a volume fraction of 0.45 ± 0.05. The deviation from the value of hard spheres was explained by electrostatic interactions. The structures of the fluid and solid phases were studied by synchrotron SAXS. Structure factors extracted in the fluid regime indicate the presence of a pronounced electrostatic contribution in the phase behavior of the CS microgels. In addition, we did not observe any osmotic deswelling in dense packings of collapsed microgels. In contrast, the samples in the solid regime showed sharp Bragg peaks and many different diffraction orders upon very slow temperature annealing of the samples. Analysis of the scattering data revealed hcp structures and domain sizes in the micrometer range. Due to the combination of synchrotron SAXS and optical spectroscopy on the very same samples, both methods probing rather large sample volumes, we were able to provide a representative correlation between the optical properties and ensemble structure of the CS microgel assemblies. From the scattering profiles of the crystalline samples, we could also directly determine the form factor of the CS microgels. Data analysis revealed osmotic deswelling with an extend that increases with increasing concentration.The unique combination of our silica-PNIPAM core–shell microgels and properly chosen shell-to-core size ratio with synchrotron SAXS is ideally suited to determine form as well as structure factors even in packings exceeding the hard sphere limit. Due to the great resolution of SAXS and the extremely short acquisition times, in situ studies on phase transitions over a broad range of packing densities will be possible in future works. A comprehensive follow-up work addressing in more detail the role of electrostatics in the phase behavior of our core–shell microgels using charged and charge-screened conditions is currently underway.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
The authors acknowledge the German Research Foundation (DFG) and the state of NRW for funding the cryo-TEM (INST 208/749-1 FUGG) and Marius Otten from Heinrich-Heine-University Düsseldorf for his assistance with the operation and image recording. The authors thank the Center for Structural Studies (CSS) that is funded by the DFG (grant numbers 417919780 and INST 208/761-1 FUGG) for access to the SAXS instrument. A. S. thanks the DFG for financial support of project A3 (project no. 191948804) within the SFB 985 – Functional Microgels and Microgel Systems. The authors acknowledge Déborah Feller from Heinrich-Heine-University Düsseldorf for her assistance with the operation of the angle-dependent dynamic light scattering setup. A. V. Petrunin, T. Höfken, and P. Mota-Santiago helped with the SAXS measurements. The SAXS measurements were performed on the CoSAXS beamline at the MAX IV laboratory (Lund, Sweden) under the proposals 20200777 and 20220526. The Research conducted at MAX IV, a Swedish national user facility, is supported by the Swedish Research council under contract 2018-07152, the Swedish Governmental Agency for Innovation Systems under contract 2018-04969, and Formas under contract 2019-02496. This work benefited from the use of the SasView application, originally developed under NSF award DMR-0520547. SasView contains code developed with funding from the European Union's Horizon 2020 research and innovation programme under the SINE2020 project, grant agreement no 654000.References
- M. Karg, A. Pich, T. Hellweg, T. Hoare, L. A. Lyon, J. J. Crassous, D. Suzuki, R. A. Gumerov, S. Schneider, I. I. Potemkin and W. Richtering, Langmuir, 2019, 35, 6231–6255 CrossRef CAS PubMed
.
- R. Pelton, Adv. Colloid Interface Sci., 2000, 85, 1–33 CrossRef CAS PubMed
.
- F. A. Plamper and W. Richtering, Acc. Chem. Res., 2017, 50, 131–140 CrossRef CAS PubMed
.
- J. D. Debord and L. A. Lyon, J. Phys. Chem. B, 2000, 104, 6327–6331 CrossRef
.
- L. A. Lyon, J. D. Debord, S. B. Debord, C. D. Jones, J. G. McGrath and M. J. Serpe, J. Phys. Chem. B, 2004, 108, 19099–19108 CrossRef CAS
.
- M. Destribats, V. Lapeyre, M. Wolfs, E. Sellier, F. Leal-Calderon, V. Ravaine and V. Schmitt, Soft Matter, 2011, 7, 7689–7698 RSC
.
- A. Scotti, S. Bochenek, M. Brugnoni, M. A. Fernandez-Rodriguez, M. F. Schulte, J. E. Houston, A. P. H. Gelissen, I. I. Potemkin, L. Isa and W. Richtering, Nat. Commun., 2019, 10, 1418 CrossRef CAS PubMed
.
- B. Brugger, B. A. Rosen and W. Richtering, Langmuir, 2008, 24, 12202–12208 CrossRef CAS PubMed
.
- Y. Hertle and T. Hellweg, J. Mater. Chem. B, 2013, 1, 5874–5885 RSC
.
- I. Berndt, J. S. Pedersen and W. Richtering, J. Am. Chem. Soc., 2005, 127, 9372–9373 CrossRef CAS PubMed
.
- M. J. Bergman, J. S. Pedersen, P. Schurtenberger and N. Boon, Soft Matter, 2020, 16, 2786–2794 RSC
.
- B. Sierra-Martin and A. Fernandez-Nieves, Soft Matter, 2012, 8, 4141–4150 RSC
.
- A. Scotti, M. F. Schulte, C. G. Lopez, J. J. Crassous, S. Bochenek and W. Richtering, Chem. Rev., 2022, 122, 11675–11700 CrossRef CAS PubMed
.
-
M. Karg, S. Prévost, A. Brandt, D. Wallacher, R. von Klitzing and T. Hellweg, Progress in Colloid and Polymer Science, Springer International Publishing, Switzerland, 2013, vol. 140, pp. 63–76 Search PubMed
.
- M. Heskins and J. E. Guillet, J. Macromol. Sci., Part A: Pure Appl. Chem., 1968, 2, 1441–1455 CrossRef CAS
.
- A. Halperin, M. Kroger and F. M. Winnik, Angew. Chem., Int. Ed., 2015, 54, 15342–15367 CrossRef CAS PubMed
.
- R. H. Pelton and P. Chibante, Colloids Surf., 1986, 20, 247–256 CrossRef CAS
.
- A. Rauh, T. Honold and M. Karg, Colloid Polym. Sci., 2016, 294, 37–47 CrossRef CAS
.
- M. Stieger, W. Richtering, J. S. Pedersen and P. Lindner, J. Chem. Phys., 2004, 120, 6197–6206 CrossRef CAS PubMed
.
- S. Nöjd, P. Holmqvist, N. Boon, M. Obiols-Rabasa, P. S. Mohanty, R. Schweins and P. Schurtenberger, Soft Matter, 2018, 14, 4150–4159 RSC
.
- X. Wu, R. H. Pelton, A. E. Hamielec, D. R. Woods and W. McPhee, Colloid Polym. Sci., 1994, 272, 467–477 CrossRef CAS
.
- E. Ponomareva, B. Tadgell, M. Hildebrandt, M. Krüsmann, S. Prévost, P. Mulvaney and M. Karg, Soft Matter, 2022, 18, 807–825 RSC
.
- J. Dubbert, T. Honold, J. S. Pedersen, A. Radulescu, M. Drechsler, M. Karg and W. Richtering, Macromolecules, 2014, 47, 8700–8708 CrossRef CAS
.
- M. Rey, M. A. Fernandez-Rodriguez, M. Karg, L. Isa and N. Vogel, Acc. Chem. Res., 2020, 53, 414–424 CrossRef CAS PubMed
.
- T. Hellweg, Angew. Chem., Int. Ed., 2009, 48, 6777–6778 CrossRef CAS PubMed
.
- M. A. Fernández-Rodríguez, R. Elnathan, R. Ditcovski, F. Grillo, G. M. Conley, F. Timpu, A. Rauh, K. Geisel, T. Ellenbogen, R. Grange, F. Scheffold, M. Karg, W. Richtering, N. H. Voelcker and L. Isa, Nanoscale, 2018, 10, 22189–22195 RSC
.
- K. Volk, F. Deißenbeck, S. Mandal, H. Löwen and M. Karg, Phys. Chem. Chem. Phys., 2019, 21, 19153–19162 RSC
.
- D. Lapkin, N. Mukharamova, D. Assalauova, S. Dubinina, J. Stellhorn, F. Westermeier, S. Lazarev, M. Sprung, M. Karg, I. A. Vartanyants and J. M. Meijer, Soft Matter, 2022, 18, 1591–1602 RSC
.
- T. Hellweg, C. D. Dewhurst, E. Brückner, K. Kratz and W. Eimer, Colloid Polym. Sci., 2000, 278, 972–978 CrossRef CAS
.
- M. Karg, T. Hellweg and P. Mulvaney, Adv. Funct. Mater., 2011, 21, 4668–4676 CrossRef CAS
.
- J. Bocanegra-Flores, C. Haro-Pérez, D. Reyes-Contreras and L. F. Rojas-Ochoa, Front. Phys., 2022, 10, 988903 CrossRef
.
- H. Senff and W. Richtering, J. Chem. Phys., 1999, 111, 1705–1711 CrossRef CAS
.
- A. M. Alsayed, M. F. Islam, J. Zhang, P. J. Collings and A. G. Yodh, Science, 2005, 309, 1207–1210 CrossRef CAS PubMed
.
- J. N. Immink, M. J. Bergman, J. J. E. Maris, J. Stenhammar and P. Schurtenberger, ACS Nano, 2020, 14, 14861–14868 CrossRef CAS PubMed
.
- P. S. Mohanty, S. Nöjd, K. van Gruijthuijsen, J. J. Crassous, M. Obiols-Rabasa, R. Schweins, A. Stradner and P. Schurtenberger, Sci. Rep., 2017, 7, 1487 CrossRef PubMed
.
- A. Scotti, U. Gasser, E. S. Herman, M. Pelaez-Fernandez, J. Han, A. Menzel, L. A. Lyon and A. Fernandez-Nieves, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 5576–5581 CrossRef CAS PubMed
.
- M. Pelaez-Fernandez, A. Souslov, L. A. Lyon, P. M. Goldbart and A. Fernandez-Nieves, Phys. Rev. Lett., 2015, 114, 098303 CrossRef CAS PubMed
.
- A. Scotti, M. Pelaez-Fernandez, U. Gasser and A. Fernandez-Nieves, Phys. Rev. E, 2021, 103, 012609 CrossRef CAS PubMed
.
- C. Pellet and M. Cloitre, Soft Matter, 2016, 12, 3710–3720 RSC
.
- G. M. Conley, P. Aebischer, S. Nöjd, P. Schurtenberger and F. Scheffold, Sci. Adv., 2017, 3, e1700969 CrossRef PubMed
.
- T. Höfken, C. Strauch, S. Schneider and A. Scotti, Nano Lett., 2022, 22, 2412–2418 CrossRef PubMed
.
- G. K. Batchelor, J. Fluid Mech., 1977, 83, 97–117 CrossRef
.
- K. D. Hartlen, A. P. T. Athanasopoulos and V. Kitaev, Langmuir, 2008, 24, 1714–1720 CrossRef CAS PubMed
.
- SasView, https://www.sasview.org/.
- S. Förster, L. Apostol and W. Bras, J. Appl. Crystallogr., 2010, 43, 639–646 CrossRef
.
- S. W. Provencher, Comput. Phys. Commun., 1982, 27, 213–227 CrossRef
.
- C. A. Schneider, W. S. Rasband and K. W. Eliceiri, Nat. Methods, 2012, 9, 671–675 CrossRef CAS PubMed
.
- A. Rauh, N. Carl, R. Schweins and M. Karg, Langmuir, 2018, 34, 854–867 CrossRef CAS PubMed
.
- B. Tadgell, E. Ponomareva, M. Karg and P. Mulvaney, J. Phys. Chem. C, 2022, 126, 4118–4131 CrossRef CAS
.
- M. Hildebrandt, S. Lazarev, J. Pérez, I. A. Vartanyants, J. M. Meijer and M. Karg, Macromolecules, 2022, 55, 2959–2969 CrossRef CAS
.
- A. Scotti, Soft Matter, 2021, 17, 5548–5559 RSC
.
- B. J. Alder, W. G. Hoover and D. A. Young, J. Chem. Phys., 1968, 49, 3688–3696 CrossRef CAS
.
- J. K. Percus and G. J. Yevick, Phys. Rev., 1958, 110, 1–13 CrossRef CAS
.
- T. Eckert and W. Richtering, J. Chem. Phys., 2008, 129, 124902 CrossRef PubMed
.
- U. Gasser and A. Fernandez-Nieves, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 81, 052401 CrossRef CAS PubMed
.
- A. Scotti, A. R. Denton, M. Brugnoni, J. E. Houston, R. Schweins, I. I. Potemkin and W. Richtering, Macromolecules, 2019, 52, 3995–4007 CrossRef CAS
.
- A. Scotti, A. R. Denton, M. Brugnoni, R. Schweins and W. Richtering, Phys. Rev. E, 2021, 103, 022612 CrossRef CAS PubMed
.
- J. M. Meijer, A. Shabalin, R. Dronyak, O. M. Yefanov, A. Singer, R. P. Kurta, U. Lorenz, O. Gorobstov, D. Dzhigaev, J. Gulden, D. V. Byelov, A. V. Zozulya, M. Sprung, I. A. Vartanyants and A. V. Petukhov, J. Appl. Crystallogr., 2014, 47, 1199–1204 CrossRef CAS
.
- A. V. Petukhov, I. P. Dolbnya, D. G. A. L. Aarts, G. J. Vroege and H. N. W. Lekkerkerker, Phys. Rev. Lett., 2003, 90, 028304 CrossRef CAS PubMed
.
- J. M. Meijer, V. W. A. de Villeneuve and A. V. Petukhov, Langmuir, 2007, 23, 3554–3560 CrossRef CAS PubMed
.
- J. Brijitta, B. V. R. Tata, R. G. Joshi and T. Kaliyappan, J. Chem. Phys., 2009, 131, 074904 CrossRef CAS PubMed
.
- U. Gasser, J. J. Lietor-Santos, A. Scotti, O. Bunk, A. Menzel and A. Fernandez-Nieves, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88, 052308 CrossRef CAS PubMed
.
- I. Sanchez-Burgos, E. Sanz, C. Vega and J. R. Espinosa, Phys. Chem. Chem. Phys., 2021, 23, 19611–19626 RSC
.
- E. A. Sulyanova, A. Shabalin, A. V. Zozulya, J. M. Meijer, D. Dzhigaev, O. Gorobtsov, R. P. Kurta, S. Lazarev, U. Lorenz, A. Singer, O. Yefanov, I. Zaluzhnyy, I. Besedin, M. Sprung, A. V. Petukhov and I. A. Vartanyants, Langmuir, 2015, 31, 5274–5283 CrossRef CAS PubMed
.
- R. Borrega, M. Cloitre, I. Betremieux, B. Ernst and L. Leibler, Europhys. Lett., 1999, 47, 729–735 CrossRef CAS
.
- U. Gasser, A. Scotti and A. Fernandez-Nieves, Phys. Rev. E, 2019, 99, 042602 CrossRef CAS PubMed
.
- A. S. Iyer and L. A. Lyon, Angew. Chem., Int. Ed., 2009, 48, 4562–4566 CrossRef CAS PubMed
.
- F. Scheffold, P. Díaz-Leyva, M. Reufer, N. Ben Braham, I. Lynch and J. L. Harden, Phys. Rev. Lett., 2010, 104, 128304 CrossRef PubMed
.
- A. Scotti, M. Brugnoni, A. A. Rudov, J. E. Houston, I. I. Potemkin and W. Richtering, J. Chem. Phys., 2018, 148, 174903 CrossRef CAS PubMed
.
- A. Scotti, J. E. Houston, M. Brugnoni, M. M. Schmidt, M. F. Schulte, S. Bochenek, R. Schweins, A. Feoktystov, A. Radulescu and W. Richtering, Phys. Rev. E, 2020, 102, 052602 CrossRef CAS PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3sm01062g |
| This journal is © The Royal Society of Chemistry 2023 |