Open Access Article
Open Access ArticleThe structure of disintegrating defect clusters in smectic C freely suspended films
Ralf
Stannarius
 *a and
Kirsten
Harth
*a and
Kirsten
Harth
 *b
*b
aInstitute of Physics, Otto von Guericke University Magdeburg, Universitätsplatz 2, D-39106 Magdeburg, Germany. E-mail: ralf.stannarius@ovgu.de
bDepartment of Engineering, Brandenburg University of Applied Sciences, Magdeburger Straße 50, D-14770 Brandenburg an der Havel, Germany. E-mail: kirsten.harth@th-brandenburg.de
First published on 28th July 2023
Abstract
Disclinations or disclination clusters in smectic C freely suspended films with topological charges larger than one are unstable. They disintegrate, preferably in a spatially symmetric fashion, into single defects with individual charges of +1, which is the smallest positive topological charge allowed in polar vector fields. While the opposite process of defect annihilation is well-defined by the initial defect positions, disintegration starts from a singular state and the following scenario including the emerging regular defect patterns must be selected by specific mechanisms. We analyze experimental data and compare them with a simple model where the defect clusters adiabatically pass quasi-equilibrium solutions in one-constant approximation. It is found that the defects arrange in geometrical patterns that correspond very closely to superimposed singular defect solutions, without additional director distortions. The patterns expand by affine transformations where all distances between individual defects scale with the same time-dependent scaling factor proportional to the square-root of time.
1 Introduction
Topological defects play a significant role in a huge variety of physical systems, including for example anisotropic soft matter,1–9 biological matter,10–14 superfluidic liquids,15–17 quantum systems,18–20 or even cosmology.21,22 The close resemblance of topological defects in biological systems and in active nematics has been emphasized.10,13,23 Coarsening of defect patterns is a common feature in the initial evolution of dynamic systems after symmetry-breaking phase transitions. The elementary processes of such coarsening scenarios are mutual annihilations of topological defect pairs with opposite charges, a scenario that has been considered in a variety of studies in different fields. It shall be mentioned that in liquid-crystalline systems in general, disclinations are quite easily prepared and observed in experiments, and the annihilation of point defects in particular has been studied extensively. A recent review of this field can be found in ref. 24.In a previous experiment with smectic C freely suspended films, the annihilation of oppositely charged defects was studied experimentally, and the role of the anisotropy of elastic constants and of macroscopic material flow in the films was demonstrated.25 The elastic anisotropy mainly manifests itself in a preferential pinning of the director near the defect cores. A model developed earlier for nematic systems26,27 was employed and extended to describe the experimentally observed effects of mutual defect orientation on the annihilation dynamics. One key ingredient of this model is the fixed orientation of defects with topological strength S = +1 in such films, mentioned above as a consequence of the elastic anisotropy.
The motivation to study this particular system and geometry is that the smectic freely suspended liquid-crystalline films offer clear advantages for systematic studies of defect interactions: first, the films allow to investigate defect dynamics in a quasi two-dimensional (2D) geometry. The air above and below the films does not affect local orientations and has only little influence on flow in the film plane. In addition, the observation of defect motions and orientations is straightforward by means of polarizing microscopy. The timescales of defect dynamics in the range of seconds are convenient for video recording, and the continuum equations governing the film dynamics are well developed. Several, but not all involved material parameters are known from other experiments. Simple methods for the experimental preparation of defect patterns in such films have been established.25,28–32
The present study does not deal with the annihilation dynamics but focuses on the opposite scenario, the decomposition of high-strength point defects. The basis of the following theoretical analysis is an earlier experimental investigation of smectic C freely suspended films with mutually repelling topological defects of equal charges.32 The emerging single defects arrange in certain characteristic, highly symmetric patterns. The structure of these patterns has no obvious relation to the initial state. We derive a model for the pattern selection and explain why some typical patterns are found experimentally while others are avoided.
2 Experimental observations
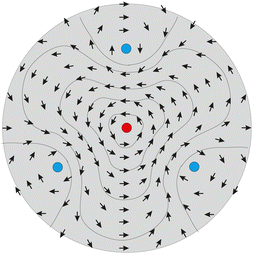
In the smectic C phase, the mesogens are on average tilted with respect to the smectic layer plane. The molecular layers in smectic free-standing films are in the film plane, perfectly stacked. The local mesogen orientation is described by the c-director field, which points in the direction of the local tilt. Because![[c with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0063_20d1.gif) is a true vector, defects with half-integer topological strength are forbidden and the defects with the lowest elastic energy are those with topological strengths S = +1 and −1. The energy of each defect is proportional to the square of its topological charge,33,34 thus defects with higher topological charges |S0| > 1 have higher elastic energies than the sum of N = |S0| defects of charges S = + 1 or −1, resp., with the same total topological charge. As a consequence, defects with strength S0 > 1 (S0 = 2, 3, 4,…) will decompose into N defects of topological charges +1, under conservation of the total charge.
is a true vector, defects with half-integer topological strength are forbidden and the defects with the lowest elastic energy are those with topological strengths S = +1 and −1. The energy of each defect is proportional to the square of its topological charge,33,34 thus defects with higher topological charges |S0| > 1 have higher elastic energies than the sum of N = |S0| defects of charges S = + 1 or −1, resp., with the same total topological charge. As a consequence, defects with strength S0 > 1 (S0 = 2, 3, 4,…) will decompose into N defects of topological charges +1, under conservation of the total charge.
When N defects of equal topological strength +1 are initially trapped within a narrow region, and then are released from this trap, they behave analogously to a decomposing single defect of topological charge S0. Such an experiment was performed earlier, and an experimental technique to prepare a restricted region where the director field has a total topological charge S0 > 1 was introduced.32 The technique basically exploits the fact that film regions with a reduced number of smectic layers (so-called ‘holes’) can trap defects. The defect energy depends linearly upon the local film thickness, thus defects in thinner film regions are caged there. When one is able to produce a local area of reduced film thickness that contains a number of topological defects of the c-director field, this will often lead to a stable configuration where the line tension of the dislocations surrounding the hole is balanced by the defect repulsion. The mutually repelling defects cannot leave the hole into the thicker surrounding film regions, so they distribute themselves along the perimeter of the hole. This arrangement prevents the hole itself from shrinking and vanishing.
The material used in the experiment was a non-chiral room-temperature SmC binary (50 vol%![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 vol%) mixture of 5-n-octyl-2-[4-(n-octyloxy)phenyl]pyrimidine and 5-n-octyl-2-[4-(n-hexyloxy)phenyl]pyrimidine.32 All experiments were performed at room temperature. Thin films were drawn across a frame with one moveable edge inside a THMS 400 hot stage. The width of the films was approximately 4 mm. The defect textures were observed using a Carl Zeiss AxioImagerPol polarizing microscope under crossed polarizers (horizontal and vertical in the images). In most of the experiments, a diagonal λ = 550 nm phase plate was inserted to distinguish the two diagonal c-director orientations in the textures. The films around the trap had uniform thicknesses roughly in the range from 300 nm to 3000 nm. After quenching the hole containing the defects, the film thicknesses were homogeneous in the observation area.
50 vol%) mixture of 5-n-octyl-2-[4-(n-octyloxy)phenyl]pyrimidine and 5-n-octyl-2-[4-(n-hexyloxy)phenyl]pyrimidine.32 All experiments were performed at room temperature. Thin films were drawn across a frame with one moveable edge inside a THMS 400 hot stage. The width of the films was approximately 4 mm. The defect textures were observed using a Carl Zeiss AxioImagerPol polarizing microscope under crossed polarizers (horizontal and vertical in the images). In most of the experiments, a diagonal λ = 550 nm phase plate was inserted to distinguish the two diagonal c-director orientations in the textures. The films around the trap had uniform thicknesses roughly in the range from 300 nm to 3000 nm. After quenching the hole containing the defects, the film thicknesses were homogeneous in the observation area.
Using the preparation method described above, we were able to create structures with total defect strengths S0 between +4 and +12 (Fig. 1) in experiments, and there seems to be no principal limit to trap more defects.32 The technique to release the defects from their cage involves a quick in-plane compression of the film so that the hole is quenched and the trap is eliminated.
The unleashed identical defects repel each other, and the local cluster will thus spread rapidly. The initial state is a cluster of defects uniformly distributed on the periphery of a tiny circular region. Thus, one might naturally expect from symmetry considerations, that after the release of these defects, they all move away radially from the cluster center, uniformly distributed on a circle. This scenario was surprisingly never observed in our experiments.
Instead, in the majority of experiments, the initial cluster decomposed with one defect remaining in the center and all others moving away radially [Fig. 2(a and b)]. In few cases, other scenarios were found like an S0 = 6 cluster consisting of two inner and four outer, nearly symmetrically arranged defects that all moved radially away from the cluster center [Fig. 2(c)]. Also, a cluster of two inner and six outer defects was found for S0 = 8 as shown below. The reason for the preference of these structures, and the absence of others, will be given in the following. We note that the absolute thickness of the homogeneous film itself after extinction of the hole does not influence the structure and dynamics of the decomposition process: the relevant quantities, e.g. the dissipation in the film and the elastic energies, both scale linearly with the film thickness.
The result of the previous experimental study32 was that the pinning of the c-director field in the vicinity of the core of a +1 defect is an essential feature that determines the disintegration process. In a strict one-constant elastic approximation, the director is not restricted to a tangential orientation near the defect core, it may have any offset angle, the defect can have a tangential or radial director field or any other phase. However, the elastic constant for bend of the c-director field, KB is actually considerably smaller than the constant for splay, KS. The experimentally determined ratio32 is KS/KB ≈ 2.2. As a consequence, a defect with a radial orientation of the c-director around its core would have a substantially larger elastic energy than a defect with purely tangential anchoring of the c-director around the core. It would thus change to tangential orientation. The tangential defects represent the lowest energy configuration, and in fact, all +1 defects in the experiments had a tangentially pinned c-director (cf.Fig. 2). Such defects can either have a clockwise or counterclockwise orientation of the c-director, with equal elastic energies. In ferroelectric smectic C* phases, this symmetry may be broken35 and there may be a preference for one of the two winding senses, but not in the smectic C material used here. In Fig. 2(a and b), the outer defects have the same winding sense, opposite to that of the central one.
3 Model for the defect configurations
It was argued in ref. 32 that a construction of a cluster of three tangential +1 defects by simple superposition of the single defect solutions is possible only if they are arranged along a straight line. Otherwise, one has to introduce additional distortions of the director field to satisfy the tangential anchoring conditions near the defect cores. In contrast, when more than three defects are involved, there are arrangements of superimposed single-defect solutions that fulfill the anchoring conditions without the necessity to add further distortions. For example, a symmetric arrangement of four defects as observed experimentally [Fig. 2(a)] can be constructed by a mere superposition of four individual +1 defects even if the defects are not lined up. Fig. 3 sketches the c-director field for the case S0 = 4, constructed as a linear superposition of the solutions for the director deflection angles obtained from four individual defects. Superficially, it might appear as if the inversion walls between the outer defects have been additionally included, but they are actually the result of the superposition of the analytical single-defect solutions. In absence of other director distortions, one can find simple analytical solutions for static defect configurations (i.e. assuming fixed defect positions) of this type in elastic one-constant approximation. During the actual cluster disintegration, the central defect remains in the original position, the other three move radially outward. Because of the spatial and temporal scaling characteristics of the involved dynamic equations for the c-director and flow fields, the solutions are self-similar when all spatial dimensions are scaled with t1/2, provided that the mutual defect distances are large compared to the defect core radii (This is in contrast to ref. 36 where the defects with overlapping cores were very close to each other and therefore different scaling factors were obtained.). This scaling behavior is fully confirmed in our experiments.We suggest a model for the pattern selection based on the following simplifying assumptions:
1. The defect patterns evolve quasi-adiabatically, i.e. they pass through states equivalent to static equilibrium solutions of the director field with fixed positions of all defects. This assumption was also made for the description of annihilation dynamics.33,34
2. The director fields for individual defects can be described in first approximation by the analytical one-constant solutions. We disregard the fact that splayed regions are expanded and bent regions are actually quenched in our material. The only effect of elastic anisotropy is the tangential pinning of the director at the core.
3. After decomposition of the initial cluster, the disclinations are arranged in such a way that additional distortions are avoided, and they choose patterns where the tangential pinning at each defect core is fulfilled by a mere superposition of single defect solutions.
4. Once these patterns have formed, they expand in a self-similar way. The scaling factor of all distances is proportional to t(1/2), where t is the time from the begin of the disintegration process.
The close resemblance of the experimentally observed textures with those obtained from superimposed single-defect solutions will serve as the main argument to justify this model. As explained above, Fig. 2(a) and 3 represent a structure that meets our conditions. Other such solutions for higher S0 are shown in Fig. 2(b and c), as will be demonstrated below.
In our ‘quasi-one-constant’ elastic model, we assume that the director field far from the defect core can still be described satisfactorily by the one-constant approximation, but the actually existing elastic anisotropy leads to the tangential pinning of the director at the cores of the +1 disclinations. There are reasonable arguments for this: at the core, the elastic energy diverges and the difference between splay and bend plays a decisive role, while outside the cores, the elastic anisotropy will merely lead to certain local corrections but not to qualitatively new solutions.
4 Disintegration dynamics
The simplest model for defect interactions33 assumes that the elastic constants for splay and bend of the c-director are equal, flow is neglected, and the orientational deformations are assumed as a linear superposition of isolated defects. The force between two such defects separated by a distance r12 is:34,37| f12 = 2πKS1S2/r12. | (1) |
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) 12. K is a mean elastic constant, and S1,2 are the defect strengths. Disclinations of the same sign, such as considered in our study, repel each other. This equation was derived for nematics, but it can be used for the smectic C films as well with a proper redefinition of K. A defect motion with velocity V relative to the film material is counteracted by a drag force fdrag = 2γV
12. K is a mean elastic constant, and S1,2 are the defect strengths. Disclinations of the same sign, such as considered in our study, repel each other. This equation was derived for nematics, but it can be used for the smectic C films as well with a proper redefinition of K. A defect motion with velocity V relative to the film material is counteracted by a drag force fdrag = 2γV![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(3.6/Er), where Er = γvrc/K is the Ericksen number, γ the rotational viscosity, v a characteristic velocity scale, and rc the defect core radius.37 This adjusts the defect velocities in this overdamped system to
ln(3.6/Er), where Er = γvrc/K is the Ericksen number, γ the rotational viscosity, v a characteristic velocity scale, and rc the defect core radius.37 This adjusts the defect velocities in this overdamped system to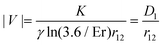 | (2) |
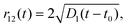 | (3) |
It should be noted that Radzihovsky39 raised the objection that a moving defect may not necessarily have the same structure as a defect at rest relative to the film material. Experimentally, such effects have not been detected, presumably they are too small in the present experiments.
Finally, one also has to consider the effects of material flow on the defect dynamics: it is well known that the motion of a disclination in the film plane causes material flow, in particular in the vicinity of defects with topological charge +1.36 This flow field has several consequences: first, it speeds up the motion of the +1 defect because the material locally flows in the same direction as the defect core is displaced relative to the film. Second, it leads to an asymmetry in the annihilation of defect pairs.36 In experiments, flow generated in the annihilation process of defect pairs in freely suspended Smectic C films has been demonstrated using fluorescence microscopy and a photo-bleaching technique.40 In the present cluster disintegration scenario, however, an experimental confirmation of backflow has not been tackled yet. Nevertheless, we hypothesize that near the positions of the outer +1 defects, the flow field is directed outward, with the defect motion, thus increasing the defect speed. A compensating flow directed inward is expected in the inversion wall regions between the outer defects, in order to fulfill the continuity equation. When more defects are on the periphery, the distance between these defects becomes smaller and shear forces will dampen the supporting flow field, therefore, it can be expected that the acceleration of the defects by flow will be particularly effective for small S0, whereas it will rapidly decrease with larger S0.
5 Geometrical analysis of groups of tangential +1 defects
In the following geometrical considerations, we will neglect flow and consider the static solutions in one-constant approximation. The advantage of the one-constant model without flow is that it yields a crude but analytical approximation for the patterns and their dynamics. A square-root law, similar to eqn (3), will remain effective even when the neglected terms related to material flow and elastic anisotropy are included.The experiments show that the geometry of the growing defect pattern, once it has formed, remains constant. Thus, it is sufficient for the following discussion to consider an arbitrarily chosen snapshot of the video sequences and discuss the defect arrangement in order to obtain the full description of the spatio-temporal behavior.
We will discuss, which types of defect configurations can be constructed under the model assumptions given above, as superpositions of single-defect equilibrium solutions. For the analysis of these configurations, a 2D vector field ![[n with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006e_20d1.gif) 0(x, y) = [nx(x, y), ny(x, y)] is considered in the (x, y) plane, and the azimuthal angle θ is defined such that nx = |
0(x, y) = [nx(x, y), ny(x, y)] is considered in the (x, y) plane, and the azimuthal angle θ is defined such that nx = |![[n with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006e_20d1.gif) 0|cos
0|cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ(x, y), ny = |
θ(x, y), ny = |![[n with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006e_20d1.gif) 0|sin
0|sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ(x, y). N defects of identical topological charges Si = +1 (i = 1, 2, 3,…N) are distributed in the plane. In the vicinity of the core of the i-th defect, θ = φi + θi, where φi is the azimuthal angle of the spatial vector from the defect center and θi is a phase angle. Tangential orientation means that θi = (ni + 1/2)π, (integer ni). For even ni, the rotation of the director around the core is counterclockwise, and for odd ni this rotation is clockwise. In the system considered here, all defects have a tangential orientation of the director near the core as a result of the minimization of the free energy when bend is favored over splay. In a material where splay deformations are energetically favored, an analogous treatment is possible. The solutions are the same except that an offset of π/2 has to be added to θ(x, y).
θ(x, y). N defects of identical topological charges Si = +1 (i = 1, 2, 3,…N) are distributed in the plane. In the vicinity of the core of the i-th defect, θ = φi + θi, where φi is the azimuthal angle of the spatial vector from the defect center and θi is a phase angle. Tangential orientation means that θi = (ni + 1/2)π, (integer ni). For even ni, the rotation of the director around the core is counterclockwise, and for odd ni this rotation is clockwise. In the system considered here, all defects have a tangential orientation of the director near the core as a result of the minimization of the free energy when bend is favored over splay. In a material where splay deformations are energetically favored, an analogous treatment is possible. The solutions are the same except that an offset of π/2 has to be added to θ(x, y).
In absence of other director distortions, the c-director angle θ(x, y) in the film plane is additively composed of the sum of N contributions φi and a constant offset θo. The phase angle θk of a given defect k thus results from the contributions of the other N − 1 defects and the offset:
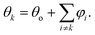 | (4) |
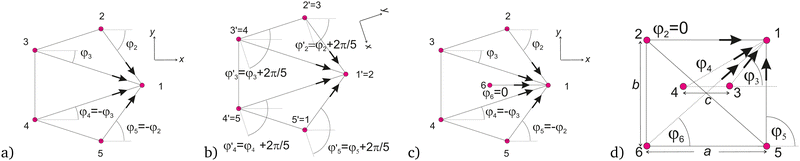
Let us now analyze configurations without central defect, where the outer N defects are arranged symmetrically in a distance R from the center in angular directions 2π(i − 1)/N (Fig. 4a and b).
In that case, a superposition of the distortions yields different phases for all five defects according to eqn (4). This can be derived straightforwardly. We demonstrate it for the example N = 5, shown in Fig. 4a: the sum of the four contributions to defect 1 is θ1 = φ2 + φ5 + φ3 + φ4 = θo, because symmetry requires φ4 = −φ3 and φ5 = −φ2 when defect 1 is located in x direction from the center. For the second defect, k = 2, it is easiest to find the phase by rotating the coordinate system by 2π/N and re-labeling the defects as shown in Fig. 4b. Now, each of the four (i.e. N − 1) azimuth angles φi, (i ≠ k) is increased by the rotation angle 2π/N, yielding the total phase 2π(N − 1)/N + θ0 for defect 2. In the same way, one finds that all defects k = 1, 2, 3, 4, 5 obtain the phases
| θk = 2π(k − 1)(N − 1)/N + θ0. |
One can nevertheless force configurations as solutions of the director field where all N defects in such an arrangement become tangential, but this would require the introduction of additional deformations of the director field, and thus additional elastic energy. It should be noted that in the experiments,32 we have never found this type of configurations after the disintegration of the central defect cluster. This is a strong indication that the system tries to avoid the additional elastic distortions. It applies even though the system is naturally not in equilibrium when the defect cluster spreads.
When one analyzes the second case, with a symmetric arrangement of N − 1 defects outside and one central defect, the situation changes completely. For N = 3, these are the trivial three lined-up defects. The case N = 6 is shown in Fig. 4c. The outer defects 2, 3, 4 and 5 contribute a total phase of zero to θ1, as indicated in the figure. On the other hand, these defects k = 2, 3, 4, 5, as in the previous case, gain the contributions 2π(k − 1)(N − 1)/N to θk from the other outer defects. However, the central defect additionally contributes a phase 2π(k − 1)/N to each of them so that the outer defects obtain the phases θk = 2π(k − 1) + θo. Thus, the θk are integer multiples of 2π plus the offset. For the central defect, the sum of all outer defects yields π, because contributions of defects 2…N − 1 cancel each other for symmetry reasons. Only the contribution of the first defect, φ1 = π, remains besides θo. As a consequence, the arrangement shown in Fig. 4 and all structurally similar arrangements for N ≥ 3 can be constructed by the superposition of the individual single-defect solutions without adding other deformations. With a proper choice of θo (depending on the orientation of the coordinate system) one can make all defects tangential.
Another configuration that was also observed in the experiment [Fig. 2(c)] is that of two inner defects and a group of outer defects, shown exemplarily for six defects in Fig. 4d. It is easy to see that defects 3 and 4 have phases θ3 = θo and θ4 = π + θo (the contributions of the four outer defects to the phase angles cancel each other pairwise). The phases of the two inner defects thus differ by π, so when one of them is tangential clockwise, the other one is anticlockwise. The phase θ1 is composed of the contributions θ0, φ5 = π/2, φ2 = 0 and the sum φ3 + φ4 + φ6. The latter three angles can be expressed by the ratios of the sides a, b, c as φ6 = arctan(b/a), φ3 = arctan[b/(a − c)], and φ4 = arctan[b/(a + c)] (see Fig. 4d). In order to bring the phase θ1 to some nπ + θo with an integer n, one needs to solve the transcendental equation
 | (5) |
This equation can be simplified using the addition theorem for the arctan function,
arctan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) X + arctan X + arctan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Y = arctan[(X + Y)/(1 − XY)] Y = arctan[(X + Y)/(1 − XY)] |
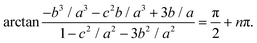 | (6) |
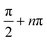 for the argument ±∞, the denominator in the argument must vanish. The solution is obviously
for the argument ±∞, the denominator in the argument must vanish. The solution is obviously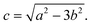 | (7) |
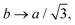 c goes to zero and the two inner defects approach each other very closely, with the same effect. The system obviously chooses a configuration of c/b where the total potential energy is near an optimum. This is the case in the experiment. Fig. 5 shows the experimental observation again (a) and the simulated texture (b) for the experimentally determined ratio a/b ≈ 1.83 and c determined from eqn (7), c/b ≈ 0.6. Instead of the director field, we show a color presentation where the intensity of the red channel of the image was set proportional to 1 + sin
c goes to zero and the two inner defects approach each other very closely, with the same effect. The system obviously chooses a configuration of c/b where the total potential energy is near an optimum. This is the case in the experiment. Fig. 5 shows the experimental observation again (a) and the simulated texture (b) for the experimentally determined ratio a/b ≈ 1.83 and c determined from eqn (7), c/b ≈ 0.6. Instead of the director field, we show a color presentation where the intensity of the red channel of the image was set proportional to 1 + sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ, the blue channel to 1 − sin
θ, the blue channel to 1 − sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ, the green channel to 0.4(1 + sin
θ, the green channel to 0.4(1 + sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ). The color scale at the right of Fig. 5 visualizes the relation between the director and the simulated texture color. This reproduces the positions of the diagonal (blueish and reddish arms in the experimental textures. Evidently, not only the defect positions but also the distortions that were generated by linear superposition of the six individual solutions are in satisfactory agreement. One has to keep in mind that we made two simplifying assumptions here: first, we assumed that the director field for a given defect arrangement is an equilibrium solution, and second, we used the solutions for one-constant approximation which we know is not exact here because KS > KB. The sense of rotation of the c-director is the same for defects 1, 4 and 5 in Fig. 4d, and opposite for the other three defects 2, 3 and 6.
θ). The color scale at the right of Fig. 5 visualizes the relation between the director and the simulated texture color. This reproduces the positions of the diagonal (blueish and reddish arms in the experimental textures. Evidently, not only the defect positions but also the distortions that were generated by linear superposition of the six individual solutions are in satisfactory agreement. One has to keep in mind that we made two simplifying assumptions here: first, we assumed that the director field for a given defect arrangement is an equilibrium solution, and second, we used the solutions for one-constant approximation which we know is not exact here because KS > KB. The sense of rotation of the c-director is the same for defects 1, 4 and 5 in Fig. 4d, and opposite for the other three defects 2, 3 and 6.
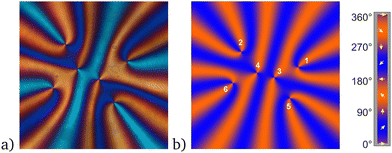 | ||
| Fig. 5 Comparison of a 2 + 4 cluster in experiment and simulation. (a) is the experimental texture. (b) was simulated to roughly represent the model texture. The outer defects were placed in positions (±a/2,±b/2) as in the experiment, and the two inner defects at (±c/2,0) with c computed from eqn (7). The colors were chosen as a crude approximation to the optics under crossed polarizers and a diagonal phase plate (see text). | ||
The arrangement for six defects shown in Fig. 5 can thus be explained easily by purely geometrical considerations, except for the experimentally selected ratio a/b which is presumably related to a local minimum of the elastic energy.
Another structure that also lacks a central defect but fulfills the requirements to be a mere superposition of single defect solutions was found coincidentally in the experiment for S0 = 8. It is shown in Fig. 6. The experimental pattern suggested that one should seek for a superposition with four defects 1, 2, 3, 4 distributed equidistantly on a straight line (distance ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ), and an appropriate addition of defect pairs 5, 6 and 7, 8 on each side of the central line. We found that defects 5 and 6 have to have a separation 2
), and an appropriate addition of defect pairs 5, 6 and 7, 8 on each side of the central line. We found that defects 5 and 6 have to have a separation 2![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) and form two equilateral triangles 1, 2, 5 and 3, 4, 6 with side length
and form two equilateral triangles 1, 2, 5 and 3, 4, 6 with side length ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) , respectively. At the opposite side of the central line, 7, 1, 2 and 8, 3, 4 in a similar arrangement form another two equilateral triangles. The comparison with the experiment shows that the two configurations are nearly identical. Small deviations may occur as a consequence of the elastic anisotropy which was disregarded in the simulated pattern. One can calculate the phases θi (i = 1, 2,…8) using the positions described above in a one-constant model to confirm the correctness. We did not search for further geometrical solutions but we hypothesize that other special configurations may exist, particularly for larger S0, which also meet the requirements listed above.
, respectively. At the opposite side of the central line, 7, 1, 2 and 8, 3, 4 in a similar arrangement form another two equilateral triangles. The comparison with the experiment shows that the two configurations are nearly identical. Small deviations may occur as a consequence of the elastic anisotropy which was disregarded in the simulated pattern. One can calculate the phases θi (i = 1, 2,…8) using the positions described above in a one-constant model to confirm the correctness. We did not search for further geometrical solutions but we hypothesize that other special configurations may exist, particularly for larger S0, which also meet the requirements listed above.
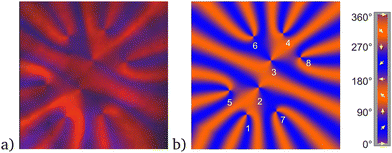 | ||
| Fig. 6 Comparison of a 2-4-2 cluster of eight defects in experiment and simulation. (a) is the experimental texture. (b) was simulated to roughly represent the texture. Four defects were distributed equidistantly on a straight line. The other four defects were placed such that they formed equilateral triangles with the first two and with the last two defects on the straight line, respectively. All direct neighbors thus have the same mutual distances. Colors as in Fig. 5. | ||
In all cases described above, the experimentally observed dynamic defect patterns simply expanded self-similarly with a scaling factor proportional to the square-root of time, until the defects approached the film boundaries or layer steps or other disclinations that might coincidentally be present in the film. Thus, the snapshots shown are representative for the complete cluster disintegration process. The square-root law evidences that the elastic energies decrease inversely proportional to the length scale ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) of the pattern.
of the pattern.
6 Discussion and summary
It has been demonstrated that the textures observed during the disintegration of defect clusters with topological charges S0 ≥ 4 can be described satisfactorily by a sequence of quasi-static equilibrium configurations that are passed in an adiabatic way. Even though the elastic anisotropy was disregarded in our analytical model, and used only for the tangential director pinning near the cores, the resemblance of analytically derived and experimentally observed textures is convincing. The total defect strength S0 of the cluster determines the geometry of the created pattern that expands continuously in a congruent, self-similar fashion. The c-director field can be described in reasonably good approximation by the superposition of the individual point defects without addition of surplus director deflections. The particular geometrical arrangements of the defects are enforced by the condition that the director is pinned tangentially near the defect cores. In a one-constant approximation, the configurations as well as their textures are obtained analytically. When the two elastic constants for splay and bend differ, then details of the texture differ but the global structure is the same. Apart from the forced pinning of the director near the defect cores, the actual elastic anisotropy has no qualitative consequences for the observed patterns. This is evident, e.g., in the satisfactory agreement between the experimental and calculated images in Fig. 5 and 6.In the experiments, almost all disintegrating clusters formed patterns with a single defect remaining at the original cluster position and N − 1 symmetrically departing defects around. The winding sense of all peripheral defects is the same, opposite to that of the central one.
Defect configurations where all single defects were distributed uniformly on a circle without a central defect cannot be constructed under the condition of tangential pinning, and they were never observed in our experiments.
In some cases, the disintegration led to two inner and N − 2 outer defects in the experiment. The two inner defects have opposite winding sense and the director field has mirror symmetry with respect to a line perpendicular to the connection of the two inner defects. An example was shown in Fig. 5. An initial S0 = 6 cluster could also decay theoretically into one central and five peripheral defects according to our model, even though we could not obtain experimental evidence for this type.
In Fig. 6, a similar structure was shown for S0 = 8. In this figure, defects with odd/even numbers have the same winding sense, respectively. This special arrangement also fulfills our conditions for the superposition model, provided that the required geometric ratios are obeyed. Note that, because of the symmetry properties of the latter two patterns without a single central defect, these solutions exist only for even values of S0.
In the experiments, we did not find any other arrangements than the two principal types with one or two inner defects, and thus we have not searched for other analytical defect configurations that might meet our conditions. Yet it cannot be excluded that such solutions exist, in particular when more than 12 defects are involved. Since all experiments started with a cluster where the individual defects were arranged at the periphery of a small circular hole, all patterns break the initial symmetry of the cluster. The reason for that must be sought in the avoidance of energetically costly additional director distortions.
The present model is by far not complete. In a more realistic dynamic model, one has to consider the induction of flow fields by the moving defects, and also the anisotropy of the elastic constants. This task was not tackled here, and is presumably not achievable analytically. It will not lead to qualitative changes of the model. One has to start with the known continuum equations for the c-director field. In the 2D film geometry, these can be directly derived from the nematic Leslie–Ericksen equations. Then, one can adopt the ideas of Svenšek and Žumer41 for that purpose, and use the projection ![[n with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006e_20d1.gif) 0 = (nx, ny) = (sin
0 = (nx, ny) = (sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β
β![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ, sin
θ, sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β
β![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ) of the director
θ) of the director ![[n with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006e_20d1.gif) onto the xy-layer plane instead of the c-director. This vector is in the same direction as
onto the xy-layer plane instead of the c-director. This vector is in the same direction as ![[c with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0063_20d1.gif) but has a length that varies with the sine of the local smectic tilt angle β. The latter serves as an order parameter variable. This tilt angle and thereby the length of
but has a length that varies with the sine of the local smectic tilt angle β. The latter serves as an order parameter variable. This tilt angle and thereby the length of ![[n with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006e_20d1.gif) 0) can deviate locally from its equilibrium value in the vicinity of the defect cores. This task is in progress.42
0) can deviate locally from its equilibrium value in the vicinity of the defect cores. This task is in progress.42
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The German science foundation (DFG) is acknowledged for support within projects STA 425/42-1 and HA 8467/2, and the German Space Administration (DLR) is acknowledged for support within grant 50WM2054.References
- W. F. Brinkman and P. E. Cladis, Phys. Today, 1982, 35, 48 CrossRef CAS.
- P. E. Cladis, W. van Saarloos, P. L. Finn and A. R. Kortan, Phys. Rev. Lett., 1987, 58, 222 CrossRef CAS PubMed.
- P. Poulin and D. Weitz, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 1998, 57, 626–637 CrossRef CAS.
- I. Muševič, M. Skarabot, U. Tkaleč, M. Ravnik and S. Žumer, Science, 2006, 313, 954–958 CrossRef PubMed.
- U. Tkaleč, M. Ravnik, S. Čopar, S. Žumer and I. Muševič, Science, 2011, 333, 62–65 CrossRef PubMed.
- I. Muševič, Eur. Phys. J. ST, 2019, 227, 2455–2485 CrossRef.
- P. V. Dolganov and N. A. Spiridenko, Liq. Cryst., 2022, 49, 1933 CrossRef CAS.
- Z. Gan, X. Hu and F. Lin, SIAM J. Math. Analysis, 2022, 54, 1695–1717 CrossRef.
- J.-C. Loudet, A. Choudhury, M. Qiu and J. J. Feng, Phys. Rev. E, 2022, 105, 044607 CrossRef CAS PubMed.
- A. Doostmohammadi, J. Ignés-Mullol, J. M. Yeomans and F. Sagués, Nat. Commun., 2018, 9, 3246 CrossRef PubMed.
- A. Ardaseva and A. Doostmohammadi, Nat. Rev. Phys., 2022, 4, 354 CrossRef.
- K. Copenhagen, R. Alert, N. S. Wingreen and J. W. Shaevitz, Nat. Phys., 2021, 17, 211 Search PubMed.
- O. J. Meacock, A. Doostmohammadi, K. R. Foster, J. M. Yeomans and W. M. Durham, Nat. Phys., 2021, 17, 205–210 Search PubMed.
- A. Amiri, R. Mueller and A. Doostmohammadi, J. Phys. A: Math. Theor., 2022, 55, 094002 CrossRef.
- V. M. H. Ruutu, V. B. Eltsov, A. J. Gill, T. W. B. Kibble, M. Krusius, Y. G. Makhlin, B. Placais, G. E. Volovik and W. Xu, Nature, 1996, 382, 334 CrossRef CAS.
- C. Bäuerle, Y. M. Bunkov, S. Fisher, H. Godfrin and G. R. Picket, Nature, 1996, 382, 332 CrossRef.
- C. Bäuerle, Y. M. Bunkov, S. N. Fisher, H. Godfrin and G. R. Pickett, Nature, 1996, 383, 570 CrossRef.
- C. N. Weiler, T. W. Neely, D. R. Scherer, A. S. Bradley, M. J. Davis and B. P. Anderson, Nature, 2008, 455, 948–951 CrossRef CAS.
- A. Polkovnikov, K. Sengupta, A. Silva and M. Vengalattore, Rev. Mod. Phys., 2011, 83, 863 CrossRef.
- J. He and S.-P. Kou, Chin. Phys. B, 2016, 25, 117310 CrossRef.
- G. E. Volovik and V. P. Mineev, Sov. Phys, 1977, 73, 767–773 CAS.
- I. Chuang, R. Durrer, B. Yurke and N. Turok, Science, 1991, 251, 1336–1342 CrossRef CAS PubMed.
- M. A. Fardin and B. Ladoux, Nat. Phys., 2021, 17, 172–173 Search PubMed.
- K. Harth and R. Stannarius, Front. Phys., 2020, 8, 112 Search PubMed.
- A. Missaoui, K. Harth, P. Salamon and R. Stannarius, Phys. Rev. Res., 2020, 2, 013080 Search PubMed.
- A. J. Vromans and L. Giomi, Soft Matter, 2016, 12, 6490–6495 RSC.
- X. Tang and J. V. Selinger, Soft Matter, 2017, 13, 5481 RSC.
- A. N. Pargellis, P. Finn, J. W. Goodby, P. Panizza, B. Yurke and P. E. Cladis, Phys. Rev. A: At., Mol., Opt. Phys., 1992, 46, 7765 CrossRef PubMed.
- C. D. Muzny and N. A. Clark, Phys. Rev. Lett., 1992, 68, 804–807 CrossRef PubMed.
- C. Muzny, PhD thesis, University of Colorado at Boulder, 1994.
- K. Wachs, B.A. Thesis, University of Colorado at Boulder, 2014.
- R. Stannarius and K. Harth, Phys. Rev. Lett., 2016, 117, 157801 CrossRef CAS PubMed.
- C. M. Dafermos, Quart. J. Mech. Appl. Math., 1970, 23, S49 CrossRef.
- M. Kleman and O. D. Lavrentovich, Soft Matter Physics: An Introduction, Springer Verlag, 2003 Search PubMed.
- C. Bohley and R. Stannarius, Eur. Phys. J. E, 2007, 23, 25 CrossRef CAS PubMed.
- D. Svenšek and S. Žumer, Phys. Rev. Lett., 2003, 90, 155501 CrossRef PubMed.
- S. Chandrasekhar and G. S. Ranganath, Adv. Phys., 1986, 35, 507–596 CrossRef CAS.
- This paper [32] contains a misprint: The square-root law for two repelling defects must read r = 2(Dt)1/2.
- L. Radzihovsky, Phys. Rev. Lett., 2015, 115, 247801 CrossRef PubMed.
- A. Missaoui, E. Lacaze, A. Eremin and R. Stannarius, Crystals, 2021, 11, 430 CrossRef CAS.
- D. Svenšek, Backflow-affected reorientation dynamics in liquid crystals, PhD thesis, Ljubljana, 2003.
- K. Harth, unpublished.
| This journal is © The Royal Society of Chemistry 2023 |