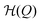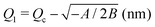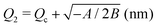Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Mean-field models for the chemical fueling of transient soft matter states†
Sven
Pattloch
 ab and
Joachim
Dzubiella
ab and
Joachim
Dzubiella
 *ab
*ab
aApplied Theoretical Physics-Computational Physics, Physikalisches Institut, Albert-Ludwigs-Universität Freiburg, D-79104 Freiburg, Germany. E-mail: joachim.dzubiella@physik.uni-freiburg.de
bCluster of Excellence livMatS@FIT-Freiburg Center for Interactive Materials and Bioinspired Technologies, Albert-Ludwigs-Universität Freiburg, D-79110 Freiburg, Germany
First published on 28th September 2023
Abstract
The chemical fueling of transient states (CFTS) is a powerful process to control the nonequilibrium structuring and the homeostatic function of adaptive soft matter systems. Here, we introduce a simple mean-field model of CFTS based on the activation of metastable equilibrium states in a tilted ‘Landau’ bistable energy landscape along a coarse-grained reaction coordinate (or ‘order parameter’) triggered by a nonmonotonic two-step chemical fueling reaction. Evaluation of the model in the quasi-static (QS) limit-valid for fast system relaxation-allows us to extract useful analytical laws for the critical activation concentration and duration of the transient states in dependence of physical parameters, such as rate constants, fuel concentrations, and the system's distance to its equilibrium transition point. We apply our model in the QS limit explicitly to recent experiments of CFTS of collapsing responsive microgels and find a very good performance with only a few global and physically interpretable fitting parameters, which can be employed for programmable material design. Moreover, our model framework also allows a thermodynamic analysis of the energy and performed work in the system. Finally, we go beyond the QS limit, where the system's response is slow and retarded versus the chemical reaction, using an overdamped Smoluchowski approach. The latter demonstrates how internal system time scales can be used to tune the time-dependent behavior and programmed delay of the transient states in full nonequilibrium.
I. Introduction
The transient assembly and ordering of active materials fueled by a chemical reaction is a key process in the nonequilibrium structuring and function of biomolecular systems, e.g., to perform work or reach homeostatic mechanical responses.1,2 These versatile and adaptive material features have triggered plenty of research recently, on one hand, to understand the fundamental physical properties of nonequilibrium transient states, but also, on the other hand, to develop synthetic active materials which display biomimetic or other novel useful behavior, driven by fuel consumption through chemical reaction networks.3–10 Experimental examples are the fuel-driven self-assembly of synthetic molecules into fibers11 or gels12,13 with variable and controllable lifetime and stiffness, the fueled nucleation and coacervation14 and spinodal decomposition15 in phase separating systems, as well as the fueled collapse of functional macromolecules such as hydrogel colloids.16,17The desired goal of the ongoing research efforts is to establish rational design principles that enable a generic access to nonequilibrium soft matter systems with adaptive and predicable dynamics,6,18 for example, to demonstrate programmable hydrogel-based model systems.19,20 Hydrogels are soft, responsive and deformable, and thus of special interest for the development, e.g., of chemically fueled mechanical actuators.21,22 However, realizing programmable or even adaptive structural dynamics has proven challenging because it requires harmonization of the chemical energy uptake and dissipation events within the steady states.9 The full nonequlibrium is even more difficult to control due to the intricate coupling of the time-dependent chemical, thermodynamic, as well as mechanical degrees of freedom of the supramolecular systems.3,4,23 The theoretical modeling is therefore often either too complex to derive simple laws, or relies only on the numerical solution and phenomenological interpretation of the underlying chemical networks.10,15,17,24 The latter typically disregard the coupling to the emerging mechanical or structural (order) parameters during the spatiotemporal evolution of the whole system to converge to a holistic modeling approach.
Here, we make a first step towards a simple theoretical treatment of the coupling of the chemical fueling to the emerging structure, thermodynamics and mechanics of the system within a generic model framework. The latter is motivated by a Landau-type of mean-field model which was historically introduced to access the qualitative behavior of phase transitions, e.g., as of magnetic systems in external fields.25 Since often we consider state- or phase-switching systems, it makes sense to use the Landau model as a starting point. In particular, we assume that the fueled system is to some degree bistable (two-state), featuring a stable state and a highly unstable state, the latter of which can then be activated by an external field. We further assume that the chemical fueling acts like an energetic field which can modify the Landau energy landscape. In other words, fueling increases the probability of the unlikely ‘hidden’ state over the initial state for a certain time, thus stabilizing a transient state with variable lifetime. In contrast to the classical Landau model, the external field enters in our approach through the action of a time-dependent chemical reaction (or chemical network). As a first approximation, the field enters linearly into our model analogous to the popular m-value approach to describe biomolecular state transitions; here, the Gibbs free energy of a two-state protein unfolding/denaturation is modified by interface free energy changes through ad- or desorption of cosolutes26–28 or the change of electrostatic intra-polymer interaction energies.29
We apply and exemplify the usefulness of our model in the quasi-static (QS) limit (where system relaxation is fast compared to the chemical reaction) explicitly to fit the experimental data of chemical fueling of hydrogel collapse recently put forward by Heckel et al.16 In these experiments, the chemical fuel N-ethyl-N′-(3-dimethy-laminopropyl)carbodiimide (EDC) was used to trigger the volume phase transition (VPT) for poly(methacrylic acid) (PMAA) microgels, to demonstrate that the collapsed hydrophobic state can be programmed in time using the fuel concentration in a cyclic reaction network. The EDC addition enables two neighboring carboxylic acid groups to form a cyclic carboxylic anhydride which increases the hydrophobicity of the hydrogel, leading to a time-dependent collapse and swelling dynamics. The measured time-dependent observable was then the mean finite hydrogel radius R(t), averaged over an ensemble of particles in dilute solution for fixed time t.
Although simple and mean-field, we demonstrate at hand of this explicit case study of transiently collapsing hydrogels that many useful scaling laws can be drawn from our model already in the QS limit, in particular, for the relations between fuel concentration, chemical rates, and the duration of the transient states between the equilibra. Moreover, we show that, like in the Landau framework,25 such a Hamiltonian-based model can then also be employed by using simple diffusive relaxational dynamics to study a full nonequilibrium fueling process. This is relevant in situations when the chemical and the system time scales are comparable and temporal effects like delay and retarded response come into play. We discuss further possible applications and extensions of these models in the final outlook section of this work.
II. General model
A. Coarse-grained bistable Hamiltonian
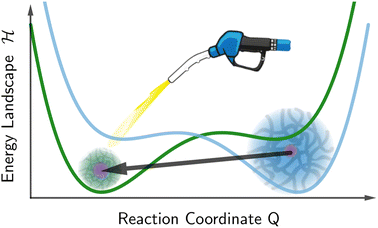
In our model, the fueled system is described by a coarse-grained one-dimensional reaction coordinate, Q, e.g., the instantaneous radius of a single responsive particle, cf.Fig. 1, or, in general, any meaningful structural (order) parameter. In order to allow for state transitions of the system (as, e.g., in the hydrogel volume transition,30,31) the coordinate is assumed to live in a bimodal energy landscape,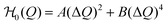 , which we model by a simple quartic form as put forward in the simplest case by Landau to model phase transitions.25 Here, ΔQ = Q − Qc, and A, B, and Qc describe the intrinsic energy landscape, with Qc being the center of the symmetric quartic form. For A < 0 and B > 0 it exhibits two local minima at Q1 and Q2. If Q is, for example, a particle volume or size, then the interpretation of such a Hamiltonian would be that it essentially represents a nonlinear elastic energy including a volume transition.
, which we model by a simple quartic form as put forward in the simplest case by Landau to model phase transitions.25 Here, ΔQ = Q − Qc, and A, B, and Qc describe the intrinsic energy landscape, with Qc being the center of the symmetric quartic form. For A < 0 and B > 0 it exhibits two local minima at Q1 and Q2. If Q is, for example, a particle volume or size, then the interpretation of such a Hamiltonian would be that it essentially represents a nonlinear elastic energy including a volume transition.
The action of the chemical fuel is considered by a time-dependent energy contribution 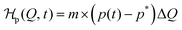 , which both Q and the product concentration p(t) enter linearly, like an external magnetic field in the Landau picture. The products are generated by the fuel by a chemical reaction and modify the energetics of the system. The total form of the Hamiltonian is thus
, which both Q and the product concentration p(t) enter linearly, like an external magnetic field in the Landau picture. The products are generated by the fuel by a chemical reaction and modify the energetics of the system. The total form of the Hamiltonian is thus
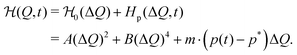 | (1) |
The value of m defines the strength of the action of the chemical products p. For the critical concentration p* the chemical contribution 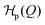 vanishes and the two coarse-grained states are equally probable. In other words, p* describes the initial bias (tilt) of the bimodal landscape in equilibrium. The Hamiltonian (1) is explicitly time-dependent because of the time-dependent product concentration p(t). The increase of the latter leads to large tilts of the landscape, activating metastable states into transient probable states, cf.Fig. 1.
vanishes and the two coarse-grained states are equally probable. In other words, p* describes the initial bias (tilt) of the bimodal landscape in equilibrium. The Hamiltonian (1) is explicitly time-dependent because of the time-dependent product concentration p(t). The increase of the latter leads to large tilts of the landscape, activating metastable states into transient probable states, cf.Fig. 1.
A few notes on the model assumptions are in order: a linear change of thermodynamic two-state energies is not always justified but it is simple and can almost always be derived from a Taylor expansion as a first order correction of external energetic field contributions. Importantly, in the field of polymeric state transitions, a linear potential is established and well accepted within the ‘m-value’ framework for the action of simple cosolutes on the coil-to-globule (or folding/unfolding) transition in bio- and polymer physics.26–28 The chemical ‘field’ of physically binding cosolutes leads to interfacial free energy changes, expressed in magnitude through m, and can thus be included as part of the total (Gibbs) free energy. In charged systems, salt and electroneutralizing chemically binding molecules (such as protons) lead to changes in the electrostatic contribution to the total free energy, which can also be included and taylored to linear potentials.29 In that sense mp* in the equation above can also be interpreted as a thermodynamic distance to the (coil-to-globule or volume) transition temperature Tcrit and is essentially related to a temperature difference ∝T − Tcrit times transition entropy.28 In other words, for a certain responsive system with a thermodynamic transition temperature, the initial tilt p* can be pre-designed by temperature, transition entropy, and the chemistry specific m-value, which are often known or measurable quantities.
B. Chemical fueling reaction
The chemical fueling is assumed to follow effectively a simple two-step reaction processHere, the fuel, f(t), is converted in the homogeneous solution to a product, p(t), binding at and modifying the considered system, e.g., the hydrogels, with a rate constant
![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) +. The products in the modified system* decay with a rate constant k−. Such a simple two-step reaction follows the rate equations
+. The products in the modified system* decay with a rate constant k−. Such a simple two-step reaction follows the rate equations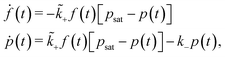 | (2) |
![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) + is a second order rate, (because the system has a concentration of binding sites,) which we denote by the tilde symbol. Moreover, we impose a saturation concentration, psat, to account for the effect of a finite maximal number of products because of limited binding sites. In equilibrium, ṗ = 0, we recover the Langmuir isotherm for the function p(f) with equilibrium constant
+ is a second order rate, (because the system has a concentration of binding sites,) which we denote by the tilde symbol. Moreover, we impose a saturation concentration, psat, to account for the effect of a finite maximal number of products because of limited binding sites. In equilibrium, ṗ = 0, we recover the Langmuir isotherm for the function p(f) with equilibrium constant ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) +/k−.32 During time evolution, the products reach a single maximum, pmax := max(p) ≤ psat, as further exemplified below.
+/k−.32 During time evolution, the products reach a single maximum, pmax := max(p) ≤ psat, as further exemplified below.
Generally, we can distinguish various regimes depending on whether the ratio of fuel to psat and the ratio of ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) +psat to k− is low/high. In a related discussion by Sharko et al.10 it is shown that to activate the transient state, we need either very high fuel concentrations, or higher activation than deactivation rates in order to obtain sufficiently many active products. We will quantify this more in the following for our model. Since we focus on systems with controllable lifetime we restrict ourselves to the activation dominant case
+psat to k− is low/high. In a related discussion by Sharko et al.10 it is shown that to activate the transient state, we need either very high fuel concentrations, or higher activation than deactivation rates in order to obtain sufficiently many active products. We will quantify this more in the following for our model. Since we focus on systems with controllable lifetime we restrict ourselves to the activation dominant case ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) +psat > k−.
+psat > k−.
Analytic solutions for p(t) we only obtain for the unsaturated case psat ≫ p for all times, where we can approximate psat − p ≃ psat and introduce a new pseudo first order rate constant k+ = ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) +psat. The analytical solution is then analogous to the double-exponential two chain reaction of radioactive decay33
+psat. The analytical solution is then analogous to the double-exponential two chain reaction of radioactive decay33
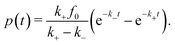 | (3) |
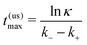 | (4) |
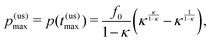 | (5) |
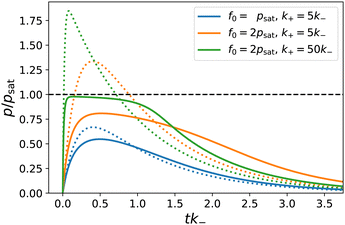 | ||
| Fig. 2 Product concentration p(t) (scaled by psat) for different parameter settings. Solid lines are according to the numerical solutions of eqn (2). Dotted lines show the concentration profiles for the same parameters without saturation, following the analytical solution, eqn (3). Besides the initial fuel concentration f0 we vary k+, cf. legend. | ||
C. Quasi-static (QS) chemical fueling
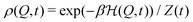 | (6) |
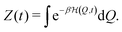 | (7) |
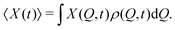 | (8) |
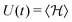 , the (Helmholtz) free energy F(t) = −kBT
, the (Helmholtz) free energy F(t) = −kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Z(t), entropy S(t) = (U(t) − F(t))/T, and the power P = dF/dt. Using the exact relation dF/dt = 〈dH/dt〉, one can derive the useful relation for our model that the power is
Z(t), entropy S(t) = (U(t) − F(t))/T, and the power P = dF/dt. Using the exact relation dF/dt = 〈dH/dt〉, one can derive the useful relation for our model that the power is| P = m(dp/dt) 〈ΔQ(t)〉, | (9) |
We note that the free energy F above is considered as the contribution stemming from the Q-state distributions, in excess over the constant ideal gas translation contributions, or other constant contributions not depending on Q. Experimentally, the constant-pressure Gibbs ensemble would be more appropriate rather than the Helmholtz ensemble we use here. However, we neglect the volume work term because we assume that its contribution at normal conditions (1 bar) are negligible compared to the relevant changes in the intrinsic energy landscape 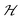 .
.
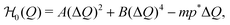 | (10) |
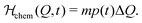 | (11) |
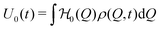 | (12) |
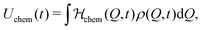 | (13) |
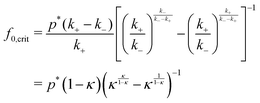 | (14) |
If we are above the threshold concentration for fueling, we can analytically estimate the duration of the times of the transient states. This we can do in two ways:
(i) Symmetry definition of the transient time
In the case of a sufficiently high saturation limit, psat > p*, and the condition p(t) > p* holds, the stability bounds of the transiently stable state are very well defined by the times t1 and t2 > t1 where p(t) = p*, i.e., where the Hamiltonian is symmetric in Q around Qc and the two states are equally likely. (Note again that in our simple two-step chemical reaction the condition p(t) = p* is met only twice, during on-fueling and decay.) The duration of the transient state can then be formally defined as| τtrans = [t2 − t1]p=p* | (15) |
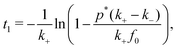 | (16) |
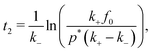 | (17) |
Interestingly, we can show that for a bistable Hamiltonian of form (1) the times defining the transient states at p(t) = p* are extrema of thermodynamic state functions, such as the free energy. Taking the derivative of the partition function Z with respect to p, we find
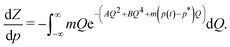 | (18) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Z(t). Using the modified Bessel functions of the second kind Kα(x), we can write the extremum of the free energy:
Z(t). Using the modified Bessel functions of the second kind Kα(x), we can write the extremum of the free energy: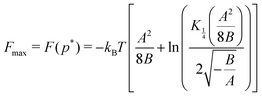 | (19) |
(ii) Plateau definition of the transient time
In the case of strong saturation (that is, small psat < p(us)max), we obtain a longer period of a plateau behavior, for which p(t) ≃ psat = pmax. Then the duration period of the transient state is mostly given by the time spent in the plateau. This we can estimate by the following: at the plateau we have p ≃ psat = constant and thus ṗ = ḟ − k−p ≃ 0, cf.eqn (2), and a linear decrease of the remaining fuel f(t) ≃ f0 − k−psatt. The plateau decays when most of the fuel is consumed f(t) ≪ f0. Hence, we find for the duration of the plateau approximately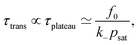 | (20) |
Note also that for saturating systems, the symmetry definition (i) should lead to values very close to the plateau definition (ii). The symmetry definition is more general and holds also for non-saturating systems, while for both p > p*. Only the plateau behavior (ii) leads to the clear linear scaling given by eqn (20).
D. Slow system relaxation: Smoluchowski approach
If the system relaxation is slow compared to the chemical reaction, its response to the time-dependent Hamiltonian will be retarded. As a simple start, we can assume the system is following an overdamped diffusive dynamics following the Smoluchowski (drift-diffusion) equation:34,35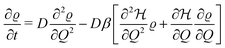 | (21) |
For an interpretation of the results during slow dynamics we need to briefly discuss the timescales in this problem: A diffusion timescale can now be defined by τD = (Q2 − Qc)/D, where Q2 is the position of the initial global minimum of 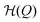 . Note, that this position changes slightly over time as the linear term of the Hamiltonian does. For our definition, we thus use the symmetric situation at p(t) = p* where it holds that
. Note, that this position changes slightly over time as the linear term of the Hamiltonian does. For our definition, we thus use the symmetric situation at p(t) = p* where it holds that 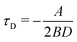 . This time expresses how long the system needs to diffuse from the minimum to the barrier position.
. This time expresses how long the system needs to diffuse from the minimum to the barrier position.
A reasonable quantity putting in relation the reactions and the diffusive time scale is the dimensionless second Damköhler number37 which we define as
| α = τDk+. | (22) |
Another relevant timescale in this bistable system, if energy barriers are significant 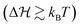 , is the so-called Kramers time for diffusive barrier crossing.38,39 There are several expressions for it depending on the approximations made. For simplicity, we define the Kramers time with τD as a prefactor to the important exponential Arrhenius-factor to have it consistent in the vanishing barrier limit, hence,
, is the so-called Kramers time for diffusive barrier crossing.38,39 There are several expressions for it depending on the approximations made. For simplicity, we define the Kramers time with τD as a prefactor to the important exponential Arrhenius-factor to have it consistent in the vanishing barrier limit, hence,
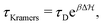 | (23) |
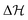 . (For the interested reader, in eqn (S10) of the ESI† we define the Kramers time with the more conventional prefactor considering the curvatures of the energy landscape, and plot a comparison in Fig. S8, ESI†) For large barriers, the Kramers time is limiting for the distribution to flood the metastable state once activated by the fuel, and also for the reverse process. Note that
. (For the interested reader, in eqn (S10) of the ESI† we define the Kramers time with the more conventional prefactor considering the curvatures of the energy landscape, and plot a comparison in Fig. S8, ESI†) For large barriers, the Kramers time is limiting for the distribution to flood the metastable state once activated by the fuel, and also for the reverse process. Note that 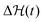 as well as the location of the extrema are themselves time-dependent meaning that also the crossing time is in general time-dependent and not very well defined. For simplicity, we follow the rule that we calculate the Kramers time using
as well as the location of the extrema are themselves time-dependent meaning that also the crossing time is in general time-dependent and not very well defined. For simplicity, we follow the rule that we calculate the Kramers time using 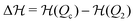 from the symmetric, non-skewed energy landscape at p = p*. The ratio between Kramers time and the chemical fueling time, we denote then by αK = τKramersk+.
from the symmetric, non-skewed energy landscape at p = p*. The ratio between Kramers time and the chemical fueling time, we denote then by αK = τKramersk+.
III. Case study: chemical fueling of hydrogel collapse
We now apply our model in the QS limit to explicitly fit the experimental data of chemical fueling of hydrogel collapse recently put forward by Heckel et al.,16 as described in the Introduction. The measured observable was the finite hydrogel radius R(t), see Fig. 3, averaged over many particles for fixed time t. We consider R(t) = 〈Q(t)〉 as an ensemble average over a hypothetically infinitely large sample of spheres.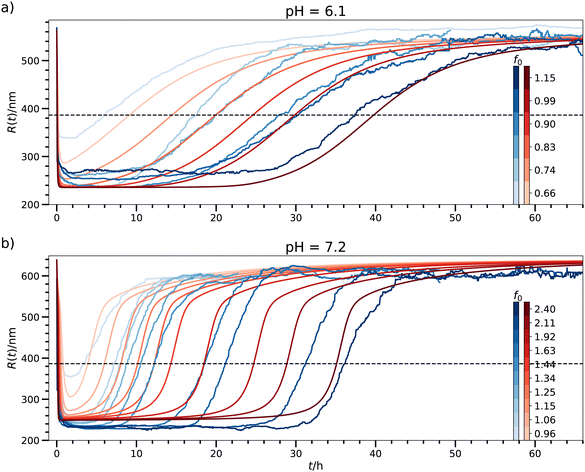 | ||
| Fig. 3 Model fits for a fixed energy barrier of 2kBT to the data set of chemically fueled hydrogel collapse16 in the QS limit for (a) pH = 6.1 and (b) pH = 7.1. The color bar codes the different fueling concentrations f0. The blueish hues represent the experimental and the reddish ones the theoretical data. The horizontal dashed line indicates the radius at the symmetric state, R(p*), below which the transient state is activated. Note that in contrast to the original work by Heckel et al.16 we choose f0 in units of mmol l−1, but not in ‘equivalent EDC’ which is stoichiometrically scaled by twice the concentration of carboxylic acid groups. These units can be converted via 1 equiv. EDC = 0.96 mmol l−1. | ||
A. Fitting procedure
Our fit is based on the numerical solution of the coupled eqn (1) and (2) including saturation. The EDC fuel concentration is translated to f0 in units of 1 mmol l−1. In Heckel et al. we find several measurement curves for two pH-values, pH = 6.1 and pH = 7.2, with differing initial fuel concentration f0. We reconcile our model and the experimental data by minimizing the total mean squared deviations (MSD) between theory curves and experimental data for a fixed pH (details in the ESI†). The model takes the initial fuel concentration f0 as an input, while the other parameters listed in Table 1 are fitting parameters, now with real experimental units assigned. However, all of the fitting parameters are kept constant for a fixed pH value. When a fitting parameter is called global, it means that it is constant also for both pH values.| Unit | Description | |
|---|---|---|
| A | k B T nm−2 | Bimodal energy landscape parameter |
| B | k B T nm−4 | Bimodal energy landscape parameter |
| Q c | nm | Center of symmetric energy landscape |
| m | k B T lmmol−1 nm−1 | Impact of p on the energy landscape |
![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) +
+
|
l mmol−1 h−1 | p-Forming rate |
| k − | h−1 | p-Decomposition rate |
| p sat | mmol l−1 | Saturation value for p |
| p* | mmol l−1 | Initial skew/transient threshold |
| f 0 | mmol l−1 | Initial fuel concentration (taken from experiment) |
We treat the parameters for the energy landscape A, B and Qc as global parameters, because we expect them to be intrinsic properties of the hydrogel colloids, which do not depend on the pH-value. We also globally fix psat, which should be constant because pH-dependent side reactions changing the amount of binding sites in the microgels are not included in our model. In contrast, the chemical reaction rates40,41 and also the m-value describing their impact on the energy landscape may depend on the pH-value. (We note that removing the constraints of pH-independent energy landscape parameters we obtain slightly improved fits, but because the improvement is only little (see ESI† Fig. S1), we consider a pH-dependent m-value as sufficient.
Moreover, we observe some arbitrariness (i.e., some insensitivity) of the fits regarding the precise magnitude of the energy barrier. We avoid this problem by fixing the energy barrier for a fixed pH through the exact expression in the symmetric landscape, 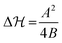 . Interestingly, unimodal potentials of the simple form ∝ΔQ2n with n = 1,2 were not able to reproduce the relatively fast sigmoidal transitions from one state to the other (see ESI† Fig. S2 and S3). Improved fits were achieved by broader n = 3 and a square-well ‘box’ potential. But here the radius distribution functions become relatively broad, in contrast to the experiments,16 with unrealistically unbound values of the radius R. Hence, a Landau-like quartic potential including the presence of transition barriers
. Interestingly, unimodal potentials of the simple form ∝ΔQ2n with n = 1,2 were not able to reproduce the relatively fast sigmoidal transitions from one state to the other (see ESI† Fig. S2 and S3). Improved fits were achieved by broader n = 3 and a square-well ‘box’ potential. But here the radius distribution functions become relatively broad, in contrast to the experiments,16 with unrealistically unbound values of the radius R. Hence, a Landau-like quartic potential including the presence of transition barriers 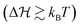 was most adequate to fit the data. Note that hydrogel charge content can tune the location and the width of the VPT.30
was most adequate to fit the data. Note that hydrogel charge content can tune the location and the width of the VPT.30
Further modifications of the fitting constraints are conceivable. For example, we can pre-fix psat to the number of available reaction partners, allow an offset for f0, or change pH-dependent variables to global ones. Similarly, we tested purely unsaturated equations for p, eqn (3), but dropped them due to the following reasons. Without saturation, the maximum value of p is not bounded but can exceed the (experimentally roughly known) number of reaction partners. In addition, the pronounced peaks in p(t) without saturation make it hard to reproduce the flat plateaus we observe in R(t) for large f0 (see Fig. 2). Finally, without saturation the fast conversion to p and thus enhanced fuel consumption leads to a sublinear scaling between f0 and the transient time, which is in contrast to the fully linear experimental observation, cf.Fig. 5 later.
B. Fitting results
The results of an exemplary best fit are displayed in Fig. 3. Here, we fixed the energy barrier to 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kBT. We obtain comparable results using other energy barriers (see Fig. S6, ESI† for
kBT. We obtain comparable results using other energy barriers (see Fig. S6, ESI† for 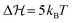 ; fits based on potentials other than defined in eqn (1) can also be found in the ESI†), which confirms that the exact choice of the barrier height is of minor importance in the QS case, as long as is it not vanishing
; fits based on potentials other than defined in eqn (1) can also be found in the ESI†), which confirms that the exact choice of the barrier height is of minor importance in the QS case, as long as is it not vanishing 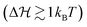 . Later we will see, however, that the precise value of
. Later we will see, however, that the precise value of 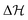 makes a substantial difference in the full nonequilibrium when the system relaxation is comparable to the chemical reaction times.
makes a substantial difference in the full nonequilibrium when the system relaxation is comparable to the chemical reaction times.
The parameters of this fit are summarized in Table 2. The fits themselves are not quantitative, but considering the relatively large error in the time domain of the experiments of a few hours (cf.Fig. 2b in Heckel et al.16), they are satisfactory, in particular, they agree very well in several qualitative aspects: They describe the fast drop of R(t) in the experiments down to 236 nm and 224 nm for pH = 6.1 and 7.2, respectively (compared to the values obtained by our fits: 236 nm and 249 nm), the plateau behavior, the slow rise of the radius, and, in particular, the trends and magnitudes of the transient times, as in detail discussed later.
Note that our model fits allow to reversely calculate the time evolution of fuel f(t) and/or products p(t) in the system. For the parameter set of Fig. 3 and the exemplary choices pH = 6.1 and f0 = 0.99 mmol l−1, we show the temporal evolution of the products p(t) together with the corresponding time evolution of the energy landscape 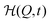 in Fig. 4. One can nicely compare the features of products and mechanical response at different characteristic times, including the saturation behavior and the symmetric states at p = p*.
in Fig. 4. One can nicely compare the features of products and mechanical response at different characteristic times, including the saturation behavior and the symmetric states at p = p*.
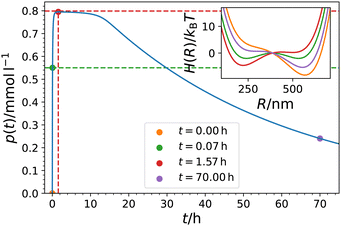 | ||
Fig. 4 Model prediction of the temporal evolution of the product concentration p(t) in the system of Heckel et al.16 Parameters were taken from Table 2 (pH = 6.1, f0 = 0.99 mmol l−1). The colored symbols depict different times for which the bimodal landscape 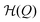 is plotted in the inset using the same color code. The values of psat and p* are indicated by horizontal red and green dashed lines, respectively. The time of the maximum tmax, when p(tmax) = psat = pmax, is indicated by the red vertical line. is plotted in the inset using the same color code. The values of psat and p* are indicated by horizontal red and green dashed lines, respectively. The time of the maximum tmax, when p(tmax) = psat = pmax, is indicated by the red vertical line. | ||
More conclusions can be drawn from the fitting numbers in Table 2. Since f0/psat ≤ 2.5, we expect high k+/k− ratios because of the pronounced plateaus. Indeed, our k+ are about three orders of magnitude larger than k−. This means, with respect to Sharko et al.,10 we are moving through different fueling regimes depending on the initial fuel concentration f0. In particular, our model captures the transition from small dips (minima) to ever-widening plateaus. Furthermore, we find that the expected pH-dependent reactivity changes with our parameters: when pH increases, we expect slower anhydride formation40,41 and faster hydrolysis,42 which is expressed in smaller k+ and lower k− for pH = 7.2 than for 6.1. This change in reactivity explains in turn, why we need more fuel for the same drop in radius for pH = 7.2. Moreover, we find excellent agreement between the saturation concentration psat when compared to the experimental numbers.16
Of special interest is the behavior of the duration of the transient times and how they are controlled by the physical and chemical parameters in the system. In the experimental paper16 the transient times were defined as the timespans between R* = (R(t = 0) + Rmin)/2, where Rmin is the minimum radius for each individual curve. We denote this half collapse time by τ1/2 in the following. This definition we can in principle also apply to the data generated by our model.
However, we evaluate the transient times, τtrans, in our model according to our well-defined symmetry definition eqn (15), which is similar but not exactly the same as τ1/2. The definition is applied to the fitting curves in Fig. 3 and plotted vs. f0 in Fig. 5, in which we compare also to the experimental definition τ1/2. There is overall very good agreement. In particular, this plot suggests a linear connection between τ and f0, as predicted from our analysis of the transient times in the saturated plateau regime, eqn (20). Using the fitted values in Table 2 we obtain slopes of 1.01 × 105 and 3.59 × 104 h l mmol−1 for pH = 6.1 and 7.2, respectively. They are shown as straight lines in Fig. 5 where the y-intercept is chosen consistently from our fits where τ(p*) = 0, i.e., where activation of the transient state starts:
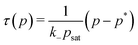 | (24) |
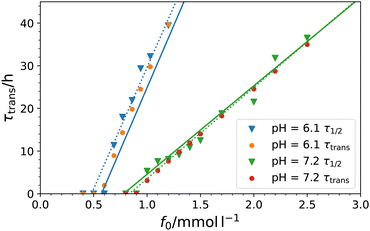 | ||
| Fig. 5 Duration times of transient states, τtrans, eqn (15), for both pH-values in dependency of the initial fuel concentration f0 (solid circles) compared to the experimentally evaluated times τ1/216 (filled triangles, fitted linearly by the dotted lines). The solid lines show slopes calculated by the theoretical ‘plateau regime’ prediction, eqn (20), with y-intercept fixed consistently with τ(p*) = 0 (cf.eqn (24)) with p* from Table 2. | ||
C. Thermodynamic analysis in the QS limit
In the QS limit, thermodynamic quantities such as energy, entropy, etc., are time-dependent but still well defined. For selected parameters (cf.Table 2, at pH = 6.1, f0 = 0.99 mmol l−1) we show U(t), S(t) and the free energy F(t) in Fig. 6. We have already discussed F(p) and found that it has a maximum at p(t) = p* where the Hamiltonian is symmetric and which is realized two times in the system: at very short times (t ≃ 0 on this linear scale; see Fig. S8 in ESI† for logarithmic time scales) where F(t) jumps up and down in a δ-peak like fashion and again at about t ≃ 30 h. (Note that if we do not reach the transient state because pmax < p*, then F would only have one maximum.) The behavior of F(t) looks complex, since F drops to a local minimum between the two maxima, at which we have the transient plateau behavior, during which p ≃ psat = pmax. After the second maximum F(t) relaxes back to the initial state. The apparently complexity essentially arises from the mapping of the asymmetric chemical kinetics p(t) on the behavior of F(p) according to the bistable Hamiltonian, eqn (1). As one can see in Fig. 6(a), U and S have similar functional forms than F. For an unimodal Hamiltonian less complex behavior can be expected.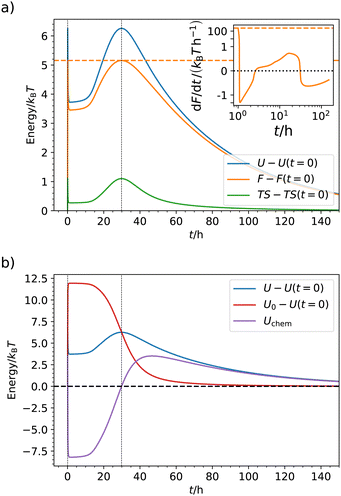 | ||
| Fig. 6 (a) Temporal evolution of the energy U(t), free energy F(t) and entropic contribution TS(t) subtracted by their initial values at time t = 0 for f0 = 0.99 mmol l−1 and parameters taken from Table 2 at pH = 6.1. The maximum of F given by eqn (19) is marked by the horizontal dashed (orange) while the vertical dotted lines mark the two times where p = p*. The inset shows the power (work per time, P = dF/dt) as a function of t (with time axis shifted by 1 h to allow for a logarithmic scale. Because of negative values of P, the scale on the y-axis is linear between −0.01 and 0.01kBT h−1 and logarithmic elsewhere. For the negative part, we show − log(−P)). The horizontal dashed line shows the analytical limit of eq. (9) at t = 0. (b) The total energy U split in mechanical (U0) and chemical contributions (Uchem) according to eqn (12) and (13). Plots with logarithmic time-axis can be found in in Fig. S8 ESI† | ||
The inset of Fig. 6(a) shows the derivative of the free energy, P = dF/dt, which we can interpret as the thermodynamic power. It has its largest absolute values immediately at the addition of the fuel at t = 0, meaning that the system is most active initially. This makes sense given the high k+ to k− ratio. It can also be understood from the analytical results, eqn (9) which is largest at the beginning where the radius is biggest and products massively produced, P(t = 0) ≃mf0k+(Q2 − Qc). For later times during relaxation then broader and flatter peaks in the power develop at around t ≃ 30 h, when F(t) peaks again and the system transitions back to the initial state. Hence, most work is performed chemically and elastically at the transitions to and from the transient state in a bistable system. The same qualitative behavior is exhibited by the entropy production (see Fig. S7 in ESI†).
Part (b) of Fig. 6 displays the course of the total energy U(t) and its mechanical and chemical contributions, U0 and Uchem, respectively. The most intuitive is the mechanical energy U0. By addition of the fuel we force the hydrogel very quickly to the collapsed state whereby energy is stored (increased) elastically. Its time of maximum coincides with that of maximum products, p = psat, and then we observe relaxation, where the stored energy is released again. For the total U, the shape is different. Here, we observe the maxima as in F(t) where p = p*, otherwise the energy is always lower. To understand this, let us consider the chemical (or external) part Uchem, being the difference of U and U0: it increases δ-peak like in the very beginning (t ≃ 0 on this scale) when chemical energy is quickly pumped into the system and converted to mechanical one. When the mechanical energy starts relaxing, Uchem rapidly decreases and turns negative. Subsequently, the process is reversed but not chemically fueled, driven by the stored elastic energy. Note that Uchem has zeros at short times p(t) ≃ 0 (on this scale) and at p(t) = p*. This is accompanied with maxima in the entropy, cf.Fig. 6(a), indicating heat exchange with the bath along the evolution of the internal energy.
D. Effects of slow system relaxation
We finally discuss the effects of slow relaxation, such as possible delays in the system's response,22 in the context of the just discussed case of chemically fueled hydrogel collapse. For this, we fix the parameters according to Table 2, for pH = 6.1 and f0 = 0.99 mmol l−1. We now tune the timescale separation parameter α in eqn (22) from 0.1 to 10 and solve numerically the Smoluchowski eqn (21) for the distribution ρ(Q,t) to calculate averages, such as R(t). The results are shown in Fig. 7(a). For α = 0.1 we are still very close to the QS limit because the diffusive system relaxation is still 10-fold faster than the fast rate k+. However, moving to α = 0.5 or 1, we observe clear retardation effects, involving less collapse and a delay of the minimum in time. For α = 5 and larger, the system becomes quite inert and the response effects less and less pronounced. The chemical power transforms mostly into dissipative losses and cannot be used to perform work. Clearly, a change of internal timescales can change the nonequilibrium time evolution and thermodynamics massively.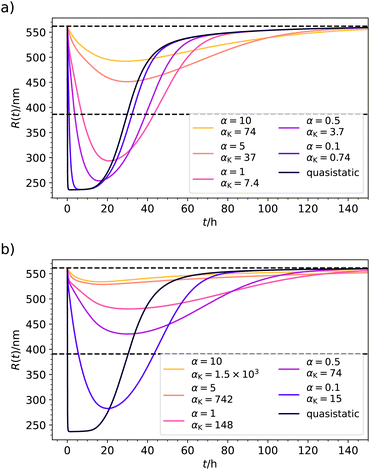 | ||
| Fig. 7 (a) Exemplary results for the time evolution of hydrogel radius R(t) in the case of slow system relaxation calculated from the Smoluchowski approach. Values for the energy landscape were taken from Table 2 (for pH = 6.1, f0 = 0.99 mmol l−1). The timescale ratio α = τDk+ defines the ratio of a typical system diffusion time and the chemical timescale k+−1. Additionally, we provide the Kramers reference αK defined by eqn (23). For very fast relaxation α ≪ 1 we reach the QS limit. By the horizontal dashed lines we show the radius before fueling R(t = 0) and the threshold radius R(p*). (b) Same as (a) but now the parameters are chosen such that the transition barrier is increased from 2kBT to 5kBT. Here, the system relaxation is too sluggish for the considered α from which we can deduce that αK provides the more precise time scale estimate. | ||
In the just described system we have still a relatively small barrier of 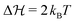 . If we raise the barrier, the system relaxation time should be more adequately described by the Kramers crossing time, eqn (23), leading to the time scale ratio αK = τKramerk+. This is exemplified in Fig. 7(b) where we use the alternative fit with a barrier height of
. If we raise the barrier, the system relaxation time should be more adequately described by the Kramers crossing time, eqn (23), leading to the time scale ratio αK = τKramerk+. This is exemplified in Fig. 7(b) where we use the alternative fit with a barrier height of 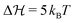 . The Kramers time is now about 150 times larger than τD resulting, for example, in αK = 15 for α = 0.1 for a response which is already clearly non-QS (brown curve in Fig. 7(b)). Hence, the Kramers time is naturally more appropriate to characterize delayed systems involving internal barriers. (Results with a slightly different definition of the Kramers time based on energy landscape curvatures time shown in Fig. S9 in the ESI† do not change our conclusion.)
. The Kramers time is now about 150 times larger than τD resulting, for example, in αK = 15 for α = 0.1 for a response which is already clearly non-QS (brown curve in Fig. 7(b)). Hence, the Kramers time is naturally more appropriate to characterize delayed systems involving internal barriers. (Results with a slightly different definition of the Kramers time based on energy landscape curvatures time shown in Fig. S9 in the ESI† do not change our conclusion.)
IV. Concluding remarks
In this contribution, we have put forward a Landau type of mean-field model to describe the quasi-static and nonequilibrium chemical fueling of transient states (CFTS) in a bistable system. Already the analysis of the quasi-static (QS) limit led to useful scaling laws and relations between chemical and mechanical parameters, which could serve for the future design of experiments. We demonstrated their usefulness explicitly for the case study of the chemically fueled volume (collapse) transition of responsive hydrogel colloids. Moreover, we provided a thermodynamic (energy, work, and power) analysis in the QS limit and also showed how internal (diffusive) relaxation times scales can substantially alter the time evolution if they compete with the chemical timescales of fueling.Several extensions of this model for CFTS shall be interesting in future studies. In our manuscript we focused on the induction and relaxation of the collapsed state, following a simple two-step reaction. If a continuous supply of fuel could be realized, e.g., as in a flow reactor, one could expect that the hydrogel would initially monotonically reach and then remain in the collapsed state. Generally, the question becomes important, how can we define chemical reaction (networks) and/or experimental protocols to program a pre-defined time-dependent macroscopic response into the system. Also, by including more complex order parameters, higher dimensions of the reaction coordinate, or structural gradients in the Hamiltonian, the extension and application of our model to self-assembling12 and phase separating systems14,15 could be attempted. From the chemical side, as indicated above, higher order reaction networks8,20,43 than only two-step reactions could be envisioned. Finally, further increasing complexity could be obtained by imposing a negative feedback cycle within the system, e.g., by coupling the mechanical response back to the chemical reaction.44–46 Here, much more intricate transient dynamics and responses, including regimes of mono- and bistability, excitability, damped oscillations, as well as sustained oscillatory states can be expected during the time evolution.8,47
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank Andreas Walther for useful discussions and sharing details of the fueling experiments on hydrogels. The authors also thank Nils Göth and Sebastian Milster for a critical reading of the manuscript. The authors further acknowledge support by the state of Baden-Württemberg through bwHPC and the German Research Foundation (DFG) through grant no INST 39/963-1 FUGG (bwForCluster NEMO) and funding from the DFG under Germany's Excellence Strategy – EXC-2193/1 – 390951807 (‘LivMatS’).References
- A. Desai and T. J. Mitchison, Annu. Rev. Cell Dev. Biol., 1997, 13, 83–117 CrossRef CAS PubMed.
- G. M. Whitesides and B. Grzybowski, Science, 2002, 295, 2418–2421 CrossRef CAS PubMed.
- V. V. Yashin, K. J. Van Vliet and A. C. Balazs, Phys. Rev. E, 2009, 79, 046214 CrossRef PubMed.
- A. P. Dhanarajan, G. P. Misra and R. A. Siegel, J. Phys. Chem. A, 2002, 106, 8835–8838 CrossRef CAS.
- R. Merindol and A. Walther, Chem. Soc. Rev., 2017, 46, 5588–5619 RSC.
- A. Walther, Adv. Mater., 2020, 32, 1905111 CrossRef CAS PubMed.
- Q. Wang, Z. Qi, M. Chen and D.-H. Qu, Aggregate, 2021, 2, e110 CrossRef CAS.
- A. V. Straube, S. Winkelmann, C. Schütte and F. Höfling, J. Phys. Chem. Lett., 2021, 12, 9888–9893 CrossRef CAS PubMed.
- D. M. Busiello, S. Liang, F. Piazza and P. De Los Rios, Communi. Chem., 2021, 4, 16 CrossRef CAS PubMed.
- A. Sharko, D. Livitz, S. De Piccoli, K. J. M. Bishop and T. M. Hermans, Chem. Rev., 2022, 122, 11759–11777 CrossRef CAS PubMed.
- J. Boekhoven, W. Hendriksen, G. Koper, R. Eelkema and J. van Esch, Science, 2015, 349, 1075–1079 CrossRef CAS PubMed.
- T. Heuser, E. Weyandt and A. Walther, Angew. Chem., Int. Ed., 2015, 54, 13258–13262 CrossRef CAS PubMed.
- S. Panja, C. Patterson and D. J. Adams, Macromol. Rapid Commun., 2019, 40, 1900251 CrossRef PubMed.
- J. Deng and A. Walther, Chem, 2020, 6, 3329–3343 CAS.
- J. Heckel, F. Batti, R. T. Mathers and A. Walther, Soft Matter, 2021, 17, 5401–5409 RSC.
- J. Heckel, S. Loescher, R. T. Mathers and A. Walther, Angew. Chem., Int. Ed., 2021, 60, 7117–7125 CrossRef CAS PubMed.
- M. Nakamoto, S. Kitano and M. Matsusaki, Angew. Chem., Int. Ed., 2022, 61, e202205125 CrossRef CAS PubMed.
- L. Heinen and A. Walther, Sci. Adv., 2019, 5, eaaw0590 CrossRef CAS PubMed.
- H. Zhang, H. Zeng, A. Priimagi and O. Ikkala, Nat. Commun., 2019, 10, 3267 CrossRef PubMed.
- B. Klemm, R. W. Lewis, I. Piergentili and R. Eelkema, Nat. Commun., 2022, 13, 6242 CrossRef CAS PubMed.
- L. Ionov, Mater. Today, 2014, 17, 494–503 CrossRef.
- G. Fusi, D. Del Giudice, O. Skarsetz, S. Di Stefano and A. Walther, Adv. Mater., 2023, 35, 2209870 CrossRef CAS.
- X. He, M. Aizenberg, O. Kuksenok, L. D. Zarzar, A. Shastri, A. C. Balazs and J. Aizenberg, Nature, 2012, 487, 214–218 CrossRef CAS.
- S. G. J. Postma, I. N. Vialshin, C. Y. Gerritsen, M. Bao and W. T. S. Huck, Angew. Chem., Int. Ed., 2017, 56, 1794–1798 CrossRef CAS PubMed.
- P. Hohenberg and A. Krekhov, Phys. Rep., 2015, 572, 1–42 CrossRef.
- C. N. Pace, CRC Crit. Rev. Biochem., 1975, 3, 1–43 CrossRef CAS PubMed.
- J. A. Schellman, Biopolymers, 1978, 17, 1305–1322 CrossRef CAS.
- J. Heyda and J. Dzubiella, J. Phys. Chem. B, 2014, 118, 10979–10988 CrossRef CAS PubMed.
- J. Heyda, S. Soll, J. Yuan and J. Dzubiella, Macromolecules, 2014, 47, 2096–2102 CrossRef CAS.
- R. Elancheliyan, G. Del Monte, E. Chauveau, S. Sennato, E. Zaccarelli and D. Truzzolillo, Macromolecules, 2022, 55, 7526–7539 CrossRef CAS.
- M. A. Fernandez-Rodriguez, S. Orozco-Barrera, W. Sun, F. Gámez, C. Caro, M. L. García-Martín and R. A. Rica, Small, 2023, 2301653 CrossRef CAS.
- I. Langmuir, J. Am. Chem. Soc., 1918, 40, 1361–1403 CrossRef CAS.
- H. Bateman, Proc. Cambridge Philos. Soc., 1910, 15, 423–427 CAS.
- M. Doi and S. F. Edwards, The Theory of Polymer Dynamics, Oxford University Press, 1988 Search PubMed.
- H. Risken, The Fokker-Planck equation, Springer, 1996 Search PubMed.
- V. Holubec, K. Kroy and S. Steffenoni, Phys. Rev. E, 2019, 99, 032117 CrossRef CAS PubMed.
- H. S. Fogler, Elements of Chemical Reaction Engineering, Prentice Hall, 4th edn, 2005 Search PubMed.
- H. Kramers, Physica, 1940, 7, 284–304 CrossRef CAS.
- P. Hänggi, P. Talkner and M. Borkovec, Rev. Mod. Phys., 1990, 62, 251–341 CrossRef.
- L. S. Kariyawasam, J. C. Kron, R. Jiang, A. J. Sommer and C. S. Hartley, J. Organic Chem., 2020, 85, 682–690 CrossRef CAS PubMed.
- A. Williams and I. T. Ibrahim, J. Am. Chem. Soc., 1981, 103, 7090–7095 CrossRef CAS.
- C. W. Woodruff, G. E. Peck and G. S. Banker, J. Pharm. Sci., 1972, 61, 1916–1921 CrossRef CAS.
- J. Deng and A. Walther, Nat. Commun., 2021, 12, 5132 CrossRef CAS PubMed.
- B. Li and R. A. Siegel, Chaos, 2000, 10, 682 CrossRef CAS PubMed.
- D. J. Bell, D. Felder, W. G. von Westarp and M. Wessling, Soft Matter, 2021, 17, 592–599 RSC.
- M. Jain and B. J. Ravoo, Angew. Chem., Int. Ed., 2021, 60, 21062–21068 CrossRef CAS PubMed.
- S. Milster, N. Göth, A. Darwish and J. Dzubiella, Phys. Rev. E, 2023, 108 CrossRef , https://arxiv.org/abs/2306.05181.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3sm00742a |
| This journal is © The Royal Society of Chemistry 2023 |