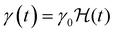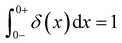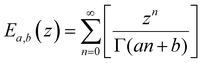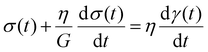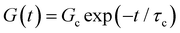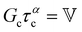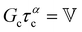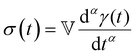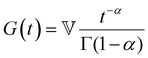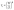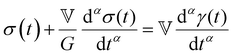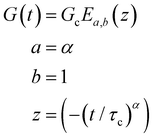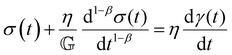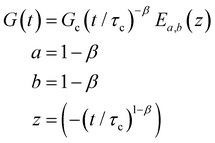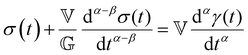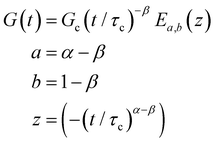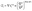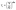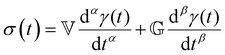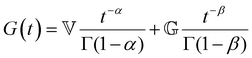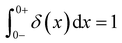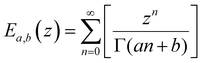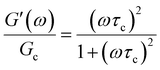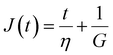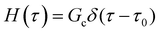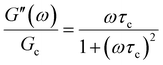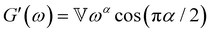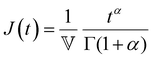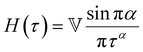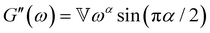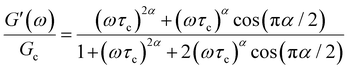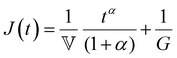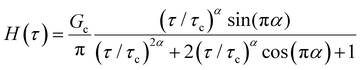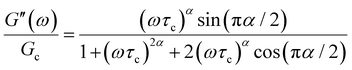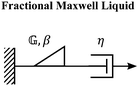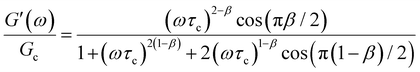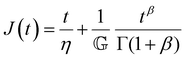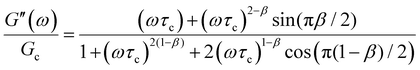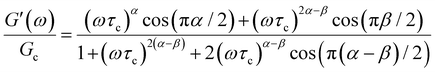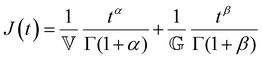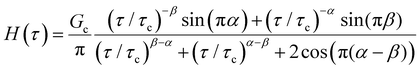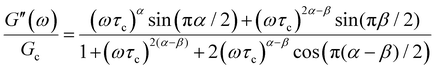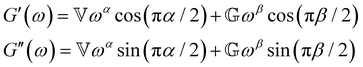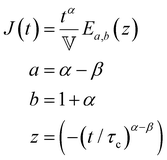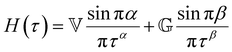Open Access Article
Open Access ArticleNon-Maxwellian viscoelastic stress relaxations in soft matter†
Jake
Song
 *abc,
Niels
Holten-Andersen
*abc,
Niels
Holten-Andersen
 ade and
Gareth H.
McKinley
ade and
Gareth H.
McKinley
 *b
*b
aDepartment of Materials Science and Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
bDepartment of Mechanical Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139, USA. E-mail: gareth@mit.edu
cDepartment of Mechanical Engineering, Stanford University, Stanford, CA 94305, USA. E-mail: jakesong@stanford.edu
dDepartment of Bioengineering, Lehigh University, Bethlehem, PA 18015, USA
eDepartment of Materials Science and Engineering, Lehigh University, Bethlehem, PA 18015, USA
First published on 28th August 2023
Abstract
Viscoelastic stress relaxation is a basic characteristic of soft matter systems such as colloids, gels, and biological networks. Although the Maxwell model of linear viscoelasticity provides a classical description of stress relaxation, it is often not sufficient for capturing the complex relaxation dynamics of soft matter. In this Tutorial, we introduce and discuss the physics of non-Maxwellian linear stress relaxation as observed in soft materials, the ascribed origins of this effect in different systems, and appropriate models that can be used to capture this relaxation behavior. We provide a basic toolkit that can assist the understanding and modeling of the mechanical relaxation of soft materials for diverse applications.
Soft matter systems are characterized by dynamic fluctuations and rearrangements within the microstructure, which play an important role in the function of a wide range of soft materials, such as cell-matrix interactions in biology,1,2 or energy dissipation and self-healing in engineered soft materials.3,4 These rearrangement events give rise to a time-dependent response in the mechanical properties, i.e., viscoelasticity.5 The measurement of viscoelasticity can thus provide meaningful information into the dynamics of the soft material of interest. This is most commonly done at bulk scales using a dynamic mechanical analyzer6 or a rheometer,5 though microscopic-scale measurements can also be made via microrheology7 and scattering.8
The dynamics of soft matter systems are non-trivial, and are characterized by a viscoelastic response that is often more complex than the Maxwell model of linear viscoelasticity (hence the term “complex fluids”). The Maxwell model is a canonical model introduced in elementary studies of linear viscoelasticity, which is characterized by a single characteristic relaxation time. However, measurements on real soft matter systems commonly exhibit a viscoelastic response that underscores a broad distribution of relaxation modes. These distributions of relaxation processes are generally interpreted as arising from a wide range of structural length-scales or relaxation mechanisms by which stress can relax, though the exact origins of these mechanisms are often not clear. Indeed, there is a vast literature on the microscopic origins of the broadly distributed relaxation modes observed in a wide range of soft matter systems, as well as on the modeling strategies to capture such viscoelastic responses. Navigating this literature to distill meaningful insights from, and appropriate models for, rheological measurements of different soft materials can therefore be a considerable challenge.
The aim of the Tutorial is to provide an overview of non-Maxwellian viscoelastic relaxation in soft matter, including the microscopic origins of the relaxation responses observed in different classes of soft materials, and for making an informed choice on suitable models to capture these relaxation responses. We first briefly recall the properties of the Maxwell model, and establish some of the basic physical scenarios in which a single Maxwell model succeeds in capturing the essential physics underlying the stress relaxation of soft matter (Section 1). We then illustrate deviations from the single-mode Maxwell model in soft matter and summarize the putative origins of such effects which have been proposed across different systems (Section II). We next establish a basic mathematical language for describing viscoelastic relaxation in soft matter (Section III). We highlight common relaxation functions (Section IV) and corresponding mechanical models (Section V) that can be used to model non-Maxwellian viscoelasticity in soft matter, and lastly, outline basic statistical considerations when applying these models to experimental data (Section VI).
I. Maxwell model of linear viscoelasticity
Exponential decays of the form ϕ = ϕ0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−t/τc), where ϕ is an observable thermo-physical property and ϕ0 is the initial value at t = 0, are often used to model relaxation events arising from simple dynamical processes. For instance, exponential decays are exact solutions to describe the correlation of Brownian motion of particles, the correlation of dipoles in the rotational diffusion of a polar molecule (giving rise to the Debye dielectric relaxation9,10), and the kinetics of first-order reactions. The characteristic time-constant for the relaxation process is denoted τc in this review, though λ is also often used in the complex fluids literature.11
exp(−t/τc), where ϕ is an observable thermo-physical property and ϕ0 is the initial value at t = 0, are often used to model relaxation events arising from simple dynamical processes. For instance, exponential decays are exact solutions to describe the correlation of Brownian motion of particles, the correlation of dipoles in the rotational diffusion of a polar molecule (giving rise to the Debye dielectric relaxation9,10), and the kinetics of first-order reactions. The characteristic time-constant for the relaxation process is denoted τc in this review, though λ is also often used in the complex fluids literature.11
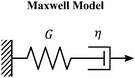
In linear viscoelasticity, exponential decays in stress are exact solutions to step strain deformations applied to the Maxwell model.12 This model is eponymously named after James C. Maxwell, who showed that a linear mechanical combination of a Hookean spring and dashpot in series give rise to a viscoelastic stress relaxation governed by a single time-scale, τc. We recall the essential results of the model here, but defer a detailed discussion of the Maxwell model to ref. 5 and 11.
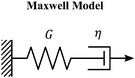
The Maxwell model (Fig. 1A) has a constitutive relation:
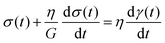 | (1) |
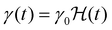 (where
(where 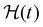 is the Heaviside step function), or small-amplitude oscillatory strain perturbations, γ(t) = γ0
is the Heaviside step function), or small-amplitude oscillatory strain perturbations, γ(t) = γ0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(ωt) (Fig. 1B and C). Solving the constitutive relation in the case of a step strain experiment, we find that the relaxation modulus G(t) of a soft material system described by eqn (1) exhibits an exponential decay (Fig. 1D):
sin(ωt) (Fig. 1B and C). Solving the constitutive relation in the case of a step strain experiment, we find that the relaxation modulus G(t) of a soft material system described by eqn (1) exhibits an exponential decay (Fig. 1D):G(t) = G0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−t/τc) exp(−t/τc) | (2) |
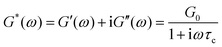 | (3) |
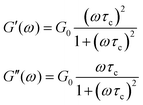 | (4) |
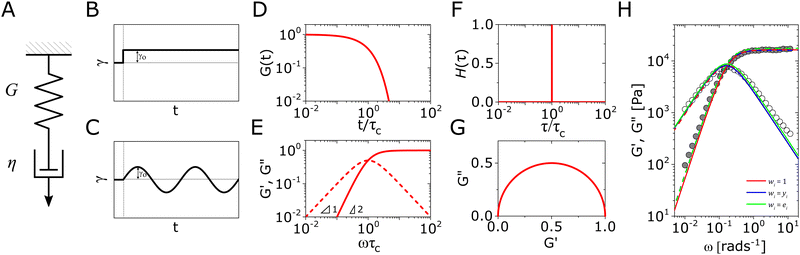 | ||
| Fig. 1 The Maxwell model of linear viscoelasticity. (A) The Maxwell model consists of a spring with an elasticity of G, and a dashpot with viscosity of η, arranged in series. (B) and (C) Illustration of the step strain and oscillatory strain input for studying viscoelastic properties of soft matter, and (D) and (E) corresponding linear viscoelastic responses of the Maxwell model under step strain and oscillatory strain (G0 = 1). (F) The relaxation spectrum of H(τ) for the Maxwell model, represented by a delta function centered around τ = τc. (G) A Cole–Cole plot of the loss modulus G′′(ω) as a function of the storage modulus G′(ω). (H) Transient polymer networks as an example of soft materials exhibiting near-Maxwellian viscoelasticity. This particular example shows the viscoelastic response of a metal-coordinating transient polymer network consisting of histidine-functionalized poly(ethylene glycol) with Ni2+ ions.13 Here we also demonstrate this fitting process using three different weights in the residual function – see eqn (26) in Section VI and discussion thereof – which leads to a statistical difference in the values of the final fitting parameters. | ||
In addition to the typical frequency sweep plot showing the storage and loss moduli as a function of frequency (Fig. 1E), there are other methods for representing G′(ω) and G′′(ω) data which are used in the literature. For instance, the storage and loss moduli are also sometimes represented in a cross-plot, i.e., G′′(ω) vs. G′(ω) – in similar vein to the plotting methods used for real and imaginary values of the electrochemical impedances (the Nyquist plot) and dielectric constants (the Cole–Cole plot). This cross-plot of the real and imaginary response to oscillatory strain for a Maxwell material is a perfect semicircle (Fig. 1G); this provides a useful and demanding test of the accuracy of the Maxwell model when analyzing the dynamical response of soft materials. Another useful plotting strategy for oscillatory strain data is to plot the loss tangent tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ = G′′(ω)/G′(ω) versus the mangnitude of the complex shear modulus |G*(ω)|, which is often referred to as the van Gurp–Palmen plot.14 The van Gurp–Palmen plot is essentially a simpler representation of the dynamic modulus data, which reveals the solid or liquid-like response of the system (since tan
δ = G′′(ω)/G′(ω) versus the mangnitude of the complex shear modulus |G*(ω)|, which is often referred to as the van Gurp–Palmen plot.14 The van Gurp–Palmen plot is essentially a simpler representation of the dynamic modulus data, which reveals the solid or liquid-like response of the system (since tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ = 1/ωτc = 1/De) without needing to decompose the modulus into a storage and loss component as done in Fig. 1E.
δ = 1/ωτc = 1/De) without needing to decompose the modulus into a storage and loss component as done in Fig. 1E.
Yet another useful representation for describing the viscoelasticity of soft matter is the continuous relaxation spectrum H(τ), which encodes the distribution of relaxation modes in a given system (more detail in Section III).15,16 The continuous relaxation spectrum is encoded in the hereditary integral formulation of linear viscoelasticity (via the Boltzmann superposition principle),17 and describes the relaxation modulus via:
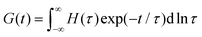 | (5) |
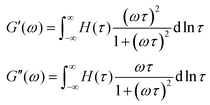 | (6) |
As the implication of the Maxwell model is the existence of a single characteristic relaxation time, τc = η/G, the continuous relaxation spectrum of the Maxwell model is a delta function centered at τc, and can be written in the compact form H(τ)/G0 = δ(τ − τc), where the integral over the delta function is equal to 1 such that 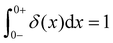 (Fig. 1F).
(Fig. 1F).
Finally, in response to a step stress of amplitude σ0, the Maxwell model exhibits an instantaneous increase in creep compliance J(t) = γ(t)/σ0 (thus exhibiting a retardation time of zero), followed by a linear increase in creep compliance J(t) with time that is given by the relation:
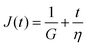 | (7) |
To keep the Tutorial concise and focused on viscoelastic relaxation phenomena, we omit extensive discussion of creep behavior (which measures the retardation response of the material). However, the topic of this review still applies broadly to creep responses, as linear viscoelastic properties such as G(t), G*(ω), and J(t) are interconvertible via the Boltzmann superposition theorem.11,15 It is also noted that creep tests can be quite a natural choice for measuring time-dependent mechanical properties in soft matter when using stress-controlled devices (i.e. most commercial rheometers). Using creep compliances can also be particularly advantageous in certain situations, for instance in analyzing entanglement plateaus in polymers18 or analyzing microrheological data.19
Though most viscoelastic stress relaxation responses of soft materials are more complex than a single exponential decay (eqn (2)), there are a few exceptional cases where essentially Maxwellian behavior is observed. A prototypical example of materials exhibiting Maxwellian viscoelasticity are transient polymer networks, such as those consisting of star poly(ethylene glycol) (PEG) which are end-functionalized with diverse binding motifs such as metal-coordinating end-groups (Fig. 1H),20 dynamic-covalent end-groups,21,22 and ionic end-groups.23 These materials are of interest due to the biocompatibility of the PEG as well as the shear-thinning behavior that arises from the disruption of the network that arises at high shear rates, which facilitates applications ranging from injectable hydrogels to cell culture.24,25 Maxwellian behavior is also observed in other network materials as long as they are governed by first-order kinetics, such as DNA nanostars with controlled base-pair interactions,26 telechelic polymers with hydrophobic domains such as the hydrophobic-ethoxylate urethane (HEUR) system,27,28 and worm-like micelles, which are dimer networks where the interaction lifetimes define a single relaxation time between an entangled solid and a fluid.29–31
The relaxation dynamics of these Maxwellian networks can be most readily understood within the framework of transient network theory.32–39 This theory describes the relaxation of polymer chains which are reversibly cross-linked by non-covalent bonds that serve as junction points of a rubbery network. In this picture, the polymer chains become affinely stretched when the network is rapidly deformed (e.g. via step strain); the accrued stress is relaxed when bond dissociation occurs, allowing the stretched polymer chains to re-associate with other polymer chains in a relaxed configuration. The relaxation process is thus governed by the bond dissociation time (which is often modeled by an Arrhenius-type expression), as well as by the density of elastically-active chains, the elastic force-extension response of the chains,32,35 and cooperative effects arising from having several interaction sites on a single polymer chain.40
II. Deviations from Maxwellian relaxation in soft matter
Soft materials commonly exhibit complex non-Maxwellian rheological behavior. We present a selection of such responses in Fig. 2, which illustrate deviations from Maxwell viscoelasticity that can occur in a diverse range of soft matter systems such as polysaccharide networks,41 muscle tissues and food systems, polymer glasses,42 mucin hydrogels,43 cytoskeletal networks,44 colloidal gels,45 supramolecular polymers,46 worm-like micelles,29 and foams.47 The extent to which the viscoelastic response of system deviates from the Maxwellian prediction can vary substantially depending on the specific microstructural features of the system. Here, we present a short survey of some of the microstructural features that have been associated with non-Maxwellian viscoelastic responses in different soft matter systems.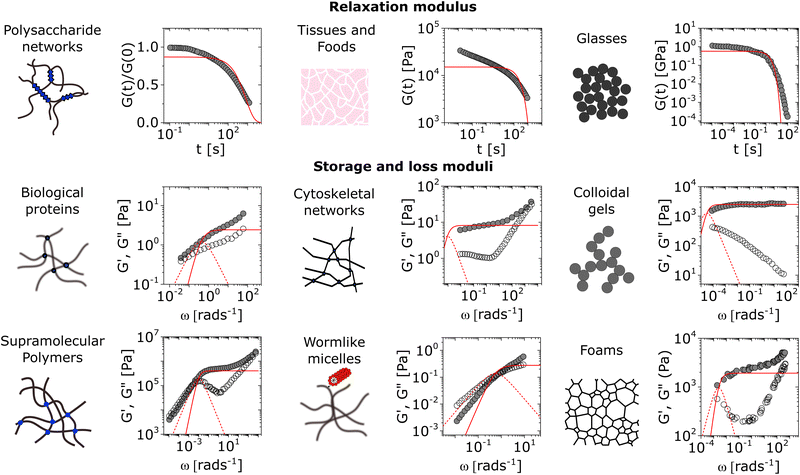 | ||
| Fig. 2 A partial survey of deviations from Maxwellian viscoelasticity across different forms of soft matter. The single-mode Maxwellian viscoelastic predictions are shown for comparison as solid lines for the relaxation modulus G(t) and the storage modulus G′(ω), and dashed lines for the loss modulus G′′(ω). All single-mode representations are obtained by non-linear fitting, and setting the weighting function wi = yi (see Section VI). Shown here are the rheological behaviors of alginate reversibly cross-linked by Ca2+,41 muscle tissue of Yellowfin tuna, m-toluidine molecular glasses,42 porcine gastric mucin,43 actin-fascin networks,44 silica colloidal gels,45 supramolecular polymers bound by ureido-pyrimidinone moieties,46 worm-like micelles of cetylpyridinium salicylate and sodium salicylate,29 and shaving foam.47 All data are digitized directly from original references, and are within the linear viscoelastic range as determined by the authors. The muscle tissue data are measured directly by performing shear rheology on a thin section of myotome of a Yellowfin tuna at room temperature (step strain γ0 = 0.5%). | ||
A. Non-first-order reaction kinetics
Deviations from Maxwellian viscoelastic relaxation can arise in telechelic networks when the bond interactions between polymers do not follow first-order reaction kinetics. A representative example of these kinds of interactions come from host–guest interactions, which are often structurally complex and can give rise to a complex dissociation pathway with many intermediate steps.48 Indeed, studies have shown that multi-arm PEGs functionalized with cyclodextrin and cholesterol exhibit strong deviations from Maxwellian rheology,49 in contrast to multi-arm PEGs functionalized with dynamic covalent linkages which exhibit Maxwellian linear viscoelastic responses.21,25,50 The use of such complex interaction moieties provides an interesting, chemically-oriented approach to tuning the relaxation spectrum of the polymeric network.B. Chain dynamics
Deviations from single-mode Maxwell viscoelastic responses are also expected based on classical models of polymer dynamics. In the Rouse model, the relaxation dynamics are assumed to arise from the Brownian motion of beads connected by springs, wherein the terminal relaxation time depends on the polymer chain length. This leads to a stress relaxation response arising from a linear summation of individual (exponential) Rouse relaxation modes, which results in a power-law scaling of the relaxation modulus preceding a terminal relaxation, of the form:51G(t) ∼ G0(t/τ0)−1/2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−t/τR) exp(−t/τR) | (8) |
Non-Maxwellian stress relaxation becomes more prominent for polymer melts with long entangled chains, in which Rouse and Zimm modes are followed at longer times by entanglement effects.52 This can result in the addition of stress relaxation mechanisms, such as reptation, contour-length fluctuations and constraint release.53 More complex relaxation processes can also arise specifically due to entanglement effects in polymer systems of more complex topologies, such as entangled star polymers54 and entangled ring polymers.55
Semiflexible polymers such as cytoskeletal polymers and extracellular matrix polymers have been shown to exhibit unique chain relaxation dynamics – distinct from Rouse and Zimm dynamics of polymers – which arise due to the significant thermal undulations of the semiflexible polymer backbone. Studies have shown that in such systems, the viscoelastic moduli exhibit a power-law scaling of G′(ω) ∼ G′′(ω) ∼ ωn, in which n = 3/4 in the high frequency regime.56–58
C. Sticky chain dynamics
Though Rouse dynamics are expected to occur even in swollen gels such as the Maxwellian transient networks introduced in Section I, these relaxation modes occur at much shorter time-scales than those arising from the reversible interactions in these systems, and are often not measurable. However, when there is a sufficient concentration of interacting stickers per polymer chain in such transient networks, we may instead observe the emergence of sticky chain dynamics.One such manifestation is the sticky Rouse model,36,40,59 in which the associations between neighboring polymer chains are understood to constrain the polymer chains and lead to a Rouse-like dynamical regime at long times. This results in the observation of power-law relaxation of the form G(t) ∼ t−1/2 in associative polymers, most commonly in systems where the main chain has been functionalized by binding motifs such that multiple stickers exist per chain.59–62 In similar vein, the concept of sticky dynamics have also been applied to reptation dynamics for studying associative networks with longer entangled chains.63–65
Sticky dynamics can also give rise to non-Maxwellian viscoelasticity in semiflexible polymer networks. Modeling studies have shown that dissociation events along the backbone of a semiflexible polymer generate transverse relaxation modes, in which successive relaxation modes become progressively slower as more dissociation events need to occur; this leads to a terminal power-law relaxation of G(t) ∼ t−1/2, which is commonly observed in semiflexible polymer networks.66 Experimentally, this power-law region has also been shown to be characterized by stress fluctuations indicative of collective dynamics.67
D. Multiple relaxation modes
Non-Maxwellian viscoelastic responses are a natural outcome for systems which intrinsically have multiple relaxation modes, such as those with chain length polydispersity, sticker heterogeneity, or multiple relaxation mechanisms.Polydispersity in the chain length can result in heterogeneous chain dynamics, and thus a broad distribution of relaxation modes. The observation of non-Maxwellian stress relaxations can be leveraged to gain insight into the polydispersity of polymer systems. For instance, for melt systems undergoing reptation, the observed distribution of relaxation modes (from H(τ)) can be retraced to the molecular weight distribution of the system.68
For associative polymers, multiple relaxation modes can arise due to factors such as the sticker distribution on chains69 and sticker clustering.70 Stickers can also introduce spatial mismatches in the binding of two chains, resulting in formation of defects such as chain loops. This can generate energetic penalties in the chain and cause broadening in the viscoelastic relaxation curve.71 These effects – especially in tandem with chain length polydispersity – can lead to complicated linear viscoelastic responses which can be challenging to ascribe to a single factor.
For composite materials such as polymer–particle systems, non-Maxwellian viscoelastic responses can arise due to multiple relaxation mechanisms that arise intrinsically from the composite microstructure. For instance, latex particles which are bridged by HEUR micelles exhibit a composite response of Rouse dynamics, bridging interactions, and large-scale cluster dynamics, the sum of which can lead to complex non-Maxwellian viscoelastic behavior.72,73 Furthermore, each of these relaxation mechanisms can be governed by a distribution of relaxation modes. For the contribution arising from Rouse dynamics, such distribution can arise as a result of chain polydispersity. For the bridging dynamics, it is well understood that the number of bridging linkers can significantly change the terminal relaxation time of a pair of particles due to cooperativity.74 As such, a Poisson distribution of linkers in associating particle systems can lead to a significantly non-Maxwellian viscoelastic response, which can be useful for understanding the dynamics of particle-polymer systems such as latex and HEUR, metal-coordinating nanoparticle hydrogels and coordination cage hydrogels.75 Finally, cluster dynamics can also be influenced by a distribution in cluster sizes, which we treat separately in Section IIE.
Lastly, a broad distribution in relaxation modes can arise in systems which are characterized by a distribution of activation energies. For instance, a Gaussian distribution in the activation energy of relaxation can facilitate a log-normal distribution in the stress relaxation time (see Section IVA). This approach has been taken to model the relaxation of a metal-coordinate polymer material76 (in which bond strengths are assumed to be distributed in a Gaussian manner) as well as glassy systems (in which relaxation is assumed to arise from local domains with a Gaussian distribution of activation energies).77,78
E. Convolution of relaxation processes
A stretched exponential relaxation of the formG(t) = G0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[(−t/τc)β] exp[(−t/τc)β] | (9) |
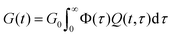 | (10) |
An example of this idea is the work of Douglas et al.,85–87 which evaluates the relaxation function of polymeric systems that form clusters. In these works, it is assumed that the cluster relaxation time depends on diffusion processes that scale with the size of the cluster. It is thus shown that the relaxation time scales as τ ∼ L2/D0 with L being the characteristic length of the cluster and D0 being the diffusivity of the cluster. Assuming that clusters take a Boltzmann (exponential) size distribution, one can derive the convolution function Φ(τ) = exp(−L) = exp(−τ1/2). A steepest descent approximation of eqn (10) with this convolution function results in the following derivation:
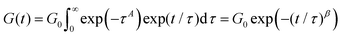 | (11) |
A similar derivation has been proposed by Cates et al. for wormlike micelles undergoing reptation,29 with the main difference being an additional assumption that the diffusivity D0 ∼ 1/L arises due to the curvilinear diffusion of the chains along their confining tubes. The convolution function thus becomes Φ(τ) = exp(−L) = exp(−τ1/3), resulting in a final stretched exponential function of G(t) ∼ exp(−(t/τ)1/4). Overall, the examples by Douglas et al., and Cates et al., show that the stretched exponential stress relaxation is a mathematical outcome of convoluted relaxation events in which there is a size polydispersity of the relaxing units, for instance clusters or tubes.
Finally, a related approach is the work of Curro et al.,88 who have shown that permanently cross-linked systems such as elastomers can also exhibit a power-law stress relaxation. This relaxation is ascribed to dangling chain ends in the system, such that 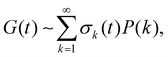 where k is the length of the chain branch, σk(t) = k − l(t) describes the stress arising from parts of the dangling chains which have not relaxed (l(t) is the lognormally-dependent relaxation rate of dangling chain ends as derived by de Gennes), and P(k) is the probability of having a dangling chain of length k. The convolution of the probability of k by the time-dependent stress arising from k is shown to result in a power law relaxation G(t) ∼ t−(q/a) where q is the ratio of cross-link density to monomer density, and a is a material constant related to the reptation time of the chain.88 This idea of the disentanglement of dangling chain ends has also been utilized by Rubinstein et al. to explain the power-law stress relaxation in block copolymers, see ref. 89.
where k is the length of the chain branch, σk(t) = k − l(t) describes the stress arising from parts of the dangling chains which have not relaxed (l(t) is the lognormally-dependent relaxation rate of dangling chain ends as derived by de Gennes), and P(k) is the probability of having a dangling chain of length k. The convolution of the probability of k by the time-dependent stress arising from k is shown to result in a power law relaxation G(t) ∼ t−(q/a) where q is the ratio of cross-link density to monomer density, and a is a material constant related to the reptation time of the chain.88 This idea of the disentanglement of dangling chain ends has also been utilized by Rubinstein et al. to explain the power-law stress relaxation in block copolymers, see ref. 89.
F. Criticality and fractals
The rheological response of an associating soft material near critical points are often characterized by a power-law response in the frequency-dependent viscoelastic moduli such that G′(ω) ∼ G′′(ω) ∼ ωn. This is observed in cross-linking polymers approaching gelation,90 in soft colloidal systems approaching jamming,91 and in fiber networks approaching critical connectivities.92 Though these studies have canonically predicted n = 1/2 across the different systems, the actual exponent underlying the power-law relaxation has been shown to vary significantly depending on the specific nature of the system.One important factor that appears to govern n is the underlying fractal structure of the associated material. In branched polymeric materials, Muthukumar et al. has shown that n can be related to the fractal dimension df of the polymer network that forms at the percolation threshold.93–95 Other works have shown that the fractal nature of the percolating system remains in the gel structure well beyond the percolation threshold, and that these structures result in remnant signatures in the loss modulus96 and the relaxation spectrum of the resulting gel.97,98 In marginal spring networks, the underlying fractal structure has also been associated with a value of n that is substantially lower than 1/2 at high frequencies,99 though a direct relation between df and n is not yet clear in those systems.100
Another important factor is viscous coupling and hydrodynamics. In polymeric systems, hydrodynamic interactions lead to a different expression of n as a function of df.95 Through normal mode analysis of weak colloidal gels it has been shown that hydrodynamic interactions can drive a power-law relaxation response.101 Finally, the viscous coupling of spring networks with solvents have also been shown to affect the value of n.102 In all of these studies, it has been shown that hydrodynamic interactions result in an increase in n, accelerating the stress relaxation of soft materials.
G. Colloidal gel dynamics
Several studies have also reported unique factors that give rise to the non-Maxwellian relaxation dynamics of colloidal gels. It has been shown in prior work that the density correlations within a single cluster of the gel follows a stretched exponential response.103,104 A microrheological conversion19 of this effect using the generalized Stokes–Einstein approach results in a Kelvin–Voigt like mechanical response, wherein the material acts like a solid at long times (low ω) and a liquid at short times (high ω). In such permanent systems there is another collective relaxation mode at longer times that can also manifest as a result of mutual constraints imposed by steric hindrance; this leads to subdiffusive dynamics, and thus a power-law decrease in G′(ω) and G′′(ω).105Zaccone et al., have shown that relating the cluster size distributions arising from attractive gelation of colloids to the continuous relaxation spectrum H(τ) can result in different relaxation spectra based on the fractal dimension of the associative colloidal gel (for instance, from gelation that proceeds via reaction-limited aggregation or diffusion-limited aggregation). Using this approach, a stretched exponential form of the continuous relaxation spectrum H(τ) (see additional detail on H(τ) in Section IVA) is obtained for diffusion-limited aggregation, and a power-law H(τ) is obtained for reaction-limited aggregation and chemical gelation.106
H. Non-linearity, non-affinity, and intermittency
A popular approach to understand non-Maxwellian relaxation in soft systems (particularly those that show aging dynamics) is through the soft glassy rheology (SGR) model,107,108 in which a power-law relaxation is obtained as a result of activated local yielding processes governed by an exponentially-distributed energy landscape. A “noise temperature” exponent can be extracted from the exponent of the power-law relaxation x from G′(ω) ∼ ωx−1, which indicates how close the material is to a glass transition. The exponentially-distributed energy landscape is motivated by a trap model used for weakly aging systems.109 This local yielding process can also be interpreted in terms of shear-transformation zones,110–114 which has since become a popular method for interpreting relaxation dynamics of glassy and disordered systems.115,116Studies have also shown the importance of non-affine deformations on the power-law viscoelasticity of soft matter. This has been explored in particular detail in spring networks, which experience an increase in non-affine deformations near critical connectivity.117 Studies have shown that such non-affine deformations can therefore directly affect the scaling response of the power law exponent governing G′(ω) ∼ G′′(ω) ∼ ωn.92,118 Recent works have also shown that such non-affine deformations can also arise in dense suspensions,119 suggesting that the underlying physics governing spring networks and dense colloidal suspensions may be similar. In emulsions, it has also been shown that the power-law response in the loss modulus G′′ can arise due to dissipation arising from non-affine motions.120
Other studies have also demonstrated the importance of non-linear mechanical driving on the non-Maxwellian rheology of soft materials. For instance, non-linear mechanical stresses can significantly slow down the power-law relaxation observed in semiflexible polymers, with a corresponding decrease in the exponent n in the relation G(t) ∼ t−n from n = 1/2 as discussed previously in sticky semiflexible polymers, to a value as low as n = 1/10.121 Our recent studies also support the picture of a non-linear mechanical process, where we show that the characteristic relaxation time τc of dynamically arrested soft materials such as gels are governed by internal stresses, and that mechanical driving leads to intermittent avalanches which result in a significant broadening in the continuous relaxation spectrum H(τ).122 In this picture, the stretched-exponential-like stress relaxation of dynamically arrested solids are a manifestation of local viscoplasticity arising from the marginal stability of these systems under imposed mechanical deformations.123–125
Studies have also shown that the scaling exponent governing the displacement trajectories of intermittent avalanches in materials that exhibit such marginal behavior (with power-law free energy landscapes) can be quantitatively linked to the scaling exponent of power-law stress relaxation of soft materials. In this framework, the superdiffusive exponent α obtained from the mean-square displacement relation Δr2(τ) ∼ τa can be related to the power-law exponent n obtained from G(t) ∼ t−n. This requires the knowledge of the power spectrum of stress fluctuations 〈Δσ2(τ)〉 ∼ τΔ; derivations for arrested materials that exhibit spontaneous and random localized motion due to force dipoles (for instance, due to internal stresses126,127) result in Δ = 1,128 and a similar value is directly observed in coarsening foams129 and cells.130 The power-law exponent n can be derived via a generalized Stokes–Einstein approach to obtain n = (a−Δ)/2.129
III. Introduction to modeling non-Maxwellian relaxations
The various proposed origins of non-Maxwellian relaxation processes in Section II invoke various functional forms of stress relaxation. We now introduce a basic mathematical toolkit to describe these non-exponential relaxation processes.A. The relaxation spectrum H(τ)
The relaxation time spectrum H(τ) reveals the underlying relaxation modes governing the stress relaxation response. Each individual relaxation mode is assumed to be exponential, though strictly speaking they can be modified to take other forms, for instance a compressed exponential form.122 It is also possible to interconvert H(τ) into a retardation spectrum L(τ),18 and either of these spectra can be used to evaluate G(t) or any other linear viscoelastic functions through the Boltzmann superposition integral (see eqn (5) and (6)).131–134 Thus, H(τ) encodes the distribution of relaxation modes which drive the linear viscoelastic behavior of a system. A Maxwellian system exhibits a single characteristic relaxation time τc corresponding to a δ function representation of H(τ) (Section I), while a non-Maxwellian system will exhibit a broader distribution of H(τ), thus allowing one to diagnose the statistical origins of non-Maxwellian responses in the rheological responses of the soft material in question.Deriving the expression for G(t) from a known distribution of H(τ) is fairly simple, and involves a simple numerical integration of the known functional form of H(τ). The reverse is not true, however. Obtaining H(τ) from measurements of G(t) or G*(ω) (which are inherently of limited temporal or frequency ranges) is challenging as it requires inverse Laplace transformations. This procedure is ill-posed, meaning that small variations in G(t), including those arising from measurement uncertainties, can cause large variations in H(τ). This has mandated the use of approximation-based methods to obtain estimates of H(τ) from experimental data. There are various strategies to perform this operation,132,134–136 but the use of Tikhonov regularizations is arguably the most established. This was first demonstrated in problems of viscoelasticity by Honerkamp et al.,137 but the regularization method is commonly used in other disciplines as well.138 The regularization method works by finding the optimal solution for H(τ) that minimizes the square error of the solution as well as a measure of the roughness of the resulting solution; for the sake of brevity we defer to references for more detailed instruction on the application of the method.137–139 Regularization-based methods for obtaining H(τ) are now readily available for users via commercial rheometer software and independent codes.139
The relaxation spectrum can be used in the form of discrete modes – in which the relaxation curve is deconstructed into a “line spectrum” of Maxwell modes140 – or in the form of a continuous curve.131,132 Using discrete relaxation modes can be advantageous when the viscoelastic relaxation can be associated directly with well-known underlying relaxation processes, for instance in telechelic metal-coordination-based polymer networks with multiple metal–ligand complexes.13 Otherwise, discrete modes can lead to an unnecessarily large number of fitting parameters, as we show in the next section. A continuous parameterized curve for H(τ) is a more compact method for studying the underlying relaxation processes arising from a stress relaxation curve, though directly estimating the distribution a priori from experimental data can be challenging due to the errors incurred from the inverse Laplace transformation process.137,141 Alternatively, fitting the experimental data to common functional forms utilized in rheology (see Sections IV and V) and obtaining their analytical solutions of H(τ) can sometimes provide a clearer description of the relaxation dynamics that underlie an observed non-Maxwellian viscoelastic response in soft materials.
B. Discrete relaxation spectrum and the generalized Maxwell model
The most straightforward method to model non-Maxwellian relaxation is to assume the presence of discrete Maxwell modes in the relaxation function. A mechanical arrangement in which i Maxwell elements are arranged in parallel gives rise to a Prony series of the Maxwell relaxation equation in eqn (2) such that: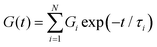 | (12) |
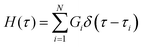 | (13) |
A useful heuristic approach is to assume the presence of a relaxation mode per decade of time.143 We demonstrate the application of this from the relaxation data of a nanoparticle-crosslinked hydrogel which follows a stretched exponential relaxation behavior (Fig. 4A).122 As shown in the data, taking N = 5 Maxwell modes results in an excellent fit to the data, but the utility of this method is poor as we now have 10 fitting parameters with no discernible physical meaning. One can employ more sophisticated methods to determine a “parsimonious” relaxation spectrum144 with the minimal number of modes, for instance by adding a penalty factor for overfitting via a Bayesian information criteria.145 Of course, a purely statistical approach to model selection will be agnostic to the plausibility of the implied physics of the system and therefore must be used with care. There is ongoing research to incorporate such physical insights into statistical models (for instance, increasing the statistical likelihood of models in which the parameters can be restricted to a narrower range of values based on physical insight).142
C. Continuous relaxation spectrum
A continuous relaxation spectrum provides a quantitative basis for interpreting the underlying physics of the relaxation phenomenon. Obtaining the continuous relaxation spectrum can be challenging, however, as the regularization process to convert rheological data to H(τ) as described above can lead to noisy results unless the collected data cover a wide range of times or frequencies. Thus, a useful strategy is to fit the rheological data to analytical solutions of microscopic models with well-known forms of H(τ). For some functional forms of H(τ) that do not have a simple analytical function for G(t) or G*(ω), a direct numerical integration viaeqn (5) and (6) can provide the relaxation modulus or the real and imaginary components of the complex shear modulus. A demonstration of this can be seen in the ref. 76, where a log-normal distribution in sticker strength is assumed to model the rheological response of an associative polymer system.D. Mittag–Leffler functions
We lastly introduce here the Mittag–Leffler (ML) functions, which are a family of generalized functions that include the exponential function. This function occurs frequently as a solution to fractional order differential and integral equations in areas such as diffusive transport, chemical kinetics and viscoelasticity (see Section V for detail on fractional models of viscoelasticity).10,146–154 The ML function of the variable z can have up to three parameters {a, b, c}, and takes the form:155,156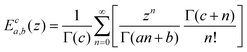 | (14) |
IV. Common relaxation functions
We apply the fundamentals laid out in Section III to highlight common functions used to model non-Maxwellian relaxation processes: the log-normal function, the Cole–Cole or fractional Maxwell gel function, the stretched exponential function, and the Cole–Davidson function. All functions here are valid under normalized conditions such that the initial modulus G0 = 1.A. Log-normal function
A log-normal distribution of relaxation times has an analytical solution of the form:161–164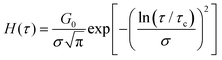 | (15) |
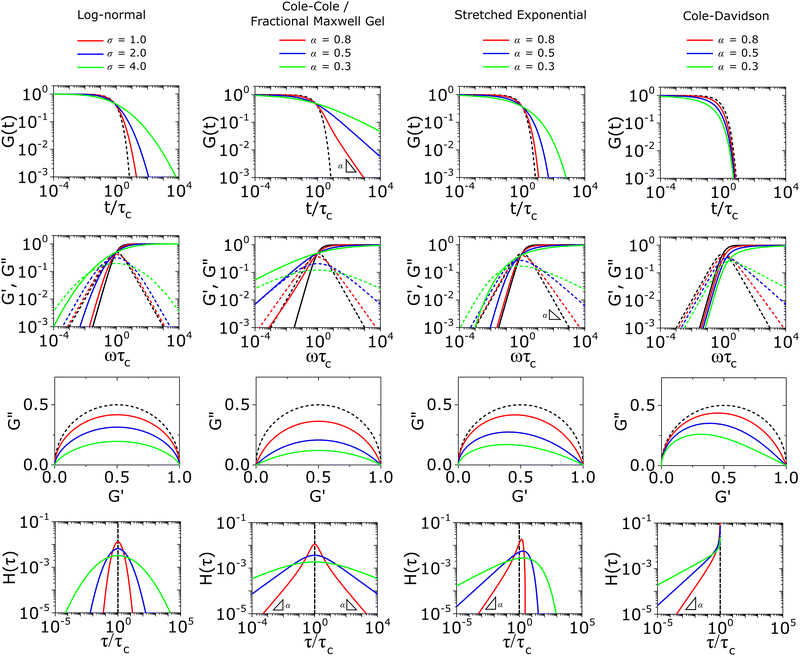 | ||
| Fig. 3 The viscoelastic response of common relaxation functions for modeling non-Maxwellian viscoelastic responses introduced in the main text. All moduli are normalized by the initial modulus G0, and horizontally scaled by the characteristic relaxation time τc. Dashed lines illustrate the viscoelastic response of the Maxwell model (Fig. 1). | ||
The main challenge with using the log-normal function is the absence of easily implementable analytical solutions for the relaxation modulus or the storage and loss moduli. Therefore, G(t) or G*(ω) are usually evaluated by numerical integration of H(τ) in eqn (15) using eqn (5) and (6);145,161,162,166–168 see Fig. 4C and D for demonstration.76 We have also included a simple MATLAB protocol for performing these fitting procedures (see Resources).
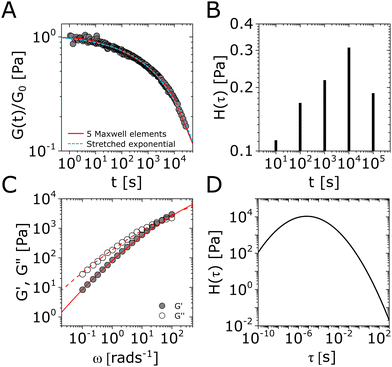 | ||
| Fig. 4 Demonstration of common relaxation functions for modeling non-Maxwellian viscoelastic responses. (A) Stress relaxation modulus G(t) of nitrocatechol-functionalized poly(ethylene glycol) networks reversibly cross-linked by Fe3O4 nanoparticles (time temperature superposition of data taken at temperatures 25 °C ≤ T ≤ 55 °C).122 Shown alongside the data are the predictions of a generalized Maxwell model with N = 5 elements (one element per decade of time, as demonstrated in the classical ref. 143), and a stretched exponential function. Both functions capture the relaxation behavior well, though the stretched exponential function3 contains substantially less fitting parameters than the generalized Maxwell model.10 (B) The obtained discrete relaxation spectrum H(τ) of the generalized Maxwell model used for fitting the data. The asymmetry in H(τ) is in agreement with the good fit of the data to the stretched exponential function which also has an asymmetric H(τ) (Fig. 3). (C) Storage modulus G′(ω) (solid symbols) and loss modulus G′′(ω) (open symbols) of spiropyran-functionalized polymer networks with transition metal cross-linking junctions.76 A fitting procedure based on the log-normal distribution of relaxation modes H(τ) results in a good fit to the storage and loss modulus (solid and dashed lines, respectively). (D) Corresponding log-normal H(τ) underlying the fitted results in (C). All fitting parameters are shown in Table S1 in the ESI.† | ||
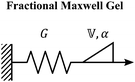
B. Cole–Cole and fractional Maxwell gel functions
The one-parameter version of the ML function with z = −(t/τc)α and a = α occurs frequently in the modeling of broadly distributed relaxation phenomena that can be described by fractional differential equations.151,154 This ML function provides an analytical solution to the Cole–Cole model, which is a classical model used to describe deviations from the Debye dielectric relaxation model (the dielectric analogue to the Maxwell viscoelastic model), given by χ*(ω) = 1/(1 + (iωτc)α).169 An exact mathematical analogue to the Cole–Cole model exists in viscoelastic models in the form of the fractional Maxwell gel model, which we introduce in greater detail later in the review.The analytical description of the Cole–Cole or fractional Maxwell gel relaxation follows:150,152
| G(t) = G0E1α,1[ − (t/τc)α] | (16) |
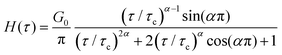 | (17) |
The storage and loss moduli can also be derived analytically. The complex shear modulus G*(ω) is described by the form:150,152,153
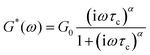 | (18) |
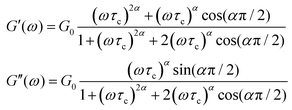 | (19) |
We show numerical evaluations of the relaxation modulus, the dynamic moduli, and the relaxation spectrum for different values of α in Fig. 3. This relaxation function proves to be highly useful in capturing the viscoelastic relaxation of gel-like systems, as we discuss in Section VB and show in Fig. 6B.
C. Stretched exponential function
The stretched exponential function is widely used to model relaxation in soft and disordered materials. It is a direct solution to convolution-based integrals (Section IIE), and is most commonly known in the form of eqn (9). The Fourier transform of the stretched exponential does not have an analytical solution, and thus fitting the stretched exponential function to storage and loss moduli G′ and G′′ also requires numerical integration of H(τ).25 The relaxation spectrum can be expanded in a power series of the form:170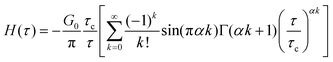 | (20) |
D. Cole–Davidson function
A similar function to the stretched exponential function, the Cole–Davidson function is also sometimes used to capture asymmetric relaxation in materials which show a heavy-tailed distribution in relaxation modes at short times, and an abrupt single Maxwell relaxation mode at long times.170,171 The function is less utilized than the stretched exponential function in modeling viscoelastic relaxation, but this function is commonly used in the modeling of dielectric relaxation.151,170,172 We outline the analytical solutions below.For mechanical relaxation, the Cole–Davidson function is most commonly known through the functional form below:
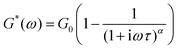 | (21) |
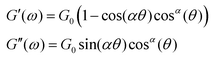 | (22) |
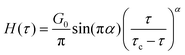 | (23) |
| G(t) = G0(1 − (t/τc)α)Eα1,α+1(−t/τc) | (24) |
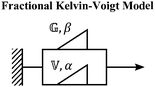
V. Fractional mechanical models
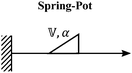
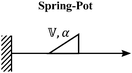
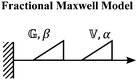
We now introduce a family of mechanical models which are particularly useful for capturing the myriad of power-law relaxation responses in soft materials. This entails the use of a spring-pot mechanical element, which can interpolate between a spring (which has a constitutive equation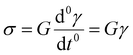 ) and a dashpot (which has a constitutive equation
) and a dashpot (which has a constitutive equation 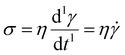 ). This is done through a fractional differentiation of strain with respect to time, such that:
). This is done through a fractional differentiation of strain with respect to time, such that: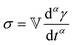 | (25) |
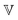 is a “quasi-property”174 which interpolates between a spring-like response in G and dashpot-like response in η, and has the units of Pa sα (an excellent polar representation of the quasi-property in terms of G and η can be found in p. 68 of ref. 175). Though the exact physical meaning of the spring-pot may appear nebulous, it has been shown that the fractional constitutive behavior of the spring-pot can be derived exactly with an infinite ladder arrangement of springs (with spring constants of G1, G2,…GN) and dashpots (with viscosities η1, η2,…ηN) with N → ∞ (Tables 1 and 2).10,16,85,160,176–178 In the ladder arrangement, the fractional exponent α is dictated by the scaling of G and η as a function of N, such that G ∼ η ∼ N1−2a.178 It has also been shown that a fractal network of spring and dashpots can also fulfill this kind of power-law relaxation (the ladder model can be interpreted as a variant of a fractal system).85,178 This makes the spring-pot particularly appealing for describing relaxation processes driven by fractal structures, such as in critical gels. Other effects that result in power-law relaxations have also been linked to fractional models, such as Rouse dynamics.179
is a “quasi-property”174 which interpolates between a spring-like response in G and dashpot-like response in η, and has the units of Pa sα (an excellent polar representation of the quasi-property in terms of G and η can be found in p. 68 of ref. 175). Though the exact physical meaning of the spring-pot may appear nebulous, it has been shown that the fractional constitutive behavior of the spring-pot can be derived exactly with an infinite ladder arrangement of springs (with spring constants of G1, G2,…GN) and dashpots (with viscosities η1, η2,…ηN) with N → ∞ (Tables 1 and 2).10,16,85,160,176–178 In the ladder arrangement, the fractional exponent α is dictated by the scaling of G and η as a function of N, such that G ∼ η ∼ N1−2a.178 It has also been shown that a fractal network of spring and dashpots can also fulfill this kind of power-law relaxation (the ladder model can be interpreted as a variant of a fractal system).85,178 This makes the spring-pot particularly appealing for describing relaxation processes driven by fractal structures, such as in critical gels. Other effects that result in power-law relaxations have also been linked to fractional models, such as Rouse dynamics.179
This mechanical model is also convenient as one can incorporate spring-pots into any conventional spring-dashpot mechanical configuration. The constitutive mechanical behavior then can be directly solved with fractional calculus operations (through either Riemann-Liouville or Caputo operators), the details of which we defer to ref. 10, 150, 152, 153 and 159. The relaxation functions for many of the fractional models feature the Mittag–Leffler functions introduced in Section IIID, which represents a natural solution to fractional differential equations, and is also encountered in other dynamical problems ranging from anomalous diffusion154,157 to infectious disease modeling.180 Fractional mechanical models thus represent a natural choice for modeling the relaxation of soft materials exhibiting fractional kinetics.181
We introduce the more commonly used models below. All analytical results – the constitutive relation, responses to common rheological perturbations such as G(t), G′(ω), G′′(ω), and J(t), as well as the relaxation spectrum H(τ) are listed in Tables 1 and 2, with representative forms shown in Fig. 5. We also defer the readers to the references for more detail on the mathematical properties and applications of these models.10,153,154,159,160,182 Finally, we provide a basic repository of MATLAB codes which demonstrates the application of these models in the fitting of viscoelastic relaxation data (Resources).
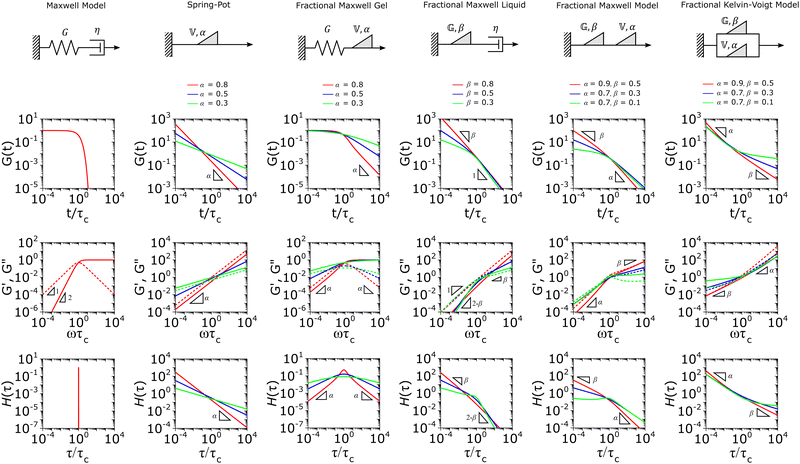 | ||
| Fig. 5 Illustration of the viscoelastic response of the fractional mechanical models discussed in the main text. All analytical functions corresponding to these graphic representations are listed in Tables 1 and 2. The values of the characteristic modulus Gc and characteristic relaxation time τc are set to unity for clarity. | ||
A. Spring-pot
The spring-pot represents the basic building block of fractional mechanical models.10,159,160 Individually, it can produce a power-law response in the relaxation modulus (Tables 1, 2 and Fig. 5). The model is thus quite useful in the modeling of critical gels, in which both G′(ω) and G′′(ω) share a common power-law.90 It is noted that critical gels are often also described by a gel strength parameter S;183 this term can be described by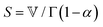 where Γ(x) is the complete Gamma function. The spring-pot is a natural choice for modeling critical gels, due to the fractal nature of both the mechanical configuration of the spring-pot as well as the fractal microstructure of critical gels. A spring-pot indeed provides an excellent fit to a critical mucus gel network, as we show in Fig. 6A.184
where Γ(x) is the complete Gamma function. The spring-pot is a natural choice for modeling critical gels, due to the fractal nature of both the mechanical configuration of the spring-pot as well as the fractal microstructure of critical gels. A spring-pot indeed provides an excellent fit to a critical mucus gel network, as we show in Fig. 6A.184
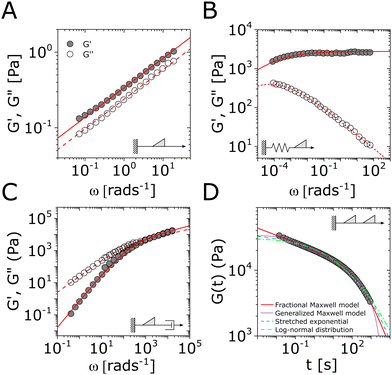 | ||
| Fig. 6 Demonstration of the use of fractional mechanical models for modeling non-Maxwellian linear viscoelastic responses. Viscoelastic responses of (A) pig gastric mucin at pH = 4,184 (B) a colloidal silica gel,45 (C) a poly(4-vinylpyridine) complex coacervate network (time-temperature superposition of data at T = −7 °C and T = 25 °C),185 and (D) myotome (muscle) tissue of Yellowfin tuna (see Fig. 2 caption for experimental protocol). Excellent fits to these data are obtained using a spring-pot, a fractional Maxwell gel (FMG), a fractional Maxwell liquid (FML), and a fractional Maxwell model (FMM) (solid and dashed lines for G′(ω) and G′′(ω) respectively), and solid line for G(t). In (D) we compare the fit to the fractional Maxwell model with fits to the stretched exponential function, the log-normal function, and the generalized Maxwell model; the fractional Maxwell model is deemed to be the most statistically likely as inferred from Bayesian information criteria (see ESI†). All fitting parameters are shown in Table S1 in the ESI.† | ||
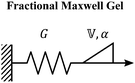
B. Fractional Maxwell gel
When a spring-pot is used in place of a dashpot in the Maxwell model, we obtain the fractional Maxwell gel model. The viscoelastic response of the fractional Maxwell gel model follows exactly the Mittag–Leffler function described in Section IVB and Fig. 3.150,152 In this sense, the fractional Maxwell gel is an exact mechanical analog to the Cole–Cole model186 which has been historically used in modeling anomalous dielectric relaxation in complex materials.151,154,158,187The fractional Maxwell gel model enables the modeling of the stress relaxation response of materials that exhibit a plateau modulus in a dynamic frequency sweep, and interpolates between a stretched exponential relaxation at short times and a power-law relaxation at long times.154 It is thus useful for modeling gel-like materials45,97,182 and we demonstrate the application of the fractional Maxwell gel model for fitting the G′(ω) and G′′(ω) of a colloidal gel, see Fig. 6B.45
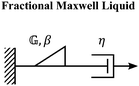
C. Fractional Maxwell liquid
When a spring-pot is used in place of a spring in the Maxwell model, we obtain the fractional Maxwell liquid model. This model is useful for capturing the response of viscoelastic liquids which may exhibit a power-law relaxation mode preceding near-exponential relaxation (for instance, Rouse-like dynamics). We demonstrate this application on polyelectrolyte complexes in Fig. 6C.185 It is worth noting, however, that the terminal relaxation in this model is not an exact exponential – because the relaxation follows a two-parameter Mittag–Leffler relaxation, the terminal slope of the storage modulus at low frequencies is G′(ω) ∼ ω2−β where β is the fractional exponent. Because the model contains a dashpot, the relaxation spectrum is integrable and yields a constant zero-shear viscosity.188,189D. Fractional Maxwell model
When both the spring and the dashpot are replaced by spring-pots, we obtain the fractional Maxwell model. This represents the most generalized linear viscoelastic model to capture mechanical responses to controlled strain (e.g., G(t), G′(ω), G′′(ω)) as it combines the benefits of the fractional Maxwell gel and the fractional Maxwell liquid models; the fractional Maxwell model can easily be reduced into either of these models by setting one of the fractional exponents to 0 or 1, respectively. The stress relaxation response follows a two-parameter variant of the Mittag–Leffler function in eqn (14), and is useful for modeling viscoelastic materials which exhibit a smooth transition between two power-law regimes. This model is also particularly useful in modeling complex materials such as tissues and food composites.190,191 We show a representative example of this in modeling the rheological response of the muscle tissues of Yellowfin tuna, which is more accurately modeled by the fractional Maxwell model than other functions such as the stretched exponential function, the log-normal function, and the generalized Maxwell model (Fig. 6D). In the limit of α = 1 and β = 0, the model reduces to that of the single spring-pot.E. Fractional Kelvin–Voigt model, fractional Zener model, and beyond
We also provide a short introduction to the fractional analog of the Kelvin–Voigt model, which is the counterpart of the fractional Maxwell gel model for studying controlled stress responses. Indeed, just as the G(t) response of the fractional Maxwell model followed a two-parameter Mittag–Leffler function, the creep compliance J(t) follows a two-parameter Mittag–Leffler function. In terms of modeling strain-dependent functions such as G′(ω), and G′′(ω), the fractional Kelvin–Voigt model may be useful in modeling rheological responses of soft materials exhibiting a high-frequency power-law. The fractional Kelvin Voigt model can be further modified by adding an extra spring-pot to one of the arms to create the fractional Zener model. For strain-dependent measurements (e.g., G(t), G′(ω), G′′(ω)), the constitutive response of the fractional Zener model involves the simple addition of the response of the fractional Maxwell model and another spring-pot.175 The fractional Zener model is quite useful in modeling viscoelastic responses of gels and tissues as well.192,193 Overall, in the same way that traditional spring-dashpot configurations can be generalized into larger structures, fractional models can be generalized into larger structures, allowing flexible and customizable modeling of non-Maxwell viscoelastic relaxation in soft materials.VI. Statistical considerations in modeling rheological data
Using the many models introduced in the tutorial review to fit a given set of rheological data is a process which is inherently governed by statistical methods. When the functional form of a model is known a priori, a common method to obtain the “right” parameters for the model that best describes a given set of data is to minimize the weighted residual sum of squares (RSSwi):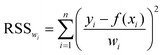 | (26) |
When the expected form of the relaxation process is not known a priori, one can infer the most likely model for a given set of rheological data using an appropriate statistical information criterion. Though the most straightforward method is to simply minimize the RSSwi, this method can be prone to overfitting.142 This overfitting problem can be compensated for by adding a term that penalizes large number of parameters. One such approach is the Bayesian information criterion (BIC):
BIC = −2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln( ln(![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) ) + np ) + np![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(ni) ln(ni) | (27) |
![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) is the maximum of the likelihood function, np is the number of fitting parameters, and ni is the number of data points. For data arising from a Gaussian process with a known variance (for instance, ei), this relation simplifies to:195
is the maximum of the likelihood function, np is the number of fitting parameters, and ni is the number of data points. For data arising from a Gaussian process with a known variance (for instance, ei), this relation simplifies to:195BIC = RSSwi=ei + np![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(ni) ln(ni) | (28) |
We can obtain the BIC values of the fractional Maxwell model, the generalized Maxwell model (with 5 elements), the stretched exponential function, and the log-normal function used to fit the stress relaxation data of Yellowfin tuna in Fig. 6D (see attached MATLAB demo and Fig. S1 in the ESI†). We see that the fractional Maxwell model has the lowest BIC value of the four models, and thus represents the most statistically likely model. A similar operation on the small-amplitude oscillatory shear measurements on the metal-coordinating polymer network of Epstein et al. (from Fig. 4C) shows that the log-normal function is the most statistically likely model (Fig. S2, ESI†).
These analyses also show that the effect of the penalty term is relatively small compared to the likelihood term; the generalized Maxwell models (np = 10 for the tuna data and np = 6 for the metal-coordinating polymer network data) have a lower BIC value than the stretched exponential models (np = 3) in both cases, despite the stretched exponential exhibiting reasonably good fits to the data. This may be because the ei values used to assume the absolute error in this analysis – obtained from uncertainties arising from measured variables on the rheometer194 – provides an under-estimation of the actual errors of the obtained data. More realistic estimations of errors must also consider uncertainties arising from experimental setup (for instance, sample underfilling and overfilling, step strain equilibration time) and from intrinsic heterogeneities in the samples, which would be challenging to quantify. Using larger weighting functions with eqn (27) will lower the magnitude of the likelihood term of the equation and increase the relevance of the penalty term.
Conclusions
We have provided a summary of non-Maxwellian viscoelastic relaxation processes in soft materials, reviewing their diverse origins in different soft materials, and introducing mathematical models and statistical tools to model the observed relaxation responses. The review is aimed at guiding the readers on selecting appropriate mathematical and mechanical models for capturing non-Maxwellian relaxation responses, and drawing meaningful conclusions on the underlying physics of the system based on knowledge of microstructural features of the system (which we have also highlighted in the review). A deep understanding of the principles of soft matter relaxation will have widespread implications in understanding and engineering natural and synthetic soft matter systems, respectively.Resources
We have uploaded a collection of MATLAB codes to demonstrate fitting small-amplitude oscillatory strain and step strain data to continuous relaxation spectra and fractional mechanical models to the File Exchange at https://www.mathworks.com/matlabcentral/fileexchange/111170-analysis-of-non-maxwellian-viscoelastic-data. Fitting results using these demonstrations can also be found in the ESI† (Fig. S1 and S2).Conflicts of interest
There are no conflicts to declare.Acknowledgements
J. S. acknowledges financial support from the MIT Mathworks Fellowship. J. S. and G. H. M. would like to acknowledge R. H. Ewoldt (UIUC), P. K. Singh (Dow Chemical Company), J. D. Rathinaraj (MIT), and J. F. Douglas (NIST) for helpful discussions, and J.-H. Cho (UCSB) for feedback on the manuscript.References
- O. Chaudhuri, J. J. Cooper-White, P. A. Janmey, D. J. Mooney and V. B. Shenoy, Effects of extracellular matrix viscoelasticity on cellular behaviour, Nature, 2020, 584(7822), 535–546 CrossRef CAS PubMed.
- M. Hofer and M. P. Lutolf, Engineering organoids, Nat. Rev. Mater., 2021, 6(5), 402–420 CrossRef CAS PubMed.
- B. J. Blaiszik, S. L. Kramer, S. C. Olugebefola, J. S. Moore, N. R. Sottos and S. R. White, Self-healing polymers and composites, Annu. Rev. Mater. Res., 2010, 40, 179–211 CrossRef CAS.
- A. Campanella, D. Döhler and W. H. Binder, Self-healing in supramolecular polymers, Macromol. Rapid Commun., 2018, 39(17), 1700739 CrossRef PubMed.
- C. W. Macosko and R. G. Larson, Rheology: principles, measurements, and applications, Wiley, 1994 Search PubMed.
- K. P. Menard and N. R. Menard, Dynamic mechanical analysis, CRC Press, 2020 Search PubMed.
- E. M. Furst and T. M. Squires, Microrheology, Oxford University Press, 2017 Search PubMed.
- F. Scheffold, S. Romer, F. Cardinaux, H. Bissig, A. Stradner and L. Rojas-Ochoa, et al., New trends in optical microrheology of complex fluids and gels, Trends Colloid Interface Sci. Xvi, 2004, 141–146 CAS.
- P. Debye, Polare Molekeln, Hirzel, Leipzig, 1929 Search PubMed.
- H. Schiessel, R. Metzler, A. Blumen and T. Nonnenmacher, Generalized viscoelastic models: their fractional equations with solutions, J. Phys. A: Math. Gen., 1995, 28(23), 6567 CrossRef CAS.
- R. B. Bird, R. C. Armstrong and O. Hassager, Dynamics of Polymeric Liquids. Fluid Mechanics, Wiley, 2nd edn, 1987, vol. 1 Search PubMed.
- J. C. Maxwell, On the dynamical theory of gases, Philos. Trans. R. Soc. London, 1867, 157, 49–88 CrossRef.
- S. C. Grindy, R. Learsch, D. Mozhdehi, J. Cheng, D. G. Barrett and Z. Guan, et al., Control of hierarchical polymer mechanics with bioinspired metal-coordination dynamics, Nat. Mater., 2015, 14(12), 1210 CrossRef CAS PubMed.
- M. Van Gurp and J. Palmen, Time-temperature superposition for polymeric blends, Rheol Bull., 1998, 67(1), 5–8 Search PubMed.
- J. D. Ferry, Viscoelastic Properties of Polymers, John Wiley & Sons, 1980 Search PubMed.
- N. W. Tschoegl, The Phenomenological Theory of Linear Viscoelastic Behavior: An Introduction, Springer Science & Business Media, 2012 Search PubMed.
- M. Mours and H. Winter, Mechanical Spectroscopy of Polymers, Experimental Methods in Polymer Science, Elsevier, 2000, pp. 495–546 Search PubMed.
- D. J. Plazek and I. Echeverrıa, Don’t cry for me Charlie Brown, or with compliance comes comprehension, J. Rheol., 2000, 44(4), 831–841 CrossRef CAS.
- T. G. Mason, Estimating the viscoelastic moduli of complex fluids using the generalized Stokes–Einstein equation, Rheol. Acta, 2000, 39(4), 371–378 CrossRef CAS.
- N. Holten-Andersen, A. Jaishankar, M. J. Harrington, D. E. Fullenkamp, G. DiMarco, L. He, G. H. McKinley, P. B. Messersmith and K. Y. Lee, Metal-coordination: using one of nature’s tricks to control soft material mechanics, J. Mater. Chem. B, 2014, 2(17), 2467–2472 RSC.
- V. Yesilyurt, M. J. Webber, E. A. Appel, C. Godwin, R. Langer and D. G. Anderson, Injectable self-healing glucose-responsive hydrogels with pH-regulated mechanical properties, Adv. Mater., 2016, 28(1), 86–91 CrossRef CAS PubMed.
- G. A. Parada and X. Zhao, Ideal reversible polymer networks, Soft Matter, 2018, 14(25), 5186–5196 RSC.
- C. Chassenieux, R. Johannsson, D. Durand, T. Nicolai, P. Vanhoorne and R. Jérôme, Telechelic ionomers studied by light scattering and dynamic mechanical measurements, Colloids Surf., A, 1996, 112(2–3), 155–162 CrossRef CAS.
- A. M. Rosales and K. S. Anseth, The design of reversible hydrogels to capture extracellular matrix dynamics, Nat. Rev. Mater., 2016, 1(2), 1–15 Search PubMed.
- S. Tang, H. Ma, H. C. Tu, H. R. Wang, P. C. Lin and K. S. Anseth, Adaptable Fast Relaxing Boronate-Based Hydrogels for Probing Cell–Matrix Interactions, Adv. Sci., 2018, 5(9), 1800638 CrossRef PubMed.
- N. Conrad, T. Kennedy, D. K. Fygenson and O. A. Saleh, Increasing valence pushes DNA nanostar networks to the isostatic point, Proc. Natl. Acad. Sci., India, 2019, 116(15), 7238–7243 CAS.
- T. Annable, R. Buscall, R. Ettelaie and D. Whittlestone, The rheology of solutions of associating polymers: comparison of experimental behavior with transient network theory, J. Rheol., 1993, 37(4), 695–726 CrossRef CAS.
- Y. Serero, R. Aznar, G. Porte, J.-F. Berret, D. Calvet and A. Collet, et al., Associating polymers: from “flowers” to transient networks, Phys. Rev. Lett., 1998, 81(25), 5584 CrossRef CAS.
- M. Cates and S. Candau, Statics and dynamics of worm-like surfactant micelles, J. Phys.: Condens. Matter, 1990, 2(33), 6869 CrossRef CAS.
- M. Cates, Reptation of living polymers: dynamics of entangled polymers in the presence of reversible chain-scission reactions, Macromolecules, 1987, 20(9), 2289–2296 CrossRef CAS.
- H. Rehage and H. Hoffmann, Viscoelastic surfactant solutions: model systems for rheological research, Mol. Phys., 1991, 74(5), 933–973 CrossRef CAS.
- F. Tanaka and S. Edwards, Viscoelastic properties of physically crosslinked networks: Part 1. Non-linear stationary viscoelasticity, J. Non-Newtonian Fluid Mech., 1992, 43(2–3), 247–271 CrossRef CAS.
- A. Tripathi, K. C. Tam and G. H. McKinley, Rheology and Dynamics of Associative Polymers in Shear and Extension: Theory and Experiments, Macromolecules, 2006, 39(5), 1981–1999 CrossRef CAS.
- F. Meng, R. H. Pritchard and E. M. Terentjev, Stress relaxation, dynamics, and plasticity of transient polymer networks, Macromolecules, 2016, 49(7), 2843–2852 CrossRef CAS.
- R. D. Groot, A. Bot and W. G. Agterof, Molecular theory of the yield behavior of a polymer gel: application to gelatin, J. Chem. Phys., 1996, 104(22), 9220–9233 CrossRef CAS.
- Z. Zhang, Q. Chen and R. H. Colby, Dynamics of associative polymers, Soft Matter, 2018, 14(16), 2961–2977 RSC.
- Z. Zhang, C. Huang, R. Weiss and Q. Chen, Association energy in strongly associative polymers, J. Rheol., 2017, 61(6), 1199–1207 CrossRef CAS.
- M. Green and A. Tobolsky, A new approach to the theory of relaxing polymeric media, J. Chem. Phys., 1946, 14(2), 80–92 CrossRef CAS.
- R. B. Bird, C. F. Curtiss, R. C. Armstrong and O. Hassager, Dynamics of polymeric liquids, Kinetic theory, Wiley, 1987, vol. 2 Search PubMed.
- M. Rubinstein and A. N. Semenov, Thermoreversible gelation in solutions of associating polymers. 2, Linear Dyn. Macromol., 1998, 31(4), 1386–1397 CAS.
- O. Chaudhuri, L. Gu, D. Klumpers, M. Darnell, S. A. Bencherif and J. C. Weaver, et al., Hydrogels with tunable stress relaxation regulate stem cell fate and activity, Nat. Mater., 2016, 15(3), 326 CrossRef CAS PubMed.
- B. Xu and G. B. McKenna, Evaluation of the Dyre shoving model using dynamic data near the glass temperature, J. Chem. Phys., 2011, 134(12), 124902 CrossRef PubMed.
- J. P. Celli, B. S. Turner, N. H. Afdhal, S. Keates, I. Ghiran and C. P. Kelly, et al., Helicobacter pylori moves through mucus by reducing mucin viscoelasticity, Proc. Natl. Acad. Sci., India, 2009, 106(34), 14321–14326 CAS.
- O. Lieleg and A. R. Bausch, Cross-linker unbinding and self-similarity in bundled cytoskeletal networks, Phys. Rev. Lett., 2007, 99(15), 158105 CrossRef CAS PubMed.
- S. Aime, L. Cipelletti and L. Ramos, Power law viscoelasticity of a fractal colloidal gel, J. Rheol, 2018, 6(2), 1429–1441 CrossRef.
- C. L. Lewis, K. Stewart and M. Anthamatten, The influence of hydrogen bonding side-groups on viscoelastic behavior of linear and network polymers, Macromolecules, 2014, 47(2), 729–740 CrossRef CAS.
- A. Gopal and D. J. Durian, Relaxing in foam, Phys. Rev. Lett., 2003, 91(18), 188303 CrossRef CAS PubMed.
- C. Velez-Vega and M. K. Gilson, Force and Stress along Simulated Dissociation Pathways of Cucurbituril–Guest Systems, J. Chem. Theory Comput., 2012, 8(3), 966–976 CrossRef CAS PubMed.
- F. van de Manakker, T. Vermonden, N. el Morabit, C. F. van Nostrum and W. E. Hennink, Rheological behavior of self-assembling PEG-β-cyclodextrin/PEG–cholesterol hydrogels, Langmuir, 2008, 24(21), 12559–12567 CrossRef CAS PubMed.
- B. Marco-Dufort, R. Iten and M. W. Tibbitt, Linking molecular behavior to macroscopic properties in ideal dynamic covalent networks, J. Am. Chem. Soc., 2020, 142(36), 15371–15385 CrossRef CAS PubMed.
- M. Rubinstein and R. H. Colby, Polymer Physics, Oxford University Press, 2003 Search PubMed.
- M. Doi and S. F. Edwards, The Theory of Polymer Dynamics, Oxford University Press, 1988 Search PubMed.
- A. E. Likhtman and T. C. McLeish, Quantitative theory for linear dynamics of linear entangled polymers, Macromolecules, 2002, 35(16), 6332–6343 CrossRef CAS.
- S. T. Milner and T. C. B. McLeish, Parameter-free theory for stress relaxation in star polymer melts, Macromolecules, 1997, 30(7), 2159–2166 CrossRef CAS.
- M. Kapnistos, M. Lang, D. Vlassopoulos, W. Pyckhout-Hintzen, D. Richter and D. Cho, et al., Unexpected power-law stress relaxation of entangled ring polymers, Nat. Mater., 2008, 7(12), 997–1002 CrossRef CAS PubMed.
- F. Gittes and F. MacKintosh, Dynamic shear modulus of a semiflexible polymer network, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1998, 58(2), R1241 CrossRef CAS.
- D. C. Morse, Viscoelasticity of tightly entangled solutions of semiflexible polymers, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1998, 58(2), R1237 CrossRef CAS.
- C. P. Broedersz and F. C. MacKintosh, Modeling semiflexible polymer networks, Rev. Mod. Phys., 2014, 86(3), 995 CrossRef CAS.
- Q. Chen, G. J. Tudryn and R. H. Colby, Ionomer dynamics and the sticky Rouse model, J. Rheol., 2013, 57(5), 1441–1462 CrossRef CAS.
- M. Ahmadi, L. G. D. Hawke, H. Goldansaz and E. van Ruymbeke, Dynamics of Entangled Linear Supramolecular Chains with Sticky Side Groups: Influence of Hindered Fluctuations, Macromolecules, 2015, 48(19), 7300–7310 CrossRef CAS.
- S. Tang, M. Wang and B. D. Olsen, Anomalous self-diffusion and sticky Rouse dynamics in associative protein hydrogels, J. Am. Chem. Soc., 2015, 137(11), 3946–3957 CrossRef CAS PubMed.
- T. Indei and J. Takimoto, Linear viscoelastic properties of transient networks formed by associating polymers with multiple stickers, J. Chem. Phys., 2010, 133(19), 194902 CrossRef PubMed.
- M. Rubinstein and A. N. Semenov, Dynamics of entangled solutions of associating polymers, Macromolecules, 2001, 34(4), 1058–1068 CrossRef CAS.
- I. Nyrkova and A. Semenov, Correlation effects in dynamics of living polymers, EPL, 2007, 79(6), 66007 CrossRef.
- C. Schaefer, P. R. Laity, C. Holland and T. C. McLeish, Silk Protein Solution: A Natural Example of Sticky Reptation, Macromolecules, 2020, 53(7), 2669–2676 CrossRef CAS PubMed.
- C. P. Broedersz, M. Depken, N. Y. Yao, M. R. Pollak, D. A. Weitz and F. C. MacKintosh, Cross-link-governed dynamics of biopolymer networks, Phys. Rev. Lett., 2010, 105(23), 238101 CrossRef PubMed.
- K. W. Müller, R. F. Bruinsma, O. Lieleg, A. R. Bausch, W. A. Wall and A. J. Levine, Rheology of semiflexible bundle networks with transient linkers, Phys. Rev. Lett., 2014, 112(23), 238102 CrossRef PubMed.
- C. Pattamaprom and R. G. Larson, Predicting the linear viscoelastic properties of monodisperse and polydisperse polystyrenes and polyethylenes, Rheol. Acta, 2001, 40(6), 516–532 CrossRef CAS.
- A. Shabbir, I. Javakhishvili, S. Cerveny, S. Hvilsted, A. L. Skov and O. Hassager, et al., Linear viscoelastic and dielectric relaxation response of unentangled UPy-based supramolecular networks, Macromolecules, 2016, 49(10), 3899–3910 CrossRef CAS.
- M. Ahmadi, A. Jangizehi, E. van Ruymbeke and S. Seiffert, Deconvolution of the Effects of Binary Associations and Collective Assemblies on the Rheological Properties of Entangled Side-Chain Supramolecular Polymer Networks, Macromolecules, 2019, 52(14), 5255–5267 CrossRef CAS.
- A. Semenov, A. Charlot, R. Auzély-Velty and M. Rinaudo, Rheological properties of binary associating polymers, Rheol. Acta, 2007, 46(5), 541–568 CrossRef CAS.
- S. Wang and R. G. Larson, Multiple relaxation modes in suspensions of colloidal particles bridged by telechelic polymers, J. Rheol., 2018, 62(2), 477–490 CrossRef CAS.
- V. V. Ginzburg, T. Chatterjee, A. I. Nakatani and A. K. Van Dyk, Oscillatory and steady shear rheology of model hydrophobically modified ethoxylated urethane-thickened waterborne paints, Langmuir, 2018, 34(37), 10993–11002 CrossRef CAS PubMed.
- J. Huskens, L. J. Prins, R. Haag and B. J. Ravoo, Multivalency: Concepts, Research and Applications, John Wiley & Sons, 2018 Search PubMed.
- H. L. Roy, J. Song, G. H. McKinley, N. Holten-Andersen and M. Lenz, Valence can control the non-exponential viscoelastic relaxation of reversible multivalent gels, arXiv, 2021, preprint, arXiv:2112.07454, DOI:10.48550/arXiv.2112.07454.
- E. S. Epstein, L. Martinetti, R. H. Kollarigowda, O. Carey-De La Torre, J. S. Moore and R. H. Ewoldt, et al., Modulating noncovalent cross-links with molecular switches, J. Am. Chem. Soc., 2019, 141(8), 3597–3604 CrossRef CAS PubMed.
- R. J. Masurel, S. Cantournet, A. Dequidt, D. R. Long, H. Montes and F. Lequeux, Role of dynamical heterogeneities on the viscoelastic spectrum of polymers: a stochastic continuum mechanics model, Macromolecules, 2015, 48(18), 6690–6702 CrossRef CAS.
- W. Schirmacher, G. Ruocco and V. Mazzone, Theory of heterogeneous viscoelasticity, Philos. Mag., 2016, 96(7–9), 620–635 CrossRef CAS.
- K. Ngai, Relaxation and Diffusion in Complex Systems, Springer Science & Business Media, 2011 Search PubMed.
- J. Phillips, Stretched exponential relaxation in molecular and electronic glasses, Rep. Prog. Phys., 1996, 59(9), 1133 CrossRef CAS.
- G. C. Berry and D. J. Plazek, On the use of stretched-exponential functions for both linear viscoelastic creep and stress relaxation, Rheol. Acta, 1997, 36(3), 320–329 CrossRef CAS.
- K. A. Erk and J. F. Douglas, Stretched exponential stress relaxation in a thermally reversible, physically associating block copolymer solution, MRS Online Proc. Libr., 2012, 1418 Search PubMed.
- O. Chaudhuri, L. Gu, D. Klumpers, M. Darnell, S. A. Bencherif and J. C. Weaver, et al., Hydrogels with tunable stress relaxation regulate stem cell fate and activity, Nat. Mater., 2016, 15(3), 326–334 CrossRef CAS PubMed.
- A. Bunde, S. Havlin, J. Klafter, G. Graff and A. Shehter, Stretched-exponential relaxation: the role of system size, Philos. Mag. B, 1998, 77(5), 1323–1329 CrossRef CAS.
- A. A. Gurtovenko and A. Blumen, Generalized Gaussian Structures: Models for Polymer Systems with Complex Topologies, Polymer Analysis Polymer Theory, Springer, 2005. pp. 171–282 Search PubMed.
- J. F. Douglas and J. B. Hubbard, Semiempirical theory of relaxation: concentrated polymer solution dynamics, Macromolecules, 1991, 24(11), 3163–3177 CrossRef CAS.
- E. B. Stukalin, J. F. Douglas and K. F. Freed, Multistep relaxation in equilibrium polymer solutions: a minimal model of relaxation in “complex” fluids, J. Chem. Phys., 2008, 129(9), 094901 CrossRef PubMed.
- J. G. Curro and P. Pincus, A theoretical basis for viscoelastic relaxation of elastomers in the long-time limit, Macromolecules, 1983, 16(4), 559–562 CrossRef CAS.
- M. Rubinstein and S. Obukhov, Power-law-like stress relaxation of block copolymers: disentanglement regimes, Macromolecules, 1993, 26(7), 1740–1750 CrossRef CAS.
- H. H. Winter and M. Mours, Rheology of polymers near liquid–solid transitions, Neutron Spin Echo Spectroscopy Viscoelasticity Rheology, Springer, 1997, pp. 165–234 Search PubMed.
- B. P. Tighe, Relaxations and rheology near jamming, Phys. Rev. Lett., 2011, 107(15), 158303 CrossRef PubMed.
- M. Yucht, M. Sheinman and C. Broedersz, Dynamical behavior of disordered spring networks, Soft Matter, 2013, 9(29), 7000–7006 RSC.
- M. Muthukumar, Dynamics of polymeric fractals, J. Chem. Phys., 1985, 83(6), 3161–3168 CrossRef CAS.
- M. Muthukumar and H. H. Winter, Fractal dimension of a crosslinking polymer at the gel point, Macromolecules, 1986, 19(4), 1284–1285 CrossRef CAS.
- M. Muthukumar, Screening effect on viscoelasticity near the gel point, Macromolecules, 1989, 22(12), 4656–4658 CrossRef CAS.
- D. Adolf and J. E. Martin, Ultraslow relaxations in networks: evidence for remnant fractal structures, Macromolecules, 1991, 24(25), 6721–6724 CrossRef CAS.
- B. Keshavarz, D. G. Rodrigues, J.-B. Champenois, M. G. Frith, J. Ilavsky and M. Geri, et al., Time-connectivity superposition and the gel/glass duality of weak colloidal gels, Proc. Natl. Acad. Sci. U. S. A., 2021, 118(15), e2022339118 CrossRef CAS PubMed.
- M. Bantawa, B. Keshavarz, M. Geri, M. Bouzid, T. Divoux and G. H. McKinley, The hidden hierarchical nature of soft particulate gels, Nat. Phys., 2023, 19, 1178–1184 Search PubMed.
- D. Head, Viscoelastic scaling regimes for marginally rigid fractal spring networks, Phys. Rev. Lett., 2022, 129(1), 018001 CrossRef CAS PubMed.
- A. Karakoulaki and D. Head, Distinct viscoelastic scaling for isostatic spring networks of the same fractal dimension. arXiv, 2022, preprint, arXiv:220802026.
- Z. Varga and J. W. Swan, Normal modes of weak colloidal gels, Phys. Rev. E, 2018, 97(1), 012608 CrossRef CAS PubMed.
- M. Dennison and H. Stark, Viscoelastic properties of marginal networks in a solvent, Phys. Rev. E, 2016, 93(2), 022605 CrossRef CAS PubMed.
- A. Krall and D. Weitz, Internal dynamics and elasticity of fractal colloidal gels, Phys. Rev. Lett., 1998, 80(4), 778 CrossRef CAS.
- J. H. Cho, R. Cerbino and I. Bischofberger, Emergence of Multiscale Dynamics in Colloidal Gels, Phys. Rev. Lett., 2020, 124(8), 088005 CrossRef CAS PubMed.
- J. H. Cho and I. Bischofberger, Two modes of cluster dynamics govern the viscoelasticity of colloidal gels, Phys. Rev. E, 2021, 103(3), 032609 CrossRef CAS PubMed.
- A. Zaccone, H. H. Winter, M. Siebenbürger and M. Ballauff, Linking self-assembly, rheology, and gel transition in attractive colloids, J. Rheol., 2014, 58(5), 1219–1244 CrossRef CAS.
- P. Sollich, F. Lequeux, P. Hébraud and M. E. Cates, Rheology of soft glassy materials, Phys. Rev. Lett., 1997, 78(10), 2020 CrossRef CAS.
- S. M. Fielding, P. Sollich and M. E. Cates, Aging and rheology in soft materials, J. Rheol., 2000, 44(2), 323–369 CrossRef CAS.
- J.-P. Bouchaud, Weak ergodicity breaking and aging in disordered systems, J. Phys. I, 1992, 2(9), 1705–1713 CrossRef.
- J. S. Langer, Shear-transformation-zone theory of plastic deformation near the glass transition, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 77(2), 021502 CrossRef CAS PubMed.
- M. L. Falk and J. S. Langer, Deformation and failure of amorphous, solidlike materials, Annu. Rev. Condens. Matter Phys., 2011, 2(1), 353–373 CrossRef CAS.
- I. Fuereder and P. Ilg, Nonequilibrium thermodynamics of the soft glassy rheology model, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88(4), 042134 CrossRef PubMed.
- E. Bouchbinder and J. S. Langer, Nonequilibrium thermodynamics and glassy rheology, Soft Matter, 2013, 9(37), 8786–8791 RSC.
- P. Sollich and M. E. Cates, Thermodynamic interpretation of soft glassy rheology models, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 85(3), 031127 CrossRef PubMed.
- A. Nicolas, E. E. Ferrero, K. Martens and J.-L. Barrat, Deformation and flow of amorphous solids: insights from elastoplastic models, Rev. Mod. Phys., 2018, 90(4), 045006 CrossRef CAS.
- E. E. Ferrero, K. Martens and J.-L. Barrat, Relaxation in yield stress systems through elastically interacting activated events, Phys. Rev. Lett., 2014, 113(24), 248301 CrossRef CAS PubMed.
- J. L. Shivers, S. Arzash, A. Sharma and F. C. MacKintosh, Scaling theory for mechanical critical behavior in fiber networks, Phys. Rev. Lett., 2019, 122(18), 188003 CrossRef CAS PubMed.
- L. Rizzi, S. Auer and D. Head, Importance of non-affine viscoelastic response in disordered fibre networks, Soft Matter, 2016, 12(19), 4332–4338 RSC.
- J. L. Shivers, A. Sharma and F. C. MacKintosh, Nonaffinity controls critical slowing down and rheology near the onset of rigidity, arXiv, 2022, preprint, arXiv:220304891.
- A. J. Liu, S. Ramaswamy, T. Mason, H. Gang and D. Weitz, Anomalous viscous loss in emulsions, Phys. Rev. Lett., 1996, 76(16), 3017 CrossRef CAS PubMed.
- Y. Mulla, F. MacKintosh and G. H. Koenderink, Origin of slow stress relaxation in the cytoskeleton, Phys. Rev. Lett., 2019, 122(21), 218102 CrossRef CAS PubMed.
- J. Song, Q. Zhang, F. de Quesada, M. H. Rizvi, J. B. Tracy and J. Ilavsky, et al., Microscopic dynamics underlying the stress relaxation of arrested soft materials, Proc. Natl. Acad. Sci., India, 2022, 119(30), e2201566119 CAS.
- B. Shang, P. Guan and J.-L. Barrat, Elastic avalanches reveal marginal behavior in amorphous solids, Proc. Natl. Acad. Sci., India, 2020, 117(1), 86–92 CAS.
- P. Cao, M. P. Short and S. Yip, Potential energy landscape activations governing plastic flows in glass rheology, Proc. Natl. Acad. Sci., India, 2019, 116(38), 18790–18797 CAS.
- P. Charbonneau, J. Kurchan, G. Parisi, P. Urbani and F. Zamponi, Fractal free energy landscapes in structural glasses, Nat. Commun., 2014, 5(1), 1–6 Search PubMed.
- J.-P. Bouchaud and E. Pitard, Anomalous dynamical light scattering in soft glassy gels, Eur. Phys. J. E: Soft Matter Biol. Phys., 2001, 6(3), 231–236 CrossRef CAS.
- L. Cipelletti, L. Ramos, S. Manley, E. Pitard, D. A. Weitz and E. E. Pashkovski, et al., Universal non-diffusive slow dynamics in aging soft matter, Faraday Discuss., 2003, 123, 237–251 RSC.
- P. T. Underhill and M. D. Graham, Correlations and fluctuations of stress and velocity in suspensions of swimming microorganisms, Phys. Fluids, 2011, 23(12), 121902 CrossRef.
- H. J. Hwang, R. A. Riggleman and J. C. Crocker, Understanding soft glassy materials using an energy landscape approach, Nat. Mater., 2016, 15(9), 1031–1036 CrossRef CAS PubMed.
- A. W. Lau, B. D. Hoffman, A. Davies, J. C. Crocker and T. C. Lubensky, Microrheology, stress fluctuations, and active behavior of living cells, Phys. Rev. Lett., 2003, 91(19), 198101 CrossRef CAS PubMed.
- M. Baumgaertel and H. H. Winter, Determination of discrete relaxation and retardation time spectra from dynamic mechanical data, Rheol. Acta, 1989, 28(6), 511–519 CrossRef CAS.
- M. Baumgaertel and H. H. Winter, Interrelation between continuous and discrete relaxation time spectra, J. Non-Newtonian Fluid Mech., 1992, 44(1), 15–36 CrossRef CAS.
- E. A. Jensen, Determination of discrete relaxation spectra using simulated annealing, J. Non-Newtonian Fluid Mech., 2002, 107(1–3), 1–11 CrossRef CAS.
- K. Soo Cho and G. Woo Park, Fixed-point iteration for relaxation spectrum from dynamic mechanical data, J. Rheol., 2013, 57(2), 647–678 CrossRef.
- J.-E. Bae and K. S. Cho, Logarithmic method for continuous relaxation spectrum and comparison with previous methods, J. Rheol., 2015, 59(4), 1081–1112 CrossRef CAS.
- F. J. Stadler and C. Bailly, A new method for the calculation of continuous relaxation spectra from dynamic-mechanical data, Rheol. Acta, 2009, 48(1), 33–49 CrossRef CAS.
- J. Honerkamp and J. Weese, A nonlinear regularization method for the calculation of relaxation spectra, Rheol. Acta, 1993, 32(1), 65–73 CrossRef CAS.
- D. C. Forney and D. H. Rothman, Common structure in the heterogeneity of plant-matter decay, J. R. Soc., Interface, 2012, 9(74), 2255–2267 CrossRef PubMed.
- A. Takeh and S. Shanbhag, A computer program to extract the continuous and discrete relaxation spectra from dynamic viscoelastic measurements, Appl. Rheol., 2013, 23(2), 24628 Search PubMed.
- I. Emri and N. Tschoegl, Generating line spectra from experimental responses. Part I: relaxation modulus and creep compliance, Rheol. Acta, 1993, 32, 311–322 CrossRef CAS.
- R. S. Anderssen and A. Davies, Simple moving-average formulae for the direct recovery of the relaxation spectrum, J. Rheol., 2001, 45(1), 1–27 CrossRef CAS.
- J. B. Freund and R. H. Ewoldt, Quantitative rheological model selection: Good fits versus credible models using Bayesian inference, J. Rheol., 2015, 59(3), 667–701 CrossRef CAS.
- H. Laun, Description of the non-linear shear behaviour of a low density polyethylene melt by means of an experimentally determined strain dependent memory function, Rheol. Acta, 1978, 17(1), 1–15 CrossRef CAS.
- H. Winter, M. Baumgaertel and P. Soskey, A parsimonious model for viscoelastic liquids and solids, Techniques in rheological measurement, Springer, 1993, pp. 123–160 Search PubMed.
- L. Martinetti, J. M. Soulages and R. H. Ewoldt, Continuous relaxation spectra for constitutive models in medium-amplitude oscillatory shear, J. Rheol., 2018, 62(5), 1271–1298 CrossRef CAS.
- F. Mainardi, On some properties of the Mittag-Leffler function Eα(−tα), completely monotone for t > 0 with 0 < α <1, arXiv, 2013, preprint, arXiv:13050161 DOI:10.48550/arXiv.13050161.
- R. Gorenflo, A. A. Kilbas, F. Mainardi and S. V. Rogosin, Mittag–Leffler functions, related topics and applications, Springer, 2014 Search PubMed.
- S. Rogosin, The role of the Mittag–Leffler function in fractional modeling, Mathematics, 2015, 3(2), 368–381 CrossRef.
- C. Rosa and E. Capelas de Oliveira, Relaxation equations: fractional models, J. Phys. Math., 2015, 6(2), 1–7, DOI:10.4172/2090-0902.1000146.
- S. W. Katicha and G. Flintsch, Fractional viscoelastic models: master curve construction, interconversion, and numerical approximation, Rheol. Acta, 2012, 51(8), 675–689 CrossRef CAS.
- R. Garrappa, F. Mainardi and M. Guido, Models of dielectric relaxation based on completely monotone functions, Fract. Calculus Appl. Anal., 2016, 19(5), 1105–1160 CrossRef.
- K. Adolfsson, M. Enelund and P. Olsson, On the fractional order model of viscoelasticity, Mech. Time-Depend. Mater., 2005, 9(1), 15–34 CrossRef CAS.
- N. Heymans, Hierarchical models for viscoelasticity: dynamic behaviour in the linear range, Rheol. Acta, 1996, 35(5), 508–519 CrossRef CAS.
- R. Metzler and J. Klafter, From stretched exponential to inverse power-law: fractional dynamics, Cole–Cole relaxation processes, and beyond, J. Non-Cryst. Solids, 2002, 305(1–3), 81–87 CrossRef CAS.
- T. R. Prabhakar, A singular integral equation with a generalized Mittag Leffler function in the kernel, Yokohama Math J., 1971, 19(1), 7–15 Search PubMed.
- R. Garra and R. Garrappa, The Prabhakar or three parameter Mittag–Leffler function: theory and application, Commun. Nonlinear Sci. Numerical Simulation, 2018, 56, 314–329 CrossRef.
- R. Metzler, E. Barkai and J. Klafter, Anomalous diffusion and relaxation close to thermal equilibrium: a fractional Fokker-Planck equation approach, Phys. Rev. Lett., 1999, 82(18), 3563 CrossRef CAS.
- E. C. De Oliveira, F. Mainardi and J. Vaz, Models based on Mittag–Leffler functions for anomalous relaxation in dielectrics, Eur. Phys. J.: Spec. Top., 2011, 193(1), 161–171 Search PubMed.
- A. Jaishankar and G. H. McKinley, Power-law rheology in the bulk and at the interface: quasi-properties and fractional constitutive equations, Proc. R. Soc. A, 2013, 469(2149), 20120284 CrossRef.
- H. Schiessel and A. Blumen, Hierarchical analogues to fractional relaxation equations, J. Phys. A: Math. Gen., 1993, 26(19), 5057 CrossRef.
- A. S. Nowick and B. S. Berry, Lognormal distribution function for describing anelastic and other relaxation processes I. theory and numerical computations, IBM J. Res. Dev., 1961, 5(4), 297–311 Search PubMed.
- A. S. Nowick and B. S. Berry, Lognormal distribution function for describing anelastic and other relaxation processes II. data analysis and applications, IBM J. Res. Dev., 1961, 5(4), 312–320 Search PubMed.
- E. Wiechert, Gesetze der elastischen Nachwirkung für constante Temperatur, Ann. Phys., 1893, 286(11), 546–570 CrossRef.
- K. W. Wagner, Zur theorie der unvollkommenen dielektrika, Ann. Phys., 1913, 345(5), 817–855 CrossRef.
- W. Schirmacher, G. Ruocco and V. Mazzone, Heterogeneous viscoelasticity: a combined theory of dynamic and elastic heterogeneity, Phys. Rev. Lett., 2015, 115(1), 015901 CrossRef PubMed.
- R. Flores and J. Perez, Mechanical Spectroscopy of the. beta. Relaxation in Poly(vinyl chloride), Macromolecules, 1995, 28(21), 7171–7179 CrossRef CAS.
- P. Feltham, On the representation of rheological results with special reference to creep and relaxation, Br. J. Appl. Phys., 1955, 6(1), 26 CrossRef CAS.
- R. Fulchiron, A. Michel, V. Verney and J. Roustant, Correlations between relaxation time spectrum and melt spinning behavior of polypropylene. 1: calculation of the relaxation spectrum as a log-normal distribution and influence of the molecular parameters, Polym. Eng. Sci., 1995, 35(6), 513–517 CrossRef CAS.
- K. S. Cole and R. H. Cole, Dispersion and absorption in dielectrics I. Alternating current characteristics, J. Chem. Phys., 1941, 9(4), 341–351 CrossRef CAS.
- C. Lindsey and G. Patterson, Detailed comparison of the Williams–Watts and Cole–Davidson functions, J. Chem. Phys., 1980, 73(7), 3348–3357 CrossRef CAS.
- B. Shang, J. Rottler, P. Guan and J.-L. Barrat, Local versus global stretched mechanical response in a supercooled liquid near the glass transition, Phys. Rev. Lett., 2019, 122(10), 105501 CrossRef CAS PubMed.
- B. Gross, Dielectric relaxation and the Davidson–Cole distribution function, J. Appl. Phys., 1985, 57(6), 2331–2333 CrossRef.
- T. C. Dotson, J. Budzien, J. D. McCoy and D. B. Adolf, Cole–Davidson dynamics of simple chain models, J. Chem. Phys., 2009, 130(2), 024903 CrossRef PubMed.
- G. S. Blair, B. Veinoglou and J. Caffyn, Limitations of the Newtonian time scale in relation to non-equilibrium rheological states and a theory of quasi-properties, Proc. R. Soc. London, Ser. A, 1947, 189(1016), 69–87 CAS.
- A. Jaishankar, The Linear and Nonlinear Rheology of Multiscale Complex Fluids, PhD thesis, Massachusetts Institute of Technology, 2014.
- B. Gross and R. M. Fuoss, Ladder structures for representation of viscoelastic systems, J. Polym. Sci., 1956, 19(91), 39–50 CrossRef.
- C. Friedrich, H. Schiessel and A. Blumen, Constitutive behavior modeling and fractional derivatives, Rheology Series, Elsevier, 1999, vol. 8, pp. 429–66 Search PubMed.
- H. Schiessel and A. Blumen, Mesoscopic pictures of the sol-gel transition: ladder models and fractal networks, Macromolecules, 1995, 28(11), 4013–4019 CrossRef CAS.
- R. L. Bagley and P. Torvik, A theoretical basis for the application of fractional calculus to viscoelasticity, J. Rheol., 1983, 27(3), 201–210 CrossRef CAS.
- M. S. Abdo, K. Shah, H. A. Wahash and S. K. Panchal, On a comprehensive model of the novel coronavirus (COVID-19) under Mittag–Leffler derivative, Chaos, Solitons Fractals, 2020, 135, 109867 CrossRef PubMed.
- I. M. Sokolov, J. Klafter and A. Blumen, Fractional kinetics, Phys. Today, 2002, 55(11), 48–54 CrossRef CAS.
- J. D. J. Rathinaraj, G. H. McKinley and B. Keshavarz, Incorporating rheological nonlinearity into fractional calculus descriptions of fractal matter and multi-scale complex fluids, Fractal Fract., 2021, 5(4), 174 CrossRef.
- H. H. Winter and F. Chambon, Analysis of linear viscoelasticity of a crosslinking polymer at the gel point, J. Rheol., 1986, 30(2), 367–382 CrossRef CAS.
- J. P. Celli, B. S. Turner, N. H. Afdhal, R. H. Ewoldt, G. H. McKinley and R. Bansil, et al., Rheology of gastric mucin exhibits a pH-dependent sol–gel transition, Biomacromolecules, 2007, 8(5), 1580–1586 CrossRef CAS PubMed.
- K. Sadman, Q. Wang, Y. Chen, B. Keshavarz, Z. Jiang and K. R. Shull, Influence of hydrophobicity on polyelectrolyte complexation, Macromolecules, 2017, 50(23), 9417–9426 CrossRef CAS.
- B. Gross, On creep and relaxation, J. Appl. Phys., 1947, 18(2), 212–221 CrossRef.
- G. Legrand, S. Manneville, G. H. McKinley and T. Divoux, Dual origin of viscoelasticity in polymer-carbon black hydrogels: a rheometry and electrical spectroscopy study, Macromolecules, 2023, 56(6), 2298–2308 CrossRef CAS.
- J. D. J. Rathinaraj, J. Hendricks, G. H. McKinley and C. Clasen, OrthoChirp: a fast spectro-mechanical probe for monitoring transient microstructural evolution of complex fluids during shear, J. Non-Newtonian Fluid Mech., 2022, 301, 104744 CrossRef CAS.
- J. D. J. Rathinaraj, B. Keshavarz and G. H. McKinley, Why the Cox–Merz rule and Gleissle mirror relation work: a quantitative analysis using the Wagner integral framework with a fractional Maxwell kernel, Phys. Fluids, 2022, 34(3), 033106 CrossRef CAS.
- T. Faber, A. Jaishankar and G. H. McKinley, Describing the firmness, springiness and rubberiness of food gels using fractional calculus. Part I: theoretical framework, Food Hydrocolloids, 2017, 62, 311–324 CrossRef CAS.
- T. Faber, A. Jaishankar and G. H. McKinley, Describing the firmness, springiness and rubberiness of food gels using fractional calculus. Part II: measurements on semi-hard cheese, Food Hydrocolloids, 2017, 62, 325–339 CrossRef CAS.
- J. Song, M. H. Rizvi, B. B. Lynch, J. Ilavsky, D. Mankus and J. B. Tracy, et al., Programmable Anisotropy and Percolation in Supramolecular Patchy Particle Gels, ACS Nano, 2020, 14(12), 17018–17027 CrossRef CAS PubMed.
- K. J. Parker, T. Szabo and S. Holm, Towards a consensus on rheological models for elastography in soft tissues, Phys. Med. Biol., 2019, 64(21), 215012 CrossRef CAS PubMed , 31530765.
- P. K. Singh, J. M. Soulages and R. H. Ewoldt, On fitting data for parameter estimates: residual weighting and data representation, Rheol. Acta, 2019, 58(6), 341–359 CrossRef CAS.
- P. K. Singh, Rheological Inferences with Uncertainty Quantification, PhD thesis, University of Illinois at Urbana-Champaign, 2019.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3sm00736g |
| This journal is © The Royal Society of Chemistry 2023 |