Open Access Article
Open Access ArticleDynamics of bubbles spontaneously entering into a tube†
Alexis
Commereuc
,
Manon
Marchand
 ,
Emmanuelle
Rio
,
Emmanuelle
Rio
 and
François
Boulogne
and
François
Boulogne
 *
*
Laboratoire de Physique des Solides, Université Paris-Saclay, CNRS, 91405, Orsay, France
First published on 6th July 2023
Abstract
When an open tube of small diameter touches a bubble of a larger diameter, the bubble spontaneously shrinks and pushes a soap film into the tube. We characterize the dynamics for different bubble sizes and number of soap films in the tube. We rationalize this observation from a mechanical force balance involving the Laplace pressure of the bubble and the viscous force from the advancing soap lamellae in the tube. We propose a numerical resolution of this model, and an analytical solution in an asymptotic regime. These predictions are then compared to the experiments. The emptying duration is primarily affected by the initial bubble to tube diameter ratio and by the number of soap films in the tube.
1 Introduction
Spontaneous entrance of a liquid in capillary tubes is a well studied problem. The equilibrium solution of capillary rise is the well known Jurin's law and was derived in the 18th century.1 It is then two centuries later that the pioneering work by Bell, Lucas and Washburn allowed the understanding of the dynamics of this problem. They considered the viscous dissipation in the liquid flow driven by the capillary suction.2–4 More recently, this problem has been revisited to provide a finer description of the role of inertia and the possibility of interfacial oscillations for fluids of extremely low viscosity was revealed.5,6Liquid invading capillary tubes has been extended also to drops. Wang et al. performed numerical simulations on the penetration of drop in non-wetting capillaries7 that has been studied experimentally by Willmott et al. highlighting the effect of the wetting conditions and the drop size to tube ratio.8 For drops, the dynamics is dominated by inertia and capillarity, with a noticeable correction due to viscous forces.9
Besides drops, bubbles are also prone to shrinkage due to the Laplace pressure for which Leidenfrost wrote observations in a monograph entitled De aquae communis nonnullis qualitatibus tractatus published in 1756.10 Leidenfrost is renowned for describing a phenomenon where a liquid drop is placed on a hot surface whose temperature is larger than the boiling temperature of the liquid. This Treatise on the Properties of Common Water not only contains a text on levitating drops, but also a less known part on soap films and bubbles. Leidenfrost commented on the soap film thickness, colored fringes, and also on surface tension and induced dynamics. Notably, Leidenfrost reports observations in paragraph 46 on the bubble shrinkage when placed at the extremity of a tube.
A well known configuration where bubble shrinkage is encountered is foam aging, in which the smaller bubbles tend to empty into the larger ones because of their higher Laplace pressure. In such a situation, the motor, which is the pressure difference between the bubbles is balanced by the gas diffusion in the liquid film.11
Another situation where a bubble shrinkage dynamics is observed has been reported recently by Clerget et al. who studied experimentally and theoretically the emptying of a hemispherical bubble through a pierced surface.12 The air motion is driven by the Laplace pressure in the bubble limited by the air flow through the orifice and eventually by the friction of the bubble on the surface.
In this article, we propose to investigate the situation closely related to the observations made by Leidenfrost: the shrinkage of a bubble placed at the end of a tube of a smaller diameter. A careful observation reveals that the entering motion shows a characteristic pattern of acceleration–deceleration, as the bubble shrinks. This scenario can be repeated by bringing additional bubbles to the tube extremity or even more simply by dipping the tube in foam. The successive bubble draining leads to the formation of the so-called bamboo foam as shown in Fig. 1.
 | ||
| Fig. 1 Bamboo foam in capillary tubes placed in contact with the surface of a glass containing a monodisperse foam. The tube diameter is 1 mm. | ||
These observations are quantified and rationalized through experimental measurements in which bubbles are manually brought in contact with the tube, described in Section 2. A simple model for the dynamics of the soap lamellae formed in the tube is presented in Section 3. This model is solved numerically, and with some approximations analytically. We show that the problem differs from the one of the spontaneous entrance of a drop in a capillary tube8,9 because first, inertia is negligible for bubbles and second, viscous dissipation is due to the motion of the lamellae.
2 Experimental protocol and qualitative observations
We prepare a soap solution by diluting a commercial dish washing soap (Fairy purchased at a concentration in anionic surfactant of 5–15%) at a concentration of 10 wt% in pure water. The liquid-vapor surface tension is γ = 24.5 ± 0.1 mN m−1 and the viscosity is μ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 1.0 ± 0.2 mPa s−1.
= 1.0 ± 0.2 mPa s−1.
A glass tube (Jeulin) of inner radius a = 3.1 mm and length L = 0.75 m is pre-wetted with the soap solution and held horizontally. Then, a bubble produced with a syringe of controlled initial volume Ωbubble is placed at one extremity of the tube as shown in Fig. 2. We consider the situation of an initial radius R0, associated with an initial volume  , larger than the tube radius a. The bubble empties in the tube such that a soap lamella enters into the tube. This lamella stops when the bubble has fully entered into the tube. A movie from which this time series has been extracted is available in the ESI.†
, larger than the tube radius a. The bubble empties in the tube such that a soap lamella enters into the tube. This lamella stops when the bubble has fully entered into the tube. A movie from which this time series has been extracted is available in the ESI.†
 | ||
| Fig. 2 Bubble approached at the extremity of a tube where a bamboo foam is already made from previous bubbles. The plot is a space–time diagram along the red line shown on the photograph that illustrates the dynamics of soap films inside the tube when a bubble empties. The constant distance between soap films is experimental evidence of the incompressible air flow. The scale bar represents 1 cm. See video in the ESI.† | ||
When the motion is completed, a new bubble of the same volume is placed following the same procedure. A new lamella is produced and the one originally present in the tube is pushed forward. The Mach number, defined as ratio of the lamellar velocity and the speed of sound in air, is between 10−6 and 10−5, which is much smaller than unity. Thus, the air flow is at a very good approximation incompressible such that both lamellae move at the same velocity and the distance between them is set by conservation of the initial bubble air volume as shown in the space–time diagram in Fig. 2.
The addition of bubbles is repeated until most of the tube is filled with soap lamellae. The dynamics is recorded on a DSLR camera (Nikon D750 with a 50 mm objective) at 60 fps. We denote as z the position of the nearest soap film from the tube entrance. We measure the time evolution of this position as a function of the number n of soap films in the tube. In Fig. 3, we plot the experimental position z(t) where color corresponds to different n values and for R0/a≃ 1.5.
By experimental design, all the bubbles have the same volume. Consequently, the same final z positions are reached once the bubbles are totally inside the tube. A contrario, the time taken to reach this final position increases as the number of preceding bubbles – and thus of soap lamellae contributing to friction – increases. We observe two regimes: the soap film moves with a slight acceleration in the first regime and decelerates in a second regime to reach the final position.
3 Model
We propose the rationalization of these observations using a simple model. Then, the predictions of this model will be compared quantitatively to the experiments.3.1 Volume conservation
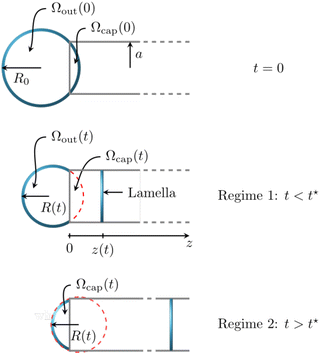
During the emptying dynamics, the bubble shape is modeled at any time as a portion of sphere, as depicted in Fig. 4, because this shape results from the minimization of surface tension energy. Initially, the bubble volume can be decomposed as where Ωout is the volume outside the tube and Ωcap is the complementary part in the tube. The volume of the cap is defined as
where Ωout is the volume outside the tube and Ωcap is the complementary part in the tube. The volume of the cap is defined as | (1) |
 .
.
From geometrical considerations (Fig. 4), the time evolution of the volume Ωout(t) outside the tube follows two regimes.13 The bubble radius of curvature first decreases until R = a during the first regime, and then increases toward a zero curvature in the second regime. We denote t* the switching time between Regimes 1 and 2 correspond to R(t*) = a. In Regime 1, we have
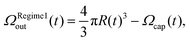 | (2) |
| ΩRegime2out (t) = Ωcap (t). | (3) |
| Ωout(t) + z(t) πa2 = Ωout(0), | (4) |
3.2 Force balance
Due to the bubble curvature, the pressure difference between the enclosed air and the atmospheric pressure is given by the Laplace pressure | (5) |
The motion of a lamella is associated with a viscous stress dissipation14–18
 | (6) |
Therefore, the stress balance between the Laplace pressure and the opposing dissipation writes Pcap = nσfilm where n ≥ 1 is the number of lamellae.
We define two characteristic parameters: the traveling distance zr = Ωbubble/πa2 and the timescale τ = μ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) zrξ3/2/γ. Then, the stress balance in a dimensionless form is
zrξ3/2/γ. Then, the stress balance in a dimensionless form is
 | (7) |
![[R with combining tilde]](https://www.rsc.org/images/entities/i_char_0052_0303.gif) = R/a and
= R/a and  .
.
The volume conservation defined in eqn (4) becomes
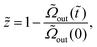 | (8) |
![[capital Omega, Greek, tilde]](https://www.rsc.org/images/entities/char_e133.gif) out = Ωout/a3.
out = Ωout/a3.
The differential eqn (7) can be solved numerically with eqn (8). We obtain the solution z(t) by using the function odeint implemented in scipy,19,20 from which we also compute the numerical traveling duration Tnum. The resulting dynamics z(t) is plotted in black in Fig. 3. The fitting parameter ξ = 32 is used to describe all the experiments. To circumvent the small experimental variations of the initial experimental volume, the volume for the numerical resolution is chosen to match each experiment that is precisely determined from the final z position. Fig. 3 shows that the numerical solution is in good agreement with the experimental measurements.
3.3 Approximated analytical solution
To get a better insight into the effect of the physical parameters, we derive an analytical solution of eqn (7). To do so, we make two approximations for which the validity will be checked both against the numerical solution and the experimental results.First, in Regime 1, we neglect the contribution of Ωcap in eqn (2). This approximation is found to be lower than 10% on the total volume for R/a > 1.25 as shown in Section 1.1 of the ESI.† In addition, we assume that the contribution of Regime 2 on the total duration of the dynamics is small. This assumption is also expected to be realistic for an initial bubble radius R0 much larger than the tube radius a.
Under these conditions, we have  , which simplifies the volume conservation from eqn (8) and reads
, which simplifies the volume conservation from eqn (8) and reads ![[z with combining tilde]](https://www.rsc.org/images/entities/i_char_007a_0303.gif) = 1 −
= 1 − ![[R with combining tilde]](https://www.rsc.org/images/entities/i_char_0052_0303.gif) (
(![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) )3/
)3/![[R with combining tilde]](https://www.rsc.org/images/entities/i_char_0052_0303.gif) 03. Thus, the differential eqn (7) reduces to
03. Thus, the differential eqn (7) reduces to
 | (9) |
 , with the initial condition
, with the initial condition ![[R with combining tilde]](https://www.rsc.org/images/entities/i_char_0052_0303.gif) (0) =
(0) = ![[R with combining tilde]](https://www.rsc.org/images/entities/i_char_0052_0303.gif) 0.
0.
In this limit, the emptying duration Tapprox has an analytical form that writes
 | (10) |
In Fig. 5, we analyze the impact of the approximations by comparing the numerical and the analytical durations. The numerical solution provides a timescale that is always larger than Tapprox. The typical dynamics z(t) is illustrated in the inset of Fig. 5, where we observe that the approximated model stops near the inflection point (t*, z*) of the numerical solution. Thus, the approximated model predicts a shorter duration than the full resolution. Nevertheless, we observe that the approximated duration converges rapidly toward Tnum as the dimensionless radius R0/a increases. In particular, the difference becomes less than 10% above R0/a ≈ 1.7 and is independent of the number of lamellae as shown in Section 1 of the ESI.† As a consequence, the timescale associated with the numerical resolution also scales as n3/2.
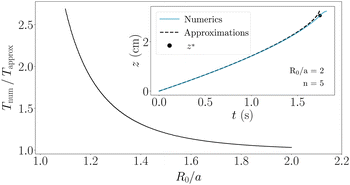 | ||
| Fig. 5 Ratio between the numerical traveling duration Tnum and the approximated time Tapprox as a function of the dimensionless initial bubble size R0/a for n = 5 for ξ = 32. We show in Section 1.2 of the ESI† that this ratio is independent of n. In the inset, both numerical and approximated position of the lamella are plotted against the numerical time for R0/a = 2 and n = 5. The inflection point (t*, z*) of the curve obtained from numerics is marked with a filled circle. | ||
3.4 Discussion
To validate the model, we repeated the experiments described in Section 2 for bubble sizes R0/a ∈ [1.5, 1.9, 2.2, 2.5] with a total number of bubbles varying between 20 and 43. The dynamics of the positions for all these experiments are well fitted for ξ = 32 (See Section 2 of the ESI†). We report in Fig. 6 the emptying duration Texp of each bubble as a function of both our prediction from the approximated model and the traveling duration Tnum. The equality between those times, represented by the black line, slightly underestimates most of the data especially the first bubbles (in red) and the last ones (squares in purple) for the approximated time (Fig. 6(a) and Section 2 of the ESI†). On the other hand, only the traveling durations Tnum of the first bubbles are underestimated (Fig. 6(b)).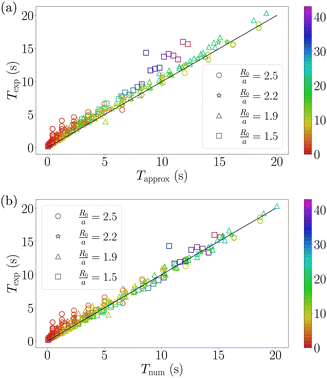 | ||
| Fig. 6 (a) Experimental emptying duration Texp of a bubble as the function of Tapprox from eqn 10 for ξ = 32. (b) Experimental emptying duration Texp of a bubble as the function of Tnum from the numerical resolution for ξ = 32. On both plots, the solid black lines represent the equality between axes and each point corresponds to a bubble where the color indicates the number of lamellae in the tube from n = 1 to n = 43. | ||
The first bubbles have a Texp comparable to the time needed to put the bubble in contact with the tube. Thus, a significant part of the dynamics is not captured by the model because the initial conditions are not matching the experimental ones. This leads to a larger Texp than both Tapprox and Tnum. Additionally, for data at R0/a = 1.5 (squares) there is 20% of discrepancy between the numerical and approximated solutions compared to less than 5% for the other experiments (see Fig. 5). In Fig. 6(a), the purple dots come from experiments with this aspect ratio, explaining why these measurements are more underestimated by the approximated model than the others.
In Fig. 6(b), we show the comparison with the numerical prediction, which is in even better agreement for the purple points but not especially for the first ones in red, supporting our argumentation. Nevertheless, the analytical prediction correctly estimates the trend and the emptying timescales.
4 Conclusions
In this paper, we investigated the emptying of a bubble placed at the extremity of a tube. We have shown that the bubble Laplace pressure is responsible for this motion and pushes a soap film into the tube. This film motion dissipates energy through the liquid viscosity with a Bretherton-like behavior. The proposed model, balancing these two forces and solved numerically, successfully describes the dynamics of this system. Under some additional hypothesis, we obtained an analytical prediction of the emptying duration that scales with the initial bubble radius as R09/2 and with the number of soap films as n3/2. The model is validated with a unique fitting parameter value ξ = 32, which is a dimensionless prefactor of the viscous friction force, whose physical origin remains to be elucidated.17,18,21The present study focused on single bubbles deposited at the extremity of a tube. For tubes plunged in foam, we expect that additional parameters can affect the dynamics such as the foam rheology at play in the necessary bubble rearrangements in the foam. Describing these dynamics will require extending the model that we proposed, which will be the purpose of future studies.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank N. Beserman and M. Dupuy for preliminary experiments, M. Hénot for useful discussions, F. Restagno for proofreading the manuscript, and L. Courbin for sharing their work of a prior publication. We acknowledge funding support from the Ecole Doctorale de Physique en Ile de France (EDPIF) and from the French Agence Nationale de la Recherche in the framework of the project AsperFoam − 19-CE30-0002-01.References
- J. Jurin, II. An account of some experiments shown before the Royal Society; with an enquiry into the cause of the ascent and suspension of water in capillary tubes, Philos. Trans. R. Soc. London, 1719, 30(355), 739–747 CrossRef.
- J. M. Bell and F. K. Cameron, The Flow of Liquids through Capillary Spaces, J. Phys. Chem., 1906, 10(8), 658–674 CrossRef.
- R. Lucas, Rate of capillary ascension of liquids, Kolloid Z., 1918, 23, 15 CrossRef CAS.
- E. W. Washburn, The Dynamics of Capillary Flow, Phys. Rev., 1921, 17, 273–283 CrossRef.
- D. Quéré, Inertial capillarity, Europhys. Lett., 1997, 39(5), 533–538 CrossRef.
- D. Quéré, E. Raphaël and J. Y. Ollitrault, Rebounds in a Capillary Tube, Langmuir, 1999, 15(10), 3679–3682 CrossRef.
- Y. Wang, S. Chen and B. Wu, Self-driven penetration of droplets into non-wetting capillaries, Comput. Fluids, 2017, 154, 211–215 CrossRef CAS . ICCFD8.
- G. R. Willmott, C. Neto and S. C. Hendy, Uptake of water droplets by non-wetting capillaries, Soft Matter, 2011, 7, 2357–2363 RSC.
- G. R. Willmott, A. Briole and F. Szczepaniak, Inertial capillary uptake of drops, Phys. Rev. E, 2020, 101, 043109 CrossRef CAS PubMed.
- J. G. Leidenfrost, De aquae communis nonnullis qualitatibus tractatus, Ovenius, 1756 Search PubMed.
- I. Cantat, S. Cohen-Addad, F. Elias, F. Graner, R. Höhler, O. Pitois, et al., Foams: Structure and Dynamics, OUP, Oxford, 2013 Search PubMed.
- M. Clerget, A. Delvert, L. Courbin and P. Panizza, Different scenarios of shrinking surface soap bubbles, Am. J. Phys., 2021, 89(3), 244–252 CrossRef.
- D. P. Jackson and S. Sleyman, Analysis of a deflating soap bubble, Am. J. Phys., 2010, 78(10), 990–994 CrossRef.
- F. P. Bretherton, The motion of long bubbles in tubes, J. Fluid Mech., 1961, 3(10), 166–188 CrossRef.
- G. J. Hirasaki and J. B. Lawson, Mechanisms of foam flow in porous media: apparent viscosity in smooth capillaries, Soc. Pet. Eng. J., 1985, 25(02), 176–190 CrossRef.
- K. G. Kornev, A. V. Neimark and A. N. Rozhkov, Foam in porous media: thermodynamic and hydrodynamic peculiarities, Adv. Colloid Interface Sci., 1999, 82(1), 127–187 CrossRef CAS.
- C. Raufaste, A. Foulon and B. Dollet, Dissipation in quasi-two-dimensional flowing foams, Phys. Fluids, 2009, 21(5), 053102 CrossRef.
- I. Cantat, Liquid meniscus friction on a wet plate: Bubbles, lamellae, and foams, Phys. Fluids, 2013, 25(3), 031303 CrossRef.
- E. Jones, T. Oliphant, P. Peterson, et al., SciPy: Open source scientific tools for Python, 2001 Search PubMed.
- P. Virtanen, R. Gommers, T. E. Oliphant, M. Haberland, T. Reddy and D. Cournapeau, et al., SciPy 1.0: Fundamental Algorithms for Scientific Computing in Python, Nat. Methods, 2020, 17, 261–272 CrossRef CAS PubMed.
- J. Emile, H. Tabuteau, F. Casanova and O. Emile, Bubble-wall friction in a circular tube, Soft Matter, 2013, 9, 4142–4144 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3sm00677h |
| This journal is © The Royal Society of Chemistry 2023 |