Open Access Article
Open Access ArticleUnderstanding the role of crosslink density and linear viscoelasticity on the shear failure of pressure-sensitive-adhesives†
Anthony
Arrowood
 a,
Mohammad A.
Ansari
a,
Mohammad A.
Ansari
 b,
Matteo
Ciccotti
b,
Matteo
Ciccotti
 c,
Rui
Huang
b,
Kenneth M.
Liechti
b and
Gabriel E.
Sanoja
c,
Rui
Huang
b,
Kenneth M.
Liechti
b and
Gabriel E.
Sanoja
 *a
*a
aMcKetta Department of Chemical Engineering, The University of Texas at Austin, Austin, TX 78712, USA. E-mail: gesanoja@che.utexas.edu
bDepartment of Aerospace Engineering and Engineering Mechanics, The University of Texas at Austin, Austin, TX 78712, USA
cLaboratoire Sciences et Ingénierie de la Matière Molle, ESPCI Paris, Université PSL, Sorbonne Université, CNRS UMR 7615, 75005 Paris, France
First published on 28th July 2023
Abstract
Pressure-sensitive-adhesives (PSAs) are ubiquitous in electronic, automobile, packaging, and biomedical applications due to their ability to stick to numerous surfaces without undergoing chemical reactions. Although these materials date back to the 1850s with the development of surgical tapes based on natural rubber, their resistance to shear loads remains challenging to predict from molecular design. This work investigates the role of crosslink density on the shear resistance of model PSAs based on poly(2-ethylhexyl acrylate-co-acrylic acid) physically crosslinked with aluminum acetylacetonate. The key result is that crosslinking PSAs leads to notable stress concentrations ahead of the peel front, as well as a transition from cohesive to adhesive failure. The shear stress distributions, as evaluated by means of a linearly viscoelastic shear lag model, suggest that this transition is related to the evolution of the ratio of the load transfer length to the bond length as dictated by the mechanical properties of the backing and adhesive layers, and the geometry of the tape.
1 Introduction
Pressure-sensitive-adhesives (PSAs) are commonly used as protective films, labels, packaging tapes, and heavy-duty double-sided tapes because of their ability to stick to numerous surfaces without undergoing chemical reactions.1 This behavior results from the hysteresis of the thermodynamic work of adhesion or, namely, the difference between the energy gained upon adhesive–substrate bonding and that dissipated upon debonding. Thus, PSAs are soft viscoelastic polymers with linear and non-linear mechanical properties that, when subject to large deformations, provide a fine balance between reversible elasticity and strain energy dissipation.PSAs that span a wide range of viscoelastic properties are frequently based on rubbery and loosely crosslinked polymer networks.1,2 These materials date to the 1850s with the development of surgical tapes, and became widespread in the mid-1900s with the upsurge of acrylic polymers. In a typical manufacturing process, long-side chain 2-ethylhexyl acrylate (or n-butyl acrylate), short side-chain methyl acrylate, and electron donor acrylic acid are copolymerized in solution, physically crosslinked with an electron acceptor such as aluminum acetylacetonate, and blade coated on a stiff backing of, for example, polyethylene terephthalate (i.e. PET). By leveraging the composition and molecular weight of the copolymer, as well as the density of crosslinks, it is possible to readily tune viscoelastic properties like the glass transition temperature, Tg, complex moduli, G′ and G′′, and loss factor, tan(δ). As such, acrylic PSAs are often the material of choice in heavy-duty applications where, for example, high shear loads are applied for long periods of time.
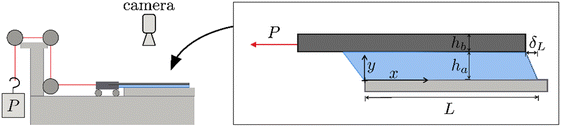
Since the development of PSAs, it has proved challenging to relate their molecular architecture and failure under static shear loads.3–7 This behavior is typically characterized with a lap shear test, where a tape is subjected to a fixed load at ca. zero-degree angle for long periods of time (Fig. 1). The lap shear test is often used in industry to assess the time-to-failure or shear-holding-power (ASTM D6463), even if it does not provide much insight on the molecular and mesoscopic processes underpinning failure. In this geometry, soft8–13 and structural14–17 adhesives have been characterized, using shear lag models (i.e. cohesive-zone analysis, and solid mechanics) to estimate the stress and stretch distributions in the adhesive and backing layers.18–27 Although the approach is common, it presents two important challenges. The first is the need to describe the adhesive layer at small and large deformations with an appropriate constitutive stress–stretch relation. And the second is the presence of a 3-D stress concentration in the vicinity of an interfacial crack that depends on time. Nonetheless, shear lag models have provided some interesting insights that are worth noting. Mojdehi et al. used a critical force criterion in a linearly elastic model to argue that the shear failure of PSAs is governed by a characteristic length scale referred to as load transfer length.22 Hui et al. and Liu et al. outlined a non-linearly elastic model to demonstrate that, within the load transfer length, the lateral stress is much larger than the shear stress and the hydrostatic pressure potentially sufficient to induce cavity nucleation and growth.23,24 And finally, Guo et al. introduced a non-linearly viscoelastic model to illustrate that strain energy dissipation ahead of the peel front can drastically mitigate stress concentrations and delay shear failure by, for example, viscoelastic creep.25,28
From a scaling standpoint, shear lag models have also enabled identification of an important non-dimensional group governing shear failure: the ratio of the load transfer length, LLT, to the bond length, L.21,22,26 When elastic adhesives are subjected to constant shear rates, shear failure is progressive or catastrophic depending on L/LLT.21,22,26,29 However, whether this scaling law can be readily extended to viscoelastic adhesives subject to static shear loads, where the load transfer length and stress concentration presumably evolve with time, remains unclear. In addition, though scaling laws are useful in designing PSAs, they rely on the continuum approximation and do not capture the role of polymer architecture on shear failure. Such a molecular picture still remains elusive.
Here, we aim to understand the relationship between polymer architecture and shear failure in viscoelastic PSAs. By subjecting a family of acrylic PSAs to static shear loads, and mapping the displacement distribution in the backing layer using Digital Image Correlation (DIC); we demonstrate that physically crosslinking a polymer melt leads to (i) notable stress concentrations in the vicinity of the peel front, and (ii) a transition from cohesive to adhesive failure under static shear loads. These results agree with predictions from linearly viscoelastic shear lag models for Maxwell liquids and Kelvin-Voigt solids, where the mechanism by which the load is transferred into the adhesive layer is notably different. Thus, this investigation unveils a clear relationship between polymer architecture, load transfer length, and shear failure.
2 Experimental
2.1 Materials
Unless otherwise specified, all chemicals were used as received. 2-Ethylhexyl acrylate (2EHA) was sourced from TCI; acrylic acid (AA), 2-cyano-2-propyl benzodithioate (2C2PB), aluminum acetylacetonate Al(acac)3, azobisisobutyronitrile (AIBN), and hydroquinone from Millipore-Sigma; and ethyl acetate, aluminum oxide, and methanol from VWR. Before use, monomers 2EHA and AA were purified by eluting in a stationary phase of aluminum oxide, and initiator AIBN was recrystallized in methanol.2.2 Synthesis and formulation of PSAs
To 110.9 ml of ethyl acetate in a 250 ml round bottom flask, 155 mmol of 2EHA, 20.4 mmol AA, 87.7 mmol of 2C2PB and 17.6 mmol of AIBN were added. This solution was subjected to five (5) consecutive freeze–pump–thaw cycles and transferred to a nitrogen-filled glovebox, whereby the solution was split evenly among four (4) vials each equipped with a magnetic stir bar. The solutions were allowed to react at 80 °C for ca. 48 h stirring at 300 rpm, and the resulting copolymers precipitated twice in 500 ml of methanol, stabilized with hydroquinone, decanted, and dried overnight under vacuum at 80 °C. The copolymers were physically crosslinked into PSAs by dissolving in ethyl acetate at ca. 1 g ml−1, and mixing with a solution of 1 mg ml−1 of Al(acac)3 at varying weight fractions, relative to polymer, of 0, 0.5, 1, and 1.5 wt%. The PSAs were stored at 15 °C until ready for use. Noteworthy, the PSA crosslinked at 1.5 wt% was too solid to be processed into a tape.2.3 Processing of PSAs into tapes
The PSAs were removed from the vials and subsequently placed between two (2) 36 μm thick non-stick silicone release liners (Drytac Inc.). With the PSAs between the sheets, the outside surfaces of the liners were heated to 80 °C and the sheet-PSA-sheet laminates pressed under a film coater of gap set to a desired thickness. The PSAs in these laminates were homogeneous, and stored at room temperature until use.Specimens for probe-tack tests were prepared by die cutting the laminates into 12 mm diameter disks of thickness ≈100 μm. Similarly, specimens for linear amplitude oscillatory shear rheology were prepared by die cutting into 8 mm diameter disks of thickness ≈500 μm. Finally, specimens for lap shear tests were prepared in two steps. First, by peeling one liner from the laminate, adhering the PSA to a speckled LDPE backing of thickness 50.8 μm, and cutting the LDPE-PSA-sheet laminate into rectangles of width 20 mm, thickness ≈100 μm, and varying bond length, L. Then, by peeling the second liner from the laminate, adhering the PSA to a glass substrate pre-washed with acetone and lens paper, and rolling the resulting LDPE-PSA-glass composite ten (10) times with a 4.5 lb rubber roller (Cheminstruments Inc. HR-100) at ≈10 mm s−1. A contact time of ≈1 h was provided before applying a fixed shear load, P.
2.4 Molecular and thermomechanical characterization
The molecular weight of the poly(2-ethylhexyl acrylate-co-acrylic acid) copolymer was determined by Gel Permeation Chromatography (GPC), eluting with tetrahydrafuran over a T6000M column (Malvern Panalytical).The glass transition temperature, Tg, was determined by Differential Scanning Calorimetry (DSC 250 TA Instruments Inc.) using the midpoint method, scanning three (3) times from −90 to 200 °C at 1 °C min−1.
The linearly viscoelastic properties, G* and tan(δ), were determined in a TA Instruments HR2 Hybrid Rheometer; using a 8 mm probe equilibrated at 30 °C, and subjecting the family of PSAs to an oscillatory shear strain of 1% amplitude and frequencies ranging from 0.01 to 100 rad s−1.
2.5 Adhesive characterization
The adhesion energy, Wadh, of PSAs was determined by probe tack tests, using an Instron 34TM5 equipped with a 100 N load cell and affixed with a 12 mm probe. PSAs of thickness ≈100 μm were adhered to the probe, and compressed at a rate of 10 μm s−1 until reaching a compressive force of 50 N. Thereafter, the probe was retracted at a constant rate of 50 μm s−1, and the resulting force–displacement curves used to estimate the stress, σ = F/A, strain, ε = (h − h0)/h0, and adhesion energy,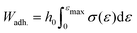 . Here, h0 is the initial thickness, and A the cross-sectional area of the probe, A = πD2/4.
. Here, h0 is the initial thickness, and A the cross-sectional area of the probe, A = πD2/4.
PSAs were also subjected to lap shear tests by adhering the tapes to a glass slide affixed to a horizontal platform clamped to a rolling carriage inclined at ≈1° (see Fig. 1, and Fig. S7, ESI†). The carriage ensured that the stress was evenly distributed along the width of the tape, and prevented any inertial effects that may arise upon loading. A static load, P, was applied by suspending a fixed weight from a string via a series of pulleys connected to the carriage. Optical images of the speckled backing were recorded from top down, and used to determine displacement distributions over time.
2.6 Linearly viscoelastic shear lag model
The theoretical stress distribution in the tape was determined with a linearly viscoelastic shear lag model,18 considering the adhesive layer either as a Maxwell liquid or a Kelvin-Voigt solid. The development of the model begins with a statement of mechanical equilibrium between the backing and the adhesive layers: | (1) |
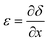 | (2) |
 | (3) |
| ε = σ/E | (4) |
Combining eqn (1)–(4) leads to:
 | (5) |
If the adhesive is also linearly elastic, then eqn (5) becomes:
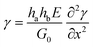 | (6) |
 | (7) |
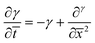 | (8) |
![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) ≡ x/LLT for a characteristic length scale (i.e. load transfer length),
≡ x/LLT for a characteristic length scale (i.e. load transfer length),  and
and ![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) = t/tR for a characteristic time scale (i.e. relaxation time), tR = η/G0. Alternatively, if the adhesive is described as a Maxwell liquid, the constitutive equation is:
= t/tR for a characteristic time scale (i.e. relaxation time), tR = η/G0. Alternatively, if the adhesive is described as a Maxwell liquid, the constitutive equation is: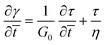 | (9) |
Combining eqn (5) and (9), and non-dimensionalizing now results in:
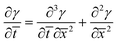 | (10) |
Eqn (8) and (10) can be numerically integrated to solve for the spatio-temporal distributions of the shear strain, γ, and the shear stress, τ, in the adhesive layer. However, some insight can be obtained by analytically integrating with Schapery's “direct method” of Laplace Transform inversion,30 where the adhesive is assumed to relax notably before shear failure. This method is particularly appropriate for describing the stress in linearly viscoelastic solids subject to quasi-static loads and negligible inertia. Details of the Laplace Transform and Schapery's inversion are summarized in Section 2 of the ESI,† but the closed form solution for the shear stress τ, in the adhesive layer is given by:
 | (11) |
 is a time-dependent load transfer length which depends on the constitutive stress–stretch relation of the PSA, (see Table 1, Table S3, and Section 2.1 in the ESI†). This closed form solution agrees rather well with the numerical solution (see Section 2.2 and Fig. S2–S5 in ESI†), and provides a physical understanding of how the stress distribution evolves in linearly viscoelastic PSAs subject to shear loads.
is a time-dependent load transfer length which depends on the constitutive stress–stretch relation of the PSA, (see Table 1, Table S3, and Section 2.1 in the ESI†). This closed form solution agrees rather well with the numerical solution (see Section 2.2 and Fig. S2–S5 in ESI†), and provides a physical understanding of how the stress distribution evolves in linearly viscoelastic PSAs subject to shear loads.
In addition, if the peel front is considered as the tip of an interfacial crack, the energy release rate,  , can be estimated from the J-integral as:
, can be estimated from the J-integral as:
 | (12) |
Or alternatively:
 | (13) |
The first term in eqn (12) and (13) is the energy release rate of a tape with an infinite bond length,  and the second term is the energy release rate of a tape with a short length
and the second term is the energy release rate of a tape with a short length  . This result is similar to that presented by Liu et al. and Wang et al. for an elastic tape;24,26,29 but with a time-dependent load transfer length,
. This result is similar to that presented by Liu et al. and Wang et al. for an elastic tape;24,26,29 but with a time-dependent load transfer length,  . After all, we treat the adhesive layer as linearly viscoelastic rather than elastic.
. After all, we treat the adhesive layer as linearly viscoelastic rather than elastic.
A couple of interesting points are worth noting. First, the time-dependence of the adhesive mechanical properties is captured within the load transfer length,  . Second, if failure is assumed to occur at a critical energy release rate,
. Second, if failure is assumed to occur at a critical energy release rate,  , then the critical force required for interfacial crack propagation is constant for a tape with an infinite bond length,
, then the critical force required for interfacial crack propagation is constant for a tape with an infinite bond length, 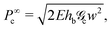 and notably dependent on the bond length, L, and time,
and notably dependent on the bond length, L, and time, ![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) , for a tape with a short bond length,
, for a tape with a short bond length,  . Third, irrespective of the constitutive behavior of the adhesive layer, interfacial crack propagation is either unstable or neutrally stable, with
. Third, irrespective of the constitutive behavior of the adhesive layer, interfacial crack propagation is either unstable or neutrally stable, with  . And finally, when
. And finally, when 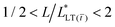 or, namely, when
or, namely, when  the energy release rate drastically changes and the tape presumably fails (see Fig. S6, ESI†).
the energy release rate drastically changes and the tape presumably fails (see Fig. S6, ESI†).
2.7 Digital-image-correlation and estimates of the stress distribution in the adhesive layer
Inspired by the seminal work of Minsky et al. on viscoelastic creep of PSAs subject to shear loads;28 a combination of Digital Image Correlation and the Linearly Viscoelastic Shear Lag Model was used to estimate the spatio-temporal stress and stretch distributions in the tape, ignoring axial stresses in the free region of the tape due to the modulus mismatch between the adhesive and backing layers, EPSA/Ebacking ≈ 10−3 (see Fig. S7 and S8, ESI†). First, the backing displacement, δ, was measured by DIC and numerically differentiated to compute the axial strain, ε, using central differences and eqn (2). Then, the axial strain, ε, was fitted to a polynomial to provide an expression for the axial stress, σ, using a modulus for the backing layer, E = 170 MPa (see Fig. S9, ESI†), and eqn (4). Next, the axial stress, σ, was analytically differentiated to estimate the shear stress, τ, with eqn (1) and a backing thickness, hb = 36 μm (see Section 3.1 and Fig. S10–S12 in the ESI†). And finally, the backing displacement, δ, was used to compute the shear strain, γ, with eqn (3) and an adhesive thickness, ha ≈ 100 μm.This procedure is remarkable because it affords the stress and strain distributions in the adhesive layer independent of the constitutive behavior of the PSA. However, we also note that it is limited by inaccuracies in estimating the first- and second-derivatives of the backing displacement, δ, in regions that undergo large deformations.
3 Results and discussion
3.1 Polymer characteristics
The molecular weight of the poly(2-ethylhexyl acrylate-co-acrylic acid) copolymer is Mn = 361 kDa, and the dispersity, PDI = 1.9 (see GPC trace in Fig. S16, ESI†). When physically crosslinked with Al(acac)3, the glass transition temperature remains unchanged at Tg = −62 °C over a range of weight fractions, 0 to 1 wt% (see DSC in Fig. S17, ESI†). Thus, this copolymer is rubbery and moderately entangled near room temperature (i.e., Mn/Me ≈ 9).3.2 Material viscoelastic properties
To adhere like PSAs, the acrylic copolymers must be soft, dissipative, and creep resistant when subject to small and large deformations.1Fig. 2 summarizes the magnitude of the complex modulus, G*, and the loss factor, tan(δ), revealing some interesting features worth noting. First, the magnitude of the complex modulus, G*, at 1 rad s−1 is ≈0.01 MPa irrespective of the crosslinking density, indicating that the materials are able to readily conform and adhere to rough surfaces upon application of light pressures. Second, the loss factor, tan(δ), is above 0.2, meaning that the materials can dissipate considerable strain energy and resist shear failure, for example, by creep. Third, both G* and tan(δ) at low frequencies, ω < 1 rad s−1, demonstrate that the materials become more creep resistant (i.e., solid-like) upon crosslinking. And finally, the frequency at which tan(δ) = 1, herein defined as the inverse of the relaxation time, ωR = 1/tR, decreases with the weight fraction of Al(acac)3. Overall, Fig. 2 confirms that, within the linear regime, our family of physically crosslinked acrylic copolymers exhibits viscoelastic properties like those of conventional PSAs.3.3 Probe-tack: short-term adhesion
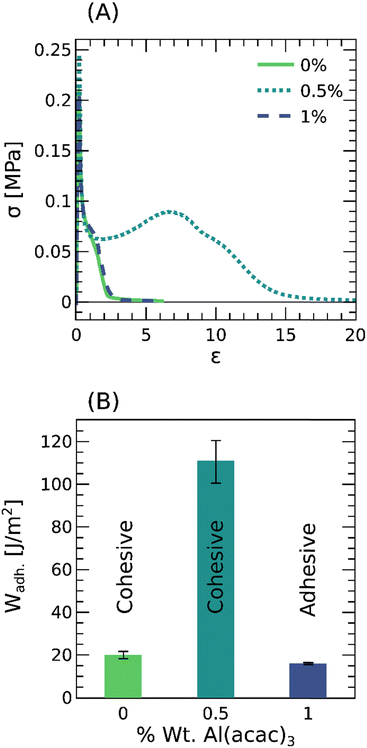
A common test to evaluate the adhesion of PSAs is the probe tack test, where a probe is pulled at a constant velocity from the adhesive layer and the force is monitored over the displacement.31 This test is ideal to unravel debonding mechanisms such as cavitation and fibrillation at μm-length scales, and is summarized here in Fig. 3(A). In the absence of crosslinker, the PSA is unable to sustain large deformations and fails cohesively by creep. This behavior is characteristic of entangled polymer melts and consistent with a loss factor, tan(δ) = 1, at frequencies as low as 1 rad s−1. At a crosslinker concentration of 0.5 wt%, the PSA presumably cavitates at a peak force of ≈0.25 MPa, strain hardens, and ultimately fails cohesively in the bulk. This behavior is distinctive of weakly crosslinked and entangled polymer networks that sustain large deformations while dissipating considerable strain energy. Finally, at a crosslinker concentration of 1%, the PSA is again unable to sustain large deformations, though this time it fails adhesively at the interface with the rigid probe. This behavior is typical of well crosslinked and entangled polymer networks that are soft but not excessively dissipative. Thus, crosslinking the acrylic PSAs with varying amounts of Al(acac)3 leads not only to more solid-like properties at small deformations (Fig. 2A) but also to a transition from cohesive to adhesive failure and a maximum in the adhesion energy, Wadh. ≈ 100 J m−2, at large deformations (Fig. 3B). Although useful for evaluating the adhesive properties at short times, ω ≈ 1 rad s−1, in a state of nearly hydrostatic tension; these probe tack tests are not necessarily appropriate for assessing shear failure over long times.3.4 Lap shear: long-term adhesion
To better understand the long term behavior, ω ≤ 10−3 Hz, PSAs were subjected to a static shear load, P ≈ 2.5 N, and the displacement distribution in the backing layer monitored over time. Fig. 1 illustrates the methodology, and Fig. 4 the evolution of the displacement at the trailing edge, δL, over time for a representative bond length, L = 10 mm. Two stages can be identified: a first stage where the velocity of the trailing edge scales with time, and a second stage where it rapidly diverges until failure (see Section 3.3 and Fig. S18 in the ESI†). The exponent β depends on the creep resistance of the PSA, being ≈0.5 for an entangled melt, and −1.0 for a crosslinked network. By identifying the transition between these stages, it is possible to evaluate a critical time, tc, and displacement, δc, at which the PSAs undergo shear failure (see example in Fig. 4, and more details in Fig. S19, ESI†).
and a second stage where it rapidly diverges until failure (see Section 3.3 and Fig. S18 in the ESI†). The exponent β depends on the creep resistance of the PSA, being ≈0.5 for an entangled melt, and −1.0 for a crosslinked network. By identifying the transition between these stages, it is possible to evaluate a critical time, tc, and displacement, δc, at which the PSAs undergo shear failure (see example in Fig. 4, and more details in Fig. S19, ESI†).
 | ||
| Fig. 4 Shear tests of acrylic tapes with L = 10 mm and different weight fractions of Al(acac)3. These tests yield a critical time, tc, and displacement, δc, at failure. | ||
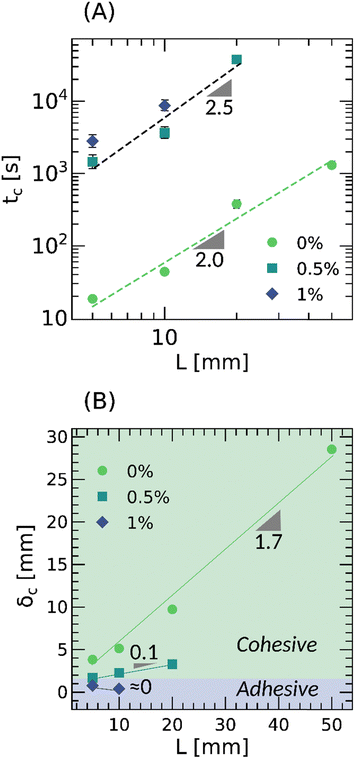
Consistent with the linearly viscoelastic properties at low frequency reported in Fig. 2, crosslinking acrylic PSAs with varying amounts of Al(acac)3 results in more solid-like behavior and delayed shear failure. Fig. 5 summarizes the results and unveils some important features worth noting. First, the time-to-failure, tc, increases by ≈ 100 s upon crosslinking. Second, the critical displacement, δc, notably decreases upon crosslinking. Third, the scaling of tc with the bond length, L, is intimately coupled to the crosslinking concentration, with tc ∼ L2.0 in the absence of crosslinker and tc ∼ L2.5 otherwise. Fourth, the critical displacement, δc, transitions from a cohesive regime where it increases, δc ∼ L, to an adhesive regime where it remains rather constant. And finally, for the crosslinked PSAs, the bond length is restricted to L = 20 mm because otherwise the time-of-failure, tc, is prohibitively long (i.e., more than 2 weeks). Overall, these observations indicate that weakly crosslinked and entangled polymer networks with optimal adhesion in tack are not necessarily optimal in shear. Instead, well crosslinked and entangled networks are preferred due to their ability to dissipate sufficient strain energy to prevent instantaneous debonding, and sustain large deformations near the peel front to resist shear failure.
Changes in the macroscopic time-to-failure, tc, and critical displacement, δc, are also reflected in the mesoscopic strain and stress distributions as measured by Digital Image Correlation and eqn (1)–(5). Fig. 6 summarizes the results and reveals the role of crosslinking density on the shear stress throughout the bond. At low crosslinking densities, the shear stress is low near the peel front, τ ≈ 2.0 kPa, and the load is readily transferred over the bond length,  ; whereas at high crosslinking densities, instead, the shear stress is high near the peel front, τ ≈ 4.5 kPa, and the load is transferred over shorter length scales,
; whereas at high crosslinking densities, instead, the shear stress is high near the peel front, τ ≈ 4.5 kPa, and the load is transferred over shorter length scales,  . This effect of crosslinking density on the stress distribution of acrylic PSAs points to an inherent coupling between the polymer architecture, load transfer length, and mechanism of shear failure.
. This effect of crosslinking density on the stress distribution of acrylic PSAs points to an inherent coupling between the polymer architecture, load transfer length, and mechanism of shear failure.
 | ||
| Fig. 6 Evolution of the shear stress profile in 50 mm long tapes of acrylic PSAs crosslinked with (A) 0% and (B) 1 wt% Al(acac)3 as determined by DIC and eqn (1)–(5). Crosslinking PSAs with Al(acac)3 leads to a stress concentration near the peel front. | ||
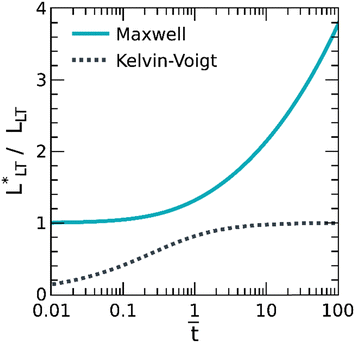
To understand such coupling, the shear stress distributions depicted in Fig. 6 were interpreted within a linearly viscoelastic shear lag model, considering the PSAs crosslinked with 0 and 1 wt% Al(acac)3 as a Maxwell liquid and Kelvin-Voigt solid, respectively. However, we note that this linearly viscoelastic shear lag model only offers a qualitative understanding of how the shear stress distribution evolves in PSAs idealized as Maxwell liquids or Kelvin-Voigt solids. After all, in a typical shear test, the deformations in the adhesive layer are far from linear, and the constitutive stress–stretch relations more complex.23,24 The closed form solutions for the shear stress in the adhesive layer, τ, as estimated from eqn (11), are presented in Fig. 7. Two points are worth noting. First, irrespective of the constitutive behavior, the stress is first concentrated near the peel front, x = 0, and then delocalized throughout the bond. And second, the load transfer mechanism depends on the linearly viscoelastic properties, with the Maxwell liquid homogenizing the stress, τ = 5 kPa at long times, t = 500 s, and the Kelvin-Voigt solid retaining a stress concentration near the peel front that depends on the modulus, G0. In other words, the Maxwell liquid develops a load transfer length,  that readily pervades the bond; whereas the Kelvin-Voigt solid, instead, relaxes to a steady-state where
that readily pervades the bond; whereas the Kelvin-Voigt solid, instead, relaxes to a steady-state where  after tR ≡ η/G0 (see Fig. 8).
after tR ≡ η/G0 (see Fig. 8).
 | ||
| Fig. 7 Theoretical evolution of the shear stress profile in the adhesive layer of a 50 mm long tape for a (A) Maxwell liquid, with G0 = 0.01 MPa and η = 0.03 MPa s, and a (B) Kelvin-Voigt solid, with G0 = 0.01 MPa and η = 3 MPa s, as determined from a linearly viscoelastic shear lag model. Consistent with Fig. 6, solid-like adhesives sustain a higher shear stress near the peel front. | ||
Interpretation of our experimental results within the linearly viscoelastic shear lag model also serves to understand the scaling of the time-to-failure (or critical time), tc, with the bond length, L. In the absence of crosslinker, the PSA is composed of a moderately entangled polymer melt, the stress is readily delocalized throughout the bond, and the failure is cohesive (i.e., progressive) by creep. If failure occurs at  then it follows from the constitutive behavior of a Maxwell liquid that:
then it follows from the constitutive behavior of a Maxwell liquid that:
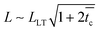 | (14) |
Namely, the time-to-failure is expected to scale with the bond length as tc ∼ L2, in agreement with the experimental data presented in Fig. 5. Instead, at 1 wt% Al(acac)3, the PSA is composed of a well crosslinked and entangled polymer network, and the steady-state load transfer length can be smaller or larger than the bond length. If  , there is no failure and the load can be sustained for long times (i.e., longer than those experimentally accessible. In our experiments, 2 weeks). Conversely, if
, there is no failure and the load can be sustained for long times (i.e., longer than those experimentally accessible. In our experiments, 2 weeks). Conversely, if  then it follows from the constitutive behavior of a Kelvin-Voigt solid that:
then it follows from the constitutive behavior of a Kelvin-Voigt solid that:
 | (15) |
That is, the time-to-failure should also scale with the bond length as tc ∼ L2. The discrepancy with Fig. 5 is not yet understood, but it could be a result of contributions from the PSA large-strain mechanical properties and interfacial slippage on the stress concentration ahead of the peel front, and the resistance to shear loads.
4 Conclusions
Acrylic PSAs find widespread use in society as they readily stick to numerous surfaces without undergoing chemical reactions. These materials remain challenging to design, with an elusive relationship between molecular architecture and bulk adhesive properties. Thus, we investigated the role of crosslink density on shear failure on model PSAs based on poly(2-ethylhexyl acrylate-co-acrylic acid) copolymers physically crosslinked with Al(acac)3.The key result is that PSAs composed of well crosslinked, entangled, and load-bearing polymer networks are able to resist shear failure for long times, as long as the shear stress is delocalized over a region smaller than the bond length. Otherwise, they will fail adhesively by interfacial crack propagation. Instead, when PSAs are composed of entangled polymer melts, where the chains can reptate or self-diffuse when subject to a macroscopic load, they readily delocalize the shear stress throughout the bond and fail cohesively by creep.
We interpreted this result within a linearly viscoelastic shear lag model to gain insights into the time-to-failure, considering the well-crosslinked polymer networks as Kelvin-Voigt solids and the moderately entangled polymer melts as Maxwell liquids. Whereas in well crosslinked polymer networks the time-to-failure depends on the tape geometry and the moduli of the backing and adhesive layers, in entangled polymer melts it is primarily controlled by the dynamics of the polymer chains as dictated by the molecular weight and entanglement density.
Acrylic PSAs, thus, suffer from an inherent compromise between short- and long-term adhesion, which can be finely tuned through the concentration of Al(acac)3 crosslinker. When the molecular architecture resembles that of an entangled and crosslinked polymer network; PSAs can resist instantaneous debonding by readily dissipating strain energy, and sustain shear loads by evolving a stable stress concentration near the peel front. Here, we outline various means to design the shear resistance of PSAs and confine the steady-state load transfer length within the bond length, such as tailoring the moduli and thickness of the backing and adhesive layers. However, we also note that it remains challenging to engineer the long-term modulus of PSAs without impacting the short-term dissipative properties or, at the molecular level, to control the number of chemical crosslinks independent from that of entanglements. In this regard, we deem it worthwhile to investigate how novel molecular architectures like bottlebrush polymer networks behave in shear.32,33
Author contributions
Research was designed by A. A., M. C., and G. E. S. Model was developed by A. A., M. A. A., M. C., R. H., and K. M. L. Synthesis, rheology, probe-tack test, shear test, and DIC were conducted by A. A., and data interpreted by A. A., and G. E. S. The manuscript was written by A. A. and G. E. S. and critically revised by all authors. All authors have given final approval to the final version.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was funded by The University of Texas at Austin. The authors acknowledge the use of shared research facilities supported in part by the Texas Materials Institute, the Center for Dynamics and Control of Materials: an NSF MRSEC (DMR-1720595); and Costantino Creton and Helen Minsky for helpful discussions.References
- C. Creton and E. Papon, MRS Bull., 2003, 28, 419–423 CrossRef CAS.
- C. Creton and M. Ciccotti, Rep. Prog. Phys., 2016, 79, 046601 CrossRef PubMed.
- A. Zosel, J. Adhes., 1994, 44, 1–16 CrossRef CAS.
- P. L. Geiss and W. Brockmann, J. Adhes., 1997, 63, 253–263 CrossRef CAS.
- K. A. Vaynberg, A. T. Berta and P. M. Dunckley, J. Adhes., 2001, 77, 275–284 CrossRef CAS.
- F. Sosson, A. Chateauminois and C. Creton, J. Polym. Sci., Part B: Polym. Phys., 2005, 43, 3316–3330 CrossRef CAS.
- A. Lindner, B. Lestriez, S. Mariot, C. Creton, T. Maevis, B. Lühmann and R. Brummer, J. Adhes., 2006, 82, 267–310 CrossRef CAS.
- D. H. Kaelble, Trans. Soc. Rheol., 1960, 4, 45–73 CAS.
- K. Kendall, J. Phys. D: Appl. Phys., 1975, 8, 512–522 CrossRef CAS.
- M. D. Bartlett, A. B. Croll and A. J. Crosby, Adv. Funct. Mater., 2012, 22, 4985–4992 CrossRef CAS.
- D. R. King and A. J. Crosby, ACS Appl. Mater. Interfaces, 2015, 7, 27771–27781 CrossRef CAS.
- Y. Wang, X. Yang, G. Nian and Z. Suo, J. Mech. Phys. Solids, 2020, 143, 103988 CrossRef.
- J. Ju, L. Cipelletti, S. Zoellner, T. Narita and C. Creton, J. Rheol., 2022, 66, 1269–1283 CrossRef CAS.
- E. Sancaktar, S. C. Schenck and S. Padgliwar, Ind. Eng. Chem. Prod. Res. Dev., 1984, 23, 426–434 CrossRef CAS.
- E. Sancaktar and S. C. Schenck, Ind. Eng. Chem. Prod. Res. Dev., 1985, 24, 257–263 CrossRef CAS.
- A. J. Kinloch, J. H. Lee, A. C. Taylor, S. Sprenger, C. Eger and D. Egan, J. Adhes., 2003, 79, 867–873 CrossRef CAS.
- C. J. Higginson, K. G. Malollari, Y. Xu, A. V. Kelleghan, N. G. Ricapito and P. B. Messersmith, Angew. Chem., 2019, 131, 12399–12407 CrossRef.
- O. Volkersen, Luftahrt Forschungen, 1938, 15, 41–47 Search PubMed.
- Z. Suo and J. W. Hutchinson, Int. J. Fracture, 1990, 43, 1–18 CrossRef.
- M. Kafkalidis and M. Thouless, Int. J. Solids Struct., 2002, 39, 4367–4383 CrossRef.
- S. Ponce, J. Bico and B. Roman, Soft Matter, 2015, 11, 9281–9290 RSC.
- A. R. Mojdehi, D. P. Holmes and D. A. Dillard, Soft Matter, 2017, 13, 7529–7536 RSC.
- C.-Y. Hui, Z. Liu, H. Minsky, C. Creton and M. Ciccotti, Soft Matter, 2018, 14, 9681–9692 RSC.
- Z. Liu, H. Minsky, C. Creton, M. Ciccotti and C.-Y. Hui, Extreme Mech. Lett., 2019, 32, 100518 CrossRef.
- J. Guo, A. T. Zehnder, C. Creton and C.-Y. Hui, Soft Matter, 2020, 16, 6163–6179 RSC.
- Y. Wang, G. Nian and Z. Suo, Mech. Mater., 2021, 158, 103845 CrossRef.
- J. Gorman and M. Thouless, Int. J. Solids Struct., 2022, 253, 111442 CrossRef.
- H. Minsky, Z. Liu, C. Y. Hui, V. Aguilar, G. E. Sanoja, C. Creton and M. Ciccotti, Submitted to Extreme Mechanics Letters.
- Y. Wang, X. Yang, G. Nian and Z. Suo, J. Mech. Phys. Solids, 2020, 143, 103988 CrossRef.
- R. A. Schapery, 4th U.S. National Congress of Applied Mechanics, 1962, pp. 1075–1085 Search PubMed.
- H. Lakrout, P. Sergot and C. Creton, J. Adhes., 1999, 69, 307–359 CrossRef CAS.
- M. Maw, E. Dashtimoghadam, A. N. Keith, B. J. Morgan, A. K. Tanas, E. Nikitina, D. A. Ivanov, M. Vatankhah-Varnosfaderani, A. V. Dobrynin and S. S. Sheiko, ACS Cent. Sci., 2023, 9, 197–205 CrossRef CAS PubMed.
- H. Kim, J. J. Watkins and A. J. Crosby, Soft Matter, 2023, 59, 479–486 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3sm00562c |
| This journal is © The Royal Society of Chemistry 2023 |