Open Access Article
Open Access ArticlePredicting the size and morphology of nanoparticle clusters driven by biomolecular recognition†
Pablo
Palacios-Alonso
 *af,
Elena
Sanz-de-Diego
a,
Raúl P.
Peláez
*af,
Elena
Sanz-de-Diego
a,
Raúl P.
Peláez
 b,
A. L.
Cortajarena
b,
A. L.
Cortajarena
 cd,
F. J.
Teran
cd,
F. J.
Teran
 ae and
Rafael
Delgado-Buscalioni
ae and
Rafael
Delgado-Buscalioni
 bf
bf
aiMdea Nanociencia, Campus Universitario de Cantoblanco, 28049 Madrid, Spain
bDpto. Física Teórica de la Materia Condensada, Universidad Autónoma de Madrid, 28049 Madrid, Spain. E-mail: rafael.delgado@uam.es
cCIC biomaGUNE-BRTA, 20014, Donostia-San Sebastián, Spain
dIkerbasque, Basque Foundation for Science, Bilbao, Spain
eNanobiotecnología (iMdea-Nanociencia), Unidad Asociada al Centro Nacional de Biotecnología (CSIC), 28049 Madrid, Spain
fCondensed Matter Physics Center, IFIMAC, Spain
First published on 20th July 2023
Abstract
Nanoparticle aggregation is a driving principle of innovative materials and biosensing methodologies, improving transduction capabilities displayed by optical, electrical or magnetic measurements. This aggregation can be driven by the biomolecular recognition between target biomolecules (analytes) and receptors bound onto nanoparticle surface. Despite theoretical advances on modelling the entropic interaction in similar systems, predictions of the fractal morphologies of the nanoclusters of bioconjugated nanoparticles are lacking. The morphology of resulting nanoclusters is sensitive to the location, size, flexibility, average number of receptors per particle ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) , and the analyte–particle concentration ratio. Here we considered bioconjugated iron oxide nanoparticles (IONPs) where bonds are mediated by a divalent protein that binds two receptors attached onto different IONPs. We developed a protocol combining analytical expressions for receptors and linker distributions, and Brownian dynamics simulations for bond formation, and validated it against experiments. As more bonds become available (e.g., by adding analytes), the aggregation deviates from the ideal Bethe's lattice scenario due to multivalence, loop formation, and steric hindrance. Generalizing Bethe's lattice theory with a (not-integer) effective functionality feff leads to analytical expressions for the cluster size distributions in excellent agreement with simulations. At high analyte concentration steric impediment imposes an accessible limit value facc to feff, which is bounded by facc < feff <
, and the analyte–particle concentration ratio. Here we considered bioconjugated iron oxide nanoparticles (IONPs) where bonds are mediated by a divalent protein that binds two receptors attached onto different IONPs. We developed a protocol combining analytical expressions for receptors and linker distributions, and Brownian dynamics simulations for bond formation, and validated it against experiments. As more bonds become available (e.g., by adding analytes), the aggregation deviates from the ideal Bethe's lattice scenario due to multivalence, loop formation, and steric hindrance. Generalizing Bethe's lattice theory with a (not-integer) effective functionality feff leads to analytical expressions for the cluster size distributions in excellent agreement with simulations. At high analyte concentration steric impediment imposes an accessible limit value facc to feff, which is bounded by facc < feff < ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) . A transition to gel phase, is correctly captured by the derived theory. Our findings offer new insights into quantifying analyte amounts by assessing nanocluster size, and predicting nanoassembly morphologies accurately is a first step towards understanding variations of physical properties in clusters formed after biomolecular recognition.
. A transition to gel phase, is correctly captured by the derived theory. Our findings offer new insights into quantifying analyte amounts by assessing nanocluster size, and predicting nanoassembly morphologies accurately is a first step towards understanding variations of physical properties in clusters formed after biomolecular recognition.
1 Introduction
While pioneer studies on colloids were applied to prevent their aggregates, the last two decades1 has witnessed a growing interest in controlling colloid aggregation starting from the nanoscopic details up to the meso and macroscales. Self-assembly yields novel mesoscopic structures with applications in smart materials, self-healing structures,2 drug delivery,3,4 light-matter interaction5,6 or biomolecular sensors. One route to programmable self-assembly consists on designing the directionality or spatial arrangement of surface patches for colloid–colloid interactions.7 Another route, considered hereby, consists on nanoparticle conjugation, where bonds are mediated by high-affinity molecular linkers (the analytes in biosensing) binding to receptors located at the nanoparticles surface. Clusters of bioconjugated nanoparticles driven by analyte–receptor interactions are usually based on antibody–antigen couples,8 protein pairs,9 or complementary ssDNA sequences.10,11 Aggregates created by specific biomolecular recognition are opening new routes in biosensing, to detect from proteins to viruses.12 As in nature's self-assembled biochemical networks (some of them recently reproduced in living cells using two-protein mixtures13), the concentration of free linker molecules in solution enables an extra thermodynamic parameter with subtle antagonistic effects, such as reversible re-entrant transition to fluid phase at high linker concentration11 (owing to saturation of receptors) or a softening the otherwise strong dependence on gelation with temperature.14 Non-specific interactions are key to understand aggregation by analyte–receptor bonds10 as they lead to either effective repulsion between particles (e.g. excluded volume, steric effects),11,14 or to attractive interaction (e.g. dispersion forces). While non-specific attraction is inherent to colloids, in these systems, the effective repulsion depends non-trivially on the functionality of the particle, the size and flexibility of the linker and receptor,10 and probably even their surface mobility.14 Interestingly, these non-trivial effects could in principle be tuned to modify the effective functionality (or valence) of the conjugated nanoparticles,10 an effect which we also study hereby. Recent theoretical and computational works on polymer-linked colloidal gels15–17 report features which are qualitatively similar to those found here for protein-linked nanoparticles: high sensitivity to the receptor location,15 to the linker size and flexibility,16 to the average number of receptors per particle![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) , and to the analyte–particle concentration ratio. General features of the phase diagram, such as the re-entrant phase behaviour17 can be captured by thermodynamic approaches such as Wertheim's thermodynamic perturbation theory (ref. 18 and references therein). More specific analytical efforts based on statistical mechanics have focused on predicting the binding free energy (and mean field potentials) from the combinatorial and configurational entropy associated to analyte–receptor mixtures, also including effective repulsion.11,14,19 Theoretical and experimental works show that the structures of these aggregates depend on how much nanoscopic details can be kept under control: from “addressable complexity” in weak (reversible) attractive interaction, leading to crystal phases,7 to aperiodic, amorphous or irreversibly gellified phases.14 Concerning the kinetics of aggregation, following the foundational works by Flory20 and Stockmayer21 and subsequent developments for equilibrium polymerization,22,23 theoretical and computational generalizations for different types of linker-mediated complexes have been more recently proposed by several groups.15,17,24–27 The aggregation strongly dependent on the relative size of the linkers and host particles, and usually treated as diffusion limited. Despite these advances, there is still a lack of studies on the fractal structure of linker mediated aggregates. For a certain parameter range we show that these aggregates also share some features with limited-valence colloids28 with strong biding energy (Ebind/kBT ∼ 10), which percolate at low packing fraction forming open structures, or “empty fluids”.29
, and to the analyte–particle concentration ratio. General features of the phase diagram, such as the re-entrant phase behaviour17 can be captured by thermodynamic approaches such as Wertheim's thermodynamic perturbation theory (ref. 18 and references therein). More specific analytical efforts based on statistical mechanics have focused on predicting the binding free energy (and mean field potentials) from the combinatorial and configurational entropy associated to analyte–receptor mixtures, also including effective repulsion.11,14,19 Theoretical and experimental works show that the structures of these aggregates depend on how much nanoscopic details can be kept under control: from “addressable complexity” in weak (reversible) attractive interaction, leading to crystal phases,7 to aperiodic, amorphous or irreversibly gellified phases.14 Concerning the kinetics of aggregation, following the foundational works by Flory20 and Stockmayer21 and subsequent developments for equilibrium polymerization,22,23 theoretical and computational generalizations for different types of linker-mediated complexes have been more recently proposed by several groups.15,17,24–27 The aggregation strongly dependent on the relative size of the linkers and host particles, and usually treated as diffusion limited. Despite these advances, there is still a lack of studies on the fractal structure of linker mediated aggregates. For a certain parameter range we show that these aggregates also share some features with limited-valence colloids28 with strong biding energy (Ebind/kBT ∼ 10), which percolate at low packing fraction forming open structures, or “empty fluids”.29
Biomolecular recognition-mediated nanoassembling is relevant in many applications related to medical care, based on nanoparticles (NP) of different compositions, sizes, and shapes.30–32 Most of the available biosensing methodologies benefit from nanoparticle aggregation.33 This is the case of photothermal34 converter, colorimetric34–37 optical,5,38 electrical39 or magnetic readouts.40
Uniform nanoparticles can be now prepared with rather well defined surface characteristics, allowing for covalent stoichiometric attachment of oligonucleotides, nucleic acids, small molecules, peptides, proteins, antibodies, etc.41 The linkers might have a valence larger than one, capturing several receptors, while nanoparticles can be decorated with multiple receptors. In bioconjugation, the number of receptors per particle is a random variable f, whose statistics (binomial distribution) can be only fixed by experimentally controlling its average value ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) . The complexity of linker-mediated clusters thus lies some where between standard colloids with non-specific interactions and the addressable complexity of some patchy colloids (fixing f and the patches surface location). Their aggregates structures highly depend on the particle and analyte concentrations, the particle and receptor sizes and the average functionality
. The complexity of linker-mediated clusters thus lies some where between standard colloids with non-specific interactions and the addressable complexity of some patchy colloids (fixing f and the patches surface location). Their aggregates structures highly depend on the particle and analyte concentrations, the particle and receptor sizes and the average functionality ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) . We note however that
. We note however that ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) is seldom experimentally controlled;42 suspensions are often saturated with receptors which physically adsorb to the particles forming a coating.
is seldom experimentally controlled;42 suspensions are often saturated with receptors which physically adsorb to the particles forming a coating.
There is great practical interest in relating all these physico-chemical details with the resulting cluster size distribution and morphology, notably in the case of biosensors, either based on magnetic nanoparticles,43,44 plasmonic resonance and colorimetric biosensors45 and many other techniques where the transduced signal is enhanced by cluster formation.46 We present a general analysis of this problem, which combines experiments, theory and simulations to study the morphology and abundance of clusters of bioconjugated nanoparticles, with experimentally controlled stoichiometric constraints. We show that the information about the average stoichiometry of the receptor–analyte bond is essential to control the cluster distribution, for instance by tuning the relative analyte–particle concentration.
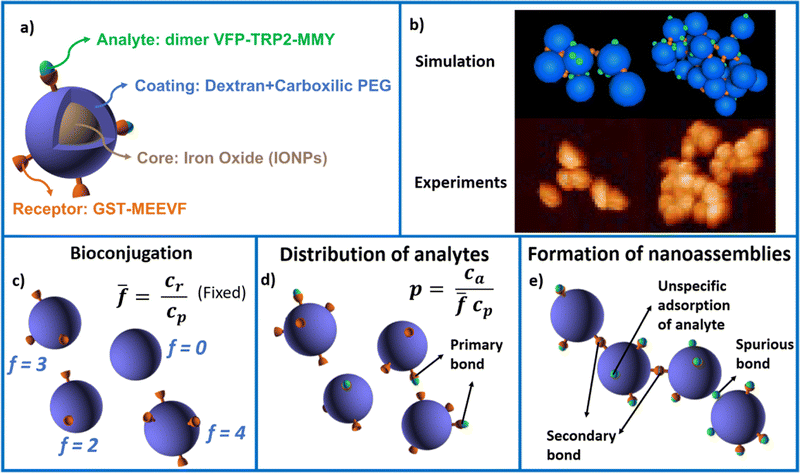
The system studied is illustrated in Fig. 1. Iron oxide nanoparticles (IONP) coated with dextran and carboxylic PEG are bioconjugated with the protein GST-MEEVF47 which binds to the divalent protein dVFP-TPR2-MMY.48 In experiments, we control the ensemble average number of MEEVF receptors per IONP (we consider ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) = {4,8,12}), the nanoparticle concentration cp and linker (analyte) concentration ca. The system's modeling was conducted by integrating analytical techniques to solve the distribution of receptors over the IONPs (Fig. 1c) and the formation of primary analyte–receptor bonds (Fig. 1d), along with numerical simulations employing Brownian Dynamics (see Methods) to address the slow IONP–IONP polymerization 1e) process.49 Simulations are successfully validated against experimental measurements of the average cluster size, polydispersity index (PDI) and the transition to a condensed colloidal phase (experimentally observed by pellet formation). Simulations indicate that this condensed phase correspond to a percolated network of protein-linked nanoparticles.‡ We analyze the effect of steric hindrance by neighboring particles in reducing their effective functionality and derive a simple expression for the accessible number of receptors (facc <
= {4,8,12}), the nanoparticle concentration cp and linker (analyte) concentration ca. The system's modeling was conducted by integrating analytical techniques to solve the distribution of receptors over the IONPs (Fig. 1c) and the formation of primary analyte–receptor bonds (Fig. 1d), along with numerical simulations employing Brownian Dynamics (see Methods) to address the slow IONP–IONP polymerization 1e) process.49 Simulations are successfully validated against experimental measurements of the average cluster size, polydispersity index (PDI) and the transition to a condensed colloidal phase (experimentally observed by pellet formation). Simulations indicate that this condensed phase correspond to a percolated network of protein-linked nanoparticles.‡ We analyze the effect of steric hindrance by neighboring particles in reducing their effective functionality and derive a simple expression for the accessible number of receptors (facc < ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) ) at high bond concentration. We then investigate the morphology of the clusters (number of bonds per particle and fractal dimension) as a function of
) at high bond concentration. We then investigate the morphology of the clusters (number of bonds per particle and fractal dimension) as a function of ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) . A generalization of Bethe's lattice analytic results, using a non-integer effective functionality feff is shown to successfully recover the cluster size distributions n(s). The effective valence varies with the analyte concentration: from feff ≈
. A generalization of Bethe's lattice analytic results, using a non-integer effective functionality feff is shown to successfully recover the cluster size distributions n(s). The effective valence varies with the analyte concentration: from feff ≈ ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) (Bethe's limit at low bond density) to feff ≈ 〈facc〉 (high bond concentration). Using the high density limit, facc, into Bethes lattice theory we predict the locus of the gelation transition observed both in experiments and simulations. Concluding remarks are given after the discussion of the results.
(Bethe's limit at low bond density) to feff ≈ 〈facc〉 (high bond concentration). Using the high density limit, facc, into Bethes lattice theory we predict the locus of the gelation transition observed both in experiments and simulations. Concluding remarks are given after the discussion of the results.
2 Methods
2.1 Experimental protocol
Experiments were carried out with magnetic iron oxide nanoparticles (IONPs) coated with dextran and carboxylic PEG synthesised by Micromode (product code is 104-56-701). The core diameter of the IONPs is 30 ± 4 nm size, the hydrodynamic diameter is 64 nm and the PDI is 0.08. Analyte–receptor recognition. IONPs were bioconjugated with a specific peptide sequence MEEVF,47 that is recognized by the design TPR domain TPR2-MMY48 that was used as target divalent analyte. Bioconjugation of magnetic nanoparticles. For the bioconjugation of IONPs coated with carboxylic PEG, three samples of 500 μL of IONPs at 3.5 mg of Fe per mL were incubated 4 hour at 37 °C with 150 mmol of EDC per g of Fe and 150 mmol of NHS per g of Fe. Samples were washed with amicon ultra centrifugal filters and redispersed in 10 mM sodium phosphate buffer pH 7.4 (PB buffer) at least 3 times. These pre-activated IONPs were incubated overnight at 37 °C with different concentrations of the receptor in order to estimate a ratio of 4, 8 and 12 receptors per particle. After that, the bioconjugated IONPs were purified by filtration through a sepharose 6 CLB column using PB buffer. Receptor-bioconjugated IONPs incubation. 50 μL of MEEVF-IONPs at 1 g L−1 of Fe were incubated 1 hour at room temperature with different concentrations of divalent analytes (dVFP-TPR2-MMY) in PB buffer. Quantification of magnetic nanoparticles. We employed a Nanosight NS300 (Malvern Instruments, USA) in order to determine the number of IONPs per unit volume in magnetic suspensions with iron contents of 1 g Fe per L. The samples were diluted 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5000 in DDW and injected into the instrument chamber using a 1 mL syringe. Camera settings were adjusted in order to focus the objective. The video data were collected for 60 seconds and repeated 3 times per sample. Colloidal Characterization of selected IONPs was performed through hydrodynamic size measurement by dynamic light scattering (DLS) in a Zetasizer Nano ZS equipment (Malvern Instruments, USA). In order to perform DLS measurements, the bioconjugated magnetic nanoparticles at 1 g Fe per L were incubated with increasing concentration of the analytes. After 60 minutes, each sample was diluted in buffer PB to a final concentration of 0.05 g Fe per L in a commercial cuvette. The energy source was a laser emitting at 633 nm, and the angle between sample and detector was 173°. DLS uses the Stokes–Einstein relation to determine the hydrodynamic size of solutes (either isolated particles or clusters), as DH = kBT/(3πηDt), where Dt is the translational diffusion coefficient measured from DLS. Using dilute IONP suspensions we measured single-particle size DH → σ = 64 nm. Moreover, DLS permits us to determine the nanoclusters average size and their polydispersity index (PDI). As explained below, above a critical value of the analyte concentration c(g)a, experiments show the formation and precipitation of a condensed (pellet) phase. In such case, we performed DLS measurements after having resuspended the solution (note however that such measurements are not representative).
5000 in DDW and injected into the instrument chamber using a 1 mL syringe. Camera settings were adjusted in order to focus the objective. The video data were collected for 60 seconds and repeated 3 times per sample. Colloidal Characterization of selected IONPs was performed through hydrodynamic size measurement by dynamic light scattering (DLS) in a Zetasizer Nano ZS equipment (Malvern Instruments, USA). In order to perform DLS measurements, the bioconjugated magnetic nanoparticles at 1 g Fe per L were incubated with increasing concentration of the analytes. After 60 minutes, each sample was diluted in buffer PB to a final concentration of 0.05 g Fe per L in a commercial cuvette. The energy source was a laser emitting at 633 nm, and the angle between sample and detector was 173°. DLS uses the Stokes–Einstein relation to determine the hydrodynamic size of solutes (either isolated particles or clusters), as DH = kBT/(3πηDt), where Dt is the translational diffusion coefficient measured from DLS. Using dilute IONP suspensions we measured single-particle size DH → σ = 64 nm. Moreover, DLS permits us to determine the nanoclusters average size and their polydispersity index (PDI). As explained below, above a critical value of the analyte concentration c(g)a, experiments show the formation and precipitation of a condensed (pellet) phase. In such case, we performed DLS measurements after having resuspended the solution (note however that such measurements are not representative).
2.2 Theoretical and computational modeling
We decompose the overall process of nanoassembly formation in three separate steps, illustrated in Fig. 1. First, we analytically derive the distribution of receptors per nanoparticle, for a given average number of receptors per particle![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) . This step is independent of the rest as in experiments the particles are first incubated with receptor proteins prior to linker molecules addition. Second, we solve (both analytically and by random sampling) the distribution of primary analyte–receptor links, which permit us to draw ensembles of particles with the expected distribution of loaded and void receptors for given values of
. This step is independent of the rest as in experiments the particles are first incubated with receptor proteins prior to linker molecules addition. Second, we solve (both analytically and by random sampling) the distribution of primary analyte–receptor links, which permit us to draw ensembles of particles with the expected distribution of loaded and void receptors for given values of ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) , particle concentration cp and analyte concentration ca. Third, for each particular realization of the ensemble of bioconjugated particles, we use Brownian dynamics (BD) simulations to model the aggregation via the formation of secondary (receptor–analyte–receptor) bonds (Fig. 1). Statistics of nanoassembly formation are gathered by repeating this three-step protocol. In the experiments, the second and third steps occur concurrently. However, as illustrated in Fig. 1, both stages can be independently solved due to the large time scale separation between the (fast) kinetics of formation of primary analyte–receptor bonds and the subsequent (slow) IONP–IONP polymerization.49 Both processes are diffusion-limited and irreversible due to the high receptor–analyte affinity (binding free energies of about 13kBT). This fact, and the large size discrepancy of the analyte proteins and the nanoparticles, ensures a solid separation between primary and secondary bond formation. In particular, the hydrodynamic diameter of the IONPs particles is 64 nm, while that of analyte proteins is around 4 nm, leading to diffusion times of τIONPs ≈ 1200 μs and τanalytes ≈ 0.3 μs where τ = Dt/σ2. We now provide details on each of the three steps of our modelling approach.
, particle concentration cp and analyte concentration ca. Third, for each particular realization of the ensemble of bioconjugated particles, we use Brownian dynamics (BD) simulations to model the aggregation via the formation of secondary (receptor–analyte–receptor) bonds (Fig. 1). Statistics of nanoassembly formation are gathered by repeating this three-step protocol. In the experiments, the second and third steps occur concurrently. However, as illustrated in Fig. 1, both stages can be independently solved due to the large time scale separation between the (fast) kinetics of formation of primary analyte–receptor bonds and the subsequent (slow) IONP–IONP polymerization.49 Both processes are diffusion-limited and irreversible due to the high receptor–analyte affinity (binding free energies of about 13kBT). This fact, and the large size discrepancy of the analyte proteins and the nanoparticles, ensures a solid separation between primary and secondary bond formation. In particular, the hydrodynamic diameter of the IONPs particles is 64 nm, while that of analyte proteins is around 4 nm, leading to diffusion times of τIONPs ≈ 1200 μs and τanalytes ≈ 0.3 μs where τ = Dt/σ2. We now provide details on each of the three steps of our modelling approach.
![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) . However, the number of receptors on each IONP follows a binomial distribution. It can be assumed that the maximum number of receptors that each particle can have (that depends on the number of free carboxilic groups in the dextran coating) is much larger than the average number receptors per particle. Hence, the bonding of a receptor to a particle is independent of the number of receptors that the particle already had. Consequently, if there are Np particles, each receptor can be bonded to a specific particle with a probability pr = 1/Np, and the probability of a particle having f receptors bonded follows a binomial distribution,
. However, the number of receptors on each IONP follows a binomial distribution. It can be assumed that the maximum number of receptors that each particle can have (that depends on the number of free carboxilic groups in the dextran coating) is much larger than the average number receptors per particle. Hence, the bonding of a receptor to a particle is independent of the number of receptors that the particle already had. Consequently, if there are Np particles, each receptor can be bonded to a specific particle with a probability pr = 1/Np, and the probability of a particle having f receptors bonded follows a binomial distribution,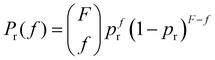 | (1) |
![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) is the total number of receptors in the system. The number of particles in the simulations and especially in the experiments is very high, consequently pr ≪ 1 and F ≫ 1 and the binomial distribution can be approximated by a Poisson distribution,
is the total number of receptors in the system. The number of particles in the simulations and especially in the experiments is very high, consequently pr ≪ 1 and F ≫ 1 and the binomial distribution can be approximated by a Poisson distribution,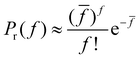 | (2) |
In practice, instead of using eqn (2) it is faster to use random sampling to distribute the receptors among the particles: we generate F = Np![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) random numbers uniformly distributed between 1 and Np. Then, the number of receptors associated to a particle i is just the number of times that the number i appears in the list of generated numbers.
random numbers uniformly distributed between 1 and Np. Then, the number of receptors associated to a particle i is just the number of times that the number i appears in the list of generated numbers.
In Fig. S4 (ESI†) we have compared the predictions for Pr(f) using the Poisson distribution, the Binomial distribution and random sampling. An excellent agreement is found for the two limiting cases considered hereby (![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) = 2 and
= 2 and ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) = 12). Thus, for computational convenience, we deploy random sampling to populate the receptors on the IONPs.
= 12). Thus, for computational convenience, we deploy random sampling to populate the receptors on the IONPs.
The random sampling protocol samples the probability of a particle having focc occupied receptors, P(focc). To verify the numerical sampling we need to derive an analytical relation for P(focc). We derive in the ESI† (Section S.5) a compact form for P(focc) which consist on another Poisson distribution,
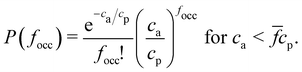 | (3) |
![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) , provided that the number of receptors in the system is greater than or equal to the number of analytes ca <
, provided that the number of receptors in the system is greater than or equal to the number of analytes ca < ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) cp. Note that when the system is saturated of analytes, ca >
cp. Note that when the system is saturated of analytes, ca > ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) cp, the distribution of occupied receptors is trivially equal to the distribution of receptors, eqn (2). In Fig. S5 (ESI†) we compare the distribution of particles having focc receptors initially occupied obtained by random sampling and by eqn (3). The comparison is basically perfect, so that to fasten up computations, random sampling is the preferred choice to set the initial conditions of the BD simulations.
cp, the distribution of occupied receptors is trivially equal to the distribution of receptors, eqn (2). In Fig. S5 (ESI†) we compare the distribution of particles having focc receptors initially occupied obtained by random sampling and by eqn (3). The comparison is basically perfect, so that to fasten up computations, random sampling is the preferred choice to set the initial conditions of the BD simulations.
Simulations were performed in cubic periodic boxes of side L = 2000 nm ≈ 31σ. The translational diffusion coefficient Dt (given by the Stokes–Einstein relation Dt = kbT/(6πηa) provides the physical time scale of the simulation. The time step was set to dt = 1 × 10−4 in units of τ = a2/Dt. Individual runs reached 1.5 × 107 time steps, which is enough for a particle to diffuse through the full box τbox = Lbox2/Dt. As shown in Fig. S7 (ESI†), these simulation times are enough to guarantee that the number of bonds formed saturates to a stationary value. While two or three of these runs are enough to obtain a good estimation of the mean hydrodynamic size and PDI of the clusters, we need between 30 and 200 runs to extract the cluster-size distributions.
All simulations have been conducted using a particle concentration of cp = 1.27 μM, which corresponds to 6111 particles in our simulation box, with the exception of those in which we aimed to study the effect of particle concentration on the average hydrodynamic size and the PDI of the nanoclusters. In these cases, we varied the concentration of MNP from 0.049 μM up to 2.9 μM (i.e., from 200 IONP to 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 IONP). Additionally, throughout all simulations, we used analyte concentrations ranging from 0.1 to 4.0 μM (i.e., 411 analytes to 19
000 IONP). Additionally, throughout all simulations, we used analyte concentrations ranging from 0.1 to 4.0 μM (i.e., 411 analytes to 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 270 analytes).
270 analytes).
Brownian dynamics for the particle displacements were solved using the Euler–Maruyama method,50 a generalization of the Euler method to stochastic differential equations. Not being interested in the precise aggregation kinetics, but rather on the statistics of the nanoclusters, we did not include hydrodynamic correlations between particles displacements, which might modify cluster formation dynamics but not their structure.51 The interaction forces between IONPs are just steric to prevent overlapping. The steric force was implemented using the Weeks–Chandler–Andersen (WCA) potential52 which is a purely repulsive, short range potential based on Lennard-Jones interaction, truncated at r = 21/6σ,
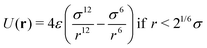 | (4) |
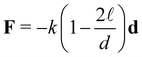 | (5) |
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 4 nn is the equilibrium distance between the surface of two bonded particles and ui, uj are the unitary vectors pointing the position of the receptors on the IONP surfaces (see Fig. S8, ESI†). The spring constant k was set to k = 100kBT/a2, which yields bond fluctuations of about 2 nm, within the expected range for the sum of thermal variations in receptors, analyte–protein and dextran-coating (in any case, results were not observed to vary using larger values of k).
= 4 nn is the equilibrium distance between the surface of two bonded particles and ui, uj are the unitary vectors pointing the position of the receptors on the IONP surfaces (see Fig. S8, ESI†). The spring constant k was set to k = 100kBT/a2, which yields bond fluctuations of about 2 nm, within the expected range for the sum of thermal variations in receptors, analyte–protein and dextran-coating (in any case, results were not observed to vary using larger values of k).
The translational displacement of each particle over time dt, is described by standard Brownian dynamics,
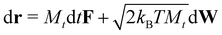 | (6) |
In analogy to the translational movement, the overdamped Langevin equation for the rotational motion includes a drag torque, a stochastic torque and all the external torques acting on the particles, which in our case they arise from the harmonic forces between the linked receptors,
| τi = aui × Fi | (7) |
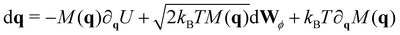 | (8) |
To integrate eqn (8), we choose a set of generalised coordinates q such that the angular velocity ω, is ω = dq/dt. Using this choice ∂qU is the total torque that acts on the particles and the mobility matrix M(q) is the rotational mobility, Mr, that relates the torque with the angular velocity as t = Mrω. In addition if we consider quasi-spherical particles the stochastic drift term kBT∂qM(q) is 0 and the mobility tensor is a diagonal matrix. Using this assumptions eqn (8) can be rewritten as,
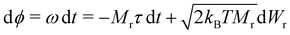 | (9) |
In the literature, we can find multiple ways of parameterize the orientations and rotations of each particle53 (i.e., using the Euler Angles, storing the directions of the three-coordinate axis of the particles…). We describe the orientation of each particle using quaternions (Qi(t))55 because they provide a singularity-free description of rotations and they are very efficient in the use of the memory (only 4 numbers are required to store the orientation of each particle).
The rotation vector that actualize the orientation of each particle can be easily transformed to a quaternion Qϕ,56
| Qϕ = (cos(θ/2), sin(θ/2)uϕ) | (10) |
The orientation of the particle in the time t + dt, Qi(t + dt), can be obtained by multiplying their orientation in the time t, Q(t), by Qϕ,
| Qi(t + dt) = Qϕ·Qi(t) | (11) |
The position of the receptors on the surface of the IONP was stored using the polar and the azimuthal angles in the reference system of the IONP. The code was written and compiled in CUDA-C/C++ using the library UAMMD57 and simulations were performed in our own groups GPU cluster.
3 Results and discussion
A key difference between colloidal aggregation via nonspecific interactions and directed aggregation of bioconjugated nanoparticles mediated by free analytes in solution, is that the latter is limited by valence (stoichiometry) and bond competition. The total number of available receptors per unit volume is![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) cp/2 where the factor 2 reflects two receptors per bond. The number of secondary (IONP-analyte-IONP) bonds depends non-trivially on the particle and analyte concentrations (cp, ca) and the IONP average functionality
cp/2 where the factor 2 reflects two receptors per bond. The number of secondary (IONP-analyte-IONP) bonds depends non-trivially on the particle and analyte concentrations (cp, ca) and the IONP average functionality ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) . Yet, an upper bound for the density of bonds can be easily derived. Forming one bond requires one receptor–analyte complex (loaded receptor) encountering a free receptor. At low analyte concentration (ca < cp
. Yet, an upper bound for the density of bonds can be easily derived. Forming one bond requires one receptor–analyte complex (loaded receptor) encountering a free receptor. At low analyte concentration (ca < cp![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) /2) the number of bonds per unit volume increases linearly with the analytes cbond = ca. The number of secondary bonds reaches a maximum value at the stoichiometric or balance mixture
/2) the number of bonds per unit volume increases linearly with the analytes cbond = ca. The number of secondary bonds reaches a maximum value at the stoichiometric or balance mixture 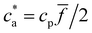 . Within this range
. Within this range 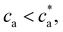 the probability of forming a bond is given by,
the probability of forming a bond is given by,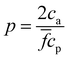 | (12) |
![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) and takes place in the balanced mixture (all the receptors may form a bond). In the range
and takes place in the balanced mixture (all the receptors may form a bond). In the range 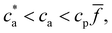 receptors start to saturate and the number of available bonds starts to decrease as cbond = cp
receptors start to saturate and the number of available bonds starts to decrease as cbond = cp![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) − ca, in this range p = 2[1 − ca/(
− ca, in this range p = 2[1 − ca/(![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) cp)]. Finally for ca >
cp)]. Finally for ca > ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) cp all the receptors are filled with analyte and no bond can be formed. While this trend roughly determines the size of the nanoclusters, it is altered by several collective deviatoric effects: notably the presence of non-accessible receptors shadowed by neighboring particles (steric hindrance) and the formation of non-specific “fake” bonds between IONP not involving receptors (Fig. 1e). We first validate our theoretical approach against experimental results for the average size and polydispersity of the IONP nanoclusters. Then, we analyze in detail the structure of these aggregates and the (experimentally observed) gelation transitions. In doing so, we show that Bethe's theory can be satisfactorily generalized to explain the cluster distributions and percolation transitions for different
cp all the receptors are filled with analyte and no bond can be formed. While this trend roughly determines the size of the nanoclusters, it is altered by several collective deviatoric effects: notably the presence of non-accessible receptors shadowed by neighboring particles (steric hindrance) and the formation of non-specific “fake” bonds between IONP not involving receptors (Fig. 1e). We first validate our theoretical approach against experimental results for the average size and polydispersity of the IONP nanoclusters. Then, we analyze in detail the structure of these aggregates and the (experimentally observed) gelation transitions. In doing so, we show that Bethe's theory can be satisfactorily generalized to explain the cluster distributions and percolation transitions for different ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) .
.
3.1 Nanoclusters size and dispersion: comparison with experiments
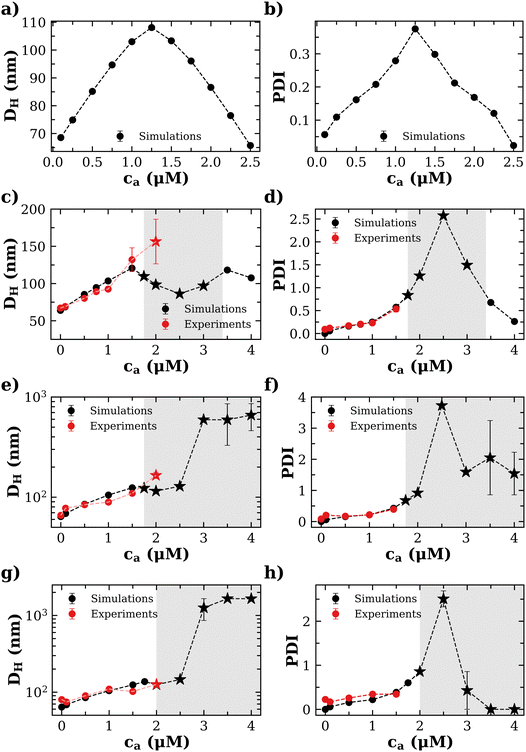
Experimental and simulation results for the average size (cluster hydrodynamic diameter DH) and polydispersity index (PDI) of the IONP clusters as a function of analyte and IONP concentrations are illustrated in Fig. 2 for cp = 1.27 μM (i.e. 7.64 × 1014 IONP mL−1). In simulations, the hydrodynamic diameter of a cluster of mass s is obtained from ref. 58,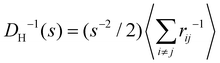 (average over independent cluster configurations). Notably, for all the functionalities
(average over independent cluster configurations). Notably, for all the functionalities ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) considered, simulation estimates for the average 〈DH〉 over the cluster ensemble (we gather about a tens of thousand of individual clusters) and the corresponding polydispersity index PDI = Std[DH]/〈DH〉 are in quantitative agreement with the experimental measurements. These quantities are related to the first and second moment of the cluster distribution and it is convenient to analyze them concurrently for increasing analyte concentration ca. As shown in Fig. 2, the case
considered, simulation estimates for the average 〈DH〉 over the cluster ensemble (we gather about a tens of thousand of individual clusters) and the corresponding polydispersity index PDI = Std[DH]/〈DH〉 are in quantitative agreement with the experimental measurements. These quantities are related to the first and second moment of the cluster distribution and it is convenient to analyze them concurrently for increasing analyte concentration ca. As shown in Fig. 2, the case ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) = 2 (two receptors per particle in average) perfectly follows the stoichiometric trend for the bond formation, explained above. In particular, the maximum average cluster size and the maximum polydispersity take place at
= 2 (two receptors per particle in average) perfectly follows the stoichiometric trend for the bond formation, explained above. In particular, the maximum average cluster size and the maximum polydispersity take place at 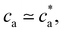 with
with 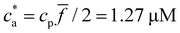 . For
. For 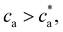 most receptors are loaded with analytes and secondary bond formation starts to saturate, leading to smaller clusters with smaller PDI.
most receptors are loaded with analytes and secondary bond formation starts to saturate, leading to smaller clusters with smaller PDI.
At small analyte concentration, the case ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) = 4 (where experimental results are available) shares features with
= 4 (where experimental results are available) shares features with ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) = 2. Simulations perfectly capture the increase in average cluster size and PDI in experiments. However, for
= 2. Simulations perfectly capture the increase in average cluster size and PDI in experiments. However, for ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) = 4 (in fact for any
= 4 (in fact for any ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) > 2) simulations predict the formation of a percolating cluster (corresponding to gel phase). For
> 2) simulations predict the formation of a percolating cluster (corresponding to gel phase). For ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) = 4 the onset of gelation takes place in the range 1.5 μM < cga ≤ 1.75 μM and the gel phase persists up to ca ∈ [3.0,3.5) μM. The observation of the gel phase is indicated in Fig. 2 with larger (black) star-shaped symbols and a shadowed region. The onset of the gel phase predicted by simulations coincides quite precisely with the formation of a pellet in the experiments (i.e. a solid-like phase of condensed IONPs which precipitates). This experimental event is indicated by red stars in Fig. 2. We note that in the experiments, pellet precipitation was observed for ca ≥ 2.0 μM; hence in this range it is not possible to compare with simulations.
= 4 the onset of gelation takes place in the range 1.5 μM < cga ≤ 1.75 μM and the gel phase persists up to ca ∈ [3.0,3.5) μM. The observation of the gel phase is indicated in Fig. 2 with larger (black) star-shaped symbols and a shadowed region. The onset of the gel phase predicted by simulations coincides quite precisely with the formation of a pellet in the experiments (i.e. a solid-like phase of condensed IONPs which precipitates). This experimental event is indicated by red stars in Fig. 2. We note that in the experiments, pellet precipitation was observed for ca ≥ 2.0 μM; hence in this range it is not possible to compare with simulations.
For ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) = 4 the stoichiometric balance (for which the maximum number of available bonds is attained) takes place at
= 4 the stoichiometric balance (for which the maximum number of available bonds is attained) takes place at 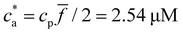 . Unlike the
. Unlike the ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) = 2 case, the system gelates before the stoichiometric condition is attained
= 2 case, the system gelates before the stoichiometric condition is attained 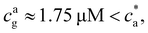 as a consequence, a peak in average cluster size at
as a consequence, a peak in average cluster size at 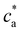 is not to be observed. Above the transition, the fraction of particles composing the percolating cluster is 0.6. Thus, close to the gel transition, a high enough number of particles remain unbounded or forming finite clusters and the average cluster size does not significantly increase for ca > cga (Fig. 2c). By contrast, this effect creates a large cluster polydispersity and the PDI reaches a maximum value at
is not to be observed. Above the transition, the fraction of particles composing the percolating cluster is 0.6. Thus, close to the gel transition, a high enough number of particles remain unbounded or forming finite clusters and the average cluster size does not significantly increase for ca > cga (Fig. 2c). By contrast, this effect creates a large cluster polydispersity and the PDI reaches a maximum value at 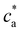 (Fig. 2d). For
(Fig. 2d). For 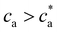 the number of available bonds decreases, and so it does the PDI, as the infinite cluster grows up to 95% of the particles. Interestingly, for ca ≥ 3.5 μM most receptors are saturated with analytes and simulations predict re-entrant melting (reverse gel–sol transition) as indicated in Fig. 2c (the gel phase is indicated with a shadowed area). Indeed, as the available secondary bonds scarce, the scenario becomes similar to
the number of available bonds decreases, and so it does the PDI, as the infinite cluster grows up to 95% of the particles. Interestingly, for ca ≥ 3.5 μM most receptors are saturated with analytes and simulations predict re-entrant melting (reverse gel–sol transition) as indicated in Fig. 2c (the gel phase is indicated with a shadowed area). Indeed, as the available secondary bonds scarce, the scenario becomes similar to 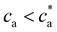 . A similar re-entrant network formation (without phase separation) as a function of linker concentration and centered at the stoichiometric ratio, was recently observed in simulations of linker-mediated aggregation of colloids.17 This re-entrant transition is however not always easily observed in experiments. As shown in Fig. 2c, under experimental conditions, aggregates are still large enough to form precipitates at ca ≥ 3.5 μM. A plausible hypothesis for such a deviation from simulations is the formation of non-specific bonds, whereby analytes physisorb to the dextran-coated IONP surfaces acting as bridges for another IONP and creating spurious bonds, as illustrated in Fig. 1e. These non-specific (spurious) bonds become more frequent as ca surpasses the corresponding dissociation constant for non-specific protein-dextran adhesion, and when specific interacting partners are not available. To validate this hypothesis, experiments were repeated without receptors (f = 0) and fixed cp: indeed, the formation of aggregates was observed for large enough values of ca, confirming the presence of non-specific interactions in absence of receptors. We note that non-specific adhesion can be easily included in the theoretical model. However, we deliberately exclude this effect in the theory to validate, by comparison, the region where specific ligand–analyte bonds are dominant in experiments.
. A similar re-entrant network formation (without phase separation) as a function of linker concentration and centered at the stoichiometric ratio, was recently observed in simulations of linker-mediated aggregation of colloids.17 This re-entrant transition is however not always easily observed in experiments. As shown in Fig. 2c, under experimental conditions, aggregates are still large enough to form precipitates at ca ≥ 3.5 μM. A plausible hypothesis for such a deviation from simulations is the formation of non-specific bonds, whereby analytes physisorb to the dextran-coated IONP surfaces acting as bridges for another IONP and creating spurious bonds, as illustrated in Fig. 1e. These non-specific (spurious) bonds become more frequent as ca surpasses the corresponding dissociation constant for non-specific protein-dextran adhesion, and when specific interacting partners are not available. To validate this hypothesis, experiments were repeated without receptors (f = 0) and fixed cp: indeed, the formation of aggregates was observed for large enough values of ca, confirming the presence of non-specific interactions in absence of receptors. We note that non-specific adhesion can be easily included in the theoretical model. However, we deliberately exclude this effect in the theory to validate, by comparison, the region where specific ligand–analyte bonds are dominant in experiments.
The trends for ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) = 8 and 12 (Fig. 2e–h) share most of the features of
= 8 and 12 (Fig. 2e–h) share most of the features of ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) = 4. Simulations and experiments observe the formation of a gel phase (percolating in simulations and precipitating in experiments) at a slightly larger analyte concentration cga ∈ (1.75–2.0] μM. For ca < cga simulations quantitatively agree with experimental measurements of the average cluster size and PDI. In these cases, the stoichiometric balance would take place at high analyte concentration (respectively
= 4. Simulations and experiments observe the formation of a gel phase (percolating in simulations and precipitating in experiments) at a slightly larger analyte concentration cga ∈ (1.75–2.0] μM. For ca < cga simulations quantitatively agree with experimental measurements of the average cluster size and PDI. In these cases, the stoichiometric balance would take place at high analyte concentration (respectively 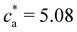 and 7.62 μM). But, the percolating cluster grows as ca is increased above cga and well before
and 7.62 μM). But, the percolating cluster grows as ca is increased above cga and well before 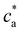 , the infinite cluster ends up by gathering the total number of particles in the simulation box, leading to a vanishing PDI at large enough ca.
, the infinite cluster ends up by gathering the total number of particles in the simulation box, leading to a vanishing PDI at large enough ca.
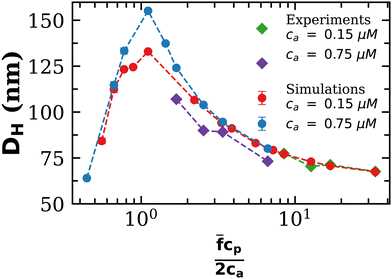
To further validate our theoretical and computational models for cluster formation, Fig. 3 compares two assays with fixed analyte concentration (ca = 0.15 μM and 0.75 μM) and varying IONP concentration (average valence ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) = 4). As expected, a rather sharp peak in the average cluster size is observed at the stoichiometric mixture
= 4). As expected, a rather sharp peak in the average cluster size is observed at the stoichiometric mixture 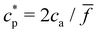 . For ca = 0.15 μM the peak takes place around 0.45 × 1014 IONP mL−1 (cp = 0.075 μM) while for ca = 0.75 μM the maximum cluster size is found when 2.25 × 1014 IONP mL−1 (or cp = 0.37 μM). Experimental results are in good agreement with simulations, although small deviations are noticed for the ca = 0.75 μM case. As an aside, it has to be stressed that details of these assemblies are rather sensitive to each parameter of the system. For instance, simulations showed deviations of about 15% in the cluster average size if the same functionality was used for all IONPs (f =
. For ca = 0.15 μM the peak takes place around 0.45 × 1014 IONP mL−1 (cp = 0.075 μM) while for ca = 0.75 μM the maximum cluster size is found when 2.25 × 1014 IONP mL−1 (or cp = 0.37 μM). Experimental results are in good agreement with simulations, although small deviations are noticed for the ca = 0.75 μM case. As an aside, it has to be stressed that details of these assemblies are rather sensitive to each parameter of the system. For instance, simulations showed deviations of about 15% in the cluster average size if the same functionality was used for all IONPs (f = ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) ) instead of using eqn (2). More examples are provided below. As a relevant conclusion in Fig. 3, it is possible to maximize the average cluster size by working close to the optimal ratio cp/ca = 2/
) instead of using eqn (2). More examples are provided below. As a relevant conclusion in Fig. 3, it is possible to maximize the average cluster size by working close to the optimal ratio cp/ca = 2/![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) . However, we shall later show that the system percolates when p =
. However, we shall later show that the system percolates when p = ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) cp/ca > pc, where the threshold pc is derived later (in eqn (20)). Thus working too close to p = 1 will lead to pellet formation, which is undesirable for biosensor applications. In particular, in Fig. 3 simulations with ca = 0.75 μM and p ≈ 1, produced pre-percolated structures with large clusters (in some cases with 400 NPs). In the dilute case, ca = 0.15 μM, and for p ≈ 1, we observed clusters with up to a 20% of the total number of NPs. While Fig. 3 should be a master curve (as even in dilute suspensions one should expect the formation of percolated structures around p ≃ 1) waiting times becomes prohibitively long as the concentration is reduced (this could actually be a benefit for biosensor experiments).
cp/ca > pc, where the threshold pc is derived later (in eqn (20)). Thus working too close to p = 1 will lead to pellet formation, which is undesirable for biosensor applications. In particular, in Fig. 3 simulations with ca = 0.75 μM and p ≈ 1, produced pre-percolated structures with large clusters (in some cases with 400 NPs). In the dilute case, ca = 0.15 μM, and for p ≈ 1, we observed clusters with up to a 20% of the total number of NPs. While Fig. 3 should be a master curve (as even in dilute suspensions one should expect the formation of percolated structures around p ≃ 1) waiting times becomes prohibitively long as the concentration is reduced (this could actually be a benefit for biosensor experiments).
3.2 Steric hindrance and accessible links
After validating our theoretical and computational approach against experiments we analyze the statistics of receptors and bonds obtained from simulations. To start with, we consider the effect of steric hindrance in limiting the number of available receptors. This effect is illustrated in Fig. 4, where it is seen that the area described by a solid angle θex around one bond linking two particles (shadowed region in the bottom panel in Fig. 4a), cannot be reached by the receptor of a third. More precisely, for an excluded angle θex, the area excluded around one IONP receptor is Aex = Asp(1 − cos(θex))/2 ≈ θex2Asp/2 with Asp = 4πa2. Following the sketch in Fig. 4b is not difficult to derive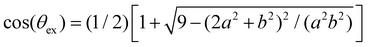 with b = a +
with b = a + ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) and
and ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) the linker length (the bond length is 2
the linker length (the bond length is 2![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ). In our case, the particle radius is a ≈ 32 nm and
). In our case, the particle radius is a ≈ 32 nm and ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 2 nm, so one bond excludes a net area of Aex = 0.11Asp. As a simple estimation, a particle with
= 2 nm, so one bond excludes a net area of Aex = 0.11Asp. As a simple estimation, a particle with ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) receptors but having only facc of them accessible, will exclude a fraction faccAex/Asp of the particle area. Making the approximation that the ratio between accessible and total receptors equals the fraction of accessible area, facc/
receptors but having only facc of them accessible, will exclude a fraction faccAex/Asp of the particle area. Making the approximation that the ratio between accessible and total receptors equals the fraction of accessible area, facc/![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) ≈ (1 − faccAex/Asp), one gets,
≈ (1 − faccAex/Asp), one gets,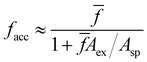 | (13) |
![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) → ∞ in eqn (13), we find that, on average, the maximum number of bonds a particle can form is close to 9, which is larger than the close packing limit for the coordination number,59 6, probably due to the linkers excluded area and the finite separation between particles. Within the range of interest of
→ ∞ in eqn (13), we find that, on average, the maximum number of bonds a particle can form is close to 9, which is larger than the close packing limit for the coordination number,59 6, probably due to the linkers excluded area and the finite separation between particles. Within the range of interest of ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) , the agreement with the approximation in eqn (13) is excellent, which suggests that, at least for small linker length
, the agreement with the approximation in eqn (13) is excellent, which suggests that, at least for small linker length ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) , the excluded area can be understood as sum of two-body exclusions. The present analysis indicates the strong effect that the receptor length
, the excluded area can be understood as sum of two-body exclusions. The present analysis indicates the strong effect that the receptor length ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) might have on the number of accessible receptors facc. For instance, for a = 32 nm, and
might have on the number of accessible receptors facc. For instance, for a = 32 nm, and ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) → 0 nm, the fraction of excluded area per bond grows to 0.25, while for
→ 0 nm, the fraction of excluded area per bond grows to 0.25, while for ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) > 13.25 nm, θex = 0, so in that case no receptor will become unavailable due to steric effects (however, for long linkers -and depending on their flexibility-another way of “loosing” receptors is the formation of multiple bonds between two particles16). In any case, tuning the length of the linker might be an alternative10 way to control the effective valence of bioconjugated particles. For instance, linkers such as ssDNA strands will expand/shorten by modifying the pH or the electrolyte concentration, while proteins are sensitive to temperature or chaotropic agents (urea).
> 13.25 nm, θex = 0, so in that case no receptor will become unavailable due to steric effects (however, for long linkers -and depending on their flexibility-another way of “loosing” receptors is the formation of multiple bonds between two particles16). In any case, tuning the length of the linker might be an alternative10 way to control the effective valence of bioconjugated particles. For instance, linkers such as ssDNA strands will expand/shorten by modifying the pH or the electrolyte concentration, while proteins are sensitive to temperature or chaotropic agents (urea).
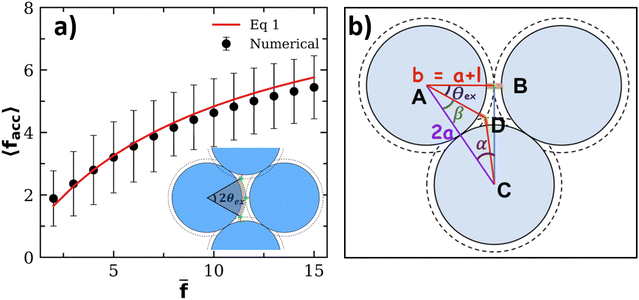 | ||
Fig. 4 (a) Average number of accessible receptors 〈facc〉: symbols obtained from random sampling (see text, error bars indicate the standard deviation) and the line is the theoretical estimation in eqn (13). The angle θex excluded by two bonded particles to a third partner is illustrated in the inset. (b) Geometry to estimate θex: using the triangles ABC and ADC we obtain sin(α) and cos(β) respectively, and then use α + β + θex = 90° to derive θex. The receptor length is ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ≈ 2 nm and particle radius a ≈ 32 nm, providing θex = 38.4°. ≈ 2 nm and particle radius a ≈ 32 nm, providing θex = 38.4°. | ||
3.3 Bond statistics
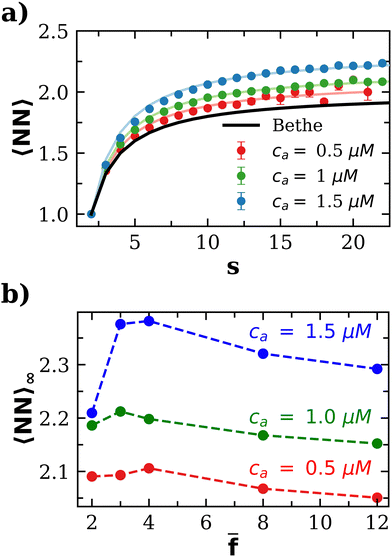
Another important quantity is the number of bonds nbonds, which is directly related to the average number of nearest neighbors 〈NN〉 in a cluster. Here we take the Bethe's lattice60,61 as reference (see S.1. and Fig. S1, ESI†). Each node of the Bethe's lattice has a fixed number of neighbors (fixed valence f) and there is a fixed probability p of creating a link between two nodes. In a Betthe's lattice the number of bonds formed in a cluster with s particles is nbonds = s − 1. This simple relation follows from the fact that cyclic structures (rings, etc.) are not allowed (Fig. S1b, ESI†). Consequently, in the Bethe lattice, on average, each particle will be connected to a number of neighbors given by,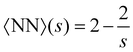 | (14) |
Compared with the Bethe's lattice (Fig. S1b, ESI†), nanoclusters of bioconjugated IONP will certainly present a larger number of bonds and neighbors because of the formation of cyclic structures, shown in the AFM images of Fig. 1b (see also Fig. S1c, ESI†). The deviations from the ideal Betthe's lattice trend increase with the number of bonds available and therefore with ca (as long as 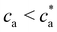 ). This fact is clearly observed in Fig. 5a where the symbols represent simulation results for 〈NN〉 for increasing values of ca without reaching the percolation of the system. Taking the analogy with the Bethe's lattice limit for s → ∞, we propose a helpful analytical relation for NN which only depends on 〈NN〉∞; the mean number of neighbors that a particle would have in a cluster with infinite particles (note that 〈NN〉Bethe∞ = 2)
). This fact is clearly observed in Fig. 5a where the symbols represent simulation results for 〈NN〉 for increasing values of ca without reaching the percolation of the system. Taking the analogy with the Bethe's lattice limit for s → ∞, we propose a helpful analytical relation for NN which only depends on 〈NN〉∞; the mean number of neighbors that a particle would have in a cluster with infinite particles (note that 〈NN〉Bethe∞ = 2)
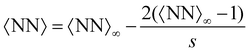 | (15) |
![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) for ca = 0.5 μM, 1.0 μM and 1.5 μM). As an interesting outcome, at low bond concentration (ca < 0.5 μM) the number of neighbours in the IONP assemblies approaches the ideal Bethe's lattice value NN → NNBethe. At high bond concentration and large clusters, 〈NN〉∞ is maximum for
for ca = 0.5 μM, 1.0 μM and 1.5 μM). As an interesting outcome, at low bond concentration (ca < 0.5 μM) the number of neighbours in the IONP assemblies approaches the ideal Bethe's lattice value NN → NNBethe. At high bond concentration and large clusters, 〈NN〉∞ is maximum for ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) = 3 or 4. For
= 3 or 4. For ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) > 4, the number of options for the formation of a new bond increases with
> 4, the number of options for the formation of a new bond increases with ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) and this explains a decrease in NN. This gain in entropy leads to less compact clusters for
and this explains a decrease in NN. This gain in entropy leads to less compact clusters for ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) > 4, as we reveal below by analyzing the Flory exponent.
> 4, as we reveal below by analyzing the Flory exponent.
3.4 Compactness of nanoclusters: Flory exponent
In fractal aggregates, the relation between the cluster size Rg(s) and the number of particles it contains s tends to a power law Rg ∼ sν for large enough s. The fractal dimension dF = 1/ν is related to the Flory exponent ν which can be extracted from the scaling of the cluster gyration radius62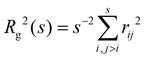 where rij is the distance between pairs of cluster particles. We gathered enough statistics from simulations to examine subtle details in the Flory exponent which provide information on the shape and the kinetics of the nanoclusters. The cluster size and shape have a strong influence on the cluster's transduction signal (e.g. its magnetic response33) and for the applied sake, it is interesting to study how ν varies with the number of particles in the cluster, s. To that end we calculate a “local” exponent as,
where rij is the distance between pairs of cluster particles. We gathered enough statistics from simulations to examine subtle details in the Flory exponent which provide information on the shape and the kinetics of the nanoclusters. The cluster size and shape have a strong influence on the cluster's transduction signal (e.g. its magnetic response33) and for the applied sake, it is interesting to study how ν varies with the number of particles in the cluster, s. To that end we calculate a “local” exponent as,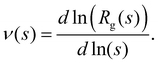 | (16) |
| Rg(s) = −c1s−c2 + c3sν∞ | (17) |
![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) . The analysis was performed at ca = 1.5 μM and cp = 1.27 μM, which are values close to (slightly below) the gelation transition. In agreement with previous studies, we observe that the fractal dimension of clusters df = 1/ν increases with the number of particles.61 The limiting values of the Flory exponent for s → ∞ (which apply for about s > 102) are plotted as a function of
. The analysis was performed at ca = 1.5 μM and cp = 1.27 μM, which are values close to (slightly below) the gelation transition. In agreement with previous studies, we observe that the fractal dimension of clusters df = 1/ν increases with the number of particles.61 The limiting values of the Flory exponent for s → ∞ (which apply for about s > 102) are plotted as a function of ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) in Fig. 6c (see also Table S1 in ESI†).
in Fig. 6c (see also Table S1 in ESI†).
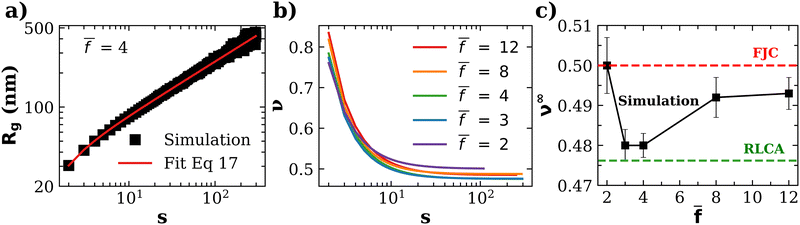 | ||
Fig. 6 (a) An example of the scaling of the gyration radius of clusters against the number of particles in the cluster, illustrating the fit with eqn (17) (red line, details in ESI†). (b) The “local” Flory coefficient ν(s) defined in eqn (16). (c) The limiting value of the Flory exponent ν∞ ≡ ν(s → ∞) against the average functionality ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) . . | ||
The variation of ν∞ with ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) is not large, yet, it reflects relevant aspects of cluster formation. Notably, values of ν∞ lie between that of reaction limited cluster aggregation (RLCA) νRLCA = 1/2.1 ≈ 0.476 and a Gaussian freely jointed chain (FJC) νFJC = 0.5.
is not large, yet, it reflects relevant aspects of cluster formation. Notably, values of ν∞ lie between that of reaction limited cluster aggregation (RLCA) νRLCA = 1/2.1 ≈ 0.476 and a Gaussian freely jointed chain (FJC) νFJC = 0.5.
Clusters obtained for ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) = 2 are Gaussian-like (ν∞ ≃ 0.5). If the polymerization were linear, this would correspond to new bonds completely uncorrelated with the previous bond direction. However, according to the binomial distribution in eqn (1), for
= 2 are Gaussian-like (ν∞ ≃ 0.5). If the polymerization were linear, this would correspond to new bonds completely uncorrelated with the previous bond direction. However, according to the binomial distribution in eqn (1), for ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) = 2, a percentage of the IONPs present f > 2, which leads to the formation of branches. Another subset presents f = 1, leading to dead-ends in some of the branches. To investigate the effect of branches and dead-ends, we performed simulations with a single functionality f =
= 2, a percentage of the IONPs present f > 2, which leads to the formation of branches. Another subset presents f = 1, leading to dead-ends in some of the branches. To investigate the effect of branches and dead-ends, we performed simulations with a single functionality f = ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) = 2 for all IONPs. In such a case we obtained an exponent corresponding to an expanded chain (self-avoiding walk) ν ≈ 0.6. Therefore, for a polydisperse functionality with
= 2 for all IONPs. In such a case we obtained an exponent corresponding to an expanded chain (self-avoiding walk) ν ≈ 0.6. Therefore, for a polydisperse functionality with ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) = 2, the origin of more compact assemblies (ν ≈ 0.5) is the formation of branches f ≥ 3 and dead-ends f = 1. For
= 2, the origin of more compact assemblies (ν ≈ 0.5) is the formation of branches f ≥ 3 and dead-ends f = 1. For ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) = 3 and 4, we found even more compact structures with ν∞ = 0.473, quite close to the RLCA value 0.476. RLCA corresponds to a bond formation which is hampered by a repulsive barrier, so that the probability of forming bond of two “colliding” particles is smaller than one. In the present scenario, such a barrier is purely entropic, corresponding to a smaller number of available spots to create a new bond in these clusters. As shown in Fig. 5, for
= 3 and 4, we found even more compact structures with ν∞ = 0.473, quite close to the RLCA value 0.476. RLCA corresponds to a bond formation which is hampered by a repulsive barrier, so that the probability of forming bond of two “colliding” particles is smaller than one. In the present scenario, such a barrier is purely entropic, corresponding to a smaller number of available spots to create a new bond in these clusters. As shown in Fig. 5, for ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) = 3 (and 4), the clusters present the largest number of neighbors (e.g. 〈NN〉∞ ≈ 2.4 for ca = 1.5 μM). Remarkably, this number is quite close to the average accessible receptors per particle 〈facc〉 (Fig. 4). This implies that the chance to find a new available site in clusters with
= 3 (and 4), the clusters present the largest number of neighbors (e.g. 〈NN〉∞ ≈ 2.4 for ca = 1.5 μM). Remarkably, this number is quite close to the average accessible receptors per particle 〈facc〉 (Fig. 4). This implies that the chance to find a new available site in clusters with ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) = 3 or 4, is smaller than for larger
= 3 or 4, is smaller than for larger ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) . For instance, for
. For instance, for ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) = 12, a new particle joining a cluster may encounter up to 〈facc〉 ≈ 5 available receptors, while particles in a cluster only typically have up to 〈NN〉∞ ≈ 2.25 neighbors (Fig. 5b). At very large
= 12, a new particle joining a cluster may encounter up to 〈facc〉 ≈ 5 available receptors, while particles in a cluster only typically have up to 〈NN〉∞ ≈ 2.25 neighbors (Fig. 5b). At very large ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) , the particle corona is filled with receptors and, for large bonding probability p ∼ 1, one expects to approach the diffusion limited (DLCA) scenario (colliding particles form a bond with probability one, leading to more open structures νDLCA = 1/1.8 ≈ 0.56). Consistently with this line, the value of ν∞ gradually increases for
, the particle corona is filled with receptors and, for large bonding probability p ∼ 1, one expects to approach the diffusion limited (DLCA) scenario (colliding particles form a bond with probability one, leading to more open structures νDLCA = 1/1.8 ≈ 0.56). Consistently with this line, the value of ν∞ gradually increases for ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) > 4, reaching 0.493 for
> 4, reaching 0.493 for ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) = 12 (and p = 0.2), as shown in Fig. 6.
= 12 (and p = 0.2), as shown in Fig. 6.
3.5 Distribution of IONP clusters
A more detailed level of description concerns n(s), the distribution of clusters of mass s (S.3, eqn (S20), ESI†). To analyze n(s) we deploy the analytical predictions for a Bethe lattice61 (summarized in the S.1, ESI†). A Bethe's lattice is characterized by particles having an equal number of linkers f and a probability p of forming a link. Bethe's theory derives an analytical relation for the probability density of forming clusters with s particles,| n(s) = gsps−1(1 − p)2+s(f−2) | (18) |
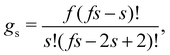 | (19) |
In order to use Bethe's theory as a template for our system, we fix the probability of forming a bond p, defined in eqn (12). Although steric hindrance limits the number of available receptors, these unusable linkers can also trap analytes, reducing the number of bond-forming analytes to a fraction, c(acc)a = ca〈facc〉/![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) . Therefore, consideration of steric hindrance leads to the same binding probability as eqn (12), p = 2c(acc)a/(〈facc〉cp).
. Therefore, consideration of steric hindrance leads to the same binding probability as eqn (12), p = 2c(acc)a/(〈facc〉cp).
In our system, deviations from Bethe's lattice are certainly expected. First, particles have a different functionalities f, determined by a binomial distribution with mean ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) . Secondly, structures with cyclic bonds are formed, and become significant as the available number of bonds increases. Finally, due to steric hindrance the average functionality is gradually reduced with the local particle and bond concentration, becoming 〈facc〉 <
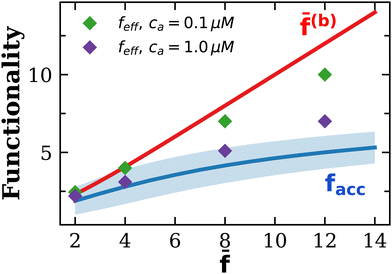
. Secondly, structures with cyclic bonds are formed, and become significant as the available number of bonds increases. Finally, due to steric hindrance the average functionality is gradually reduced with the local particle and bond concentration, becoming 〈facc〉 < ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) (Fig. 4). In order to compare with simulation results for n(s), we will abuse Bethe's theory and insert a real number as the “effective valence” feff in the analytical relation for n(s), eqn (18) (we note however that p is fixed, by eqn (12)). As p increases, cyclic-bonding structures become more frequent, as revealed by a significant deviation in the mean number of neighbors per particle, with respect Bethe's lattice (see 〈NN〉 in Fig. 5). At high bond concentration, steric hindrance gradually leads to the limit of accessible receptors. Therefore the effective functionality feff (fitting n(s) viaeqn (18) needs to decrease with ca, within the range 〈facc〉 ≤ feff ≤
(Fig. 4). In order to compare with simulation results for n(s), we will abuse Bethe's theory and insert a real number as the “effective valence” feff in the analytical relation for n(s), eqn (18) (we note however that p is fixed, by eqn (12)). As p increases, cyclic-bonding structures become more frequent, as revealed by a significant deviation in the mean number of neighbors per particle, with respect Bethe's lattice (see 〈NN〉 in Fig. 5). At high bond concentration, steric hindrance gradually leads to the limit of accessible receptors. Therefore the effective functionality feff (fitting n(s) viaeqn (18) needs to decrease with ca, within the range 〈facc〉 ≤ feff ≤ ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) . A way to estimate feff is to combine the information about the fractal dimension of the clusters Rg(s) ∼ sν and the cluster size distribution n(s;feff,p) in eqn (18): the effective functionality feff should recover the experimental trends for the average cluster size:
. A way to estimate feff is to combine the information about the fractal dimension of the clusters Rg(s) ∼ sν and the cluster size distribution n(s;feff,p) in eqn (18): the effective functionality feff should recover the experimental trends for the average cluster size: 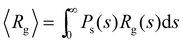 , where Ps(s) = sn(s)/C is the probability of a particle being in a cluster of size s and
, where Ps(s) = sn(s)/C is the probability of a particle being in a cluster of size s and 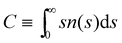 . Numerical solution of this inverse problem leads to values of feff which are consistent with those derived from direct fitting of n(s) (see below). In particular, feff decreases with ca, going from
. Numerical solution of this inverse problem leads to values of feff which are consistent with those derived from direct fitting of n(s) (see below). In particular, feff decreases with ca, going from ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) to 〈facc〉. Note that this procedure is also a fast and useful way to approximate n(s) from very limited information (e.g. from the average cluster size), an idea already used in ref. 63. However, we need to verify that the shape of n(s) is indeed recovered by eqn (18). To that end, we calculate n(s) from BD simulations providing a direct and more accurate estimation of feff.
to 〈facc〉. Note that this procedure is also a fast and useful way to approximate n(s) from very limited information (e.g. from the average cluster size), an idea already used in ref. 63. However, we need to verify that the shape of n(s) is indeed recovered by eqn (18). To that end, we calculate n(s) from BD simulations providing a direct and more accurate estimation of feff.
![[f with combining macron]](https://www.rsc.org/images/entities/b_i_char_0066_0304.gif) = 2.
The case
= 2.
The case ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) = 2 is qualitatively different from
= 2 is qualitatively different from ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) > 2 and deserves a separate discussion. Fig. 7a–d shows simulation results for n(s) for different concentration of analytes: from low concentration ca = 0.1 μM up to the balanced mixture ca = cp = 1.27 μM. Even at ca = 0.1 μM (low binding probability) the IONPs cluster distribution for
> 2 and deserves a separate discussion. Fig. 7a–d shows simulation results for n(s) for different concentration of analytes: from low concentration ca = 0.1 μM up to the balanced mixture ca = cp = 1.27 μM. Even at ca = 0.1 μM (low binding probability) the IONPs cluster distribution for ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) = 2 differ from the Bethe lattice with functionality f = 2 (blue lines), presenting a larger population of large clusters and a deviation from the exponential trend. For
= 2 differ from the Bethe lattice with functionality f = 2 (blue lines), presenting a larger population of large clusters and a deviation from the exponential trend. For ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) = 2, these deviations from the Bethe's scenario are due to the dispersion in the receptor number f. We confirmed this statement upon comparison with simulations of mono-disperse case (f = 2 for all IONPs) which showed n(s) ∼ exp[−s/ξ(p)] with ξ(p) in quite good agreement with Bethe's prediction up to ca ≈ 1 μM (however, percolation was not observed due to loop formation). According to the binomial distribution of receptors P(f = 0) = e−
= 2, these deviations from the Bethe's scenario are due to the dispersion in the receptor number f. We confirmed this statement upon comparison with simulations of mono-disperse case (f = 2 for all IONPs) which showed n(s) ∼ exp[−s/ξ(p)] with ξ(p) in quite good agreement with Bethe's prediction up to ca ≈ 1 μM (however, percolation was not observed due to loop formation). According to the binomial distribution of receptors P(f = 0) = e−![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) (see eqn (1), and inset of Fig. S4, ESI†) which for
(see eqn (1), and inset of Fig. S4, ESI†) which for ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) = 2, means that a significant fraction (13%) of particles have no linker f = 0, and will never polymerize. Excluding these impaired particles (f = 0) from the ensemble of
= 2, means that a significant fraction (13%) of particles have no linker f = 0, and will never polymerize. Excluding these impaired particles (f = 0) from the ensemble of ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) = 2, leads to an average of
= 2, leads to an average of ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) (b) = 2.31 receptors per binding-viable particles (f > 0). Note that this effect is already negligible for
(b) = 2.31 receptors per binding-viable particles (f > 0). Note that this effect is already negligible for ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) = 4 as,
= 4 as, ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) (b)(4) = 4.07. One thus expects that feff (2) > 2, even at low ca, which is consistent with the deviation of n(s) from the single exponential (Fig. 7a). Notably, the generalized Bethe relation with a real effective valence feff (red lines) nicely matches all the observed distributions. As expected, the values of feff obtained from the best fit to eqn (18) (Fig. 7a–d) decrease as ca approaches
(b)(4) = 4.07. One thus expects that feff (2) > 2, even at low ca, which is consistent with the deviation of n(s) from the single exponential (Fig. 7a). Notably, the generalized Bethe relation with a real effective valence feff (red lines) nicely matches all the observed distributions. As expected, the values of feff obtained from the best fit to eqn (18) (Fig. 7a–d) decrease as ca approaches  ; being feff ≈
; being feff ≈ ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) (b) at moderate ca, and approaching the high cluster density limit 〈facc〉 ≃ 1.9 close to
(b) at moderate ca, and approaching the high cluster density limit 〈facc〉 ≃ 1.9 close to  .
.
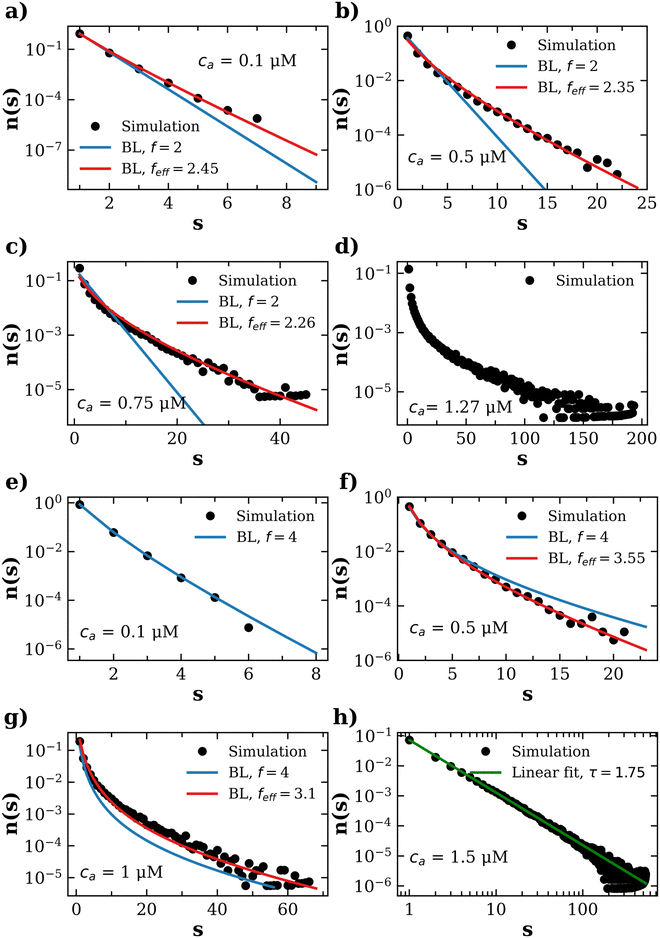 | ||
Fig. 7 Cluster distributions obtained for IONP concentration cp = 1.27 μM and average receptors per IONP equal to ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) = 2 (a–d) and = 2 (a–d) and ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) = 4 (e–h). Symbols correspond to simulation results, blue lines to the Bethe's lattice (BL) with single functionality f = = 4 (e–h). Symbols correspond to simulation results, blue lines to the Bethe's lattice (BL) with single functionality f = ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) and red lines are the best fits using Bethe's analytical relation eqn (18) with an effective functionality feff. For and red lines are the best fits using Bethe's analytical relation eqn (18) with an effective functionality feff. For ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) = 4, results for ca = 1.5 μM correspond to the onset of percolation. = 4, results for ca = 1.5 μM correspond to the onset of percolation. | ||
For the balanced mixture  the binding probability is p = pc = 1 and Bethe's theory with f = 2, predicts the formation of a large unique chain in an infinite time.22,23 However, for
the binding probability is p = pc = 1 and Bethe's theory with f = 2, predicts the formation of a large unique chain in an infinite time.22,23 However, for ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) = 2 the bioconjugated IONPs reached an equilibrium state with no infinite clusters. Consistently with the absence of percolation transition, Fig. 7d shows that the distribution n(s) obtained for
= 2 the bioconjugated IONPs reached an equilibrium state with no infinite clusters. Consistently with the absence of percolation transition, Fig. 7d shows that the distribution n(s) obtained for  presents an exponential decay for s > 50. As verified by comparison with the mono-disperse f = 2, for
presents an exponential decay for s > 50. As verified by comparison with the mono-disperse f = 2, for ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) = 2 we find formation of branches (particles with f > 2) and to a lesser extent loops. However, it should be noted that in the case of mixtures of patchy colloids (where saturation of available bonds is not a limiting factor, as it happens in linker-mediated aggregation), an infinitesimal fraction of f = 3 particles leads to percolation.24
= 2 we find formation of branches (particles with f > 2) and to a lesser extent loops. However, it should be noted that in the case of mixtures of patchy colloids (where saturation of available bonds is not a limiting factor, as it happens in linker-mediated aggregation), an infinitesimal fraction of f = 3 particles leads to percolation.24
![[f with combining macron]](https://www.rsc.org/images/entities/b_i_char_0066_0304.gif) = 4, 8, 12.
Fig. 7e–h shows simulation results for the distribution n(s) obtained from
= 4, 8, 12.
Fig. 7e–h shows simulation results for the distribution n(s) obtained from ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) = 4 and compare them with the best fit to the generalized Bethe's relation eqn (18). For
= 4 and compare them with the best fit to the generalized Bethe's relation eqn (18). For ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) > 2 the effect of receptor poly-dispersion becomes less important (e.g.
> 2 the effect of receptor poly-dispersion becomes less important (e.g. ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) ≃
≃ ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) (b)). And in this line, for
(b)). And in this line, for ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) = 4 we find that when the analyte concentration is small (ca = 0.1 μM, binding probability p ≈ 0.04), the cluster distribution is quite close to that produced by a Bethe lattice with f =
= 4 we find that when the analyte concentration is small (ca = 0.1 μM, binding probability p ≈ 0.04), the cluster distribution is quite close to that produced by a Bethe lattice with f = ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) , with n(s) being a single exponential. For ca = 0.5 μM (or p ≈ 0.2) steric hindrance and cyclic structures become relevant and n(s) starts to deviate from the Bethe lattice with f = 4. An excellent fit to n(s) is obtained using a smaller effective functionality feff = 3.55 into eqn (18). As ca is further increased and larger clusters are formed, steric hindrance tends to further reduce feff, becoming feff ≃ 3.1 for ca = 1 μM (p = 0.4), which is close to the high-concentration accessible limit 〈facc〉 ≈ 2.8. A similar outcome is found for the distributions for
, with n(s) being a single exponential. For ca = 0.5 μM (or p ≈ 0.2) steric hindrance and cyclic structures become relevant and n(s) starts to deviate from the Bethe lattice with f = 4. An excellent fit to n(s) is obtained using a smaller effective functionality feff = 3.55 into eqn (18). As ca is further increased and larger clusters are formed, steric hindrance tends to further reduce feff, becoming feff ≃ 3.1 for ca = 1 μM (p = 0.4), which is close to the high-concentration accessible limit 〈facc〉 ≈ 2.8. A similar outcome is found for the distributions for ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) = {8, 12} (ESI†) which can be also mapped to the effective Bethe's distribution. As
= {8, 12} (ESI†) which can be also mapped to the effective Bethe's distribution. As ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) becomes larger, however, the formation of loops becomes more probable and the effective functionality feff starts to deviate from
becomes larger, however, the formation of loops becomes more probable and the effective functionality feff starts to deviate from ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) at smaller values of ca.
at smaller values of ca.
Fig. 8 collects the results for the effective functionality against ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) , showing its upper
, showing its upper ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) (b) and lower 〈facc〉 boundaries. Values of feff for small analyte concentration ca = 0.1 μM (purple diamonds) approach the Bethe's scenario, where loops are unlikely to be formed and most of the receptors are accessible. At ca = 1.0 μM (green diamonds) loop formation and the steric hindrance within the larger clusters induce a decrease of feff to values much closer to the accessible limit facc.
(b) and lower 〈facc〉 boundaries. Values of feff for small analyte concentration ca = 0.1 μM (purple diamonds) approach the Bethe's scenario, where loops are unlikely to be formed and most of the receptors are accessible. At ca = 1.0 μM (green diamonds) loop formation and the steric hindrance within the larger clusters induce a decrease of feff to values much closer to the accessible limit facc.
![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) ≥ 4), the exponential tail becomes distorted and at the percolation threshold, n(s) fully exhibits a power law scaling. This transition is illustrated in Fig. 7h. Concerning the Fisher exponent τ governing the critical scaling n(s) ∼ s−τ, we find τ = 1.75 (green line in Fig. 7h. This value is smaller than the Fisher exponent for the Bethes lattice, which (S.1, ESI†) turns out to be independent on the valence (τBethe = 5/2). When compared with Bethes picture, our nanoclusters present a broader distribution close to the gel transition. This is expected considering that the possibility of forming multiple bonds between particles within the same cluster (rings, polyhedrons, etc.) enhances the diversity in cluster sizes, with respect the Bethe model.
≥ 4), the exponential tail becomes distorted and at the percolation threshold, n(s) fully exhibits a power law scaling. This transition is illustrated in Fig. 7h. Concerning the Fisher exponent τ governing the critical scaling n(s) ∼ s−τ, we find τ = 1.75 (green line in Fig. 7h. This value is smaller than the Fisher exponent for the Bethes lattice, which (S.1, ESI†) turns out to be independent on the valence (τBethe = 5/2). When compared with Bethes picture, our nanoclusters present a broader distribution close to the gel transition. This is expected considering that the possibility of forming multiple bonds between particles within the same cluster (rings, polyhedrons, etc.) enhances the diversity in cluster sizes, with respect the Bethe model.
It is possible to estimate the locus for the transition to gel phase by generalizing Bethe's prediction for the critical probability using the functionality at the accessible limit, pc = (〈facc〉 − 1)−1 = 2c(g)a/(![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) cp). This relation leads to,
cp). This relation leads to,
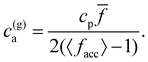 | (20) |
![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) = 4, 〈facc〉 ≈ 2.5 and cp is varied at fixed ca) we consistently observed formation of large structures only for p > pc = 0.66. In terms of ca (and fixed cp = 1.27 μM) for
= 4, 〈facc〉 ≈ 2.5 and cp is varied at fixed ca) we consistently observed formation of large structures only for p > pc = 0.66. In terms of ca (and fixed cp = 1.27 μM) for ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) = 4, 8 and 12 relation 20 provides the direct (sol–gel) transition at c(g)a = 1.41, 1.70 and 1.91 μM, respectively. These predictions are in quite good agreement with simulations and experiments. As shown in Fig. 2, the sol–gel transition takes place within the range cga ∈ (1.5–1.75] μM for
= 4, 8 and 12 relation 20 provides the direct (sol–gel) transition at c(g)a = 1.41, 1.70 and 1.91 μM, respectively. These predictions are in quite good agreement with simulations and experiments. As shown in Fig. 2, the sol–gel transition takes place within the range cga ∈ (1.5–1.75] μM for ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) = 4 and 8, while for
= 4 and 8, while for ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) = 12 it lies within cga ∈ (1.75–2.0] μM. Also, according to the prediction pc ≈ 0.66 for
= 12 it lies within cga ∈ (1.75–2.0] μM. Also, according to the prediction pc ≈ 0.66 for ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) = 4, the reverse gel–sol transition should take place for ca ≈ 3.4 μM which is in the range of Fig. 2. In line with the prediction of eqn (20), as
= 4, the reverse gel–sol transition should take place for ca ≈ 3.4 μM which is in the range of Fig. 2. In line with the prediction of eqn (20), as ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) is increased, the sol–gel transition takes places at slightly larger values of the analyte concentration. One possible reason for the small discrepancies observed between the predictions of eqn (20) and the simulation results could be the formation of loops, as discussed by Lindquist et al. for linker-mediated aggregation.27 These loops hinder the percolation of the system, thus requiring a higher concentration of analytes to reach the percolation transition.
is increased, the sol–gel transition takes places at slightly larger values of the analyte concentration. One possible reason for the small discrepancies observed between the predictions of eqn (20) and the simulation results could be the formation of loops, as discussed by Lindquist et al. for linker-mediated aggregation.27 These loops hinder the percolation of the system, thus requiring a higher concentration of analytes to reach the percolation transition.
To conclude, it is interesting to compare our aggregates with other linker-mediated aggregates. As an example, for ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) = 4, we observe the gelation transition for IONP packing fraction of ϕ = cp[m−3](4πa3/3) ≈ 0.085 with facc ≃ 2.8 and inverse binding energy kBT/Ebind ≈ 0.08. In the case of the so called “empty fluids”, formed by open percolating structures formed by limited valence colloids29 these values are quite consistent with the “empty fluid” phase of limited valence colloids.29 In the case of linker-mediated colloids27 where linkers and particles have the same size, for a volume fraction 0.09, the percolation thresholds were found around kBT/Ebind ≈ 0.11. In the case of polymer-linked colloids,15 the spinodal line obtained using dumbbells as linkers and patchy colloids with f = 6 and orthogonally placed receptors, is indeed very close to our result kBT/Ebind ≈ 0.06 for colloid volume fraction around 0.08.
= 4, we observe the gelation transition for IONP packing fraction of ϕ = cp[m−3](4πa3/3) ≈ 0.085 with facc ≃ 2.8 and inverse binding energy kBT/Ebind ≈ 0.08. In the case of the so called “empty fluids”, formed by open percolating structures formed by limited valence colloids29 these values are quite consistent with the “empty fluid” phase of limited valence colloids.29 In the case of linker-mediated colloids27 where linkers and particles have the same size, for a volume fraction 0.09, the percolation thresholds were found around kBT/Ebind ≈ 0.11. In the case of polymer-linked colloids,15 the spinodal line obtained using dumbbells as linkers and patchy colloids with f = 6 and orthogonally placed receptors, is indeed very close to our result kBT/Ebind ≈ 0.06 for colloid volume fraction around 0.08.
4 Conclusions
We reported on an experimental and theoretical study on predicting the formation of nanoparticle clustering driven by biomolecular recognition. These clusters strongly depend on molecular details, such as the size and binding energy of the receptor–analyte interaction, as well as the average number of receptors per particle![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) , and the concentration of nanoparticles cp and analytes ca. Iron oxide nanoparticles displaying superparamagnetic behaviour were decorated with molecular receptors which specifically bind to the target molecule (analyte protein) with selectivity and affinity (a dissociation constant of about 1 μM). We proposed a theoretical and computational approach and successfully validate it against experimental results for the average size and polydispersity index (PDI) of the so-formed IONP nanoclusters. The theoretical route consists in three separate steps: (i) distribute the receptors amongst nanoparticles with a fixed (experimentally controlled) average valence
, and the concentration of nanoparticles cp and analytes ca. Iron oxide nanoparticles displaying superparamagnetic behaviour were decorated with molecular receptors which specifically bind to the target molecule (analyte protein) with selectivity and affinity (a dissociation constant of about 1 μM). We proposed a theoretical and computational approach and successfully validate it against experimental results for the average size and polydispersity index (PDI) of the so-formed IONP nanoclusters. The theoretical route consists in three separate steps: (i) distribute the receptors amongst nanoparticles with a fixed (experimentally controlled) average valence ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) , (ii) distribute the analytes amongst the receptors according to the given set of parameters (cp, ca and
, (ii) distribute the analytes amongst the receptors according to the given set of parameters (cp, ca and ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) ) and (iii) perform Brownian dynamics simulations for the formation of bonds between IONPs, in the limit of irreversible binding. The IONPs are considered spherical particles with excluded volume interactions, having translational and rotational degrees of freedom, while receptor–analyte–receptor bonds consists on harmonic springs.
) and (iii) perform Brownian dynamics simulations for the formation of bonds between IONPs, in the limit of irreversible binding. The IONPs are considered spherical particles with excluded volume interactions, having translational and rotational degrees of freedom, while receptor–analyte–receptor bonds consists on harmonic springs.
Experimental results for the mean hydrodynamic size and PDI of clusters are reproduced with considerable accuracy. For ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) = 2, a peak in the cluster size and PDI takes place at the stoichiometric mixture
= 2, a peak in the cluster size and PDI takes place at the stoichiometric mixture 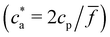 . For this ratio ca/cp = 2/
. For this ratio ca/cp = 2/![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) , the number of possible bonds is maximum. For
, the number of possible bonds is maximum. For ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) > 2 (and using cp = 1.27 μM) we found that the system gelates at a smaller analyte concentration
> 2 (and using cp = 1.27 μM) we found that the system gelates at a smaller analyte concentration 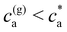 . Notably, the numerical predicted sol–gel transition precisely coincides with the precipitation of a pellet phase in experiments. In the second part of this work we have used Bethe's lattice theory as a template for an analysis on the statistics of the IONP clusters. We consider deviatoric effects from Bethe's scenario, such as the effect of receptor poly-dispersity, steric hindrance (some receptors are not accessible due to the “shadow” of neighboring IONPs) and the formation of cyclic structures in the clusters. We analyzed the fractal structure of the clusters, providing a “local” Flory exponent ν(s). Interestingly, we found a close relation between the fractal dimension df = 1/ν, the number of accessible receptors, and the average number of neighbors per IONP. Finally, we have studied the distribution of aggregates n(s) as a function of ca and average functionality
. Notably, the numerical predicted sol–gel transition precisely coincides with the precipitation of a pellet phase in experiments. In the second part of this work we have used Bethe's lattice theory as a template for an analysis on the statistics of the IONP clusters. We consider deviatoric effects from Bethe's scenario, such as the effect of receptor poly-dispersity, steric hindrance (some receptors are not accessible due to the “shadow” of neighboring IONPs) and the formation of cyclic structures in the clusters. We analyzed the fractal structure of the clusters, providing a “local” Flory exponent ν(s). Interestingly, we found a close relation between the fractal dimension df = 1/ν, the number of accessible receptors, and the average number of neighbors per IONP. Finally, we have studied the distribution of aggregates n(s) as a function of ca and average functionality ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) . Introducing a real effective functionality feff into Bethe's relation, allow us to excellently recover the measured cluster distributions. This effective valence feff decreases with the analyte concentration (i.e. with the binding probability) starting from f ≈
. Introducing a real effective functionality feff into Bethe's relation, allow us to excellently recover the measured cluster distributions. This effective valence feff decreases with the analyte concentration (i.e. with the binding probability) starting from f ≈ ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) at low ca towards feff ∼ 〈facc〉 as ca is increased. This analysis enabled us to estimate the effect of polydispersion in receptor number (note that P(f) is a binomial distribution), and the creation of branches and cyclic structures. Notably, these two effects induce significant deviations between
at low ca towards feff ∼ 〈facc〉 as ca is increased. This analysis enabled us to estimate the effect of polydispersion in receptor number (note that P(f) is a binomial distribution), and the creation of branches and cyclic structures. Notably, these two effects induce significant deviations between ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) = 2 and the mono-valence f = 2 counterpart, even at low ca. For
= 2 and the mono-valence f = 2 counterpart, even at low ca. For ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) ≥4 a sol–gel transition is observed, characterized by a power-law dependence for the cluster size distribution ns(s) ∼ s−τ. Generalizing Bethe's lattice prediction, we derived a relation (eqn (20)) which correctly forecast the locus of the sol–gel transition in the parameter space (ca, cp and
≥4 a sol–gel transition is observed, characterized by a power-law dependence for the cluster size distribution ns(s) ∼ s−τ. Generalizing Bethe's lattice prediction, we derived a relation (eqn (20)) which correctly forecast the locus of the sol–gel transition in the parameter space (ca, cp and ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) ). Interestingly, for
). Interestingly, for ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) = 4, a re-entrant transition towards gas phase occurs as ca is further increased, however this was not experimentally observed due to non-specific adsorption. Understanding the self-assembly of nanoparticles mediated by biomolecular recognition is essential to decipher their response under external fields, for instance the hysteresis cycles of bioconjugated magnetic nanoparticles under AC magnetometry. In a future work we will consider nanoclusters of bioconjugated ferromagnetic nanoparticles, where one expects that equilibrium structures will non-trivially depend on the interplay between the magnetic energy (dipolar interactions between particles) and the chemical energy of the bonds.
= 4, a re-entrant transition towards gas phase occurs as ca is further increased, however this was not experimentally observed due to non-specific adsorption. Understanding the self-assembly of nanoparticles mediated by biomolecular recognition is essential to decipher their response under external fields, for instance the hysteresis cycles of bioconjugated magnetic nanoparticles under AC magnetometry. In a future work we will consider nanoclusters of bioconjugated ferromagnetic nanoparticles, where one expects that equilibrium structures will non-trivially depend on the interplay between the magnetic energy (dipolar interactions between particles) and the chemical energy of the bonds.
Author contributions
Pablo Palacios: conceptualization, methodology (theory and simulations), software, writing-original draft, review and editing. Elena Sand-de Diego: methodology (experiments), review and editing. Raúl Pérez Peláez: software. A. L. Cortajarena: resources (analytes), review. Francisco J. Terán: conceptualization, methodology (experiments), resources (nanoparticles), review and editing. Rafael Delgado-Buscalioni: conceptualization, methodology (theory and simulations), writing original draft, review and editing.Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
This work has been partially funded by the Spanish Research Agencies (PID2020-117080RB-C51, PDC2021-121441-C21, PCI2019-103600,CEX2020-001039-S, PID2019-111649RB-I00 PID2020-117080RB-C53, MDM-2017-0720, RED2018-102626-T) and Comunidad de Madrid (NANOMAGCOST, S2018/NMT-4321). European COST Actions CA17115 (MyWave), and CA17140 (Nano2Clinic) are also acknowledged. ESD thanks Comunidad de Madrid for financial support (PEJ-2017-AI/BMD-7517). Authors thank Dr Patricia Pedraz for carefull acquisition of AFM images.Notes and references
- A. L. Hiddessen, S. D. Rodgers, D. A. Weitz and D. A. Hammer, Langmuir, 2000, 16, 9744–9753 CrossRef CAS.
- L. Zhai, A. Narkar and K. Ahn, Nano Today, 2020, 30, 100826 CrossRef CAS.
- A. R. Town, J. Taylor, K. Dawson, E. Niezabitowska, N. M. Elbaz, A. Corker, E. Garcia-Tuñón and T. O. McDonald, J. Mater. Chem. B, 2019, 7, 373–383 RSC.
- Y. Gao, A. Ahiabu and M. Serpe, ACS Appl. Mater. Interfaces, 2014, 6, 13749–13756 CrossRef CAS PubMed.
- Y. Wang, Z. Gao, Z. Han, Y. Liu, H. Yang, T. Akkin, C. Hogan and J. Bischof, Sci. Rep., 2021, 11, 898 CrossRef CAS.
- I. Isnaeni and Y. Herbani, J. Phys.: Conf. Ser., 2017, 817, 012039 CrossRef.
- N. A. Mahynski, E. Pretti, V. K. Shen and J. Mittal, Nat. Commun., 2019, 2028 CrossRef.
- S. Neupane, Y. Pan, S. Takalkar, K. Bentz, J. Farmakes, Y. Xu, B. Chen, G. Liu, S. Qian and Z. Yang, J. Phys. Chem. C, 2016, 121, 1377–1386 CrossRef.
- K. L. Gurunatha, A. C. Fournier, A. Urovas, M. Valerio-Lepiniec, V. Marchi, P. Minar and E. Dujardin, ACSNano, 2016, 10, 3176–3185 CrossRef CAS PubMed.
- S. Angioletti-Uberti, P. Varilly, B. M. Mognetti and D. Frenkel, Phys. Rev. Lett., 2014, 113, 128303 CrossRef PubMed.
- W. Rogers, J. Chem. Phys., 2020, 153, 124901 CrossRef CAS PubMed.
- K. Wu, R. Saha, D. Su, V. D. Krishna, J. Liu, M. C.-J. Cheeran and J.-P. Wang, ACS Appl. Nano Mater., 2020, 3, 9560–9580 CrossRef CAS.
- M. Heidenreich, J. M. Georgeson, E. Locatelli and L. Rovigatti, et al. , Nat. Chem. Biol., 2020, 16, 939–945 CrossRef CAS PubMed.
- X. Xiuyang, H. Hu, M. P. Ciamara and R. Ni, Sci. Adv., 2020, 6, eaaz6921 CrossRef.
- M. P. Howard, R. B. Jadrich, B. A. Lindquist, F. Khabaz, R. T. Bonnecaze, D. J. Milliron and T. M. Truskett, J. Chem. Phys., 2019, 151, 124901 CrossRef PubMed.
- M. P. Howard, Z. M. Sherman, A. N. Sreenivasan, S. A. Valenzuela, E. V. Anslyn, D. J. Milliron and T. M. Truskett, J. Chem. Phys., 2021, 154, 074901 CrossRef CAS PubMed.
- T. Kwon, T. A. Wilcoxson, D. J. Milliron and T. M. Truskett, J. Chem. Phys., 2022, 157, 184902 CrossRef CAS PubMed.
- M. S. Wertheim, J. Stat. Phys., 1986, 42, 459 CrossRef.
- P. Varilly, S. Angioletti-Uberti, M. M. Bortolo and D. Frenkel, J. Chem. Phys., 2012, 137, 094108 CrossRef PubMed.
- P. Flory, J. Am. Chem. Soc., 1941, 63, 3083–3090 CrossRef CAS.
- W. H. Stockmayer, J. Chem. Phys., 1943, 11, 45–55 CrossRef CAS.
- R. M. Ziff and G. Stell, J. Chem. Phys., 1980, 73, 3492–3499 CrossRef CAS.
- P. G. van Dongen and M. Ernst, J. Stat. Phys., 1984, 37, 301 CrossRef.
- D. de Las Heras, J. M. Tavares and M. Telo da Gama, Soft Matter, 2010, 7, 5615–5626 RSC.
- J. M. Tavares, G. C. Antunes, C. S. Dias, M. M. Telo da Gama and N. A. M. Araújo, Soft Matter, 2020, 16, 7513–7523 RSC.
- R. Teixeira, D. de Las Heras, J. Tavares and M. Telo da Gama, J. Chem. Phys., 2021, 155, 044903 CrossRef PubMed.
- B. A. Lindquist, R. B. Jadrich, D. J. Milliron and T. M. Truskett, J. Chem. Phys., 2016, 145, 074906 CrossRef CAS.
- F. Sciortino and E. Zaccarelli, Curr. Opin. Colloid Interface Sci., 2017, 30, 90–96 CrossRef CAS.
- E. Bianchi, J. Largo, P. Tartaglia, E. Zaccarelli and F. Sciortino, Phys. Rev. Lett., 2006, 97, 168301 CrossRef PubMed.
- D. Mendez-Gonzalez, M. Laurenti, A. Latorre, A. Somoza, A. Vázquez González, A. Negredo, E. López-Cabarcos, O. Calderón, S. Melle and J. Rubio Retama, ACS Appl. Mater. Interfaces, 2017, 9, 12272–12281 CrossRef CAS PubMed.
- L. Gloag, M. Mehdipour, D. Chen, R. Tilley and J. Gooding, Adv. Mater., 2019, 31, 1904385 CrossRef CAS PubMed.
- C. Pina-Coronado, Á. Martínez-Sobrino, L. Gutiérrez-Gálvez, R. Del Caño, E. Martínez-Periñán, D. García-Nieto, M. Rodríguez-Peña, M. Luna, P. Milán-Rois, M. Castellanos, M. Abreu, R. Cantón, J. C. Galán, T. Pineda, F. Pariente, Á. Somoza, T. García-Mendiola, R. Miranda and E. Lorenzo, Sens. Actuators, B, 2022, 369, 132217 CrossRef CAS PubMed.
- L. Gutiérrez, L. de la Cueva, M. R. del Árbol, E. Mazarío, S. de Bernardo, J. M. de la Fuente, M. P. Morales and G. Salas, Nanotechnology, 2019, 30, 112001 CrossRef.
- W. Zhou, K. Hu, S. Kwee, L. Tang, Z. Wang, J. Xia and X. Li, Anal. Chem., 2020, 92, 2739–2747 CrossRef CAS PubMed.
- F. Ghasemi, M. Hormozi-Nezhad and M. Mahmoudi, Nanoscale, 2018, 10, 6361–6368 RSC.
- P. Moitra, M. Alafeef, K. Dighe, M. Frieman and D. Pan, ACS Nano, 2020, 14, 7617–7627 CrossRef CAS PubMed.
- A. Latorre, C. Posch, Y. Garcimartín, S. Ortiz-Urda and A. Somoza, Chem. Commun., 2014, 50, 3018–3020 RSC.
- M. Donolato, P. Antunes, R. Bejhed, T. Torre, F. Østerberg, M. Strömberg, M. Nilsson, M. Strømme, P. Svedlindh, M. Hansen and P. Vavassori, Anal. Chem., 2014, 87, 1622–1629 CrossRef PubMed.
- A. Moyano, M. Salvador, J. Martínez-García, V. Socoliuc, L. Vekas, D. Peddis, M. Alvarez, M. Fernández, M. Rivas and M. C. Blanco-López, Anal. Bioanal. Chem., 2019, 411, 6615–6624 CrossRef CAS PubMed.
- J. Perez, F. J. Simeone, Y. Saeki, L. Josephson and R. Weissleder, J. Am. Chem. Soc., 2003, 125, 10192–10193 CrossRef CAS PubMed.
- J. M. Perez, L. Josephson, T. O'Loughlin, D. Högemann and R. Weissleder, Nat. Biotechnol., 2002, 20, 816–820 CrossRef CAS PubMed.
- K. Wu, J. Liu, D. Su, R. Saha and J.-P. Wang, ACS Appl. Mater. Interfaces, 2019, 11, 22979–22986 CrossRef CAS PubMed.
- I. Morales, R. Costo, N. Mille, J. Carrey, A. Hernando and P. de la Presa, Nanoscale Adv., 2021, 3, 5801–5812 RSC.
- C. Iacovita, J. Hurst, G. Manfredi, P. A. Hervieux, B. Donnio, J. L. Gallani and M. V. Rastei, Nanoscale, 2020, 12, 1842–1851 RSC.
- Y. You, S. Lim and S. Gunasekaran, ACS Appl. Nano Mater., 2020, 1900 CrossRef CAS.
- K. Wu, D. Su, R. Saha, J. Liu, V. K. Chugh and J. P. Wang, ACS Appl. Nano Mater., 2020, 3, 4972–4989 CrossRef CAS.
- M. E. Jackrel, R. Valverde and L. Regan, Protein Sci., 2009, 18, 762–774 CAS.
- R. P. Ilagan, E. Rhoades, D. F. Gruber, H.-T. Kao, V. A. Pieribone and L. Regan, FEBS J., 2010, 277, 1967–1978 CrossRef CAS PubMed.
- C. S. Dias, C. A. Custódio, G. C. Antunes, M. M. Telo da Gama, J. F. Mano and N. A. M. Araújo, ACS Appl. Mater. Interfaces, 2020, 12, 48321–48328 CrossRef CAS.
- P. Kloeden and E. Platen, The Numerical Solution of Stochastic Differential Equations, Springer, Berlin, Heidelberg, 1992, vol. 23 Search PubMed.
- A. Vázquez-Quesada and R. Delgado-Buscalioni, Phys. Rev. Fluids, 2020, 5, 053301 CrossRef.
- J. D. Weeks, D. Chandler and H. C. Andersen, J. Chem. Phys., 1971, 54, 5237–5247 CrossRef CAS.
- S. Delong, F. Balboa Usabiaga and A. Donev, J. Chem. Phys., 2015, 143, 144107 CrossRef PubMed.
- T. Evensen, S. Naess and A. Elgsaeter, Macromol. Theory Simul., 2008, 17, 403–409 CrossRef CAS.
- W. R. Hamilton, London, Edinburgh Dublin Philos. Mag. J. Sci., 1844, 25, 10–13 CrossRef.
- N. Rösch, Int. J. Quantum Chem., 1987, 32, 401 CrossRef.
- R. P. Peláez, Universally Adaptable Multiscale Molecular Dynamics, https://github.com/RaulPPelaez/UAMMD.
- J. G. Kirkwood, J. Polym. Sci., Part B: Polym. Phys., 1996, 34, 597–610 CrossRef.
- G. T. Nolan and P. Kavanagh, Powder Technol., 1992, 72, 149 CrossRef CAS.
- M. Fixman, J. Chem. Phys., 1962, 36, 306–310 CrossRef CAS.
- D. Liu, W. Zhou, X. Song and Z. Qiu, Fract. Fractional, 2017, 1, 12 CrossRef.
- M. E. Fisher, Phys. Physique Fizika, 1967, 3, 255–283 CrossRef.
- J. Tavares, P. Teixeira, M. M. Telo da Gama and F. Sciortino, J. Chem. Phys., 2010, 132, 234502 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3sm00536d |
| ‡ Here, we ascribe this percolation transition to a gel phase, although, viscoelastic characterization of the condensed phase were not performed. |
| This journal is © The Royal Society of Chemistry 2023 |