Rheology of a 2D granular film

Abstract

We study experimentally the rheology of a macroscopic particle-laden soap film, designated as a “Granular Film”, in the simple shear configuration. Macroscopic particles are dispersed in a soap film, while being large enough that they bridge both fluid interfaces. We simultaneously perform macroscopic rheological measurements with a classical rheometer and investigate interactions at the particle scale with a camera underneath the film. The determination of the velocity field of the grains reveals the presence of an inhomogeneous shear within the granular film. Trying to correlate both measurements unveils the non-locality of the rheology of the granular film: similar to what has been observed in a dry granular material, we find an highly-sheared zone close to the moving wall contrasting with a large quasistatic area. This behavior can be accounted for through extended kinetic theory and correlated with a transition in the dominant component of the stress.

---

1 Introduction

Particle-laden interfaces are far from uncommon in nature. The stabilization effect of adding solid particles on such interfaces¹ has always been used by animals for instance against natural disasters² or as a reproductive strategy.³ Particle laden interfaces are also ubiquitous in industry (e.g. oil recovery,^4,5 filtration processes,⁶ armored drops used as microreactors⁷ and for liquid manipulation⁸) for which the interface stabilisation effect might be either sought or fought. Due to their countless applications, since the pioneering works of Ramsden⁹ and Pickering,¹⁰ numerous studies have been devoted to understanding the mechanical behavior of particle laden interfaces.^11–14 Most of the studies have dealt with colloidal particles at a single interface.^15–17 They have shown that particle laden interface stability depends on the particle fluid contact angle, surface tension and shear stress. Energetic transition has increased the interest for interfacial composite materials^18–20 such as concrete foams,^21–23 where particles might be larger than the liquid film thus bridge both interfaces, making particle-laden films. During the foaming process, to create particle stabilized foams, the interfaces are highly stretched and sheared. Recent studies^24–26 have shown that the mechanical properties of particle-laden films differ from those of single particle laden interfaces, though the origin of the differences remains unclear. From a fundamental point of view, particle-laden films consist of particles dispersed in a continuous liquid phase that are subject to capillary attractive forces,²⁷ and might belong to the class of attractive granular media.²⁸ Many studies have been devoted to this class of material;^29–31 most are numerical and little is known from an experimental point of view.³² Moreover the capillary interactions between particles trapped in a soap film differ from the single interface problem.³³ Therefore understanding the behavior of particle-laden films requires well-controlled experiments of sheared and stretched particle laden soap films. In a recent paper Timounay et al.³⁴ inferred from particle diffusion the effective viscosity of a particle-laden soap film in a compression flow.

In this letter we report quantitative rheological measurements of particle-laden soap films in a simple shear configuration. We first show that in this configuration and for small shear-rates, particle-laden soap films don't exhibit viscous behavior but are more likely granular media. In the second part we highlight the inhomogeneous nature of the flow linked to the non-locality of the rheology of the material. While a hydrodynamic model in the framework of kinetic theory renders the inhomogeneity of the flow, it also gives a microscopic interpretation of the inter-particulate interactions and delimits two co-existing flow regimes in two regions of the granular film. We compute the density probability functions of elementary strains in the two zones and reveal two different forms of scaling, suggesting a change in the nature of the interactions between particles.

From a rheological point of view, for a 3D dense granular material, a single dimensionless inertial number can be used to fully describe the rheological behavior of the flowing material, where [small gamma, Greek, dot above]_{[small script l]} is the local shear rate, P is the confining pressure, d is the particle diameter, and ρ is their density. This dimensionless number is related to the effective friction coefficient μ = τ/P, where τ is the shear stress, and the packing fraction ϕ, through local constitutive laws.^35–38 However in many cases of globally-sheared granular materials, a quasistatic region appears and is attributed to a non-local effect. In these situations, the local constitutive law for granular materials is no longer valid and several models have been established to describe this non-locality.^39–45

Similarly, for granular films, one can build an inertial number that compares a microscopic characteristic rearrangement time t_c to the solicitation time 1/[small gamma, Greek, dot above]_l. Given that the only stress scale results from the surface tension of the soap film χ, the confining pressure in the granular film is p = σ/d with σ = χ cos(ζ) where ζ is the contact angle between the liquid and the particles. The microscopic time then assumes the form and one can define a capillary inertial number .

2 Experimental methods

2.1 Fluid and particles

Particle-laden soap films are obtained through extraction from a granular raft: silanized polystyrene spheres of diameter d = 80 μm and wetting contact angle ζ ≈ 80° are spread on a surfactant solution of Tetradecyl Trimethyl Ammonium Bromide (TTAB) water and glycerin that almost matches the density of the particles. There is little to no leeway in the surface tension allowing for an experimentally stable soap film,^46,47 we thus exceed the CMC leading to a value of χ = 34 mN m⁻¹. Then a cylindrical frame is dipped in the solution, piercing the raft, and is taken out. A soap film forms between the frame and the raft pulling out a great number of particles. It creates a dense monolayer of grains, trapped by the surface tension and large enough to bridge both liquid–air interfaces of the film (Fig. 1a), that we call a granular film. This method produces little variation of the granular film packing fraction ϕ (around 0.77). The detection of particles during the experiment allowed us to determine that there is no spatial variation of the surface fraction, with a precision of 1%.

Fig. 1 (a) Sketch of the experimental setup: an annular granular film is sheared in a rheometer. (b) Velocity field for an imposed velocity of Ω = 0.1 Hz using DIC software. (c) Normalized velocity profile v as a function of the normalized distance s inside the gap. The solid lines are fits deduced from eqn (3). Colors and symbols refer to the ones used in the inset, with colors referring to the velocity. () [small gamma, Greek, dot above]_m = 1.6 s⁻¹μ = 0.53, () [small gamma, Greek, dot above]_m = 0.55 s⁻¹μ = 0.46, () [small gamma, Greek, dot above]_m = 0.17 s⁻¹μ = 0.41, () [small gamma, Greek, dot above]_m = 0.06 s⁻¹μ = 0.31, and () [small gamma, Greek, dot above]_m = 0.02 s⁻¹μ = 0.21. Inset: Shear stress τ_s/σ as a function of mean strain for different films of solid fractions: (▽) ϕ = 0.76, (□) ϕ = 0.77, (△) ϕ = 0.78, (⋄) ϕ = 0.78 and (×) ϕ = 0.78.

2.2 Set-up

The cylindrical frame holding the granular film is then placed horizontally into a MCR 302 rheometer and pierced in its center with an hollow cylinder mounted on the rheometer axis, to constitute a Couette cell of inner radius R = 13.7 mm and gap e = 3.5 mm (Fig. 1a). Both cylinders are made coarse by gluing a thin layer of beads identical to the one used to form the granular films. After a pre-shear at a constant velocity of 6.3 rad s⁻¹ for 30 s, we impose constant velocities Ω of the inner wall which range from 10⁻³ to 10⁻¹ rad s⁻¹ for 100 s each, roamed in a random order to mask the effects of the aging of the film through evaporation. A permanent regime in the resisting torque measured is almost immediately registered. At these velocities, the flow radial pressure is five orders of magnitude lower than the capillary pressure scale.

2.3 Velocity field

Taking advantage of the 2D-nature of the granular film, we placed a camera underneath the cell to capture, through a glass window, the movement of the particles in the sheared film (Fig. 1(a)). The images are then processed with DIC software (DaVis, LaVision) to compute the instantaneous velocity field V(r,θ,t) of the granular film (Fig. 1(b)). Given the axisymmetry of the setup, the results are discussed in polar coordinates (r,θ) with a reduced radial position defined as s = (r − R)/e. In the permanent regime, we consider the mean velocity as 〈V(s,θ,t)〉 = V_r(s,θ)e_r + V_θ(s,θ)e_q, with e_r (resp. e_q) the unit vector in the radial (resp. orthoradial) direction and 〈·〉 the temporal average. Finally, the velocities will be discussed through their normalized values v = 〈V(s,θ,t)〉/V_w, with V_w = RΩ the velocity of the moving wall.

In the steady state, the velocity is found to be essentially azimuthal (V_r ≈ 0) and varying only radially (V_θ(s)e_q). From the local velocity profiles averaged over time and the azimuthal direction, we plot the normalized v(s) in Fig. 1c. All profiles are similar, without clear dependence on Ω: the velocity decreases drastically over a few grains away from the moving wall, to reach a quasi-zero, slowly decreasing the value well before the middle of the gap. This implies an inhomogeneity of the local shear rate [small gamma, Greek, dot above]_{[small script l]} = rd(V_θ/r)/dr ≃ dV_θ/dr. This inhomogeneity of the flow is a classical feature of dry granular media.^39,48–50

3 Results

3.1 Rheometry

Because of the 2D nature of the granular film, we define a surface stress τ_s that can be seen as a shear stress integrated over the thickness of the film. The rheological measurements (inset of Fig. 1c) show the evolution of the effective friction coefficient μ = τ_s/σ as a function of a mean capillary inertial number I_m = [small gamma, Greek, dot above]_mt_c where [small gamma, Greek, dot above]_m = V_w/e is the mean shear rate. It reveals that the state of stress is not directly dependent on the imposed velocity. This is coherent to what is usually seen in dry granular media at such low inertial number.^37,51 At this range of I_m, macroscopic and local models with a constant and homogeneous effective friction coefficient μ are not incompatible with inhomogeneous shear rates, but fail to predict them and their subsequent observed velocity profiles (Fig. 1c). To account for this localization of the flow, we introduce a diffusive quantity and we develop a hydrodynamic model in the framework of extended kinetic theory.

3.2 Hydrodynamic model

Several hydrodynamic models have been used in dry granular media to account for the localization of the flow by introducing a diffusive quantity. In the case of a homogeneous state of stress, kinetic theory can be successfully applied while providing a microscopic understanding of the velocity fluctuations.^{48,49,52–55} This introduces a granular temperature T and is related to the variance of velocity at a given point in space: T(s) = 〈V²(s,t)〉 − 〈V(s,t)〉². The flow is then self-induced: the temperature is generated by the forcing at the moving wall; which drags the particles in contact with it. It then increases locally the granular temperature, thus allowing for the neighboring particles to move in turn. This is propagated until a steady state is reached; the spatial distribution of T is then dictated by its evolution through the contacts between grains as it diffuses and dissipates.

In the present experiment, given the size of the setup (with a small gap approximation, e/2R ∼ 0.1) and the mechanical equilibrium, we assume the state of stress to be spatially homogeneous, so p and τ are uniform in the gap. The effective local viscosity then varies such that η ∼ 1/[small gamma, Greek, dot above]_{[small script l]}. Moreover, the kinetic theory of granular systems^48–50,56 gives the relationship between the effective viscosity η and the granular temperature T as η = η₀T^{−(2β−1)/2}, where η₀ depends on the pressure p, the density ρ, the mechanical properties and diameter d of the particles, which are all constant in the experiment, and a phenomenological exponent β equal to one in dilute and moderately dense systems, and larger than one in highly dense systems to account for the divergence of the viscosity (for instance in a dry granular shear flow, β ≃ 1.75^48,49). Thus it exists as a power-law linking T to [small gamma, Greek, dot above]_{[small script l]}: [small gamma, Greek, dot above]_{[small script l]} ∝ T^(2β−1)/2, valid in the inertial regime, where the collisions are of prime importance in the overall dynamics of the granular film. Calculating T from the measured velocity fields and plotting its square-root against the local capillary inertial number I_c, that we derive from the velocity profiles (Fig. 2a), we will consider a linear relationship between the two quantities (β = 1); I_c = [small gamma, Greek, dot above]_{[small script l]}t_c ≈ τT^1/2t_c/η₀.

Fig. 2 (a) Dimensionless velocity fluctuations T^1/2/(d/t_c) as a function of I_c for a film at different wall velocities Ω and for a fixed value ϕ = 0.78. The solid line corresponds to T^1/2/(d/t_c) = I_c^1/(2β−1), with β = 1. The dashed line corresponds to the critical value delimiting the inertial and quasistatic regime (b) I_c as a function of s. The same colors as in Fig. 1.

For all stresses, the spatial distribution of T is expected to obey a heat equation whose coefficients themselves are dependent on T. An equilibrium is found between diffusion (with a diffusive coefficient κ = κ₀T^−1/2), dissipation (with a dissipation coefficient ε = ε₀T^−1/2) and production through inner forces τ[small gamma, Greek, dot above]_{[small script l]}. κ₀ and ε₀ are solely dependent on grain properties (mechanical properties, diameter, density) and pressure p, which again are constant in the experiment. The hydrodynamic equation for T(s) then comes down to:

which, once integrated, gives the differential equation for v:where δ is a characteristic length that explicitly depends on applied stress, even though in a non-trivial way. In the velocity-independent regime for the shear stress, as is the case here, it is expected that the diffusion length does not vary. Particles are glued on both walls, leading to non-slip conditions v(0) = 1 and v(1) = 0. A third boundary condition comes from the consideration that at the static wall no heat is produced, and the granular film may be considered insulated (as per⁴⁸). Then dT/ds(1) = 0 and it follows:where δ is the only fitting parameter. This equation is fitted on the velocity profile in Fig. 1c with good agreement to the data, with δ/e = 0.17 ± 0.04. As the variation of the fitted diffusion length does not follow the trend set by the variation of the measured shear-stress through its ageing, this variation of length should be interpreted as the manifestation of statistical variations and experimental biases that disturb the expected behavior.

3.3 Quasistatic regime

Though the velocity profiles derived from eqn (3) are in good agreement with the experimental data (Fig. 1c), Fig. 2a displays more scattered data below a critical capillary inertial number and there is no unique relationship between T and [small gamma, Greek, dot above]_l anymore. For sheared dry granular material this feature is the signature of the transition between a collisional regime (for I > 10⁻¹) and an elastoplastic regime (for I < 10⁻²).^44,57–59 In this plastic regime velocity fluctuations are sustained through boundary conditions and local rearrangements happen occasionally and can be seen as elementary strains [small gamma, Greek, dot above]_i(s,θ,t). It is then interesting to describe and to understand the nature of the plastic regime in such attractive granular medium. To do so, we plot the probability density function of elementary strains at a given position (as proposed in ref. 44) normalized by its mean value [small gamma, Greek, dot above]_{[small script l]} (Fig. 3). At s = 0.1 and for 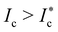for example, the PDF scale with [small gamma, Greek, dot above]_{[small script l]} and few negative strains are recorded compared to positive strains (Fig. 3a). This behavior is characteristic of the collisional regime of the flow and so 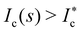. However, at s = 0.8, the PDFs show that almost half of the recorded strains occur in opposition to the forcing, inhibiting the onset of a macroscopic shear (Fig. 3b). This feature is a signature of the quasistatic regime and consequently (Fig. 2b). The lower I_c, the wider the PDF, thus showing that important strain events still occur.

Fig. 3 PDF of elementary strains [small gamma, Greek, dot above]_i normalized: by the mean strain [small gamma, Greek, dot above]_{[small script l]} in the flowing region (s = 0.1 and ) (a) and (d) and in the quasistatic regime (s = 0.8, ) (b) and (e), by [small gamma, Greek, dot above]_i^3/4 in the quasistatic regime (s = 0.8, ) (c) and (f). In (a)–(c), the colors represent the imposed wall velocity as per Fig. 1c. In (d)–(f), the particle diameter is varied: d = 40 μm (green), d = 80 μm (blue), and d = 250 μm (black).

In the quasistatic regime, the elastic energy is stored into film meniscus between grains and released through avalanche-like mechanisms.⁶⁰ During these events, due to the continuous liquid phase the elastic energy loss might be balanced by the viscous dissipation. Thus for 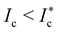, the granular might be described by a viscoplastic model. A theoretical and numerical study²⁹ based on the bubble model for foams⁶¹ predicts [small gamma, Greek, dot above]_i scales with [small gamma, Greek, dot above]_{[small script l]}^3/4. Rescaling the PDF of elementary strains for s = 0.8 by [small gamma, Greek, dot above]_{[small script l]}^3/4t_q^−1/4, where t_q is the characteristic viscous time different from t_c, shows that indeed they collapse on a single curve (Fig. 3c). Varying the particles diameter reveals that, while we recover the same behavior for collisional and the quasistatic regimes (Fig. 3d and e), the viscous time t_q does not depend on particle diameter d. Adapting the bubble model for foam to the 2D nature of the granular soap film, we define the viscous time t_q with the so-called surface viscosity η_s.⁶² Though no consensus exists on the value of surface viscosity, η_s ∈ [10⁻⁸, 10⁻⁵] Pa m s for soap films, we used in Fig. 3ft_q = η_s/χ = 10⁻⁴ s.

4 Conclusion

We have studied for the first time the behavior of particle-laden soap films in simple shear flow, revealing a rich rheology. When sheared, a dense granular soap film behaves like 2D attractive granular media. Within the range of applied velocity Ω the granular soap film is in a global plastic regime. The flow is well-described by the use of a capillary inertial number I_c that compares inertial effects to capillary attraction. It should be noted however that the evaluation of a Stokes number in the heterogeneous flow produces values between 10⁻⁴ and 10², not ruling out the existence of viscous effects in some regions of the film. Upon studying the velocity fluctuations we delimit 2 sub regimes: a collisional regime for I_c > 3 × 10⁻⁵ well described with the kinetic theory, and a quasistatic regime for I_c < 3 × 10⁻⁵ described with the bubble model for foam. The consistency of these findings has been checked for different sizes of particles, while the description of the quasistatic regime would benefit from further study on interfacial rheology.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We are grateful to L. Auffray, J. Amarni, A. Aubertin, C. Manquest and R. Pidoux for the development of the experimental setup. The authors thank N. Retailleau, Y. Khidas, X. Chateau, V. Langlois, O. Pitois and F. Rouyer for fruitful discussions. This work is supported by the project PhyGaMa ANR-19-CE30-0009-02 and “Investissements d'Avenir” LabEx Physique: Atomes Lumière Matière (ANR-10-LABX-0039-PALM).

References

1. B. P. Binks and R. Murakami, Nat. Mater., 2006, 5, 865–869.
2. N. J. Mlot, C. A. Tovey and D. L. Hu, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 7669–7673.
3. R. S. Seymour and J. P. Loveridge, J. Exp. Biol., 1994, 197, 31–46.
4. S. Kokal, SPE Prod. Facil., 2005, 20, 5–13.
5. B. P. Binks and B. Vishal, Adv. Colloid Interface Sci., 2021, 291, 102404.
6. S. Mehrabian, M. Bussmann and E. Acosta, Colloids Surf., A, 2015, 483, 25–35.
7. P. S. Bhosale and M. V. Panchagnula, Langmuir, 2010, 26, 10745–10749.
8. Y. Zhao, J. Fang, H. Wang, X. Wang and T. Lin, Adv. Mater., 2010, 22, 707–710.
9. W. Ramsden, Proc. R. Soc. London, 1904, 72, 156–164.
10. S. U. Pickering, J. Chem. Soc., Trans., 1907, 91, 2001–2021.
11. P. Cicuta and D. Vella, Phys. Rev. Lett., 2009, 102, 138302.
12. P. Petit, A.-L. Biance, E. Lorenceau and C. Planchette, Phys. Rev. E, 2016, 93, 042802.
13. C. Planchette, E. Lorenceau and A.-L. Biance, Soft Matter, 2018, 14, 6419–6430.
14. W. He, Y. Sun and A. D. Dinsmore, Soft Matter, 2020, 16, 2497–2505.
15. P. M. Kruglyakov, S. I. Elaneva and N. G. Vilkova, Adv. Colloid Interface Sci., 2011, 165, 108–116.
16. A. Maestro, E. Rio, W. Drenckhan, D. Langevin and A. Salonen, Soft Matter, 2014, 10, 6975–6983.
17. S. Li, Z. Li and P. Wang, Ind. Eng. Chem. Res., 2016, 55, 1243–1253.
18. A. Bala Subramaniam, M. Abkarian, L. Mahadevan and H. A. Stone, Nature, 2005, 438, 930.
19. A. B. Subramaniam, M. Abkarian, L. Mahadevan and H. A. Stone, Langmuir, 2006, 22, 10204–10208.
20. I. B. Liu, N. Sharifi-Mood and K. J. Stebe, Annu. Rev. Condens. Matter Phys., 2018, 9, 283–305.
21. K. Ramamurthy, E. K. Nambiar and G. I. S. Ranjani, Cem. Concr. Compos., 2009, 31, 388–396.
22. P. Petit, I. Javierre, P.-H. Jézéquel and A.-L. Biance, Cem. Concr. Res., 2014, 60, 37–44.
23. D. A. Abdourahman, A. Geniere, M. Auriol, F. Dalas, A.-L. Biance and M. Le Merrer, Soft Matter, 2021, 17, 2429–2438.
24. N. Denkov, I. Ivanov, P. Kralchevsky and D. Wasan, J. Colloid Interface Sci., 1992, 150, 589–593.
25. N. Taccoen, F. Lequeux, D. Z. Gunes and C. N. Baroud, Phys. Rev. X, 2016, 6, 011010.
26. Y. Timounay, O. Pitois and F. Rouyer, Phys. Rev. Lett., 2017, 118, 228001.
27. D. Vella and L. Mahadevan, Am. J. Phys., 2005, 73, 817–825.
28. G. Lois, J. Blawzdziewicz and C. S. O'Hern, Phys. Rev. Lett., 2008, 100, 028001.
29. B. P. Tighe, E. Woldhuis, J. J. Remmers, W. van Saarloos and M. van Hecke, Phys. Rev. Lett., 2010, 105, 088303.
30. E. Irani, P. Chaudhuri and C. Heussinger, Phys. Rev. Lett., 2014, 112, 188303.
31. D. J. Koeze, L. Hong, A. Kumar and B. P. Tighe, Phys. Rev. Res., 2020, 2, 032047.
32. O. Pitois and F. Rouyer, Curr. Opin. Colloid Interface Sci., 2019, 43, 125–137.
33. A. Yadav, E. J. Hinch and M. S. Tirumkudulu, Phys. Rev. Lett., 2019, 122, 098001.
34. Y. Timounay and F. Rouyer, Soft Matter, 2017, 13, 3449–3456.
35. GDR MiDi, Eur. Phys. J. E: Soft Matter Biol. Phys., 2004, 14, 341–365.
36. C. Cassar, M. Nicolas and O. Pouliquen, Phys. Fluids, 2005, 17, 103301.
37. P. Jop, Y. Forterre and O. Pouliquen, Nature, 2006, 441, 727–730.
38. F. Boyer, É. Guazzelli and O. Pouliquen, Phys. Rev. Lett., 2011, 107, 188301.
39. K. Reddy, Y. Forterre and O. Pouliquen, Phys. Rev. Lett., 2011, 106, 108301.
40. M. Bouzid, M. Trulsson, P. Claudin, E. Clément and B. Andréotti, Phys. Rev. Lett., 2013, 111, 238301.
41. M. Bouzid, A. Izzet, M. Trulsson, E. Clément, P. Claudin and B. Andreotti, Eur. Phys. J. E: Soft Matter Biol. Phys., 2015, 38, 125.
42. D. L. Henann and K. Kamrin, Phys. Rev. Lett., 2014, 113, 178001.
43. A. Thomas, Z. Tang, K. E. Daniels and N. Vriend, Soft Matter, 2019, 15, 8532–8542.
44. J. Gaume, G. Chambon and M. Naaim, Phys. Rev. Lett., 2020, 125, 188001.
45. K. Kamrin and G. Koval, Phys. Rev. Lett., 2012, 108, 178301.
46. P.-G. De Gennes, F. Brochard-Wyart and D. Quéré, Gouttes, bulles, perles et ondes, Belin Paris, 2002.
47. M. Pasquet, L. Wallon, P.-Y. Fusier, F. Restagno and E. Rio, Eur. Phys. J. E: Soft Matter Biol. Phys., 2022, 45, 101.
48. W. Losert, L. Bocquet, T. C. Lubensky and J. P. Gollub, Phys. Rev. Lett., 2000, 85, 1428–1431.
49. L. Bocquet, W. Losert, D. Schalk, T. C. Lubensky and J. P. Gollub, Phys. Rev. E, 2001, 65, 011307.
50. A. Seguin, Y. Bertho, P. Gondret and J. Crassous, Phys. Rev. Lett., 2011, 107, 048001.
51. F. Da Cruz, S. Emam, M. Prochnow, J.-N. Roux and F. Chevoir, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 72, 021309.
52. L. Bocquet, A. Colin and A. Ajdari, Phys. Rev. Lett., 2009, 103, 036001.
53. K. Kamrin, Front. Phys., 2019, 7, 116.
54. S. Kim and K. Kamrin, Phys. Rev. Lett., 2020, 125, 088002.
55. D. Berzi and J. T. Jenkins, Soft Matter, 2015, 11, 4799–4808.
56. A. Seguin and P. Gondret, Phys. Rev. E, 2017, 96, 032905.
57. G. Koval, J.-N. Roux, A. Corfdir and F. Chevoir, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 79, 021306.
58. O. Pouliquen and Y. Forterre, Philos. Trans. R. Soc., A, 2009, 367, 5091–5107.
59. S. Khamseh, J.-N. Roux and F. Chevoir, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 92, 022201.
60. J. Lin, E. Lerner, A. Rosso and M. Wyart, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 14382–14387.
61. D. J. Durian, Phys. Rev. Lett., 1995, 75, 4780.
62. I. Cantat, S. Cohen-Addad, F. Elias, F. Graner, R. Höhler, O. Pitois, F. Rouyer and A. Saint-Jalmes, Les mousses: structure et dynamique, Belin, 2010.

---