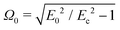DOI:
10.1039/D3SM00298E
(Paper)
Soft Matter, 2023,
19, 6825-6837
On the absence of collective motion in a bulk suspension of spontaneously rotating dielectric particles†
Received
8th March 2023
, Accepted 10th August 2023
First published on 14th August 2023
Abstract
A suspension of dielectric particles rotating spontaneously when subjected to a DC electric field in two dimensions next to a no-slip electrode has proven to be an ideal model for active matter [Bricard et al., Nature, 2013, 503, 95–98]. In this system, an electrohydrodynamic (EHD) instability called Quincke rotation was exploited to create self-propelling particles which aligned with each other due to EHD interactions, giving rise to collective motion on large length scales. It is natural to question whether a suspension of such particles in three dimensions will also display collective motion and spontaneously flow like bacterial suspensions do. Using molecular dynamics type simulations, we show that dielectrophoretic forces responsible for chaining in the direction of the applied electric field in conventional electrorheological fluids and the counter-rotation of neighboring particles in these chains prevent collective motion in suspensions undergoing spontaneous particle rotations. Our simulations discover that the fundamental microstructural unit of a suspension under Quincke rotation is a pair of counter-rotating spheres aligned in the direction of the electric field. We perform a linear stability analysis that explains this observation.
1. Introduction
Suspensions of particles dispersed in a liquid medium are commonly found in food, cosmetic, pharmaceutical and construction industries. Typical examples include milk, ink, paint, cement, slurries and blood.1,2 Adding particles to liquids imparts properties that are otherwise difficult or impossible to achieve. From a fluid mechanics viewpoint, the apparent viscosity of a suspension can be increased by incorporating solid particles or more viscous fluid droplets, or decreased by adding less viscous fluid droplets compared to the medium. In certain applications,3–5 it is desirable to tune the viscosity of a suspension by the application of an external field. If the constituent particles are susceptible to electric polarisation, they can respond to electric fields in addition to flow fields. These suspensions are termed electrorheological (ER) fluids. The first experiments on ER fluids date back to 1949, when Winslow6 applied an electric field to a concentrated suspension of semiconductive spheres with a high dielectric constant. Upon applying a shear flow, he observed an increase in the apparent viscosity of the suspension. For a detailed history of experimental and theoretical work on electrorheological phenomena, we refer the reader to review articles.7–9
Microscopically, ER fluids are two-phase materials, and our interest lies in the macroscopic properties of such complex media. Early studies focused on solid inclusions within solid materials. Determining the effective conductivity of a medium has been central in seminal investigations.10–13 In two-phase fluid mechanical problems, Einstein14 and Taylor15 examined the effective viscosity of suspensions with solid particles and fluid droplets, respectively. Incorporating gravity, which induces particle sedimentation, into these theoretical calculations adds considerable complexity. To address this, Batchelor16–18 devised the renormalization technique to account for hydrodynamic interactions among sedimenting particles and those exposed to shear flows.
In a fluid medium, suspended particles can also undergo motion due to electric and viscous forces. The aforementioned theoretical approaches do not apply when the suspension's structure is unknown and changes with time. In the case of ER fluids, accounting for both electric and hydrodynamic interactions significantly enhances the problem's complexity. Therefore, numerical simulations become necessary to unveil the microstructure of an ER suspension. Early computational investigations into ER fluids were conducted by Zukoski and co-workers.19,20 They employed the point-dipole approximation to compute the dielectrophoretic (DEP) force acting on particles while ignoring hydrodynamic interactions. This approximation enabled simulations of 100–300 particles in two dimensions. Bonnecaze and Brady,21,22 on the other hand, employed the more precise Stokesian dynamics method23,24 to calculate the effective conductivity of a medium containing solid inclusions. Subsequently, they solved the complete electrohydrodynamic (EHD) problem for ER fluids, capturing the microstructure of a suspension subjected to shear flow. These simulations considered higher-order electric and flow interactions, resulting in increased accuracy. However, the computationally intensive nature of the Stokesian dynamics method limited them to simulating a monolayer of 25 particles. Both research groups successfully replicated experimental findings.6,25,26 However, their assumption of instantaneously polarized particles is valid only when both particles and the fluid act as perfect dielectrics, leading to the neglect of the charge conservation equation in the Taylor-leaky dielectric model27 described below.
Allan28 and Mason29 reported anomalous observations on oblate drops that were inexplicable by existing theories and led Taylor29 to discard the notion that the suspending fluids could be treated as insulators. Despite the poor conductivity of the suspending fluids, Taylor recognized that even a slight conductivity would enable electric charge to reach the drop interface, leading to the formulation of the leaky dielectric model. ER fluids that have finite but relatively poor conductivity are well described by this model; refer to Saville30 for a comprehensive review. This model lacks electrokinetic effects that generate electroosmotic flows around a particle's surface. Additionally, magnetic fields arising from electric currents are absent, resulting in the exclusive coupling of electric and flow fields at the interface. The initial rigorous experiments on EHD interactions of spheres suspended in a fluid were conducted by Mason and co-workers.31,32
Surprisingly, an electrorotational instability, well described by the leaky dielectric model, had gone unnoticed by most researchers, including Rayleigh, Taylor and Mason. This phenomenon, discovered in 1896 by Quincke,33 is observed when a dielectric particle is suspended in a weakly conducting dielectric fluid such that τp > τf, where τ = ε/σ is the charge relaxation time, ε is the permittivity and σ is the conductivity. The subscripts ‘p’ and ‘f’ stand for the particle and fluid phases, respectively. When the applied electric field E0 = E0ez is sufficiently strong (greater than a critical value Ec), the particle starts rotating spontaneously.34–36 The direction of the angular velocity Ω is indeterminate but always remains perpendicular to the applied field, Ω·E0 = 0. In this configuration, the viscous torque is balanced by the electric torque acting on the particle. Quincke electrorotation of isolated drops has also been observed and studied in detail.37–42
A sequence of experiments investigating the dynamics of a suspension containing rigid dielectric particles under Quincke rotation was conducted by Lemaire and co-workers. Lobry and Lemaire43 were the first to report the behaviour of a suspension of weakly conducting PMMA particles subject to a Couette flow and a strong DC electric field, simultaneously. The particles were placed inside a parallel plate rheometer filled with a mixture of transformer oil and another dielectric liquid, Ugilec. A constant shear stress was applied to the upper plate for 20 seconds so that all particles rotated in the vorticity direction. The applied torque was subsequently gradually decreased to zero, facilitating the measurement of the plate's equilibrium angular velocity. Under strong fields, they observed that the apparent viscosity declined to zero, and the rheometer continued to rotate without the need for an external torque. These findings stand in contrast to the experiments of Winslow,6 Marshall1 et al.,25 Klingenberg and Zukoski IV26 and simulations of Klingenberg et al.19 and Bonnecaze and Brady22 where inclined chains between the electrodes were detected, leading to an augmentation in the apparent viscosity of the suspension.
In a different set of experiments, Lemaire et al.44 placed dielectric particles in a Poiseuille flow and reported an increase in flow rate when Quincke rotation occurred. The authors derived an expression for the flow rate but neglected EHD interactions. A discrepancy between experiment and theory was observed when the particle concentration was increased. The authors speculated that hydrodynamic interactions between particles could modify the spin direction as well as the rotation rate of individual particles so that the average spin rate of the whole suspension is reduced. They also speculated that the role played by dipolar interactions between particles in their experiments was to drive particle chaining as in conventional ER fluids without rotation. The emergence of layered structures perpendicular to the vorticity direction was also reported, which was attributed to the suspension's diminished flow rate. Through simulations, we will demonstrate the validity of both these speculations in the absence of a shear flow, with similar implications expected in its presence.
All the aforementioned experimental works were concerned with rheological properties of an ER fluid, which required application of a shear flow by definition. More recently, Quincke rotation has seen a resurgence of interest in the context of synthetic active matter. In these systems, the external field does not dictate the direction of collective motion. The fundamental constituent of active matter is a self-propelled particle powered by an external field but whose direction of motion remains indeterminate. This allows its direction to be influenced by its neighbours and the possibility of emergence of collective motion. Bricard et al.45,46 realized that the spontaneous rotation of a particle under Quincke rotation can be converted to spontaneous translation simultaneously when placed next to a no-slip wall, giving rise to so-called Quincke rollers. EHD interactions in collections of Quincke rollers were shown to give rise to macroscopic flocking dynamics. Recent experiments with the same physical system have also reproduced the run-and-tumble dynamics of bacteria47,48 and oscillatory dynamics.49 We also note experimental work that highlighted the short-ranged electrostatic interactions on collective motion of Quincke rollers,50 recent simulations of Quincke rollers using the smoothed profile method51 and isolated self-propelled particles in bulk powered by Quincke rotation.52,53
With the renewed interest in ER suspensions from an active matter perspective, we identify a significant gap in the existing literature. No experiments or simulations have explored a bulk fluid suspension of particles under Quincke rotation without the influence of an external flow. Our present study endeavors to address this void by focusing on a suspension of rigid spherical particles experiencing Quincke rotation. This paper addresses two fundamental inquiries. Firstly, does a system exhibiting collective motion in two dimensions alongside a surface replicate the same behavior in three dimensions? Secondly, do particle suspensions undergoing Quincke rotation indeed develop chains due to dipolar interactions, as speculated by Lemaire et al.,44 and, if so, are these chains stable?
To answer these questions, we extend our previous work54 on the EHD interaction of a pair of spherical particles under Quincke rotation to multiple particles (N = 500–1000). Our simulations may also be seen as extending those of Klingenberg et al.20 and Bonnecaze and Brady,55 as we use the complete leaky dielectric model which results in a dipole evolution equation depending on both permittivity and conductivity ratios rather than an instantaneous dipole solely dependent on the permittivity ratio. This work also complements the previously published results on suspensions subject to the combined electrohydrodynamic effects of dielectrophoresis and induced-charge electrophoresis (ICEP).56,57 We note the work of Hu et al.58 on the dynamics of a suspension of spontaneously spinning particles. They focused on the effect of a non-uniform electric field and did not address the questions raised here.
The paper is organized as follows. In Section 2, we describe the problem set up. We review the dynamics of a single particle under Quincke rotation in Section 2.1 and extend the governing equations for multiple particles capturing EHD interactions in Section 2.2. In Section 3, we discuss the relevant parameters for the simulations. In Section 3.1, we reproduce the familiar effect of DEP chaining when the applied electric field is below the critical value for Quincke rotation. This is followed by a discussion on the microstructure of a suspension under Quincke rotation in Section 3.2. We show that DEP forces in three dimensions that cause chaining or fibration in conventional ER fluids impede collective motion in ER fluids with Quincke rotation. In Section 3.3, we focus on isolated single chains and discuss their dynamics. In Section 3.4, we turn our attention to the fundamental building block of the suspension microstructure: a pair of counter-rotating particles, and we discuss its stability when it is aligned in parallel and perpendicular directions to the electric field. We end with conclusions and directions for future work in Section 4.
2. Problem formulation
Our physical system consists of spherical dielectric particles of radius a, permittivity εp, and conductivity σp, suspended in a dielectric fluid of permittivity εf, conductivity σf and viscosity η, subject to an electric field E0 = E0ez, see Fig. 1. We first review the dynamics of a single isolated spherical particle in an infinite fluid medium, before discussing the case of multiple interacting particles.
 |
| | Fig. 1 Schematic diagram showing a pair of spherical particles undergoing Quincke rotation at locations xα and xβ, respectively. The vector pointing from the centre of α to β is denoted as Rαβ = xβ − xα. The applied field is in the z-direction, E0 = E0ez. The translational and angular velocities of the spheres are denoted with U and Ω, respectively. Permittivity and conductivity are denoted as ε and σ. The particle and fluid phases are denoted with the subscripts ‘p’ and ‘f’, respectively. | |
2.1 Single particle in an infinite fluid
The dynamics of a single particle under Quincke rotation in an infinite fluid medium has been discussed by Jones34 and Turcu.35 The leaky dielectric model postulates the formation of charge 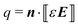 on the particle-fluid interface arising due to a jump in the Ohmic current
on the particle-fluid interface arising due to a jump in the Ohmic current  across the interface. Here, n is the outward unit normal vector on the surface, and
across the interface. Here, n is the outward unit normal vector on the surface, and  denotes the jump of variable f across the interface in the direction of n. The interfacial charge density gets convected with the interfacial velocity u, and thus obeys the conservation equation,
denotes the jump of variable f across the interface in the direction of n. The interfacial charge density gets convected with the interfacial velocity u, and thus obeys the conservation equation,| |  | (1) |
where ∇s = (I − nn)·∇ is the surface divergence operator. In the case when the rigid particle is rotating at an angular velocity Ω, its interfacial velocity is u = Ω × an. Note that Ω is unknown and must be found by balancing torques on the spherical particle. Upon expanding the electric potential on the basis of spherical harmonics, the surface charge conservation eqn (1) can be used to derive an evolution equation for the dipole moment induced in the particle:| |  | (2) |
Readers are referred to Das and Saintillan54 for details. The characteristic time scale at which the dipole relaxes to its steady state is the Maxwell–Wagner relaxation time, denoted as τMW, and εpf, σpf are the Clausius–Mossotti factors,36 given as,| |  | (3) |
The particle may experience a dielectrophoretic force and torque due to interaction of the induced dipole with the applied electric field and its gradient,| | | Fe = 4πεfP·∇E0, Te = 4πεfP × E0. | (4) |
The DEP force and torque will be resisted by the viscous force and torque acting on the spherical particle due to its motion,| | | Ff = −6πηaU, Tf = −8πηa3Ω, | (5) |
where U and Ω are the translational and rotational velocities, respectively. As the effect of inertia can be ignored owing to the particle's size, usually a few micrometers, electric and viscous forces and torques balance each other,| | | Fe + Ff = 0, Te + Tf = 0. | (6) |
Here, we only consider a uniform external field as a consequence of which a single isolated particle does not experience any DEP force, Fe = 0, and thus remains fixed in space. However, it can undergo rotation with an angular velocity obtained by balancing electric and viscous torques acting on the body,| | | −8πηa3Ω + 4πεfP × E0 = 0. | (7) |
At steady state, solving the governing eqn (2) and (7) for the angular velocity yields the trivial solution Ω = 0, implying no rotation. A second solution also exists with a constant non-zero angular velocity with magnitude| |  | (8) |
where Ec is the critical electric field strength above which Quincke rotation can take place,| |  | (9) |
The direction of rotation is indeterminate and depends on the initial condition. However, it can be shown to be always perpendicular to the electric field. For a given particle-fluid system, real values of Ec exist only if εpf > σpf. This simplifies to the condition required for Quincke rotation to take place, τp > τf.
2.2 Multiple particles subject to an electric field in a periodic domain
Next, we consider pairwise interactions of multiple particles subject to a uniform DC electric field when all the directions, x, y, z, are periodic, see Fig. 2. Periodicity is imposed to remove the effects of free boundaries. The particles colored in red are in the physical box highlighted with blue colored faces, while their periodic images are in green in the immediate neighbouring boxes. In total, there are 1 physical box and 8 + 9 + 9 periodic image boxes. The physical box is cubic with dimensions L × L × L.
 |
| | Fig. 2 Schematic diagram showing a collection of dielectric particles in a periodic domain subject to an electric field. The physical box is highlighted with blue faces and red spherical particles while their periodic images are shown in green color. Only the boxes in the (x, y) plane with z = −L/2 to z = L/2 to are shown. There are 9 additional periodic boxes behind and in front of the real box not shown in the diagram. Each particle in the physical box interacts with N − 1 particles in the physical box and 26N particles in the image boxes. | |
The detailed derivations capturing the EHD interactions of dielectric particles are given in Das and Saintillan54 and not repeated here for brevity. We simply extend the equations from a pair in an infinite domain to N particles in a periodic domain. The electric and flow field around a particle α are disturbed by the remaining N − 1 particles in the physical domain and 26N particles in the 26 periodic images boxes, denoted as β. We only retain leading-order interactions: point-dipole electric field and point-rotlet flow field interactions between the spherical particles. The dipole moment Pα of a spherical particle α ∈ [1, N] located at xα and rotating at an angular velocity Ωα satisfies the dipole moment evolution equation,
| |  | (10) |
where
Eα is the electric field experienced by it that includes perturbations
Eαβ due to the dipole moments of all the other spheres,
| |  | (11) |
where,
| |  | (12) |
Rαβ =
xβ −
xα is the vector pointing from the centre of the sphere
α to
β, and
![[R with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0052_0302.gif) αβ
αβ =
Rαβ/
Rαβ. We note that the last transient term in
eqn (10) was missing in our previous article.
54 This term is non-zero because the electric field
Eα around particle
α depends on the dipole moments
Pβ of neighboring particles and on the relative position vectors
Rαβ, which are functions of time. We neglect the latter effect in the following since it is of a higher order

. Corrections to the electric field,
Eα, due to higher-order multipole moments are of order

and hence neglected in
eqn (11). The torque balance equation provides us with an expression for the angular velocity of sphere
α in terms of the dipole moments of all the particles,
| |  | (13) |
The first term on the left hand side is the net electric torque experienced by sphere
α that takes into account electric interactions. The term
ωαβ takes into account hydrodynamic interactions due to the rotational flow field created by the motion of all other spheres. The vorticity due to the translational velocity of other spheres is of the order

and hence neglected. The rotlet flow at
xα due to a rotating sphere located at
xβ is,
| |  | (14) |
from which the disturbance vorticity is found as
| |  | (15) |
For a given set of
N spheres with known dipole moments, one needs to solve a linear system of equations to obtain the angular velocities
Ωα using
eqn (13). However, realising that we only need to retain the leading order term in the angular velocity of sphere
β,
eqn (15) simplifies to,
| | 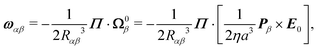 | (16) |
so that the angular velocity of each sphere can be computed directly for a given set of dipole moments.
When particles are interacting, they can also undergo translational motion as they are transported in each other's flow fields and also experience dielectrophoretic forces due to gradients in electric field. The translational velocity of sphere α is obtained by balancing DEP and viscous forces acting on it,
| | 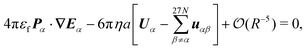 | (17) |
where the gradient of the electric field is,
| |  | (18) |
with higher order terms

being neglected. The first term on the left hand side of
eqn (17) is the DEP force
Fe and captures dipolar interactions through the gradient of the perturbed electric field
∇Eα. The second term
uαβ given in
eqn (14) captures hydrodynamic interactions due to the disturbance flow field created by the motion of all other spheres. Higher-order corrections

arising from flows created by Stokeslets are neglected.
In the rest of the paper, we use the radius of the sphere as the characteristic length scale a, the Maxwell–Wagner relaxation time τMW as the time scale, and E0 as the electric field strength to non-dimensionalise physical quantities. The dipole moment is non-dimensionalised with a3E0. Non-dimensionalising the torque and force balance eqn (13) and (17) gives rise to a dimensionless number, called the Mason number,7 that captures the ratio of viscous to electric stresses,
| |  | (19) |
Note there is a factor of 2 difference in the definition of the Mason number in our previous article.
54 We also note that the formation of particle chains under Quincke rotation and their rupture in a shear flow was described with a modified Mason number in a previous paper.
59 The particles are randomly distributed in space initially at time
t = 0 with dipole moment
P =
εpfez equivalent to zero charge
q = 0 on the fluid–particle interface. After non-dimensionalization, the governing equations can be summarized as follows. The electric dipoles
Pα, angular velocities
Ωα, and translational velocity
Uα, satisfy the 3
N coupled vector ordinary differential equations:
| | 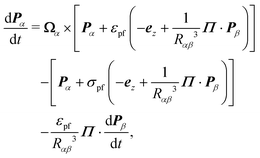 | (20a) |
| | 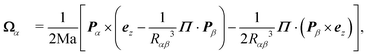 | (20b) |
| |  | (20c) |
where summation over all the particles
β ≠
α is implied and
α ∈ [1,
N]. This system of equations is integrated numerically using an explicit 4th order Runge–Kutta method. The transient term
Ṗβ on the right-hand side of
eqn (20a) is unknown at time
t =
tn: to avoid inverting a large system of equations, we treat this term explicitly by using its known value at the previous time step
t =
tn−1 (it is omitted during the first time step at time
t = 0). Note that the method presented here relies on a far-field approximation and is therefore quantitatively inaccurate for small separation gaps
R ≈ 2–5. To resolve near-field effects, one would need to implement more accurate but computationally expensive methods such as the boundary element method.
39,42,52,60 Nevertheless, the qualitative behaviour of the suspension is expected to remain unaffected when using far-field expansions, as has been shown to be the case in other related physical systems.
61 Since the simulation box is periodic, when a particle exits the box, it re-enters from the opposite face with the same dipole moment and linear and angular velocities. A short-range repulsive interaction force is added to the force balance equation to prevent particles from overlapping,
| |  | (21) |
where
C =
D = 200 was found to be a stable choice that prevented overlaps while not posing severe restrictions on the time step. Similar short-range repulsive forces have been used in Stokesian Dynamics simulations for the same purpose.
23 Since the repulsive force acts along the direction of the vector joining the centres of two spheres, it does not induce any torque on the particles. More sophisticated versions of steric interaction models can be implemented
54,62,63 but are not considered here for simplicity.
3. Results
We simulate the coupled ODEs eqn (20) for two system sizes, N = 500 and 1000. Most of the plots shown are for N = 500 for visual clarity, while results for both system sizes are used when particle averages are considered. We did not find any qualitative differences between the results for these two system sizes. Since our formulation is based on far-field expansions, we restrict our simulations to density ratios ranging from ϕ = 0.02–0.1. The ratio of conductivities R = σf/σp = 30 and Q = εp/εf = 0.5 were chosen, which results in σpf = −0.48 and εpf = −0.20. Note that Quincke rotation occurs for RQ > 1 and E0/Ec > 1,54 the latter condition being strictly true for an isolated spherical particle. In Section 3.1, we choose E0 = 0.9Ec so that there is no Quincke rotation, while in Section 3.2, we choose E0 = 2Ec. We have also performed simulations for E0 = 3Ec and found no qualitative difference in the results, most important of which is the absence of collective motion of the suspended particles. Particle averages of quantities, f for example, are denoted as 〈f〉.
3.1 Suspension dynamics with E0/Ec < 1
First, we perform simulations below the critical field for Quincke rotation (E0/Ec = 0.9) and reproduce the well-known chaining effect in a conventional ER fluid, observed in both experiments7 and previous simulations.19,55 In most prior simulation studies, the dipole moment at any instant was kept fixed and given by P = εpfa3E0, neglecting electrical interactions. In contrast, we solve the complete dipole moment evolution equation that accounts for finite solid and fluid phase conductivities, eqn (20a). This still reproduces chaining because the tensorial form of the DEP force and, in particular, its dependence on the vector joining the centre of two spheres Rαβ remains the same, see eqn (18). Consequently, the particles experience attraction in the direction of the electric field and repulsion in the direction perpendicular to it. Fig. 3a shows particles randomly distributed in the simulation box initially at time t = 0, and Fig. 3b shows the same particles aligned along the direction of the electric field at time t = 500 in the absence of Quincke rotation. Small isolated clusters are evident, containing particles that revolve around their respective axes. However, the majority of particles do not exhibit rotation. This observation is consistent with our previous finding54 that the critical electric field for the Quincke rotation of a pair of particles can either increase or decrease based on their configuration.
 |
| | Fig. 3 (a) and (b) Three-dimensional views of a suspension at times t = 0 and t = 500 with E0/Ec = 0.9. The suspension contains N = 500 particles in a box of linear size L = 47, corresponding to volume fraction ϕ = 0.02. The corresponding top views are shown in (c) and (d). Panels (b) and (d) clearly show the formation of chains in the direction to the electric field. The normalized porosity is f/fm = 0.56 at t = 0 and f/fm = 0.75 at t = 500. Also see movies of the dynamics, Video S1, in the ESI.† | |
The bottom row Fig. 3c–d show the particle structure at t = 0 and t = 500 when viewed in the direction opposite to the electric field (negative z-direction). We project the particles onto the (x, y) plane, equivalent to averaging in the z-direction, and define a porosity, f, denoting the fraction of area that is unoccupied by particles in that top view. Note that the maximum possible chain length is equal to the box size L. For a given particle number N and box size L, there is a maximum porosity fm corresponding to the case when all the particles form perfect vertical chains spanning the length of the box. For a given microstructure, we normalize the porosity by this maximum porosity value as a way to quantify the degree of chaining and alignment in the suspension. For a random distribution of particles, we find the porosity to be f/fm = 0.56 at time t = 0, see Fig. 3c, and in the steady state t = 500 when chaining is observed, we find the porosity to be f/fm = 0.75, see Fig. 3d. These numbers were obtained by an image processing tool in MATLAB. The stability of these chains in the absence of Quincke rotation has been discussed extensively2,26,55 and is reproduced in Section 3.4.
We characterize the statistics of particle distributions in more detail in Fig. 4. We first plot in Fig. 4a the probability density function P(N) of the number of particles N residing in small randomly placed cubic interrogation boxes with a size chosen to have a mean of 〈N〉 = 4. In a perfectly random distribution of non-interacting point particles, a Poisson distribution P(N) = 〈N〉Ne−〈N〉/N! is expected as shown in red in Fig. 4a. The density function measured in our simulations follows the Poisson distribution fairly well on this particular length scale, despite the occurrence of chains in the vertical direction. Chaining is quantified more precisely in Fig. 4b, where we plot the pair distribution function64 in the (r, z) plane, where  is the distance from the vertical axis in cylindrical coordinates. The pair distribution function exhibits a series of bright spots along the direction of the electric field at roughly an interval of z = 2 equal to the particle diameter, indicative of regular chains along the vertical direction, as seen in previous work on dielectric particles.56
is the distance from the vertical axis in cylindrical coordinates. The pair distribution function exhibits a series of bright spots along the direction of the electric field at roughly an interval of z = 2 equal to the particle diameter, indicative of regular chains along the vertical direction, as seen in previous work on dielectric particles.56
 |
| | Fig. 4 (a) Probability density function P(N) of the number of particles N falling in small randomly placed cubic interrogation boxes with a size chosen to have a mean of 〈N〉 = 4. The red curve shows the Poisson distribution P(N) = 〈N〉Ne−〈N〉/N! (b) Pair distribution function in the (r, z) plane, where r is the distance from the vertical axis in cylindrical coordinates, for the suspension shown in Fig. 3b at time t = 500. The bright spots along the vertical axis, spaced at a distance of 2, are an indication of particle chaining in the suspension. The inset shows a close-up of the first peak. | |
3.2 Suspension dynamics with E0/Ec > 1
Next, we subject the suspension to a stronger electric field, E0 > Ec, so that Quincke rotation can occur, keeping other simulation parameters fixed as in Section 3.1. Fig. 5 show the three-dimensional and top views of the suspension under Quincke rotation for volume fractions ϕ = 0.02 (a, c) and ϕ = 0.10 (b, d). Also see movies in the ESI† for a visualisation of particle rotations. The suspension porosity in the z-direction decreases from f/fm = 0.56 to f/fm = 0.37 with an increase in particle volume fraction, as expected. For a dilute concentration of ϕ = 0.02, we still find chaining similar to that in suspensions with no rotation under weaker electric fields. This is a rather surprising observation because individually each particle is rotating around its center and thus creates a disturbance flow field.
 |
| | Fig. 5 (a) and (b) Three-dimensional views of two suspensions with volume fractions ϕ = 0.02 and ϕ = 0.10 undergoing Quincke rotation (E0/Ec = 2) at t = 500. The particle number is N = 500 in both cases, while the linear system size is varied: L = 47 for (a) and L = 28 for (b). The corresponding top views are shown in (c) and (d). Imperfect alignment with the field can be noted in comparison with Fig. 3, with some chains appearing to be tilted at an angle with respect to the electric field. The normalized porosity f/fm for the two different volume fractions is 0.67 and 0.35, respectively. Also see movies of the dynamics, Videos S2 and S3, in the ESI.† | |
The components of the particle-averaged angular and translational velocities are shown in Fig. 6a–f, respectively, as functions of volume fraction ϕ and for two different system sizes N = 500 and 1000. We find that the average velocities are of the order of 10−3 to 10−2, indicating that there is no large-scale collective motion of the particles despite individual particle rotations and EHD interactions between them. This is also seen by considering the histograms of the individual components of the angular and translational velocities in Fig. 7a and b. All the components of both the angular and translational velocities have a zero mean indicating the absence of any collective motion. The x and y components of the angular velocities are broadly distributed between [−1, 1], corresponding to the angular velocities pointing in arbitrary directions in the x–y plane. The z component Ωz, however, is sharply peaked around 0 as the Quincke effect does not cause rotation around the field direction: rotations around the z-axis are instead caused by hydrodynamic interactions and therefore much weaker. All the translational velocity components show similar deviations from the zero mean.
 |
| | Fig. 6 Components of the mean particle angular (a)–(c) and translational velocity (d)–(f) as functions of volume fraction ϕ in suspensions undergoing Quincke rotation (E0/Ec = 2) for systems with N = 500 and 1000 particles. The mean angular velocity is scaled by the angular velocity of an isolated particle,  . All quantities have also been time-averaged over the interval t ∈ [490, 500]. . All quantities have also been time-averaged over the interval t ∈ [490, 500]. | |
 |
| | Fig. 7 Time-averaged histograms over the interval t ∈ [490, 500] of the components of the N = 500 particles (a) angular and (b) translational velocities with volume fraction ϕ = 0.02 undergoing Quincke rotation (E0/Ec = 2). The components of the angular velocity are scaled by the angular velocity of an isolated particle, 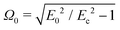 . The x and y-components of the angular velocities of the particles are broadly distributed between [−1, 1] while the z-component is sharply peaked around 0. The translational velocity components have a zero mean as well indicating the absence of any large-scale collective motion. . The x and y-components of the angular velocities of the particles are broadly distributed between [−1, 1] while the z-component is sharply peaked around 0. The translational velocity components have a zero mean as well indicating the absence of any large-scale collective motion. | |
We plot the average magnitude of the angular speed of the particles in Fig. 8a and find it to remain nearly constant with varying particle volume fraction ϕ, for both N = 500 and 1000. However, its average value is always less than the angular speed of an isolated sphere, indicating that EHD interactions tend to slow down Quincke rotation. The average translational speed is found to increase with ϕ in Fig. 8b, whereas the porosity f/fm decreases with ϕ in Fig. 8c. This suggests that particle–particle interactions enhance velocity fluctuations and thereby disrupt chain alignment in the vertical direction, despite the lack of large-scale collective dynamics; we characterize this in more detail below. The effect of the system size is found to be relatively minor, with the small system with N = 500 exhibiting slightly higher values for both the average angular and translational velocities when ϕ > 0.06.
 |
| | Fig. 8 Particle-averaged values of: (a) the angular velocity |Ω|, scaled by the angular velocity  of an isolated particle under Quincke rotation; (b) the translational speed |U|; and (c) the normalized porosity f/fm of the suspension, as functions of volume fraction ϕ for two different particle numbers N = 500 and 1000. All quantities have also been time-averaged over the interval t ∈ [490, 500]. of an isolated particle under Quincke rotation; (b) the translational speed |U|; and (c) the normalized porosity f/fm of the suspension, as functions of volume fraction ϕ for two different particle numbers N = 500 and 1000. All quantities have also been time-averaged over the interval t ∈ [490, 500]. | |
We observe that the microstructure in Fig. 5c appears less porous when compared to Fig. 3d, indicating that the chains in these two cases have some dissimilarities. Visual inspection of the three-dimensional structure of suspensions under Quincke rotation (also see movies in the ESI†) reveals that the longer chains are not completely aligned with the electric field and that smaller isolated chains are titled at an angle to it regardless of particle concentration. This is further evidenced when comparing the pair distribution functions for the case when there is Quincke rotation in Fig. 9a with the case with no rotation in Fig. 4b. When Quincke rotation takes place, the second and third bright yellow spots along the z-direction are found to be weaker, which indicates that alignment along the field direction is not as strong. The particle chains are even less straight when the particle concentration is increased, see Fig. 5d. This is also evidenced in the pair distribution function of Fig. 9b, where the brightest yellow spot near z = 2 is seen to be stretched in the radial direction.
 |
| | Fig. 9 (a) and (b) Pair distribution functions in the (r, z) plane, where r is the distance from the vertical axis in cylindrical coordinates, for two suspensions of N = 500 particles undergoing Quincke rotation (E0/Ec = 2.0) at volume fractions ϕ = 0.02, and ϕ = 0.10. The insets show close-ups of the first peaks. (c) and (d) Corresponding distributions of  for the same two systems. Blue spots indicate counter-rotation while red spots indicate co-rotation with respect to a particle located at the origin. (e) and (f) Probability density function P(N) of the number of particles N falling in small randomly placed cubic interrogation boxes with a size chosen to have a mean of 〈N〉 = 4, for the same two systems. The red curve shows the Poisson distribution P(N) = 〈N〉Ne−〈N〉/N! In all figures, the data has been time-averaged over the interval t ∈ [490, 500]. for the same two systems. Blue spots indicate counter-rotation while red spots indicate co-rotation with respect to a particle located at the origin. (e) and (f) Probability density function P(N) of the number of particles N falling in small randomly placed cubic interrogation boxes with a size chosen to have a mean of 〈N〉 = 4, for the same two systems. The red curve shows the Poisson distribution P(N) = 〈N〉Ne−〈N〉/N! In all figures, the data has been time-averaged over the interval t ∈ [490, 500]. | |
Another question of interest is whether particles are co-rotating or counter-rotating with respect to their immediate neighbours. To answer this quantitatively, we plot the distribution function of  as a function of relative position between two particles in Fig. 9. We find that neighbouring particles forming the chains are counter-rotating, as evidenced by alternating blue (negative) spots and yellow (positive) spots along the z-direction, regardless of the particle concentration, see Fig. 9c and d. We also compare the probability density P(N) of the particle number inside cubic interrogation boxes with mean number 〈N〉 = 4 to the Poisson distribution in Fig. 9e and f, and find a much stronger deviation from the Poisson distribution than when Quincke rotation is absent, especially at the lower volume fraction of ϕ = 0.02. We have also performed simulations with a higher electric field E0 = 3Ec and did not find any qualitative differences.
as a function of relative position between two particles in Fig. 9. We find that neighbouring particles forming the chains are counter-rotating, as evidenced by alternating blue (negative) spots and yellow (positive) spots along the z-direction, regardless of the particle concentration, see Fig. 9c and d. We also compare the probability density P(N) of the particle number inside cubic interrogation boxes with mean number 〈N〉 = 4 to the Poisson distribution in Fig. 9e and f, and find a much stronger deviation from the Poisson distribution than when Quincke rotation is absent, especially at the lower volume fraction of ϕ = 0.02. We have also performed simulations with a higher electric field E0 = 3Ec and did not find any qualitative differences.
Here, we find it useful to contrast the two-dimensional Quincke roller system of Bricard et al.45,46 with its three-dimensional counterpart analyzed here. In the former case, the presence of the wall serves two important roles in giving rise to collective motion: (1) it couples angular and translational velocities, thereby enabling isolated particles to self-propel, and (2) it promotes alignment of two self-propelled particles due to the symmetry of the hydrodynamic rotlet flow near a no-slip wall. In the three-dimensional case, an isolated particle can never self-propel. Therefore, only electrohydrodynamic interactions between particles can potentially give rise to either self-propulsion or large-scale directed motion. As discussed previously, we see neither of these effects in our simulations. We also note that the DEP force in the two-dimensional Quincke roller system favored alignment of one roller either behind or in front of another roller, further helping in flock formation. In the three-dimensional case, the DEP force hinders any such collective motion.
3.3 Isolated chains in an infinite fluid
The suspensions with particles under Quincke rotation display chains that are imperfectly aligned with the electric field. Relatively isolated smaller chains were found to be either tilted with respect to the electric field or in a bow-shaped configuration. To uncover the mechanism behind this observation, we simulate isolated chains in an infinite domain. We place particles in the direction of the electric field and introduce small perturbations in the dipole moments in the x-direction at time t = 0 to induce counter-rotation of particles in the chain in the y-direction. The steady state configurations of these chains with counter-rotating particles in an infinite fluid are found to be very similar to those in the suspensions. The even-numbered chains form a bow-shaped configuration (Fig. 10a) while the odd-numbered chains are tilted at an angle (Fig. 10b) with respect to the electric field. To quantify this misalignment with the field, we plot in Fig. 10c the projection of the vector ![[R with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0052_0302.gif) α,α+1 along the vertical axis joining pairs of subsequent particles inside the chain as a function of α ∈ [1, N − 1], for two chains with an even (N = 10) and odd (N = 11) number of particles. With this definition, a value of 1 corresponds to perfect alignment with the z-direction. As shown in Fig. 10c, chains with even numbers of particles display stronger misalignment near their free ends consistent with the bow-shaped conformation shown in Fig. 10b, whereas misalignment is nearly uniform along chains with odd numbers of particles, since these are simply tilted at an angle as shown in Fig. 10a. The ends of the even-numbered chains were found to make an angle of 5–20° with respect to the positive z-direction, regardless of chain size, N. Similarly, the averaged angle of tilt was found be 5–20° in the odd-numbered chains. We confirm that neighbouring particles inside chains are counter-rotating in Fig. 10d, where plot
α,α+1 along the vertical axis joining pairs of subsequent particles inside the chain as a function of α ∈ [1, N − 1], for two chains with an even (N = 10) and odd (N = 11) number of particles. With this definition, a value of 1 corresponds to perfect alignment with the z-direction. As shown in Fig. 10c, chains with even numbers of particles display stronger misalignment near their free ends consistent with the bow-shaped conformation shown in Fig. 10b, whereas misalignment is nearly uniform along chains with odd numbers of particles, since these are simply tilted at an angle as shown in Fig. 10a. The ends of the even-numbered chains were found to make an angle of 5–20° with respect to the positive z-direction, regardless of chain size, N. Similarly, the averaged angle of tilt was found be 5–20° in the odd-numbered chains. We confirm that neighbouring particles inside chains are counter-rotating in Fig. 10d, where plot  as function of α and find that it is uniformly equal to −1 in both even- and odd-numbered chains.
as function of α and find that it is uniformly equal to −1 in both even- and odd-numbered chains.
 |
| | Fig. 10 (a) and (b) Steady-state conformations of isolated finite particle chains undergoing Quincke rotation (E0/Ec = 2.0): (a) even-numbered chains (N = 10) adopt a bow-shaped configuration, whereas (b) odd-numbered chains (N = 11) remains nearly straight but are tilted at an angle with respect to the field direction. Red and blue colors correspond to the direction of rotation. (c) Vertical projection of the vector ![[R with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0052_0302.gif) α,α+1 joining pairs of subsequent particles inside the chains as a function of α ∈ [1, N − 1], for N = 10 and 11. (d) Correlation between the angular velocity direction of subsequent particles inside the chains, α,α+1 joining pairs of subsequent particles inside the chains as a function of α ∈ [1, N − 1], for N = 10 and 11. (d) Correlation between the angular velocity direction of subsequent particles inside the chains,  , as a function of α. Also see movies of the dynamics, Videos S4 and S5, in the ESI.† , as a function of α. Also see movies of the dynamics, Videos S4 and S5, in the ESI.† | |
Interestingly, the bow-shaped configuration of even-numbered chains is similar to that of a non-rotating chain subject to an electric field but placed in a Poiseuille flow. Similarly, the titled configuration appears similar to that under a shear flow (see Fig. 8 and 10 in Parthasarathy and Klingenberg65). These configurations in our simulations are a result of free-end effects. This is best explained by looking at chains of sizes three and four, respectively, as depicted in Fig. 11, and by only considering nearest neighbor interactions. The black arrows in the schematic show the directions of rotation in the chains, with subsequent particles rotating in opposite directions consistent with observations. The colored arrows correspond to the linear velocities induced at a particle's centre by its direct neighbors due to their rotlet flows. For example, the induced velocity due to a red particle is represented with a red colored arrow and so on. First, consider the odd chain with three particles. The net velocity experienced by the central blue particle is zero due to symmetry. The velocity induced by the central particle at the locations of its neighbors are in the opposite directions (left on green particle and right on red particle). Hence, the particles situated at the ends translate in opposite directions. Since the particles are no longer aligned parallel to the electric field, there is a component of the DEP force in the direction perpendicular to the electric field. The particles stop moving when the component of the DEP force perpendicular to the electric field balances the induced flow due to the central blue particle. The DEP force acting on the central blue particle is zero due to symmetry. If we sum the translational velocities of all the particles (colored arrows), the net result is zero, and the chain remains stationary. Similarly, if we add one more particle to the previous case, we get a chain with an even number of particles. In this case, the two central particles stay fixed relative to the chain due to symmetry. A similar argument as above applies to the top green particle and shows that it moves to the right. The yellow colored particle moves due to the induced velocity arising from its neighboring red particle. Both the particles at the ends of the chain stop moving relative to the chain when the DEP forces balance the induced rotlet velocities. However, summing the translational velocities of all the particles in this case results in a net translational velocity of the entire chain and the chain self-propels towards the right direction. In our suspension simulations, these free-end effects are reduced due to periodicity and we observe these two configurations mainly at dilute concentrations where crowding effects are lower.
 |
| | Fig. 11 Schematic diagram explaining the formation of tilted (odd) and bow (even) shaped chains when neighboring particles are perturbed to have angular velocities in opposite directions in the Quincke regime. The black arrows denote the directions of rotation. The colored arrows show the translational velocities induced by rotlet flows generated by the particles of the corresponding colors. | |
The dependence of the angular speed on chain length for both odd- and even-numbered chains is shown in Fig. 12a. We find that the mean velocity of the particles decreases with an increase in chain size due to hydrodynamic interactions and is always lower than the angular speed of an isolated spherical particle,  for E0/Ec = 2 in these simulations. One additional feature of the even-numbered chains is self-propulsion. This was observed as one of the outcomes of the simulations for a pair of particles in our previous work.54 The velocity of self-propulsion is seen to decrease with number of particles in the chain N, i.e., longer chains propel with a lower velocity, see Fig. 12b. This is simply because propulsion arises due to the force experienced by the particles near the free ends, which remains finite as the chain increases in size. On the other hand, the hydrodynamic drag experienced by the chain increases with N. Finally, we also plot the mean of
for E0/Ec = 2 in these simulations. One additional feature of the even-numbered chains is self-propulsion. This was observed as one of the outcomes of the simulations for a pair of particles in our previous work.54 The velocity of self-propulsion is seen to decrease with number of particles in the chain N, i.e., longer chains propel with a lower velocity, see Fig. 12b. This is simply because propulsion arises due to the force experienced by the particles near the free ends, which remains finite as the chain increases in size. On the other hand, the hydrodynamic drag experienced by the chain increases with N. Finally, we also plot the mean of ![[R with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0052_0302.gif) αβ·ez for each chain as a function of N in Fig. 12c. As the chain is made longer, the particles in the centre become more aligned with the z-direction, and hence the value of
αβ·ez for each chain as a function of N in Fig. 12c. As the chain is made longer, the particles in the centre become more aligned with the z-direction, and hence the value of ![[R with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0052_0302.gif) αβ·ez approaches unity. However, it never reaches one, because chains larger than N ≳ 75 break into smaller chains. This explains the observation of stable chains in these suspensions even when particles are under Quincke rotation. The effect of periodicity in the suspension helps in making the chains less titled. Since the chains are not isolated, the particles forming these chains experience EHD interactions from the neighbouring chains and become slightly misaligned, assuming a zig-zag configuration in concentrated suspensions.
αβ·ez approaches unity. However, it never reaches one, because chains larger than N ≳ 75 break into smaller chains. This explains the observation of stable chains in these suspensions even when particles are under Quincke rotation. The effect of periodicity in the suspension helps in making the chains less titled. Since the chains are not isolated, the particles forming these chains experience EHD interactions from the neighbouring chains and become slightly misaligned, assuming a zig-zag configuration in concentrated suspensions.
 |
| | Fig. 12 (a) Mean angular velocity magnitude |Ωα·ey|, scaled by the angular velocity  of an isolated particle, in finite particle chains undergoing Quincke rotation (E0/Ec = 2.0) as a function of chain length N, for both odd and even values of N. (b) Mean translational velocity |Uα · ex| of the chains as a function of N. Only chains with even numbers of particles have a non-zero velocity. (c) Mean value of the vertical projection of the vector of an isolated particle, in finite particle chains undergoing Quincke rotation (E0/Ec = 2.0) as a function of chain length N, for both odd and even values of N. (b) Mean translational velocity |Uα · ex| of the chains as a function of N. Only chains with even numbers of particles have a non-zero velocity. (c) Mean value of the vertical projection of the vector ![[R with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0052_0302.gif) α,α+1 joining pairs of subsequent particles forming the chains as a function of N. α,α+1 joining pairs of subsequent particles forming the chains as a function of N. | |
3.4 Stability of a pair of counter-rotating particles
In this section, we focus on the most fundamental microstructural unit of the suspension, namely a pair of counter-rotating particles, and show that this pair is stable when aligned in the direction of the electric field. Consider two counter-rotating particles with the assumption Ω1 = −Ω2. The translational velocities of the spherical particles are,| |  | (22a) |
| |  | (22b) |
without any steric interactions. Noting that R12 = −R21, and substituting P1 = Pxex + Pzez, P2 = −Pxex + Pzez and ![[R with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0052_0302.gif) 12 = Rxex + Rzez, the rate of change of the vector pointing from sphere 1 to 2 is,
12 = Rxex + Rzez, the rate of change of the vector pointing from sphere 1 to 2 is,| |  | (23) |
where we have dropped the subscripts 12 for convenient reading. The components of Ṙ in the x- and z-directions read,| |  | (24a) |
| |  | (24b) |
Note that the effect of rotational flow field is absent in the expression for Ṙ in eqn (24). However, the effect of Quincke rotation comes into play through the dipole moment in the plane perpendicular to E0, i.e. Px. Next we consider two basic configurations: one when the vector R is perpendicular to the applied electric field and another when R is parallel to it. In the first case, substituting Rz = 0 in eqn (24) yields| |  | (25) |
Since 2Px2 + Pz2 ≥ 2, we find that dRx/dt > 0, i.e., the two particles will separate in the x direction. Note that this is also true for non-rotating conventional ER fluids26,55 where Px = 0. To investigate the stability of the perpendicular configuration, we perturb it as R = Rxex + δRzez, where δ is a small number, and linearize eqn (24b) to obtain| |  | (26) |
The prefactor on the right-hand side can be seen to positive, which indicates that the perpendicular configuration Rz = 0 is unstable: the pair of particles will separate along the perpendicular direction while at the same time rotating away from that configuration.
Next, we perform a similar analysis for the parallel case and first substitute Rx = 0 in eqn (24), yielding
| |  | (27) |
In this case, we find that d
Rz/d
t < 0,
i.e., the distance between the two particles in the field direction will decrease with time, which is also true for non-rotating particles in weak fields. Eventually, this motion will be counteracted by steric interactions, and the two particles will form a pair with
Rz = 2. To probe the stability of the parallel configuration, we introduce a perturbation as
R = δ
Rxex +
Rzez and linearize
eqn (24a) to find
| |  | (28) |
The prefactor on the right-hand side is negative in this case, indicating that the parallel configuration is stable for counter-rotating particles and is responsible for the microstructure observed in isolated chains and periodic suspensions simulations. From
eqn (26) and (28), we see that the DEP forces are a quadratic function of
Px,z. Increasing the electric field will increase the strength of the induced dipole moments and the chaining effect will become even more pronounced. This is consistent with the results of our simulations with
E0 = 3
Ec, which show the same phenomenology as for
E0 = 2
Ec with yet clearer chain formation.
4. Conclusions
In this article, we performed simulations of a relatively large number of dielectric particles (N = 500–1000) in a periodic domain suspended in a weakly conducting fluid and subject to a DC electric field. We reproduced the chaining phenomenon in a conventional ER fluid where individual particles do not spin. On increasing the electric field beyond the critical value, the particles start to spontaneously spin in the suspension. While a suspension of such particles confined to two dimensions and rotating next to a wall is known to display collective motion, the same was found not to be true in three dimensions. Instead, we found that the dielectrophoretic (DEP) forces also caused chaining in these suspensions under Quincke rotation. Adjacent particles were found to counter-rotate in the chains. There was no net particle motion in any direction and hence no spontaneous collective motion in these suspensions. Flows created by individual particle rotation were unable to break the chains formed by DEP forces. This is in contrast to the related phenomenon of dipolophoresis, where particle chaining due to DEP was significantly suppressed by induced-charge electrophoresis (ICEP).56,57,61
We then analysed isolated chains in an electric field and found two distinct configurations depending on whether the number of particles in the chain was odd or even. The odd-numbered chains were found to be tilted at an angle to the electric field akin to a flexible fibre subject to a Couette flow. On the other hand, even-numbered chains formed a bow-shaped configuration similar to a flexible fibre subject to a Poiseuille flow. The even-numbered chains were found to self-propel with a velocity that decreases with the chain size. These effects were found to be a result of free-end effects and less likely to be seen in concentrated periodic suspensions. Finally, we focused on the fundamental building unit of the suspension microstructure: a pair of counter-rotating spheres. A stability analysis showed that such a pair is stable in the direction of the electric field but unstable perpendicular to it.
Future research work should consider the effect of shear flow on such suspensions to study their rheological properties. This will enable one to answer questions raised by experiments where an increase in flow rate has been observed when these suspensions are subjected to a Couette59,66,67 and Poiseuille flow.44 The simulations should then be compared with theoretical continuum models.68–70 An apparent increase in conductivity has also been reported.71 Since, we used normal contact forces to model steric interactions, the role of friction is unknown in such suspensions. Hence, sophisticated contact models accounting for surface asperities and roughness should also be considered, particularly for dense suspensions.62 Our simulations, based on far-field results, could be extended to account for near-field interactions by using Stokesian dynamics simulations or the boundary element method. The latter is particularly suitable for studying suspensions of non-spherical particles, such as spheroids72 or helices.52 Finally, our simulations could be extended to include wall effects and reproduce recent experiments on magnetic control of Quincke rollers,73 dynamics of Quincke dimers and trimers,74 and pear-shaped Quincke rollers.75
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
We thank Jae Sung Park for helpful discussions on post-processing of the results and Michael McDougall for pointing out the missing transient term in our previous publication.54 We also thank the referees for their constructive criticism of the manuscript. D. S. acknowledges funding from National Science Foundation grant no. CBET-1934199.
References
-
E. Guazzelli and J. F. Morris, A Physical Introduction to Suspension Dynamics, Cambridge University Press, 2011 Search PubMed.
-
N. J. Wagner and J. Mewis, Theory and Applications of Colloidal Suspension Rheology, Cambridge University Press, 2021 Search PubMed.
- Z. P. Shulman, R. G. Gorodkin, E. V. Korobko and V. K. Gleb, J. Non-Newtonian Fluid Mech., 1981, 8, 29–41 CrossRef.
- R. Stanway, J. L. Sproston and A. K. El-Wahed, Smart Mater. Struct., 1996, 5, 464 CrossRef CAS.
- L. Hines, K. Petersen, G. Z. Lum and M. Sitti, Adv. Mater., 2017, 29, 1603483 CrossRef PubMed.
- W. M. Winslow, J. Appl. Phys., 1949, 20, 1137–1140 CrossRef CAS.
- P. A. Arp, R. T. Foister and S. G. Mason, Adv. Colloid Interface Sci., 1980, 12, 295–356 CrossRef.
- Y. F. Deinega and G. V. Vinogradov, Rheol. Acta, 1984, 23, 636–651 CrossRef CAS.
- A. P. Gast and C. F. Zukoski, Adv. Colloid Interface Sci., 1989, 30, 153–202 CrossRef CAS.
-
J. C. Maxwell, A Treatise on Electricity and Magnetism, Clarendon Press, 1873, vol. 1 Search PubMed.
- L. Rayleigh, Phil. Mag., 1892, 34, 481–502 Search PubMed.
- R. C. McPhedran and D. R. McKenzie, Proc. R. Soc. Lond. A, 1978, 359, 45–63 CAS.
- J. B. Keller, J. Appl. Phys., 1963, 34, 991–993 CrossRef.
- A. Einstein, Ann. Physik, 1911, 34, 592 Search PubMed.
- G. I. Taylor, Proc. R. Soc. Lond. A, 1932, 138, 41–48 CAS.
- G. K. Batchelor, J. Fluid Mech., 1970, 41, 545–570 CrossRef.
- G. K. Batchelor and J. T. Green, J. Fluid Mech., 1972, 56, 401–427 CrossRef.
- G. K. Batchelor, Annu. Rev. Fluid Mech., 1974, 6, 227–255 CrossRef.
- D. J. Klingenberg, F. Van Swol and C. F. Zukoski, J. Chem. Phys., 1989, 91, 7888–7895 CrossRef CAS.
- D. J. Klingenberg, F. Van Swol and C. F. Zukoski, J. Chem. Phys., 1991, 94, 6160–6169 CrossRef CAS.
- R. T. Bonnecaze and J. F. Brady, Proc. R. Soc. Lond. A, 1990, 430, 285–313 CAS.
- R. T. Bonnecaze and J. F. Brady, Proc. R. Soc. Lond. A, 1991, 432, 445–465 Search PubMed.
- G. Bossis and J. F. Brady, J. Chem. Phys., 1984, 80, 5141–5154 CrossRef CAS.
- J. F. Brady and G. Bossis, Annu. Rev. Fluid Mech., 1988, 20, 111–157 CrossRef.
- L. Marshall, C. F. Zukoski and J. W. Goodwin, J. Chem. Soc. Faraday I, 1989, 85, 2785–2795 RSC.
- D. J. Klingenberg and C. F. Zukoski IV, Langmuir, 1990, 6, 15–24 CrossRef CAS.
- J. R. Melcher and G. I. Taylor, Annu. Rev. Fluid Mech., 1969, 1, 111–146 CrossRef.
- R. S. Allan and S. G. Mason, Proc. R. Soc. Lond. A, 1962, 267, 45–61 Search PubMed.
- G. I. Taylor, Proc. R. Soc. Lond. A, 1966, 291, 159–166 Search PubMed.
- D. A. Saville, Annu. Rev. Fluid Mech., 1997, 29, 27–64 CrossRef.
- R. S. Allan and S. G. Mason, Proc. R. Soc. Lond. A, 1962, 267, 62–76 Search PubMed.
- C. E. Chaffey and S. G. Mason, J. Colloid Sci., 1964, 19, 525–548 CrossRef.
- G. Quincke, Ann. Phys. Chem., 1896, 59, 417 CrossRef.
- T. Jones, IEEE Trans. Ind. Appl., 1984, IA–20, 845–849 Search PubMed.
- I. Turcu, J. Phys. A, 1987, 20, 3301 CrossRef.
-
T. B. Jones, Electromechanics of Particles, Cambridge University Press, 2005 Search PubMed.
- S. Krause and P. Chandratreya, J. Colloid Interface Sci., 1998, 206, 10–18 CrossRef CAS PubMed.
- P. F. Salipante and P. M. Vlahovska, Phys. Fluids, 2010, 22, 112110 CrossRef.
- D. Das and D. Saintillan, J. Fluid Mech., 2017, 829, 127–152 CrossRef CAS.
- D. Das and D. Saintillan, J. Fluid Mech., 2021, 914, A22 CrossRef CAS.
- P. M. Vlahovska, Annu. Rev. Fluid Mech., 2019, 51, 305–330 CrossRef.
- M. Firouznia, S. H. Bryngelson and D. Saintillan, J. Comp. Phys., 2023, 112248 CrossRef.
- L. Lobry and E. Lemaire, J. Electrostat., 1999, 47, 61 CrossRef CAS.
- E. Lemaire, L. Lobry and N. Pannacci, J. Electrostat., 2006, 64, 586–590 CrossRef.
- A. Bricard, J.-B. Caussin, N. Desreumaux, O. Dauchot and D. Bartolo, Nature, 2013, 503, 95–98 CrossRef CAS PubMed.
- A. Bricard, J.-B. Caussin, D. Das, C. Savoie, V. Chikkadi, K. Shitara, O. Chepizhko, F. Peruani, D. Saintillan and D. Bartolo, Nat. Commun., 2015, 6, 1–8 Search PubMed.
- H. C. Berg and D. A. Brown, Nature, 1972, 239, 500–504 CrossRef CAS PubMed.
- H. Karani, G. E. Pradillo and P. M. Vlahovska, Phys. Rev. Lett., 2019, 123, 208002 CrossRef CAS PubMed.
- Z. Zhang, H. Yuan, Y. Dou, M. O. De La Cruz and K. J. M. Bishop, Phys. Rev. Lett., 2021, 126, 258001 CrossRef CAS PubMed.
- S. Q. Lu, B. Y. Zhang, Z. C. Zhang, Y. Shi and T. H. Zhang, Soft Matter, 2018, 14, 5092–5097 RSC.
- S. Imamura, K. Sawaki, J. J. Molina, M. S. Turner and R. Yamamoto, Adv. Theory Simul., 2022, 2200683 Search PubMed.
- D. Das and E. Lauga, Phys. Rev. Lett., 2019, 122, 194503 CrossRef CAS PubMed.
- E. Han, L. Zhu, J. W. Shaevitz and H. A. Stone, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2022000118 CrossRef CAS PubMed.
- D. Das and D. Saintillan, Phys. Rev. E, 2013, 87, 043014 CrossRef PubMed.
- R. T. Bonnecaze and J. F. Brady, J. Chem. Phys., 1992, 96, 2183–2202 CrossRef CAS.
- J. S. Park and D. Saintillan, J. Fluid Mech., 2010, 662, 66–90 CrossRef.
- J. S. Park and D. Saintillan, Phys. Rev. E, 2011, 83, 041409 CrossRef PubMed.
- Y. Hu, P. M. Vlahovska and M. J. Miksis, Phys. Rev. E, 2018, 97, 013111 CrossRef CAS PubMed.
- N. Pannacci, L. Lobry and E. Lemaire, Rheol. Acta, 2007, 46, 899–904 CrossRef CAS.
- D. Das and D. Saintillan, J. Fluid Mech., 2017, 810, 225–253 CrossRef.
- D. Saintillan, Phys. Fluids, 2008, 20, 067104 CrossRef.
- S. Luding, Granular Matter, 2008, 10, 235–246 CrossRef.
- E. Corona, L. Greengard, M. Rachh and S. Veerapaneni, J. Comp. Phys., 2017, 332, 504–519 CrossRef.
-
D. Frenkel and B. Smit, Understanding Molecular Simulation: From Algorithms to Applications, Elsevier, 2001 Search PubMed.
- M. Parthasarathy and D. J. Klingenberg, Mater. Sci. Eng., 1996, 17, 57–103 CrossRef.
- A. Cēbers, E. Lemaire and L. Lobry, Phys. Rev. E, 2000, 63, 016301 CrossRef PubMed.
- E. Lemaire, L. Lobry, N. Pannacci and F. Peters, J. Rheol., 2008, 52, 769–783 CrossRef CAS.
- A. Cēbers, Phys. Rev. E, 2014, 90, 032305 CrossRef PubMed.
- M. Belovs and A. Cēbers, Phys. Rev. E, 2014, 89, 052310 CrossRef CAS PubMed.
- M. Belovs and A. Cēbers, Phys. Rev. Fluids, 2020, 5, 013701 CrossRef.
- N. Pannacci, L. Lobry and E. Lemaire, Phys. Rev. Lett., 2007, 99, 094503 CrossRef CAS PubMed.
- A. Cebers, E. Lemaire and L. Lobry, Int. J. Mod. Phys. B, 2002, 16, 2603–2609 CrossRef.
- R. R. Garza, N. Kyriakopoulos, Z. M. Cenev, C. Rigoni and J. V. I. Timonen, Sci. Adv., 2023, 9(26), eadh2522 CrossRef PubMed.
- A. Mauleon-Amieva, M. P. Allen, T. B. Liverpool and C. P. Royall, Sci. Adv., 2023, 9(20), eadf5144 CrossRef PubMed.
- B. Zhang, A. Sokolov and A. Snezhko, Nat. Commun., 2020, 11, 4401 CrossRef CAS PubMed.
|
| This journal is © The Royal Society of Chemistry 2023 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *a and
David
Saintillan
*a and
David
Saintillan
 b
b
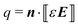 on the particle-fluid interface arising due to a jump in the Ohmic current
on the particle-fluid interface arising due to a jump in the Ohmic current  across the interface. Here, n is the outward unit normal vector on the surface, and
across the interface. Here, n is the outward unit normal vector on the surface, and  denotes the jump of variable f across the interface in the direction of n. The interfacial charge density gets convected with the interfacial velocity u, and thus obeys the conservation equation,
denotes the jump of variable f across the interface in the direction of n. The interfacial charge density gets convected with the interfacial velocity u, and thus obeys the conservation equation,







![[R with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0052_0302.gif) αβ = Rαβ/Rαβ. We note that the last transient term in eqn (10) was missing in our previous article.54 This term is non-zero because the electric field Eα around particle α depends on the dipole moments Pβ of neighboring particles and on the relative position vectors Rαβ, which are functions of time. We neglect the latter effect in the following since it is of a higher order
αβ = Rαβ/Rαβ. We note that the last transient term in eqn (10) was missing in our previous article.54 This term is non-zero because the electric field Eα around particle α depends on the dipole moments Pβ of neighboring particles and on the relative position vectors Rαβ, which are functions of time. We neglect the latter effect in the following since it is of a higher order  . Corrections to the electric field, Eα, due to higher-order multipole moments are of order
. Corrections to the electric field, Eα, due to higher-order multipole moments are of order  and hence neglected in eqn (11). The torque balance equation provides us with an expression for the angular velocity of sphere α in terms of the dipole moments of all the particles,
and hence neglected in eqn (11). The torque balance equation provides us with an expression for the angular velocity of sphere α in terms of the dipole moments of all the particles,
 and hence neglected. The rotlet flow at xα due to a rotating sphere located at xβ is,
and hence neglected. The rotlet flow at xα due to a rotating sphere located at xβ is,

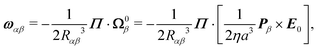
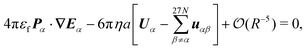

 being neglected. The first term on the left hand side of eqn (17) is the DEP force Fe and captures dipolar interactions through the gradient of the perturbed electric field ∇Eα. The second term uαβ given in eqn (14) captures hydrodynamic interactions due to the disturbance flow field created by the motion of all other spheres. Higher-order corrections
being neglected. The first term on the left hand side of eqn (17) is the DEP force Fe and captures dipolar interactions through the gradient of the perturbed electric field ∇Eα. The second term uαβ given in eqn (14) captures hydrodynamic interactions due to the disturbance flow field created by the motion of all other spheres. Higher-order corrections  arising from flows created by Stokeslets are neglected.
arising from flows created by Stokeslets are neglected.

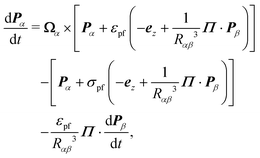
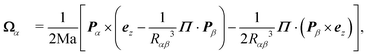



 is the distance from the vertical axis in cylindrical coordinates. The pair distribution function exhibits a series of bright spots along the direction of the electric field at roughly an interval of z = 2 equal to the particle diameter, indicative of regular chains along the vertical direction, as seen in previous work on dielectric particles.56
is the distance from the vertical axis in cylindrical coordinates. The pair distribution function exhibits a series of bright spots along the direction of the electric field at roughly an interval of z = 2 equal to the particle diameter, indicative of regular chains along the vertical direction, as seen in previous work on dielectric particles.56

 as a function of relative position between two particles in Fig. 9. We find that neighbouring particles forming the chains are counter-rotating, as evidenced by alternating blue (negative) spots and yellow (positive) spots along the z-direction, regardless of the particle concentration, see Fig. 9c and d. We also compare the probability density P(N) of the particle number inside cubic interrogation boxes with mean number 〈N〉 = 4 to the Poisson distribution in Fig. 9e and f, and find a much stronger deviation from the Poisson distribution than when Quincke rotation is absent, especially at the lower volume fraction of ϕ = 0.02. We have also performed simulations with a higher electric field E0 = 3Ec and did not find any qualitative differences.
as a function of relative position between two particles in Fig. 9. We find that neighbouring particles forming the chains are counter-rotating, as evidenced by alternating blue (negative) spots and yellow (positive) spots along the z-direction, regardless of the particle concentration, see Fig. 9c and d. We also compare the probability density P(N) of the particle number inside cubic interrogation boxes with mean number 〈N〉 = 4 to the Poisson distribution in Fig. 9e and f, and find a much stronger deviation from the Poisson distribution than when Quincke rotation is absent, especially at the lower volume fraction of ϕ = 0.02. We have also performed simulations with a higher electric field E0 = 3Ec and did not find any qualitative differences.![[R with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0052_0302.gif) α,α+1 along the vertical axis joining pairs of subsequent particles inside the chain as a function of α ∈ [1, N − 1], for two chains with an even (N = 10) and odd (N = 11) number of particles. With this definition, a value of 1 corresponds to perfect alignment with the z-direction. As shown in Fig. 10c, chains with even numbers of particles display stronger misalignment near their free ends consistent with the bow-shaped conformation shown in Fig. 10b, whereas misalignment is nearly uniform along chains with odd numbers of particles, since these are simply tilted at an angle as shown in Fig. 10a. The ends of the even-numbered chains were found to make an angle of 5–20° with respect to the positive z-direction, regardless of chain size, N. Similarly, the averaged angle of tilt was found be 5–20° in the odd-numbered chains. We confirm that neighbouring particles inside chains are counter-rotating in Fig. 10d, where plot
α,α+1 along the vertical axis joining pairs of subsequent particles inside the chain as a function of α ∈ [1, N − 1], for two chains with an even (N = 10) and odd (N = 11) number of particles. With this definition, a value of 1 corresponds to perfect alignment with the z-direction. As shown in Fig. 10c, chains with even numbers of particles display stronger misalignment near their free ends consistent with the bow-shaped conformation shown in Fig. 10b, whereas misalignment is nearly uniform along chains with odd numbers of particles, since these are simply tilted at an angle as shown in Fig. 10a. The ends of the even-numbered chains were found to make an angle of 5–20° with respect to the positive z-direction, regardless of chain size, N. Similarly, the averaged angle of tilt was found be 5–20° in the odd-numbered chains. We confirm that neighbouring particles inside chains are counter-rotating in Fig. 10d, where plot  as function of α and find that it is uniformly equal to −1 in both even- and odd-numbered chains.
as function of α and find that it is uniformly equal to −1 in both even- and odd-numbered chains.

![[R with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0052_0302.gif) α,α+1 joining pairs of subsequent particles inside the chains as a function of α ∈ [1, N − 1], for N = 10 and 11. (d) Correlation between the angular velocity direction of subsequent particles inside the chains,
α,α+1 joining pairs of subsequent particles inside the chains as a function of α ∈ [1, N − 1], for N = 10 and 11. (d) Correlation between the angular velocity direction of subsequent particles inside the chains,  , as a function of α. Also see movies of the dynamics, Videos S4 and S5, in the ESI.†
, as a function of α. Also see movies of the dynamics, Videos S4 and S5, in the ESI.† for E0/Ec = 2 in these simulations. One additional feature of the even-numbered chains is self-propulsion. This was observed as one of the outcomes of the simulations for a pair of particles in our previous work.54 The velocity of self-propulsion is seen to decrease with number of particles in the chain N, i.e., longer chains propel with a lower velocity, see Fig. 12b. This is simply because propulsion arises due to the force experienced by the particles near the free ends, which remains finite as the chain increases in size. On the other hand, the hydrodynamic drag experienced by the chain increases with N. Finally, we also plot the mean of
for E0/Ec = 2 in these simulations. One additional feature of the even-numbered chains is self-propulsion. This was observed as one of the outcomes of the simulations for a pair of particles in our previous work.54 The velocity of self-propulsion is seen to decrease with number of particles in the chain N, i.e., longer chains propel with a lower velocity, see Fig. 12b. This is simply because propulsion arises due to the force experienced by the particles near the free ends, which remains finite as the chain increases in size. On the other hand, the hydrodynamic drag experienced by the chain increases with N. Finally, we also plot the mean of ![[R with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0052_0302.gif) αβ·ez for each chain as a function of N in Fig. 12c. As the chain is made longer, the particles in the centre become more aligned with the z-direction, and hence the value of
αβ·ez for each chain as a function of N in Fig. 12c. As the chain is made longer, the particles in the centre become more aligned with the z-direction, and hence the value of ![[R with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0052_0302.gif) αβ·ez approaches unity. However, it never reaches one, because chains larger than N ≳ 75 break into smaller chains. This explains the observation of stable chains in these suspensions even when particles are under Quincke rotation. The effect of periodicity in the suspension helps in making the chains less titled. Since the chains are not isolated, the particles forming these chains experience EHD interactions from the neighbouring chains and become slightly misaligned, assuming a zig-zag configuration in concentrated suspensions.
αβ·ez approaches unity. However, it never reaches one, because chains larger than N ≳ 75 break into smaller chains. This explains the observation of stable chains in these suspensions even when particles are under Quincke rotation. The effect of periodicity in the suspension helps in making the chains less titled. Since the chains are not isolated, the particles forming these chains experience EHD interactions from the neighbouring chains and become slightly misaligned, assuming a zig-zag configuration in concentrated suspensions.

![[R with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0052_0302.gif) 12 = Rxex + Rzez, the rate of change of the vector pointing from sphere 1 to 2 is,
12 = Rxex + Rzez, the rate of change of the vector pointing from sphere 1 to 2 is,