Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Dynamics of elastoviscoplastic filament stretching
P.
Moschopoulos
 ,
E.
Kouni
,
E.
Kouni
 ,
K.
Psaraki
,
K.
Psaraki
 ,
Y.
Dimakopoulos
,
Y.
Dimakopoulos
 and
J.
Tsamopoulos
and
J.
Tsamopoulos
 *
*
Laboratory of Fluid Mechanics and Rheology, Department of Chemical Engineering, University of Patras, Greece. E-mail: tsamo@chemeng.upatras.gr; Web: https://fluidslab.chemeng.upatras.gr
First published on 6th June 2023
Abstract
We study theoretically the stretching dynamics of a yield stress material that exhibits both elastic and viscoplastic behavior. The material is confined between two coaxial disks, forming initially a cylindrical liquid bridge and then a neck when the disks are pulled apart. The material follows the Saramito–Herschel–Bulkley constitutive model and yields according to the von Mises criterion. We find that an elongated thin neck is formed when elasticity prevails, connecting the upper and lower parts of the filamentous bridge. This neck has been observed in breakup experiments of yield stress bridges, but this is the first theoretical study that predicts it. Earlier numerical and theoretical studies of filament stretching of yield stress materials failed to do so, because they excluded elasticity from the constitutive model they used in the simulations. Our results indicate that increasing elasticity leads to shorter pinching times and filament length than the viscoplastic case. This is caused by the fact that larger areas of the filament remain unyielded, while they undergo small deformation even before yielding, and only the remaining smaller yielded areas carry the burden of visible deformation. Our findings suggest that the value of the yield strain, defined as the ratio of the yield stress to the elastic modulus, should be used with caution to determine whether elastic effects will affect the filament stretching procedure or not.
1. Introduction
Yield-stress materials are an ambiguous class of non-Newtonian fluids that flow only when a specific stress threshold is surpassed. This particular stress threshold, termed “yield stress”, is the distinct property that differentiates these materials from all others.1 The range of materials categorized as yield-stress materials is broad. Notable examples are waxy crude oil,2 fresh cement,3,4 various foodstuffs like mayonnaise,5,6 cosmetic materials like hair gels, shaving foam, and toothpaste, and biocompatible hydrogels used in 3D printing.7,8 They exhibit two kinds of behavior: solid-like when the applied stress is smaller than the yield stress and fluid-like when the applied stress surpasses the yield stress.Historically, elasticity was excluded when yield-stress materials were investigated. As a result, two distinct material groups emerged, viscoelastic and viscoplastic. However, excluding elasticity could not explain and predict many experimental observations with yield-stress materials. For example, initially Putz & Burghelea9 and later Holenberg et al.10 reported the loss of fore-and-aft symmetry under creeping flow conditions and the occurrence of the negative wake structure behind a sedimentating spherical particle through a Carbopol gel. In the case of a bubble rising through a yield-stress material, the negative wake structure was reported,11 and even more intriguingly, the bubble attained an inverted teardrop shape.12–14 These experimental observations were clear manifestations of the elasticity in yield stress materials. To overcome the deficiency of viscoplastic models, Fraggedakis et al.15 used the proposed elastoviscoplastic model of Saramito,16 which was based on the original ideas of Oldroyd.17 They predicted accurately the loss of the fore-and-aft symmetry and the negative wake behind the particle. Moreover, Varchanis et al.18 studied experimentally the flow of a Pluronic aqueous solution in the optimized shape cross-slot extensional rheometer (OSCER), conducted simulations using Saramito's model16 and got excellent agreement between experiments and simulations. Later, Moschopoulos et al.19 employed a refined version of the Saramito model that accounted also for strain rate thinning20 and captured the inverted teardrop shape of a bubble, found in bubble rising experiments in Carbopol solutions. This experimental evidence and the accompanied simulations showed that elasticity should not be excluded lightheartedly when we investigate the flows of yield-stress materials, especially in flows with a predominant extensional deformation.
Filament stretching is another procedure to create an extensional flow field. The easiest way to create such a configuration is to place a small amount of material between two coaxial disks of equal radius and pull the upper disk vertically. The material elongates, thins, and, finally, pinches off under capillarity. To probe the filament stretching dynamics, especially when we want to measure very short relaxation times, several well-controlled processes and instruments exist, like the Capillary Breakup Extensional Rheometer21,22 (CaBER), the Rayleigh Ohnesorge Jetting Extensional Rheometer (ROJER)23 and Dripping-onto-Substrate.24,25 The way the material deforms, and breaks is of paramount importance for many industrial processes like fiber spinning, ink-jet printing, 3D printing or spraying fertilizers. Newtonian22,26 and Generalized Newtonian27 materials have been investigated already. The literature is richer for viscoelastic materials28,29 due to their abundance, and importance in practical applications and the intriguing phenomena that arise. As viscoelastic materials thin, significant tensile stresses develop that oppose the necking of the fluid thread. These are responsible for the increased lifetime of the bridge and for the appearance of a long and cylindrical thread30,31 that connects the two pendant drops. Also, for specific material properties where both elastic and inertial effects are comparable, a second, small satellite drop grows between the larger beads, which simulations capture accurately.32,33
The literature focused mainly on determining the so-called extensional yield stress for viscoplastic materials. Martinie et al.34 and Niedzwiedz et al.35 tried to measure the value of the extensional yield stress experimentally using the CaBER experimental protocol. However, their measurements did not agree with the ideal viscoplastic theory that predicted the extensional yield stress to be  times the shear yield stress. This inconsistency originated from the contributions of elastic stresses in the Von Mises criterion, as Varchanis et al.18 explained. Nelson et al.36 studied yield stress materials that achieved extremely large extensional deformations and they reported the evolution of the engineering stress versus extensional strain. On the other hand, Balmforth et al.37 investigated drips and bridges of different yield-stress materials and compared their experimental results with the viscoplastic slender theory they developed. Also, they used this theory to study the pinching dynamics of yield stress materials.38 During the last stages before pinching, the break-up dynamics became universal, and dictated by simple power laws which depended only on material properties. They predicted that the scaling laws were the same as the ones for Generalized Newtonian fluids39,40 and that the yield stress had almost no effect on the scaling law. Also, Huisman et al.6 studied the pinching dynamics of yield stress materials experimentally. Even though their experimental results demonstrated that yield stress materials followed the scaling laws of shear-thinning materials, a small cylindrical neck was formed connecting the upper and lower conical parts of the bridge, which was also found in the experiments of Niedzwiedz et al.35 However, neither Huisman et al.6 nor Niedzwiedz et al.35 reported the elastic modulus of their materials. Later, Moschopoulos et al.41 performed 2D simulations and presented a parametric study for the bulk and pinching dynamics of the thread in viscoplastic bridges. Their simulations also verified the previously mentioned scaling laws for viscoplastic materials.6 However, their simulations did not capture the cylindrical neck that Huisman et al.6 and Niedzwiedz et al.35 reported.
times the shear yield stress. This inconsistency originated from the contributions of elastic stresses in the Von Mises criterion, as Varchanis et al.18 explained. Nelson et al.36 studied yield stress materials that achieved extremely large extensional deformations and they reported the evolution of the engineering stress versus extensional strain. On the other hand, Balmforth et al.37 investigated drips and bridges of different yield-stress materials and compared their experimental results with the viscoplastic slender theory they developed. Also, they used this theory to study the pinching dynamics of yield stress materials.38 During the last stages before pinching, the break-up dynamics became universal, and dictated by simple power laws which depended only on material properties. They predicted that the scaling laws were the same as the ones for Generalized Newtonian fluids39,40 and that the yield stress had almost no effect on the scaling law. Also, Huisman et al.6 studied the pinching dynamics of yield stress materials experimentally. Even though their experimental results demonstrated that yield stress materials followed the scaling laws of shear-thinning materials, a small cylindrical neck was formed connecting the upper and lower conical parts of the bridge, which was also found in the experiments of Niedzwiedz et al.35 However, neither Huisman et al.6 nor Niedzwiedz et al.35 reported the elastic modulus of their materials. Later, Moschopoulos et al.41 performed 2D simulations and presented a parametric study for the bulk and pinching dynamics of the thread in viscoplastic bridges. Their simulations also verified the previously mentioned scaling laws for viscoplastic materials.6 However, their simulations did not capture the cylindrical neck that Huisman et al.6 and Niedzwiedz et al.35 reported.
In this work, we aim to deepen our understanding of the dynamics of filament stretching of yield stress materials accounting for the elasticity that these materials possess. To accomplish this, we undertake a computational study of an extending elastoviscoplastic bridge. To introduce elastic effects, we employ the Saramito–Hershel–Bulkley model.20 As a base material, we use a 0.2% Carbopol solution.12 We monitor the time evolution of the filament, its minimum radius, velocity, and the net traction force on the upper plate generated by the imposed velocity on the upper plate which we maintain constant. Also, we visualize the yielded/unyielded region inside the material as time progresses as well as the developed stresses, something that experiments cannot do until now. We show that at the last stages prior to pinching, a cylindrical neck develops connecting the upper and the lower part because viscoelastic stresses prevail when the strain rate in the neck increases rapidly. We find also that elasticity decreases the lifetime of the filament compared to the case where it is absent. Moreover, we perform a detailed parametric study varying all the important material properties, like the elastic modulus or the yield stress. For all the examined cases, we also simulate the corresponding viscoplastic materials to explore the difference that elasticity induces in filament stretching dynamics of yield stress materials not only in the bridge shape but also in the evolution of the minimum radius and the force on the upper plate.
The present work is organized as follows. In Section 2, the problem formulation is presented, and the equations and boundary conditions that govern the problem are introduced. In Section 3, we review, briefly, the solution method. We dedicate Section 4 to discussing our 2D results concerning the filament stretching of elastoviscoplastic materials. Finally, we summarize our findings in Section 5.
2. Problem formulation
We consider a bridge of an incompressible yield-stress material, as shown in Fig. 1. The sample is confined between two coaxial disks of radius![[R with combining tilde]](https://www.rsc.org/images/entities/i_char_0052_0303.gif) ; and an initial separation
; and an initial separation ![[L with combining tilde]](https://www.rsc.org/images/entities/i_char_004c_0303.gif) 0. Throughout the remainder of the paper, a tilde (∼) denotes a dimensional variable or parameter, while the absence of one denotes its dimensionless counterpart. The complex material exhibits an elastoviscoplastic response characterized by yield stress,
0. Throughout the remainder of the paper, a tilde (∼) denotes a dimensional variable or parameter, while the absence of one denotes its dimensionless counterpart. The complex material exhibits an elastoviscoplastic response characterized by yield stress, ![[small tau, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e5.gif) y, and elastic modulus,
y, and elastic modulus, ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) , and its rheological response is modeled by the Saramito–Hershel–Bulkley (SHB) model.20 We suppose that the material yields according to the von Mises criterion. A dynamically inactive, inert gas surrounds the filament. The surface tension,
, and its rheological response is modeled by the Saramito–Hershel–Bulkley (SHB) model.20 We suppose that the material yields according to the von Mises criterion. A dynamically inactive, inert gas surrounds the filament. The surface tension, ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) , of the fluid/gas interface remains spatially uniform and constant. At time
, of the fluid/gas interface remains spatially uniform and constant. At time ![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) = 0, the upper disk starts suddenly to move upwards with constant velocity, Ũ, in the vertical direction. Then, the material yields driven by the continuous stretching, a characteristic neck is formed connecting the upper and lower part of the bridge, and the filament eventually breaks.
= 0, the upper disk starts suddenly to move upwards with constant velocity, Ũ, in the vertical direction. Then, the material yields driven by the continuous stretching, a characteristic neck is formed connecting the upper and lower part of the bridge, and the filament eventually breaks.
We adopt a cylindrical coordinate system {![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) ,
, ![[z with combining tilde]](https://www.rsc.org/images/entities/i_char_007a_0303.gif) , θ}, where
, θ}, where ![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) is the radial coordinate,
is the radial coordinate, ![[z with combining tilde]](https://www.rsc.org/images/entities/i_char_007a_0303.gif) is the axial coordinate, and θ is the azimuthal angle. We position its origin at the center of the bottom disk. The
is the axial coordinate, and θ is the azimuthal angle. We position its origin at the center of the bottom disk. The ![[z with combining tilde]](https://www.rsc.org/images/entities/i_char_007a_0303.gif) coordinate is aligned vertically along the gravity vector, which points in the negative direction, i.e
coordinate is aligned vertically along the gravity vector, which points in the negative direction, i.e![[g with combining tilde]](https://www.rsc.org/images/entities/b_i_char_0067_0303.gif) = −
= −![[g with combining tilde]](https://www.rsc.org/images/entities/i_char_0067_0303.gif) ez. Also, we assume independence from the azimuthal angle; thus, we solve for the axisymmetric case. We employ the non-dimensionalization proposed by Balmforth et al.37,38 as we did in Moschopoulos et al.41 for the case of viscoplastic filaments. We use the disk radius
ez. Also, we assume independence from the azimuthal angle; thus, we solve for the axisymmetric case. We employ the non-dimensionalization proposed by Balmforth et al.37,38 as we did in Moschopoulos et al.41 for the case of viscoplastic filaments. We use the disk radius ![[R with combining tilde]](https://www.rsc.org/images/entities/i_char_0052_0303.gif) as a characteristic length. To obtain a characteristic time, we balance the capillary stress,
as a characteristic length. To obtain a characteristic time, we balance the capillary stress, ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) /
/![[R with combining tilde]](https://www.rsc.org/images/entities/i_char_0052_0303.gif) with the viscous stress,
with the viscous stress, ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) (1/
(1/![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) vc)n and the resulting viscous-capillary time scale is
vc)n and the resulting viscous-capillary time scale is  where
where ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) is the consistency parameter, and n is the shear-thinning exponent of the SHB model.20 Consequently, the characteristic velocity is
is the consistency parameter, and n is the shear-thinning exponent of the SHB model.20 Consequently, the characteristic velocity is ![[R with combining tilde]](https://www.rsc.org/images/entities/i_char_0052_0303.gif) /
/![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) vc and the characteristic stress is defined as
vc and the characteristic stress is defined as ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) (
(![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) vc)−n ≡
vc)−n ≡ ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) /
/![[R with combining tilde]](https://www.rsc.org/images/entities/i_char_0052_0303.gif) . In our problem, four dimensionless numbers arise: Oh, Bo, Ys, and Ec, given by:
. In our problem, four dimensionless numbers arise: Oh, Bo, Ys, and Ec, given by:
 | (1) |
Based on the previous arguments, the dimensionless momentum and mass conservation equations take the following form:
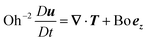 | (2) |
| ∇·u = 0 | (3) |
The extra stress tensor follows the SHB model, which can be expressed in dimensionless form as:
 | (4) |
 is the magnitude of the deviatoric part of the extra stress tensor, τd = τ − tr(τ)/tr(I),
is the magnitude of the deviatoric part of the extra stress tensor, τd = τ − tr(τ)/tr(I), ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e0a2.gif) = ∇u + (∇u)T is the deformation rate tensor, and the symbol ∇ over the stress tensor denotes the upper convected derivative, which is defined as:
= ∇u + (∇u)T is the deformation rate tensor, and the symbol ∇ over the stress tensor denotes the upper convected derivative, which is defined as: | (5) |
| n·(u − um) = 0, on Sf | (6) |
 | (7) |
 is the mean curvature of the free surface, ∇s = (I − nn)·∇ is the surface gradient operator,
is the mean curvature of the free surface, ∇s = (I − nn)·∇ is the surface gradient operator,  is the velocity of the mesh nodes in the fluid domain, and rf is the position vector of the free surface, which is given as rf = her + ζez, where h is its radial component and ζ is its respective axial one.
is the velocity of the mesh nodes in the fluid domain, and rf is the position vector of the free surface, which is given as rf = her + ζez, where h is its radial component and ζ is its respective axial one.
We solve for the axisymmetric case here; thus, we impose the symmetry conditions along the axis As:
| ns·T·ts = 0, on As | (8) |
| ns·u = 0, on As | (9) |
Also, we impose the no slip and no penetration conditions along the two disks
| u = Uez at z = L | (10) |
| u = 0 at z = 0 | (11) |
Regarding initial conditions, we assume that the bridge is initially motionless and under no stress:
| u(r, z, t = 0), τ(r, z, t = 0) = 0. | (12) |
| h(z, t = 0) = 1, ∀ζ ∈ [0, L0]. | (13) |
3. Numerical implementation
3.1 Finite element formulation
We employ the newly developed finite element formulation for free surface flow problems by Varchanis et al.42 to solve numerically the preceding system of equations. It permits using equal interpolants in all variables by optimally generalizing the PSPG formulation43 for viscoelastic materials, thus reducing the computational cost. It also uses the DEVSS numerical scheme44 to preserve the elliptic nature of the momentum equations and the SUPG45 formulation to cope with the hyperbolic character of the constitutive model equation. Varchanis et al.42 summarize the weak form of the momentum and mass balance equations and note essential implementation guidelines. This method has been already successfully implemented for the solution of viscoelastic filament stretching and other flows of elastoviscoplastic materials, like the flow through the cross-slot geometry18,46 and the bubble rise problem.19 It has been used also to solve long-standing problems in viscoelastic flows, such as the sharkskin instability.47We approximate all variables with linear, three-node Lagrangian basis functions. We use the arbitrary Lagrangian–Eulerian (ALE) method to track the deformation of the free surface of the filament as it stretches. We choose the quasi-elliptic grid generation scheme proposed by Dimakopoulos & Tsamopoulos48 with its corresponding boundary conditions. The computational domain, which remains undeformed and time-independent, coincides with the initial shape of the bridge. Regarding its implementation, the interested reader is referred to the works of Dimakopoulos & Tsamopoulos,48 and Chatzidai et al.49
3.2 Solution procedure
We discretize the solution domain using triangular elements. Initially, we create a structured mesh of quadrilateral elements that are subsequently split into two triangles. We prefer triangles over quadrangles because they accommodate better the large domain deformations that the stretching introduces. Next, we perform a systematic mesh convergence study to determine the spatial discretization required to obtain mesh-independent results. To this end, we solve a representative case on three different meshes. We generate the two finer meshes by sequentially doubling the elements of the previous mesh in both directions. We find that the optimal mesh, regarding the accuracy and computational cost, consists of 300 elements in the axial direction and 100 elements in the radial direction. We use this discretization to model the whole domain, from the top to the bottom plate and throughout the simulation. Hence at any value of the local radius, there are 100 elements in the radial direction within the filament. The larger number of elements in the axial direction are necessary to avoid remeshing procedures which inevitably induce numerical diffusion, while we achieve the same accuracy even when the bridge has elongated considerably towards the end of each simulation.Concerning the time integration, we employ the implicit Euler method for the first five time-steps. A first-order forward difference predictor precedes each implicit Euler step. Subsequently, we use a second order backward finite difference method for increased accuracy, preceded by a quadratic extrapolation for the predicted solution at each time step. We set the initial time step to 10−3. After 100 time-steps, it varies accordingly to control the time integration error by requiring the norm of the truncation error at the next time step to be equal to a tolerance of 10−5. For a detailed description of the procedure, the interested reader is referred to Syrakos et al.50 We implement Newton's iterative method to solve the resulting non-linear algebraic equations and calculate the Jacobian entries via finite differences. The iterations of Newton's method terminate when the norm of the residual vector falls below 10−8.
4. Results
In the present study, we examine the bulk dynamics of elastoviscoplastic filaments and how the various parameters affect them. The yielded regions of the bridge are drawn in red, while the unyielded ones are in blue. We consider that the filament break-up takes place when the minimum radius reduces to 10−2 times the initial radius. Beyond this minimum radius, the dynamics of the neck evolve so fast that the bulk shape changes very little. Thus, the simulations are terminated at this point, because they do not provide any additional insight concerning the bulk dynamics, whereas they become too expensive because they require finer meshes, longer times and higher computational cost near the pinching point. Detailed studies of the pinching dynamics will be pursued in later publications.As a base material, we choose the 0.2% Carbopol solution of Lopez et al.12 The parameters of the SHB model for this specific concentration are determined following a non-linear regression. The interested reader is referred to Moschopoulos et al.19 for more details. In Fig. 2, we plot the prediction of our EVP model superimposed on the experimental values, and we summarize the parameter values in Table 1. It is evident that the SHB model can accurately reproduce the steady shear experiments. Unfortunately, Lopez et al.12 did not perform experiments to measure extensional properties. As Moschopoulos et al.19 noted in the case of the bubble rise through an elastoviscoplastic material, when the model parameters were fitted only on shear data, the elastic nature of the material was slightly underestimated. Nonetheless, this did not present problems in understanding how elasticity affects the dynamics of elastoviscoplastic materials.
 | ||
| Fig. 2 Steady-state flow curve for the 0.2% Carbopol solution of Lopez et al.12 The symbols represent the experimental data, and the continuous line represents the model predictions. | ||
![[small tau, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e5.gif) y
y
|
![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif)
|
n |
![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif)
|
|---|---|---|---|
| 29.24 Pa | 7.893 Pa sn | 0.45 | 169.4 Pa |
We use the value of 0.073 N m−1 for the interfacial tension, ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) , for all simulations. Also, we assume that the disks have a radius of 3 mm, the upper-plate velocity is 14.8 mm s−1 and the initial separation is 6 mm. In experimental works,6,37 the upper-plate velocity varies typically between 0.6–26 mm s−1, and the initial separation varies between 3–12 mm. Based on these assumptions, we summarize the dimensionless numbers corresponding to the base material in Table 2.
, for all simulations. Also, we assume that the disks have a radius of 3 mm, the upper-plate velocity is 14.8 mm s−1 and the initial separation is 6 mm. In experimental works,6,37 the upper-plate velocity varies typically between 0.6–26 mm s−1, and the initial separation varies between 3–12 mm. Based on these assumptions, we summarize the dimensionless numbers corresponding to the base material in Table 2.
| Oh−2 | Y s | Bo | Ec | U | L 0 |
|---|---|---|---|---|---|
| 0.046 | 1.25 | 1.26 | 0.14 | 0.45 | 2 |
4.1 Base case – time evolution
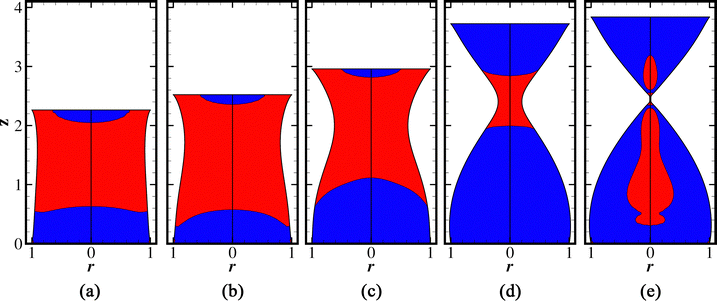
We start our study by investigating the time evolution of the bridge choosing the value of 0.45 for the dimensionless upper-plate velocity, and the value of 2 for the initial separation.Initially, the material liquefies almost entirely because of the sudden extension (Fig. 3(a)). Small portions of the material remain unyielded near the lower and the upper plate due to the no-slip and no-penetration boundary conditions. As time progresses (Fig. 3(b)), most of the yielded material concentrates near the neck, where larger elongational and shear stresses develop due to the conical shape of the neck, as Moschopoulos et al.41 showed in the case of viscoplastic filaments. The lower part of the material becomes increasingly unyielded. Also, the bridge grows to be asymmetric because of the asymmetry in the motion (only the upper plate is pulled, and inertia is accounted for) and the gravity force. Later (Fig. 3(c)), stronger necking of the bridge occurs. At the same time, the accelerating thinning of the neck is enough to counterbalance the increase of the height of the filament due to stretching and to conserve the mass of the material. Stresses drop below the yield stress in most of the filament because material deforms slightly. Thus, most of the material becomes unyielded. The neck now carries the burden of the deformation and shrinks faster to zero. From Fig. 3(d), we observe that the radius of the lower part increases slightly even though the material remains unyielded. This is permitted by the elastoviscoplastic constitutive equation, which models the unyielded phase as a hyperelastic solid that deforms elastically even below the yield limit. On the contrary, this was not observed in the case of viscoplastic filament stretching41 because viscoplastic models assumed the unyielded material to remain undeformed disallowing such deformation.
At the last stages prior to pinching (Fig. 3(e)), material elasticity opposes the abrupt shrinkage of the neck, by developing significant elastic stresses, which give rise to the observed elongated neck that connects the upper and lower part of the filament. Notice that the minimum radius decreases from 0.2 to 0.01 in approximately 0.25 dimensionless time.
This neck structure is typically observed in viscoelastic filament stretching dynamics29 but was not predicted in earlier viscoplastic simulations.37,41 Still, it was demonstrated in experimental works regarding filament stretching of yield stress materials,6,35 but the ideal viscoplastic theory could not explain it because it excluded elasticity. For example, for a concentrated water acrylic paint mixtures (Fig. 16 in ref. 6 and Fig. 3 (top row) in ref. 35), a long neck was formed connecting the upper and lower parts of the filament. Another interesting point is that the yielded areas are not extremely localized very near the neck but extend inside the lower and the upper part of the filament. The reason for this is the following: the neck is evacuated extremely fast; thus, the generated axial velocity is quite large. In conjunction with the intermediate Ys number, this yields the material near the neck and the evacuating material penetrates and compresses it. The yielded area in the lower part of the filament extends much further in the axial direction than its upper counterpart due to the effect of gravity which pulls material downwards.
It is important to compare the stretching of an elastoviscoplastic material with the case of a viscoplastic one with the same material parameters excluding elasticity. Hence, we set Ec = 0 to obtain the Hershel–Bulkley (HB) model51 and we perform the same simulation again. To deal with the stress indeterminacy that viscoplastic models possess, we employ the stabilized PAL method.52 The interested reader can find more information on the implementation of this method in ref. 52. In Fig. 4(a)–(c), we compare side by side the filament shapes of the two cases at three instants. For early times (Fig. 4(a)), the differences between the two materials are small. The EVP material presents larger unyielded regions because it can deform elastically prior to yielding compared to the VP case, where any deformation yields the material. The same pattern persists for intermediate times (Fig. 4(b)). However, as we approach pinch-off, larger differences arise, and the VP filament breaks much later in time. In the examined case, the VP bridge breaks at a time equal to 5.932, whereas the EVP counterpart breaks at 4.085. In the VP case, the absence of elasticity does not permit any deformation below the yield stress. So, more material yields and drifts upwards, leading to longer filaments and increasing the pinching time. Moreover, as time progresses, most of the material becomes unyielded in the EVP counterpart, as shown in Fig. 3(d). Even though the solid phase can deform slightly, the accelerating shrinking of the yielded areas in the neck region compensates mainly for the filament stretching. Thus, elasticity paves the way for the neck region to carry alone the burden of deformation. The neck of the EVP filament shrinks eventually faster to zero compared to the VP case. We plot the neck shape for both materials at pinch-off (Fig. 4(d)). The neck of the EVP material is clearly long and slender like the one observed when viscoelastic materials are stretched.29 On the other hand, the VP case is neither slender (n < 0.66) nor long, in accordance with the findings of Renardy & Renardy53 and Suryo & Basaran40 for power law fluids. The difference in the pinching times between the two materials motivate us to reexamine Fig. 2 in the work of Moschopoulos et al.,41 where they compare viscoplastic numerical simulations against the experiments of Balmforth et al.37 Even though the 2D simulations show very good agreement with experiments regarding the bridge shape, they predict larger pinching times for both materials, namely Carbopol solution and Kaolin suspension. Following the present study, we suggest that viscoplasticity fails to predict accurately the pinching times in these cases because elasticity is excluded.
In Fig. 4(e), we plot the time evolution of the minimum radius, hmin, for EVP and VP materials to visualize their differences better. Up to time equal to 3, the evolution of the minimum radius is approximately the same. After this point, the thinning of the neck accelerates in the EVP filament for the reasons explained above, and it becomes abrupt after a value of the minimum radius equal to 0.1. On the other hand, the thinning is gradual for the VP counterpart because more material is yielded, and the fast evacuation of the neck occurs after the minimum radius reaches approximately the value of 0.02.
An important quantity to measure during filament stretching is the applied force on the upper disk. A force balance relates its value to the stress difference in the fluid, making the calculation of the extensional viscosity possible. A thorough analysis of the force balance that includes the effects of inertia and surface tension is presented in the work of Szabo.54 Also, the time evolution of the plate force can be used to quantify the tackiness of a viscoelastic material.55–57 In our case, the normal force, FPL, is obtained from the following expression:
 | (14) |
At this point, we examine the importance of surface tension in the propagation of the shear wave. Note that the present nondimensionalization does not permit excluding capillarity, because we use surface tension to scale stresses and pressure. To this end, we use as characteristic velocity the velocity of the upper plate and we rescale stresses and pressure with the viscous stress scale, namely  . Note that in this case, the capillary force is not equal to the viscous stress scale. Now, the capillary number,
. Note that in this case, the capillary force is not equal to the viscous stress scale. Now, the capillary number,  arises that divides the curvature terms in the interface force balance (right-hand side of eqn (7)). Assuming for the sake of the present examination that Ca is very large, we can neglect the surface tension terms in the eqn (7) and perform the simulations again. Oscillations develop also when surface tension is excluded, and we conclude that it plays a minor role in the propagation dynamics of the shear wave.
arises that divides the curvature terms in the interface force balance (right-hand side of eqn (7)). Assuming for the sake of the present examination that Ca is very large, we can neglect the surface tension terms in the eqn (7) and perform the simulations again. Oscillations develop also when surface tension is excluded, and we conclude that it plays a minor role in the propagation dynamics of the shear wave.
Having clarified the nature of these oscillations, we can also calculate their period. Up to time equal to 0.9, the elapsed time between two maxima in the plate force is approximately 0.2 (Fig. 4(f)). As a first approximation, the wave travels a 2L0 = 4 distance during this period, which is the distance from the upper to the bottom plate and back. Of course, the upper plate moves constantly upwards, but the total length increase of the filament up to time equal to 1 is 0.45 which is small compared to the initial length of the filament (L0 = 2). The shear wave speed, VSW, is calculated as the square root of the ratio of the elastic modulus over the density of the material  which reads in dimensionless form:
which reads in dimensionless form:
 | (15) |
 which compares nicely with the 0.2 value found in simulations. Note that if we disregard gravity via setting Bo = 0, we find the wave period equal to 0.25 from simulations, which is even closer to the theoretical value. During this period, the material does not yield because the upper-plate velocity is small enough. Thus, a viscous dissipation mechanism does not exist to lessen these oscillations. If we add numerically a minuscule amount of dissipation in the solid phase, these oscillations do not appear. As time progresses, the material yields, and viscous dissipation increases, damping the oscillations, which cease to exist after a time equal to 1.
which compares nicely with the 0.2 value found in simulations. Note that if we disregard gravity via setting Bo = 0, we find the wave period equal to 0.25 from simulations, which is even closer to the theoretical value. During this period, the material does not yield because the upper-plate velocity is small enough. Thus, a viscous dissipation mechanism does not exist to lessen these oscillations. If we add numerically a minuscule amount of dissipation in the solid phase, these oscillations do not appear. As time progresses, the material yields, and viscous dissipation increases, damping the oscillations, which cease to exist after a time equal to 1.
On the other hand, the VP material starts from a large force on the upper plate and then the force decreases gradually. Here, the material yields immediately following a generalized Newtonian constitutive law. No oscillations are encountered, and the force does not increase from zero because elasticity is excluded. After this initial different response, the forces show a similar trend as both decrease assuming comparable values. However, the decrease is steeper for the EVP filament because smaller yielded areas exist than in the VP counterpart, and the neck thins faster, which results in a smaller required force because the upper-plate velocity remains constant. During the last stages of the stretching, the force even changes sign becoming negative. Notice that the filament radius has not reached yet its minimum permitted value in this instance. Now, capillarity is strong enough to drive the process, and in conjunction with the strain rate thinning nature of the EVP and VP materials, the fluid evacuates the neck much faster. At these moments, the thinning evolves so fast that the location of the upper plate barely moves upwards. Thus, the evacuating material “sees” the other parts of the filament as if they are immobile and compresses them. This compression is why the upper-plate force changes sign, which denotes that the material pushes the upper plate in the direction of its motion. Still, the rate of decrease grows for the EVP, which is not the case for the VP counterpart. In the latter, the force decreases at a lower rate.
Our results for EVP materials are qualitatively similar to the experiments by Nelson et al.36 We cannot perform a quantitative comparison because they have not reported the elastic modulus of the materials they have used. In their paper, they have plotted the engineering stress, which is related to the force on the upper plate, versus the extensional strain. The latter corresponds to the dimensionless time in our plots. Their figures clearly depict the initial growth of the force on the upper plate followed by its decrease. However, oscillations cannot be distinguished, and the rate at which the force decreases is lower in experiments. The initial, transient oscillations are not observed in experiments because the solid phase of yield stress materials possesses viscous dissipation and does not behave as a hyperelastic solid. We attribute the slower decrease of the force to the fact that we use the surface tension of water which is larger than in most yield stress materials. Nelson et al.36 do not report the surface tension of their materials. Also, the accurate measurement of surface tension is in fact not easy because plasticity and the experimental protocol influence the measured value.62
Having compared the evolution of the force on the upper plate between EVP and VP material, we choose to make such a comparison between elastoviscoplastic and viscoelastic materials. During the filament stretching of viscoelastic bridges, the measured force decreases but then increases suddenly.63 Viscoelastic materials show strain-hardening effects, and the extensional viscosity increases considerably.28 The material in the neck region becomes increasingly difficult to stretch further, and the unstretched material near the plates becomes relatively easier to pull, which increases the required force on the upper plate. However, as Kordalis et al.46 explain, the microstructure of these EVP materials cannot support strain-hardening effects, and the extensional viscosity decreases when the strain rate increases. Thus, the force does not increase monotonically but reaches a maximum. The same observations with ours are made in the work of Zhang et al.,64 where they measured the needed force to stretch the examined yield stress materials using rough and smoothed plates (Fig. 1 in ref. 64).
A key finding of the present study is the formation of a cylindrical neck that stems from the increased viscoelastic response of the material that opposes the sudden shrinkage of the neck. To support our argument, we track the evolution of the local extension rate at the location of the minimum radius, which is given by:
 | (16) |
 for EVP and VP materials. In both cases, the local extension rate remains fairly small until the very last moments before pinching. Small differences arise during the initial transient. In the EVP fluid, oscillations are encountered due to the aforementioned reasons. Also, the extension rate of EVP material is slightly lower than the VP one. VP simulations show extensive yielding of the filamentous bridge; thus, surface tension pushes material inwards. When we account for elasticity, the material stays unyielded for longer, and surface tension does not influence the dynamics. Near pinch-off, the extension rate diverges suddenly, and its value grows larger for the EVP material
for EVP and VP materials. In both cases, the local extension rate remains fairly small until the very last moments before pinching. Small differences arise during the initial transient. In the EVP fluid, oscillations are encountered due to the aforementioned reasons. Also, the extension rate of EVP material is slightly lower than the VP one. VP simulations show extensive yielding of the filamentous bridge; thus, surface tension pushes material inwards. When we account for elasticity, the material stays unyielded for longer, and surface tension does not influence the dynamics. Near pinch-off, the extension rate diverges suddenly, and its value grows larger for the EVP material  than its VP counterpart
than its VP counterpart  . This behavior of extension rate in EVP material triggers their elastic response, and the thread is formed. Viscoplastic simulations exclude elasticity, so the increase in the extension rate does not alter the filament dynamics. In the same figure, we plot also a locally defined Weissenberg number, Wilocal, which reads as follows:
. This behavior of extension rate in EVP material triggers their elastic response, and the thread is formed. Viscoplastic simulations exclude elasticity, so the increase in the extension rate does not alter the filament dynamics. In the same figure, we plot also a locally defined Weissenberg number, Wilocal, which reads as follows: | (17) |
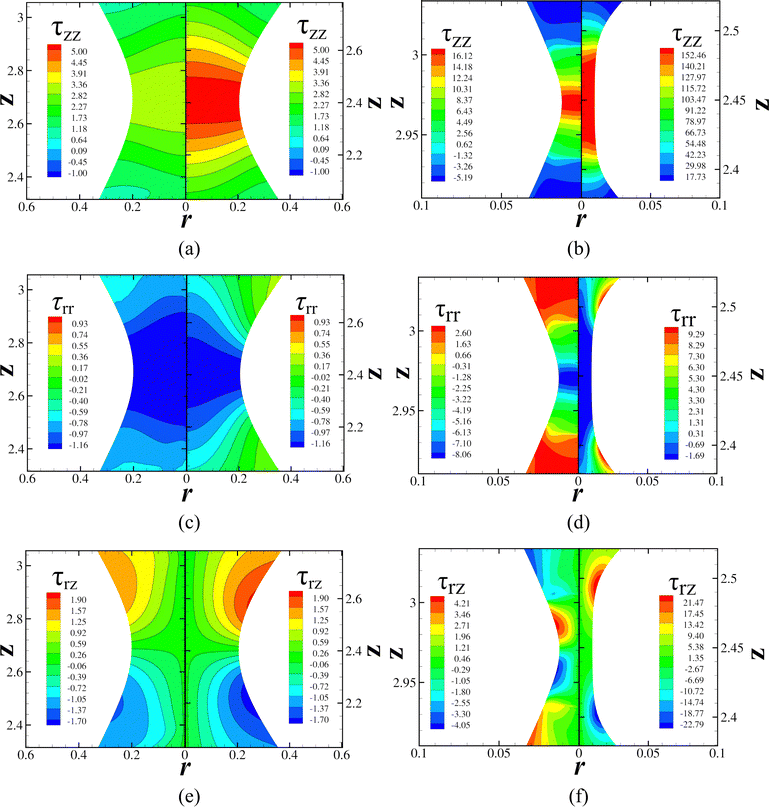
To understand the extensional flow dynamics further it is customary to measure the stress field inside the fluid experimentally. Although techniques have been developed to measure the stress field, like flow birefringence,65,66 and applied successfully in viscoelastic flows, they have not been adapted to yield stress materials. On the other hand, numerical simulation results, like the present ones, provide insights into the developed stresses. We compare the contours of the τzz, τrr, and τrz stress components between the EVP and VP materials in the neck region for two minimum radius values, hm = 0.2 (Fig. 5(a), (c) and (e)) and hm = 0.01 (Fig. 5(b), (d) and (f)). Note that the required time for each filament to reach the selected radius value is different. In all figures, the left-hand side corresponds to the VP material and the right-hand side corresponds to the EVP one.
We examine initially the axial stress component, τzz, for hm = 0.2 (Fig. 5(a)). In both fluids, τzz shows the same variation. Near the minimum radius, τzz is almost independent of the radial coordinate, but the region that this holds is small. When we move away from the neck, the radial dependence becomes apparent. The positive values denote that the material elements are stretched along the axial coordinate. The difference between the two materials is mainly found in the value of the axial stress, which is larger for the EVP material. The increased stresses arise from the presence of elasticity in the EVP material and the faster evacuation of the neck, which can be clearly seen in Fig. 4(e) and (g). Next, we plot the contours of the radial stress component, τrr, for hm = 0.2 (Fig. 5(c)). Again, their radial dependence fades away when we are near the neck, and they are negative because the material is compressed radially. Although the values of the radial component are comparable between the two materials, they decrease greatly as we move from the neck region in the EVP case and become positive. For the VP case, they remain negative around the neck and change sign very far from it (not shown here). This axial variation of τrr is an indirect consequence of elasticity in the EVP constitutive model. As we have shown in Fig. 4(b), which corresponds to the case of hm = 0.2, the unyielded areas in the EVP material are closer to the neck and act as an “obstacle” that opposes the axial motion of the material elements. Thus, the material gets slightly compressed as it reaches the unyielded regions, and a radial flow develops to satisfy the continuity constraint, leading to positive radial stresses. We do not observe important differences between the two materials for the shear stress component, τrz, shown in Fig. 5(e). They are concentrated in the region of maximum free surface curvature or where the curvature changes fast, which is very close to the neck region, as Moschopoulos et al.41 have shown. Once more, the EVP material shows slightly larger shear stresses resulting from the faster neck evacuation.
Next, we investigate the dynamics of the stress components when the minimum radius is equal to 0.01. Regarding the axial stress component (Fig. 5(b)), it increases abruptly during the final stages prior to pinching in the EVP material and withstands the fast evacuation of the neck. As a result, a cylindrical neck is formed, as shown in Fig. 4(d). We observe that inside the formed thread, τzz does not vary radially or axially, but it does so closer to the top and bottom plates. Thus, inside the neck, we can assume that an almost ideal uniaxial elongation flow field is developed. In the VP material, the value of τzz is much smaller than the EVP one. Specifically, in the under-investigation case, τEVPzz is equal to 152.46 whereas its VP counterpart τEVPzz is equal to 16.12, which results in one order of magnitude difference. Near the necking region, it does not vary radially like the EVP counterpart, but we observe axial dependence as we move away from the point of the minimum radius.
Differences arise also regarding τrr. EVP simulations (Fig. 5(d)) predict smaller radial stresses than VP ones in the neck region, where in the latter, the value is four times larger than the former. Radial stresses are found independent of the radial and axial coordinates inside the thread for the EVP material, whereas the filament area that this holds true is smaller in the VP case. As far as the shear stresses are concerned, they are much larger in the EVP fluid (Fig. 5(f)) than the VP counterpart away from the neck. On the contrary, inside the cylindrical neck they are very small (Fig. 5(f)), strengthening our argument that a uniaxial elongational flow field is developed in the EVP case. In contrast, in the VP counterpart, this applies only in a very confined area around the point of minimum radius. As we move away from the neck, the sign of the shear stresses changes both for VP and EVP material (not shown in Fig. 5(f) due to the magnification around the thread). Right above the locus of the minimum radius, material moves towards the axis of symmetry with negative radial velocity, and at the same time, it has a positive axial one. When we consider the curvature change in the region, positive shear stresses arise. However, when we move further above, the material continues translating upwards with a positive radial velocity. So, the shear stresses become negative. The same arguments apply when we move towards the bottom plate, but now the axial velocity is negative, resulting in the opposite sign of the shear stresses.
4.2 Effect of the yield stress parameter
We continue our study by investigating the effect of the yield stress parameter, Ys, on the bulk dynamics. In Fig. 6(a), we present the case of Ys = 0.125. We observe that the plastic nature of the material weakens. The whole material yields except for a minimal unyielded area around the center of the upper disk. The shape is qualitatively different from that of a viscoplastic filament, where the decrease of Ys leads to a simple viscous response and a very long cylindrical neck.41 The viscoelastic nature of the present material is not affected by the decrease of Ys, thus the upper and lower part of the filament are connected with a small, elongated neck. In addition, the effect of flow asymmetry and gravity are prominent because the asymmetry of the bridge increases, and the lower part of the filament resembles a sessile drop.Increasing Ys (Fig. 6(b), which is the case shown in Fig. 3(d)), a larger portion of the material becomes unyielded because the developed internal stresses are below the yield limit. Plasticity also hinders the effect of gravity because the asymmetry between the upper and the lower part of the filament decreases.
A further increase of Ys makes plasticity predominant, and the yielded areas concentrate exclusively around the neck. However, flow asymmetry and gravity are still dominant in contrast with the case of viscoplastic materials, where their effect diminishes for large plasticity, and symmetric filaments are predicted.41 Notice that Ys = 2.25 is the largest Ys we examine here, which results in 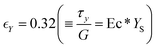 . We choose not to exceed this value of the yield strain because we prefer our parametric study to follow closely “real” yield stress materials. It is quite interesting that the length of the neck increases slightly for Ys = 2.25. As Varchanis et al.18 and Kordalis et al.46 argue, a large yield strain number (which corresponds to the case of Ys = 2.25) results in a stronger elastic response. Thus, the material reacts forcefully with the sudden decrease of the neck radius that results in the observed length increase. Still, lengthy, elongated necks like the ones found in viscoelastic materials cannot be supported by the elastoviscoplastic theory, because it predicts monotonic extension-rate thinning, which eventually decreases viscoelastic stresses.
. We choose not to exceed this value of the yield strain because we prefer our parametric study to follow closely “real” yield stress materials. It is quite interesting that the length of the neck increases slightly for Ys = 2.25. As Varchanis et al.18 and Kordalis et al.46 argue, a large yield strain number (which corresponds to the case of Ys = 2.25) results in a stronger elastic response. Thus, the material reacts forcefully with the sudden decrease of the neck radius that results in the observed length increase. Still, lengthy, elongated necks like the ones found in viscoelastic materials cannot be supported by the elastoviscoplastic theory, because it predicts monotonic extension-rate thinning, which eventually decreases viscoelastic stresses.
In Fig. 6(d), we plot the time evolution of the minimum radius for each case of Ys both for EVP and VP materials. The time for pinching decreases monotonically as we increase Ys in the EVP model, but non-monotonically for the VP cases. For small Ys values, most of the material is yielded and surface tension drives the evacuation of the liquid from the neck both in EVP and in VP bridges. For intermediate (Ys = 1.25) values of Ys, decreasing pinching times are predicted for an EVP material, but increasing ones are found for the VP counterpart. This can be explained as follows: with increased plastic nature, the elastoviscoplastic material is mainly unyielded in the upper and lower parts of the bridge. These unyielded parts present increased viscoplastic resistance to deformation. So, the neck carries all the burden of stretching and shrinks faster to zero. However, in the VP material, larger yielded areas are located in the upper and lower parts of the filament and present an increased viscous resistance that opposes the thinning of the neck, resulting in longer filaments. For large enough (Ys = 2.25) values of Ys, both materials show decreasing pinching times. Now, the increased viscoplastic resistance of the materials leads to smaller yielded areas, and the neck thins faster to zero because it carries alone the deformation burden. Independently from the Ys value or from simulating an EVP or VP material, the minimum radius falls rapidly when it reaches a critical point (Fig. 6(d)).
We visualize the effect of YS on the upper-plate force in Fig. 6(e). In the EVP case, the duration of the initial oscillations depends on Ys. As we increase Ys, greater deformation is needed for the material to yield, leading to a larger force maximum, which is also attained later in time. Prior to their fluidization, these materials are assumed to be Neo-Hookean solids with the same elastic modulus. The evolution of the force is the same (even the local oscillation extrema) irrespective of Ys until yielding, because the shear wave does not depend on Ys (eqn (15)). However, for small Ys, the filament yields sooner in time, and the viscous effects damp sooner the oscillations. In the VP filament, the force attains its maximum value immediately, which depends on Ys. The increased plastic nature of the material necessitates stronger forces so that the material yields and starts to deform. After the maximum force value of the EVP bridge, the force evolution is very similar irrespective of the type of material we simulate. Especially for the smallest Ys (Ys = 0.125), their differences are almost indistinguishable, except from the last stages prior to pinching, where we predict a shorter pinching time for the EVP material for reasons explained in Section 4.1. Also, we observe that the force decreases faster for the intermediate and large Ys than the small Ys. For small Ys, the plastic nature of the material cannot affect the stretching dynamics, and most of the material is yielded. Thus, most of the material deforms in response to the imposed stretch, and the neck does not thin fast. This holds also for the viscoplastic case, but the differences in the slope of the upper-plate force are much smaller.
4.3 Effect of the pulling velocity
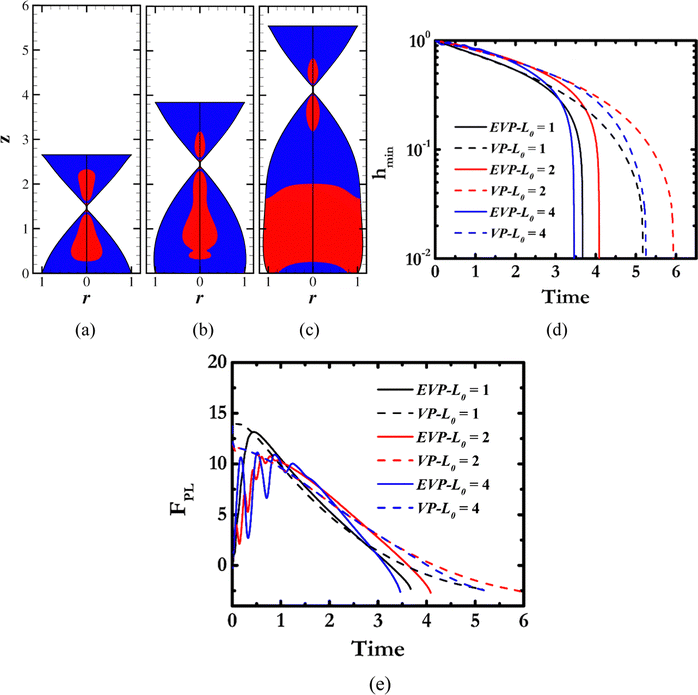
We continue by examining the effect of the upper-plate velocity when we increase it by an order of magnitude at a time. For the smallest velocity (U = 0.045), the neck that connects the upper and the lower part of the filament is smaller than the one found for U = 0.45. When we increase the velocity, we amplify the elastic response of the material, and the elongated neck is longer. This comparison shows how important it is to correctly characterize the sample and not assume that elastic effects are not important only from flow experiments, especially if the extensional flow field is not strong enough. Also, the filament reaches a somewhat larger height for a larger velocity. The small upper-plate velocity (Fig. 5(a)) induces small deformations during the early stages that do not result in extensive yielding of the material. As a result, a smaller portion of the filament carries the burden of deformation, and the upper plate cannot reach the same height as for U = 0.45 (Fig. 7(b)).However, clearer differences in shape arise when we further increase the plate velocity (Fig. 7(c)). Now, a prolonged and distinct neck is formed, and its shape is qualitatively different from the previous cases. At a time well before break-up, we have the minimum radius only at one axial location, as in Fig. 7(a) and (b), but when pinching approaches, the radius of the bridge develops two minima at two axial positions. As a result, a satellite drop tends to form between the upper and lower part of the filament, which we visualize better by plotting the radial and axial velocity contours side by side near the neck at the stage prior to pinching in Fig. 7(d). This phenomenon is usually observed in low-viscosity fluids, but it has not been reported for viscoplastic materials. The mechanism that leads to the present structure reads as follows. The increased velocity of the upper plate amplifies the elastic response of the material, which opposes the extremely fast evacuation of the neck, so a longer neck is formed. However, the continuously increasing extensional components of the rate-of-strain tensor decrease the extensional viscosity of the material and render viscoelastic stresses weaker. Consequently, inertia grows dominant due to the large upper-plate velocity, despite the small value of Oh−2 (Oh−2 = 0.046) leading to the formation of the satellite drop structure. The shape and size of the yielded part of the material in its lower section does not vary too much, but its size increases particularly in the highest velocity in the upper part.
In Fig. 7(d), we plot the evolution of the minimum radius of the bridge. As expected, for small velocities, the filament breaks later (t ≈ 40). Larger velocities induce increased viscoelastic forces that drag more material upwards and lead to longer filaments (Fig. 7(b) and (c)). Nevertheless, material evacuates the neck faster, resulting in shorter break-up times. Also, VP materials follow the same trend. Still, the VP filament is stretched for a longer time and the difference in pinching time increases with the upper-plate velocity.
We also examine the time evolution of the upper-plate force (Fig. 7(e)). Here, the initial, transient evolution of the force depends strongly on the upper-plate velocity, especially in the EVP material. For small U (U = 0.045) values, the force starts from a very small but negative value. The free surface has deformed slightly, and the surface tension pushes material inwards. However, the viscoelastic stresses do not increase to oppose the movement of the plate during the early stages of stretching because the plate velocity is quite small. After some time, oscillations appear, and they fade away when the material yields. The corresponding VP case does not predict a negative force because viscous stresses increase abruptly in response to the sudden stretching. However, they remain constant for a longer period. Increasing U (U = 0.45), the oscillations are short lived in the EVP filament and the force does not start from negative values. We notice that the forces for both materials start to decrease approximately at the same time. For very large values of the upper-plate velocity (U = 4.5), the oscillations are almost gone in the EVP bridge because the material yields faster due to the faster stretching. Also, the force does not increase from zero but from a finite value because at the first time step the amplified inertial effects oppose the pulling of the upper plate. The VP counterpart predicts a very large value (≈42) for the upper-plate force due to inertia effects, which is not shown in the figure due to the choice in the range of the ordinate. Also, irrespective of the upper-plate velocity, the force on the upper plate decreases more abruptly in EVP than in VP materials.
4.4 Effect of the shear thinning exponent
Next, we examine the effect of the shear thinning exponent on the stretching dynamics. Fig. 8 shows results for n = 0.2 (Fig. 8(a)), n = 0.3 (Fig. 8(b)) and n = 0.45 (Fig. 8(c)). We choose not to exceed the critical value of n = 0.5. This choice stems from the fact that the SHB model predicts extension rate hardening for n > 0.5, which the microstructure of yield stress materials cannot support, as Kordalis et al.46 explain. Decreasing the shear thinning exponent, we amplify the shear and extension rate thinning nature of the material. The material around the neck presents a smaller viscoelastic force for smaller n, which cannot oppose the effect of the capillary force.Thus, the neck shrinks faster, and the filament breaks sooner. We observe that a smaller part of the material yields for smaller n (Fig. 8(a)) because only the neck carries all the burden of the deformation, which enables the stresses to relax, and the material becomes unyielded. Note that an island of yielded material is predicted to be surrounded by unyielded regions. This was not predicted in viscoplastic simulations37,41 because the ideal viscoplastic theory did not permit it. For ideal viscoplastic materials, the strain rate is zero in the unyielded parts. So, a yielded area where the strain rate is not zero cannot exist inside an unyielded one. In Fig. 8(d), we plot the time evolution of the minimum filament radius for EVP and VP materials. We predict that the break-up time monotonically decreases, when the shear-thinning exponent decreases, as explained above. Also, the HB model predicts extension rate thinning. Thus, smaller pinching times are predicted when we decrease the shear thinning exponent.
The variations of the shear thinning exponent present minimal alteration in the measured force on the upper plate (Fig. 8(e)). The predicted initial oscillations are not affected by its value because the elastic part of the constitutive equation does not depend on the shear-thinning exponent. For both materials, the force on the upper plate decreases with a slope that becomes steeper for smaller values of the shear thinning exponent because of the amplified extension rate thinning.
4.5 Effect of the elastocapillary number
To examine the effect of material elasticity, we vary the elastocapillary number. By selecting a small value (Ec = 0.014 in Fig. 9(a)), the viscoplastic nature of the material overcomes the elastic one. This becomes apparent primarily from the absence of an elongated neck, characteristic of the elastic response, and from the increased yielded areas. If we increase its value (Fig. 9(b) and (c)), a prolonged neck is formed, and its length increases further with larger values of Ec (Fig. 9(c)). We do not examine values of Ec greater than 0.25 because we do not wish to exceed the value of 0.32 for the yield strain, , and we are not aware of yield stress materials that have larger values of
, and we are not aware of yield stress materials that have larger values of 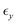 . Another important observation is that larger unyielded areas exist inside the bridge for increasing Ec number, originating from the increased elasticity that enables the unyielded regions to deform much more before they yield. However, this also affects the break-up time, which decreases monotonically with increasing Ec values (Fig. 9(d)). This can be explained as follows. The small Ec value (Fig. 9(a)) corresponds to a material that can sustain only slight deformations causing the nearly complete yielding of the filamentous bridge. The yielded material drifts upwards more easily, resulting in longer filaments and later break-up times, which are comparable to the VP case with Ec = 0. On the other hand, as we increase the Ec number, a smaller portion of the material yields because the solid phase can sustain larger deformations. When a neck is formed, and the material inevitably yields around it, its apparent viscosity is smaller than in the upper and lower unyielded parts of the filament. Thus, the deformation is concentrated only in the neck region, and the neck carries all the burden of the stretching and breaks eventually sooner. This phenomenon resembles the one presented previously in relation to Fig. 2(c) for Ys = 2.12.
. Another important observation is that larger unyielded areas exist inside the bridge for increasing Ec number, originating from the increased elasticity that enables the unyielded regions to deform much more before they yield. However, this also affects the break-up time, which decreases monotonically with increasing Ec values (Fig. 9(d)). This can be explained as follows. The small Ec value (Fig. 9(a)) corresponds to a material that can sustain only slight deformations causing the nearly complete yielding of the filamentous bridge. The yielded material drifts upwards more easily, resulting in longer filaments and later break-up times, which are comparable to the VP case with Ec = 0. On the other hand, as we increase the Ec number, a smaller portion of the material yields because the solid phase can sustain larger deformations. When a neck is formed, and the material inevitably yields around it, its apparent viscosity is smaller than in the upper and lower unyielded parts of the filament. Thus, the deformation is concentrated only in the neck region, and the neck carries all the burden of the stretching and breaks eventually sooner. This phenomenon resembles the one presented previously in relation to Fig. 2(c) for Ys = 2.12.
The great decrease of the elastic effects for the small Ec (Ec = 0.014) value is visualized even better when we plot the evolution of the upper-plate force in Fig. 9(e). This force grows suddenly for the elastoviscoplastic material and obtains the same value as the VP material. Still, there are oscillations that cease to exist in a short time. After this point, the EVP filament evolves just like the VP one, and slight differences arise in the last stages prior to pinching. When we increase the Ec number (Ec = 0.14 and Ec = 0.24), we amplify the elastic nature of the material. Thus, the viscoelastic stresses do not develop fast because the material remembers its previous stress state, resulting in a slower evolution of the upper-plate force. The increase of Ec also affects the period of the oscillations, which increases. This observation follows our argument that these oscillations are manifestations of a traveling shear wave whose velocity is given by eqn (15).
4.6 Effect of inertia
Thus far, we did not analyze inertia in depth because its effects were observed only in the case of a very large velocity (Fig. 7(c)) and only in the last stages before pinching. To examine the effect of inertia on the bulk dynamics we vary Oh−2. The importance of inertia depends on the pulling velocity, and therefore we select a large value of U = 3 for this examination.In Fig. 10(a), we plot the results for the case of zero inertia (Oh−2 = 0) and in Fig. 10(b) for the case of Oh−2 = 0.04. Despite this very small difference, qualitative differences arise between the two cases. The crucial one is the absence of a satellite drop between the upper and lower part in Fig. 10(a), because of the absence of inertia. The filament develops an elongated neck with only a single point of minimum radius at which the bridge eventually breaks. On the other hand, two pinching points appear in the case of Oh−2 = 0.04. If we increase further Oh−2 (Fig. 10(c)), we get a very different bridge shape. The satellite drop structure is absent. However, if we examine the filament closer, we find that there is also a second location, at z ≈ 2.9, which starts to evolve into a second break-up point, but the bridge breaks before a satellite drop grows. The early dynamics of the stretching dictate the peculiar shape of the filamentous bridge. For the large inertia, only the material very close to the upper plate “senses” the sudden extension. This part deforms and starts to thin earlier than the rest of the material, and the pinching point moves closer to the upper plate.
We visualize the effect of inertia on the break-up time by plotting the time evolution of the minimum radius (Fig. 10(d)) for elastoviscoplastic and viscoplastic materials. Initially, the radius evolution of the two smaller values of Oh−2 presents the same behavior, but the radius decreases faster for the larger Oh−2 As explained before, the deformation is not transmitted quickly to the whole filament for Oh−2 = 0.4, but it is localized only near the upper part of the material, which deforms earlier and shrinks faster to zero. However, as time progresses, the increased inertia decreases the rate of liquid evacuation from the neck, opposing the breakage driven by capillarity. Thus, we obtain larger break-up times and longer filaments. These observations hold true both for EVP and VP materials. However, the effect of inertia in VP materials is smaller than the one found in their EVP counterparts.
In Fig. 10(e), we plot the force on the upper plate for all cases. When inertia is absent (Oh−2 = 0), oscillations are not observed in the case of EVP. For negligible inertia, the shear wave speed tends to infinity because it is inversely proportional to Oh−2. So, we need infinitely small time-steps to observe the wave translation, which we are unable to do. When inertia is increased (Oh−2 = 0.04) coupled with the large U, the VP simulation predicts a very high value of the plate force, which decreases rapidly and follows the typical time evolution observed in previous cases. On the other hand, the EVP material does not exhibit a significant increase in the force on the upper plate. Also, the effect of the shear wave on the upper plate force is minor because the intense stretch of the material leads to its sooner yielding. The further increase of Oh−2 (Oh−2 = 0.4) just amplifies inertial effects without changing the previously explained pattern, and again no oscillations are present. When we increase Oh−2, we decrease the propagation speed of the shear wave (eqn (15)). However, the material yields before the wave reaches the upper plate, and viscous dissipation impedes it.
4.7 Effect of gravity
To investigate the effect of gravity, we choose to vary the initial separation of the disks. It is common to assess the importance of gravity by the value of the Bond number. However, the Bond number based on the characteristic scales we use does not depend on the height of the filament. Thus, it is helpful to introduce a modified Bond number, which we define as the ratio of the characteristic gravity force to a characteristic capillary force: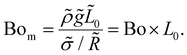 | (18) |
We plot the results for three different initial separations (and modified Bond numbers) in Fig. 11. For small separation or small modified Bond number (Fig. 11(a)), we obtain an almost symmetric filament because the effect of gravity is small. As we increase the separation (Fig. 11(b)), asymmetrical filamentous bridges arise, and a slightly larger area of the lower part of the filament deforms elastically. For the largest L0 that we examine (Fig. 11(c)), the effect of gravity is amplified even more, and the bulkier lower part yields under its own weight. Thus, the lower part of the bridge sags and extends sideways beyond the original radius of r = 1. However, the change of the initial separation does not bring any noticeable differences regarding the formed neck that connects the upper and the lower part of the bridge.
In Fig. 11(d), we plot the time evolution of the minimum radii, which shows a non-monotonic behavior with respect to the initial separation, irrespective of the presence of elasticity or not. From L0 = 1 to L0 = 2, the break-up time increases approximately by 0.25 for the EVP material and by 0.75 for the VP one, but this pattern is reversed for L0 = 4, where the shortest break-up time is predicted. We attribute this variation to the amplified gravitational force, which pulls the material downwards, accelerating the evacuation of the neck and the break-up of the filament.
The initial separation affects the transient response of the force on the upper plate in the EVP filament, but its effect is smaller in the VP material. For L0 = 1 with an EVP material, the oscillations are absent. For small L0, the effective extension rate (≡U/L0) is large, and the material yields sooner in time. Also, significant shear stresses develop near the plate due to the small aspect ratio and the applied no-slip condition, both of which contribute to the fast yielding of the material. Thus, the short-lived shear wave cannot affect the upper plate force. When we increase L0, the material remains unyielded for a longer period. Both the amplitude of the oscillation and the period increase with increasing L0. Let us explain this behavior in the framework established in Section 4.1. The period of the shear wave is proportional to the traveled distance. If we double it and keep constant the material properties, we expect the period to double, which we observe if we compare the red and blue lines in Fig. 11(e). Approximately three maxima of the upper force for the case of L0 = 2 (red line) develop, where two maxima are found for the case of L0 = 4 (blue line) for the same elapsed time, demonstrating period doubling. The increase of the amplitude in the upper plate force stems from the larger “resonant” cavity formed by the liquid bridge. Regarding the VP bridge, a larger force is needed to set the plate in motion for the small aspect ratio (L0 = 1) than the larger ones. As explained for the EVP counterpart, the higher effective extension rate yields most of the viscoplastic bridge and the material poses a greater viscous resistance to the imposed stretching. For the two larger L0 (L0 = 2 and L0 = 4), the force evolves independently of the initial aspect ratio, except from the last stages prior to pinching.
5 Conclusions
We investigated the stretching dynamics of a liquid bridge composed of yield stress material that exhibits both plastic and elastic effects simultaneously. We used the Saramito–HB constitutive equation20 to model the rheological response of these materials. We selected as a base case for our analysis a 0.2% Carbopol solution.12 We predict that the filament deforms initially as a hyperelastic solid. The sudden pulling of the upper plate generates a shear wave that translates through the medium. When it reaches the upper plate, it aids its upward motion. The material inevitably yields due to the constant stretching, and the viscous dissipation damps this wave, and the bridge evolves almost like a viscoplastic material. However, as the final stages prior to pinching are approached, a long and slender neck is formed, which connects the upper and the lower part of the filament. This structure appeared before in experimental studies dealing with yield stress materials,6,35 but the ideal viscoplastic theory cannot explain its presence because it excludes elasticity. Also, experiments36 show that the measured force on the upper plate grows gradually in time which agrees with our numerical results for elastoviscoplastic bridges. However, quantitative comparison between our numerical results with the experimental ones cannot be made because the elastic modulus of the materials is not reported. In these late stages, when the material evacuation rate in the pinching point is accelerating, elastic stresses grow abruptly, and oppose filament pinch-off. These stresses are responsible also for creating the long neck found in simulations and experiments of viscoelastic materials.The effect of elasticity is manifested also in the shape of the lower unyielded areas, which swell radially as opposed to the viscoplastic materials. Here, the unyielded areas can deform prior to yielding because they are assumed to behave as Neo-Hookean materials. Thus, the permitted, small deformation of the unyielded materials results in a more curved lower part of the filament. Also, elasticity leads to shorter pinching times compared with the case where it is not accounted for. The shorter times are caused by the larger areas inside the material that remain unyielded, which produce large differences in the apparent viscosity between the yielded regions found in the neck and the rest of the material. Eventually, the neck carries the burden of deformation and shrinks faster to zero.
We conducted a detailed parametric study varying all the dimensional parameters governing the dynamics of elastoviscoplastic filament stretching. The primary outcomes can be summarized as follows:
• Increasing the elastic nature of the material results in a longer neck, connecting the upper and lower parts of the filament. Still, shorter pinching times are predicted. Larger elasticity amplifies the growth of the elastic stresses when the strain rate increases. At the same time, more material remains unyielded because it can withstand greater deformation before yielding. Thus, the smaller yielded areas found in the filament lead to faster evacuation of the neck.
• Increasing material plasticity induces shorter filaments with shorter pinching times. An elongated neck is formed in all cases. We expected the formation of the elongated neck for large Ys leading to large yield strains based on the arguments of Varchanis et al.18 and Kordalis et al.46 that large yield strains result in a stronger elastic response of the material. However, even for the smallest Ys (εY = 0.0175) case (Fig. 4(a)), elasticity is unexpectedly still important, and a long neck appears. We can conclude safely that the yield strain alone cannot indicate whether elastoviscoplastic materials will show a viscoplastic behavior or not in filament stretching dynamics. To strengthen our argument, we simulated a case with smaller Ec, but with the same yield strain (Fig. 7(a)) as before. For small Ec, the viscoplastic nature of the material prevails and no neck is formed.
• For large enough upper-plate velocities, the filament develops two pinch-off points, despite the small value of Oh−2. The large strain rates inside the elongated neck lead to a considerable decrease in the viscoelastic stresses because the SHB model predicts monotonic strain rate thinning. Thus, inertia becomes dominant, and the filament breaks in two points.
In a forthcoming study, we will examine the pinching dynamics of elastoviscoplastic materials. We will investigate whether similarity solutions exist in elastoviscoplastic materials, as in Newtonian,67 viscoplastic,38,41 and viscoelastic31,68 materials. Also, we will determine the effect of elasticity on the values of the scaling exponents. Moreover, we will incorporate thixotropy. It has been shown that the properties of yield stress materials, such as the yield stress or the elastic modulus, can change and exhibit a time-dependent behavior. We will explore this and employ constitutive models proposed in ref. 69 and 70 that include this mechanism.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
We would like to thank the anonymous reviewers for their insightful comments that led to the improvement of our presentation of our work. This work was supported by the Hellenic Foundation of Research and Innovation, under grant HFRI FM17-2309, MOFLOWMAT. PM has been supported by the Hellenic Foundation for Research and Innovation (HFRI) under the 3rd Call for HFRI PhD Fellowships (Fellowship Number 5854).References
- I. Frigaard, Curr. Opin. Colloid Interface Sci., 2019, 43, 80–93 CrossRef CAS.
- C. J. Dimitriou and G. H. McKinley, Soft Matter, 2014, 10, 6619–6644 RSC.
- C. Hu and F. De Larrard, Cem. Concr. Res., 1996, 26, 283–294 CrossRef CAS.
- F. Mahmoodzadeh and S. E. Chidiac, Cem. Concr. Res., 2013, 49, 1–9 Search PubMed.
- L. Ma and G. V. Barbosa-Cánovas, J. Food Eng., 1995, 25, 409–425 CrossRef.
- F. M. Huisman, S. R. Friedman and P. Taborek, Soft Matter, 2012, 8, 6767–6774 RSC.
- J. M. Townsend, E. C. Beck, S. H. Gehrke, C. J. Berkland and M. S. Detamore, Prog. Polym. Sci., 2019, 91, 126–140 CrossRef CAS PubMed.
- V. H. M. Mouser, F. P. W. Melchels, J. Visser, W. J. A. Dhert, D. Gawlitta and J. Malda, Biofabrication, 2016, 8, 035003 CrossRef PubMed.
- A. M. V. Putz, T. I. Burghelea, I. A. Frigaard and D. M. Martinez, Phys. Fluids, 2008, 20, 033102 CrossRef.
- Y. Holenberg, O. M. Lavrenteva, U. Shavit and A. Nir, Phys. Rev. E: Stat. Nonlinear, Soft Matter Phys., 2012, 86, 066301 CrossRef PubMed.
- N. Mougin, A. Magnin and J. M. Piau, J. Non-Newton. Fluid Mech., 2012, 171–172, 42–55 CrossRef CAS.
- W. F. Lopez, M. F. Naccache and P. R. de Souza Mendes, J. Rheol., 2018, 62, 209–219 CrossRef CAS.
- D. Sikorski, H. Tabuteau and J. R. de Bruyn, J. Non-Newton. Fluid Mech., 2009, 159, 10–16 CrossRef CAS.
- A. Pourzahedi, M. Zare and I. A. Frigaard, J. Non-Newton. Fluid Mech., 2021, 292, 104531 CrossRef CAS.
- D. Fraggedakis, Y. Dimakopoulos and J. Tsamopoulos, Soft Matter, 2016, 12, 5378–5401 RSC.
- P. Saramito, J. Non-Newton. Fluid Mech., 2007, 145, 1–14 CrossRef CAS.
- J. G. Oldroyd, Math. Proc. Cambridge Philos. Soc., 1947, 43, 100–105 CrossRef CAS.
- S. Varchanis, S. J. Haward, C. C. Hopkins, A. Syrakos, A. Q. Shen, Y. Dimakopoulos and J. Tsamopoulos, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 12611–12617 CrossRef CAS PubMed.
- P. Moschopoulos, A. Spyridakis, S. Varchanis, Y. Dimakopoulos and J. Tsamopoulos, J. Non-Newton. Fluid Mech., 2021, 297, 104670 CrossRef CAS.
- P. Saramito, J. Non-Newton. Fluid Mech., 2009, 158, 154–161 CrossRef CAS.
- L. E. Rodd, T. P. Scott, J. J. Cooper-White and G. H. McKinley, Appl. Rheol., 2005, 15, 12–27 CAS.
- G. H. McKinley and A. Tripathi, J. Rheol., 2000, 44, 653 CrossRef CAS.
- B. Keshavarz, V. Sharma, E. C. Houze, M. R. Koerner, J. R. Moore, P. M. Cotts, P. Threlfall-Holmes and G. H. McKinley, J. Non-Newton. Fluid Mech., 2015, 222, 171–189 CrossRef CAS.
- J. Dinic, L. N. Jimenez and V. Sharma, Lab Chip, 2017, 17, 460–473 RSC.
- M. Rosello, S. Sur, B. Barbet and J. P. Rothstein, J. Non-Newton. Fluid Mech., 2019, 266, 160–170 CrossRef CAS.
- X. Zhang, R. S. Padgett and O. A. Basaran, J. Fluid Mech., 1996, 329, 207–245 CrossRef CAS.
- O. E. Yildirim and O. A. Basaran, Chem. Eng. Sci., 2001, 56, 211–233 CrossRef CAS.
- G. H. McKinley and T. Sridhar, Annu. Rev. Fluid Mech., 2002, 34, 375–415 CrossRef.
- S. L. Anna and G. H. McKinley, J. Rheol., 2001, 45, 115–138 CrossRef CAS.
- T. Sridhar, V. Tirtaatmadja, D. A. Nguyen and R. K. Gupta, J. Non-Newton. Fluid Mech., 1991, 40, 271–280 CrossRef CAS.
- C. Clasen, J. Eggers, M. A. Fontelos, J. Li and G. H. McKinley, J. Fluid Mech., 2006, 556, 283–308 CrossRef CAS.
- P. P. Bhat, S. Appathurai, M. T. Harris, M. Pasquali, G. H. McKinley and O. A. Basaran, Nat. Phys., 2010, 6, 625–631 Search PubMed.
- S. Varchanis, Y. Dimakopoulos, C. Wagner and J. Tsamopoulos, Soft Matter, 2018, 14, 4238–4251 RSC.
- L. Martinie, H. Buggisch and N. Willenbacher, J. Rheol., 2013, 57, 627–646 CrossRef CAS.
- K. Niedzwiedz, H. Buggisch and N. Willenbacher, Rheol. Acta, 2010, 49, 1103–1116 CrossRef CAS.
- A. Z. Nelson, R. E. Bras, J. Liu and R. H. Ewoldt, J. Rheol., 2018, 62, 357 CrossRef CAS.
- N. J. Balmforth, N. Dubash and A. C. Slim, J. Non-Newton. Fluid Mech., 2010, 165, 1147–1160 CrossRef CAS.
- N. J. Balmforth, N. Dubash and A. C. Slim, J. Non-Newton. Fluid Mech., 2010, 165, 1139–1146 CrossRef CAS.
- P. Doshi, R. Suryo, O. E. Yildirim, G. H. McKinley and O. A. Basaran, J. Non-Newton. Fluid Mech., 2003, 113, 1–27 CrossRef CAS.
- R. Suryo and O. A. Basaran, J. Non-Newton. Fluid Mech., 2006, 138, 134–160 CrossRef CAS.
- P. Moschopoulos, A. Syrakos, Y. Dimakopoulos and J. Tsamopoulos, J. Non-Newton. Fluid Mech., 2020, 284, 104371 CrossRef CAS.
- S. Varchanis, A. Syrakos, Y. Dimakopoulos and J. Tsamopoulos, J. Non-Newton. Fluid Mech., 2020, 284, 104365 CrossRef CAS.
- T. J. R. Hughes, L. P. Franca and M. Balestra, Comput. Methods Appl. Mech. Eng., 1986, 59, 85–99 CrossRef.
- R. Guénette and M. Fortin, J. Non-Newton. Fluid Mech., 1995, 60, 27–52 CrossRef.
- A. N. Brooks and T. J. R. Hughes, Comput. Methods Appl. Mech. Eng., 1982, 32, 199–259 CrossRef.
- A. Kordalis, S. Varchanis, G. Ioannou, Y. Dimakopoulos and J. Tsamopoulos, J. Non-Newton. Fluid Mech., 2021, 296, 104627 CrossRef CAS.
- S. Varchanis, D. Pettas, Y. Dimakopoulos and J. Tsamopoulos, Phys. Rev. Lett., 2021, 128(8), 088001, DOI:10.1103/PhysRevLett.127.088001.
- Y. Dimakopoulos and J. Tsamopoulos, J. Comput. Phys., 2003, 192, 494–522 CrossRef.
- N. Chatzidai, A. Giannousakis, Y. Dimakopoulos and J. Tsamopoulos, J. Comput. Phys., 2009, 228, 1980–2011 CrossRef.
- A. Syrakos, Y. Dimakopoulos and J. Tsamopoulos, J. Non-Newton. Fluid Mech., 2020, 275, 104216 CrossRef CAS.
- W. H. Herschel and R. Bulkley, Kolloid-Zeitschrift, 1926, 39, 291–300 CrossRef.
- P. Moschopoulos, S. Varchanis, A. Syrakos, Y. Dimakopoulos and J. Tsamopoulos, J. Non-Newton. Fluid Mech., 2022, 309, 104883 CrossRef CAS.
- M. Renardy and Y. Renardy, J. Non-Newton. Fluid Mech., 2004, 122, 303–312 CrossRef CAS.
- P. Szabo, Rheol. Acta, 1997, 36, 277–284 CAS.
- S. Varchanis, A. Kordalis, Y. Dimakopoulos and J. Tsamopoulos, Phys. Rev. Fluids, 2021, 6, 013301 CrossRef.
- A. Zosel, Colloid Polym. Sci., 1985, 263, 541–553 CrossRef CAS.
- H. Lakrout, P. Sergot and C. Creton, J. Adhes., 1999, 69, 307–359 CrossRef CAS.
- F. R. S. Lamb, Proc. R. Soc. London, Ser. A, 1917, 93, 114–128 Search PubMed.
- R. Buscall, J. W. Goodwin, M. W. Hawkins and R. H. Ottewill, J. Chem. Soc., Faraday Trans. 1, 1982, 78, 2873–2887 RSC.
- D. D. Joseph, A. Narain and O. Riccius, J. Fluid Mech., 1986, 171, 289–308 CrossRef CAS.
- D. D. Joseph, O. Riccius and M. Arney, J. Fluid Mech., 1986, 171, 309–338 CrossRef CAS.
- L. Jørgensen, M. Le Merrer, H. Delanoë-Ayari and C. Barentin, Soft Matter, 2015, 11, 5111–5121 RSC.
- M. Yao and G. H. McKinley, J. Non-Newton. Fluid Mech., 1998, 74, 47–88 CrossRef CAS.
- X. Zhang, O. Fadoul, E. Lorenceau and P. Coussot, Phys. Rev. Lett., 2018, 120, 048001 CrossRef CAS PubMed.
- S. J. Haward and J. A. Odell, Rheol. Acta, 2004, 43, 350–363 CrossRef CAS.
- S. J. Haward and G. H. McKinley, Phys. Fluids, 2013, 25, 083104 CrossRef.
- J. Eggers, Phys. Rev. Lett., 1993, 71, 3458–3460 CrossRef PubMed.
- E. Turkoz, J. M. Lopez-Herrera, J. Eggers, C. B. Arnold and L. Deike, J. Fluid Mech., 2018, 851, R2 CrossRef.
- S. Varchanis, G. Makrigiorgos, P. Moschopoulos, Y. Dimakopoulos and J. Tsamopoulos, J. Rheol., 2019, 63, 609–639 CrossRef CAS.
- Y. Wei, M. J. Solomon and R. G. Larson, J. Rheol., 2018, 62, 321–342 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2023 |