 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Fluid interfaces laden by force dipoles: towards active matter-driven microfluidic flows
Kuntal
Patel
 * and
Holger
Stark
* and
Holger
Stark

Institut für Theoretische Physik, Technische Universität Berlin, Hardenbergstr. 36, 10623 Berlin, Germany. E-mail: kuntal.h.patel@tu-berlin.de
First published on 13th March 2023
Abstract
In recent years, nonlinear microfluidics in combination with lab-on-a-chip devices has opened a new avenue for chemical and biomedical applications such as droplet formation and cell sorting. In this article, we integrate ideas from active matter into a microfluidic setting, where two fluid layers with identical densities but different viscosities flow through a microfluidic channel. Most importantly, the fluid interface is laden with active particles that act with dipolar forces on the adjacent fluids and thereby generate flows. We perform lattice-Boltzmann simulations and combine them with phase field dynamics of the interface and an advection–diffusion equation for the density of active particles. We show that only contractile force dipoles can destabilize the flat fluid interface. It develops a viscous finger from which droplets break up. For interfaces with non-zero surface tension, a critical value of activity equal to the surface tension is necessary to trigger the instability. Since activity depends on the density of force dipoles, the interface can develop steady deformation. Lastly, we demonstrate how to control droplet formation using switchable activity.
I. Introduction
Rapid advancement in processing fluids on the micron scale has given rise to various applications in chemical analyses,1 biology,2,3 medical diagnosis,4,5 and many more. Such miniaturized flow-control platforms are referred to as microfluidic lab-on-a-chip devices.6–8 Typically, microfluidic flows occur at low Reynolds numbers and, therefore, obey kinematic reversibility, which sets restrictions on the realizable flows and their applications.9 To extend the use of microfluidic devices, one needs to introduce nonlinearities, for example, through inertial microfluidics or viscoelastic fluids.9,10 This field of nonlinear microfluidics has opened new avenues for droplet generation11–13 and cell sorting applications.14–18 In addition, nonlinear processes in microfluidic devices are also initiated by an external electric field, which induces electroosmotic flows,19–21 and acoustic fields, which generate surface acoustic waves traveling along substrates.22,23 Furthermore, microfluidic devices with compliant structures are known to cause a nonlinear response of the flow rate to the pumping pressure.9,24 Aside from nonlinear microfluidics, the development of other microfluidic techniques has immensely contributed to the overall progress of the field. Two such examples are light-driven25 and digital microfluidics26 for manipulating droplets. In this article we introduce yet another mechanism to design and control microfluidic flow by introducing active particles at fluid interfaces.We investigate a microfluidic system in combination with ideas from the field of active matter. This is a relatively new and less explored strategy to control and shape fluid flow at low Reynolds numbers. The entities of living or artificial active systems consume the ambient free energy to propel themselves and exert forces.27–30 In practice, the scale of active matter systems ranges from nanometers to meters.31,32 A bacterial suspension is one example that belongs to a micron-sized active matter system. It is well known now that the collective motion of bacteria can generate chaotic flow structures called active turbulence.33–35 Researchers36–39 have also demonstrated that such a bacterial bath can drive the continuous rotation of microscopic gears, which can be utilized as microfluidic mixers or energy harvesters. Another interesting system is a suspension of flexible active filaments made, e.g., by mixing microtubule with motor proteins40 and termed active nematic fluid.29,41 Without activity it assumes an isotropic ground state. However, tuning the activity beyond a critical value, a hydrodynamic instability occurs and the fluid begins to flow.42 Later, using numerical simulations, Chandragiri et al.43 demonstrated that the turbulent flow becomes unidirectional in sufficiently narrow microchannels resulting in the net transport of fluid along the channel. Hence, active fluids are an alternative for driving fluid flow without using microfluidic pumps. Recently, Rorai et al.44 studied the channel flow of active nematics with hybrid alignment at the channel walls. Within microfluidic applications, we also mention theoretical work on active matter logic45 and experimental work on active matter in circular channels46 and driven by light.47
In this article, we take up the idea of combining microfludic flow with active entities. We focus on a multi-component microfluidic setup, in contrast to the systems with a single fluid component described in the last paragraph. Earlier, Alonso and Mikhailov48 employed interfacial active molecules to generate turbulence at the liquid–air interface of a thin liquid film. They noted that the destabilization of the interface occurs only for a sufficiently high value of particle concentration and activity. Following this, Pototsky et al.49 looked at the dynamics of a micron-sized thin liquid film with self-propelling point-like swimmers, which act as insoluble surfactants. As a result of the upward motion of swimmers against the film interface, they observed interesting interfacial patterns in their numerical simulations. Most recent experiments by Adkins et al.50 revealed a highly dynamic fluid interface between an active and passive fluid, which is caused by the chaotic flow within the active fluid. They also reported that a gradual increase in activity eventually disrupts the fluid interface, which results in the formation of active emulsions. Further examples of active surfaces are described in ref. 51 and 52. Although there have been some efforts to leverage active matter into microfluidics, developing such a strategy for multi-component microfluidic systems remains scarce. In the present study, we introduce theoretical ideas as early steps for designing multi-component microfluidic flow devices fueled by active matter. The practical realization of these concepts holds great potential to impact a broad spectrum of applications, e.g., cell encapsulation,53 drug delivery,54 and particle synthesis.55
In the present work, we consider a microfluidic channel that contains two fluid layers separated by a fluid interface with surface tension σ. The fluids have identical densities but different viscosities. Most importantly, we cover the fluid interface with active particles that act with force dipoles on the surrounding fluid, one of the typical characteristics of active matter systems. The setup with two fluid layers is of fundamental relevance and ubiquitous in various microfluidic devices.56 We study the flow induced by the interfacial force dipoles and its effect on the fluid interface using hybrid lattice-Boltzmann finite-difference simulations, where the fluid interface is described by a phase field model. Our numerical results show that contractile force dipoles destabilize the flat fluid interface so that multiple breakups occur, where droplets form. In contrast, when laden with extensile dipoles, the interface stays flat. For interfaces with non-zero surface tension, we derive the critical value of activity necessary to trigger the instability. Since activity depends on the density of force dipoles, the interface can develop a steady deformation. Finally, we show how to control droplet formation with a switchable activity.
The outline of the article is as follows. In Section II we first introduce our microfluidic configuration with an active fluid interface, followed by the explanation of the governing laws and numerical methodology. The simulation results of our systematic investigations are presented in Section III. We conclude our work with final remarks in Section IV.
II. Methods
A. Setup of active microfluidics
The schematic of our computational setup is depicted in Fig. 1. We consider a two-dimensional microfluidic channel by placing two parallel walls at a distance w from each other in the y-direction while along the x-direction periodic boundary conditions are used [see Fig. 1(a)]. The channel is filled with two fluid layers of thickness h (bottom layer) and w–h (top layer), respectively. Both fluid layers have identical densities ρ while the bottom fluid (fluid 1) is more viscous than the top fluid (fluid 2), which we quantify by the viscosity contrast m = μ1/μ2 > 1. Finally, the fluid interface separating fluids 1 and 2 has surface tension σ. In the following, it is disturbed by imposing an interfacial perturbation of wavelength λ.The important feature of the present problem is that the fluid interface contains active particles, as shown in Fig. 1(b). The activity of these particles gives rise to force dipoles as depicted in Fig. 1(b) that generate flows in the fluids adjacent to the interface. We assume that the active particles are much smaller than the channel width w, so that they can be considered as point particles. The dipole-laden interface in a continuum approximation is shown in Fig. 1(c), where the two opposing forces of the dipole are represented by red and blue colors. We impose the following constraints on the active particles to simplify the present problem:
• They are tied to the fluid interface, while they are free to slide along it, and
• They are always oriented perpendicular to the fluid interface.
The notion of active particles residing at the fluid interface is inspired by insoluble surfactants found in practice, which get adsorbed at the interface.57 Motivated by this, Alonso and Mikhailov48 and Pototsky et al.49 also implemented interfacial active agents. In addition, two-fluid setups with Janus particles trapped at the interface have also been widely studied.58–60 The surface of Janus particles can be treated to have different wettabilities so that the top and bottom halves of particles prefer opposite fluids adjoining the interface, orienting particles perpendicular to the interface.61 The wettability contrast suppresses perturbations in the orientation and reorients particles perpendicular to the interface, as shown by Gao et al.62 This justifies our simplification of the particle orientation.
The force dipoles at the interface generate stresses, which we describe by the active stress tensor63
| Taij = WC(x,t)ninjδs, | (1) |
Thus, the fluid interface is not a sharp boundary but we describe it with the help of a phase field ϕ that is represented by a smooth step function varying between ϕ = 0 (fluid 2) and ϕ = 1 (fluid 1). The dynamics of ϕ follows a phase field equation as we detail in Section II B [see eqn (7)]. The interface normal is then given by n = ∇ϕ/|∇ϕ| and δs = n·∇ϕ = |∇ϕ|. Note that δs is normalized to one, as it should, since ϕ varies between 0 and 1.
By taking the divergence of the active stress tensor, the effect of activity can also be formulated as an active body force
 | (2) |
 [see Fig. 1(b)] and extensile force dipoles
[see Fig. 1(b)] and extensile force dipoles  for W < 0.63 The flowchart in Fig. 2 describes how our system evolves in the presence of a non-zero active body force Fa. To fully describe such a system, we need laws that govern the concentration of active particles at the interface as well as the motion of the interface and the flow of the bulk fluids. Since the interface implicitly determines the orientation of active particles, we do not need an additional equation to describe the orientation of active particles. We now proceed to discuss the required governing laws and numerical methods to solve them using computer simulations.
for W < 0.63 The flowchart in Fig. 2 describes how our system evolves in the presence of a non-zero active body force Fa. To fully describe such a system, we need laws that govern the concentration of active particles at the interface as well as the motion of the interface and the flow of the bulk fluids. Since the interface implicitly determines the orientation of active particles, we do not need an additional equation to describe the orientation of active particles. We now proceed to discuss the required governing laws and numerical methods to solve them using computer simulations.
 | ||
| Fig. 2 Time evolution of the fluid interface in the active microfluidic setup (see Fig. 1). The active body force drives fluid flow viaeqn (4), which displaces and deforms the interface described by phase field ϕ and its dynamics in eqn (7). This reorients the force dipoles and modifies their density C viaeqn (6), so that the body force needs to be updated viaeqn (2). | ||
B. Governing equations
The flow arising in the bottom and top fluids due to the force dipoles (see Fig. 1) is governed by the continuity equation (conservation of mass)| ∇·u = 0 | (3) |
 | (4) |
Since in our model the total number of active particles along the deforming fluid interface S(t) is conserved,
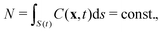 | (5) |
 | (6) |
 is the gradient operator and
is the gradient operator and  the velocity vector, both projected onto the fluid interface. The third term on the left-hand side arises since any curvature κ = ∇s·n = ∇·n of the fluid interface enhances the surface area and thereby changes the concentration. Since we are working with a smooth interface, one can show that eqn (6) is still valid with C replaced by Cδs and the projection (index s) is not needed.66
the velocity vector, both projected onto the fluid interface. The third term on the left-hand side arises since any curvature κ = ∇s·n = ∇·n of the fluid interface enhances the surface area and thereby changes the concentration. Since we are working with a smooth interface, one can show that eqn (6) is still valid with C replaced by Cδs and the projection (index s) is not needed.66
The presence of finite-sized particles at the fluid interface deforms the interface due to their weight, giving rise to capillary interactions.67,68 Nevertheless, capillary interactions can be safely neglected for micron or submicron-sized particles with smooth surfaces.67 Furthermore, closely placed active particles that induce force dipoles undergo hydrodynamic interactions.69,70 The leading-order hydrodynamic interactions drive particles closer (extensile dipoles) or away (contractile dipoles) from each other and reorient them.71 In the dilute limit, hydrodynamic interactions between active particles can be neglected. Moreover, since we consider the fixed particle orientation with respect to the fluid interface, it is sufficient to use the interfacial advection–diffusion equation [eqn (6)] to describe particle dynamics.
As introduced earlier, the phase field ϕ describes the diffuse interface between fluid 1 and 2 centered around the isoline with ϕ = 0.5 (see Fig. 3). Its time evolution is governed by the conservative advection equation13,64,72
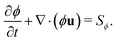 | (7) |
 | (8) |
 | (9) |
 | ||
| Fig. 3 One-fluid representation of the current multi-component system with density ρ(x,t) and viscosity μ(x,t) in the framework of a diffuse interface using the phase field ϕ. | ||
Now, choosing the mobility M in eqn (8) sufficiently large, the equilibrium shape of the profile is approximately preserved even if the system becomes dynamic.73,74 Note that the hyperbolic tangent profile agrees with the equilibrium solution of the Cahn–Hilliard phase field equation, which has been derived using physical arguments.75 In the following we will use the modified phase field eqn (7) since the computational implementation of the second-order differential equation is relatively simple compared to the fourth-order Cahn–Hilliard equation.
To formulate an equation for the body force Fs related to surface tension, we start with a two-fluid free-energy functional that captures the energy of the fluid interface,76–78
 | (10) |
Deforming a plane interface, generates a surface-tension body force, which can be given as79,80
 | (11) |
 | (12) |
 | (13) |
 . We will use this later for some qualitative arguments, while in the simulations we employ the full expression of eqn (13).
. We will use this later for some qualitative arguments, while in the simulations we employ the full expression of eqn (13).
C. Numerical methodology
We employ a hybrid lattice-Boltzmann finite-difference scheme to solve the governing equations numerically. Specifically, the lattice-Boltzmann method81 is applied to determine the fluid flow [eqn (3) and (4)] and to simulate the interface dynamics [eqn (7)], while the interfacial advection–diffusion equation [eqn (6)] is discretized and solved using the finite-difference scheme. The details of the lattice-Boltzmann implementation can be found in our recent work.13 The same approach is used for the current solver. To implement the finite-difference solver for eqn (6), we follow the methodology proposed by Teigen et al.66 This approach solves eqn (6) in the entire domain by extending the interfacial concentration C(x,t) as a constant in the direction normal to the fluid interface, such that where V is the domain volume. Furthermore, we use the modified Crank–Nicolson method82 to integrate in time and the 5th-order accurate WENO (Weighted Essentially Non-Oscillatory) scheme83 to handle the advection term.
where V is the domain volume. Furthermore, we use the modified Crank–Nicolson method82 to integrate in time and the 5th-order accurate WENO (Weighted Essentially Non-Oscillatory) scheme83 to handle the advection term.
In the simulations we use 512 grid points across the channel width w and set the interface width ξ to 4 lattice units. In our earlier work,13 we successfully tested and used the same grid resolution (derived using grid convergence) for a similar geometry and fluid parameters but with two interfaces and without activity. There, the problem was even more complex because of the high inertia of the background flow and complex interface topology (see Fig. 18 and 21 of ref. 13). For the remaining discussion, all fluid properties and parameters related to the activity (i.e., ρ, μ, σ, C, D, and W) are in units of the lattice-Boltzmann method. To non-dimensionalize thickness h, perturbation wavelength λ, amplitude A(τ), and time τ, we use channel width w and viscous time scale w2ρ/μm, where μm = 2μ1μ2/(μ1 + μ2) is the mean viscosity. Unless stated otherwise, we fix the thickness of the bottom fluid layer to h = 0.5 and the diffusivity of active particles to D = 0.11, which guarantees a uniform distribution of the active particles along the deforming interface.
III. Results and discussion
A. Activity-induced instability of the interface
To understand the role of active interfacial stresses in our system, we start with two fluids with a viscosity ratio of m = 30. Furthermore, we select an initial active particle concentration of C(x,0) = 0.5 and set interfacial tension σ to zero, so that one can clearly notice the effect of activity (a discussion on the influence of σ will follow in Section III B). On perturbing the fluid interface by a sinusoidal modulation of wavelength λ = 0.5, we observe that the interface covered with contractile force dipoles of force dipole moment W = 2 × 10−5 becomes unstable. In contrast, extensile force dipoles with W = −2 × 10−5 attenuate the interfacial perturbation [see Fig. 4(e)]. The contractile dipoles drive a vortex pair that lets the interfacial perturbation grow, as shown in Fig. 4(a). The vortex pair consists of counter-clockwise and clockwise circulation zones situated halfway between the peak and the two valleys of the interfacial height profile. For extensile force dipoles, the direction of circulation reverses [see Fig. 4(b)], driving the system back to the flat fluid interface.To qualitatively explain the activity-driven instability, we consider the schematic shown in Fig. 4(g). The neutral state represents the flat fluid interface laden by contractile force dipoles. Orange and blue-colored circles represent the two forces in the dipole. They are of the same magnitude and act normal to the interface on the respective fluids as indicated by the arrows. On bending the fluid interface the density of the outer forces (blue) decreases, while the density of the inter forces (red) increases. This generates a normal stress across the interface that drives the destabilizing flow for W > 0. One can compare this with the Laplace pressure acting across the interface, which balances the interfacial tension due to the increased interface. Later, in Section III B, we will elaborate more on the similarities and differences between the destabilizing active force and the stabilizing surface-tension force.
We further substantiate our qualitative explanation using mathematical reasoning. The magnitude of the active body force fa already introduced in eqn (2) can be written in expanded form as
 | (14) |
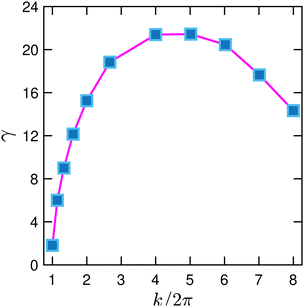
We further quantify the interfacial instability using dispersion curves. As before, we employ the same viscosity ratio m = 30 and force dipole moment W = 2 × 10−5 and set the interfacial tension σ to zero. We start from a flat fluid interface and impose single-mode interfacial perturbations with the rescaled wavenumber k/2π = λ−1 ranging from one to eight and an amplitude A = 2.5 × 10−2. Here, k = 2π corresponds to a wavelength λ equal to the channel width w. The flat interface is initially covered by contractile force dipoles with the areal concentration of C(x) = 0.5. Note that otherwise we always choose C(x,0) as the initial areal concentration along the perturbed interface. Upon increasing the wavenumber, the growth rate γ rises and peaks at k/2π = 4 as shown in Fig. 5. This is because for larger wavenumbers (or smaller wavelengths) the interface curvature κ increases and with it the destabilizing active force component fa2 in eqn (14). Then, the growth rate γ declines for k/2π > 4 as the area of the perturbed interface increases with k. Therefore, the force-dipole concentration along the perturbed interface and thus the destabilizing force decreases. Note that the growth rate does not tend to zero for k → 0 as expected for vanishing curvature. Instead, it approaches zero at k/2π = λ−1 ≈ 1. We attribute this to the nearby channel walls, which hinder the destabilizing flow to develop fully.
Dispersion curves identify and quantify the unstable modes. They are determined in a linear stability analysis, which we performed here by direct numerical simulations. Now, we observe how the most unstable mode at k/2π = 4(λ = 0.25) evolves further in time. We choose N = 131 active dipoles, which gives a concentration C(x,0) = 0.94 at the interface, nearly twice as large compared to the linear stability analysis. Increasing the concentration of the force dipoles speeds up the instability and thereby helps to reduce the computational cost. We observe that as the instability evolves, the symmetry of the interfacial perturbation about the channel centerline breaks because of the viscosity contrast. Ultimately, the more viscous bottom fluid invades the less viscous top fluid, and the fluid interface takes the form of a finger, as shown in Fig. 6. The continued elongation of the finger results in its breakup near the tip and generates a droplet. We call this a droplet breakup via active tip streaming. A similar interface dynamics has also been observed in electrohydrodynamic (EHD) flows (see Fig. 1 of ref. 84), commonly known as EHD tip streaming. Later, in Section III C we will demonstrate how one can exploit the breakup process in Fig. 6 to systematically form droplets.
Recently, Ruske and Yeomans85 reported the formation of fingerlike protrusions in three-dimensional active nematic droplets due to the active flow around disclination lines near the interface. The formation of fluid fingers also occurs in hydrodynamic instabilities such as Rayleigh–Taylor86 and Saffman–Taylor,87 which, however, have different origins. The Saffman–Taylor instability originates when a less viscous fluid is continuously pumped against a more viscous stagnant fluid in a Hele–Shaw cell. Thus, it exhibits fingers that consist of a less viscous fluid, opposite of that in Fig. 6 for the present instability. This distinction arises because curved regions of the active interface penetrate the less viscous top fluid with relative ease than the more viscous bottom fluid. Moreover, unlike the Saffman–Taylor instability, the activity-driven instability prevails in the absence of viscosity contrast (m = 1) since it is solely driven by the interface curvature κ, as previously discussed. The presence of the viscosity contrast in our two-fluid setup enables us to realize the asymmetric interface height profile about the channel centerline, which lets us systematically deposit droplets in the top fluid, as described later in Section III C.
We further studied the influence of the viscosity ratio m on the breakup dynamics. On increasing the viscosity ratio by decreasing the viscosity of the top fluid, the bottom fluid displaces the top fluid more easily. Hence, the instability develops faster as demonstrated in Fig. 7(a). This, in turn, speeds up the breakup of the finger. However, we also observe that the size of the emitted droplet is slightly smaller [compare insets of Fig. 7(a)]. To quantify the influence of the viscosity ratio m on the growth rate, we first rescale time by m−1, which results in a master curve for the amplitudes A(τ) at early times [see inset of Fig. 7(b)]. This is expected for the linear regime of the interface dynamics. Deviations occur at later times in the nonlinear regime when approaching the breakup point. On introducing a weakly nonlinear scaling, τ ∝ m−1.25, we obtain a master curve with a good agreement near the breakup point [see main plot of Fig. 7(b)]. At early times, we see a slight deviation from the master curve for m = 30.
Next, we investigate how the activity-driven interfacial instability progresses after the first breakup. We consider a relatively thin layer of the bottom fluid with thickness h = 0.1. This allows sufficient room for the interface to penetrate the top fluid at later times. Furthermore, we set the viscosity ratio to m = 100 where the instability grows fastest [see Fig. 7(a)]. The other simulation parameters are kept the same. Snapshots from a long enough simulation run in Fig. 8(a)–(g) reveal the formation of droplets through multiple breakup events. The time variation of the perturbation amplitude A(τ) in Fig. 8(h) (main plot) shows that these breakup events are not regular, i.e., the time elapsed between two successive breakups is not unique. The second breakup in Fig. 8(b) follows quickly after the first [see Fig. 8(h)]. After the second breakup, the perturbation amplitude continues to grow and the interface pushes the separated pair of droplets further up. Eventually, the fluid interface regains a height similar to that during the first breakup [compare Fig. 8(a) and (c)]. Then a third droplet forms, merges with the preceding droplet, and bow-tie-shaped viscous ligaments form, which ultimately form a fluid chain by merging together [see Fig. 8(d)–(f)]. However, the newly formed fluid chain is unstable and disintegrates into a train of droplets [see Fig. 8(g)]. We add two comments. For the present case, where we implemented a thin bottom film, the first breakup occurs faster than with a thick bottom layer for the viscosity ratio of m = 30 [compare the case of m = 30 in the inset of Fig. 8(h) with Fig. 7(a)]. We attribute this to the presence of the channel wall. For the higher viscosity ratio of m = 100, the speedup in the breakup is very marginal.
B. Influence of interfacial tension on the activity-induced instability
So far we set the surface tension σ of the interface to zero. For σ ≠ 0, perturbing a plane interface, enhances its area and thereby its surface energy. So the non-zero surface tension always tries to damp the perturbation. Thus, for a fluid interface covered with contractile force dipoles (W > 0), surface tension and active body forces compete against each other and we expect that below a critical value σ* the interface becomes unstable.To determine σ*, we recall that the relevant part of the surface-tension body force Fs in eqn (13) is
 | (15) |
 | (16) |
 . Furthermore, we set the perturbation wavelength and viscosity ratio to λ = 0.25 and m = 30, respectively.
. Furthermore, we set the perturbation wavelength and viscosity ratio to λ = 0.25 and m = 30, respectively.
The outcome of the direct numerical simulations is illustrated in Fig. 9(a), where we show the time evolution of the perturbation amplitude. Indeed, for an interface with strong enough surface tension (σ > WC), the perturbation dies out, while for σ < WC we observe the interfacial instability. As predicted, on setting σ = WC(x,0), the initial interfacial perturbation remains static, as illustrated in the inset of Fig. 9(a). Now, studying the instability for σ < WC(x,0) for a longer duration, we find that the amplitude of the interfacial perturbation eventually reaches a plateau [see the main plot and inset in Fig. 9(b)]. Similarly, for a higher viscosity ratio of m = 100, the instability also comes to a halt after an even shorter period. The reason for reaching a statically deformed interface is because the area of the growing interface increases and thus the areal concentration C(x,τ) continuously drops. Ultimately, when σ = WC(x,τeq) is reached at time τeq, the motion of the fluid interface is arrested. We also note that the steady-state amplitude of the perturbation is a bit higher for m = 100 compared to m = 30 because the viscous finger is slightly more pointed. Fig. 9(c) summarizes the instability controlled by the surface tension. Below σ* the growth rate of the interfacial perturbation is positive, while the perturbation is damped for σ > σ*. The qualitative nature of the dispersion curve in Fig. 5 also holds for unstable active interfaces with non-zero surface tension (WC > σ) since the stabilizing surface tension force Fs and the destabilizing active force fa2n have the same mathematical form.
Formally, one can interpret contractile force dipoles (W > 0) as imparting a negative surface tension −WC to the fluid interface and vice versa for extensile force dipoles (W < 0). Then, for contractile force dipoles the instability is triggered when the total surface tension becomes negative. This is reminiscent of the effectively negative surface tension, which is induced by the overpopulation of surfactants at the fluid interface as reported in ref. 88.
C. Controlling droplet production using particles with switchable activity
Till now, we discussed two cases with contractile force dipoles: the breakup of droplets from a fluid interface at zero surface tension and the stabilizing property of the surface tension. Here, we demonstrate that by varying the destabilizing activity at the fluid interface, one can control the formation of microfluidic droplets. Such droplets can be utilized in various practical applications, e.g., as chemical reactors on lab-on-a-chip platforms.89We select the parameter combination {λ, m, W, N} = {0.25, 30, 2 × 10−5, 131} and two values of interfacial tension σ = 10−8 and 10−6. Since both values always satisfy σ < WC, the interfacial perturbation grows with time and a droplet breaks up from the fluid interface, as shown in Fig. 10(a). Once the breakup is detected in our simulation, we switch off the activity by setting W = 0. As a result, the viscous finger retracts due to the stabilizing surface-tension force and leaves the droplet behind in the top fluid layer [see snapshots of fluid interface at different time instances in the insets of Fig. 10(a)]. Hence, one droplet-generation cycle consists of forming a viscous finger, the breakup of a droplet, and the damping of the interfacial perturbation due to surface tension once the activity is switched off. Increasing the surface tension from σ = 10−8 to 10−6 does not significantly impact the finger formation. However, it dramatically speeds up the retraction of the interface [see Fig. 10(a)]. The idea of switching off activity is inspired by light-switchable active particles90 and surfactants,25,91 which are used in practice. In theory, one can realize the continuous formation of droplets by periodically switching on and off the activity. However, after each droplet-formation cycle, the strength of activity at the main interface will weaken because of the gradual reduction in the areal concentration C since the droplets carry away active particles.
The generation of a droplet speeds up considerably for the higher viscosity ratio of m = 100, as shown in Fig. 10(b). Furthermore, upon increasing the perturbation wavelength to λ = 0.5 in Fig. 10(c), we observe droplet formation for m = 100 but not for m = 30. In the latter case, a long finger with a broad basis and a thin tip develops, but the breakup of a droplet is hindered by the upper wall as the inset of Fig. 10(c) shows. Interestingly, we find that the droplet radius Rd remains nearly unchanged irrespective of the studied perturbation wavelength λ and viscosity ratio m. For the different combinations we find {λ, m, Rd} = {0.25, 30, 0.037}, {0.25, 100, 0.031}, and {0.5, 100, 0.039}.
IV. Concluding remarks
Designs of microfluidic lab-on-a-chip devices have continuously evolved to meet practical requirements as well as to increase robustness and efficiency. In contrast to mainstream design ideas, we proposed a fairly novel approach that relies on active matter to generate microfluidic flows in a multi-component setting. Our microfluidic setup consists of an active fluid interface separating two fluids of different viscosities. The activity is due to interfacial particles that exert dipolar forces on the two fluids close to the interface. In our numerical study, we use lattice-Boltzmann simulations to determine fluid flow, which is coupled to a phase field equation for the dynamics of the interface. In addition, an advection–diffusion equation governs the active-particle density at the curved interface.Our direct numerical simulations uncovered that flat fluid interfaces laden with contractile force dipoles can become unstable, while extensile force dipoles never destabilize the interface. The instability is driven by the interface curvature, which creates an imbalance between the densities of the two dipolar force components at the interface. For zero surface tension of the interface, a viscous finger develops which breaks up into multiple droplets. For non-zero surface tension, a sufficiently large active-force density is needed to destabilize the flat interface (WC > σ). Since the active-force density decreases for a deformed interface, a static deformation can develop. For sufficiently large active forces, a droplet breakup occurs. Using switchable activity, we show how one can control droplet formation.
To realize the activity-driven droplet formation, one needs to fulfill WC > σ. Typical values for the surface tension of the fluid interface are close to σ = 10−4 N m−1.92 To estimate the force-dipole strength, we follow ref. 93 and take W ∼ μUls2, where ls is the length of the active particle and U its swimming speed. A good estimate for the concentration is C ∼ g2/ls2, where g refers to the aspect ratio of the active particle, and one finds WC ∼ g2μU. For larger rodlike microswimmers such as Bacillus subtilis with U = 100 μm s−1 and g = 10,33 and a more viscous fluid such as silicone oil with μ = 10−2 kg ms−1,94 one obtains indeed WC ∼ σ. Another strategy to fulfill WC > σ is to use fluid interfaces with an ultra-low surface tension such as σ = 10−6 N m−1 reported in ref. 95. This allows to reduce the size of the active particles and the viscosity. Finally, the fluid interface is also unstable under Poiseuille flow,13 which can help to induce the droplet formation.
Microfluidic lab-on-a-chip systems often take advantage of the inherent nonlinearities of viscoelastic flows to systematically steer17 and encapsulate96 particles. Likewise, incorporating viscoelastic fluids in the proposed active microfluidic setup may extend the utility of the current design. For example, characterizing the response of the active interface in the presence of a neighboring viscoelastic fluid can open up a new way to implicitly determine the rheological properties of viscoelastic fluids in practice. There already exists microfluidic rheometers, which employ the cross-stream particle migration in viscoelastic channel flows97 and stagnation point flows in cross-slot geometries98 to assess the elasticity of viscoelastic fluids. Devising such microfluidic rheometers is one of the topical microfluidic applications with immense practical value.
The present work on active fluid interfaces provides theoretical insights into how to combine microfluidics and active matter. More importantly, our results on the activity-driven formation of droplets are convincing enough that active-matter microfluidics is a promising concept for multi-component flows on the micron scale. Bringing these theoretical ideas to life will have far-reaching consequences due to their utility in lab-on-a-chip applications. For example, having solute particles in the more viscous fluid, one can controllably encapsulate them into droplets. Active-matter microfluidics is still an emerging field. We hope our work will motivate experiments that explore the potential of combining multi-component microfluidics with active matter.
Conflicts of interest
There are no conflicts of interest to declare.Appendix A: Validation of the interfacial advection–diffusion solver
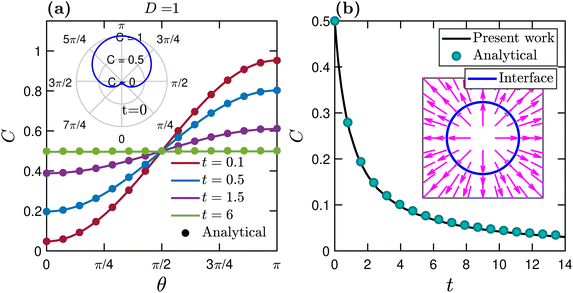
The benchmarking of our finite difference implementation for the interfacial advection–diffusion equation [eqn (6)] is carried out using two different test cases proposed by Teigen et al.82 In the first test case, we consider a static interface in the absence of the background flow to check the correctness of the numerical implementation of the diffusion term in eqn (6). For the second test case, we set the diffusivity D to zero and impose a predefined flow field to verify the advection-driven transport of active particles. Moreover, in the second test case, the interface location is known analytically at all times. Thus we do not need to solve the phase field equation. The time step is set to Δt = 10−4 in both test cases. The outcome of our test cases is compared with the analytical solution proposed by Teigen et al.82 As plotted in Fig. 11, excellent agreement is found between the analytical and present numerical results.Acknowledgements
We acknowledge support from the Deutsche Forschungsgemeinschaft in the framework of the Collaborative Research Center SFB 910. We thank the anonymous reviewers for carefully reading our manuscript and for their insightful suggestions and comments.References
- E. Livak-Dahl, I. Sinn and M. Burns, Annu. Rev. Chem. Biomol. Eng., 2011, 2, 325–353 CrossRef CAS PubMed.
- D. J. Beebe, G. A. Mensing and G. M. Walker, Annu. Rev. Biomed. Eng., 2002, 4, 261–286 CrossRef CAS PubMed.
- C. M. Leung, P. de Haan, K. Ronaldson-Bouchard, G.-A. Kim, J. Ko, H. S. Rho, Z. Chen, P. Habibovic, N. L. Jeon, S. Takayama, M. L. Shuler, G. Vunjak-Novakovic, O. Frey, E. Verpoorte and Y.-C. Toh, Nat. Rev. Methods Primers, 2022, 2, 33 CrossRef CAS.
- P. Yager, T. Edwards, E. Fu, K. Helton, K. Nelson, M. R. Tam and B. H. Weigl, Nature, 2006, 442, 412–418 CrossRef CAS PubMed.
- S. F. Berlanda, M. Breitfeld, C. L. Dietsche and P. S. Dittrich, Anal. Chem., 2020, 93, 311–331 CrossRef PubMed.
- H. Stone, A. Stroock and A. Ajdari, Annu. Rev. Fluid Mech., 2004, 36, 381–411 CrossRef.
- G. M. Whitesides, Nature, 2006, 442, 368–373 CrossRef CAS PubMed.
- J. K. Nunes and H. A. Stone, Chem. Rev., 2022, 122, 6919–6920 CrossRef CAS PubMed.
- H. M. Xia, J. W. Wu, J. J. Zheng, J. Zhang and Z. P. Wang, Lab Chip, 2021, 21, 1241–1268 RSC.
- D. Stoecklein and D. D. Carlo, Anal. Chem., 2018, 91, 296–314 CrossRef PubMed.
- X. Hu and T. Cubaud, J. Fluid Mech., 2020, 887, A27 CrossRef.
- T. Dinh and T. Cubaud, Langmuir, 2021, 37, 7420–7429 CrossRef CAS PubMed.
- K. Patel and H. Stark, Eur. Phys. J. E: Soft Matter Biol. Phys., 2021, 44, 144 CrossRef CAS PubMed.
- D. D. Carlo, D. Irimia, R. G. Tompkins and M. Toner, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 18892–18897 CrossRef PubMed.
- K. Patel and H. Stark, Soft Matter, 2021, 17, 4804–4817 RSC.
- B. Owen and T. Krüger, J. Fluid Mech., 2022, 937, A4 CrossRef PubMed.
- J. Zhou and I. Papautsky, Microsyst. Nanoeng., 2020, 6, 113 CrossRef CAS PubMed.
- S. R. Bazaz, A. Mashhadian, A. Ehsani, S. C. Saha, T. Krüger and M. E. Warkiani, Lab Chip, 2020, 20, 1023–1048 RSC.
- S.-C. Wang, Y.-W. Lai, Y. Ben and H.-C. Chang, Ind. Eng. Chem. Res., 2004, 43, 2902–2911 CrossRef CAS.
- M. Z. Bazant and T. M. Squires, Phys. Rev. Lett., 2004, 92, 066101 CrossRef PubMed.
- T. M. Squires and M. Z. Bazant, J. Fluid Mech., 2004, 509, 217–252 CrossRef.
- L. Y. Yeo and J. R. Friend, Annu. Rev. Fluid Mech., 2014, 46, 379–406 CrossRef.
- W. Connacher, N. Zhang, A. Huang, J. Mei, S. Zhang, T. Gopesh and J. Friend, Lab Chip, 2018, 18, 1952–1996 RSC.
- S. Battat, D. A. Weitz and G. M. Whitesides, Chem. Rev., 2022, 122, 6921–6937 CrossRef CAS PubMed.
- D. Baigl, Lab Chip, 2012, 12, 3637 RSC.
- M. J. Jebrail, M. S. Bartsch and K. D. Patel, Lab Chip, 2012, 12, 2452 RSC.
- M. C. Marchetti, J. F. Joanny, S. Ramaswamy, T. B. Liverpool, J. Prost, M. Rao and R. A. Simha, Rev. Mod. Phys., 2013, 85, 1143–1189 CrossRef CAS.
- A. Zöttl and H. Stark, J. Phys.: Condens. Matter, 2016, 28, 253001 CrossRef.
- M. J. Bowick, N. Fakhri, M. C. Marchetti and S. Ramaswamy, Phys. Rev. X, 2022, 12, 010501 CAS.
- A. Zöttl and H. Stark, Annu. Rev. Condens. Matter Phys., 2023, 14 DOI:10.1146/annurev-conmatphys-040821-115500.
- F. Cichos, K. Gustavsson, B. Mehlig and G. Volpe, Nat. Mach. Intell., 2020, 2, 94–103 CrossRef.
- G. Volpe, C. Bechinger, F. Cichos, R. Golestanian, H. Löwen, M. Sperl and G. Volpe, npj Microgravity, 2022, 8, 54 CrossRef PubMed.
- H. H. Wensink, J. Dunkel, S. Heidenreich, K. Drescher, R. E. Goldstein, H. Löwen and J. M. Yeomans, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 14308–14313 CrossRef CAS PubMed.
- V. Bratanov, F. Jenko and E. Frey, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 15048–15053 CrossRef CAS PubMed.
- A. W. Zantop and H. Stark, Soft Matter, 2022, 18, 6179–6191 RSC.
- L. Angelani, R. D. Leonardo and G. Ruocco, Phys. Rev. Lett., 2009, 102, 048104 CrossRef PubMed.
- A. Sokolov, M. M. Apodaca, B. A. Grzybowski and I. S. Aranson, Proc. Natl. Acad. Sci. U. S. A., 2009, 107, 969–974 CrossRef PubMed.
- R. D. Leonardo, L. Angelani, D. Dell'Arciprete, G. Ruocco, V. Iebba, S. Schippa, M. P. Conte, F. Mecarini, F. D. Angelis and E. D. Fabrizio, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 9541–9545 CrossRef PubMed.
- S. P. Thampi, A. Doostmohammadi, T. N. Shendruk, R. Golestanian and J. M. Yeomans, Sci. Adv., 2016, 2, e1501854 CrossRef PubMed.
- T. Sanchez, D. T. N. Chen, S. J. DeCamp, M. Heymann and Z. Dogic, Nature, 2012, 491, 431–434 CrossRef CAS PubMed.
- A. Doostmohammadi, J. Ignés-Mullol, J. M. Yeomans and F. Sagués, Nat. Commun., 2018, 9, 3246 CrossRef PubMed.
- R. Green, J. Toner and V. Vitelli, Phys. Rev. Fluids, 2017, 2, 104201 CrossRef.
- S. Chandragiri, A. Doostmohammadi, J. M. Yeomans and S. P. Thampi, Phys. Rev. Lett., 2020, 125, 148002 CrossRef CAS PubMed.
- C. Rorai, F. Toschi and I. Pagonabarraga, Phys. Rev. Fluids, 2021, 6, 113302 CrossRef.
- F. G. Woodhouse and J. Dunkel, Nat. Commun., 2017, 8, 15169 CrossRef PubMed.
- J. Hardoüin, J. Laurent, T. Lopez-Leon, J. Ignés-Mullol and F. Sagués, Soft Matter, 2020, 16, 9230–9241 RSC.
- Z. Qu, D. Schildknecht, S. Shadkhoo, E. Amaya, J. Jiang, H. J. Lee, D. Larios, F. Yang, R. Phillips and M. Thomson, Commun. Phys., 2021, 4, 198 CrossRef.
- S. Alonso and A. S. Mikhailov, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 79, 061906 CrossRef PubMed.
- A. Pototsky, U. Thiele and H. Stark, Eur. Phys. J. E: Soft Matter Biol. Phys., 2016, 39, 51 CrossRef PubMed.
- R. Adkins, I. Kolvin, Z. You, S. Witthaus, M. C. Marchetti and Z. Dogic, Science, 2022, 377, 768–772 CrossRef CAS PubMed.
- A. J. Mathijssen, F. Guzmán-Lastra, A. Kaiser and H. Löwen, Phys. Rev. Lett., 2018, 121, 248101 CrossRef CAS PubMed.
- S. Alonso, H.-Y. Chen, M. Bär and A. Mikhailov, Eur. Phys. J.: Spec. Top., 2010, 191, 131–145 CAS.
- S. Köster, F. E. Angilè, H. Duan, J. J. Agresti, A. Wintner, C. Schmitz, A. C. Rowat, C. A. Merten, D. Pisignano, A. D. Griffiths and D. A. Weitz, Lab Chip, 2008, 8, 1110 RSC.
- Q. Xu, M. Hashimoto, T. T. Dang, T. Hoare, D. S. Kohane, G. M. Whitesides, R. Langer and D. G. Anderson, Small, 2009, 5, 1575–1581 CrossRef CAS PubMed.
- J. K. Nunes, S. S. H. Tsai, J. Wan and H. A. Stone, J. Phys. D: Appl. Phys., 2013, 46, 114002 CrossRef PubMed.
- X. Hu and T. Cubaud, Phys. Rev. Lett., 2018, 121, 044502 CrossRef CAS PubMed.
- V. Garbin, J. C. Crocker and K. J. Stebe, Langmuir, 2011, 28, 1663–1667 CrossRef PubMed.
- X. Wang, M. In, C. Blanc, M. Nobili and A. Stocco, Soft Matter, 2015, 11, 7376–7384 RSC.
- P. Malgaretti, M. N. Popescu and S. Dietrich, Soft Matter, 2016, 12, 4007–4023 RSC.
- J. Deng, M. Molaei, N. G. Chisholm, T. Yao, A. Read and K. J. Stebe, Curr. Opin. Colloid Interface Sci., 2022, 61, 101629 CrossRef CAS.
- B. D. Frank, M. Perovic, S. Djalali, M. Antonietti, M. Oschatz and L. Zeininger, ACS Appl. Mater. Interfaces, 2021, 13, 32510–32519 CrossRef CAS PubMed.
- H.-M. Gao, Z.-Y. Lu, H. Liu, Z.-Y. Sun and L.-J. An, J. Chem. Phys., 2014, 141, 134907 CrossRef PubMed.
- S. Ramaswamy, Annu. Rev. Condens. Matter Phys., 2010, 1, 323–345 CrossRef.
- A. Fakhari, M. Geier and T. Lee, J. Comput. Phys., 2016, 315, 434–457 CrossRef CAS.
- H. A. Stone, Phys. Fluids, 1990, 2, 111–112 CrossRef CAS.
- K. E. Teigen, P. Song, J. Lowengrub and A. Voigt, J. Comput. Phys., 2011, 230, 375–393 CrossRef CAS PubMed.
- L. Botto, E. P. Lewandowski, M. Cavallaro and K. J. Stebe, Soft Matter, 2012, 8, 9957 RSC.
- G. B. Davies, T. Krüger, P. V. Coveney, J. Harting and F. Bresme, Adv. Mater., 2014, 26, 6715–6719 CrossRef CAS PubMed.
- I. O. Götze and G. Gompper, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 82, 041921 CrossRef PubMed.
- F. Alarcón and I. Pagonabarraga, J. Mol. Liq., 2013, 185, 56–61 CrossRef.
- E. Lauga and T. R. Powers, Rep. Prog. Phys., 2009, 72, 096601 CrossRef.
- P.-H. Chiu and Y.-T. Lin, J. Comput. Phys., 2011, 230, 185–204 CrossRef CAS.
- Y. Sun and C. Beckermann, J. Comput. Phys., 2007, 220, 626–653 CrossRef.
- R. Folch, J. Casademunt, A. Hernández-Machado and L. Ramírez-Piscina, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1999, 60, 1724–1733 CrossRef CAS PubMed.
- W. J. Boettinger, J. A. Warren, C. Beckermann and A. Karma, Annu. Rev. Mater. Res., 2002, 32, 163–194 CrossRef CAS.
- J. W. Cahn and J. E. Hilliard, J. Chem. Phys., 1958, 28, 258–267 CrossRef CAS.
- A. Bray, Adv. Phys., 1994, 43, 357–459 CrossRef.
- T. Qian, X.-P. Wang and P. Sheng, J. Fluid Mech., 2006, 564, 333 CrossRef CAS.
- J. Kim, J. Comput. Phys., 2005, 204, 784–804 CrossRef.
- R. Chella and J. Viñals, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 1996, 53, 3832–3840 CrossRef CAS PubMed.
- T. Krüger, H. Kusumaatmaja, A. Kuzmin, O. Shardt, G. Silva and E. M. Viggen, The Lattice Boltzmann Method: Principles and Practice, Springer, Berlin, Heidelberg, 2016 Search PubMed.
- K. E. Teigen, X. Li, J. Lowengrub, F. Wang and A. Voigt, Commun. Math. Sci., 2009, 7, 1009–1037 CrossRef PubMed.
- G.-S. Jiang and D. Peng, SIAM J. Sci. Comput., 2000, 21, 2126–2143 CrossRef.
- R. T. Collins, J. J. Jones, M. T. Harris and O. A. Basaran, Nat. Phys., 2007, 4, 149–154 Search PubMed.
- L. J. Ruske and J. M. Yeomans, Phys. Rev. X, 2021, 11, 021001 Search PubMed.
- A. Fakhari, T. Mitchell, C. Leonardi and D. Bolster, Phys. Rev. E, 2017, 96, 053301 CrossRef PubMed.
- T. T. Al-Housseiny, P. A. Tsai and H. A. Stone, Nat. Phys., 2012, 8, 747–750 Search PubMed.
- A. Z. Patashinski, R. Orlik, K. Paclawski, M. A. Ratner and B. A. Grzybowski, Soft Matter, 2012, 8, 1601–1608 RSC.
- H. Song, D. L. Chen and R. F. Ismagilov, Angew. Chem., Int. Ed., 2006, 45, 7336–7356 CrossRef CAS PubMed.
- H. R. Vutukuri, M. Lisicki, E. Lauga and J. Vermant, Nat. Commun., 2020, 11, 2628 CrossRef CAS PubMed.
- J. Kim, H. Yun, Y. J. Lee, J. Lee, S.-H. Kim, K. H. Ku and B. J. Kim, J. Am. Chem. Soc., 2021, 143, 13333–13341 CrossRef CAS PubMed.
- T. Cubaud, B. Conry, X. Hu and T. Dinh, Phys. Rev. Fluids, 2021, 6, 094202 CrossRef.
- A. P. Berke, L. Turner, H. C. Berg and E. Lauga, Phys. Rev. Lett., 2008, 101, 038102 CrossRef PubMed.
- X. Hu, Z. Wang, D. J. Hwang, C. E. Colosqui and T. Cubaud, Soft Matter, 2021, 17, 879–886 RSC.
- G. Bolognesi, A. Hargreaves, A. D. Ward, A. K. Kirby, C. D. Bain and O. Ces, RSC Adv., 2015, 5, 8114–8121 RSC.
- K. Shahrivar and F. D. Giudice, Soft Matter, 2021, 17, 8068–8077 RSC.
- F. D. Giudice, G. DAvino, F. Greco, I. D. Santo, P. A. Netti and P. L. Maffettone, Lab Chip, 2015, 15, 783–792 RSC.
- S. J. Haward, Biomicrofluidics, 2016, 10, 043401 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2023 |








![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)