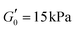Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Dynamically tunable lamellar surface structures from magnetoactive elastomers driven by a uniform magnetic field†
Izidor
Straus
a,
Gašper
Kokot
 *b,
Gaia
Kravanja
c,
Luka
Hribar
c,
Raphael
Kriegl
d,
Mikhail
Shamonin
*b,
Gaia
Kravanja
c,
Luka
Hribar
c,
Raphael
Kriegl
d,
Mikhail
Shamonin
 d,
Matija
Jezeršek
c and
Irena
Drevenšek-Olenik
d,
Matija
Jezeršek
c and
Irena
Drevenšek-Olenik
 ab
ab
aUniversity of Ljubljana, Faculty of Mathematics and Physics, Ljubljana, Slovenia
bJožef Stefan Institute, Ljubljana, Slovenia. E-mail: gasper.kokot@ijs.si
cUniversity of Ljubljana, Faculty of Mechanical Engineering, Ljubljana, Slovenia
dOstbayerische Technische Hochschule Regensburg, Regensburg, Germany
First published on 12th April 2023
Abstract
Stimuli responsive materials are key ingredients for any application that requires dynamically tunable or on-demand responses. In this work we report experimental and theoretical investigation of magnetic-field driven modifications of soft-magnetic elastomers whose surface was processed by laser ablation into lamellar microstructures that can be manipulated by a uniform magnetic field. We present a minimal hybrid model that elucidates the associated deflection process of the lamellae and explains the lamellar structure frustration in terms of dipolar magnetic forces arising from the neighbouring lamellae. We experimentally determine the magnitude of the deflection as a function of magnetic flux density and explore the dynamic response of lamellae to fast changes in a magnetic field. A relationship between the deflection of lamellae and modifications of the optical reflectance of the lamellar structures is resolved.
1. Introduction
Soft stimuli-responsive materials are crucial ingredients of soft robotics1 and an important member of future advanced materials that can dynamically adapt their properties depending on the requirements of a particular moment. An important class of such materials are dynamic surfaces that can adjust their wettability in response to environmental cues2–9 or on demand by applying a suitable stimulus.5–13 For magnetic materials the use of a magnetic field for controlling their properties is an obvious choice. The magnetic field needed to induce the required changes can be created either by electromagnets or mechanically (by moving permanent magnets), which further extends the flexibility of this approach.A promising class of smart materials susceptible to magnetic fields are magnetoactive elastomers (MAEs).14–28 They consist of magnetic microparticles dispersed in an elastomer matrix. A MAE surface can be (micro)structured into various topographies leading to intriguing new functionalities.12 One of the common choices is lamellar topography that enables dynamic modification of optical,29,30 wetting13,31 and friction32–34 properties. The cantilever-type MAE structures have been shown to controllably deflect both in non-uniform and uniform magnetic fields. If a cantilever is fabricated from an MAE filled with hard-magnetic particles, the driving force behind its deflection is the propensity of the particle's magnetic moment to align parallel to the applied magnetic field.35–37 In contrast, a theoretical description of the deflection of MAE cantilevers incorporating soft-magnetic particles is more complicated, because the induced magnetic moment of an individual particle is determined by the local magnetic field and its magnetic properties (i.e., dependence of the magnetic moment on the magnetic field strength) are nonlinear. For example, Romeis et al.38 presented a theoretical approach for calculating the stress induced by a uniform magnetic field in confined magnetoactive elastomers of an arbitrary shape. As far as soft-magnetic MAEs are concerned, the deflection of cantilevers made from such MAEs in non-uniform fields could be attributed to the force on an individual magnetic moment in a non-uniform field (F = ∇(mnB), where mn is the magnetic moment and B is the magnetic flux density). The case of a soft-magnetic MAE cantilever (or a beam) in a uniform magnetic field is somewhat different. If a homogeneous, soft-magnetic planar cantilever was oriented perpendicular to the uniform magnetic field, it would not bend.39 To induce bending of this kind of cantilever, the symmetry should be destroyed. For example, a slight inclination of the normal to the MAE plane with respect to the external magnetic field leads to the torque acting on the MAE cantilever.39,40 Moreover, the magnetized particles within soft MAEs tend to re-arrange and aggregate into some new configuration in a magnetic field.41 This phenomenon is known as restructuring of the filler.27
Hitherto, the research has been focused mainly on the magnetic-field-induced bending of hard-magnetic MAE cantilevers and much less effort has been spent on studies of soft-magnetic MAE beams. In particular, systematic investigations of deformations of the arrays of soft-magnetic MAE beams (e.g. lamellar structures), are missing in the literature. The purpose of this paper is to fill this gap. We acknowledge the questions, why and how a single MAE lamella would deflect in a uniform magnetic field, have already been addressed. However, we focus instead on an experimental investigation of lamellar MAE arrays and offer some insight on how their geometry influences lamellar deflection, for example we demonstrate a pitch dependence. In order to minimize the computing time, we formulate a very simplified model that ignores restructuring details within a single lamella38,39,41 and instead describes how the forces between neighbouring lamellae influence each other. We treat the elastic properties of lamellae as a continuum, but take into account point-like dipole forces between magnetic microparticles, i.e., the magnetic properties are considered to be discontinuous. We show that such a simple hybrid model can readily account for situations when the neighbouring lamellae stick together. We demonstrate that the magnetizable surrounding of a selected lamella can contribute to its deflection and investigate how spatial distribution of magnetic micro-particles within the polymer matrix affects the magnitude and direction of the deflection. We experimentally explore the deflection process of lamellar structures with different structural parameters and characterize their hysteresis behaviour. We also investigate the dynamic response of lamellae to rapid modifications of magnetic flux density and identify the corresponding relaxation processes. We discuss the connection between lamellae deflection and changes in optical reflectance of the lamellar structures.
2. Methods and model
2.1 Experimental section
The samples studied in this paper were manufactured from larger sheets of MAE exhibiting two different shear storage moduli of 15 and 65 kPa measured at a circular frequency of 10 s−1 and a shear amplitude of 0.01%. The liquid MAE mixture was spread on a substrate, in this case 0.2 mm PET foil, using a film applicator. An adjustable blade set to a 2 mm distance was then moved over the liquid at a constant rate of 1 mm s−1 to form a MAE film of the desired thickness. The MAE film was then transferred onto a flat baking sheet and placed in an oven for 1 h at 80 °C followed by 24 h at 60 °C to fully cure.
of 15 and 65 kPa measured at a circular frequency of 10 s−1 and a shear amplitude of 0.01%. The liquid MAE mixture was spread on a substrate, in this case 0.2 mm PET foil, using a film applicator. An adjustable blade set to a 2 mm distance was then moved over the liquid at a constant rate of 1 mm s−1 to form a MAE film of the desired thickness. The MAE film was then transferred onto a flat baking sheet and placed in an oven for 1 h at 80 °C followed by 24 h at 60 °C to fully cure.
Patterning into lamellar surface structures was realized by the laser micro-machining method using a procedure detailed in ref. 12. Configurations with varying surface geometries (see Fig. 1) were inscribed into the top surface layer of MAE sheets.
The MAE sheets were approximately 2 mm thick and were deposited on transparent polyethylene terephthalate (PET) foil. The manufacturing process followed a standardized procedure42,43 that consists of mixing and curing a base polymer, a chain extender modifier, a reactive diluent polymer, a crosslinker, a Pt-catalyst with a compatible inhibitor, silicone oil, and carbonyl iron powder (CIP) (mean particle size of 4.5 μm). By varying the ratio of the molar concentrations of vinyl and hydride groups in the initial compound by altering the doses of the crosslinker, materials with different shear storage moduli  can be manufactured. Surface structuring was performed using a pulsed Nd:YAG fiber laser (wavelength of 1064 nm, maximum average power of 20 W, a pulse duration of 12 ns, and a repetition rate of 35 kHz) as described in ref. 12. We prepared numerous samples with different geometrical parameters and we present here a selection of the results that display the resolved trends. We focus on two sets of samples, the first one with the constant height h ≈ 250 μm and varying pitches in the range of p ≈ 100–500 μm, and the second one with the constant pitch p ≈ 170 μm and varying heights in the range h ≈ 130–300 μm, while other parameters were kept constant (w ≈ 70 μm,
can be manufactured. Surface structuring was performed using a pulsed Nd:YAG fiber laser (wavelength of 1064 nm, maximum average power of 20 W, a pulse duration of 12 ns, and a repetition rate of 35 kHz) as described in ref. 12. We prepared numerous samples with different geometrical parameters and we present here a selection of the results that display the resolved trends. We focus on two sets of samples, the first one with the constant height h ≈ 250 μm and varying pitches in the range of p ≈ 100–500 μm, and the second one with the constant pitch p ≈ 170 μm and varying heights in the range h ≈ 130–300 μm, while other parameters were kept constant (w ≈ 70 μm,  ).
).
After surface structuring the samples were trimmed into smaller pieces (<1 cm2) and glued to a 3D printed plastic holder with water soluble PVA glue. The holders were placed on a custom 3D printed arm which enabled xyz translations for precise positioning of samples between the cores of an electromagnet (GMW 3470, Buckley Systems Limited) and also in-plane rotations of the sample to customize the angles between magnetic field lines and surface structure axes. A DC power supply (GWinstek GPD-3303S) was wired through a multimeter (KEITHLEY 2700 Multimeter) to the electromagnet, driving it with a maximum current of 3 A, which produced magnetic fields between the magnetic cores up to 300 mT depending on the employed configuration (the cores can be adjusted for a stronger and more uniform magnetic field).
A light emitting diode (LED) illumination source (Thorlabs MNWHL4) was used in combination with a monochrome camera (USB 3.0, BFLY-U3-23S6M-C), an extension tube (Edmund Optics), and an optical objective with magnification of 1.8 (Mitutoyo) to capture images and videos of lamellar assembly from a vertical point of view (as shown in Fig. 1). A typical measurement was executed by synchronously capturing the video of the selected area while changing the applied current to the electromagnet and monitoring it with a multimeter. All devices were controlled in sync with a proprietary Python code.
2.2 Simulation model
We model a single MAE lamella as an Euler–Bernoulli beam which is sliced along the y axis into equal sections and numerically calculate its bending based on the total force experienced by each of the slices. This means that we employ classical continuum theory for the elastomer bending, whose properties enter the equations only through the Young's modulus E0. For non-compressible neo-Hookean solids E0 = 3G0.44 Assuming that the displacement happens in the x direction (as per choice of coordinate system in Fig. 1) and that the beam has a constant second moment of area I = (w3l)/12, where w is the width and l the length of the lamella, we write the basic non-linear equation (the dot denotes the derivative on y) governing the deflection δx:45,46 | (1) |
In our model we do not include any explicit torques, only the ones arising from forces. We consider two contributions to the force per slice: gravity Fg and magnetic dipolar forces. For two magnetic dipoles ![[m with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006d_20d1.gif) i and
i and ![[m with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006d_20d1.gif) j separated by a distance
j separated by a distance ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) the pair force
the pair force ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) md reads:
md reads:
 | (2) |
![[m with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006d_20d1.gif) i is the magnetic moment of the i-th particle. In our simple model we take
i is the magnetic moment of the i-th particle. In our simple model we take ![[m with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006d_20d1.gif) i =
i = ![[m with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006d_20d1.gif) j =
j = ![[m with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006d_20d1.gif) n = const, i.e. magnetic moments of all particles are equal and pointing in the direction of the external magnetic field μ0H. This corresponds to the case of magnetic saturation where an external magnetic field is so high that the local variations of magnetic field can be neglected. Obviously, this model does not allow any conclusions about field dependence of the observed deflections, but it may nevertheless lead to meaningful insights into inter-lamellar interaction. As pointed out at the onset, in order to isolate the influence of the lamella's neighbourhood, we are not considering interactions within the lamella. Aligned with the choice of sketch colours in Fig. 2, this means that all
n = const, i.e. magnetic moments of all particles are equal and pointing in the direction of the external magnetic field μ0H. This corresponds to the case of magnetic saturation where an external magnetic field is so high that the local variations of magnetic field can be neglected. Obviously, this model does not allow any conclusions about field dependence of the observed deflections, but it may nevertheless lead to meaningful insights into inter-lamellar interaction. As pointed out at the onset, in order to isolate the influence of the lamella's neighbourhood, we are not considering interactions within the lamella. Aligned with the choice of sketch colours in Fig. 2, this means that all ![[m with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006d_20d1.gif) i come from blue and all
i come from blue and all ![[m with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006d_20d1.gif) j from green lamella. In the last step we sum all
j from green lamella. In the last step we sum all  experienced by particles within a particular slice, add Fg, and consider this to be a point force generating a point torque acting on the beam in a particular slice (see Fig. 2b). For the calculation we choose typical experimental parameters h = 300 μm and w = 70 μm, and a limited length l = 30 μm. We consider that the elastomer matrix has a density close to pure PDMS (ρ = 965 kg m−3) and incorporates 75 wt% of particles that are assumed to be iron (ρ = 7874 kg m−3) spheres with a diameter of 4.5 μm. According to these parameters the volume of one lamella in our calculations is populated by n = 3549 particles, which we randomly distribute throughout.
experienced by particles within a particular slice, add Fg, and consider this to be a point force generating a point torque acting on the beam in a particular slice (see Fig. 2b). For the calculation we choose typical experimental parameters h = 300 μm and w = 70 μm, and a limited length l = 30 μm. We consider that the elastomer matrix has a density close to pure PDMS (ρ = 965 kg m−3) and incorporates 75 wt% of particles that are assumed to be iron (ρ = 7874 kg m−3) spheres with a diameter of 4.5 μm. According to these parameters the volume of one lamella in our calculations is populated by n = 3549 particles, which we randomly distribute throughout.
In this first step, the purpose of the model is to provide a qualitative explanation for experimental observations. We are not trying to explain the field dependence of deflection, therefore we assume mn to be saturated (i.e., it does not explicitly depend on the applied magnetic field strength H). We also ignore the fact that the value of E0, when MAE is subjected to a magnetic field, can change by several orders of magnitude even for a bulk material, which is another feature to be implemented in the future developments of this model. For the calculations presented in this work specific values of E0, I and mn are relevant only as the ratio μ0mn2/(E0I). We identify the ratios Fg/(E0I) = 2 × 104 m−2 and μ0mn2/(E0I) = 10−17 m2 to give reasonable deflections that do not corrupt our numerical procedure. Together with the number of particles n and dipolar force summation these ratios determine the parameters α and β that enter into the numerical scheme of eqn (1).
3. Results and discussion
3.1 Hysteresis of structure response
In addition to subsequent image analysis of captured videofiles of lamellar deflection in a magnetic field, we also tested an alternative method for the detection of deflection processes based on optical reflectivity modifications. Being fast, simple and noncontact in its nature, optical sensing of surface modifications can be a very convenient in situ method for their characterization or control. We obtain the lamella deflection δx by fitting a Gaussian distribution to the inverse intensity profile then detecting and tracking the top edges of lamellae (see Fig. 3, middle). In order to establish a link between δx and optical reflectance R, we started with a careful inspection of both of them in response to a slowly increasing and decreasing magnetic field. More precisely, we measured a relative reflectance defined as: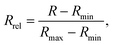 | (3) |
We increased and decreased the current in a stepwise manner, each time waiting for the structure to reach equilibrium before capturing the image from the top. We analyzed the images in terms of δx as well as Rrel. Careful inspection of the deflection process reveals that, as the lamella is deflecting, it also casts a shadow on the neighbouring parts, which was characterized as the width of the fitted Gaussian function. The presence of a shadow explains a qualitative difference between the hysteresis (Fig. 3 bottom) of δx (green full squares) and hysteresis of Rrel (blue empty triangles). Most notably, one can see an increase in the shadow area exactly when Rrel stays flat or even has a negative value, despite the fact that δx is already responding to B. Recognizing the decisive role that the shadow plays for the obtained R values, the conclusion is that mounting details of the sample and the light source determine the Rrel hysteresis parameters, such as the area or initial plateau length, which makes sample to sample comparison futile. Nevertheless, the result shown in Fig. 3 demonstrates that measurements of Rrel are suitable as a convenient proxy variable for δx as long as B is sufficiently large.
3.2 Relaxation times of the lamellar structure
We explored the lamella's deflecting dynamics in terms of Rrel because of two considerations. Firstly, measuring R is much simpler and more robust than edge tracking which becomes more complex as edges become poorly defined, curved along the z axis or are deflected out of frame. Measuring R also enables comparison between different types of surface morphology (not just lamellar) or, as we show below, for material responses that are different from pure deflection. Secondly, for optical applications R is in any case a more relevant parameter than δx. The measurements of the dynamic relaxation times were carried out in the same setup as the hysteresis measurements. Each sample was rigidly fixed between the magnetic poles and firstly stressed by subjecting it to a series of on–off pulses, where we switched the magnetic field from 0 to 145 mT and back, to ensure independence from the rearrangement of particles that MAEs usually experience during the initial driving cycles. Afterwards, we followed the changes in Rrel (see Fig. 4 for an example) while applying a series of 10 alternating on–off pulses with a 5 s dwell time. For comparison a δx measurement is also plotted alongside the Rrel data. We treated each lamella in the video independently and report mean values over several lamellae (Fig. 4 shows the results obtained for one of the lamellae). Simultaneously, we measured the current through the electromagnet in order to pinpoint the time at which the current in the coils does not change anymore and therefore a magnetic field applied to the MAE is truly constant. | ||
Fig. 4 Top: Example of structure relaxation time measurement ( , w = 70 μm, h = 280 μm, p = 355 μm). The black line shows the time dependence of the external magnetic field (left axis) and the connected dots represent the reflectance R (blue) and deflection δx (green) of an individual lamella (right axes). When the field is switched off, R and δx drop in accordance with lamellae straightening back to their original shapes. Bottom: An example of the corresponding relaxation process, when the field is switched off (see also Fig. S1 and S2, ESI†). The curves represent the time relaxation of Rrel and δx for 10 consecutive off pulses (annotated with gray rectangles on the top graph). A two exponential decay is fitted (R-squared >0.97 for both) and two relaxation times are extracted from the fit (short τ1 and long τ2). Their values are averaged over multiple lamellae for each sample. , w = 70 μm, h = 280 μm, p = 355 μm). The black line shows the time dependence of the external magnetic field (left axis) and the connected dots represent the reflectance R (blue) and deflection δx (green) of an individual lamella (right axes). When the field is switched off, R and δx drop in accordance with lamellae straightening back to their original shapes. Bottom: An example of the corresponding relaxation process, when the field is switched off (see also Fig. S1 and S2, ESI†). The curves represent the time relaxation of Rrel and δx for 10 consecutive off pulses (annotated with gray rectangles on the top graph). A two exponential decay is fitted (R-squared >0.97 for both) and two relaxation times are extracted from the fit (short τ1 and long τ2). Their values are averaged over multiple lamellae for each sample. | ||
The involvement of several relaxation processes on significantly different timescales is a known property of MAE.42 It is therefore not surprising that the change in Rrel facilitated by a change in δx shows similar complex dynamics. We focus on the part of the measurement where both δx and Rrel display a double exponential decay ∝ A1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−t/τ1) + A2
exp(−t/τ1) + A2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−t/τ2) with the two characteristic times τ1,2 of quite similar values (Fig. 4). We denote τ1 as the short and τ2 as the long relaxation time. Rrel has a typical ratio of
exp(−t/τ2) with the two characteristic times τ1,2 of quite similar values (Fig. 4). We denote τ1 as the short and τ2 as the long relaxation time. Rrel has a typical ratio of  demonstrating that the short relaxation process dominates. The green full circles in Fig. 5a show a weak rise in
demonstrating that the short relaxation process dominates. The green full circles in Fig. 5a show a weak rise in  as we move from stretching to sticking, indicating that the second relaxation process is the most pronounced for stretching. It should be highlighted that we identify less relaxation processes than in ref. 42. This is attributed to the fact that the dwell time between switching events in our experiments is relatively short (5 s), therefore any longer relaxation process is not encompassed by our measurements. We interpret τ2 as the time constant of the collective response of MAE lamellae. Regardless of the changes in the pitch p, height h, and shear storage modulus
as we move from stretching to sticking, indicating that the second relaxation process is the most pronounced for stretching. It should be highlighted that we identify less relaxation processes than in ref. 42. This is attributed to the fact that the dwell time between switching events in our experiments is relatively short (5 s), therefore any longer relaxation process is not encompassed by our measurements. We interpret τ2 as the time constant of the collective response of MAE lamellae. Regardless of the changes in the pitch p, height h, and shear storage modulus  , τ1 remains practically constant and is similar to the time constant of the electromagnet. This means the shortest material relaxation time is much faster and the lamellar surface simply follows the electromagnet switching on and off. We are unable to determine the shortest relaxation time, because we cannot change the time constant of the electromagnet. This is the reason τ1 is independent from any other parameter in the experiment. In contrast, τ2 reveals a non-trivial dependence on structural parameters (Fig. 5) which we interpret as the final restructuring of the iron particles inside MAE.
, τ1 remains practically constant and is similar to the time constant of the electromagnet. This means the shortest material relaxation time is much faster and the lamellar surface simply follows the electromagnet switching on and off. We are unable to determine the shortest relaxation time, because we cannot change the time constant of the electromagnet. This is the reason τ1 is independent from any other parameter in the experiment. In contrast, τ2 reveals a non-trivial dependence on structural parameters (Fig. 5) which we interpret as the final restructuring of the iron particles inside MAE.
Based on the measurements of samples with constant p, we identify three regimes with regards to h that exhibit observable qualitative differences in lamellar response (Fig. 5a). The boundaries between regimes are blurred and a mixed response is typical. We define the boundary where more than half of the lamellae in the sample display predominantly one type of behaviour. At low h there exists the stretching regime, in which a predominantly bulk material below the lamellae stretches via magnetostriction. As h increases, we encounter the deflecting regime, where in addition to stretching, the lamellae deflect due to an external magnetic field. Finally, there appears a sticking regime that takes place when lamellae are tall enough that they stick to the closest neighbouring lamellae, form pairs or triplets, and tend to stay in the same position even after a larger magnetic field is applied. These regimes are qualitative in nature and are apparently connected with τ2 values (Fig. 5a), which are the largest at lowest h, followed by a plateau and then exhibit a decrease at the highest value of h. If we fix h and observe how Rrel changes as a function of p (Fig. 5b), a non-monotonic behaviour of τ2 is observed again: with increasing p the value of τ2 at first rises and then drops. This outcome suggests that the neighbouring lamellae influence the deflection process. This property opens up diverse possibilities to design deflection characteristics of lamellar MAEs structures via appropriate selection of their structural parameters.
3.3 Mutual effect of neighbouring lamellae
The identification of three qualitative regimes for sequential lamellae behaviour implies that many physical mechanisms are at play. This problem was already partially studied previously in an investigation of how MAE cylinders change shape under the influence of a magnetic field.38 We believe that the same effects are involved in the stretching and partially also in the deflecting regime. We present here a hybrid model that, despite its simplicity, elucidates the sticking regime as a consequence of magnetic dipolar forces acting between neighbouring lamellae. The way in which we formulate the model allows us to isolate contributions of different parts of the structural geometry to the deflection of a selected lamella (see Fig. 2b). We purposefully ignore any internal mechanisms, for example the one that explains the critical bending of a single lamella,39 because we set out to separate the effects native to inter-lamellar interaction. For a selected deflecting lamella (Fig. 2 blue) we sum up all![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) md arising from the particles in its neighbourhood (Fig. 2 green), while the magnetic field and hence all mn are pointing in the x axis direction (Fig. 1a) and both lamellae are still upright. The lamellae deflect towards each other (Fig. 2b). Of course this is only the first calculation step, because in the deflected state we have to recalculate the
md arising from the particles in its neighbourhood (Fig. 2 green), while the magnetic field and hence all mn are pointing in the x axis direction (Fig. 1a) and both lamellae are still upright. The lamellae deflect towards each other (Fig. 2b). Of course this is only the first calculation step, because in the deflected state we have to recalculate the ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) md contributions (as the relative particle positions changed) until the solution for x(y) converges to the final deflection which is greater than the one obtained in the first step. This requires modifying eqn (1) to include arbitrary curvature, but before we complicate the model further, important lessons can, surprisingly, be learned from just calculating the first step. Experimentally, this is equivalent to the moment of the very first application of the magnetic field.
md contributions (as the relative particle positions changed) until the solution for x(y) converges to the final deflection which is greater than the one obtained in the first step. This requires modifying eqn (1) to include arbitrary curvature, but before we complicate the model further, important lessons can, surprisingly, be learned from just calculating the first step. Experimentally, this is equivalent to the moment of the very first application of the magnetic field.
Our results offer insight into the initial tip-off of a selected lamella. They also qualitatively explain numerous experiments in which we observed frustration of the lamellae deflection (Fig. 2e). In these cases a single lamella deflects in opposite directions along its length l and neighbouring lamellae randomly stick together. To explain this behaviour, we analyze δx for a blue lamella (Fig. 2a, blue) with a single neighbouring lamella (Fig. 2a, green). The corresponding ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) md provide the force both in x and y directions and gravity acts only in the y direction with the resultant force native to each slice as shown in Fig. 2b. Gravity is larger than the magnetic dipolar force contribution (notice the scale bar in x is an order of magnitude smaller than in the y direction), yet gravity alone (self-buckling scenario) does not deflect the lamella. This is akin to a known effect from construction engineering that has to be accounted for in order to avoid instability and catastrophic failure. A centrally loaded pillar (our case with gravity only) can carry much more weight than a pillar where forces also act perpendicular to its axis, for example a chimney that collapses due to strong enough winds. Of course the situation can be mirrored and we can calculate the deflection of the green lamella in the same manner (the
md provide the force both in x and y directions and gravity acts only in the y direction with the resultant force native to each slice as shown in Fig. 2b. Gravity is larger than the magnetic dipolar force contribution (notice the scale bar in x is an order of magnitude smaller than in the y direction), yet gravity alone (self-buckling scenario) does not deflect the lamella. This is akin to a known effect from construction engineering that has to be accounted for in order to avoid instability and catastrophic failure. A centrally loaded pillar (our case with gravity only) can carry much more weight than a pillar where forces also act perpendicular to its axis, for example a chimney that collapses due to strong enough winds. Of course the situation can be mirrored and we can calculate the deflection of the green lamella in the same manner (the ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) md comes from particles in the blue lamella in this case) producing identical results. Therefore, for the sake of simplicity of the discussion we present results only for the blue lamella. As we increase the separation (pitch p) between the blue and green lamella, δx monotonously decreases as ∝1/p3 (Fig. 2c), compliant with the arbitrary far-field approximation of the dipolar field B ∝ p−3. For larger values of mn2/(E0I), the curve keeps its shape albeit it translates to larger p.
md comes from particles in the blue lamella in this case) producing identical results. Therefore, for the sake of simplicity of the discussion we present results only for the blue lamella. As we increase the separation (pitch p) between the blue and green lamella, δx monotonously decreases as ∝1/p3 (Fig. 2c), compliant with the arbitrary far-field approximation of the dipolar field B ∝ p−3. For larger values of mn2/(E0I), the curve keeps its shape albeit it translates to larger p.
Intriguingly, for a chosen p, the exact configuration of particles within both lamellae determines the amplitude of δx. Repeating the calculation for 200 random cases reveals a histogram with a wide Gaussian distribution (Fig. 2d, yellow) and a peak in the direction towards the green lamella. For the symmetric case (Fig. 2d, red), with one green lamella on each side, δx is distributed around zero while keeping the width. The symmetric case is a more accurate representation of the experiments because lamellae have two closest neighbours, one on each side. The two closest neighbours (and not other neighbours further away) dominant contribution to δx is supported by a cubic decrease of δx on p (Fig. 2c). These results imply that a particular random configuration is the decisive factor for the direction and the size of δx. In reality, one can rarely have perfect geometric symmetry because the fabrication procedure inevitably introduces defects and lamella width variations, therefore locally the δx distribution is mostly shifted to one of the two possible sides. Moreover, a qualitative explanation for Fig. 2e emerges: moving along l is equivalent to sampling from the δx histogram in Fig. 2d, because particular particle configurations change along l.
As pointed out before, our minimal model neglects the internal processes taking place inside the selected lamella due to complex magnetic fields that form inside. This is a crucial ingredient to be added, if one wishes to compare the dependence of δx on B observed in the experiments. Also a comparison study that includes both internal processes and the effects of geometry, is needed to elucidate which of the two processes dominates and at which parameters. Models focused on explaining the changes in surface roughness of MAEs induced by magnetic fields have identified that strong local deformations are possible due to chaining and clustering of particles.19,27 Our model treats particles as fixed and does not consider the time evolution of the particle positions (neither due to restructuring41 nor due to deflection), they only act as a source of force. To obtain a point force per slice, which is a compulsory form of the input for the δx calculation as we perform it, we simply sum up the contributions of all the particles within a particular slice. Another aspect we did not address here is the role of the material below the lamellas. Our lamellar structures also have MAE underneath and it is not straightforward to predict how this influences δx. To avoid this complication we propose for future experiments a system that will be composed of an array of MAE lamellae positioned on a hard diamagnetic substrate such as glass.
We identified that, even for a geometrically symmetric case, a particular (random) particle arrangement can lead to forces between lamellae that promote deflection. We also demonstrate that introducing geometric asymmetry makes deflection in one direction preferable. In practice, a certain degree of asymmetry is very often present in the samples due to manufacturing limitations.
4. Conclusions
Deflection of sequential lamellar MAE microstructures exposed to a uniform magnetic field was investigated experimentally and theoretically. We identified three response regimes for an array of MAE lamellae: stretching, deflecting, and sticking, which are mostly determined by lamella height. We resolved the connection between deflection of lamellae and modifications of surface optical reflectivity from lamellar structure, which can be conveniently used as a proxy variable to study the system dynamics. Both of them display hysteresis responses to changes in magnetic field, but they are not identical because of the shadow the lamellae cast during the deflection.On the timescale of the experiments we identified two relaxation processes. The shorter of them more or less follows the electronic response time of the coils that were used to generate the magnetic field. Most of the R variation (>93%) happened within this first relaxation process, meaning that in practical applications the driving speed is limited predominantly by the rapidness of the magnetic field switching. This relatively fast instrumentally limited response together with broad possibilities for changing the shape and size of the sculptured patterns makes MAE surface microstructures very promising for applications requiring dynamically adaptive surfaces.
We demonstrate that a simple model which attributes the deflection of lamellae to the magnetic dipolar forces acting between magnetic microparticles dispersed in the neighbouring lamellae can qualitatively explain the observed sticking regime. We show that even in a geometrically symmetric case the inevitable granular microstructure of MAEs can generate a force (and corresponding torque) imbalance for a particular magnetic particle configuration resulting in equally probable deflections backward and forward with respect to the direction of the external magnetic field. The distribution of deflection magnitudes is Gaussian and has a large width, which remains alike even when the symmetry is increased, and only the peak position is shifted. Neglecting the internal physical processes within a single lamella allowed us to elucidate the influence of geometry on the lamellar deflection and explain certain behaviours such as pitch dependence of deflection and frustration of deflection direction. To truly understand the interplay between internal MAE processes and the specific geometry resulting in lamellar bending requires a more comprehensive model incorporating all known physical effects38,41,42 as well as a procedure leading to self-consistent solutions accounting for all the deflections. This is especially important for resolving which contribution (internal or external) is dominant in the response properties of a lamellar structure with specific structural parameters.
Author contributions
I. S. performed experiments and analyzed the measurements. G. Ko. developed the model and performed numerical calculations. G. Kr. and L. H. fabricated the lamellar structures. R. K. prepared the MAE material. M. S., M. J. and I. D. O. supervised the work. I. S. and G. Ko. prepared the manuscript. All authors commented on the manuscript and discussed the results.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors would like to acknowledge funding for this project. Slovenian Research Agency (ARRS): research programs P1-0192, P2-0392, and research project J1-3006. The work of R. K. and M. S. in Regensburg was funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation), project number 437391117.Notes and references
- B. Mazzolai, A. Mondini, E. Del Dottore, L. Margheri, F. Carpi, K. Suzumori, M. Cianchetti, T. Speck, S. K. Smoukov and I. Burgert, et al. , Multifunct. Mater., 2022, 5, 032001 CrossRef.
- D. H. Carey and G. S. Ferguson, J. Am. Chem. Soc., 1996, 118, 9780–9781 CrossRef CAS.
- T. Okano, A. Kikuchi, Y. Sakurai, Y. Takei and N. Ogata, J. Controlled Release, 1995, 36, 125–133 CrossRef CAS.
- G. d Crevoisier, P. Fabre, J.-M. Corpart and L. Leibler, Science, 1999, 285, 1246–1249 CrossRef PubMed.
- K. Ichimura, S.-K. Oh and M. Nakagawa, Science, 2000, 288, 1624–1626 CrossRef CAS PubMed.
- C. L. Feng, Y. J. Zhang, J. Jin, Y. L. Song, L. Y. Xie, G. R. Qu, L. Jiang and D. B. Zhu, Langmuir, 2001, 17, 4593–4597 CrossRef CAS.
- D. Liu and D. J. Broer, Responsive Polymer Surfaces: Dynamics in Surface Topography, John Wiley & Sons, 2017 Search PubMed.
- A. Hozumi, L. Jiang, H. Lee and M. Shimomura, Stimuli-Responsive Dewetting/Wetting Smart Surfaces and Interfaces, Springer, 2018 Search PubMed.
- C. Li, M. Li, Z. Ni, Q. Guan, B. R. Blackman and E. Saiz, J. R. Soc., Interface, 2021, 18, 20210162 CrossRef CAS PubMed.
- S. L. Gras, T. Mahmud, G. Rosengarten, A. Mitchell and K. Kalantar-zadeh, Chem. Phys. Chem., 2007, 8, 2036–2050 CrossRef CAS PubMed.
- G. Kravanja, I. A. Belyaeva, L. Hribar, I. Drevenšek-Olenik, M. Jezeršek and M. Shamonin, Adv. Mater. Interfaces, 2021, 8, 2100235 CrossRef CAS.
- G. Kravanja, I. A. Belyaeva, L. Hribar, I. Drevenšek-Olenik, M. Shamonin and M. Jezeršek, Adv. Mater. Technol., 2022, 7, 2101045 CrossRef CAS.
- R. Kriegl, G. Kravanja, L. Hribar, L. Čoga, I. Drevenšek-Olenik, M. Jezeršek, M. Kalin and M. Shamonin, Polymers, 2022, 14, 3883 CrossRef CAS PubMed.
- Y. Li, J. Li, W. Li and H. Du, Smart Mater. Struct., 2014, 23, 123001 CrossRef.
- J. Sutrisno, A. Purwanto and S. A. Mazlan, Adv. Eng. Mater., 2015, 17, 563–597 CrossRef.
- A. M. Menzel, Phys. Rep., 2015, 554, 1–45 CrossRef CAS.
- M. Lopez-Lopez, J. D. Durán, L. Y. Iskakova and A. Y. Zubarev, J. Nanofluids, 2016, 5, 479–495 CrossRef.
- M. A. Cantera, M. Behrooz, R. F. Gibson and F. Gordaninejad, Smart Mater. Struct., 2017, 26, 023001 CrossRef.
- M. Shamonin and E. Y. Kramarenko, Novel Magnetic Nanostructures, Elsevier, 2018, pp. 221–245 Search PubMed.
- R. Weeber, M. Hermes, A. M. Schmidt and C. Holm, J. Phys.: Condens. Matter, 2018, 30, 063002 CrossRef PubMed.
- T. Liu and Y. Xu, Smart and Functional Soft Materials, 2019, ch. 4, vol. 5, pp. 63–86 Search PubMed.
- J. R. Morillas and J. de Vicente, Soft Matter, 2020, 16, 9614–9642 RSC.
- M. Arslan Hafeez, M. Usman, M. A. Umer and A. Hanif, Polymers, 2020, 12, 3023 CrossRef PubMed.
- A. K. Bastola and M. Hossain, Composites, Part B, 2020, 200, 108348 CrossRef CAS.
- A. K. Bastola and M. Hossain, Mater. Des., 2021, 211, 110172 CrossRef.
- S. Odenbach, Magnetic Hybrid-Materials: Multi-Scale Modelling, Synthesis, and Applications, Walter de Gruyter GmbH & Co KG, 2021 Search PubMed.
- T. A. Nadzharyan, M. Shamonin and E. Y. Kramarenko, Polymers, 2022, 14, 4096 CrossRef CAS PubMed.
- G. Glavan, W. Kettl, A. Brunhuber, M. Shamonin and I. Drevenšek-Olenik, Polymers, 2019, 11, 594 CrossRef PubMed.
- Z. Yang, J. K. Park and S. Kim, Small, 2018, 14, 1702839 CrossRef PubMed.
- M. Lovšin, D. Brandl, G. Glavan, I. A. Belyaeva, L. Cmok, L. Čoga, M. Kalin, M. Shamonin and I. Drevenšek-Olenik, Polymers, 2021, 13, 4422 CrossRef PubMed.
- G. Glavan, P. Salamon, I. A. Belyaeva, M. Shamonin and I. Drevenšek-Olenik, J. Appl. Polym. Sci., 2018, 135, 46221 CrossRef.
- R. Li, D. Ren, X. Wang, X. Chen, S. Chen and X. Wu, J. Intell. Mater. Syst. Struct., 2018, 29, 160–170 CrossRef CAS.
- R. Li, X. Li, Y. Li, P.-A. Yang and J. Liu, Friction, 2020, 8, 917–929 CrossRef CAS.
- A. Kovalev, I. A. Belyaeva, C. von Hofen, S. Gorb and M. Shamonin, Adv. Eng. Mater., 2022, 24, 2200372 CrossRef CAS.
- P. V. von Lockette, S. Lofland, J. Biggs, J. Roche, J. Mineroff and M. Babcock, Smart Mater. Struct., 2011, 20, 105022 CrossRef.
- R. Sheridan, J. Roche and S. E. Lofland, et al. , Smart Mater. Struct., 2014, 23, 094004 CrossRef CAS.
- W. Zhang, S. Ahmed, S. Masters, J. Hong, Z. Ounaies and M. Frecker, J. Intell. Mater. Syst. Struct., 2018, 29, 3983–4000 CrossRef.
- D. Romeis, S. Kostrov, E. Y. Kramarenko, G. V. Stepanov, M. Shamonin and M. Saphiannikova, Soft Matter, 2020, 16, 9047–9058 RSC.
- V. Kalita, Y. I. Dzhezherya, S. Cherepov, Y. B. Skirta, A. Bodnaruk and G. Levchenko, Smart Mater. Struct., 2021, 30, 025020 CrossRef CAS.
- G. Glavan, I. A. Belyaeva, K. Ruwisch, J. Wollschläger and M. Shamonin, Sensors, 2021, 21, 6390 CrossRef CAS PubMed.
- P. A. Sánchez, E. S. Minina, S. S. Kantorovich and E. Y. Kramarenko, Soft Matter, 2019, 15, 175–189 RSC.
- I. A. Belyaeva, E. Y. Kramarenko, G. V. Stepanov, V. V. Sorokin, D. Stadler and M. Shamonin, Soft Matter, 2016, 12, 2901–2913 RSC.
- V. V. Sorokin, I. A. Belyaeva, M. Shamonin and E. Y. Kramarenko, Phys. Rev. E, 2017, 95, 062501 CrossRef PubMed.
- S. Chougale, D. Romeis and M. Saphiannikova, J. Magn. Magn. Mater., 2021, 523, 167597 CrossRef CAS.
- F. P. Beer, E. R. Johnston Jr., J. T. DeWolf and D. F. Mazurek, Mechanics of materials, McGraw Hill, 2020 Search PubMed.
- F. A. Chouery, Exact and numerical solutions for large deflection of elastic non-prismatic beams, FAC Systems INC., WA, 2006 Search PubMed.
- V. V. Sorokin, G. V. Stepanov, M. Shamonin, G. J. Monkman, A. R. Khokhlov and E. Y. Kramarenko, Polymer, 2015, 76, 191–202 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: An SI file with additional details and a video example of top-view lamellar deflection hysteresis measurement of a MAE surface (height ≈ 280 μm, width ≈ 70 μm, pitch ≈ 355 μm, and shear storage modulus ≈ 15 kPa). See DOI: https://doi.org/10.1039/d3sm00012e |
| This journal is © The Royal Society of Chemistry 2023 |