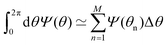DOI:
10.1039/D2SM01565J
(Paper)
Soft Matter, 2023,
19, 2127-2137
An exact expression of three-body system for the complex shear modulus of frictional granular materials
Received
30th November 2022
, Accepted 16th February 2023
First published on 17th February 2023
Abstract
We propose a simple model comprising three particles to study the nonlinear mechanical response of jammed frictional granular materials under oscillatory shear. Owing to the introduction of the simple model, we obtain an exact analytical expression of the complex shear modulus for a system including many monodispersed disks, which satisfies a scaling law in the vicinity of the jamming point. These expressions perfectly reproduce the shear modulus of the many-body system with low strain amplitudes and friction coefficients. Even for disordered many-body systems, the model reproduces the results by introducing a single fitting parameter.
1 Introduction
The rheological property of densely dispersed grains, e.g., granular materials, colloidal suspensions, and emulsions, plays an important role in physics and engineering. This rheological property mainly depends on the packing fraction ϕ of the grains. The materials behave like fluids for ϕ < ϕJ with jamming fraction ϕJ and exhibit a solid-like elastic response above ϕJ.1,2 In the linear response regime (i.e., for small strains), the shear modulus is characterized by the density of states3–5 and satisfies scaling laws.6–9 However, the linear response region becomes narrower as ϕ approaches ϕJ,10,11 and the nonlinear response becomes relevant due to the plastic deformation associated with the yielding.12–20
If we are interested in a nonlinear response to an applied oscillatory shear strain, it exhibits a complicated stress–strain curve. Although the storage and loss moduli G′ and G′′ were originally introduced to characterize the linear viscoelasticity of materials, they can be used to characterize nonlinear viscoelasticity or visco-elastoplastic responses to applied strains.21 In this case, G′ and G′′ are no longer constants but strongly depend on the strain amplitude γ0. In particular, we have recognized that G′ decreases with γ011,22–25 and G′′ remains non-zero in the low frequency limit24,25 for densely dispersed grains.
The theoretical analysis of densely dispersed grains is challenging as a typical many-body problem in non-equilibrium systems. To date, a few theoretical approaches have been proposed for systems related to frictionless particles. The scaling laws for the linear elastic response were derived in terms of the vibrational density of states.7,8 The Fourier analysis of particle trajectories helps to generate semi-analytical expressions for G′ and G′′.25 Unfortunately, these theories cannot apply to frictional particles because of the history-dependent contact force.9,24
It is helpful to analyze a simple model with small degrees of freedom to understand the behavior of many-body systems, including densely dispersed grains. This approach has been used in statistical mechanics. The mean-field approximation of the Ising model is a typical example in which the system contains only one Ising spin under the influence of a self-consistently determined mean field.26 For atomic liquids, a cell model, in which a single atom exists in a cage, was used to derive the equation of state.27,28 The coherent potential approximation for disordered solids has been used to understand electronic band structures.29 The effective medium theory reveals the elastic response of random spring networks.30 In addition, a simple model consisting of two particles was proposed to reproduce the liquid–solid phase transition.31 The advantage of such few-body models is that we can obtain exact solutions. The qualitative behavior of the corresponding many-body systems can be determined based on the solutions of the few-body models. Thus, we adopt this approach to determine the nonlinear responses of the frictional dispersed grains.
This study proposes a model consisting of three identical particles to describe the mechanical response of jammed frictional granular materials under oscillatory shear. In Section 2, we introduce the three-body system (TBS). This model can be analytically solved for low-strain amplitudes and friction coefficients near the jamming point in Section 3. In Section 4, we demonstrate that the analytical solution reproduces the storage and loss moduli of many-body systems (MBSs) without any fitting parameter if there is no disorder in the particle configuration. Even if disorder exists, a scaling law for the complex shear modulus for the TBS semi-quantitatively agrees with the numerical simulations of the MBS by introducing a fitting parameter. We discuss and conclude our results in Section 5. In Appendix A, we show the details of the MBS when the particles are initially placed on a triangular lattice. The effect of particle rotation is described in Appendix B. In Appendix C, we derive the analytical expressions for the shear stress and pressure in the TBS. In Appendix D, we relate the complex shear modulus with the hysteresis loop of the stress–strain curve. The details of the disordered MBS are presented in Appendix E. We present the numerical shear modulus for the TBS in Appendix F.
2 Three-body system
We consider two-dimensional granular materials consisting of many grains under oscillatory shear (Fig. 1). Here, the grains constituting granular materials are modeled as frictional spherical particles. Moreover, we introduce a system of three identical particles to simply describe the MBS (Fig. 2). The MBS can contain polydisperse particles, while we assume that the TBS is a monodisperse system. In the TBS, the position ri(t) = (xi(t), yi(t)) of particle i with diameter d at time t is given by| |  | (1) |
| |  | (2) |
| | 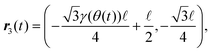 | (3) |
where ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) is the initial distance between particles. We also introduce ε:= 1 −
is the initial distance between particles. We also introduce ε:= 1 − ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) /d as the compressive strain. The compressive strain ε in the TBS corresponds to ϕ − ϕJ in the MBS, as shown in Appendix A. We apply shear strain as
/d as the compressive strain. The compressive strain ε in the TBS corresponds to ϕ − ϕJ in the MBS, as shown in Appendix A. We apply shear strain as| | γ(θ) = γ0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ θ | (4) |
with strain amplitude γ0, phase θ = ωt, and angular frequency ω. Note that we need at least three particles to realize a stable interlocking state.
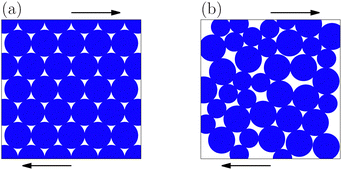 |
| | Fig. 1 Schematics of the ordered MBS (a) and the disordered MBS (b). | |
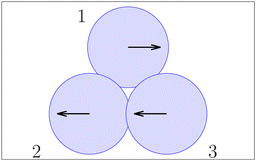 |
| | Fig. 2 A schematic of the TBS. | |
We adopt the interaction force fij between particles i and j given by
| | | fij = (f(n)ijnij + f(t)ijtij)H(rij − d), | (5) |
where
f(n)ij and
f(t)ij denote the normal and tangential forces between the particles
i and
j.
32 The distance between the particles
i and
j is
rij = |
rij| with
rij :=
ri −
rj = (
xij,
yij). Here,
H(
x) is Heaviside's step function satisfying
H(
x) = 1 for
x > 0 and
H(
x) = 0 otherwise. The normal and tangential unit vectors are denoted by
nij :=
rij/
rij = (
nij,x,
nij,y) and
tij := (−
nij,y,
nij,x), respectively. For simplicity, we do not consider the torque balance and, thus, the rotation of the particles. See Appendix B for the effect of the rotation.
The normal force is assumed to be
with the normal elastic constant
kn and normal relative displacement
u(n)ij :=
rij −
d. Moreover, the tangential force is assumed to be
| | f(t)ij = min(|![[f with combining tilde]](https://www.rsc.org/images/entities/i_char_0066_0303.gif) (t)ij|,μf(n)ij)sgn( (t)ij|,μf(n)ij)sgn(![[f with combining tilde]](https://www.rsc.org/images/entities/i_char_0066_0303.gif) (t)ij), (t)ij), | (7) |
where
![[f with combining tilde]](https://www.rsc.org/images/entities/i_char_0066_0303.gif) (t)ij
(t)ij = −
ktu(t)ij;
kt denotes the tangential elastic constant, and
μ denotes the friction coefficient. Here, min(
a,
b) selects the smaller value between
a and
b, sgn(
x) = 1 for
x ≥ 0, and sgn(
x) = −1 for
x < 0. The tangential displacement
u(t)ij satisfies
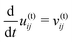
for |
![[f with combining tilde]](https://www.rsc.org/images/entities/i_char_0066_0303.gif) (t)ij
(t)ij| <
μf(n)ij with the tangential velocity
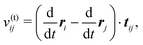
whereas
u(t)ij remains unchanged for |
![[f with combining tilde]](https://www.rsc.org/images/entities/i_char_0066_0303.gif) (t)ij
(t)ij| ≥
μf(n)ij. We refer to the contact with |
![[f with combining tilde]](https://www.rsc.org/images/entities/i_char_0066_0303.gif) (t)ij
(t)ij| <
μf(n)ij as the stick contact and the contact with |
![[f with combining tilde]](https://www.rsc.org/images/entities/i_char_0066_0303.gif) (t)ij
(t)ij| ≥
μf(n)ij as the slip contact. The tangential displacement,
u(t)ij, is initially set to zero.
The (symmetric contact) shear stress is given by
| | | σ(θ; γ0, μ) = σ(n)(θ; γ0, μ) + σ(t)(θ; γ0, μ) | (8) |
with the normal component of
σ| |  | (9) |
and tangential component of
σ| |  | (10) |
Here,
A corresponds to the area of the system, and we choose

as shown in Appendix A. The pressure is given by
| |  | (11) |
In the right-hand sides of
eqn (9)–(11), we have omitted the arguments
θ,
γ0, and
μ. Similar abbreviations are used below. As we are interested in quasistatic processes, we do not consider the kinetic parts of
σ and
P and the dependence on
ω. After several cycles of oscillatory shear,
σ(
θ) becomes periodic. The storage and loss moduli are given by
33| | 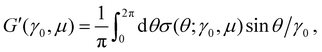 | (12) |
| |  | (13) |
3 Theoretical analysis
Assuming γ0 ≪ ε ≪ 1, we analytically obtain G′ and G′′ for the TBS. The derivation of the analytical results can be found in Appendix C.
First, the normal component of the shear stress is given by
| |  | (14) |
The tangential component of the shear stress is given by
| |  | (15) |
for
γ0 <
γc(
μ) with a critical amplitude
| |  | (16) |
which characterizes the transition from stick to slip states in the contact between the particles. For
γ0 ≥
γc(
μ), the tangential component of the shear stress is given by
| |  | (17) |
where
Θ = cos
−1(1 − 2
γc(
μ)/
γ0). Regions with
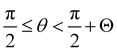
and

correspond to the stick state, and the other regions correspond to the slip state. Owing to this transition in the contact, the stress–strain curve given by
eqn (14)–(17) exhibits a hysteresis loop.
Eqn (17) does not exhibit a viscoelastic response but a typical elastoplastic response without viscous effect.
Fig. 3 shows the scaled shear stress σ/γ0 against the scaled strain γ/γ0 using eqn (4), (8) and (14)–(17) for various values of γ0 with kt/kn = 1.0 and μ = 0.01. The shape of the scaled stress–strain curve is characterized by a parallelogram as a typical elastoplastic response. As γ0 increases, the maximum value ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) max = (σ/γ0)|γ/γ0=1 decreases from a larger value
max = (σ/γ0)|γ/γ0=1 decreases from a larger value 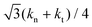 to a smaller value
to a smaller value 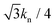 . As shown in Appendix D, the storage modulus G′ is approximately given by
. As shown in Appendix D, the storage modulus G′ is approximately given by ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) max. Hence, the decrease of
max. Hence, the decrease of ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) max in Fig. 3 indicates the decrease of G′. For γ0 = 0.00003 and 0.0001, the hysteresis loop exists, but the area of the loop is negligible for γ0 = 0.00001 and 0.001. The loss modulus G′′ is proportional to the area of the loop, as shown in Appendix D. Hence, the dependence of the area on γ0 indicates that there is a peak in G′′ as γ0 increases.
max in Fig. 3 indicates the decrease of G′. For γ0 = 0.00003 and 0.0001, the hysteresis loop exists, but the area of the loop is negligible for γ0 = 0.00001 and 0.001. The loss modulus G′′ is proportional to the area of the loop, as shown in Appendix D. Hence, the dependence of the area on γ0 indicates that there is a peak in G′′ as γ0 increases.
 |
| | Fig. 3 Scaled shear stress σ/γ0 against γ/γ0 using eqn (4), (8) and (14)–(17) for various values of γ0 with kt/kn = 1.0, ε = 0.001, and μ = 0.01. | |
Substituting eqn (8) and (14)–(17) into eqn (12), we obtain the storage modulus as
| |  | (18) |
As
γ0 increases beyond
γc(
μ),
G′ decreases from a higher value to a lower value. The corresponding behavior has been observed in the MBS in previous studies.
9,24
Substituting eqn (8) and (14)–(17) into eqn (13), the loss modulus is given by
| | 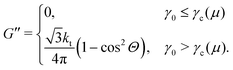 | (19) |
The loss modulus
G′′ is zero for
γ0 <
γc(
μ), whereas
G′′ sharply increases with
γ0 when
γ0 exceeds
γc(
μ) and decreases to 0 after a peak. The behavior of
G′′ for the TBS qualitatively reproduces that of the MBS in previous studies.
24
We adopt the abbreviation for the pressure at γ = 0 as
| | | P0 := P(θ = 0; γ0, μ), | (20) |
which is also obtained as
| |  | (21) |
From
eqn (16), (18), (19) and (21), we derive scaling laws for a given
ε as
| |  | (22) |
| |  | (23) |
where
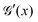
and

denote scaling functions. The maximum values of
G′ and
G′′ are denoted as
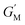
and

, respectively. In the TBS, they are given as
| |  | (24) |
| |  | (25) |
| |  | (26) |
with
T(
x) = cos
−1(1 − 2
xc/
x),
S(
x) = sin(2
T(
x))/2, and

.
4 Comparison with the MBS
We demonstrate the relevance of the TBS analysis based on the simulation of a two-dimensional MBS consisting of N frictional grains. First, we consider a system corresponding to the TBS, where all the particles are identical and initially placed on the triangular lattice with a unit length ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) (Fig. 1(a)). The details are shown in Appendix A. Next, we consider a bidisperse system where the number of particles with diameter d is equal to that of particles with diameter d/1.4, and the particles are randomly placed with packing fraction ϕ (Fig. 1(b)). The mass densities of the particles are identical. The details of the disordered MBS are shown in Appendix E. In both systems, the shear strain given by eqn (4) is applied for Nc cycles using the SLLOD equation under the Lees–Edwards boundary condition.34 In the MBS, we replace the normal force as
(Fig. 1(a)). The details are shown in Appendix A. Next, we consider a bidisperse system where the number of particles with diameter d is equal to that of particles with diameter d/1.4, and the particles are randomly placed with packing fraction ϕ (Fig. 1(b)). The mass densities of the particles are identical. The details of the disordered MBS are shown in Appendix E. In both systems, the shear strain given by eqn (4) is applied for Nc cycles using the SLLOD equation under the Lees–Edwards boundary condition.34 In the MBS, we replace the normal force as| | | f(n)ij→ −(knu(n)ij + ηnv(n)ij) | (27) |
with the normal viscous constant ηn and the normal velocity  to include the viscous force depending on the relative velocity. The tangential force is replaced by
to include the viscous force depending on the relative velocity. The tangential force is replaced by| | f(t)ij → min(|![[f with combining tilde]](https://www.rsc.org/images/entities/i_char_0066_0303.gif) (t)ij|,μf(n,el)ij)sgn( (t)ij|,μf(n,el)ij)sgn(![[f with combining tilde]](https://www.rsc.org/images/entities/i_char_0066_0303.gif) (t)ij), (t)ij), | (28) |
with| | ![[f with combining tilde]](https://www.rsc.org/images/entities/i_char_0066_0303.gif) (t)ij → −(ktu(t)ij + ηtv(t)ij), (t)ij → −(ktu(t)ij + ηtv(t)ij), | (29) |
where f(n,el)ij = −knu(n)ij denotes the elastic part of the normal force with a tangential viscous constant ηt. We measure G′, G′′, and P0 in the last cycle using eqn (11)–(13). For the ordered MBS, we use N = 64, kt/kn = 1.0, and ε = 0.001, whereas N = 1000, kt/kn = 0.2, and ϕ = 0.87 are used for the disordered MBS. In both systems, the other parameters are identical: Nc = 20,  and
and  with a mass m of larger particles.
with a mass m of larger particles.
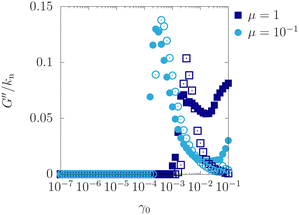
As shown in Fig. 4, we plot G′ for the ordered MBS against γ0 with kt/kn = 1.0 and ε = 0.001 for various values of μ as points. Moreover, we plot the analytical results of the TBS obtained using eqn (18) as thin solid lines. Surprisingly, the results of the TBS agree with those of the MBS for γ0 < 0.003 without any fitting parameters. As γ0 increases beyond γc(μ) shown by the vertical dashed lines, G′ for μ > 0 decreases and converges to a constant, which is equal to G′ for μ = 0. For larger γ0, G′ for the MBS decreases again, whereas the theoretical G′ for the TBS is constant. This discrepancy results from the violation of condition γ0 ≪ ε for the analytical calculation. If we numerically solve the TBS to obtain G′ without the assumption γ0 ≪ ε, G′ decreases after a plateau again as in the case of MBS, although its value in the TBS for γ0 → 0.1 slightly deviates from that of the MBS, as shown in Appendix F.
 |
| | Fig. 4 Storage modulus G′ against γ0 with kt/kn = 1.0 and ε = 0.001 for various values of μ. The points represent the results of the ordered MBS. The thin solid lines represent the analytical result given by eqn (18). The vertical dashed lines represent the critical amplitude γc(μ) given by eqn (16) for μ = 10−4, 10−3, 10−2, 10−1, and 1 from left to right. | |
As shown in Fig. 5, we plot G′′ for the MBS on the triangular lattice against γ0 with kt/kn = 1.0 and ε = 0.001 for various values of μ as points. Moreover, we plot the analytical results of the TBS obtained using eqn (19) as thin solid lines. The analytical result agrees perfectly with the MBS for γ0 < 0.003 without any fitting parameters. As γ0 increases beyond γc(μ) shown by the vertical dashed lines, G′′ for μ > 0 increases from 0 and decreases after reaching a peak. The peak position of G′′ against γ0 increases with μ. Thus, our analytical results fail to capture the behavior of G′′ for μ = 1.
 |
| | Fig. 5 Loss modulus G′′ against γ0 with kt/kn = 1.0 and ε = 0.001 for various values of μ. The points represent the results of the ordered MBS. The thin solid lines represent the analytical results obtained using eqn (19). The vertical dashed lines represent the critical amplitude γc(μ) given by eqn (16) for μ = 10−4, 10−3, 10−2, 10−1, and 1 from left to right. | |
Consider the disordered MBS shown in Fig. 1(b). Fig. 6 shows the scaled shear stress σ/γ0 against the scaled strain γ/γ0 in the disordered MBS with μ = 0.0001. The maximum value ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) max decreases as γ0 increases. The area S of the curve is the largest for γ0 = 0.00003. It is interesting that stress–strain curves are not characterized by parallelograms in this case in contrast to Fig. 3. This means that the disordered configuration of particles creates an effective viscosity, and thus, the response to an applied strain becomes visco-elastoplastic.
max decreases as γ0 increases. The area S of the curve is the largest for γ0 = 0.00003. It is interesting that stress–strain curves are not characterized by parallelograms in this case in contrast to Fig. 3. This means that the disordered configuration of particles creates an effective viscosity, and thus, the response to an applied strain becomes visco-elastoplastic.
 |
| | Fig. 6 Scaled shear stress σ/γ0 against γ/γ0 in the disordered MBS for various values of γ0 with μ = 0.01 and ϕ = 0.870. | |
The behaviors of G′ and G′′ in the disordered MBS are similar to those of the TBS as shown in Appendix E. Therefore, it is expected that the scaling laws in eqn (22) and (23) for a given ε in the TBS can be used even in this system with corresponding ϕ. This expectation is verified by Fig. 7, in which we plot the scaled moduli  and
and  against the scaled strain ktγ0/(μP0(γ0, μ)) for various values of μ in the disordered MBS. Moreover, we plot the analytical results for the TBS obtained using eqn (25) and (26) as solid lines, which qualitatively reproduce the MBS results for small scaled strain, while the scaling is apparently violated for large scaled strain. Here, we choose kt/kn = 1.5 for the TBS to fit the second plateau to that of the MBS. At present, we do not know the relationship between ϕ and the fitting parameter.
against the scaled strain ktγ0/(μP0(γ0, μ)) for various values of μ in the disordered MBS. Moreover, we plot the analytical results for the TBS obtained using eqn (25) and (26) as solid lines, which qualitatively reproduce the MBS results for small scaled strain, while the scaling is apparently violated for large scaled strain. Here, we choose kt/kn = 1.5 for the TBS to fit the second plateau to that of the MBS. At present, we do not know the relationship between ϕ and the fitting parameter.
 |
| | Fig. 7 (a) Scaled storage modulus  against the scaled strain ktγ0/(μP0(γ0, μ)) with ϕ = 0.87 and kt/kn = 0.2 for various values of μ in the disordered MBS. The solid line represents the analytical result of the TBS given by eqn (25) with kt/kn = 1.5. (b) Scaled loss modulus against the scaled strain ktγ0/(μP0(γ0, μ)) with ϕ = 0.87 and kt/kn = 0.2 for various values of μ in the disordered MBS. The solid line represents the analytical result of the TBS given by eqn (25) with kt/kn = 1.5. (b) Scaled loss modulus  against the scaled strain ktγ0/(μP0(γ0, μ)) with ϕ = 0.87 and kt/kn = 0.2 for various values of μ in the disordered MBS. The solid line represents the analytical result of the TBS given by eqn (26) with kt/kn = 1.5. against the scaled strain ktγ0/(μP0(γ0, μ)) with ϕ = 0.87 and kt/kn = 0.2 for various values of μ in the disordered MBS. The solid line represents the analytical result of the TBS given by eqn (26) with kt/kn = 1.5. | |
5 Conclusions
We demonstrated the relevancy of a model of the TBS to describe the complex modulus of jammed frictional granular materials under oscillatory shear. We obtained the analytical expressions for the γ0-dependence of G′ and G′′ as shown in eqn (16), (18), and (19), which predict the μ-dependence of the critical amplitude γc, the decrease of G′, and the peak of G′′ above γc for crystalline solids. The analytical expressions lead to the scaling laws given by eqn (22) and (23). Although we have ignored the non-affine motion for crystalline solids, these analytical results quantitatively agree with those of the ordered MBS. Surprisingly, some characteristic features of disordered solids for low strain (or high pressure) can be captured. These results indicate that the analysis of the toy model gives a basis for understanding the nonlinear rheology of frictional granular materials under small strain.
Although the values of the plateaus in G′ for disordered MBS depended on ϕ − ϕJ,6,9 the corresponding values of the TBS are independent of ϕ − ϕJ, as expressed in eqn (18). In addition, our analytical expressions cannot reproduce the second decrease of G′ and increase of G′′ near γ0 = 10−2 in the MBS. The discrepancy should result from the disorder because it leads to the ϕ-dependence of G′.7 To include the disorder effect, we regarded kt/kn as a fitting parameter. In previous studies on models with small degrees of freedom, e.g., the coherent potential approximation,26,29,30 the corresponding fitting parameters were self-consistently determined. In future studies, we will discuss the self-consistent determination of the parameter for the TBS.
Some researchers are interested in contributions from higher harmonics characterizing the nonlinear response to oscillatory shear,21 but the nonlinear viscoelastic moduli characterizing the higher harmonics are negligibly small for jammed frictionless particles.25 However, the higher harmonics in the frictional granular materials require further careful investigation.
Conflicts of interest
There are no conflicts to declare.
Appendix A: details of Ordered MBS
This section explains the details of the ordered MBS consisting of monodispersed particles initially placed on a triangular lattice. We consider a two-dimensional assembly of N frictional particles in a periodic box with sizes along the x and y directions Lx and Ly, respectively. Here, we initially place N = 2NxNy particles of diameter d with integers nx and ny at ri as| |  | (30) |
for 0 ≤ i < NxNy with integers nx, ny, and i = nx + Nxny. For NxNy ≤ i < 2NxNy, ri is defined as| |  | (31) |
with i = nx + Nxny + NxNy. The initial configuration is illustrated in Fig. 8. We choose Lx = Nx![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) and
and 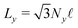 with
with ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = d(1 − ε).
= d(1 − ε).
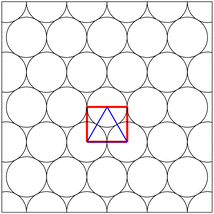 |
| | Fig. 8 Initial configuration of mono-dispersed particles on a triangular lattice. The red rectangle, including interactions represented by the blue lines, corresponds to the TBS. | |
The position ri and peculiar momentum pi of particle i with mass mi and diameter di are driven by the SLLOD equation under the Lees–Edwards boundary condition as34
| | 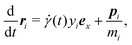 | (32) |
| |  | (33) |
where
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif)
(
t) =
γ0ω![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
cos
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ωt
ωt and
ex = (1,0) is the unit vector along the
x direction. The interaction force
fi is defined as
| |  | (34) |
with
dij = (
di +
dj)/2,
nij =
rij/
rij,
tij = (−
nij,y,
nij,x), and
rij =
ri −
rj = (
xij,
yij). The normal force is given by
| | | f(n)ij = −(knu(n)ij + ηnv(n)ij) | (35) |
with a normal viscous constant
ηn and
| | | v(n)ij = (vi − vj)·nij, | (36) |
where the velocity of particle
i is given by
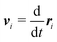
. The following model is adopted for the tangential force:
| | f(t)ij = min(|![[f with combining tilde]](https://www.rsc.org/images/entities/i_char_0066_0303.gif) (t)ij|,μf(n,el)ij)sgn( (t)ij|,μf(n,el)ij)sgn(![[f with combining tilde]](https://www.rsc.org/images/entities/i_char_0066_0303.gif) (t)ij), (t)ij), | (37) |
where
f(n,el)ij = −
knu(n)ij denotes the elastic part of the normal force. Here,
![[f with combining tilde]](https://www.rsc.org/images/entities/i_char_0066_0303.gif) (t)ij
(t)ij is given by
| | ![[f with combining tilde]](https://www.rsc.org/images/entities/i_char_0066_0303.gif) (t)ij = −(ktu(t)ij + ηtv(t)ij) (t)ij = −(ktu(t)ij + ηtv(t)ij) | (38) |
with a tangential viscous constant
ηt. The tangential velocity
v(t)ij is given by
| | | v(t)ij = (vi − vj)·tij. | (39) |
The tangential displacement
u(t)ij satisfies

for |
![[f with combining tilde]](https://www.rsc.org/images/entities/i_char_0066_0303.gif) (t)ij
(t)ij| <
μf(n,el)ij, whereas
u(t)ij remains unchanged for |
![[f with combining tilde]](https://www.rsc.org/images/entities/i_char_0066_0303.gif) (t)ij
(t)ij| ≥
μf(n,el)ij. The tangential displacement
u(t)ij is set to zero if
i and
j are detached.
If all the particles are separated, the packing fraction ϕ for the ordered MBS is defined as
| |  | (40) |
Even if contacts exist between the particles, we use
eqn (40) by assuming that the contact length
dij −
rij is sufficiently lower than
dij. Using
eqn (40),
ϕ is defined as
| |  | (41) |
The jamming point of this system is
| |  | (42) |
with
ε = 0. The distance from the jamming point is proportional to
ε as
| |  | (43) |
for
ε ≪ 1.
The shear stress σ is defined by eqn (8) in the main article with the normal component
| |  | (44) |
and tangential component
| |  | (45) |
The pressure is defined as
| |  | (46) |
We use Nx = 8, Ny = 4, Nc = 20, kt = kn, and 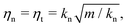 where m denotes the mass of a particle with diameter d. This model corresponds to a restitution coefficient e = 0.043. We adopt the leapfrog algorithm considering a time step of Δt = 0.05t0. We choose
where m denotes the mass of a particle with diameter d. This model corresponds to a restitution coefficient e = 0.043. We adopt the leapfrog algorithm considering a time step of Δt = 0.05t0. We choose  as the quasistatic shear deformation because G′ and G′′ are almost independent of ω for
as the quasistatic shear deformation because G′ and G′′ are almost independent of ω for 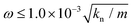 .
.
As shown in Fig. 4 and 5, the behaviors of G′ and G′′ of the TBS agree with that of the MBS. We explain the theoretical background of the TBS. The initial configuration is shown in Fig. 8; it contains the unit cell represented by the red rectangle with length ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) and height
and height  . It contains interactions between the three particles represented by blue lines. Here, we assume that the particles move affinely as
. It contains interactions between the three particles represented by blue lines. Here, we assume that the particles move affinely as
| | | ri(t) = ri(0) + γ(θ(t))yi(0)ex. | (47) |
In this case, the corresponding relative distances between the particles in any unit cell are identical.
In particular, in a unit cell containing particles i = i1, i2, and i3 with i1 = NxNy, i2 = 0, and i3 = 1, the positions of the particles are given by
| | 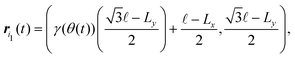 | (48) |
| |  | (49) |
| | 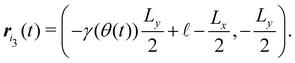 | (50) |
The relative distances between these particles are identical to those of the TBS, given by
eqn (1)–(3), which indicates that the TBS provides the interaction forces among the three particles. This system includes 2
NxNy unit cells with identical interaction forces. Hence, the normal and tangential components of
σ are given by
| |  | (51) |
| | 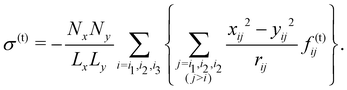 | (52) |
The pressure is also given by:
| |  | (53) |
Using the relation

corresponding to
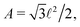 σ(n)
σ(n),
σ(t), and
P coincide with
eqn (8)–(11). Hence, if the assumptions of the affine motion,
i.e.,
eqn (48)–(50), are satisfied,
G′ and
G′′ in the ordered MBS coincide with those in the TBS.
Appendix B: effect of particle rotation
In this section, we illustrate the effect of particle rotation, which was not described in Appendix A. In the model with rotation, the tangential velocity v(t)ij is given by| | | v(t)ij = (vi − vj)·tij − (diωi + djωj)/2 | (54) |
instead of eqn (39), where ωi denotes the angular velocity of particle i. The time evolution of ωi is given by| | 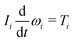 | (55) |
with the moment of inertia Ii = midi2/8 and torque  .
.
As shown in Fig. 9, we plot G′ in the ordered MBS with and without rotation with kt/kn = 1.0 and ε = 0.001 for various values of μ = 0.01. The values of other parameters are the same as those in Appendix A. The effect of particle rotation is negligible, except for the region near γc.
 |
| | Fig. 9 Storage modulus G′ against γ0 for the ordered MBS with μ = 0.01 and ε = 0.001. The open and filled symbols represent the results of the particles with and without rotation, respectively. | |
As shown in Fig. 10, we plot G′′ in the ordered MBS with and without rotation with kt/kn = 1.0 and ε = 0.001 for μ = 10−2, 10−3, 10−4, 10−5 and 0.00001. The values of other parameters are the same as those in Appendix A. There are slight deviations in the peak position near γc between particles with and without rotation.
 |
| | Fig. 10 Loss modulus G′′ against γ0 for the ordered MBS with μ = 10−2, 10−3, 10−4, 10−5 and ε = 0.001. The open and filled symbols represent the results of the particles with and without rotation, respectively. | |
In Fig. 11, we plot G′′ in the ordered MBS with and without rotation with kt/kn = 1.0 and ε = 0.001 for μ = 1.0 and 0.1. There are slight deviations in the peak position near γc between particles with and without rotation even for these higher μ. In addition, the second increase in G′′ around γ0 = 0.1 for particles without rotation disappears for those with rotation.
 |
| | Fig. 11 Loss modulus G′′ against γ0 for the ordered MBS with μ = 1.0,0.1 and ε = 0.001. The open and filled symbols represent the results of the particles with and without rotation, respectively. | |
Appendix C: analytical calculation of shear stress and pressure
This section briefly explains the derivation of the normal and tangential components of shear stress and pressure for a small value of γ0. From eqn (1)–(3), the relative distance rij is given by| |  | (56) |
| | 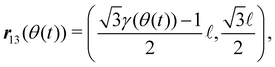 | (57) |
| | r23(θ(t)) = (−![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ,0). ,0). | (58) |
Substituting these equations into u(n)ij = rij − d, the normal displacements are given by| |  | (59) |
| |  | (60) |
Substituting these equations into eqn (6), we obtain the normal force as| | 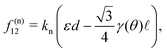 | (62) |
| |  | (63) |
up to O(γ0).
By differentiating eqn (56)–(58) with time t, we obtain the relative velocity as
| | 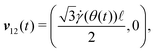 | (65) |
| |  | (66) |
with the strain rate

. The tangential unit vector is given by
| |  | (68) |
| | 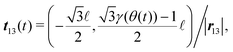 | (69) |
By considering the inner product of
vij and
tij, the tangential velocity is given by
| |  | (71) |
| |  | (72) |
If the transition from the stick state to the slip state does not occur under oscillatory shear, the tangential displacement is obtained by integrating
v(t)ij(
t) as
| | 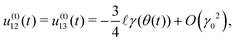 | (74) |
u(t)23(
t) = 0.(75)Substituting these equations into
f(t)ij = −
ktu(t)ij yields
| | f(t)12 = f(t)13 = 3ktγ(θ(t))![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) /4, /4, | (76) |
up to
O(
γ0). The condition that the transition does not occur is satisfied when
f(t)12 <
μf(n)12 for
γ =
γ0. Using
eqn (64) and (77) with the assumption
γ0 ≪
ε, the condition is replaced by
γ0 <
γc with
γc given by
eqn (16).
For γ0 > γc, there exist regions where u(t)ij is unchanged in the slip state as
| |  | (78) |
where
Θ satisfies
| | 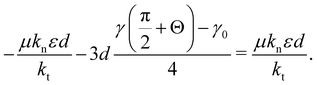 | (81) |
This equation provides Θ = cos−1(1 − 2γc/γ0). Substituting these equations into f(t)ij = −ktu(t)ij yields
| | 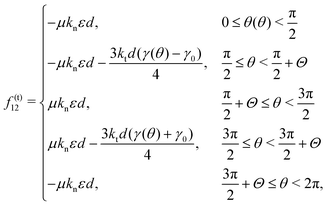 | (82) |
The normal component of σ in eqn (9) is given by
| | | σ(n) = σ(n)12 + σ(n)13 | (85) |
with
| |  | (86) |
| |  | (87) |
Substituting
eqn (58) and (57) with
eqn (64) and (63) into
eqn (86) and (87) and using
eqn (85), we obtain
σ(n) as
eqn (14).
The tangential component of σ in eqn (10) is given by
| | | σ(t) = σ(t)12 + σ(t)13 | (88) |
with
| | 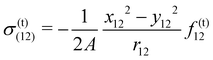 | (89) |
| | 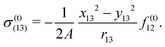 | (90) |
Substituting
eqn (58) and (57) with
eqn (77) into
eqn (88), (89), and (90), we obtain
σ(t) as
eqn (15) for
γ0 <
γc. Using
eqn (84) and (83) instead of
eqn (77), we obtain
σ(t) as
eqn (17) for
γ0 ≥
γc.
The pressure, i.e., P, in eqn (11) is defined as
with
| |  | (92) |
Substituting
eqn (56)–(58) with
eqn (62)–(64) into
eqn (91) and (92) with
γ = 0, we obtain
P0(
γ0,
μ) as
eqn (21).
Appendix D: relation between shear modulus and stress–strain curve
In this section, we relate the shape of the stress–strain curve to the complex shear modulus. The shear stress σ(θ) is expanded using the Fourier series as| |  | (93) |
where 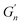 and
and  with n > 1 denote the higher harmonics,
with n > 1 denote the higher harmonics,  , and
, and  . By neglecting
. By neglecting  and
and  for n > 1,
for n > 1,| |  | (94) |
which is the maximum value of the scaled stress–strain curve illustrated in Fig. 3(b). This expression and the scaled stress–strain curve in Fig. 3(b) explain the decrease of G′ defined by eqn (18).
The area S of the curve for σ(θ)/γ0 against γ(θ)/γ0 is given by
| |  | (95) |
Substituting
eqn (4) into
eqn (95) with
eqn (12), we obtain
| | 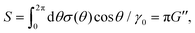 | (96) |
which results in
G′′ =
S/π. As
γ0 increases, the area
S of the scaled stress–strain curve in
Fig. 3(b) increases first and decreases later, which explains the
γ0-dependence of
G′′ provided by
eqn (19).
Appendix E: details of disordered MBS
In this section, we present the details of the disordered MBS. This model is an extension of the monodisperse model used in Appendix A, including the dispersion of the particles and disordered initial configuration.
The system is bidisperse and includes an equal number of particles with diameters d and d/1.4. To simulate the disordered MBS, we randomly place the particles in a rectangular box with an initial packing fraction of ϕI = 0.75. The system is slowly compressed until the packing fraction reaches ϕ.24 In each compression step, the packing fraction is increased by Δϕ = 1.0 × 10−4 with an affine transformation. Thereafter, the particles are relaxed to a mechanical equilibrium state with the kinetic temperature  . Here, we choose Tth = 1.0 × 10−8knd2. After compression, the oscillatory shear strain given by eqn (4) is applied for Nc cycles. In the last cycle, we measure G′ and G′′ using eqn (12) and (13) with eqn (8)–(10). The pressure, P0(γ0, μ) is obtained using eqn (11) after the last cycle. We use ϕ = 0.87, N = 1000, Nc = 20, Ly/Lx = 1, kt = 0.2kn, and
. Here, we choose Tth = 1.0 × 10−8knd2. After compression, the oscillatory shear strain given by eqn (4) is applied for Nc cycles. In the last cycle, we measure G′ and G′′ using eqn (12) and (13) with eqn (8)–(10). The pressure, P0(γ0, μ) is obtained using eqn (11) after the last cycle. We use ϕ = 0.87, N = 1000, Nc = 20, Ly/Lx = 1, kt = 0.2kn, and 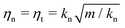 .
.
Fig. 12 shows the storage modulus G′ against γ0 in the disordered MBS for various values of μ. The storage modulus G′ is almost independent of γ0 for a small γ0 and decreases as γ0 increases. The endpoint of the first plateau increases with μ except for μ = 0. A second plateau of G′ exists for μ = 10−4 and 10−5. The behavior of G′ for relatively small γ0 is similar to that of crystalline solids as depicted in Fig. 4. On the other hand, the decrease of G′ for larger γ0 cannot be captured by the analytical results of the TBS. Note that G′ for μ = 0.1 in the limit γ0 → 0 is different from that for μ ≤ 0.01, which results from the μ dependence of the jamming point ϕJ.9
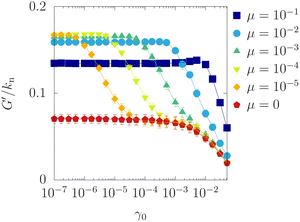 |
| | Fig. 12 Storage modulus G′ in the disordered MBS against γ0 with ϕ = 0.870 for various values of μ. | |
Fig. 13 shows the loss modulus G′′ in the disordered MBS against γ0 for various values of μ. For sufficiently small γ0, G′′ is zero, while G′′ becomes non-zero as γ0 increases. The loss modulus G′′ starts to increase for smaller γ0 as μ decreases. Similar to the case of G′, TBS captures only the behavior of relatively small γ0 (see Fig. 5 and 13).
 |
| | Fig. 13 Loss modulus G′′ in the disordered MBS against γ0 with ϕ = 0.870 for various values of μ. | |
Appendix F: numerical shear modulus for TBS
In this section, we show the behaviors of G′ and G′′ in the TBS without the assumption used to obtain the analytical solution. Here, we numerically obtain G′ and G′′ under quasistatic oscillation using eqn (12) and (13) based on the left Riemann sum, where the integration of Ψ(θ), i.e.,| |  | (97) |
is approximated as| | 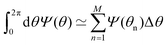 | (98) |
with Δθ = 2π/M and θn = (n − 1)Δθ. We use ε = 0.001 and Δθ = 5.0 × 10−5 in our simulation.
As shown in Fig. 14, we plot the storage modulus G′ numerically obtained from the TBS against γ0 with kt/kn = 1.0 for various values of μ as points. Moreover, we plot the analytical results derived from eqn (18) as thin solid lines. The numerical results agree with the analytical results for γ0 < 0.003 and reproduce the second plateau of the MBS shown in Fig. 4.
 |
| | Fig. 14 Storage modulus G′ against γ0 with kt/kn = 1.0 and ε = 0.001 for various values of μ. The points represent the numerical results of the TBS, while the thin solid lines represent the analytical result given by eqn (18). The vertical dashed lines represent the critical amplitude γc(μ) given by eqn (16) for μ = 10−4, 10−3, 10−2, 10−1, 100 from left to right. | |
Fig. 15 shows the loss modulus G′′ numerically obtained from the TBS against γ0 with kt/kn = 1.0 for various values of μ as points. We also plot the analytical results given by eqn (19) as thin solid lines. The numerical results agree with the analytical results for γ0 < 0.003.
 |
| | Fig. 15 Loss modulus G′′ against γ0 with kt/kn = 1.0 and ε = 0.001 for various values of μ. The points represent the numerical results of the TBS, while the thin solid lines represent the analytical results obtained from eqn (19). The vertical dashed lines represent the critical amplitude γc(μ) obtained from eqn (16) for μ = 10−4, 10−3, 10−2, 10−1, 100 from left to right. | |
Acknowledgements
The authors thank K. Saitoh, D. Ishima, and S. Takada for fruitful discussions. This study was supported by JSPS KAKENHI under Grant No. JP19K03670 and JP21H01006.
References
- M. van Hecke, J. Phys.: Condens. Matter, 2010, 22, 033101 CrossRef CAS PubMed.
- R. P. Behringer and B. Chakraborty, Rep. Prog. Phys., 2019, 82, 012601 CrossRef CAS PubMed.
- C. Maloney and A. Lemaître, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 93, 195501 Search PubMed.
- C. E. Maloney and A. Lemaître, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 74, 016118 CrossRef PubMed.
-
D. Ishima, K. Saitoh, M. Otsuki and H. Hayakawa, 2022, arXiv:2207.06632.
- C. S. O'Hern, S. A. Langer, A. J. Liu and S. R. Nagel, Phys. Rev. Lett., 2002, 88, 075507 CrossRef PubMed.
- M. Wyart, Ann. Phys., 2005, 30, 1 Search PubMed.
- B. P. Tighe, Phys. Rev. Lett., 2011, 107, 158303 CrossRef PubMed.
- M. Otsuki and H. Hayakawa, Phys. Rev. E, 2017, 95, 062902 CrossRef PubMed.
- C. Coulais, A. Seguin and O. Dauchot, Phys. Rev. Lett., 2014, 113, 198001 CrossRef CAS PubMed.
- M. Otsuki and H. Hayakawa, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 90, 042202 CrossRef PubMed.
- K. H. Nagamanasa, S. Gokhale, A. K. Sood and R. Ganapathy, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 89, 062308 CrossRef PubMed.
- E. D. Knowlton, D. J. Pine and L. Cipelletti, Soft Matter, 2014, 10, 6931–6940 RSC.
- T. Kawasaki and L. Berthier, Phys. Rev. E, 2016, 94, 022615 CrossRef PubMed.
- P. Leishangthem, A. D. S. Parmar and S. Sastry, Nat. Commun., 2017, 8, 14653 CrossRef PubMed.
- A. H. Clark, J. D. Thompson, M. D. Shattuck, N. T. Ouellette and C. S. O'Hern, Phys. Rev. E, 2018, 97, 062901 CrossRef CAS PubMed.
- J. Boschan, S. Luding and B. P. Tighe, Granular Matter, 2019, 21, 58 CrossRef.
- J. Boschan, D. VÅgberg, E. Somfai and B. P. Tighe, Soft Matter, 2016, 12, 5450–5460 RSC.
- D. Nakayama, H. Yoshino and F. Zamponi, J. Stat. Mech.: Theory Exp., 2016, 2016, 104001 CrossRef.
-
T. Kawasaki and K. Miyazaki, arXiv, 2020, preprint, arXiv:2003.10716, DOI:10.48550/arXiv.2003.10716.
- K. Hyun, M. Wilhelm, C. O. Klein, K. S. Cho, J. G. Nam, K. H. Ahn, S. J. Lee, R. H. Ewoldt and G. H. McKinley, Prog. Polym. Sci., 2011, 36, 1697 CrossRef CAS.
- S. Dagois-Bohy, E. Somfai, B. P. Tighe and M. van Hecke, Soft Matter, 2017, 13, 9036–9045 RSC.
- D. Ishima and H. Hayakawa, Phys. Rev. E, 2020, 101, 042902 CrossRef CAS PubMed.
- M. Otsuki and H. Hayakawa, Eur. Phys. J. E: Soft Matter Biol. Phys., 2021, 44, 70 CrossRef CAS PubMed.
- M. Otsuki and H. Hayakawa, Phys. Rev. Lett., 2022, 128, 208002 CrossRef CAS PubMed.
-
N. Goldenfeld, Lectures on Phase Transitions and the Renormalization Group, CRC Press, 1992 Search PubMed.
- J. E. Lennard-Jones and A. F. Devonshire, Proc. R. Soc. A, 1937, 163, 53–70 CAS.
- J. E. Lennard-Jones and A. F. Devonshire, Proc. R. Soc. A, 1938, 165, 1–11 CAS.
- F. Yonezawa and K. Morigaki, Prog. Theor. Phys. Suppl., 1973, 53, 1–76 CrossRef CAS.
- S. Feng, M. F. Thorpe and E. Garboczi, Phys. Rev. B: Condens. Matter Mater. Phys., 1985, 31, 276–280 CrossRef CAS PubMed.
- A. Awazu, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2001, 63, 032102 CrossRef CAS PubMed.
- P. A. Cundall and O. D. L. Strack, Géotechnique, 1979, 29, 47–65 CrossRef.
-
M. Doi and S. F. Edwards, The theory of polymer dynamics, Oxford University Press, 1986 Search PubMed.
-
D. J. Evans and G. Morriss, Statistical Mechanics of Nonequilibrium Liquids, Cambridge University Press, 2008 Search PubMed.
|
| This journal is © The Royal Society of Chemistry 2023 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *a and
Hisao
Hayakawa
*a and
Hisao
Hayakawa
 b
b


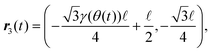
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) is the initial distance between particles. We also introduce ε:= 1 −
is the initial distance between particles. We also introduce ε:= 1 − ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) /d as the compressive strain. The compressive strain ε in the TBS corresponds to ϕ − ϕJ in the MBS, as shown in Appendix A. We apply shear strain as
/d as the compressive strain. The compressive strain ε in the TBS corresponds to ϕ − ϕJ in the MBS, as shown in Appendix A. We apply shear strain as![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ
θ![[f with combining tilde]](https://www.rsc.org/images/entities/i_char_0066_0303.gif) (t)ij|,μf(n)ij)sgn(
(t)ij|,μf(n)ij)sgn(![[f with combining tilde]](https://www.rsc.org/images/entities/i_char_0066_0303.gif) (t)ij),
(t)ij),![[f with combining tilde]](https://www.rsc.org/images/entities/i_char_0066_0303.gif) (t)ij = −ktu(t)ij; kt denotes the tangential elastic constant, and μ denotes the friction coefficient. Here, min(a,b) selects the smaller value between a and b, sgn(x) = 1 for x ≥ 0, and sgn(x) = −1 for x < 0. The tangential displacement u(t)ij satisfies
(t)ij = −ktu(t)ij; kt denotes the tangential elastic constant, and μ denotes the friction coefficient. Here, min(a,b) selects the smaller value between a and b, sgn(x) = 1 for x ≥ 0, and sgn(x) = −1 for x < 0. The tangential displacement u(t)ij satisfies 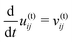 for |
for |![[f with combining tilde]](https://www.rsc.org/images/entities/i_char_0066_0303.gif) (t)ij| < μf(n)ij with the tangential velocity
(t)ij| < μf(n)ij with the tangential velocity 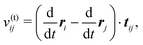 whereas u(t)ij remains unchanged for |
whereas u(t)ij remains unchanged for |![[f with combining tilde]](https://www.rsc.org/images/entities/i_char_0066_0303.gif) (t)ij| ≥ μf(n)ij. We refer to the contact with |
(t)ij| ≥ μf(n)ij. We refer to the contact with |![[f with combining tilde]](https://www.rsc.org/images/entities/i_char_0066_0303.gif) (t)ij| < μf(n)ij as the stick contact and the contact with |
(t)ij| < μf(n)ij as the stick contact and the contact with |![[f with combining tilde]](https://www.rsc.org/images/entities/i_char_0066_0303.gif) (t)ij| ≥ μf(n)ij as the slip contact. The tangential displacement, u(t)ij, is initially set to zero.
(t)ij| ≥ μf(n)ij as the slip contact. The tangential displacement, u(t)ij, is initially set to zero.


 as shown in Appendix A. The pressure is given by
as shown in Appendix A. The pressure is given by
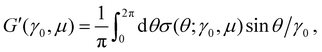





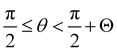 and
and  correspond to the stick state, and the other regions correspond to the slip state. Owing to this transition in the contact, the stress–strain curve given by eqn (14)–(17) exhibits a hysteresis loop. Eqn (17) does not exhibit a viscoelastic response but a typical elastoplastic response without viscous effect.
correspond to the stick state, and the other regions correspond to the slip state. Owing to this transition in the contact, the stress–strain curve given by eqn (14)–(17) exhibits a hysteresis loop. Eqn (17) does not exhibit a viscoelastic response but a typical elastoplastic response without viscous effect.
![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) max = (σ/γ0)|γ/γ0=1 decreases from a larger value
max = (σ/γ0)|γ/γ0=1 decreases from a larger value 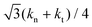 to a smaller value
to a smaller value 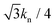 . As shown in Appendix D, the storage modulus G′ is approximately given by
. As shown in Appendix D, the storage modulus G′ is approximately given by ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) max. Hence, the decrease of
max. Hence, the decrease of ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) max in Fig. 3 indicates the decrease of G′. For γ0 = 0.00003 and 0.0001, the hysteresis loop exists, but the area of the loop is negligible for γ0 = 0.00001 and 0.001. The loss modulus G′′ is proportional to the area of the loop, as shown in Appendix D. Hence, the dependence of the area on γ0 indicates that there is a peak in G′′ as γ0 increases.
max in Fig. 3 indicates the decrease of G′. For γ0 = 0.00003 and 0.0001, the hysteresis loop exists, but the area of the loop is negligible for γ0 = 0.00001 and 0.001. The loss modulus G′′ is proportional to the area of the loop, as shown in Appendix D. Hence, the dependence of the area on γ0 indicates that there is a peak in G′′ as γ0 increases.

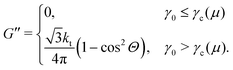



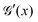 and
and  denote scaling functions. The maximum values of G′ and G′′ are denoted as
denote scaling functions. The maximum values of G′ and G′′ are denoted as 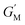 and
and  , respectively. In the TBS, they are given as
, respectively. In the TBS, they are given as


 .
.
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) (Fig. 1(a)). The details are shown in Appendix A. Next, we consider a bidisperse system where the number of particles with diameter d is equal to that of particles with diameter d/1.4, and the particles are randomly placed with packing fraction ϕ (Fig. 1(b)). The mass densities of the particles are identical. The details of the disordered MBS are shown in Appendix E. In both systems, the shear strain given by eqn (4) is applied for Nc cycles using the SLLOD equation under the Lees–Edwards boundary condition.34 In the MBS, we replace the normal force as
(Fig. 1(a)). The details are shown in Appendix A. Next, we consider a bidisperse system where the number of particles with diameter d is equal to that of particles with diameter d/1.4, and the particles are randomly placed with packing fraction ϕ (Fig. 1(b)). The mass densities of the particles are identical. The details of the disordered MBS are shown in Appendix E. In both systems, the shear strain given by eqn (4) is applied for Nc cycles using the SLLOD equation under the Lees–Edwards boundary condition.34 In the MBS, we replace the normal force as to include the viscous force depending on the relative velocity. The tangential force is replaced by
to include the viscous force depending on the relative velocity. The tangential force is replaced by![[f with combining tilde]](https://www.rsc.org/images/entities/i_char_0066_0303.gif) (t)ij|,μf(n,el)ij)sgn(
(t)ij|,μf(n,el)ij)sgn(![[f with combining tilde]](https://www.rsc.org/images/entities/i_char_0066_0303.gif) (t)ij),
(t)ij),![[f with combining tilde]](https://www.rsc.org/images/entities/i_char_0066_0303.gif) (t)ij → −(ktu(t)ij + ηtv(t)ij),
(t)ij → −(ktu(t)ij + ηtv(t)ij), and
and  with a mass m of larger particles.
with a mass m of larger particles.


![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) max decreases as γ0 increases. The area S of the curve is the largest for γ0 = 0.00003. It is interesting that stress–strain curves are not characterized by parallelograms in this case in contrast to Fig. 3. This means that the disordered configuration of particles creates an effective viscosity, and thus, the response to an applied strain becomes visco-elastoplastic.
max decreases as γ0 increases. The area S of the curve is the largest for γ0 = 0.00003. It is interesting that stress–strain curves are not characterized by parallelograms in this case in contrast to Fig. 3. This means that the disordered configuration of particles creates an effective viscosity, and thus, the response to an applied strain becomes visco-elastoplastic.
 and
and  against the scaled strain ktγ0/(μP0(γ0, μ)) for various values of μ in the disordered MBS. Moreover, we plot the analytical results for the TBS obtained using eqn (25) and (26) as solid lines, which qualitatively reproduce the MBS results for small scaled strain, while the scaling is apparently violated for large scaled strain. Here, we choose kt/kn = 1.5 for the TBS to fit the second plateau to that of the MBS. At present, we do not know the relationship between ϕ and the fitting parameter.
against the scaled strain ktγ0/(μP0(γ0, μ)) for various values of μ in the disordered MBS. Moreover, we plot the analytical results for the TBS obtained using eqn (25) and (26) as solid lines, which qualitatively reproduce the MBS results for small scaled strain, while the scaling is apparently violated for large scaled strain. Here, we choose kt/kn = 1.5 for the TBS to fit the second plateau to that of the MBS. At present, we do not know the relationship between ϕ and the fitting parameter.
 against the scaled strain ktγ0/(μP0(γ0, μ)) with ϕ = 0.87 and kt/kn = 0.2 for various values of μ in the disordered MBS. The solid line represents the analytical result of the TBS given by eqn (25) with kt/kn = 1.5. (b) Scaled loss modulus
against the scaled strain ktγ0/(μP0(γ0, μ)) with ϕ = 0.87 and kt/kn = 0.2 for various values of μ in the disordered MBS. The solid line represents the analytical result of the TBS given by eqn (25) with kt/kn = 1.5. (b) Scaled loss modulus  against the scaled strain ktγ0/(μP0(γ0, μ)) with ϕ = 0.87 and kt/kn = 0.2 for various values of μ in the disordered MBS. The solid line represents the analytical result of the TBS given by eqn (26) with kt/kn = 1.5.
against the scaled strain ktγ0/(μP0(γ0, μ)) with ϕ = 0.87 and kt/kn = 0.2 for various values of μ in the disordered MBS. The solid line represents the analytical result of the TBS given by eqn (26) with kt/kn = 1.5.

![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) and
and 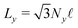 with
with ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = d(1 − ε).
= d(1 − ε).

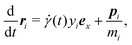

![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) (t) = γ0ω
(t) = γ0ω![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ωt and ex = (1,0) is the unit vector along the x direction. The interaction force fi is defined as
ωt and ex = (1,0) is the unit vector along the x direction. The interaction force fi is defined as
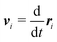 . The following model is adopted for the tangential force:
. The following model is adopted for the tangential force:![[f with combining tilde]](https://www.rsc.org/images/entities/i_char_0066_0303.gif) (t)ij|,μf(n,el)ij)sgn(
(t)ij|,μf(n,el)ij)sgn(![[f with combining tilde]](https://www.rsc.org/images/entities/i_char_0066_0303.gif) (t)ij),
(t)ij),![[f with combining tilde]](https://www.rsc.org/images/entities/i_char_0066_0303.gif) (t)ij is given by
(t)ij is given by![[f with combining tilde]](https://www.rsc.org/images/entities/i_char_0066_0303.gif) (t)ij = −(ktu(t)ij + ηtv(t)ij)
(t)ij = −(ktu(t)ij + ηtv(t)ij) for |
for |![[f with combining tilde]](https://www.rsc.org/images/entities/i_char_0066_0303.gif) (t)ij| < μf(n,el)ij, whereas u(t)ij remains unchanged for |
(t)ij| < μf(n,el)ij, whereas u(t)ij remains unchanged for |![[f with combining tilde]](https://www.rsc.org/images/entities/i_char_0066_0303.gif) (t)ij| ≥ μf(n,el)ij. The tangential displacement u(t)ij is set to zero if i and j are detached.
(t)ij| ≥ μf(n,el)ij. The tangential displacement u(t)ij is set to zero if i and j are detached.







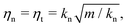 where m denotes the mass of a particle with diameter d. This model corresponds to a restitution coefficient e = 0.043. We adopt the leapfrog algorithm considering a time step of Δt = 0.05t0. We choose
where m denotes the mass of a particle with diameter d. This model corresponds to a restitution coefficient e = 0.043. We adopt the leapfrog algorithm considering a time step of Δt = 0.05t0. We choose  as the quasistatic shear deformation because G′ and G′′ are almost independent of ω for
as the quasistatic shear deformation because G′ and G′′ are almost independent of ω for 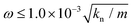 .
.![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) and height
and height  . It contains interactions between the three particles represented by blue lines. Here, we assume that the particles move affinely as
. It contains interactions between the three particles represented by blue lines. Here, we assume that the particles move affinely as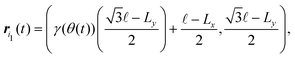

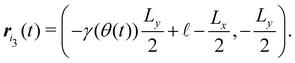

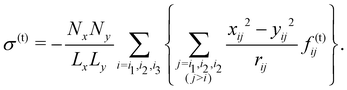

 corresponding to
corresponding to 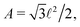 σ(n), σ(t), and P coincide with eqn (8)–(11). Hence, if the assumptions of the affine motion, i.e., eqn (48)–(50), are satisfied, G′ and G′′ in the ordered MBS coincide with those in the TBS.
σ(n), σ(t), and P coincide with eqn (8)–(11). Hence, if the assumptions of the affine motion, i.e., eqn (48)–(50), are satisfied, G′ and G′′ in the ordered MBS coincide with those in the TBS.
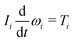
 .
.



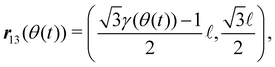
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ,0).
,0).

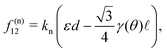

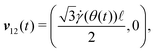

 . The tangential unit vector is given by
. The tangential unit vector is given by
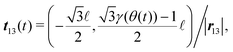


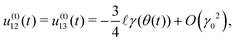
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) /4,
/4,
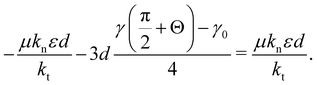
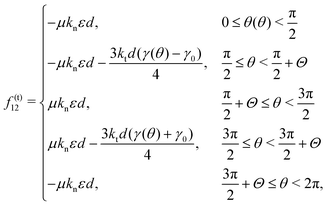


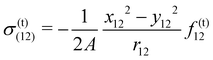
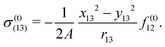


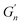 and
and  with n > 1 denote the higher harmonics,
with n > 1 denote the higher harmonics,  , and
, and  . By neglecting
. By neglecting  and
and  for n > 1,
for n > 1,

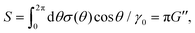
 . Here, we choose Tth = 1.0 × 10−8knd2. After compression, the oscillatory shear strain given by eqn (4) is applied for Nc cycles. In the last cycle, we measure G′ and G′′ using eqn (12) and (13) with eqn (8)–(10). The pressure, P0(γ0, μ) is obtained using eqn (11) after the last cycle. We use ϕ = 0.87, N = 1000, Nc = 20, Ly/Lx = 1, kt = 0.2kn, and
. Here, we choose Tth = 1.0 × 10−8knd2. After compression, the oscillatory shear strain given by eqn (4) is applied for Nc cycles. In the last cycle, we measure G′ and G′′ using eqn (12) and (13) with eqn (8)–(10). The pressure, P0(γ0, μ) is obtained using eqn (11) after the last cycle. We use ϕ = 0.87, N = 1000, Nc = 20, Ly/Lx = 1, kt = 0.2kn, and 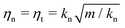 .
.