Open Access Article
Open Access ArticleLiquid structure of bistable responsive macromolecules using mean-field density-functional theory
Arturo
Moncho-Jordá
 *ab,
Nils
Göth
*ab,
Nils
Göth
 c and
Joachim
Dzubiella
c and
Joachim
Dzubiella
 *c
*c
aInstitute Carlos I for Theoretical and Computational Physics, Facultad de Ciencias, Universidad de Granada, Campus Fuentenueva S/N, 18071 Granada, Spain. E-mail: moncho@ugr.es
bDepartamento de Física Aplicada, Universidad de Granada, Campus Fuentenueva S/N, 18071 Granada, Spain
cPhysikalisches Institut, Albert-Ludwigs-Universität Freiburg, Hermann-Herder Straße 3, D-79104 Freiburg, Germany. E-mail: joachim.dzubiella@physik.uni-freiburg.de
First published on 17th March 2023
Abstract
Macromolecular crowding typically applies to biomolecular and polymer-based systems in which the individual particles often feature a two-state folded/unfolded or coil-to-globule transition, such as found for proteins and peptides, DNA and RNA, or supramolecular polymers. Here, we employ a mean-field density functional theory (DFT) of a model of soft and bistable responsive colloids (RCs) in which the size of the macromolecule is explicitly resolved as a degree of freedom living in a bimodal ‘Landau’ energy landscape (exhibiting big and small states), thus directly responding to the crowding environment. Using this RC-DFT we study the effects of self-crowding on the liquid bulk structure and thermodynamics for different energy barriers and softnesses of the bimodal energy landscape, in conditions close to the coil-to-globule transition. We find substantial crowding effects on the internal distributions, a complex polydispersity behavior, and quasi-universal compression curves for increasing (generalized) packing fractions. Moreover, we uncover distinct signatures of bimodal versus unimodal behavior in the particle compression. Finally, the analysis of the pair structure – derived from the test particle route – reveals that the microstructure of the liquid is quite inhomogeneous due to local depletion effects, tuneable by particle softness.
1 Introduction
The phenomenon of macromolecular crowding in biomolecular and polymer-based systems has attracted great attention during the last decades due to its huge implications on the macromolecular structure, stability, as well as conformational transitions and dynamics.1–7 All these properties have profound implications on (bio)chemical reactions in physiological or synthetic media.8 Indeed, biological macromolecules have evolved and function within intracellular environments that are surrounded by other macromolecules at large concentrations. Within these crowded environments, the interactions between macromolecules become substantial, driven not only by volume exclusion effects, but also by other nonspecific interactions, such as electrostatics and hydrophobicity.3,9,10 Better understanding of the mechanisms and consequences of molecular crowding is not only of fundamental and biological interest but will improve the design of functional materials, e.g., synthetic cellular nanosystems.11Theoretical studies of macromolecular crowding usually assume that the macromolecules are hard and stiff entities, and have no internal degrees of freedom (DoFs). However, due their polymeric nature the particles feature large conformational behavior and rather behave in many cases effectively as soft and responsive, and so are able to modify their effective size in response to the external stimuli. For instance, organelle sizes inside the cell fluctuate in demand, swelling or shrinking, to preserve the cell homeostasis,12 and soft and compressible lipid vesicles undergo compaction by increasing the concentration of high molecular weight PEG-based crowders.13
Furthermore, the conformation of biological or functional macromolecules often displays a two-state behavior, such as in folded/unfolded or globule/coil transitions of proteins and polymers.5,14–19 Crowding leads to a restriction of the available space that usually promotes the folded (deswollen or globular) state.5,7,20 Simple models to explain two-state behavior are either based on discrete state models14–16 or on continuous bistable Landau-like models.21,22 However, the consequences of bimodal behavior on the systems’ bulk structure and compression behavior are not well understood. In particular, playing with particle softness/stiffness (defined as a measure of how easily the particle size changes under pressure) and particle hardness (defined as a measure of the interparticle penetrability) is expected to allow fine control and tuneability of the bulk structure and thermodynamics, but is yet unexplored.
In this work, we consider systems formed by identical bistable macromolecular species, each modeled by soft repulsive spheres with a generic Landau-like bimodal size distribution.21,22 We employ the model of ‘Responsive Colloids’ (RCs) where an internal DoF (here, the particle size, σ) is explicitly resolved in an one-body contribution to the Hamiltonian, defining an internal ‘parent’ energy landscape, ψ(σ).23σ represents an internal coarse-grained property of the particle that is explicitly altered by the environment and particle–particle interactions. The RC model has already been applied, e.g., to study the equilibrium structure and dynamics of unimodal, elastic (‘Hertzian’) colloids in bulk using overdamped Brownian dynamics (BD) simulations.24 The polydispersity in such a model is dynamical, and interesting many-body correlations and novel diffusion effects were uncovered, some in line with earlier Monte-Carlo simulations of explicitly compressible microgels.25 Moreover, using a bimodal parent landscape of the colloidal size, the influence of crowding on the internal switching kinetics was examined using BD simulations.26 However, the explicit effects of particle softness and hardness on particle's mean size, polydispersity, packing fraction and other structural bulk properties have not been systematically considered. In addition, it would be desirable to have complementary theoretical tools than BD simulations to study the structure and thermodynamics of larger systems in equilibrium and nonequilibrium more efficiently.27
For these purposes, we combine the RC model with classical density-functional theory (DFT), which is a powerful machinery to efficiently describe the structure and thermodynamics of liquids.28 In equilibrium, the RC model is equivalent to conventional polydisperse systems in the thermodynamic limit,23 for which DFT was successfully constructed.29,30 We note that the research of polydisperse systems surprisingly calmed down, and studies beyond hard spheres with simple unimodal Gaussian parents have been rare since. As a noteworthy exception, Schmidt and Denton showed, using DFT of models of colloid–polymer mixtures which resolved the polymer size as an explicit DoF, how crowding leads to polymer compression and shifts the demixing fluid binodal compared to incompressible systems.31 Here, we adapt and extend these methods in accordance with our bistable RC model and solve it for soft, Gaussian pair potentials assuming a mean-field approximation for the inhomogeneous free energy functional. The RC-DFT machinery is then employed to study bulk structure, polydispersity, and pressure systematically for different forms of the bimodal energy landscape characterized by its energy barrier and its softness. By comparing to the unimodal case (no bistability),24,25 we find large differences for the bistable colloids and some key signatures of bistability in the compression curves.
Our model is sufficiently generic to describe the qualitative behavior of a wide range of crowded soft systems and represents a first approximation to describe conformational (coil-to globule) transitions of globular proteins and peptides having two (e.g., folded/unfolded) conformations,32,33 including intrinsically disordered proteins17 or synthetic supramolecular polymers,18 but also DNA or RNA chains,5,19 and prototypical thermosensitive polymers.34–36
The paper is organized as follows. In Section 2 we introduce the theory and present the main DFT mean-field equations required to determine the one-body density profile, the local size distribution and the microstructure of the RC model (Section 3). We complement our numerical DFT study with perturbation theory described in Section 4. Then, in Section 5 we apply this theoretical framework to investigate how particle squeezing modifies the particle size and volume distribution, the packing fraction, polydispersity, osmotic pressure, as well as the colloidal microstructure (pair distribution functions) of the homogeneous RC systems. We close with a brief summary, concluding remarks, and an outlook on worthwhile future work.
2 Theory
2.1 Distributions of responsive colloids
In ordinary DFT, the equilibrium properties of a non-responsive colloidal system immersed in an external potential, uext(r), are determined by the inhomogeneous one-body density profile, ρ(r), where r is the particle position. Integration over the entire volume V of the system gives the total number of particles,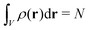 . This framework assumes that the particles forming the system do not have any internal DoFs.
. This framework assumes that the particles forming the system do not have any internal DoFs.
In the more general case of responsive colloids (RCs), the size of the colloids (σ) changes in response to the interactions with other particles or with an applied external potential. In addition, this external field not only depends on position, but also it could vary with the particle size, i.e. uext(r,σ). In other words, the external potential makes the colloidal system inhomogeneous in terms of position and also size distribution. Therefore, we have to consider the joint distribution of the particle position and size, ρ(r,σ). In the following we briefly recall the most basic statistical relations between distributions and means.23
Integration over the four coordinates provides the total number of particles,
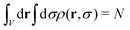 | (1) |
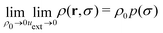 | (2) |
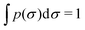 . Hence, p(σ) is the size distribution of a single isolated responsive particle that does not interact with external forces or with other particles. We can express p(σ) as
. Hence, p(σ) is the size distribution of a single isolated responsive particle that does not interact with external forces or with other particles. We can express p(σ) as| p(σ) = p0e−βψ(σ), | (3) |
If the particle concentration is increased beyond the dilute regime and/or the external potential uext is turned on, interactions with the surrounding particles and with the external potential will affect this single-particle property distribution. We denote by f(σ) = N(σ)/N the emergent probability distribution, where N(σ)dσ is the number of particles with internal property within [σ,σ + dσ] in the system. In particular, in the absence of any external field, we have
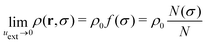 | (4) |
Integration of ρ(r,σ) leads to partial distribution functions. Integrating over the σ-space provides the one-body number density distribution of the RC fluid,
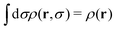 | (5) |
The position dependent mean size is given by
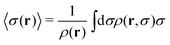 | (6) |
In a similar way, integrating over the volume V we obtain the size distribution
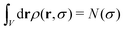 | (7) |
Finally, the position-dependent size distribution is
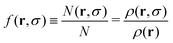 | (8) |
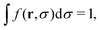 and provides the local size distribution at position r. Its knowledge allows to measure the effect of the applied external potential uext(r,σ) on the size distribution locally.
and provides the local size distribution at position r. Its knowledge allows to measure the effect of the applied external potential uext(r,σ) on the size distribution locally.
2.2 Density functional theory of a RC fluid
Let us consider a RC fluid immersed in the external potential, uext(r,σ). In the same way, the particle–particle pair potential not only depends on the positions r and r′ of both particles, but also has explicit dependence on the size of both interacting particles, σ and σ′, that is u(r,r′;σ,σ′).The inhomogeneous free energy functional of a RC fluid can be written as23,30
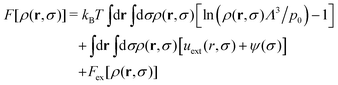 | (9) |
The grand canonical potential energy functional of a RC fluid is
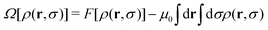 | (10) |
The equilibrium density profile is the one that minimizes the grand canonical functional
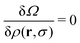 | (11) |
Applying this functional differentiation to eqn (10) and using eqn (9) leads to the so-called Euler–Lagrange equation
kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(ρ(r,σ)Λ3/p0) + uext(r,σ) + ψ(σ) + μex(r,σ) − μ0 = 0 ln(ρ(r,σ)Λ3/p0) + uext(r,σ) + ψ(σ) + μex(r,σ) − μ0 = 0 | (12) |
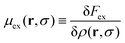 | (13) |
Solving eqn (12) for the particle density ρ(r,σ), we find
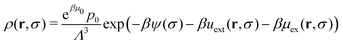 | (14) |
The prefactor q = eβμ0/Λ3 is a constant number with the dimensions of length−3. Using eqn (3) for the single-particle distribution property p(σ) (which is assumed to be known) we finally find
| ρ(r,σ) = qp(σ)exp(−βuext(r,σ) − βμex(r,σ)) | (15) |
The constant q can be calculated by normalization of the density profile
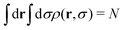 | (16) |
Eqn (15) and (16) must be solved iteratively until convergence is achieved, leading to the equilibrium position and size distribution ρeq(r,σ).
2.3 Mean-field approximation
Although the exact expression of Fex is typically unknown, it is confirmed that the mean-field approximation works quite well for a wide range of bounded potentials representing soft colloids, such as linear polymer chains, dendrimers, star polymers or polyelectrolyte stars, becoming more accurate when increasing the particle density.37,38 The mean-field excess free energy functional is given by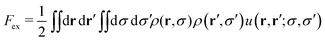 | (17) |
Performing the functional differentiation leads to the explicit expression of the excess chemical potential
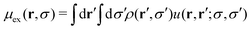 | (18) |
Therefore, given the total number of particles in the system, N, the equilibrium one-body density profile of the mean-field RC is obtained by solving the following set of equations
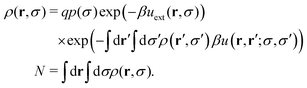 | (19) |
To determine the equilibrium density profiles with a finite particle concentration ρ0 as input parameter, eqn (19) is solved numerically starting from the uniform distribution ρ(r,σ)|0 = ρ0p(σ). For this purpose, this initial guess is inserted into the convolution integral of eqn (19) and then normalized 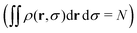 to calculate the next iteration,
to calculate the next iteration, 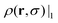 . This iterative procedure is repeated to obtain further interactions, n. In order to improve the stability of the method, the new solution is mixed with the old one, as ρ(r,σ)|n+1 = αρ(r,σ)|n+1 + (1 − α)ρ(r,σ)|n, with α = 0.1. We consider that the procedure has converged to the final equilibrium distribution when
. This iterative procedure is repeated to obtain further interactions, n. In order to improve the stability of the method, the new solution is mixed with the old one, as ρ(r,σ)|n+1 = αρ(r,σ)|n+1 + (1 − α)ρ(r,σ)|n, with α = 0.1. We consider that the procedure has converged to the final equilibrium distribution when 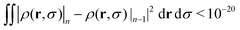 . The r and σ-space are both discretized in intervals of 10−2σ0.
. The r and σ-space are both discretized in intervals of 10−2σ0.
In the particular of considering a homogeneous bulk suspension of RCs (without any applied external field) eqn (19) take the form
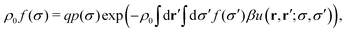 | (20) |
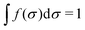 .
.
2.4 Generalized radial distribution functions (RDFs)
The distribution functions that characterize the microstructure of a dispersion can be also generalized for the RC fluid. In particular, the two-body distribution function is defined as23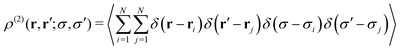 | (21) |
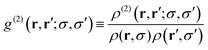 | (22) |
If the system is homogeneous and isotropic, then ρ(r,σ) = ρ0f(σ) and the pair distribution depends only on the distance between particles, so we can define the radial pair–property distribution function g(r;σ,σ′), where r represents the distance between both RCs.
A powerful procedure to obtain g(r;σ,σ′) can be developed by making use of the Test Particle Route (TPR).39,40 Within this method, a test particle of size σ′ is fixed at the origin r = 0. This central particle acts as an external potential for the RC fluid, so uext(r,σ) = u(r;σ,σ′), where r here represents the distance to the test particle. Solving iteratively the mean-field DFT expression given by eqn (19) with this external potential provides the resulting equilibrium density profile of the RCs around the central test particle, ρ(r,σ)|σ′. Rewriting eqn (19) for the particular case radial symmetry we find
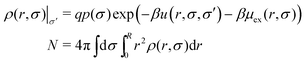 | (23) |
From this density profile, we can extract the RDF as ρ(r,σ)|σ′ = ρ0f(σ)g(r;σ,σ′). Using this method, the radial pair–property distribution functions g(r;σ,σ′) can be calculated as
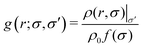 | (24) |
It can be shown that, for large values of r, g(r;σ,σ′) → 1. In addition, for a very diluted system, we obtain
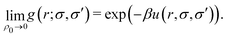 | (25) |
To perform the TPR calculation, we chose a sufficiently large cavity of radius R = 16σ0 and confine the RC fluid inside. This value of the radius is large enough to guarantee that ρ(r) is uniform at the middle distance from the center of the cavity, r = R/2. Then, the total number of RC particles was selected in order to obtain the desired particle density ρ(r = R/2) = ρ0.
3 RC model
We apply the mean-field DFT to investigate the compression effects of an interacting fluid of bistable RCs in bulk solution and investigate its microstructure making use of the TPR described above. We now define our specific RC model.In all cases, to model two-state behavior, we choose a generic bimodal form of the explicit double-Gaussian function
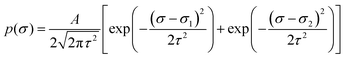 | (26) |
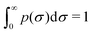 .
.
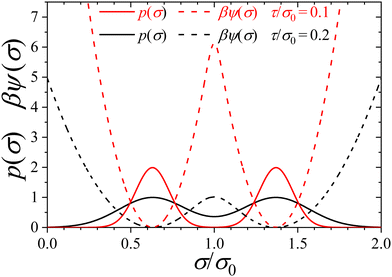
At this point, it is important to explain the physical meaning of the parameter τ. For this purpose, we show in Fig. 1 both, p(σ) and the corresponding elastic free-energy landscape, ψ(σ), for τ = 0.1σ0 and τ = 0.2σ0. As observed, τ provides the thickness of the size distribution. From the perspective of the energy landscape, decreasing τ leads to a sharper energy landscape and to a larger energy barrier separating the two potential wells located at σ1 and σ2. Therefore, τ provides an estimate of the particle softness (conversely, τ−1 represents the stiffness of the RC). In other words, the energy cost of compressing a RC is larger for small τ.
In order to study how bimodality affects the compression effects, we also explore RCs that follow an unimodal Gaussian distribution, defined as
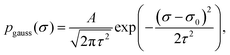 | (27) |
We focus in our work on systems composed by soft interpenetrable responsive spherical colloids, for which we assume the following size-dependent Gaussian pair potential for the particle–particle pair interaction
βu(r,r′;σ,σ′) = ε![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−4|r − r′|2/(σ + σ′)2), exp(−4|r − r′|2/(σ + σ′)2), | (28) |
The choice of the Gaussian pair potential represents a good approximation of the effective interaction between the centers of mass of ultrasoft colloids such as linear polymers chains and dendrimers.37,43–48 The equilibrium properties of soft Gaussian particles described by eqn (28) are well represented by a weakly correlated mean-field fluid over a surprisingly wide density and temperature range, being more accurate for increasing particle densities.37 In addition, the accuracy of mean-field DFT approach for bistable systems has been recently probed comparing the theoretical predictions for (active) two-state switching Gaussian colloids to reactive Brownian Dynamics simulation, finding good quantitative agreement.49–51
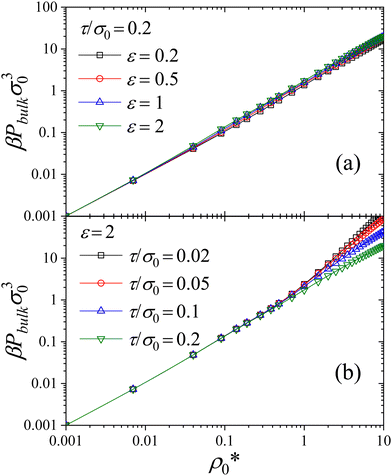
Note that the hardness ε and the stiffness τ−1 are typically not independent quantities, as stiffer colloids also repel each other more strongly. However, in order to investigate the role of both parameters, we treat ε and τ as independent variables. In particular, the calculations were performed choosing ε = 0.2, 0.5, 1, and 2 for the particle hardness. In addition, we explore particles softness values given by τ/σ0 = 0.2 (super soft), 0.1, 0.05 and 0.02 (super stiff). The corresponding free energy barriers are 1kBT, 6.1kBT, 26.7kBT and 170kBT, respectively. In addition, the particle density, ρ0, is also varied to study the role of compression of the size distribution and RDFs in bulk.
4 Perturbation theory
To complement the numerical DFT results with approximate analytical equations and limiting universal scaling laws, we perform a perturbation theory. For this, we use the isolated RC as basis and disturb it with a non-zero density ρ0.24 The mean force of a particle with size σ from particle–particle pair interactions is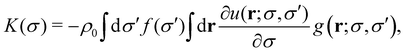 | (29) |
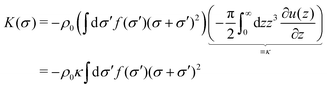 | (30) |
Eqn (30) can be written as expectation values of the emergent distribution
| K(σ) = −ρ0κ(σ2 + 2〈σ〉σ + 〈σ2〉). | (31) |
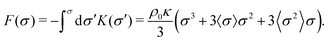 | (32) |
| ftot(σ) = f0e−βψtot(σ) = f0e−βψ(σ)e−βF(σ) = f0p(σ)e−βF(σ). | (33) |
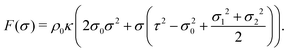 | (34) |
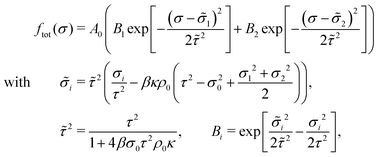 | (35) |
![[small tau, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e5.gif) and each with a new center
and each with a new center ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) i and weight Bi. The prefactor A0 is just for normalization and is explicitly given in Appendix A. For the mean size we finally obtain
i and weight Bi. The prefactor A0 is just for normalization and is explicitly given in Appendix A. For the mean size we finally obtain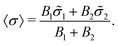 | (36) |
5 Results and discussion
5.1 Compression effects on internal distributions and size
For a homogeneous bulk suspension without we need to solve eqn (20). Using the Gaussian pair potential (eqn (28)) and performing analytically the integral leads to the following expression for f(σ) (see Appendix B):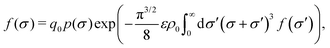 | (37) |
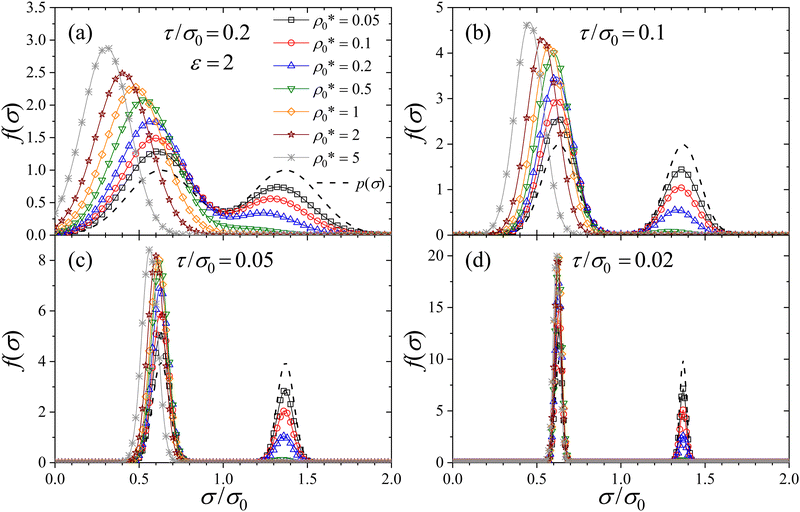
Fig. 2 shows the resulting size distributions for different particle densities from 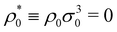 to 5, for ε = 2. Each plot (from (a) to (d)) depicts the distributions for increasing particle stiffness. We first analyze the case of a soft RC, τ/σ0 = 0.2 (Fig. 2(a)). As observed, increasing ρ0 modifies the bimodal distribution in such a way that small sizes occur with a larger probability than the big ones. For sufficiently large concentrations such as
to 5, for ε = 2. Each plot (from (a) to (d)) depicts the distributions for increasing particle stiffness. We first analyze the case of a soft RC, τ/σ0 = 0.2 (Fig. 2(a)). As observed, increasing ρ0 modifies the bimodal distribution in such a way that small sizes occur with a larger probability than the big ones. For sufficiently large concentrations such as 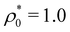 , the peak originally located at σ2 = 1.37σ0 (large sizes) has completely disappeared due to compression, and only small particles remain. In other words, crowding promotes the deswollen state due to the volume exclusion exerted by the soft RCs. This behavior has been reported in many bistable macromolecules such as flexible polymer chains, DNA and globular proteins.5,7,20,32,41,52
, the peak originally located at σ2 = 1.37σ0 (large sizes) has completely disappeared due to compression, and only small particles remain. In other words, crowding promotes the deswollen state due to the volume exclusion exerted by the soft RCs. This behavior has been reported in many bistable macromolecules such as flexible polymer chains, DNA and globular proteins.5,7,20,32,41,52
In addition to this particle redistribution, compression also provokes the shift of both peaks to smaller σ values. This effect is clearly seen for 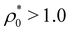 , for which the peak located initially at σ1 = 0.63σ0 experiences a notable increase and shifts to smaller sizes upon compression of the system. By increasing the particle stiffness (Fig. 2(b)–(d)) we still observe the size redistribution effect that converts big RC into small ones. However, the shifting to smaller sizes diminishes and becomes negligible in the limit of very stiff particles (τ/σ0 = 0.02), which means that it is extremely difficult to compress the volume of the RCs. This effect arises because the form of ψ(σ) becomes very steep upon decreasing τ, so the energy cost of compressing the soft colloids tends to be large, too.
, for which the peak located initially at σ1 = 0.63σ0 experiences a notable increase and shifts to smaller sizes upon compression of the system. By increasing the particle stiffness (Fig. 2(b)–(d)) we still observe the size redistribution effect that converts big RC into small ones. However, the shifting to smaller sizes diminishes and becomes negligible in the limit of very stiff particles (τ/σ0 = 0.02), which means that it is extremely difficult to compress the volume of the RCs. This effect arises because the form of ψ(σ) becomes very steep upon decreasing τ, so the energy cost of compressing the soft colloids tends to be large, too.
Fig. 3(a) depicts the average particle diameter of the RC fluid 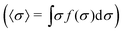 as a function of the bulk concentration, ρ0, for different values of the repulsion strength, ε, assuming soft RCs with τ/σ0 = 0.2. For dilute systems and large mean pair distances, the compression effects are negligible, leading to 〈σ〉σ0 ≈ 1. However, by increasing ρ0, the interparticle repulsion provokes a significant decrease of the mean size for larger values of ε.
as a function of the bulk concentration, ρ0, for different values of the repulsion strength, ε, assuming soft RCs with τ/σ0 = 0.2. For dilute systems and large mean pair distances, the compression effects are negligible, leading to 〈σ〉σ0 ≈ 1. However, by increasing ρ0, the interparticle repulsion provokes a significant decrease of the mean size for larger values of ε.
 | ||
Fig. 3 (a) Average particle diameter, 〈σ〉, as a function of the particle concentration, 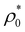 , for ε = 0.2, 0.5, 1 and 2. Inset: All curves for different ε collapse into a single curve when 〈σ〉 is plotted against , for ε = 0.2, 0.5, 1 and 2. Inset: All curves for different ε collapse into a single curve when 〈σ〉 is plotted against 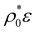 . For large particle densities, . For large particle densities, 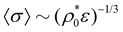 . (b) 〈σ〉 as a function of . (b) 〈σ〉 as a function of 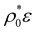 for different values of the particle softness: τ/σ0 = 0.02, 0.05, 0.1 and 0.2. Lines with solid symbols correspond to the bimodal distribution (eqn (26)). Lines with open symbols show the results for the unimodal Gaussian distribution (eqn (27)). Dashed lines depict the predictions provided by the analytical perturbation theory (eqn (35) and (36)). for different values of the particle softness: τ/σ0 = 0.02, 0.05, 0.1 and 0.2. Lines with solid symbols correspond to the bimodal distribution (eqn (26)). Lines with open symbols show the results for the unimodal Gaussian distribution (eqn (27)). Dashed lines depict the predictions provided by the analytical perturbation theory (eqn (35) and (36)). | ||
By plotting 〈σ〉 against the coupling parameter ρ0ε, we find that the different curves collapse onto a universal scaling curve (see orange line in the inset of Fig. 3(a)). This scaling behavior arises from the fact that the equilibrium distribution of a mean-field fluid, given by eqn (37), depends on the product ερ0, so increasing the interparticle interaction strength, ε, at fixed ρ0 has exactly the same effect on the probability distribution of sizes than increasing ρ0 at fixed ε. At very large particle crowding, this scaling curve finally tends to follow an asymptotic power law decay, given by 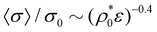 . Please note that similar results for the mean size and the size distribution will be obtained for any other non-Gaussian interparticle pair potential because of the rescalability of the potential dependent prefactor with the density ρ0. The effect of the particle stiffness on 〈σ〉 is displayed in Fig. 3(b). We first describe the results for the bimodal p(σ), given by eqn (26) (lines with symbols in Fig. 3(b)). It occurs that the mean size decreases in two stages due to two different processes: in the dilute regime conversion of big colloids into small ones takes place, whereas in the dense regime
. Please note that similar results for the mean size and the size distribution will be obtained for any other non-Gaussian interparticle pair potential because of the rescalability of the potential dependent prefactor with the density ρ0. The effect of the particle stiffness on 〈σ〉 is displayed in Fig. 3(b). We first describe the results for the bimodal p(σ), given by eqn (26) (lines with symbols in Fig. 3(b)). It occurs that the mean size decreases in two stages due to two different processes: in the dilute regime conversion of big colloids into small ones takes place, whereas in the dense regime 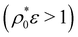 particle compression dominates. For smaller values of τ both mechanisms become more and more separated. In other words, the big-to-small switching still occurs in the dilute regime, but the particle deswelling in the small state requires a further increase of the particle density due to particle stiffness. For sufficiently large densities, the scaling
particle compression dominates. For smaller values of τ both mechanisms become more and more separated. In other words, the big-to-small switching still occurs in the dilute regime, but the particle deswelling in the small state requires a further increase of the particle density due to particle stiffness. For sufficiently large densities, the scaling 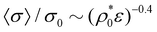 is recovered, but larger compression is required to reach it (see for instance the curve for τ/σ0 = 0.1). In the limit of very small τ (such as τ/σ0 = 0.02), the particles are so stiff that they are not able to further reduce their volume under compression and we find a plateau located at 〈σ〉 ≈ σ1 = 0.63σ0. We point out that, although microgels cannot be modeled as ultrasoft Gaussian colloids, very similar behavior has also been reported in simulations of soft hollow microgels, which clearly show that deswelling of the particles under compression also follows two stages, with an intermediate region nearly having a plateau.53 Note that within the validity of the mean-field approximation, other soft but non-Gaussian interaction potentials would lead to the same scaling behavior with
is recovered, but larger compression is required to reach it (see for instance the curve for τ/σ0 = 0.1). In the limit of very small τ (such as τ/σ0 = 0.02), the particles are so stiff that they are not able to further reduce their volume under compression and we find a plateau located at 〈σ〉 ≈ σ1 = 0.63σ0. We point out that, although microgels cannot be modeled as ultrasoft Gaussian colloids, very similar behavior has also been reported in simulations of soft hollow microgels, which clearly show that deswelling of the particles under compression also follows two stages, with an intermediate region nearly having a plateau.53 Note that within the validity of the mean-field approximation, other soft but non-Gaussian interaction potentials would lead to the same scaling behavior with 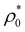 .
.
We remark here that the phase diagram of non-responsive repulsive Gaussian colloids shows crystallization and a reentrant fluid phase at high densities, but only for interaction strengths above ε > 100.54,55 However, the values of ε explored in our work are well below this threshold. In addition, we believe that size responsiveness will promote even more the fluid phase due to the inherent size polydispersity of the system. Therefore, we do not expect the formation of solid phases, no matter the particle density.
These results for the bimodal RCs can be compared to the ones obtained for an unimodal Gaussian distribution (lines with open symbols in Fig. 3(b)). In this case, the responsive colloids are not able to adapt to the density increase by converting big particles into small ones: the only possible mechanism is to reduce the particle size by uniform compression. As a consequence of this, the curves only show a single decay mode with 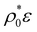 , also exhibiting the same scaling behavior for large compression of soft RCs. For the stiffer system (τ/σ0 = 0.02), the reduction of the particle volume is almost negligible, so the particles behaves effectively as uncompressible non-responsive colloids.
, also exhibiting the same scaling behavior for large compression of soft RCs. For the stiffer system (τ/σ0 = 0.02), the reduction of the particle volume is almost negligible, so the particles behaves effectively as uncompressible non-responsive colloids.
We complement this discussion comparing the results for the mean size obtained with our mean-field responsive DFT with the theoretical predictions attained by the analytical perturbation theory (eqn (35) and (36) in Section 4), shown as dashed lines in Fig. 3(b) for different stiffnesses as a function of 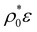 . For small τ we find two decreases of 〈σ〉 that are separated by a plateau. Again, the interpretation is the same: the first one characterizes the transition of large particles into the small state, whereas the second decrease comes from the shrinking of the small state particles. As observed, although perturbation theory (involving low-density and mean-field approximation) is not able to exactly match the DFT predictions nor the right scaling trend for large
. For small τ we find two decreases of 〈σ〉 that are separated by a plateau. Again, the interpretation is the same: the first one characterizes the transition of large particles into the small state, whereas the second decrease comes from the shrinking of the small state particles. As observed, although perturbation theory (involving low-density and mean-field approximation) is not able to exactly match the DFT predictions nor the right scaling trend for large 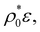 at least it provides an excellent qualitative justification of the results in terms of an analytical expression.
at least it provides an excellent qualitative justification of the results in terms of an analytical expression.
5.2 Polydispersity
Another interesting property to investigate is the polydispersity of the size distribution, δ, defined as the ratio between the standard deviation and the mean size, i.e.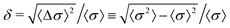 . For the sake of simplicity, we start analysing the behavior of the RC with the Gaussian parent distribution (lines with open symbols in Fig. 4). As seen before, increasing
. For the sake of simplicity, we start analysing the behavior of the RC with the Gaussian parent distribution (lines with open symbols in Fig. 4). As seen before, increasing 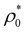 (or increasing ε) involves a progressive decrease of the particle mean size, especially for the softer colloids. Compression of the particles also entails a reduction of the absolute value of the standard deviation,
(or increasing ε) involves a progressive decrease of the particle mean size, especially for the softer colloids. Compression of the particles also entails a reduction of the absolute value of the standard deviation, 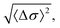 as expected (not shown). However, the polydispersity δ increases upon particle compression due to the reduction of the mean size. This effect is insignificant for the stiff systems (τ/σ0 = 0.02 and 0.05), but becomes quite relevant for the softer system τ/σ0 = 0.2, for which a significant increase of δ arises for
as expected (not shown). However, the polydispersity δ increases upon particle compression due to the reduction of the mean size. This effect is insignificant for the stiff systems (τ/σ0 = 0.02 and 0.05), but becomes quite relevant for the softer system τ/σ0 = 0.2, for which a significant increase of δ arises for 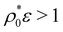 . In other words, increasing the particle concentration leads to more polydisperse systems. This curious effect has been observed also in BD simulations of RCs interacting with an elastic Hertzian pair potential24 as well as in experiments of soft microgel compression.56
. In other words, increasing the particle concentration leads to more polydisperse systems. This curious effect has been observed also in BD simulations of RCs interacting with an elastic Hertzian pair potential24 as well as in experiments of soft microgel compression.56
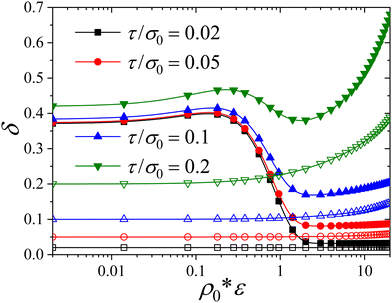 | ||
Fig. 4 RC polydispersity, δ = 〈Δσ2〉1/2/〈σ〉, as a function of 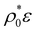 for different values of the particle softness: τ/σ0 = 0.02, 0.05, 0.1 and 0.2. Lines with solid symbols corresponding to the bimodal distribution (eqn (26)) and lines with open symbols to the unimodal Gaussian distribution (eqn (27)). for different values of the particle softness: τ/σ0 = 0.02, 0.05, 0.1 and 0.2. Lines with solid symbols corresponding to the bimodal distribution (eqn (26)) and lines with open symbols to the unimodal Gaussian distribution (eqn (27)). | ||
The behavior of the polydispersity δ for the bimodal RC system is more complex because of the two involved mechanisms (switching and compression) for the bistable particles. The corresponding curves are depicted as lines with solid symbols in Fig. 4. We first focus on the stiffer system, τ/σ0 = 0.02. For small particle densities (or weak interparticle interaction), in the regime 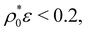 the reduction of the mean size due to the big-to-small conversion mechanism induces a slight increase of the polydispersity. For
the reduction of the mean size due to the big-to-small conversion mechanism induces a slight increase of the polydispersity. For 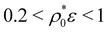 the bimodal distribution becomes completely unimodal, with a mean size located at σ1 = 0.63σ0, which obviously entails a substantial decrease of the polydispersity. In the regime
the bimodal distribution becomes completely unimodal, with a mean size located at σ1 = 0.63σ0, which obviously entails a substantial decrease of the polydispersity. In the regime 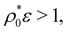 the polydispersity remains constant because the colloids are too stiff. This last regime is different for the softer colloids, for which the unimodal distribution obtained from switching from big to small sizes is still able to shift leftwards due to particle compression, giving rise to an increase of δ. This effect is clearly seen for τ/σ0 = 0.2, where a very important growth is observed for
the polydispersity remains constant because the colloids are too stiff. This last regime is different for the softer colloids, for which the unimodal distribution obtained from switching from big to small sizes is still able to shift leftwards due to particle compression, giving rise to an increase of δ. This effect is clearly seen for τ/σ0 = 0.2, where a very important growth is observed for 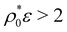 .
.
5.3 Packing fraction behavior
Particle compressibility can also be characterized by means of the particle volume fraction, defined from the emergent mean particle volume through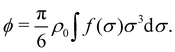 | (38) |
Alternatively, we can also use the so-called generalized volume fraction, ζ, defined as the volume fraction of the soft particles assuming that they do not interact with each other (having the isolated particle distribution p(σ)),25,57–59
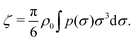 | (39) |
It is important to emphasize that the definition of the packing fraction given in eqn (38) does not take into account the mutual volume overlap or shape deformation of the soft colloids upon compression, which cannot be accessed by means of this theoretical framework. Therefore, eqn (38) represents only a possible reasonable definition for ϕ that provides an estimate of how particle squeezing depends on the density and the softness for interacting systems.
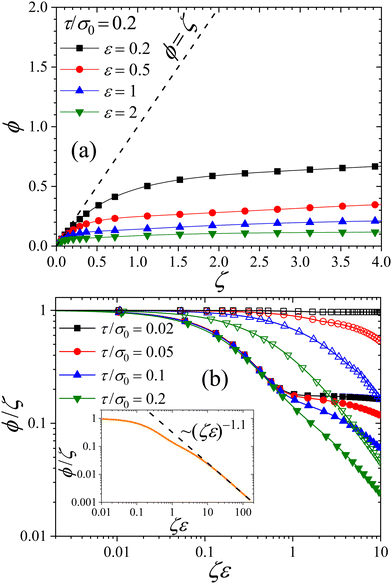
Fig. 5(a) illustrates ϕ(ζ) for our bistable RCs with τ/σ0 = 0.2. At high dilution, particle interactions are so weak that particle compression is practically negligible, leading to ϕ = ζ. Increasing the particle concentration, the compression of the soft colloids leads to ϕ < ζ. Please note that ζ can rise well above 1, which means that our RCs are able to significantly modify their volume in presence of crowding or other external interactions. This reduction in the particle volume becomes emphasized as we increase the interparticle repulsion strength. Indeed, for ε = 0.2 particle squeezing starts to become relevant above ζ > 0.3, whereas for ε = 2 particle compression is important already for ζ > 0.1, and becomes even more significant for larger ζ. In fact, soft colloids become about 15 times smaller in volume for ζ = 1.5 due to particle interactions for ε = 2.
The behavior of the ratio ϕ/ζ as a function of ζε for a fixed stiffness is plotted in Fig. 5(b) for different values of τ (solid symbols correspond to the bimodal distribution and open symbols to the unimodal one). As observed, the curves for the bimodal parent distribution (eqn (26)) follow the same trends than the ones discussed for 〈σ〉: for ζε < 0.7 (dilute or weakly interacting colloids), the particle volume diminishes due to conversion of big colloids into small ones, whereas for large enough ζε the decrease in particle volume is caused by the continuous shrinking of the particles. Again, the curves scale into a common form due to the mean-field character of our RC fluid. This is clearly seen in the inset of Fig. 5(b), in which the orange line represents the curves obtained for different values of ε. For large particle densities, the scaling finally tends to follow a power law decay given by ϕ/ζ ∼ (ζε)−1.1.
The results for the unimodal Gaussian parent distribution (eqn (27)) do not show the big-to-small transition, as expected. In this case, the curves have two well-defined regimes: in the low-density regime ζε < 0.3–0.4 the responsive colloids do not reduce their internal volume. This regime corresponds to a mutual interpenetration due to the overlap of the particles, without particle compression. For larger concentrations, the interpenetration regime saturates, and the only mechanism able to accommodate the RCs is reducing their particle volume, being more significant for softer colloids.
5.4 Osmotic pressure
In the mean-field approximation, the bulk pressure of a homogeneous multi-component colloidal system with M particle species of different sizes σi and with a total number density ρ0 is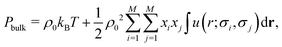 | (40) |
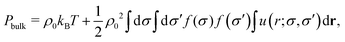 | (41) |
Inserting the Gaussian pair potential given by eqn (28) leads to the following expression for the bulk pressure,
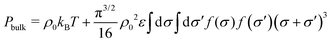 | (42) |
Fig. 6(a) shows the bulk pressure as a function of the particle density for a bimodal distribution of particles (eqn (26)) with τ/σ0 = 0.2 (soft colloids), for four different values of the interaction strength, going from ε = 0.2 to 2. As expected, Pbulk increases with ρ0. In principle, one would expect to find an increase of Pbulk also with the interparticle repulsion (that is, the particle hardness), ε. In fact, this would be the case for an ordinary non-responsive system of colloids. However, we find here a surprising observation: the equilibrium pressure is rather insensitive to ε in the range of studied particle densities. This result implies that, when particle hardness is enhanced, the RC fluid modifies the size distribution by conversion/squeezing to smaller sizes in order to reduce the interparticle repulsion, leading to a the pressure that remains almost unaltered. Such a homeostatic effect is a characteristic feature of responsive colloids and can also be observed e.g., for self-diffusion.24
In Fig. 6(b) we plot the dependence of the bulk pressure on density and varying the particle softness. As observed, decreasing particle softness does not modify Pbulk for 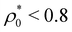 , because in this dilute regime the compression of the systems leads to a rearrangement of the bimodal distribution in such a way that the population of the big colloids decreases whereas the population of the small ones increases. This redistribution of sizes occurs independently of the particle stiffness, leading to the same pressure of the system in all cases. The situation changes when
, because in this dilute regime the compression of the systems leads to a rearrangement of the bimodal distribution in such a way that the population of the big colloids decreases whereas the population of the small ones increases. This redistribution of sizes occurs independently of the particle stiffness, leading to the same pressure of the system in all cases. The situation changes when 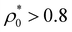 . In this regime, big colloids have already disappeared in the system, so increasing the particle concentration only provokes the progressive compression of the small colloids. Since squeezing stiff colloids involves an additional energy cost compared to soft ones, we find that the bulk pressure becomes dependent on the particle stiffness, with larger Pbulk for smaller τ.
. In this regime, big colloids have already disappeared in the system, so increasing the particle concentration only provokes the progressive compression of the small colloids. Since squeezing stiff colloids involves an additional energy cost compared to soft ones, we find that the bulk pressure becomes dependent on the particle stiffness, with larger Pbulk for smaller τ.
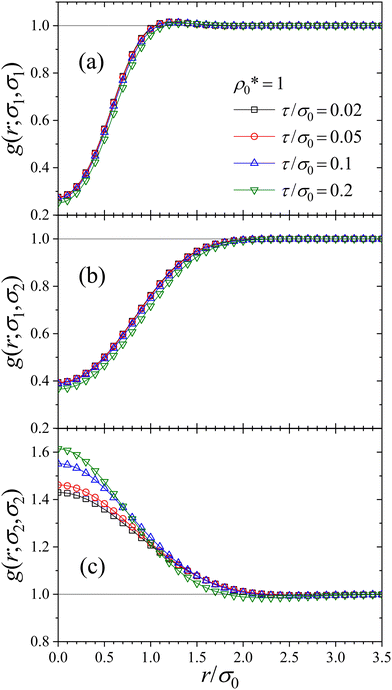
5.5 Radial distribution functions (RDFs)
The RDFs are obtained solving iteratively eqn (23) and then using eqn (24). The calculation of μex(r,σ) for the particular case of a Gaussian pair potential is shown in Appendix C (see eqn (57)).
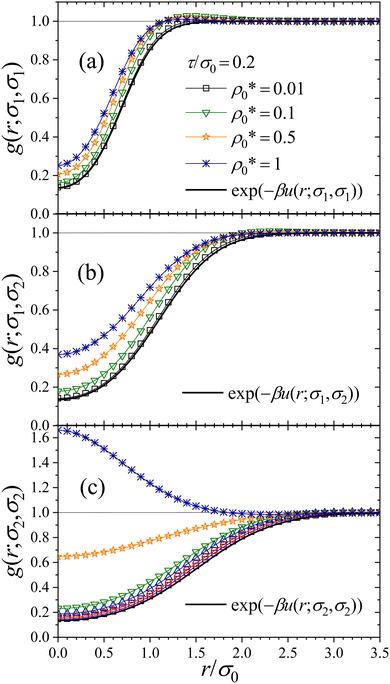
Fig. 7(a)–(c) shows the resulting g(r;σ,σ′) of a uniform RC fluid for τ/σ0 = 0.2 and for several combinations of σ and σ′, i.e. small–small (σ1-σ1), big–small (σ1-σ2), and big–big (σ2-σ2). The RDFs usually feature an excluded-volume ‘correlation’ hole at small distances that grows with the size of both particles. This depletion region is the consequence of the existent soft repulsive particle–particle interactions.37 In the regime of low particle concentration 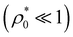 , the DFT results clearly show that the equilibrium RDF tends to
, the DFT results clearly show that the equilibrium RDF tends to 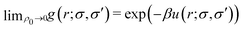 , as expected. Increasing ρ0 yields a progressive reduction of the soft correlation hole. This is a typical behavior of finite core interacting colloids, which tend to overlap under compression, leading to an ideal-gas-like behavior of g(r) in the high density limit.37,49 Surprisingly, the RDF between two big colloids develops a maximum at r = 0 upon increasing the particle concentration (see blue curve in Fig. 7(c)), indicating the existence of a depletion attraction between them. Indeed, for
, as expected. Increasing ρ0 yields a progressive reduction of the soft correlation hole. This is a typical behavior of finite core interacting colloids, which tend to overlap under compression, leading to an ideal-gas-like behavior of g(r) in the high density limit.37,49 Surprisingly, the RDF between two big colloids develops a maximum at r = 0 upon increasing the particle concentration (see blue curve in Fig. 7(c)), indicating the existence of a depletion attraction between them. Indeed, for 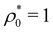 the big colloids are scarce in the system. So, when two big RC approach each other, small particles are excluded from the region between the big particles, inducing a depletion interaction given by βudepl(r) = − ln
the big colloids are scarce in the system. So, when two big RC approach each other, small particles are excluded from the region between the big particles, inducing a depletion interaction given by βudepl(r) = − ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) g(r;σ2,σ2).
g(r;σ2,σ2).
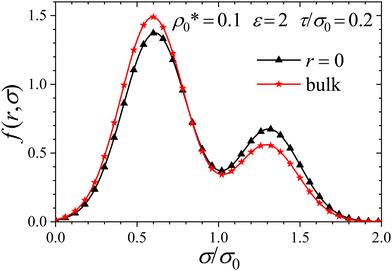
It is important to emphasize that the size distribution of the homogeneous RC fluid is position-dependent with respect to a fixed test particle. In other words, the distribution changes locally when we examine it close to one particle or far away from it. This effect is visible in Fig. 8, where the position-dependent size distribution (f(r,σ)) of the colloids surrounding a central big particle with size σ2 = 1.37σ0 is plotted for the particles located at r = 0 and at r → ∞ (i.e. in bulk solution), for 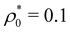 , ε = 2 and τ/σ0 = 0.2. The size distribution in bulk (red curve) is in accordance with the results shown before in Fig. 2(a). However, when approaching r = 0, the repulsion exerted by the central big colloid induces a decrease of the local density, as predicted by the depletion observed in g(r;σ1,σ2). Since the concentration of particles is smaller in this region, the RC fluid becomes less squeezed, allowing the increase of population of big colloids, as seen in the black curve of Fig. 8.
, ε = 2 and τ/σ0 = 0.2. The size distribution in bulk (red curve) is in accordance with the results shown before in Fig. 2(a). However, when approaching r = 0, the repulsion exerted by the central big colloid induces a decrease of the local density, as predicted by the depletion observed in g(r;σ1,σ2). Since the concentration of particles is smaller in this region, the RC fluid becomes less squeezed, allowing the increase of population of big colloids, as seen in the black curve of Fig. 8.
Finally, we explore the role of the particle stiffness on the microstructure of the RC fluid. On the one hand, calculations performed for different values of τ show that the RDFs g(r;σ,σ′) are barely dependent on the particle stiffness for dilute systems 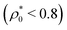 . Somehow, it happens that the effect of the stiffness is compensated by the already discussed rearrangement of the bimodal size distribution, leaving the bulk properties as well as the pressure and the microstructure unaltered (results not shown). On the other hand, for
. Somehow, it happens that the effect of the stiffness is compensated by the already discussed rearrangement of the bimodal size distribution, leaving the bulk properties as well as the pressure and the microstructure unaltered (results not shown). On the other hand, for 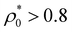 , big colloids have almost disappeared from the system, and the only way to react under compression is by isotropic shrinking of the colloids. In this regime, the microstructure becomes sensitive to the particle stiffness, as seen in Fig. 9. Indeed, increasing stiffness makes the particle more repulsive, increasing the bulk pressure, and pushing the colloids closer, which leads to a reduction of the correlation hole of g(r,σ1,σ1) and g(r,σ1,σ2) (see Fig. 9(a) and (b)). As a consequence of the reduction of the depletion region of small colloids around the big ones, the maximum observed in g(r;σ2,σ2) also decreases. This result implies that softer colloids are able to induce stronger depletion forces than stiff ones in RC fluids.
, big colloids have almost disappeared from the system, and the only way to react under compression is by isotropic shrinking of the colloids. In this regime, the microstructure becomes sensitive to the particle stiffness, as seen in Fig. 9. Indeed, increasing stiffness makes the particle more repulsive, increasing the bulk pressure, and pushing the colloids closer, which leads to a reduction of the correlation hole of g(r,σ1,σ1) and g(r,σ1,σ2) (see Fig. 9(a) and (b)). As a consequence of the reduction of the depletion region of small colloids around the big ones, the maximum observed in g(r;σ2,σ2) also decreases. This result implies that softer colloids are able to induce stronger depletion forces than stiff ones in RC fluids.
6 Conclusions
In this work, we applied a mean-field DFT to characterize the structural properties of a homogeneous fluid comprised by soft (Gaussian) responsive colloids in which the particle size (σ) is explicitly responsive and bistable. This fundamental model represents a first approach to describe macromolecular crowding effects in soft two-state biomolecules and polymer-based systems, which are able to modify the particle internal conformation in response to changes in the particle concentration and particle–particle interactions. The results show that compressing the system shifts the bimodal free-energy landscape to promote smaller sizes following a two-stage transition that can be tuned by varying the particle softness. In the first stage, for low particle densities, compression of the system shifts big colloids into small ones. In the second stage, at high particle densities, compression induces a progressive reduction of the size of the small colloids. The separation between these two compression regimes is enhanced by increasing the stiffness of the individual particles. This behavior represents a new feature that is not observed in simpler unimodal landscapes. In addition, particle–particle interactions significantly lower volume fractions compared to the ones observed in noninteracting systems. More precisely, we find for both the mean size and the particle volume fraction follow a scaling law in the regime of high densities with particle concentration (ρ0) and interaction strength (ε) as basis. Furthermore, a study of the osmotic pressure demonstrates that the bulk pressure is almost independent of the interaction strength. This surprising effect is attributed to the responsiveness of the soft particles. Finally, we show that mean-field DFT with the Test Particle Route also provides micro-structural information of the fluid of responsive colloids, through the radial pair–property distribution, g(r;σ,σ′). Here, for increased densities the remaining large particles possess an effective attraction to each other due to depletion effects.Overall, by comparing unimodal to bimodal size distributions in our model systems we uncover typical signatures of bistability in the compression behavior. For example, saddle-point like behavior in the mean size or packing fraction versus density, or intriguing non-monotonicities in the particle polydispersity.
Our model could also serve as a very preliminary description of the physics behind microgel volume transitions arising close to the LCST.60–62 In fact, experiments performed with a single thermo-responsive microgel using optical tweezers clearly show that the transition from the swollen to the collapsed state is discontinuous, suggesting that this process represents a first-order phase transition, and thus leading to a distinct two-state behavior and hysteresis.63,64 In fact, hysteresis – as a marker for bistability – in swelling–deswelling cycles of (ionized and non-ionized) hydrogels were found induced by temperature,65–67 pH,22,66,68 or the addition of cosolutes.69,70 However, it is important to emphasize that the application of our method to the description of microgels implies important changes of the model presented here. First, the Gaussian pair potential must be replaced by a more adequate interaction model, such as the Hertzian pair potential, and also include the size-dependence on the interaction strength, ε(σ,σ′), as suggested by Scotti et al.53 Second, the mean-field approach described in the work should be improved using a more accurate DFT to account for the harder character of the particle interactions arising by the presence of crosslinker inside the microgel particle. Finally, experiments and simulations with squeezed microgel systems indicate the existence of a deformation regime (faceting) that appears between the interpenetration and the compression regimes, in which the individual particles change their shapes without reducing their volume.71–77 To account for faceting, additional internal coarse-grained parameters beyond σ should also be included in the model.
In the future we would like to investigate how RC fluids behave under different external potentials. The relevance of external potentials is given in both in vitro and in vivo. They can exist either as an immutable present field (e.g., gravitation) or a tuneable perturbation (e.g., light) to obtain a control mechanism. Finally, we would like to study how the presence of internal DoF affects the phase behavior of RC fluids in the presence of interparticle attractions, for both unimodal and bimodal distribution. For the case of repulsion, it is well known that the phase diagram of non-responsive Gaussian colloids shows crystallization and a reentrant fluid phase at large enough densities for ε > 100.54,55 Therefore, it would be very interesting to investigate how particle responsiveness modifies this phase behavior as a function of the particle softness, possibly enhancing the fluid phase and reducing the regions with solid phases. Extending our method to other repulsive ultrasoft repulsive potentials as the generalized exponential models (GEM-n) would also allow to explore the effect of responsiveness on the anomalous formation of microclusters arranged into crystal structures observed in this kind of systems.38,78–81
Conflicts of interest
There are no conflicts to declare.Appendices
Appendix A: calculation of the emergent distribution in the perturbation theory
The goal of this calculation is to obtain the emergent distribution ftot(σ) from the perturbation theory (eqn (33) and (34)). The last two equations read| ftot(σ) = f0p(σ)e−βF(σ), | (43) |
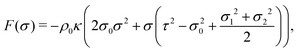 | (44) |
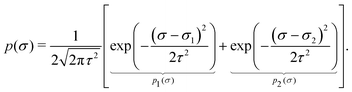 | (45) |
| ftot(σ) = f0(p1(σ) + p2(σ))e−βF(σ). | (46) |
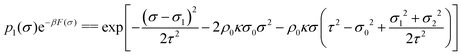 | (47) |
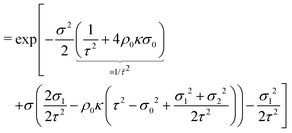 | (48) |
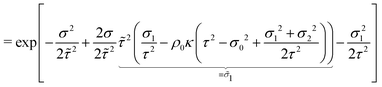 | (49) |
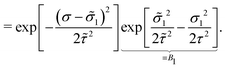 | (50) |
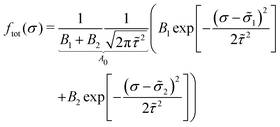 | (51) |
Appendix B: calculation of μex for an homogeneous mean-field fluid
For a homogeneous RC fluid (no external fields), the particle density can be written as ρ(r,σ) = ρ0f(σ), so it does not depend on r. Consequently, the double integral involved in the calculation of μex(r,σ) in the mean-field approximation can be simplified as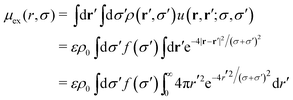 | (52) |
Integration over the r′ radial coordinate leads to an excess chemical potential that only depends on the particle size, σ:
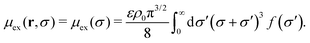 | (53) |
Appendix C: calculation of μex for a RC fluid confined inside a spherical cavity
For spherical symmetry, the density profile depends on ρ(r,σ) = ρ(r,σ), where r is the radial coordinate, or distance to the center of the cavity. In this case, the excess chemical potential of a mean-field fluid of Gaussian colloids is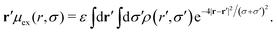 | (54) |
Without the lose of generality, We can chose r to be oriented in the z direction, r = r![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) , so
, so
|r − r′|2 = r2 + r′2 − 2rr′![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ′, θ′, | (55) |
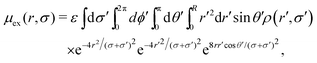 | (56) |
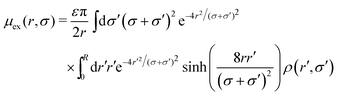 | (57) |
Acknowledgements
The authors thank M. A. Fernández-Rodríguez (University of Granada) for helpful discussions. A. M.-J. thanks the financial support provided by the Junta de Andalucía and European Regional Development Fund – Consejería de Conocimiento, Investigación y Universidad, Junta de Andalucía (Projects PY20-00241, A-FQM-90-UGR20) and the program Visiting Scholars funded by the Plan Propio of the University of Granada (Project PPVS2018-08).References
- S. B. Zimmerman and A. P. Minton, Annu. Rev. Biophys. Biomol. Struct., 1993, 22, 27–65 CrossRef CAS PubMed.
- R. Ellis, Trends Biochem. Sci., 2001, 26, 597–604 CrossRef CAS PubMed.
- H.-X. Zhou, G. Rivas and A. P. Minton, Annu. Rev. Biophys., 2008, 37, 375–397 CrossRef CAS PubMed.
- Y. C. Kim and J. Mittal, Phys. Rev. Lett., 2013, 110, 208102 CrossRef PubMed.
- H. Kang, P. A. Pincus, C. Hyeon and D. Thirumalai, Phys. Rev. Lett., 2015, 114, 068303 CrossRef PubMed.
- J. Shin, A. G. Cherstvy and R. Metzler, Soft Matter, 2015, 11, 472–488 RSC.
- M. P. Taylor, C. Vinci and R. Suzuki, J. Chem. Phys., 2020, 153, 174901 CrossRef CAS PubMed.
- A. P. Minton, J. Biol. Chem., 2001, 276, 10577–10580 CrossRef CAS PubMed.
- G. Rivas, J. A. Fernández and A. P. Minton, Proc. Natl. Acad. Sci. U. S. A., 2001, 98, 3150–3155 CrossRef CAS PubMed.
- S. L. Speer, C. J. Stewart, L. Sapir, D. Harries and G. J. Pielak, Annu. Rev. Biophys., 2022, 51, 267–300 CrossRef PubMed.
- C. Tan, S. Saurabh, M. P. Bruchez, R. Schwartz and P. LeDuc, Nat. Nanotechnol., 2013, 8, 602–608 CrossRef CAS PubMed.
- K. P. Amiri, A. Kalish and S. Mukherji, Phys. Rev. Lett., 2023, 130, 018401 CrossRef CAS PubMed.
- S. D. Quinn, L. Dresser, S. Graham, D. Conteduca, J. Shepherd and M. C. Leake, Front. Bioeng. Biotechnol., 2022, 10, 958026 CrossRef PubMed.
- K. W. Plaxco, K. T. Simons, I. Ruczinski and D. Baker, Biochemistry, 2000, 39, 11177–11183 CrossRef CAS PubMed.
- X. Zeng, K. M. Ruff and R. V. Pappu, Proc. Natl. Acad. Sci. U. S. A., 2022, 119, e2200559119 CrossRef CAS PubMed.
- H. K. Murnen, A. R. Khokhlov, P. G. Khalatur, R. A. Segalman and R. N. Zuckermann, Macromolecules, 2012, 45, 5229–5236 CrossRef CAS.
- U. B. Choi, J. J. McCann, K. R. Weninger and M. E. Bowen, Structure, 2011, 19, 566–576 CrossRef CAS PubMed.
- S. Dhiman, A. Jain and S. J. George, Angew. Chem., Int. Ed., 2017, 56, 1329–1333 CrossRef CAS PubMed.
- N. F. Dupuis, E. D. Holmstrom and D. J. Nesbitt, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 8464–8469 CrossRef CAS PubMed.
- N. Tokuriki, M. Kinjo, S. Negi, M. Hoshino, Y. Goto, I. Urabe and T. Yomo, Protein Sci., 2004, 13, 125–133 CrossRef CAS PubMed.
- E. Sato Matsuo and T. Tanaka, J. Chem. Phys., 1988, 89, 1695–1703 CrossRef.
- A. Suzuki and H. Suzuki, J. Chem. Phys., 1995, 103, 4706–4710 CrossRef CAS.
- Y.-C. Lin, B. Rotenberg and J. Dzubiella, Phys. Rev. E, 2020, 102, 042602 CrossRef CAS PubMed.
- U. Baul and J. Dzubiella, J. Phys.: Condens. Matter, 2021, 33, 174002 CrossRef CAS PubMed.
- M. Urich and A. R. Denton, Soft Matter, 2016, 12, 9086–9094 RSC.
- U. Baul, N. Götth, M. Bley and J. Dzubiella, J. Chem. Phys., 2021, 155, 244902 CrossRef CAS PubMed.
- M. Schmidt, Rev. Mod. Phys., 2022, 94, 015007 CrossRef CAS.
- J.-P. Hansen and I. McDonald, Theory of Simple Liquids, Academic Press, 4th edn, 2013 Search PubMed.
- J. L. Barrat and J. P. Hansen, J. Phys., 1986, 47, 1547–1553 CrossRef CAS.
- I. Pagonabarraga, M. E. Cates and G. J. Ackland, Phys. Rev. Lett., 2000, 84, 911–914 CrossRef CAS PubMed.
- A. R. Denton and M. Schmidt, J. Phys.: Condens. Matter, 2002, 14, 12051–12062 CrossRef CAS.
- M. S. Cheung, D. Klimov and D. Thirumalai, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 4753–4758 CrossRef CAS PubMed.
- C. L. Vestergaard, P. C. Blainey and H. Flyvbjerg, Nucleic Acids Res., 2018, 46, 2446–2458 CrossRef CAS PubMed.
- J. Heyda, S. Soll, J. Yuan and J. Dzubiella, Macromolecules, 2014, 47, 2096–2102 CrossRef CAS.
- P. G. Bolhuis, A. A. Louis, J. P. Hansen and E. J. Meijer, J. Chem. Phys., 2001, 114, 4296–4311 CrossRef CAS.
- A. A. Louis, P. G. Bolhuis, J. P. Hansen and E. J. Meijer, Phys. Rev. Lett., 2000, 85, 2522–2525 CrossRef CAS PubMed.
- A. A. Louis, P. G. Bolhuis and J. P. Hansen, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2000, 62, 7961–7972 CrossRef CAS PubMed.
- C. N. Likos, N. Hoffmann, H. Löwen and A. A. Louis, J. Phys.: Condens. Matter, 2002, 14, 7681 CrossRef CAS.
- J. K. Percus, Phys. Rev. Lett., 1962, 8, 462–463 CrossRef.
- A. J. Archer, P. Hopkins and M. Schmidt, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 75, 040501 CrossRef PubMed.
- E. Sherman and G. Haran, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 11539–11543 CrossRef CAS PubMed.
- I. C. Sanchez, Macromolecules, 1979, 12, 980–988 CrossRef CAS.
- P. J. Flory and W. R. Krigbaum, J. Chem. Phys., 1950, 18, 1086–1094 CrossRef CAS.
- O. F. Olaj, W. Lantschbauer and K. H. Pelinka, Macromolecules, 1980, 13, 299–302 CrossRef CAS.
- B. Kruger, L. Schäfer and A. Baumgärtner, J. Phys., 1989, 50, 3191–3222 CrossRef.
- J. Dautenhahn and C. K. Hall, Macromolecules, 1994, 27, 5399–5412 CrossRef CAS.
- C. N. Likos, M. Schmidt, H. Löwen, M. Ballauff, D. Pötschke and P. Lindner, Macromolecules, 2001, 34, 2914–2920 CrossRef CAS.
- C. N. Likos, S. Rosenfeldt, N. Dingenouts, M. Ballauff, P. Lindner, N. Werner and F. Vögtle, J. Chem. Phys., 2002, 117, 1869–1877 CrossRef CAS.
- M. Bley, J. Dzubiella and A. Moncho-Jordá, Soft Matter, 2021, 17, 7682–7696 RSC.
- M. Bley, P. I. Hurtado, J. Dzubiella and A. Moncho-Jordá, Soft Matter, 2022, 18, 397–411 RSC.
- A. Moncho-Jordá, Phys. Rev. Lett., 2020, 125, 078001 CrossRef PubMed.
- C. Miller, Y. Kim and J. Mittal, Biophys. J., 2016, 111, 28–37 CrossRef CAS PubMed.
- A. Scotti, A. R. Denton, M. Brugnoni, J. E. Houston, R. Schweins, I. I. Potemkin and W. Richtering, Macromolecules, 2019, 52, 3995–4007 CrossRef CAS.
- A. Lang, C. N. Likos, M. Watzlawek and H. Löwen, J. Phys.: Condens. Matter, 2000, 12, 5087 CrossRef CAS.
- S. Prestipino, F. Saija and P. V. Giaquinta, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 71, 050102 CrossRef PubMed.
- A. Scotti, Soft Matter, 2021, 17, 5548–5559 RSC.
- H. Senff and W. Richtering, J. Chem. Phys., 1999, 111, 1705–1711 CrossRef CAS.
- M. Pelaez-Fernandez, A. Souslov, L. A. Lyon, P. M. Goldbart and A. Fernandez-Nieves, Phys. Rev. Lett., 2015, 114, 098303 CrossRef CAS PubMed.
- A. Scotti, U. Gasser, E. S. Herman, J. Han, A. Menzel, L. A. Lyon and A. Fernandez-Nieves, Phys. Rev. E, 2017, 96, 032609 CrossRef CAS PubMed.
- K. Nothdurft, D. H. Müller, S. D. Mürtz, A. A. Meyer, L. P. B. Guerzoni, A. Jans, A. J. C. Kühne, L. De Laporte, T. Brands, A. Bardow and W. Richtering, J. Phys. Chem. B, 2021, 125, 1503–1512 CrossRef CAS PubMed.
- G. D. Monte, D. Truzzolillo, F. Camerin, A. Ninarello, E. Chauveau, L. Tavagnacco, N. Gnan, L. Rovigatti, S. Sennato and E. Zaccarelli, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2109560118 CrossRef CAS PubMed.
- R. Elancheliyan, G. Del Monte, E. Chauveau, S. Sennato, E. Zaccarelli and D. Truzzolillo, Macromolecules, 2022, 55, 7526–7539 CrossRef CAS.
- M. R. R. Kannan, B. V. R. Tata, R. Dasgupta, S. Ahlawat and P. K. Gupta, AIP Conf. Proc., 2011, 1391, 359–362 CrossRef CAS.
- D. Karthickeyan, D. K. Gupta and B. V. R. Tata, J. Opt., 2016, 18, 105401 CrossRef.
- Y. Hirokawa and T. Tanaka, J. Chem. Phys., 1984, 81, 6379–6380 CrossRef.
- M. Annaka and T. Tanaka, Nature, 1992, 355, 430–432 CrossRef CAS.
- P. Werner, M. Münzberg, R. Hass and O. Reich, Anal. Bioanal. Chem., 2017, 409, 807–819 CrossRef CAS PubMed.
- J. P. Baker and R. A. Siegel, Macromol. Rapid Commun., 1996, 17, 409–415 CrossRef CAS.
- S. Koga, S. Sasaki and H. Maeda, J. Phys. Chem. B, 2001, 105, 4105–4110 CrossRef CAS.
- J. Gernandt and P. Hansson, J. Phys. Chem. B, 2015, 119, 1717–1725 CrossRef CAS PubMed.
- G. M. Conley, P. Aebischer, S. Nöjd, P. Schurtenberger and F. Scheffold, Sci. Adv., 2017, 3, e1700969 CrossRef PubMed.
- I. Bouhid de Aguiar, T. van de Laar, M. Meireles, A. Bouchoux, J. Sprakel and K. Schroën, Sci. Rep., 2017, 7, 10223 CrossRef CAS PubMed.
- A. Scotti, M. Brugnoni, A. A. Rudov, J. E. Houston, I. I. Potemkin and W. Richtering, J. Chem. Phys., 2018, 148, 174903 CrossRef CAS PubMed.
- J. Brijitta and P. Schurtenberger, Curr. Opin. Colloid Interface Sci., 2019, 40, 87–103 CrossRef CAS.
- M. Karg, A. Pich, T. Hellweg, T. Hoare, L. A. Lyon, J. J. Crassous, D. Suzuki, R. A. Gumerov, S. Schneider, I. I. Potemkin and W. Richtering, Langmuir, 2019, 35, 6231–6255 CrossRef CAS PubMed.
- S. V. Nikolov, A. Fernandez-Nieves and A. Alexeev, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 27096–27103 CrossRef CAS PubMed.
- A. Scotti, M. F. Schulte, C. G. Lopez, J. J. Crassous, S. Bochenek and W. Richtering, Chem. Rev., 2022, 122, 11675–11700 CrossRef CAS PubMed.
- C. N. Likos, A. Lang, M. Watzlawek and H. Löwen, Phys. Rev. E, 2001, 63, 031206 CrossRef CAS PubMed.
- C. N. Likos, B. M. Mladek, D. Gottwald and G. Kahl, J. Chem. Phys., 2007, 126, 224502 CrossRef PubMed.
- C. N. Likos, B. M. Mladek, A. J. Moreno, D. Gottwald and G. Kahl, Comput. Phys. Commun., 2008, 179, 71–76 CrossRef CAS.
- D. Coslovich and A. Ikeda, Soft Matter, 2013, 9, 6786–6795 RSC.
| This journal is © The Royal Society of Chemistry 2023 |