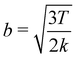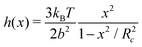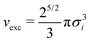Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
An extensible density-biasing approach for molecular simulations of multicomponent block copolymers
Aravinthen
Rajkumar
 *a,
Peter
Brommer
*a,
Peter
Brommer
 b and
Łukasz
Figiel
b and
Łukasz
Figiel
 c
c
aEPSRC Centre for Doctoral Training in Modelling of Heterogeneous Systems (HetSys), University of Warwick, Coventry, CV4 7AL, UK. E-mail: arre.rajkumar@warwick.ac.uk
bWarwick Centre for Predictive Modelling (WCPM), School of Engineering, University of Warwick, Coventry, CV4 7AL, UK
cInternational Institute for Nanocomposites Manufacturing (IINM), WMG, University of Warwick, Coventry, CV4 7AL, UK. E-mail: l.w.figiel@warwick.ac.uk
First published on 27th January 2023
Abstract
A node-density biased Monte Carlo methodology is proposed for the molecular structure generation of complex block copolymers. Within this methodology, the block copolymer is represented as bead-spring model. Using self-consistent field theory, a density field for all monomer species within the system is calculated. Block copolymers are generated by random walk configuration biased by the density fields. The proposed algorithm then modifies the generation process by taking the global structure of the polymer into account. It is then demonstrated that these global considerations can be built into the sampling procedure, specifically through functions that assign a permissible difference in density field value between relevant monomer species to each step of the random walk. In this way, the random walk may be naturally controlled to provide the most appropriate conformations. The overall viability of this approach has been demonstrated by using the resulting configurations in molecular dynamics simulations. This new methodology is demonstrated to be powerful enough to generate molecular configurations for a much wider variety of materials than the original approach. Two key examples of the new capabilities of the method are viable configurations for ABABA pentablock copolymers and ABC triblock terpolymers.
1. Introduction
Block copolymers represent a class of materials with an enormous design space. They can assume the large variety of architectures exhibited by homopolymers1,2 and, for each architecture, may be further differentiated by the degree of polymerisation and the chemical details of the monomers comprising the full structure.3An important property of block copolymers and a defining feature of many soft matter systems is their tendency to self-assemble into a variety of morphologies4via microphase separation. The thermal and mechanical properties of a block copolymer material are naturally dependent on the morphology that the system assumes, but the interplay between the phases that constitute the self-assembled material can be complex. For example, a system composed of a copolymer whose blocks have different glass transition temperatures can lead to the self-assembly of glassy spheres embedded in a soft rubber matrix. The resulting material will be a thermoplastic elastomer whose properties are directly influenced by the underlying morphology.
It is therefore not difficult to envisage the need to discover and understand block copolymer structure–morphology–property relations. However, the experimental exploration of this design space is infeasible due to its size. This provides strong motivation for the development of computer simulation methodologies for block copolymers, specifically for the investigation of the effects of complex block copolymer architectures on their end-use properties.
Block copolymers present a range of interesting fundamental challenges, ranging from the increasingly sophisticated synthesis and characterization techniques5 to poorly understood mechanical behaviours.6 The capability of building models of a self-assembled block copolymer system will allow for the detailed study of such themes.
The problem of devising a simulation approach for the calculation of structure–morphology–property relations thus contains two essential aspects, these being the prediction of morphology from structural information and the simulation methodologies by which the properties of the predicted morphology are determined.
The first of these aspects, block copolymer morphology prediction, poses challenges to both its theoretical description and numerical simulation.7 There are a number of methods by which this may be accomplished, ranging from phase field calculations of the Ohta–Kawasaki model8,9 to self-consistent field theory (SCFT) and associated methodologies.10,11 The output of these calculations typically includes a density field representing the monomers comprising the system. Whilst the problem of block copolymer self-assembly is relatively well understood in the case of simple binary systems,12 the problem of identifying morphologies becomes significantly more intensive with more heterogeneous examples.5,13,14
For the second aspect, molecular simulation emerges as the natural approach to predicting properties for block copolymers. A variety of approaches to the molecular simulation of block copolymers in equilibrium exist,15 but in many systems it is important to capture dynamical aspects that give rise to physical crosslinking and thermal motion. One methodology that incorporates all of these effects whilst preserving efficiency is coarse-grained molecular dynamics, the use of which has proven highly successful in studying a variety of polymeric systems without being encumbered by atomic detail.16–19
When the means for morphology prediction and coarse-grained molecular dynamics have been selected, the final remaining step is the process of combining these methodologies. This is an exceptionally complex problem as the two methodologies are fundamentally different: the former relies on a field theory, whereas the latter is based around a discrete molecular description.
In the present study, we examine an existing solution for this problem, the node-density biased Monte Carlo algorithm, which has been successfully applied to diblock and triblock copolymer systems. We first describe the existing approach by casting the algorithm into a theoretical perspective, specifically a means of sampling from a polymer conformation probability density function. Then, we demonstrate the flaws that render it unable to model any given linear block copolymer system, limiting it to only the diblock and triblock copolymer case. These flaws indicate that it cannot serve as a general simulation approach for the discovery and study of block copolymer structure–morphology–property relations. By modifying the probability distribution described through the theoretical perspective, we motivate a novel algorithmic approach that operates by immediately rejecting unrealistic polymer conformations. We demonstrate the power of our improved algorithm by using it to create molecular configurations of significantly more complex polymer structures, such as pentablock copolymers and ABC triblock terpolymers.
2. Background
2.1. The node-density biased Monte Carlo algorithm
In this work, the general approach used to create initial configurations of coarse-grained block copolymers is a variant of the node density-biased Monte Carlo algorithm (NDBMC) proposed by Aoyagi et al.20 The NDBMC algorithm is an elegant example of a hierarchical calculation methodology in that it relies upon two methods at differing length and timescales.Initially, it uses self-consistent field theory (SCFT) to predict the equilibrium morphology. The result of an SCFT algorithm typically includes the monomer number density field of the system: this is then converted into a particle representation by running a series of biased random walks, where each random walk builds a polymer monomer by monomer. The biasing procedure is carried out at each step by generating a random number between 0 and 1 and comparing said number to the monomer density of the relevant monomer type at a potential position. On the occasion that the random number is less than monomer density, the potential position is accepted. As such, there is a high likelihood of acceptance of a step when the monomer density of the desired monomer type is sufficiently large. In principle, these ideas are not unique to the NDBMC algorithm: one example of this methodology being used to guide the placement of molecules in a system can be found in work by Rodgers et al.,21 where a density field ansatz is used to study the solubility of alcohol molecules in a mesoscopic model of the lipid bilayer. On the other hand, a separate example where SCFT calculations are used to inform an external potential for the generation of self-assembled diblock copolymer systems can also be found in Padmanabhan et al.22
It is natural to ask why this scheme is necessary, as all capabilities required to replicate the experimental procedure for block copolymer self-assembly are in theory easy to reproduce virtually. This replication would entail the random initialization of a large number of block copolymer chains in liquid form at high temperature, followed by quenching such that microphase separation is induced.23 This is however unfeasible, as the timescale in which block copolymers typically undergo phase separation is many orders of magnitude above what is currently accessible with molecular dynamics simulations.
The NDBMC algorithm has been successfully used as a starting point in modelling diblock (AB) and triblock copolymer (ABA) systems24–26 and serves as an excellent first step to the main problem of obtaining equilibrium block copolymer structures in a form amenable to molecular dynamics. It differs in this regard from theoretically informed coarse-grained simulation (TICG),27,28 another important technique used in the bridging of SCFT to molecular simulation. The NDBMC algorithm is designed to build configurations for molecular dynamics, whereas the TICG approach consists of polymer Monte Carlo simulations whose configurations are directly motivated from the field-theoretic Hamiltonian underlying the system. A key difference is that the former uses a trial move approach solely for the purpose of building configurations, whereas the latter uses Monte Carlo moves to actively calculate ensemble averages of the system. TICG simulations are elegant and exceptionally powerful when considering polymer systems in equilibrium. Despite the implicit use of δ-function interactions, it would not be difficult to employ similar equilibration routines to develop a realistic molecular configuration. However, a unique strength of the NDBMC approach is its indifference to the components that it uses: there is no real necessity for the use of self-consistent field theory. In contrast, TICG is built directly from the SCFT Hamiltonian and is thus dependent on it. For the NDBMC algorithm, one might easily use a technique such as the aforementioned phase-field simulation or a novel scheme that allows the simulation of nanocomposite systems.29 The NDBMC algorithm needs only an appropriate field, whereas most other approaches to multiscale simulation have unavoidable dependencies in methodology.
Despite this versatility, we believe that there are a number of issues that both prevent the adoption of the NDBMC algorithm as a general technique and limit the level of heterogeneity that may be explored with it. Essentially, it cannot be used as a stand-alone technique and must always be employed in tandem with a means of correction. In order to shed light on the issues surrounding the algorithm, we will first describe the NDBMC algorithm through formalism.
2.2. The NDBMC algorithm as a high-dimensional sampling technique
The NDBMC algorithm can be framed as sampling from the distribution of possible polymer conformations in an external field. The external field here is the chemical potential of the system that drives the constituents to self-assemble.Defining a polymer configuration as a set of N individual steps RN = (r1,r2…rN), the probability that any given configuration is sampled via the NDBMC algorithm can be written as
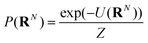 | (1) |
The majority of theoretical treatments express Z in an integral formulation, as this form is typically easier to utilize in analytical calculation. We maintain the summation notation as a means of motivating a computational method. A single configuration RN is constructed by first randomly choosing a starting position within the system volume, carrying out a density biasing procedure as outlined in the previous section. The NDBMC algorithm does not employ self-avoiding random walks, instead opting to treat chains as ideal and allowing chains to cross over each other. This feature, which is markedly unphysical, is corrected by gradually introducing excluded volume in a later simulation stage.
It is to be noted that there are many possible variants of U(RN) that incorporate a variety of features and models. In the study in which the NDBMC algorithm was originally used, the polymer chains were treated as ideal, so any interaction between beads that are not adjacent on the same chain are not considered. In combination with the effect of the external field, the energy can be decomposed as
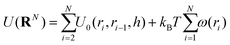 | (2) |
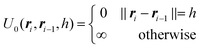 | (3) |
We note here that additional aspects of a random walk model, such as self-avoiding and interactions between solvents and other non-polymeric objects, may be included in U(RN). However, these features do not impact the exposition of our methodology and so we proceed with the simplest case.
The NDBMC algorithm attempts to sample from (1) by building RN by trialing each ri independently. It should be noted that whilst (1) makes use of the chemical potential, the NDBMC algorithm makes use of the number density. The number density is the conjugate thermodynamic variable of the chemical potential. The energetic contribution of the chemical potential is thus solved through the use of SCFT and need not be given special attention.
2.3. Motivating a new approach
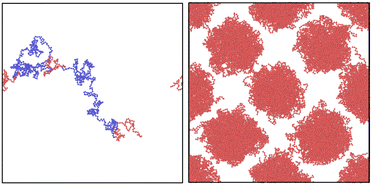
The probability distribution depicted in (1) is of dimension D = 3N. The smallest and largest use-cases for chain generation with the NDBMC algorithm in literature are N = 40 and N = 120 respectively, leading to dimensional spaces of D = 120 to D = 360. It is worth mentioning that these are relatively small coarse-grained chains, with recent block copolymer simulations investigating cases as large as N = 800.30The total number of possible configurations for even relatively small chains is enormous, yet within the set of possible samples there exist many that would not be suitable for molecular dynamics simulation. As such, (1) as written is not a suitable probability distribution from which to sample configurations for the purpose of simulation. In information-theoretic terms, one might describe (1) to have a higher entropy than what would be useful for the task of sampling random walks for molecular simulation. When specifically considering the distribution of the configuration of a polymer subject to an external field, an unsuitable sample will manifest as chains with a number of segments that reside in regions of unfavorable chemical potential as illustrated in Fig. 1. Statistically, these segments are insignificant. A very large number of samples should in theory tend to a reasonable configuration. However, as a molecular dynamics simulation can only run on a single configuration, the statistical properties of an ensemble of configurations is not particularly useful. With this in mind, a useful outcome of any algorithm bridging SCFT with a molecular simulation is not necessarily one that succeeds in reproducing the density profile obtained by the self-consistent field calculation. In the NDBMC algorithm, the role of the self-consistent field calculation is primarily used to predict the likely morphology that the system finds itself in.
Monte Carlo simulations use rejection as an integral algorithmic component. Rejection plays a important part in ensuring that the samples drawn from a probability distribution are not outliers. Whilst the NDBMC algorithm possesses a mechanism for local rejection in that single bead position is rejected based on its local number density, the quality of the walk overall is not considered. The rejection of a single bead position based on local number density plays a large part in guiding the configuration from one region to another, but it does not guarantee that the configuration itself is likely according to (1).
The NDBMC algorithm possesses a unique flaw that manifests as a tendency of generating substandard configurations. Consider a symmetric (A)N(B)N diblock copolymer, comprised of generic monomer types A and B and with a degree of polymerisation 2N. As per the NDBMC method, the random walk configuration representing the A block will eventually find itself in a region where the chemical potential is favorable to type A beads. Naturally, one would expect that the Nth bead will have through gradual maximisation found itself in an A-type rich region. However, the (N + 1) th bead is of the B-type. As such, the first bead of the type B block will find itself in an initial position that is wholly unsuited to it. Even in such an unsuitable position the algorithm will continuously generate potential new positions until by chance a random number is generated such that it is lower than the number density. The aforementioned lack of rejection becomes a serious flaw in this situation.
This situation is illustrated in Fig. 2 and is an unavoidable complexity that emerges at the junction between two blocks. It must be noted that this flaw is amplified when dealing with more complex architectures.
A workaround for these problems exists in the form of an artificial potential that directly uses the predicted number density field to drive phase separation. This is the approach used in the original use-case of the NDBMC algorithm. This method would be highly effective for smaller chains, but it falls victim to the overarching problem that necessitates the use of SCFT in the first place: chains subjected to a potential still move through reptation, which we have already established is prohibitively slow in most cases. Even if chains treated as ideal at first and are allowed to pass through each other when undergoing a relaxation procedure, the process of incorporating excluded volume into the system is exceptionally challenging and time-consuming due to the enormous energies that most coarse-grained potentials will exhibit upon intersection. Further, when the NDBMC algorithm returns a poor configuration for sufficiently long chains, a given chain segment may be pulled to multiple regions of favorable chemical potential, which drastically increases any equilibration time. The NDBMC algorithm cannot be expected to fare well in situations more complicated than a copolymer melt composed of more than two monomer types. Taking a terpolymer as an example, the gradients of monomer density calculated by SCFT are typically more gradual than what is typical from diblock monomer densities. Gradual changes in a density profile permit a far larger number of configurations to traverse it, leading to a larger number of possible configurations. This, like before, manifests as a very high likelihood of sampling lower-quality chains. The aforementioned problem involving poorly placed junction monomers is also exacerbated, as there are more opportunities for the junction monomers to find themselves in unsuitable positions. The density-driven potential is also limited in its ability to correct the configuration, as the poor configurations obtained by the NDBMC algorithm are usually too far from the SCFT number density prediction to be corrected.
It is important to realise that these difficulties are the result of the drastic difference in scale between SCFT and CGMD. Despite dealing with the same system, they are fundamentally different paradigms that are built on disparate frameworks for the representation of polymers. This can be motivated by imagining a configuration in which a large number of chains are sampled from (1): that is, where the number of polymers Np → ∞. In this situation, the number density of the monomers will be exactly equal to the monomer density field predicted by SCFT. However, this fictitious configuration will still contain a large number of monomers in regions that are not suitable for the associated monomer type, even if the statistical features of the configuration are accurate.
It should be noted that these are flaws specific to the NDBMC algorithm. When attempting to bridge the scale between SCFT and MD, the thermodynamic aspects of a field-theoretic calculation and a molecular dynamics calculation must be in agreement. For a truly multi-scale approach, this agreement is imperative. The aspects pertaining to this multiscale modelling approach are discussed further in Section 5.2.
Notwithstanding these barriers and despite advancements in the twenty years since its first demonstration, we believe that the NDBMC algorithm is the most versatile method developed so far to model block copolymer morphologies with molecular simulation. It is attractive as a practical problem-solving approach in that it depends on no specific theoretical or technological developments: like all good software, the individual components that it is composed of may be upgraded or indeed replaced entirely with a new and more suitable methods. Despite the discussed flaws, it serves as an appropriate starting point for the development of newer and more involved algorithms. In the subsequent section, we discuss two techniques that may be employed to tackle more complex systems than the previously discussed copolymer structures.
3. Methodology
3.1. Construction of a more useful probability distribution
We have justified that (1) is unsuitable for the purpose of sampling random walk configurations. Our specific reason for this is the excessively high number of configurations permissible through the energies described in (2) that are not useful when subjected to molecular dynamics simulation. It would thus be desirable to construct a new probability distribution by reducing the entropy of (1): this could be carried out by incorporating additional information about the random walk that we would expect from an intuitive understanding of the system. Specifically, we would expect that a sampled random walk representing a single block in a copolymer should follow some trends regarding the position of the monomers that constitute the junction. These monomers should be located at a region where the chemical potential is favorable to both of the monomer types of each block. In practice, this is a region where the number densities of two different types, ρi(r) and ρj(r), are at least approximately equal at a position r. We will refer to these regions as density interfaces.The concept of a density interface motivates a measure that can be exploited when considering a means of biasing a random walk. The introduction of such a bias would naturally result in a more appropriate distribution than (1). First, we define the density difference of a given point as
| Δij(r) = ρi(r) − ρj(r) | (4) |
| ΔNij(k) = {Δij(rk)|rk ∈ RN} | (5) |
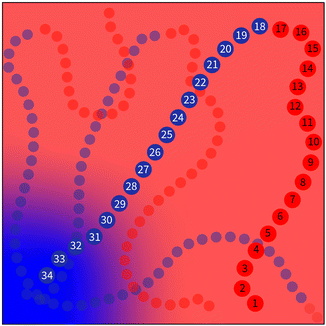
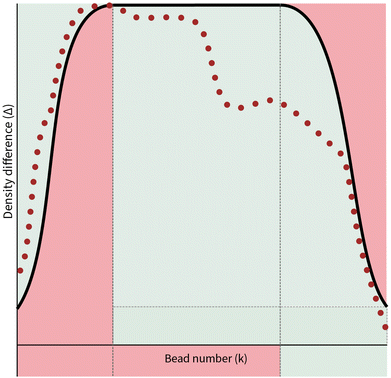
The values of ΔNij(k) can be associated with the desired behaviour of the chain. Without loss of generality, we will only consider a single block in a polymer chain. As illustrated in Fig. 3, we would expect three regions where the behaviour of the chain constituting a block takes on distinct characteristics.
• In the first region arbitrarily specified by the set of bead numbers [0,a), the chain should be driven away from an interface and deeper into a region that is favorable to it. This could be interpreted as a region in which the density difference is gradually maximised for k ∈ [0,a).
• When in second region, specified as [a,b], the chain should be discouraged from entering a region that is not favourable to it. Otherwise, it should be able to travel freely in order to maintain random walk behavior.
• Finally in third region, specified by (b,N], the chain should be driven away from a region favorable to it and back to an interface. In contrast with the first region, the density difference should be gradually minimised for the values k ∈ (b,N].
These constraints motivate the existence of a function f(k) such that
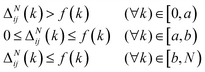 | (6) |
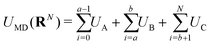 | (7) |
When (7) is added to the existing energies outlined in (2), polymer chains that do not satisfy the specified behaviour expected are automatically removed from the original probability distribution. The entropy of the resulting distribution is significantly reduced, but the chains that may be sampled from it are guaranteed to have reasonable configurations for the purpose of molecular dynamics simulation.
There are two issues that must be considered before using this methodology. First, it is important to recognize that there is a fundamental difference in the nature of UA and UC in that the latter is a necessary condition. The segment must find itself terminating at a region that is favorable to both types. However, UA has no such requirement and should in principle allow a much wider variety of chain conformations. It would thus be unrealistic to demand that every single chain within a polymer melt follow the conditions outlined by a single form of the domain of f(k) that pertains to UA. However, the general tendency that the segment chains tend towards regions denser to their type must be satisfied. A reasonable approach would be to generate a different form of f(k) for every chain comprising a melt, where the initial domain varies with respect to a statistical distribution. This is however difficult to implement, as any such statistical distribution must be carefully derived. Instead, we present a faster and simpler approach to accomplish the same effect in Section 3.1.
Secondly, it should also be noted that this technique essentially breaks down on the final block of a copolymer chain, as there is no next type along the chain by which the density difference may be computed. However, the final block is not required to fulfil the characteristics outlined for the three specified regions. As such, the basic NDBMC algorithm is sufficient to guide the configuration of the last block, with the additional benefit that the steps involving the final block are essentially guaranteed to begin at a density interface.
3.2. Sample generation
The new probability distribution would be sampled from in a similar way as the NDBMC algorithm, although with the additional condition such that the positions of the polymer configurations are forbidden from accessing density values that do not agree with the constraints used to form (3).In the previous subsection we outlined the requirement that the initial domain [0,a) of f(k) should not be as strictly constrained as the domain [b,N). Our methodology for implementing this difference is to allow for a significantly more lenient Monte Carlo move in the domain [0,a). In the previous development we have operated under the assumption that any move not satisfying the conditions outlined in (7) is rejected outright. In our implementation, this is still the case for the second and third domains. However, for the first domain, the random walk is allowed to enter an unfavorable region of density difference with the caveat that all steps will be subject to the standard Monte Carlo move of the original NDBMC algorithm. Conversely, a step that occurs in a favourable region is accepted automatically and will thus never be rejected. This is an effective means of biasing the first region and thus satisfies the issues raised.
There are a number of additional features that we have made to the sampling procedure that are not incorporated in the constructed distribution of the previous section. These features are primarily centred around software design: they are intended to improve the speed and applicability of structure generation.
The first of these features is the use of the self-avoiding walk rather than the typical ideal walk combined with energy minimisation. Self-avoiding walks are slower to generate, but typically require very little post-processing when compared to energy minimisation. In our experience, it is typically faster and less resource intensive to use self-avoiding walks in lieu of equilibrating chains that interact via the potentials described in the next section. There are however limitations that self-avoiding walks introduce. The closer a configuration is to an ideal walk, the better the quality of the sample obtained from the new probability distribution. Further, self-avoiding walks become progressively harder to sample when attempting to create a melt structure. This is due to the gradual incorporation of excluded volume. The implementation of self-avoiding walks and the manner in which this implementation is extended to include a SCFT calculation is discussed in the appendix. We note however that it is not strictly necessary to run our version of the NDBMC algorithm with self-avoiding walks. There is nothing wrong with the approach of using ideal walks and gradually introducing excluded volumes into the system. This method benefits from the extensive work carried out regarding the equilibration and relaxation of polymer melts, including schemes developed after the original NDBMC approach was first published. One such scheme proposed by Parker and Rottler31 consists of the use of soft repulsive potentials derived from the free energy functional. There are however important considerations to take into account when this method is used. The rate at which the excluded volume is introduced to the system has direct effect on the chain statistics32 of the system and care must be taken to ensure that these are preserved.
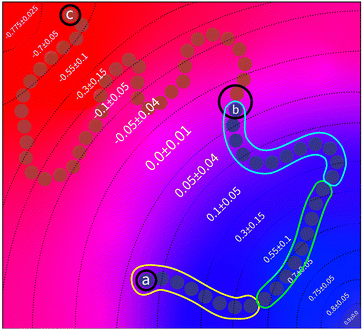
Given the apparent strictness of the constraints incorporated in the new probability distribution, it is from a computational perspective unwise to follow them exactly. There are two ways in which we may relax the constraints in order to improve the sampling speed of a polymer configuration. Firstly, in the formulation of the conditions (6) that the function f(k) must follow, the idea of the density interface is implicitly included by setting the lowest value of f(k) to be 0. This is extremely strict, as it only allows the random walk to begin and end on the two-dimensional surface upon which the density interface is defined on. It is therefore desirable and indeed more realistic to introduce an interface gap comprised of a range of values that a walk might start and finish. Such a function can be seen in Fig. 4.
A second means by which the constraints of the new distribution may be relaxed is the way the chain reacts when it reaches the boundary defined by f(k). In our implementation, we have allowed the random walk configuration to step outside the boundary and temporarily find itself in a region outside of the conditions imposed by (6). However, we do not allow the chain to go any further, requiring it to return to an allowed value of ΔNij(k) immediately on the next step. This significantly improves the speed at which configurations may be sampled.
As justified in Section 2.3, the NDBMC algorithm does not contain a mechanism that allows for sample rejection. There are of course many ways in which rejection could be built into the algorithm. For example, if the algorithm fails to generate a valid position after a sufficiently large number of attempts, the configuration can be rejected. However, this rejection procedure does not serve to provide better samples. It will only prolong the amount of time required for a valid sample to be generated. With the stricter constraints motivated within this work, a rejection based upon the global validity of a configuration presents itself naturally.
We do not outright reject the configuration, instead employing retraction. Here, a random walk configuration that has become arrested during generation may remove up to half of its current configuration and begin at a previously attained position. Retraction is preferable to outright rejection, as it serves as a method of salvaging a configuration that may have required a non-negligible amount of time to build. In practice, retraction is carried out after a user-defined number of failures.
A hitherto-unanswered question is the form of the function f(k) specified in (6). This is a flexible condition and there are likely a variety of possible solutions, but we have opted to use the very simplest: a piece-wise function constructed of three linear sub-functions,
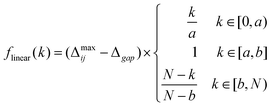 | (8) |
It may be noted that the essential goal of the biasing function is to constrain the value of the density difference with respect the stationary points of the density profile, but one might wonder why the density difference needs to be considered at all. A more useful measure might be the gradient of a single density profile. Using a method close to the well-known gradient descent algorithm would still perform the basic function of directing a random walk to a region where it is most appropriate. An effective way of constructing f(k) might take the form of incorporating the gradient of a single density profile and systematically introducing regions and conditions for when the minimisation might occur. Indeed, the gradient and higher order derivatives of a density profile can even be linked to the free energies of the block copolymer system and ensure close thermodynamic consistency between any sampled random walk configurations.
Relying on the gradient to build f(k) may work exceptionally well for copolymers composed of two monomer types, but will typically be less effective when considering systems with more monomer types such as the terpolymer case. This is because in the latter situation, the minima of a single density field will correspond to the maxima of multiple other density fields. To illustrate, an ABC terpolymer may begin at an A-type monomer dense region and find itself in a minimum where the density of C-type monomers is maximized instead of that of B-type monomers. Our solution necessarily takes into account the correct minima by working on minimizing density differences rather than the density itself. We believe that the local density difference between the current type and the next type on a chain is the most effective way of incorporating this additional information without relying on more expensive global methods.
3.3. Molecular dynamics simulations
Once the structure is generated via the previously described method, molecular simulations may be carried with the myriad methodologies developed for polymer simulation. As justified in the introduction, we have opted to use molecular dynamics simulations to calculate the physical properties of the system.The fundamental tool required to convert a random walk into a macromolecule fit for simulation are coarse-grained interatomic potentials. To this end, we employ the finitely extensible nonlinear elastic (FENE) model to capture interactions between beads that are neighbors on the same chain.
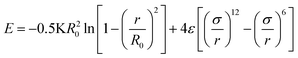 | (9) |
Here we use the same parameters for the FENE potential as those in the Kremer–Grest model.33
Another standard consideration in any kind of molecular simulation is the requirement that the constituent particles should not overlap with each other. A time-tested solution to this requirement is to use the Lennard-Jones potential,
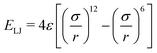 | (10) |
In simulations of block copolymers, the Lennard-Jones potential allows for an additional benefit in that it provides a driving mechanism for phase separation. There are multiple ways in which the parameters of the Lennard-Jones potential may be modified in order to capture this effect. In previously cited studies by Aoyagi, phase separation between the two phases A and B is achieved by setting different values of numerical cutoff distance of (10): self-assembly is driven by directly controlling the effect of the attractive component of the Lennard Jones potential. By setting the cut-off distance of (10) to the potential minimum, the beads within the system may be made to repel each other exclusively.
In another study by Parker and Röttler,30 the same kinetic behavior is accomplished by changing the dispersion energy εAB between two different types A and B. Here, the differences in the depth of potential wells between particles are used to drive phase separation. We have opted to use the second approach, as there is a direct relationship to the dispersion energies and the Flory Huggins parameter. In work by Chremos et. al.,35 a linear relation is proposed between the Lennard-Jones parameters and the Flory–Huggins parameter such that
| χ = α/T + β, | (11) |
| α(εBB,εAB) = 9.8εBB − 18.4εAB + 8.6 |
| β(εBB,εAB) = −4.6εBB + 6.9εAB − 2.4 |
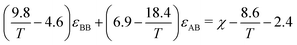 | (12) |
However, it must be noted that any values for the Lennard-Jones parameters obtained in this way run the risk of representing systems that are nothing more than toy models that have unrealistic physical properties. This issue is elaborated upon in Section 5.3.
4. Results
In this section we compare our algorithm with the original NDBMC algorithm and demonstrate additional useful features that emerge from our own methodology. We focus exclusively on the BCC morphology, as this morphology is by far the most difficult to reproduce using the standard approach of the NDBMC method. This is because a random walk must successfully be driven to a spherical region, the locations of which being significantly more specific than other morphologies. We only perform simulations for the ABA triblock copolymer, as this system has a range of parameters already used in previous research. Further, we demonstrate how our algorithm is successfully able to build configurations for significantly more complex systems, such as those comprised of pentablock copolymers and ABC triblock terpolymers. The last case, whilst being novel in own right, is also a demonstration of what may be possible for more complex morphologies. BCC configurations can in principle be obtained through the use of centro-symmetric potentials whose minima correspond to the minima of the density fields obtained from the SCFT calculation. However, potentials are less effective for gyroidal morphologies and as can be seen in the final example it is common for ABC block copolymers to have features common to both gyroidal phases and spheroid phases. We demonstrate that our method is versatile enough to deal with any of these configurations.4.1. ABA triblock copolymer
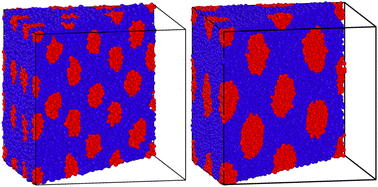
In this section, we first produce the initial guesses for the ABA triblock morphology for different chain lengths with the old NDBMC algorithm. We use ideal walks to remain faithful to the original methodology. It should be noted that ideal walks will always produce configurations that accurately reproduce density profile described by the biased distribution, although this occurs at the cost of minimisation time. Even despite the benefits of using ideal walks, the original algorithm demonstrates a number of serious issues that are exacerbated at shorter chain lengths. In Fig. 5, we juxtapose these results with the output of our improved algorithm. As can be seen, our method provides excellent initial guesses for configurations for molecular simulation. It is to be noted that our method, despite being perfectly able to run and indeed provide slightly better results with ideal walks, uses fully self-avoiding walks. As such, all of the results produced from our algorithm require minimal equilibration. For all blocks, the parameters used for (8) are a = 0.2, b = 0.8 and Δgap = 0.05: little quantitative difference was observed for slight variations of these parameters. The Flory–Huggins parameter used to generate the underlying SCFT simulation is χ = 62.18, which corresponds to a simulation with εAA = 1.0, εBB = 0.5 and εBA = 0.2 at T = 0.15 in Lennard-Jones units. The original algorithm results are computed using walks of length N = 100 (top left), N = 1000 (middle left) and N = 2000 (bottom left). On the right column, walks are of length N = 100 (top right), N = 500 (middle right) and N = 1000 (bottom right). The chains being samples are symmetric ABA triblock copolymers with number fraction fA = 0.2 and fB = 0.8, where A represents the red spherical region and B represents the blue matrix region.As can be seen, there is little use in comparing samples from the original NDBMC algorithm until a sufficiently high number of beads is reached: all samples are of exceptionally poor quality. When N = 1000, however, the beads demonstrate a vaguely BCC morphology, which improves markedly when N reaches a much higher number. On the other hand, our algorithm is so effective that it provides an essentially perfect BCC configuration with just N = 100 beads. Indeed, it can very clearly be seen that a chain length of N = 100 is in fact unrealistic at the given volume, as the chain is not long enough to cover the entire box: note however that the fundamental reason for this lack of reality is discussed in Section 5.2. This demonstrates that our method is powerful enough to operate in even sub-optimal conditions, although this confers the responsibility of choosing reasonable chain lengths onto the user. As we have used self-avoiding walks for our version of the NDBMC algorithm, we have not simulated chains of length N = 2000, as this would result in too many beads being crammed into the space-limited red regions for a single random walk. The extreme limit of our approach occurs when a single A block of just one copolymer configuration occupies all available space in a bead. However, this is markedly unrealistic given the enormous molecular weights that such a polymer configuration would require.
We also employ values used in previous simulations to demonstrate just how effective this approach is when molecular simulations are carried out. As can be seen in Fig. 6, the hard phase depicted with blue beads naturally coalesces into a nearly perfectly spherical structure. No potentials or in-simulation tools have been used to achieve these spherical beads: they emerge naturally from thermal motion. It should however be noted that in this situation, it appears that the temperature required by (11) to achieve a Flory–Huggins parameter is in fact too low. Despite starting our simulations at a temperature of 0.2kbT, we found that raising the temperature in our simulations up to 0.29 as in previously cited work still maintains the BCC configuration and the spherical form taken by the hard phase. This is likely an indication of a discrepancy in the semi-empirical law, a fact which is discussed in Section 5.3.
4.2. ABABA pentablock copolymer
There are markedly few studies regarding the pentablock copolymers in a self-assembled state. In this result, we demonstrate the viability of our method to the generation of such molecular configurations. It should be noted however that, in this example, the Flory–Huggins parameter χ was not motivated by the values of the Lennard-Jones parameters: we began by finding a value of χ that results in self-assembly for a pentablock copolymer. Self assembly was easily achieved by using a Flory Huggins parameter χ = 100. The results, shown in Fig. 7, are quantitatively similar to the ABA triblock copolymer case albeit with larger beads. Molecular dynamics simulations have not been performed on this sample, as clarification on appropriate values for the Lennard-Jones parameters is necessary. The parameters used for the A block were (8) are a = 0.1, b = 0.9 and Δgap = −0.05: we selected these values the ensure that the chain could, if required, pass entirely through an A-type region if necessary. For the B block, we used the same parameters as in the ABA system.4.3. ABC triblock terpolymer
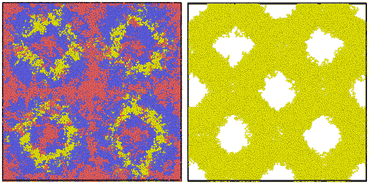
Like the previous case, there are very few studies of the ABC triblock terpolymer melts in which the primary methodology relies on molecular dynamics. We present a valid configuration for an ABC triblock terpolymer in Fig. 8. The Flory–Huggins parameters used are χAB = 13, χBC = 13 and χCA = 35: these parameters were selected because of the certainty with which they would result in a self-assembled field. The process of generating chains for this number density field is unique because the polymer may either begin at an A block or a C block. As justified in Section 3.1, the final block will typically follow the normal NDBMC algorithm whereas the initial block will be subject to the constraints demonstrated in (6). If all random walks began at the A-block, a bias would naturally become present within the simulation. In order to ensure that the density profile of the generated beads are not biased to a particular type, we randomly begin our walks at either the C block or the A block. The parameters used for the A and C blocks (8) are a = 0.1, b = 0.9 and Δgap = 0.1, whilst the B block uses the same parameters as the ABA system: we observed that the acceptance rate was noticeably affected by the parameter choice for this particular example.Our algorithm will successfully generate ABC morphologies given sufficient time. However, it must be noted that the time taken for this particular case is typically quite lengthy. One successful approach is to reduce the extent of the self-avoiding capability of a random walk by reducing the σ parameter used to represent the bead size, before subjecting the system to energy minimisation. This approach will naturally require a longer time to equilibrate the configuration, but the reduction in structure generation time is likely a more efficient trade-off.
5. Discussion
It is to be noted that, despite not posing a significant issue in our work, our choice for the constraining function f(k) that satisfies the conditions stated in (6) is by no means the most efficient implementation. It is however functional, as it achieves the goal of driving the polymer to the required interfaces. An ideal constraining function would be one that balances control of the random walk, or the efficiency by which the walk reaches an interface, whilst still maximising the number of possible configurations that might potentially be sampled. Our choice, flinear, prioritises the latter condition. It is worth considering that the only drawback of prioritizing the number of configurations available to a chain is the increased rejection rate, which in turn increases the time taken to sample a single configuration.Finding the most efficient form of f(k) is a complex problem considering the variety of morphologies that might be sampled. It is likely that the form of the optimal constraining function is also dependent on the morphology that underlies the sampling approach. However, we anticipate that the determination of the optimal form of f(k) will be of increasing importance for the block copolymer systems more complex than those we have shown in our results. Subtle differences, such as the size of the chain and the volume of the box, will likely have to be incorporated into the form of f(k) in order for maximum effectiveness.
There are of course standard limitations to the algorithm which are most aptly described as depending on the sound judgement of the user. Attempting to fit a chain more suited for a gyroid morphology into a body-centred crystal morphology, for instance, will not result in a successful configuration sample for obvious reasons. The excluded volume of a single chain segment of a given type must be well below the volume corresponding to the number density of the segment monomer type. However, in more complex morphologies, the efficiency of the algorithm can become quite sensitive to chain length and box volume.
Our focus in this publication has been the generation of structure upon the assumption that the SCFT calculation employed indeed provides the equilibrium morphology of the system, or at least provides a valid approximation. In the following section we demonstrate how such a valid approximation may be improved through the use of more sophisticated random walk generation and sampling methods. We believe that our variant of the node-density biased Monte Carlo algorithm effectively solves the problem of connecting a number-field density to a coarse-grained molecular configuration. The validity of the technique is thus dependent exclusively on the manner in which SCFT agrees with molecular dynamics simulation. A further important feature to consider is the effect that the Lennard-Jones parameters have an effect on the system as it undergoes molecular simulation.
5.1. Random walk generation
The parameters of the random walk strongly influence the effectiveness of the overall algorithm. It is not difficult to see why a smaller step would be more effective at traversing a density profile: smaller steps are capable of navigating smaller changes in density. This suggests that a powerful method of producing high quality configurations might make use of fine-graining. Indeed, for many applications it may even be more useful to eschew the use of coarse-grained beads and build the configuration with fully atomistic models. For reasons of computational performance, this may not be desirable for simulation purposes. However, through techniques such as the Newton inversion method36 applied to polymers, it is still possible to improve the performance of the NDBMC algorithm using the concept of fine-graining.In both the original NDBMC algorithm and our variation of it, the random walk generation process is relatively simple: the former simply generates an ideal random walk position constrained by the bond length between coarse-grained beads while the latter produces a self-avoiding configuration naturally. The ideal chain is the most basic case and must undergo preprocessing if it is to be used in a molecular dynamics simulation. On the other extreme, the self-avoiding random walk consciously avoids overlaps, but at the same time it excludes a large number of reasonable configurations. These are examples of simple sampling schemes for obtaining configurations for RN and naturally, there are more sophisticated examples. A key example that would be a good replacement for the schemes outlined in this work is an off-lattice variant of the Rosenbluth and Rosenbluth algorithm.37 This scheme operates by the standard importance sampling approach common to most Monte Carlo algorithms, where the energies of the walk positions are taken into account as the walk is built. A significant benefit of the Rosenbluth sampling technique is the fact that it may be used to calculate relative probabilities of chains. This in turn allows for the use of the Metropolis–Hastings algorithm: effectively, a configuration may be directly sampled from the Boltzmann distribution. Further improvements to the Rosenbluth sampling scheme exist, such as the Pruned and Enriched Rosenbluth Method and Configurational-bias Monte Carlo.
In the case of block copolymers, the Rosenbluth sampling scheme is enhanced when combined with our variant of the NDBMC algorithm. The algorithm operates by considering local energies and has no mechanism to guide a chain to a given region: it simply seeks to reduce the energy of the chain, a strategy that is not useful when a segment composed of A-type monomers has found itself surrounded by B-type monomers. Likewise, the Rosenbluth scheme is significantly faster than the simple self-avoiding walk scheme described in this work as it deals with the problem of overlaps in a more intelligent, thermodynamically consistent manner. We note that the use of the biasing function to guide the random walk will not need to be incorporated into the energy calculations carried out by the Rosenbluth–Rosenbluth algorithm, as the density profiles are completely independent of the molecular simulation.
Whilst this additional change may add rigor as a means of sampling from the Boltzmann distribution, one might question the necessity of carrying out a Monte Carlo calculation when the step immediately following the construction of RN is a MD simulation. Molecular dynamics simulation is the essential component in our approach, with the NDBMC algorithm being used as a precursor step. As such, we would prioritise that the final configuration should be closer to the MD Hamiltonian than the SCFT Hamiltonian. We believe that a Monte Carlo simulation may be useful in the case of a discrepancy between the SCFT Hamiltonian and the MD Hamiltonian, as it will naturally correct the configuration towards the latter.
5.2. Molecular chains and the Gaussian chain model
In the results presented so far, we have remained faithful to the original molecular simulation specifications presented in the original work in which the NDBMC algorithm was presented. It is to be noted, however, that there exists a subtle discrepancy in these specifications with the model underlying the SCFT calculation. As described in Section 3.3, we use the FENE potential in combination with the Lennard-Jones potential to represent the covalent bonds of the polymer. However, all SCFT calculations shown so far use the continuous Gaussian chain model, the energy of which is determined by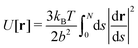 | (13) |
There is no guarantee that the thermodynamics of a system described by (13) are equivalent to the thermodynamics of a system that uses the FENE chain. Unless the thermodynamics of these two systems are proven to be equivalent, one can never be certain that the equilibrium configurations predicted by SCFT will provide equilibrium configurations on the molecular scale. This would imply that the overarching approach of converting an SCFT calculation into a molecular configuration is generally unfeasible. However, there are two strategies that can minimise or even wholly eliminate this issue.
The first option is to use a different potential in molecular simulation that explicitly follows the same assumptions of the Gaussian chain model. The FENE chain appears to be the standard for polymer simulations of entangled polymeric systems, as it eliminates any chance of chains passing through each other. However, this is not the technique by which this condition may be achieved. In the already discussed work by Chremos et. al., the harmonic bond
| E = k(r − R0)2 | (14) |
which suggests that for the spring constant described previously a representative Kuhn length should be 0.008σN. This value indeed allows for fast-converging SCFT simulations, but it admittedly places quite a restriction on the systems that may be studied. It is worth however noting that this analysis may only become significant in highly energetic situations where chains on the molecular scale are deformed considerably. This is because the forces arising from the FENE potential, aptly described by Warner's relationship38
reduces to the standard harmonic potential for weak bond extensions x/R2c ≪ 1.
The second option is in a way a reverse of the previous suggestion. Instead of modifying the potentials used in the molecular dynamics simulation, one might develop a SCFT simulation that includes as part of its underlying model the same potentials as the molecular dynamics simulation. Indeed, SCFT can be built around a large variety of underlying chain models, ranging from discrete chains with a finite number of beads39 to compressible systems.40 Both of these modifications would significantly improve the accuracy of the SCFT calculation in providing equilibrium configurations. This option, if achieved, would be as close to infallible as possible when combined with the sampling algorithm presented in this paper. It is however a difficult and time-intensive undertaking. A tailored SCFT code presents the additional caveat that there is no guarantee that the modified code would result in self-assembly. Further, it is worth mentioning that the Gaussian chain model is specifically used because it significantly simplifies calculations in practice. A more complicated model based around a molecular potential is not guaranteed to be at all solvable in the framework of SCFT.
However, the considerable progress has been made in field-based simulation methods over two decades since the publication of the original NDBMC algorithm. Field-theoretic simulations, which introduce fluctuation corrections to SCFT, are one example of this progress. Field-theoretic simulations typically deal with excluded volume interactions with idealised δ-function interactions, but recently work by Weyman et. al.41,42 have explored field theoretic simulations that implicitly incorporate the effect of realistic interatomic potentials. One key result of their research is that field-theoretic methods are not suitable ground for the strict 12-6 Lennard-Jones potential. This is because a key feature required for the field-theoretic simulation, the functional inverse of the interatomic potential u, does not exist for the Lennard-Jones potential. On the other hand, this requirement is satisfied for the Morse potential
| V(r) = De−2a(r−r0) − 2De−a(r−r0) | (15) |
On a related note, we note that chain length presents a subtle but important discrepancy that exists between the SCFT calculation used in the original NDBMC algorithm and the assumptions underlying the molecular structure used in the MD simulation. The SCFT calculation used in the original formulation makes the assumption that the underlying chain model is a Gaussian chain, which implicitly approximates a polymer composed of infinitely many segments. This is of course too drastic a simplification when attempting to obtain useful molecular-level comparisons and is undoubtedly a flaw in the entire approach. However, as mentioned, the progress in field-theoretic methodologies is such that this simplification is no longer necessary. There are a variety of techniques that operate with a finite number of segments, with Single-Chain-in-Mean-Field (SCMF) simulations and discrete chain self-consistent field theory (DCSCFT) as notable examples.44
As mentioned, this paper is devoted to Monte Carlo sampling: our concern is the process of generating configurations upon the assumption that the number density predicted by SCFT is valid. An in-depth investigation of the strategies presented in this discussion is not included in this work, but we believe these considerations to be important enough to warrant explicit mention.
Indeed, we consider the capability of the NDBMC algorithm to work seamlessly with any field-based solution to be its most powerful feature. In this sense, the capabilities of the NDBMC algorithm are limited only by the sophistication of field-theoretic simulation.
Whilst we have recommended a variety of replacements for the original SCFT approach, we also note that more efficient molecular simulation tools may be used. Essentially, any simulation approach that requires an initial configuration stands to benefit from our improved version of the NDBMC algorithm. This may in fact be a necessity when anticipating the structural complexities of terpolymers and pentablock systems. One strong candidate for this replacement is dissipative particle dynamics,45 a mesoscopic particle-based method that has successfully been used to model block copolymer self assembly.46,47 We do note that it is important that the Hamiltonian of any method chosen should match as closely as possible to field theory.
5.3. Dependence of mechanical properties on Lennard-Jones parameters
We have demonstrated molecular simulation only for the example of the ABA triblock copolymer, using values of the Lennard-Jones ε parameters that have been used in previous research. For the latter examples, we have explicitly excluded mention of the Lennard-Jones parameters and proceeded with a version of the Flory–Huggins parameter that leads to self-assembly.The application of (12) would have provided a large range of possible values for εAA, εBB and εAB. The Flory–Huggins parameter χ = 100 employed in Section 4.2 could, for instance, be obtained with a T = 0.15 with εAA = 1.0, εBB = 0.9327 and εAB = 0.1. However, given that (11) is a semi-empirical law obtained from Monte Carlo simulations, it would be appropriate to verify the validity of any Lennard-Jones ε parameters that vary from the assumptions made in deriving them. This verification can naturally be carried out using the same method used to derive (11). On a further note, it is also important to note that this relation might indeed by too simple to capture the self-assembly behavior of more complex systems than the standard diblock. This was briefly alluded to in Section 4.1, where the Flory–Huggins parameter provided by (11) for the system only resulted in self-assembly at a lower temperature than those studied in previous work. This discrepancy suggests that the architecture of a polymer should be taken into account when designing schemes by which to predict the Flory–Huggins parameter. Further evidence to this feature is the fact that the pentablock ABABA simulation required a significantly larger value for the Flory–Huggins parameter in order to self-assemble than the ABA triblock simulation.
Another and more serious concern is related to the purpose for which the molecular configurations are generated. Our preliminary investigations have demonstrated that varying the Lennard-Jones ε parameters has a complex effect on the mechanical properties of the simulation, specifically the manner in which the hard phase evolves throughout deformation. This is an interesting and multifaceted problem that provides a number of insights regarding the structure-property relations of a generic block copolymer material. We thus defer detailed discussion to a future study.
6. Conclusion
In this work, we have provided a new algorithm based around extending the node-density biased Monte Carlo algorithm, whereby a set of desirable conditions is motivated and are then incorporated into the sampling scheme. These conditions make use of the difference of number densities between two different types, a local quantity that nevertheless serves well to govern the global structure of the random walk configuration of a segment. The inclusion of these density-difference based constraints represents a general methodology by which mesoscopic calculations may be used to build microscopic configurations of complex macro-molecular systems.The effectiveness of our method is demonstrated by the quality of the molecular dynamics simulations that it yields for systems that have already received extended study. With our method it is no longer necessary to build complex simulation workflows for the investigation of the bead morphology, as near-perfect spherical beads are automatically obtained by ensuring that the chains that form them are high quality samples.
Further, our application of the extended node-density biased Monte Carlo method has yielded simulations that have before now received very little attention from the lens of molecular dynamics simulation, likely due to the difficulty of obtaining high quality initial configurations of such systems. One example of this is the pentablock copolymer melt simulated in this publication. Pentablock copolymers have received limited attention in previous research, but to the authors knowledge these systems have never been investigated in an already self-assembled form via molecular dynamics simulation. Our extended algorithm allows for the investigation of a number of difficult questions, chief of which is the relationship between the thermo-mechanical properties of an N-block copolymer and the value of N.
The most interesting and challenging example of polymer systems that our extended algorithm allows the investigation of are ABC triblock terpolymer, whose extraordinarily rich spectrum of morphologies is seemingly limited only to SCFT literature. We believe that our variant of the NDBMC method might allow this vibrant domain of soft matter simulation to be opened up to more traditional particle-based methodologies. We consider this to be an important objective, as a detailed description of polymer motion in a block copolymer is not possible with just the coarse-grained self-consistent field representation.
We consider that our variant of the NDBMC method to be a reasonably complete solution to finding initial configurations of a variety of block copolymer morphologies. The further development of this technique is limited only by the capabilities of its constituent methodologies, namely SCFT and molecular dynamics. The extent of this method's application is dependent entirely on the number and quality of phases SCFT, or indeed a more sophisticated mesoscopic methodology such as field-theoretic simulation, can achieve. As explored in the discussion however, it is important to note that the energies attained with the bead-spring model when combined with the Lennard-Jones potential are not the same as those that the SCFT calculation is based on. For a truly consistent multi-scale modelling approach, a SCFT calculation that incorporates the exact potentials should be used. This development will likely require further investigation. Finally, we demonstrate that it is possible to justify the algorithm rigorously by reframing it in terms of Rosenbluth sampling. We believe that with the incorporation of biasing functions and the enhancements we have suggested that the NDBMC algorithm will prove itself to be a powerful tool for the molecular dynamics simulation of self-assembled multicomponent block copolymers.
Data-availability
The versions of our software used in the generation of Fig. 5–8 can be found at https://doi.org/10.5281/zenodo.7327034.48 The current version of the code can be found at its dedicated GitHub repository.49Author contributions
All authors contributed equally to this work.Conflicts of interest
The authors have no conflicts of interest to declare.Appendix
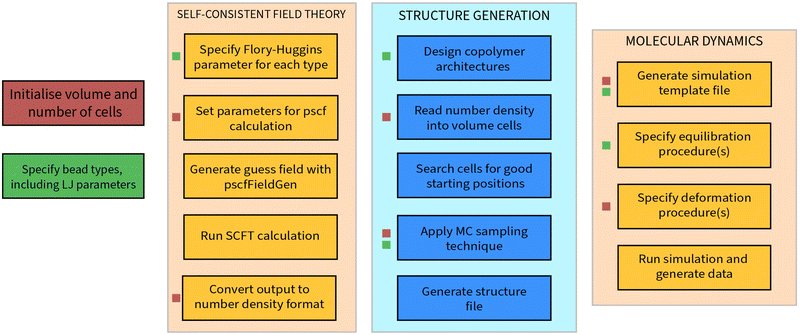
A. NanoPoly: a structure generation tool for block copolymer melts
Every process described in this research can be carried out in a streamlined fashion using nanoPoly, a software suite designed to model a variety of polymer structures. In this section, we will outline some of the design principles behind this software that informed many of implementation details in our approach. It is worth noting that nanoPoly is not limited to building and simulating self-assembled block copolymer morphologies: general polymer melts for a large variety of user-defined architectures are also possible. We will limit exposition of nanoPoly features to aspects relevant to the simulations carried out in this paper. A generic workflow is shown in Fig. 9.The essential component of nanoPoly is the self-avoiding walk and the entire software is designed around the rapid generation of self-avoiding random walk configurations. In the structure generation phase, all monomers are treated as hard-spheres whose contribution to the excluded volume is
The most computationally intensive component of constructing a self-avoiding random walk is the requirement that every position be checked for overlap with the accepted bead positions that have already been placed within the box. This achieved in nanoPoly by partitioning the volume into cells that are at least as large as the equilibrium distance of the FENE potential used to model a given random walk. Typically, this equilibrium corresponds to the minimum of the Lennard-Jones potential, σmin = 21/6. When multiple FENE potentials are used for different architectures, the largest equilibrium distance is used as the smallest possible cell length. Thus, the fundamental data structure that nanoPoly makes use of is a collection of ordered volume cells that, when combined, represent a full volume. The problem of verifying the validity of a position for a self-avoiding random walk is reduced from checking every existing position to checking only the bead positions that share the cell of the position being verified.
The collection of ordered volume cells also lends well to the problem of reading in the number density configurations that are calculated through SCFT. All SCFT calculations described in this paper were carried out using the pscf software developed by Morse and coworkers,51 as well as the additional pscfFieldGen software for initial guess generation. We emphasize that the choice of a mean field theory is consequential only in the quality of the final result: nanoPoly need only a number density file in order to generate a coarse-grained molecular configuration.
The pscf calculations are carried out automatically by nanoPoly after key parameters are specified. Once the SCFT calculation is carried out for a grid of N × N × N points, it may be read into the corresponding collection of volume cells defined in nanoPoly. The option to read an N × N × N SCFT calculation into a collection containing (aN)3 volume cells also exists such that one volume grid may include a unit cells of a given SCFT morphology. It is worth noting that this is in fact a departure from the original formulation of the NDBMC algorithm, which instead relies on representing the number density as a continuous field through interpolation. With nanoPoly, this option is available. However, we have found that maintaining the discrete number density field in combination with an optimally selected volume-cell size guarantees a noticeable change in density difference. Whilst this makes little impact on the original NDBMC algorithm, for the development discussed in this publication it significantly increases the efficiency of the algorithm.
The biasing of a walk is conducted in a similar manner to the original NDBMC algorithm as described in Section 2.1, with the exception being when a step of the walk does not satisfy the conditions outlined by (6). Once a volume is defined and populated with a variety of random walks, it may be subjected to molecular dynamics simulation. The exact sequence of the molecular simulation may be outlined directly in nanoPoly, which provides an interface to lammps. Our interface is reasonably complete for the purpose of designing molecular dynamics simulations in which deformations play an important part. Using nanoPoly, it is simple to write a routine that either builds a large number of configurations and simulates each one in turn. It is also possible and in many cases desirable to instead generate a single configuration and simulate it many times with differing parameters. This facility was used liberally to obtain the results discussed in Section 4.
Acknowledgements
The work presented in this paper benefited immensely from discussions with Dr Bart Vorselaars of the University of Lincoln, who provided much needed input from the view of an expert in SCFT. The work presented in this paper would have been incomplete without his advice and suggestions, for which we are extremely grateful. This work was funded and supported by the EPSRC Centre for Doctoral Training in the Modelling of Heterogeneous Systems (EP/S022848/1), with PhD scholarship (AR) being gratefully acknowledged. For the purpose of open access, the author has applied a Creative Commons Attribution (CC BY) licence to any Author Accepted Manuscript version arising from this submission.Notes and references
- M. Rubinstein and R. H. Colby, Polymer Physics, Oxford University Press, Oxford, England, UK, 2003 Search PubMed.
- G. Polymeropoulos, G. Zapsas, K. Ntetsikas, P. Bilalis, Y. Gnanou and N. Hadjichristidis, Macromolecules, 2017, 50, 1253–1290 CrossRef CAS.
- S. L. Perry and C. E. Sing, ACS Macro Lett., 2020, 9, 216–225 CrossRef CAS PubMed.
- F. S. Bates and G. H. Fredrickson, Block Copolymer Thermodynamics: Theory and Experiment, Annual Reviews, 2003 Search PubMed.
- C. M. Bates and F. S. Bates, Macromolecules, 2017, 50, 3–22 CrossRef CAS.
- J. Diani, B. Fayolle and P. Gilormini, Eur. Polym. J., 2009, 45, 601–612 CrossRef CAS.
- M. W. Matsen and M. Schick, Phys. Rev. Lett., 1994, 72, 2660–2663 CrossRef CAS PubMed.
- T. Ohta and K. Kawasaki, Equilibrium morphology of block copolymer melts, ACS Publications, 2002 Search PubMed.
- D. Kay, V. Styles, A. Muünch and Q. Parsons, AIP Conf. Proc., 2020, 2293, 020002 CrossRef CAS.
- G. Fredrickson, The Equilibrium Theory of Inhomogeneous Polymers, Oxford University Press, Oxford, England, UK, 2013 Search PubMed.
- M. W. Matsen and T. M. Beardsley, Polymers, 2021, 13, 2437 CrossRef CAS PubMed.
- M. W. Matsen, Macromolecules, 2012, 45, 2161–2165 CrossRef CAS.
- S. Li, Y. Jiang and J. Z. Y. Chen, Soft Matter, 2013, 9, 4843–4854 RSC.
- F. S. Bates and G. H. Fredrickson, Phys. Today, 2008, 52, 32 CrossRef.
- V. G. Mavrantzas, Front. Phys., 2021, 9, 173 Search PubMed.
- D. Hossain, M. A. Tschopp, D. K. Ward, J. L. Bouvard, P. Wang and M. F. Horstemeyer, Polymer, 2010, 51, 6071–6083 CrossRef CAS.
- H. A. Karimi-Varzaneh, N. F. A. van der Vegt, F. Muüller-Plathe and P. Carbone, ChemPhysChem, 2012, 13, 3428–3439 CrossRef CAS PubMed.
- F. Schmid, ACS Polym. Au, 2022 DOI:10.1021/acspolymersau.2c00049.
- M. Zhang, Z. Cui and L. C. Brinson, J. Polym. Sci., Part B: Polym. Phys., 2018, 56, 1552–1566 CrossRef CAS.
- T. Aoyagi, F. Sawa, T. Shoji, H. Fukunaga, J.-I. Takimoto and M. Doi, Comput. Phys. Commun., 2002, 145, 267–279 CrossRef CAS.
- J. M. Rodgers, M. Webb and B. Smit, J. Chem. Phys., 2010, 132, 064107 CrossRef PubMed.
- P. Padmanabhan, F. Martinez-Veracoechea and F. A. Escobedo, Computation of Free Energies of Cubic Bicontinuous Phases for Blends of Diblock Copolymer and Selective Homopolymer, ACS Publications, 2016 Search PubMed.
- E. L. Thomas and R. L. Lescanec, Proc. R. Soc. London, Ser. A, 1994, 348, 149–166 CAS.
- T. Aoyagi, T. Honda and M. Doi, J. Chem. Phys., 2002, 117, 8153–8161 CrossRef CAS.
- T. Aoyagi, Nihon Reoroji Gakkaishi, 2009, 37, 75–79 CrossRef CAS.
- T. Aoyagi, Polymer, 2022, 243, 124624 CrossRef CAS.
- D. Q. Pike, F. A. Detcheverry, M. Muüller and J. J. de Pablo, J. Chem. Phys., 2009, 131, 084903 CrossRef PubMed.
- A. Ramírez-Hernaández, F. A. Detcheverry, B. L. Peters, V. C. Chappa, K. S. Schweizer, M. Muüller and J. J. de Pablo, Macromolecules, 2013, 46, 6287–6299 CrossRef.
- K. M. Langner and G. J. A. Sevink, Soft Matter, 2012, 8, 5102–5118 RSC.
- A. J. Parker and J. Rottler, ACS Macro Lett., 2017, 6, 786–790 CrossRef CAS.
- A. J. Parker and J. Rottler, Macromol. Theory Simul., 2014, 23, 401–409 CrossRef CAS.
- R. Auhl, R. Everaers, G. S. Grest, K. Kremer and S. J. Plimpton, J. Chem. Phys., 2003, 119, 12718–12728 CrossRef CAS.
- K. Kremer and G. S. Grest, J. Chem. Phys., 1990, 92, 5057–5086 CrossRef CAS.
- X. Wang, S. Ramírez-Hinestrosa, J. Dobnikar and D. Frenkel, Phys. Chem. Chem. Phys., 2020, 22, 10624–10633 RSC.
- A. Chremos, A. Nikoubashman and A. Z. Panagiotopoulos, J. Chem. Phys., 2014, 140, 054909 CrossRef PubMed.
- A. Lyubartsev, A. Mirzoev, L. Chen and A. Laaksonen, Faraday Discuss., 2009, 144, 43–56 RSC.
- M. N. Rosenbluth and A. W. Rosenbluth, J. Chem. Phys., 1955, 23, 356–359 CrossRef CAS.
- R. Bird, O. Hassager, R. C. Armstrong and C. F. Curtiss, Dynamics of Polymeric Liquids, vol. 2, 1977 Search PubMed.
- M. W. Matsen, Macromolecules, 2012, 45, 8502–8509 CrossRef CAS.
- E. Helfand, J. Chem. Phys., 1975, 62, 999–1005 CrossRef CAS.
- A. Weyman, V. G. Mavrantzas and H. C. OÖttinger, J. Chem. Phys., 2021, 155, 024106 CrossRef CAS.
- A. Weyman, V. G. Mavrantzas and H. C. OÖttinger, J. Chem. Phys., 2022, 156, 224115 CrossRef CAS PubMed.
- G. Kacar, Chem. Phys. Lett., 2017, 690, 133–139 CrossRef CAS.
- S. J. Park and J. U. Kim, Soft Matter, 2020, 16, 5233–5249 RSC.
- P. Espanñol and P. B. Warren, J. Chem. Phys., 2017, 146, 150901 CrossRef PubMed.
- R. D. Groot and T. J. Madden, J. Chem. Phys., 1998, 108, 8713 CrossRef CAS.
- H. Huang and A. Alexander-Katz, J. Chem. Phys., 2019, 151, 154905 CrossRef PubMed.
- A. Rajkumar, nanoPoly-v1, 2022 DOI:10.5281/zenodo.7327034.
- A. Rajkumar, nanoPoly, 2022, https://github.com/aravinthen/nanoPoly, [Online; accessed 16. Nov. 2022].
- E. Polak and G. Ribiere, Recherche Opertionelle, 3e année, 1969, 16, 35–43.
- A. Arora, J. Qin, D. C. Morse, K. T. Delaney, G. H. Fredrickson, F. S. Bates and K. D. Dorfman, Macromolecules, 2016, 49, 4675–4690 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2023 |

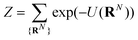

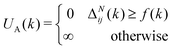
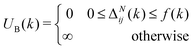
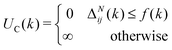

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 beads. For denser systems, the soft phase composed of blue beads has been removed for visibility purposes.
000 beads. For denser systems, the soft phase composed of blue beads has been removed for visibility purposes.