Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
A new hyperelastic lookup table for RT-DC
Lucas Daniel
Wittwer
 abc,
Felix
Reichel
abc,
Felix
Reichel
 cd,
Paul
Müller
cd,
Paul
Müller
 c,
Jochen
Guck
c,
Jochen
Guck
 *cd and
Sebastian
Aland
*cd and
Sebastian
Aland
 ab
ab
aInstitute of Numerical Mathematics and Optimisation, TU Freiberg, Akademiestrasse 6, 09599 Freiberg, Germany
bFaculty of Informatics/Mathematics, HTW Dresden, Friedrich-List-Platz 1, 01069 Dresden, Germany
cMax Planck Institute for the Science of Light and Max-Planck-Zentrum für Physik und Medizin, Staudtstrasse 2, 91058 Erlangen, Germany. E-mail: jochen.guck@mpl.mpg.de
dChair of Biological Optomechanics, FAU Erlangen-Nürnberg, Universitätsstraße 40, 91054 Erlangen, Germany
First published on 20th February 2023
Abstract
Real-time deformability cytometry (RT-DC) is an established method that quantifies features like size, shape, and stiffness for whole cell populations on a single-cell level in real-time. A lookup table (LUT) disentangles the experimentally derived steady-state cell deformation and the projected area to extract the cell stiffness in the form of the Young's modulus. So far, two lookup tables exist but are limited to simple linear material models and cylindrical channel geometries. Here, we present two new lookup tables for RT-DC based on a neo-Hookean hyperelastic material numerically derived by simulations based on the finite element method in square and cylindrical channel geometries. At the same time, we quantify the influence of the shear-thinning behavior of the surrounding medium on the stationary deformation of cells in RT-DC and discuss the applicability and impact of the proposed LUTs regarding past and future RT-DC data analysis. Additionally, we provide insights about the cell strain and stresses, as well as the influence resulting from the rotational symmetric assumption on the cell deformation and volume estimation. The new lookup tables and the numerical cell shapes are made freely available.
Cell stiffness emerged as an important phenotypical marker linked to many biological processes and can reveal pathological changes of cells.1,2 The emergence of high-throughput techniques to measure single-cell deformability enables the use of cell deformation as a tool in clinical diagnostics.1,3 In this work, we concentrate on the microfluidic technique real-time deformability cytometry (RT-DC).4 RT-DC is used for high-throughput and label-free mechanical characterization of cells and has been applied in the past to address biological research questions5–10 and for blood diagnostics.1–3,11
In RT-DC, cells flow through a narrow microfluidic channel where they get deformed by hydrodynamic stresses from the flow field around them, reaching a steady state configuration. On the timescale of an RT-DC measurement, viscous effects have no influence on the steady state and the deformation is purely due to the elastic cellular response. The deformed cells are imaged, and the contour is analyzed in real-time at a throughput of up to 1000 cells s−1. Based on this stationary deformation, not only base properties like the cell circumference L, projected area A, and volume V are deduced but also material properties like the cell's stiffness (elasticity) in the form of the Young's modulus. For the latter, the influence of the cell size, measured by the area A, needs to be decoupled from the stationary deformation D, here defined as
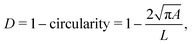 | (1) |
With these LUTs, it is possible to check for structural differences in cell populations of different sizes where the deformation parameter alone is not suited to compare cell stiffness. This becomes important when cells undergo size changes, e.g., during development,5,6 or in disease or treatment.1,3,14
RT-DC measurements are done for various flow rates, channel widths, and measurement buffer viscosities. Mietke et al.12 showed analytically that isoelasticity lines – the level set for a fixed Young's modulus – of the lookup table can be scaled to a different channel width L′, flow rate Q′ and viscosity of the buffer medium η′ for a Newtonian carrier and linear elastic cell material by E′ = E(η′Q′L3/ηQL′3) and A′ = A(L′/L)2. Here, η, Q, and L are the parameters used to generate the lookup tables. Thus, the same lookup table can be used for different flow rates, microfluidic channels, and buffers. Those lookup tables and the scaling are implemented in dclab,15 the Python library for the post-measurement analysis of real-time deformability cytometry.
However, these two models use three simplifications. First, the square cross-section of the channel is assumed to be cylindrical to employ rotational symmetry. Second, they do not consider the non-Newtonian shear-thinning nature of the suspension buffers used in RT-DC, e.g., methyl-cellulose dissolved in phosphate-buffered saline (MC-PBS).16,17 And last, both assume a small strain linear elasticity bulk model for the cell. Especially for larger cells or higher hydrodynamic stresses, the small strain assumption does not hold. Recent work on probing viscoelastic properties of cells in RT-DC, dynamic real-time deformability cytometry dRT-DC,18 showed large deformation in the inflow region of the narrow channel. A numerical study of the viscoelastic behavior of cells and beads in RT-DC has been conducted in the axisymmetric case in Schuster et al.19 and in full three-dimensional channels in Wittwer et al.20 Both studies model the cell as a neo-Hookean hyperelastic material model. The apparent viscosity η is linked to the apparent Young's modulus by η = Eτ, where τ is the relaxation timescale of the cell. But E is only deducible by a lookup table based on the same material model. Thus, a LUT based on the neo-Hookean hyperelastic material model is necessary to deduce the apparent Young's modulus E and viscosity η.
Here, we introduce two new improved LUTs – one for a cylindrical and one for a square channel – to extract the stiffness of cells in RT-DC based on fully coupled fluid–solid interaction finite element simulations. We use a hyperelastic neo-Hookean material to get the cells' elastic response in a full three-dimensional square channel with a shear-thinning buffer. We show that, like the initial analytical and numerical LUTs, the two proposed LUTs uniquely map every combination of area and deformation to a Young's modulus. The scaling concept still holds, including shear-thinning. The new and improved LUTs for RT-DC will help reveal stiffness changes between cell types or due to cell state changes with unprecedented accuracy. Additionally, we report the resulting strains and hydrodynamic surface stresses acting on the cells for the first time. And finally, we investigate the systematic error in volume computation introduced by the widely-used assumption of rotationally symmetric cell deformation.
1 Methods
We start by describing the computational domain and the new fluid–solid interaction (FSI) model with a shear-thinning non-Newtoinan fluid (the buffer) and a hyperelastic neo-Hookean solid (the cell). Based on this model, we describe the generation of the new lookup tables by sampling the area-deformation space. At the end of this section, we describe the experimental setup used to measure the HL60 cells and PAAm beads in Fig. 6.1.1 Fluid–solid interaction model
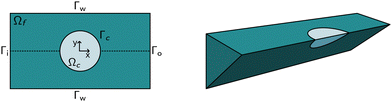
The computational domain, as illustrated in Fig. 1, is split into the fluid subdomain Ωf and the subdomain representing the cell Ωc. The subdomains are separated by the interface Γ. We model the fluid in the Ωf by the incompressible Navier–Stokes equations given by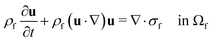 | (2) |
| σf = −pI + η(u)(∇u + (∇uT)) in Ωf | (3) |
| ρf∇·u = 0 in Ωf | (4) |
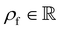 is the fluid density,
is the fluid density, 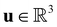 the fluid velocity,
the fluid velocity, 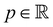 the pressure, and
the pressure, and 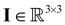 the identity matrix. The power-law rheology model with
the identity matrix. The power-law rheology model with 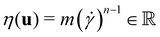 accounts for the velocity-dependent viscosity where
accounts for the velocity-dependent viscosity where 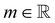 is the fluid consistency coefficient,
is the fluid consistency coefficient, ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) is the shear rate and
is the shear rate and 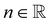 the flow behavior index.
the flow behavior index.
Following Mokbel et al.,13 we assume the cells to be incompressible but not linear elastic but as a non-linear neo-Hookean hyperelastic material described by
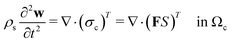 | (5) |
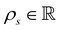 is the cell density,
is the cell density, 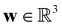 the displacement vector, F is the deformation gradient and S is the second Piola–Kirchhoff stress. The strain energy density of the neo-Hookean material Ws is
the displacement vector, F is the deformation gradient and S is the second Piola–Kirchhoff stress. The strain energy density of the neo-Hookean material Ws is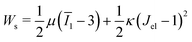 | (6) |
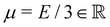 with the Young's modulus E and the bulk modulus
with the Young's modulus E and the bulk modulus 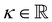 .
.
On the interface Γ, we impose the kinematic condition u = ∂tw (continuity of velocities) as well as the dynamic condition nf·σf = −nc·σc (balance of forces). The mechanical model is described in more detail in Wittwer et al.20
1.2 Finite-element implementation
The above system of equations is discretized and solved by the finite element method using COMSOL Multiphysics. For the full three-dimensional simulations of the square channel, we reduced the computational effort by exploiting the 4-fold rotational symmetry and 2-fold reflection symmetry of the rectangular channel cross-section (see Fig. 1 on the right). We can exploit the rotational symmetry and reduce the computational domain to a two-dimensional surface for the cylindrical channel lookup table. The radius R of the cylindrical channel is adapted to R = 1.094 × lc, where lc is the square channel width, such that the pressure drop over the cylindrical channel is equal to the square channel (see the concept of equivalent channel described in Mietke et al.12). The resulting computational domain is meshed with a combination of tetrahedral, prisms and pyramid elements to efficiently reduce the number of degrees of freedom even further. To resolve the high gradient in the flow profile on the channel walls and the cell surface, we added a boundary layer on Γw and Γc. We choose linear Lagrange elements (P1) to discretize the Navier–Stokes equation for both the velocity field and pressure and stabilize the saddle-point problem with streamline and crosswind diffusion. Linear elements are used to discretize the displacement field of the hyperelastic material. We did not experience any locking behavior during our model validation by comparing the solution with quadratic elements for the solid.The correct inflow profile ui is precomputed in the absence of a cell, based on the flow rate, channel width, and the non-Newtonian parameters of the fluid and used as Dirichlet boundary condition at the inlet. At the outlet Γ0, the pressure is fixed to p0 = 0, and we suppressed any eventual backflow. To keep the cell centered in the computational domain, we describe all quantities in a coordinate system that moves with the cell. We use a proportional integral derivative (PID) controller to adjust the wall speed uw on Γw based on the barycentre of the cell. This wall speed is subtracted from the inflow profile such that the resulting system is the same as if the cell moves through the channel. The arbitrary Lagrangian–Eulerian (ALE) description is employed for the deformation of the fluid domain Ωf. The grid movement on Γ is extended into the interior of the domain and smoothed by treating the vertex displacements as a neo-Hookean hyperelastic material.
To improve the stability of the simulations, we add an artificial viscosity to the cell in a Kelvin–Voigt-like manner, and we monotonically ramp up the inflow profile from u = 0 to ui. We stop the simulation as soon as the steady state deformation is reached by measuring the absolute deformation change 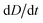 and set as the stop criteria
and set as the stop criteria 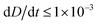 . The artificial viscous term and the ramp-up do not influence the steady state. The fully bidirectional coupled geometrical non-linear system is solved with a Newton method in time and the PARDISO direct solver in space.
. The artificial viscous term and the ramp-up do not influence the steady state. The fully bidirectional coupled geometrical non-linear system is solved with a Newton method in time and the PARDISO direct solver in space.
1.3 Creation of the new lookup tables
We indirectly sampled the area-deformation space for the new lookup tables by the radius and Young's modulus of the cells. The radii R are chosen equidistant in R2 such that the resulting projected areas should be in the range of [30 μm2, 290 μm2] (the actual projected cell area is not conserved). Similar, the Young's modulus E ∈ [0.3 kPa, 30 kPa] is equally sampled in E−1/2. For each R × E combination, we ran two simulations, one in a square channel with a channel width of lc = 20 μm and one in an equivalent cylindrical channel (see above). The cell has a density of ρs = 1000 kg m−3 and we set the bulk modulus κ = 2.15 GPa corresponding to the bulk modulus of water, leading to a quasi-incompressible cell. The artificial cell viscosity is set to 10 mPa s. For both lookup tables, the flow rate is 0.04 μL s−1. The fluid parameters are based on 0.6% MC-PBS (see below). Additionally, we set the density to ρf = 1000 kg m−3.We did several data-cleaning steps for both lookup tables to ensure that the simulations converge and are not numerical artifacts. We automatically detect and delete outliers based on polynomial regression and the random sample consensus (RANSAC) method. Additionally, we drop all the simulations with a deformation D ≤ 5 × 10−4, since such deformation values are not measurable by RT-DC and are close to the perfect sphere discretized by the mesh. The final lookup tables are built by linearly interpolating the 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 558 obtained cell shapes for the cylindrical (2D axisymmetric) channel and 1206 cell shapes for the square (3D) channel to a uniform grid for fast lookup.
558 obtained cell shapes for the cylindrical (2D axisymmetric) channel and 1206 cell shapes for the square (3D) channel to a uniform grid for fast lookup.
1.4 Cell culture
The HL60/S4 cell subline (ATCC Cat# CRL-3306, RRID:CVCL_II77) was cultured in RPMI 1640 medium with 2 mM L-Glutamine (Thermo Fisher #A1049101) with 1% penicillin and streptomycin (Gibco) and 10% heat-inactivated fetal bovine serum (Sigma Aldrich, catalog no. F4135, lot no. 13C519). Cells were grown at 37 °C, with 5% CO2, at densities between 105–106 cells per mL with subculturing every 48–72 hours.1.5 Buffer production for RT-DC
Samples for RT-DC experiments were suspended in a buffer solution made from 0.594 w/w% methyl cellulose (MC; 4000 cPs, Alfa Aesar 036, 718.22, CAS#9004-67-5) dissolved in phosphate-buffered saline (PBS) without Mg2+ and Ca2+ (Gibco Dulbecco 14190144). Buffers were adjusted to have a viscosity of 25 mPa s when measured in a HAAKE Falling Ball Viscometer type C (Thermo Fisher Scientific, Dreieich, Germany) using ball number 3 at 24 °C.The rheology of the 0.6% MC-PBS solutions was measured with an Anton Paar MCR 502WESP TwinDrive rheometer (Anton Paar GmbH, Graz, Austria) at 25 °C controlled with a PTD 180 MD Peltier element (Anton Paar GmbH, Graz, Austria). At shear rates over 5.000 s−1, the solutions showed power-law behavior, and the fluid consistency coefficient was found at m = 0.4057 Pa s and the flow behavior index at n = 0.6039. For the 0.5% MC-PBS buffer in the scaling validation, we used the measured fluid consistency coefficient of 0.2671 Pa s and a flow behavior index of 0.6264. For a detailed description of the buffer rheology, see Büyükurgancı et al.21
1.6 Cell and beads measurements
Cell and beads experiments were performed with a commercially available RT-DC device (AcCellerator, Zellmechanik Dresden GmbH). The measurement principle of RT-DC is described in detail in Otto et al.4 Briefly, a microfluidic chip containing the measurement channels with a cross-section of 20 × 20 μm, that were simulated in this work, is mounted on an inverted microscope (Axiovert 200 M, ZEISS, Oberkochen, Germany) and flow is introduced with syringe pumps. Images are captured with a CMOS camera (Mikrotron, Unterschleissheim, Germany). Syringe pumps (Cetony Nemesys, Korbussen, Germany) and camera were controlled with the measurement software ShapeIn (Zellmechanik Dresden, Dresden, Germany), which analyses contours in real-time.For the beads experiments, 2.5 μL of polyacrylamide (PAAm)-beads solution (monomer concentration = 7.9%; for details, see Girardo et al.22) were resuspended in 47.5 μL of 0.6% MC-PBS and measured at a flow rate of 0.04 μL s−1.
For cell experiments, 2 mL of HL60-cell solution (5 × 105 cells mL−1) was centrifuged at 188 RCF for 4 minutes. After the supernatant was removed, the cell pellet was resuspended in 100 μL of 0.6% MC-PBS for a final cell concentration of 107 cells mL−1 and measured at 0.04 μL s−1.
In both cases, the measured sizes have been pixelation corrected (see Herold et al.16 for more details), and only cells and beads with a ratio of convex-hull area to the raw area of 1.0–1.05 are considered.23,24 This step guarantees that noisy contours that could lead to overestimated deformation values are not considered in the analysis.
2 Results
The new lookup tables are based on finite element simulations, where we indirectly sample the area-deformation space by varying the cell radius and Young's modulus. Thereby, we get for each fixed Young's modulus an isoelasticity line (see Mietke et al.12) in the area-deformation space. We begin by describing one of these numerically obtained cell shapes and show the flow field around the in silico cell and the surface stresses acting on it. Next, we validate the new LUTs by comparing to the linear elastic lookup table from Mokbel et al.13 and show that the scaling still holds. We compare the new lookup tables in the cylindrical and square channel to the previous lookup table. Following this, we show the influence of the different lookup tables on the resulting apparent Young's modulus. We conclude this section by reporting the engineering strains and surface stresses on biological cells and the relative volume error resulting from the axisymmetric channel assumption in the steady-state configuration.2.1 Cell shape and stress distribution
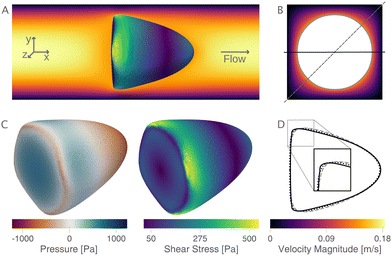
The new proposed LUTs assume a neo-Hookean hyperelastic material for biological cells and are deduced from full three-dimensional finite element simulations and two-dimensional axisymmetric simulations. In Fig. 2, we show one of the three-dimensional simulations. The in silico cell reaches a bullet-shaped stationary deformation (see Fig. 2A) due to the hydrodynamic stresses from the surrounding fluid. The stationary configuration of the cell is not rotationally symmetric. The flow profile around the cell from the front is shown in Fig. 2B. The stresses on the cell surface can be split into normal (pressure) and tangential (shear) stress contributions. Fig. 2C shows the pressure on the cell surfaces and the shear stress distribution. We subtract the average surface pressure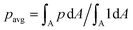 since the pressure enters the system as a gradient only and, thus, the absolute value is not meaningful. The pressure is non-symmetric, with the highest absolute value at the front of the cell. Here, we define the shear stress ‖P(σc·n)‖ where P = I − n ⊗ n is the surface projection, σc the stress tensor of the cell and n the surface normal. The peak shear stress is located in the regions closest to the channel wall.
since the pressure enters the system as a gradient only and, thus, the absolute value is not meaningful. The pressure is non-symmetric, with the highest absolute value at the front of the cell. Here, we define the shear stress ‖P(σc·n)‖ where P = I − n ⊗ n is the surface projection, σc the stress tensor of the cell and n the surface normal. The peak shear stress is located in the regions closest to the channel wall.
Only the projected area and deformation of the resulting cell shape are used for the lookup creation. In Fig. 2D, we plot this projected contour for the cylindrical channel overlaid with the projected contour in the square channel. The corresponding deformation values are Dcylindrical = 0.071 and Dsquare = 0.086. For comparison, the contour of the cell along the diagonal is shown with a dashed line.
2.2 Model and scaling validation
Next, we validate that the resulting lookup tables are – like the linear elastic LUT – bijective (no isoelasticity lines cross each other), and the scaling holds for the hyperelastic material model, the non-Newtonian shear-thinning buffer as well as the square channel geometry. Isoelasticity lines for different Young's moduli in the cylindrical channel with and without a shear-thinning buffer are shown in Fig. 3 (left). In Fig. 3 (right), the same is shown for the square channel with a shear-thinning buffer only. In both plots, the isoelasticity lines from Mokbel et al.13 for the linear material model without shear thinning, and cylindrical channel are added for comparison (dotted lines). All three lookup tables are bijective, meaning that for each area-deformation pair, there is a unique apparent Young's modulus associated. For small deformations (read small strains), the linear elastic LUT does agree with the hyperelastic material based LUTs. For stiff beads, this is the case for almost all cell sizes. Reducing the cell stiffness leads to increased divergences of the isoelasticity lines for larger beads. For soft beads, the isoelasticity lines diverge already for small bead sizes. This holds true for the cylindrical channel simulations as well as for the square channel simulations. In the case of a cylindrical channel, the isoelasticity lines flatten out for Young's moduli around 1 kPa for larger cells. In contrast, the linear elastic material predicts a higher increase in deformation. The square channel lookup table (Fig. 3 (right)) shows a similar pattern. There, the isoelasticity lines agree for stiff cells. For softer cells, the isoelasticity lines diverge already at smaller cell sizes, and the deformations are larger. For larger cells with Young's modulus ≤1.5 kPa, the isoelasticity lines seem to flatten out too, but the range in terms of numerically stable simulations is smaller, resulting in a smaller lookup table than in the cylindrical channel. Additionally, for the cylindrical channel, we investigate the influence of shear-thinning on the isoelasticity lines by comparing to the deformations in a Newtonian fluid with a fixed apparent viscosity η = 6 mPa s (see Herold et al.16 for derivation from a shear-thinning fluid). The resulting isoelasticity lines are shown again in Fig. 3 (left) as dashed lines. For smaller cells, shear thinning is negligible for all cell elasticities. Again, a Newtonian fluid results in a higher deformation for the larger cells. This leads to an underestimation of the apparent Young's modulus for larger cells. Overall, the agreement between the linear elastic and hyperelastic isoelasticity lines for small strains validates the new numerical results.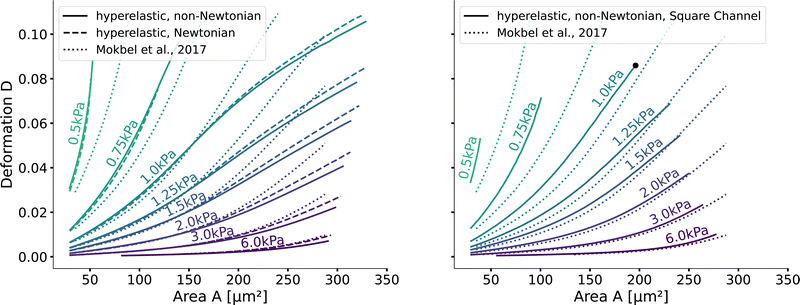 | ||
| Fig. 3 Comparison of the stationary deformation for the linear and hyperelastic cells: Isoelasticity lines for different Young's moduli E ∈ [0.5, 0.75, 1.0, 1.25, 1.5, 2.0, 3.0, 6.0] kPa for the linear elastic material model without shear-thinning (dotted, see Mokbel et al.13), the new hyperelastic material model with shear-thinning (solid) and without shear-thinning (dashed). On the (left) for the cylindrical (2D-axisymmetric) channel. On the (right) for the square (full 3D) channel geometry. The black dot corresponds to the simulation shown in Fig. 2. Parameters: L = 20 μm, Q = 0.04 μL s−1, buffer characteristics of 0.6% MC-PBS for the shear-thinning isoelasticity lines, η = 6 mPa s for the apparent viscosity of 0.6% MC-PBS in the Newtonian case. Contours of Mokbel et al.13 extracted from Wittwer et al.25 | ||
Validating the scaling discussed above12 is non-trivial, as we include the non-linear shear-thinning behavior of 0.6% MC-PBS and hyperelastic neo-Hookean material model for the cell and consider the full three-dimensional geometry. The new lookup tables are based on a channel side length L = 20 μm, a flow rate of Q = 0.04 μL s−1 and an apparent viscosity of 0.6% MC-PBS which results in η = 6 mPa s. Here, to validate the scaling numerically, we perform two in silico experiments in square channels with a side length of L′ = 30 μm, a flow rate of Q′ = 0.16 μL s−1 and with 0.5% MC-PBS and 0.6% MC-PBS, resulting in apparent viscosities 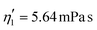 and
and 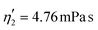 . We scaled the Young's moduli and derived the deformation values from the adapted simulations. After rescaling the area A′, the isoelasticity lines in Fig. 4 (left) agree perfectly except at the boundary, indicating that the scaling still holds at least for the most part of the LUT and only at the boundary it might become inaccurate.
. We scaled the Young's moduli and derived the deformation values from the adapted simulations. After rescaling the area A′, the isoelasticity lines in Fig. 4 (left) agree perfectly except at the boundary, indicating that the scaling still holds at least for the most part of the LUT and only at the boundary it might become inaccurate.
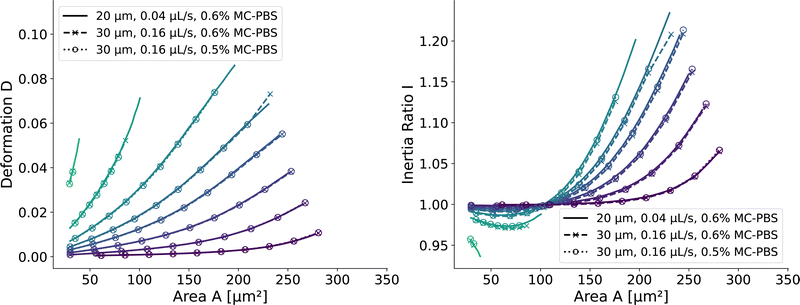 | ||
| Fig. 4 Scaling of the square channel lookup table: isoelasticity lines of the new lookup table (solid) in the square channel compared to rescaled data with a wider channel geometry and a higher flow rate (dashed), and additionally a different fluid (dotted). The isoelasticity lines and coloring are the same as in Fig. 5 (left). The Young's modulus E′ and the projected cell area A′ were scaled to match the new channel geometry, flow rate, and apparent viscosities. (left) Isoelasticity lines and rescaled isoelasticity lines for area-deformation, (right) Isoelasticity lines and rescaled isoelasticity lines for area-inertia ratio. | ||
The ratio between the two axial second moments of area is another dimensionless integral quantity to describe cell deformation, introduced in Mokbel et al.13 We use the definition of this inertia ratio I implemented in dclab,15 which for horizontally symmetric shapes is defined by
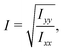 | (7) |
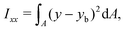 | (8) |
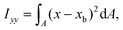 | (9) |
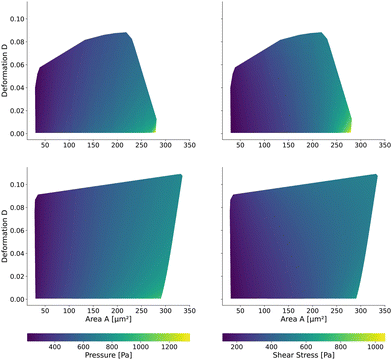
2.3 The New Lookup Tables and the Geometric Influence
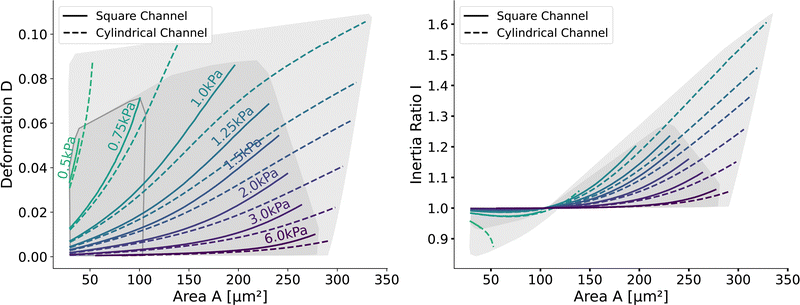
Having validated the numerical simulations and the scaling, we can construct the final lookup tables based on many simulations. As already described above, the lookup tables are based on simulations with a channel side length L = 20 μm, a flow rate of Q = 0.04 μL s−1 and 0.6% MC-PBS. The cylindrical channel simulations are numerically more stable as the confinement – the ratio between the cell diameter and channel width – is smaller, i.e., the channel width is larger to account for the changed pressure drop. For more details of the concept of equivalent channel between the square and cylindrical channel, see Mietke et al.12Fig. 5 shows the region of all simulations for the two new lookup tables in the area-deformation space as well as area-inertia ratio space. The space of the cylindrical lookup table spans [28 μm2, 335 μm2] × [0.377 kPa, 23.753 kPa] and the square channel [29 μm2, 281 μm2] × [0.469 kPa, 27.669 kPa]. Since the area is not conserved and not all radius-Young's modulus pairs are numerically stable, the resulting LUTs are not rectangular. Again, we show the isoelasticity lines for the same Young's moduli as in Fig. 3. The area where the inertia ratio of the square channel is I < 1 is enclosed in Fig. 5 (left) by the grey line.The channel geometry does have an observable influence on the deformations. On the technical side, the simulations are more stable in the axisymmetric setting, as discussed above, resulting in a larger lookup table. For small cells as well as stiff cells, the isoelasticity lines from the two new LUTs overlay. But for larger and softer cells, the isoelasticity lines of the cylindrical and square channel diverge. As the deformation is smaller in the cylindrical channel, the cylindrical lookup table underestimates the apparent Young's modulus.
2.4 Applying the new LUTs to Measurements
With the validated new lookup tables, it is possible to extract the apparent Young's modulus from RT-DC measurements. To demonstrate this, we measured poly-acrylamide (PAAm) hydrogel beads22 and HL60 cells (see Methods). The kernel density estimations of the measured bead and cell distributions in the area-deformation plot are shown in Fig. 6 (left). All three measurements fall within the region of definition of both new LUTs, with a few sample points outside the square channel LUT (resulting in omitted data points). The resulting apparent Young's moduli are shown in Fig. 6 (right). The cylindrical LUT predicts similar elasticity values and distribution than the linear elastic LUT of Mokbel et al.13 For small beads, the new cylindrical channel LUT predicts a higher Young's modulus compared to the linear elastic LUT, whereas for the larger beads the Young's moduli decrease (see the gray dashed lines in Fig. 6 (right)). This is due to the non-linear material response discussed above and seen in the flattening isoelasticity lines. For the HL60 cells, which have a higher deformation than the small beads, the stiffness increases compared to the linear elastic LUT too. Comparing the two new LUTs, the square channel LUT predicts higher Young's moduli for all three measurements. This holds true compared to the old linear elastic material model in the cylindrical channel. At the same time, the shape of the distribution changes compared to the cylindrical LUT, supporting the importance of the channel geometry.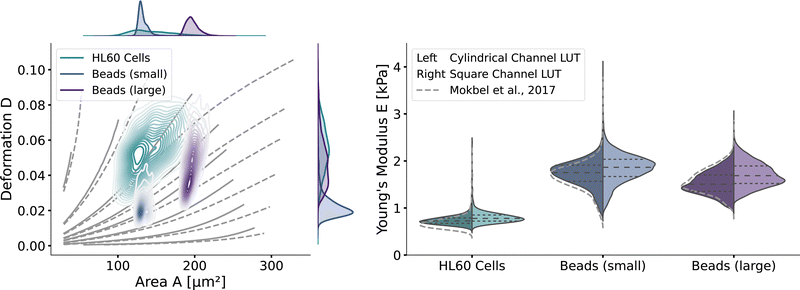 | ||
| Fig. 6 RT-DC measurements of PAAm beads and HL60: (left) The distributions of PAAm beads with two different sizes and HL60 cells from separate measurements (by bivariate kernel density estimation). The marginal distributions for area and deformation are shown on the top and on the right. The isoelasticity lines from Fig. 5 (left) are shown in grey. (right) Violin plots of the estimated Young's modulus from the three measurements. The resulting Young's modulus distribution with the cylindrical LUT is on the left in each violin, for the square channel LUT on the right. The dashed lines within the violins are the quartiles (25%/50%/75%). The grey dashed lines indicate the Young's modulus distribution from the cylindrical LUT of Mokbel et al.13 | ||
Remarkably, the HL60 cells show a greater spread of the data points in the area-deformation plot than the PAAm beads but a much narrower distribution of Young's moduli for all types of LUTs. On closer inspection, the HL60 fall along the trajectory of a few isoelasticity lines, while the beads cross several lines. This highlights an important use case of the LUTs: when comparing samples of different size in RT-DC, the deformation parameter alone is not sufficient because it is dependent on the area. In our example it shows that the HL60 are quite homogeneous in Young's modulus compared to the PAAm beads even though they are more heterogeneous in size. The heterogeneity of the Young's modulus of the PAAm beads is a consequence of the production process and is discussed in more detail in Girardo et al.22
2.5 Strain and stresses of the cells
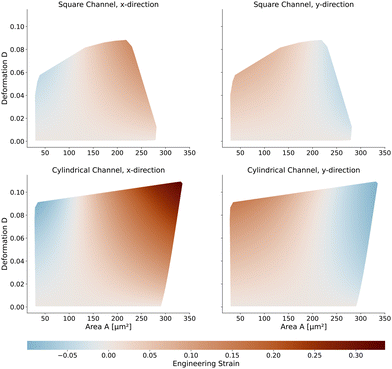
Next, we will look at the strain and stresses on the cell surface. Deformation as a measure of strain approximates the resulting shapes by a single number. In Fig. 7, we plot the strains along the horizontal x-axis and the vertical y-axis to get a better understanding of the deformed shapes. Here we use the engineering strain defined as (l − l0)/l0 and (h − h0)/h0 where l and h are the maximum extensions of the cell in x and y direction. l0 and h0 are the diameter of the cell in the undeformed state with l0 = h0 = 2R. Small cells are horizontally compressed but elongated vertically. Larger cells are exposed to higher shear force, resulting in a more stretched shape along the flow direction and compressed in the y-axis. The strains of the cells in the square channel are in the range of [−4.5%, 13%], in the cylindrical channel in the range of [−9.9%, 33.6%].The maximum stress components acting on the cells are shown in Fig. 8 for the square and cylindrical channel. The shear stresses are in the range of [117 Pa, 1058 Pa] in the square channel and [118 Pa, 624 Pa] in the cylindrical channel, again increasing with the cell size. The largest cells with a large Young's modulus are exposed to the highest shear stress, as their surface is closest to the channel wall. The maximum pressure is in the range of [226 Pa, 1346 Pa] in the square channel and [220 Pa, 1022 Pa] in the cylindrical channel, respectively. We subtract the average surface pressure pavg again (see above).
2.6 Volume estimation error
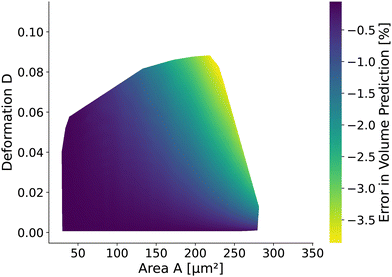
The volume of cells flowing through the microfluidic chip is a valuable cell feature. It is approximated by revolving the detected contour of the stationary shape and pixelation corrected similar to the cell deformation and area (see Methods). The rotational-symmetry assumption is only valid for small cells, perceiving the almost axisymmetric flow field in the center of the channel. The absolute value of the relative error is below 1% for cells with a radius R < 6.2 μm (i.e., confinement of less than 62%.) and any Young's modulus considered. For larger cells, the relative error depends on the Young's modulus and the cell size. Fig. 9 shows the relative error based on measured area and deformation. The relative error εvol is defined by εvol = 100 × (Vrot/V0 − 1) where Vrot is the approximated volume from revolving the contour of the in silico cell20,26 with radius R and V0 is the volume of a sphere with radius R. Interestingly, the error is only in the range of [−3.87%, −0.06%]. The volume of small cells is underestimated only slightly compared to the actual cell volume independently of the deformation and thus apparent Young's modulus. For larger cells, the influence of the deformation on the volume error increases.3 Discussion and conclusion
This work presents two new lookup tables for RT-DC for cylindrical and square channels based on the neo-Hookean hyperelastic material model. We validate the numerical model by comparing to the linear elastic LUT of Mokbel et al.13 in the small strain regime. We discuss the influence of different material models, the shear-thinning behavior of the fluid, and the channel geometry and reveal different material responses. We find that the scaling still holds for the hyperelastic material even with a shear-thinning non-Newtonian fluid. In consequence, the proposed LUTs can be used for a vast array of different channel sizes, buffer viscosities, and flow rates. Shear-thinning does affect the isoelasticity lines for large cells only. Compared to the existing linear elastic material LUT, the more accurate hyperelastic square channel LUT predicts stiffer cells, especially for small, highly deformed cells. However, the square channel LUT has a limited range of possible cell sizes and deformations due to the smaller region of numerical stable simulations. On the other hand, the cylindrical channel LUT has a similar size as the linear elastic material LUT. Depending on the position of the measurements in the area-deformation space, the distribution of the Young's modulus is altered for both proposed LUTs compared to the existing one. For both proposed LUTs, we report the strain and surface stresses of the cells depending on the projected cell area and deformation. Both new lookup tables are available in dclab15 and freely available in Wittwer et al.,27 extending the predictive power to derive the apparent Young's modulus of any biological cell type based on the given model assumptions. At the same time, the proposed LUTs complement the work in Wittwer et al.20 to derive the viscoelastic response of biological cells in a square RT-DC geometry. The reported findings and freely available data are not only applicable to RT-DC, but to similar flow cytometry setups as well. A lookup based on area and deformation ignores the actual shape of the measured cells. Extending the search space by considering the contour shapes would considerably improve the predictive power of RT-DC and could take into account different material models for different cell types and beads. However, this leads to a significant increase in parameters and is thus left for future studies.Data availability statement
The data that support the findings of this study are openly available27 on figshare at https://doi.org/10.6084/m9.figshare.20630940.Author contributions
Lucas D. Wittwer: conceptualization (equal); data curation (lead); formal analysis (lead); software (equal); visualization (lead); writing – original draft (lead); writing – review and editing (equal). Felix Reichel: data curation (supporting); writing – original draft (supporting); writing – review and editing (equal). Paul Müller: data curation (supporting); software (equal); writing – review and editing (equal). Jochen Guck: conceptualization (equal); funding acquisition (equal); supervision (equal); writing – review and editing (equal). Sebastian Aland: conceptualization (equal); funding acquisition (equal); supervision (equal); writing – review and editing (equal).Conflicts of interest
J. G. and P. M. are co-founders of Rivercyte GmbH.Acknowledgements
Simulations were performed at the Center for Information Services and High-Performance Computing (ZIH) at TU Dresden. L. W. acknowledges the COMSOL support staff for their support. S. A. acknowledges support from the German Research Foundation DFG (grant AL1705/3-2) and support from the Saxon Ministry for Science and Art (SMWK MatEnUm-2 and EUProfil). The authors acknowledge the financial support through the base funding of the Max Planck Society to J. G. We thank Christine Schweitzer and Cornelia Liebers for help with cell culture, and Ruchi Goswami for the production of PAAm beads. Open Access funding provided by the Max Planck Society.Notes and references
- N. Toepfner, C. Herold, O. Otto, P. Rosendahl, A. Jacobi, M. Kräter, J. Stächele, L. Menschner, M. Herbig, L. Ciuffreda, L. Ranford-Cartwright, M. Grzybek, Ü. Coskun, E. Reithuber, G. Garriss, P. Mellroth, B. Henriques-Normark, N. Tregay, M. Suttorp, M. Bornhäuser, E. R. Chilvers, R. Berner and J. Guck, eLife, 2018, 7, e29213 CrossRef PubMed.
- M. Koch, K. E. Wright, O. Otto, M. Herbig, N. D. Salinas, N. H. Tolia, T. J. Satchwell, J. Guck, N. J. Brooks and J. Baum, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 4225–4230 CrossRef CAS PubMed.
- M. Kubánková, B. Hohberger, J. Hoffmanns, J. Fürst, M. Herrmann, J. Guck and M. Kräter, Biophys. J., 2021, 120, 2838–2847 CrossRef PubMed.
- O. Otto, P. Rosendahl, A. Mietke, S. Golfier, C. Herold, D. Klaue, S. Girardo, S. Pagliara, A. Ekpenyong, A. Jacobi, M. Wobus, N. Töpfner, U. F. Keyser, J. Mansfeld, E. Fischer-Friedrich and J. Guck, Nat. Methods, 2015, 12, 199–202 CrossRef CAS PubMed.
- M. Urbanska, M. Winzi, K. Neumann, S. Abuhattum, P. Rosendahl, P. Müller, A. Taubenberger, K. Anastassiadis and J. Guck, Biophys. J., 2018, 114, 516a–517a CrossRef.
- R. H. Pires, T. H. Dau, E. Manu, N. Shree and O. Otto, Physiological reports, 2022, 10, e15171 CrossRef CAS PubMed.
- P. Rosendahl, K. Plak, A. Jacobi, M. Kraeter, N. Toepfner, O. Otto, C. Herold, M. Winzi, M. Herbig, Y. Ge, S. Girardo, K. Wagner, B. Baum and J. Guck, Nat. Methods, 2018, 15, 355–358 CrossRef CAS PubMed.
- S. Golfier, P. Rosendahl, A. Mietke, M. Herbig, J. Guck and O. Otto, Cytoskeleton, 2017, 74, 283–296 CrossRef CAS PubMed.
- M. Urbanska, H. E. Muñoz, J. Shaw Bagnall, O. Otto, S. R. Manalis, D. Di Carlo and J. Guck, Nat. Methods, 2020, 17, 587–593 CrossRef CAS PubMed.
- M. C. Munder, D. Midtvedt, T. Franzmann, E. Nüske, O. Otto, M. Herbig, E. Ulbricht, P. Müller, A. Taubenberger, S. Maharana, L. Malinovska, D. Richter, J. Guck, V. Zaburdaev and S. Alberti, eLife, 2016, 5, e09347 CrossRef PubMed.
- M. Kräter, S. Abuhattum, D. Soteriou, A. Jacobi, T. Krüger, J. Guck and M. Herbig, Adv. Sci., 2021, 2003743 CrossRef PubMed.
- A. Mietke, O. Otto, S. Girardo, P. Rosendahl, A. Taubenberger, S. Golfier, E. Ulbricht, S. Aland, J. Guck and E. Fischer-Friedrich, Biophys. J., 2015, 109, 2023–2036 CrossRef CAS PubMed.
- M. Mokbel, D. Mokbel, A. Mietke, N. Träber, S. Girardo, O. Otto, J. Guck and S. Aland, ACS Biomater. Sci. Eng., 2017, 3, 2962–2973 CrossRef CAS PubMed.
- F. Reichel, M. Kräter, K. Peikert, H. Glaß, P. Rosendahl, M. Herbig, A. Rivera Prieto, A. Kihm, G. Bosman and L. Kaestner, et al. , Front. Physiol., 2022, 556 Search PubMed.
- P. Müller, M. Herbig, E. O’Connell, P. Rosendahl, M. Schlögel and J. Guck, dclab version 0.34.1: Python library for the post-measurement analysis of real-time deformability cytometry data sets, [Software], 2015, https://github.com/DC-analysis/dclab Search PubMed.
- C. Herold, Mapping of Deformation to Apparent Young's Modulus in Real-Time Deformability Cytometry, arXiv, 2017 DOI:10.48550/arXiv.1704.00572.
- B. L. Micklavzina, A. E. Metaxas and C. S. Dutcher, Soft Matter, 2020, 16, 5273–5281 RSC.
- B. Fregin, F. Czerwinski, D. Biedenweg, S. Girardo, S. Gross, K. Aurich and O. Otto, Nat. Commun., 2019, 10, 415 CrossRef CAS PubMed.
- R. Schuster and O. Marti, J. Phys. D: Appl. Phys., 2021, 54, 125401 CrossRef.
- L. D. Wittwer, F. Reichel and S. Aland, in Modeling of Mass Transport Processes in Biological Media, ed. S. Becker, A. Kuznetsov, F. de Monte, G. Pontrelli and D. Zhao, Elsevier, 2022 Search PubMed.
- B. Büyükurganc, S. K. Basu, M. Neuner, J. Guck, A. Wierschem and F. Reichel, Soft Matter, 2023 10.1039/D2SM01515C.
- S. Girardo, N. Träber, K. Wagner, G. Cojoc, C. Herold, R. Goswami, R. Schlüßler, S. Abuhattum, A. Taubenberger, F. Reichel, D. Mokbel, M. Herbig, M. Schürmann, P. Müller, T. Heida, A. Jacobi, E. Ulbricht, J. Thiele, C. Werner and J. Guck, J. Mater. Chem. B Mater. Biol. Med, 2018, 6, 6245–6261 RSC.
- M. Urbanska, P. Rosendahl, M. Kräter and J. Guck, Methods Cell Biol., 2018, 147, 175–198 Search PubMed.
- M. Herbig, M. Kräter, K. Plak, P. Müller, J. Guck and O. Otto, Methods Mol. Biol., 2018, 1678, 347–369 CrossRef CAS PubMed.
- L. D. Wittwer, P. Müller, D. Mokbel, M. Mokbel, J. Guck and S. Aland, Finite element simulation data for the computation of the Young's modulus in real-time deformability cytometry, 2020.
- M. Herbig, A. Mietke, P. Müller and O. Otto, Biomicrofluidics, 2018, 12, 042214 CrossRef CAS PubMed.
- L. D. Wittwer, P. Müller, F. Reichel, S. Aland and J. Guck, Hyperelastic Lookup Table for Real-Time Deformability Cytometry (RT-DC), 2022.
| This journal is © The Royal Society of Chemistry 2023 |