A mechanistic understanding of microcolony morphogenesis: coexistence of mobile and sessile aggregates

Abstract

Most bacteria in the natural environment self-organize into collective phases such as cell clusters, swarms, patterned colonies, or biofilms. Several intrinsic and extrinsic factors, such as growth, motion, and physicochemical interactions, govern the occurrence of different phases and their coexistence. Hence, predicting the conditions under which a collective phase emerges due to individual-level interactions is crucial. Here we develop a particle-based biophysical model of bacterial cells and self-secreted extracellular polymeric substances (EPS) to decipher the interplay of growth, motility-mediated dispersal, and mechanical interactions during microcolony morphogenesis. We show that the microcolony dynamics and architecture significantly vary depending upon the heterogeneous EPS production. In particular, microcolony shows the coexistence of both motile and sessile aggregates rendering a transition towards biofilm formation. We identified that the interplay of differential dispersion and the mechanical interactions among the components of the colony determines the fate of the colony morphology. Our results provide a significant understanding of the mechano-self-regulation during biofilm morphogenesis and open up possibilities of designing experiments to test the predictions.

---

1 Introduction

Self-organization into multicellular communities such as swarms or biofilm-like aggregates is a common trait in most bacterial species in nature.^1–11 While developing a multicellular organization, various processes such as cell attachment to a surface, cell growth, division, differentiation, and secretion of extracellular polymeric substances (EPS) contribute. Furthermore, cell motility and dispersion, owing to physicochemical interaction among the cells and with the surrounding, drives the spatiotemporal dynamics of the growing colony.^12,13 In a microbial biofilm, many cells are embedded in a self-produced matrix of EPS containing polysaccharides, amyloid proteins, eDNA, etc.^14,15 Biofilms formation is a route toward structural integrity, morphological diversity, and protection of the cell complex from adverse environmental conditions.^16–19 Biofilm-like aggregates cause many diseases and inflammation in animal tissues and damage in industrial applications.^20,21 The physical interactions of the bacterial cells among themselves and with the EPS significantly influence and controls the structure and dynamics of growing biofilms.^22–26

Over the years, several experiments have provided many insights into the individual and colony level dynamics in different bacteria.^27–32 Besides, many theoretical and computational models were developed to capture various aspects of the construction of biofilm-like multicellular organization.^{22,23,33–38} Majority of these models followed continuum-based approaches. For example, how EPS contributes to the biofilm expansions and heterogeneous patterning are discussed in^28,39–41 with continuum-based models. On the other hand, in a dense bacterial colony, where mechanical interactions among the bacterial cells and the surroundings appear to be a crucial factor in driving colony expansion and morphogenesis, alternative approaches have been employed to gain insights into the mesoscopic level interactions among the components. In this context, several studies have utilized agent-based/particle-based models or a hybrid type model which can capture the individual-level interactions among the bacterial cells inside a colony.^{22,23,34,42,43} Although these pre-existing studies illuminate several aspects of the occurrence of collective phases, considerable effort is needed to understand the influence of the two significant aspects of a growing bacterial colony: cell motility and physicochemical properties of self-produced EPS. In particular, how and to what extent these two aspects in conjugation with each other regulate the microcolony morphogenesis is yet to be explored.

Motility force allows individual cells to propel themselves in a specific direction. While, in certain conditions, a group of motile cells can exhibit long-range collective motions in the form of swirls or whirls,^44–46 one of the characteristic features of developing a biofilm-like structure is the secretion of extracellular polymeric substances (EPS) in a growing colony.^{2,28,40,47–50} The existing literature suggests that the synthesis and secretion of EPS in a growing colony is a heterogeneous process.¹² It depends upon the local nutrient availability.^41,51,52 Apart from the heterogeneity in EPS production, the physicochemical property of EPS can significantly control biofilm morphogenesis. These two properties: motility and presence of EPS, appear to be counteracting in a growing colony. Therefore, learning the interplay of motility and the self-produced EPS is one of the key issues which still needs considerable effort to gain insights into the spatiotemporal dynamics of a developing biofilm.

Here, we utilized a particle-based model of motile rod-shaped bacterial cells and self-produced EPS to study the spatiotemporal dynamics of a growing and expanding bacterial colony. We observe that the physicochemical properties of the self-secreted EPS and the local nutrient availability can regulate the spatial morphology and dynamics in a growing multicellular colony. In particular, the presence of sticky EPS can facilitate the coexistence of motile and sessile aggregates within the colony rendering to the biofilm transition. The heterogeneity of EPS production across the colony profoundly impacts the coexistence of such motile and sessile cell aggregates attributing that cells do not necessarily need to be non-motile in type to develop biofilm-like structures. Instead, the heterogeneous presence of the self-produced EPS is a crucial factor. The differential dispersion among the components thereby determines the outcome of colony morphology. The present study provides a systematic understanding of the mechanoregulation of colony morphogenesis in conjugation with cell motility and the physical properties of self-secreted extracellular polymeric substances.

2 Model and method

We consider an individual-based model of bacterial cells and self-secreted extracellular polymeric substances (EPS) in two dimensions.^8,22,23 Each bacterial cell is modeled as a spherocylindrical particle with fixed diameter d₀ and variable length L = l + d₀, where l corresponds to the cylindrical length of the particle. The position and the orientation of an individual cell are given by a spatial coordinate r⃑(x, y) and a unit vector u⃑(u_x, u_y). We discretize a 2D simulation box (L_x × L_y) into a certain number of square grids and keep the nutrient concentration fixed at C₀ on each grid point at the beginning. We have used a sizable simulation box to avoid any boundary effect, ensuring that no bacterial cell can cross the boundary during the course of a simulation. Besides, the nutrient concentration is always kept at a fixed value (C₀) at the edges of the simulation box, which acts as a nutrient reservoir.

At first, a single bacterial cell is inoculated around the center of the simulation box. The cell grows along its major axis by consuming the local nutrient from the media. The dispersion of the nutrient in each grid point (C(x, y)) obeys the diffusion equation having a sink term as follows

where D is the diffusion constant of the nutrients, x_i and y_i are the spatial coordinates, A_i = πr₀²+ 2r₀l_i is the area, r₀ = d₀/2 is the radius of the end caps, and l_i is the length of the ith cell. Here, the consumption of the diffusing nutrient takes place at a rate kf(C) per unit biomass density, where f(C) is a monotonically increasing dimensionless function. In our simulations, we consider f(C) = C/(1 + C), a Monod function with a half-saturation constant equal to 1 (in arbitrary units). The linear growth of each cell obeys the equation: dl_i/dt = ϕ × (A_i/Ā) × f(C(x_i, y_i)), where ϕ is the linear growth rate of the cell and Ā = πr₀²+ (3/2)r₀l_c is the average cell area.^22,23,34

In a growing bacterial colony, in general, once a cell reaches a critical length l_c, it splits into two daughter cells, at a rate k_div, with daughter cells having slightly random orientation compared to the mother cell. This randomness in orientation assimilates the effect of various deformities like the roughness of the agar surface, slight bending of the cells, etc. This stochasticity also confirms that the cell will not form a long filament-like structure. However, quite interestingly, some species depending on environmental conditions, show asymmetric division in their growing lifestyle.³² In our model, we have also incorporated the asymmetric division in a straightforward way by defining a quantity named Division, taking the numbers from a Gaussian distribution as 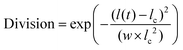, where w = 0.0055, l(t) is the time-dependent length, and l_c is the critical length of the cell. We have put a condition that the cell will divide if and only if Division > rand(), where rand() is the random number between 0 to 1. Moreover, depending on the w values, the standard deviation (STD) of the distribution will change. Fig. S1 (ESI†) shows the distribution of division for different values of w, which are 10 times larger and smaller than w = 0.0055. For a large value of w (w = 0.055), the STD of the distribution is wide, so the cell can divide in a wide range of l(t), which is unrealistic. On the other hand, for a small value of w (w = 0.00055), the scenario is the other way around. So we have chosen an intermediate value of (w = 0.0055) such that most of the cells can divide at l(t) = l_c, but there is a finite probability for dividing the cells at l_c > l(t) ⪅ 5.6 or 4.4 ⪆ l(t) < l_c. In addition, each bacterial cell can secrete EPS to the nearby region depending on the local nutrient concentration as reported in the prior experimental studies.^41,51,52 The consumption of nutrients by the cells leads to a depletion of local nutrient content. Once the local nutrient concentration C(x, y) reaches a certain low level (C*), it triggers EPS secretion, and cells commence EPS production with a rate k_eps in their surrounding medium. However, our simulation model does not have an explicit natural EPS degradation. Instead, to avert the excessive production of EPS locally, we impose a condition on the EPS production by considering that it starts when the local cell area density reaches a certain threshold and stops once the local EPS area density reaches a maximum concentration.²³ However, it is impossible to determine the conformation of individual EPS on the scale of the bacterial colony. Therefore, we have modeled the EPS as spherical particles with a radius equal to the radius of gyration.^27,53 We have chosen a radius that is half of a bacterial cell's radius but larger than the actual size of the EPS. So one can think of a single sphere as the assembly of EPS particles. Even smaller size of EPS qualitatively provides similar mechanoregulation as discussed earlier in Ref.23 However, a relatively larger size of EPS, as taken, reduces a huge computational cost.

The mechanical interaction between cell–cell, EPS–EPS, and cell–EPS is repulsive (F_rf), which is following the Hertzian theory of elastic contact^6,11 if there are spatial overlaps between them. The repulsive force between two spherocylindrical rods is assumed to be the force between two spheres placed along the major axis at such positions that their distance is minimal.^23,33 The repulsive force has been modeled by the expression: F_rf = Ed^1/2₀h^3/2, where E is the elastic modulus of the cells and h = d₀ − r represents the overlap between two interacting cells, where r corresponds to the closest distance of the approach between the two cells.^{7,8,22,23,33,34,44} Similarly, a cell and EPS particle will experience repulsive mechanical force if the closest distance of approach between them is lesser than the sum of the radii of the cell and the EPS particle. However, in our model, to mimic the sticky nature of the EPS to the cell surface, we have introduced a short-range attractive force (F_af) between them.^{12,28,51,54,55} The weak attractive interaction between cell and EPS is modeled by the attractive part of the Lennard-Jones (L-J) potential⁵⁶ as F_af = − 24εd⁶_eff/r⁷ with the range of this attraction is r_cut = 2.5d_eff where d_eff = (d^cell₀ + d^eps₀)/2 and ε is the strength of attraction. So, if there are any overlaps between the particles, they will experience a resultant repulsive force (F_rf). However, only EPS and cells will sense an attractive force (F_af) provided they are in certain cut-off distances (r_cut). Apart from the attractive and repulsive forces, each cell is equipped with a self-propulsive force (F_mf) along the cell's major axis. However, the exact generic functional form of the self-propulsion force is not precisely known. Furthermore, to study various biologically relevant properties, the motility force can be modeled in different ways, such as local density-dependent motility force in the case of quorum-sensing,^9,57 aspect ratio-dependent motility force for swarming motion,⁴⁴etc. For simplicity, we have taken a constant term for motility force, i.e., F_mf = f_mot which physically makes them active^58,59 in nature. Besides, each particle experiences a random force ζ from the surrounding medium. It is taken from a uniform distribution within a range − 10⁻³ Pa μm² to + 10⁻³ Pa μm². The schematic representation of the entire model is demonstrated in Fig. 1.

Fig. 1 (a) A schematic representation of spherocylindrical cell with diameter d₀ and cylindrical length l. Cells can grow as a function of time at a particular rate. It is more likely to split into two daughter cells when it reaches to a critical length and there is a random kick in their new positions. (b) Coil-like polymeric EPS has been modeled by spherical particles. (c) Repulsive mechanical interaction between two rod-shaped cells. (d) EPS-EPS and cell-EPS are interacting with a repulsive interaction if there are spatial overlaps. Cell-EPS are interacting via short-range attractive force if they are in a certain cut-off distance. Motility force acts along the long axis of the cell.

In our model, each particle follows over-damped dynamics, i.e., the medium viscosity dominates over the inertia. It suggests that the linear and the angular velocities are proportional to the force and the torque experienced by the particle, respectively. Therefore, the equation of motion of each particle can be written as

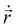where , η, ω, and τ are the linear velocity, friction coefficient per unit length, angular velocity, and torque, respectively. Each agent follows the same equation of motion, except for EPS particle F_mf = 0, as they are non-motile. Here, we are not interested in any temperature-dependent biofilm morphogenesis. We have chosen the value of ζ within the mentioned range so that the particles in our model can feel very weak randomness in their motion. To study the temperature-dependent biofilm phenomena, one should consider the Brownian dynamics simulation with a white noise that follows the fluctuation-dissipation theorem, i.e., 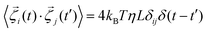. Here k_B and T denote the Boltzman constant and temperature, respectively. The particle's new positions and velocities are determined by solving the equations of motion using the simple Euler method^60,61 along with solving the diffusion equation for the nutrients. Due to the abundance of nutrients at the colony front, the cells will consume more nutrients and divide rapidly compared to the colony's center, which implies the colony will always grow with time. In our simulations, we have set a condition that if the number of agents (cells + EPS) reaches a certain number N_max = 25 000, the colony's growth will stop. This condition also ensures that within the simulation time, the front of the colony will never reach the boundary of the simulation box. In the remainder of the paper, length and time are re-scaled by the diameter of the cell (d₀) and 1/cell division rate (1/k_div) respectively to make them dimensionless. Table S1 in ESI† contains the values of all the parameters and the constants used in our simulation.

3 Results and discussion

The present study focuses on the microcolony morphogenesis facilitated by the presence of self-produced EPS, rendering towards transitions from a colony of motile cells to biofilm-like aggregate motivated by the existing experimental studies.³⁰ To get a mechanistic understanding, we consider a particle-based model of bacterial cells and explicit EPS and perform computer simulations starting from a single bacterial cell developing a multicellular spatial organization. We have investigated three significant features which influence a growing bacterial colony: (i) physicochemical property of EPS: weakly attractive/sticky in nature, (ii) self-propulsion force/cell motility, and (iii) nutrient-dependent cell-growth and EPS production. In response to the interplay of these factors, the morphology and spatiotemporal dynamics of a growing colony distinctly vary.

Sticky EPS facilitates biofilm transition rendering coexistence of motile and sessile aggregates

We begin our study by considering that an individual cell has self-propulsion ability; it elongates utilizing the available local nutrients and replicates when it reaches a threshold cell length. Additionally, each cell has a probability of secreting EPS in the surrounding media depending upon the local nutrient level, and those EPS are weakly attractive to the bacterial cells. A snapshot of a simulated growing colony is depicted in Fig. 2(a) at a sufficiently long time (tk_div = 30.0) for cells having constant motility force f_mot = 500 Pa μm², EPS production rate k_eps = 1.0 h⁻¹ and for a moderate initial nutrient concentration C₀ = 3.0 fg μm³. As given in Table S1 in ESI,† all the other parameters are kept the same throughout the text unless otherwise mentioned. The spatial organization of cells and EPS particles corresponding to Fig. 2(a) is determined by calculating the radial density of the cells and EPS particles and depicted in Fig. 2(b). To estimate the radial density, we have first determined the distance of each particle (cell and EPS) from the center of the colony. By plotting the histogram of these distances and subsequently fitting the histogram using a Kernel Density Estimation (KDE) plot,⁶² we obtain the radial density of the particles as a function of the distance from the center of the colony. The radial density plot shows the presence of both cells and EPS particles in the colony's interior, whereas a thin rim of only cells is observed at the periphery of the growing colony. Corresponding video (Video S1, ESI†) of the simulated colony demonstrates that cells grow, divide, move, secrete EPS in the nearby area depending upon the local accessibility of the nutrients and interact through mechanical forces to self-organize. The self-secreted EPS being a bit sticky, can self-regulate the spatiotemporal organization and movement of the components of a growing colony. The Video S1 (ESI†) reveals the presence of apparently distinct phases of sessile aggregates and some motile cells within the colony's interior and mobile phases (only cells retaining their motile state) at the expanding periphery. The existence of mixed phases in a growing colony attributes to biofilm morphogenesis.

Fig. 2 (a) A time snap of simulated colony of a growing bacteria at a long time tk_div = 30.0 in the presence of self-secreted sticky EPS for an initial nutrient concentration C₀ = 3.0 fg μm³ and cell motility force f_mot = 500 Pa μm². Spherocylindrical bacterial cells and spherical EPS are represented in cyan and red color respectively. Peripheral cells remains in motile state, but the interior cells have initiated to transform into sessile state (almost immobilized) in response to the interaction with the sticky EPS. The gray line represents the scale bar which corresponds to 20.0/d₀ (in length unit). (b) The radial density profile of the cells and EPS particles as a function of the distance from the center of the simulated colony determined for the Fig. 2(a). EPS particles reside mostly in the interior of the colony mixed with cells and a peripheral rim of only motile cells are observed.

In order to quantify the spatial heterogeneity within the growing colony consisting both mobile and sessile aggregates, we determine the mean squared displacement (MSD) of individual cells. For dispersal of a particle, MSD is defined as MSD (r²(τ)) = 〈|r⃑(t + τ) − r⃑(t)|²〉_t, where τ is the lag time, r⃑ is the position of the cell, and angular brackets denote the time average. In general, MSD can be fitted with a power-law as r²(τ) ∼ τ^β, where β is called MSD exponent. The time profiles of MSD and MSD exponents allow us to characterize the type of dispersion i.e., how fast or slow the particles are spreading in the space. β = 1 indicates the standard diffusion, β < 1 implies the sub-diffusion, and β > 1 specifies the super-diffusion. Since, in a growing colony, individual bacterial life span varies with time, it is not straightforward to calculate the MSD. We strategically determine the MSD by first considering a circle about the center of the colony for a particular radius (r/d₀ = 60). After a specific time (tk_div = 26.8), as the colony expands, we track those bacteria which belong to this particular radius in that period. We divide the lag time into two intervals with τ₁k_div = (0–0.2), defined as short time lag, and τ₂k_div = (0.2–0.4), defined as large time lag, to observe the different time scale behavior in observed MSD values.

Fig. 3(a and b) show the MSD as a function of lag time for 10 cells and distribution of MSD exponents for all the cells of the colony in short lag time τ₁k_div((0–0.2)) respectively. From these figures, it is clear that most cells show super-diffusion in a short time lag τ₁k_div. On the other hand, Fig. 3(c and d) depict the MSD of the 10 cells for a large lag time τ₂k_div((0.2–0.4)) which reveals the presence of both sub and super diffusion of the cells respectively. The distribution of MSD exponents of all the cells determined for large lag-time τ₂k_div as demonstrated in Fig. 3(e) also complement the fact that for a large time lag τ₂k_div, there are co-existence of cells with sub and super diffusion. As apparent from the Fig. 2 and 3(e) along with the corresponding Video S1 (ESI†), we observe that there are two dynamic phases of bacteria, i.e., the periphery of the colony cells are motile and at the center of the colony, they are undergoing a transition to a biofilm with the assistance of embedded EPS particles.

Fig. 3 (a) MSD as a function of lag time for 10 cells from the colony and (b) the distribution of MSD exponents for all of the cells in short lag time τ₁k_div. The time profiles of MSD for (c) sub-diffusive and (d) super-diffusive cells respectively with longer lag time τ₂k_div. Here we have shown 10 trajectories for both the cases. Distribution of MSD exponents of cells in presence of (e) sticky EPS and (f) in absence EPS respectively for a longer lag time τ₂k_div. For sticky EPS, there is a co-existence of super and sub-diffusive cells. But in the absence of any EPS, almost all of the cells in a colony display super-diffusion. In (a, c and d) scatter points and dotted lines represent the simulated data and fitted data respectively while the black solid line indicates the standard diffusion (slope = 1) which acts as a reference line.

To get a better insight into the EPS profile of the colony, we have determined the number of EPS particles as a function of time for the whole colony and a circular region within the colony interior. Here the circular region corresponds to the region we used for the MSD calculation. We have scaled the number of EPS between (0–1) for both cases. Fig. S2(a and b) (ESI†) represent the number of EPS particles as a function of time for the whole colony and the particular circular region, respectively. Due to the spontaneous secretion of the EPS into the medium, the EPS profile for the whole colony is an increasing function of time. On the other hand, due to the limited available space in two dimensions and local EPS density-dependent termination of EPS production, the EPS profile for the circular interior region of the colony starts to saturate in longer times. These observations are qualitatively well corroborated with the previous experimental findings in the case of an early stage of the biofilm.^63,64

In general, non-interacting active Brownian particles, in the presence of a homogeneous medium, show super diffusion at a short time scale and normal diffusion at a much larger time scale.^65,66 The super diffusion is mainly mediated by the activeness of the particles that provide the directed motion at a short time scale. On the other hand, over a long period, the orientation and direction of the particles are randomized due to their rotational motion, which bestows normal diffusion. However, in our simulations, the motile cells interact with each other and with the EPS, and the medium is no longer homogeneous due to the presence of EPS. Under these conditions, the bacterial cells show super-diffusion at a short lag time scale, and super and sub-diffusive cells coexist at a longer lag time. Self-secreting sticky EPS mainly mediates the sub-diffusion.

At this point, we simulated a growing colony in the absence of EPS production keeping all the other parameters as same as used in Fig. 2. Fig. 3(f) manifests the distribution of MSD exponents for a simulated colony in the absence of EPS production for a large lag time τ₂k_div. We observe that all the bacterial cells show super-diffusion suggesting cell motility mediated fast dispersal.

We extended our investigation on how EPS production controls the dispersion of the cells within the growing colony, by performing simulations for an increasing values of EPS production rate k_eps as: 3.0, 5.0, 7.0, and 10.0 h⁻¹. We evaluated the fraction of cells showing sub-diffusion by the ratio of the number of sub-diffusive cells and the total cells present within the circle (as discussed earlier). Fig. 4(a) represents the bar plot of the fraction of sub-diffusive cells as a function of k_eps for a particular motility force f_mot = 500 Pa μm² for a large time lag (τ₂k_div). We have also estimated the total number of EPS particles corresponding to the different values of k_eps and depicted in a bar plot (Fig. 4(b)). Both Fig. 4(a and b) reveal that the fraction of sub-diffusive cells and number of EPS increase with k_eps. However, the increase is significantly low for high values of k_eps. Since EPS production depends on several factors such as the local nutrient-concentration, cell area density and also the EPS area density on the two dimensional surface, even with the higher values of k_eps, the EPS-production will self-saturate for these constraints. Altogether these results identify that both cell motility and heterogeneous presence of sticky EPS in a growing colony are essential for the coexistence of mobile and sessile phases rendering a biofilm transition. In what follows, we will next discuss how and to what extent cell motility can regulate the colony features to get further insights into biofilm transition.

Fig. 4 Bar plots of (a) the fraction of sub-diffusive cells and (b) the number of EPS particles as a function of EPS secretion rate (k_eps). Both the fraction of sub-diffusive cells and number of EPS increase slightly with k_eps.

Cell motility regulates colony compactness and local order

For motile bacteria, self-propulsion force is a salient feature that helps them move to the nearby regions to search for nutrients for their survival. Depending on bacterial species and surrounding conditions, motility might vary. How does the variation of motility force impact the spatial architecture of a growing colony? By varying motility force, we analyze an expanding colony's spatiotemporal organization. Fig. 5(a–d) represent the snapshots of the bacterial colony at a particular time (tk_div = 35.0) for an increasing value of self-propulsion force: f_mot = 100, 300, 500, and 700 Pa μm² respectively, keeping all other parameters same as used in Fig. 2. It is apparent from Fig. 5 that the spatial morphology varies, and we observe a transition from compact to a sparse colony for the higher values of motility forces. To quantify the compactness of a growing colony, we define a quantity called “sparseness (S_p)”, as , where A_particles and A_colony are the area of the particles and area of the colony respectively. To determine S_p, we first evaluate the distance of each particle after a certain time (tk_div = 3.0) from inoculation from the center of the colony and compute the maximum distance of the particle in the growing colony. We consider a circle of a radius identical to the maximum distance of the particle at that time and calculate the area of this circle (A_colony) and the total area of those particles (A_particles) belonging to this circle. So, S_p ∼ 1.0 indicates that particle's area is very low compared to the colony area, and S_p ∼ 0.0 suggests that the particle's area and the colony area are nearly equal. Fig. 5(e) illustrates the sparseness of the colony as a function of time with a variation of motility forces. We observe that sparseness is high for each of the simulated colonies irrespective of their different motility forces (f_mot = 100–700 Pa μm²) at the early stage of micro-colony morphogenesis. However, at the later stage, sparseness values show decay and saturate to a fixed value for each case. It is also evident from the Fig. 5(e), that the sparseness value is larger for colonies with higher cell motility forces. The underlying reason of compact to sparse colony organization with increasing values of motility can be understood by considering two velocities:⁴² (1) a growth-induced velocity (v_g) and (2) the self-propeling velocity (v_mot) and their competition. For larger values of motility force, self-propulsion velocity v_mot dominates over v_g, developing more sparse colony with less order compared to the smaller values of motility force where v_g dominate over v_mot. These similar types of observations were also previously reported for a non-motile bacterial colony²⁶ where low diffusion of the particles led to the formation of compact clusters. Furthermore, we address how different values of motility forces can affect the colony dynamics by calculating the fraction of sub-diffusive cells as a function of f_mot for large time lag (τ₂k_div) and depicted in a bar diagram as given by Fig. 5(f). We observe that for f_mot = 100 Pa μm², ∼50% of the total cells are showing sub-diffusion. But for, higher values of motility forces ∼ 20% of the total cells reveal the sub-diffusive nature. This result supports that the stickiness of the EPS is not high enough to suppress the motility force of the bacterial cells.

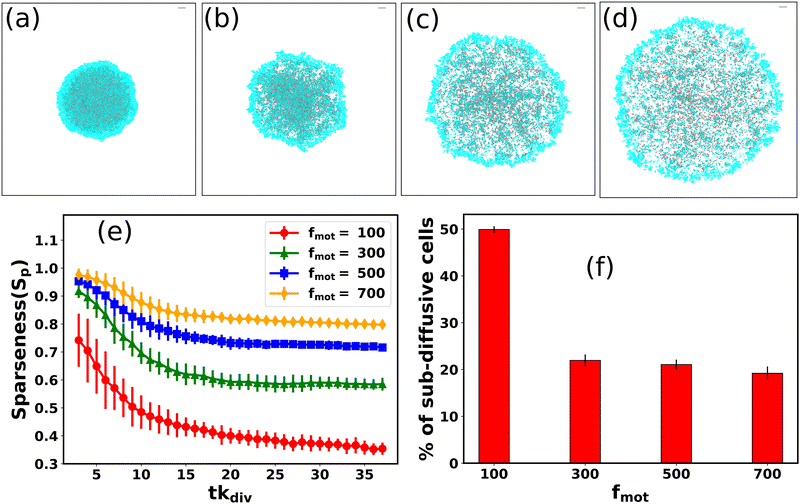Fig. 5 Snapshots of growing bacterial colony in the presence of sticky EPS for different values of the self-propulsion forces: (a) f_mot = 100 Pa μm², (b) f_mot = 300 Pa μm², (c) f_mot = 500 Pa μm², and (d) f_mot = 700 Pa μm² respectively. The gray line in each snapshot represents the scale bar which corresponds to 20.0/d₀ (in length unit). (e) Plot of sparseness (S_p) as a function of time for different motility forces. With increasing values of motility forces, the colony becomes compact to sparse. (f) Percentage of sub-diffusive cells as a function of different motility forces through a bar diagram. Here error bars represent the standard error. All the other parameters remain the same as mentioned in Table S1 (ESI†).

To shed light on how the interaction between motility and steric forces can influence the local spatial organization of the cells in a growing colony in two dimensions, we first calculate the radial distribution function of the cells. This has been done, once the colony reaches to a steady-state after a sufficiently long time (tk_div = 35.0). Here steady-state means that after a certain time the structural properties of the colony are not changing significantly with respect to the time. From Fig. 5(e), it is evident that after a sufficiently long time the sparseness of the simulated colonies show a saturation with respect to time for any value of motility force. The radial distribution function is defined as , where r⃑_ij is the distance between ith and jth particle. Fig. 6(a) depicts the radial distribution functions of cells. As demonstrated in Fig. 6(a) and inset figure, an initial sharp peak appears at a very short distance followed by a gradual decrease signifying an almost homogeneous colony spread of the cells. However, a close look reveals that for higher values of motility force the peak values are slightly larger compared to lower values of motility forces. This observation indicates that though for higher values of motility force the colony is more sparse, the cells are more ordered at shorter distances compared to the lower values of motility forces. In general, many active microorganisms such as bacteria, sperms and epithelial cells, etc., exhibit a wide variety of collective behavior and patterns.^67–70 Self-propulsion force in the form of activity is responsible for such collective motion in which in the absence of any alignment mechanism, the activity provides effective alignment and makes them cooperative.^71,72 Overall, here the observation suggests a motility-induced collective dynamics.

Fig. 6 Radial distribution functions of cells for different values of motility force. The inset figure represents the zoomed version of main figure for smaller values of r. For higher values of motility force, the cells are more collective at shorter distances compared to the lower values of motility forces which suggests motility-induced collective motion. (b) Distribution of hexatic order parameter |ψ₆| of cells for different value of motility forces. For a higher value of motility forces the high |ψ₆| values are significantly larger compared to the lower value of motility forces which implies motility induced ordering among the cells.

To gain further insights into the local organization of the cells, we compute the hexatic order parameter ψ₆,^73,74 defined as

where n_j is the number of neighbors of particle j within a certain cutoff distance and θ^k_j is the angle between the vector from particle j to its neighbor k which is (r⃑_j − r⃑_k) and the x-axis. ψ₆ can vary between 0 and 1. |ψ₆| = 1 means perfect hexagonal arrangement and |ψ₆| = 0 indicates random arrangement. Fig. 6(b) represents the probability distribution of |ψ₆| of the cells for different values of motility forces. Here probability distribution is normalized such that and for neighbor searching of each particle we have chosen the cutoff as r_cut = 8.0/d₀. From this figure, it is clear that for a higher value of motility forces the distribution is broader i.e. high |ψ₆| values are significantly larger compared to the lower value of motility forces which implies again motility induced ordering among the cells.

At this stage, we will now investigate the combined effect of the nutrient-dependent growth and motility force in colony morphodynamics.

Competition between growth-induced internal stress and motility force

In a growing bacterial colony, initial nutrient concentration C₀ is a key factor that controls the growth and associated morphological dynamics. To decipher the effect of nutrient concentration, we performed computer simulations by varying C₀ keeping all other parameters the same as Fig. 2. Fig. 7(a–d) represent the snapshots of the bacterial colony for a particular time (tk_div = 17.5) for different values of initial nutrient concentration as C₀ = 3.0, 10.0, 20.0, and 30.0 fg μm³ respectively. It is apparent from Fig. 7(a–d) that the colony is spreading more quickly for higher values of C₀. To quantify the growth dynamics concerning the variation of C₀, we calculate the total area covered by the particles (cell + EPS) and the speed at which the colony expands. The front speed of the colony is determined by computing the rate of change of the colony area occupied by the particles and defining it as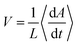 , where L is the length of the simulation box and 〈…〉 denotes the ensemble average. Fig. 7(e and f) illustrate the area covered by the colony and front speed as a function of time for different values of C₀. For larger values of C₀, cells grow faster and hit quickly to the division length and are more likely to replicate, thereby causing a rapid increase in the area of the growing colony. This observation complements the higher value of the front speed of the colony. However, we have not found any drop in the velocity profile of the colony front.⁷⁵ In our model, there exists a nutrient reservoir at the edges of the simulation box, thereby causing a constant supply of the nutrients. Subsequently, the motile bacteria consume nutrients from the medium and will divide spontaneously. It always leads to an increase in the velocity of the colony front. To verify this fact, we performed a new set of simulations by removing the nutrient reservoir from the edges of the simulation box, keeping all other parameters as same as used in Fig. 2. Fig. S3 (ESI†) presents the velocity profile of the front of the colony as a function of time in the absence of a nutrient reservoir. The plot in Fig. S3 (ESI†) shows a clear drop in the velocity profile. This observations suggest that after a certain time, the growth of the colony halted due to insufficient nutrients.

Fig. 7 Snapshots of growing bacterial colony in presence of sticky EPS with motility force f_mot = 500 Pa μm² for different values of initial nutrient concentration: (a) C₀ = 3.0 fg μm³, (b) C₀ = 10.0 fg μm³, (c) C₀ = 20.0 fg μm³, and (d) C₀ = 30.0 fg μm³ respectively at a particular time tk_div = 17.5. The gray line in each snapshot represents the scale bar which corresponds to 20.0/d₀ (in length unit). With increasing values of initial nutrient concentration, the colony is spreading more quickly. (e) Surface coverage and (f) front speed as a function of time for different values of initial nutrient concentration. Both are increasing with C₀, due to faster cells divisions. Time profiles of (g) force and (h) stress for different values of C₀. For figures (f, g and h) the color coding is the same as the legend of figure (e). Error bar represents the standard error.

Moreover, recent experimental studies^76,77 have highlighted a collective oscillation in biofilm expansion and these oscillations are coupled with the metabolic product formation and the nutrient availability within the biofilm. However, in our case, we have not found any oscillatory behavior in the front speed and the stress profiles of the colonies. We hypothesized numerous underlying reasons for such contrasting behavior in our case, such as: (i) bacterial cells are self-propelled or motile, (ii) metabolism and cell death is not included in our model, (iii) cell division and growth rate are not directly coupled with the local nutrient concentration, etc. Nonetheless, we have also computed the front speed considering a non-motile bacteria with F⃑_mf = 0, keeping all other parameters as same as used in Fig. 2. Fig. S4 (ESI†) represents the front speed of the colony as a function of time. It is evident from Fig. S4 (ESI†), that the front speed is not a smooth increasing function of time, rather there are few crests and troughs in the plot of speed in some intervals which suggests an oscillatory nature in the front speed.

For larger values of C₀, cells experience a large mechanical force that stems from growth and rapid cell division. We evaluate total force and total stress, acting on the bacterial cells. The total force and total stress are defined as and respectively, where A_tot is the total area covered by the bacterial cells. Fig. 7(g and h) represent the total force and total stress as a function of time respectively. The results manifest that both the force and stress are larger for a higher value of C₀. However, at a longer time, the stress curve saturates. The underlying reason is that for a longer time, due to fast cell growth and divisions, the rate of change of the area of the colony is almost equal to the rate of change of total force acting on the cells leading to a saturation of the total stress. This observation suggests a competition between growth-induced internal stress and self-propulsion force which diminishes the unidirectional motion of cells. To justify this argument, we compute the MSD of cells in a growing colony for initial nutrient concentration C₀ = 10.0 fg μm³ and make a distribution of MSD exponents. As depicted in Fig. S5(a and b) (ESI†), more cells show sub-diffusion for both small (τ₁k_div) and large (τ₂k_div) lag times in comparison to C₀ = 3.0 fg μm³ (Fig. 3(b and e)). Due to the larger access to the local nutrient concentration for higher C₀, cells grow, divide, and cover a certain area faster than growing in a lower C₀. A close look at the stress curves reveal that there is a small drop in the stress values for C₀ = 20 fg μm³ and C₀ = 30 fg μm³. The decrease in the stress values might be due to the presence of some vacant space inside the growing colony which are covered by the bacteria in the next time step. Under this scenario, the area of the colony increases but the force does not increase much which leads to a drop in the stress curve. However, these drops are within the standard deviation.

We now analyze how does the nutrient concentration profile change for different values of motility forces. We evaluate the mean value of nutrient concentration as denoted by C_avg = 〈C(t)/C₀〉, where C(t) and C₀ are the time-dependent and initial nutrient concentration in each grid point respectively. The angular bracket denotes the average over all the grid points. Fig. 8 illustrates the change of C_avg as a function of time (tk_div) for different values of motility forces. We notice that C_avg of the different colonies show a similar decay with respect to the time initially (up to tk_div ∼ 15) and differ in a later stage, showing a slower decay for the low motile cells compare to higher motile cells. For larger values of self-propulsion forces, as cells spread rapidly across the colony, they can utilize the available nutrients to grow fast and divide and multiply in numbers, thereby causing a quicker depletion of local nutrients. This behavior of colonies with different cell motility suggests that although high motility forces help in spreading in search of food, colonies with lower values of motility forces of the cells will survive for a longer time with the conserved initial nutrients.

Fig. 8 Mean nutrient concentration C_avg = 〈C(t)/C₀〉 as a function of time for different values of motility forces. Here error bars represent the standard error.

4 Summary and concluding remarks

Bacterial aggregation, spread, and pattern formation have immense importance for their survival and biological functioning. These features play a crucial role in infections and spreading, biofilm formation, and antibiotic resistance. Over the years, experimental and theoretical research have illuminated underlying structural complexities and dynamics in multicellular organizations. Although bacterial cells are rigid and hardly deform under external forces, their multicellular organizations, such as biofilms, are dynamic and active. At the community level, they appeared to be able to generate mechanical forces and respond to the changing environment potentially. Existing studies have established that mechanical forces and physicochemical factors can profoundly influence the spatial morphology and pattern formation in multicellular microbial communities.^{7–9,22–25,33–35,39} It is now becoming increasingly relevant to consider mechanical interactions while underpinning the spatiotemporal evolution and dynamics in multicellular systems composed of mesoscopic objects such as bacterial cells.

The dynamics, architecture, morphogenesis, etc., of a bacterial colony, can vary depending on the different variants of the same species. Here, we are mainly motivated by the recent seminal work of Worlitzer et al.,³⁰ on bacteria Bacillus Subtilis where they have reported that only the matrix builders cells can transform from a motile to a biofilm state. This transition mainly occurs in the intermediate regions between the colonial center and its edge, where cells embedded in EPS start to form dense stationary aggregates. Both physical and biological processes drive this transition, but the interplay between these is still elusive. Our work attempts to understand the role of physicochemical interactions that trigger biofilm formation. However, the exact mechanism and conditions of EPS production are lacking. A few experimental studies^41,51,52 have claimed that the depletion of nutrients triggers EPS production in a growing colony. Based on these studies, in our model, we have implemented that EPS production depends on a threshold of local nutrient concentration. From Fig. S2(b) (ESI†), it is clear that the production of EPS in the interior region of the colony is saturating slowly due to the limited available space in two dimensions and local EPS density-dependent termination of EPS production. In our model, the EPS are mainly secreting at the regions between the edge and interior of the colony but not at the exact leading edge of the colony as mentioned by previous studies.^29,78 The underlying biological origin and exact mechanism might be more complex such as EPS production might be some complicated function of local nutrient concentration.

Here, we have investigated microcolony morphogenesis focusing on the physicochemical properties of self-secreted EPS, cell growth, and motion during colony development using a particle/agent-based model from the perspective of soft matter physics. The spatiotemporal dynamics of a growing monolayered microcolony is understood in terms of its primary components, i.e., the rigid rod-like cells and the self-secreted EPS in the media. Furthermore, heterogeneous expression of EPS due to the spatial heterogeneity of the local nutrients set up concentration gradients within the biofilm, which on the other hand, generates mechanical forces relevant for spreading and spatial patterning. Moreover, the properties of EPS profoundly impact the structural integrity and morphological dynamics of the growing microcolony biofilms.

Our simulation results reveal a dynamic phase transition indicating the presence of coexisting phases of mobile and sessile aggregates during micro-colony morphogenesis. Specifically, in weakly attractive/sticky EPS, we find a dynamics phase transition where cells inside the colony interior form sessile clusters surrounded by motile cells. The cells at the outermost layer remain motile due to the high accessibility of nutrients and less EPS production. We observe the presence of coexisting cells which follow sub-diffusion and super-diffusion simultaneously for a longer lag time scale. Our control simulation of a growing colony without self-produced EPS does not show such sub-diffusive dynamics even in a longer lag time scale. These observations support that transition from motile to biofilm-like aggregates is mediated by self-secreting sticky EPS. For this type of growing bacterial colonies with motile cells, the self-propulsion force helps the cells to form small aggregates, and sticky EPS increases the adherence of the cells within the clusters. Therefore, the co-existence of two dynamical phases is conciliated by joint ventures of these two properties (cell motility and sticky EPS).

Most bacterial biofilms are sessile communities that self-organize into 3D structures, with cells embedded in a self-produced extracellular polymeric substances (EPS).^28,79 Furthermore, chemotactic aggregation, swirling, and swarming are standard features observed in multicellular bacterial colonies.^80–83 Besides, it is also evident in recent study that chemical stress can induce single to multilayer transition or three-diemnsional island formation in bacterial swarms.⁸⁴ However, the present study is focused on understanding mechanical self-regulation during colony morphogenesis following a minimal two-dimensional biophysical model of cells and self-produced EPS. Despite its simplicity, our model provides crucial insights into the spatial morphology and dynamics of a growing biofilm. We find that the combined effects of cell motility, growth-induced stress, and mechanical interactions among the biofilm components regulate the spatial heterogeneity and pattern formation during biofilm morphogenesis. One of the advantages of our model, owing to its simplicity, is that it can predict and provide biophysical intuition for the different behaviors exhibited by a multicellular microbial community for varied conditions. We believe our theoretical predictions have the potential to guide future experiments on biofilm formation.

In the future, it would be logical and interesting to extend our model in 3D to learn how different factors contribute to the shaping of a mature biofilm. Besides, it would be interesting to investigate if chemotaxis, confinement, cell death, etc., further influence biofilm morphogeneis.^33,39,85 Furthermore, incorporating nutrient-coupled division rate, nutrient-dependent sporulation, and detailed investigation of EPS production might provide much more realistic biofilm morphogenesis.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

All the authors acknowledge Tata Institute of Fundamental Research Hyderabad (TIFRH), and IISER Thiruvananthapuram India for providing the support of computing resources. Palash Bera and Abdul Wasim gratefully acknowledge TIFRH for institute fellowship.

References

1. T. Tolker-Nielsen and S. Molin, Microb. Ecol., 2000, 40, 75–84.
2. L. Hall-Stoodley, J. W. Costerton and P. Stoodley, Nat. Rev. Microbiol., 2004, 2, 95–108.
3. R. M. Donlan, Emerging Infect. Dis., 2002, 8, 881.
4. E. Ben-Jacob, I. Cohen and H. Levine, Adv. Phys., 2000, 49, 395–554.
5. H. Jeckel, E. Jelli, R. Hartmann, P. K. Singh, R. Mok, J. F. Totz, L. Vidakovic, B. Eckhardt, J. Dunkel and K. Drescher, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 1489–1494.
6. D. Volfson, S. Cookson, J. Hasty and L. S. Tsimring, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 15346–15351.
7. Z. You, D. J. Pearce, A. Sengupta and L. Giomi, Phys. Rev. Lett., 2019, 123, 178001.
8. Z. You, D. J. Pearce and L. Giomi, Sci. Adv., 2021, 7, eabc8685.
9. F. Farrell, M. Marchetti, D. Marenduzzo and J. Tailleur, Phys. Rev. Lett., 2012, 108, 248101.
10. Q. Zhang, J. Li, J. Nijjer, H. Lu, M. Kothari, R. Alert, T. Cohen and J. Yan, Proc. Natl. Acad. Sci. U. S. A., 2021, 118(31), e2107107118.
11. D. Boyer, W. Mather, O. Mondragón-Palomino, S. Orozco-Fuentes, T. Danino, J. Hasty and L. S. Tsimring, Phys. Biol., 2011, 8, 026008.
12. J. N. Wilking, T. E. Angelini, A. Seminara, M. P. Brenner and D. A. Weitz, MRS Bull., 2011, 36, 385–391.
13. J. B. Xavier and K. R. Foster, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 876–881.
14. F. Hans-Curt and J. Wingender, Nat. Rev. Microbiol., 2010, 8, 623–633.
15. A. Dragoš and Á. T. Kovács, Trends Microbiol., 2017, 25, 257–266.
16. M. J. Bradburn, T. G. Clark, S. B. Love and D. G. Altman, Br. J. Cancer, 2003, 89, 605–611.
17. J. Hou, D. H. Veeregowda, B. van de Belt-Gritter, H. J. Busscher and H. C. van der Mei, Appl. Environ. Microbiol., 2018, 84, e01516–17.
18. S. S. Branda, Å. Vik, L. Friedman and R. Kolter, Trends Microbiol., 2005, 13, 20–26.
19. G. Gebreyohannes, A. Nyerere, C. Bii and D. B. Sbhatu, Heliyon, 2019, 5, e02192.
20. L. K. Vestby, T. Grønseth, R. Simm and L. L. Nesse, Antibiotics, 2020, 9, 59.
21. J. W. Costerton, P. S. Stewart and E. P. Greenberg, Science, 1999, 284, 1318–1322.
22. F. Farrell, O. Hallatschek, D. Marenduzzo and B. Waclaw, Phys. Rev. Lett., 2013, 111, 168101.
23. P. Ghosh, J. Mondal, E. Ben-Jacob and H. Levine, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, E2166–E2173.
24. F. D. Farrell, M. Gralka, O. Hallatschek and B. Waclaw, J. R. Soc., Interface, 2017, 14, 20170073.
25. Z. You, D. J. Pearce, A. Sengupta and L. Giomi, Phys. Rev. X, 2018, 8, 031065.
26. R. D. Acemel, F. Govantes and A. Cuetos, Sci. Rep., 2018, 8, 1–9.
27. G. Dorken, G. P. Ferguson, C. E. French and W. C. Poon, J. R. Soc., Interface, 2012, 9, 3490–3502.
28. M. Asally, M. Kittisopikul, P. Rué, Y. Du, Z. Hu, T. Çağatay, A. B. Robinson, H. Lu, J. Garcia-Ojalvo and G. M. Süel, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 18891–18896.
29. S. Srinivasan, I. D. Vladescu, S. A. Koehler, X. Wang, M. Mani and S. M. Rubinstein, Biophys. J., 2018, 114, 1490–1498.
30. V. M. Worlitzer, A. Jose, I. Grinberg, M. Bär, S. Heidenreich, A. Eldar, G. Ariel and A. Be’er, Sci. Adv., 2022, 8, eabn8152.
31. D. Dell’Arciprete, M. Blow, A. Brown, F. Farrell, J. S. Lintuvuori, A. McVey, D. Marenduzzo and W. C. Poon, Nat. Commun., 2018, 9, 1–9.
32. K. J. Kieser and E. J. Rubin, Nat. Rev. Microbiol., 2014, 12, 550–562.
33. P. Ghosh and H. Levine, Phys. Rev. E, 2017, 96, 052404.
34. N. Rana, P. Ghosh and P. Perlekar, Phys. Rev. E, 2017, 96, 052403.
35. M. Mukherjee and P. Ghosh, Phys. Rev. E, 2018, 97, 012413.
36. C. Zachreson, X. Yap, E. S. Gloag, R. Shimoni, C. B. Whitchurch and M. Toth, Phys. Rev. E, 2017, 96, 042401.
37. J. J. Winkle, O. A. Igoshin, M. R. Bennett, K. Josić and W. Ott, Phys. Biol., 2017, 14, 055001.
38. T. J. Rudge, P. J. Steiner, A. Phillips and J. Haseloff, ACS Synth. Biol., 2012, 1, 345–352.
39. P. Ghosh, E. Ben-Jacob and H. Levine, Phys. Biol., 2013, 10, 066006.
40. A. Seminara, T. E. Angelini, J. N. Wilking, H. Vlamakis, S. Ebrahim, R. Kolter, D. A. Weitz and M. P. Brenner, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 1116–1121.
41. W. Zhang, A. Seminara, M. Suaris, M. P. Brenner, D. A. Weitz and T. E. Angelini, New J. Phys., 2014, 16, 015028.
42. P. Nie, F. Alarcon, I. López-Montero, B. Orgaz, C. Valeriani and M. Pica Ciamarra, Soft Mater., 2021, 19, 346–358.
43. C. Zachreson, C. Wolff, C. B. Whitchurch and M. Toth, Phys. Rev. E, 2017, 95, 012408.
44. P. Bera, A. Wasim, J. Mondal and P. Ghosh, Soft Matter, 2021, 17, 7322–7331.
45. B. Ilkanaiv, D. B. Kearns, G. Ariel and A. Be’er, Phys. Rev. Lett., 2017, 118, 158002.
46. A. Be’er, B. Ilkanaiv, R. Gross, D. B. Kearns, S. Heidenreich, M. Bär and G. Ariel, Commun. Phys., 2020, 3, 1–8.
47. G. E. Dilanji, M. Teplitski and S. J. Hagen, Proc. R. Soc. London, Ser. B, 2014, 281, 20132575.
48. F. J. Lobo-Cabrera, A. Patti, F. Govantes and A. Cuetos, Phys. Rev. E, 2021, 103, 052407.
49. P. R. Secor, L. A. Michaels, A. Ratjen, L. K. Jennings and P. K. Singh, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 10780–10785.
50. J. Yan, C. D. Nadell, H. A. Stone, N. S. Wingreen and B. L. Bassler, Nat. Commun., 2017, 8, 1–11.
51. K. Myszka and K. Czaczyk, Curr. Microbiol., 2009, 58, 541–546.
52. J.-H. Ryu, H. Kim and L. R. Beuchat, J. Food Prot., 2004, 67, 2123–2131.
53. J. Schwarz-Linek, C. Valeriani, A. Cacciuto, M. Cates, D. Marenduzzo, A. Morozov and W. Poon, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 4052–4057.
54. A. Gelimson, K. Zhao, C. K. Lee, W. T. Kranz, G. C. Wong and R. Golestanian, Phys. Rev. Lett., 2016, 117, 178102.
55. K. Zhao, B. S. Tseng, B. Beckerman, F. Jin, M. L. Gibiansky, J. J. Harrison, E. Luijten, M. R. Parsek and G. C. Wong, Nature, 2013, 497, 388–391.
56. J. Jara, F. Alarcón, A. K. Monnappa, J. I. Santos, V. Bianco, P. Nie, M. P. Ciamarra, Á. Canales, L. Dinis and I. López-Montero, et al. , Front. Microbiol., 2021, 11, 588884.
57. F. Jose, S. K. Anand and S. P. Singh, Soft Matter, 2021, 17, 3153–3161.
58. Ö. Duman, R. E. Isele-Holder, J. Elgeti and G. Gompper, Soft Matter, 2018, 14, 4483–4494.
59. K. Prathyusha, S. Henkes and R. Sknepnek, Phys. Rev. E, 2018, 97, 022606.
60. M. P. Allen and D. J. Tildesley, Computer simulation of liquids, Oxford university press, 2017.
61. D. Frenkel, B. Smit and M. A. Ratner, Understanding molecular simulation: from algorithms to applications, Academic press, San Diego, 1996, vol. 2.
62. M. L. Waskom, J. Open Source Softw., 2021, 6, 3021.
63. I. Grobas, M. Polin and M. Asally, eLife, 2021, 10, e62632.
64. S. Liu, Y. Li, H. Xu, D. B. Kearns and Y. Wu, bioRxiv, 2022.
65. G. Volpe, S. Gigan and G. Volpe, Am. J. Phys., 2014, 82, 659–664.
66. C. Bechinger, R. Di Leonardo, H. Löwen, C. Reichhardt, G. Volpe and G. Volpe, Rev. Mod. Phys., 2016, 88, 045006.
67. A. Sokolov, I. S. Aranson, J. O. Kessler and R. E. Goldstein, Phys. Rev. Lett., 2007, 98, 158102.
68. B. Szabo, G. Szöllösi, B. Gönci, Z. Jurányi, D. Selmeczi and T. Vicsek, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 74, 061908.
69. I. Theurkauff, C. Cottin-Bizonne, J. Palacci, C. Ybert and L. Bocquet, Phys. Rev. Lett., 2012, 108, 268303.
70. I. Buttinoni, J. Bialké, F. Kümmel, H. Löwen, C. Bechinger and T. Speck, Phys. Rev. Lett., 2013, 110, 238301.
71. V. Narayan, S. Ramaswamy and N. Menon, Science, 2007, 317, 105–108.
72. J. Deseigne, O. Dauchot and H. Chaté, Phys. Rev. Lett., 2010, 105, 098001.
73. T. Kawasaki, T. Araki and H. Tanaka, Phys. Rev. Lett., 2007, 99, 215701.
74. A. Pasupalak, L. Yan-Wei, R. Ni and M. P. Ciamarra, Soft Matter, 2020, 16, 3914–3920.
75. X. Wang, Y. Kong, H. Zhao and X. Yan, Dev., Growth Differ., 2019, 61, 431–443.
76. J. Liu, A. Prindle, J. Humphries, M. Gabalda-Sagarra, M. Asally, D.-Y. D. Lee, S. Ly, J. Garcia-Ojalvo and G. M. Süel, Nature, 2015, 523, 550–554.
77. A. Prindle, J. Liu, M. Asally, S. Ly, J. Garcia-Ojalvo and G. M. Süel, Nature, 2015, 527, 59–63.
78. H. Vlamakis, C. Aguilar, R. Losick and R. Kolter, Genes Dev., 2008, 22, 945–953.
79. K. Drescher, J. Dunkel, C. D. Nadell, S. Van Teeffelen, I. Grnja, N. S. Wingreen, H. A. Stone and B. L. Bassler, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, E2066–E2072.
80. E. Ben-Jacob, A. Finkelshtein, G. Ariel and C. Ingham, Trends Microbiol., 2016, 24, 257–269.
81. E. J. Marsden, C. Valeriani, I. Sullivan, M. Cates and D. Marenduzzo, Soft Matter, 2014, 10, 157–165.
82. L. Turner, W. S. Ryu and H. C. Berg, J. Bacteriol., 2000, 182, 2793–2801.
83. Y. Hong, N. M. Blackman, N. D. Kopp, A. Sen and D. Velegol, Phys. Rev. Lett., 2007, 99, 178103.
84. I. Grobas, M. Asally and M. Polin, Front. Soft Matter, 2022, 2, 936779.
85. M. Asally, M. Kittisopikul, P. Rué, Y. Du, Z. Hu, T. Çağatay, A. B. Robinson, H. Lu, J. Garcia-Ojalvo and G. M. Süel, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 18891–18896.

---

Footnote

† Electronic supplementary information (ESI) available: Appendix PDF file in support of the model details, figures: S1, S2(a), S2(b), S3, S4, S5(a), S5(b) and the table S1 as mentioned in the main text. The description of Video S1 is also included. See DOI: https://doi.org/10.1039/d2sm01365g

---