Electro- and photochemical H₂ generation by Co(II) polypyridyl-based catalysts bearing ortho-substituted pyridines

Abstract

Cobalt(II) complexes featuring hexadentate amino-pyridyl ligands have been recently discovered as highly active catalysts for the Hydrogen Evolution Reaction (HER), whose high performance arises from the possibility of assisting proton transfer processes via intramolecular routes involving detached pyridine units. With the aim of gaining insights into such catalytic routes, three new proton reduction catalysts based on amino-polypyridyl ligands are reported, focusing on substitution of the pyridine ortho-position. Specifically, a carboxylate (C2) and two hydroxyl substituted pyridyl moieties (C3, C4) are introduced with the aim of promoting intramolecular proton transfer which possibly enhances the efficiency of the catalysts. Foot-of-the-wave and catalytic Tafel plot analyses have been utilized to benchmark the catalytic performances under electrochemical conditions in acetonitrile using trifluoroacetic acid as the proton source. In this respect, the cobalt complex C3 turns out to be the fastest catalyst in the series, with a maximum turnover frequency (TOF) of 1.6 (±0.5) × 10⁵ s⁻¹, but at the expense of large overpotentials. Mechanistic investigations by means of Density Functional Theory (DFT) suggest a typical ECEC mechanism (i.e. a sequence of reduction – E – and protonation – C – events) for all the catalysts, as previously envisioned for the parent unsubstituted complex C1. Interestingly, in the case of complex C2, the catalytic route is triggered by initial protonation of the carboxylate group resulting in a less common (C)ECEC mechanism. The pivotal role of the hexadentate chelating ligand in providing internal proton relays to assist hydrogen elimination is further confirmed within this novel class of molecular catalysts, thus highlighting the relevance of a flexible polypyridine ligand in the design of efficient cobalt complexes for the HER. Photochemical studies in aqueous solution using [Ru(bpy)₃]²⁺ (where bpy = 2,2′-bipyridine) as the sensitizer and ascorbate as the sacrificial electron donor support the superior performance of C3.

---

1. Introduction

The production of clean fuels from renewable energy supplies, such as solar energy, is one of the most ambitious scientific challenges, which would provide a solution to the current energy and environmental problems.^1,2 Because of the potential of hydrogen as a green fuel, most of the research has so far been focused on the development of systems for the reduction of protons to generate H₂.³ In particular, the formation of molecular hydrogen from light-driven water splitting is an attractive strategy to exploit and store the enormous amount of energy contained in solar light.^4–7 Inspired by the ability of nature to convert solar energy into chemical fuels (i.e. via the photosynthesis process), photoinduced proton reduction systems need at least three components: a light absorber (i.e. photosensitizer), a catalyst and an electron donor.⁸ Another promising way to produce H–H bonds is through electrochemical reduction of protons using solar-generated electricity.^9,10 In both cases, the final goal is to obtain highly efficient systems capable of operating under fully aqueous conditions. Nevertheless, electrochemical studies aimed at gaining insights into the performance of the catalysts are generally carried out in organic media, in which the amount of protons can be more precisely controlled.¹¹ For the development of systems active in both electro- and photochemical hydrogen production, particular attention has been paid to homogeneous molecular catalysts based on abundant, cheap, and noble-metal-free species, such as di-iron hydrogenase mimics or bioinspired cobalt and nickel complexes.^12–21 Cobaloxime complexes, in particular, have emerged as active catalysts for electrochemical proton reduction because of the low overpotential and the high catalysis rate.²² These complexes have also been employed as catalysts in photochemical systems, although the low stability in fully aqueous media due to ligand exchange and hydrolysis dramatically limits their applicability.^18,19 Recently, polypyridyl cobalt complexes have been reported as competent catalysts, showing excellent stability and impressive activity even though they display higher overpotentials with respect to cobaloximes.^23–25 We have recently reported a polypyridyl cobalt complex having an exotic heptacoordinate structure, which showed outstanding performances in light-driven hydrogen production.^26,27 Synthetic modifications by ligand substitutions enable the optimization of the catalytic properties of this class of catalysts. Indeed, the introduction of electron withdrawing groups (i.e. EWG) or electron donating groups (i.e. EDG) can affect the reduction potentials of the cobalt centre, while their position can modulate the catalytic mechanism, thus allowing the optimization of the performances.^28,29 In particular, we have recently proved that the position of the substituents plays a more prominent role in the photochemical efficiency towards hydrogen production using [Ru(bpy)₃]²⁺ (where bpy = 2,2′-bipyridine) as the sensitizer,³⁰ while electronic effects become relevant in the light-driven performance when using less powerful reducing agents.³¹ Several research groups have also performed the functionalization with carboxylic or hydroxyl groups in peripheral positions with respect to the metal centre in order to promote intramolecular proton transfer, thus enhancing the efficiency of the catalysis.³² In the same vein, Zonta, Natali and co-workers³³ introduced different substituents (i.e. –OH, –CH₂OH, –CHO, –CONH₂) on the phenyl ring of an amino polypyridine cobalt complex, in order to modify the solvent–ligand interactions without affecting the electronic properties of the metal centre. The authors observed, however, only small differences in the efficiency among the considered complexes. In particular, they attributed the slightly higher activity of the complexes bearing –OH and –CH₂OH to the presence of the hydroxyl group that could promote the formation of a H-bonded water network near the cobalt. Conversely, the low performances of the catalysts bearing –CHO and –CONH₂ were ascribed to a lower stability of the catalysts induced by these substituents. Herein, we present the synthesis and the characterization of three new amino-polypyridyl cobalt complexes bearing different functional groups i.e. –CO₂⁻, –CH₂OH and –OH (yielding C2, C3, and C4 respectively) in the ortho-position to the N of the pyridine moiety with the aim of studying their effect on the catalytic activity in the electrochemical and photochemical hydrogen production.²⁶ The presence of such substituents is expected to actively influence the role of the pyridine group in assisting the protonation of the metal centre, thus affecting the overall catalysis. The rate constants of the protonation steps are extrapolated from electrochemical studies in acetonitrile with trifluoroacetic acid (TFA) as proton source. Experiments of photoinduced H₂ evolution in water are performed in the presence of ascorbic acid as electron donor and [Ru(bpy)₃]²⁺ as sensitizer. Density Functional Theory (DFT) was employed to calculate the relative stability and structure of the intermediates involved in H₂ production, including those in the final H₂ release, making possible a comparison between different pathways for each proposed compound and allowing a reliable rationalization of the experimental results.

2. Methodology

2.1 Synthesis and characterization

The synthesis of the compounds was performed according to the procedure reported in Section S2 of the ESI.† Solid state structures were obtained by X-ray diffraction on single crystals prepared by slow diffusion of diethyl ether into methanolic solutions of the complexes.

To observe possible variations of the electronic absorption of the catalysts in the presence of a source of protons, UV-Vis spectra were measured in 4 mM solutions of complexes in CH₃CN in the presence of increasing amounts of trifluoroacetic acid (TFA) by keeping the final volume (2 mL) unchanged.

2.2 Electrochemistry

Cyclic voltammetry experiments were carried out in CH₃CN under N₂ with 0.1 M tetrabutylammonium hexafluorophosphate (TBAPF₆) as supporting electrolyte and glassy carbon as working electrode. Bulk electrolysis experiments were performed at −1.5 V and −1.63 V vs. Fc⁺/Fc on a mercury-pool electrode in 8 mL CH₃CN, in the presence of TFA (100 mM), the complexes (1 mM) and tetrabutylammonium hexafluorophosphate, TBAPF₆ (0.1 M). Foot-of-the-wave analysis (FOWA) was performed to gain information concerning the rate constants (k₁, k₂) relative to the proton transfer step of the catalytic process.^34–36 The rate constants were extrapolated as average at various concentrations of acid (TFA solutions in the range 5–20 mM) and scan rates (0.7–47 V s⁻¹). Further details of the calculations are shown in the ESI (Sections S4 and S5).

2.3 Photochemistry

Photoinduced hydrogen production experiments were performed in fully aqueous solutions with 1 M acetate buffer (pH = 4) in the presence of [Ru(bpy)₃]Cl₂ (0.5 mM) as photosensitizer, and ascorbic acid (0.1 M) as proton source and catalyst (5 μM). The solutions were irradiated with a blue light at 475 nm and 20 °C for 6 h. These conditions were selected according to the best conditions previously found for C1.^26,27 Turnover numbers (TONs), turnover frequencies (TOFs) and quantum yields (QYs) were calculated according to the procedures previously reported by us.³⁰

Nanosecond transient absorption measurements were performed with a custom laser spectrometer consisting of a Continuum Surelite II Nd:YAG laser (FWHM = 8 ns) with a frequency doubling (532 nm, 330 mJ) option, an Applied Photophysics Xe light source including a mod. 720 150 W lamp housing, a mod. 620 power-controlled lamp supply and a mod. 03-102 arc lamp pulser. Laser excitation was provided at 90° with respect to the white light probe beam. Light transmitted by the sample was focused onto the entrance slit of a 300 mm focal length Acton SpectraPro 2300i triple grating, flat field, double exit monochromator equipped with a photomultiplier detector (Hamamatsu R3896). Signals from the photomultiplier (kinetic traces) were processed by means of a TeledyneLeCroy 604Zi (400 MHz, 20 GS s⁻¹) digital oscilloscope. Before all the measurements the solutions were purged with nitrogen for 10 minutes.

2.4 Computational setup

Theoretical investigations were performed only for C2 and C3, since the two tautomeric forms of C4 impeded a straightforward comparison between the experimental and calculated properties. The general computational strategy used here for the calculation of the oxidation potentials, reaction intermediates and energy barriers is the same as that employed in our previously published studies on heptacoordinate cobalt complexes (including C1).^26,27,30 Redox potentials in acetonitrile were calculated as free energy differences in solution. The Gibbs free energy in solution of a species i (Gⁱ_solv) is defined as Gⁱ_solv = Gⁱ_vac + ΔGⁱ_solv, where Gⁱ_vac is the Gibbs free energy in the gas phase (the gas phase energy with zero-point energy and thermal corrections) and ΔGⁱ_solv is the free energy of solvation. Gⁱ_vac is obtained by performing a single point calculation at the optimized geometry in vacuo, followed by frequency calculations in order to include the vibrational contribution to the total partition function. The solvation free energy, ΔGⁱ_solv, was obtained by a single-point calculation in solution and a reference calculation in the gas phase at the geometry optimized in solution. The absolute potentials calculated vs. vacuum were converted to potentials vs. Fc⁺/Fc by adding −4.80 V as reported in ref. 44. In line with our previous studies and following the procedure reported in ref. 37 to calculate the relative free energies for the considered reaction steps, we used values of G*(H⁺_(s)) = −266.5 kcal mol⁻¹,³⁸G⁰(e⁻_(g)) = −0.868 kcal mol⁻¹ (ref. 39) and G⁰(H_2(g)) = −739.5 kcal mol⁻¹. A value of −4.44 eV was used for the vacuum level with respect to the Normal Hydrogen Electrode (NHE) in acetonitrile.³⁷ Preliminary benchmark calculations on the redox potentials of the systems considered here showed, however, that the best agreement with experiments was obtained when using the PBE0 functional (25% of Hartree–Fock exchange), instead of B3LYP, that was adopted in our previous studies.⁴⁰ Therefore, we performed all the DFT calculations to determine energy minima, transition states and relaxed scans for the different reduction and oxidation steps, by using the PBE0 exchange and correlation functional and the 6-311G* basis set. The solvent (acetonitrile) was taken into account in all cases by the implicit IEF (Integral Equation Formalism) method of the PCM (Polarizable Continuum Model).⁴¹ For a proper comparison of C2 with the experimental values, two different mechanisms were considered: (i) initial protonation by the medium, before starting the H₂ evolution process by accepting 2 electrons and 2 protons (i.e., 2E2H) or (ii) final protonation by an explicit acidic medium after reaching the second protonation step. In the latter case, a CH₃COOH molecule (weak acid), a CF₃COOH molecule (TFA, strong acid), and a protonated water cluster of 3 water molecules (i.e., 2H₂O⋯H₃O⁺) were explicitly included in the calculations (see Fig. ES25 in the ESI†).

For C2 and C3 the stability of the high and low spin configurations was preliminarily verified by single point electronic structure calculations in implicit acetonitrile solvent, using DFT (PBE0 functional) and MP2 methods with the 6-311G* basis set (Table ES5 in the ESI†).

All calculations were performed with the Gaussian16 package,⁴² including the thermochemical characterization of each stationary point on the potential energy surface (minima and transition states) through frequency calculations, thus obtaining enthalpy and Gibbs free energy.

3. Results and discussion

3.1 Synthesis and characterization

The ligands L2, L3 and L4 (Fig. 1) were synthesised from the reaction of N,N-bis-(6-(2,2′-bipyridyl)methyl)amine with the pyridine bearing various substituent groups in the presence of the base N,N-diisopropylethylamine. The synthesis of L1 was previously described.²⁶ The reaction of the ligands L2, L3 and L4 with Co(BF₄)₂·6H₂O or CoSO₄·7H₂O in methanol led to the formation of the complexes (i.e.C2: [Co(II)L2](BF₄), C3: [Co(II)L3](BF₄)₂, C4: [Co(II)L4](BF₄)₂ with BF₄⁻ and C3′: [Co(II)L3]SO₄ and C4′: [Co(II)L4]SO₄ with SO₄²⁻ as counterions, respectively) which were precipitated and washed with diethyl ether. C3′′: [Co(II)L3](PF₆)₂ (counterion = PF₆⁻) was synthesized by adding NH₄PF₆ to a solution of C3′ (counterion = SO₄²⁻) in water. Further details of the synthesis and the characterization of the compounds are shown in the ESI (Section S2). The structural study conducted on single crystals with X-ray diffraction (Fig. 2) reveals that complexes C2 and C3′′ possess a heptacoordinate geometry which can be described as a face capped octahedron, similarly to the archetypical complex C1.²⁶ The metal centre in C2 and C3′′ is coordinated to six N and to the O of the substituents on the pyridine. The coordination bonds lengths are in the range of 2.11–2.41 Å, i.e. very close to the bond length range observed in C1 (2.09–2.41 Å). The longest bond in both the complexes is Co–N1 (with a length of 2.4101(13) Å and 2.3080(17) Å for C2 and C3′′, respectively). The angles closest to linearity are N2–Co–N5 for C2 (ca. 158°) and N4–Co–N3 (ca. 161°) for C3”. In the case of complexes derived from L4, two different tautomeric structures at the pyridine level were observed, namely C4 (enol form) and C4′ (keto form). In both structures the metal centre shows a hexacoordinate geometry: in C4′ it coordinates the oxygen of the sulphate counterion (Co–O bond distance = 2.0102(14) Å), whilst in C4 it coordinates all six N of the ligand. However, in spite of the different geometry, C4 and C4′ have structural parameters and geometries similar to C2 and C3′′ with bond distances in the range of 2.01–2.34 Å and the angle close to linearity N2–Co–N5 (ca. 156° and ca. 160° for C4 and C4′, respectively). The ¹H-NMR spectra of the complexes in D₂O confirmed the paramagnetic nature of Co(II). Values of magnetic efficiency (μ_eff) = 3.9, 4.1 and 3.8 BM were calculated for C2, C3 and C4 respectively, corresponding to high spin configurations with three unpaired electrons (Fig. ES1†).^26,43 Indeed, electronic structure calculations also predict the high spin configuration to be the most stable one for both C2 and C3 (Table ES5 in the ESI†), thus corroborating the reliability of the DFT protocol. Ultraviolet-Visible (UV-Vis) absorption spectra were recorded in CH₃CN in the presence and in the absence of trifluoroacetic acid (TFA), to evaluate the possibility of protonating the complexes (Fig. 3). The final volume of the solutions (2 mL) was kept constant to minimize the dilution effect on the absorption spectra. C2 shows a broad signal around 486 nm and a less intense peak at 634 nm. In the presence of 1 to 20 equivalents of TFA, the high energy band assumes a more defined shape and it is slightly red-shifted (489 nm), while the peak at 634 nm disappears. Only a slight hypsochromic shift is observed in the presence of acid in the UV-Vis spectra of C3, characterized by a shoulder at 490 nm. C4 displays a broad absorption at 460 nm, a slightly less intense peak at 511 nm and a weak peak at 676 nm. Upon addition of the acid, the first peak is shifted to 456 nm, the second peak remains at the same position but with a slightly higher intensity with respect to the first peak and the peak at 676 nm disappears. As expected, the absorption spectrum of complex C1 (Fig. 3a) does not show any modification upon addition of acid.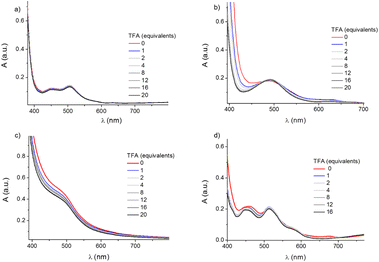

Fig. 1 Structures of the ligands L1–L4 (left) and the corresponding Co complexes (C1–C4). For the sake of clarity, the description of the different counterions of the complexes is provided in the text.

Fig. 2 Crystal structures of complexes C2, C3′′ and the two tautomers C4 (enol form) and C4′ (keto form). Colour code: Co (turquoise), N (blue), O (red), C (black), S (yellow), H (white). Non-coordinating counterions (i.e., BF₄⁻, PF₆⁻ and SO₄²⁻), solvents, and other hydrogen atoms have been omitted for clarity.

Fig. 3 UV-Vis spectra of 4 mM solutions of complexes C1 (a), C2 (b), C3 (c), and C4 (d) in CH₃CN at increasing amounts of TFA keeping the final volume (2 mL) unchanged.

3.2 Electrochemical studies

The cyclic voltammograms (CV) of each complex (Fig. 4) display two reversible and diffusion-controlled waves (Fig. ES2–ES4†). The first electrochemical waves at −1.88 V for C2, −1.64 V for C3 and −1.70 V for C4, as well as the second redox systems at −2.13 V for C2, −2.03 V for C3 and −2.14 V for C4 (all values vs. Fc⁺/Fc, Table 1) can be preferentially attributed, by DFT calculations, to bipyridine ligand-centred reduction, with substantial involvement of the metal Co^II/I reduction for the first wave (Fig. ES20†). The calculated absolute potentials for the first/second reduction obtained vs. vacuum and converted to potentials vs. Fc⁺/Fc⁴⁴ (Table ES6†) are −2.03/−2.18 and −1.80/−2.09 V for C2 and C3, respectively, in overall good agreement with the experimental values. The first signals of C2, C3 and C4 show a peak-to-peak separation of around 66 mV in accordance with the theoretical value of 59 mV for a monoelectronic Nernstian process, while the second waves have a peak-to-peak separation of 110 mV for C3 and C4 and 50 mV for C2 (Fig. ES2–ES4†). As expected, the functionalization of the ligand influences the electronic properties of the complex. In fact, the first redox signal of C2, C3 and C4 appears at potentials more negative than for the unsubstituted complex C1 (with the first reduction at −1.50 V vs. Fc⁺/Fc).

Fig. 4 Cyclic voltammograms (CVs) of 1 mM solutions of complexes (a: C2, b: C3, c: C4) recorded at 0.1 V s⁻¹ in CH₃CN with 0.1 M TBAPF₆, with glassy carbon as working electrode.

Table 1 Reduction potentials (E_1/2) in acetonitrile, half-wave potentials of the catalytic waves (E_cat) and difference between E_cat and Co^II/I for C1, C2, C3, and C4 with TFA

	First reduction (V vs. Fc^+/Fc)	Second reduction (V vs. Fc^+/Fc)	E cat (V vs. Fc^+/Fc)	E cat − ECoII/CoI (mV)
C1 (ref. 27)	−1.50	−2.06	−1.41	39
C2	−1.88	−2.13	−1.58	300
C3	−1.64	−2.03	−1.57	70
C4	−1.70	−2.14	−1.46	240

---

The second reduction of C2 and C4 also occurs at potentials more negative than those of C1 (i.e., the second reduction at −2.06 V vs. Fc⁺/Fc), whilst C3 displays the second reduction at potentials close to those of C1. However, the smaller difference (<0.1 V) between the redox potentials of the second wave with respect to those of the first wave (>0.2 V) supports a minor effect of the substituted pyridine on the ligand-based redox event, as expected on the basis of the preferential involvement of the bipyridyl moieties in the second reduction. As a final remark, while two neat redox processes can be observed for complexes C2 and C3, additional minor features can be discerned in the case of C4 (Fig. 4c) which can be associated with the coming into play of ligand tautomerism, possibly induced by trace amounts of water in the acetonitrile solvent. As a matter of fact, although the 2-pyridone tautomer is expected to be the most stable species in solution for the free ligand,⁴⁵ coordination to the cobalt centre should favour the hydroxypyridine form thus leading to a hexacoordinated species in solution. The similar redox potentials and CV shape observed for C4 and the remaining complexes C1–3 strongly support this latter hypothesis, with any changes in the tautomeric equilibrium possibly imparted by the occurrence of hydrogen bonding interactions in the presence of water (or trace amounts thereof) or acid sources (see below).

For all the complexes, the addition of increasing amounts of TFA as proton source triggers the appearance of catalytic waves at potentials more positive than those of the Co^II/I standard reduction potentials (Fig. 5 and ES5–ES7 of the ESI†). The half-wave potentials of the catalytic waves (i.e., E_cat) are shifted towards more positive potentials with respect to Co^II/I. In particular, a big shift of ca. 300 mV is observed with C2 and C4 and a less pronounced shift of 70 mV is observed with C3 (Table 1). E_cat is independent of scan rates and acid concentrations as shown in Fig. ES12.† The considerable shifts of E_cat for C2 and C4 (300 and 240 mV, respectively) together with the appreciable variation of the UV-Vis spectra in the presence of TFA (Fig. 3) suggest that a protonation of the catalyst takes place prior to the first electron transfer of the catalytic cycle (Scheme 1a). C2 protonation is expected to involve the carboxylate group of the ligand, while in the case of C4 the acid source most likely shifts the tautomeric equilibrium of the hydroxypyridine towards the 2-pyridone form leading to decoordination and protonation. Conversely, in the case of C3, the absence of major spectral changes in the UV-Vis spectra in the presence of TFA together with the small shift in potential strongly supports a catalytic mechanism similar to the one established for the prototype complex C1 (Scheme 1b).²⁷

Fig. 5 Cyclic voltammograms of 1 mM of catalysts C2 (a), C3 (b) and C4 (c) recorded in CH₃CN with 0.1 M TBAPF₆ at 30 V s⁻¹ with glassy carbon as working electrode and increasing amounts of TFA (0 red, 1 blue, 5 green, 10 brown, 15 orange and 20 navy blue mM).

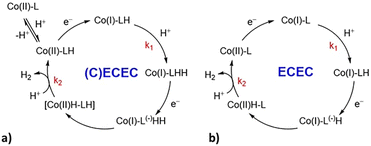Scheme 1 Proposed pathways for H₂ evolution under electrochemical conditions in acetonitrile solution with TFA as the proton source: (a) (C)ECEC for complexes C2 and C4; (b) ECEC mechanism for complexes C3 and C1.²⁷

Bulk electrolysis experiments confirmed the production of molecular hydrogen in proximity of the catalytic wave (Table ES1 and Fig. ES8†). In particular, at −1.50 V vs. Fc⁺/Fc C2, C3 and C4 gave faradaic yields of 51%, 73% and 53% respectively, while at −1.63 V vs. Fc⁺/Fc faradaic yields of 92% for C2 and 85% for C3 and C4 were achieved.

The general mechanism proposed for C3 belongs to the ECEC category (with E being the electron transfer and C the chemical, i.e. protonation, step, Scheme 1b) with the second electron transfer easier than the first and the second protonation slower than the first.⁴⁶ Foot-of-the-wave analysis (FOWA) was thus used to determine the rate constant of the first protonation step leading to a value of k₁ = 3.1 (±0.8) × 10⁷ M⁻¹ s⁻¹. Then, following the same procedure used for C1 in our previous work,²⁷ from the potential shift of the catalytic wave with respect to the Co(II)/Co(I) redox couple the rate constant of the second protonation step was attained, k₂ = 1.6 (±0.5) × 10⁵ M⁻¹ s⁻¹. In the case of C2 and C4 this approach cannot be applied because of the significant shift of the catalytic wave with respect to the Co(II)/Co(I) reduction. This observation, together with the changes of the absorption spectra in the presence of acid, is consistent with a protonation of the catalyst taking place before the catalysis (Scheme 1a). This process produces a Co(II)LH species which is the starting point of the catalytic hydrogen evolution reaction, most likely following a (C)ECEC mechanism.⁴⁷ However, the reduction potential of the Co(II)LH species is unknown, thus FOWA cannot be applied to extract kinetic information. A recently published method shows that catalytic potential measured at high scan rates (at which the catalysis is likely outrun) can actually provide the redox potential of the Co(II)LH/Co(I)LH species.⁴⁷ Unfortunately, in the case of C2 substantial catalysis can still be observed up to 47 V s⁻¹ in the presence of 15 eq. of acid (Fig. ES5†). Therefore, in the case of C2 and C4 the plateau currents extracted under scan rate independent conditions (Fig. ES11†) were used, giving catalytic rate constants as high as 1.1 (±0.2) × 10⁵ M⁻¹ s⁻¹ and 3.4 (±0.6) × 10⁴ M⁻¹ s⁻¹ for C2 and C4, respectively. Assuming that even for these complexes the second protonation is the rate-determining step of the catalysis, as observed for C1 and C3, these rate constants thus correspond to k₂ values. Further discussion on the kinetic analysis (including relevant equations and plots) is provided in the ESI (Section S5). Interestingly, in the case of C2 and C4, the use of acetic acid as the proton donor triggers the appearance of catalytic waves with E_cat near the Co^II/I couple (Fig. ES13†). These results suggest that protonation of the pristine form of the catalyst does not occur with a weaker proton source and hence the HER catalysis follows a typical ECEC mechanism (Scheme 1b). The failure to achieve protonation of the complexes under weakly acidic conditions, however, translates in the HER by C2 and C4 being promoted at more negative potentials than with TFA. This evidence is particularly relevant towards the application of C2 under photochemical conditions (see below) since a highly negative reduction potential is associated with the Co(II)/Co(I) step.

Finally, from the values of k₁ and k₂ attained for complexes C2–4 in acetonitrile using TFA as proton source, a TOF_max (turnover frequency maximum) of 1.1 × 10⁵ s⁻¹, 1.6 × 10⁵ s⁻¹ and 0.34 × 10⁵ s⁻¹ for C2, C3 and C4 respectively can be extrapolated for a 1 M acid solution, i.e., the standard conditions proposed for a rational benchmark of the performances of H₂ evolution, to obtain the catalytic Tafel plot (Fig. 6). Such a plot can be traced for each catalyst knowing TOF_max, E_cat and the apparent equilibrium potential of the H⁺/H₂ couple (0.61 V vs. Fc^+/Fc).^19,35,48 As shown in Fig. 6, the catalytic Tafel plots of the catalysts are comparable. In particular, a significant catalytic activity (i.e., log(TOF) > 1) is reached at overpotentials larger than 500 mV in the case of C1. On the other hand, the other catalysts of the series require higher overpotentials to reach a catalytic activity: 600 mV in the case of C4 and 700 mV in the case of C2 and C3.

Fig. 6 Catalytic Tafel plots relating TOFs and applied overpotentials (η) for C1 (blue), C2 (orange), C3 (green), and C4 (red).

3.3 Photochemical studies

Light-driven hydrogen production was studied upon irradiation of 5 μM solutions of each catalyst in 1.0 M acetate buffer (pH = 4) in the presence of 0.1 M ascorbic acid and 0.5 mM [Ru(bpy)₃]²⁺ (bpy = 2,2′-bipyridine) as sacrificial electron donor and photosensitizer, respectively. In this three-component system hydrogen evolution is expected to occur via a reductive route involving excitation of the [Ru(bpy)₃]²⁺, reductive quenching by the ascorbate donor, and subsequent electron transfer from the reduced sensitizer to the catalyst (HEC) either in its pristine or one-electron reduced form (eqn (1)–(3)).²³

[Ru(bpy)₃]²⁺ + hν → *[Ru(bpy)₃]²⁺ (1)

*[Ru(bpy)₃]²⁺ + Asc⁻ → [Ru(bpy)₃]⁺ + Asc˙ (2)

[Ru(bpy)₃]⁺ + HEC_ox → [Ru(bpy)₃]²⁺ + HEC_red (3)

Fig. 7a shows the evolution of H₂ during the catalysis for C3, C4 and C1 (herein used as a reference), while Fig. 7b reports the maximum turnover numbers with respect to the moles of catalysts used (TONs) and turnover frequencies (TOFs, i.e., moles of H₂ per mole of catalyst per min). The catalytic trace of C2 is not reported since negligible hydrogen evolution was observed under the present experimental conditions. Inspection of the kinetic data shows that complex C4 reached a TON of 626 with a maximum TOF of 12.5 min⁻¹, whilst C3 reached a TON of 1333 with a maximum TOF of 11.0 min⁻¹, which is slightly higher than that of C1 under the same conditions (TON of 1166 and TOF of 7.5 min⁻¹). The estimated quantum yields were 4.9%, 7.2%, and 8.2% for C1, C3 and C4, respectively. The formation of nanoparticles as decomposition products of C3 and C4 was ruled out by mercury poisoning experiments, i.e., by running the photochemical experiments in the presence of 1 mL of mercury and under the same catalytic conditions reported above. Under these conditions no appreciable variation of the photocatalytic behaviour was indeed observed, as shown in Fig. ES14.†

Fig. 7 (a) H₂ evolution in mL over time for solutions of 5 μM catalysts C1 (blue), C3 (green), and C4 (red) and without catalysts (black). The experiments were performed in 1.0 M acetate buffer at pH 4.0 with 0.1 M ascorbic acid and 0.5 mM [Ru(bpy)₃]Cl₂ at 20 °C and the solutions were irradiated with LED light at 475 nm. (b) Maximum TONs and TOFs for C1, C3 and C4.

Transient absorption spectroscopy was then employed to conduct a kinetic characterization of the photoinduced events. Upon excitation at 532 nm of a solution containing 70 μM [Ru(bpy)₃]²⁺, 0.1 M ascorbic acid, and 0.1 mM C3 in 1 M acetate buffer, a transient spectrum develops within a μs that features an absorption at 510 nm (prompt spectrum in Fig. 8a). This spectrum can be assigned to the reduced sensitizer [Ru(bpy)₃]⁺ formed via reductive quenching of the triplet excited state of the [Ru(bpy)₃]²⁺ chromophore by the ascorbate sacrificial donor (eqn (1) and (2)).^49,50 The subsequent spectral evolution (Fig. 8a) is characterized by the decrease of the 510 nm absorption and the concomitant formation of a new band at λ > 600 nm. This spectral evolution is accompanied by a clear isosbestic point at 595 nm, which can be attributed to the reduction of the cobalt complex C3 by photogenerated [Ru(bpy)₃]⁺ (eqn (3)). The broad absorptions in the visible spectrum are indeed characteristic spectral features of Co(I) species of polypyridine complexes,^27,50–54 as further confirmed by spectroelectrochemical analysis (Fig. ES15†). Similar spectral changes are monitored using complex C4 under identical experimental conditions (Fig. ES16†).

Fig. 8 (a) Transient absorption spectra between 0.7 and 35 μs obtained by laser flash photolysis (excitation at 532 nm) of a solution containing 70 μM [Ru(bpy)₃]²⁺, 0.1 M ascorbic acid, and 0.1 mM C3 in 1 M acetate buffer; (b) kinetic traces at 510 nm at 0.1–0.3 mM C3 (fitting was performed using a biexponential function in which the first component is associated with the reaction in eqn (3), and the second component with the charge recombination between Co(I) and the ascorbate radical).

Interestingly, the kinetics of the decay at 510 nm is observed to be dependent on the concentration of the cobalt complex (see Fig. 8b for C3 and Fig. ES16† for C4), as expected based upon the bimolecular nature of the electron transfer reaction in eqn (3). Under pseudo-first order kinetic conditions, fitting of the kinetic traces and subsequent normalization by the catalyst concentration (Fig. ES16 and ES17 of the ESI†) allows the determination of the bimolecular rate constant for the electron transfer process from the photogenerated [Ru(bpy)₃]⁺ to the cobalt complex (eqn (3)). These estimates yield values of 1.6 × 10⁹ M⁻¹ s⁻¹ and 1.9 × 10⁹ M⁻¹ s⁻¹ for C3 and C4, respectively, close to the diffusion-controlled kinetic regime and comparable to those experimentally determined for the parent compound C1 (2.2 × 10⁹ M⁻¹ s⁻¹) and related substituted analogues.^27,30 The transient absorption spectrum associated with the Co(I) species finally decays to the baseline within a few hundred μs with a clear second-order kinetics (Fig. ES18 and ES19† for C3 and C4, respectively) due to charge recombination with the oxidized ascorbate.^27,52 Overall, the transient absorption spectroscopic investigation establishes that: (i) similar to most polypyridine cobalt complexes both catalysts C3 and C4 rapidly react with photogenerated [Ru(bpy)₃]⁺ thus accounting for the intrinsic high catalytic activity of this class of compounds within the aforementioned photochemical reaction scheme;²³ (ii) the product of such an electron transfer event is a Co(I) catalyst species as monitored from the peculiar spectral fingerprints, (iii) the failure to observe additional spectral features upon Co(I) decay, beside those associated with charge recombination with the ascorbate radical, suggests that protonation of the one-electron reduced catalyst, likely involving a detached pyridine as supported by DFT calculations (see below), does not occur in a concerted fashion and is thus slower than experimentally detectable; (iv) the similar electron transfer kinetics observed for C1, C3, and C4 possibly indicate that any differences in terms of catalysis rates and efficiencies within the series are mainly ascribable to the kinetics of either protonation or hydrogen release. In this respect, the improved activity of complex C3 with respect to the remaining complexes of the series is well consistent with the highest catalysis rate measured in electrocatalytic experiments. On the other hand, the performance of C4 apparently contrasts with the slowest catalysis rate measured under electrochemical conditions. This can be in part attributed to possible effects exerted by the different solvent environments (acetonitrile in the electrochemical experiments vs. water in the photochemical ones) which might impact to some extent on the speciation of the catalyst, according to the observed ligand tautomerism. As to the failure to observe any activity by complex C2, this can be associated with inefficient protonation of the pristine complex in the aqueous buffer under weakly acidic conditions. Under this assumption, one-electron reduction of complex C2 (−1.88 V vs. Fc⁺/Fc, Table 1) by the photogenerated [Ru(bpy)₃]⁺ (E = −1.28 V vs. NHE in water,⁵⁵ corresponding to −1.81 V vs. Fc⁺/Fc⁵⁶) is indeed expected to be endergonic.

We would like to stress, however, that direct comparison between performance-related parameters in electrochemical and light-driven catalysis is usually too speculative and should be taken with caution since different kinetic limiting steps may actually determine the overall activity of the catalysts in either experiment. Interestingly, different rate-determining steps were recently observed by Llobet and co-workers in electrochemical and photochemical experiments when investigating the hydrogen evolution reaction of cobalt tetraazamacrocycles.⁵⁷

3.4 Computational analysis

Quantum mechanical calculations were performed on complexes C2 and C3 to corroborate the hypothesis of the different proposed mechanisms. In fact, the presence of two tautomeric forms in C4 impeded a straightforward comparison between the experimental and calculated properties.

Our previous mechanistic studies on C1 and on other related derivatives clearly pointed to an ECEC catalytic mechanism.^27,30 In more detail, based on DFT/TDDFT results and transient absorption spectroscopy measurements, we proposed that, after a first reduction of the metal centre giving a Co(I) intermediate, a protonation of the bipyridyl and/or pyridyl moieties takes place. In fact, in this family of compounds the direct protonation of the metal centre to give Co(III)–H is thermodynamically unfavourable. These first two steps are then followed by a second reduction and protonation event to form H₂ (Scheme 1b). Here, experimental evidence suggests that complexes C2 and C3 both follow an ECEC mechanism, analogously to C1, although C2 needs to be initially protonated, thus formally resulting in a (C)ECEC mechanism.

In more detail, for complex C2, both UV-Vis absorption spectroscopy (Fig. 3) and the electrochemical potential shift (Fig. 4 and 5) suggest the steady formation of a protonated complex. Consistently, the computational investigation confirms that a Co(II)-OfH (i.e. the complex protonated on the non-coordinated oxygen of the carboxylic group, the adopted nomenclature is shown in Fig. ES22†) species is formed spontaneously by proton transfer from the surrounding media. Interestingly, this species preserves the stable 7-fold coordination geometry of the metal centre. The first step is expected to involve a Co(II)-OfH + e⁻ → Co(I)-OfH reduction (see the left panel of Fig. 9). Energy shift values are given in Table ES6.† Subsequent protonation and reduction of the Co(I)-OfH species then leads to the generation of three near-in-energy intermediates involving a doubly protonated ligand, namely Co(I)-PY⁽⁻⁾H-OfH, Co(I)-BPY1⁽⁻⁾H-OfH, and Co(I)-BPY2⁽⁻⁾H-OfH. For the last protonation triggering hydrogen elimination, two different pathways were considered: (i) intermolecular proton transfer from the pyridyl/bipyridyl moiety to the cobalt centre, prior to re-protonation of the ligand and (ii) bimolecular protonation of the cobalt centre followed by hydrogen formation. The former mechanism is not feasible for the two intermediates involving the protonated pyridyl moiety (Co(I)-PY⁽⁻⁾H-OfH, activation energy barrier of 22.09 kcal mol⁻¹ and free energy difference of 13.08 kcal mol⁻¹) and those involving the bipyridyl moieties (Co(I)-BPY1⁽⁻⁾H-OfH and Co(I)-BPY2⁽⁻⁾H-OfH). Conversely, bimolecular protonation of the cobalt centre according to mechanism (ii) results in the face-to-face arrangement of two hydrogen atoms, favouring the generation of molecular hydrogen (see especially the Co(II)H-PYH-OfH structure in Fig. ES26,† as well as its energy profile, together with Co(II)H-BPY1H-OfH and Co(II)H-BPY2H-OfH, in Fig. 10, left). Interestingly, this process is particularly feasible for Co(II)H-PYH-OfH (Fig. 10, left), being almost barrierless (+0.05 eV, +1.11 kcal mol⁻¹) and slightly exergonic (−0.16 eV, −3.61 kcal mol⁻¹). This mechanistic scenario is further confirmed by theoretical analysis of the possible, alternative CEEC mechanism (Fig. ES21†). As a matter of fact, for this latter, highly endergonic pathways (by +3.18 eV and +3.34 eV) are envisioned after the first protonation towards the formation of the Co(I)-Of⁽⁻⁾H intermediate upon two electron transfer processes. At this stage hydrogen elimination is thermodynamically hampered, whilst H₂ production becomes feasible only when a strong acid such as TFA is hydrogen-bonded to the pyridyl-COOH moiety or in the presence of an acidic (H₂O)₂(H₃O⁺) cluster (Fig. ES25†). Indeed, since the hydrogen atom of the pyridyl-COOH group is required to form H₂, the acidic medium is necessary to mediate, in a concerted fashion, H₂ formation and –COOH regeneration. This computational evidence thus supports the proposed (C)ECEC mechanism. Concerning complex C3, experimental evidence suggests a typical ECEC mechanism as observed for C1. The corresponding mechanistic analysis is reported in Fig. 9 (right) with energy shift values reported in Table ES6.† After the first reduction step, Co(II) + e⁻ → Co(I), involving de-coordination of the CH₂OH group, the most favourable thermodynamic pathway goes through the formation of a Co(I)-BPY1H intermediate upon protonation (−0.10 eV, −2.3 kcal mol⁻¹). This latter is stabilized by an intramolecular N–H⋯OH bond between the protonated BPY1H moiety and the OH group of the pyridyl moiety. On the other hand, protonation of the other available bipyridyl to generate Co(I)-BPY2H as the first protonation step is predicted to be more than 1.08 eV (25 kcal mol⁻¹) higher in energy, due to the impossibility of forming any hydrogen bond. The second reduction step then involves the formation of a Co(I)-BPY1⁽⁻⁾H intermediate. Finally, to complete the ECEC mechanism the last chemical step implies protonation of the cobalt centre, thus forming a Co(II)H-BPY1H intermediate that further evolves to produce H₂ similarly to what is observed for the parent C1.²⁷ As depicted in Fig. 10 (right) and Fig. ES26† hydrogen elimination from the Co(II)H-BPY1H species occurs thanks to the close interaction between the H atom of the protonated bipyridine moiety (H_a) and the H atom (H_b) of the protonated Co centre (NH_a-BPY⋯H_b-Co distance of 1.80 Å). For this reaction a transition state of ca. 0.48 eV (11.0 kcal mol⁻¹) is predicted, whose value is similar to that estimated in the case of C1 (10 kcal mol⁻¹). On a thermodynamic basis, the final H₂ release is negligibly endergonic for C3 (+0.01 eV, +0.23 kcal mol⁻¹), while a larger ΔG was calculated for C1 (ca. +0.13 eV, +3 kcal mol⁻¹).²⁷ We should note that C3 could also follow a different pathway implying the formation of H₂ through reaction of the pyridyl OH group with cobalt-hydride species (Co(II)H-BPY1H in Fig. ES26,† H⋯H distance of 1.56 Å). Nevertheless, although it is closer in distance, such a reaction would lead to an unstable deprotonated OH group and is thus not feasible (Fig. ES24†).

Fig. 9 Calculated free energy profiles in acetonitrile for the possible reaction steps involved in the proposed mechanism for C2 (left) and C3 (right). Values and profiles of the relative free energy changes (ΔG) are given in Table ES6.† The zero is defined as the free energy of the Co(II) compound (Co(II)-OfH for C2; Co(II) for C3) plus that of two protons with an activity of 1 (apparent pH = 0 in acetonitrile) and two electrons at the potential of the NHE in acetonitrile. For C2 L′ = BPY1, BPY2, and PY. The corresponding structures can be found in Fig. ES26.†

Fig. 10 Calculated free energy profiles (ΔG) starting from the second protonation step until formation of H₂, for C2 (left) and C3 (right). At this step, once formed, H₂ is still in interaction with the complex (see structures in Fig. ES26†). The structures corresponding to stationary points (minima and transition states, TS) are given in Fig. ES26,† including the imaginary frequency of the most relevant TSs.

Akin to what was observed for the parent complex C1 and the other substituted analogues, mechanistic analysis of catalytic hydrogen evolution by complexes C2 and C3 still suggests the important role of the hexadentate polypyridine ligand wherein pendant pyridine moieties in the reduced state(s) of the catalyst act as proton relays favouring hydrogen elimination via intramolecular routes.

We believe that this ability represents a peculiar figure-of-merit of this class of molecular catalysts, resulting in enhanced catalysis rates over molecular analogues.²³

4. Conclusions

In conclusion, we have reported here a series of new polypyridyl cobalt complexes introducing –CO₂⁻, –CH₂OH and –OH ortho to the nitrogen of the pyridine group. Surprisingly, C2 and C3 display a heptacoordinate structure with the seventh coordination site directly occupied by the ligand. Electrochemical studies in acetonitrile using TFA as the proton donor confirm the ability of all complexes to act as molecular catalysts for the hydrogen evolution reaction with complex C3 displaying the highest catalysis rate. Photochemical studies under homogeneous conditions in aqueous solution confirmed improved performances for catalyst C3. The experimental electrochemical data, supported by DFT calculations, point for all complexes towards an ECEC catalytic mechanism which, in the case of both C2 and C4, requires an initial ligand protonation to trigger catalysis according to a (C)ECEC mechanism. DFT computations further support the important role of the chelating ligand in providing an internal proton relay to assist the hydrogen elimination via intramolecular proton transfer processes, thus showcasing a fundamental requisite to achieve sustained catalysis rates using polypyridine cobalt complexes.

Author contributions

FL and AR designed the molecules. FL synthesized the molecules and performed photochemical H₂ evolution studies. FD and MN performed transient absorption spectroscopy. FL, JF, AM and VA performed electrochemical investigations. ES and RS collected and resolved X-ray crystal structures. MM and MP performed computational studies. FL and AR wrote the first draft and MM, MP, MN, and VA collaborated in the finalization of the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work received funding from the Swiss National Foundation (Grant 159716, FN 7359) and French National Research Agency (Labex ARCANE, CBH-EUR-GS, ANR-17-EURE-0003). MN acknowledges the University of Ferrara (FIR2021, FAR2022) for funding. Computational resources from the mésocentre EXPLOR of Université de Lorraine (Project 2018CPMXX0602) are acknowledged.

Notes and references

1. V. Balzani, A. Credi and M. Venturi, Curr. Opin. Chem. Biol., 1997, 1, 506–513.
2. N. S. Lewis and D. G. Nocera, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 15729–15735.
3. W. T. Eckenhoff, W. R. McNamara, P. Du and R. Eisenberg, Biochim. Biophys. Acta Bioenerg., 2013, 1827, 958–973.
4. H. B. Gray and A. W. Maverick, Science, 1981, 214, 1201–1205.
5. V. Balzani, A. Credi and M. Venturi, ChemSusChem, 2008, 1, 26–58.
6. E. S. Andreiadis, M. Chavarot-Kerlidou, M. Fontecave and V. Artero, Photochem. Photobiol., 2011, 87, 946–964.
7. G. Segev, J. Kibsgaard, C. Hahn, Z. J. Xu, W.-H. Cheng, T. G. Deutsch, C. Xiang, J. Z. Zhang, L. Hammarström, D. G. Nocera, A. Z. Weber, P. Agbo, T. Hisatomi, F. E. Osterloh, K. Domen, F. F. Abdi, S. Haussener, D. J. Miller, S. Ardo, P. C. McIntyre, T. Hannappel, S. Hu, H. Atwater, J. M. Gregoire, M. Z. Ertem, I. D. Sharp, K.-S. Choi, J. S. Lee, O. Ishitani, J. W. Ager, R. R. Prabhakar, A. T. Bell, S. W. Boettcher, K. Vincent, K. Takanabe, V. Artero, R. Napier, B. R. Cuenya, M. T. M. Koper, R. Van De Krol and F. Houle, J. Phys. D: Appl. Phys., 2022, 55, 323003.
8. S. Berardi, S. Drouet, L. Francàs, C. Gimbert-Suriñach, M. Guttentag, C. Richmond, T. Stoll and A. Llobet, Chem. Soc. Rev., 2014, 43, 7501–7519.
9. M. Grätzel, Nature, 2001, 414, 338–344.
10. M. Grätzel, Inorg. Chem., 2005, 44, 6841–6851.
11. V. S. Thoi, Y. Sun, J. R. Long and C. J. Chang, Chem. Soc. Rev., 2013, 42, 2388–2400.
12. W. T. Eckenhoff, Coord. Chem. Rev., 2018, 373, 295–316.
13. P. Du and R. Eisenberg, Energy Environ. Sci., 2012, 5, 6012–6021.
14. D. Brazzolotto, L. K. Wang, H. Tang, M. Gennari, N. Queyriaux, C. Philouze, S. Demeshko, F. Meyer, M. Orio, V. Artero, M. B. Hall and C. Duboc, ACS Catal., 2018, 8, 10658–10667.
15. T. Straistari, J. Fize, S. Shova, M. Réglier, V. Artero and M. Orio, ChemCatChem, 2017, 9, 2262–2268.
16. D. Brazzolotto, M. Gennari, N. Queyriaux, T. R. Simmons, J. Pecaut, S. Demeshko, F. Meyer, M. Orio, V. Artero and C. Duboc, Nat. Chem., 2016, 8, 1054–1060.
17. D. Streich, Y. Astuti, M. Orlandi, L. Schwartz, R. Lomoth, L. Hammarström and S. Ott, Chem.–Eur. J., 2010, 16, 60–63.
18. M. Razavet, V. Artero and M. Fontecave, Inorg. Chem., 2005, 44, 4786–4795.
19. C. Baffert, V. Artero and M. Fontecave, Inorg. Chem., 2007, 46, 1817–1824.
20. X. Hu, B. M. Cossairt, B. S. Brunschwig, N. S. Lewis and J. C. Peters, Chem. Commun., 2005, 4723–4725.
21. O. Pantani, E. Anxolabéhère-Mallart, A. Aukauloo and P. Millet, Electrochem. Commun., 2007, 9, 54–58.
22. V. Artero, M. Chavarot-Kerlidou and M. Fontecave, Angew. Chem., Int. Ed., 2011, 50, 7238–7266.
23. F. Droghetti, F. Lucarini, A. Molinari, A. Ruggi and M. Natali, Dalton Trans., 2022, 51, 10658–10673.
24. N. Queyriaux, R. T. Jane, J. Massin, V. Artero and M. Chavarot-Kerlidou, Coord. Chem. Rev., 2015, 304, 3–19.
25. D. Z. Zee, T. Chantarojsiri, J. R. Long and C. J. Chang, Acc. Chem. Res., 2015, 48, 2027–2036.
26. F. Lucarini, M. Pastore, S. Vasylevskyi, M. Varisco, E. Solari, A. Crochet, K. M. Fromm, F. Zobi and A. Ruggi, Chem.–Eur. J., 2017, 23, 6768–6771.
27. F. Lucarini, J. Fize, A. Morozan, M. Marazzi, M. Natali, M. Pastore, V. Artero and A. Ruggi, Sustain. Energy Fuels, 2020, 4, 589–599.
28. M. Nippe, R. S. Khnayzer, J. A. Panetier, D. Z. Zee, B. S. Olaiya, M. Head-Gordon, C. J. Chang, F. N. Castellano and J. R. Long, Chem. Sci., 2013, 4, 3934–3945.
29. S. Schnidrig, C. Bachmann, P. Muller, N. Weder, B. Spingler, E. Joliat-Wick, M. Mosberger, J. Windisch, R. Alberto and B. Probst, ChemSusChem, 2017, 10, 4570–4580.
30. F. Lucarini, D. Bongni, P. Schiel, G. Bevini, E. Benazzi, E. Solari, F. Fadaei-Tirani, R. Scopelliti, M. Marazzi, M. Natali, M. Pastore and A. Ruggi, ChemSusChem, 2021, 14, 1874–1885.
31. A. Orlando, F. Lucarini, E. Benazzi, F. Droghetti, A. Ruggi and M. Natali, Molecules, 2022, 27, 8277.
32. C. H. Lee, D. K. Dogutan and D. G. Nocera, J. Am. Chem. Soc., 2011, 133, 8775–8777.
33. M. Natali, E. Badetti, E. Deponti, M. Gamberoni, F. A. Scaramuzzo, A. Sartorel and C. Zonta, Dalton Trans., 2016, 45, 14764–14773.
34. C. Costentin and J. M. Saveant, ChemElectroChem, 2014, 1, 1226–1236.
35. V. Artero and J. M. Saveant, Energy Environ. Sci., 2014, 7, 3808–3814.
36. C. Costentin, S. Drouet, M. Robert and J. M. Saveant, J. Am. Chem. Soc., 2012, 134, 11235–11242.
37. J. T. Muckerman and E. Fujita, Chem. Commun., 2011, 47, 12456–12458.
38. C. P. Kelly, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2007, 111, 408–422.
39. J. E. Bartmess, J. Phys. Chem., 1994, 98, 6420–6424.
40. C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170.
41. E. Cancès, B. Mennucci and J. Tomasi, J. Chem. Phys., 1997, 107, 3032–3041.
42. G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman, and D. J. Fox, Gaussian 16 Revision C.01, Gaussian, Inc., Wallingford CT, 2016.
43. K. De Buysser, G. G. Herman, E. Bruneel, S. Hoste and I. Van Driessche, Chem. Phys., 2005, 315, 286–292.
44. C. Fujisue, T. Kadoya, T. Higashino, R. Sato, T. Kawamoto and T. Mori, RSC Adv., 2016, 6, 53345–53350.
45. L. Forlani, G. Cristoni, C. Boga, P. E. Todesco, E. D. Vecchio, S. Selva and M. Monari, ARKIVOC, 2002, 2002, 198–215.
46. C. Costentin and J.-M. Savéant, ChemElectroChem, 2014, 1, 1226–1236.
47. C.-B. Li, A. J. Bagnall, D. Sun, J. Rendon, M. Koepf, S. Gambarelli, J.-M. Mouesca, M. Chavarot-Kerlidou and V. Artero, Sustain. Energy Fuels, 2022, 6, 143–149.
48. V. Fourmond, P. A. Jacques, M. Fontecave and V. Artero, Inorg. Chem., 2010, 49, 10338–10347.
49. E. Deponti and M. Natali, Dalton Trans., 2016, 45, 9136–9147.
50. M. Natali, ACS Catal., 2017, 7, 1330–1339.
51. R. S. Khnayzer, V. S. Thoi, M. Nippe, A. E. King, J. W. Jurss, K. A. El Roz, J. R. Long, C. J. Chang and F. N. Castellano, Energy Environ. Sci., 2014, 7, 1477–1488.
52. W. M. Singh, M. Mirmohades, R. T. Jane, T. A. White, L. Hammarström, A. Thapper, R. Lomoth and S. Ott, Chem. Commun., 2013, 49, 8638–8640.
53. A. Lewandowska-Andralojc, T. Baine, X. Zhao, J. T. Muckerman, E. Fujita and D. E. Polyansky, Inorg. Chem., 2015, 54, 4310–4321.
54. B. N. DiMarco, D. E. Polyansky, D. C. Grills, P. Wang, Y. Kuwahara, X. Zhao and E. Fujita, ChemPhysChem, 2021, 22, 1478–1487.
55. N. Queyriaux, E. Giannoudis, C. D. Windle, S. Roy, J. Pécaut, A. G. Coutsolelos, V. Artero and M. Chavarot-Kerlidou, Sustain. Energy Fuels, 2018, 2, 553–557.
56. V. D. Parker, K. L. Handoo, F. Roness and M. Tilset, J. Am. Chem. Soc., 1991, 113, 7493–7498.
57. S. Grau, M. Schilling, D. Moonshiram, J. Benet-Buchholz, S. Luber, A. Llobet and C. Gimbert-Suriñach, ChemSusChem, 2020, 13, 2745–2752.

---

Footnote

† Electronic supplementary information (ESI) available: Detailed synthetic procedures and compounds characterization, electrochemical and photochemical supplementary data, foot of the wave analysis, and crystallographic, spectroscopic and computational data. CCDC 2245266–2245269. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d3se00295k

---