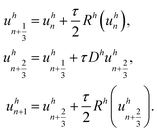Experimental and numerical investigation of microbial growth in two-phase saturated porous media at the pore-scale

Abstract

Efficient long-term storage of energy is of crucial importance for an economy which is completely based on renewable energies. Subsurface storage of green hydrogen could contribute substantially to reaching this goal. However, the injection of hydrogen into the subsurface could lead to an increased activity of microorganisms which results in gas conversion and an increase in biomass. In this work, the growth of methanogenic microorganisms was studied by a combined experimental and numerical modeling approach. For the experiments, artificial porous structures between two glass plates, referred to as glass–silicon–glass micromodels, were used. These transparent quasi-two-dimensional micromodels allow the direct observation of microbial processes by microscopic analysis. Experiments were performed under static and dynamic conditions to get a detailed insight into the temporal and spatial dynamics of the microorganisms. The experiments were accompanied by two-dimensional reactive transport modeling to further improve the understanding of microbial dynamics. The model takes into account gas and water as phases and the diffusive transport of the substrate inside both phases. A Monod model is used for describing the growth of microbes inside a partially saturated porous medium. The experimental and simulated data are in very good agreement. It has been shown that during the static experiments, nutrient-limited growth inside the liquid phase of the porous medium takes place. However, during dynamic experiments with a re-supply of nutrients, the microbial density quickly reaches a maximum near the gas/liquid interface. Growth is continuous but much slower further away from this interface. The study shows new substantial findings which can serve as a basis for developing improved models on the continuum scale and can be used to optimize the management of long-term storage systems in deep reservoirs.

---

1 Introduction

Due to the increasing share of renewable energy production and the consequent development of a hydrogen-based economy, a suitable long-term storage solution for hydrogen is necessary. Based on already established subsurface storage technologies for natural gas, hydrogen could either be stored in leached salt caverns for short-term periods or in naturally formed porous structures for long-term storage. The feasibility of cyclic underground hydrogen storage to balance electrical energy supply from renewable sources was already studied theoretically and demonstrated in first field tests.^1–3

The injection of hydrogen could lead to an increased activity of microorganisms in the subsurface. Microbial impacts are already known from former town gas storages (with up to 60% H₂) and were shown for an underground hydrogen storage field test with 10% H₂.^3,4 Four different metabolic pathways are discussed for the use of hydrogen as an energy source: methanogenesis, sulfate-reduction, homoacetogensis, and iron-reduction.⁵ The last three metabolic pathways would result in an irreversible loss of energy. In contrast, methanogenesis by methanogenic archaea could lead to the production of methane, which has advantageous chemical properties compared to hydrogen: it has a higher calorific value, could be distributed over the existing gas grid, and be used to drive existing power plants, heating systems, and vehicles. If the hydrogen produced from renewable energy would be injected together with captured carbon dioxide and any gas leaks could be excluded, the produced methane would be climate-neutral. A system designed to stimulate this process is called an underground methanation reactor.^5–7

Microbial effects are usually studied in the laboratory by incubation or batch experiments. For this purpose, brine samples are taken from the reservoir, transferred under anaerobic conditions, and incubated in the laboratory with or without the addition of additives.⁴ Subsequently, it is observed whether microbial growth or conversions take place.

Amigáň et al.⁸ conducted such experiments with samples from the Czech gas storage in Lobodice. They have shown the potential of methanogenic archaea, which have converted part of the hydrogen into methane. In the Underground Sun Storage³ and Underground Sun Conversion projects,⁹ similar reactor experiments have been conducted to study the growth of microorganisms with a mixture of brine, rocks, and a methane–carbon dioxide–hydrogen mixture (4% H₂, 0.3% CO₂ and rest methane). The results show a strong shift in the microbial consortium towards methanogenic species, a decrease in the hydrogen concentration, and an increase in the methane concentration. Thus, the potential for methanogenesis was also shown for this reservoir.

However, while incubation and batch reactor experiments can be used to determine the potential for methanation, the actual dynamics in gas storage can only be determined to a very limited extent as there are important differences between the conditions in batch reactors and storage reservoirs:

• Batch reactors have a much smaller interfacial area between the phases than partially water-saturated rocks in a reservoir.

• The liquid solution in batch reactors is well mixed while in a gas storage water has limited mobility and trapped water bodies can even be completely separated from each other.

• Interactions with flow and transport processes as they occur in a gas storage are not reflected in batch reactors.

To overcome these shortcomings, a microfluidics approach is used in this work to study microbial methanogenesis. In this experimental technique, the storage rock is represented by artificial porous structures between two glass plates, referred to as a glass–silicon–glass micromodel. These transparent quasi-two-dimensional micromodels allow the direct observation of microbial processes by microscopic analysis.

The methodology has already been used before to investigate fluid dynamics and microbial growth.

Regarding fluid dynamics during underground hydrogen storage, microfluidics was used recently to study possible wettability and relative permeability changes. Van Rooijen¹⁰ presents an experimental design where hydrogen in the gaseous phase is injected into a micromodel to study the dynamic contact angles between water, hydrogen, and solid grains. However, no microbes are used in the experiments. A second study that used microfluidics to study the flow of hydrogen in porous media was published by Lysyy et al.¹¹ Similar to the study by Van Rooijen, the focus of this research is the multi-phase flow of hydrogen and water in porous media, but no microbial growth is involved.

However, also the capability of studying microbial growth in micromodels, which represent the porous medium, is demonstrated by several authors. Liu et al.¹² presented the use of microfluidics to study sulfate-reducing microbes during underground hydrogen storage. The focus is on the effect of microbial conversion, bio-clogging, and changes in phase saturation.

Gaol et al.¹³ used microfluidics in experiments with an oil–water system. They obtained microbial growth dynamics from optical analysis and observed gas production and bio-clogging effects. Aufrecht¹⁴ studied the flow rate reduction due to clogging by microorganisms, which were externally cultivated and then injected. In contrast, Hassannayebi et al.¹⁵ performed a study where the microbes are grown in situ, and a substantial biomass increase over time was observed.

The experimental work by Hassannayebi et al.¹⁵ and Aufrecht et al.¹⁴ was combined with numerical simulations. Both studies concentrate on modeling the change of hydraulic properties on the pore-scale due to microbial growth and thus focus on the impact of biomass on hydraulic properties and not on a correct description of microbial growth during the experiments. Further numerical models for microbial growth during underground hydrogen storage were proposed by Hagemann⁵ at the field scale and by Ebigbo et al.¹⁶ at the pore-scale. However, the proposed numerical models for the growth of microbes during underground hydrogen storage lack validation by experimental or field data.

The existing gap between the theoretical assumption of substrate-limited growth (modified Monod model) and its experimental validation in a storage scenario must be closed. This study analyses newly obtained experimental data with a 2-D pore-scale model to test the viability and limitations of a growth model, obtain the necessary parameters, and improve the understanding of microbial dynamics. Such a combination of experimental study and numerical simulations with a focus on microbial growth in gas–water-saturated porous media is a novelty and essential for the implementation and optimization of underground hydrogen storage.

2 Experimental methodology

The measurement of the development of microbial density in a porous medium in traditional experiments like core-flooding is difficult, as microorganisms are not always mobile and measurements of the microbial density is not easy. Thus, in this study experiments in microfluidic chips are conducted, as they allow a visualization of the bacteria through fluorescence and a determination of microbial density by counting active cells or by determining the intensity of fluorescence.

This study focuses on methanation performed by hydrogenotrophic methanogens, which can be described by the net equation

CO₂ + 4H₂ ⇔ CH₄ + 2H₂O, (1)

where hydrogen is the electron donor (and energy source) and carbon dioxide is the electron acceptor (and carbon source). The produced biomass is accounted for with a yield coefficient in the two-dimensional model, see Section 3.

2.1 Microfluidic setup

The microfluidic setup consists of three main parts: a fluid handling system, a microscope, and a micromodel, which is placed in a holder.

2.1.1 Micromodel. The crucial part of a microfluidic setup is a microchip, which represents the porous media. It has a very small vertical extension and can be treated as an essentially 2-dimensional system. The porous structure is etched into a plate, which in this case consists of silicon. Thus, processes commonly used in computer manufacturing (masking by UV light and subsequent wet etching) can be used. The etching process removes a layer with a thickness of 50 μm and can reliably create pores with a minimal size of 8 μm, resulting in a minimal width to height ratio of 6 : 1. The difficult part of the whole process is the airtight sealing of the silicon layer. This is realized by a seal with Borofloat 33 glass layers on the top and the bottom of the silicon chip in an anodic bonding process. Two boreholes are drilled into the glass on the bottom to enable the injection of fluids into the structure.

The structure to be etched into the microchip can be chosen by the designer. The procedure also allows the production of identical replica. In our setup, the structure consists of circular grains, see Fig. 1. The distribution and arrangement of grain diameters is based on the pore and grain size distribution of a real sandstone (Bentheimer sandstone).¹⁷ The dimensions of the porous structure are 50 mm × 9 mm × 0.05 mm. The resulting porosity is 26.5% and the measured permeability is seven Darcy. The porous structure of the micromodel has a total volume of 7 μL.¹⁸

Fig. 1 Structure of the microchips used in the experiments: black indicates pore space and white color indicates the grains.

2.1.2 Fluid-handling system and holder. To enable methanation, the complete system has to be brought under strict anaerobic and sterile conditions. This puts high requirements on all tubes and connections. In order to minimize the diffusion and still keep the system as flexible as possible, polyether–ether–ketone (PEEK) was used for the tubes (Idex P-732 Natural PEEK, Upchurch Scientific Inc.). Syringe pumps (Harvard Pump 11 Elite Series, Harvard Apparatus Ltd.) with gas-tight syringes (Series 1000, Hamilton) were used to inject the liquids and gases into the micromodel. The pressure was recorded at the inlet and outlet of the micromodel via absolute pressure sensors from Keller AG with a pressure range of 10 bar and an accuracy of 0.05%.

As the chip is embedded between glass plates, the pore space is translucent. To allow the recording of high-quality pictures with a resolution high enough to capture individual bacteria, an upright epifluorescence microscope (Axio Imager.Z2m, Carl Zeiss GmbH) is used in combination with a high-quality camera. Active methanogenic bacteria produce coenzyme F420 and therefore absorb light at a wavelength of 420 nm and emit it at 520 nm. A matching filter is used to identify active bacteria.

The micromodel, introduced in Section 2.1.1, is placed into an integrated holder, which maintains a constant working temperature and enables the flow of fluids through the micromodel. The holder is made from PEEK, similar to the tubes and valves. The heating system is composed of an ITO-glass plate in which the temperature is controlled. Though the pressure in a real reservoir is much higher, the operating pressure was limited to 2 bar as the storage bottles for the liquids at the in- and outflow were made of glass. The glass bottles allow the monitoring of the turbidity of the liquids, which is an important indicator for unintended microbial growth in the glass bottles.

2.2 Microbial strains

In a natural reservoir, many different types of microorganisms could compete for hydrogen as an energy source (e.g. sulfate- or iron-reducing bacteria). However, this study only focuses on methanogenic bacteria. Methanogenic species can differ significantly in their growth behavior and conversion rate of hydrogen. An overview of methanogens and their preferred habitats was published by Thaysen et al.¹⁹ The main inhibitor for microbial growth in the subsurface could be the salt concentration in the formation water. For the experiments, two types of microorganisms with two different optimal living conditions have been selected:

• Methanothermococcus thermolithotrophicus (species 1); optimal temperature = 65 °C; optimal NaCl-concentration = 4%; optimal pH-value = 7; doubling time of population = 55 min.

• Methanolacinia petrolearia (species 2); optimal temperature = 37 °C; optimal NaCl-concentration = 1–3%; optimal pH-value = 7; doubling time of population = 10 h.

Both microorganisms were originally found living under harsh conditions. The origin of the first species is a heated seafloor in Italy, whereas species 2 was found in a deep oil reservoir in Japan. However, both species can potentially live in deep porous formations.¹⁹

In order to optimize the conditions necessary for growth and to prevent inhibiting effects by e.g. salt concentration the culture medium 141 was used. The culture medium contains iron and other tracer elements, different salt minerals (MgCl, KCl, NaCl), and low concentrations of yeast extract and acetate. The exact composition of the culture medium is given by DSMZ.²⁰ Hydrogen and carbon dioxide were provided in a stoichiometric mixture consisting of 80% hydrogen and 20% carbon dioxide.

2.3 Experimental overview and procedure

Two different types of experiments have been performed: static experiments investigate the growth of microorganisms under substrate-limited conditions, comparable to an idle/storage period in an underground hydrogen storage. After injection of the gas mixture, the model is sealed off. These series give insides if the theoretical assumption made in the numerical models proposed by Hagemann⁵ and Ebigbo et al.¹⁶ for substrate-limited growth conditions is valid. Dynamic experiments, in contrast, investigate microbial growth with an unlimited supply of nutrients provided by a continuous gas flow through the micromodel. These conditions are more realistic for underground hydrogen storage during the injection period and the results can be used to assess if microbial growth under these conditions can be reproduced by the numerical model as well.

Before each experiment, the micromodel is cleaned with acid (H₂SO₅) and then the permeability of the micromodel is measured and compared to the known permeability of the structure to verify the quality of the cleaning. The micromodel is attached to the holder, placed under the microscope and the air tightness of the system is checked. The micromodel is first flooded with isopropanol, then with distilled water, and finally with nitrogen for a duration of 12 hours to obtain anaerobic conditions. The nitrogen is then replaced by distilled and oxygen-free water. Complete saturation is validated by taking an image of the micromodel. By securing a full water-saturated system, the preparation is finished.

In total, 3 mL of a solution containing the microorganisms is injected at a very low flow rate of 10 μL min⁻¹ into the micromodel to assure a uniform distribution of the microorganisms. The system is checked for remaining gas bubbles before a gas mixture consisting of 80% hydrogen and 20% carbon dioxide is injected at a rate of 1–2 μL min⁻¹ corresponding to a velocity of approx. 3 m d⁻¹ in the micromodel until an average gas saturation of 75–80% is obtained, which is validated by subsequent image analysis. Initially, a higher inlet pressure is needed to replace the water in the system. After the breakthrough of the gas phase, the pressure in the system drops significantly to a value sustained during the experiment (Table 1).

Table 1 Microbial species, environmental conditions, and duration for the different experiments

Exp. no.	Species	Type	Temp. [°C]	Pres. [hPa]	Exp. run time [h]
1	Species 1	Static	55 ± 3	1200 ± 150	24
2	Species 1	Static	63 ± 3	1300 ± 150	24
3	Species 1	Dynamic	63 ± 3	1700 ± 200	48
4	Species 1	Dynamic	63 ± 3	1750 ± 200	52
5	Species 2	Static	37 ± 2	1100 ± 100	72
6	Species 2	Static	37 ± 2	1500 ± 100	68

---

The breakthrough marks the beginning of the actual growth experiment. Whereas in static experiments, the micromodel is now sealed off, in dynamic experiments the gas injection continues at the same rate for the duration of the experiment.

Images of the micromodel are made using a camera mounted to a microscope. The sample can be automatically and reproducibly positioned to obtain images of a certain section of the micromodel. Images can be taken at 5×, 10× and 40× magnification. Images at 5× magnification in combination with a dark light (phase) filter are used to obtain the distribution of gas and water and to calculate the gas and water saturation in the micromodel. Even at this magnification, it is necessary to take 100–120 images of the micromodel, which are stitched together later. A 10× magnification in combination with a filter for the fluorescence of the F420 enzyme (425/26 BrightLine HC and 520/35 BrightLine HC) is used to obtain images of the bacterial distribution over the whole micromodel (taking more than 200 images while repositioning the sample). After the start of each experiment, 20–30 locations are identified at which images with 40× magnification are taken every 15 minutes during the experiment to count individual microorganisms. If the liquid phase at one of the locations was displaced by the gas phase during the experiment, the location was excluded from further analysis, and a new location was selected nearby.

During the whole experiment, the pressure at the inlet and outlet as well as the temperature in the micromodel are recorded. Changes in room temperature lead to fluctuations of below 3 degrees celsius in the experiment (Table 1).

Static experiments have been conducted both with Methanococcus thermolithotrophicus (species 1) and Methanolacinia petrolearia (species 2), while dynamic experiments were only conducted with species 1 (Table 1).

2.4 Image post-processing

The images taken during the experiment are post-processed using a combination of Zen, ImageJ, and programs written in Matlab. After the removal of light scattering, the images with 40× magnification are binarized into the fluorescent microorganisms and the background. The magnification is assumed to be large enough to count individual microorganisms. Counting is performed automatically with an algorithm verified by manual counting for selected images. Thus, an estimation of the microbial density at the representative locations is possible. This process is repeated for all locations and measurement times. Fig. 2 gives an example of an image before and after processing.

Fig. 2 Image of the pore space at 40× magnification: while there is a significant amount of light scattering in the original image at the left, microorganisms (light green) can easily be distinguished from grains (black) and liquid (blue) in the post-processed image on the right.

The gas saturation in the micromodel is determined by a similar process. However, the images of subregions of the micromodel taken at 5× magnification are first stitched together using ZEN to obtain a single image of the whole micromodel. This is done for both images with the fluorescence filter as well as the dark filter, which are then combined with ImageJ to enhance the phase contrast in the images. The image is then thresholded to obtain an image of the phase distribution from which the phase saturations are calculated. An example of a resulting image is shown in Fig. 3.

Fig. 3 Distribution of gas (grey), water (blue) and solid phase (black) during a static experiment. The residual water saturation is 25%.

3 Two-dimensional physico-chemical model

Mathematically, methanation can be modelled as a system of partial differential equations describing bacterial growth as a reaction and the transport of reactants and products as a diffusive process:in [0,T] × Ω ⊂ [Doublestruck R] × [Doublestruck R]² for the components bacteria (X in cells per L), carbon dioxide (CO₂ in mol L⁻¹), hydrogen (H₂ in mol L⁻¹) and methane (CH₄ in mol L⁻¹), i.e. i ∈ {X, CO₂, H₂, CH₄}, equipped with initial and boundary conditions
Here, Ω ⊂ [Doublestruck R]² is the spatial set to be modelled, i.e. the micromodel (or microchip) introduced in 2.1.1. The boundary of Ω, called ∂Ω, is divided into the two sets ∂Ω = ∂Ω_D ∪ ∂Ω_N, on which Dirichlet or Neumann boundary conditions are applied, respectively.

With given initial and boundary conditions, a unique solution

u_i : [0,T] × Ω → [Doublestruck R]

can be obtained, which describes the concentration of component i for every time point t ∈ [0,T] and for every point x ∈ Ω ⊂ [Doublestruck R]². The spatially varying diffusion coefficients for each component i are described by a function D_i : Ω → [Doublestruck R], which is assumed to be constant over time due to a static phase distribution. The reaction term R_i : [Doublestruck R]⁴ → [Doublestruck R] can depend on the concentrations of all components of u(t,x) ∈ [Doublestruck R]⁴, resulting in a coupling of the diffusion equations.

3.1 Diffusion coefficients

To obtain the spatial distribution of diffusion coefficients D_i : Ω → [Doublestruck R] for each component i ∈ {X, CO₂, H₂, CH₄} we make the following assumptions:

• Bacteria only exist in the liquid phase. They do not diffuse and there is also no active movement of the bacteria (no flagellas and no chemotaxis). Therefore, D_X(x) = 0 for all x ∈ Ω.

• All other components can exist in both the liquid and the gas phase. We assume local thermodynamic equilibrium at the phase boundaries. Dissolution of gases can be described using Henry's law.

• We can divide Ω into three disjoint sets: Ω_g (gas), Ω_l (liquid), and Ω_s (solid) on which D_i is constant for each component. This means that every point x ∈ Ω represents either a gas, a liquid, or a solid point. This phase distribution is known from the experiment.

Diffusion between neighbouring cells with different phase states can then be calculated from the harmonic mean of the diffusion coefficients for both phases taking into account Henry's law.

The diffusion coefficients for each component in each phase and the dimensionless Henry coefficients (describing the ratio of the concentration of a component in the liquid phase to the concentration in gas in the gas phase) are given in Table 2.

Table 2 Diffusion coefficients and Henry coefficients for the components and phases

Component	H [—]	D l [dm^2 min^−1]	D g [dm^2 min^−1]
Bacteria (X)	—	0	0
Carbon dioxide (CO2)	0.830	1.15 × 10^−5	1.15 × 10^−1
Hydrogen (H2)	0.019	2.70 × 10^−5	2.70 × 10^−1
Methane (CH4)	0.035	8.94 × 10^−6	8.94 × 10^−2

---

For the simulated experiments the phase distribution was obtained from a picture taken during the experiments and post-processed as described in 2.4. Each pixel in the picture yields one spatial cell that belongs either to Ω_g, Ω_l or Ω_s.

3.2 Reaction model for microbial growth

Bacterial growth is modelled as a reaction based on Michaelis–Menten kinetics (also called the Monod model) describing the dependence of reaction speed on reactant concentrations. Let c be the concentration of a substance consumed by the bacteria, then the Michaelis–Menten kinetics is formulated as

Note that M(0) = 0, i.e. if the reactant concentration is zero, the growth rate is zero as well, and M(c) → 1 as c → ∞, i.e. there exists an upper limit to the growth rate. The parameter k_c is called half saturation constant as

A minimal set of reactants consisting of bacteria X, carbon dioxide CO₂, hydrogen H₂, and methane CH₄ was chosen to avoid an over-parametrization of the model. Rough estimates show that the produced water can be neglected. Based on the reaction given by eqn (1), we model the bacterial growth with a double Michaelis–Menten kinetics including the reactants CO₂ and H₂, i.e. the reaction rate is given by

where μ is the maximal growth rate in 1/min and k_CO2 and k_H2 are the half-saturation constants in mol L⁻¹ for carbon dioxide and hydrogen, respectively. With this, the reaction terms R_i from eqn (2) are given by
where Y is the yield coefficient in cell per mol (we assume that one yield coefficient is sufficient). Note that the reaction is nonlinear.

3.3 Numerical solution of the reaction-diffusion system

For the discretization of the coupled reaction-diffusion system, a method of lines approach is used, i.e. we first discretize in space and transform the partial differential equation into a potentially very large system of ordinary differential equations, which is then discretized in time. This is done using the Cell-Centered Finite Volume (CCFV) method. CCFV guarantees mass conservation and non-negativity, which is essential for reaction systems. The system of ODEs derived from CCFV has the formwhere

• |·| denotes the volume of element Ω_i or the area of face Ω_ij,

• the set N_i consists of the indices j of all neighbours Ω_j of Ω_i,

• Ω_ij is the face between Ω_i and Ω_j,

• D_ij is an approximation of the diffusion coefficient D on Ω_ij, determined by taking the harmonic mean between D_i on Ω_i and D_j on Ω_j (eventually additionally taking Henry's law into account),

• x_i and x_j are the cell centers of Ω_i and Ω_j, respectively.

As this system is nonlinear (due to the reaction) and spatially coupled (due to the diffusion) it is numerically very challenging to solve. Furthermore, very tight time step restrictions can occur: if the time step is too large, the reaction can cause the concentration of some components to become negative (e.g. for the reactants) in single cells. As negative concentrations are unphysical this has to be avoided. Although this issue can be solved by an automatic time step control, the step size can become prohibitively small. Local restrictions thus could lead to a huge numerical overhead.

To avoid this problem, an operator splitting (OS) approach is used, where the transport by diffusion and the reaction are calculated separately. We use Strang splitting,²¹ a common OS method for the solution of diffusion-advection-reaction systems, which is second-order accurate in time (note that the CCFV discretization is second-order accurate in space).

We rewrite (3) as

where u^h : [0,T] → [Doublestruck R]^M·N is an approximation of u : [0,T]×Ω → [Doublestruck R]^N in the sense, that with x_j the cell-center of Ω_j and D^h and R^h the associated discretized operators for diffusion and reaction. The Strang splitting OS approach can be expressed by
Here, τ > 0 is the time step size and u^h_n is the approximation of u^h at the n-th time discretization point. Note that the first and the third step (the nonlinear reaction steps) can be solved explicitly, while the second step (the linear diffusion step) has to be solved implicitly due to the stiffness of the diffusion equation. As an explicit solver the Runge–Kutta–Fehlberg 45 method is used, a higher order Runge–Kutta method with automatic step size control. The implicit diffusion step is solved using the Alexander2 scheme,²² a second-order diagonally implicit Runge–Kutta method. The resulting system of linear equations is solved using the BiCGstab method (biconjugate gradient stabilized) with an algebraic multigrid scheme as a preconditioner.

For the implementation of the discretization and the linear solvers the PDELab discretization model of the Distributed and Unified Numerics Environment (DUNE), a C++ framework for the solution of partial differential equations, was used.^23,24 This also facilitates the use of parallel computers.²⁵

Simulations from the two-dimensional model also yield an approximation of the function c_{X :} [0,T]×Ω → [Doublestruck R] describing the bacterial concentration at all spatial and temporal points. In order to verify the simulations, either the relative bacterial concentration over time, i.e. the function c̃_X : [0,T] → [Doublestruck R] defined via

for a fixed x ∈ Ω or for fixed points from a subregion x ∈ Ω_sub ⊂ Ω, or the relative spatially averaged bacterial concentration over time, i.e. the function
is compared to the experimental result.

3.4 Simulation setups

Both types of experiments conducted have been simulated:

• Static experiments are simulated using zero Neumann boundary conditions, i.e. there is no in- or outflow of the components.

• Dynamic experiments are simulated using Dirichlet boundary conditions, i.e. there is a constant value of carbon dioxide and hydrogen in the gas phase at the boundary ∂Ω. For all other phases and components zero Neumann boundary conditions are used.

Whereas the microbial concentration has to reach some termination point in the static experiment, it could in principle continue throughout the experiment in the dynamic experiment.

To obtain feasible runtimes of the simulations while maintaining the desired very high spatial resolution of 1 μm in the pore space, only a subregion with 2338 × 2372 pixel of a representative image of the phase distribution (24390 × 4390 pixel, post-processed as described in Section 2.4) is used as the domain for the simulations (Fig. 4). The phase distribution is assumed to be invariable in time over the whole simulation.

Fig. 4 Phase distribution in the subregion of the micromodel used for the simulations: gas (green), liquid (blue), solid (grey).

The simulations were conducted on one server node of the parallel computer cluster of the Institute of Mathematics, consisting of two 32-core 2.35 GHz AMD EPYC 7452 processors. The typical execution time for a two-dimensional simulation with a resolution of 2338 × 2372 pixel and a time step size of 1 minute was 2.5 hours using 64 threads.

For both simulations, the following kinetic and thermodynamic parameters were used:

• Henry and diffusion coefficients as given in Table 2.

• Half saturation constants of k_CO2 = 1.1 × 10⁻⁵ mol L⁻¹ and k_H2 = 2 × 10⁻⁵ mol L⁻¹.²⁶

• As initial conditions in the liquid phase u_X(0) = 10⁹ cells per mL, u_CO2(0) = 5.4 × 10⁻² mol L⁻¹, u_H2(0) = 1.17⋅10⁻³ mol L⁻¹ and u_CH4(0) = 0 mol L⁻¹ were used. The initial conditions in the gas phase are assumed to be in equilibrium with the liquid phase according to Henry's law.²⁷

The maximal average growth rate μ and the yield coefficient Y are derived from the experimental data.

4 Results

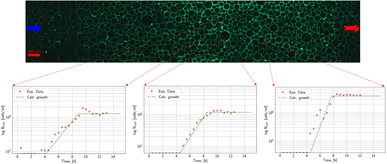
The main aim of the static experiments was a testing of the methodology, a first analysis of the growth pattern of microorganisms, and the determination of the two missing parameters of the growth model. Three characteristic time points in the temporal development of the population of Methanococcus thermolithotrophicus (species 1) at a specific region under 40× magnification are shown in Fig. 5: the distribution of microorganisms at the start of the experiment, after 8 hours in the middle of the exponential phase and after 10 h, when the microorganisms reach the stationary phase. A marked increase in microbial density over time is visible. Even in these not post-processed images it is evident that an automatic count of the microorganisms is possible (though with limited precision). Thus, the analysis of the growth of methanogenic microorganisms in the micromodel works well.

Fig. 5 Images of the development of the distribution of microorganisms over time at a fixed location in a static experiment taken at 40× magnification: water-filled pore space (dark green), grains (black), and microorganisms (light green).

Fig. 6 shows the time development of relative microbial density at three different points in the static experiment. An initial lag phase is followed by exponential growth. Finally, the relative microbial density approaches a constant value when the nutrients are exhausted.

Fig. 6 Fluorescence image of the complete micromodel in a static experiment where the initial gas flow was from left to right (top), microbial density at three positions, and the adjusted Michaelis–Menton model (bottom).

To obtain the remaining parameters for the growth model for the microorganisms (see Section 3.2), the maximal growth rate and the yield coefficient of a Michaelis–Menten model were fitted to the measured temporal development of microbial density. Model parameters for the whole micromodel were then derived by averaging over the local parameters for the two replicate experiments.

The obtained average values for the maximal growth rate and the yield coefficient in the different experiments are listed in Table 3.

Table 3 Estimated values for maximal growth rate and yield coefficient obtained for the different experimental setups and species

Species	Type	Exp. nr.	μ [min^−1]	Y [cell per mol]	[small mu, Greek, macron] [min^−1]	Ȳ [cell per mol]
Species 1	Static	1	7.3 × 10^−3	4.4 × 10^11	9.6 × 10^−3	3.8 × 10^11
		2	11.8 × 10^−3	3.3 × 10^11
	Dynamic	3	11.7 × 10^−3	4.2 × 10^11	10.8 × 10^−3	3.9 × 10^11
		4	9.9 × 10^−3	3.7 × 10^11
Species 2	Static	5	1.1 × 10^−3	1.5 × 10^11	1.2 × 10^−3	1.7 × 10^11
		6	1.3 × 10^−3	1.9 × 10^11

---

Fig. 7 shows the experimental and simulation result for the average relative microbial density in one of the static experiments with species 1. There is a very good qualitative agreement between experiment and simulation. Although the parameters were obtained with a zero-dimensional model and averaged over the different measurement points and experimental replicas, the growth dynamics are captured well by the two-dimensional model.

Fig. 7 Comparison of the time development of the average microbial density in the static experiment with the values obtained in the simulation.

The static experiments with species 2 show a similar pattern in the spatial distribution (not shown). The initial lag phase is longer and the maximal growth rate is lower (Table 3) so species 2 takes longer to reach the same microbial density as species 1. The lower estimated yield factor indicates that the metabolism of species 2 is a bit less effective.

The difference in the results obtained for the growth parameters of the two species in the static experiment is significantly larger than the difference between the two replicas with the same species.

For the subsequent simulations, the averages [small mu, Greek, macron] and Ȳ of the values measured for the static experiment with species 1 are used.

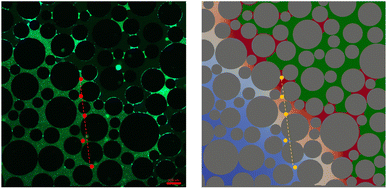
In the dynamic experiments, the total microbial density at the end of the experiment is much higher. Close to the interface it is up to 7 times higher compared to the static experiment. The fluorescence image of the microbial distribution at the end of the experiment and the final result of the simulation are shown in Fig. 8. They show a good qualitative agreement.

Fig. 8 Fluorescence image of a sub-region of the micromodel at the end of a dynamic experiment with transect highlighted in red (left). Simulated bacterial density at the end of the experiment was blue to red indicating an increasing microbial density, the gas phase is shown in green, and the solid phase in grey (right).

The growth parameters for species 1 have also been estimated for the dynamic experiment (Table 3). They are not significantly different from the parameters obtained from the static experiment.

The density of microorganisms decreases considerably with increasing distance from the gas–water interface, especially in the dynamic experiment (Fig. 9).

Fig. 9 Image of an area containing interfaces between liquid and gas phase in a dynamic experiment taken at 10× magnification (left) showing a higher fluorescence intensity in regions closer to the interface. This is confirmed by an image of the region directly at the interface taken at 40× magnification (right).

For a more detailed comparison, five points along a transect from the gas/liquid interface to the inner region of the liquid phase were chosen in the experiment (dashed line in Fig. 8). Microbial density at the end of the experiment was the highest close to the gas/liquid interface and decreased rapidly along the transect (Fig. 10). The reason for the decrease is the higher availability of nutrients close to the gas/liquid interface, whereas the transport of nutrients by diffusion is much smaller due to the higher distance for the inside regions, while a part of the nutrients will already be consumed along the path. There is again a very good agreement between measured and simulated values.

Fig. 10 Gradient of microbial density along the transect for experiment and simulation.

A comparison of the temporal evolution of experimental and simulated microbial densities at two selected points along the transect for the dynamic experiment is shown in Fig. 11. While the bacterial density is still (slowly) increasing at the end of the experiment in the region away from the interface (in contrast to the behaviour in the static experiment), it seems to have reached a saturation point close to the interface. This can no longer be explained by a lack of nutrients, but seems to be a consequence of the limited space available for the microorganisms. To obtain an agreement between simulation and experiment for the dynamic simulation a maximal microbial density had to be introduced as an additional parameter in the model. If it is assumed that the volume of a single microorganism is 10⁻¹² mL and 10% of the total fluid volume can be occupied by microorganisms, the maximal cell density is 10¹¹ cells per mL. Using this value, very good agreement of simulation and experiment shown in Fig. 8–11 is obtained.

Fig. 11 Temporal development of microbial density at two positions along the transect.

5 Conclusions and recommendations

This study provides a novel approach to study microbial growth in porous media and provides a numerical model, reproducing the results from the experiments and consequently helping to understand the experimental observations.

Two types of experiments have been conducted to study the spatial and temporal dynamics of methanogenic microorganisms with and without substrate limitations. A 2-D model coupling growth and molecular diffusion was parameterized to the experimental data to understand this phenomenon. The main findings of the combined study are:

• The experimental data gathered during the static experiments show a nutrient-limited growth inside the liquid phase of the porous medium. No significant changes in the fluid saturation were observed.

• While a similar growth dynamics can be observed in the case of unlimited nutrient supply, the microbial density quickly reaches a maximum close to the gas/liquid interface. Further away from the gas/liquid interface, the growth is continuous but slower.

• The proposed modified double Monod model could be successfully applied for both static and dynamic conditions in a partially-saturated porous medium. The estimated parameters of the growth model can be used in further studies and for modeling at a different scale. As the system is more realistic, the parameters should be more reliable than the parameters obtained from reactor experiments.

• The proposed model needed to be adapted for growth with an unlimited nutrient supply to reproduce the microbial density observed in the experiment close to the gas/liquid interface. This was realized by introducing a maximal microbial density estimated from the size of the microorganisms relative to the space available. The model then correctly reproduces the experimental findings. The slow but continuous growth away from the gas/liquid interface is caused by a limited nutrient supply modeled correctly by diffusion in the liquid phase.

• The simulations also show that it is justified to neglect microbial mobility, as there was a very good agreement between experiment and simulation even if the microorganisms were assumed to be completely immobile.

The non-uniform distribution of microbes resulting from a combination of a maximal microbial density and a spatial gradient of nutrients could significantly impact geological reservoirs with rather small pore throats, where an increase in microbial density could block pores and change the gas flow path over the storage cycles. In terms of intended microbial conversion, as in an underground methanation reactor, the substrate-diffusion limitation of the growth and conversion has to be considered. The majority of the conversion will take place near the gas/liquid interface. Thus, the injection pattern for hydrogen and carbon dioxide should be designed to produce a gas phase with as much interfacial area as possible.

Some aspects not covered by the experiments and simulations might be important as well and require further research. The maximal growth rate and the yield coefficient have only been determined by parameter estimation based on microbial density. Measuring the amount of methane produced and the amount of hydrogen and carbon dioxide consumed could lead to more accurate growth parameters. In dynamic experiments, this could be done by analyzing the gas in- and out-flow composition. In static experiments, it would need sensors to measure the gas composition in situ, which is rather difficult. It would also be interesting to perform studies with more complex microbial communities, including other microbial metabolisms like sulfate or iron reduction. The effect of the growing microbial population on the substrate's diffusion coefficients in water was not considered in the simulations. Especially close to the interface, the microorganisms could form a biofilm, which could inhibit the gas exchange and the mobility of the liquid phase.²⁸

Author contributions

All authors have contributed equally to this work.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This publication is based upon work supported and financed by the Clausthal University of Technology, project Catalytic and microbial methanation as basis for sustainable energy storage (CliMb). The authors acknowledge the support of the Research Center for Energy Storage Technologies Goslar (Forschungszentrum Energiespeichertechnologien) for the present study. This publication is based upon work partially funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation – Project No. 433108788).

Notes and references

1. V. Reitenbach, L. Ganzer, D. Albrecht and B. Hagemann, Environ. Earth Sci., 2015, 73, 6927–6937.
2. N. Heinemann, J. Alcalde, J. Miocic, S. Hangx, J. Kallmeyer, C. Ostertag-Henning, A. Hassanpouryouzband, E. Thaysen, G. Strobel, C. Schmidt-Hattenberger, K. Edlmann, M. Wilkinson, M. Bentham, R. Haszeldine, R. Carbonell and A. Rudloff, Energy Environ. Sci., 2021, 14, 853–864.
3. Underground Sun. Storage Report, https://www.underground-sun-storage.at/presse/publikationen/publikationen-1.html, accessed: 2022-07-10.
4. N. Dopffel, S. Jansen and J. Gerritse, Int. J. Hydrogen Energy, 2021, 46, 8594–8606.
5. B. Hagemann, Numerical and Analytical Modeling of Gas Mixing and Bio-Reactive Transport during Underground Hydrogen Storage, 2017.
6. G. Strobel, B. Hagemann, T. M. Huppertz and L. Ganzer, Renewable Sustainable Energy Rev., 2020, 123, 109747.
7. M. Panfilov, V. Reitenbach and L. Ganzer, Environ. Earth Sci., 2016, 75, 313.
8. P. Amigáň, M. Greksak, J. Kozánková, F. Buzek, V. Onderka and I. Wolf, FEMS Microbiol. Ecol., 1990, 6, 221–224.
9. Underground Sun. Conversion Report, https://www.underground-sun-conversion.at/presse/publikationen/publikationen-1.html, accessed: 2022-07-10.
10. W. van Rooijen, L. Hashemi, M. Boon, R. Farajzadeh and H. Hajibeygi, Adv. Water Resour., 2022, 164, 104221.
11. M. Lysyy, G. Ersland and M. Fernø, Adv. Water Resour., 2022, 163, 104167.
12. N. Liu, A. R. Kovscek, M. A. Fernø and N. Dopffel, Front. Energy Res., 2023, 11, 1–10.
13. C. Gaol, L. Ganzer, P. Verlag and M. Amro, Experimental and Numerical Investigation of Pore-Scale Mechanisms of Microbial Enhanced Oil Recovery (MEOR) Using a Microfluidics Approach, Clausthal University of Technology, 2020.
14. J. Aufrecht, J. Fowlkes, A. Bible, J. Morrell-Falvey, M. Doktycz and S. Retterer, PLoS One, 2019, 14, e0218316.
15. N. Hassannayebi, B. Jammernegg, J. Schritter, P. Arnold, F. Enzmann, M. Kersten, A. Loibner, M. Fernø and H. Ott, Transp. Porous Media, 2021, 139, 1–17.
16. A. Ebigbo, F. Golfier and M. Quintard, Adv. Water Resour., 2013, 61, 74–85.
17. J. Wegner, Investigation of Polymer Enhanced Oil Recovery (EOR) in Microfluidic Devices that Resemble Porous Media: An Experimental and Numerical Approach, Shaker, 2015.
18. G. Strobel, M. Wirth, B. Hagemann and L. Ganzer, European Association of Geoscientists & Engineers, 2021, 2021, 1–5.
19. E. Thaysen, S. McMahon, G. Strobel, I. Butler, N. Heinemann, B. Ngwenya, M. Wilkinson, A. Hassanpouryouzband, C. McDermott and K. Edlmann, Renewable Sustainable Energy Rev., 2021, 151, 1–15.
20. DSMZ Medium 141, https://bacmedia.dsmz.de/medium/141, accessed: 2022-06-08.
21. G. Strang, SIAM J. Numer. Anal., 1968, 5, 506–517.
22. R. Alexander, SIAM J. Numer. Anal., 1977, 14, 1006–1021.
23. P. Bastian, M. Blatt, A. Dedner, C. Engwer, R. Klöfkorn, M. Ohlberger and O. Sander, Computing, 2008, 82, 103–119.
24. P. Bastian, M. Blatt, A. Dedner, C. Engwer, R. Klöfkorn, R. Kornhuber, M. Ohlberger and O. Sander, Computing, 2008, 82, 121–138.
25. O. Sander, DUNE—The Distributed and Unified Numerics Environment, Springer Nature, London, 2020, vol. 140.
26. N. Schill, W. Van Gulik, D. Voisard and U. Von Stockar, Biotechnol. Bioeng., 1996, 51, 645–658.
27. W. Henry, Philos. Trans. R. Soc. London, 1803, 29–274.
28. P. S. Stewart, J. Bacteriol., 2003, 185, 1485–1491.

---