Observation of parallel intersystem crossing and charge transfer-state dynamics in [Fe(bpy)₃]²⁺ from ultrafast 2D electronic spectroscopy

Abstract

Transition metal-based charge-transfer complexes represent a broad class of inorganic compounds with diverse photochemical applications. Charge-transfer complexes based on earth-abundant elements have been of increasing interest, particularly the canonical [Fe(bpy)₃]²⁺. Photoexcitation into the singlet metal–ligand charge transfer (¹MLCT) state is followed by relaxation first to the ligand-field manifold and then to the ground state. While these dynamics have been well-studied, processes within the MLCT manifold that facilitate and/or compete with relaxation have been more elusive. We applied ultrafast two-dimensional electronic spectroscopy (2DES) to disentangle the dynamics immediately following MLCT excitation of this compound. First, dynamics ascribed to relaxation out of the initially formed ¹MLCT state was found to correlate with the inertial response time of the solvent. Second, the additional dimension of the 2D spectra revealed a peak consistent with a ∼20 fs ¹MLCT → ³MLCT intersystem crossing process. These two observations indicate that the complex simultaneously undergoes intersystem crossing and direct conversion to ligand-field state(s). Resolution of these parallel pathways in this prototypical earth-abundant complex highlights the ability of 2DES to deconvolve the otherwise obscured excited-state dynamics of charge-transfer complexes.

---

1. Introduction

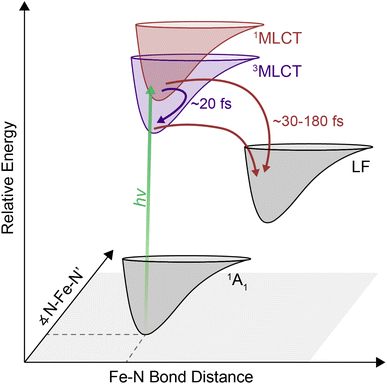
Transition metal-based polypyridyl complexes represent an important class of inorganic chromophores with photophysical properties amenable for applications ranging from solar energy conversion^1–5 to organic transformations.^6–8 Amongst this class of complexes, the prototypical chromophore is tris(2,2′-bipyridine)ruthenium(II), i.e., [Ru(bpy)₃]²⁺. The photophysical properties of [Ru(bpy)₃]²⁺ – specifically the existence of a metal-to-ligand charge-transfer (MLCT) excited state that stores ∼2 V of energy⁹ and persists for ∼1 μs in deoxygenated solution¹⁰ – lie at the heart of its utility in such a wide range of settings. Despite its advantages, the elemental scarcity of ruthenium (as well as related chromophores containing iridium, rhenium, osmium, etc.) raises important questions about the cost and scalability of processes built on these materials.¹¹ This realization has spurred recent efforts to develop alternatives that replicate the photochemical properties of compounds such as [Ru(bpy)₃]²⁺ while using components for which material availability ceases to be an issue.^12–17 Accordingly, there has been a rapid expansion of research into the synthesis and photophysical properties of chromophores based on elements of the first transition series (e.g., iron, cobalt, nickel, chromium).

Many of these efforts have focused on ions possessing a d⁶ configuration due to their valence isoelectronic relationship with Ru(II). The canonical example of this class of compounds, [Fe(bpy)₃]²⁺, exhibits similar steady-state optical properties to its second- and third-row transition metal analogs, namely a strong MLCT absorption in the mid-visible region, yet its excited-state properties bear little resemblance to its heavier group 8 congeners.¹⁸ Specifically, the absence of a spectroscopic signature associated with the bipyridyl radical anion (i.e., bpy˙⁻) within 10 ps following MLCT excitation was an early indication of an excited-state lifetime that was many orders of magnitude shorter than its Ru(II) counterpart.⁴ The sub-100 fs lifetime of the MLCT manifold for an Fe(II) polypyridyl complex was first quantified in 2000 using ultrafast time-resolved absorption spectroscopy in conjunction with spectrochemical identification of an optical signature for the MLCT excited state.¹⁹ This was later observed specifically in [Fe(bpy)₃]²⁺ using XANES²⁰ and ultraviolet transient absorption spectroscopy.²¹ Similar timescales have also been seen for a range of related compounds.^12,22–24 The dramatic attenuation in MLCT-state lifetime observed for the Fe(II) complexes results from an inversion in the relative energies of the charge-transfer and ligand-field excited states compared to what exists in the second- and third transition series due to the so-called primogenic effect.^25–27 These ligand-field states are characterized by large geometric distortions relative to both the ground- and MLCT excited states, thereby facilitating rapid non-radiative decay out of the charge transfer-state manifold and the eventual formation of the high-spin ⁵T₂ excited state on a timescale of ∼200 fs.

Following conversion from the MLCT excited state manifold to the lowest-energy ligand-field excited state, specifically the ⁵T₂ state, ground state recovery (i.e., ⁵T₂ → ¹A₁ relaxation) occurs on a timescale of ∼1 ns. Recently, Miller and McCusker identified solvent dependent kinetics for this ground-state recovery.²⁸ The dependence was attributed to solvent reorganization in response to the large decrease in molecular volume associated with the conversion from a high-spin to a low-spin configuration. Although subtle, the solvent dependence associated with electronic state evolution localized on the metal center and relatively insulated from the solvent environment raises questions about the solvent dependence of dynamics in the charge-transfer manifold. Here, the transfer of an electron from the metal to the ligand places negative charge density on the periphery of the molecule and therefore in direct contact with the surrounding solvent. Despite there being ample evidence from studies on complexes possessing long-lived charge-transfer states that ultrafast solvent-coupled processes can influence their initial evolution,^22,28–30 the effect of solvent at early timescales and its coupling to intersystem crossing processes in [Fe(bpy)₃]²⁺ have not been investigated.

Although relaxation from the MLCT manifold into the ligand-field ⁵T₂ state has been established for [Fe(bpy)₃]²⁺, the pathway involved in this relaxation is still under debate. Direct relaxation from the MLCT band into the ⁵T₂ state is formally a two-electron process, thus making a direct transition highly improbable.³¹ It has therefore been proposed that the ¹MLCT → ⁵T₂ conversion likely occurs via intermediate metal-centered states. While progress has clearly been made with regard to bringing processes localized on the metal center into better focus, details are sparse when it comes to dynamics occurring within the initially formed charge-transfer state(s). Transient absorption spectroscopy conducted by Auböck and Chergui was interpreted in terms of a ¹MLCT → ³MLCT intersystem crossing event followed by a ³MLCT → ⁵T₂ direct relaxation mechanism with an overall timescale of <50 fs,³² whereas X-ray fluorescence spectroscopy data were modeled without invoking an intersystem crossing event within the charge-transfer manifold.³³ Because the photoexcited MLCT state relaxes into the high-spin ⁵T₂ state within a few hundred femtoseconds, fast time resolution^33–36 is required to properly resolve the early-time dynamics within the MLCT manifold. A range of time-resolved methodologies are available to access this regime, but the issue is compounded by the broad and overlapping spectroscopic features associated with relevant processes in [Fe(bpy)₃]²⁺. These temporal and spectral requirements present significant challenges for determining what mediates the excited-state dynamics. Two-dimensional electronic absorption spectroscopy (2DES) is an advanced spectroscopic technique that combines the ability of transient absorption spectroscopy to probe ultrafast dynamics with direct excitation and detection frequency correlation. The additional dimension attained through this correlation allows for energetic deconvolution of different contributions to the excited-state dynamics of systems, providing information about the energy landscape that would be difficult, if not impossible, to divine from transient absorption spectroscopy alone. Although 2DES has been commonly used to study light harvesting systems,^34,37–39 inorganic nanomaterials,^40–43 and organic molecular chromophores,^35,44,45 amongst other systems, it has been underutilized as a tool to understand ultrafast dynamics in molecular, transition-metal based chromophores.

In this report, we show that challenges associated with characterizing early-time dynamics within the MLCT manifold of [Fe(bpy)₃]²⁺ can be overcome using 2DES. Here, the additional spectral separation afforded by this technique uncovered a previously hidden ¹MLCT → ³MLCT cross peak while simultaneously resolving sub-100 fs dynamics of intersystem crossing and transfer out of the MLCT manifold. Collectively, these observations revealed parallel pathways of triplet-mediated and direct relaxation to the metal centered states. These results demonstrate the ability of 2DES to be a particularly effective tool for elucidating the early-timescale excited-state dynamics in the class of transition metal-based chromophores (like [Fe(bpy)₃]²⁺) to provide new insights into the ultrafast processes underlying their functionality.⁴⁶

2. Results

2.1. Steady-state absorption features

Fig. 1A shows the steady-state absorption spectrum of [Fe(bpy)₃]²⁺ in methanol. In this frequency range, the dominant peak at ∼19 200 cm⁻¹ is the ¹A₁ → ¹MLCT transition with a tail on the red edge associated with the formally spin forbidden ¹A₁ → ³MLCT transition.⁴⁷ Consistent with this assignment, TD-DFT calculations (Fig. 1B) showed that the ³MLCT states primarily contribute to the lower-energy range of the absorption spectrum while the higher-energy range of the spectrum is dominated by a ¹MLCT transition with a large oscillator strength. The dominant calculated excitation at 21 832 cm⁻¹ seen in Fig. 1B corresponds to a doubly-degenerate ¹MLCT state (Table S9†). Only minor solvatochromic effects were observed in the absorption spectra of [Fe(bpy)₃]²⁺ (Fig. S1A and S17†).

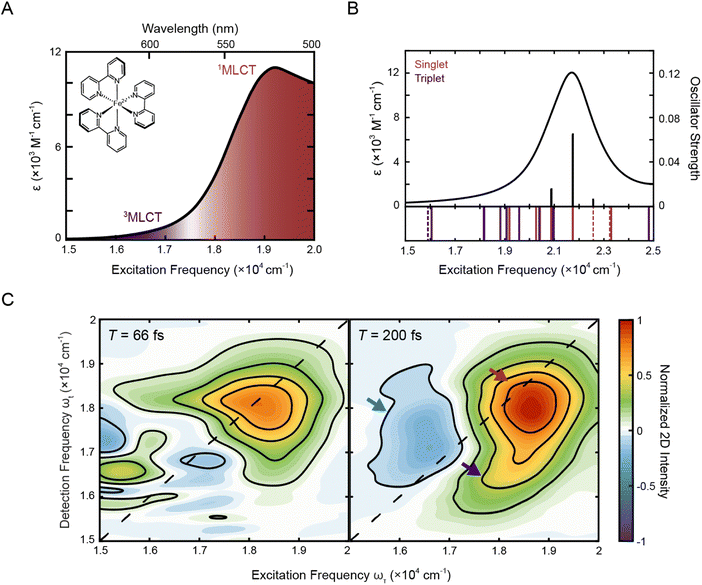Fig. 1 (A) Absorption spectrum of [Fe(bpy)₃]²⁺ in methanol with singlet and triplet metal-to-ligand charge transfer bands (¹A₁ → ¹MLCT, red; ¹A₁ → ³MLCT, purple). The molecular structure of [Fe(bpy)₃]²⁺ is shown in the inset. (B) Calculated stick spectrum (top, black sticks) and broadened line spectrum (top, black line) obtained from TD-DFT calculations of [Fe(bpy)₃]²⁺ in acetonitrile. Energy spectrum of the singlet metal-centered (dashed red lines) and ¹MLCT (solid red lines) and triplet metal-centered (dashed purple lines) and ³MLCT (solid purple lines) transitions, including those with zero oscillator strength, are shown below the plotted spectrum (see Tables S9 and S10† for full information of the calculated singlet and triplet states, respectively). (C) Phased 2D spectra of [Fe(bpy)₃]²⁺ in methanol at T = 66 fs (left) and T = 200 fs (right). Positive intensity corresponds to ground state bleach or stimulated emission signals and negative intensity corresponds to excited state absorption signal. Plots are normalized to the maximum and minimum intensities of the T = 200 fs spectrum. Contour lines are drawn at 20% intervals. Arrows denote predominant peaks.

2.2. 2DES spectra features

To investigate the dynamics of the charge-transfer transitions, 2DES was used to measure a series of spectra that map out the excited-state evolution. Correlation plots of excitation (ω_τ) and detection (ω_t) energies were created as a function of the delay time between excitation and detection events, known as the waiting time (T).^34,39 The spectra were measured with ∼10 fs temporal resolution. The nonresonant response (coherent artifact) of the pulse was also characterized spectrally (Fig. S2†). To minimize contributions from the nonresonant response, the 2D data were analyzed only for T > 47 fs. Representative 2D spectra of [Fe(bpy)₃]²⁺ in methanol are shown in Fig. 1C. For 2DES experiments performed in the BOXCARS geometry, positive intensity corresponds to ground state bleach/stimulated emission and negative intensity corresponds to excited state absorption.

The 2D spectra contain three primary features. First, the spectra are dominated by a positive peak on the diagonal at ω_τ = 18 500 cm⁻¹, ω_t = 18 000 cm⁻¹ (Fig. 1C, red arrow). Second, a positive peak grows in below the dominant peak at approximately ω_τ = 18 250 cm⁻¹ and ω_t = 16 500 cm⁻¹ at T = 200 fs (Fig. 1C, right, blue arrow, Fig. S13†). Third, a negative peak is also present, particularly at later waiting times, at approximately ω_τ = 16 500 cm⁻¹ and ω_t = 17 000 cm⁻¹ (Fig. 1C, right, purple arrow).

Previous studies of [Fe(bpy)₃]²⁺ using more traditional spectroscopic methods allow us to orient our understanding of these three features. First, the initially-formed (<200 fs) excited state is a ¹MLCT state that can be described in terms of oxidation of the metal center (i.e., Fe(II) to Fe(III)) and the creation of a radical anion associated with the bipyridyl ligand (bpy˙⁻). This formulation allows for the use of spectroelectrochemistry to approximate the optical signatures that will characterize this initial state (Fig. S4†).¹⁸ These data indicate that the ¹MLCT excited state will consist of two overlapping contributions: first, a loss of absorption (and stimulated emission at early times <100 fs) due to ground-state depletion and the concomitant change in oxidation state of the metal,⁵² which contributes positively to the 2D signal; and second, a new absorption feature associated with the bpy radical anion (bpy˙⁻), which contributes negatively to the 2D signal. The former appears at the steady-state absorption of the MLCT states (Fig. 1A) whereas the latter manifests as a broad feature starting at 16 000 cm⁻¹ and extending into the UV regime. Owing to the large oscillator strength associated with the charge-transfer band, the overall spectrum will be dominated by the former. Consistent with this picture, the dominant positive feature on the diagonal is approximately at the ¹MLCT absorption in the steady-state spectrum, although the maximum is slightly red-shifted due to the spectral profile of the ultrafast laser pulse (Fig. S1B†). Therefore, the dominant positive diagonal feature is denoted as the ¹MLCT ground-state bleach/stimulated emission (¹MLCT GSB/SE) peak. Any ESA contribution from the bpy radical anion at T < 200 fs at lower energies (ω_τ < 17 000 cm⁻¹) is obscured due to contribution from the nonresonant response signal (Fig. 1C, left). Second, the positive cross peak below the diagonal corresponds energetically to excitation into the ¹MLCT state and detection of population in the ³MLCT state at early waiting times (T < 200 fs). It is important to note that the contribution of stimulated emission to these features is tied to the persistence of the ¹MLCT state. Further details about this assignment will be discussed in Section 2.3.4.

After initial photoexcitation into the MLCT manifold, the molecule relaxes into the ligand-field excited state manifold within 200 fs.^20,21 This relaxation corresponds to the electron in the ligand-based π* orbital transferring back to the metal. Formation of these ligand-field excited state(s) has two consequences for the absorptive properties of the complex: loss of absorption associated with the bpy radical anion; and the eventual creation of an MLCT excited-state absorption feature associated with the lowest-energy ligand-field excited state of the molecule. These new net absorptive contributions to the spectrum can be expected to arise from MLCT transitions associated with the excited ligand-field states, in particular a ⁵T₂ → ⁵MLCT transition that will persist until ground-state recovery (∼1 ns). The intensity of this band is expected to be roughly an order of magnitude less than that associated with the ground state.⁵³ Its contribution to the overall signal depends on the nature of its overlap with the ground-state bleach. Thus, the ESA feature observed is assigned to the ⁵T₂ → ⁵MLCT transition, supported by TD-DFT calculations (discussed in more detail in Section 2.3.3) and a nanosecond decay consistent with ground-state recovery (Fig. S5D and Table S3†). Although previous studies of similar complexes have shown an ESA signature in this region as a result of multi-photon excitation,⁵⁴ the intensity of the laser pulse used in this study, is ten-fold below the advent of these multi-photon features. By T = 200 fs, the ¹MLCT peak, which by this time is comprised solely of the ground-state bleach, also shifts slightly below the diagonal. Given the broad peak structure of the ⁵T₂ ESA peak, the redshift in detection frequency of the ¹MLCT GSB/SE peak is therefore most likely from partial cancellation from the rise of the ⁵T₂ ESA.

2.3. Kinetic analysis of 2DES spectra

2.3.1. Early-time evolution of the ¹MLCT state. To investigate the kinetics, a waiting time trace from T = 47–1000 fs for the ¹MLCT peak was constructed by integrating the peak intensity within ω_τ = 18 500–20 000 cm⁻¹ and ω_t = 18 000–20 000 cm⁻¹ (i.e., the region indicated by the red arrow in Fig. 2A, B, S6, and S18†) and normalized to the time point with maximum intensity. The asymmetric ranges were selected to minimize the contribution from the nonresonant response at early waiting times, and thus should best capture the dynamics associated with [Fe(bpy)₃]²⁺ (Fig. S2†). The waiting time trace was fit to a biexponential function (Fig. 2B, solid line) where the where the first term (which has negative amplitude) tracks the rapid rise (with its time constant called the “rise time”) and second term tracks the slow ground-state recovery (Eqn S1, Table S1†). A biexponential function was used because additional terms did not lead to a significant improvement in fit quality, consistent with previous experiments that reported a monoexponential decay²⁸ and a monoexponential rise.³² The initial rise in peak intensity occurred on a ∼30 fs timescale. The lower intensity at early times is consistent with spectrally overlapped ¹MLCT GSB/SE and bpy˙⁻ ESA signatures generated upon photoexcitation into the MLCT manifold.¹⁸ Excited-state evolution from the MLCT manifold to the lower-lying ligand-field manifold results in the disappearance of the bpy˙⁻ (and therefore loss of the bpy˙⁻ ESA signature), leaving only the contribution from the underlying ground-state bleach signal. The increase in magnitude of the ground-state bleach can only be rationalized through the removal of a partial cancellation from an overlapping negative signal. For this reason, the intensity rise in the bleach signal can be assigned to conversion from the charge-transfer to ligand-field manifold of the compound due to loss of the partial cancellation from the ESA as opposed to relaxation within the charge-transfer band where no such change in partial cancellation would occur.

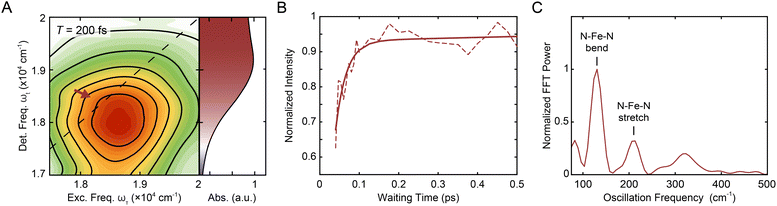Fig. 2 (A) Reproduction of the positive, on-diagonal region of the T = 200 fs 2DES spectrum in Fig. 1C with the corresponding linear absorption spectrum on the right. The red arrow indicates the GSB signal of the ¹MLCT (and, at early times, the SE signal). (B) Intensity trace (dashed line) of the ¹MLCT diagonal peak over waiting time T with its respective biexponential fit (solid lines) in methanol. See text for details. (C) Fourier transform of the residuals from the exponential fit depicted in (B) see also Fig. S12.† The peaks denoted correspond to the N–Fe–N bending (lower frequency) and N–Fe–N stretching (higher frequency) from a hot ground state during the waiting time.^48–51

The waiting time traces also exhibit rapid oscillations.

Fourier analysis of the residuals from the biexponential fitrevealed two primary frequencies at 129.4 ± 0.4 cm⁻¹ and 209 ± 1 cm⁻¹ (Fig. 2C) corresponding to a N–Fe–N bending mode (∼114–157 cm⁻¹) and a Fe–N stretching mode (∼185–280 cm⁻¹) (see also Fig. S12 and Table S4†).^49–51 Fourier filtering and subsequent biexponential fitting revealed similar rise timescales as reflected in the biexponential fit of the unfiltered data (Fig. S11†); in order to minimize assumptions made in the kinetic analysis, the unfiltered data were used. In addition, global kinetic analysis was performed on the region of the MLCT peaks using the method illustrated in Volpato et al.⁵⁵ The ESA peak was not included in the analysis as the region is dominated by the nonresonant response signal at early timescales. Consistent with the results from the analysis described above, growth of both the ¹MLCT GSB/SE peak and the ¹MLCT → ³MLCT cross peak was observed with a sub-100 fs timescale (Section 2.3.4).

2.3.2. Solvent dependent evolution of the ¹MLCT state. As a dicationic species, [Fe(bpy)₃]²⁺ is expected to be strongly solvated in polar solvents in the ground state. Upon photoexcitation into the MLCT manifold, the solvent must respond to the formation of the bpy˙⁻. DFT calculations predict the excited electron in one of these initially-excited ¹MLCT states to be delocalized over two bipyridyl ligands (Fig. S24B†) with a dipole moment of 3.94 Debye, while the second transition is localized on a single bipyridyl ligand with a dipole moment of 3.97 Debye (Fig. 3A). Any initially-excited delocalized MLCT state is expected to quickly localize on a single bipyridyl ligand, further increasing the dipole moment.^56,57 The fully optimized structure of the lowest-energy ¹MLCT, as well as the ³MLCT state, predicts stabilization of the state that localizes the electron in a π* orbital of a single bipyridyl ligand (Fig. 3B) with an overall dipole moment of 9.0 Debye and 6.7 Debye, respectively (Fig. S25†). These calculations are consistent with those obtained through Stark spectroscopy.⁵⁶

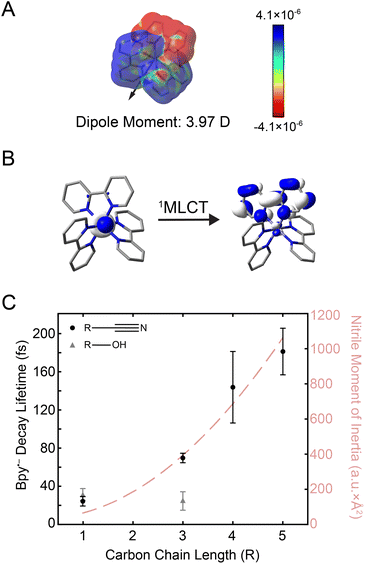Fig. 3 (A) Electron density difference surface between the ground and the initially-excited ¹MLCT state densities (isovalue = 0.0004 electrons per a.u.³). The ¹MLCT state depicted here corresponds to one of the double degenerate transitions at 21 832 cm⁻¹ shown in Fig. 1B (see Fig. S24† for both states). Red values indicate an increase in the excited-state electron density relative to the ground state (particle), while blue values indicate a decrease (hole). The excited-state dipole moment (3.97 Debye) is depicted by an arrow pointing in the positive direction. (B) Molecular orbitals associated with excitation of the ¹MLCT state (see Fig. S25† for depictions of both the singlet and triplet MLCT transitions). (C) Plot of the bpy˙⁻ decay lifetime in nitriles (black circles) and alcohols (gray triangles) as a function of carbon chain length (R). Error bars reflect standard error from three replicates. The moment of inertia (I) of the nitrile solvents is also plotted (light red dashed line).

The electron placed in the π* orbital of the bpy ligand dramatically alters the nature of the charge density with which the solvent interacts. In the ground state, the solvent organizes around an overall dicationic state wherein the charge is buried on the metal ion whereas, in the excited ¹MLCT state, the charge is localized on the periphery of the complex. Alcohols can respond by simply rotating about the C–O single bond, whereas the rigid-rod nature of nitriles requires at least a partial rotation of the entire solvent molecule. The timing of this molecular rotation is therefore dependent on the moment of inertia of the molecule,²² which can be as fast as 25 fs.^58,59 2D spectra were measured in these two classes of solvents, alcohols and nitriles, to examine the effect of these different mechanisms of reorganization in response to the creation of the MLCT excited state.

The kinetics from 2D spectra of [Fe(bpy)₃]²⁺ in methanol, 1-propanol, acetonitrile, butyronitrile, are compared in Fig. 3C, with values from the biexponential fit reported in Table 1. The rise times, shown as gray triangles in Fig. 3C, were ∼30 fs for both methanol (carbon chain length R = 1) and 1-propanol (R = 3). The similarity observed can be attributed to the fact that an extension of the aliphatic chain from methanol to 1-propanol should have little effect on the dynamics of rotation about the C–O bond.²⁸ On the other hand, the time constant for the same signal in the nitrile solvents was observed to increase from ∼30 fs acetonitrile (R = 1) to ∼70 fs for butyronitrile (R = 3). This solvent-dependent evolution observed in the nitrile solvents likely originates from the nature of the anticipated solvent response, a rotation of the entire molecule.

Table 1 Kinetics associated with the disappearance of the bpy radical anion

Solvent	bpy˙^− decay lifetime (fs)
Methanol	32 ± 6
1-Propanol	24 ± 10
Acetonitrile	25 ± 5
Butyronitrile	70 ± 5
Pentanenitrile	140 ± 40
Hexanenitrile	180 ± 20

---

To further investigate the nature of this solvent response, 2DES studies were performed in commercially-available nitriles with longer carbon chains, namely pentanenitrile (R = 5) and hexanenitrile (R = 6). The dynamics in propionitrile were not measured because [Fe(bpy)₃]²⁺ was observed to interact with impurities in the solvent and degrade too fast for 2DES experiments (ESI Section 6.1†). The bpy˙⁻ ESA decay lifetime in all nitrile solvents is as a function of carbon chain length (R) is plotted as black circles in Fig. 3C (black circles).

The reported lifetimes of the bpy˙⁻ decay increased to ∼140 fs and ∼180 fs for pentanenitrile and hexanenitrile, respectively. The overall trend follows closely with the trends of the moment of inertia (I) of the solvent, plotted as a light-red dashed curve in Fig. 3C (see also ESI Section 4†). This clear scaling reflects the ability of the surrounding solvent to stabilize the change in charge density upon photoexcitation.

These data represent the first observation of solvent dynamics coupled to MLCT-state evolution in an Fe(II) polypyridyl complex and moreover suggest that the conversion from the charge-transfer to ligand-field manifolds may indeed be gated by solvent response.

2.3.3. Properties of the ⁵T₂ ESA feature. The early-time kinetics of the negative peak could not be well-characterized as the spectral region contains significant nonresonant response at T < 100 fs (Fig. S2†). Instead, the magnitude of the peak intensity was compared to the magnitude of the positive ¹MLCT peak intensity (Fig. 4A and B) to quantify its relative contribution, or effective oscillator strength. The relative magnitude of the ESA peak was averaged for each triplicate data set in each solvent from T = 200–3000 fs to minimize contributions from both the initial photophysics and the nonresonant response. The intensity of the negative peak was integrated over ω_τ = 16 000–17 000 cm⁻¹ and ω_t = 16 800–17 800 cm⁻¹ and the intensity of the positive peak was integrated over ω_τ = 17 500–19 500 cm⁻¹ and ω_t = 17 000–19 000 cm⁻¹. These limits were selected to span the contour lines that denote this feature (Fig. 1C) as no other overlapping contributions are present in this spectral region. The magnitude of the negative peak was ∼10% of the positive peak (Fig. 4D and S16†), consistent with the order-of-magnitude reduction in intensity expected for a ⁵T₂ → ⁵MLCT absorption relative to the corresponding transition in the low-spin ground state. To further investigate the relevant states, TD-DFT calculations were performed on the ⁵T₂ states (Fig. S23†). Analysis of the transitions showed ⁵T₂ → ⁵MLCT transition with a similar energy gap (Fig. 4C), supporting the assignment. Along the waiting times sampled, the system undergoes nuclear equilibration within the ⁵T₂ state primarily assigned to be an expansion of the Fe–N bond distance.²⁸ Therefore, the differences in intensity of the ESA peak between the solvents studied (Fig. 4D) are likely reflective of differences in the nature of the nuclear equilibration due to each type of solvent interactions.

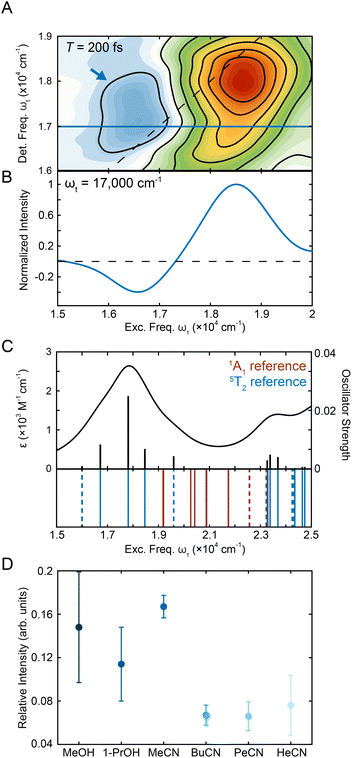Fig. 4 (A) Region of representative [Fe(bpy)₃]²⁺ 2DES spectrum in methanol centering the ESA peak (blue arrow) at T = 200 fs. (B) Horizontal slice in detection frequency at ω_t = 17 000 cm⁻¹ (shown as a blue line in Fig. 4A) that shows the presence of the negative ESA peak. (C) Absorption spectrum obtained from TD-DFT calculations in acetonitrile utilizing the fully-optimized lowest-energy quintet state (⁵T₂) of [Fe(bpy)₃]²⁺ as a reference. Calculated stick spectrum (black sticks) along the broadened line spectrum (half-width at half-maximum, HWHM = 968 cm⁻¹ (0.12 eV), black line) is shown at the top. Energy spectrum of all calculated transitions (even those with zero oscillator strength) is displayed on the bottom. Blue lines represent transitions from the ⁵T₂ state, while the red lines represent singlet transitions from the ¹A₁ state. MLCT transitions are represented by the solid lines while ligand-field transitions are represented by the dashed lines. See Tables S11 and S9† for full information about the transitions for the ⁵T₂ and ¹A₁ states, respectively. (D) Relative intensity of the negative peak compared to the positive peak in methanol, 1-propanol, acetonitrile, butyronitrile, pentanenitrile, and hexanenitrile. The error bars are standard errors from three replicates.

The relative intensities in the solvents were within error of each other for the alcohols whereas the relative intensity in acetonitrile was over double that in the longer nitriles. This observation is consistent with previous studies where solvent-dependent, outer-sphere effects influenced the dynamics of the ligand-field ⁵T₂ state.²⁸ Specifically, the solvent reorganization energy is coupled to the change in the volume of the complex as the system moves between high-spin and low-spin configurations, which in turn affects the oscillator strength of the transition. The effect of solvent on the relative oscillator strength of the ligand-field excited state can be difficult to quantify using traditional transient absorption spectroscopy experiments as the magnitude of the effect often falls below the noise threshold. In this experiment, the 2D apparatus utilizes a fully non-collinear, BOXCARS configuration for background-free detection, which vastly improves the signal-to-noise ratio^40,60–62 by almost two orders of magnitude.⁶³ The improved sensitivity was required to resolve the small changes in oscillator strength due to solvent effects. This result both establishes solvent-coupled behavior of [Fe(bpy)₃]²⁺ in the lower-lying ligand-field states and highlights the power of 2DES as a tool for understanding excited-state dynamics in transition metal complexes.

2.3.4. Evolution of the ¹MLCT → ³MLCT cross peak. A cross peak is also present in the spectrum at energetic coordinates corresponding to excitation of the ¹MLCT state and detection of population in the ³MLCT state (Fig. 5A, purple arrow). Based on these coordinates, along with its near-zero intensity at T = 0, we assign this peak to a ¹MLCT → ³MLCT intersystem crossing event. At later times (T > 200 fs), the region is dominated by the GSB of the triplet charge-transfer state, as evidenced by both the red-shift in excitation energy (Fig. S14†) and the nanosecond timescale of the signal decay (Fig. S5C and Table S3†). The ESA peak is not expected to influence these features or dynamics as it only exhibits the nanosecond decay of the overall signal (Fig. S5D†) outside of the nonresonant response. Although the triplet charge transfer state has low oscillator strength, features in 2D spectra depend on the oscillator strength of both the excitation and detection transitions, and so the cross peak is visible in part due to the oscillator strength of the singlet state. Furthermore, the decongestion afforded by a second frequency dimension allows otherwise obscured features to be observed.^36,64 The background-free nature of the 2D apparatus as noted above also makes possible the resolution of relatively weak signals,⁶³ such as the ³MLCT evolution. These features represent some of the advantages that 2DES brings to the study of the ultrafast excited-state dynamics of this class of chromophores. Specifically, direct observation of ¹MLCT → ³MLCT intersystem crossing via a time-resolved absorption measurement had not been achieved previously.

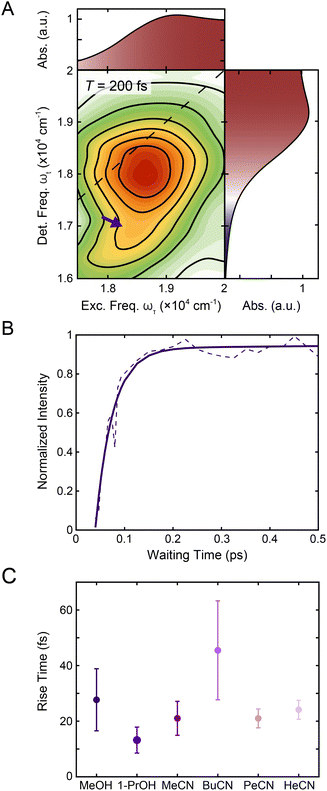Fig. 5 (A) Reproduction of the positive region of the T = 200 fs 2DES spectrum in Fig. 1C. The purple arrow indicates the contribution from ¹MLCT → ³MLCT intersystem crossing. The corresponding linear absorption spectrum is reproduced on the top and right of the 2DES spectrum for clarity. (B) Intensity trace of the ¹MLCT → ³MLCT cross peak (dashed lines) over waiting time T along with a biexponential fit (solid lines) in methanol. See text for details. (C) Rise times of the ¹MLCT → ³MLCT cross peak (purple) in methanol, 1-propanol, acetonitrile, butyronitrile, pentanenitrile, and hexanenitrile extracted from the fits of the intensity traces (Fig. S9 and S20†). Error bars are the standard error from three replicates.

To characterize the evolution of the ¹MLCT/³MLCT cross peak, waiting time traces were constructed by integrating the peak intensity within ω_τ = 17 500–20 000 cm⁻¹ and ω_t = 15 600–16 600 cm⁻¹ (Fig. 5A, purple arrow, Fig. 5B). The waiting time traces exhibited an intensity increase, which was fit to an exponential rise function (Fig. 5B, solid line, Eqn S1 and Table S2†). A rise was also observed for the diagonal peak, as discussed above, but the associated intensities were different. While the diagonal peak had ∼75% of the final intensity upon photoexcitation, the cross peak initially had a near-zero intensity, which increased to ∼40% of the diagonal peak intensity at later times (T > 200 fs, Fig. S16†). The timescales extracted from the fits captured the initial rise and were on the 20–40 fs timescale for all solvents. These values are both faster than the timescales extracted from the diagonal peak (Table 1) and lack the solvent dependence observed for that feature.

The cross peak rise time is expected to contain some contribution from intersystem crossing as well as a rise of the overlapping ³MLCT GSB signal. The ³MLCT GSB signal, which is on the diagonal, rises with the loss of the bpy˙⁻ absorption, similar to that of the ¹MLCT GSB signal. The fast (<50 fs) relaxation from the ³MLCT to the ligand field states likely limits the population accumulated in the ³MLCT states,³³ which may be the reason this feature does not become dominant in the 2D spectra. The extremely fast timescales and overlapping spectral signatures, however, mean that the intersystem crossing and relaxation to the ligand-field states cannot be fully isolated. As a result, the global kinetic analysis of the region extracted a timescale that is a mixture of the appearance of both the ¹MLCT GSB/SE peak and the cross peak (Fig. S22†). The timescale of the cross peak rise alone gives a better approximation of the intersystem crossing rate. The rise timescales extracted through the biexponential fit were predominantly ∼20 fs (Fig. 5C), particularly in the solvents with slower relaxation to the ligand field manifold, where the intersystem crossing is expected to be better isolated. These values are consistent with expectations for an intersystem crossing event in this complex.⁶⁵ Previous work proposed a sub-30 fs (ref. 32) intersystem crossing timescale based on fluorescence up-conversion measurements with an instrument response of ∼120 fs.⁴⁷ The ∼10 fs temporal response of our 2D apparatus enabled quantification of this extremely fast process, revealing that intersystem crossing occurs on a timescale similar to that reported for the same process in [Ru(bpy)₃]²⁺. This suggests that spin–orbit coupling is a necessary but not sufficient condition for describing intersystem crossing dynamics in transition metal complexes. Moreover, our data clearly reveal that intersystem crossing within the charge-transfer manifold occurs in competition with direct conversion from the initially formed ¹MLCT state to ligand-field excited states localized on the metal center as illustrated in Fig. 6.

Fig. 6 Proposed energy relaxation diagram derived from 2DES experiments. The initially-excited MLCT states relax into a lower-lying excited ligand field (LF) state at a solvent-dependent timescale. The timescales denoted represent the range reported in this study. Singlet-to-triplet intersystem crossing within the MLCT manifold occurs simultaneously on a timescale of ∼10–20 fs.

3. Concluding remarks

There is great interest in developing earth abundant photocatalysts using first-row transition metals.^66–69 Their smaller ligand field splitting, however, leads to distinct photodynamics that cannot be interpreted within the framework of their second- and third-row transition metal counterparts.⁷⁰ [Fe(bpy)₃]²⁺ is the prototypical example of a d⁶ photocatalyst with an earth abundant metal center. Similar to others in its class, it has rapid and complex dynamics within the MLCT manifold. Disentangling this complexity to understand why they differ from their second- and third-row counterparts is a key step in the development of these complexes for photochemical applications. For [Fe(bpy)₃]²⁺, uncovering the relaxation mechanisms at the early timescales can shed light into how the complex can undergo a formally two-electron relaxation process into the high-spin ⁵T₂ state within 200 fs, which is not typically observed in other complexes.

In this study, we observed a ¹MLCT → ³MLCT intersystem crossing process nearly contemporaneous with direct relaxation from the ¹MLCT state into lower-lying ligand-field states indicate parallel relaxation mechanisms. These parallel mechanisms indicate that in [Fe(bpy)₃]²⁺, electrons both undergo ¹MLCT → LF and ¹MLCT → ³MLCT → LF relaxation out of the MLCT manifold. Therefore, the previously competing models of energy relaxation may not be mutually exclusive, and in fact may be occurring simultaneously. Furthermore, the correlation between solvent response and relaxation from the MLCT manifold indicates that the solvent interacts with the relative charge associated with these states and may even control the pathway of relaxation. On the timescales of relaxation from the MLCT manifold, solvent dynamics are largely governed by the inertial response,^58,59 which can be as fast as 25 fs and so allows the solvent to mediate these ultrafast processes.

The high spectral and temporal resolution of 2DES revealed dynamics previously obscured in data measured with more traditional techniques. In particular, the GSB/SE and intersystem crossing peaks in [Fe(bpy)₃]²⁺ became spectrally separated by simply resolving the excitation dimension, allowing for greater insight into the crowded excited-state landscape of first-row transition-metal photocatalysts.

In conclusion, the early-time excited-state dynamics of [Fe(bpy)₃]²⁺ were measured using 2DES in a series of nitrile and alcohol solvents. The ultrafast pulse used in this experiment allowed for the resolution of early-time dynamics, making it possible to observe the effect of solvent dependence on the relaxation of the bipyridyl radical anion. Simultaneously, resolution along the excitation frequency axis allows for direct observation of the intersystem crossing dynamics. The timescale of this event was determined to be on the scale of ∼20 fs. The direct resolution of previously unobserved features in [Fe(bpy)₃]²⁺ shows the power of 2DES to provide new information on the excited-state dynamics in this class of photocatalysts.

4. Methods

4.1. Sample preparation

To ensure sufficient sample solubility in all four solvents, [Fe(bpy)₃]²⁺ was synthesized using reported literature methods^28,71,72 with different counteranions: tetrafluoroborate (BF₄⁻, for dissolving in acetonitrile, butyronitrile, pentanenitrile, and hexanenitrile) and bromide (Br⁻, for dissolving in methanol and 1-propanol).

For the 2DES experiments, the sample solutions were prepared by dissolving [Fe(bpy)₃]²⁺ powder in spectroscopic grade solvents purchased from Millipore Sigma.

4.2. Two-dimensional electronic spectroscopy

The 2D measurements were performed in a fully non-collinear, BOXCARS phase-matching geometry. Full details on the setup used can be found in Son et al.⁶² The laser spectrum (Fig. S1A†) has a spectral bandwidth (FWHM) of 106 nm (3300 cm⁻¹) centered at 540 nm (18 510 cm⁻¹). The pulse was compressed with two pairs of chirped mirrors (Ultrafast Innovations) and characterized by transient grating frequency-resolved optical gating (TG-FROG) at the sample position using a 0.1 mm thick quartz cuvette (Starna) filled with acetone.⁷³ The FROG trace revealed a pulse duration of 12 fs (Fig. S1B†). The samples were measured in a 0.1 mm path length quartz cuvette. The optical density of the sample in each solvent was measured to be 0.21 (acetonitrile), 0.27 (butyronitrile), 0.28 (pentanenitrile), 0.25 (hexanenitrile), 0.27 (methanol) and 0.21 (1-propanol) per 0.1 mm at 535 nm. An excitation pulse energy of 68 nJ was utilized, which corresponds to 1.9 × 10¹⁴ photons per cm² per pulse. Coherence time (τ), the time delay between the first two pulses, was sampled from −80 to 80 fs in 0.4 fs steps. Waiting time (T), the time delay between the second and third pulses, was sampled every 6.67 fs for T = 0–100 fs, every 25 fs for T = 100–2500 fs, every 500 fs for T = 2500–10 000 fs, every 5000 fs for T = 10 000–100 000 fs, and every 50 000 fs for T = 100 000–700 000 fs. The absolute-value 2D spectra were phased using the projection slice theorem.⁶⁴ After collection of each dataset, the linear absorption spectrum of the sample was measured and compared with the one measured before the 2D experiment to confirm the absence of photodegradation. Each sample was then measured an additional three (for the nitrile series) to four (for the alcohol series) times from T = 0–3000 fs to ensure reproducibility of the data.

For pentanenitrile and hexanenitrile experiments, an ND filter (0.2–0.5 OD) was added to the beam path after the sample to avoid detector saturation.

4.3. DFT calculations

Theoretical calculations on [Fe(bpy)₃]²⁺ complex were carried out with the Gaussian 16, Revision A.03 software package.⁷⁴ Geometry optimizations for the singlet and quintet states were performed with the TPSSH functional.⁷⁵ The 6-311G* basis set was employed for all atoms (C, H, N)^76,77 except for Fe, where the SDD basis sets and its accompanying pseudopotential⁷⁸ were used. Solvent effects (acetonitrile) were included in the calculations via the polarizable continuum model (PCM).⁷⁹ Vibrational frequency analysis was performed to ensure that all optimized structures are true minima with no imaginary frequencies. Natural orbital (NO) analysis was carried out to confirm the metal-centered character of the optimized quintet state.⁸⁰ The absorption spectra were calculated with linear-response time-dependent DFT (TD-DFT)^81–83 at the same level of theory as described for optimization. The UV-vis spectra were computed at the optimized singlet ground state structure utilizing the singlet reference state (30 lowest-energy singlet and 30 triplet excited states were calculated), as well as at the optimized quintet geometry utilizing the quintet reference state (30 lowest-energy excited states). The stick spectra were broadened using the Lorentzian functions with a half-width-at-half-maximum (HWHM) of 0.12 eV for the singlet and quintet states.

Data availability

All the data files used to generate the plots in this manuscript are available from the authors upon request.

Author contributions

A. L. performed ultrafast spectroscopy experiments and subsequent replicate experiments, analyzed the results, and wrote the manuscript with input from all authors. M. S. performed ultrafast spectroscopy experiments and assisted in the analysis of the results. M. D. performed the TD-DFT calculations on the complex studied. M. D. W. synthesized the complexes and precipitated the complex studied in various salts for spectroscopy experiments. S. M. H. assisted in conducting replicate experiments. H. F. B. curated the spectroelectrochemical data of the complex studied. P. T. C. curated the solvation information for the salts prepared. E. J. supervised the TD-DFT calculations. J. K. M. and G. S. S. C. supervised the project.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported as part of BioLEC, an Energy Frontier Research Center funded by the U.S. Department of Energy, Office of Science, Basic Energy Sciences under award no. DE-SC0019370. A. L. and S. M. H. acknowledge support from the National Science Foundation Graduate Research Fellowship Program. The authors would also like to thank and acknowledge Jonathan T. Yarranton for his help in identifying the cause of sample degradation in propionitrile.

References

1. E. R. Welin, C. Le, D. M. Arias-Rotondo, J. K. McCusker and D. W. C. MacMillan, Science, 2017, 355, 380–385.
2. K. Singh, S. J. Staig and J. D. Weaver, J. Am. Chem. Soc., 2014, 136, 5275–5278.
3. Z. Lu and T. P. Yoon, Angew. Chem., Int. Ed., 2012, 51, 10329–10332.
4. C. Creutz, M. Chou, T. L. Netzel, M. Okumura and N. Sutin, J. Am. Chem. Soc., 1980, 102, 1309–1319.
5. A. de Palo, G. La Ganga, F. Nastasi, M. Guelfi, M. Bortoluzzi, G. Pampaloni, F. Puntoriero, S. Campagna and F. Marchetti, Eur. J. Inorg. Chem., 2021, 2021, 861–869.
6. J. Oh, W. Ghann, H. Kang, F. Nesbitt, S. Providence and J. Uddin, Inorg. Chim. Acta, 2018, 482, 943–950.
7. J. C. Freys, J. M. Gardner, L. D'Amario, A. M. Brown and L. Hammarström, Dalton Trans., 2012, 41, 13105–13111.
8. A. Reynal, A. Forneli and E. Palomares, Energy Environ. Sci., 2010, 3, 805–812.
9. K. Kalyanasundaram, Coord. Chem. Rev., 1982, 46, 159–244.
10. A. Juris, V. Balzani, P. Belser and A. von Zelewsky, Helv. Chim. Acta, 1981, 64, 2175–2182.
11. O. S. Wenger, Chem.–Eur. J., 2019, 25, 6043–6052.
12. M. C. Carey, S. L. Adelman and J. K. McCusker, Chem. Sci., 2019, 10, 134–144.
13. M. D. Woodhouse and J. K. McCusker, J. Am. Chem. Soc., 2020, 142, 16229–16233.
14. M. Guttentag, A. Rodenberg, C. Bachmann, A. Senn, P. Hamm and R. Alberto, Dalton Trans., 2013, 42, 334–337.
15. Z. Zuo, D. T. Ahneman, L. Chu, J. A. Terrett, A. G. Doyle and D. W. C. MacMillan, Science, 2014, 345, 437–440.
16. S. K. Kariofillis, B. J. Shields, M. A. Tekle-Smith, M. J. Zacuto and A. G. Doyle, J. Am. Chem. Soc., 2020, 142, 7683–7689.
17. B. M. Hockin, C. Li, N. Robertson and E. Zysman-Colman, Catal. Sci. Technol., 2019, 9, 889–915.
18. A. M. Brown, C. E. McCusker and J. K. McCusker, Dalton Trans., 2014, 43, 17635–17646.
19. J. E. Monat and J. K. McCusker, J. Am. Chem. Soc., 2000, 122, 4092–4097.
20. C. Bressler, C. Milne, V.-T. Pham, A. ElNahhas, R. M. van der Veen, W. Gawelda, S. Johnson, P. Beaud, D. Grolimund, M. Kaiser, C. N. Borca, G. Ingold, R. Abela and M. Chergui, Science, 2009, 323, 489–492.
21. C. Consani, M. Prèmont-Schwarz, A. El Nahhas, C. Bressler, F. van Mourik, A. Cannizzo and M. Chergui, Angew. Chem., Int. Ed., 2009, 48, 7184–7187.
22. A. T. Yeh, C. V. Shank and J. K. McCusker, Science, 2000, 289, 935–938.
23. A. Cannizzo, C. Milne, C. Consani, W. Gawelda, C. Bressler, F. van Mourik and M. Chergui, Coord. Chem. Rev., 2010, 254, 2677–2686.
24. W. Zhang and K. J. Gaffney, Acc. Chem. Res., 2015, 48, 1140–1148.
25. J. K. McCusker, Science, 2019, 363, 484–488.
26. P. Pyykko, Chem. Rev., 1988, 88, 563–594.
27. M. Kaupp, J. Comput. Chem., 2007, 28, 320–325.
28. J. N. Miller and J. K. McCusker, Chem. Sci., 2020, 11, 5191–5204.
29. P. Chen and T. J. Meyer, Chem. Rev., 1998, 98, 1439–1478.
30. A. Rondi, Y. Rodriguez, T. Feurer and A. Cannizzo, Acc. Chem. Res., 2015, 48, 1432–1440.
31. C. Sousa, C. de Graaf, A. Rudavskyi, R. Broer, J. Tatchen, M. Etinski and C. M. Marian, Chem.–Eur. J., 2013, 19, 17541–17551.
32. G. Auböck and M. Chergui, Nat. Chem., 2015, 7, 629–633.
33. W. Zhang, R. Alonso-Mori, U. Bergmann, C. Bressler, M. Chollet, A. Galler, W. Gawelda, R. G. Hadt, R. W. Hartsock, T. Kroll, K. S. Kjær, K. Kubiček, H. T. Lemke, H. W. Liang, D. A. Meyer, M. M. Nielsen, C. Purser, J. S. Robinson, E. I. Solomon, Z. Sun, D. Sokaras, T. B. van Driel, G. Vankó, T.-C. Weng, D. Zhu and K. J. Gaffney, Nature, 2014, 509, 345–348.
34. S. Biswas, J. Kim, X. Zhang and G. D. Scholes, Chem. Rev., 2022, 122, 4257–4321.
35. J. Lu, Y. Lee and J. M. Anna, J. Phys. Chem. B, 2020, 124, 8857–8867.
36. S. Mukamel, Annu. Rev. Phys. Chem., 2000, 51, 691–729.
37. M. Son, A. Pinnola, R. Bassi and G. S. Schlau-Cohen, Chem, 2019, 5, 575–584.
38. V. R. Policht, A. Niedringhaus, R. Willow, P. D. Laible, D. F. Bocian, C. Kirmaier, D. Holten, T. Mančal and J. P. Ogilvie, Sci. Adv., 2022, 8, eabk0953.
39. M. Son, S. M. Hart and G. S. Schlau-Cohen, Trends Chem., 2021, 3, 733–746.
40. E. Collini, J. Phys. Chem. C, 2021, 125, 13096–13108.
41. H. Seiler, S. Palato, C. Sonnichsen, H. Baker, E. Socie, D. P. Strandell and P. Kambhampati, Nat. Commun., 2019, 10, 4962.
42. A. Liu, G. Nagamine, L. G. Bonato, D. B. Almeida, L. F. Zagonel, A. F. Nogueira, L. A. Padilha and S. T. Cundiff, ACS Nano, 2021, 15, 6499–6506.
43. A. Liu, D. B. Almeida, L. A. Padilha and S. T. Cundiff, J. Phys. Mater., 2022, 5, 021002.
44. S. M. Hart, W. J. Chen, J. L. Banal, W. P. Bricker, A. Dodin, L. Markova, Y. Vyborna, A. P. Willard, R. Häner, M. Bathe and G. S. Schlau-Cohen, Chem, 2021, 7, 752–773.
45. J. Brazard, L. A. Bizimana, T. Gellen, W. P. Carbery and D. B. Turner, J. Phys. Chem. Lett., 2016, 7, 14–19.
46. J. D. Gaynor, A. Petrone, X. Li and M. Khalil, J. Phys. Chem. Lett., 2018, 9, 6289–6295.
47. W. Gawelda, A. Cannizzo, V.-T. Pham, F. van Mourik, C. Bressler and M. Chergui, J. Am. Chem. Soc., 2007, 129, 8199–8206.
48. S. Dhamija, G. Bhutani, A. Jayachandran and A. K. De, J. Phys. Chem. A, 2022, 126, 1019–1032.
49. B. D. Alexander, T. J. Dines and R. W. Longhurst, Chem. Phys., 2008, 352, 19–27.
50. L. M. Lawson Daku, Phys. Chem. Chem. Phys., 2018, 20, 6236–6253.
51. H. T. Lemke, K. S. Kjær, R. Hartsock, T. B. van Driel, M. Chollet, J. M. Glownia, S. Song, D. Zhu, E. Pace, S. F. Matar, M. M. Nielsen, M. Benfatto, K. J. Gaffney, E. Collet and M. Cammarata, Nat. Commun., 2017, 8, 15342.
52. O. Bräm, F. Messina, A. M. El-Zohry, A. Cannizzo and M. Chergui, Chem. Phys., 2012, 393, 51–57.
53. A. L. Smeigh, M. Creelman, R. A. Mathies and J. K. McCusker, J. Am. Chem. Soc., 2008, 130, 14105–14107.
54. A. N. Tarnovsky, W. Gawelda, M. Johnson, C. Bressler and M. Chergui, J. Phys. Chem. B, 2006, 110, 26497–26505.
55. A. Volpato, L. Bolzonello, E. Meneghin and E. Collini, Opt. Express, 2016, 24, 24773–24785.
56. A. B. Maurer and G. J. Meyer, J. Am. Chem. Soc., 2020, 142, 6847–6851.
57. D. A. Hoff, R. Silva and L. G. C. Rego, J. Phys. Chem. C, 2011, 115, 15617–15626.
58. S. J. Rosenthal, X. Xie, M. Du and G. R. Fleming, J. Chem. Phys., 1991, 95, 4715–4718.
59. M. Maroncelli, P. V. Kumar, A. Papazyan, M. L. Horng, S. J. Rosenthal and G. R. Fleming, AIP Conf. Proc., 1994, 298, 310–333.
60. J. O. Tollerud and J. A. Davis, Prog. Quantum Electron., 2017, 55, 1–34.
61. J. D. Hybl, A. Albrecht Ferro and D. M. Jonas, J. Chem. Phys., 2001, 115, 6606–6622.
62. M. Son, S. Mosquera-Vázquez and G. S. Schlau-Cohen, Opt. Express, 2017, 25, 18950–18962.
63. F. Milota, C. N. Lincoln and J. Hauer, Opt. Express, 2013, 21, 15904–15911.
64. D. M. Jonas, Annu. Rev. Phys. Chem., 2003, 54, 425–463.
65. L. S. Forster, Coord. Chem. Rev., 2006, 250, 2023–2033.
66. O. S. Wenger, J. Am. Chem. Soc., 2018, 140, 13522–13533.
67. A. Hossain, A. Bhattacharyya and O. Reiser, Science, 2019, 364, eaav9713.
68. M. Kojima and S. Matsunaga, Trends Chem., 2020, 2, 410–426.
69. J. Liu, L.-Q. Lu, Y. Luo, W. Zhao, P.-C. Sun, W. Jin, X. Qi, Y. Cheng and W.-J. Xiao, ACS Catal., 2022, 12, 1879–1885.
70. M. Iwamura, S. Takeuchi and T. Tahara, Acc. Chem. Res., 2015, 48, 782–791.
71. J. K. McCusker, A. L. Rheingold and D. N. Hendrickson, Inorg. Chem., 1996, 35, 2100–2112.
72. Y. Yamamoto, E. Sumimura, K. Miyoshi and T. Tominaga, Anal. Chim. Acta, 1973, 64, 225–233.
73. R. Trebino, K. W. DeLong, D. N. Fittinghoff, J. N. Sweetser, M. A. Krumbügel, B. A. Richman and D. J. Kane, Rev. Sci. Instrum., 1997, 68, 3277–3295.
74. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision C.01, Gaussian Inc, Wallingford CT, 2016.
75. J. Tao, J. P. Perdew, V. N. Staroverov and G. E. Scuseria, Phys. Rev. Lett., 2003, 91, 146401.
76. R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72, 650–654.
77. A. D. McLean and G. S. Chandler, J. Chem. Phys., 1980, 72, 5639–5648.
78. M. Dolg, U. Wedig, H. Stoll and H. Preuss, J. Chem. Phys., 1987, 86, 866–872.
79. G. Scalmani and M. J. Frisch, J. Chem. Phys., 2010, 132, 114110.
80. P.-O. Löwdin, Phys. Rev., 1955, 97, 1474–1489.
81. R. Bauernschmitt and R. Ahlrichs, Chem. Phys. Lett., 1996, 256, 454–464.
82. M. E. Casida, C. Jamorski, K. C. Casida and D. R. Salahub, J. Chem. Phys., 1998, 108, 4439–4449.
83. R. E. Stratmann, G. E. Scuseria and M. J. Frisch, J. Chem. Phys., 1998, 109, 8218–8224.

---

Footnotes

† Electronic supplementary information (ESI) available: Data for Fig. 1–5, and further detailed analysis and calculations. Extended studies on nitriles. See DOI: https://doi.org/10.1039/d3sc02613b

‡ Current address: Department of Chemistry, Boston University, 590 Commonwealth Ave, Boston, MA 02215, USA.

§ Current address: Department of Chemistry, University of California, Berkeley, California 94720, USA.

---