Isostructural bridging diferrous chalcogenide cores [Fe^II(μ-E)Fe^II] (E = O, S, Se, Te) with decreasing antiferromagnetic coupling down the chalcogenide series

Abstract

Iron compounds containing a bridging oxo or sulfido moiety are ubiquitous in biological systems, but substitution with the heavier chalcogenides selenium and tellurium, however, is much rarer, with only a few examples reported to date. Here we show that treatment of the ferrous starting material [(^tBupyrpyrr₂)Fe(OEt₂)] (1-OEt₂) (^tBupyrpyrr₂ = 3,5-^tBu₂-bis(pyrrolyl)pyridine) with phosphine chalcogenide reagents E = PR₃ results in the neutral phosphine chalcogenide adduct series [(^tBupyrpyrr₂)Fe(EPR₃)] (E = O, S, Se; R = Ph; E = Te; R = ^tBu) (1-E) without any electron transfer, whereas treatment of the anionic starting material [K]₂[(^tBupyrpyrr₂)Fe₂(μ-N₂)] (2-N₂) with the appropriate chalcogenide transfer source yields cleanly the isostructural ferrous bridging mono-chalcogenide ate complexes [K]₂[(^tBupyrpyrr₂)Fe₂(μ-E)] (2-E) (E = O, S, Se, and Te) having significant deviation in the Fe–E–Fe bridge from linear in the case of E = O to more acute for the heaviest chalcogenide. All bridging chalcogenide complexes were analyzed using a variety of spectroscopic techniques, including ¹H NMR, UV-Vis electronic absorbtion, and ⁵⁷Fe Mössbauer. The spin-state and degree of communication between the two ferrous ions were probed via SQUID magnetometry, where it was found that all iron centers were high-spin (S = 2) Fe^II, with magnetic exchange coupling between the Fe^II ions. Magnetic studies established that antiferromagnetic coupling between the ferrous ions decreases as the identity of the chalcogen is tuned from O to the heaviest congener Te.

---

Introduction

Iron complexes with bridging chalcogenide ligands play an important role in metalloenzymes, such as the soluble methane monooxygenase^1–5 and ATP-dependent nitrogenase,^6,7 but also form the core unit of a class of semiconductor materials.^8–10 A bridging iron μ-O complex with an Fe(μ-O)₂Fe core is considered a key intermediate in the catalytic mechanism of the soluble methane monooxygenase.^11–13 Owing to their bioinorganic prevalence, hundreds of synthetic Fe(μ-O)Fe^14–29 model complexes utilizing a variety of ligand platforms have been reported. Some of these Fe(μ-O)Fe complexes have been implicated in useful transformations, such as the oxidation of water,^30–32 olefins,^33–35 alkanes,³⁶ alcohols,^37,38 and thianthrenes,³⁹ as well as in reduction processes involving carbon dioxide,^40–43 and dioxgyen.⁴⁴

Likewise, bridging iron sulfide complexes are equally prevalent in nature, since iron-sulfur clusters found in the FeMoCo of the ATP-dependent nitrogenase enzymes are responsible and indispensable in delivering multiple equivalents of electrons during the catalytic cycle for the fixation of nitrogen.^45,46 Many compounds with Fe(μ-S)₂Fe^47–55 cores and even higher nuclearities,^56–59 especially cubane-type structures,^60–63 have been well explored. Surprisingly, complexes having mono-bridged Fe(μ-S)Fe^28,57–82 cores are not as common as their O-counterparts, with crystallographically characterized synthetic examples numbering in the tens.⁸³

While iron complexes with bridging O and S ligands are more well established, the heavier congeners Se and Te have just a few examples in the literature (Scheme 1). In fact, there are only five reported crystal structures of iron complexes containing a bridging mono-selenide^{71,75,77,84,85} ligand and, surprisingly, only one example containing a bridging mono-telluride⁸⁶ ligand. Due to the scarcity of iron complexes containing Fe(μ-Se)Fe and Fe(μ-Te)Fe cores, the effect of heavier chalcogenide substitution on the electronic properties has proven to be difficult to study. Being able to systematically change the nature of the more flexible mono-bridged chalcogenide ligand – and to understand the subtle structural and electronic changes this brings about to the Fe–E–Fe core – would represent an important venture. Along these lines, Gade and co-workers^22,71 reported bridging iron chalcogenide complexes of O, S, and Se using the same carbazole-based pincer ligand (Scheme 1). Double-bridged chalcogenide complex cores Fe(μ-E)₂Fe with the heavier chalcogenides Se and Te have recently received attention due to interesting electronic properties; namely, their ability to form rare intermediate spin-states in reduced mixed valent [(nacnac)Fe(μ-E)₂Fe(nacnac)]⁻ (nacnac = HC(CMeN(2,6-diisopropylphenyl))₂; E = Se, Te) systems.⁸⁷

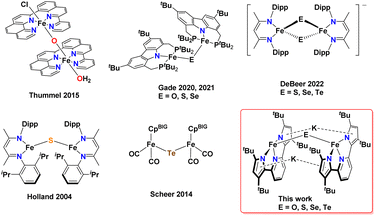Scheme 1 Reported examples of mono-bridged diiron chalcogenide complexes, DeBeer's bis-chalcogenide bridged diiron system stabilizing intermediate spin states, and this work. Cp^BIG = Cp(p-^tBuPh)₅.

Herein, we report the first isostructural series of diferrous complexes containing the mono-bridged chalcogenides O, S, Se, and Te. These complexes are supported by the same ^tBu-substituted pyridine bispyrrolide ligand platform with the core enforced through two K⁺ pyrrole π-interactions (Scheme 1). These complexes have been characterized by single crystal X-ray diffraction studies (sc-XRD), as well as ¹H NMR, UV-Vis electronic absoption, and ⁵⁷Fe Mössbauer spectroscopies. With the aid of solid-state SQUID magnetometry, we observed a marked trend of lesser antiferromagnetic coupling when expanding substitution to the heavier chalcogenide congeners which we attribute to the ∠Fe–E–Fe angle becoming more acute due to decreased hybridization in the heavier chalcogenides and poorer orbital overlap with Fe^II d-orbitals. For comparison, we also report mononuclear adducts of the phosphine chalcogenide series where E-atom transfer does not occur. Our work represents the first study to span the whole chalcogenide series for diirion cores of the type Fe(μ-E)Fe and their direct comparison as chalcogenide substitution progresses down group 16. We show how these cores can be systematically accessed via a formally end-on and bridging dinitrogen precursor with a Fe^I(μ-N₂)Fe^I core and the suitable chalcogen source as the oxidant.

Results and discussion

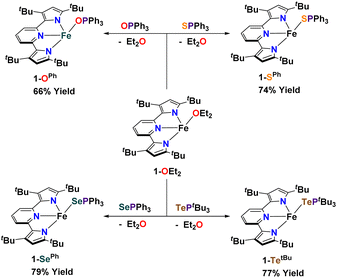
Synthesis of complexes 1-E and 2-E. Using [(^tBupyrpyrr₂)Fe(OEt₂)] (1-OEt₂)⁸⁸ (^tBupyrpyrr₂ = 3,5-^tBu₂-bis(pyrrolyl)pyridine) as a starting material, we previously showed how insertion of elemental sulfur into the ^tBupyrpyrr₂ ligand framework would form a dimeric [(pyrr-1-S-pyrrpy)Fe]₂ (pyrr-1-S-pyrrpy = 3,5-(^tBu₂-pyrrolyl)(1-S-3,5-^tBu₂-pyrrolyl)pyridine) complex, in which one pyrrole arm of the former tridentate ligand had been oxidized.⁸⁹ This reaction could, in principle, involve the formation of mono-nuclear Fe^IVS sulfido or Fe^IIIS sulfur radical species. Therefore, we explored other possible S-atom transfer reagents in hopes of trapping such an elusive species. We turned our attention to S=PPh₃ with the goal of making a hypothetical complex [(^tBupyrpyrr₂)Fe(S)(PPh₃)]. When 1-OEt₂ was treated with the phosphine–sulfide the reaction yielded instead the ferrous adduct [(^tBupyrpyrr₂)Fe(SPPh₃)] (1-S^Ph) in 74% isolated yield after workup of the mixture (Scheme 2). Single-crystals suitable for a sc-XRD were grown by slow evaporation of hexane into a concentrated toluene solution of 1-S^Ph, followed by chilling of the solution at −35 °C for one day. The solid-state structure of 1-S^Ph shows the SPPh₃ ligand to be bound to the formally Fe^II ion (Fig. 1) in a cis-divacant octahedral⁸⁸ molecular geometry, which is typical of neutral ferrous adducts with this ligand platform.^88–90

Scheme 2 Synthesis of mononuclear phosphine chalcogenide adducts 1-O^Ph, 1-S^Ph, 1-Se^Ph, and 1-Te^tBu.

Fig. 1 Solid-state molecular structures of 1-O^Ph, 1-S^Ph, 1-Se^Ph, 1-Te^tBu (top) and 2-O, 2-S, 2-Se, and 2-Te (bottom) shown at 50% probability. Hydrogen atoms and solvent molecules have been omitted for clarity.

Not surprisingly, analogous treatment of 1-OEt₂ with O=PPh₃, Se=PPh₃, and Te=P^tBu₃ yielded the corresponding phosphine chalcogenide adducts 1-O^Ph, 1-Se^Ph, and 1-Te^tBu in 66%, 79%, and 77% isolated yields, respectively (Scheme 2), and without any evidence of chalcogen-atom transfer. However, due to the instability of Te=PPh₃, a more electron-rich phosphine (P^tBu₃) had to be employed to furnish an isolable phosphine telluride reagent. Phosphine chalcogenide adducts 1-O^Ph, 1-Se^Ph, and 1-Te^tBu were crystallized using slightly different conditions (see ESI†) owing to their different solubilities in common organic solvents.

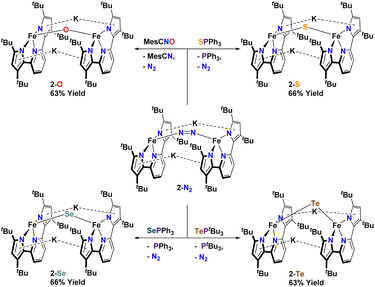
In an attempt to transfer the chalcogenide atom to iron, the phosphine chalcogenide adducts 1-E (E = O^Ph, S^Ph, Se^Ph, Te^tBu) were reduced with one equivalent of KC₈. In general, these reactions were unclean yielding various paramagnetic products. We were, however, able to isolate the bridging chalcogenide anions [K₂][(^tBupyrpyrr₂)Fe₂(μ-E)] (2-E) (E = O, S, Se, Te) from these complex reaction mixtures. Unfortunately, these reduction reactions resulted in poor yields and impure forms of 2-E. Desiring a cleaner and higher yielding route to the ate-diferrous chalcogenide compounds 2-E, we turned our attention to the dinuclear, formally mono-valent, Fe₂^I,I precursor, [K]₂[(^tBupyrpyrr₂)Fe₂(μ-N₂)] (2-N₂), which is readily prepared from 1-OEt₂ and KC₈ under an atmosphere of N₂.⁹¹ This route would allow us to preassemble the diiron-ate core while using the chalcogen source as an oxidant. Gratifyingly, when 2-N₂ is treated with phosphine chalcogenides S=PPh₃, Se=PPh₃, and Te=P^tBu₃ the reaction resulted in ready elimination of N₂ and clean formation of the corresponding bridging diiron-ate chalcogenide complexes 2-E (E = S, Se, and Te, Scheme 3). Remarkably, even a rare example of a bridging mono-telluride ate complex [K]₂[(^tBupyrpyrr₂)Fe₂(μ-Te)] (2-Te) could be prepared using this synthetic route and structurally confirmed via sc-XRD, making this a rare example of a system containing a Fe^II(μ-Te)Fe^II unit.⁸⁶ However, synthesis of the oxo-derivative using 2-N₂ with O=PPh₃ proved more challenging due to the inability of O=PPh₃ to act as an O-atom donor to 2-N₂. For this reason, we resorted to a more reactive O-atom transfer reagent, mesityl nitrile oxide (MesCNO), which is known to effect clean O-atom transfer to a variety of targets.^92–94 Accordingly, treatment of 2-N₂ with one equivalent of MesCNO resulted in clean formation of [K]₂[(^tBupyrpyrr₂)Fe₂](μ-O)] (2-O). Thus, using these synthetic strategies, compounds 2-E could be prepared reproducibly and in pure form in yields ranging from 63%–66% (see ESI†). The ability to prepare the diferrous chalcogenide series presented us with the unique opportunity to study how the variation of a single atom in complexes 2-E could affect both structural and electronic properties.

Scheme 3 Synthesis of dinuclear bridging chalcogenide anions 2-O, 2-S, 2-Se, and 2-Te.

Structural properties of complexes 1-E and 2-E

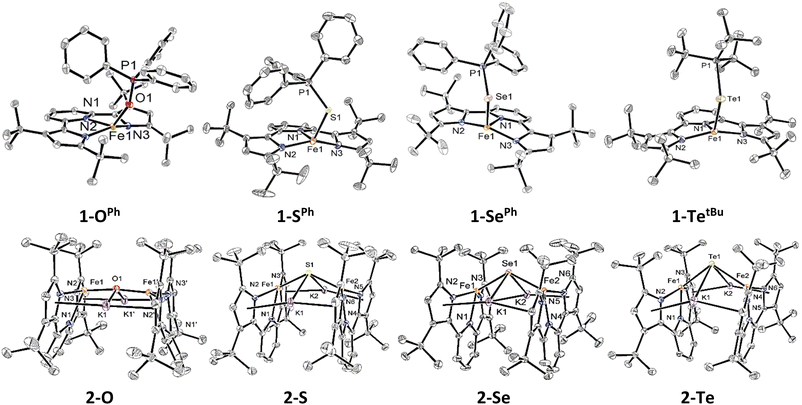
With the isostructural set of complexes 1-E and 2-E in hand, comparisons between their metrical parameters could be made. As expected, the Fe–E distance in complexes 1-E increases as the identity of E is moved down group 16 from 2.008(1) Å in 1-O^Ph to 2.7449(5) Å in 1-Te^tBu (Fig. 1 and Table 1). Additionally, the ∠N1–Fe–E angle decreases from 125.34(5)° in 1-O^Ph to 115.78(5)° in 1-Se^Ph. However, the ∠N1–Fe–E angle in 1-Te^tBu was found to be 124.90(6)°, but this departure from the trend may be due to the sterically more encumbering substitution of the phosphine on the coordinated phosphine telluride ligand as compared to the lighter congeners. Similarly, the ∠Fe–E–P angle also decreases as E becomes a heavier chalcogen from 152.58(8)° in 1-O^Ph to 111.42(2)° in 1-Se^Ph. Again, 1-Te^tBu strays from the trend with a ∠Fe–E–P angle of 113.12(2)°, due to the different substituents on the phosphine. Finally, all complexes 1-E have quite similar τ₄ values, ranging from 0.61 to 0.71 in the typical range of cis-divacant octahedral iron complexes of the ^tBupyrpyrr₂ ligand platform.^88–90

Table 1 Selected bond metrics for 1-E and 2-E

Compound	1-O^Ph	1-S^Ph	1-Se^Ph	1-Te^t^Bu	2-O	2-S	2-Se	2-Te
d(Fe1–E) (Å)/d(Fe2–E) (Å)	2.008(1)	2.4734(6)	2.5552(4)	2.7449(5)	1.8511(3)	2.2629(4)/2.2825(5)	2.3991(4)/2.4153(5)	2.6028(6)/2.6186(5)
d(E–P) (Å)	1.501(1)	2.0368(9)	2.1496(7)	2.4162(8)
∠N1–Fe1–E/∠N4–Fe2–E (°)	125.34(5)	116.00(6)	115.78(5)	124.90(6)	116.29(8)	129.28(4)/122.23(4)	130.53(4)/124.01(4)	130.65(7)/125.89(7)
∠Fe1–E–P (°)	152.58(8)	113.78(3)	111.42(2)	113.12(2)
∠Fe–E–Fe (°)					172.18(1)	131.61(2)	125.35(2)	112.12(2)
d(Fe–Fe) (Å)					3.69	4.13	4.26	4.32
τ 4 (Fe1/Fe2)	0.61	0.71	0.69	0.64	0.81	0.65/0.71	0.63/0.68	0.62/0.67

---

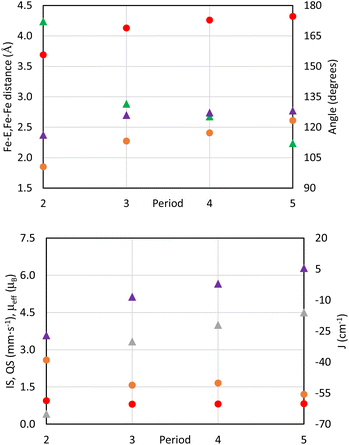
The diferrous bridging chalcogenide complexes 2-E also show systematic structural variations with differing substitution of the bridging chalcogenide core. The dinuclear complexes 2-E are held together in part by K⁺–π_arene interactions as well as coordination of K⁺ to the bridging chalcogenide ligand. Among these, complex 2-O crystallized in the centrosymmetric C2/c space group owing to a two-fold rotation axis through the oxygen atom. This symmetric feature rendered both iron atoms and associated ligand environments indistinguishable by symmetry. In contrast, the structures of complexes 2-S, 2-Se, and 2-Te possess asymmetric iron atoms due to further distortion about the ∠Fe–E–Fe angle. Table 1 lists some salient structural parameters for each iron atom. Perhaps the most notable structural trend among the complexes 2-E is the decrease in the ∠Fe–E–Fe angle as the identity of E moves down group 16 (Fig. 1). The ∠Fe–E–Fe angle significantly changes from the more linear mode of 172.18(1)° in 2-O, to 131.61(2)° in 2-S, 125.35(2)° in 2-Se, and, ultimately, a highly bent angle of 112.12(2)° is observed in 2-Te, due to a combination of hybridized orbitals in the lighter chalcogenides and structural rearrangements to accommodate larger chalcogenides under the constraints imposed by the K⁺–π_arene interactions. Likewise, the Fe–E bond distance increases as E shifts to heavier chalcogenides: from 1.8511(3) Å in 2-O to 2.2629(4)/2.2825(5) Å in 2-S, 2.3991(4)/2.4153(5) Å in 2-Se, and 2.6028(6)/2.6186(5) in 2-Te, as expected considering the greater covalent radii of the heavier chalcogenides. Due to such an increment in the distance, the Fe–Fe separation also increases from 3.69 Å in 2-O, 4.13 Å in 2-S, 4.26 Å in 2-Se, to 4.32 Å in 2-Te. Additionally, the ∠N1–Fe–E angle in 2-O is much more acute (116.29(8)°) than in 2-S, 2-Se, and 2-Te (129.28(4)°/122.23(4)° in 2-S – 130.65(7)°/125.89(7)° in 2-Te). This becomes partially manifested in a systematic decrease in the geometric index, τ₄, in complexes 2-E as the identity of E spans down the chalcogenide group. The values of τ₄ change from 0.81 in 2-O to 0.65/0.71 in 2-S, 0.63/0.68 in 2-Se, and 0.62/0.67 in 2-Te, indicating a coordination geometry closer to square planar for the heavier congeners of 2-E while still within the typical range of compounds with a cis-divacant octahedral coordination geometry.^88–90 Despite all iron ions being formally Fe^II, the primary systematic structural difference between complexes 2-E and their corresponding phosphine chalcogenide adducts 1-E is a shortening of the Fe–E bond in the anionic chalcogenide dimers, likely a result of increased covalent character of the Fe–E bond in the absence of the phosphine as well as the charged nature of the complexes.

Spectroscopic and magnetic properties of complexes 1-E and 2-E

Solution ¹H NMR spectral data of complexes 1-E are defined by the presence of 6–8 distinct paramagnetically shifted and broadened resonances (Fig. S1–S4†), indicative of a plane of symmetry bisecting the ^tBupyrpyrr₂ ligand as well as symmetrically equivalent substituents on the E = PR₃ ligand due to free rotation of the phosphine substituents. Due to the poor solubility of 1-SPh in benzene, only 7 resonances were observable in the ¹H NMR spectrum (Fig. S2†). The ¹H NMR spectrum of 1-Te^tBu shows fewer paramagnetically shifted resonances (Fig. S4†), as expected and in accordance with a similar C_s symmetric structure in solution as in 1-O^Ph, 1-S^Ph, and 1-Se^Ph. The ¹H NMR resonances for all complexes 1-E fall in the typical range of neutral, ferrous Lewis-base adducts containing the (^tBupyrpyrr₂)Fe scaffold (δ 122.14 to −5.31).^88–90

Complexes 2-E were also analyzed by ¹H NMR spectroscopy and each displayed 5 paramagnetically shifted and broadened resonances; also in accord with C_s symmetry in solution (Fig. S5–S8†). These resonances were distributed in the range from δ 72.01 to −6.89, notably up-field compared to the starting material 2-N₂.⁹¹ Interestingly, there is a trend in the pyrrolyl/meta-pyrydyl resonances, in which these resonances shift downfield from δ 32.01/19.84 in 2-O to δ 72.01/66.57 in 2-Te as the identity of the bridging chalcogen shifts to the heavier congeners of group 16. This trend may be due to a lower total spin in 2-O, 2-S, and 2-Se, thus giving rise to a smaller paramagnetic contribution to the chemical shift (vide infra).⁹⁵ The resonances for complexes 2-E are also notably sharper and occupy a smaller range of chemical shifts than the phosphine chalcogenide adducts 1-E.

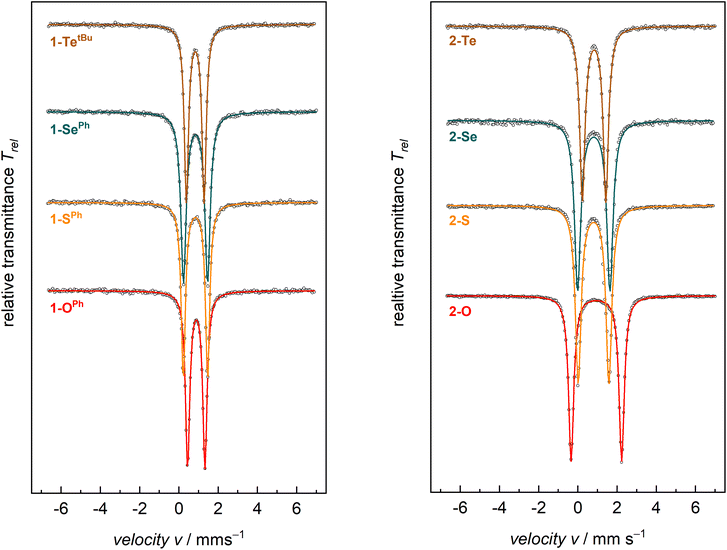
Zero-field ⁵⁷Fe Mössbauer spectroscopy in the solid state at 77 K of compounds 1-E show quadrupole doublets with isomer shifts, δ, in the narrow range of 0.88–0.83 mm s⁻¹ and quadrupole splitting parameters, ΔE_Q, in the range of 1.24–0.88 mm s⁻¹ (Fig. 2 and Table 2). These values are all in the typical range of high-spin (S = 2) Fe^II on the ^tBupyrpyrr₂ ligand platform.^88–90 Similarly, compounds 2-E show Mössbauer parameters consistent with S = 2 Fe^II ions. The isomer shifts of complexes 2-E are in the range δ = 0.94–0.80 mm s⁻¹, whereas the values for the quadrupole splitting parameter fall in the range ΔE_Q = 2.58–1.20 mm s⁻¹. However, complex 2-O has a much larger quadrupole splitting value (2.58 mm s⁻¹) than the heavier congeners 2-S, 2-Se, and 2-Te (1.20–1.65 mm s⁻¹, Table 2). The larger quadrupole splitting of 2.58 mm s⁻¹ for 2-O (compared to 1.57, 1.65, 1.20 mm s⁻¹ for 2-S, 2-Se, and 2-Te, respectively) can be explained by a higher degree of ligand contribution to the electric field gradient, expressed as the quadrupole splitting parameter ΔE_Q. This is mostly due to oxygen being the lightest and most electronegative group 16 element (EN_O: 3.44); thus, being significantly smaller and more electronegative compared to its larger and heavier homologues (EN_S: 2.58; EN_Se: 2.55, EN_Te: 2.10; according to Pauling). Consequently, the orbital overlap between metal d and chalcogen p orbitals in 2-O is more effective, as reflected by the shorter Fe–O bonds and the nearly linear ∠Fe–O–Fe angle. Since not all metal d-electrons are equally affected by the short Fe–O bond, this will enforce an electric field gradient that is higher than the one from metal d-electron distribution (valence contribution) alone. Therefore, a larger quadrupole splitting is observed in 2-O compared to 2-S, 2-Se, and 2-Te.

Fig. 2 Zero-field ⁵⁷Fe Mössbauer spectra of compounds 1-E (left) and 2-E (right) recorded at 77 K.

Table 2 Zero-field ⁵⁷Fe Mössbauer and magnetic data measured for compounds 1-E and 2-E. Effective magnetic moments μ_eff are in units of μ_B

Compound	δ (mm s^−1)	ΔEQ (mm s^−1)	Γ fwhm	μ eff (300 K, μB) SQUID	μ eff (300 K, μB) Evans method	g av	|D| (cm^−1)	J (cm^−1)
1-O^Ph	0.88	0.88	0.26	5.30	4.8	2.23	8
1-S^Ph	0.84	1.24	0.26	5.33		2.15	9
1-Se^Ph	0.84	1.23	0.33	5.16	4.4	2.08	9
1-Te^t^Bu	0.83	0.90	0.26	5.32	4.9	2.19	8
2-O	0.94	2.58	0.32	3.58	3.5	2.05		−65
2-S	0.80	1.57	0.35	5.13	5.5	2.15		−30
2-Se	0.81	1.65	0.38	5.66	5.3	2.08		−22
2-Te	0.82	1.20	0.33	6.29	5.9	2.19		−16

---

When compared to complexes 2-E, the ⁵⁷Fe Mössbauer spectra of complexes 1-E generally have smaller quadrupole splitting values. The isomer shifts, on the other hand, show negligible differences between these classes of compounds. Since the iron centers in both 1-E and 2-E share the S = 2 spin state and, therefore, the same physical oxidation state, this is reflected by similar isomer shifts for all eight compounds.

Solution state magnetic susceptibility measurements of complexes 1-O^Ph, 1-Se^Ph, and 1-Te^tBu were all consistent with the ⁵⁷Fe Mössbauer data, and in accord with these having an S = 2 ground state (Table 2). Unfortunately, due to insufficient solubility, we were unable to obtain a reliable solution-state magnetic moment for 1-S^Ph. To more conclusively understand the magnetic properties for the entire series, complexes 1-E were also analyzed by variable-temperature SQUID magnetometry. Multiple independently synthesized samples were studied, and reproducible data were analyzed and plotted as effective magnetic moment, μ_eff, vs. temperature. The magnetic data for mononuclear complexes 1-E show low μ_eff values at low temperatures followed by a sharp increase in the magnetic moment to a plateau over a large range of temperatures. Effective magnetic moments, μ_eff, at 300 K are in the range of 5.16–5.32 μ_B and are consistent with the solution-phase magnetic studies and ⁵⁷Fe Mössbauer data, again indicating an S = 2 ground state (Table 2 and Fig. 3 top). The solid-state magnetic moments are, however, larger than expected for spin-only values (μ_s.o. = 4.90 μ_B), and this could be explained by partially unquenched spin–orbit coupling which results in average g-values larger than that of the free electron. This is not unexpected, especially for complexes containing the heavier group 16 elements.

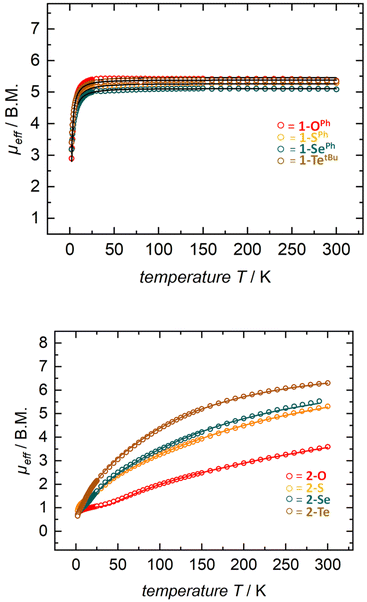Fig. 3 SQUID magnetization data of representative samples of compounds 1-E (top) and 2-E (bottom). Reproducibility was confirmed by measuring two independently synthesized samples for each compound (see the ESI†). For 1-Te, temperature-independent paramagnetism (TIP = 1.7 × 10⁻³ emu) has been considered and subtracted. Color indicates identity of chalcogen E (O-red, S-orange, Se-green, and Te-brown).

Given the dinuclear structures of complexes 2-E through the chalcogenide bridge one would anticipate the possibility of magnetic exchange coupling between the two ferrous ions. Although antiferromagnetic coupling is observed at low temperatures for all previously reported dinuclear species using the ^tBupyrpyrr₂ ligand, room temperature antiferromagnetic coupling was only observed in a ligand-sulfur oxidized species [(pyrr-1-S-pyrrpy)Fe]₂.⁸⁹ For the isostructural starting material 2-N₂, we observe room temperature ferromagnetic coupling between the Fe^II ions and the triplet N₂²⁻ fragment.⁹¹ In our situation, solution-state magnetic moments of the bridging chalcogenide anions 2-E are generally in an incremental order from E = O to Te with a range from 3.5–5.9 μ_B with 2-O being the smallest and 2-Te being the largest (Table 2). These values are significantly lower than the spin-only value of two uncoupled S₁ = S₂ = 2 ions, where μ_eff = [(μ_eff(S₁))² + (μ_eff(S₂))²]^1/2 = 6.90 μ_B.

Gratifyingly, solution-state magnetic moments were corroborated in the solid-state by SQUID magnetometry (Table 2 and Fig. 3). For instance, compounds 2-E exhibited a steady increase in μ_eff over the temperature range of 2–300 K with solid state magnetic moments at room temperature ranging between 3.58–6.29 μ_B (μ_eff for 2-O = 3.58 μ_B; 2-S = 5.13 μ_B; 2-Se = 5.66 μ_B; and 2-Te = 6.29 μ_B). These effective magnetic moments are much lower than the expected spin-only value for two isolated S = 2 iron centers and suggest spin-pairing between the ferrous iron centers. This clear trend of lower effective magnetic moments (at RT) can be explained by the antiferromagnetic coupling constant J derived from the Heisenberg–Dirac–Van Vleck exchange Hamiltonian

Ĥ_HDVV = −JŜ₁Ŝ₂.

In our systems, J is in the range of −65 to −16 cm⁻¹, with 2-O having the largest magnitude (most negative) antiferromagnetic coupling constant in the series followed in order by 2-S, 2-Se, and 2-Te (Table 2).

The marked trend of lower effective magnetic moments with lighter substitution mirrors the observed structural trends, namely, the ∠Fe–E–Fe angle, Fe–E bond length, and the Fe–Fe distance. The most dramatic structural trend is the decrease in the ∠Fe–E–Fe angle from 172.18(2)° in 2-O to 112.12(2)° in 2-Te (Table 1 and Fig. 4), which is reflected by the trend in the effective magnetic moment μ_eff and the magnitude of the antiferromagnetic coupling constant J (Fig. 4). It is well established through the Goodenough–Kanamori rules that ∠M–E–M angles close to 180° result in antiferromagnetic coupling, while ∠M–E–M angles close to 90° result in ferromagnetic coupling.^96–98 More linear ∠M–E–M angles could be caused by the enhanced ability of lighter main group elements to have hybridized orbitals as well as better orbital overlap with Fe^II d-orbitals. Greater orbital overlap between the chalcogenide core and the Fe^II ion gives rise to more magnetic exchange coupling. Hybridized chalcogenide orbitals would also lead to a larger degree of π-bonding⁹⁹ with the Fe^II ion as evidenced by the significantly larger ΔE_Q value in 2-O (Table 2) and a shorter Fe–O bond length.

Fig. 4 (Top) Scatter plots of Fe–E bond length (orange circles, Å, left axis), Fe–Fe distance (red circles, Å, left axis), ∠Fe–E–Fe angle (green triangles, degrees, right axis), and ∠N_pyr–Fe–E angle (purple triangles, degrees, right axis) of compounds 2-E as a function of the period of the chalcogenide substituent. The ∠N_pyr–Fe–E angles and Fe–E bond lengths for periods 3–5 (compounds 2-S, 2-Se, and 2-Te) are calculated as the average for the two different iron atoms. (Bottom) Scatter plots of Mössbauer isomer shift (red circles, mm s⁻¹, left axis), Mössbauer Quadrupole Splitting (orange circles, mm s⁻¹, left axis), SQUID μ_eff at 300 K (purple triangles, μ_B, left axis), and SQUID antiferromagnetic coupling J (grey triangles, cm⁻¹, right axis) as a function of the period of the chalcogenide substituent.

The effect of chalcogenide size on the observed trends in ∠Fe–E–Fe angle, Fe–E bond lengths, and Fe–Fe distances cannot, however, be overlooked. There are notable differences in the covalent and ionic radii between the different chalcogenides which leads to an increased Fe–E bond length for the heavier chalcogenides (Fig. 4). Constraining the molecular geometry by K⁺–π_arene interactions forces the ∠Fe–E–Fe angle to become smaller in order to accommodate the longer Fe–E bond distance for heavier chalcogenides. The Fe–Fe distance also increases with substitution of heavier chalcogenides from 3.69 Å in 2-O to 4.32 Å in 2-Te (Table 1 and Fig. 4) due to puckering of the ^tBupyrpyrr₂ ligand to again, accommodate the longer Fe–E bond lengths. The origin of the observed structural trends is a combination of increased hybridization of orbitals and the smaller size of lighter chalcogenides.

In contrast to the magnetic properties, the ⁵⁷Fe Mössbauer parameters remain largely consistent throughout the series of complexes 2-E (except for the significantly larger quadrupole splitting value in 2-O), thus, indicating high-spin ferrous character for all iron atoms (Table 2 and Fig. 4). Therefore, the observed magnetic trends can be primarily ascribed to the nature of the bridging ligand and the resulting ∠Fe–E–Fe angle, thus controlling the strength of antiferromagnetic coupling.

Conclusions

In conclusion, we have synthesized and characterized the entire mono-bridged chalcogenide (E) series of isostructural diferrous complexes. Treating a ferrous starting material 1-OEt₂ with one equivalent of a phosphine chalcogenide reagent generated the neutral phosphine chalcogenide adducts 1-E (E = O, S, Se, Te, R = Ph, ^tBu) without any evidence of E-transfer from the phosphine to the Fe^II ion. ⁵⁷Fe Mössbauer spectroscopy and SQUID magnetometry of these complexes show these to be high-spin S = 2 Fe^II complexes, akin to previously published neutral Lewis base adducts using this ligand framework.^88–90 When the anionic dinuclear-ate precursor 2-N₂ was used instead with suitable chalcogenide transfer reagents, the bridging chalcogenide anions 2-E were isolated and span the whole chalcogenide series E = O, S, Se, and Te. Complexes 2-E are the first reported isostructural series of diiron mono-bridged chalcogenide complexes containing the structural motif Fe(μ-E)Fe. Characterization of the series 2-E by ⁵⁷Fe Mössbauer spectroscopy indicated these to contain two S = 2 Fe^II centers, similar to the starting material 2-N₂.⁹¹ Magnetic measurements of 2-E performed both in solution and solid phases showed much lower magnetic moments than expected for isolated ferrous ions and suggest significant spin-pairing of electrons. A clear trend of decreasing magnetic moment with lighter chalcogenides is observed and is attributed to increased antiferromagnetic coupling caused by the linearity of the ∠Fe–E–Fe angle and greater Fe–E orbital overlap.

Data availability

The ESI† contains experimental details, characterization, magnetic, and various spectral data. CCDC 2242659–2242666 contain the supplementary crystallographic data for this paper.

Author contributions

Ethan Zars synthesized the complexes and helped compose the manuscript. Lisa Gravogl performed the Mössbauer and SQUID measurements and with Karsten Meyer analyzed the Mössbauer and SQUID data. Michael R. Gau and Patrick J. Carroll solved and refined the X-ray crystal structures. Daniel J. Mindiola and Karsten Meyer provided helpful direction in the project, funding, and helped revise the manuscript to its final version. All authors have given approval to the final version of the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank the University of Pennsylvania for financial support and Dr Pavel Zatsepin and Dr Orion Staples for their expertise in synthesizing chalcogenide transfer reagents and for insightful discussions. Funding was also possible by the U.S. Department of Energy (DOE), Office of Basic Energy Sciences, Division of Chemical Sciences, Geosciences, and Biosciences, Catalysis Science Program (DOE-BES-DESC0023340). EZ thanks Prof. Daniel J. Mindiola and the University of Pennsylvania for funding a trip to Germany to conduct research in the laboratories of Prof. Karsten Meyer. We also thank Dr Mehrafshan Gholi Jafari for arranging shipments of samples. KM thanks the Friedrich-Alexander-Universität Erlangen-Nürnberg (FAU) for generous funding.

References

1. E. I. Solomon, T. C. Brunold, M. I. Davis, J. N. Kemsley, S.-K. Lee, N. Lehnert, F. Neese, A. J. Skulan, Y.-S. Yang and J. Zhou, Chem. Rev., 2000, 100, 235–350.
2. R. Banerjee, J. C. Jones and J. D. Lipscomb, Annu. Rev. Biochem., 2019, 88, 409–431.
3. B. J. Wallar and J. D. Lipscomb, Chem. Rev., 1996, 96, 2625–2658.
4. M. Merkx, D. A. Kopp, M. H. Sazinsky, J. L. Blazyk, J. Müller and S. J. Lippard, Angew. Chem., Int. Ed., 2001, 40, 2782–2807.
5. A. J. Jasniewski and L. Que, Chem. Rev., 2018, 118, 2554–2592.
6. L. C. Seefeldt, B. M. Hoffman and D. R. Dean, Annu. Rev. Biochem., 2009, 78, 701–722.
7. D. C. Johnson, D. R. Dean, A. D. Smith and M. K. Johnson, Annu. Rev. Biochem., 2005, 74, 247–281.
8. F. Ma, W. Ji, J. Hu, Z.-Y. Lu and T. Xiang, Phys. Rev. Lett., 2009, 102, 177003.
9. Y. Mizuguchi and Y. Takano, J. Phys. Soc. Jpn., 2010, 79, 102001.
10. T. Hanaguri, S. Niitaka, K. Kuroki and H. Takagi, Science, 2010, 328, 474–476.
11. K. E. Liu, A. M. Valentine, D. Wang, B. H. Huynh, D. E. Edmondson, A. Salifoglou and S. J. Lippard, J. Am. Chem. Soc., 1995, 117, 10174–10185.
12. S. K. Lee, B. G. Fox, W. A. Froland, J. D. Lipscomb and E. Munck, J. Am. Chem. Soc., 1993, 115, 6450–6451.
13. L. Shu, J. C. Nesheim, K. Kauffmann, E. Münck, J. D. Lipscomb and L. Que, Science, 1997, 275, 515–518.
14. L. Zhang, L. Xiang, Y. Yu and L. Deng, Inorg. Chem., 2013, 52, 5906–5913.
15. T. Chantarojsiri, J. W. Ziller and J. Y. Yang, Chem. Sci., 2018, 9, 2567–2574.
16. C. Cordes (née Kupper), M. Morganti, I. Klawitter, C. Schremmer, S. Dechert and F. Meyer, Angew. Chem., Int. Ed., 2019, 58, 10855–10858.
17. N. A. Eckert, S. Stoian, J. M. Smith, E. L. Bominaar, E. Münck and P. L. Holland, J. Am. Chem. Soc., 2005, 127, 9344–9345.
18. E. Fleischer and S. Hawkinson, J. Am. Chem. Soc., 1967, 89, 720–721.
19. C. F. Martens, N. N. Murthy, H. V Obias and K. D. Karlin, Chem. Commun., 1996, 629–630.
20. S. Ménage, J.-B. Galey, J. Dumats, G. Hussler, M. Seité, I. G. Luneau, G. Chottard and M. Fontecave, J. Am. Chem. Soc., 1998, 120, 13370–13382.
21. M. Müller, E. Bill, T. Weyhermüller and K. Wieghardt, Chem. Commun., 1997, 705–706.
22. J. C. Ott, H. Wadepohl and L. H. Gade, Angew. Chem., Int. Ed., 2020, 59, 9448–9452.
23. D. Sil, F. S. T. Khan and S. P. Rath, Chem.–Eur. J., 2016, 22, 14585–14597.
24. E. Vogel, S. Will, A. S. Tilling, L. Neumann, J. Lex, E. Bill, A. X. Trautwein and K. Wieghardt, Angew. Chem., Int. Ed. Engl., 1994, 33, 731–735.
25. E. C. Wilkinson, Y. Dong and L. Que, J. Am. Chem. Soc., 1994, 116, 8394–8395.
26. S. Yoon and S. J. Lippard, J. Am. Chem. Soc., 2004, 126, 2666–2667.
27. S. Meyer, I. Klawitter, S. Demeshko, E. Bill and F. Meyer, Angew. Chem., Int. Ed., 2013, 52, 901–905.
28. J. A. Bellow, M. Yousif, D. Fang, E. G. Kratz, G. A. Cisneros and S. Groysman, Inorg. Chem., 2015, 54, 5624–5633.
29. E. J. Johnson, C. Kleinlein, R. A. Musgrave and T. A. Betley, Chem. Sci., 2019, 10, 6304–6310.
30. L. D. Wickramasinghe, R. Zhou, R. Zong, P. Vo, K. J. Gagnon and R. P. Thummel, J. Am. Chem. Soc., 2015, 137, 13260–13263.
31. L. M. Brines, M. K. Coggins, P. C. Y. Poon, S. Toledo, W. Kaminsky, M. L. Kirk and J. A. Kovacs, J. Am. Chem. Soc., 2015, 137, 2253–2264.
32. Y. Liu, R. Xiang, X. Du, Y. Ding and B. Ma, Chem. Commun., 2014, 50, 12779–12782.
33. N. T. Vo, Y. Mekmouche, T. Tron, R. Guillot, F. Banse, Z. Halime, M. Sircoglou, W. Leibl and A. Aukauloo, Angew. Chem., Int. Ed., 2019, 58, 16023–16027.
34. X. Wang, S. Wang, L. Li, E. B. Sundberg and G. P. Gacho, Inorg. Chem., 2003, 42, 7799–7808.
35. K. Schröder, S. Enthaler, B. Bitterlich, T. Schulz, A. Spannenberg, M. K. Tse, K. Junge and M. Beller, Chem.–Eur. J., 2009, 15, 5471–5481.
36. A. E. Tapper, J. R. Long, R. J. Staples and P. Stavropoulos, Angew. Chem., Int. Ed., 2000, 39, 2343–2346.
37. A. Ghosh, F. Tiago de Oliveira, T. Yano, T. Nishioka, E. S. Beach, I. Kinoshita, E. Münck, A. D. Ryabov, C. P. Horwitz and T. J. Collins, J. Am. Chem. Soc., 2005, 127, 2505–2513.
38. T.-A. D. Nguyen, A. M. Wright, J. S. Page, G. Wu and T. W. Hayton, Inorg. Chem., 2014, 53, 11377–11387.
39. T. P. Schlachta, M. R. Anneser, J. F. Schlagintweit, C. H. G. Jakob, C. Hintermeier, A. D. Böth, S. Haslinger, R. M. Reich and F. E. Kühn, Chem. Commun., 2021, 57, 6644–6647.
40. K. A. Andrea, T. R. Brown, J. N. Murphy, D. Jagota, D. McKearney, C. M. Kozak and F. M. Kerton, Inorg. Chem., 2018, 57, 13494–13504.
41. Y. Sakaguchi, A. Call, M. Cibian, K. Yamauchi and K. Sakai, Chem. Commun., 2019, 55, 8552–8555.
42. C. T. Saouma, C. C. Lu, M. W. Day and J. C. Peters, Chem. Sci., 2013, 4, 4042–4051.
43. X. Chai, H.-H. Huang, H. Liu, Z. Ke, W.-W. Yong, M.-T. Zhang, Y.-S. Cheng, X.-W. Wei, L. Zhang and G. Yuan, Chem. Commun., 2020, 56, 3851–3854.
44. L. Wang, M. Gennari, F. G. Cantú Reinhard, S. K. Padamati, C. Philouze, D. Flot, S. Demeshko, W. R. Browne, F. Meyer, S. P. de Visser and C. Duboc, Inorg. Chem., 2020, 59, 3249–3259.
45. O. Einsle and D. C. Rees, Chem. Rev., 2020, 120, 4969–5004.
46. K. Tanifuji and Y. Ohki, Chem. Rev., 2020, 120, 5194–5251.
47. J. Ballmann, A. Albers, S. Demeshko, S. Dechert, E. Bill, E. Bothe, U. Ryde and F. Meyer, Angew. Chem., Int. Ed., 2008, 47, 9537–9541.
48. A. Albers, S. Demeshko, S. Dechert, C. T. Saouma, J. M. Mayer and F. Meyer, J. Am. Chem. Soc., 2014, 136, 3946–3954.
49. A. Albers, S. Demeshko, K. Pröpper, S. Dechert, E. Bill and F. Meyer, J. Am. Chem. Soc., 2013, 135, 1704–1707.
50. A. Albers, S. Demeshko, S. Dechert, E. Bill, E. Bothe and F. Meyer, Angew. Chem., Int. Ed., 2011, 50, 9191–9194.
51. M. Bergner, S. Dechert, S. Demeshko, C. Kupper, J. M. Mayer and F. Meyer, J. Am. Chem. Soc., 2017, 139, 701–707.
52. M. Reiners, M. Maekawa, C. G. Daniliuc, M. Freytag, P. G. Jones, P. S. White, J. Hohenberger, J. Sutter, K. Meyer, L. Maron and M. D. Walter, Chem. Sci., 2017, 8, 4108–4122.
53. S. Yao, F. Meier, N. Lindenmaier, R. Rudolph, B. Blom, M. Adelhardt, J. Sutter, S. Mebs, M. Haumann, K. Meyer, M. Kaupp and M. Driess, Angew. Chem., Int. Ed., 2015, 54, 12506–12510.
54. A. Salifoglou, A. Simopoulos, A. Kostikas, R. W. Dunham, M. G. Kanatzidis and D. Coucouvanis, Inorg. Chem., 1988, 27, 3394–3406.
55. Q. Liang, J. C. DeMuth, A. Radović, N. J. Wolford, M. L. Neidig and D. Song, Inorg. Chem., 2021, 60, 13811–13820.
56. Y. Lee, I.-R. Jeon, K. A. Abboud, R. García-Serres, J. Shearer and L. J. Murray, Chem. Commun., 2016, 52, 1174–1177.
57. D. E. DeRosha, N. A. Arnet, B. Q. Mercado and P. L. Holland, Inorg. Chem., 2019, 58, 8829–8834.
58. A. McSkimming and D. L. M. Suess, Inorg. Chem., 2018, 57, 14904–14912.
59. H.-C. Zhou and R. H. Holm, Inorg. Chem., 2003, 42, 11–21.
60. S. C. Lee, W. Lo and R. H. Holm, Chem. Rev., 2014, 114, 3579–3600.
61. P. Venkateswara Rao and R. H. Holm, Chem. Rev., 2004, 104, 527–560.
62. M. Ye, N. B. Thompson, A. C. Brown and D. L. M. Suess, J. Am. Chem. Soc., 2019, 141, 13330–13335.
63. A. McSkimming, A. Sridharan, N. B. Thompson, P. Müller and D. L. M. Suess, J. Am. Chem. Soc., 2020, 142, 14314–14323.
64. F. Corazza, C. Floriani and M. Zehnder, J. Chem. Soc., Dalton Trans., 1987, 709–714.
65. R. N. Mukherjee, T. D. P. Stack and R. H. Holm, J. Am. Chem. Soc., 1988, 110, 1850–1861.
66. J. S. Anderson and J. C. Peters, Angew. Chem., Int. Ed., 2014, 53, 5978–5981.
67. L. Fohlmeister and C. Jones, Aust. J. Chem., 2014, 67, 1011–1016.
68. P. Berno, C. Floriani, A. Chiesi-Villa and C. Guastini, J. Chem. Soc., Dalton Trans., 1989, 551–554.
69. J. R. Dorfman, J. J. Girerd, E. D. Simhon, T. D. P. Stack and R. H. Holm, Inorg. Chem., 1984, 23, 4407–4412.
70. F. Zhang, T. J. Woods, T. B. Rauchfuss, F. Arrigoni and G. Zampella, Chem. Commun., 2021, 57, 5079–5081.
71. J. C. Ott, H. Wadepohl and L. H. Gade, Inorg. Chem., 2021, 60, 3927–3938.
72. T.-T. Zhang, M. Wang, N. Wang, P. Li, Z.-Y. Liu and L.-C. Sun, Polyhedron, 2009, 28, 1138–1144.
73. N. A. Arnet, T. R. Dugan, F. S. Menges, B. Q. Mercado, W. W. Brennessel, E. Bill, M. A. Johnson and P. L. Holland, J. Am. Chem. Soc., 2015, 137, 13220–13223.
74. N. A. Arnet, S. F. McWilliams, D. E. DeRosha, B. Q. Mercado and P. L. Holland, Inorg. Chem., 2017, 56, 9185–9193.
75. X.-D. Chen, W. Zhang, J. S. Duncan and S. C. Lee, Inorg. Chem., 2012, 51, 12891–12904.
76. D. L. Gerlach, D. Coucouvanis, J. Kampf and N. Lehnert, Eur. J. Inorg. Chem., 2013, 2013, 5253–5264.
77. J. Huang, S. Mukerjee, B. M. Segal, H. Akashi, J. Zhou and R. H. Holm, J. Am. Chem. Soc., 1997, 119, 8662–8674.
78. A. L. Nagelski, M. S. Fataftah, M. M. Bollmeyer, S. F. McWilliams, S. N. MacMillan, B. Q. Mercado, K. M. Lancaster and P. L. Holland, Chem. Sci., 2020, 11, 12710–12720.
79. C. Schneider, S. Demeshko, F. Meyer and C. G. Werncke, Chem.–Eur. J., 2021, 27, 6348–6353.
80. B. D. Stubbert, J. Vela, W. W. Brennessel and P. L. Holland, Z. Anorg. Allg. Chem., 2013, 639, 1351–1355.
81. T. Terada, T. Wakimoto, T. Nakamura, K. Hirabayashi, K. Tanaka, J. Li, T. Matsumoto and K. Tatsumi, Chem.–Asian J., 2012, 7, 920–929.
82. J. Vela, S. Stoian, C. J. Flaschenriem, E. Münck and P. L. Holland, J. Am. Chem. Soc., 2004, 126, 4522–4523.
83. C. R. Groom, I. J. Bruno, M. P. Lightfoot and S. C. Ward, Acta Crystallogr., 2016, 171–179.
84. G. F. Wong, L. F. Yeung, H. Y. Tsoi, H.-S. Chan, M.-H. Chiang and H. K. Lee, Eur. J. Inorg. Chem., 2019, 2019, 98–109.
85. C. Hecht, E. Herdtweck, J. Rohrmann, W. A. Herrmann, W. Beck and P. M. Fritz, J. Organomet. Chem., 1987, 330, 389–396.
86. S. Heinl and M. Scheer, Dalton Trans., 2014, 43, 16139–16142.
87. J. T. Henthorn, G. E. Cutsail, T. Weyhermüller and S. DeBeer, Nat. Chem., 2022, 14, 328–333.
88. K. Searles, S. Fortier, M. M. Khusniyarov, P. J. Carroll, J. Sutter, K. Meyer, D. J. Mindiola and K. G. Caulton, Angew. Chem., Int. Ed., 2014, 53, 14139–14143.
89. D. Sorsche, M. E. Miehlich, E. M. Zolnhofer, P. J. Carroll, K. Meyer and D. J. Mindiola, Inorg. Chem., 2018, 57, 11552–11559.
90. E. Zars, L. Gravogl, M. Gau, P. J. Carroll, K. Meyer and D. J. Mindiola, Inorg. Chem., 2022, 61, 1079–1090.
91. D. Sorsche, M. E. Miehlich, K. Searles, G. Gouget, E. M. Zolnhofer, S. Fortier, C.-H. Chen, M. Gau, P. J. Carroll, C. B. Murray, K. G. Caulton, M. M. Khusniyarov, K. Meyer and D. J. Mindiola, J. Am. Chem. Soc., 2020, 142, 8147–8159.
92. A. Corsaro, V. Librando, U. Chiacchio, V. Pistarà and A. Rescifina, Tetrahedron, 1998, 54, 9187–9194.
93. X. Cai, S. Majumdar, G. C. Fortman, L. M. Frutos, M. Temprado, C. R. Clough, C. C. Cummins, M. E. Germain, T. Palluccio, E. V Rybak-Akimova, B. Captain and C. D. Hoff, Inorg. Chem., 2011, 50, 9620–9630.
94. M. Joost, M. Nava, W. J. Transue and C. C. Cummins, Chem. Commun., 2017, 53, 11500–11503.
95. J. D. Satterlee, Concepts Magn. Reson., 1990, 2, 69–79.
96. J. B. Goodenough, Phys. Rev., 1955, 100, 564–573.
97. J. B. Goodenough, J. Phys. Chem. Solids, 1958, 6, 287–297.
98. J. Kanamori, J. Phys. Chem. Solids, 1959, 10, 87–98.
99. M. W. Rosenzweig, J. Hümmer, A. Scheurer, C. A. Lamsfus, F. W. Heinemann, L. Maron, M. Mazzanti and K. Meyer, Dalton Trans., 2019, 48, 10853–10864.

---

Footnote

† Electronic supplementary information (ESI) available. CCDC 2242659–2242666. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d3sc01094e

---