 Open Access Article
Open Access ArticlePolarizing agents for efficient high field DNP solid-state NMR spectroscopy under magic-angle spinning: from design principles to formulation strategies†
Georges
Menzildjian
 a,
Judith
Schlagnitweit
a,
Gilles
Casano
b,
Olivier
Ouari
a,
Judith
Schlagnitweit
a,
Gilles
Casano
b,
Olivier
Ouari
 b,
David
Gajan
*a and
Anne
Lesage
b,
David
Gajan
*a and
Anne
Lesage
 *a
*a
aCentre de RMN à, Très Hauts Champs, Université de Lyon (CNRS/ENS Lyon/UCB Lyon 1), 5 Rue de la doua, 69100 Villeurbanne, France. E-mail: anne.lesage@ens-lyon.fr; david.gajan@ens-lyon.fr
bAix Marseille Univ., CNRS, Institut de Chimie Radicalaire, UMR 7273, Marseille, France
First published on 12th May 2023
Abstract
Dynamic Nuclear Polarization (DNP) has recently emerged as a cornerstone approach to enhance the sensitivity of solid-state NMR spectroscopy under Magic Angle Spinning (MAS), opening unprecedented analytical opportunities in chemistry and biology. DNP relies on a polarization transfer from unpaired electrons (present in endogenous or exogenous polarizing agents) to nearby nuclei. Developing and designing new polarizing sources for DNP solid-state NMR spectroscopy is currently an extremely active research field per se, that has recently led to significant breakthroughs and key achievements, in particular at high magnetic fields. This review describes recent developments in this area, highlighting key design principles that have been established over time and led to the introduction of increasingly more efficient polarizing sources. After a short introduction, Section 2 presents a brief history of solid-state DNP, highlighting the main polarization transfer schemes. The third section is devoted to the development of dinitroxide radicals, discussing the guidelines that were progressively established to design the fine-tuned molecular structures in use today. In Section 4, we describe recent efforts in developing hybrid radicals composed of a narrow EPR line radical covalently linked to a nitroxide, highlighting the parameters that modulate the DNP efficiency of these mixed structures. Section 5 reviews recent advances in the design of metal complexes suitable for DNP MAS NMR as exogenous electron sources. In parallel, current strategies that exploit metal ions as endogenous polarization sources are discussed. Section 6 briefly describes the recent introduction of mixed-valence radicals. In the last part, experimental aspects regarding sample formulation are reviewed to make best use of these polarizing agents in a broad panel of application fields.
1 Introduction
While the fundamental principles of Dynamic Nuclear Polarization (DNP) and the first proofs of concept were described and carried out 70 years ago, it is only recently that this method became a game-changing technology to alleviate the sensitivity barrier of solid-state Nuclear Magnetic Resonance (NMR) spectroscopy under Magic Angle Spinning (MAS).1 For the last twenty years, ongoing advances, notably in the instrumentation, have democratized this approach, with renewed application breakthroughs. DNP relies on a microwave irradiation induced transfer of spin polarization between unpaired electrons and neighboring nuclei. The efficiency of the process critically depends on the molecular structure and physico-chemical properties of the polarization sources hosting the free electrons, the so-called polarizing agents (PAs). The design, synthesis and characterization of such polarizing agents is a complex, multi-parametric approach, requiring advanced knowledge in a number of areas such as free radical chemistry, organic synthesis, EPR spectroscopy, solid-state NMR, DFT calculations, spin physics, theoretical simulations, etc. Since the first use of nitroxide radicals in 1997 by Griffin and co-workers,2 continuous progress has been made to not only develop effective electron sources and solid-state DNP formulations, but also to rationally understand the principles governing the efficiency of polarizing agents at high magnetic field. Here, we review almost two decades of scientific developments during which key design principles could be established so as to develop ever more efficient polarizing sources for modern high field DNP enhanced solid-state NMR. This article complements previous reviews on the subject,3,4 with a focus on the most recent developments.2 DNP enhanced solid-state NMR: brief history and fundamentals
2.1 The discovery of DNP
Electrons inherently have a significantly higher spin polarization than nuclei at thermal equilibrium due to their larger gyromagnetic ratio γ (e.g. in a magnetic field, electrons are 660 times more polarized than protons or 2640 times more polarized than carbons). Thus, the idea of transferring polarization from electrons to nuclei appeared very promising from the early days of NMR.The DNP effect was first predicted theoretically by Albert Overhauser in 1953![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 for nuclei in metals, hyperpolarized by the conducting electrons. In this original paper, Overhauser postulated that, upon irradiating the electrons with a resonant microwave magnetic field that equates the populations of the electronic spin states, “dynamical processes” (or relaxation processes, hence the name of the technique) “which tend to restore the system to its equilibrium state induce nuclear transitions”, this action relying on the modulation of the hyperfine coupling interaction present between electron and nuclear spins. This effect would lead to a sizeable net steady-state hyperpolarization of the nucleus I coupled to the irradiated electron S, resulting in an enhancement of the observed NMR signal. The maximum enhancement that could be achieved in theory is approximated to the ratio of electronic and nuclear polarizations:
5 for nuclei in metals, hyperpolarized by the conducting electrons. In this original paper, Overhauser postulated that, upon irradiating the electrons with a resonant microwave magnetic field that equates the populations of the electronic spin states, “dynamical processes” (or relaxation processes, hence the name of the technique) “which tend to restore the system to its equilibrium state induce nuclear transitions”, this action relying on the modulation of the hyperfine coupling interaction present between electron and nuclear spins. This effect would lead to a sizeable net steady-state hyperpolarization of the nucleus I coupled to the irradiated electron S, resulting in an enhancement of the observed NMR signal. The maximum enhancement that could be achieved in theory is approximated to the ratio of electronic and nuclear polarizations:
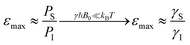 | (1) |
Thus, the expected boost in sensitivity is on the order of a few hundreds or thousands fold improvement depending on the nucleus. Overhauser already mentioned in his paper that operating DNP at low temperatures would be beneficial to maximize the obtained nuclear polarization. A few months later, Carver and Slichter validated this theoretical prediction by an experimental observation of DNP on a 7Li metal sample.6 According to their estimations, they managed to hyperpolarize lithium with a ca. 100-fold enhancement and performed similar experiments using the solvated electrons in solutions of Na in liquid NH3.7
2.2 The DNP mechanisms
Several reviews have described the polarization transfer mechanisms occurring in insulating solids.8–11 The reader is invited to refer to these already existing comprehensive publications. Nevertheless, this section will present the key details of these mechanisms, as their understanding is essential to rationalize the features of the polarization agents invoking one or the other effect. We will focus on DNP transfers based on continuous microwave (CW) irradiation. Basic notions, such as depolarization and absolute sensitivity gain, are also briefly introduced.In a coupled electron-nucleus 2-spin system, the fluctuation of the dipolar and scalar hyperfine interaction due to dynamics lead to electron and nuclear relaxation via single quantum (SQ) transitions as well as, upon saturation at the EPR frequency of the electron spin by microwave irradiation (ωμw = ωS0), to additional zero quantum (ZQ) and double quantum (DQ) relaxation pathways. The hyperpolarization in OE stems from an imbalance between the ZQ and DQ relaxation rates, the sign of the enhancement depending on the relative values of the ZQ and DQ relaxation rates.
While the Overhauser effect is an extremely effective mechanism for DNP in solution, it also shows some promise in solids, notably for high field applications as its efficiency scales favorably with the magnetic field. The difficulty is, however, to find suitable polarization sources for OE in insulating solids. For several years, only BDPA and its derivatives were shown to yield OE DNP in these conditions. Research to find new candidates for OE in solids at high fields is currently very active and recent discoveries by Pylaeva and co-workers have opened new avenues for the design of OE polarizing agents by identifying new classes of mixed-valence radical compounds that exhibit a modulation of the intramolecular hyperfine couplings on suitable timescales for OE DNP and that yields sizeable DNP enhancements.13,14 Polarizing agents for OE DNP remain however scarce and the use of this mechanism is limited by strong constraints on molecular design. While mixed-valence organic radicals will be briefly discussed (Section 7), this review will focus mostly on more widely used polarizing agents that rely on other DNP mechanisms, described below.
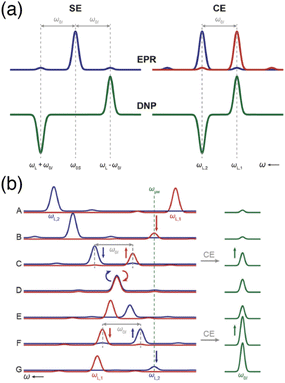 | ||
| Fig. 1 (a) Schematic EPR and DNP field profiles for SE and CE showing the separation between the positive and negative maximum enhancements. The satellite transitions visible in the EPR spectra correspond to forbidden ZQ and DQ transitions. (b) The Larmor frequency of the two electrons (in red and blue) is modulated during magic angle spinning (from A to G). Several rotor events are taking place, such as electron-microwave frequency crossing (B and G), cross-effect (C and F) or electron–electron frequency crossing (D), that result in polarization transfers to the nucleus (in green). Reproduced from ref. 22 with permission from the RSC Publishing, copyright 2016. | ||
It may sound difficult to find a system that, by chance, will match the cross-effect conditions. Yet it turns out that a few paramagnetic species are suitable for CE. The EPR inequivalence necessary for this mechanism can be found either with polarizing agents that have broad inhomogeneous EPR spectra (larger than the nuclear Larmor frequency due to a sizeable g anisotropy), such as nitroxide-based radicals (Section 3) or in mixtures or covalent pairs of radicals comprising two different moieties, that can either or both have a narrow EPR line (Section 4). Specific examples of such polarizing sources will be the extensive focus of the next two sections of this review.
Under MAS, the dynamics of the CE mechanism is quite complex as the eight energy levels of the 3-spin systems undergo a periodic modulation over the course of the rotor period. They can either cross each other or avoid crossings, yielding level anti-crossing (LAC) events. A complete theoretical model for this effect has been extensively developed by several groups.23–26 At multiple points during a rotor period, the avoided level crossings are either adiabatic, and therefore the eigenstate populations follow the energy levels, or non-adiabatic, if the time dependence of the interaction at play is not smooth enough, causing populations to stay in the same spin states across the LAC. More precisely, there are three types of so-called rotor events that can occur under MAS. The first type corresponds to a crossing between the (time-dependent) effective frequency of one electron and the microwave frequency, i.e. ωμw = ωS10 or ωμw = ωS20, which results into a partial saturation of that electron. Thurber et al. estimated that, as there are multiple events of that type during a rotor period, the electron spin polarization is perturbed by approximately 28%, the electron polarization difference being then transferred to the nucleus during the second type of event.25 The second rotor event type is the three-spin process that yields the CE transfer, occurring when the matching condition ωS10 − ωS20 = ωI0 is fulfilled in the course of the rotation. The probability for an adiabatic passage through this LAC depends on the strength of the hyperfine and electron–electron couplings. Despite sizeable couplings, this probability actually remains quite low (typically a fraction of a percent). However, this is mitigated since the typical nuclear spin-lattice relaxation time scale contains hundreds of rotor periods, allowing for the nuclear hyperpolarization to accumulate. The third significant rotor event that can occur under MAS is an electron–electron crossing, equalizing their effective Larmor frequencies, i.e. ωS10 = ωS20. Its probability for an adiabatic LAC is close to one, meaning that most of the time the electrons exchange their polarization adiabatically, therefore enabling more constructive CE events when they are again meeting the CE matching condition. However, there is still a chance for this event to be detrimental and act to equalize the polarization of the electrons, thus reducing the polarization available for a transfer to the nucleus. This effect, mostly problematic at higher MAS frequencies, leads to the phenomenon of nuclear depolarization that happens even in the absence of microwave irradiation and counteracts CE DNP.25
A typical illustration of the sequencing of such rotor events, from Corzilius and co-workers in ref. 22, is presented in Fig. 1(b) where the evolution of the effective frequencies of the two electrons is shown during a rotor period, in comparison with the observed signal intensity in NMR. The EPR lines of the two electrons are shown in blue (for the first one) and red (for the second one), while the NMR line is represented in green (panel A). The second electron becomes partially saturated when its (modulated) EPR resonance reaches the microwave frequency, creating a polarization difference between the two electrons (panel B). A three-spin inversion event (flip-flop-flip) ends up going through another LAC where the CE condition is met, transferring that polarization difference to the nucleus (panel C). Later, the two electron frequencies match each other and they most likely exchange their polarization adiabatically (panel D), preserving a difference (panel E) that will be transferred again constructively to the nucleus at another CE matching point (panel F). Further microwave irradiation of the electron matching the microwave frequency recreates a polarization difference to be later transferred via CE (panel G).
The field dependence of CE was for a while subject to debate in the literature, mostly because of the lack of experimental data points and was believed to be less severe than that of SE. However, computational and experimental work showed that the dependence of CE efficiency with field is complex, scaling between (B0)−1 and (B0)−3.26,27 Despite this unfavorable dependence, CE remains often more advantageous than SE at temperature >30 K as its power requirements are lower and its efficiency more tunable through radical design as will be described in the next sections.
The mechanisms described above rely on the application of a continuous microwave irradiation of the sample, which can be achieved with commercially available (frequency fixed) gyrotrons or klystrons.28 The introduction of frequency-agile micro-wave sources allowing the manipulation of electron spins has brought new opportunities.29–32 Several pulsed DNP methods have been proposed to more efficiently and selectively transfer electron spin polarization.33–38 While these developments leave much hope for pulsed methods to become a cornerstone of DNP MAS NMR experiments in the future, such approaches are still relying on home-build equipment and their implementation at high magnetic field remains to be demonstrated.
We finally note that dissolution DNP (d-DNP) mostly relies on trityls (for 13C polarization) and mono-nitroxides such as TEMPOL (for 1H polarization).39,40 At the very low temperatures (∼4 K and below) at which the d-DNP experiments are performed, the EPR line of nitroxides undergoes strong spectral diffusion and the polarization transfer occurs via a mechanism referred to as Thermal Mixing (TM).41
2.3 Signal quenching, nuclear depolarization and sensitivity
The DNP enhancement mentioned so far is meant in its most natural sense and is quantified by taking the ratio of the NMR signal intensity (or area) obtained in the presence (μw ON) or absence (μw OFF) of microwave irradiation: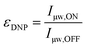 | (2) |
However, this is not an entirely fair comparison to the Boltzmann polarization recorded in conventional room temperature MAS NMR. First, as paramagnetic species are added into the sample, the hyperfine coupling induces a faster longitudinal nuclear relaxation as well as a broadening/shift of the NMR lines for the nuclei closely surrounding the PA. This effectively acts as a bleaching effect reducing the number of detectable nuclear spins in DNP conditions. This paramagnetic bleaching is present for all polarization sources, for all DNP mechanisms and whether the experiment is conducted under static or MAS conditions.42 In addition, another detrimental effect that pertains to CE under MAS, described in ref. 25 and 43, is the so-called depolarization effect that partially depletes the nucleus polarization over the course of the rotor period. This effect originates in the low probability but still existing unfavorable electron–electron anti-crossing events, as described above. This non entirely adiabatic process is active even in the absence of microwave irradiation and is strongly MAS dependent. Strong electron–electron magnetic couplings tend to mitigate depolarization, which will be further discussed in the light of PA design strategies in the following sections.
To quantify the combined impact of paramagnetic bleaching and depolarization on the signal-to-noise ratio under DNP NMR conditions, Rossini and co-workers44 suggested to use an overall sensitivity gain parameter Σ defined as follows:
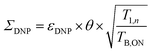 | (3) |
The sample temperature is an important parameter to assess the sensitivity of a MAS DNP NMR experiment. While in principle it is possible to obtain SE and CE DNP near ambient temperatures, most conventional MAS DNP experiments are performed at cryogenic temperatures around 100 K or lower. This not only increases the initial nuclear Boltzmann polarization but more importantly guarantees that the electron relaxation times of the PA are sufficiently long to ensure an efficient saturation of their EPR transitions upon microwave irradiation.45 The overall sensitivity gain can then be corrected to reflect the difference between low temperature (LT) DNP and ambient temperature conventional solid-state NMR experiments, for example as:
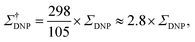 | (4) |
An interesting discussion about the actual sensitivity gain in MAS DNP experiments and the ways to quantify it is developed by Hediger and co-workers in ref. 46. The authors argue to remove T1,n from eqn (3) and (4) as it does not depend on the efficiency of the PA or the DNP process but rather on the sample to polarize. As many other parameters could and should be taken into account, and in the spirit of estimating, overall, how much the sensitivity of a given NMR experiment is increased by performing DNP instead, they ultimately suggest to simply quantify the signal-to-noise ratio per square root unit time, 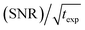 and use it as a relevant indicator of the resulting sensitivity boost.
and use it as a relevant indicator of the resulting sensitivity boost.
2.4 Propagation of the hyperpolarization
SE and CE are local phenomena that are only responsible for transferring spin polarization to the hyperfine-coupled nuclei nearby the polarization source, i.e. in the close vicinity of the electron spins. Bulk nuclear hyperpolarization is only obtained after a homonuclear spin diffusion (SD) step that relies on dipolar transfers between nuclei. Typically, for protons in a frozen solution containing a PA, the dense dipolar network is quite effective at spreading hyperpolarization via SD, while that process becomes significantly less efficient between nuclei with smaller gyromagnetic ratios.47 In the latter case, when possible, cross-polarization (CP) contacts or equivalent are often used to transfer magnetization from the hyperpolarized proton bath of the matrix to the target heteronuclei, resulting in the so-called indirect DNP transfer.In this context, the spin diffusion barrier model10,18 describes two pools of nuclear spins: those which are strongly hyperfine-coupled to the electrons and cannot be involved in a conservative dipolar flip-flop with the rest of the nuclei in the lattice, and those which are outside of a certain cut-off distance from the electron sources and virtually unaffected by the electron-induced paramagnetic effects and that can relay hyperpolarization to the rest of the bulk. This model, although challenged in modern DNP theory and specially under MAS conditions, is still investigated extensively – leading to interesting mechanistic studies such as the one performed recently by Tan and co-workers estimating that the spin diffusion barrier surrounding a trityl radical in a glycerol-water matrix is less than 6 Å from the paramagnetic center.48
The SD processes are dependent on the MAS frequency, with diffusion rate constants scaling inversely with the spinning rate. They however remain efficient at the fastest spinning frequencies available with DNP, helping to reduce the recovery periods between experiments under cryogenic conditions down to durations similar to those used in conventional ambient temperature MAS NMR. Detailed spin diffusion models are out of the scope of this review, but the reader is invited to refer to the work of Pinon and co-workers for analytical developments on the optimization of polarization transfers in various samples and as a function of their SD behaviour.49,50 Perras and co-workers also managed to include an extensive full-scale description of SD in advanced MAS DNP numerical simulation packages.51,52
3 Design principles for nitroxide-based polarizing agents
3.1 From mononitroxides to the first generation of binitroxides
The developments led by Griffin and co-workers in the 1990s2,53 paved the way for modern MAS DNP experiments at high fields and cryogenic temperatures. In the early 2000s, i.e. twenty years ago, a state-of-the-art DNP experiment exploited the CE mechanism using highly concentrated (ca. 40 mM) solutions of 4-amino-TEMPO (2,2,6,6-tetramethylpiperidinyl-1-oxyl) in a glycerol/water mixture to produce in these conditions a ca. 15-fold enhancement.54TEMPO derivatives belong to the family of stable nitroxides, which are a class of free radicals typically based on a 5 or 6-membered ring containing an aminoxyl moiety bearing an unpaired electron. These radicals are characterized by an inhomogeneously broadened EPR profile, typically spanning across a range on the order or larger than the hydrogen nuclear Larmor frequency at a given magnetic field, as their g-tensor principal values typically range from 2.0090 for gxx to 2.0025 for gzz.4 Thus, nitroxides are suitable PAs for CE DNP as the matching condition can be satisfied within a pair of magnetically coupled nitroxide radicals with non colinear respective g-tensor orientations. In 2004, Hu, Griffin and co-workers, under the assumption that the size of the electron–electron coupling affects the efficiency of the DNP process, and despite the lack of an extensive theoretical framework describing CE under MAS, have introduced the groundbreaking idea of chemically tethering two nitroxide moieties, thus forming a biradical.55 Efficient CE was demonstrated in the bTnE series where n = 2, 3, 4 is the number of ethylene glycol units linking the two nitroxides. This first series of biradicals exhibits increasing electron–electron (e–e) dipolar coupling (D) strength as the linker is shortened from 4 to 2 ethylene glycol units. This trend correlates with the proton DNP enhancement and a ca. 4-fold improvement from monomeric TEMPO to bT2E was achieved (Fig. 2), resulting in a record enhancement factor at the time of 175 at 5 T and 90 K, under 3.5 kHz MAS in a 4 mm rotor and with a 5 mM solution of biradical. Biradicals were therefore shown to not only be extremely efficient at producing CE DNP, but also to allow the use of much lower radical concentration, mitigating the paramagnetic bleaching effects.
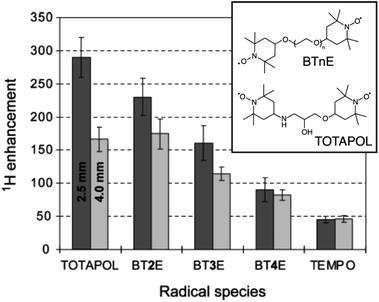 | ||
| Fig. 2 Structures of BTnE and TOTAPOL radicals and measured DNP enhancements at 5 T and 90 K. Reproduced and adapted from ref. 56 with permission from American Chemical Society, copyright 2006. | ||
Pushing this concept, Griffin and co-workers later designed a new dinitroxide biradical based on two TEMPO units tethered by a shorter linker, dubbed TOTAPOL (1-(TEMPO-4-oxy)-3-(TEMPO-4-amino)propan-2-ol).56 Reducing the number of atoms in the linker further increases the electron–electron dipolar coupling strength in the biradical and in turn the CE DNP enhancement. Although its performance is comparable to that of bT2E in a 4 mm rotor, TOTAPOL yields 290-fold enhancement factors at 90 K in a 2.5 mm rotor (where the microwave penetration is more efficient) under otherwise similar conditions, as reported on Fig. 2, thus achieving overall better CE DNP at the same magnetic field. This radical also had the added benefit of being more soluble in water and aqueous solutions in general due to the alcohol and amine groups in its linker, resulting in a wider applicability to DNP formulations involving biologically relevant samples.
Building upon the molecular structure of TOTAPOL, interesting attempts have been made to evaluate the performance of the DOTOPA family, which is comprised of a series of tri- or tetra-nitroxide based PAs, all chemically tethered within one molecule.57,58 Despite the difficulty in comparing the results obtained in these studies to the rest of the MAS DNP literature, as the authors were carrying out experiments either in static or ultra-low temperature (below 30 K) conditions, it can be said that while tetranitroxides were poorly soluble, thus yielding modest enhancements, trinitroxides were promising for low temperature MAS DNP. In particular, an aqueous solution of DOTOPA–ethanol at neutral pH yielded 15-fold proton enhancements under typical MAS DNP conditions at 9.4 T and 100 K, and 100-fold enhancements at the same field when the temperature was lowered to 26 K. The authors pointed out that triradicals could be a good compromise to maximize the number of favorable CE matching events since more two-by-two pairs of nitroxides would experience proper relative orientations of their g-tensors during a rotor period, while still preventing a too fast (and therefore detrimental) electronic spectral diffusion from happening.
3.2 Towards more rigidified binitroxides
In the seminal studies mentioned above, the idea that some relative orientations of the two g-tensors would contribute positively to the DNP, mainly in cases where these tensors are nearly orthogonal, while others would be non-effective or detrimental, was already present in ref. 55 and 56, without any attempt to control this parameter. Hu and co-workers subsequently conducted a detailed multiple frequency EPR study on a several binitroxides to evaluate their distribution of conformations and correlate them with their DNP performance. In particular they noticed that the DNP efficiency of the shortly tethered BT2E and TOTAPOL was correlated with conformational constraints.59 Similarly, they found that the underwhelming DNP performance of bTurea and bTOXA, two other bis-TEMPO tethered by a urea and oxalyl amide structure respectively, could be justified by nearly co-axial g-tensors, diminishing the EPR frequency separation between the two nitroxides required for CE. Notably, the urea-based linker in bTurea provides a limited number of different conformations, locking the biradical in an intermediate g-tensor orientation that yields moderate 125-fold enhancements at 5 T. This biradical is however interesting for its well-defined structure and will fortunately not be discarded by the MAS DNP community. A particularly rigid biradical structure was later obtained by tethering two nitroxides with a bisketal linker, yielding the bTbK molecule.60 This PA was shown to produce a ca. 40% improvement in CE DNP enhancement compared to TOTAPOL, which was attributed to its remarkably rigid structure that strongly constrains the two g-tensors in a near-orthogonal orientation while maintaining a similar dipolar coupling between the electrons. Other studies by Ysacco et al. later confirmed that an orthogonal relative orientation of electron g tensors is essential to obtain high enhancements.61,62The results and concepts presented here have been revisited and further rationalized in the light of recent theoretical studies. In 2017, Perras and co-workers have performed a series of numerical simulations varying different EPR parameters of a model binitroxide radical (a three-spin system for CE) in order to screen, among others, optimal values of the Euler angles (α, β, γ) (Fig. 3(a)) describing the relative orientation of the two g-tensors.63 While a very narrow condition was expected, translating into the necessity of having strictly orthogonal tensors, a rather broad set of angular parameters was instead found that yield similar (maximum) enhancements sampling the orientational space (Fig. 3(b)), at least as long as the gzz components of the two tensors are orthogonal (β ≈ 90°). This in turn allows synthetic chemists some degree of flexibility in the design of efficient PAs for CE DNP.
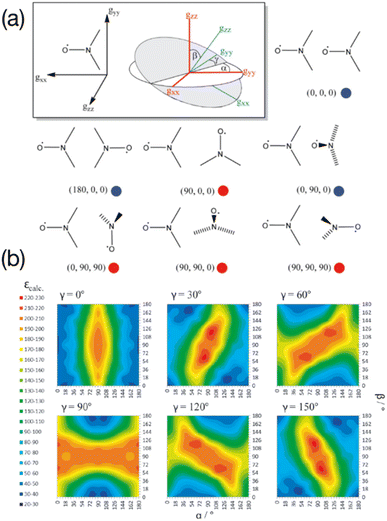 | ||
| Fig. 3 (a) The orientation of the g-tensor in the nitroxide molecular frame as well as the coordinate frame defining the three Euler angles. Different biradical orientations are outlined and their corresponding Euler angle values are listed. Red circles indicate favorable orientations while blue circles indicate disfavorable orientations. (b) Calculated enhancements for six ensembles of (α, β, γ) Euler angles between the g-tensors. Reproduced and adapted from ref. 63 with permission from John Wiley & Sons, copyright 2017. | ||
Mentink-Vigier recently proposed a refinement to the notions of orthogonality and proximity between the two g-tensors of a binitroxide radical by introducing a new metric based on the Frobenius norm that quantifies the “distance” associated to how differently they are oriented via their set of relative Euler angles.64 A correlation could be established between the g-tensor's distance of a given radical and its CE enhancement, i.e. maximizing the former will maximize the latter. Depolarization properties were also shown to be dependent on the relative orientation of the two tensors. The study confirms that the β angle needs to be close to 90°, while also highlighting the influence of the α and γ angles in the overall DNP process. The authors conclude that the distances corresponding to the best binitroxide radicals available to date approach, but without reaching, the maximum value.
3.3 The importance of electronic relaxation parameters
As described in the previous sections, the early studies on the design of dinitroxides for solid-state DNP emphasized the importance of both the electron dipolar coupling and the relative orientation of the two g-tensors.55,60,65 Notably, the necessity to adapt the e–e distance to the nuclear Larmor frequency was well-realized, dipolar coupling values larger than the ωI0 preventing the realization of the CE matching condition. While bTbK was considered as near optimum, there was still room for improvement entering the 2010 decade, as the theoretical maximum enhancement of 660 for protons was yet out of reach.The critical role of electronic relaxation parameters, namely the longitudinal relaxation time T1e and the transverse relaxation time T2e, was hypothesized to be important in the efficiency of the CE DNP process as slower electronic relaxation is expected to facilitate the saturation of electronic transitions upon microwave irradiation.3,8 In the light of this assumption and works by Eaton and coworkers,66,67 Emsley, Tordo and co-workers attempted to lengthen the electronic relaxation times of bTbK by replacing the methyl groups on the nitroxide rings by bulkier spirocyclohexyl moieties, obtaining a binitroxide radical dubbed bCTbK.68 This functionalization yielded a significant increase by nearly a factor 2 in electronic relaxation times. Concomitantly with this change in relaxation properties, the authors reported significant improvements in the DNP performance, recording a 52-fold enhancement factor for 29Si NMR of a mesoporous silica sample via1H–29Si CP at 9.4 T, 100 K and 12 kHz MAS with a 20 mM bCTbK solution, while bTbK only yielded a 21-fold enhancement in the same conditions, hence a tremendous improvement. The authors also showed, with the help of EPR and DFT, that the magnitude of the magnetic interactions between the two electrons in both binitroxides as well as their respective g-tensors relative orientations are practically unchanged, the difference being later estimated to be less than 3°.69 Building upon the structure of bCTbK, Zagdoun et al. ultimately synthesized a series of new functionalized binitroxides, varying the spiro groups (cyclohexyl, 1-acetylpiperidinyl, tetrahydropyranyl or 4-phenylcyclohexyl) and the number of substituents on the α-positions of the nitroxide rings.70 The authors verified a correlation between the molecular weight (i.e. the degree of functionalization) of these radicals and the increase of their relaxation times (Fig. 4). The increase of both the inversion recovery time Tir and the phase memory time TM (reflecting longitudinal and transverse relaxation times respectively) leads to an increase of the saturation factor (defined as the product of the two). Measuring the DNP enhancements for these binitroxides, the authors then established a clear correlation between the increase in saturation factor (via further functionalization with bulkier groups) and the increase in DNP performance. Within this series, TEKPol, yielded the highest enhancements, enabling a ca. 200-fold amplification at 9.4 T, 100 K and 12 kHz MAS on the proton signal in a frozen 1,1,2,2-tetrachloroethane (TCE) solution, largely outclassing all other binitroxide radicals.
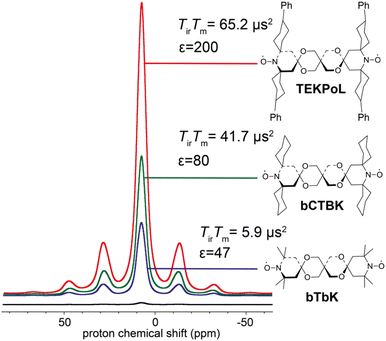 | ||
| Fig. 4 Proton enhancement and saturation factors measured for 16 mM bTbK, bCTbK and TEKPOL in frozen solution of TCE at 100 K. The black spectrum is the microwave off signal. Adapted from ref. 70. | ||
While a significant improvement was made in the field of binitroxide PAs with the introduction of TEKPol, the latter was not compatible with aqueous solutions. In the same year, Sauvée and co-workers also re-examined the bTurea radical and designed improved versions of it to achieve high enhancements in aqueous media at 9.4 T.71 Driven by the same principle of introducing large functional groups on the nitroxide moieties in order to lengthen their electronic relaxation times, the authors proposed to functionalize bTurea with 4 spirotetrahydropyranyl groups, thus forming the PyPol radical. This modification also guarantees a good water solubility for this PA, and another radical dubbed AMUPol, with an extra 4-unit PEG chain grafted on the linker to prevent aggregation in solution, was also synthesized (the structure of AMUPol is shown later in Fig. 6). These two radicals were shown to be highly soluble in water/glycerol mixtures, as well as to exhibit significantly longer electronic relaxation times than bTurea. In turn, their DNP performance was 3 to 4 times better than that of bTurea, achieving a ca. 235-fold enhancement for AMUPol in water/glycerol solutions at 9.4 T and 100 K. Enhancement factors up to 400 or 500-fold were reported by Kubicki and co-workers with AMUPol and TEKPol used in conjunction with KBr crystals to improve the microwave penetration in 3.2 mm rotors.72
An in-depth study of the Zeeman field profile for AMUPol by Buntkowsky and co-workers confirmed that, while a slight contribution of SE cannot be excluded, the dominant mechanism responsible for the performance of AMUPol at 9.4 T is attributed to CE, highlighting that this radical achieves very efficient CE at this field by combining all the design principles discussed so far.73 Recent work by Mentink-Vigier and co-workers also brought additional insights into the DNP efficiency of AMUPol and TEKPol by recording Zeeman field profiles for these radicals at 14.1 T, successfully reproducing these profiles as well as the polarization build-up times with high accuracy in silico, using spin dynamics simulations.74
3.4 Screening for the most efficient binitroxides at intermediate magnetic field (9.4 T)
Having reached a point where very efficient polarizing agents (namely TEKPol for organic solvents and AMUPol for aqueous media) were available for MAS DNP experiments, yielding unprecedented 200-fold enhancements at 9.4 T, the aforementioned binitroxides opened the possibility for many applications in solid-state NMR of materials or biological samples. In the following years, research was dedicated to refining the structure of these radicals and screening for potentially better performing PAs. In 2016, Kubicki and co-workers have extensively compared the DNP performance of an ensemble of 37 different biradicals in a glassy matrix of TCE at 9.4 T and 100 K.75 These radicals derivate from different families of binitroxide scaffolds (including bTurea, PyPol, bTbk and TEKPol). This study confirms that sizeable electron–electron couplings, near-orthogonal g-tensors orientation and long electron relaxation times constructively add up to improve progressively the DNP performance of the tested biradicals. This study reiterates that TEKPol and its bulkier derivatives such as TEKPOL2 are dinitroxides of choice at 9.4 T. In parallel, in another systematic study, Sauvée and co-workers have focused on 18 water-soluble bTurea derivatives, functionalized with various bulky groups on their nitroxide moities or with various PEG-like chains on their linker.76 The latter contributes to improve the solubility of the biradical, but only to a certain extent, as illustrated by the poor DNP performance of the TetraPEG compound in that study. The authors confirm that AMUPol and similar structures are optimum binitroxides for MAS DNP in aqueous media at 9.4 T. Interestingly, it can be noted that presence of PEG chains, while twisting the relative orientation of the g-tensors and setting the angle between their mean planes to be ca. 30°, does not seem to hinder the efficiency of these PAs, in agreement with the simulations performed by Perras and discussed at the end of the previous section.63Work conducted by Oschkinat and co-workers also led to the introduction of an efficient water-soluble binitroxide PA, derivative of PyPol with hydroxycyclohexyl groups decorating the nitroxides, dubbed bcTol, that was shown to perform comparably to AMUPol.77 A slight improvement was later reported by the addition of methyl groups in the linker, shortening the polarization build-up time and therefore increasing the overall sensitivity gain provided by the so-called bcTol-M biradical.78 A recent theoretical study by Mentink-Vigier advocates for a higher average g-tensor's distance in bcTol-M compared to AMUPol and bcTol, in line with its high efficiency.79
Some developments are also noteworthy in an attempt to design nitroxide-based polarizing agents tailored for a specific application. Spin-labeled lipids were developed for the study of membrane proteins, as demonstrated by Bechinger and co-workers80,81 as well as Long and co-workers.82,83 By adequately doping a lipid bilayer with 3 mol% of such spin-labeled lipids, the latter showed that the dipolar couplings between two neighboring nitroxide moieties are close to those of AMUPol, hence providing an optimum performance, yielding promising results despite still modest enhancement factors due to the high mobility in such a matrix, even at 100 K where motional freedom of methyl groups is not completely frozen. Another recent attempt with TOAC (2,2,6,6-tetramethylpiperidine-N-oxyl-4-amino-4-carboxylic acid)-based binitroxide spin-labelled peptides enabled 20-fold DNP enhancements on 13C and 31P in lipid bilayers.84 When studying a specific protein, a high-affinity binitroxide-based tag can also be designed to stoichiometrically bind the protein at micromolar concentration and therefore providing sizeable signal enhancement while limiting paramagnetic bleaching, as demonstrated by McDermott and co-workers.85 Alternatively, site-directed spin labeling of proteins using tailor-designed biradicals can be employed to induce local paramagnetic relaxation effects and produce effective DNP enhancements.86 Recently, another example of targeted polarizing agent was proposed by Debelouchina and co-workers by exploiting the bio-orthogonal combination of a tetrazin-based binitroxide with modified norbornene-lysine sites in a protein, yielding satisfactory 24-fold DNP enhancements.87 A trimodal polarizing agent has been presented for in-cell NMR applications, which contains a targeting peptide for cell penetration as well as a fluorophore for intracellular localization with confocal microscopy, besides the nitroxide biradical.88
Polarizing agent design is a complex and multi-factorial problem that requires fine-tuning of interdependent EPR parameters via chemical synthesis. Predicting the DNP performance of a binitroxide radical is a tedious task, however simulations can be helpful in that respect. The critical point then becomes the accuracy of the input parameters. Two remarkable multifrequency EPR studies can be mentioned as successful attempts to fit and extract such parameters in the case of AMUPol by Baldus and co-workers89 and the bTurea and PyPol families by Mathies and co-workers.35 This method, despite being quite demanding in experimental EPR data and requiring careful computation of fitting routines, provided a key insight in radical design by confirming and quantifying the presence of a strong Heisenberg exchange coupling J between the two electrons in AMUPol and alike binitroxides. Previously, the vision of the electron–electron couplings was often limited to through-space interactions whereas these studies confirm that the sum of the dipolar and scalar couplings should be considered and optimized to reach optimum CE.
Overall, the different studies following the introduction of AMUPol and TEKPol, while reinforcing the rational understanding of key parameters in PA efficiency, and despite the discovery of a few binitroxides that provided modest improvements, have not achieved a significant jump forward in DNP enhancement via CE at 9.4 T. Added to the fact that these two radicals have become quickly commercially available, they remain widely used as gold standards for MAS DNP applications up to date and constitute the current glass ceiling in PA design at intermediate fields.
3.5 Solvent accessibility
In the search of more efficient PAs for CE DNP, a new design parameter, the local geometry around the unpaired electron, has been recently introduced and its importance demonstrated at both 9.4 and 21.1 T.90 The DNP performance was shown to be dramatically affected by changes in the local structure around the unpaired electron in mono- and binitroxides, for otherwise identical constitution. This effect is illustrated in Fig. 5(a) for two mono-radicals with open and closed ring conformations of the spirorings in the vicinity of the N–O bond. Irrespective of the radical concentration, the open conformer yields higher enhancement factors than its closed analog. Here, the conformation of the tetrahydropyran ring substituents was controlled by the inclusion of locking methyl groups. The open version of AMUPOL, dubbed O-MAMUPOL (structure shown in Fig. 5(c)) was shown to provide significantly higher ε (by around 40%). Enhancements as high as 330 could be measured at 9.4 T and 100 K in a DMSO/water mixture for the HydrOPol biradical (Fig. 5(b)) that features a shorter PEG chain in the linker. To our best knowledge, the outstanding performance of this HydrOPol has not yet been overcome in these field and temperature conditions.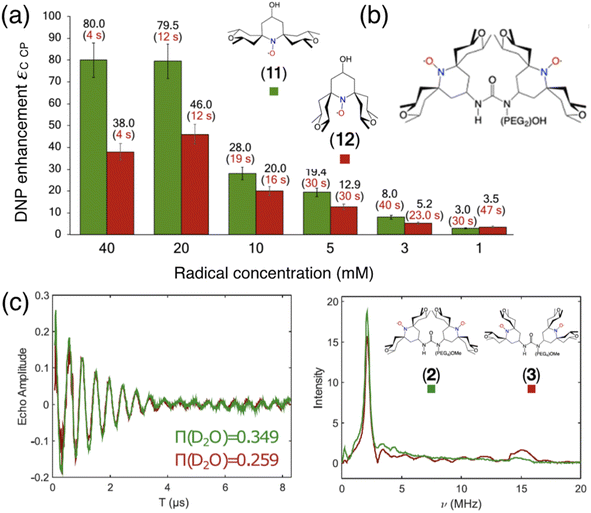 | ||
Fig. 5 (a) Proton MAS DNP enhancements measured via1H–13C CP for the monoradicals O-MbPyTol (in green) and C-MbPyTol (in red) in DMSO-d6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D2O D2O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2O (60 H2O (60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 v/v/v) at different radical concentrations at 9.4 T and 100 K. The enhancement value is indicated in black above the bar. The build-up time of the solvent 1H signals is given in parentheses. (b) Structure of the HydrOPol. (c) Three-pulse ESEEM time-domain data and the corresponding magnitude spectra (obtained after Fourier transform of the normalized nuclear modulation function) for O-MAMUPOL (in green) and C-MAMUPOL (in red) in glycerol-d8 10 v/v/v) at different radical concentrations at 9.4 T and 100 K. The enhancement value is indicated in black above the bar. The build-up time of the solvent 1H signals is given in parentheses. (b) Structure of the HydrOPol. (c) Three-pulse ESEEM time-domain data and the corresponding magnitude spectra (obtained after Fourier transform of the normalized nuclear modulation function) for O-MAMUPOL (in green) and C-MAMUPOL (in red) in glycerol-d8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D2O D2O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2O (60 H2O (60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 v/v/v) at 50 K and 200 μM. The solvent accessibility parameter π(D2O), obtained from the modulation depth defined as the peak-to-peak distance between the first maximum and the first minimum in the deuterium modulation,90 is always larger for the open form. Reproduced from ref. 90 with permission from American Chemical Society, copyright 2020. 10 v/v/v) at 50 K and 200 μM. The solvent accessibility parameter π(D2O), obtained from the modulation depth defined as the peak-to-peak distance between the first maximum and the first minimum in the deuterium modulation,90 is always larger for the open form. Reproduced from ref. 90 with permission from American Chemical Society, copyright 2020. | ||
Pulsed EPR was applied to demonstrate that the differences in the ring conformation around the N–O bond led to differences in terms of solvent accessibility to the unpaired electrons. Electron spin echo envelope modulation (ESEEM) experiments indicated that the improved efficiency of the open conformers is correlated with a higher local concentration of solvent molecules next to the electron spin, as illustrated in Fig. 5(c). A differential distribution of protons in the vicinity of the unpaired electron is expected to affect the first steps of the polarization transfer process, which would translate into the observed changes in the bulk DNP enhancements. The mean electron–electron distances and electron relaxation properties being nearly the same, this study highlights the – so far overlooked – crucial importance of local conformational changes near the nitroxides, introducing a new design principle for the synthesis of efficient radicals tailored for solid-state DNP.
3.6 Limitations of binitroxide radicals
The ever-growing complexity of the samples investigated by solid-state NMR requires the highest possible sensitivity gains provided by MAS DNP jointly with the finest spectral resolution accessible at very high magnetic fields. Transposing the tremendous sensitivity boosts obtained at intermediate magnetic fields (9.4 T) to the highest fields available (18.8 and 21.1 T) is one of the key challenges of modern DNP. For binitroxide radicals, the expected trend of CE efficiency is a severe drop with increasing field, as the breath of the EPR profile of these PAs scales with the latter, rendering the saturation of electronic transitions less effective. The probability of adiabatic three-spin crossing events resulting in a polarization transfer, as detailed in the previous section, actually decreases as (ωI0)−2.23 Even more drastic drops are often observed experimentally. For instance, the enhancement produced by AMUPOL in glycerol/water solutions decreases from εDNP ∼ 250 at 9.4 T in a 3.2 mm rotor to ∼140 at 14.1 T,71 and ∼30 at 18.8 T.91 This is a severe drawback of dinitroxides and one of the main reasons for the limited democratization of very high field DNP, with only five 800 MHz/527 GHz and one 900 MHz/592 GHz Bruker commercial MAS DNP systems currently installed worldwide.While most DNP MAS NMR experiments are carried out in 3.2 mm rotors spinning at 14 kHz at 100 K, the use of smaller diameter rotors enables to spin DNP samples up to frequencies of 40 kHz (resp. 65 kHz) in a 1.3 mm (resp. 0.7 mm) LT MAS probes. While fast spinning is beneficial in terms of resolution and sensitivity, and opens new opportunities such as the implementation of proton-detected experiments, the depolarization effects observed for CE with binitroxide radicals severely intensify in fast MAS regimes.25,43 For AMUPol, this leads to a sizeable drop in the contribution factor θ from 0.85 at 10 kHz to 0.45 at 40 kHz (Fig. 6(a)), as reported by Chaudhari and co-workers.91 The DNP build-up time is also increased in this case due to less efficient spin diffusion processes at high spinning frequencies, thus making less favorable the overall sensitivity gain ΣDNP expected with such biradicals.
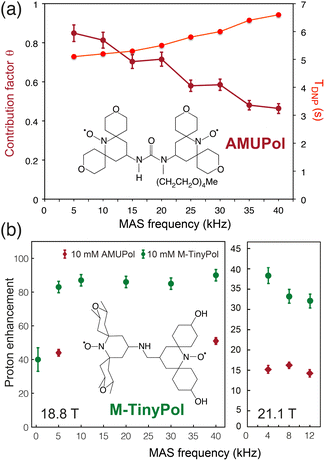 | ||
| Fig. 6 (a) Contribution and build-up times for a 10 mM AMUPol solution in d8-glycerol/D2O/H2O (60/30/10, v/v/v) at 18.8 T as a function of MAS rate. The structure of AMUPol is shown. Adapted from ref. 91 with permission from RSC Publishing, copyright 2016. (b) Enhancement factors of M-TinyPol at 10 mM measured in bulk solution of d8-glycerol/D2O/H2O (60/30/10, v/v/v) at 18.8 T and 21.1 T as a function of MAS frequency. Adapted from ref. 94 with permission from RSC Publishing, copyright 2020. | ||
3.7 Perspectives at high magnetic fields
In order to mitigate the detrimental trends observed at high fields and fast spinning frequencies, binitroxides were re-examined with fresh eyes by the community. While aiming for high field DNP, it became clear, following the benchmark study by Thurber and Tycko,23 that further increasing the magnitude of magnetic interactions between the two electrons within a binitroxide radical would be beneficial to its CE efficiency, while preventing excessive depolarization at fast MAS. The work from ref. 89 and 92 also highlighted the key role of the Heisenberg exchange interaction J between the two electrons, that was previously assumed to be small or negligible, whereas it turns out to constitute a significant portion of the total magnetic interaction, for instance in the case of AMUPol where both the dipolar and exchange coupling terms are of the same order of magnitude (∼30–40 MHz). The J coupling is of particular interest for enhancing the DNP performance of biradicals at fast MAS as, unlike the dipolar coupling, this interaction is not modulated by sample spinning.While there is a synthetic challenge in producing adequate values of J couplings by playing on the linker length, its conjugation and the type of atoms involved, the complexity of this interaction stems from the distribution of conformations adopted by biradicals in the glassy DNP matrix, which in turn generates a distribution of coupling values in the frozen state. As shown by Han and co-workers,93 solution X-band EPR spectra of AMUPol in several usual solvents taken at different temperatures reflect different distributions of J coupling values. In addition to the design of the polarizing agent itself, the freezing history of the sample and the conformational dynamics of the molecule in a given DNP matrix, is therefore also affecting the pool of conformers available for efficient CE. The authors performed DFT calculations to map the exchange coupling value in AMUPol as a function of the relative torsion angle between the nitroxide moieties, showing that the orientational dependence of this interaction is strong, causing broad distributions that should be taken into account when fitting EPR data on binitroxide PAs. With the help of spin dynamics simulations, the authors also estimate that the combination of a favorable relative g-tensor orientation and a threshold mean J value (at a given magnetic field) should facilitate high enhancements and negligible depolarization with MAS.
A few experimental studies have reported the synthesis and characterization of binitroxides with increased J coupling strength in an attempt to produce higher enhancement factors at high magnetic fields. The design of such biradicals with short linkers and rigidified (partly conjugated) backbone has been reported by Buntkowsky and co-workers, but their performance was unfortunately only assessed at intermediate fields.95 A noteworthy attempt was made by De Paëpe and co-workers in 2018 who introduced the AsymPol family.96 These radicals, designed to have a short tether and a conjugated carbon–carbon double bond in the five-membered ring, yield dipolar and exchange couplings on the order of 56 and 70 MHz respectively (absolute values). The authors show that these coupling values fall into an optimum range for efficient CE DNP at 18.8 T according to spin dynamics simulations. Despite an effectively modest 27-fold enhancement in MAS DNP conditions at 18.8 T in 3.2 mm rotors, the best radical in this series, AsymPol-POK, is shown to yield a satisfying overall sensitivity gain as it benefits from short polarization build up times and limited depolarization. Very recently, an improved version of AsymPol-POK was obtained by grafting cyclohexyl moieties to the five-membered nitroxide to lengthen electronic relaxation times.97 This radical, dubbed cAsymPol-POK, yields comparable enhancements to AMUPol at 18.8 T, but its short build-up times and near-absence of depolarization are preserved through this modification, making it relevant for applications in proton-dense solids such as pharmaceutical formulations.
Another family of binitroxides successfully achieving sizeable enhancement values at 18.8 T are the TinyPols, introduced in 2020 by Lesage, Ouari and co-workers. The authors demonstrated that, by reducing the distance between the two unpaired electrons, the unfavorable field dependence could be significantly reduced.94 With the best radical in the series, dubbed M-TinyPol, εDNP as high as 90 at 18.8 T in 1.3 mm rotors (40 kHz MAS frequency), and 38 at 21.1 T in 3.2 mm rotors (12 kHz MAS frequency), versus respectively 54 and 14 for AMUPol, were achieved in glycerol/water solutions (Fig. 6(b)). The performance of TinyPols was attributed to higher e–e dipolar couplings, as both the electron relaxation times and J coupling values were unchanged with respect to AMUPol. Thus, AsymPol- and TinyPol-like families of polarization agents opens up new opportunities for very high-field DNP, promoting hyperpolarized solid-state NMR as an accessible technique over a broad range of magnetic fields. Outstanding performances at very high magnetic fields were also recently achieved with the design of hybrid radicals, having only one nitroxide moiety, as described in the next section.
4 Hybrid radicals, a new paradigm for high-field DNP MAS NMR
While, since the mid-2000, the search for new PAs structures has predominantly been focusing on purely nitroxide-based radicals, carbon-centered radicals with narrow EPR line such as trityl and BDPA have been recognized as efficient electron sources for SE since the early days of modern MAS DNP. In the recent years, the community has pivoted towards these other types of radicals with a renewed attention and in the light of the insights gained in the study of nitroxides.4.1 Non covalent mixtures of organic radicals
As early as in 2007, Hu, Griffin and co-workers experimented with mixtures of trityl and 4-hydroxy-TEMPO monoradicals in an attempt to produce efficient CE DNP.98 The motivation behind this approach was, instead of exploiting only a fraction of the molecular orientations present in a frozen solution of a broad EPR line mononitroxide, or constraining the relative orientation of two nitroxides in a biradical in order to select conformations with an electron frequency difference on the order of the nuclear Larmor frequency ωI0, to achieve the correct g-value difference with the separation between a narrow EPR line and the maximum position of a broad EPR line. The authors noted that, ideally, a very efficient PA for CE could be obtained by combining two isotropic radicals separated by the nuclear Larmor frequency. However, such a theoretical mixture or biradical would be nucleus dependent and does not yet exist. Protons have a 211 MHz Larmor frequency at 5 T. Hence, the ca. 80 G (i.e. 225 MHz at this field) separation between the quasi-isotropic trityl line and the position of the gyy component at the maximum of the nitroxide powder pattern closely matches that frequency. The authors demonstrated that, while trityl and TEMPO lead to maximum enhancements of ca. 15 and 55-fold respectively in these conditions, their 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture (in moles of electrons, for a 40 mM total concentration) yielded an impressive ca. 160-fold boost on the urea 13C cross-polarization (CP) signal in a DMSO/water solution, at 5 T, 90 K and 5 kHz MAS (Fig. 7(a)). The Zeeman field profile of the mixture clearly indicates that the DNP effect observed surpasses the sum of SE from trityl and CE between mononitroxides, while the asymmetric shape of the profile and the ca. 76 G separation between its positive and negative maxima provide the evidence of trityl-nitroxide intermolecular CE. The chosen concentration is a trade-off between high enhancement values (with short build-up times on the order of 5 s) and significant bleaching effects.
1 mixture (in moles of electrons, for a 40 mM total concentration) yielded an impressive ca. 160-fold boost on the urea 13C cross-polarization (CP) signal in a DMSO/water solution, at 5 T, 90 K and 5 kHz MAS (Fig. 7(a)). The Zeeman field profile of the mixture clearly indicates that the DNP effect observed surpasses the sum of SE from trityl and CE between mononitroxides, while the asymmetric shape of the profile and the ca. 76 G separation between its positive and negative maxima provide the evidence of trityl-nitroxide intermolecular CE. The chosen concentration is a trade-off between high enhancement values (with short build-up times on the order of 5 s) and significant bleaching effects.
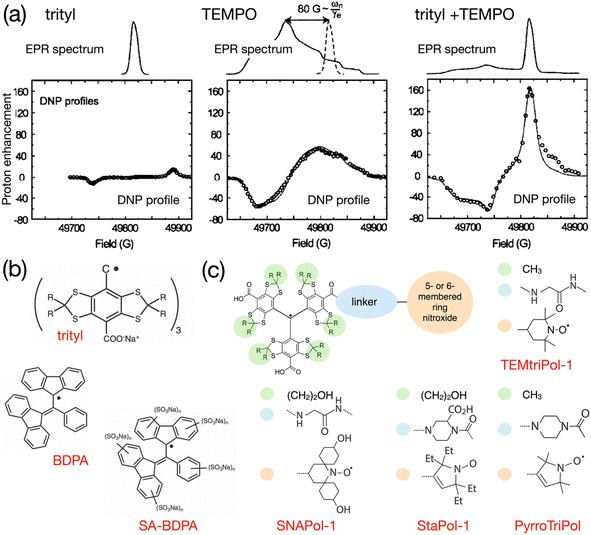 | ||
Fig. 7 (a) EPR spectra and Zeeman field profiles recorded at 5 T and 90 K for trityl, 4-hydroxy-TEMPO and a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture of these radicals. Reproduced and adapted from ref. 98 with permission from American Chemical Society, copyright 2007. (b) Molecular structure of trityl, BDPA and the water-soluble sulfonated BDPA. (c) Schematic structure of trityl-nitroxide hybrid radicals, and substituents for TEMtriPil-1,103 SNAPol-1,104 StaPol105 and PyrroTriPol.106 1 mixture of these radicals. Reproduced and adapted from ref. 98 with permission from American Chemical Society, copyright 2007. (b) Molecular structure of trityl, BDPA and the water-soluble sulfonated BDPA. (c) Schematic structure of trityl-nitroxide hybrid radicals, and substituents for TEMtriPil-1,103 SNAPol-1,104 StaPol105 and PyrroTriPol.106 | ||
In 2012, Swager, Griffin and co-workers proposed a synthetic route for a sulfonated version of BDPA, hence enabling the use of this PA in aqueous solutions. This SA-BDPA monoradical (Fig. 7(b)) was shown to yield 100-fold SE enhancements at 5 T, overperforming trityl.99 Subsequently, the authors proposed the use of a mixture of SA-BDPA and trityl OX063, the EPR frequencies of which being separated by approximately the 13C Larmor frequency, and evidenced a very efficient direct 13C polarization transfer resulting in enhancements up to 600-fold in a frozen solution of 13C-labelled glycerol/water (the theoretical maximum being at 2600 for 13C).100 In this paper, the authors point out, however, based on the recorded field profiles, that this significant enhancement value is a combination of SE from both monoradicals, possibly CE from trityl (that has a broader EPR line than SA-BDPA) and CE between the two different radicals. Noticing that SA-BDPA is more efficient in this sample than in the pure sample, they measured the longitudinal electronic relaxation times and found them to be one order of magnitude shorter for SA-BDPA in the mixture compared to its pure form (3.6 versus 28.9 ms) while the trityl T1e remains around 1.4 ms in both pure and mixed forms. This short T1e for SA-BDPA allows this radical to be extremely efficient at directly polarizing 13C nuclei by SE. The difference in relaxation times between the two coupled radicals is also beneficial as, while the saturated radical (SA-BDPA) has a longer T1e that facilitates its saturation, the non-saturated electron of trityl has a shorter relaxation time (1.4 ms versus 28.9 ms for pure SA-BDPA) that allows for a fast recovery of the polarization difference between the two electrons, therefore maximizing the polarization transfers at each CE event. This is the first illustration of this principle, already discussed on a theoretical level by Hu and co-workers.8
Finally, a recent study by Han and co-workers revisited mixtures of different monoradicals by questioning the ideal ratio between nitroxide and trityl spins to maximize CE efficiency.101 Although their experimental conditions – using a home-made low-temperature MAS probe, operating at 5 kHz and at 25 K, and with a low-power 350 mW microwave source – are quite far from the commercial DNP instrumentation, the authors pointed out that a 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 TEMPO–trityl mixture yielded a 25% improvement on the value of the positive CE maximum enhancement with respect to the 1
1 TEMPO–trityl mixture yielded a 25% improvement on the value of the positive CE maximum enhancement with respect to the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture. This increase, accompanied with a slight reduction in polarization build-up time, is then confirmed via spin dynamics simulations highlighting the greater probability of constructive CE events with this composition. A 3
1 mixture. This increase, accompanied with a slight reduction in polarization build-up time, is then confirmed via spin dynamics simulations highlighting the greater probability of constructive CE events with this composition. A 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture, while maintaining short build-ups, is however detrimental for the enhancement, most likely due to a concomitant shortening of the trityl T1e with the increased overall spin concentration. Therefore, the authors foresee improvements to existing biradicals by tethering a trityl moiety to two or more nitroxides.
1 mixture, while maintaining short build-ups, is however detrimental for the enhancement, most likely due to a concomitant shortening of the trityl T1e with the increased overall spin concentration. Therefore, the authors foresee improvements to existing biradicals by tethering a trityl moiety to two or more nitroxides.
4.2 Trityl-nitroxide hybrid radicals
The first successful attempt to tether chemically a trityl and a nitroxide radical, following Hu's seminal work on mixtures,98 was reported by Liu and co-workers.102 While not performing DNP experiments in their study, the authors show via a thorough EPR analysis that this chemistry offers a wide range of tunability for the electron–electron couplings while varying the length and nature of the linker. The sum of the dipolar and scalar interactions can thus be modulated from a few MHz to ca. 3300 MHz thanks to the combined effect of the distance between the two free electrons in the biradical and the chemical nature of the linker allowing for overlap of spin densities. The authors predict that this system is therefore a good candidate for efficient DNP at high magnetic fields as the magnitude of magnetic interactions can be adjusted to produce optimal CE.A first demonstration of this concept was provided in 2015 by Mathies, Griffin and co-workers who introduced the TEMTriPol family.103 This paper has been extremely impactful as it not only evidenced CE DNP with such biradicals but also showed how efficient it could be at high fields. The best radical in the series, TEMTriPol-1 (Fig. 7(c)) yielded a 65-fold enhancement at 18.8 T, 100 K and moderate spinning frequencies. The magnitude of the Heisenberg exchange interaction in TEMTriPol-1 is on the order ca. 73 MHz. This turns out to be adapted to such high fields, while remaining reasonably-sized, so that the CE matching condition can be fulfilled. In contrast, ProxTriPol, another radical in the series, did not produce observable enhancements, in line with its ca. 820 MHz J coupling value. Interestingly, TEMTriPol-1 performs better at 14.1 T than 18.8 T, providing insights on the target values of couplings necessary to tune such a biradical for maximum CE efficiency at a given magnetic field. A complementary study of TEMTriPol-1 refined the characterization of its J coupling value that was previously estimated via the splitting observed in solution state X-band EPR spectra of the radical.107 Advanced fitting of new EPR data combined with spin dynamics simulations allowed the authors to estimate a distribution of J values, more representative of the couplings at play in frozen solutions of TEMTriPol-1. They also demonstrated the absence of nuclear depolarization due to the strong isotropic coupling between the electrons, which is an advantageous feature of hybrid trityl-nitroxide PAs.
Other designs have been suggested to link a trityl and nitroxide moiety together, such as a series synthesized by Buntkowsky and co-workers in 2018 with variable linker length, containing zero, one or two ester functions.95 Unfortunately, the authors only tested these PAs at an intermediate field of 9.4 T. The 1H and 13C enhancements factors ranged from 2-fold for the shorter linker, 50-fold for the intermediate one and 15-fold for the longest in the series. This illustrates once again the existence of an optimal magnitude for the electron–electron coupling interactions. CE efficiency can be maximized in hybrid radicals and controlled in part by choosing the linker length accordingly. A follow-up study by the same team demonstrated the feasibility of the design of hybrid trityl-nitroxide biradicals with controlled g values and magnetic interaction strength via a rigid organic tether such as phenylene or naphtalene.108 The goal here was also to broaden the scope of applications of such radicals by making them more soluble in organic solvents. While only reporting a modest 30-fold CE DNP enhancement at 9.4 T with Tr-Ph-NO in TCE, this study nicely expanded the available tools to engineer hybrid biradical PAs for high field DNP.
Liu, Baldus and co-workers also highlighted a new feature of hybrid trityl-nitroxide biradicals that could help fine-tune their geometry and performances. Given that trityl can in principle adopt either an M or P helix conformation, and using a chiral L-proline tether, they synthesized four different diastereoisomers that each differs (two by two) by the configuration of one steric center.109 These chiral biradicals were studied via EPR and turned out to form two very different sets of molecules with either very strong (ca. 550 MHz) or moderate (ca. 15 MHz) Heisenberg exchange couplings, while all having a similar dipolar coupling strength about 10 G at low temperatures around 220 K. In correlation with this difference in magnetic interactions, diastereoisomers with a too strong J value were found to perform poorly in DNP conditions at 18.8 T, yielding a 7-fold enhancement, while the PAs with a moderate J value achieved a ca. 40-fold enhancement in the same conditions, slightly underperforming TEMTriPol-1. This piece of work is however an important proof of concept that chirality may be used as an additional lever to tailor the DNP performances of hybrid radicals.
Recently, the same group of researchers has achieved significant progress on the DNP performance of water-soluble trityl-nitroxide by revisiting the structure of TEMTriPols. They first introduced a post-modification of the linker to help solubilizing the biradical.110 The resulting series, dubbed NATriPols, was evaluated at 18.8 T and 103 K at different concentrations. It was found that the DNP performance of these radicals correlates well with their parting coefficient between water and octanol – in other words, the more hydrophilic the NATriPols are, the better they perform at CE DNP. The best biradical in series, NATriPol-3, slightly overperforms TEMTriPol-1 at 18.8 T in a frozen bulk aqueous solution. More interestingly, when measured on biomolecules, NATriPol-3 was shown to preserve a sizeable 30-fold gain. Further functionalization of both the trityl and nitroxide moieties with various hydrophylic groups to limit aggregation processes led to the introduction of the SNAPol family with an increased solubility and the best performances reported for a water-soluble hybrid radical at 18.8 T up to date.104 In particular, SNAPol-1 (Fig. 7(c)) yields a 135-fold proton enhancement in DNP juice in 3.2 mm rotors while maintaining short (ca. 4 s) polarization build-up times, representing over a 500-fold overall sensitivity gain compared to an undoped sample. The authors show that SNAPols, which combines appropriate electron–electron coupling interactions magnitude and water-compatible functionalization, open up new avenues at high fields for challenging applications of MAS DNP on biologically relevant samples, including in cells where radicals having a gem-diethyl pyrroline nitroxide such as StaPol-1 (Fig. 7(c)) were shown to be highly stable in reducing environments.105 We note that the performance of these hybrid biradicals was only evaluated at intermediate MAS frequencies, leaving room for improvement if used in conjunction with faster spinning probes that benefit from better microwave penetration.
More recently, a new family of trityl-nitroxide hybrid radicals having a rigid piperazine linker and a 5-membered ring nitroxide, named PyrroTriPols, was introduced that are suitable for both aqueous and organic solutions, and that provide higher overall sensitivity than TEMTriPols at magnetic fields ranging from 9.4 to 18.8 T.106 The good performance of PyrroTriPol (Fig. 7(c)) was assigned to a relatively narrow distribution of conformations as evidenced by MD simulations and an average distance of 13.7 Å between the two electrons. Interestingly, attempts to prepare triradicals composed of one trityl and two nitroxides were also reported. However, the latter were shown be less efficient than their biradical analogs at a fixed electron concentration.
4.3 BDPA-nitroxide hybrid radicals for efficient high field DNP in organic solvents
In parallel to the trityl-nitroxide route, another type of hybrid biradicals has been recently developed for efficient CE DNP in organic solvents, by tethering a nitroxide with a BDPA moiety. BDPA has a more isotropic EPR line than trityl and has longer electron relaxation times, which is advantageous at high fields where saturating electron transition in inhomogeneously broadened EPR spectra becomes increasingly difficult. The first attempt at connecting a BDPA moiety to a nitroxide was reported by Swager and co-workers in 2009,111 when they synthesized a BDPA-amide-TEMPO biradical. The DNP performance of this radical was however not reported, and current understanding of the critical role of magnetic interactions in biradical PAs leads to believe that this radical would perform quite poorly, in agreement with the too large J coupling value of ca. 140 MHz as determined by EPR. Here we note by passing that a BDPA-ester-TEMPO biradical with a strong J coupling value was successfully used in the context of dissolution DNP at 3.35 T and 1.4 K.112The only series of hybrid BDPA-nitroxide biradicals for which successful high field DNP cross effect has been reported to date is the HyTEK series.113 This study highlighted two key design principles for such PAs: (i) controlling the magnitude of electron couplings is paramount to tailor biradicals to very high fields, which was already hinted at by prior work notably on nitroxide–nitroxide and trityl-nitroxide biradicals; (ii) lengthening the electronic relaxation times in the nitroxide moiety is also very impactful. This second aspect was not straightforward to anticipate in these asymmetric biradicals as the BDPA resonance is the one saturated in the DNP NMR experiment.
Although the linker and substituents were not systematically varied, a series of structures were investigated that are schematically represented in Fig. 8(a). Varying the linker length within the series was shown to affect not only the strength of the dipolar interaction (from 4 to 28 MHz) but also the Heisenberg spin exchange interaction which becomes more pronounced as the linker is shortened (from 0 to 30–70 MHz), and in turn the DNP efficiency. For example, going from HyPTEK with one phenylene unit in the linker to HyTEK with none considerably influences the interactions between the two electrons, which tremendously improves the DNP performance, from 81 to 143-fold enhancement factors recorded at 9.4 T and 40 kHz MAS (Fig. 8(b)). The strong electron couplings in the shortest radicals broaden the BDPA line and slightly shorten its relaxation times, yet without affecting the efficiency of the saturation process.
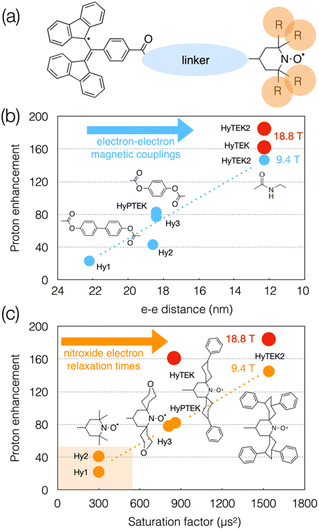 | ||
| Fig. 8 (a) Schematic structure of BDPA-nitroxide hybrid radicals. (b) and (c) Plots showing the evolution of the enhancement factor with electron–electron distance (b) and saturation factor (c) in the HyTEK series. The blue and orange dots correspond to data acquired at 9.4 T, while the red dots are values measured at 18.8 T. Adapted from ref. 113. | ||
The functionalization of the nitroxide moiety with increasingly bulkier groups, reminiscent of the design strategy that led from bTbK to bCTbK, then TEKPol and TEKPol2, proved to be also very efficient in this family of hybrid biradicals. Hence the concomitant increase of the electron relaxation time on the nitroxide upon increasing the size of the functionalization groups between Hy-3 and HyPTEK when the linker has one phenylene moiety, or between HyTEK and HyTEK2 when the linker has none, which were both accompanied by improved enhancements (Fig. 8(c)). This experimental study also brings new insights into the complexity of balancing relaxation times in an asymmetric biradical, as the simple principle of one long and one short T1e discussed previously no longer applies and as both are modulated by structural changes. Ultimately, the best radical in this series, HyTEK2 combines sizeable magnetic interactions and long nitroxide electron relaxation times, ensuring an optimum cross effect efficiency, yielding enhancements as high as 185-fold at 18.8 T and 40 kHz MAS in a 32 mM frozen solution of TCE. A version of HyTEK2 with an even shorter linker, dubbed “short-HyTEK2”, and corresponding to a functionalized version of the BDPA-amide-TEMPO radical reported in ref. 111, was shown to yield significantly lower enhancements, in agreement with too strong magnetic interactions. We finally note that the design principles unraveled in this study also help understanding the beneficial role of the functionalization in the SNAPol series discussed earlier.
In practice, beyond the high enhancement values achieved by these hybrid biradicals, the polarization build-up times were shown to be quite short (<3 s), which is beneficial to the overall sensitivity. In addition, depolarization was quantified and found to be negligible at 18.8 T over the whole spinning frequency range. This not only further improves the overall signal boost offered by these PAs but also confirms that strong magnetic interactions increase the adiabaticity of electron–electron crossing events under fast MAS, maintaining at best the polarization difference between the electrons involved in CE in hybrid radicals.107 The efficiency of HyTEK2 was also evaluated at the highest field available for DNP, i.e. 21.1 T, in the initial study, yielding sizeable 64-fold enhancement at 10 kHz in a 3.2 mm rotor. Additional measurements were later performed at this field with a 0.7 mm LT MAS prototype probe capable of spinning rotors up to 65 kHz and offering excellent microwave penetration and homogeneity. The authors showed that the very good performance of HyTEK2 was preserved at 21.1 T, reaching an impressive 200-fold enhancement factor at the fastest spinning frequency.114 This record performance confirms that the magnetic interactions in this PA are optimal for efficient CE at high magnetic fields.
In addition to the experimental data at 18.8 T and 21.1 T, Equbal and co-workers performed numerical simulations in an attempt to map the CE enhancement as a function of the sum of electron–electron magnetic interactions.115 While this value pilots the efficiency of a PA, they suggested that its performance also depends on the ratio between the scalar (or exchange J) and dipolar (D) contribution of the electron–electron couplings, with an optimum around a 1.5 for the J/D ratio for hybrid radicals. These simulations back up the experimental conclusions about HyTEK2 as this radical falls into the calculated optimum J/D range.
While developments in trityl-nitroxide and BDPA-nitroxide hybrid PAs both provide solid candidates for high field DNP, the latter category benefits from one additional feature that has only been observed for this type of biradical so far: the enhancement value is monotonously increasing as a function of the spinning frequency, yielding the highest values of enhancements at 40 kHz and 65 kHz from the experiments carried out in a 1.3 mm probe and 18.8 T and in a 0.7 mm probe at 21.1 T respectively.113,114 While the enhancements obtained with other symmetric or asymmetric biradicals tend to decrease or plateau at higher MAS rate, this advantageous behavior of HyTEK2 is favorable as it facilitates high sensitivity boosts in combination with faster spinning and improved spectral resolution. This behavior was explained by modeling the spin diffusion processes at play, relying on a source-sink model previously developed to explain similar effects obtained for OE DNP with BDPA in a rigid ortho-terphenyl (OTP) matrix:116 faster spinning effectively isolates the sinks and allows higher levels of steady-state polarization to build up.
One major limitation of BDPA-based hybrid biradicals is however their limited stability in solution, as they tend to degrade over the course of a few days, mostly due to interactions with oxygen. In an attempt to stabilize BDPA-based hybrid radicals in solution and especially in polar solvents, Sigurdsson and co-workers reported the synthesis of a water soluble version of BDPA-nitroxide decorated with positively charged tetraalkyl-ammonium groups on the fluorenyl moieties.117 The MAS DNP performance of such promising water-compatible hybrid radicals yet remains to be evaluated.
5 Metal ions: a versatile alternative approach for exogenous and endogenous DNP
While the recent developments in organic radical based PAs are promising, exploring other sources of polarization is relevant to increase the versatility and applicability of MAS DNP. The very first DNP experiment used free conduction electrons in metallic 7Li to produce hyperpolarization. In that respect, another important class of PAs to be discussed is metal ions, whether under the form of exogenous molecular complexes added to the sample formulation, or endogenous, i.e. present in the lattice of the solid of interest. The following section will review successful attempts at producing DNP with a variety of metal ions in the context of MAS NMR, while leaving aside the advanced theoretical framework underlying SE and CE with metal ions that is well described in ref. 22 and 118.5.1 Exogenous molecular metal ion complexes for MAS DNP
The first DNP experiment using a metal ion complex was performed in static conditions, at 1.5 K and low field, by Abragam and co-workers with chromium Cr(V) in complexes with diols and glycerol.119 The transition metal complex used here had a single unpaired electron (S = 1/2) and its g-anisotropy was found to be very small in the glassy matrix of frozen glycerol, yielding a symmetric SE Zeeman field profile with proton polarization levels near 50% at both maxima. Another successful DNP experiment with spin S = 1/2 transition metal complexes was reported recently by Han and co-workers, featuring vanadium V(IV) ions, bound in assemblies of various sizes such that the only intramolecular protons were located between 4 and 12.6 Å away from the paramagnetic center.120 While this experiment was conducted in static conditions at 4 K, it should be noted that the authors managed to harness hyperpolarization at an intermediate field of 6.9 T from the V(IV) ions and transfer it efficiently to the intramolecular protons in the complex, even for the longest distance available, where the protons to polarize lie beyond the estimated spin diffusion barrier. This proof of principle is promising as it shows that, provided the SE condition can be matched instrumentally, such complexes could be of use in MAS DNP.Apart from the above-mentioned examples, research on transition metal complexes for MAS DNP has mainly been focused on high-spin ions. Indeed, among the available paramagnetic metal ions, few are suitable for hyperpolarized solid-state NMR experiments. The main reason is the current instrumental limitation of commercially available devices. While gyrotrons outputs a fixed frequency, the main field of the NMR magnet can in principle be adjusted via a sweep coil so as to match several SE or CE conditions of the metal complexes, yet only within a range of a few tens of mT from its nominal value. Amidst the metal ions presenting an accessible EPR resonance, those which experience a strong broadening of their EPR line induced by zero field splitting (ZFS) or spin orbit coupling (SOC) are also hampered by the subsequent inefficiency of their saturation upon microwave irradiation.121 In a seminal study published by Corzilius and Griffin in 2011, manganese Mn(II) and gadolinium Gd(III), with S = 5/2 and S = 7/2 respectively, were shown to have g factors sufficiently close to that of the free electron and EPR lines sufficiently narrow to produce DNP at 5 T.122 Thanks to their respective ground states being 6S and 8S, the SOC vanishes, leading to narrow central transitions in both cases. Their satellite transitions are significantly broadened by the first order ZFS, while the central transition is only affected at the second order, resulting in an overall narrow pseudo spin S = 1/2 EPR profile in highly symmetric high-spin complexes for these two metals.10 Originally inspired by bio-compatible MRI contrast agents, the authors tested the DNP performance of Mn(DOTA), Gd(DOTA) and Gd(DTPA) in a typical water/glycerol DNP matrix at 86 K (see Fig. 9 for their structures (a) and EPR profiles (b)). While the Zeeman field profile obtained for Mn(DOTA) clearly shows six SE sub-profiles intertwined (Fig. 9(b)), each corresponding to an irradiation near one of its EPR lines among a hyperfine sextet, the 2-fold maximum enhancement factors obtained reflect the small fraction of spins involved in DNP as they are spread between the hyperfine lines (Fig. 9(c)). The overlay between the profiles of Gd(DTPA) and Gd(DOTA) allows to identify SE as the main DNP mechanism for these complexes and highlights a factor of 4 in performance in favor of the latter, yielding a 13-fold enhancement factor. This was attributed by the authors to the particularly narrow central transition in Gd(DOTA), which was measured to be of 29 MHz breath versus 55 MHz for the trityl radical.122 The central transition in these complexes is expected to get narrower at higher field, hence the interest in these PAs despite the detrimental field dependence of SE and their relatively low starting enhancements.
 | ||
| Fig. 9 Structures (a), EPR profiles (b) and Zeeman field profiles (c) recorded under MAS DNP conditions at 5 T for Gd(DOTA) in blue and Gd(DTPA). Reproduced from ref. 122 with permission from American Chemical Society, copyright 2011. (d) Proton DNP enhancement at 9.4 T for 4 mM solutions in DNP juice of seven different Gd(III) complexes as a function of their axial zero field splitting parameter D. The red curve is a fit to the theoretical inverse quadratic relationship. Reproduced from ref. 127 with permission from American Chemical Society, copyright 2022. | ||
Following this work, Corzilius and co-workers demonstrated that a Mn(II) ion bound in a 13C-labelled ribozyme could produce an 8-fold direct carbon enhancement factor at 9.4 T, realizing a DNP transfer internal to a biomolecule.123 Despite moderate gains in sensitivity and long 13C polarization build-up times, this method is expected to be valuable to produce site-specific DNP in the context of structural biology and could supplement the conventional use of binitroxide PAs. This concept is further expanded in a subsequent publication from the same group where a site-directed approach is deployed, combining small molecular chelate polarizing agents such as Gd(DOTA) and specific protein isotopic labeling.124 In addition to the possibilities offered by this method for biomolecule characterization, two very important results are reported in this work. First, as the Zeeman field profile for Gd(DOTA) is carefully examined for direct 1H and 13C SE, the authors note that a slight enhancement is present at the 1H maximum positions on the 13C profile, with opposite sign, when recorded in a proton-rich matrix. This interesting effect, attributed to heteronuclear cross-relaxation, similar to the nuclear Overhauser case, now serves as a basis for a series of fruitful experiments dubbed SCREAM-DNP, as described in ref. 125. Second, when investigating the effect of metal ion complex concentration on the Zeeman field profiles, the authors realized that the 15N profile – and also to a lesser extent the 13C profile – was dependent on that concentration. Using a simple statistical model, they estimated the nearest neighbouring Gd(III) ions to be located between 2.4 nm at 20 mM and 5.2 nm at 2 mM. In the latter case, the dipolar interactions between PAs can be neglected while in the former they are sizeable enough to induce a large contribution of CE to the DNP, in addition to the expected SE. Based on this last observation, Corzilius and co-workers designed bis-gadolinium complexes with variable linker length, enabling electron–electron dipolar couplings ranging from 1 to 32 MHz, in order to study the competition between SE and CE DNP with such a PA.126 The authors observed a shift of the maximum enhancement position in the profile as a function of the linker length as well as new features emerging for either 1H, 13C or 15N profiles. However the CE proton enhancements obtained remained modest, mostly due to a significant broadening of the EPR line upon decreasing the distance between the gadolinium centers. Interesting mechanistic considerations could however be derived from this study, including a clear illustration of the limitations in PA design imposed by the simplified CE condition, which falls apart when the dipolar coupling value come close to the 15N Larmor frequency.
Later, Emsley and co-workers focused on the design of better performing molecular metal complexes to increase the enhancement ceiling with this class of PAs.128 Noting that binitroxides are not resilient to reducing (and potentially biologically relevant) environments, the goal of their study was to capitalize on a versatile, water-soluble, stable PA with a narrow EPR central transition, hence the choice to pursue with Gd(III). In agreement with the theoretical predictions in ref. 22, the authors derive a simple analytical expression of the enhancement factor dependance on ZFS. Assuming that the ZFS dominates the EPR linewidth and subsequently governs the efficiency of the SE process for these complexes, two complexes noted (1) and (2) with respective axial ZFS components D1 and D2 would yield enhancement factors verifying:
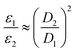 | (5) |
Thus, reducing the ZFS of the Gd(III) complex would thus benefit the SE efficiency, unlocking higher orders of magnitudes for enhancements with metal complexes. The authors therefore introduce a new complex, Gd(tpatcn) (Fig. 9(d)), which has a pseudo-C3 symmetry. The measured ZFS axial component for this complex amounts 410 MHz versus 599 MHz for Gd(DOTA). According to the previous equation, a factor of two improvement on the enhancement is therefore expected for Gd(tpatcn). The authors demonstrate successfully that this factor, measured on the negative SE maximum for both complexes, is not only observed on 1H (measured via CP), 13C and 15N enhancements, bringing the new record for metal complexes to a 37-fold proton enhancement at 9.4 T, but also reproducible over a wide range of concentrations in a water/glycerol mixture. These results confirm the design principle hypothesized by the authors as the two complexes investigated have otherwise similar g-anisotropy and electronic relaxation properties. In a recent publication, the DNP performance of four new Gd(III) complexes was evaluated along with the measurement of their ZFS parameters, validating the robustness of this postulated structure–properties relationship.127 While none of the four PAs introduced in this wok overperforms Gd(dota) or Gd(tpatcn), a clear correlation between the ZFS and enhancement factor (with an inverse quadratic dependence) was verified (Fig. 9(d)). Among all the complexes, Gd(tbptcn) and Gd(tpptcn) were shown to have a non-negligible offset form the curve. This deviation was explained by their relatively large mean saturation factors (0.40 and 0.32 μs2 respectively) in comparison to the other complexes, which range between 0.20 and 0.23 μs2, which facilitates their saturation. We finally note that moderate SE 13C and 15N enhancement factors were reported in water/glycerol mixtures using the Gd(NO3)3, a widely available and inexpensive Gd complex.129 All these studies provided rational criteria for the search of improved Gd(III) polarizing agents in the future. To date however, Gd(tpatcn) remains the best performing Gd(III) water-soluble complex for MAS DNP at 9.4 T due to its remarkably low ZFS value, in turn due to the symmetry and nature of its ligands.
5.2 Endogenous metal ions present or added into inorganic materials
Despite the relatively modest enhancement factors discussed in the previous section, the interest of metal ions as polarization sources remains their versatility. This section will discuss outstanding DNP results obtained with such PAs when used endogenously, i.e. as internal spies into bulk or nanostructured inorganic materials, whether they are intrinsically present or added via doping during synthesis. This allows for site specific and in situ investigations of multiple classes of functional materials, with notable applications in the field of energy storage. First, we mention a recent study by Hope and co-workers that very well illustrates the power of this endogenous approach. In this work, using conditions similar to the very first DNP experiment by Carver and Slichter,6 the authors exploited the OE from conduction electrons to produce 1H, 7Li and 19F enhancements at room temperature and intermediate fields of 9.4 to 14.1 T in a cycled lithium metal anode.130 Despite relatively low enhancement factors (of ∼10-fold), they managed to get specific and targeted local information, gaining invaluable insight into the structure of the solid-electrolyte interface formed in their system.Stepping back into the past, multiple transition metals have shown their ability to produce hyperpolarization from SE DNP in inorganic solids. Very early experiments feature cerium Ce(III) impurities in a trigonal lanthanum magnesium nitrate phase that produce sizeable proton hyperpolarization at a few Kelvins.131 Note here that the spin orbit coupling (SOC) is large for this ion, resulting in a broadening of the EPR line that makes DNP impractical at regular cryogenic temperatures. This illustrates the need to ideally have an isotropic and symmetric environment for the metal ion in the lattice in order to minimize the broadening and relaxation effects of SOC and zero field splitting (ZFS) on its central transition. Another relevant aspect of endogenous DNP emerging from this study is the need for only a small percentage of dopants to produce DNP, ca. 1%. The introduction of metal ions in a lattice, if they are not already present, is therefore not expected to perturb significantly the spatial arrangement of the material of interest but requires dedicated synthetic routes that can vary from one target to another.121 An example of the incorporation of ∼1% of paramagnetic chromium Cr(III) by substitution was reported by Corzilius and co-workers for octahedral sites of a molecular cobalt crystal.132 In this material, the Cr(III) ions are in a ground state with vanishing angular momentum, therefore do not have any SOC and only limited ZFS broadening. Interestingly, modest 1H but sizeable 13C and 59Co SE DNP enhancements could be obtained at 5 T and high doping ratios. A contribution of CE could be identified as the maxima of enhancements in the Zeeman field profiles did not fall exactly at the expected pure SE positions. This was attributed to the matching between the central transition of one Cr(III) center and the broader satellite transition of neighboring chromium metal ions, despite the large distance ranges of ca. 8 Å between dopants.
Over the recent years, the MAS DNP community has conducted several fruitful studies using endogenous metal ions dopants such as iron Fe(III), manganese Mn(II) and gadolinium Gd(III), led by the pioneering contribution of Leskes and co-workers in the context of NMR characterization of electrode and battery materials. Most of this work focuses on lithium titanium oxide (LTO) of generic formula Li4Ti5O12, where 6Li, 7Li and 17O are the nuclei of interest. Mn(II) and Gd(III) doped LTO were first examined in static conditions, where a 14-fold 7Li sensitivity boost was reported with 0.5% and 1% doping respectively, paving the way for significant sensitivity gains for nuclei with even lower gyromagnetic ratios.133 A series of anode materials were then investigated combining endogenous DNP from Mn(II) doping with MAS.134 Looking at the enhancements obtained on lithium resonances as a function of dopant concentration, the authors established that the previously mentioned compositions stand as optimum Mn(II) concentrations to hyperpolarize lithium in LTO, yielding 142 and 24-fold gains on 6Li and 7Li respectively (Fig. 10). The shape of the NMR spectra was shown to vary significantly with the Mn(II) ion concentration, with the appearance of a broad component and with significant quenching at the highest dopant contents in a 10 to 14 Å radius around the metal ions. This effect, while detrimental for sensitivity, can be exploited to highlight different lithium resonances as well as their spatial distribution. In parallel, the approach enables the detection of hyperpolarized 17O signals at natural abundance.
 | ||
| Fig. 10 Signal enhancement factors for (a) 7Li and (b) 6Li obtained at the optimal field position as a function of the Mn(II) concentration in LTO of formula of Li4Ti5O12. The insets show the μW on and off spectra for Mn concentration of 0.05 (7Li) and 0.025 (6Li). εabs corresponds to the absolute sensitivity enhancement factor taking into account the difference in longitudinal build-up times and contribution factor, as described in Section 2.3. Reproduced from ref. 134 with permission from American Chemical Society, copyright 2019. | ||
Leskes and co-workers later introduced Fe(III) as another dopant for endogenous DNP NMR of LTO.135 This doping was shown to be of particular relevance as the Fe(III) ions were not only included in a very symmetric spinel environment, producing large SE DNP enhancements (up to 180-fold on 6Li at 9.4 T), but were also electrochemically active in the cycling conditions of the electrode, therefore offering a way to monitor the activity of the material by following changes in the enhancement. This study also showed that Fe(III) was efficient at SE DNP over a wide range of dopant concentration, which led the authors to investigate the mechanistic behavior of polarization transfer. In a following paper and in the context of endogenous 17O DNP, they carefully derived theoretical expressions and conducted spin dynamics simulations assuming that the nuclear relaxation was dominated by the PRE effect induced by the added polarization source.136 Under this hypothesis, they showed that the distance dependence of the electron-nucleus dipolar coupling and the nuclear paramagnetic relaxation time cancel out, resulting in the ability to spread the same level of steady-state polarization across the sample regardless of the distance between the PA and the target. This mechanism allows efficient direct hyperpolarization of insensitive nuclei through the bulk of a doped material, broadening the scope of applications of endogenous metal ion PAs. A very recent paper by the same group shows that the nuclear relaxation parameters can be, in that context, related to the electronic relaxation time of the dopant, such as Mn(II) or Fe(III). Quenching and enhancement factor intensities vary as a function of dopant content and can be mapped by following the nuclear T1 and T2, which reflect the decrease in T1e with the increasing dipolar coupling between unpaired electron spins at higher concentrations.137
Similar approaches have been deployed for the study of different materials such as cathode coating layers.138 In this case, an approach combining endogenous Fe(III) doping and the exogenous introduction of AMUPol enabled to probe complementary information about both the bulk and the interface of active particles and to gain structural insights on the role and composition of their LixSiyOz coating layer. Metal-doped oxide glasses, such as lithium borates, lithium silicates or zinc phosphates, were also successfully characterized by Pruski and co-workers using either Mn(II) or Gd(III) dopants.139 Challenging 89Y–89Y correlations were also obtained in yttrium-doped ceria via endogenous gadolinium doping, which pave the way to atomic level understanding of ionic conductivity in solid electrolytes.140
Finally we note that Grey, Emsley and co-workers reported DNP NMR experiments of 17O-enriched ceria CeO2 doped with 0.01 to 1% of Gd(III) ions, which can be readily substituted to Ce(IV), with concomitant oxygen vacancies to balance the charge.14117O enhancement factors up 652-fold were reported at 9.4 T and 100 K for the lowest doping ratio. Interestingly very efficient hyperpolarization could still be achieved at elevated temperatures, with enhancement factors of 320-fold at room temperature and 150-fold at 370 K, establishing the feasibility of endogenous DNP at temperatures where materials are typically operational. The authors showed that Gd(III) doping allows the investigation of interfaces in vertically aligned nanocomposite (VAN) thin films, composed of gadolinium-doped 17O-enriched ceria nanopillars embedded in a strontium titanate SrTiO3 matrix, with the implementation of two-dimensional 17O correlation experiments, highlighting spin diffusion between ceria and the solid–solid interface.
5.3 DNP from other endogenous paramagnetic centers
Some of the first DNP MAS NMR experiments were performed in the 80s at low magnetic field (1.4 T) and slow spinning frequencies (∼3 kHz) on materials with endogenous unpaired electrons, such as coal naturally containing organic radicals, amorphous silicons with paramagnetic defects or diamond crystals containing nitrogen impurities.142–144 Such approaches were recently revisited for example in undoped crystalline silicon particles,145–147 where the unpaired electrons result from structural defects in amorphous regions nearby the surface of the materials or dangling bonds. Notably, using a commercial DNP apparatus operating at 9.4 T and cryogenic temperatures, Michaelis et al. reported enhancements of up to 6 for the 29Si resonance of the core of nanometric silicon particles using a direct polarization transfer from the unpaired electrons with polarization build-up time >4000 s and radical concentration lower than 1 mM.147 DNP enhanced 29Si and 13C cross-polarization experiments were also implemented from endogenous free radicals in carbonized mesoporous silicons.148 The potential of diamonds particles for MAS DNP NMR at high magnetic field (9.4 T) was also explored.149,150 In particular, Frydman and co-workers shown that carbon-13 resonances of micro and nanoparticles of diamonds could be enhanced in the solid-state at low and ambient temperatures from nitrogen defects, the signal boost decreasing with the size of the particles. For long microwave irradiation times (>1000 s), DNP MAS enhancements as high as 300 and 140 were reported for the largest diamond particles (1 μm) at respectively 100 K and room temperature.149 Such amplification factors were attributed to the extremely long electronic and nuclear spin-lattice relaxation times in diamond, opening perspectives to use these particles as a source of polarization to hyperpolarize other compounds.6 Mixed-valence compounds for OE DNP at high magnetic fields
Mixed-valence compounds contains moieties undergoing intramolecular charge transfers that lead to different oxidation states. In 2014, Griffin and co-workers demonstrated BDPA and its derivatives could provide efficient OE DNP in insulating solids.12 Enhancements of above 100 were reported for BDPA in the rigid OTP matrix at 18.8 T and 40 kHz spinning.116 While it was already established in the first studies that the presence of a pool of protons located on the fluorenyl moieties of BDPA with ca. 5 MHz fold hyperfine couplings to the free electron was essential to obtain a DNP effect,9 a recent study provided a fundamental understanding of the dynamics at play in BDPA, showing that this radical is a mixed-valence compound in which the electron spin density is jumping between two sites.14,151This process induces fast geometric changes in the bond length, leading to a fluctuation of the scalar hyperfine couplings at a rate of approximately 650 GHz, i.e. on the same order of magnitude as the electron Larmor frequencies at the high magnetic fields used in NMR (10–20 T range). A recent study by Griffin and co-workers has refined this understanding by applying selective deuteration schemes during the synthesis of BDPA and has identified the protons on the α and γ positions to be determining both the sign of the OE DNP enhancement and the polarization transfer mechanism to the matrix surrounding the radical.152 More recently Pylaeva and co-workers introduced new family of mixed-valence organic compounds, the tetra-arylbenzene-1-3-diamine and 1-4-diamine radicals (dubbed 1-3-amine and 1-4-amine) shown in Fig. 11. The authors reported OE DNP enhancements of 20 to 30 at 18.8 T and 8 kHz MAS using these PAs (with a favorable spinning frequency dependence), confirming the idea that the OE mechanism relies on fluctuations between two different valence structures, leading to the required modulation of the electron to nuclei couplings.
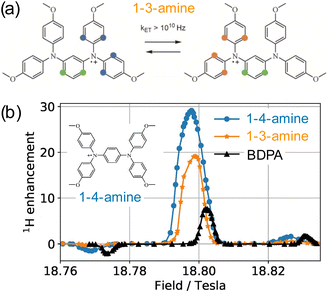 | ||
| Fig. 11 (a) Structure of the 1-3-amine mixed valence radical. The two inequivalent structures are shown where the electron spin density is fluctuating from one side to the other side of the molecule, modulating the hyperfine couplings to the nearest protons, highlighted in color. (b) Field profiles for the BDPA, 1-3-amine and 1-4-amine (structure shown in the inset) measured at 18.8 T and 100 K in TCE (MAS frequency 8 kHz) for a 15 mM radical concentration. Reproduced from ref. 13 with permission from Wiley-VCH GmbH, copyright 2021. | ||
7 Formulation strategies for DNP solid-state NMR across disciplines
Table 1 lists the DNP performance of the latest and most efficient rationally-designed PAs described in Sections 3 to 6. The enhancement values are reported in bulk frozen solutions. These values are usually lower when the radicals are formulated in a target substrate. In this section, experimental aspects regarding sample formulation are reviewed to make best use of the polarizing agents described above, in a broad panel of application fields.| Radical | DNP matrix | B 0 | ω r | ε ON,OFF | θ | T B,ON (s) | Ref. |
|---|---|---|---|---|---|---|---|
| a Here, the θ value corresponds only to the depolarization losses, i.e. signal attenuation due to paramagnetic bleaching was not considered. | |||||||
| AMUPol | 10 mM in d8-glycerol/D2O/H2O 60/30/10 (v/v/v) | 9.4 T | 10 kHz | 235 | n.d. | 3.5 | 71 |
| AMUPol | 10 mM in d8-glycerol/D2O/H2O 60/30/10 (v/v/v) | 9.4 T | 40 kHz | 290 | n.d. | 3.8 | 94 |
| AMUPol | 10 mM in d8-glycerol/D2O/H2O 60/30/10 (v/v/v) | 18.8 T | 40 kHz | 48 | 0.46 | 10 | 94 |
| AMUPol | 5 mM in d8-glycerol/D2O/H2O 60/30/10 (v/v/v) | 21.1 T | 12 kHz | 18 | 0.64 | 14.4 | 94 |
| HydrOpol | 5 mM d6-DMSO/D2O/H2O (60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10) v/v/v 10) v/v/v |
9.4 T | 12 kHz | 293 | 0.51 | 5.5 | 90 |
| TinyPol | 5 mM in d8-glycerol/D2O/H2O 60/30/10 (v/v/v) | 9.4 T | 40 kHz | 225 | n.d. | 11.2 | 94 |
| TinyPol | 5 mM in d8-glycerol/D2O/H2O 60/30/10 (v/v/v) | 18.8 T | 40 kHz | 73 | 0.73 | 15.5 | 94 |
| TinyPol | 5 mM in d8-glycerol/D2O/H2O 60/30/10 (v/v/v) | 21.1 T | 12 kHz | 29 | 0.59 | 13.3 | 94 |
| AsymPol-POK | 10 mM in d8 – d8-glycerol/D2O/H2O 60/30/10 (v/v/v) with 20 mM 13C-urea | 9.4 T | 10 kHz | 105 | 0.79a | 3.5 | 96 |
| AsymPol-POK | 10 mM in d8 – d8-glycerol/D2O/H2O 60/30/10 (v/v/v) with 20 mM 13C-urea | 18.8 T | 8 kHz | 27 | 0.89a | 5.8 | 96 |
| cAsymPol-POK | 10 mM in d8 – d8-glycerol/D2O/H2O 60/30/10 (v/v/v) | 9.4 T | 40 kHz | 140 | n.d. | 2.5 | 97 |
| cAsymPol-POK | 10 mM in d8 – d8-glycerol/D2O/H2O 60/30/10 (v/v/v) | 14.4 T | 8 kHz | 110 | 0.78a | 1.9 | 97 |
| cAsymPol-POK | 10 mM in d8 – d8-glycerol/D2O/H2O 60/30/10 (v/v/v) | 18.8 T | 40 kHz | 50 | n.d. | 3.6 | 97 |
| TEMTripol-1 | 10 mM in d8-glycerol/D2O/H2O 60/30/10 (v/v/v) | 18.8 T | 8 kHz | 65 | 0.84 | 3.7 | 103 |
| NATriPol-3 | 10 mM in d8-glycerol/D2O/H2O 60/30/10 (v/v/v) | 18.8 T | 8 kHz | 70 | 0.85 | 4.8 | 104 |
| SNAPol-1 | 10 mM in d8-glycerol/D2O/H2O 60/30/10 (v/v/v) | 18.8 T | 8 kHz | 133 | 0.87 | 4.2 | 104 |
| TEKPol | 16 mM in TCE | 9.4 T | 8 kHz | 205 | 0.65 | 3 | 75 |
| TEKPol | 16 mM in TCE | 18.8 T | 40 kHz | 13 | 0.71 | 4.5 | 113 |
| HyTEK2 | 32 mM in TCE | 9.4 T | 40 kHz | 143 | n.d. | 1.6 | 113 |
| HyTEK2 | 32 mM in TCE | 18.8 T | 40 kHz | 185 | 0.70 | 3.3 | 113 |
| BDPA | 60 mM in 95% d14-OTP, OE | 18.8 T | 40 kHz | 105 | 1.0 | 45 | 116 |
| BDPA | 15 mM in TCE | 18.8 T | 8 kHz | 8 | n.d. | n.d. | 13 |
| 1-4-Amine | 15 mM in TCE | 18.8 T | 8 kHz | 30 | n.d. | 44 | 13 |
| Gd(tpatcn) | 5 mM in d8-glycerol/D2O/H2O 60/30/10 (v/v/v) | 9.4 T | 8 kHz | 35 | 0.38 | 8.6 | 127 |
7.1 Formulation protocols for materials and molecular solids
As most materials or molecular solids do not inherently contain unpaired electrons (except, for example, for those mentioned in the previous section in the context of endogenous DNP with metal ions), the usual DNP formulation consists in impregnating them with an aqueous or organic solution containing typically 5 to 20 mM of radicals that forms a glassy matrix at 100 K. The quality of the glass is essential to ensure an even distribution of the radicals (the PA being excluded from crystalline domains) and heavily influences the efficiency of the DNP process. For aqueous formulations, water/DMSO or water/glycerol mixtures have been identified as yielding good glassy matrices in DNP conditions. The most commonly found composition is the so-called “DNP juice”, a mixture consisting of 60% of d8-glycerol, 30% of D2O and 10% of H2O. It has been optimized empirically since the early days of MAS DNP and seems to provide a good compromise in terms of solubility of the PAs, glass quality and proton density for spin diffusion.153 Its composition is regularly challenged but remains one of the most efficient to date, as pointed out in ref. 154. A screening of multiple organic solvents has enabled to identify 1,1,2,2-tetrachloroethane (TCE), 1,2-dichloroethane and 1,2-dichlorobenzene as organic solvents of choice for materials with hydrophobic or water-sensitive surfaces.155 The polarizing solution typically wets the surfaces of particulate solids, while penetrating by capillary action inside porous materials. This versatile strategy allows the selective signal amplification (by one or two orders of magnitude) of surfaces in functional materials, an approach dubbed DNP SENS (surface enhanced NMR spectroscopy)156 and has found many applications on materials as diverse as heterogeneous catalysts, functionalized metal–organic frameworks, zeolites, polymer thin films, ligand-capped nanoparticles, biominerals, etc.157,158 Interestingly, an additional 2-fold DNP enhancement was reported in frozen solutions containing dielectric particles such as sapphire, KBr, and PTFE, enabling to reach εH > 500 at 100 K and 9.4 T, an effect later exploited to obtain high-sensitivity 31P NMR spectra from as little as 160 picomoles of DNA deposited onto sapphire wafers.159Thereafter, numerous efforts have been made to adapt the DNP sample formulation to highly reactive surfaces that lead to the degradation/reduction of the PA, and/or to a modification of the properties of the material (e.g. catalyst deactivation upon coordination of the free exogeneous radical). Approaches have been notably proposed to prevent a close approach of the paramagnetic dopant to the materials surfaces that are summarized schematically in Fig. 12a–d. Carbosilane dendrimeric structures that encapsulate binitroxides were first proposed to restore sizable enhancements on highly reactive catalysts (a).160 It has been later shown that reactive surface species could be characterized by DNP if they were immobilized inside a porous support with suitably small pores that hinder the penetration of bulky radicals (b).161 It was also shown that detrimental interactions with the paramagnetic dopant could be reduced by tuning the surface hydrophobicity of nanoparticles, so as to promote their aggregation in the polarizing solution (c) and prevent the PAs from diffusing between particles and reach surface functional groups.162 Finally, the adsorption of probe molecules such as pyridine prior to impregnation can be employed to prevent a close proximity between radicals and reactive acid sites (d).163 In parallel, dedicated strategies were deployed for DNP NMR of colloidal quantum dots, avoiding their aggregation at cryogenic temperatures (Fig. 12e–g). Significant enhancement factors were thus reported by homogeneously dispersing the PAs and the nanoparticles into mesoporous silica (e).164 More recently, DNP enhancements could be improved by dispersing the particles onto hexagonal boron nitride (h-BN), a support with favorable dielectric properties (f).165 In an alternative approach, the nanoparticles can be precipitated as powders and mixed with h-BN, before impregnation with radical solution, which leads to further 4-fold sensitivity enhancements (g).165 Aqueous acrylamide gels were also proposed as efficient DNP media.166 The enhancements were shown to increase with cross-linker concentration and, at low concentrations of the AMUPol biradical, ε of around 200 were obtained in pure water at 9.4 T and 100 K. This formulation was also successfully used to enhance the surface signal of quantum dots.
 | ||
| Fig. 12 (a–d) Schematic views of strategies implemented for DNP SENS on reactive surfaces, in non-porous (a, c and d) or porous (b) materials. (a) The reactive surfaces are represented as grey balls while the orange spheres represent the radical (e–g) general schemes of sample preparation methods for DNP SENS on nanoparticles and quantum dots. (e) The particles (in yellow) are dispersed inside the mesopores of silica or (f) on hexagonal boron nitride (h-BN). (g) A powdered mixture of the particles and the h-BN support is impregnated with the radical solution, which increases the concentration of NPs in the formulated sample. (e–g) Adapted with permission from ref. 165. The sample preparation schemes (a–g) are not drawn to scale. | ||
Depending on the composition of the substrate, the huge polarization generated at surfaces from the hyperpolarized solvent molecules may be transported by 1H–1H spin diffusion167 or by spin diffusion between low-gamma nuclei.168 The former effect is exploited to polarize the inner core of porous materials such as zeolites169 or metal organic frameworks170 in which the PA does not enter (or only partially), but where the protons relay the hyperpolarization, or microcrystalline organic solids,167 pharmaceutical tablets,171 cellulose fibrils,172etc. The latter effect can be used to polarize proton-free substrates.
7.2 Formulation protocols for DNP MAS NMR biomolecules and cells
Water soluble radicals and aqueous matrices are most relevant to biological systems. Similar to small molecules and materials (Section 7.1), DNP experiments on biological systems can be carried out in a frozen solution of 5 to 20 mM biradical in DNP juice. However, alternatives to reduce the solvent amount and fraction of cryoprotectant, therefore maximizing the signal per rotor volume and avoiding interference of the cryoprotectant with the sample integrity, have been developed. One possible way to prepare biomolecular DNP samples is to impregnate a pelleted protein with a stock radical solution followed by soaking and removal of the supernatant, prior to rotor packing. In the so-called matrix-free approach the solvent can be removed almost completely by further drying of the sample. Sedimentation is an alternative way where the solution of the biomolecule, also containing the radical, is ultracentrifuged into the MAS rotor. Strategies to prepare various biological samples, including membrane proteins, for DNP have been detailed in ref. 173 and aspects of bio-DNP sample preparation have also been discussed in two recent reviews.174,175The fact that DNP is carried out at cryogenic temperatures, a temperature at which cells can be frozen and preserved makes DNP a suitable technique for in-cell NMR.176 The first attempts to detect specific biomolecules or drugs in mammalian cells used DNP juice177 or a variation where glycerol was replaced with DMSO.178,179 Cryoprotectants are crucial to avoid water crystallization and keep the cells intact and viable as is the case for any standard cell freezing medium. Frederick's and Barnes' groups have recently demonstrated that mammalian cells formulated with 10% DMSO-d6 or 15% glycerol-d8, i.e. with a lower concentration of cryoprotectant, displayed good DNP performances and increased viability after the DNP measurements.180,181 While DNP samples are usually flash frozen by inserting the NMR rotor directly into the cold stator of the probe, a slow-freeze protocol outside the magnet, consisting in cooling the sample at a rate of 1 °C min−1 prior to the transfer to the sample catcher, was proposed in order to keep cell membranes intact and further improve post-DNP viability.182 It should be noted that while this procedure is ideal from a cell-biological perspective, metabolic or structural changes which occur during such a slow reduction of temperature might justify flash freezing the sample from a physical-chemistry perspective for some applications, despite losing the possibility to revive the cells after the measurement. The easiest approach to add the radical is using incubation, i.e. resuspending the pelleted cells in a radical solution for example composed of 10 mM AMUPol in 15% (v/v) d8-glycerol, 75% (v/v) D2O and 10% (v/v) H2O (perdeuterated PBS). The Baldus group, using confocal microscopy, showed that the radical PyPOL-TMR, a variant of AMUPol, is well distributed in both nuclear and cytoplasmic compartments of the cell following the incubation method.177 More recently Ghosh et al. showed, based on differences in enhancements for certain 13C chemical shift regions, that it is necessary to electroporate AMUPol in the cells in order to achieve a homogenous distribution of the radical throughout the cell.181 They also highlighted that care has to be taken to monitor the time between radical delivery and sample freezing as the reductive environment of the cell inactivates AMUPol. Metal ions that are resistant to reducing conditions were suggested as suitable PAs for DNP NMR of cells,128 but to our best knowledge they were never evaluated in such a context. Very recently, Debelouchina and co-workers investigated the stability of various binitroxides in cellular environment, including a new structure based on five-membered pyrrolidine rings that displays improved resistance towards reduction in cellular media.183
7.3 Polarizing matrices of high glass transition temperature
As discussed in the first section, sufficiently long electron relaxation times are critical to ensure an adequate saturation of the EPR line and in turn an effective polarization transfer by DNP. Exogenous organic radicals typically feature short relaxation times, of the order of tens or hundreds of microseconds in frozen samples at temperature ca. 100 K. Hence, continuous wave DNP MAS NMR experiments are usually carried out around 100 K or lower, so as to lengthen T1e and T2e. These cryogenic temperatures also ensure that the glassy matrix is sufficiently rigid and that the network of dipolar-coupled protons efficiently distributes the enhanced polarization by spin diffusion. In practice, hardly any DNP amplification is observed above 200 K for organic PAs in conventional polarizing matrices, such as glycerol/water mixtures or TCE due to the softening of such matrices. This paragraph briefly reviews a few formulation strategies to produce sizeable enhancement factors using DNP in solids at temperatures close to ambient. First, we note that a series of approaches, referred to as “optical DNP”, that generate electron hyperpolarization upon irradiation with a monochromatic laser, exploiting either negatively charged nitrogen vacancies in diamonds184 or photo-excited triplet states in conjugated molecules, such as pentacene and derivatives,185,186 were shown to produce DNP at room temperature. Similarly, sizeable enhancements were reported over a broad temperature range, including room temperature, by pulsed DNP (or time-domain DNP) techniques, where the microwaves are applied as phase-modulated pulses.33 However, these powerful approaches that undoubtedly represent promising alternatives to continuous-wave DNP currently remain limited to low fields and require specific instrumentation.Exploiting endogenous radicals (of narrow EPR line) generated in situ by γ-ray irradiation is a first promising approach for high temperature continuous-wave DNP, which has been demonstrated by Rossini and co-workers in 2019 on a series of inorganic and organic solids.187 Thus, a 29Si enhancement of 400 was reported on γ-irradiated fused quartz at cryogenic temperatures and 9.4 T, with a recycle delay of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 s. As long electron T1e are preserved at high temperature, the authors demonstrated that DNP remained effective at 298 K with a 150-fold enhancement. They also reported an 8-fold 13C enhancement at room temperature on a molecular solid of maleic acid irradiated with γ-rays at 298 K.188 Here, we mention again the work by Grey and co-workers who exploited the conduction electrons of lithium metal to achieve a 10-fold enhancement in lithium metal anode at room temperature130 and who also reported ε > 100 at 370 K in Gd-doped oxides featuring sharp EPR spectra.141
000 s. As long electron T1e are preserved at high temperature, the authors demonstrated that DNP remained effective at 298 K with a 150-fold enhancement. They also reported an 8-fold 13C enhancement at room temperature on a molecular solid of maleic acid irradiated with γ-rays at 298 K.188 Here, we mention again the work by Grey and co-workers who exploited the conduction electrons of lithium metal to achieve a 10-fold enhancement in lithium metal anode at room temperature130 and who also reported ε > 100 at 370 K in Gd-doped oxides featuring sharp EPR spectra.141
Aside from the PA, the matrix itself can be chosen and tuned to facilitate DNP at elevated temperature. The rigidity of the glassy polarizing matrix was shown to play a major role in preserving high DNP enhancements at high temperatures since the early days of modern MAS DNP. Griffin and co-workers demonstrated a sizeable 10-fold DNP SE enhancement on protons at room temperature and 5 T using BDPA dissolved in polystyrene.53 Since then, several media, suitable for DNP at non-cryogenic temperatures, were screened. ortho-Terphenyl (OTP) was shown to be an appropriate rigid DNP matrix for experiments at elevated temperatures as it forms a stable glassy amorphous phase up to its glass transition temperature (Tg), i.e. 243 K. Thus, a 80-fold enhancement was reported for TEKPol in OTP at 9.4 T, just below the Tg of the matrix by Lelli et al., while enhancement factors from 10 to 20 were preserved near room temperature.189 Similar performances were also reported with BDPA,189 and more recently with HyTEK2 in the OTP matrix,190 for which an enhancements of ∼65 was obtained at 230 K. Above this temperature, a sizeable fall of the enhancement was observed, ascribed to the reduction of the more efficient electron relaxation, and in particular to the drastic jump of the two phase memory times at Tg. More recently, trehalose (Tg = 379 K) jointly with a biradical tailored for a facilitated dispersion into the rigid sugar matrix was used for DNP at elevated temperatures.191 A smooth decay of the 13C enhancements monitored on the resonances of casein embedded in trehalose was reported as a function of temperature. A 10-fold enhancement was maintained at 230 K, a temperature where conventional formulations fail. Overall, these results highlight the major contribution of the polarizing matrix that must preserve long electron relaxation times for effective DNP at non cryogenic temperatures.
7.4 Polarizing solids
Several types of solid supports functionalized with nitroxide radicals have been proposed as polarizing matrices for DNP MAS NMR. A series of hybrid mesoporous silica materials containing covalently bonded radicals were first introduced that efficiently polarize impregnated frozen solutions and analytes. In 2013, Thieuleux and co-workers reported enhancements as high as ∼35 at 100 K and 9.4 T from mesostructured silica matrices featuring a two-dimensional hexagonal arrangement of the porous network (analogous to SBA-15 materials), which were post-grafted with mono- or biradicals.192 The homogeneous distribution as well as the concentration of the PAs were shown to be key determinants in the DNP efficiency. Tailor-made polarizing solids were then developed by improving the nanostructuration of the silica matrix, with the introduction of functionalized three-dimensional cubic networks with interconnected pores (analogous to SBA-16 materials)193 or by tuning the linker attaching the PAs to the silica surface.194 Materials that incorporate the nitroxide radicals within the walls of the silica were also proposed to minimize interactions between the electron sources and the analyte.195–197 While the potential of these polarizing matrices has been successfully exploited for dissolution DNP, their interest in DNP MAS NMR has so far remained limited. It is noteworthy however that mesoporous SBA-15 silica materials with wall-embedded TEMPO radicals were used as a polarizing platform to monitor by crystallization processes in confined media by DNP enhanced solid-state NMR.198 In parallel, substantial DNP enhancements were achieved from covalent organic frameworks containing rigidly attached and evenly distributed proxyl radicals, suggesting that these materials could be used as polarizing “crystalline sponges”.1998 Conclusion
Twenty years of developments have led to the introduction of more and more efficient PAs, as well as, equally important, to the elaboration of fundamental principles for the rational design of these polarization sources. These efforts were largely driven by the need for PAs suitable for solid-state DNP at high magnetic fields. The first experiments carried out with bis-TEMPO radicals, back to the early 2000s, reported proton enhancements values at 90 K of ∼175 at 211 MHz and 3.5 kHz MAS. Today, εH of up to 300 can be reached at 400 MHz in a 10–40 kHz frequency range using binitroxides of tailor-designed geometries (from the length of the linker, its rigidity or its conjugation to the structure and functionalization of the NO rings or the local geometry around the unpaired electrons). Hybrid biradicals in which a nitroxide is covalently linked to a trityl or a BDPA moiety have emerged as extremely efficient PAs for very high field solid-state DNP, with proton enhancement factors between 100 and 200 at 800 and 900 MHz for the most optimized structures, and little depolarization losses at fast MAS. New generations of binitroxides were also introduced that offer decent performances at these high magnetic fields. While PAs with metal ions still yield modest enhancement factors (εH ∼ 30–40 at 400 MHz), the DNP performance of G(III) complexes could be significantly improved by tuning the ligands around the metal center. In parallel, the use of metal ions as endogenous polarization source has become a highly valuable approach, providing drastic signal amplifications in doped materials or metallic substrates. These advances have been done jointly with the introduction of new polarizing matrices, from rigid glassy solutions to gels, sugars or functionalized solids, as well of dedicated formulation strategies for different application fields.Overall, these developments have led to a better understanding of the basic principles that govern the efficiency of PAs. Thus, over the years, the determinant role of the electron dipolar and spin exchange interactions, the electronic relaxation times, the width and shape of the EPR line in the polarization (and depolarization) mechanisms, the solvent accessibility or the zero-field splitting were highlighted, in relation with the chemical structure and dynamics of the polarizing agent as well as the composition of the matrix and its glass transition. This progress has been achieved at the cost of significant experimental efforts. Numerical approaches modelling the spin dynamics have also been essential.
The ideal PA for CE DNP that would consist of two chemically-tethered narrow EPR line radicals does not exist yet. The use of metal ions as polarizing sources for SE DNP is still at its early stages. The introduction of novel mixed valence compounds opens new perspectives for OE DNP at high fields. Future studies should keep searching for diversified polarizing sources, aiming at further deciphering how these polarizing agents can be refined for an optimum efficiency in specific application areas.
Author contributions
Conceptualization: GM, AL and DG; writing – original draft: GM, JS, GC, OO, DG and AL; writing – review and editing: DG, OO and AL.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Financial support from the ANR grant ANR-22-CE09-0017 and from the PANACEA project from the European Union's Horizon 2020 research and innovation program under Grant Agreement 101008500 is acknowledged. The authors are very grateful to Moreno Lelli, Lyndon Emsley, Christophe Copéret, Brad Chmelka, Maxim Yulikov, Gunnar Jeschke, Gabriele Stevanato, Ganesan Karthikeyan, Dorothea Wisser, Alicia Lund, Amrit Venkatesh, Aaron Rossini, Arthur Pinon, Lorenzo Niccoli, Bob Griffin and their collaborators for fruitful collaborations and discussions.References
- J. Eills, D. Budker, S. Cavagnero, E. Y. Chekmenev, S. J. Elliott, S. Jannin, A. Lesage, J. Matysik, T. Meersmann, T. Prisner, J. A. Reimer, H. Yang and I. V. Koptyug, Chem. Rev., 2023, 123, 1417–1551 CrossRef CAS PubMed.
- D. A. Hall, D. C. Maus, G. J. Gerfen, S. J. Inati, L. R. Becerra, F. W. Dahlquist and R. G. Griffin, Science, 1997, 276, 930–932 CrossRef CAS PubMed.
- K.-N. Hu, Solid State Nucl. Magn. Reson., 2011, 40, 31–41 CrossRef CAS PubMed.
- G. Casano, H. Karoui and O. Ouari, eMagRes, 2018, 195–208 CAS.
- A. W. Overhauser, Phys. Rev., 1953, 92, 411–415 CrossRef CAS.
- T. R. Carver and C. P. Slichter, Phys. Rev., 1953, 92, 212–213 CrossRef CAS.
- C. P. Slichter, Phys. Chem. Chem. Phys., 2010, 12, 5741–5751 RSC.
- K.-N. Hu, G. T. Debelouchina, A. A. Smith and R. G. Griffin, J. Chem. Phys., 2011, 134, 125105 CrossRef PubMed.
- T. V. Can, Q. Z. Ni and R. G. Griffin, J. Magn. Reson., 2015, 253, 23–35 CrossRef CAS PubMed.
- A. S. L. Thankamony, J. J. Wittmann, M. Kaushik and B. Corzilius, Prog. Nucl. Magn. Reson. Spectrosc., 2017, 102–103, 120–195 CrossRef PubMed.
- B. Corzilius, Annu. Rev. Phys. Chem., 2020, 71, 143–170 CrossRef CAS PubMed.
- T. V. Can, M. A. Caporini, F. Mentink-Vigier, B. Corzilius, J. J. Walish, M. Rosay, W. E. Maas, M. Baldus, S. Vega, T. M. Swager and R. G. Griffin, J. Chem. Phys., 2014, 141, 064202 CrossRef CAS PubMed.
- A. Gurinov, B. Sieland, A. Kuzhelev, H. Elgabarty, T. D. Kühne, T. Prisner, J. Paradies, M. Baldus, K. L. Ivanov and S. Pylaeva, Angew. Chem., Int. Ed., 2021, 60, 15371–15375 CrossRef CAS PubMed.
- S. Pylaeva, P. Marx, G. Singh, T. D. Kuhne, M. Roemelt and H. Elgabarty, J. Phys. Chem. A, 2021, 125, 867–874 CrossRef CAS PubMed.
- A. Abragam and W. G. Proctor, C. R. Hebd. Seances Acad. Sci., 1958, 246, 2253–2256 CAS.
- Y. Hovav, A. Feintuch and S. Vega, J. Magn. Reson., 2010, 207, 176–189 CrossRef CAS PubMed.
- B. Corzilius, A. A. Smith and R. G. Griffin, J. Chem. Phys., 2012, 137, 054201 CrossRef PubMed.
- A. A. Smith, B. Corzilius, A. B. Barnes, T. Maly and R. G. Griffin, J. Chem. Phys., 2012, 136, 015101 CrossRef PubMed.
- A. V. Kessenikh and A. A. Manenkov, Phys. Solid State, 1963, 5, 835–837 Search PubMed.
- C. F. Hwang and D. A. Hill, Phys. Rev. Lett., 1967, 19, 1011–1014 CrossRef CAS.
- Y. Hovav, A. Feintuch and S. Vega, J. Magn. Reson., 2012, 214, 29–41 CrossRef CAS PubMed.
- B. Corzilius, Phys. Chem. Chem. Phys., 2016, 18, 27190–27204 RSC.
- K. R. Thurber and R. Tycko, J. Chem. Phys., 2012, 137, 084508 CrossRef PubMed.
- F. Mentink-Vigier, Ü. Akbey, Y. Hovav, S. Vega, H. Oschkinat and A. Feintuch, J. Magn. Reson., 2012, 224, 13–21 CrossRef CAS PubMed.
- K. R. Thurber and R. Tycko, J. Chem. Phys., 2014, 140, 184201 CrossRef PubMed.
- F. Mentink-Vigier, U. Akbey, H. Oschkinat, S. Vega and A. Feintuch, J. Magn. Reson., 2015, 258, 102–120 CrossRef CAS PubMed.
- D. Mance, P. Gast, M. Huber, M. Baldus and K. L. Ivanov, J. Chem. Phys., 2015, 142, 234201 CrossRef PubMed.
- M. Rosay, M. Blank and F. Engelke, J. Magn. Reson., 2016, 264, 88–98 CrossRef CAS PubMed.
- E. P. Saliba, E. L. Sesti, F. J. Scott, B. J. Albert, E. J. Choi, N. Alaniva, C. Gao and A. B. Barnes, J. Am. Chem. Soc., 2017, 139, 6310–6313 CrossRef CAS PubMed.
- T. V. Can, R. T. Weber, J. J. Walish, T. M. Swager and R. G. Griffin, Angew. Chem., Int. Ed., 2017, 56, 6744–6748 CrossRef CAS PubMed.
- F. J. Scott, E. P. Saliba, B. J. Albert, N. Alaniva, E. L. Sesti, C. Gao, N. C. Golota, E. J. Choi, A. P. Jagtap, J. J. Wittmann, M. Eckardt, W. Harneit, B. Corzilius, S. T. Sigurdsson and A. B. Barnes, J. Magn. Reson., 2018, 289, 45–54 CrossRef CAS PubMed.
- P. T. Judge, E. L. Sesti, N. Alaniva, E. P. Saliba, L. E. Price, C. K. Gao, T. Halbritter, S. T. Sigurdsson, G. B. Kyei and A. B. Barnes, J. Magn. Reson., 2020, 313, 106702 CrossRef CAS PubMed.
- T. V. Can, J. J. Walish, T. M. Swager and R. G. Griffin, J. Chem. Phys., 2015, 143, 054201 CrossRef CAS PubMed.
- G. Mathies, S. Jain, M. Reese and R. G. Griffin, J. Phys. Chem. Lett., 2016, 7, 111–116 CrossRef CAS PubMed.
- S. K. Jain, G. Mathies and R. G. Griffin, J. Chem. Phys., 2017, 147, 164201 CrossRef PubMed.
- K. O. Tan, C. Yang, R. T. Weber, G. Mathies and R. G. Griffin, Sci. Adv., 2019, 5, eaax2743 CrossRef CAS PubMed.
- T. V. Can, K. O. Tan, C. Yang, R. T. Weber and R. G. Griffin, J. Magn. Reson., 2021, 329, 107012 CrossRef CAS PubMed.
- V. S. Redrouthu and G. Mathies, J. Am. Chem. Soc., 2022, 144, 1513–1516 CrossRef CAS PubMed.
- J. H. Ardenkjaer-Larsen, Emagres, 2018, 7, 63–77 CAS.
- D. Kurzbach and S. Jannin, Emagres, 2018, 7, 117–131 CAS.
- W. T. Wenckebach, J. Magn. Reson., 2017, 277, 68–78 CrossRef CAS PubMed.
- B. Corzilius, L. B. Andreas, A. A. Smith, Q. Z. Ni and R. G. Griffin, J. Magn. Reson., 2014, 240, 113–123 CrossRef CAS PubMed.
- F. Mentink-Vigier, S. Paul, D. Lee, A. Feintuch, S. Hediger, S. Vega and G. De Paëpe, Phys. Chem. Chem. Phys., 2015, 17, 21824–21836 RSC.
- A. J. Rossini, A. Zagdoun, M. Lelli, D. Gajan, F. Rascon, M. Rosay, W. E. Maas, C. Coperet, A. Lesage and L. Emsley, Chem. Sci., 2012, 3, 108–115 RSC.
- A. B. Barnes, B. Corzilius, M. L. Mak-Jurkauskas, L. B. Andreas, V. S. Bajaj, Y. Matsuki, M. L. Belenky, J. Lugtenburg, J. R. Sirigiri, R. J. Temkin, J. Herzfeld and R. G. Griffin, Phys. Chem. Chem. Phys., 2010, 12, 5861–5867 RSC.
- S. Hediger, D. Lee, F. Mentink-Vigier and G. De Paëpe, MAS-DNP Enhancements: Hyperpolarization, Depolarization, and Absolute Sensitivity, in eMagRes, John Wiley & Sons, Ltd, 2018, pp. 105–116 Search PubMed.
- A. Abragam and M. Goldman, Rep. Prog. Phys., 1978, 41, 395 CrossRef CAS.
- K. O. Tan, M. Mardini, C. Yang, J. H. Ardenkjær-Larsen and R. G. Griffin, Sci. Adv., 2019, 5, eaax2743 CrossRef CAS PubMed.
- A. C. Pinon, J. Schlagnitweit, P. Berruyer, A. J. Rossini, M. Lelli, E. Socie, M. Tang, T. Pham, A. Lesage, S. Schantz and L. Emsley, J. Phys. Chem. C, 2017, 121, 15993–16005 CrossRef CAS.
- N. A. Prisco, A. C. Pinon, L. Emsley and B. F. Chmelka, Phys. Chem. Chem. Phys., 2021, 23, 1006–1020 RSC.
- F. A. Perras and M. Pruski, J. Chem. Phys., 2018, 149, 154202 CrossRef PubMed.
- F. A. Perras, M. Raju, S. L. Carnahan, D. Akbarian, A. C. T. van Duin, A. J. Rossini and M. Pruski, J. Phys. Chem. Lett., 2020, 11, 5655–5660 CrossRef CAS PubMed.
- L. R. Becerra, G. J. Gerfen, R. J. Temkin, D. J. Singel and R. G. Griffin, Phys. Rev. Lett., 1993, 71, 3561–3564 CrossRef CAS PubMed.
- M. Rosay, V. Weis, K. E. Kreischer, R. J. Temkin and R. G. Griffin, J. Am. Chem. Soc., 2002, 124, 3214–3215 CrossRef CAS PubMed.
- K.-N. Hu, H.-h. Yu, T. M. Swager and R. G. Griffin, J. Am. Chem. Soc., 2004, 126, 10844–10845 CrossRef CAS PubMed.
- C. Song, K.-N. Hu, C.-G. Joo, T. M. Swager and R. G. Griffin, J. Am. Chem. Soc., 2006, 128, 11385–11390 CrossRef CAS PubMed.
- K. R. Thurber, W.-M. Yau and R. Tycko, J. Magn. Reson., 2010, 204, 303–313 CrossRef CAS PubMed.
- W.-M. Yau, K. R. Thurber and R. Tycko, J. Magn. Reson., 2014, 244, 98–106 CrossRef CAS PubMed.
- K. N. Hu, C. Song, H. H. Yu, T. M. Swager and R. G. Griffin, J. Chem. Phys., 2008, 128, 052302 CrossRef PubMed.
- Y. Matsuki, T. Maly, O. Ouari, H. Karoui, F. Le Moigne, E. Rizzato, S. Lyubenova, J. Herzfeld, T. Prisner, P. Tordo and R. G. Griffin, Angew. Chem., Int. Ed., 2009, 48, 4996–5000 CrossRef CAS PubMed.
- C. Ysacco, E. Rizzato, M. A. Virolleaud, H. Karoui, A. Rockenbauer, F. Le Moigne, D. Siri, O. Ouari, R. G. Griffin and P. Tordo, Phys. Chem. Chem. Phys., 2010, 12, 5841–5845 RSC.
- C. Ysacco, H. Karoui, G. Casano, F. Le Moigne, S. Combes, A. Rockenbauer, M. Rosay, W. Maas, O. Ouari and P. Tordo, Appl. Magn. Reson., 2012, 43, 251–261 CrossRef CAS.
- F. A. Perras, A. Sadow and M. Pruski, ChemPhysChem, 2017, 18, 2279–2287 CrossRef CAS PubMed.
- F. Mentink-Vigier, Phys. Chem. Chem. Phys., 2020, 22, 3643–3652 RSC.
- C. Ysacco, E. Rizzato, M.-A. Virolleaud, H. Karoui, A. Rockenbauer, F. Le Moigne, D. Siri, O. Ouari, R. G. Griffin and P. Tordo, Phys. Chem. Chem. Phys., 2010, 12, 5841–5845 RSC.
- H. Sato, V. Kathirvelu, A. Fielding, J. P. Blinco, A. S. Micallef, S. E. Bottle, S. S. Eaton and G. R. Eaton, Mol. Phys., 2007, 105, 2137–2151 CrossRef CAS.
- V. Kathirvelu, C. Smith, C. Parks, M. A. Mannan, Y. Miura, K. Takeshita, S. S. Eaton and G. R. Eaton, Chem. Commun., 2009, 454–456 RSC.
- A. J. Rossini, A. Zagdoun, M. Lelli, D. Gajan, F. Rascón, M. Rosay, W. E. Maas, C. Copéret, A. Lesage and L. Emsley, Chem. Sci., 2012, 3, 108–115 RSC.
- C. Ysacco, H. Karoui, G. Casano, F. Le Moigne, S. Combes, A. Rockenbauer, M. Rosay, W. Maas, O. Ouari and P. Tordo, Appl. Magn. Reson., 2012, 43, 251–261 CrossRef CAS.
- A. Zagdoun, G. Casano, O. Ouari, M. Schwarzwälder, A. J. Rossini, F. Aussenac, M. Yulikov, G. Jeschke, C. Copéret, A. Lesage, P. Tordo and L. Emsley, J. Am. Chem. Soc., 2013, 135, 12790–12797 CrossRef CAS PubMed.
- C. Sauvée, M. Rosay, G. Casano, F. Aussenac, R. T. Weber, O. Ouari and P. Tordo, Angew. Chem., Int. Ed., 2013, 52, 10858–10861 CrossRef PubMed.
- D. J. Kubicki, A. J. Rossini, A. Purea, A. Zagdoun, O. Ouari, P. Tordo, F. Engelke, A. Lesage and L. Emsley, J. Am. Chem. Soc., 2014, 136, 15711–15718 CrossRef CAS PubMed.
- S. Bothe, M. M. Hoffmann, T. Gutmann and G. Buntkowsky, J. Phys. Chem. C, 2017, 121, 27089–27097 CrossRef CAS.
- F. Mentink-Vigier, A.-L. Barra, J. van Tol, S. Hediger, D. Lee and G. De Paëpe, Phys. Chem. Chem. Phys., 2019, 21, 2166–2176 RSC.
- D. J. Kubicki, G. Casano, M. Schwarzwälder, S. Abel, C. Sauvée, K. Ganesan, M. Yulikov, A. J. Rossini, G. Jeschke, C. Copéret, A. Lesage, P. Tordo, O. Ouari and L. Emsley, Chem. Sci., 2016, 7, 550–558 RSC.
- C. Sauvée, G. Casano, S. Abel, A. Rockenbauer, D. Akhmetzyanov, H. Karoui, D. Siri, F. Aussenac, W. Maas, R. T. Weber, T. Prisner, M. Rosay, P. Tordo and O. Ouari, Chem.–Eur. J., 2016, 22, 5598–5606 CrossRef PubMed.
- A. P. Jagtap, M.-A. Geiger, D. Stöppler, M. Orwick-Rydmark, H. Oschkinat and S. T. Sigurdsson, Chem. Commun., 2016, 52, 7020–7023 RSC.
- M.-A. Geiger, A. P. Jagtap, M. Kaushik, H. Sun, D. Stöppler, S. T. Sigurdsson, B. Corzilius and H. Oschkinat, Chem.–Eur. J., 2018, 24, 13485–13494 CrossRef CAS PubMed.
- F. Mentink-Vigier, T. Dubroca, J. V. Tol and S. T. Sigurdsson, J. Magn. Reson., 2021, 329, 107026 CrossRef CAS PubMed.
- E. S. Salnikov, H. Sarrouj, C. Reiter, C. Aisenbrey, A. Purea, F. Aussenac, O. Ouari, P. Tordo, I. Fedotenko, F. Engelke and B. Bechinger, J. Phys. Chem. B, 2015, 119, 14574–14583 CrossRef CAS PubMed.
- E. S. Salnikov, S. Abel, G. Karthikeyan, H. Karoui, F. Aussenac, P. Tordo, B. Bechinger and O. Ouari, ChemPhysChem, 2017, 18, 2103–2113 CrossRef CAS PubMed.
- A. N. Smith, M. A. Caporini, G. E. Fanucci and J. R. Long, Angew. Chem., Int. Ed., 2015, 54, 1542–1546 CrossRef CAS.
- A. N. Smith, U. T. Twahir, T. Dubroca, G. E. Fanucci and J. R. Long, J. Phys. Chem. B, 2016, 120, 7880–7888 CrossRef CAS PubMed.
- S. Zhu, E. Kachooei, J. R. Harmer, L. J. Brown, F. Separovic and M.-A. Sani, Biophys. J., 2021, 120, 4501–4511 CrossRef CAS PubMed.
- R. Rogawski, I. V. Sergeyev, Y. Li, M. F. Ottaviani, V. Cornish and A. E. McDermott, J. Phys. Chem. B, 2017, 121, 1169–1175 CrossRef CAS PubMed.
- E. A. W. van der Cruijsen, E. J. Koers, C. Sauvee, R. E. Hulse, M. Weingarth, O. Ouari, E. Perozo, P. Tordo and M. Baldus, Chem.–Eur. J., 2015, 21, 12971–12977 CrossRef CAS PubMed.
- B. J. Lim, B. E. Ackermann and G. T. Debelouchina, ChemBioChem, 2020, 21, 1315–1319 CrossRef CAS PubMed.
- B. J. Albert, C. K. Gao, E. L. Sesti, E. P. Saliba, N. Alaniva, F. J. Scott, S. T. Sigurdsson and A. B. Barnes, Biochemistry, 2018, 57, 4741–4746 CrossRef CAS PubMed.
- P. Gast, D. Mance, E. Zurlo, K. L. Ivanov, M. Baldus and M. Huber, Phys. Chem. Chem. Phys., 2017, 19, 3777–3781 RSC.
- G. Stevanato, G. Casano, D. J. Kubicki, Y. Rao, L. Esteban Hofer, G. Menzildjian, H. Karoui, D. Siri, M. Cordova, M. Yulikov, G. Jeschke, M. Lelli, A. Lesage, O. Ouari and L. Emsley, J. Am. Chem. Soc., 2020, 142, 16587–16599 CrossRef CAS PubMed.
- S. R. Chaudhari, P. Berruyer, D. Gajan, C. Reiter, F. Engelke, D. L. Silverio, C. Copéret, M. Lelli, A. Lesage and L. Emsley, Phys. Chem. Chem. Phys., 2016, 18, 10616–10622 RSC.
- J. Soetbeer, P. Gast, J. J. Walish, Y. Zhao, C. George, C. Yang, T. M. Swager, R. G. Griffin and G. Mathies, Phys. Chem. Chem. Phys., 2018, 20, 25506–25517 RSC.
- K. Tagami, A. Equbal, I. Kaminker, B. Kirtman and S. Han, Solid State Nucl. Magn. Reson., 2019, 101, 12–20 CrossRef CAS PubMed.
- A. Lund, G. Casano, G. Menzildjian, M. Kaushik, G. Stevanato, M. Yulikov, R. Jabbour, D. Wisser, M. Renom-Carrasco, C. Thieuleux, F. Bernada, H. Karoui, D. Siri, M. Rosay, I. V. Sergeyev, D. Gajan, M. Lelli, L. Emsley, O. Ouari and A. Lesage, Chem. Sci., 2020, 11, 2810–2818 RSC.
- S. Bothe, J. Nowag, V. Klimavičius, M. Hoffmann, T. I. Troitskaya, E. V. Amosov, V. M. Tormyshev, I. Kirilyuk, A. Taratayko, A. Kuzhelev, D. Parkhomenko, E. Bagryanskaya, T. Gutmann and G. Buntkowsky, J. Phys. Chem. C, 2018, 122, 11422–11432 CrossRef CAS.
- F. Mentink-Vigier, I. Marin-Montesinos, A. P. Jagtap, T. Halbritter, J. van Tol, S. Hediger, D. Lee, S. T. Sigurdsson and G. De Paëpe, J. Am. Chem. Soc., 2018, 140, 11013–11019 CrossRef CAS PubMed.
- R. Harrabi, T. Halbritter, F. Aussenac, O. Dakhlaoui, J. van Tol, K. Damodaran, D. Lee, S. Paul, S. Hediger, F. Mentink-Vigier, S. Sigurdsson and G. De Paepe, Angew. Chem., Int. Ed., 2022, e2021141 Search PubMed.
- K.-N. Hu, V. S. Bajaj, M. Rosay and R. G. Griffin, J. Chem. Phys., 2007, 126, 044512 CrossRef PubMed.
- O. Haze, B. Corzilius, A. A. Smith, R. G. Griffin and T. M. Swager, J. Am. Chem. Soc., 2012, 134, 14287–14290 CrossRef CAS PubMed.
- V. K. Michaelis, A. A. Smith, B. Corzilius, O. Haze, T. M. Swager and R. G. Griffin, J. Am. Chem. Soc., 2013, 135, 2935–2938 CrossRef CAS PubMed.
- Y. Li, A. Equbal, K. Tagami and S. Han, Chem. Commun., 2019, 55, 7591–7594 RSC.
- Y. Liu, F. A. Villamena, A. Rockenbauer, Y. Song and J. L. Zweier, J. Am. Chem. Soc., 2013, 135, 2350–2356 CrossRef CAS PubMed.
- G. Mathies, M. A. Caporini, V. K. Michaelis, Y. Liu, K.-N. Hu, D. Mance, J. L. Zweier, M. Rosay, M. Baldus and R. G. Griffin, Angew. Chem., Int. Ed., 2015, 54, 11770–11774 CrossRef CAS PubMed.
- X. Cai, A. Lucini Paioni, A. Adler, R. Yao, W. Zhang, D. Beriashvili, A. Safeer, A. Gurinov, A. Rockenbauer, Y. Song, M. Baldus and Y. Liu, Chem.–Eur. J., 2021, 27, 12758–12762 CrossRef CAS PubMed.
- R. Yao, D. Beriashvili, W. X. Zhang, S. Li, A. Safeer, A. Gurinov, A. Rockenbauer, Y. Yang, Y. G. Song, M. Baldus and Y. P. Liu, Chem. Sci., 2022, 13, 14157–14164 RSC.
- T. Halbritter, R. Harrabi, S. Paul, J. van Tol, D. Lee, S. Hediger, S. T. Sigurdsson, F. Mentink-Vigier and G. De Paepe, Chem. Sci., 2023, 14, 3852–3864 RSC.
- F. Mentink-Vigier, G. Mathies, Y. Liu, A.-L. Barra, M. A. Caporini, D. Lee, S. Hediger, R. G. Griffin and G. De Paëpe, Chem. Sci., 2017, 8, 8150–8163 RSC.
- K. Sato, R. Hirao, I. Timofeev, O. Krumkacheva, E. Zaytseva, O. Rogozhnikova, V. M. Tormyshev, D. Trukhin, E. Bagryanskaya, T. Gutmann, V. Klimavicius, G. Buntkowsky, K. Sugisaki, S. Nakazawa, H. Matsuoka, K. Toyota, D. Shiomi and T. Takui, J. Phys. Chem. A, 2019, 123, 7507–7517 CrossRef CAS PubMed.
- W. Zhai, Y. Feng, H. Liu, A. Rockenbauer, D. Mance, S. Li, Y. Song, M. Baldus and Y. Liu, Chem. Sci., 2018, 9, 4381–4391 RSC.
- W. Zhai, A. Lucini Paioni, X. Cai, S. Narasimhan, J. Medeiros-Silva, W. Zhang, A. Rockenbauer, M. Weingarth, Y. Song, M. Baldus and Y. Liu, J. Phys. Chem. B, 2020, 124, 9047–9060 CrossRef CAS.
- E. L. Dane, T. Maly, G. T. Debelouchina, R. G. Griffin and T. M. Swager, Org. Lett., 2009, 11, 1871–1874 CrossRef CAS PubMed.
- L. F. Pinto, I. Marín-Montesinos, V. Lloveras, J. L. Muñoz-Gómez, M. Pons, J. Veciana and J. Vidal-Gancedo, Chem. Commun., 2017, 53, 3757–3760 RSC.
- D. Wisser, G. Karthikeyan, A. Lund, G. Casano, H. Karoui, M. Yulikov, G. Menzildjian, A. C. Pinon, A. Purea, F. Engelke, S. R. Chaudhari, D. Kubicki, A. J. Rossini, I. B. Moroz, D. Gajan, C. Copéret, G. Jeschke, M. Lelli, L. Emsley, A. Lesage and O. Ouari, J. Am. Chem. Soc., 2018, 140, 13340–13349 CrossRef CAS PubMed.
- P. Berruyer, S. Björgvinsdóttir, A. Bertarello, G. Stevanato, Y. Rao, G. Karthikeyan, G. Casano, O. Ouari, M. Lelli, C. Reiter, F. Engelke and L. Emsley, J. Phys. Chem. Lett., 2020, 11, 8386–8391 CrossRef CAS PubMed.
- A. Equbal, K. Tagami and S. Han, Phys. Chem. Chem. Phys., 2020, 22, 13569–13579 RSC.
- S. R. Chaudhari, D. Wisser, A. C. Pinon, P. Berruyer, D. Gajan, P. Tordo, O. Ouari, C. Reiter, F. Engelke, C. Copéret, M. Lelli, A. Lesage and L. Emsley, J. Am. Chem. Soc., 2017, 139, 10609–10612 CrossRef CAS PubMed.
- S. Mandal and S. T. Sigurdsson, Chem. Commun., 2020, 56, 13121–13124 RSC.
- B. Corzilius, Paramagnetic Metal Ions for Dynamic Nuclear Polarization, in eMagRes, John Wiley & Sons, Ltd, 2018, pp. 179–194 Search PubMed.
- H. Glättli, M. Odehnal, J. Ezratty, A. Malinovski and A. Abragam, Phys. Lett. A, 1969, 29, 250–251 CrossRef.
- S. K. Jain, C.-J. Yu, C. B. Wilson, T. Tabassum, D. E. Freedman and S. Han, Chem, 2021, 7, 421–435 CAS.
- D. Jardón-Álvarez and M. Leskes, Dynamic nuclear polarization in inorganic solids from paramagnetic metal ion dopants, 2021 Search PubMed.
- B. Corzilius, A. A. Smith, A. B. Barnes, C. Luchinat, I. Bertini and R. G. Griffin, J. Am. Chem. Soc., 2011, 133, 5648–5651 CrossRef CAS PubMed.
- P. Wenk, M. Kaushik, D. Richter, M. Vogel, B. Suess and B. Corzilius, J. Biomol. NMR, 2015, 63, 97–109 CrossRef CAS PubMed.
- M. Kaushik, T. Bahrenberg, T. V. Can, M. A. Caporini, R. Silvers, J. Heiliger, A. A. Smith, H. Schwalbe, R. G. Griffin and B. Corzilius, Phys. Chem. Chem. Phys., 2016, 18, 27205–27218 RSC.
- V. Aladin and B. Corzilius, Solid State Nucl. Magn. Reson., 2019, 99, 27–35 CrossRef CAS PubMed.
- M. Kaushik, M. Qi, A. Godt and B. Corzilius, Angew. Chem., Int. Ed., 2017, 56, 4295–4299 CrossRef CAS PubMed.
- Y. Rao, C. T. Palumbo, A. Venkatesh, M. Keener, G. Stevanato, A. S. Chauvin, G. Menzildjian, S. Kuzin, M. Yulikov, G. Jeschke, A. Lesage, M. Mazzanti and L. Emsley, J. Phys. Chem. C, 2022, 126, 11310–11317 CrossRef CAS PubMed.
- G. Stevanato, D. J. Kubicki, G. Menzildjian, A.-S. Chauvin, K. Keller, M. Yulikov, G. Jeschke, M. Mazzanti and L. Emsley, J. Am. Chem. Soc., 2019, 141, 8746–8751 CrossRef CAS PubMed.
- S. J. Elliott, B. B. Duff, A. R. Taylor-Hughes, D. J. Cheney, J. P. Corley, S. Paul, A. Brookfield, S. Pawsey, D. Gajan, H. C. Aspinall, A. Lesage and F. Blanc, J. Phys. Chem. B, 2022, 126, 6281–6289 CrossRef CAS PubMed.
- M. A. Hope, B. L. D. Rinkel, A. B. Gunnarsdóttir, K. Märker, S. Menkin, S. Paul, I. V. Sergeyev and C. P. Grey, Nat. Commun., 2020, 11, 2224 CrossRef CAS PubMed.
- O. S. Leifson and C. D. Jeffries, Phys. Rev., 1961, 122, 1781–1795 CrossRef CAS.
- B. Corzilius, V. K. Michaelis, S. A. Penzel, E. Ravera, A. A. Smith, C. Luchinat and R. G. Griffin, J. Am. Chem. Soc., 2014, 136, 11716–11727 CrossRef CAS PubMed.
- T. Chakrabarty, N. Goldin, A. Feintuch, L. Houben and M. Leskes, ChemPhysChem, 2018, 19, 2139–2142 CrossRef CAS PubMed.
- T. Wolf, S. Kumar, H. Singh, T. Chakrabarty, F. Aussenac, A. I. Frenkel, D. T. Major and M. Leskes, J. Am. Chem. Soc., 2019, 141, 451–462 CrossRef CAS PubMed.
- A. Harchol, G. Reuveni, V. Ri, B. Thomas, R. Carmieli, R. H. Herber, C. Kim and M. Leskes, J. Phys. Chem. C, 2020, 124, 7082–7090 CrossRef CAS PubMed.
- D. Jardón-Álvarez, G. Reuveni, A. Harchol and M. Leskes, J. Phys. Chem. Lett., 2020, 11, 5439–5445 CrossRef PubMed.
- D. Jardón-Álvarez, T. Malka, J. v. Tol, Y. Feldman, R. Carmieli and M. Leskes, J. Magn. Reson., 2022, 336, 107143 CrossRef PubMed.
- S. Haber, Rosy, A. Saha, O. Brontvein, R. Carmieli, A. Zohar, M. Noked and M. Leskes, J. Am. Chem. Soc., 2021, 143, 4694–4704 CrossRef CAS PubMed.
- A. L. Paterson, F. A. Perras, M. F. Besser and M. Pruski, J. Phys. Chem. C, 2020, 124, 23126–23133 CrossRef CAS.
- D. Jardón-Álvarez, N. Kahn, L. Houben and M. Leskes, J. Phys. Chem. Lett., 2021, 12, 2964–2969 CrossRef PubMed.
- M. A. Hope, S. Björgvinsdóttir, D. M. Halat, G. Menzildjian, Z. Wang, B. Zhang, J. L. MacManus-Driscoll, A. Lesage, M. Lelli, L. Emsley and C. P. Grey, J. Phys. Chem. C, 2021, 125, 18799–18809 CrossRef CAS.
- H. Lock, R. A. Wind, G. E. Maciel and N. Zumbulyadis, Solid State Commun., 1987, 64, 41–44 CrossRef CAS.
- R. A. Wind, M. J. Duijvestijn, C. Vanderlugt, A. Manenschijn and J. Vriend, Prog. Nucl. Magn. Reson. Spectrosc., 1985, 17, 33–67 CrossRef CAS.
- R. A. Wind, F. E. Anthonio, M. J. Duijvestijn, J. Smidt, J. Trommel and G. M. C. Devette, J. Magn. Reson., 1983, 52, 424–434 CAS.
- M. L. Guy, K. J. van Schooten, L. H. Zhu and C. Ramanathan, J. Phys. Chem. C, 2017, 121, 2748–2754 CrossRef CAS.
- A. E. Dementyev, D. G. Cory and C. Ramanathan, Phys. Rev. Lett., 2008, 100, 127601 CrossRef CAS PubMed.
- M. Ha, A. N. Thiessen, I. V. Sergeyev, J. G. C. Veinot and V. K. Michaelis, Solid State Nucl. Magn. Reson., 2019, 100, 77–84 CrossRef CAS PubMed.
- J. Riikonen, S. Rigolet, C. Marichal, F. Aussenac, J. Lalevee, F. Morlet-Savary, P. Fioux, C. Dietlin, M. Bonne, B. Lebeau and V. P. Lehto, J. Phys. Chem. C, 2015, 119, 19272–19278 CrossRef CAS.
- C. O. Bretschneider, U. Akbey, F. Aussenac, G. L. Olsen, A. Feintuch, H. Oschkinat and L. Frydman, ChemPhysChem, 2016, 17, 2691–2701 CrossRef CAS PubMed.
- C. Presti, A. S. L. Thankamony, J. G. Alauzun, P. H. Mutin, D. Carnevale, C. Lion, H. Vezin, D. Laurencin and O. Lafon, J. Phys. Chem. C, 2015, 119, 12408–12422 CrossRef CAS.
- S. Pylaeva, K. L. Ivanov, M. Baldus, D. Sebastiani and H. Elgabarty, J. Phys. Chem. Lett., 2017, 8, 2137–2142 CrossRef CAS PubMed.
- L. Delage-Laurin, R. S. Palani, N. Golota, M. Mardini, Y. Ouyang, K. O. Tan, T. M. Swager and R. G. Griffin, J. Am. Chem. Soc., 2021, 143, 20281–20290 CrossRef CAS PubMed.
- A. B. Barnes, G. De Paepe, P. C. A. van der Wel, K. N. Hu, C. G. Joo, V. S. Bajaj, M. L. Mak-Jurkauskas, J. R. Sirigiri, J. Herzfeld, R. J. Temkin and R. G. Griffin, Appl. Magn. Reson., 2008, 34, 237–263 CrossRef CAS PubMed.
- A. Leavesley, C. B. Wilson, M. Sherwin and S. Han, Phys. Chem. Chem. Phys., 2018, 20, 9897–9903 RSC.
- A. Zagdoun, A. J. Rossini, D. Gajan, A. Bourdolle, O. Ouari, M. Rosay, W. E. Maas, P. Tordo, M. Lelli, L. Emsley, A. Lesage and C. Copéret, Chem. Commun., 2012, 48, 654–656 RSC.
- A. Lesage, M. Lelli, D. Gajan, M. A. Caporini, V. Vitzthum, P. Miéville, J. Alauzun, A. Roussey, C. Thieuleux, A. Mehdi, G. Bodenhausen, C. Coperet and L. Emsley, J. Am. Chem. Soc., 2010, 132, 15459–15461 CrossRef CAS PubMed.
- P. Berruyer, L. Emsley and A. Lesage, Emagres, 2018, 7, 93–104 CAS.
- W.-C. Liao, B. Ghaffari, C. P. Gordon, J. Xu and C. Copéret, Curr. Opin. Colloid Interface Sci., 2018, 33, 63–71 CrossRef CAS.
- B. J. Walder, C. Berk, W. C. Liao, A. J. Rossini, M. Schwarzwalder, U. Pradere, J. Hall, A. Lesage, C. Coperet and L. Emsley, ACS Cent. Sci., 2019, 5, 515–523 CrossRef CAS PubMed.
- W. C. Liao, T. C. Ong, D. Gajan, F. Bernada, C. Sauvee, M. Yulikov, M. Pucino, R. Schowner, M. Schwarzwalder, M. R. Buchmeiser, G. Jeschke, P. Tordo, O. Ouari, A. Lesage, L. Emsley and C. Coperet, Chem. Sci., 2017, 8, 416–422 RSC.
- E. Pump, J. Viger-Gravel, E. Abou-Hamad, M. K. Samantaray, B. Hamzaoui, A. Gurinov, D. H. Anjum, D. Gajan, A. Lesage, A. Bendjeriou-Sedjerari, L. Emsley and J. M. Basset, Chem. Sci., 2017, 8, 284–290 RSC.
- E. Pump, A. Bendjeriou-Sedjerari, J. Viger-Gravel, D. Gajan, B. Scotto, M. K. Samantaray, E. Abou-Hamad, A. Gurinov, W. Almaksoud, Z. Cao, A. Lesage, L. Cavallo, L. Emsley and J. M. Basset, Chem. Sci., 2018, 9, 4866–4872 RSC.
- A. Yakimov, J. Xu, K. Searles, W. C. Liao, G. Antinucci, N. Friederichs, V. Busico and C. Coperet, J. Phys. Chem. C, 2021, 125, 15994–16003 CrossRef CAS.
- L. Piveteau, T. C. Ong, A. J. Rossini, L. Emsley, C. Coperet and M. V. Kovalenko, J. Am. Chem. Soc., 2017, 139, 17700 CrossRef CAS PubMed.
- M. P. Hanrahan, Y. Chen, R. Blome-Fernández, J. L. Stein, G. F. Pach, M. A. S. Adamson, N. R. Neale, B. M. Cossairt, J. Vela and A. J. Rossini, J. Am. Chem. Soc., 2019, 141, 15532–15546 CrossRef CAS PubMed.
- J. Viger-Gravel, P. Berruyer, D. Gajan, J. M. Basset, A. Lesage, P. Tordo, O. Ouari and L. Emsley, Angew. Chem., Int. Ed., 2017, 56, 8726–8730 CrossRef CAS PubMed.
- A. J. Rossini, A. Zagdoun, F. Hegner, M. Schwarzwalder, D. Gajan, C. Coperet, A. Lesage and L. Emsley, J. Am. Chem. Soc., 2012, 134, 16899–16908 CrossRef CAS PubMed.
- S. Bjorgvinsdottir, B. J. Walder, A. C. Pinon and L. Emsley, J. Am. Chem. Soc., 2018, 140, 7946–7951 CrossRef CAS PubMed.
- P. Wolf, M. Valla, A. J. Rossini, A. Comas-Vives, F. Nunez-Zarur, B. Malaman, A. Lesage, L. Emsley, C. Coperet and I. Hermans, Angew. Chem., Int. Ed., 2014, 53, 10179–10183 CrossRef CAS PubMed.
- A. J. Rossini, A. Zagdoun, M. Lelli, J. Canivet, S. Aguado, O. Ouari, P. Tordo, M. Rosay, W. E. Maas, C. Coperet, D. Farrusseng, L. Emsley and A. Lesage, Angew. Chem., Int. Ed., 2012, 51, 123–127 CrossRef CAS PubMed.
- A. J. Rossini, C. M. Widdifield, A. Zagdoun, M. Lelli, M. Schwarzwalder, C. Coperet, A. Lesage and L. Emsley, J. Am. Chem. Soc., 2014, 136, 2324–2334 CrossRef CAS PubMed.
- J. Viger-Gravel, W. Lan, A. C. Pinon, P. Berruyer, L. Emsley, M. Bardet and J. Luterbacher, J. Phys. Chem. C, 2019, 123, 30407–30415 CrossRef CAS.
- B. Itin and I. V. Sergeyev, Strategies for Efficient Sample Preparation for Dynamic Nuclear Polarization Solid-State NMR of Biological Macromolecules, 2017, pp. 133–154 Search PubMed.
- W. Y. Chow, G. De Paepe and S. Hediger, Chem. Rev., 2022, 122, 9795–9847 CrossRef CAS PubMed.
- T. Biedenbander, V. Aladin, S. Saeidpour and B. Corzilius, Chem. Rev., 2022, 122, 9738–9794 CrossRef PubMed.
- A. L. Paioni, M. A. M. Renault and M. Baldus, Emagres, 2018, 7, 51–61 CAS.
- S. Narasimhan, S. Scherpe, A. L. Paioni, J. van der Zwan, G. E. Folkers, H. Ovaa and M. Baldus, Angew. Chem., Int. Ed., 2019, 58, 12969–12973 CrossRef CAS PubMed.
- J. Schlagnitweit, S. F. Sandoz, A. Jaworski, I. Guzzetti, F. Aussenac, R. J. Carbajo, E. Chiarparin, A. J. Pell and K. Petzold, ChemBioChem, 2019, 20, 2474–2478 CrossRef CAS PubMed.
- A. Bertarello, P. Berruyer, M. Artelsmair, C. S. Elmore, S. Heydarkhan-Hagvall, M. Schade, E. Chiarparin, S. Schantz and L. Emsley, J. Am. Chem. Soc., 2022, 144, 6734–6741 CrossRef CAS PubMed.
- S. A. Overall and A. B. Barnes, Front. Mol. Biosci., 2021, 8, 743829 CrossRef CAS PubMed.
- R. Ghosh, Y. L. Xiao, J. Kragelj and K. K. Frederick, J. Am. Chem. Soc., 2021, 143, 18454–18466 CrossRef CAS PubMed.
- R. Ghosh, J. Kragelj, Y. L. Xiao and K. K. Frederick, J. Vis. Exp., 2020 DOI:10.3791/61733.
- B. E. Ackermann, B. J. Lim, N. Elathram, S. Narayanan and G. T. Debelouchina, ChemBioChem, 2022, 23, e202200577 CrossRef CAS PubMed.
- J. P. King, K. Jeong, C. C. Vassiliou, C. S. Shin, R. H. Page, C. E. Avalos, H. J. Wang and A. Pines, Nat. Commun., 2015, 6, 8965 CrossRef PubMed.
- S. Fujiwara, M. Hosoyamada, K. Tateishi, T. Uesaka, K. Ideta, N. Kimizuka and N. Yanai, J. Am. Chem. Soc., 2018, 140, 15606–15610 CrossRef CAS PubMed.
- S. Fujiwara, N. Matsumoto, K. Nishimura, N. Kimizuka, K. Tateishi, T. Uesaka and N. Yanai, Angew. Chem., Int. Ed., 2022, 61, e202115792 CrossRef CAS PubMed.
- S. L. Carnahan, A. Venkatesh, F. A. Perras, J. F. Wishart and A. J. Rossini, J. Phys. Chem. Lett., 2019, 10, 4770–4776 CrossRef CAS PubMed.
- S. L. Carnahan, Y. Chen, J. F. Wishart, J. W. Lubach and A. J. Rossini, Solid State Nucl. Magn. Reson., 2022, 119, 101785 CrossRef CAS PubMed.
- M. Lelli, S. R. Chaudhari, D. Gajan, G. Casano, A. J. Rossini, O. Ouari, P. Tordo, A. Lesage and L. Emsley, J. Am. Chem. Soc., 2015, 137, 14558–14561 CrossRef CAS PubMed.
- G. Menzildjian, A. Lund, M. Yulikov, D. Gajan, L. Niccoli, G. Karthikeyan, G. Casano, G. Jeschke, O. Ouari, M. Lelli and A. Lesage, J. Phys. Chem. B, 2021, 125, 13329–13338 CrossRef CAS PubMed.
- M. Kaushik, H. Lingua, G. Stevanato, M. Elokova, M. Lelli, A. Lesage and O. Ouari, Phys. Chem. Chem. Phys., 2022, 24, 12167–12175 RSC.
- D. Gajan, M. Schwarzwalder, M. P. Conley, W. R. Gruning, A. J. Rossini, A. Zagdoun, M. Lelli, M. Yulikov, G. Jeschke, C. Sauvee, O. Ouari, P. Tordo, L. Veyre, A. Lesage, C. Thieuleux, L. Emsley and C. Coperet, J. Am. Chem. Soc., 2013, 135, 15459–15466 CrossRef CAS PubMed.
- D. Baudouin, H. A. van Kalkeren, A. Bornet, B. Vuichoud, L. Veyre, M. Cavailles, M. Schwarzwalder, W. C. Liao, D. Gajan, G. Bodenhausen, L. Emsley, A. Lesage, S. Jannin, C. Coperet and C. Thieuleux, Chem. Sci., 2016, 7, 6846–6850 RSC.
- W. R. Gruning, H. Bieringer, M. Schwarzwalder, D. Gajan, A. Bornet, B. Vuichoud, J. Milani, D. Baudouin, L. Veyre, A. Lesage, S. Jannin, G. Bodenhausen, C. Thieuleux and C. Coperet, Helv. Chim. Acta, 2017, 100, e1600122 CrossRef.
- E. Besson, F. Ziarelli, E. Bloch, G. Gerbaud, S. Queyroy, S. Viel and S. Gastaldi, Chem. Commun., 2016, 52, 5531–5533 RSC.
- D. L. Silverio, H. A. van Kalkeren, T. C. Ong, M. Baudin, M. Yulikov, L. Veyre, P. Berruyer, S. Chaudhari, D. Gajan, D. Baudouin, M. Cavailles, B. Vuichoud, A. Bornet, G. Jeschke, G. Bodenhausen, A. Lesage, L. Emsley, S. Jannin, C. Thieuleux and C. Coperet, Helv. Chim. Acta, 2017, 100, e1700101 CrossRef.
- E. Besson, A. Vebr, F. Ziarelli, E. Bloch, G. Gerbaud, S. Queyroy, P. Thureau, S. Viel and S. Gastaldi, Phys. Chem. Chem. Phys., 2022, 24, 25279–25286 RSC.
- M. Juramy, R. Chevre, P. C. Vioglio, F. Ziarelli, E. Besson, S. Gastaldi, S. Viel, P. Thureau, K. D. M. Harris and G. Mollica, J. Am. Chem. Soc., 2021, 143, 6095–6103 CrossRef CAS PubMed.
- W. Cao, W. D. Wang, H. S. Xu, I. V. Sergeyev, J. Struppe, X. L. Wang, F. Mentink-Vigier, Z. H. Gan, M. X. Xiao, L. Y. Wang, G. P. Chen, S. Y. Ding, S. Bai and W. Wang, J. Am. Chem. Soc., 2018, 140, 6969–6977 CrossRef CAS PubMed.
Footnote |
| † This manuscript is dedicated to R. G. Griffin on the occasion of his 80th birthday. |
| This journal is © The Royal Society of Chemistry 2023 |
