 Open Access Article
Open Access ArticleAccelerating reaction modeling using dynamic flow experiments, part 2: development of a digital twin†
Klara
Silber
 ab,
Peter
Sagmeister
ab,
Peter
Sagmeister
 ab,
Christine
Schiller
ab,
Christine
Schiller
 ab,
Jason D.
Williams
ab,
Jason D.
Williams
 ab,
Christopher A.
Hone
ab,
Christopher A.
Hone
 *ab and
C. Oliver
Kappe
*ab and
C. Oliver
Kappe
 *ab
*ab
aCenter for Continuous Flow Synthesis and Processing (CC FLOW), Research Center Pharmaceutical Engineering GmbH (RCPE), Inffeldgasse 13, 8010 Graz, Austria. E-mail: christopher.hone@rcpe.at
bInstitute of Chemistry, University of Graz, NAWI Graz, Heinrichstrasse 28, 8010 Graz, Austria. E-mail: oliver.kappe@uni-graz.at
First published on 31st July 2023
Abstract
In this paper, we describe the development of a digital twin for a Michael addition continuous-flow process using data generated from dynamic flow experimentation. We commenced our investigation by creating a virtual flowsheet representation of the “real-life” continuous-flow system. The residence time distribution (RTD) within the system was assessed using an automated step change protocol which examined the performance at different flow rates. The RTD study generated an understanding of the influence of dispersion on the intrinsic reaction kinetics. The dynamic flow experiments were fitted to a parallel reaction network for the reaction of 1,2,4-triazole with acrylonitrile in the presence of base to form the desired product and a regioisomer. The reaction network comprised of four kinetic parameters (A1, Ea1, A2 and Ea2). The fitted model closely corresponded to the experimental data, with R2 = 0.974. The model was then further validated with additional dynamic flow experiments and a self-optimization study. The established digital twin was then used to explore the influence of disturbances within the system.
Introduction
The pharmaceutical industry is placing more focus on data-rich experimentation and the generation of in-depth reaction understanding through process modeling.1 Furthermore, regulatory authorities are encouraging a greater emphasis on quality by design (QbD) principles, whereby quality is built-in by having a thorough understanding of processes.2 Pharma 4.0 is a framework devised for developing digital approaches in the context of pharmaceutical manufacturing.3One technological tool that remains underdeveloped in the pharmaceutical industry is the application of digital twins.4,5 A digital twin is a virtual model of a physical system, where the conditions, properties and characteristics are represented by digital information (Fig. 1). The creation of digital twins will help to accelerate pharmaceutical development workflows, enable better control over quality, as well as improve efficiency and sustainability. In particular, digital twins would be of great utility for the in silico investigation of different manufacturing scenarios, thus reducing experimental costs and improving efficiency. A digital twin can also be implemented to simulate process disturbances, therefore supporting the development of process control strategies.6–9 Subsequently, experimental validation can be restricted to only a small selection of experiments, thus reducing the experimental burden.
As reported in part 1 of this contribution, autonomous dynamic flow experimentation, also referred to as transient or non-steady state experimentation, can be used to collect data in less time and save on material use.10 Autonomous dynamic flow methods enable the entirety of the design space to be explored within a single experiment.11,12 In recent years, a number of different research groups have established different dynamic flow approaches to explore different model structures and for kinetic parameter estimation.10–12 However, this data has not yet been utilized for the development of a digital twin.13 In alignment with the framework of Pharma 4.0, we were interested in the extension of this type of data-rich approach for the creation of a digital twin.
There are only a limited number of reports that provide a full virtual representation of a flow system as a digital twin for pharmaceutically-relevant organic chemistry examples. Jolliffe and Gerogiorgis created a digital twin for the multistep continuous manufacture of ibuprofen using a series of three plug flow reactors.14 Previously, we reported the development of a digital twin for a gas–liquid aerobic oxidation.15 In this instance, a hybrid modeling approach was implemented, whereby a combination of data-driven and physics-driven approaches were applied to obtain parameter values for the creation of a digital twin. Another interesting contribution was made in a series of papers from researchers working at Amgen, who discussed the development of a virtual plant for integrated continuous manufacturing.16–18 The team used the digital twin to assess the impact of process disturbances and model uncertainties on critical quality attributes (CQAs), which then supported their process control strategy.
A shortcoming of the previous reports is the limited connection between efficient experimental design and the modeling aspects to create a digital twin. There are certain limitations that hinder the development of digital twins: i) limited data availability over a wide range of operating conditions, including across the time domain; ii) missing knowledge for reliable representation; iii) limited model fidelity across the entirety of the design space; and iv) the high level of mathematical and computational expertise deemed necessary to create the process models. We propose that the implementation of dynamic experiments will facilitate the rapid and efficient exploration of the design space for this purpose. Furthermore, by using off-the-shelf software with pre-defined reactor models, we believe that this lowers the barrier of entry for the creation of a digital twin, thus making it accessible to process chemists and engineers. In this paper, we discuss our efforts in the creation of a digital twin using the transient experimental flow data. We outline the stages in our workflow: i) model discrimination, ii) kinetic parameter estimation, iii) model validation, and iv) utilization for in silico optimization and disturbance analysis.
Results and discussion
Chemistry
A parallel reaction network was defined for the system, see Scheme 1, comprising of the reaction of 1,2,4-triazole (1), in the presence of N,N-diisopropylethylamine (DIPEA, 2), reacting with acrylonitrile (3) to give either the desired product 4 or the regioisomer 5.Flowsheet
A flowsheet, see Scheme 2, was created as a representation of the physical system within gPROMS (PSE/Siemens, FormulatedProducts 2.3.1). This software uses equation-oriented flowsheeting.19–21 A one-dimensional tubular one-phase plug flow reactor model was selected (see ESI,† section S4). The physical properties (molecular weight, density, physical states) for all the chemical species were inputted into a database (gPROMS FormulatedProducts Utilities 1.0.020190705). The system was simulated in dynamic mode. The flow ramps and step intervals were defined using the piecewise constant setting in the software. Isothermal temperature control was assumed: the high heat transfer provided a consistent temperature across the reactor. The concentration of 1, 3, 4 and 5 were measured by inline FTIR and online NMR. The mass balance of the system for the experiments is based on the measured concentration of species 1, 3, 4 and 5. More details regarding the analytical setup are described in part 1 of this contribution.10 | ||
| Scheme 2 a) Physical flow system configuration for a Michael addition reaction; b) digital twin flowsheet in gPROMS FormulatedProducts. | ||
Dispersion
We performed an automated step experiment at the maximum, midpoint and minimum total flow rates (4 mL min−1, 1.33 mL min−1 and 0.67 mL min−1) to understand the residence time distribution (RTD) within the system. These flow rates correspond to the range of residence times used in our study (30 s, 90 s and 180 s). The RTD was investigated to assess the effect of dispersion within the system, especially related to its impact on the kinetic analysis. The RTD was investigated by introducing 1 in MeOH through one pump and MeOH through a second pump. The step change experiment was performed by switching from the substrate pump to the solvent pump and the concentration of 1 was measured by NMR. It is important to note that the measured values assume a perfect pulse input, since no measurements were made before the reactor. The concentration data were then used to calculate the Bodenstein number (Bo) (see Fig. 2 and ESI,† section S3).22 Due to the analytics displaying a limit of detection (LOD) > 0 M, the F-curves were only fitted using normalized data from the step ups. A Bodenstein number close to 20 was obtained at the lowest flow rate, indicating more CSTR-type behavior. Whereas, for 1.33 mL min−1 and 4.00 mL min−1 Bo numbers of >40 were calculated. Based on this analysis, moderate axial dispersion and some small deviations from plug flow were expected, with further deviation expected for shorter reactor residence times closer to 30 s. An axial dispersion coefficient, Dax, of 5.10 × 10−3 m2 s−1 was obtained at a flow rate of 4 mL min−1. This value for Dax was fixed within the flowsheet. We were also interested in comparing the online NMR dispersion results to the inline FTIR measurements (see also ESI,† Fig. S1). In this case, Bodenstein numbers above 100 were obtained, indicating that ideal plug flow could be assumed. The results from measuring the RTD using FTIR demonstrate that there is minimal axial dispersion within the reactor itself and that under all flow rates the reactor displays ideal plug flow behavior. These results highlight the difference between using an inline and an online analytical method. The inline FTIR displayed performance across the range of flow rates. It is the additional volume and subsampling system for the NMR which is the cause for the difference in the performance. Analysis should be performed as close to the reactor as possible for it to be most representative of the reaction itself. The difference in the results between the FTIR and NMR shows that scientists should be careful to consider the point of analysis and the acquisition time when configuring PAT, as this can sometimes be overlooked. | ||
| Fig. 2 RTD study: measurement of F curves within the reactor system using NMR data, and Bo and Dax values calculated at different flow rates using NMR and FTIR. Reactor temperature at 100 °C. | ||
We used an upwind discretization method for our reactor model. However, upwind differences can result in “numerical diffusion”, therefore we looked at the influence of different grid points on the numerical diffusion.23 As can be expected, using a higher number of finite volume compartments resulted in less numerical diffusion, see Fig. 3a, but the computational time to simulate was also noticeably longer without a significant change in the numerical diffusion. We selected 10 finite volumes for the reactor as a compromise between accuracy and computational requirements. The trajectory of the experimental concentration for 1,2,4-triazole (1) determined by NMR was compared to the simulated concentration (Fig. 3b). At moderate and high flow rates (1.33 mL min−1 and 4 mL min−1) the simulated trajectory closely corresponded to the experimental data. However, a larger deviation was observed at the lowest flow rate, probably due to the subsampling routine for the online NMR.
Flow ramp
1,2,4-Triazole (1) (0.75 to 1.5 M), DIPEA (2) equiv. (0–0.1 eq.), acrylonitrile (3) equiv. (0.8 to 2 eq.) and temperature (100 to 140 °C) were all varied as part of the flow ramp (Fig. 5a). Different residence times (70 to 120 s) were explored by using step changes. Longer residence times were not explored in the ramp used for kinetic fitting due to the higher dispersion observed during the RTD study at shorter residence times.Kinetic fitting
There are two key components to kinetic modelling: model discrimination and kinetic parameter estimation. Model discrimination is the selection of the best fitting rate expression from a set of a priori rate expressions, and kinetic parameter estimation is the fitting of parameters to a priori rate expressions to estimate values of rate parameters. The mass balance for the species within the competitive reaction model was based on the following derived rate laws for the species generation and consumption: | (1) |
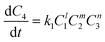 | (2) |
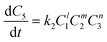 | (3) |
Model discrimination
An Arrhenius expression modified for parameter estimation and optimization with reference temperature was used for the simultaneous fitting of the product 4 and regioisomer 5 formation (see ESI,† eqn (S11)). Parameter estimation within gPROMS was carried out by solving a maximum likelihood model validation problem, the formulation (see ESI,† eqn (S13)) Seven candidate model structures were considered for the reaction system. The dynamic experiment given in Fig. 5a was used to fit the parameters to the data for each model in turn by minimizing Chi-squared (χ)2 (Fig. 4). The order with respect to components 1, 2 and 3 were investigated by using fixed interval values for the orders (l, m, n = 0 or 1). A higher χ2 value indicates higher lack-of-fit, the best fit was achieved for model 011. This corresponds to first order with respect to DIPEA (2), first order with respect to the acrylonitrile (3) and zero order in 1,2,4-triazole (1) displaying the best fit.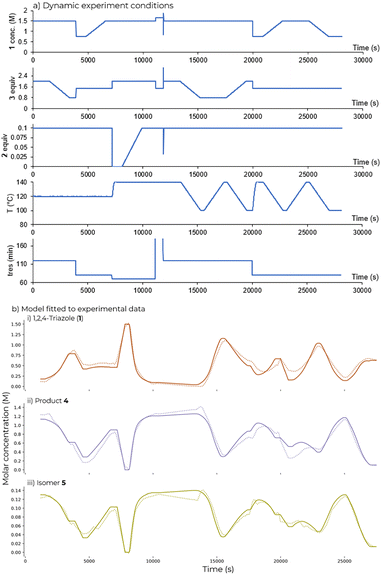 | ||
| Fig. 5 a) Conditions explored in the dynamic experiment used for fitting; b) fitted model and measured data for dynamic experiment using parameter values obtained in Table 1. Lines show fitted concentration; points show experimental data. | ||
Parameter estimation
The parameter estimates for the logarithmic form of the pre-exponential factors, A1 and A2, and the activation energies, Ea1 and Ea2, are shown in Table 1. A1 and A2 are re-parameterized pre-exponential factors at the reference temperature (T0 = 120 °C). All of the kinetic parameters were fitted with very good precision. The model predicted concentration values closely corresponded to the experimental values, with a R2 of 0.974 for species 1, 4 and 5 (see Fig. 5b and ESI,† Fig. S4 for parity plots). The activation energies for Ea1 and Ea2 were determined to be very similar, 70.6 kJ mol−1 and 68.5 kJ mol−1, respectively. To further validate the optimality of the parameter estimates a multistart solver, #MINLPSolver, was utilized with a maximum number of 10 initial guess points to ensure a local optimum had not been identified. The multistart solver was used to sample a wider range of initial guesses (±20% of the first set of initial guesses) to check the solution is a global rather than local optimum. In all cases the same optimum parameters were estimated, suggesting that the global optimum had been identified. Furthermore, almost the same parameter values were obtained when including the concentration values for acrylonitrile (3) as without acrylonitrile (see ESI,† Table S2 vs.Table 1), therefore further calculations were performed without using the values obtained for acrylonitrile.| log(AT0) ± SE (mol−1 m3 s−1) | E a ± SE (kJ mol−1) | |
|---|---|---|
| Formation of 4 | −9.27 ± 0.001 | 70.6 ± 0.1 |
| Formation of 5 | −11.4 ± 0.002 | 68.5 ± 0.2 |
The results show that higher conversion is achieved at higher temperatures, but also that favorable selectivity towards a particular product cannot be achieved by temperature manipulation due to the similar activation energies. The results also showed that the base concentration highly influences the conversion and reaction rate.
Model validation
A number of additional experimental automated flow ramps were then performed for model validation. The simulated trajectories closely correspond to the experimentally-measured data (see ESI,† Fig. S5–S7). Although the model appears to fit to all the data well, slight deviations were observed at lower concentrations of starting material 1 and also when less than 1 equivalent of acrylonitrile 3 were used.Optimization
The digital twin was used to visualize the design space, with both increasing equivalents of acrylonitrile 3 and a longer residence time increasing the yield of 4 (Fig. 6). A shorter residence time could be used to achieve the same yield of 4 through increasing the temperature, thus enabling a higher productivity. | ||
| Fig. 6 Simulated response surface for product 4 yield using parameter values obtained in Table 1. Fixed conditions: 1 conc. = 1.5 M and 2 equiv. = 0.1 eq. | ||
Automated self-optimizing continuous-flow systems based on optimization algorithms have been reported for the identification of optimal operating conditions.24,25 We were interested in comparing the predictive capability of our digital twin to the experimental data obtained from a self-optimization campaign (Fig. 7 and ESI,† Fig. S8). Product 4 displayed a small difference between the experimental and simulated values, but the same general trend could be observed. However, in the case of isomer 5 the model showed very close agreement with the experimental data. Even though there is some discrepancy between the predicted and experimental values for product 4, the in silico experiments still serve as a method for pre-screening experiments to identify those that would be the most valuable to run in the laboratory, such as those on the pareto front.26 The benefit of using a kinetic-based approach is that a clear understanding regarding the relative rates between the two parallel reactions is obtained, thus enabling better control over selectivity.27 The digital twin can be used to explore outside of the experimental design space. Although, it is important to note that any predictions will not include the impact of new mechanisms (e.g., a new reaction pathway) that were not considered as part of the fitted kinetic model, therefore any extrapolation should be done with caution. Typically, kinetic models should not be used to extrapolate far outside the experimentally explored space.
 | ||
| Fig. 7 Experimental data and simulated trajectories using parameter values obtained in Table 1 for self-optimization campaign for: a) product 4 and b) isomer 5. Lines show simulated concentration; orange points show experimental data and purple points show steady state values for the self-optimization algorithm. | ||
Disturbance simulation
We were also interested in the predictive capability of our model for when the system experienced disturbances.28,29 Thus, we simulated the influence of switching off the acrylonitrile pump at set intervals, which decreased the consumption of starting material (1). The simulated results for 1,2,4-triazole (1) are compared to the experimentally-measured values in Fig. 8 (see also ESI,† Fig. S9). The change in the simulated concentration values closely matched the measured values. The NMR needed longer to settle its baseline when compared to the FTIR which immediately returned. This result shows an advantage of having multiple complementary process analytical techniques (PAT) approaches (both inline and online) within a single system,30 whereby NMR can be used to generate a kinetic model, but a process monitoring and control strategy could afterwards be devised with FTIR due to its faster response time. | ||
| Fig. 8 Simulated trajectories and experimental data for disturbance tests using parameter values obtained in Table 1: a) compared to online NMR data; b) compared to inline FTIR data. The times given on the figure refer to the length of the time interval for which the acrylonitrile pump was switched off. For a comparison of all the main species, see ESI,† Fig. S9. | ||
Conclusions and outlook
The implementation of automated dynamic experimentation facilitated the efficient exploration of a wide range of experimental conditions within a single experiment (<8 h of operating time). The data were then used to establish a kinetic model and for the fitting of parameter estimates, which resulted in a model that closely described the experimental data (R2 = 0.974). The model was successfully validated with additional automated flow ramps. This then led to the creation of a digital twin which could be used to investigate the system using in silico experimentation. The comparison of simulated experiments to a self-optimization routine showed the ability to use a digital twin for pre-screening experiments before entering the laboratory.One consideration in the design our combined approaches in part 1 and 2 was to reflect the constraints placed on process development within the pharmaceutical industry. In general, the chemistry is developed first, which is followed by the development of a deeper understanding of the reactor system dynamics. Therefore, firstly a rough model was developed for the system in part 1, prior to developing more refined models for the reactor system dynamics and parameter estimation for the creation of a digital twin in this second contribution. Our approach allows process models to be generated much earlier in reaction optimization, allowing early estimation of the sensitivity of product quality to input parameter changes. This type of approach will reduce the experimental burden in the lab, where optimization is performed in silico and then only the most important experiments are validated experimentally. We demonstrated that the digital twin could be used to reliably evaluate potential disturbances through in silico experimentation. The ability to perform in silico disturbance analysis and visualize the design space will support in the establishment of advanced control strategies in API manufacture. The combined dynamic experimentation and digital twin approach can be extended to new reaction chemistries. This work is ongoing in our laboratories. Future work will focus on the development of a platform whereby the physical and digital systems can interact in a closed-loop fashion in real-time, and provide “on-the-fly” learning to the digital twin.
Data availability
The experimental data generated during this study can be found online at: https://doi.org/10.5281/zenodo.7829131.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors gratefully acknowledge funding by Land Steiermark/Zukunftsfonds Steiermark (No. 9003) for acquiring the infrastructure used in this work. The Research Center Pharmaceutical Engineering (RCPE) is funded within the framework of COMET – Competence Centers for Excellent Technologies by BMK, BMDW, Land Steiermark and SFG. The COMET program is managed by the FFG. The authors are thankful to Niall Mitchell and Meera Mahadevan (Siemens Process Systems Enterprise) for helpful discussions.Notes and references
- S. Caron and N. M. Thomson, J. Org. Chem., 2015, 80, 2943–2958 CrossRef CAS PubMed.
- S. L. Lee, T. F. O. Connor, X. Yang, C. N. Cruz, L. X. Yu and J. Woodcock, J. Pharm. Innov., 2015, 10, 191–199 CrossRef.
- V. Steinwandter, D. Borchert and C. Herwig, Drug Discovery, 2019, 24, 1795–1805 Search PubMed.
- N. Kockmann, React. Chem. Eng., 2019, 4, 1522–1529 RSC.
- Y. Chen, O. Yang, C. Sampat, P. Bhalode, R. Ramachandran and M. Ierapetritou, Processes, 2020, 8, 1088–1120 CrossRef.
- P. Sagmeister, R. Lebl, I. Castillo, J. Rehrl, J. Kruisz, M. Sipek, M. Horn, S. Sacher, D. Cantillo, J. D. Williams and C. O. Kappe, Angew. Chem., 2021, 60, 8139–8148 CrossRef CAS PubMed.
- I. Castillo, J. Rehrl, P. Sagmeister, R. Lebl, J. Kruisz, S. Celikovica, M. Sipek, D. Kirschneck, M. Horn, S. Sacher, D. Cantillo, J. D. Williams, J. G. Khinast and C. O. Kappe, J. Process Control, 2023, 152, 59–62 CrossRef.
- R. Lakerveld, B. Benyahia, P. L. Heider, H. Zhang, A. Wolfe, C. J. Testa, S. Ogden, D. R. Hersey, S. Mascia, J. M. B. Evans, R. D. Braatz and P. I. Barton, Org. Process Res. Dev., 2015, 19, 1088–1100 CrossRef CAS.
- A. Mesbah, J. A. Paulson, R. Lakerveld and R. D. Braatz, Org. Process Res. Dev., 2017, 21, 844–854 CrossRef CAS.
- For more detail, see part 1 of this contribution, entitled “Accelerating Reaction Modeling Using Dynamic Flow Experiments, Part 1: Design Space Exploration”, P. Sagmeister, C. Schiller, P. Weiss, K. Silber, S. Knoll, C. A. Hone, J. D. Williams and C. O. Kappe, React. Chem. Eng., 2023 10.1039/D3RE00243H.
- S. Mozharov, A. Nordon, D. Littlejohn, C. Wiles, P. Watts, P. Dallin and J. M. Girkin, J. Am. Chem. Soc., 2011, 133, 3601–3608 CrossRef CAS PubMed.
- J. S. Moore and K. F. Jensen, Angew. Chem., Int. Ed., 2014, 53, 470–473 CrossRef CAS PubMed.
- C. J. Taylor, J. A. Manson, G. Clemens, B. A. Taylor, T. W. Chamberlain and R. A. Bourne, React. Chem. Eng., 2022, 7, 1037–1046 RSC.
- H. G. Jolliffe and D. I. Gerogiorgis, Chem. Eng. Res. Des., 2015, 97, 175–191 CrossRef CAS.
- G. Vernet, M.-S. Salehi, P. Lopatka, S. K. Wilkinson, S. K. Bermingham, R. Munday, A. O'Kearney-McMullan, K. Leslie, C. A. Hone and C. O. Kappe, Chem. Eng. J., 2021, 416, 129045 CrossRef CAS.
- E. Içten, A. J. Maloney, M. G. Beaver, D. E. Shen, X. Zhu, L. R. Graham, J. A. Robinson, S. Huggins, A. Allian, R. Hart, S. D. Walker, P. Rolandi and R. D. Braatz, Org. Process Res. Dev., 2020, 24, 1861–1875 CrossRef.
- E. Içten, A. J. Maloney, M. G. Beaver, X. Zhu, D. E. Shen, J. A. Robinson, A. T. Parsons, A. Allian, S. Huggins, R. Hart, P. Rolandi, S. D. Walker and R. D. Braatz, Org. Process Res. Dev., 2020, 24, 1876–1890 CrossRef.
- A. J. Maloney, E. Içten, G. Capellades, M. G. Beaver, X. Zhu, L. R. Graham, D. B. Brown, D. J. Griffin, R. Sangodkar, A. Allian, S. Huggins, R. Hart, P. Rolandi, S. D. Walker and R. D. Braatz, Org. Process Res. Dev., 2020, 24, 1891–1908 CrossRef CAS.
- gPROMS FormulatedProducts, https://www.psenterprise.com/products/gproms/formulatedproducts, Accessed: 22nd March 2023 Search PubMed.
- S. Diab, G. Bano, C. Christodoulou, N. Hodnett, A. Benedetti, M. Anderson and S. Zomer, J. Pharm. Innov., 2022, 17, 1333–1346 CrossRef.
- S. Diab, C. Christodoulou, G. Taylor and P. Rushworth, Org. Process Res. Dev., 2022, 26, 2864–2881 CrossRef CAS.
- O. Levenspiel, Chemical Reaction Engineering, John Wiley & Sons, Inc., New York, 3rd edn, 1964 Search PubMed.
- S. D. Schaber, S. C. Born, K. F. Jensen and P. I. Barton, Org. Process Res. Dev., 2014, 18, 1461–1467 CrossRef CAS.
- C. Mateos, M. J. Nieves-Remacha and J. A. Rincón, React. Chem. Eng., 2019, 4, 1536–1544 RSC.
- M. Abolhasani and E. Kumacheva, Nat. Synth., 2023, 2, 483–492 CrossRef.
- A. M. Schweidtmann, A. D. Clayton, N. Holmes, E. Bradford, R. A. Bourne and A. A. Lapkin, Chem. Eng. J., 2018, 352, 277–282 CrossRef CAS.
- For an example of using self-optimization data to fit kinetic model, see: B. L. Hall, C. J. Taylor, R. Labes, A. F. Massey, R. Menzel, R. A. Bourne and T. W. Chamberlain, Chem. Commun., 2021, 57, 4926–4929 RSC.
- C. Armstrong, Y. Miyai, A. Formosa, P. Kaushik, L. Rogers and T. D. Roper, J. Flow Chem., 2023 DOI:10.1007/s41981-023-00266-0.
- M. Glace, W. Wu, H. Kraus, D. Acevedo, T. D. Roper and A. Mohammad, React. Chem. Eng., 2023, 8, 1032–1042 RSC.
- P. Sagmeister, J. D. Williams, C. A. Hone and C. O. Kappe, React. Chem. Eng., 2019, 4, 1571–1578 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3re00244f |
| This journal is © The Royal Society of Chemistry 2023 |




