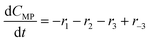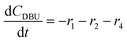Mechanistic insights into amination via nucleophilic aromatic substitution†
Received
11th April 2023
, Accepted 29th April 2023
First published on 19th May 2023
Abstract
Extensive kinetic investigations were performed to identify novel reaction pathways and assess their feasibility to resolve contradictions in the reported understanding of an amination reaction via nucleophilic aromatic substitution. The use of different bases in a reaction system resulted in distinct concentration profiles, such as sigmoidal profiles in both the starting material and the product. The generated profiles could be rationalized by the evolution of a species during the reaction working as a catalyst, suggesting that the mechanism of the reaction changes depending on the specific base. The kinetic studies using confidence intervals narrowed down the window of investigation by assessing the feasibility of different reaction pathways. This study presents novel identification of reaction conditions and additives leading to a change in mechanism, while elucidating the catalytic effect of a newly discovered species formed during the reaction. The findings resolve the previously conflicting explanation of the reaction pathways. The insights gained in this study can have significant implications for planning synthesis strategies for the SNAr reaction towards greener processes with higher yields. Furthermore, the finding of the new catalytic effect opens up new possibilities for optimizing reaction conditions and designing chemical processes in a broader context beyond the specific reaction studied. The approach can be also advantageous for conducting further detailed reaction mechanism analysis in cases where the intermediates are difficult to detect and where the reactions involve larger sized molecules of small molecule drugs. This approach can facilitate application of quantum chemistry calculation by speeding up the process of generating initial chemical structures for larger sized molecules with reduced time and computational cost.
1. Introduction
Amination via nucleophilic aromatic substitution (SNAr) is one of the most important reaction types in pharmaceutical synthesis.1 Heteroatom alkylation and arylation account for the most common reaction types used in the pharmaceutical industry, and N-arylation with aryl halide is the most used reaction in this category.1
There is an ongoing debate regarding the SNAr reaction mechanism. The generally accepted mechanism involves stepwise addition and elimination via a Meisenheimer complex (MC) as an intermediate.2,3 However, recent research using the kinetic isotope effect and computer analyses using density functional theory (DFT) calculation have provided convincing contradictory evidence about the mechanism of the reaction.4 According to a study, the SNAr reaction proceeds through a concerted pathway in most cases, with a stepwise pathway occurring only in special cases.4 Examples of such cases include when nitro substrates possess high levels of anionic resonance, or when fluoride substrates possess a poor leaving group. The reaction mechanisms from that work are shown in Scheme 1.
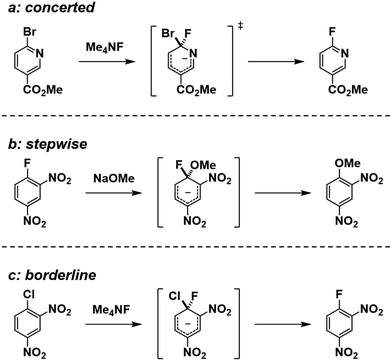 |
| | Scheme 1 Previously reported SNAr reaction mechanisms.4 | |
In the case of the SNAr reaction, a base is often added to enhance the reaction. A generally acceptable explanation would be that the addition of a base enhances the nucleophilicity of the reactant and accelerates the reaction. However, the role of the base in the mechanism has not been fully investigated.5,6 In our experiments, it was observed that the addition of a base resulted in a unique behaviour of the reaction system, which could not be explained by the conventional understanding of the reaction mechanism. The utilization of kinetic studies is well established in the field of chemical engineering. The kinetic studies offer an understanding of the reaction mechanism and determine reaction rate equations. This knowledge can be used to optimize chemical processes, predict the behaviour of a reaction under different conditions, and develop models that can be used for process simulation and optimization. The use of kinetic studies also extends to the pharmaceutical industry, where recent applications have included comparisons of batch and flow syntheses for doripenem,7 modelling the production of ibuprofen on a plant-wide scale,8 kinetic study of lomustine in flow synthesis,9 and the continuous manufacturing of acetylsalicylic acid.10 The purpose of this study is to improve the understanding of the SNAr amination reaction mechanism through a combination of experiments and kinetic studies. In this work, the kinetic study approach was applied to resolve the uncertainties regarding the reaction mechanism and to explore potential reaction pathways. The impact of the base addition on the reaction mechanism was also investigated, leading to new insights. The general workflow developed in this work can be applied to other reactions that have limited understanding or unresolved disputes regarding their mechanism.
2. Materials and methods
2.1. Experimental
Target reaction.
The overview of the target reaction is shown in Scheme 2. In this work, SM refers to the starting material (3,4-difluorobenzonitrile); MP refers to morpholine (tetrahydro-1,4-oxazine); DBU refers to diazabicycloundecene (2,3,4,6,7,8,9,10-octahydropyrimido[1,2-a]azepine); DP refers to the desired product (3-fluoro-4-morpholinobenzonitrile); MC refers to the Meisenheimer complex. The formation of a C–N bond occurs through the reaction between SM and MP, resulting in the formation of DP. As a by-product of this reaction, HF is generated, which is subsequently captured by the base (MP or DBU) that is present in the reaction system. Under the condition where only MP is used as a base, two moles of MP are consumed, with one being consumed by the reaction and the other reacting with the HF.
 |
| | Scheme 2 Target overall reaction to produce 3-fluoro-4-morpholinobenzonitrile. | |
General information.
All reactions were run under a nitrogen atmosphere. Solvents and reagents were purchased from commercial sources and used without further purification. 3,4-Difluorobenzonitrile (SM) was purchased from AstaTech Inc. Morpholine (MP) and 1,8-diazabicyclo[5.4.0]undec-7-ene (DBU) were purchased from Tokyo Chemical Industry Co., Ltd. Isopropyl acetate was purchased from Wako Pure Chemical Industries Ltd. The reaction was conducted using a Mettler Toledo Easy Max 102. HPLC analysis was carried out using a Shimadzu LC-2010CHT. 1H NMR spectra were recorded on a Bruker AVANCE III HD 400 MHz.
Typical batch procedure to obtain kinetic data.
A typical batch procedure was conducted to obtain kinetic data for 16 experimental runs, where material amounts and reactor temperatures were varied. Runs 1–3 tested the conditions where DBU was not added, but 2.0 eq. amount of MP was added instead. Runs 4–12 tested combinations of three different molality and temperature conditions. In run 13, the experiment was performed using equimolar amounts of all reagents. In each of runs 14–16, the amount of each reagent was increased to 2.0 eq., respectively. Table 1 shows the summary of the conditions used in each of the 16 runs. For example, in run 10 from Table 1, a solution of SM (1.39 g, 10.00 mmol) in iPrOAc (7.0 mL) was heated to 80 °C in a batch reactor (EasyMax 100 mL). MP (958.3 mg, 11.00 mmol, 1.1 eq.) and DBU (2.28 g, 15.00 mmol, 1.5 eq.) were added to the batch reactor sequentially. The reaction mixture was stirred using a three-blade retreat curve impeller at 400 rpm (maximum stirring speed in EasyMax) for 2.5 hours at 80 °C. 10 wt% aqueous solution of HCl (15 mL) was added to the reaction mixture. One sample of the reaction mixture (50 μL) was added to MeCN/H2O [9950 μL, 80/20 (v/v)] at regular intervals and analysed by HPLC.
Table 1 Experimental conditions
| Run |
SM [mmol] |
MP [mmol] |
DBU [mmol] |
Solvent [mL] |
Temperature [K] |
| 1 |
10 |
20 |
0 |
8.16 |
313 |
| 2 |
10 |
20 |
0 |
8.16 |
333 |
| 3 |
10 |
20 |
0 |
8.16 |
353 |
| 4 |
10 |
11 |
15 |
7.00 |
313 |
| 5 |
10 |
11 |
15 |
14.0 |
313 |
| 6 |
5.0 |
5.5 |
7.5 |
14.0 |
313 |
| 7 |
10 |
11 |
15 |
7.00 |
333 |
| 8 |
5.0 |
5.5 |
7.5 |
7.00 |
333 |
| 9 |
10 |
11 |
15 |
28.0 |
333 |
| 10 |
10 |
11 |
15 |
7.00 |
353 |
| 11 |
10 |
11 |
15 |
14.0 |
353 |
| 12 |
10 |
11 |
15 |
28.0 |
353 |
| 13 |
10 |
10 |
10 |
6.67 |
313 |
| 14 |
10 |
20 |
10 |
6.67 |
313 |
| 15 |
10 |
10 |
20 |
6.67 |
313 |
| 16 |
20 |
10 |
10 |
6.67 |
313 |
2.2. General methodology
The overall methodology to understand the reaction mechanism and acquire the corresponding models is shown in Fig. 1. Fig. 1(a) shows the overall workflow. The research process starts with a question regarding the reaction mechanism. If there is consensus regarding the understanding of the reaction mechanism and existing models fit the available experimental data, then the models can be directly used for process design and optimization. However in the case where there is limited understanding, there is contradicting theories on the reaction mechanism, or it is not possible to fit the model based on the commonly accepted understanding, then further steps should be taken to determine feasible reaction pathways and model generation. Fig. 1(b) shows the details of the required steps for model development. First, a priori knowledge and available experimental data are analysed to generate potential reaction pathways and the corresponding kinetic models. The models are tested to fit the experimental data, and the obtained parameter estimates with their confidence intervals are used to eliminate infeasible reaction pathways and refine the model hypotheses. Additional experiments can be conducted, and the cycle is repeated until sufficient mechanistic understanding is developed.
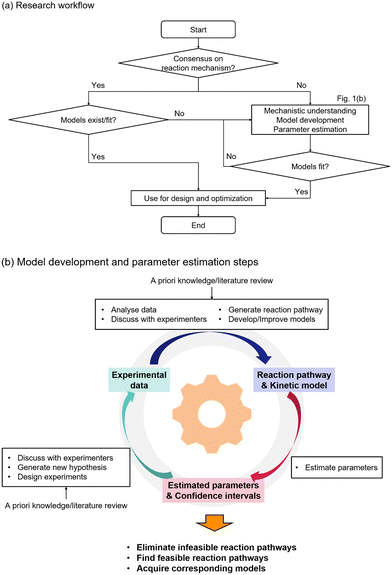 |
| | Fig. 1 Methodology of this research. (a) Research workflow and (b) model development and parameter estimation steps to eliminate infeasible reaction pathways, to identify feasible reaction pathways, and to acquire kinetic models. | |
2.3. Model equations and parameter estimation
Assuming homogenous conditions in a batch reactor, the general form of differential equations used in this study is shown in eqn (1). Here, i is the species, νj is the stoichiometric ratio, and rj is the reaction rate of reaction route j. The Arrhenius equation used in this study is shown in eqn (2), and the pre-exponential factor and activation energy were the parameters fitted to the experimental data. Different reaction mechanisms were investigated in the kinetic study to identify the most fitting pathways or to eliminate infeasible ones. Detailed model equations are provided for each investigated reaction mechanism either in the following section or in the ESI.†| |  | (1) |
| |  | (2) |
The Runge–Kutta method was used to solve the ordinary differential equations. Python 3.7.11 was used to implement the algorithm. To evaluate the fitting accuracy, the coefficient of determination was used in this study and is shown in eqn (3). It is calculated using the sum of squares of residuals and the total sum of squares. Minimizing the coefficient of determination allows for minimizing the squared residuals considering multiple materials, experiments, and conditions at once during the parameter fitting. Here, yi and yj are the measured values, fi is the estimated value, and ȳ is the mean of the measured values. The objective function in the parameter estimation is shown in eqn (4). Here, l is the experiment run, m is the species (SM or DP in this study), and n is the number of data points (which varies for different experimental runs). The vector of fitted parameters for each reaction pathway θ is summarized in Table 2. The minimisation was performed using Python's Nelder–Mead technique from the scipy.optimize.minimize package.11 Both constrained and unconstrained minimizations were tested for the parameter estimation. The constrained approach ensured that the parameter values remained positive. The initial parameter values were examined over a broad range to detect the ranges of solutions with high accuracy and stability. The confidence intervals were determined using the Levenberg–Marquardt technique and the lmfit minimisation package.12
| |  | (3) |
| | | min(∑ − Rl,m2(Cnexp, Cncal(θ))) | (4) |
Table 2 Summary of the fitted parameters for each modelled case. A1 and E1 were initially estimated using runs 1–3, and then kept fixed for subsequent parameter estimations
| Reaction pathway |
Fitting parameters |
| Reaction pathway without DBU |
A
1, E1 |
| Reaction with DBU based on concerted pathways |
A
2, E2 |
| Reaction with DBU based on stepwise pathways |
A
5, A6, E5, E6 |
| Reaction with DBU based on the proposed reaction pathways: (a) concerted and (b) stepwise with a reverse reaction |
A
2, A3, A4, A−3, E2, E3, E4, E−3 |
| Reaction with DBU based on the proposed reaction pathways: (a) concerted and (b) stepwise without a reverse reaction |
A
2, A3, A4, E2, E3, E4 |
| Reaction with DBU based on the proposed reaction pathways: (a) concerted and (b) concerted |
A
2, A7, E2, E7 |
3. Kinetic study of the amination reaction
3.1. Investigation of the amination reaction
The developed workflow was applied to resolve the uncertainty around the SNAr amination reaction and to test the feasibility of the conflicting mechanisms shown in Scheme 1, specifically, the concerted and stepwise reaction pathways.
Runs 1–3 were conducted to investigate the role of the base in the reaction. They were conducted in the presence of additional MP instead of DBU addition. Scheme 3 shows the potential reaction pathways without DBU. Scheme 3(a) shows both the concerted and stepwise reaction pathways. The concerted pathway refers to either the concerted or short-lived intermediate pathway, and the stepwise pathway refers to either the stepwise or long-lived transition state pathway. Parameter estimation was conducted for both pathways. The stepwise pathway could not be fitted well to the experimental results with a high accuracy. Improved accuracy in the fitting results can only be achieved when the parameter values were not constrained and became negative. It is worth noting that the experimental data, in this case, did not exhibit sigmoidal patterns in the product concentration profile, which is a characteristic of stepwise reactions. This could be used to further confirm the elimination of the stepwise pathway in this case. The concerted pathway, on the other hand, provided a satisfactory match to the experimental data with feasible solutions for the pre-exponential factor and activation energy, indicating that the reaction is carried out in a concerted manner (or with a short-lived intermediate). Scheme 3(b) shows the detailed reaction mechanism for the concerted pathway. The generated corresponding model equations are given in section S1 in the ESI.†Fig. 2 shows the kinetic analysis results for runs 1–3 using the concerted pathway. The high accuracy of the fit (the coefficients of determination for SM and DP are shown above the graphs) confirms the hypothesis of a concerted pathway in the absence of DBU.
 |
| | Scheme 3 Reaction without DBU. (a) Two potential reaction pathways, concerted and stepwise and (b) a detailed illustration of reaction mechanism for the concerted pathway which was found to fit the experimental data (runs 1–3) well. | |
 |
| | Fig. 2 Kinetic study results for the conditions without DBU based on the concerted pathways in Scheme 3(b). | |
Subsequently, the kinetic investigation was conducted in the presence of DBU (runs 4–16). Scheme 4 shows the reaction with DBU, with two potential pathways presented in Scheme 4(a): the concerted reaction, in which MC exists as a transition state, and the stepwise reaction, in which MC exists as an intermediate. Scheme 4(b) and (c) show the detailed reaction mechanisms for the concerted and stepwise pathways, respectively.
 |
| | Scheme 4 Reaction with DBU. (a) The overall reactions with two potential reaction pathways; (b) and (c) detailed steps in the reaction pathways of the concerted and stepwise, respectively. | |
The concerted route was the first to be examined, as it was successfully identified in the previous runs without DBU. The results of fitting the experimental data in the presence of DBU to this route were unsatisfactory. The generated corresponding model equations are given in section S2 in the ESI.†Fig. 3 depicts the best results obtained for fitting the experimental data for runs 4, 5, and 6. Similar results were obtained for the other runs (runs 7–16). The complete set of results for runs 4–16 is shown in ESI† Fig. S1. The error could not be minimized further from the results shown in Fig. 3, despite the wide range of employed initial parameter values for the pre-exponential factor and activation energy. The concentration profiles of both SM and DP in the experimental data exhibited sigmoidal profiles. This is consistent with our conclusion about the change in reaction mechanism since such sigmoidal profiles cannot be observed in the case of concerted reaction routes.
 |
| | Fig. 3 Kinetic study results for the conditions with DBU based on the concerted pathways in Scheme 4(b). | |
Stepwise reaction pathways were then kinetically examined and fitted to the experimental data. Scheme 4(c) shows the detailed stepwise reaction pathways, and Fig. 4 shows the results of the kinetic study based on the stepwise pathways for runs 4, 5, and 6 as an example (the complete set of results for runs 4–16 is shown in section S3 in the ESI†). Sigmoidal patterns are more common for the final products than for the starting materials in stepwise reactions. A potential explanation for the sigmoidal patterns in SM was that SM and MC could not be distinguished in the measurements due to similarities in their structures. As such, the sigmoidal profiles would be the result of the sum of SM and MC in the measurements, which was taken into consideration for the calculation of SM values in Fig. 4 and S2 in the ESI.† The sigmoidal profile could be captured for both SM and DP in runs 4 and 5. However, while concentrations at earlier time points were relatively well captured, deviations were observed after some time, yielding poor fitting results. The simulated reactions were slower at later time points than those in the experiments. All other run simulations also showed discrepancies when compared to the experimental results. The sigmoidal profile is not visible in lower concentration conditions, for example in run 6. Reaction pathways with a reverse reaction were also examined in this case. However, they could also not be well fitted to the data, and the accuracy showed no significant improvement.
 |
| | Fig. 4 Kinetic study results for the conditions with DBU based on the stepwise pathways in Scheme 4(c). | |
As a satisfactory conclusion regarding the reaction mechanism could still not be reached, a new cycle of model development was initiated, according to Fig. 1(b). A new hypothesis was generated based on literature review of other reactions involving DBU. The hypothesis was strengthened through discussions with industrial experts.
3.2. New proposed reaction pathways
We deduced from the results in Fig. 4 that one or more species that were generated during the reaction accelerated the reaction in the later stages. DP or DBU·HF were two possible candidates. DP may speed up the reaction by having π–π interactions with SM. This interaction, on the other hand, can occur in the absence of DBU and is not limited to the conditions with DBU. A more likely explanation involves the interactions of DBU·HF. According to a previous study,13 DBUH+ can potentially interact with electrophiles and/or π bonds in an addition–cyclization reaction. Assuming that the presence of equivalent interactions in the nucleophilic substitution reactions would be consistent with the results from our experiments, DBUH+ can catalyse the reaction by activating SM. DBUH+ can interact with the fluorine in the para position of SM or with the π bonds in SM. The latter is more feasible from the standpoint of hard and soft acid and base (HSAB) theory. Therefore, we further conducted a kinetic analysis based on this new hypothesized reaction pathway.
Scheme 5 depicts the potential new reaction pathways, including one (a) that is accelerated by DBU and another (b) that is triggered by DBUH+. For each, a concerted or stepwise reaction pathway was considered, resulting in a total of four possibilities. The consideration of a reverse reaction in the stepwise pathway results in more possibilities.
 |
| | Scheme 5 Potential new reaction pathways including one (a) that is accelerated by DBU and another (b) that is initiated by DBUH+. The final proposed reaction pathways exclude the stepwise option in reaction pathway (a). | |
After investigating all possibilities, it was observed that satisfactory results could be achieved when the reaction route in Scheme 5(a) was considered as concerted, independent of the considerations for the reaction route (b). When the reaction pathway (a) was regarded as stepwise, the pre-exponential factor in the second stage of the stepwise reaction could not be determined. The solutions could not be obtained within the given tolerance range. Therefore, we concluded that the reaction (a) follows a concerted pathway (or a short-lived intermediate route).
If the reaction pathway (a) is fixed as concerted, then three possible pathways for the reaction route (b) remain as shown in Scheme 5, including stepwise with a reverse reaction, stepwise without a reverse reaction, and concerted pathways. Scheme 6 shows a detailed description of the pathway with concerted (a) and stepwise (b) with a reverse reaction. Scheme 7 shows the pathway without a reverse reaction for stepwise (b). Meanwhile Scheme 8 shows the pathway with concerted (a) and concerted (b).
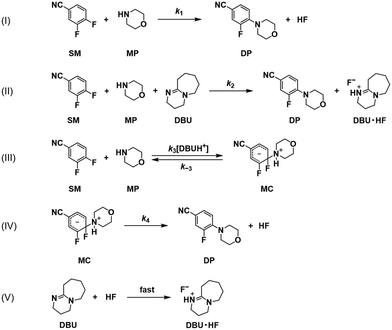 |
| | Scheme 6 Detailed reaction pathways with concerted (a) and stepwise (b) with a reverse reaction in Scheme 5. | |
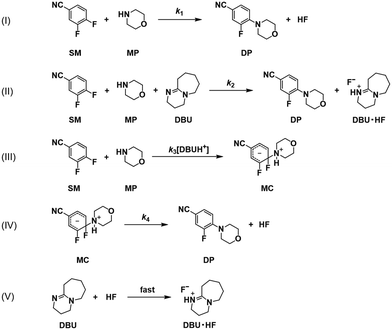 |
| | Scheme 7 Detailed reaction pathways with concerted (a) and stepwise (b) without a reverse reaction in Scheme 5. | |
 |
| | Scheme 8 Detailed reaction pathways with concerted (a) and concerted (b) in Scheme 5. | |
Model development.
The models developed based on the reactions in Scheme 6 are shown in eqn (5)–(15). The models for Schemes 7 and 8 are presented in section S5 and S6 in the ESI.† The HF dissociation was considered in the reaction network, where the HF was assumed to react instantly with the strongest base in the mixture. Under the conditions where MP is present, HF reacts with it resulting in the consumption of two moles of MP (one being consumed by the reaction to give DP and the other reacting with HF), and under the conditions where a stronger base, DBU, is present, it reacts selectively with DBU, where the reaction of HF with DBU results in the formation of DBUH+.The kinetic study was conducted by solving the following differential equations of a batch reactor (eqn (10)–(15)).| |  | (10) |
| | 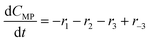 | (11) |
| | 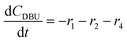 | (12) |
| |  | (13) |
| |  | (14) |
| |  | (15) |
Model fitting and parameter estimation.
A good fit was obtained for Schemes 6–8 as shown in Fig. 5–7, respectively. Results for runs 4, 5, and 6 are shown in the figures as an example (the complete results for runs 4–16 are shown in Fig. S3–S5†). The calculation results showed a good match to the experimental data. The unique sigmoidal profiles in both SM and DP could be well described. The consideration of the catalytic effect of DBUH+ to accelerate the reaction resulted in a good model fit for all reaction runs (runs 4–16) throughout the duration of each experimental run. Narrow confidence intervals were also obtained, indicating high parameter certainty. T-Tests were conducted to compare the experimental data to the simulated results. Table 3 shows the t- and p-values for each reaction pathway in Schemes 6–8, which were calculated for the reference, upper, and lower boundaries. The simulation used the estimated parameter values for the reference, and the boundaries were determined based on the confidence intervals. The upper boundaries correspond to the largest pre-exponential factor and lowest activation energy values within the confidence intervals, and vice versa. The p-values were all above 0.05, indicating no significant difference between the experimental data and simulated results with parameter values within the confidence intervals. This confirms the reproducibility of the models and the narrow confidence interval ranges. Narrowing down the reaction pathway further could not be achieved with the available data. As a result, three potential pathways can explain the observed sigmoidal patterns, which are (a) concerted and (b) concerted, (a) concerted and (b) stepwise with a reverse reaction, and (a) concerted and (b) stepwise without a reverse reaction, but this kinetic study alone cannot differentiate further.
 |
| | Fig. 5 Kinetic study results for Scheme 6, with (a) concerted and (b) stepwise pathways with a reverse reaction in Scheme 5. | |
 |
| | Fig. 6 Kinetic study results for Scheme 7, with (a) concerted and (b) stepwise pathways without a reverse reaction in Scheme 5. | |
 |
| | Fig. 7 Kinetic study results for Scheme 8, with (a) concerted and (b) concerted reaction pathways in Scheme 5. | |
Table 3
T-Test results comparing the experimental data to the simulated results. The t- and p-values for each reaction pathway in Schemes 6–8 are given for the reference, upper, and lower boundaries
|
T-Test values |
(a) Concerted |
(a) Concerted |
(a) Concerted |
| (b) Stepwise with a reverse reaction |
Stepwise without a reverse reaction |
(b) Concerted |
| Reference |
Upper |
Lower |
Reference |
Upper |
Lower |
Reference |
Upper |
Lower |
|
t-Value |
−0.275 |
−0.275 |
−0.275 |
−0.273 |
−0.273 |
−0.273 |
−0.274 |
−0.274 |
−0.274 |
|
p-Value |
0.784 |
0.784 |
0.784 |
0.785 |
0.785 |
0.785 |
0.784 |
0.784 |
0.784 |
3.3. Discussion
Kinetic studies were used to identify reaction routes, as well as to gain insights into the reaction mechanism. The sigmoidal profiles could be well fitted by considering DBUH+ catalysed reaction pathways. Sigmoidal profiles were not observed under the conditions without DBU (runs 1–3 in Table 1). In runs 1–3, MP, which is also a base, was added in excess. The generated HF was captured by MP, and MPH+ was generated. However, similar sigmoidal patterns were not observed in the presence of MPH+, which demonstrates the unique role of DBUH+ in this reaction. The electron delocalization with DBUH+ makes it a soft acid to interact with SM, which is a soft base, in contrast to MPH+, where the electronic charge cannot be delocalized. This could support the hypothesis concerning the role of DBUH+ in activating the reaction through the interaction with π bonds in SM. Expanding the range of the experiments to test other substrates and bases would help further clarify their roles in the reaction. This would help to categorize the catalytic effects observed in this study for further utilization in different reactions.
The insights gained in this study can aid in the planning of synthesis strategies for the SNAr reaction when adding DBU as a base. In our experiments, the generated HF reacts with the reactant MP if DBU is not available in excess, causing a decrease in yield. To avoid the yield loss, in this case, addition of an excess amount of a base (DBU or MP in this case) is necessary. The decision of which base to add could be based on different environmental indicators, e.g., process mass intensity (PMI), or safety considerations based on the properties of each reagent. As a result, greener alternatives can be evaluated. Furthermore, further acceleration of the reaction could be achieved by adding a catalytic amount of DBUH+ at the start of the reaction. This can support reaction condition optimization towards a greener process with a higher yield and reduced reaction time.
We found that sigmoidal profiles can be well described in both SM and DP concentrations with the new proposed pathways, where the generated species, during the reaction, subsequently accelerate it. We also found that the sigmoidal characteristic in the SM profile can be rationalized by the assumption that the starting material and intermediate are detected as one compound in the measurements.
The ability to fit model parameters with narrow confidence intervals provided a decent insight into the feasibility of different reaction pathways examined in the kinetic studies. In this study, the confidence intervals could aid in eliminating infeasible reaction pathways, e.g., the stepwise pathway in Scheme 5(a). It is worth noting that inter-parameter correlations may exist, particularly in instances of a stepwise reaction with a reverse reaction pathway where the intermediate species is not experimentally measured. However, the results of this analysis were highly accurate and did not hinder the ability to eliminate mechanisms that could not be fitted.
In some cases, such as the reaction in Scheme 5(b), this kinetic investigation may not be sufficient to determine one reaction pathway. Further investigation using quantum chemistry calculation may aid in determining precise reaction mechanisms or other aspects such as the electronic structure, bonding, and energetics of the reacting molecules. The kinetic studies with confidence intervals, on the other hand, can narrow the window that should be examined in further analysis. The kinetic study approach is particularly advantageous for such cases where the intermediates are difficult to detect14,15 and where the reactions involve larger sized molecules in small molecule drugs. This can aid in the application of quantum chemistry calculation by providing the chemical structures for the examination. This can reduce the time and computational cost of such analysis for larger sized molecules.
The novelty of this work is in the elucidation of the mechanism of the amination reaction in the presence of different bases through the application of a kinetic modelling approach. In addition, the methodology presented in this work can be extended to other systems where a consensus could not be reached regarding the reaction mechanism. Additionally, the approach can be used for transitioning from batch to flow or vice versa, where the mechanism or equations can be different.16 The method can also be useful for studying fast reactions in flow chemistry, such as Grignard reactions. The in silico exploration using the developed models from the methodology can save time and experimental cost while determining optimal operating conditions, such as design space,17 without the need for excessive physical experimentation.
4. Conclusions
Comprehensive kinetic studies were conducted to enhance the mechanistic understanding and assess the feasibility of different reaction pathways in an amination reaction via nucleophilic aromatic substitution. A general workflow was developed to resolve contradictions in the reported reaction pathways. The resulting kinetic studies were used to identify new reaction pathways, which were able to better fit different reaction conditions. In the new pathways, the generated DBUH+ was identified as a catalyst, which enhanced the performance in later reaction phases and yielded the unique sigmoidal profiles in both SM and DP. This finding challenges the existing assumptions and provides new insights into the underlying mechanisms of the reaction. The implications of these insights can be significant in terms of planning synthesis strategies for the SNAr reaction and chemical processes in a broader context beyond the specific reaction studied.
Abbreviations
| SM | Starting material, 3,4-difluorobenzonitrile |
| MP | Morpholine, tetrahydro-1,4-oxazine |
| DBU | Diazabicycloundecene, 2,3,4,6,7,8,9,10-octahydropyrimido[1,2-a]azepine |
| DP | Desired product, 3-fluoro-4-morpholinobenzonitrile |
| MC | Meisenheimer complex |
Nomenclature
|
A
|
Adjusted pre-exponential factor |
h−1 or m3 mol−1 h−1 or m6 mol−2 h−1 |
|
C
cal
|
Calculated concentration |
mol m−3 |
|
C
exp
|
Concentration in experiments |
mol m−3 |
|
C
i
|
Concentration of i |
mol m−3 |
|
E
|
Activation energy |
J mol−1 |
|
i
|
Compound (SM, MP, DBU, DP, MC, DBUH+) |
|
|
k
|
Reaction rate constant |
h−1 or m3 mol−1 h−1 or m6 mol−2 h−1 |
|
R
|
Gas constant |
J K−1 mol−1 |
|
R
2
|
Coefficient of determination |
— |
|
r
j
|
Reaction rate of reaction j |
mol m−3 h−1 |
|
T
|
Temperature |
K |
|
t
|
Time |
h |
|
θ
|
Vector of fitting parameters for each reaction pathway |
|
Author contributions
Junu Kim: conceptualization, data curation, formal analysis, investigation, methodology, software, visualization, writing – original draft, and writing – review & editing. Yusuke Hayashi: conceptualization and writing – review & editing the draft. Sara Badr: conceptualization and writing – review & editing the draft. Kazuya Okamoto: data curation and writing – review & editing the draft. Toshikazu Hakogi: data curation and writing – review & editing the draft. Haruo Furukawa: writing – review & editing the draft. Satoshi Yoshikawa: writing – review & editing the draft. Hayao Nakanishi: writing – review & editing the draft. Hirokazu Sugiyama: conceptualization, funding acquisition, project administration, resources, supervision, and writing – review & editing the draft.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
The study was funded by a research grant from Shionogi Pharma Co., Ltd. J. K. is thankful for the financial support from the Leading Graduate Schools Program, “Global Leader Program for Social Design and Management”, by the Ministry of Education, Culture, Sports, Science and Technology.
References
- S. D. Roughley and A. M. Jordan, J. Med. Chem., 2011, 54, 3451–3479 CrossRef CAS PubMed.
-
A. Williams, Concerted organic and bio-organic mechanisms, CRC Press, 2000 Search PubMed.
-
F. Terrier, Modern nucleophilic aromatic substitution, Wiley-VCH, 2013, https://onlinelibrary.wiley.com/doi/book/10.1002/9783527656141 Search PubMed.
- E. E. Kwan, Y. Zeng, H. A. Besser and E. N. Jacobsen, Nat. Chem., 2018, 10, 917–923 CrossRef CAS PubMed.
- C. Sun, W. Yao, X. Chen, Y. Zhao, Q. Wei, Z. Chen, J. Wu, F. Hao and H. Xie, ACS Omega, 2019, 4, 10534–10538 CrossRef CAS PubMed.
- R. P. Tangallapally, R. Yendapally, R. E. Lee, A. J. M. Lenaerts and R. E. Lee, J. Med. Chem., 2005, 48, 8261–8269 CrossRef CAS PubMed.
- J. Kim, H. Yonekura, T. Watanabe, S. Yoshikawa, H. Nakanishi, S. Badr and H. Sugiyama, Comput. Chem. Eng., 2022, 156, 107541 CrossRef CAS.
- F. C. C. Montes, K. Gernaey and G. Sin, Ind. Eng. Chem. Res., 2018, 57, 10026–10037 CrossRef CAS.
- S. Diab, M. Raiyat and D. I. Gerogiorgis, React. Chem. Eng., 2021, 6, 1819–1828 RSC.
- B. Nagy, B. Szilágyi, A. Domokos, B. Vészi, K. Tacsi, Z. Rapi, H. Pataki, G. Marosi, Z. K. Nagy and Z. K. Nagy, Chem. Eng. J., 2021, 419, 129947 CrossRef CAS.
- scipy.optimize.minimize — SciPy v1.9.3 Manual, https://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.minimize.html, (accessed 21 November 2022).
- Performing Fits and Analyzing Outputs — Non-Linear Least-Squares Minimization and Curve-Fitting for Python, https://lmfit.github.io/lmfit-py/fitting.html#, (accessed 21 November 2022.
- P. Zhao, Q. Liao, H. Gao and C. Xi, Tetrahedron Lett., 2013, 54, 2357–2361 CrossRef CAS.
- M. P. Mower and D. G. Blackmond, J. Am. Chem. Soc., 2015, 137, 2386–2391 CrossRef CAS PubMed.
- D. G. Blackmond and D. G. Blackmond, Angew. Chem., Int. Ed., 2005, 44, 4302–4320 CrossRef CAS PubMed.
- J. Kim, Y. Hayashi, S. Badr, H. Nakanishi and H. Sugiyama, Chem. Eng. Res. Des., 2023, 189, 156–166 CrossRef CAS.
- S. Diab, C. Christodoulou, G. Taylor and P. Rushworth, Org. Process Res. Dev., 2022, 26, 2864–2881 CrossRef CAS.
|
| This journal is © The Royal Society of Chemistry 2023 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article a,
Yusuke
Hayashi
a,
Yusuke
Hayashi
 a,
Sara
Badr
a,
Sara
Badr
 a,
Kazuya
Okamoto
b,
Toshikazu
Hakogi
b,
Haruo
Furukawa
b,
Satoshi
Yoshikawa
c,
Hayao
Nakanishi
c and
Hirokazu
Sugiyama
a,
Kazuya
Okamoto
b,
Toshikazu
Hakogi
b,
Haruo
Furukawa
b,
Satoshi
Yoshikawa
c,
Hayao
Nakanishi
c and
Hirokazu
Sugiyama
 *a
*a