 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Impact of residence time distributions in reacting magnesium packed beds on Grignard reagent formation – pump-induced flow behaviour in non-reacting magnesium beds (part 1)†
Eva
Deitmann
ab,
Michael
Maskos
a,
Gabriele
Menges-Flanagan
 *a and
Dirk
Ziegenbalg
*a and
Dirk
Ziegenbalg
 *b
*b
aFraunhofer IMM, Carl-Zeiss-Strasse 18-20, 55129 Mainz, Germany. E-mail: gabriele.menges-flanagan@imm.fraunhofer.de
bUlm University, Helmholtz-Strasse 16, 89081 Ulm, Germany. E-mail: dirk.ziegenbalg@uni-ulm.de
First published on 28th June 2023
Abstract
Grignard reagent formation in continuously operated magnesium packed-bed reactors can be influenced by fine tuning the residence time distribution within the magnesium packing. By decreasing the magnesium turning size and increasing the packing density, narrower residence time distributions and therefore improved Bodenstein numbers can be obtained. The utilized pump system and its induced flow behaviour also have an impact on the residence time distributions in packed-bed reactors. By using oscillatory flow rates instead of pulsation-free pumps, Bodenstein numbers within a magnesium filled reactor cartridge can be increased by 25% for fine magnesium turnings and by 70% for coarse magnesium turnings, resulting in minimized backmixing and approaching plug flow behaviour.
Introduction
Organomagnesium halides, also known as Grignard reagents, are important intermediates for the formation of new carbon–carbon bonds in synthetic chemistry. In the pharmacy sector, they became especially useful for the formation of active pharmaceutical ingredients, e.g. pain-reliever ibuprofen and breast cancer drug tamoxifen.1 Grignard reagents originate from an exothermic reaction of metallic magnesium (mostly powder or turnings) and a halide in a water free ethereal solvent. Side product formation due to the Wurtz coupling reaction can occur, in which a Grignard reagent molecule (product) reacts with a halide molecule (educt), diminishing the yield of the Grignard reagent.2 Therefore, reducing the contact between the formed Grignard reagent and the halide educt would prevent Wurtz coupling. Consequently, residence time distributions (RTDs) in tubular flow reactors equipped with a packed bed of magnesium turnings will have an impact on product distribution. To minimize the contact between the halide educt and the Grignard reagent, a plug-flow like behaviour is favourable, ideally having a constant velocity across the cross-section of the tube and no backmixing, resulting in a narrow residence time distribution. The residence time distribution of chemical reactors depends on the flow and mixing conditions and is a long-known tool of reactor development to estimate the hydrodynamic characteristics of a reactor. The data obtained can also be used to make statements about the average residence time of a volume element within the investigated system, and by applying a model, the dimensionless Bodenstein number Bo can be estimated.Several approaches to realize near-plug flow behaviour within continuously operated reactor systems do exist, which are focused on the manipulation of the fluid flow itself, on separating a bigger reactor into a number of smaller reactors or on a combination of both principles, e.g. operating tubular reactors within a turbulent flow regime, application of static mixers or structured microchannels and application of several stirred tank reactors in series. Operating tubular reactors in a turbulent flow regime results in a plug flow-like velocity profile, but high flow rates are required to achieve turbulent flow, resulting in short residence times, which requires long reactors and increases capital costs.3 Static mixers and structured microchannels can achieve a mixing effect even in laminar flow by repeatedly separating, rearranging and merging the flow.4,5 A cascade of continuously stirred tank reactors also exhibits a residence time distribution similar to a plug flow reactor but requires formally an infinite number of tanks.3,6 Except for the application of a turbulent flow profile in a tubular reactor, the other concepts are not applicable for packed-bed reactors and are difficult to realize when a solid reactant is involved. Another concept to narrow residence time distributions and minimize backmixing, finally approaching plug flow behaviour and high Bodenstein numbers under laminar conditions, is the application of continuous oscillatory baffled reactors (COBRs). The COBR is a tubular reactor with internal baffles, which are equidistantly spaced. By superimposing an oscillating flow on the main flow, vortices are generated at the backside of the baffles that cause intense mixing within the vortices and improved heat and mass transfer.7 Mixing is decoupled from the net flow rate and depends on the oscillation conditions and the configuration of the oscillatory reactor. While maintaining intense convection due to the oscillation, low flow rates are possible, allowing for a compact set-up with reduced axial dispersion.8 This oscillatory flow concept utilising baffles or even without baffles has been used not only for gas–liquid9–16 and liquid–liquid reaction systems17–21 but also for solid-containing22–31 reaction systems. The platform SciFinder refers to 3782 publications from 1950 to 2022 considering the term “oscillatory flow” with a steady increase in publications per year, showing the rising interest in and application of this reactor concept. Some literature reviews do exist, dealing with the concept of oscillatory flow reactors (OFRs) and giving an overview of the broad potential and applications of this specific reactor type.3,8,32–35 Investigated solid-containing reaction systems operated under oscillating flow conditions consider solid particles being suspended in the fluid on the one hand27–29,31 and being placed in packed beds on the other hand.23,24,30,36–38 For packed beds, the application of baffleless reactors36,39,40 and baffled reactors23,24,30,41,42 is mentioned in the literature. Considering a baffleless packed bed of spherical particles, the relationship between axial dispersion and the amplitude and frequency of the superimposed oscillatory flow was found to be similar to that in baffled columns.36 When increasing the amplitude from zero, the axial dispersion decreases with increasing amplitude towards a minimum. A further increase in amplitude results in an increase in axial dispersion. A minimum in axial dispersion could be found at an amplitude similar to the particle size.36 Mostly spheres or beads are studied packing materials, which have a uniform, round shape and can be packed as a homogeneous bed. Other materials like Raschig rings and static mixers are investigated only occasionally, though they can be considered as uniform materials as well since every element has the same geometry and dimensions. The application of non-uniform, non-spherical particles as a packing material results in broadened particle size distributions, a random, non-homogeneous packing and increased potential for disturbances in flow. The impact of pump-induced flow behaviour and oscillatory flow on residence time distributions within these types of packed beds is not reported in the literature yet.
In the case of the flow tube reactor used in this publication, it is not a COBR type reactor, but a tubular reactor fitted with a packed bed of non-uniform, non-spherical magnesium turnings. The magnesium turnings in the reactor cartridge present obstacles to the flow through the reactor, influencing flow behaviour, so the fluid usually does not flow through the reactor in a uniform way. By using different pumps (syringe pump, pulsating valveless rotary piston pump and pulsation-free micro annular gear pump) and by applying oscillating flow conditions, the residence time distribution of the magnesium-filled reactor cartridge and its dependence on the pump-induced flow behaviour were determined and the Bodenstein numbers and mean residence times were calculated to draw conclusions on the general applicability of oscillatory flow for baffleless, non-homogeneous and randomly packed beds of a non-uniform and non-spherical packing material. In part 2 of this publication, the impact of residence time distribution and backmixing on the selectivity of Grignard reagent formation was investigated by utilizing the synthesis of benzylmagnesium bromide. This exemplary synthesis is prone to Wurtz coupling and a specific application example of the reactor system described within this part 1 of the publication.
Experimental section
Investigated reactor concept
The investigated reactor is a laboratory-scaled tubular reactor designed by Fraunhofer IMM and manufactured by 3D laser melting for the formation of organomagnesium halide reagents.43,44Fig. 1 shows the reactor in more detail.It consists of a reactor cartridge and a replenishment unit that can be attached to the main reactor body for replenishing metal turnings during organometallic halide reagent synthesis. Since the reactor is used for Grignard reagent synthesis, the residence time measurements are performed by utilizing a reactor cartridge filled with magnesium turnings. Although the reactor cartridge including the magnesium packing is used for the synthesis of magnesium-based organometallic halide reagents and, as a result, the magnesium packing is being subject to continuous change during synthesis, the actual state of the magnesium bed at the beginning of the synthesis is used to determine the residence time distributions, i.e., without taking synthesis into account.
Materials and methods for residence time measurements
All solvents and reagents are used without further purification: magnesium turnings (coarse: Merck KGaA, fine: Almamet GmbH), tetrahydrofuran (>99.9%, p.a., Th. Geyer GmbH & Co. KG), and toluene (≥99.7%, Honeywell International Inc.).The following pumps are used: Postnova syringe pump with 2.5 mL Hamilton glass syringes, Landgraf syringe pump with a syringe size depending on the amplitude and frequency to be achieved (B. Braun Melsungen GmbH), HNP micro annular gear pump, and Ismatec valveless rotary piston pump. Further details on the specific pumps are mentioned in Table 1.
| Pump | Pump type | Pump name | Manufacturer | Operating conditions |
|---|---|---|---|---|
| A | Syringe pump | PN1610 syringe dosing system | Postnova Analytics GmbH | Flow rate: max. 20 mL min−1 (2.5 mL syringes) |
| B | Syringe pump | LA-120 | Landgraf Laborsysteme HLL GmbH | Stroke volume: depending on syringe size |
| No limits on the number of withdrawing/dosing cycles per minute noted but pump is not designed for frequent changes | ||||
| Flow rate: max. 35 mL min−1 (depending on syringe size) | ||||
| C | Micro annular gear pump | mzr-7205 | HNP Mikrosysteme GmbH | Flow rate: 0.048–288 mL min−1 |
| Dosing precision: variation coefficient <1% | ||||
| D | Valveless rotary piston pump | Reglo-CPF digital with ISM321 drive and RH1CKC pump head | Ismatec, Cole-Parmer Instrument Company LTD | Stroke volume: 10–100 μl |
| Speed: 40–1800 min−1 | ||||
| Flow rate: 0.40–180 mL min−1 | ||||
A Matrix-MF infrared (IR) spectrometer with a diamond micro ATR probe from Bruker Optik GmbH is used for concentration measurements. Experimental data are recorded using the software OPUS (version 6.5, Bruker Optik GmbH).
The residence time measurements are conducted by using the displacement marking method (step function), in which a tracer-free inlet flow is exchanged for a tracer-containing flow (or vice versa) of the same size at time t = 0. Toluene is selected as the tracer substance (toluene peak at 732 cm−1), since it does not react with the magnesium metal and can be used as a solvent in Grignard reagent synthesis as well.45,46 Since residence time determinations under reactive synthesis conditions are also planned in the further course of the investigations (see part 2), the tracer must also behave inertly towards the chemicals used in the Grignard reagent synthesis and in particular towards the Grignard reagent itself, and the chosen analytics in terms of hardware and software must not be affected in a negative way by the chemicals.
Evaluation of residence time measurements
The evaluation of the measurement data obtained by IR spectroscopy is done by using the dispersion model, considering an open system in terms of dispersion, meaning that dispersion can also occur across the inlet and the outlet of the reaction section. The dispersion model is used to describe nonideal tubular reactors and it takes into account that a deviation from the ideal plug flow can occur in real tube reactors by means of axial dispersion superimposed onto the bulk flow, leading to a parabolic velocity profile.47 Axial dispersion can occur due to molecular diffusion and backmixing, introduced by turbulent eddies and fluctuations in velocity. The dimensionless number to describe these effects is the axial dispersion coefficient Dax, which is considered constant throughout the reaction section.48The residence time distribution can be defined by the cumulative distribution function F(t) (eqn (1), dimensionless form), describing the volume fractions leaving a reactor in a residence time between 0 (entering reactor volume) and t, and by the residence time distribution function E(t), describing the probability of a volume element leaving the reactor at a certain time t. Eqn (2) represents the dimensionless distribution function for a nonideal flow tube reactor under consideration of the dispersion model and an open system in terms of dispersion.
 | (1) |
 | (2) |
![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) . The mean residence time
. The mean residence time ![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) resembles the time after which 50% of a tracer substance has left the reactor. The hydrodynamic residence time τ is the ratio of the reactor volume VR and the volumetric flow rate
resembles the time after which 50% of a tracer substance has left the reactor. The hydrodynamic residence time τ is the ratio of the reactor volume VR and the volumetric flow rate ![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) . For an ideal plug flow behaviour in which every fluid element experiences the same residence time, τ equals
. For an ideal plug flow behaviour in which every fluid element experiences the same residence time, τ equals ![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) .
. | (3) |
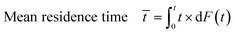 | (4) |
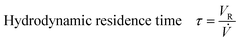 | (5) |
![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) (eqn (4)).
(eqn (4)). | (6) |
Procedure for determination of magnesium turning size distribution
To obtain a representative sample for particle size measurements, the method of “coning and quartering” is used, in which a larger sample quantity is piled up into a uniform cone and divided into four equal parts with the aid of a dividing cross. Two opposing quarters are combined and quartered again using the dividing cross until a suitable magnesium turning quantity is obtained.Using a transmitted light stage, high resolution photographs of the prepared magnesium turning samples are taken. For this, magnesium turnings were spread out to avoid touching each other. These photos were then analysed using ImageJ Particle Size Analyzer software to determine the maximum and minimum Feret diameter. Assuming that the magnesium turnings are flat and angular, the maximum Feret diameter should be slightly larger than the actual magnesium turning length and the minimum Feret diameter should be approximately equal to the magnesium turning width.
Procedure for residence time distribution measurement
The flow sheet for performing residence time distribution measurements is shown in Fig. 2. The reactor cartridge R1 is charged within one minute from the top of the replenishing unit Mg with magnesium turnings (23 g for coarse magnesium turnings, 27 g for fine magnesium turnings) while the jogging motor M at the bottom of the reactor cartridge is already started. After the reactor cartridge has been filled, the magnesium bed is allowed to settle and be compacted by the vibrations generated by the jogging motor for another 30 minutes. Residence time measurements are performed at room temperature with the jogging motor running at 6 V electrical voltage. The determination of the residence time distribution in the magnesium-filled reactor cartridge is performed using infrared spectroscopy. The IR probe is placed within a PTFE-T-piece directly at the reactor inlet for measuring the inlet concentrations and directly at the reactor outlet for measuring the outlet concentrations. | ||
| Fig. 2 Flow sheet for residence time distribution measurement within a magnesium-filled reactor cartridge. | ||
The measurements are conducted with 2 mol L−1 toluene in tetrahydrofuran (THF) solution. By simultaneously using 3/2-way valves V2 and V4 in front of the inlet T-piece, switching between toluene solution and pure THF is possible while pumps are running. A concentration change is generated at the reactor inlet as a signal either by introducing the toluene solution into the THF filled reactor cartridge or by displacing the toluene solution from the reactor by using pure THF. The flow rates used are 2 mL min−1 utilising Postnova syringe pumps unless otherwise specified. The incoming signal is detected at the reactor outlet and recorded for further evaluation.
In the case of applying oscillatory flow, pump B or pump D (P3) is integrated into the set-up and placed before the reactor inlet. To generate an oscillating flow, the possible amplitudes and frequencies are limited by the specific pump and its operating range. During oscillatory flow experiments, the jogging motor is turned off to investigate solely the influence of oscillations, unless otherwise specified. No relevant changes in the magnesium bed are to be expected during a single measurement run.
To obtain the mean Bo and mean ![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) , multiple measurement runs are performed.
, multiple measurement runs are performed.
Results and discussion
Characterization of magnesium turnings
Commercially available magnesium turnings for Grignard reagent synthesis are a mixture of particles with different sizes (Fig. 3). The coarse magnesium turnings (Fig. 4) had a mean Feretmax diameter of 1.38 mm and a mean Feretmin diameter of 0.90 mm. The size distribution ranged from 0.35 mm to 3.35 mm. The fine magnesium turnings (Fig. 5) had a mean Feretmax diameter of 0.85 mm and a mean Feretmin diameter of 0.54 mm. For these turnings, the size distribution of the maximum diameter ranged from 0.44 mm to 1.64 mm, with 70% of the turnings having a maximum Feret diameter between 0.55 mm and 1.04 mm. The particle size distribution is narrower than for the coarse turnings. | ||
| Fig. 3 Magnesium turnings (left side: coarse magnesium turnings from Merck KGaA, right side: fine magnesium turnings from Almamet GmbH). | ||
The void fraction ε within the reactor cartridge when using a packed bed of coarse or fine magnesium turnings was 0.58 or 0.51, respectively. Thus, a denser magnesium packing can be achieved when using smaller magnesium turnings. From the particle size distributions of the representative Mg turning samples and the void fraction, the total magnesium surface within a filled reactor cartridge can be obtained: 0.33 m2 for the fine and 0.14 m2 for the coarse turnings, with specific surface areas of 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 350 m2 m−3 and 10
350 m2 m−3 and 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 934 m2 m−3, respectively.
934 m2 m−3, respectively.
To determine the amount of Mg turnings per cross section through the packed bed, the assumption was made that within a cross-section the magnesium turnings lie flat. From the known particle size distribution and the bed porosity, 474 and 154 turnings per cross section were calculated for the fine and coarse magnesium turnings, respectively.
The flow path diameter and length vary between experiments due to the statistical nature of the poured magnesium bed and the varying geometries of the turnings, but according to Kraume,49 the determination of the hydraulic pore diameter is sufficient enough by assuming straight, parallel and uniform flow paths. The hydraulic pore diameter dh is used to specify the mean pore size and can be calculated by eqn (7), with ε = void fraction and d32 = Sauter diameter of magnesium turnings (fine turnings: d32 = 2.81 μm, coarse turnings: d32 = 5.48 μm).
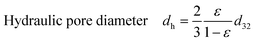 | (7) |
Residence time measurements in beds of metal turnings
The selection of the tracer used for residence time measurements is of great importance. It must be an inert substance that does not affect the physical properties of the reactor contents and can be measured easily. In particular, the viscosity and density of the tracer should be similar to the actual reaction solution.6 Furthermore, the tracer must be added at the same flow rate as the carrier solution is added to the reactor system under investigation. For the measurements presented here, THF was used as the carrier solution and toluene as the tracer. Though both solvents slightly differ in density and viscosity, THF is one of the most frequently used solvents for Grignard reagent syntheses and toluene represents a solvent which can also be used for Grignard reagent synthesis and which behaves inertly towards THF and the magnesium turnings but has a very similar density and viscosity to THF (Table 2). Using the slightly lighter toluene as the tracer and introducing the tracer into the reactor cartridge, effects and counter effects on the axial dispersion and the Bodenstein number by means of the pump system or the jogging motor are more easily detectable, since axial dispersion is already pronounced due to the small difference in density. On the other hand, by displacing the toluene tracer from the reactor cartridge with the denser pure THF, a stable displacement50 and therefore recording of actual residence time distribution and mean residence time should be possible. Hennico et al. obtained a significant effect of viscosity on the axial dispersion coefficient at large Reynolds numbers,51 but since the particle Reynolds numbers of the systems studied here were low (0.11 for fine magnesium turnings, 0.19 for coarse magnesium turnings), the influence of viscosity of THF or toluene on the flow behaviour was neglected.| Toluene | Tetrahydrofuran | |
|---|---|---|
| Density (25 °C)/(g mL−1) | 0.87 | 0.89 |
| Viscosity/(mPa s) | 0.58 | 0.48 |
Larger Bodenstein numbers were registered for the fine magnesium turnings (see Table 3). This is particularly related to the denser magnesium packing and the smaller voids in the magnesium packing (ε = 0.51 for fine vs. ε = 0.58 for coarse magnesium turnings). The broader particle size distribution of the coarse turnings results in an increased axial dispersion and thus lower Bo. Compared to a packed bed of fine magnesium turnings, larger voids or flow paths might occur. Since the cross-section of the flow channel has an influence on the flow velocity at a constant volumetric flow rate, lower flow velocities might be achieved with coarse magnesium turnings. According to the definition of the Bodenstein number (eqn (6)), smaller flow velocities and larger axial dispersions cause a reduction in the Bodenstein number.
| Magnesium turnings | Pump | Introduce/displace tracer | Mean Bo/1 | Standard deviation of Bo/1 | τ/s | Mean ![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) /s /s |
Δ![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) (mean-hydrodyn.)/s (mean-hydrodyn.)/s |
Δ![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) (displ.-introd.)/s (displ.-introd.)/s |
|---|---|---|---|---|---|---|---|---|
| Coarse | Syringe pump A | Displace | 81 | 13 | 652 | 595 | −57 | −2 |
| Introduce | 61 | 10 | 597 | −55 | ||||
| Micro annular gear pump C | Displace | 91 | 34 | 608 | −44 | 2 | ||
| Introduce | 47 | 10 | 606 | −46 | ||||
| Valveless rotary piston pump D | Displace | 96 | 5 | 683 | 31 | 110 | ||
| Introduce | 53 | 3 | 573 | −79 | ||||
| Fine | Syringe pump A | Displace | 154 | 49 | 583 | 514 | −69 | −16 |
| Introduce | 161 | 22 | 530 | −53 | ||||
| Micro annular gear pump C | Displace | 170 | 60 | 516 | −67 | 16 | ||
| Introduce | 184 | 39 | 500 | −83 | ||||
| Valveless rotary piston pump D | Displace | 212 | 35 | 590 | 7 | 103 | ||
| Introduce | 191 | 30 | 487 | −96 | ||||
| Mixed | Syringe pump A | Displace | 148 | 17 | 601 | 590 | −10 | 43 |
| Introduce | 57 | 7 | 547 | −53 | ||||
| Valveless rotary piston pump D | Displace | 145 | 43 | 615 | 14 | 20 | ||
| Introduce | 49 | 1 | 595 | −6 | ||||
For Bo >100, only small deviations from ideal plug flow occur, but already from Bo ≥7 one can speak of a flow behaviour approaching plug flow behaviour.48 For the fine magnesium turnings, higher Bodenstein numbers and thus a more pronounced plug flow behaviour were registered. On average, pump D achieved the highest Bodenstein numbers, followed by pump C and pump A. This is remarkable because pump D is a pump type with comparatively strong pulsation, depending on the set stroke volume and speed (RPM). Pump A also exhibits a short, albeit significant, deviation from constant volume flow when switching between the alternating syringes. Pump C, on the other hand, generates an almost pulsation-free volumetric flow rate (Fig. 6).
Standard deviations of the obtained Bodenstein numbers show the following correlations:
• Higher deviations are obtained when displacing the tracer compared to the introduction of the tracer.
• Pump C exhibits the highest standard deviations among all pumps.
• Using fine turnings results in higher standard deviations compared to using coarse turnings.
The reproducibility of Bo depends on the reproducibility of the magnesium bed. Thus, the results also show that similarity of beds is difficult to obtain. For the fine turnings, the formation of voids or preferred flow channels in an otherwise dense bed will have a stronger impact on the obtained results than in a bed of coarse turnings, where more or bigger voids (higher void fraction) do already exist. The standard deviations demonstrate that for the description of a statistical, poured packed-bed, no conclusions can be drawn from individual or single measurements. Therefore, to make a statement about residence time distributions in an average packed bed, multiple measurement runs must be performed. On average, five measurement runs were investigated to calculate the mean Bodenstein number listed in Table 3.
A comparison of the mean residence times with the hydrodynamic residence times shows that, apart from the use of pump D (displace), the mean residence times in the reactor cartridge were in some cases even more than one minute below the ideal residence time (Table 3). Since this deviation is present during both injection and displacement of the tracer, this gives evidence for poorly accessible volumes in the magnesium bed. Based on the residence times, it can be concluded that these poorly perfused portions account for up to 3 mL. Here, pump D shows the most distinct deviation from the ideal residence time for both the fine and coarse magnesium turnings. This is related to the comparatively strong pulsation of the pump, which seems to have an effect on the flow conditions leading to lower or higher residence times compared to the hydrodynamic residence time and depending on the introduction and the displacement of the tracer, respectively.
It is noticeable that pump C and pump A show the same residence time differences in absolute values between introduction and displacement, but the smallest deviation to the hydrodynamic residence times was obtained with pump A introducing 2 mol L−1 toluene-in-THF, whereas with pump C using pure THF to displace the tracer toluene. However, compared to the fine turnings, the difference in absolute values between pump C and pump A is less pronounced for the coarse magnesium turnings. This is related to the overall more inhomogeneous magnesium bed, in which the slight differences in the operation of pump C and pump A are less noticeable. In contrast to pump D, pump A experiences only a brief stop in liquid delivery followed by a slower increase in volume flow, when the syringes are switched. Thus, pump A has less impact on the flow behaviour. Since pump C generates a pulsation-free volume flow, the effects of the pump are least pronounced here, so that the results of pump C show the Bodenstein numbers and residence times without additional influence of the hydrodynamics imposed by the pumping characteristics. Considering the standard deviations of the obtained Bodenstein numbers, the pump-induced flow behaviour of pump A and pump D in terms of flow pulsation has a positive impact on the reproducibility of residence time distributions.
Mixed magnesium turnings
A magnesium bed of mixed magnesium turnings resulting in a considerably broader particle size distribution corresponds more to a changing magnesium bed during an ongoing Grignard reagent synthesis. For a mixture of fine magnesium turnings (75%) and coarse magnesium turnings (25%), the void fraction ε was 0.52 and the magnesium mass was 26 g. This is close to the bed porosity of a magnesium bed of exclusively fine turnings due to the higher density of fine magnesium turnings. A larger fraction of fine turnings was used because during an ongoing synthesis, the average size of the magnesium turnings in the reactor shifts to smaller sizes and only the magnesium turnings replenished by means of the replenishing unit have their original size.For the mixed turnings, the difference in Bo between the introduction and displacement of the tracer is much more pronounced (Table 3). For the introduction of toluene, the Bodenstein numbers are in a range comparable to the coarse magnesium turnings. In contrast, when pure THF is used (displacement), the measured Bo values are more like those of fine magnesium turnings alone. The standard deviations are also more like those of fine or coarse turnings, respectively, depending on the introduction or the displacement of the tracer. Probably, the slight difference in density of the solvents is decisive for the differences in the results obtained. The lighter toluene rises through the THF due to buoyancy, leading to shorter residence times but higher axial dispersion. When the toluene tracer is displaced from the magnesium bed by using pure THF, the THF displaces the toluene, only driven by the pump pressure. The axial dispersion is less pronounced (larger Bo) and larger residence times are observed. The broad particle size distribution of the mixed magnesium turnings leads to even further axial dispersion.50 For these reasons, wide particle size distributions (mixed turnings but also coarse turnings alone) cause deviations of the RTD between the two different ways of generating the tracer signal. The broader the particle size distribution, the more pronounced this effect is.
The displacement of the tracer toluene by pure THF with pump D leads to residence times above the hydrodynamic residence time independent of the bed composition (Table 3). The average residence time of one component can be higher than the ideal hydrodynamic residence time calculated on the basis of the reactor volume and (theoretical) volumetric flow rate, if either the real reactor volume is larger or the real volumetric flow rate is smaller than assumed, or if there is more backmixing or short-circuiting flow of one component.
Influence of the jogging motor
The jogging motor placed at the bottom of the reactor cartridge is used to maintain a homogeneous and dense magnesium bed. It has been demonstrated in previous work that the use of the jogging motor has a positive influence on the reaction start and yields of Grignard reagent syntheses.43 The generated vibrations cause abrasion of the passivating oxide layer on the magnesium surface and thus a larger active magnesium surface is accessible for Grignard reagent synthesis.This jogging motor also plays an important role during the initial filling of the reactor cartridge in preparation of the synthesis. Fig. 7 depicts the Bodenstein numbers over a flow range of 1 mL min−1 to 4 mL min−1 when using a cartridge filled with coarse magnesium turnings and introducing the tracer toluene to a THF-filled reactor cartridge. If the jogging motor is used during filling of the reactor cartridge and during RTD measurements, Bodenstein numbers increase up to a value of 90. In contrast, if the jogging motor is only used during RTD measurements, the Bo values are lower by about 25 and this behaviour is independent of the chosen flow rate. This behaviour is mainly due to less magnesium turnings being filled in the reactor cartridge when not using the jogging motor during the initial filling. Even though Fig. 7 shows the results for the coarse magnesium turnings, independent of the size of the turnings, around 10% less magnesium mass fits in the reactor cartridge when not using the jogging motor due to the missing compaction. If the jogging motor is used only for filling the reactor cartridge, Bodenstein numbers are equally low as for the case of RTD measurement only. Since missing compaction and less magnesium mass cannot be the reason for this observation, this indicates that the jogging motor also influences the flow behaviour during RTD measurements. At low volumetric flow rates, both effects influence the RTD. This can be observed especially at a flow rate of 3 mL min−1 compared to 4 mL min−1: using the jogging motor only for filling, the mean Bodenstein numbers decrease (46 to 41), while when using it only for RTD measurements, the mean Bodenstein numbers show a still increasing trend (52 to 56), and in combination of filling and measurement, the trend remains almost constant (80 to 81). The decreasing trend in Bodenstein numbers for the case of “filling only” at 3 mL min−1 to 4 mL min−1 indicates an increasing influence of the lighter toluene shooting through at increasing volumetric flow rates. In contrast, the cases of using the jogging motor during RTD measurements indicate that the jogging motor superimposes a transverse movement of the fluid counteracting the axial movement due to the difference in densities. From Fig. 7, it can be deduced that it is favourable to use the jogging motor for filling with magnesium turnings to ensure compaction and also during the introduction of a fluid of lower density to a fluid of higher density, as it occurs in Grignard reagent synthesis, in which the lighter halide educt solution enters the reactor from the bottom with the higher density Grignard reagent already formed within the reactor cartridge. When using fine magnesium turnings, only a few differences between the Bodenstein numbers for using the jogging motor only during filling of the magnesium cartridge or additionally during the residence time measurement are noticeable (Fig. 8). Furthermore, the fluctuations of Bo increase with increasing volumetric flow rate. Both effects are due to the more compact and more homogeneous packing which is possible because of the smaller magnesium turnings. The influence of the jogging motor on the flow behaviour is less prominent when using finer magnesium turnings, and thus a denser magnesium bed, since axial dispersion is already less pronounced in comparison to coarse Mg turnings.
 | ||
| Fig. 7 Influence of the jogging motor on the Bodenstein number for coarse magnesium turnings (introduction of tracer, pump A) and the use of the jogging motor for different occasions: filling only, RTD measurement only and combination of both (for exemplary distribution functions see the ESI†). Lines within the data are solely to guide the eyes. | ||
 | ||
| Fig. 8 Influence of the jogging motor on the Bodenstein number for fine magnesium turnings (introduction of tracer, pump A) and the use of the jogging motor for different occasions: filling only and during filling and RTD measurement (for exemplary distribution functions see the ESI†). Lines within the data are solely to guide the eyes. | ||
Deviations in Bo are mainly caused by deviations between the magnesium beds in different experiments. One reason for the inhomogeneity of the beds is the so-called Brazil nut effect. Ripple et al.52 described that when soil columns are packed by vibration, radial segregation and separation by particle size can occur, resulting in inhomogeneities in the packing. For the magnesium bed, this would cause larger turnings to move to the top of the bed when it is shaken. It is known that the dispersion coefficient increases and Bo values decrease when packed beds are not well packed. Though packing of the magnesium cartridge was done by using the same procedure every time to minimize this influence, having particles of non-uniform shape and size does not allow for perfectly packed beds and deviations within the bed and between beds must be accepted.
Oscillating flow conditions in packed magnesium beds
Since the impact of the flow conditions on the RTD was already observed, oscillating flow conditions were evaluated as a strategy to realize narrow residence time distributions by fine-tuning the stroke frequency and stroke amplitude. Oscillatory flow conditions can be described by a specific Reynolds number, the oscillatory Reynolds number Re0. This Reynolds number and the bulk flow Reynolds number ReN (eqn (8) and (9)) can be correlated by the velocity ratio Ψ (eqn (10)). | (8) |
 | (9) |
 | (10) |
To ensure comparability between the results, a net volumetric flow rate of 2 mL min−1 toluene/THF solution was maintained in the results presented here. This volumetric flow rate was generated by means of a pulsation-free micro annular gear pump (pump C). In the case of the fine magnesium turnings, an additional valveless rotary piston pump (pump D) ensured the oscillation of the volume flow. In the case of coarse magnesium turnings, a programmable syringe pump (pump B) was used to generate the oscillation. The maximum amplitudes and frequencies that can be achieved depend on the pump used and its technically possible operating conditions (Table 1).
The results for the fine and coarse turnings (Fig. 9 and 10, respectively) show a clear dependency of the Bodenstein numbers on the oscillatory Reynolds number. For the fine magnesium turnings, Bo values decrease with increasing oscillatory Reynolds number (Fig. 9). An average Bodenstein number of 184 was registered for the pulsation-free operation (compare Table 3). For small oscillatory Reynolds numbers, an increase of Bo by 25% up to 230 was possible. Correlating Bo to the pulsation frequency and amplitude reveals a decrease with increasing frequency and with increasing amplitude (Fig. 11 and 12). The scattering of the data points in Fig. 12 results from the coupled impact of the amplitude and the frequency. Even for a constant amplitude, different Bo values were obtained at different frequencies.
 | ||
| Fig. 9 Bodenstein numbers as a function of oscillatory Reynolds number and velocity ratio for the use of fine magnesium turnings and different stroke volumes (for exemplary distribution functions see the ESI†). | ||
 | ||
| Fig. 10 Bodenstein numbers as a function of oscillatory Reynolds number and velocity ratio for the use of coarse magnesium turnings and different stroke volumes (for exemplary distribution functions see the ESI†). | ||
 | ||
| Fig. 11 Bodenstein numbers as a function of oscillation frequency for the use of fine magnesium turnings and different stroke volumes. | ||
 | ||
| Fig. 12 Bodenstein numbers as a function of oscillation amplitude for the use of fine magnesium turnings and different stroke volumes. | ||
With the coarse magnesium turnings, an improvement in Bo can be observed too due to the additional oscillation. An increase of the Bodenstein numbers with increasing oscillatory Reynolds number up to Re0 = 1.38 was found for coarse magnesium turnings (Fig. 10). At Re0 = 1.38, a maximum is reached and a further increase of the oscillatory Reynolds number leads to a drop of Bo. Whereas without oscillation, a mean Bodenstein number of 47 (pulsation-free pump C) is achieved, with a superimposed oscillation, a Bodenstein number of up to 80 is possible, an increase by 70%. In contrast to the use of fine magnesium turnings, no clear dependency of Bo on the amplitude was found (Fig. 13). Instead, Bo depends strongly on the stroke frequency (Fig. 14). The comparison of two different sizes of magnesium turnings with different particle size distributions reveals that especially packed beds of broader particle size distributions can benefit from a superimposed oscillation.
 | ||
| Fig. 13 Bodenstein numbers as a function of oscillation amplitude for the use of coarse magnesium turnings and different stroke volumes. | ||
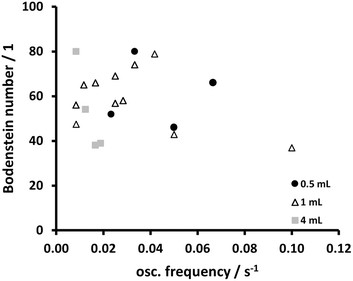 | ||
| Fig. 14 Bodenstein numbers as a function of oscillation frequency for the use of coarse magnesium turnings and different stroke volumes. | ||
Interestingly, application of pump D (which was operated at higher stroke frequencies) instead of pump B did not lead to an improvement in Bo for coarse magnesium turnings. Bodenstein numbers between 26 and 40 were measured, which are even lower than those without oscillation (Fig. 15). Despite the low amplitudes that can be realized with this pump, a dependency of Bo on the amplitude is recognizable, with the optimum being 50 μl stroke volume. Nevertheless, the operating range of this pump is not suited for narrowing the RTD for coarse Mg turnings, and the Bodenstein numbers are close to those obtained by means of the syringe pump induced oscillation.
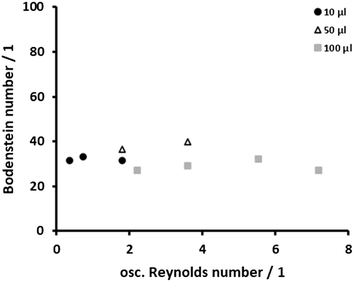 | ||
| Fig. 15 Bodenstein numbers for different stroke volumes as a function of oscillatory Reynolds number for the use of coarse magnesium turnings and pump D for inducing oscillation. | ||
Considering the velocity ratio, for the use of coarse magnesium turnings, the optimum (Bo ≈ 80) lies within a range of Ψ = 3–8, depending on the amplitude (Fig. 10). For the finer magnesium turnings, the highest Bo can be obtained by using a stroke volume of 10 μl, and by using this value, elevated Bo values due to oscillatory flow are possible up to Ψ = 8 (Fig. 9). Therefore, independent of the used size of magnesium turnings, the optimum in terms of Bo and a minimum in axial dispersion can be realized by paying attention to a velocity ratio below 8. For smaller particles, the optimum velocity ratio is lower than for larger particles. The optimal range of velocity ratio values found for the reactor investigated in this work is comparable to the results by P. Stonestreet et al. (Ψ = 2–4 for a reactor with 24 mm in diameter)53 and A. N. Phan et al. (Ψ = 4–10 for a reactor with 5 mm in diameter, dependent on the used baffle type),54 even though small-sized COBRs were used in these studies and not a baffleless, magnesium-filled reactor cartridge with a non-homogeneous, randomly packed bed of non-uniform and non-spherical metal turnings. Although the data gathered within the experiments are specific to the used pumps and pump systems and their behaviour when it comes to oscillation or dips within the flow rate, the use of the dimensionless numbers to analyse the flow behaviour enables a generalization of the findings. The results obtained expand the general applicability of the oscillatory flow concept to baffleless, non-homogeneous, randomly packed beds of a non-uniform and non-spherical packing material. The presented findings also clearly underline the necessity of choosing a suitable pump system, since the pumping characteristics certainly do have an influence on the residence time distribution in this kind of packed bed reactor. Since residence time distributions are known to have an impact on the yields and selectivities of reactions, a thoughtful pump selection has the potential to enhance product quantity and quality.
During oscillatory flow operation, the jogging motor was only used for the initial compaction of the magnesium bed and for the compaction in between measurement runs, but not during actual residence time measurements. Using coarse magnesium turnings and low oscillatory Reynolds numbers, a Bodenstein number of 47 is achieved, while a maximum of 80 is possible at higher Reynolds numbers. This range of Bo correlates to the Bodenstein numbers at 2 mL min−1 found for non-oscillating flow conditions (Fig. 7) and indicates a similar influence of the vibrations introduced by the jogging motor and the oscillatory flow on the actual flow behaviour within a bed of coarse magnesium turnings. When using fine turnings, the vibrations generated by the jogging motor during measurements are not sufficient to reduce the axial dispersion, but a superimposed oscillatory flow does. The Bodenstein numbers could be increased up to 230. For coarse as well as fine magnesium turnings, the optimum oscillatory Reynolds numbers achieving the highest Bodenstein numbers lie in a range of 0 to 1.5. Fine tuning of operational conditions is more easily manageable by using oscillatory flow instead of a jogging motor, but since oscillatory flow will not lead to compaction of the magnesium bed, the use of the jogging motor and its influence is not negligible.
Conclusions
The residence time distribution in non-homogeneous and randomly packed magnesium beds was found to strongly depend on the properties of the used magnesium turnings and the operational conditions. Axial dispersion could be reduced by using finer magnesium turnings. The characteristics of the pump (pulsation-free pump, pump exhibiting intermittent pulsation, strongly and regularly pulsating pump) were also found to have an influence on the residence time distributions. Strongly and regularly pulsating pumps were found to lead to narrower residence time distributions in a packed bed reactor.The general applicability of using superimposed oscillating flows to influence axial dispersion in non-homogeneous, randomly packed beds of non-uniform and non-spherical metal turnings was successfully demonstrated. Especially packed beds with broader particle size distributions can benefit from a superimposed oscillatory flow in terms of a narrowed residence time distribution. To minimize the axial dispersion, fine tuning of the oscillation amplitude and frequency to the properties of the packed bed is required. In the case presented, magnesium turnings are used, but the concept should be easily transferable to other packed beds of metal turnings.
Analysis of dimensionless numbers enabled generalization of the findings of the effect of oscillating flow behaviour. The optimum velocity ratio found for the investigated non-homogeneous, randomly packed beds of non-uniform and non-spherical magnesium turnings is comparable to the optimum velocity ratio of small-sized COBRs mentioned in the literature.
For a magnesium-filled reactor, intended to be used for Grignard reagent synthesis, it must be considered that magnesium is one of the reactants in Grignard reagent formation. Thus, the magnesium bed is subject to changes. The impact of the changing bed on the residence time distribution as well as the correlation to the selectivity of the Grignard reagent formation is presented in part 2 of this contribution.
Notation
| Bo | Bodenstein number | 1 |
| d 32 | Sauter diameter | m |
| d h | Hydraulic pore diameter | m |
| D ax | Axial dispersion coefficient | m2 s−1 |
| E | Residence time distribution function | 1 |
| F | Cumulative distribution function | 1 |
| f | Frequency | s−1 |
| L | Channel length | m |
| ReN | Bulk flow Reynolds number | 1 |
| Re0 | Oscillatory Reynolds number | 1 |
| u | Flow velocity | m s−1 |
![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif)
|
Flow rate | m3 s−1 |
| V R | Reactor volume | m3 |
| t | Time | s |
![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif)
|
Mean residence time | s |
| x 0 | Amplitude | m |
Greek letters
| ε | Void fraction | 1 |
| θ | Dimensionless residence time | 1 |
| μ | Dynamic viscosity | kg m−1 s−1 |
| ρ | Fluid density | kg m−3 |
| τ | Hydrodynamic residence time | s |
| Ψ | Velocity ratio | 1 |
Author contributions
Conceptualization: E. D. (supporting), D. Z. (lead); data curation: E. D. (lead); formal analysis: E. D. (lead); funding acquisition: E. D. (lead), M. M. (supporting); investigation: E. D. (lead); methodology: E. D. (equal), D. Z. (equal); project administration: E. D. (lead); resources: E. D. (supporting), M. M. (supporting), G. M.-F. (supporting), D. Z. (supporting); supervision: M. M. (supporting), G. M.-F. (supporting), D. Z. (lead); validation: E. D. (lead), D. Z. (supporting); visualization: E. D. (lead); writing – original draft: E. D. (lead); writing – review & editing: E. D. (equal), D. Z. (equal).Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors would like to acknowledge the Fraunhofer IMM and the Fraunhofer Organization for internal funding via the Fraunhofer development and career program TALENTA. The authors would also like to acknowledge the funding of part of the presented research through the project InnomodA. InnomodA was funded by the Ministry of Science, Education and Culture of Rhineland-Palatinate and by the European Union via the European Regional Development (funding reference: Europäischer Strukturfond für die regionale Entwicklung (EFRE) – “Investitionen in Wachstum und Beschäftigung (IWB) – Rheinland-Pfalz”; funding period: 2014–2020. Proposal no.: 84004713). The authors thank Lisa Pokropp (Fraunhofer IMM) for the creation of the table of content graphic.References
- A. Kadam, M. Nguyen, M. Kopach, P. Richardson, F. Gallou, Z.-K. Wan and W. Zhang, Comparative performance evaluation and systematic screening of solvents in a range of Grignard reactions, Green Chem., 2013, 15, 1880 RSC.
- Handbook of Grignard reagents, ed. G. S. Silverman and P. E. Rakita, CRC Taylor & Francis Group, Boca Raton, London, New York, 1996, vol. 64 Search PubMed.
- T. McGlone, N. E. B. Briggs, C. A. Clark, C. J. Brown, J. Sefcik and A. J. Florence, Oscillatory Flow Reactors (OFRs) for Continuous Manufacturing and Crystallization, Org. Process Res. Dev., 2015, 19, 1186–1202 CrossRef CAS.
- T. van Gerven and A. Stankiewicz, Structure, Energy, Synergy, Time—The Fundamentals of Process Intensification, Ind. Eng. Chem. Res., 2009, 48, 2465–2474 CrossRef CAS.
- D. Hobbs and F. Muzzio, The Kenics static mixer: a three-dimensional chaotic flow, Chem. Eng. J., 1997, 67, 153–166 CrossRef CAS.
- E. Müller-Erlwein, Chemische Reaktionstechnik, Springer Spektrum, Wiesbaden, 3rd edn, 2015 Search PubMed.
- A. Stankiewicz, T. van Gerven and G. Stefanidis, The fundamentals of process intensification, Wiley-VCH, Weinheim, 2019 Search PubMed.
- P. Bianchi, J. D. Williams and C. O. Kappe, Oscillatory flow reactors for synthetic chemistry applications, J. Flow Chem., 2020, 10, 475–490 CrossRef CAS.
- S. M. R. Ahmed, A. N. Phan and A. P. Harvey, Scale-Up of Gas–Liquid Mass Transfer in Oscillatory Multiorifice Baffled Reactors (OMBRs), Ind. Eng. Chem. Res., 2019, 58, 5929–5935 CrossRef CAS.
- F. Almeida, F. Rocha, J. A. Teixeira and A. Ferreira, The influence of electrolytes in aqueous solutions on gas-liquid mass transfer in an oscillatory flow reactor, Chem. Eng. Sci., 2022, 263, 118048 CrossRef CAS.
- A. Ferreira, J. A. Teixeira and F. Rocha, O2 mass transfer in an oscillatory flow reactor provided with smooth periodic constrictions. Individual characterization of kL and a, Chem. Eng. J., 2015, 262, 499–508 CrossRef CAS.
- M. R. Hewgill, M. R. Mackley, A. B. Pandit and S. S. Pannu, Enhancement of gas-liquid mass transfer using oscillatory flow in a baffled tube, Chem. Eng. Sci., 1993, 48, 799–809 CrossRef CAS.
- M. S. N. Oliveira and X.-W. Ni, Characterization of a gas-liquid OBC: Bubble size and gas holdup, AIChE J., 2004, 50, 3019–3033 CrossRef CAS.
- N. Reis, P. C. Mena, A. A. Vicente, J. A. Teixeira and F. A. Rocha, The intensification of gas–liquid flows with a periodic, constricted oscillatory-meso tube, Chem. Eng. Sci., 2007, 62, 7454–7462 CrossRef CAS.
- N. Reis, R. N. Pereira, A. A. Vicente and J. A. Teixeira, Enhanced Gas−Liquid Mass Transfer of an Oscillatory Constricted-Tubular Reactor, Ind. Eng. Chem. Res., 2008, 47, 7190–7201 CrossRef CAS.
- H. Zhu, J. Duan, H. Cui, Q. Liu and X. Yu, Experimental research of reciprocating oscillatory gas-liquid two-phase flow, Int. J. Heat Mass Transfer, 2019, 140, 931–939 CrossRef CAS.
- E. Lobry, T. Lasuye, C. Gourdon and C. Xuereb, Liquid–liquid dispersion in a continuous oscillatory baffled reactor – Application to suspension polymerization, Chem. Eng. J., 2015, 259, 505–518 CrossRef CAS.
- S. S. Mongeon, D. M. Roberge, M. Bittel, P. Elsner and A. Macchi, Liquid–Liquid Mass Transfer in an Oscillatory-Flow Mesoscale Coil Reactor without Baffles, Org. Process Res. Dev., 2016, 20, 733–741 CrossRef CAS.
- A. P. Harvey, M. R. Mackley and P. Stonestreet, Operation and Optimization of an Oscillatory Flow Continuous Reactor, Ind. Eng. Chem. Res., 2001, 40, 5371–5377 CrossRef CAS.
- A. N. Phan, A. P. Harvey and V. Eze, Rapid Production of Biodiesel in Mesoscale Oscillatory Baffled Reactors, Chem. Eng. Technol., 2012, 35, 1214–1220 CrossRef CAS.
- A. Mazubert, J. Aubin, S. Elgue and M. Poux, Intensification of waste cooking oil transformation by transesterification and esterification reactions in oscillatory baffled and microstructured reactors for biodiesel production, Green Processes Synth., 2014, 3, 1646 Search PubMed.
- L. N. Ejim, S. Yerdelen, T. McGlone, I. Onyemelukwe, B. Johnston, A. J. Florence and N. M. Reis, A factorial approach to understanding the effect of inner geometry of baffled meso-scale tubes on solids suspension and axial dispersion in continuous, oscillatory liquid–solid plug flows, Chem. Eng. J., 2017, 308, 669–682 CrossRef CAS.
- V. C. Eze, J. C. Fisher, A. N. Phan and A. P. Harvey, Intensification of carboxylic acid esterification using a solid catalyst in a mesoscale oscillatory baffled reactor platform, Chem. Eng. J., 2017, 322, 205–214 CrossRef CAS.
- V. C. Eze and A. P. Harvey, Continuous reactive coupling of glycerol and acetone – A strategy for triglyceride transesterification and in-situ valorisation of glycerol by-product, Chem. Eng. J., 2018, 347, 41–51 CrossRef CAS.
- R. Kacker, S. I. Regensburg and H. J. Kramer, Residence time distribution of dispersed liquid and solid phase in a continuous oscillatory flow baffled crystallizer, Chem. Eng. J., 2017, 317, 413–423 CrossRef CAS.
- M. Zaki, I. Nirdosh, M. H. I. Baird and G. H. Sedahmed, Effect of Superimposed Pulsating Flow on Liquid-Solid Mass Transfer in Fixed Beds, Can. J. Chem. Eng., 2005, 83, 593–598 CrossRef CAS.
- G. Jimeno, Y. C. Lee and X.-W. Ni, The effect of particle size on flow in a continuous oscillatory baffled reactor using CFD, Can. J. Chem. Eng., 2022, 100, 223 CrossRef.
- P. C. Cruz, C. R. Silva, F. A. Rocha and A. M. Ferreira, Mixing Performance of Planar Oscillatory Flow Reactors with Liquid Solutions and Solid Suspensions, Ind. Eng. Chem. Res., 2021, 60, 2663–2676 CrossRef CAS.
- D. Slavnić, B. Bugarski and N. Nikačević, Solids flow pattern in continuous oscillatory baffled reactor, Chem. Eng. Process., 2019, 135, 108–119 CrossRef.
- H. Zheng, Z. Yan, S. Chu and J. Chen, Continuous synthesis of isobornyl acetate catalyzed by a strong acid cation exchange resin in an oscillatory flow reactor, Chem. Eng. Process., 2018, 134, 1–8 CrossRef CAS.
- B. J. Doyle, B. Gutmann, M. Bittel, T. Hubler, A. Macchi and D. M. Roberge, Handling of Solids and Flow Characterization in a Baffleless Oscillatory Flow Coil Reactor, Ind. Eng. Chem. Res., 2020, 59, 4007–4019 CrossRef CAS.
- M. S. R. Abbott, A. P. Harvey, G. V. Perez and M. K. Theodorou, Biological processing in oscillatory baffled reactors: operation, advantages and potential, Interface Focus, 2013, 3, 20120036 CrossRef CAS PubMed.
- M. Abolhasani and K. F. Jensen, Oscillatory multiphase flow strategy for chemistry and biology, Lab Chip, 2016, 16, 2775–2784 RSC.
- J. R. McDonough, A. N. Phan and A. P. Harvey, Rapid process development using oscillatory baffled mesoreactors – A state-of-the-art review, Chem. Eng. J., 2015, 265, 110–121 CrossRef CAS.
- X. Ni, M. R. Mackley, A. P. Harvey, P. Stonestreet, M. Baird and N. V. Rama Rao, Mixing Through Oscillations and Pulsations—A Guide to Achieving Process Enhancements in the Chemical and Process Industries, Chem. Eng. Res. Des., 2003, 81, 373–383 CrossRef CAS.
- B. D. Crittenden, A. Lau, T. Brinkmann and R. W. Field, Oscillatory flow and axial dispersion in packed beds of spheres, Chem. Eng. Sci., 2005, 60, 111–122 CrossRef CAS.
- B. D. Crittenden, R. W. Field and M. I. Pervez, Oscillatory flow in packed beds and baffled tubes. A unifying approach to the interpretation of experimental data, Chem. Eng. Sci., 1995, 50, 3839–3845 CrossRef CAS.
- A. Motamed Dashliborun, F. Larachi and M. Schubert, Hydrodynamics of gas-liquid cocurrent upflow in oscillating packed beds for offshore marine applications, Chem. Eng. Sci., 2017, 170, 583–596 CrossRef CAS.
- A. Lau, Enhancement of liquid phase adsorption column performance by means of oscillatory flow: an experimental study, Sep. Purif. Technol., 2004, 35, 113–124 CrossRef CAS.
- J. C. Göebel, K. Booij and J. Fortuin, Axial dispersion in single-phase flow in pulsed packed columns, Chem. Eng. Sci., 1986, 41, 3197–3203 CrossRef.
- A. Mak, C. Koning, P. J. Hamersma and J. Fortuin, Axial dispersion in single-phase flow in a pulsed packed column containing structured packing, Chem. Eng. Sci., 1991, 46, 819–826 CrossRef CAS.
- H. M. Kefas, R. Yunus, U. Rashid and Y. H. Taufiq-Yap, Enhanced biodiesel synthesis from palm fatty acid distillate and modified sulfonated glucose catalyst via an oscillation flow reactor system, J. Environ. Chem. Eng., 2019, 7, 102993 CrossRef CAS.
- G. Menges-Flanagan, E. Deitmann, L. Gössl, C. Hofmann and P. Löb, Scalable Continuous Synthesis of Grignard Reagents from in Situ-Activated Magnesium Metal, Org. Process Res. Dev., 2020, 24, 315–321 CrossRef CAS.
- G. Menges-Flanagan, E. Deitmann, L. Gössl, C. Hofmann and P. Löb, Scalable Continuous Synthesis of Organozinc Reagents and Their Immediate Subsequent Coupling Reactions, Org. Process Res. Dev., 2021, 25, 427–433 CrossRef CAS.
- M. Sassian, D. Panov and A. Tuulmets, Grignard reagents in toluene solutions, Appl. Organomet. Chem., 2002, 16, 525–529 CrossRef CAS.
- H. Simuste, D. Panov, A. Tuulmets and B. T. Nguyen, Formation of phenylmagnesium halides in toluene, J. Organomet. Chem., 2005, 690, 3061–3066 CrossRef CAS.
- Lehrbuch der technischen Chemie, ed. M. Baerns, H. Hofmann and A. Renken, Thieme, Stuttgart, 2nd edn, 1992 Search PubMed.
- J. Hagen, Chemiereaktoren. Auslegung und Simulation, Wiley-VCH, Weinheim, 1st edn, 2012 Search PubMed.
- M. Kraume, Transportvorgänge in der Verfahrenstechnik. Grundlagen und apparative Umsetzungen, Springer Berlin Heidelberg, Berlin, Heidelberg, 3rd edn, 2020 Search PubMed.
- J. M. P. Q. Delgado, A critical review of dispersion in packed beds, Heat Mass Transfer, 2006, 42, 279–310 CrossRef CAS.
- A. Hennico, G. Jacques and T. Vermeulen, Longitudinal dispersion in single-phase liquid flow through ordered and random packings, Lawrence Rad Lab Rept, 1963 Search PubMed.
- C. D. Ripple, R. V. James and J. Rubin, Packing-Induced Radial Particle-Size Segregation: Influence on Hydrodynamic Dispersion and Water Transfer Measurements, Soil Sci. Soc. Am. J., 1974, 38, 219–222 CrossRef.
- P. Stonestreet and P. van der Veeken, The Effects of Oscillatory Flow and Bulk Flow Components on Residence Time Distribution in Baffled Tube Reactors, Chem. Eng. Res. Des., 1999, 77, 671–684 CrossRef CAS.
- A. N. Phan and A. Harvey, Development and evaluation of novel designs of continuous mesoscale oscillatory baffled reactors, Chem. Eng. J., 2010, 159, 212–219 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Distribution functions for residence time measurements. See DOI: https://doi.org/10.1039/d3re00190c |
| This journal is © The Royal Society of Chemistry 2023 |




