Unravelling catalytic activity trends in ceria surfaces toward the oxygen reduction and water oxidation reactions†
Received
12th January 2023
, Accepted 28th February 2023
First published on 3rd March 2023
Abstract
Improved catalysts are critical for more environmentally friendly, and long-term oxygen electrochemical reactions. Computational catalysis can provide atomic level information that is critical for optimizing the next generation of electrocatalysts. It has been demonstrated that by varying the exposed planes, the catalytic performance of metallic oxides can be tuned. Herein, we investigate the role of CeO2 surface orientations (100), (110), (111), (221), and (331) in enhancing catalytic activity toward various oxygen electrochemical reactions ranging from 4- and 2-electron oxygen reduction reactions (ORR) to 4-, 2- and 1-electron water oxidation reactions (WOR) using density functional theory (DFT) calculations in conjunction with the computational hydrogen electrode. Our results indicate that the CeO2(100) facet is the most promising for 4-electron ORR, with a theoretical limiting potential of 0.52 V. We also show that the presence of oxygen vacancies can enhance the 4-electron ORR activity of the CeO2(110) and CeO2(111) surfaces. Besides, CeO2(100) is selective for the 4-electron WOR while CeO2(110) and CeO2(111) are selective for the 2-electron and 1-electron WOR, respectively. Oxygen vacancies shift all the above three facets towards the 4-electron WOR. This work sheds light on the role of different ceria facets in various oxygen electrochemical reactions which is critical for developing better catalysts.
Introduction
The ever-increasing worldwide energy demand along with the depletion of fossil fuels, a significant part of the current energetic matrix, has brought attention to the urgent need for novel technologies and more sustainable energy generation alternatives.1–3 In this regard, fuel cells and electrolyzers have emerged as versatile and efficient devices for energy conversion and chemical production.4 Fuel cells have shown promise in powering vehicles, household appliances, electronics, and even medical and military equipment.5–9 The 4-electron oxygen reduction reaction (4e-ORR) is known to limit the efficiency of fuel cells due to sluggish kinetics.10 For large-scale applications, new materials must be created because the majority of the currently available commercial fuel cell catalysts are based on noble metals.11
The ORR is also gaining interest from the scientific community as an attractive reaction for water treatment when the reaction follows a 2-electron pathway.10,12–15 In this case, the final product is hydrogen peroxide, which can be converted to hydroxyl radicals and they break organic pollutants.16 The reverse reaction to ORR is the water oxidation reaction (WOR) which is a key process for green production of hydrogen. Using an electrolyzer the WOR, can follow a 4-electron pathway evolving oxygen (4e-WOR), a 2-electron pathway, producing hydrogen peroxide (2e-WOR), or a 1-electron pathway, producing hydroxyl radicals (1e-WOR).17 Understanding the role of various different ceria facets is critical for determining catalytic activity and selectivity towards each of these oxygen electrochemical reaction routes.18
A very promising direction for the electrocatalyst development is the utilization of metal oxides, due to their low cost compared to noble metals, high versatility, stability under harsh conditions, controllable shapes, and exposed surfaces through a wide range of nanostructures, and catalytic performance.19–22 Among oxides, ceria (CeO2) has stood out with remarkable catalytic properties for various reactions.23–25 CeO2 is an abundant oxide,26 has high oxygen mobility26,27 and shows an easy conversion between Ce3+ and Ce4+ species, and its nanostructures can be experimentally shaped by controlled synthesis.28,29
Density functional theory (DFT) calculations provide a powerful tool for gaining atomic scale understanding of catalytic behavior30–33 and guiding the design of improved catalyst materials with the desired properties.34–36 Theoretical studies on CeO2 have provided valuable information on activity descriptors,20 nanoparticle stable geometries,37 magnetic properties,38 and oxygen vacancy formation.39 However, the effect of different ceria crystal planes on catalytic activity towards the ORR and WOR is still unknown. Recent studies have emphasized the important role of different exposed facets in oxides in the catalytic activity.19,40 Herein, we used DFT calculations to investigate the activity of different ceria crystal planes towards both the oxygen reduction and water oxidation reactions. We show that (100) is the most active CeO2 crystal plane for the 4e-ORR, with the lowest theoretical overpotential value, and that oxygen vacancies can boost the catalytic activity of surfaces that would otherwise be inactive, such as (100) and (110). (111). Furthermore, CeO2 low-index planes are active and exhibit different selectivities for the WOR, with (100), (110), and (111) favoring the 4e-WOR, 2e-WOR, and 1e-WOR, respectively. We show that the presence of oxygen vacancies changes the selectivity to the 4e-WOR on all low-index surfaces.
Experimental
Density functional theory (DFT) calculations were performed with the plane-wave basis sets available on the Quantum ESPRESSO package.41 The core electrons were treated as frozen and described with standard solid-state efficiency pseudopotentials (SSSPs), which allow minimum wave function cutoff values to be employed and optimize computational time.42,43 The valence electrons were described with plane-wave basis functions with a 50 Ry kinetic energy cutoff. To describe the exchange–correlation energy, generalized gradient approximation functionals as parametrized by Perdew, Burke, and Ernzerhof (GGA-PBE)44 were used.43,45 To describe the adsorbate–surface interaction, slab models from Matz and Calatayud46 were constructed with a bulk lattice parameter of 5.50 Å. Their original work presents a careful and detailed convergence in terms of atomic layers and superficial energy for each Miller index surface. The (100) Ce terminated, (110), (111), (221), and (331) Ce–O mixed terminated CeO2 surfaces were built for this study. According to this study, the calculated superficial energies, indicative of surface thermal stability, follow the order: (111) < (221) < (331) < (110) < (100)-Ce.46 A vacuum layer of 15 Å along the surface perpendicular direction was used to avoid any interaction between periodic images and to correctly describe the species adsorption.47–50 A k-point grid of 2 × 2 × 1 was used for all the slab calculations. CeO2 is a strongly correlated system, and it is established in the literature that standard DFT approaches cannot accurately describe its electronic properties.51,52 Thus, a Hubbard-like parameter of Ueff = 5 eV (ref. 53) was applied to account for the on-site Coulomb interaction and describe Ce-4f localized states, chosen based on previous studies.48–52 This value has also been reported to well describe partial reduction/reoxidation of Ce atoms, which makes it suitable for investigating the ORR/WOR over CeO2 surfaces.54–56 The slabs were initially optimized until a convergence threshold on the forces acting on each atom of 10−3 a.u. and of 10−4 a.u. on total energy, with half of the bottom layers kept fixed. The surface atoms together with adsorbates were allowed to relax. The optimized structures were then used for the adsorption calculations, via the following equation:57| | | ΔEADS = Eslab+adsorbate − (Eslab + Eadsorbate) | (1) |
where Eslab+adsorbate is the total energy of the surface and adsorbates, and Eslab and Eadsorbate refer to the isolated surface slab adsorbed species, respectively.
The associative mechanism was considered for investigating the 4e-ORR activity on ceria surfaces. In this mechanism, the oxygen molecule is reduced at the surface and forms *OOH without O–O bond scission. The following reduction steps shown in (2)–(5) will form the other intermediates O* and OH* along with two water molecules:
| | | O2 + * + H+ + e− → *OOH | (2) |
| | | *OOH + H+ + e− → *O + H2O | (3) |
| | | *OH + H+ + e− → * + H2O | (5) |
The computational hydrogen electrode (CHE) framework developed by Nørskov et al.10,32 was adapted, which exploits the free energy of an electron–proton pair equivalent to the free energy of H2 in the gas phase (pH = 0). The free energies of the ORR intermediate steps were calculated via the following equations:
| | | ΔE(*OOH) = E(*OOH) − E(*) + 3/2EH2 − 2EH2O | (6) |
| | | ΔE(*OH) = E(*OH) − E(*) + 1/2EH2 − 2EH2O | (7) |
| | | ΔE(*O) = E(*O) − E(*) + EH2 − EH2O | (8) |
The Gibbs free energy of each reaction intermediate was calculated using the following equation:
| | | ΔG = ΔEelec. + ΔZPE − TΔS − neU | (9) |
where Δ
Eelec. is the energy obtained from DFT calculations, ΔZPE and Δ
S refer to zero-point energy and entropy contributions,
U is an applied electrode potential
vs. reversible hydrogen electrode (RHE) and
n is the number of electrons that are transferred.
U = 0 V indicates an open-cell circuit and no applied potential on the electrode, whereas
U = 1.23 V is the reaction equilibrium potential for the 4-electron pathway, which is the maximum thermodynamically allowed value.
10,32 The solvation correction was neglected because it has been shown that the double-layer effect on the predicted potential is usually small.
32 The free energy diagram is constructed at
U =0.0 V and at equilibrium potential
E0 = 1.23 V, for the 4e-ORR. If the reaction follows the 2e-ORR pathway, the equilibrium potential is
E0 = 0.70 V. For the associative mechanism, the free energy of each reaction step is calculated as follows:
| | | ΔG1 = ΔG(*OOH) − 4.92 eV | (10) |
| | | ΔG2 = ΔG(*O) − ΔG(*OOH) | (11) |
| | | ΔG3 = ΔG(*OH) − ΔG(*O) | (12) |
The overpotential is given by the largest difference between the reaction steps at the equilibrium potential, according to the following equation:
| | η = max [ΔG1,![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ΔG2, ΔG2,![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ΔG3, ΔG3,![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ΔG4]/e ΔG4]/e | (14) |
For the WOR, the reaction intermediates are the same and the free energy diagram is similar to eqn (10)–(13), in the opposite direction. The mechanism, in this case, can be calculated according to the different equilibrium potentials: 1-electron pathway (E0 = 2.5 V), 2-electron pathway (E0 = 1.76 V), and 4-electron pathway (E0 = 1.23 V). Previous studies showed that binding energies of OH* and O* can be used as a selectivity parameter for different products of the WOR.17,58 If ΔG (*OH) > 2.73 eV, the 1e-WOR is dominant and ˙OH is the major product. If 1.65 < ΔG (*OH) < 2.73 eV and ΔG (*O) > 3.52 eV, the catalyst is selective towards the 2e-WOR and H2O2 is the major product. Finally, if ΔG (*OH) < 1.76 eV, the 4e-WOR is dominant with O2 as the product.
Results and discussion
It has been shown that the trends in ORR catalytic activity can be rationalized based on the adsorption energies of the oxygen intermediates.10 The majority of transition metals and oxides follows linear scaling relationships for the oxygenated species since all three intermediates bind to the surface through the same atom.10 The calculated adsorption free energies for all three ORR reaction intermediates can be found in Table S1.†Fig. 1 displays the scaling relation between *OOH and *OH adsorption energies on different ceria surfaces considered in this study. It can be seen that all low-index ceria surfaces, (100), (110), and (111), follow linear scaling. That is also the case for the stepped surface (221) and its non-equivalent surface sites, although with a small deviation. The (331) surface, on the other hand, does not follow the same linear scaling relationship, which is due to the strong adsorption free energies of *O and *OH intermediates on this surface. The “ideal catalyst” should have a free energy difference of 1.23 eV for each subsequent reaction step, so these values were expected to lie around 2.46 eV and 1.23 eV, respectively. Deviation from this accounts for the observed overpotential.59 For the (331)-Ce2 sites, these values are 0.86 eV and 0.78 eV, respectively, which have around 0.4 eV difference from 1.23 eV. The distinct catalytic profiles among ceria surfaces, with a considerable activity difference between different planes, are somewhat similar to what has been observed by Matz and Calatayud46 for hydrogen activation. The calculated ΔG(*OH) for the (100) Ce-terminated surface is 0.96 eV which is closer to 1.23 eV and higher than the predicted value (0.65 eV) for ΔG(*OH) on Pt(111) by Nørskov et al.10 This indicates that the (100) Ce-terminated surface should have less overpotential than Pt(111). This is also the case on the (331) facet with Ce2 as the active sites. The (110) (111) and (221) facets of ceria bind both (*OOH) and (*OH) too weakly, indicating a poor catalytic activity for the ORR. These results show how important it is to investigate different surface orientations, which is in line with the finding in the recent report by Gunasooriya and Nørskov.19 To achieve the limit of zero overpotential which results in higher activity, breaking the linear scaling relations is required, as suggested in the literature.36
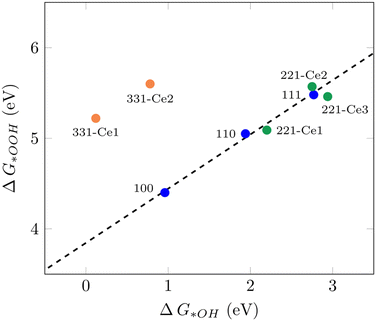 |
| | Fig. 1 Scaling relation between ΔG*OOH and ΔG*OH for various CeO2 facets examined in this study. | |
Fig. 2 shows the free energy diagrams following the associative mechanism for the low index ceria surfaces (100), (110), and (111). The data for each plot are listed in Table S2.† The reaction is thermodynamically favorable on the (100) surface, with the lowest overpotential value. With an applied U = 1.23 V, it can be seen that the reaction is still feasible, and the limiting step is the O–O bond breaking, *OOH → *O (i.e. the higher positive ΔG value). This results in a theoretical overpotential of 0.71 V (defined by the largest ΔG difference between reaction steps). This value is similar to the one for Pt, the commercial reference material for this application,10 therefore making the (100) surface a really promising surface. As can be seen in Fig. 2a, the *OH formation is energetically favorable, and the O–O bond breaking would be the limiting step indicated by the higher positive ΔG. As for the (110) surface, shown in Fig. 2b, the *OOH formation is higher in free energy (0.13 eV), and at U = 1.23 V it becomes considerably unfavourable, which means low catalytic activity. On the other hand, there are prohibitive ΔG values, especially at the equilibrium potential (ΔG = 1.81 V, positive and higher than 1.23 V, the thermodynamic limit for this reaction).
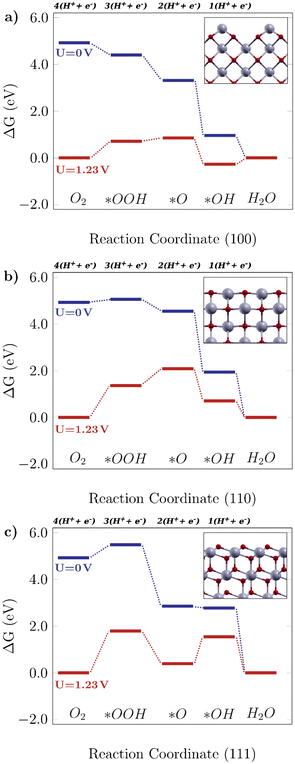 |
| | Fig. 2 Free energy diagrams for the associative mechanism of the oxygen reduction reaction on low-index CeO2 surfaces: the a) (100) facet, b) (110) facet and c) (111) facet. The insets display the corresponding structures for each case. | |
The same tendency is observed for the (111) surface, indicated in Fig. 2c, which can be seen by similar theoretical overpotential values (1.79 V) to (110), both being unfavorable for this reaction. Thus, among the stoichiometric low-index surfaces considered in this work, only (100) is viable for the 4-electron ORR. Gunasooriya and Nørskov19 also observed more favorable (100) surfaces in comparison with (110), for example, in oxides such as Ti(WO4)2 and Ni(SbO3)2. As for (221) and (331), it was observed that these might not contribute to the overall catalytic activity of the material, with considerably high overpotential values. The free energy diagrams for stepped surfaces are shown in Fig. S1. It is interesting to see that non-equivalent sites also have different catalytic properties. On (331), for example, ΔG(*O) is considerably lower on Ce2 sites than on Ce1 ones. On (221), the oxygen binds so strongly on Ce3 sites that the following hydrogenation step becomes unlikely to occur. Nonetheless, the reaction is unfavorable on both surfaces, as can be seen in the positive ΔG values even for U = 0 V. The difference between (331)-Ce1 and (331)-Ce2 activities might arise from the different superficial Ce–O bond lengths, which is 2.33 Å for the (331)-Ce2 site, whereas for (331)-Ce1, the neighboring atoms of the relaxed surface have slightly asymmetric distances of 2.31 Å and 2.44 Å. From a structural point of view, the most promising ceria sites for the ORR are the ones where the Ce atom is more exposed, whereas nearby O atoms are below the surface level.
The results obtained in this work are in agreement with what has been observed experimentally, where XRD patterns of experimentally synthesized CeO2 nanostructures57,58 indicate that the (100) planes, which are predominant in nanorods, are the most active facets for the 4e-ORR. The relationship between ceria structures and catalytic activity for hydroxyl radical generation has also been investigated experimentally by Fisher, T. J et al.,28 where the authors observed that nanorods with a combination of (100) and (111) facets yielded the best results. Another theoretical and experimental study indicated that (100) surfaces have higher oxygen mobility than (110) and (111)62 while acting as supports, which is a desirable characteristic and might also play a role in their great catalytic activity.
Given that the reaction is highly unlikely to occur on any other stoichiometric surface than (100), we further investigated the role of oxygen vacancies as a means of improving the catalytic activity of other crystallographic planes. This is mainly motivated by experimental reports in the literature, where ceria catalytic activity has been correlated to the presence of oxygen vacancies on the synthesized materials.28,59,60 For that investigation, we selected the (110) and (111) planes due to their great stability and facile synthesis.28,59,60 To create vacancies, the two uppermost surface layers were considered and labelled V1 and V2, respectively, as indicated in Fig. S3.† The vacancy formation energies were calculated taking the oxygen chemical potential (μO2) as the reference and according to the following equation:
| | | ΔEF = Eslab+vacancy − (Eslab − 1/2μO2) | (15) |
The oxygen vacancy formation is slightly more favourable on (110) in comparison to (111) (Table S3†), which agrees with what has previously been reported in the literature.61 The 4e-ORR was then calculated on Ce sites adjacent to the removed oxygen sites. The presence of oxygen vacancies on the surfaces can considerably lower the oxygen intermediate species adsorption free energies in both cases, as shown in Fig. 3. The dashed lines indicate the thermodynamic limit after which the overpotentials are high enough so that the reaction would not occur, and the surfaces would not have good catalytic activity. The oxygen vacancies significantly reduce the overpotentials from what would be prohibitive values for the reaction to occur to reasonable ones, as indicated by the red bars – from 1.81 V to 1.12 V on (110) and 1.79 V to 0.66 V on (111), for the 4e-ORR; from 1.28 V to 0.57 V on (110) and 1.26 V to 0.13 V on (111), for the 2e-ORR. Considering the low overpotential observed on (111) with oxygen vacancies, as well as the ΔG(*OH) value of 3.50 eV (Table S3†), close to the H2O2 reference (3.52 eV), this surface with subsurface oxygen vacancies could favor the 2e-ORR pathway. We noted that on both (110) and (111), a sub-surface oxygen vacancy results in the lowest overpotential value, in agreement with what has been reported for other reactions in the literature.63 Zhang et al.63 also observed that oxygen vacancies improve the catalytic activity of the (110) surface for the water oxidation reaction, thus corroborating the obtained results in this work. The theoretical overpotential values on the (110) and (111) surfaces with oxygen vacancies are very close to what was obtained for (100) as shown in Fig. 3, which summarizes these results, indicating that oxygen vacancies can significantly improve the catalytic activity of the (110) and (111) surfaces towards the oxygen reduction reaction.
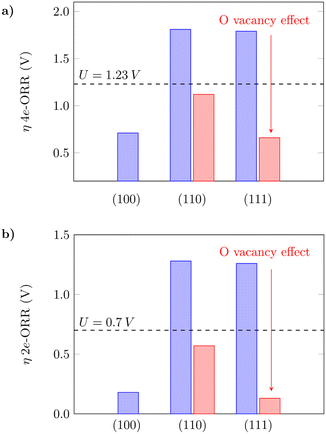 |
| | Fig. 3 Calculated overpotentials for the a) 4-electron and b) 2-electron ORRs on low-index CeO2 planes and the effect of oxygen vacancies. | |
For the WOR, on the other hand, the relationship between the reaction intermediate free energies ΔG(*OH) and ΔG(*O) can be used to identify the selectivity towards each of the possible reaction products, as proposed by Siahrostami et al.17Fig. 4 shows the selectivity diagram obtained in this case. Interestingly, it can be seen that each low-index ceria surface favors a different pathway. The (100) surface lies in the O2 evolution region, even though its proximity to the H2O2 evolution limit might indicate a competing route, while the (110) surface lies in the H2O2 evolution region and the (111) in ˙OH generation. This map indicates that both stepped surfaces (221) and (331) would favor the O2 evolution; however, the high overpotential observed for (331) in this case excludes it as a viable surface for the 4-electron pathway to occur. The free energy diagrams of the stepped surfaces can be found in Fig. S2,† and the discussion below will focus on the most relevant low-index cases, identifying the factors that play a role in each surface's different selectivities for the WOR.
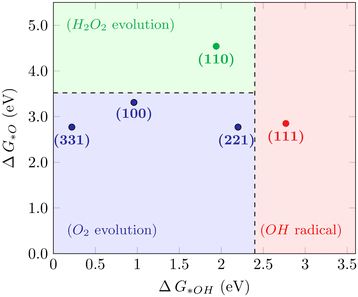 |
| | Fig. 4 Selectivity diagram for the WOR on CeO2 surfaces, showing that the (111) facet predominantly produces OH radicals while (110) is selective towards H2O2. | |
The Gibbs free energy diagrams shown in Fig. 5 can help to rationalize the activity trends among different low-index surfaces, and the selectivity of each facet towards different WOR products is shown in Fig. 4. It can be seen in Fig. 5a that for the (100) surface, ΔG(*O) is lower in energy than H2O2, so the reaction can follow the 4e-WOR. This finding is consistent with a recent report by Feng et al.,64 on synthesized ceria nanorods with a dominant (100) exposed facet, which found that pure ceria nanorods did not exhibit significant O2 evolution and that they were improved with different surface functionalization approaches. This makes (100) ceria surfaces very promising for energy applications, based on green hydrogen production, which is currently still limited by the lack of suitable catalysts for the oxygen evolution reaction.64 The (110) surface, as shown in Fig. 5b, promotes the 2e-WOR and H2O2 formation with a low overpotential of 0.18 V, and it can be seen that this happens because the H2O2 energy level is lower than ΔG(*O), and therefore the 2e-WOR will be the preferred route in this case. This is in agreement with the recent experimental results in the literature.65 Finally, the (111) surface (Fig. 5c) is selective for hydroxyl radical formation as previously shown in Fig. 4, because both ΔG(*OH) and ˙OH are very close. The Gibbs free energy profile of the (111) facet is similar to the free energy diagram reported on TiO2, an oxide where theoretical and experimental studies show that the ˙OH generation is favorable.17 H2O2 generation, as promoted by the (110) surface, or ˙OH generation, as promoted by the (111) surface, are undesirable reactions for green energy generation, but interesting from an environmental perspective, since both could be employed in advanced electrooxidative processes for water treatment.16Fig. 5d shows the calculated overpotentials for each reaction mechanism on these surfaces. The (100) surface, despite its position on the 4e-WOR region of the selectivity diagram from Fig. 4, has a lower overpotential for the 2e-WOR, which might provide some theoretical insight into the work of Feng et al.,64 since the O2 generation might be hampered by a competing route. The overpotentials for the 2e-WOR lie below 1.76 V for all surfaces, which suggests that either this will be a competing route on all low-index stoichiometric ceria surfaces or some structural factor might account for tuning the selectivity towards one or another mechanism. It is noteworthy that the introduction of an oxygen vacancy shifts the selectivity of both (110) and (111) surfaces towards the O2 evolution, lowering the 4e-WOR overpotential, but the 2e-WOR will still have low values such as this and remains a competing route. This is in agreement with a study from Mansingh et al.,66 where it was observed that the selectivity of the (111) ceria surface towards either O2 evolution or ˙OH generation could be tuned by controlling the concentration of oxygen vacancies. In summary, our results show that ceria is a very promising material and that oxygen vacancies can play an important role in tuning the catalytic properties of ceria surfaces towards the desirable applications.
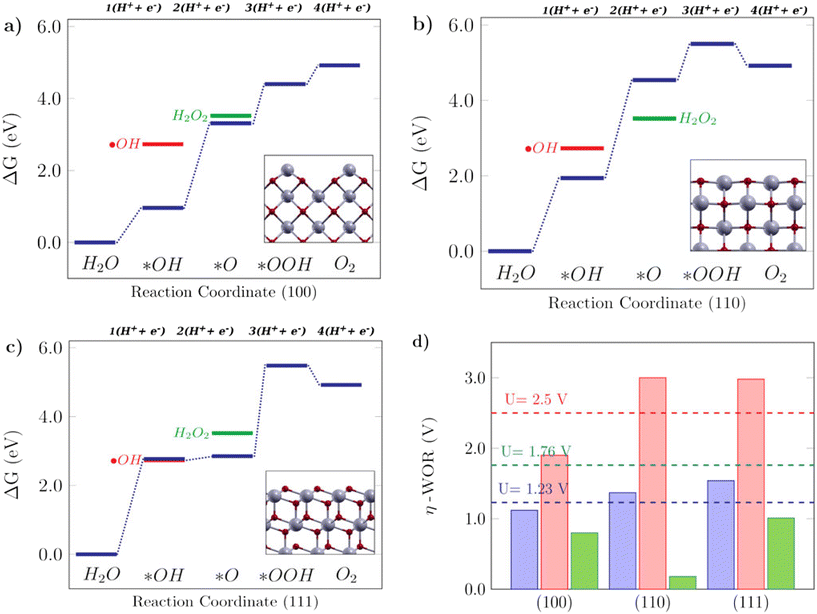 |
| | Fig. 5 Free energy diagrams for the water oxidation reaction on low-index CeO2 surfaces: a) the (100) facet, b) (110) facet and c) (111) facet. The insets in the free energy diagrams display the side view of the corresponding structures. d) Calculated theoretical overpotentials for the 1e-WOR, 2e-WOR, and 4e-WOR on low-index CeO2 surfaces. | |
Conclusions
Using DFT+U calculations and the computational hydrogen electrode model, various CeO2 planes were investigated to determine the most promising crystalline orientations toward the oxygen reduction and water oxidation reactions. Among the selected surfaces, (100) has the closest to the ideal adsorption G(*OOH) versus G(*OH) relation, and the reaction has the lowest theoretical overpotential for the 4e-ORR. It is worth noting that (331) exhibits distinct non-linear behavior between intermediate species, but stepped surfaces (221) and (331) do not appear to contribute significantly to 4e-ORR catalytic activity. Despite their stability, (110) and (111) stoichiometric surfaces appear unsuitable for this application. However, in the presence of oxygen vacancies, the catalytic activity of the (110) and (111) surfaces can be significantly enhanced, with overpotential values approaching those observed for (100) surfaces. CeO2 is a very promising material for WOR applications, and surface orientation is very important. Among the crystallographic planes considered, (100), (110), and (111) promote O2, H2O2, and ˙OH evolution, respectively. Our results also show that the presence of oxygen vacancies shifts the selectivity of (110) and (111) towards O2 evolution. This research provides a comprehensive picture of CeO2's ability to catalyze various oxygen electrochemistry reactions ranging from the ORR to the WOR. Other parameters, such as different proportions of oxygen vacancies and doping with other metals, are expected to improve the catalytic properties of CeO2 further.
Author contributions
Lanna E. B. Lucchetti: conceptualization, data curation, formal analysis, investigation, methodology, software, writing – original draft, and writing – review & editing. James M. de Almeida: conceptualization, formal analysis, investigation, methodology, project administration, software, supervision, validation, writing – original draft, and writing – review & editing. Pedro A. S. Autreto: conceptualization, formal analysis, investigation, methodology, writing – original draft, and writing – review & editing. Samira Siahrostami: conceptualization, data curation, formal analysis, investigation, methodology, project administration, resources, software, supervision, and writing – review & editing. Mauro C. Santos: conceptualization, funding acquisition, project administration, resources, supervision, validation, visualization, and writing – review & editing.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
The authors would like to thank FAPESP (2019/01925-4, 2017/10118-0), CNPq (310045/2019-3, 429727/2018-6), CAPES, and PRH/ANP for the financial support. The authors would also like to thank CCM-UFABC for the computational resources. S. S. acknowledges the support from the University of Calgary's Canada First Research Excellence Fund Program, the Global Research Initiative in Sustainable Low Carbon Unconventional Resources.
Notes and references
-
British Petroleum, Statistical Review of World Energy, 2020.
-
H. Ritchie, M. Roser and P. Rosado, Energy, Our World in Data, 2022 Search PubMed.
- S. Chu, Y. Cui and N. Liu, The path towards sustainable energy, Nat. Mater., 2016, 16, 16–22 CrossRef PubMed.
-
R. G. Akay and A. B. Yurtcan, Direct Liquid Fuel Cells: Fundamentals, Advances and Future, Academic Press, 2020 Search PubMed.
- W. Cai, L. Yan, C. Li, L. Liang, W. Xing and C. Liu, Development of a 30 W class direct formic acid fuel cell stack with high stability and durability, Int. J. Hydrogen Energy, 2012, 37, 3425–3432 CrossRef CAS.
-
M. Choi, S. Yang, J. Kim, H. Jin and C. K. Rhee, Development of 200W Class Direct Formic Acid Fuel Cell Stack Using Bi-Modified Pt/C Catalyst By Irreversible Adsorption, ECS Meeting Abstracts, 2017 Search PubMed.
- A. Kundu, J. H. Jang, J. H. Gi, L. C. R. Jung, H. R. Lee, S.-H. Kim, B. Ku and Y. S. Oh, Micro-fuel cells—Current development and applications, J. Power Sources, 2007, 170, 67–78 CrossRef CAS.
- B. Filanovsky, E. Granot, I. Presman, I. Kuras and F. Patolsky, Long-term room-temperature hydrazine/air fuel cells based on low-cost nanotextured Cu–Ni catalysts, J. Power Sources, 2014, 246, 423–429 CrossRef CAS.
- L. van Biert, M. Godjevac, K. Visser and P. V. Aravind, A review of fuel cell systems for maritime applications, J. Power Sources, 2016, 327, 345–364 CrossRef CAS.
- A. Kulkarni, S. Siahrostami, A. Patel and J. K. Nørskov, Understanding Catalytic Activity Trends in the Oxygen Reduction Reaction, Chem. Rev., 2018, 118, 2302–2312 CrossRef CAS PubMed.
- J. Huang, J. Zhang and M. Eikerling, Unifying theoretical framework for deciphering the oxygen reduction reaction on platinum, Phys. Chem. Chem. Phys., 2018, 20, 11776–11786 RSC.
- X. Tian, X. F. Lu, B. Y. Xia and X. W. Lou, Advanced Electrocatalysts for the Oxygen Reduction Reaction in Energy Conversion Technologies, Joule, 2020, 4, 45–68 CrossRef CAS.
- C. Sun, J. A. Alonso and J. Bian, Recent Advances in Perovskite-Type Oxides for Energy Conversion and Storage Applications, Adv. Energy Mater., 2020, 11, 2000459 CrossRef.
- J. Stacy, Y. N. Regmi, B. Leonard and M. Fan, The recent progress and future of oxygen reduction reaction catalysis: A review, Renewable Sustainable Energy Rev., 2017, 69, 401–414 CrossRef CAS.
- S. Jang, K. Moon, Y. Park, S. Park and K. H. Park, Recent Studies on Multifunctional Electrocatalysts for Fuel Cell by Various Nanomaterials, Catalysts, 2020, 10, 621 CrossRef CAS.
- M. C. Santos, V. S. Antonin, F. M. Souza, L. R. Aveiro, V. S. Pinheiro, T. C. Gentil, T. S. Lima, J. P. C. Moura, C. R. Silva, L. E. B. Lucchetti, L. Codognoto, I. Robles and M. R. V. Lanza, Decontamination of wastewater containing contaminants of emerging concern by electrooxidation and Fenton-based processes – A review on the relevance of materials and methods, Chemosphere, 2022, 307, 135763 CrossRef CAS PubMed.
- S. Siahrostami, G.-L. Li, V. Viswanathan and J. K. Nørskov, One- or Two-Electron Water Oxidation, Hydroxyl Radical, or H2O2 Evolution, J. Phys. Chem. Lett., 2017, 8, 1157–1160 CrossRef CAS PubMed.
- A. S. Malik, T. Liu, M. Dupuis, R. Li and C. Li, Water Oxidation on TiO2: A Comparative DFT Study of 1e–, 2e–, and 4e– Processes on Rutile, Anatase, and Brookite, J. Phys. Chem. C, 2020, 124, 8094–8100 CrossRef CAS.
- G. T. K. K. Gunasooriya and J. K. Nørskov, Analysis of acid-stable
and active oxides for the oxygen evolution reaction, ACS Energy Lett., 2020, 5, 3778–3787 CrossRef CAS.
- M. Capdevila-Cortada, G. Vilé, D. Teschner, J. Pérez-Ramírez and N. López, Reactivity descriptors for ceria in catalysis, Appl. Catal., B, 2016, 197, 299–312 CrossRef CAS.
- M. L. Cerón, T. Gomez, M. Calatayud and C. Cárdenas, Computing the Fukui Function in Solid-State Chemistry: Application to Alkaline Earth Oxides Bulk and Surfaces, J. Phys. Chem. A, 2020, 124, 2826–2833 CrossRef PubMed.
- H. Metiu, S. Chrétien, Z. Hu, B. Li and X. Sun, Chemistry of Lewis acid–base pairs on oxide surfaces, J. Phys. Chem. C, 2012, 116, 10439–10450 CrossRef CAS.
- A. Trovarelli, Catalytic properties of Ceria and CeO2-containing materials, Catal. Rev.: Sci. Eng., 1996, 38, 439–520 CrossRef CAS.
- A. P. Amrute, C. Mondelli, M. Moser, G. Novell-Leruth, N. López, D. Rosenthal, R. Farra, M. E. Schuster, D. Teschner, T. Schmidt and J. Pérez-Ramírez, Performance, structure, and mechanism of CeO2 in HCl oxidation to Cl2, J. Catal., 2012, 286, 287–297 CrossRef CAS.
- Q. Li, L. Song, Z. Liang, M. Sun, T. Wu, B. Huang, F. Luo, Y. Du and C. Yan, A review on CeO2 -based electrocatalyst and photocatalyst in energy conversion, Adv. Energy Sustainability Res., 2021, 2, 2000063 CrossRef CAS.
- M. Ziemba, C. Schilling, M. V. Ganduglia-Pirovano and C. Hess, Toward an Atomic-Level Understanding of Ceria-Based Catalysts: When Experiment and Theory Go Hand in Hand, Acc. Chem. Res., 2021, 54, 2884–2893 CrossRef CAS.
- J. Paier, C. Penschke and J. Sauer, Oxygen defects and surface chemistry of ceria: quantum chemical studies compared to experiment, Chem. Rev., 2013, 113, 3949–3985 CrossRef CAS PubMed.
- T. J. Fisher, Y. Zhou, T. Wu, M. Wang, Y. Soo and C. L. Cheung, Structure-activity relationship of nanostructured ceria for the catalytic generation of hydroxyl radicals, Nanoscale, 2019, 11, 4552–4561 RSC.
- Z.-A. Qiao, Z. Wu and S. Dai, Shape-controlled ceria-based nanostructures for catalysis applications, ChemSusChem, 2013, 6, 1821–1833 CrossRef CAS PubMed.
- B. Hammer and J. K. Nørskov, Theoretical surface science and catalysis—calculations and concepts, Adv. Catal., 2000, 45, 71–129 CAS.
-
J. K. Nørskov, F. Studt, F. Abild-Pedersen and T. Bligaard, Fundamental Concepts in Heterogeneous Catalysis, John Wiley & Sons, New Jersey, 2014 Search PubMed.
- J. K. Nørskov,
et al., Origin of the Overpotential for Oxygen Reduction at a Fuel-Cell Cathode, J. Phys. Chem. B, 2004, 108, 17886–17892 CrossRef.
- B. Hammer and J. K. Nørskov, Electronic factors determining the reactivity of metal surfaces, Surf. Sci., 1995, 343, 211–220 CrossRef CAS.
- J. K. Nørskov, T. Bligaard, J. Rossmeisl and C. H. Christensen, Towards the computational design of solid catalysts, Nat. Chem., 2009, 1, 37–46 CrossRef PubMed.
- V. Stamenkovic,
et al., Changing the activity of electrocatalysts for oxygen reduction by tuning the surface electronic structure, Angew. Chem., 2006, 118, 2963–2967 CrossRef.
- S. Siahrostami, A. Verdaguer-Casadevall, M. Karamad, D. Deiana, P. Malacrida, B. Wickman, M. Escudero-Escribano, E. A. Paoli, R. Frydendal, T. W. Hansen, I. Chorkendorff, I. E. L. Stephens and J. Rossmeis, Enabling direct H2O2 production through rational electrocatalyst design, Nat. Mater., 2013, 12, 1137–1143 CrossRef CAS PubMed.
- C. Loschen, A. Migani, S. T. Bromley, F. Illas and K. M. Neyman, Density functional studies of model cerium oxide nanoparticles, Phys. Chem. Chem. Phys., 2008, 10, 5730–5738 RSC.
- A. N. Ribeiro and N. S. Ferreira, Systematic study of the physical origin of ferromagnetism in CeO2−δ nanoparticles, Phys. Rev. B, 2017, 95, 144430 CrossRef.
- J. Vecchietti, A. Bonivardi, W. Xu, D. Stacchiola, J. J. Delgado, M. Calatayud and S. E. Collins, Understanding the role of oxygen vacancies in the water gas shift reaction on Ceria-supported platinum catalysts, ACS Catal., 2014, 4, 2088–2096 CrossRef CAS.
- B. Wei and M. Calatayud, The subsurface diffusion of hydrogen on rutile TiO2 surfaces: A periodic DFT study, Top. Catal., 2021, 65, 270–280 CrossRef.
- P. Giannozzi,
et al., QUANTUM ESPRESSO: a modular and open-source software project for quantum simulations of materials, J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef PubMed.
- G. Prandini, A. Marrazzo, I. E. Castelli, N. Mounet and N. Marzari, Precision and efficiency in solid-state pseudopotential calculations, npj Comput. Mater., 2018, 4, 1–13 CrossRef.
- K. Lejaeghere,
et al., Reproducibility in density functional theory calculations of solids, Science, 2016, 351, 1415 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
-
D. Sholl and J. A. Steckel, Density Functional Theory: A Practical Introduction, John Wiley and Sons, New Jersey, 2009 Search PubMed.
- O. Matz and M. Calatayud, Breaking H2 with CeO2: Effect of Surface Termination, ACS Omega, 2018, 3, 16063–16073 CrossRef CAS PubMed.
- C. W. M. Castleton, J. Kullgren and K. Hermansson, Tuning LDA+U for electron localization and structure at oxygen vacancies in ceria, J. Chem. Phys., 2007, 127, 244704 CrossRef CAS PubMed.
- T. Zacherle, A. Schriever, R. A. De Souza and M. Martin, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 134104 CrossRef.
- P. R. L. Keating, D. O. Scanlon, B. J. Morgan, N. M. Galea and G. W. Watson, Analysis of Intrinsic Defects in CeO2 Using a Koopmans-Like GGA+U Approach, J. Phys. Chem. C, 2012, 116, 2443–2452 CrossRef CAS.
- N. M. Galea, D. O. Scanlon, B. J. Morgan and G. W. Watson, A GGA+U study of the reduction of ceria surfaces and their partial reoxidation through NO2 adsorption, Mol. Simul., 2009, 35, 577–583 CrossRef CAS.
- C. W. M. Castleton, J. Kullgren and K. Hermansson, Tuning LDA+U for electron localization and structure at oxygen vacancies in ceria, J. Chem. Phys., 2007, 127, 244704 CrossRef CAS PubMed.
- J. J. Plata, A. M. Márquez and J. F. Sanz, Communication: improving the density functional theory+U description of CeO2 by including the contribution of the O2p electrons, J. Chem. Phys., 2012, 136, 041101 CrossRef PubMed.
- M. Cococcioni and S. de Gironcoli, Linear response approach to the calculation of the effective interaction parameters in the LDA+U method, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 035105 CrossRef.
- M. Nolan, S. Grigoleit, D. C. Sayle, S. C. Parker and G. W. Watson, Density functional theory studies of the structure and electronic structure of pure and defective low index surfaces of ceria, Surf. Sci., 2005, 576, 217–229 CrossRef CAS.
- H.-L. Chen and H.-T. Chen, Role of hydroxyl groups for the O2 adsorption on CeO2 surface: A DFT U study, Chem. Phys. Lett., 2010, 493, 269–272 CrossRef CAS.
- X. Shi, S. Siahrostami, G.-L. Li, Y. Zhang, P. Chakthranont, F. Studt, T. F. Jaramillo, X. Zheng and J. K. Nørskov, Understanding activity trends in electrochemical water oxidation to form hydrogen peroxide, Nat. Commun., 2017, 8, 701 CrossRef PubMed.
- H.-Y. Su, Y. Gorlin, I. C. Man, F. Calle-Vallejo, J. K. Nørskov, T. F. Jaramillo and J. Rossmeisl, Identifying active surface phases for metal oxide electrocatalysts: a study of manganese oxide bi-functional catalysts for oxygen reduction and water oxidation catalysis, Phys. Chem. Chem. Phys., 2012, 14, 14010–14022 RSC.
- V. S. Pinheiro, E. C. Paz, L. R. Aveiro, L. S. Parreira, F. M. Souza, P. H. C. Camargo and M. C. Santos, Ceria high aspect ratio nanostructures supported on carbon for hydrogen peroxide electrogeneration, Electrochim. Acta, 2018, 259, 865–872 CrossRef CAS.
- V. S. Pinheiro, F. M. Souza, T. C. Gentil, L. S. Parreira, B. L. Batista and M. C. Santos, Hybrid palladium-ceria nanorod electrocatalysts applications in oxygen reduction and ethanol oxidation reactions in alkaline media, Int. J. Hydrogen Energy, 2021, 46, 15896–15911 CrossRef CAS.
- A. H. Mahadi,
et al., Beyond surface redox and oxygen mobility at pd-polar ceria (100) interface: Underlying principle for strong metal-support interactions in green catalysis, Appl. Catal., B, 2020, 270, 118843 CrossRef CAS.
- T. Wu, N. López, T. Vegge and H. A. Hansen, Facet-dependent electrocatalytic water splitting reaction on CeO2: A DFT + U study, J. Catal., 2020, 388, 1–10 CrossRef CAS.
- N. Baumann, J. Lan and M. Iannuzzi, CO2 adsorption on the pristine and reduced CeO2 (111) surface: Geometries and vibrational spectra by first principles simulations, J. Chem. Phys., 2021, 154, 094702 CrossRef CAS PubMed.
- Y.-C. Zhang, Z. Li, L. Zhang, L. Pan, X. Zhang, L. Wang, Fazal-e-Aleem and J.-J. Zou, Role of oxygen vacancies in photocatalytic water oxidation on ceria oxide: Experiment and DFT studies, Appl. Catal., B, 2018, 224, 101–108 CrossRef CAS.
- T. Feng,
et al., Amorphous Fe(OH)3 passivating CeO2 nanorods: A noble-metal-free photocatalyst for water oxidation, ChemSusChem, 2021, 14, 3382–3390 CrossRef CAS PubMed.
- M. Cheng, Z. Li, T. Xu, Y. Mao, Y. Zhang, G. Zhang and Z. Yan, Efficient overall 2e- oxygen electrolysis to H2O2 on CeO2 nanocubes, Electrochim. Acta, 2022, 430, 141091 CrossRef CAS.
- S. Mansingh, D. Kandi, K. K. Das and K. Parida, A Mechanistic Approach on Oxygen Vacancy-Engineered CeO2 Nanosheets Concocts over an Oyster Shell Manifesting Robust Photocatalytic Activity toward Water Oxidation, ACS Omega, 2020, 5, 9789–9805 CrossRef CAS PubMed.
|
| This journal is © The Royal Society of Chemistry 2023 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article a,
Pedro
A. S. Autreto
a,
Pedro
A. S. Autreto
 a,
James M.
de Almeida
a,
James M.
de Almeida
 ab,
Mauro C.
Santos
ab,
Mauro C.
Santos
 a and
Samira
Siahrostami
a and
Samira
Siahrostami
 *c
*c
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ΔG2,
ΔG2,![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ΔG3,
ΔG3,![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ΔG4]/e
ΔG4]/e




