Processing on crystal growth, structure, thermal property, and nuclear magnetic resonance of organic–inorganic hybrid perovskite type [NH₃(CH₂)₆NH₃]ZnCl₄ crystal

Abstract

Organic–inorganic hybrid compounds have recently gained significant attention in recent years due to their diverse applications. Herein, [NH₃(CH₂)₆NH₃]ZnCl₄ crystals were grown, and their triclinic structure, phase transition temperature (T_C = 408 K), and high thermal stability (T_d = 584 K) was determined using X-ray diffraction (XRD), differential scanning calorimetry, and thermogravimetry measurements. By analyzing the chemical in response to temperature changes, we observed that the coordination geometry around ¹H and ¹³C were highly symmetric below T_C, whereas their symmetry was lowered above T_C. The change of N–H⋯Cl hydrogen bond from XRD results and the change of ¹⁴N NMR chemical shifts was due to the changes to the coordination geometry of Cl⁻ around Zn²⁺ in the ZnCl₄ anion. The activation energy of ¹H was three times greater than that of ¹³C, and this result indicates that the energy transfer of ¹³C was easier than those of ¹H. We compared the results for [NH₃(CH₂)_nNH₃]ZnCl₄ (n = 6) studied here with those for n = 2, 3, 4, and 5 obtained from previous studies. The characteristics of the length of CH₂ in the methylene chain are expected to be used for potential applications in the near future.

---

1. Introduction

The research on organic–inorganic hybrid compounds has garnered significant interest lately due to their wide range of applications and rapid advancement. The structural flexibility and optical properties of these organic–inorganic hybrid compounds are determined by organic cations,^1,2 while the inorganic anions govern their thermal and mechanical properties. These materials are receiving increasing attention due to their unique ability to selectively harness the benefits of both organic and inorganic materials, creating diverse and exceptional materials.

The development of ferroelastic semiconductors is hindered by the significant challenge associated with fabricating hybrid perovskites.³ Moreover, the successful incorporation of ferroelectric properties in hybrid perovskites renders them ideal for application in flexible wearable devices.^4,5 Organic–inorganic hybrid compounds utilizing CH₃NH₃PbX₃ (X = Cl, Br, or I) have demonstrated successful applications in solar cells.^6–8 Nonetheless, the toxic nature of Pb in these perovskites and its susceptibility to decomposition in humid air necessitates the exploration of environmentally friendly alternatives. A class of environmentally friendly free-Pb hybrid organic–inorganic compounds, [NH₃(CH₂)_nNH₃]MX₄ (n = 2, 3, 4, …; M = Co, Zn, Mn, Cd, Fe, Cu; X = Cl, Br), has emerged.^9–14 These compounds are characterized by organic [NH₃(CH₂)_nNH₃] cations arranged along the longest axis, with inorganic MX₄ anions positioned between them. The physical and chemical properties of the organic–inorganic hybrid perovskites depend on the characteristics of the organic cations, the geometry of the inorganic anions (metal halide ions; (MX₆)²⁻ or (MX₄)²⁻), and reaction stoichiometry. When M is Mn, Cu, or Cd, the structure comprises alternating corner-shared octahedral (MX₆)²⁻ units with organic layers. However, in the case of M = Co or Zn, the structures consist of tetrahedral (MX₄)²⁻ units sandwiched between layers of organic cations.^15–24 Recently, researches of 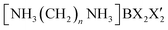with different halogen ions were reported by Abdel-Aal et al.^25–27 The organic and inorganic layers form infinite 0D or 2D structures, connected by N–H⋯Cl hydrogen bonds.^28–31 In particular, the structural rearrangements due to changes along the length of cations are also very important factors.

One interesting hybrid compound is 1,6-hexanediammonium tetrachlorozincate (II), ([NH₃(CH₂)₆NH₃]ZnCl₄), which contains a [NH₃(CH₂)₆NH₃] cation and a ZnCl₄ anion, and has phase transition temperatures of 289 K, 342 K, and 385 K as measured by differential scanning calorimetry (DSC). The structure of the [NH₃(CH₂)₆NH₃]ZnCl₄ crystal at room temperature is triclinic with unit cell parameters of a = 7.2816 Å, b = 10.0996 Å, c = 10.0972 Å, α = 74.368°, β = 88.046°, γ = 85.974°, and Z = 2.³² The terminal ammonium ions of the [NH₃(CH₂)₆NH₃] cation are connected by hydrogen bonds with the Cl ions (i.e., N–H⋯Cl) in the ZnCl₄ anion.

The growth and structures of [NH₃(CH₂)_nNH₃]ZnCl₄ (n = 2–5) single crystals along the length of cations have been previously confirmed by X-ray diffraction analyses.^19,33–36 The thermal stabilities and spin–lattice relaxation times with temperature change were mainly utilized to study the physicochemical properties and structural dynamics of the single crystals.^35–38 Despite the numerous applications of these compounds, there has been limited discussion regarding the thermal properties and structural dynamics attributed to variations in the methylene chain length.

In this study, organic–inorganic hybrid [NH₃(CH₂)₆NH₃]ZnCl₄ single crystals replacing with eco-friendly were grown using the aqueous solution method, and their crystal structures, phase transition temperatures (T_C), and thermal properties were studied. The effect of temperature on coordination geometry, which can provide valuable insights into the physical and chemical properties of compounds, was discussed based on information obtained from ¹H, ¹³C, and ¹⁴N nuclear magnetic resonance (NMR) chemical shifts. The energy transfer was investigated by employing the spin–lattice relaxation time (T_1ρ). Moreover, the interplay of N–H⋯Cl hydrogen bonds connecting the organic cation and inorganic anion was considered. The results of this study demonstrated comparability and provided explanations for research on structural dynamics of [NH₃(CH₂)_nNH₃]ZnCl₄ (n = 2, 3, 4, 5, and 6) where the methylene length chain length varies as a parameter.

2. Experimental

[NH₃(CH₂)₆NH₃]ZnCl₄ single crystals were grown by the slow evaporation method at 300 K after dissolving NH₂(CH₂)₆NH₂·2HCl (Aldrich, 99%) and ZnCl₂ (Aldrich, 98%) in a ratio of 1 : 1 in distilled water. The single crystal grown here had a size of about 7 mm × 3 mm × 2 mm and was colorless and transparent.

The lattice constants at 250, 300, and 350 K were obtained by single-crystal X-ray diffraction (SCXRD) at the Seoul Western Center of the Korea Basic Science Institute (KBSI). Single crystal experiments were performed using a Bruker diffractometer (D8 Venture PHOTON III M14) with Mo-Kα radiation source and a nitrogen cold flow (−50 °C). Data collection was obtained using SMART APEX3 (Bruker 2016) and SAINT (Bruker, 2016) software. The structure was analyzed by full-matrix least-squares on F² using SHELXTL.³⁹ All hydrogen atoms were represented in geometric positions. Additionally, powder X-ray diffraction (PXRD) patterns were obtained at various temperatures using an XRD system equipped with a Mo-Kα as the same target used in SCXRD.

Differential scanning calorimetry experiments (TA, DSC 25) were performed at temperatures ranging from 193 to 573 K at a heating rate of 10 °C min⁻¹ under N₂ gas.

Thermogravimetry analysis (TGA) and differential thermal analysis (DTA) measurements were conducted from 300 to 873 K under N₂ gas at a heating rate of 10 °C min⁻¹ using a thermogravimetric analyzer (TA Instrument).

Temperature-dependences for NMR spectra and spin-lattice relaxation times (T_1ρ) were measured using a 400 MHz (AVANCE III HD) solid-state NMR spectrometer (Bruker, Germany) in the same laboratory as above. The Larmor frequency for the ¹H magic angle spinning (MAS) NMR experiment was 400.13 MHz, and TMS (tetramethylsilane) was used as the standard material to accurately measure the ¹H NMR chemical shifts. The Larmor frequency for the ¹³C MAS NMR experiment was 100.619 MHz, and adamantane was used as the standard material for measuring the ¹³C NMR chemical shifts. Static ¹⁴N NMR chemical shifts were measured using the one-pulse method at a Larmor frequency of 28.90 MHz, and NH₄NO₃ was used as the reference material. Meanwhile, the spin–lattice relaxation time T_1ρ values were measured using a π/2–τ pulse by a spin-lock pulse of duration τ, where the pulse width of π/2 for ¹H and ¹³C were 4.0 and 3.6 μs, respectively. The spinning rate to minimize the sideband of the NMR signal was 10 kHz. N₂ gas flow and heater current were used to adjust and maintain the desired temperature.

3. Results and discussion

3.1 Single-crystal XRD measurements

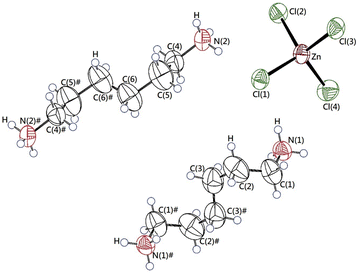
The single-crystal XRD patterns of [NH₃(CH₂)₆NH₃]ZnCl₄ were obtained at 250, 300, and 350 K. The SCXRD result at three temperatures showed a triclinic system with P1 (bar) space group and the cell constants of a = 7.2844 (2) Å, b = 10.1024 (3) Å, c = 10.1051 (3) Å, α = 74.3060 (10)°, β = 85.9270 (10)°, γ = 88.0170 (10)°, and Z = 2 at 300 K. These results were in good agreement with data at 300 K reported by Mostafa and El-khiyami.³² On the other hand, the structures and lattice parameters were unchanged at 250, 300, and 350 K, as shown in Table 1, and it between 300 K and 350 K does not change to be significantly at the phase transition temperature of 340 K previously reported.³² Fig. 1 shows the structure of the [NH₃(CH₂)₆NH₃] cation and ZnCl₄ anion, the atomic numbering scheme, and the thermal ellipsoids of the H atoms in the [NH₃(CH₂)₆NH₃]ZnCl₄ crystal. In ZnCl₄, the Zn atom is surrounded by four Cl atoms, forming a tetrahedron. Infinite chains consisting of face-shared ZnCl₄ tetrahedra and four doubly bridging chloride ions link the adjacent Zn centers. This crystal is characterized by the N–H⋯Cl hydrogen bonds, connecting the cation to the anion. Bond lengths for Zn–Cl, N–C, C–C, C–H, N–H at three temperatures, are shown in Table 2. At 250 and 300 K, three N–H⋯Cl hydrogen bonds were formed, however, one N–H⋯Cl was broken at 350 K, and two N–H⋯Cl hydrogen bonds remained. The CIF files results of SCXRD for the crystal structures at 250, 300, and 350 K are shown in the ESI (1, 2, and 3†).

Table 1 Crystal data and structure refinement for [NH₃(CH₂)₆NH₃]ZnCl₄ at 250 K, 300 K, and 350 K

Temperature	250 K	300 K	350 K
Chemical formula	C6H18N2ZnCl4	C6H18N2ZnCl4	C6H18N2ZnCl4
Weight	325.39	325.39	325.39
Crystal system	Triclinic	Triclinic	Triclinic
Space group	P1 (bar)	P1 (bar)	P1 (bar)
a (Å)	7.2757 (4)	7.2844 (2)	7.2972 (3)
b (Å)	10.0165 (6)	10.1024 (3)	10.1542 (4)
c (Å)	10.0348 (6)	10.1051 (3)	10.1812 (3)
α (°)	75.028 (2)	74.3060 (10)	73.8420 (10)
β (°)	86.496 (2)	85.9270 (10)	87.9390 (10)
γ (°)	88.354 (2)	88.0170 (10)	85.6380 (10)
Z	2	2	2
V (Å^3)	705.10 (7)	714.01 (4)	722.41 (5)
Radiation type	Mo-Kα	Mo-Kα	Mo-Kα
Wavelength (Å)	0.71073	0.71073	0.71073
Reflections collected	14 848	26 702	27 217
Independent reflections	3539 (Rint = 0.0242)	3538 (Rint = 0.0272)	3595 (Rint = 0.0295)
Goodness-of-fit on F^2	1.039	1.042	1.021
Final R indices [I > 2 sigma(I)]	R1 = 0.0283, wR2 = 0.0687	R1 = 0.0359, wR2 = 0.0964	R1 = 0.0446, wR2 = 0.1405
R indices (all data)	R1 = 0.0369, wR2 = 0.0740	R1 = 0.0480, wR2 = 0.1046	R1 = 0.0656, wR2 = 0.1613

---

Fig. 1 The thermal ellipsoid plots for [NH₃(CH₂)₆NH₃]ZnCl₄ crystal structure at 300 K.

Table 2 The bond lengths (Å) of [NH₃(CH₂)₆NH₃]₂ZnCl₄ at 250 K, 300 K, and 350 K

Temperature	250 K	300 K	350 K
Zn–Cl (1)	2.2454 (7)	2.2795 (8)	2.2749 (10)
Zn–Cl (2)	2.2787 (6)	2.2776 (8)	2.2765 (11)
Zn–Cl (3)	2.2828 (6)	2.2686 (8)	2.2449 (12)
Zn–Cl (4)	2.2691 (6)	2.2442 (9)	2.2707 (11)
N (1)–C (1)	1.480 (3)	1.479 (4)	1.458 (6)
N (2)–C (4)	1.487 (3)	1.467 (4)	1.466 (6)
C (1)–C (2)	1.479 (4)	1.482 (6)	1.365 (9)
C (2)–C (3)	1.556 (4)	1.578 (7)	1.585 (11)
C (3)–C (3)#	1.496 (6)	1.454 (9)	1.476 (19)
C (4)–C (5)	1.507 (4)	1.435 (6)	1.431 (10)
C (5)–C (6)	1.547 (4)	1.584 (7)	1.620 (12)
C (6)–C (6)#	1.498 (6)	1.465 (11)	1.399 (15)
C–H	0.980	0.970	0.970
N–H	0.900	0.890	0.890
N (1)–H (1)–Cl (2)		3.287
N (2)–H (2)–Cl (2)		3.479
N (2)–H (2)–Cl (4)		3.738

---

3.2 Phase transitions and powder XRD measurements

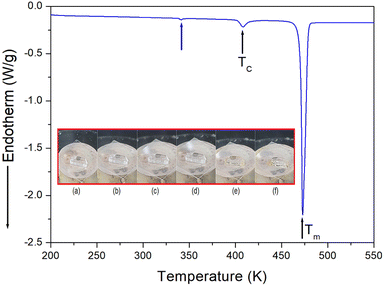
The phase transition temperature of the [NH₃(CH₂)₆NH₃]ZnCl₄ crystal was investigated using a DSC experiment which involved heating the crystal from 200 K to 550 K at a rate of 10 °C min⁻¹, with a sample size of 8.8 mg. The DSC curve, shown in Fig. 2, revealed the presence of two weak endothermic peaks at 340 K and 408 K, respectively, along with a strong endothermic peak at 473 K. The endotherm peak at 340 K was relatively small, making it challenging to accurately measure the enthalpy. However, at 408 K and 473 K, the enthalpy values of 796 J mol⁻¹ and 21 kJ mol⁻¹ were obtained, respectively. The temperature-induced variations in the single crystal were examined using an optical polarization microscope to accurately confirm the three peaks seen in DSC. It was observed that the crystal exhibited minimal changes in the temperature range of 300–450 K, and melting of the single crystal began at near 470 K (i.e., T_m = 470 K) as shown in the inset of Fig. 2.

Fig. 2 Differential scanning calorimetry (DSC) curve of [NH₃(CH₂)₆NH₃]ZnCl₄ (inset: changes in the crystal at various temperatures: (a) 300 K, (b) 370 K, (c) 420 K, (d) 440 K, (e) 470 K, and (f) 490 K).

The temperature-dependent PXRD experiment was conducted, and the corresponding results are presented in Fig. 3, covering a range of 8–60° (2θ). The PXRD patterns below 400 K, indicated by red color, exhibited slight differences compared to those recorded at 410 K, represented by the olive color. This difference was attributed to T_C (= 408 K). Notably, the PXRD results were well consistent with the DSC findings. The PXRD patterns did not exhibit any changes corresponding to the small endothermic peak near 340 K observed in the DSC analysis. Also, the triclinic structure derived from SCXRD results at 300 K and 350 K remained unchanged. And, the simulated XRD pattern based on the CIF file at 300 K is shown is represented in Fig. 3, and this result agrees well with the pattern obtained from PXRD experiment.

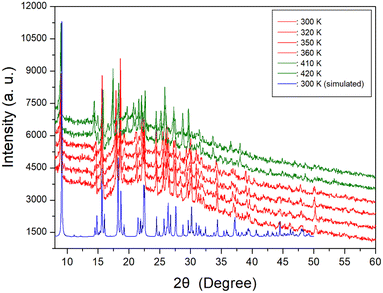Fig. 3 Powder X-ray diffraction (PXRD) patterns at various temperatures, and the blue color is simulated PXRD pattern at 300 K.

Therefore, the phase transition temperature (T_C) determined from DSC, PXRD, SCXRD, and optical polarizing microscopy experiments, was found to be 408 K. These results were not consistent with the previously reported values of 289 K, 342 K, and 385 K.³²

3.3 Thermal properties

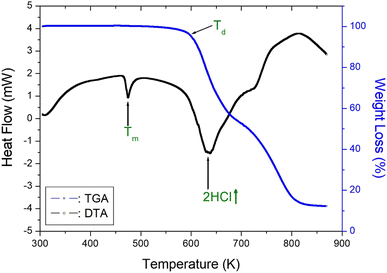
To understand the thermal characteristics, the [NH₃(CH₂)₆NH₃]ZnCl₄ crystal were assessed through TGA and DTA experiments at the heating rate of 10 °C min⁻¹ with a method similar to that of the DSC experiment. As shown in Fig. 4, the endothermic peak at 408 K in the DSC curve of Fig. 2 is very small, so there is almost no change in the TGA and DTA curves. In other words, it shows thermal stability near the phase transition temperature of 408 K. And, the DTA curve exhibited a peak around 474 K, which correlates with the melting temperature determined from the DSC and optical polarizing microscope analyses. The TGA and DTA results indicated that the crystal displayed thermal stability up to approximately 584 K, referred to as the partial thermal decomposition temperature (T_d). Beyond this temperature, [NH₃(CH₂)₆NH₃]ZnCl₄ experienced weight loss, and the amount of solid residue was determined using the molecular weight. The weight loss rapidly declined between 600 and 800 K, and approximately 22% weight loss occurred near 636 K due to the decomposition of 2HCl. Around 800 K, a weight loss of 90% was observed, resulting from the decomposition of NH₂(CH₂)₆NH₂·2HCl, leaving behind only the inorganic ZnCl₂ anions.⁴⁰

Fig. 4 Thermogravimetry analysis and differential thermal analysis curves of [NH₃(CH₂)₆NH₃]ZnCl₄.

3.4 ¹H and ¹³C MAS NMR spectra

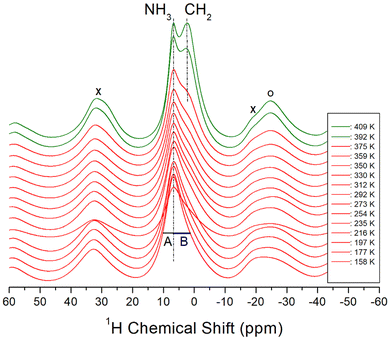
The ¹H MAS NMR spectra of the [NH₃(CH₂)₆NH₃]ZnCl₄ crystal were acquired in situ as a function of temperature, and the corresponding ¹H chemical shifts are shown in Fig. 5. The TMS reference signal was used as the standard for ¹H chemical shifts. At lower temperatures, a single resonance signal with an asymmetric shape was observed, resulting from the overlapping ¹H resonance lines of NH₃ and CH₂ in the organic [NH₃(CH₂)₆NH₃] cations. The left (A) and right (B) sides of the resonance signal exhibited unequal half-full width at half maximum (FWHM). At 158 K, a single resonance line was detected at a chemical shift of 6.07 ppm. With increasing the temperature to 410 K, the NMR line displayed a separation into two distinct resonance lines at chemical shifts of 6.79 and 2.13 ppm for NH₃ and CH₂, respectively. The NH₃ spinning sidebands are marked with crosses, and the sidebands for CH₂ are marked with open circles in Fig. 5. Above 392 K, near T_C, the ¹H NMR signals for NH₃ and CH₂ began to separate. In addition, the narrow line width of the left signal (i.e., NH₃) and the broader line width of the right signal (i.e., CH₂) aligned well with the respective number of ¹H in the NH₃ and CH₂ groups. The ¹H chemical shifts for NH₃ remained almost unchanged as the temperature increased, whereas those of CH₂ experienced changes. These observations suggest that the surrounding environments of ¹H of the NH₃ changes little and that of the CH₂ changes slightly.

Fig. 5 ¹H MAS NMR chemical shifts for NH₃ and CH₂ in [NH₃(CH₂)₆NH₃]ZnCl₄ as a function of temperature, and the spinning rate is 10 kHz. The cross (×) and open circle (○) indicate the sidebands for NH₃ and CH₂, respectively. A and B show the half-full width at half maximum for NH₃ and CH₂.

The variations of ¹³C chemical shifts in the MAS NMR spectra with temperature are shown in Fig. 6. The adamantane reference signal was used as the standard for the ¹³C chemical shifts. In the [NH₃(CH₂)₆NH₃] cation illustrated in Fig. 1, the CH₂ groups positioned adjacent to the NH₃ are designated as C (1) and C (1)#, while the centrally located CH₂ groups are denoted as C (3) and C (3)#. The CH₂ groups situated between C (1) and C (3) are labeled as C (2) and C (2)#, respectively. At 292 K, three distinct ¹³C NMR signals were observed; C (1) at 41.76 ppm, C (2) at 27.23 ppm, and C (3) at 25.71 ppm. As the temperature increased, the chemical shifts of C (1) remained largely unchanged, while those of C (2) and C (3) shifted positively. Near the T_C temperature, C (1) was resolved into C (1)# with a different environment, and C (2) was separated into C (2)# with a different environment. No notable changes were observed in C (1), C (2), and C (3) around 340 K. And, the difference of the chemical shift between (2) and C (2)# is larger than that between C (1) and C (1)#. Separation into C (1) and C (1)# and C (2) and C (2)# above T_C means that the symmetry of cations above T_C is lowered.

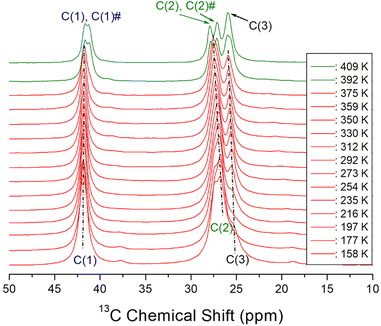Fig. 6 ¹³C MAS NMR chemical shifts for C (1), C (1)#, C (2), C (2)#, and C (3) in [NH₃(CH₂)₆NH₃]ZnCl₄ as a function of temperature, and the spinning rate is 10 kHz.

3.5 ¹⁴N static NMR spectrum

The ¹⁴N static NMR spectrum of [NH₃(CH₂)₆NH₃]ZnCl₄ single crystal was obtained in the temperature range of 180–420 K (Fig. 7). The ¹⁴N chemical shift range exhibited a significantly wider span compared to the ¹H chemical shift range, making it valuable for determining the surrounding environment of ¹⁴N. In this study, the external magnetic field was measured in an arbitrary direction of the single crystal. Considering the spin number of ¹⁴N as I = 1, the NMR spectrum predicts two resonance lines due to the quadrupole interaction.⁴¹ However, due to the very low Larmor frequency of 28.90 MHz for obtaining the ¹⁴N NMR spectrum, the signal acquisition was challenging. The ¹⁴N NMR chemical shifts shown in Fig. 7 disappeared above 340 K. The SCXRD results listed in Table 2 indicated the formation of three N–H⋯Cl hydrogen bonds at 250 and 300 K. However, one N–H⋯Cl at 350 K was broken, leaving two N–H⋯Cl hydrogen bonds intact. This observation aligned with the disappearance of the ¹⁴N NMR signal above 340 K. The continuous change in the ¹⁴N chemical shifts with increasing temperature indicated a variation in the local environment and coordination geometry of the ¹⁴N atoms.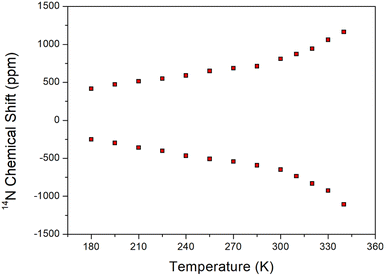

Fig. 7 Static ¹⁴N NMR chemical shifts of [NH₃(CH₂)₆NH₃]ZnCl₄ single crystal as a function of temperature.

3.6 ¹H and ¹³C spin–lattice relaxation times

The spin–lattice relaxation time T_1ρ for ¹H and ¹³C was determined by acquiring an FID after applying the spin-lock pulse. The intensity changes of the measured magnetization are described by the following equation:⁴²

S(t)/S(0) = exp(−τ/T_1ρ), (1)

where S(t) is the intensity of the resonance line at the delay time t, S(0) is the intensity of the NMR spectrum at the delay time t = 0. The experiment was conducted with various τ values, and the corresponding T_1ρ values were determined from the slopes of the resulting intensities plotted against the delay time according to eqn (1). The T_1ρ values of the ¹H of NH₃ and CH₂ in [NH₃(CH₂)₆NH₃]ZnCl₄ were obtained, and are represented in Fig. 8 as a function of the 1000/temperature. The T_1ρ value for ¹H in NH₃ and CH₂ decreased slightly with increasing temperature, followed by a rapid increase above 177 K. Moreover, the ¹H T_1ρ values in NH₃ and CH₂ reached a maximum near 340 K, followed by a subsequent decrease in a similar manner. At 177 K, the minimum T_1ρ value for ¹H in CH₂ and NH₃ were 4.6 ms and 6.2 ms, respectively. These patterns in T_1ρ values indicate active molecular motion. According to the Bloembergen–Pound–Purcell (BPP) theory,^43,44 the experimental T_1ρ value is directly related to the correlation time τ_C as shown in eqn (2).

(T_1ρ)⁻¹ = R[4f₁(ω₁) + f₂(ω_C − ω_H) + 3f₃(ω_C) + 6f₄(ω_C + ω_H) + 6f₅(ω_H)], f₁ = τ_C/[1 + ω₁²τ_C²], f₂ = τ_C/[1 + (ω_C − ω_H)²τ_C²], f₃ = τ_C/[1 + ω_C²τ_C²], f₄ = τ_C/[1 + (ω_C + ω_H)²τ_C²], f₅ = τ_C/[1 + ω_H²τ_C²], (2)

where R (γ_H γ_C ħ/r³)²; constant, ω₁; the spin-lock field, and ω_C and ω_H; the Larmor frequencies for carbon and proton. When ω₁τ_C = 1, a minimum value is obtained for T_1ρ, enabling the determination of the constant R using τ_C. R, ω₁, ω_H, ω_C, and T_1ρ are then used to calculate τ_C at a given temperature change. Local field fluctuations around ¹H can be explained by the thermal motion of thermally activated protons. For the correlation time τ_C, the activation energy E_a can be obtained using eqn (3) shown below ⁴¹

τ_C = τ_C (0) exp(−E_a/k_BT) (3)

where τ_C (0); the pre-correlation time, E_a; the activation energy, k_B; the Boltzmann constant, and T; the temperature. The magnitude of E_a is related to molecular kinetics. When 1000/T for ¹H is plotted against τ_C on a logarithmic scale, as shown in Fig. 8, E_a values of 16.82 ± 1.71 kJ mol⁻¹ and 19.61 ± 1.71 kJ mol⁻¹ for ¹H in NH₃ and for ¹H in CH₂ can be obtained from the slopes of the solid lines, which were almost similar within the error range.

Fig. 8 ¹H spin–lattice relaxation times T_1ρ and correlation times τ_C for NH₃ and CH₂ in [NH₃(CH₂)₆NH₃]ZnCl₄ as a function of 1000/temperature. The solid lines represent the ¹H activation energies (E_a) in NH₃ and CH₂.

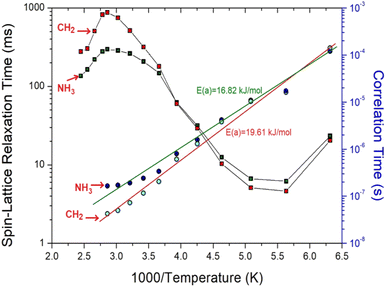
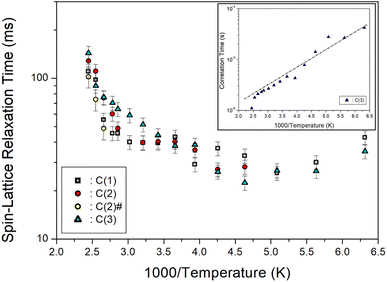
Furthermore, the T_1ρ values of C (1), C (2), C (2)#, and C (3) for ¹³C in [NH₃(CH₂)₆NH₃]ZnCl₄ were measured, and their results are represented in Fig. 9 as a function of the 1000/temperature. The T_1ρ values for ¹³C of all three types kinds exhibited a slight decrease as the temperature rose and showed a slow increase at temperatures above 216 K. Notably, the T_1ρ values of C (1), C (2), C (2)#, and C (3) demonstrated trends similar to each other. Regarding the T_1ρ value of ¹H, C (3) exhibits a minimum value of 22 ms, and their ¹³C T_1ρ patterns underwent active molecular motion. The logarithmic plot of the τ_C versus 1000/T for ¹³C is shown as an inset in Fig. 9. The slope of the dotted line in the figure yielded E_a = 6.56 ± 0.63 kJ mol⁻¹, and the values for C (1), C (2), and C (2)# were nearly identical within the margin of error.

Fig. 9 ¹³C spin–lattice relaxation times T_1ρ for C (1), C (2), C (2)#, and C (3) of [NH₃(CH₂)₆NH₃]ZnCl₄ as a function of 1000/temperature (inset: correlation time τ_C for C (3) as a function of 1000/temperature).

3.7 [NH₃(CH₂)_nNH₃]ZnCl₄ (n = 2, 3, 4, 5, and 6) crystals

We then conducted a comparison between our study on [NH₃(CH₂)_nNH₃]ZnCl₄ (n = 6) and previous studies on n = 2, 3, 4, and 5.^35–38 The structures, space groups, and lattice constants of [NH₃(CH₂)_nNH₃]ZnCl₄ (n = 2, 3, 4, 5, and 6) crystals were shown in Table 3. Correspondingly, the crystal structure was found to be monoclinic for odd values of n, triclinic for even values of n, and orthorhombic for n = 2. By analyzing the physicochemical properties of these organic–inorganic compounds, we examined the impact of the methylene chain length. With an increase in the length of the methylene chain, the thermal stability is enhanced, and it is related to intermolecular forces. This trend is clearly illustrated in Fig. 10, where the results showed an increase to 534, 549, 559, 581, and 584 K for n = 2, 3, 4, 5, and 6, respectively. The changes of T_d can be considered as electronic configuration; the 3d electron of the M shell is filled, and the valence electron is 4s².

Table 3 The structures, space groups, and lattice constants (Å) of [NH₃(CH₂)_nNH₃]ZnCl₄ (n = 2, 3, 4, 5, and 6) crystals

n	2	3	4	5	6
Structure	Orthorhombic	Monoclinic	Triclinic	Monoclinic	Triclinic
Space group	P212121	P21/n	P1 (bar)	C2/c	P1 (bar)
Lattice constant
a (Å)	8.832	10.670	7.2839	21.4175	7.2844
b (Å)	9.811	10.576	8.1354	7.3574	10.1024
c (Å)	11.089	10.755	10.4592	19.1079	10.1051
α (°)			77.6527		74.3060
β (°)		118.477	80.3358	120.5190	85.9270
γ (°)			82.8355		88.0170
Z	4	4	2	8	2
Ref.	33	31 and 34	35	36	32, present

---

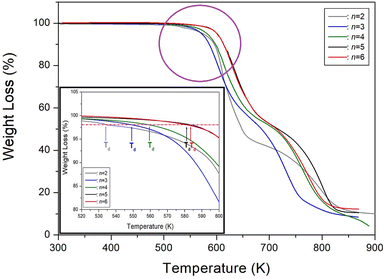Fig. 10 Thermogravimetry analysis (TGA) curves of [NH₃(CH₂)_nNH₃]ZnCl₄ (n = 2, 3, 4, 5, and 6) according to the methylene chain length.

On another note, as n increased, the ¹H T_1ρ below 300 K became shorter, while the behavior of T_1ρ above 300 K varied, as shown in Fig. 11. Similarly, Fig. 12 illustrates the overall temperature-dependent behavior of ¹³C T_1ρ. The substantial difference between ¹³C T_1ρ (10 times less) and ¹H T_1ρ indicates that energy transfer for ¹³C is more efficient. However, when n is 2, both ¹H and ¹³C T_1ρ displayed different characteristics compared to when n = 3, 4, 5, and 6. Furthermore, the length of the chain (i.e., n) did not distinctly affect the temperature dependence of ¹H and ¹³C T_1ρ, but it increased the temperature dependence of T_d.

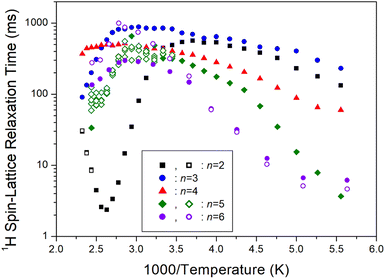Fig. 11 ¹H spin–lattice relaxation times T_1ρ of [NH₃(CH₂)_nNH₃]ZnCl₄ (n = 2, 3, 4, 5, and 6) for various methylene chain lengths as a function of 1000/temperature.

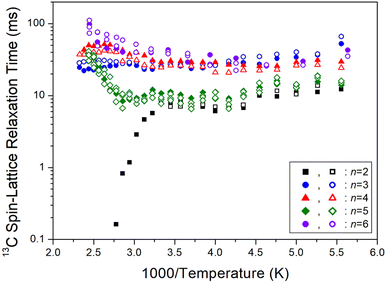Fig. 12 ¹³C spin–lattice relaxation times T_1ρ of [NH₃(CH₂)_nNH₃]ZnCl₄ (n = 2, 3, 4, 5, and 6) for different methylene chain lengths as a function of 1000/temperature.

4. Conclusion

Studying the physical properties of [NH₃(CH₂)₆NH₃]ZnCl₄ crystals is essential for their practical application. In this study, we successfully grew these crystals with triclinic structures. Through comprehensive examinations utilizing DSC, SCXRD, and PXRD, we established that the phase transition temperature of these crystals occurred at 408 K. Remarkably, this phase transition temperature was different from those observed in other groups, indicating that slight differences in crystal growth conditions may be the underlying cause.

Additionally, exceptionally high thermal stability was observed, with the crystals exhibiting remarkable stable up to approximately 584 K. The NMR analyses of the [NH₃(CH₂)₆NH₃]ZnCl₄ crystal showed that the chemical shifts caused by the local field surrounding ¹H, ¹³C, and ¹⁴N of the cation and anion as the temperature increases, and the surrounding environment of their atoms also changes. Based on the temperature-dependent chemical, it was found that the coordination geometry around ¹H and ¹³C exhibited high symmetry below T_C, whereas it showed low symmetry above T_C. The structural analysis using SCXRD revealed no changes in the structure below 350 K. However, at 250 and 300 K, three N–H⋯Cl hydrogen bonds were identified. At 350 K, one N–H⋯Cl hydrogen broke, leaving two intact. This finding appears to be connected to the significant change observed in the ¹⁴N chemical shifts. The variations in the N–H⋯Cl hydrogen bond arises from alterations in the coordination geometry of Cl⁻ around Zn²⁺ in the ZnCl₄ anion. Notably, the activation energy of ¹H was three times higher than that of ¹³C, suggesting that the energy transfer of ¹³C is smaller than that of ¹H.

As a result, the effect of cation length can be attributed to an increase in the decomposition temperature T_d by the intermolecular forces. These findings suggest that the characteristics of the CH₂ chain length hold promise for potential future applications.

Author contributions

A. R. Lim performed X-ray experiments, and wrote the manuscript. S. H. Kim measured NMR experiments.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the national Research Foundation of Korea (NRF) grant funded by the Korea government (MSIT) (2023R1A2C2006333). This research was also supported by the Basic Science Research Program through the National Research Foundation of Korea (NRF), funded by the Ministry of Education, Science, and Technology (2016R1A6A1A03012069).

References

1. W. Zang and R.-G. Xiong, Chem. Rev., 2012, 112, 1163.
2. A. R. Lim and S. H. Kim, ACS Omega, 2021, 6, 27568.
3. C. Su, M. Lun, Y. Chen, Y. Zhou, Z. Zhang, M. Chen, P. Huang, P. D. Fu and Y. Zhang, CCS Chem., 2022, 4, 2009.
4. Y. Xie, Y. Ai, Y.-L. Zeng, W.-H. He, X.-Q. Huang, D.-W. Fu, J.-X. Gao, X.-G. Chen and Y.-Y. Tang, J. Am. Chem. Soc., 2020, 142, 12486.
5. D.-W. Fu, J.-X. Gao, W.-H. He, X.-Q. Huang, Y.-H. Liu and Y. Ai, Angew. Chem., Int. Ed., 2020, 59, 17477.
6. S. K. Abdel-Aal, A. S. Abdel-Rahman, G. G. Kocher-Oberlehner, A. Ionov and R. Mozhchil, Acta Crystallogr., Sect. A: Found. Adv., 2017, 70, C1116.
7. Y. Liu, L. Collins, R. Proksch, S. Kim, B. R. Watson, B. Doughty, T. R. Calhoun, M. Ahmadi, A. V. levlev, S. Jesse, S. T. Retterer, A. Belianinov, K. Xiao, J. Huang, B. G. Sumpter, S. V. Kalinin, B. Hu and O. S. Ovchinnikova, Nat. Mater., 2018, 17, 1013.
8. J. Lee, W. Lee, K. Kang, T. Lee and S. K. Lee, Chem. Mater., 2021, 33, 370.
9. C. Sourisseau, G. Lucazeau and A. J. Dianoux, J. Phys., 1983, 44, 967.
10. K. Chhor, J. F. Bocquet and C. Pommier, J. Chem. Thermodyn., 1985, 17, 379.
11. V. V. Eremenko, V. I. Fomin and V. S. Kurnosov, Phys. B, 1994, 194–196, 187.
12. J.-C. Bissey, N. Filloleau, N.-B. Chanh, R. Berger and S. Flandrois, Solid State Commun., 1998, 106, 385.
13. M. M. Bogdan, M. I. Kobets and E. N. Khats'ko, Low Temp. Phys., 1999, 25, 192.
14. S. J. Lee, M. Y. Choi and A. R. Lim, ACS Omega, 2021, 6, 15392.
15. N. Narita and I. Yamada, J. Phys. Soc. Jpn., 1996, 65, 4054.
16. D. B. Mitzi, K. Chondroudis and C. R. Kagan, IBM J. Res. Dev., 2001, 45, 29.
17. H. Manaka, I. Yamada and T. Goto, J. Phys. Soc. Jpn., 2002, 71, 2822.
18. Y. Wei, P. Audebert, L. Galmiche, J. S. Lauret and E. Deleporte, Materials, 2014, 7, 4789.
19. D. B. Mitzi, J. Chem. Soc., Dalton Trans., 2001, 1, 1.
20. S. Ahmad, C. Hanmandlu, P. K. Kanaujia and G. Vijaya Prakash, Opt. Mater. Express, 2014, 4, 1313.
21. I. Saikumar, S. Ahmad, J. J. Baumberg and G. Vijaya Prakash, Scr. Mater., 2012, 67, 834.
22. K. Pradeesh, G. S. Yadav, M. Singh and G. Vijaya Prakash, Mater. Chem. Phys., 2010, 124, 44.
23. K. Pradeesh, J. Baumberg and G. Vijaya Prakash, Appl. Phys. Lett., 2009, 95, 173305.
24. S. K. Abdel-Aal and A. S. Abdel-Rahman, J. Cryst. Growth, 2017, 457, 282.
25. S. K. Abdel-Aal and A. Ouasri, J. Mol. Struct., 2022, 1251, 131997.
26. S. K. Abdel-Aal, M. F. Kandeel, A. F. El-Sherif and A. S. Abdel-Rahman, Phys. Status Solidi A, 2021, 218, 2100136.
27. S. K. Abdel-Aal, A. S. Abdel-Rahman, W. M. Gamal, M. Abdel-Kader, H. S. Ayoub, A. F. El-Sherif, M. F. Kandeel, S. Bozhko, E. E. Yakimov and E. B. Yakimov, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2019, 75, 880.
28. S. K. Abdel-Aal, G. Kocher-Oberlehner, A. Ionov and R. N. Mozhchil, Appl. Phys. A, 2017, 123, 531.
29. W. Liu, J. Xing, J. Zhao, X. Wen, K. Wang, P. Lu and Q. Xiong, Adv. Opt. Mater., 2017, 5, 1601045.
30. J.-C. Bissey, N. Filloleau, N.-B. Chanh, R. Berger and S. Flandrois, Solid State Commun., 1998, 106, 385.
31. A. R. Lim, S. H. Kim and Y. L. Joo, Sci. Rep., 2021, 11, 8408.
32. M. F. Mostafa and S. S. El-khiyami, J. Solid State Chem., 2014, 209, 82.
33. W. T. A. Harrison, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2005, 61, m1951–m1952.
34. A. Kallel, J. Fail, H. Fuess and A. Daoud, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1980, 36, 2788.
35. A. R. Lim, RSC Adv., 2021, 11, 37824.
36. A. R. Lim and J. Cho, Sci. Rep., 2022, 12, 16901.
37. A. R. Lim, ACS Omega, 2020, 5, 31417.
38. A. R. Lim, S. H. Kim and Y. L. Joo, Sci. Rep., 2021, 11, 8408.
39. SHELXTL v6.10, Bruker AXS, Inc., Madison, Wisconsin, USA, 2000.
40. A. R. Lim and S. H. Kim, ACS Omega, 2021, 6, 27568.
41. A. Abragam, The Principles of Nuclear Magnetism, Oxford University press, 1961.
42. J. L. Koenig, Spectroscopy of Polymers, Elsevier, 1999.
43. N. Bloembergen, E. M. Purcell and R. V. Pound, Phys. Rev., 1948, 73, 679.
44. R. K. Harris, Nuclear Magnetic Resonance Spectroscopy, Pitman Pub, 1983.

---

Footnote

† Electronic supplementary information (ESI) available. CCDC 2278866, 2302890 and 2302891. See DOI: https://doi.org/10.1039/d3ra05752f

---