Open Access Article
Open Access ArticleUnderstanding the charge carriers dynamics in the La0.55Ca0.45Mn0.8Nb0.2O3 perovskite: scaling of electrical conductivity spectra
Y. Moualhi*a,
M. Smari b and
H. Rahmouni
b and
H. Rahmouni a
a
aUnité de Recherche Matériaux Avancés et Nanotechnologies (URMAN), Institut Supérieur des Sciences Appliquées et de Technologie de Kasserine, Université de Kairouan, 1200 Kasserine, BP 471, Tunisia. E-mail: moualhiyoussef7@gmail.com
bA. Chełkowski Institute of Physics, University of Silesia in Katowice, 75 Pułku Piechoty 1, Chorzów, 41-500, Poland
First published on 13th October 2023
Abstract
The present work proposes the best realistic theoretical approaches to examine the experimental conductivity data taken for La0.55Ca0.45Mn0.8Nb0.2O3. For this purpose, we comprehensively discussed the structural, microstructural, and electrical properties of the La0.55Ca0.45Mn0.8Nb0.2O3 perovskite. Both X-ray diffraction and Rietveld analysis show the orthorhombic structure of the ceramic. Scanning electron microscope showed the existence of well-defined irregularly shaped particles with a grain-size distribution of 0.843 μm. The X-ray photoemission spectroscopy reveals the existence of Mn3+ and Mn4+ states. The complicated behavior of the lanthanum states is demonstrated using the La3d line. AC-conductivity responses are related to the correlated barrier hopping contribution. At high temperatures, the compound's semiconductor behavior is attributed to the activation of the polaronic transport. At low temperatures, the occurrence of semiconductor behavior in the La0.55Ca0.45Mn0.8Nb0.2O3 ceramic is attributed to the effect of the variable range hopping conduction process. The application of the time-temperature-superposition-principle and the Summerfield scaling formalisms leads to the superposition of the isotherms. Using the Ghosh formalism, the superposition of the spectra confirms that the number density and the hopping distance are temperature-dependent. The superposition of the spectra suggested the temperature-independent relaxation and polaronic processes. In addition, it confirms that the relaxation mechanism is independent of the microstructure response.
1. Introduction
Since the discovery of the colossal magnetoresistance property, the magnetocaloric effect, and related effects, perovskite-based ceramics have attracted excessive attention as active compounds in innovative alternatives to well-known technologies.1–3 Therefore, perovskites show increasing attention thanks to their multifunctional applications that include the new generation spintronic field, optoelectronics, information storage, solid oxide fuel cells (SOFCs),4 and photovoltaic devices.5 The most intensively investigated perovskite families are the manganite ceramics. Those materials are used in numerous solid-state devices such as batteries, as they are characterized by the contribution of numerous conduction and polarization processes to transport, relaxation, and dielectric properties.6 With the development of alternative current conductivity techniques, impedance investigation become a well-conventional description means. Therefore, a variety of theoretical and experimental works is conducted to confirm that the conductivity, for numerous semiconducting compounds, obeys universal laws.7–9 Accordingly, it is well-identified that the electrical conductivity of manganites increases rapidly with both frequency and temperature due to the contribution of various hopping and tunneling conduction mechanisms.6,10,11 Among numerous solid oxides, the manganites-based perovskite family belongs to electronically conducting compounds in which the DC electrical conductivity follows the polaron hopping theory.12 They are categorized among the materials that reveal scale invariant comportment and offer themselves to simplify and habitually universal description.13 In doped manganites, the polaronic transport originates from the electron transfer between Mn3+ and Mn4+ ions and, therefore, displays a strong dependence on several parameters like the fraction of the mixed valence ions, the average distance and the amount of manganese oxide.14,15 The manganite systems covering transition-metal ions display semiconductor character due to the multivalent states of the Mn-ions. In this material family, the occurrence of semiconductor behavior results from the hopping movement of polaron charge carriers between transition metal ions that reveal multi-valence states.14,15 Accordingly, at high temperatures, mobile charge carriers achieve thermally activated hopping motions between nearest sites to contribute to the transport phenomena and favor the appearance of a semiconductor behavior.12 At the low-temperature range, the electrical DC-conductivity variation is already analyzed via the variable range hopping conduction model.12 According to previous works,16,17 the electrical experimental data make it possible to attain information on the dynamics of charges in various material compounds. Therefore, open-handed the possibility to choose the greatest appropriate composition of the raw material. Therefore, several researchers have studied the electrical characteristics of numerous materials and shown that the overlapping of the conductivity spectra on a single master curve indicated the occurrence of the conductivity relaxation phenomena at diverse temperatures that display frequency-independent dynamical processes.16,17In the last few years, the frequency dependent-conductivity, at various temperatures, and the contribution of numerous conduction mechanisms to the transport phenomena have been studied in low-hole-doped manganites.11,13 The AC conductivity variation and the dynamic of the charge carriers are mainly attributed to the motion of ion charge carriers. In the same material family, the experimental frequency-dependent conductivity data, at high frequencies, are usually interpreted using universal power laws (Jonscher law,7 Bruce (double Jonscher) law,9 superlinear power law,18,19 and nearly constant loss20). Several conduction mechanisms are suggested to identify the origin of the power variation, and they vary from hopping to tunneling processes.11 The aforementioned mechanisms give limited evidence about the potential energy and the charge carrier interactions. So far, only a limited number of publications are concerned with the comprehensive investigation of the charge carrier transports in the substituted manganites based on the scaling approaches.15 Accordingly, varieties of other theoretical approaches are put forward utilizing diverse assumptions concerning the charge carrier's network and Coulomb mobile charge carrier's interactions.21 Taylor proposes scaling formalism by plotting the evolution of the scaled conductivity isotherms (master curve) against the scaled frequency. After that, Isard revised the scaling formalism according to the following expression:22
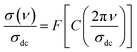 | (1) |
The scaling factor F is temperature-independent. For each temperature value, the frequency axis is scaled by introducing the dc conductivity (σdc) value and a scaled constant C. Since it is possible to calculate the value of the constant C, an improvement to the Taylor-Isard scaling formalism is proposed by introducing the time-temperature superposition principle (TTSP).23 The latter labels the microscopic processes under investigation in various electrical compounds.23 Accordingly, the superposition of the electrical conductivity spectra into a single master curve can be effectuated by choosing suitable direct and indirect scaling parameters. In this case, the existence of a conductivity master curve indicates that the microscopic process is temperature-independent.16,17 For a large number of materials, the superposition of the spectra on a single master curve confirms resemblance in the physical processes.23 In addition, the superposition of the spectra into a single curve indicates that the microscopic process is temperature-independent.23 The existence of the aforementioned master curve is referred to as the “time-temperature superposition principle. For numerous materials, the determination of the suitable scaling frequency value is continuously a matter of discussion. Hence, different expressions are proposed to define the adequate form of the characteristic frequency that permits the superposition of the conductivity curves. Based on the Summerfield approach, the characteristic frequency can be directly calculated from the dc-conductivity and the temperature quantities.24,25 To get precise information about the dynamics of the charge carriers in sodium borate glasses, the Summerfield scaling approach is mainly employed by Roling et al.26–28 In alkali glasses, Sidebottom has found that the Summerfield scaling formalism failed on the superposition of the conductivity spectra.29 As the temperature decreases, Sidebottom has found that the isotherms are shifted to elevated values on 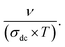 29 On one hand, the spectra do collapse onto a single master curve when a supplementary scaling factor is added for the frequency axis. In this case, the scaling formalism is established in the random free energy barrier (RFEB) model without the Coulomb interactions between the mobile particles.30 Based on the RFEB model, the correction to the Summerfield deviation is introduced to account for the inhomogeneities created by the chemical composition of the material.30 On the other hand, the divergence of the conductivity spectra is corrected by introducing a characteristic scaling frequency that depends on the conductivity σdc, the permittivity of the free space (ε0), the static permittivity (εs) at low frequencies and the high-frequency permittivity (ε∞).29 For lithium tellurite glasses, Ghosh et al.31,32 establish that the Summerfield scaling approach did not scale the conductivity spectra into a single curve. Furthermore, they have found that it is difficult to find a well-defined static permittivity value for numerous materials and therefore the application of the Sidebottom scaling formalism is difficult.31,32 In this case, Ghosh et al. suggested that the hopping frequency that takes into account the change in permittivity and Haven ratio could be used as a scaling factor.31 In this paper, a detailed investigation of the structural, morphological, X-ray photoemission (XPS) and electrical properties of the La0.55Ca0.45Mn0.8Nb0.2O3 manganite that is prepared using the ball-milling route has been performed. The XPS analysis is presented to confirm the mixed valence state of the Mn ions. With the assistance of a wide variety of previously developed scaling theories, the novelty of this paper is to discuss the procedure of scaling the AC conductivity data and find the correlation between the AC and DC conductivity regimes. We report our study on scaling behavior using the hopping frequency vH, the conductivity (σdc), and the absolute temperature as scaling parameters. To get a consistent standpoint on the charge carrier's dynamics, various conduction models and theories are proposed. Given this, the concept of the correlated barrier hopping conduction mechanism is incorporated into the conductivity analysis to comprehend the charge carrier's conduction process.
29 On one hand, the spectra do collapse onto a single master curve when a supplementary scaling factor is added for the frequency axis. In this case, the scaling formalism is established in the random free energy barrier (RFEB) model without the Coulomb interactions between the mobile particles.30 Based on the RFEB model, the correction to the Summerfield deviation is introduced to account for the inhomogeneities created by the chemical composition of the material.30 On the other hand, the divergence of the conductivity spectra is corrected by introducing a characteristic scaling frequency that depends on the conductivity σdc, the permittivity of the free space (ε0), the static permittivity (εs) at low frequencies and the high-frequency permittivity (ε∞).29 For lithium tellurite glasses, Ghosh et al.31,32 establish that the Summerfield scaling approach did not scale the conductivity spectra into a single curve. Furthermore, they have found that it is difficult to find a well-defined static permittivity value for numerous materials and therefore the application of the Sidebottom scaling formalism is difficult.31,32 In this case, Ghosh et al. suggested that the hopping frequency that takes into account the change in permittivity and Haven ratio could be used as a scaling factor.31 In this paper, a detailed investigation of the structural, morphological, X-ray photoemission (XPS) and electrical properties of the La0.55Ca0.45Mn0.8Nb0.2O3 manganite that is prepared using the ball-milling route has been performed. The XPS analysis is presented to confirm the mixed valence state of the Mn ions. With the assistance of a wide variety of previously developed scaling theories, the novelty of this paper is to discuss the procedure of scaling the AC conductivity data and find the correlation between the AC and DC conductivity regimes. We report our study on scaling behavior using the hopping frequency vH, the conductivity (σdc), and the absolute temperature as scaling parameters. To get a consistent standpoint on the charge carrier's dynamics, various conduction models and theories are proposed. Given this, the concept of the correlated barrier hopping conduction mechanism is incorporated into the conductivity analysis to comprehend the charge carrier's conduction process.
2. Experimental details
Environmentally benign mechanical milling, in a high-energy ball mill, produces the examined La0.55Ca0.45Mn0.8Nb0.2O3 manganite. Using the solid-state method, the precursor powder is produced with stoichiometric quantities of La2O3 (99.8%, Sigma-Aldrich), CaCO3 (99.8%, Sigma-Aldrich), NbO2 (99.8%, Sigma-Aldrich), and MnO2 (99%, Sigma-Aldrich) of high purity. Before the powder is crushed for 10 hours in a high-energy ball mill (rotation speed of 450 rpm), it is weighed and mixed in stainless steel jars in a planetary mill-PM 100. Before quenching, the powder is annealed in the air for two hours at 1300 °C to achieve de-carbonization. In total, the ball weighed 99.946 g, with a ceramic ball-to-powder ratio of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.
1.
The X-ray Powder Diffraction (XRD) results are used to study the structure of the sample at room temperature. So, a Bragg-Brentano θ–2θ geometry is used on an Empyrean Panalytical diffractometer with a monochromatic Cu Kα source at λ = 1.5406 Å. The Rietveld method and the Fullprof program are used to find out the crystal structure and the lattice parameters. The X-ray photoemission spectroscopy (XPS) results are made on an Escalab 250 IX Thermal Fisher platform through a monochromatic Al Kα X-ray source (1486.6 eV) with a micro spot size of 650 μm and a 180° hemisphere analyzer. High-resolution core-level spectra are obtained with an energy step of 0.1 eV and a pass energy of 20 eV. All the reported measurements are conducted at room temperature and under an Ultra High Vacuum (UHV) with a base pressure of around 10−10 mbar. After a proper Shirley background subtraction, the deconvolution of the spectra is performed with a Voigt profile (GL (30)). A clean wooden stick is employed to push the compound onto the carbon tape. This step is made to prevent it from flying away in the vacuum chamber. An Avantage software, licensed by the Thermal Fisher XPS Company is employed to fit the experimental data. At standard atmospheric pressure, measurements of the electrical conductivity as a function of frequency are collected using a dielectric spectrometer (Novo-Control Alpha) throughout a wide frequency range. The studied manganite is placed between two stainless-steel electrodes (diameter: 5 mm, gap: 2 mm) and mounted on a cryostat. During measurements, the sample is maintained under dry nitrogen gas flow. During measurements, the sample is kept in a vacuum or a stream of dry nitrogen gas. The conductivity data are performed between 153 K and 400 K.
3. Results and discussions
3.1. X-ray diffraction and diamond structure
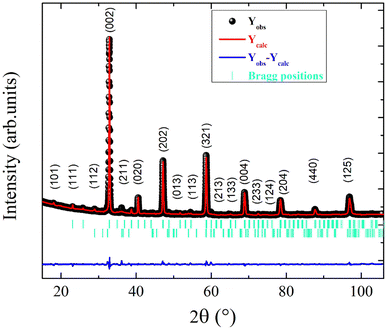
Fig. 1 shows the room temperature X-ray diffraction (XRD) pattern of the ball-milling derived La0.55Ca0.45Mn0.8Nb0.2O3 ceramic. The observed sharp peaks for the XRD data confirm the crystalline nature of the studied manganite. Based on the Rietveld refinement results, the observed peaks that are allocated to the principle-identified crystal phase are indexed in the orthorhombic structure through the Pnma space group. The computed lattice parameters for the sample, following Rietveld refinement, are a = 5.4446(2) Å, b = 7.7146(5) Å, c = 5.4458(1) Å, and V = 228.7396(9) Å3. The Mn–O bond lengths and Mn–O–Mn bond angle values are 1.9576(6) Å and 157.0847(2)°, respectively. The supplementary peaks (with low intensity) are attributed to the presence of the Mn3O4 phase that crystallizes in the I41/amd space group.33 For the Mn3O4 phase, Mn3+ ions are located at the B-octahedral 8d site and Mn2+ ions at the A-tetrahedral 4a sites.3.2. Scanning electron microscopy analysis
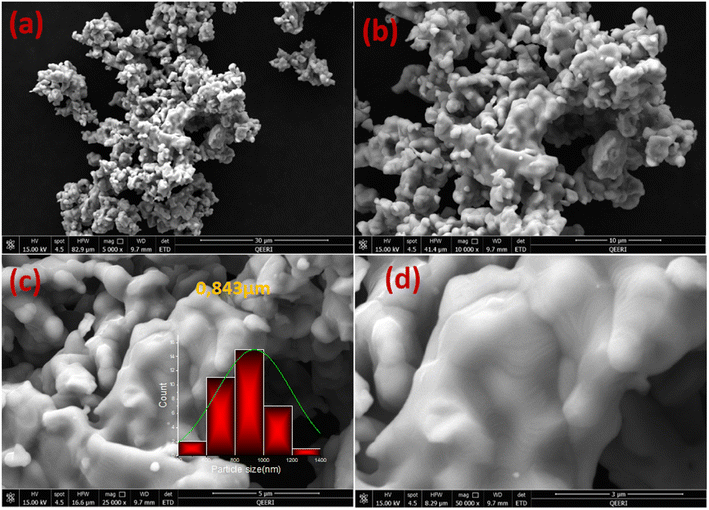
The particle size distribution and the powder stoichiometry of the La0.55Ca0.45Mn0.8Nb0.2O3 sample are investigated using Scanning Electron Microscope (SEM) pictures and Energy Dispersive Spectroscopy (EDS) analyses. As can be seen in Fig. 2(a)–(d), most microparticles take the shape of homogenous linked granular forms. After the application of the lognormal distribution function, the fitting of the size histogram in Fig. 2(c) shows that the average particle size in the La0.55Ca0.45Mn0.8Nb0.2O3 compound is 0.843 μm.3.3. X-ray photoelectron spectra analysis
To get information about the surface properties, chemical composition, and valence states of the La0.55Ca0.45Mn0.8Nb0.2O3 material, an X-ray photoelectron spectra (XPS) examination is provided. Fig. 3(a) shows a survey spectrum of the La3d, Ca2p, Mn2p, and Nb3d signals from −5 eV to 1350 eV. After taking out the Shirley background, the Gaussian–Lorentzian profile (GL (30)) is used to straighten out the experimental results of all chemical elements. Fig. 3(b) illustrates the deconvolution of the La3d line of the studied compound. The La3d line is composed of three doublets and overlapped Auger peaks and plasmons at the same energy range. A clear spin–orbit (L–S) splitting of the La3d line and further splitting of both the 3d5/2 and 3d3/2 components are documented since electron transport between the oxygen valence band and the empty La4f states.34 As reported for numerous lanthanum perovskite structures,34 the ground state for the La3+ ions is pronounced as 3d94f0L, where L signifies the oxygen ligand. After the photoionization, two possible final states can be observed in the La-based perovskites. Accordingly, for both 3d spaces, the presence of lower 3d94f0L and higher 3d94f1L binding energy peaks is confirmed. The energy separation, after the La3d deconvolution, for the lower and higher binding energy lines is equal to 4.3 eV. The deduced energy separation value confirms the impact of mixed overlapped La2O3 and La(OH)3 states in such separation. The appearance of two final states is observed when a 3d core hole is produced. Formerly, the vacant f orbital accepts an electron charge carrier from the lower energy valence in the p orbital of oxygen. This implies the appearance of a hole in the oxygen valence state. The observed additional satellite structures at 835.3 eV and 852 eV positions can be attributed to the multiple interaction effects between the La3d hole-core and 4f1 states.34 Between the satellite line and the lower banding energy peak, the energy separation (ΔE = 2.1 eV) also confirms the mixed La-based species.34 The L–S splitting of high 3d5/2 and low 3d3/2 peaks with a characteristic value of ΔE ≈ 16.8 eV is well reported for La-based samples.35 For dominated Ca2p3/2 with BE ≈ 345.6 eV and Ca2p1/2 with BE ≈ 349.2 eV, the L–S spitting for the p-type photoemission line is noted at about ΔE ≈ 3.6 eV. After the deconvolution of the Ca2p core-level line (Fig. 3(c)), the noted BE value is characteristic of the CaO states. The second observed doublet with suggestively minor intensity and slightly higher L–S of ΔE ≈ 3.9 eV is standard for CaCO3.36 In comparison with the metallic signal, the oxidation of the Mn element (Fig. 3(d)) is characterized by a better binding energy location. Fig. 3(d) shows that the Mn2p is spin split with an energy gap of 11.2 eV. The fitting line of Mn2p3/2 has three doublets that are located at 640.1 eV, 641.1 eV, and 643.2 eV. As revealed after deconvolution, the dominated lines can be assigned to Mn3+ with ΔE = 11.7 eV. The second one is typical for Mn4+ with the same LS parameter. Both lines are standard for manganites, where the super-exchange and double-exchange interactions are realized.37 Such a higher parameter may point to the partial origin of Mn3+ ions from octahedral sites of Mn3O4. Similarly, the third noted doublet assigned to Mn2+ states (ΔE = 11.3 eV), may probably originate from the tetrahedral site impurity of the Mn3O4 phase. Additionally, the Mn3+/Mn2+ ratio equals about 5.9. Fig. 3(e) shows Nb3d data, including the splitting of Nb3d5/2 and Nb3d3/2 with an energy gap of 2.8 eV. The deconvolution consists of a strong Nb4+ signal at 206.1 eV and a faint Nb2+ signal at 205.1 eV. As a result, the Nb4+ and Nb2+ signals can be ascribed to the NbO2 bonding and the Nb–CO associated state, respectively.38,39 Fig. 3(f) shows the deconvolution of the O1s data. At about BE ≈ 528.7 eV, the observed state can be attributed to the La–O, probably partly overlapped with Mn–O at BE ≈ 529.6 eV. The latter peaks are attributed to the hydroxylation (OH) and carbon oxidation states (C–O). The global element concentration is listed in Table 1 based on the intensity of the core level spectra as discussed above. The optimal fit for the oxygen content 3 − δ was found to be δ = 0.582(3), where the experimental error of the refinement is indicated between parentheses. Even so, the oxygen deficiency extracted from the XPS analysis yields the value δ = 0.727(2). The difference between the XPS and XRD fitting values is because the calculated from the XPS analysis corresponds to the combination of surface and bulk vacancy of oxygen, whereas the calculated from the XRD refinement corresponds to the bulk vacancy. In manganites, it is usually known that the oxygen anion plays a crucial role in determining the physical properties of this material family.40–42 According to previous works, it is found that the perovskite-structured manganite is a class of materials that exhibit an interesting interplay involving oxygen content, orbital, and charge-ordering phenomena.41 This interplay affects mainly the structural, magnetic, dielectric, and electrical transport properties of the manganite materials. Accordingly, oxygen non-stoichiometry can efficiently modify the ratio of the Mn3+/Mn4+ ions and promote the hopping movement governed by the Mn3+–O–Mn4+ angle and the Mn3+–O bond distance.41 In addition, it is found that the oxygen content variation affects the Curie point (TC) and the metal-semiconductor transition temperatures (TM–SC).40–42 Moreover, variation in the oxygen content can modify the percentage of Mn3+ and Mn4+ ions (the Mn3+/Mn4+ mixed valence state) and the unit cell volume, which affects the double and the superexchange processes.41 This affects mainly the magnetoresistance phenomenon and the magnetocaloric behavior of the manganite ceramics.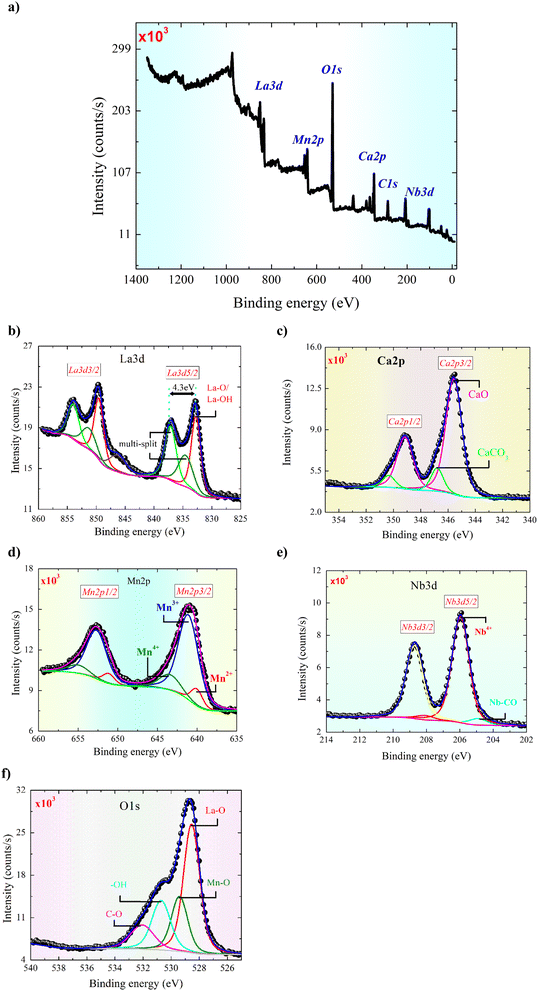 | ||
| Fig. 3 (a–e) Survey spectrum (−5 eV to 1350 eV) of the La3d, Ca2p, Mn2p and Nb3d signal (a); XPS core level of the La3d, Ca2p, Mn2p, Nb3d and O1s, respectively (b–f). | ||
| Element | Peak BE | FWHM (eV) | Area (P) CPS. eV | Atomic (%) |
|---|---|---|---|---|
| Nb3d | 206.53 | 1.24 | 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 178.34 178.34 |
3.36 |
| C1s | 285.22 | 2.39 | 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 504.98 504.98 |
24.87 |
| Ca2p | 346.19 | 1.53 | 26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 588.02 588.02 |
8.98 |
| O1s | 529.34 | 2.02 | 71![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 742.87 742.87 |
52.89 |
| Mn2p | 641.32 | 3.18 | 37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 054.38 054.38 |
6.62 |
| La3d | 833.50 | 2.75 | 75![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 522.72 522.72 |
3.27 |
According to previous investigations, it is observed that the variation in the oxygen content can destroy the large grains, which reduces in turn particle/crystallite size.40,42 This can modify the electrical resistivity and the dielectric characteristics of the materials. The pursuit of a novel approach to generate vacancies in oxygen sites (with an oxygen content below 3) has garnered attention owing to the significant technological implications of these vacancies. These include their potential applications in solid oxide fuel cells, high-temperature electrolysis, oxygen sensors, and catalysis.40,42
3.4. Conductivity investigation
In the literature, it is reported that the Anderson-localized charges contribute significantly to the transport properties of various classes of materials.43 Under the effect of the frequency increase, the contribution of the hopping conduction processes increases the electrical conductivity leading to the appearance of a power law variation with a frequency exponent (s < 1).7,44,45 Considering the dc conductivity plateau, the frequency dependences of the conductivity and the universal dielectric response are commonly described as:7| σ(ν,T) = σdc(T) + A(T) × νs | (2) |
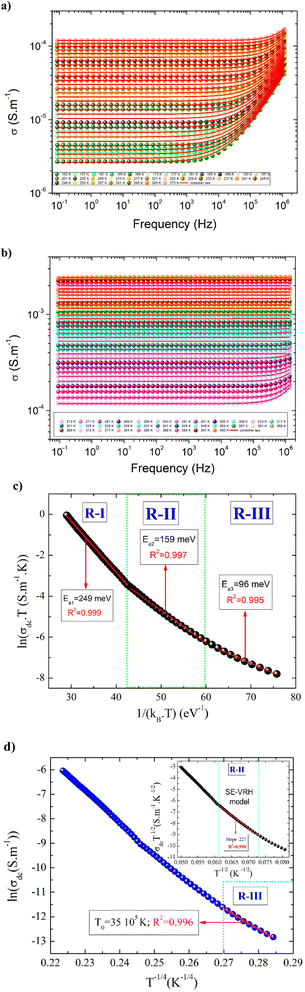
The first term (σdc(T)) describes the dc conductivity response. A (T) and “s” are two temperature-dependent functions. The physical significance of the low-frequency region correlates with the long-range translational hopping of charge carriers or ions among neighboring localized states and arises due to the availability of an important time scale. However, the electrical transport properties, at the high-frequency range, are attributed to the short-range hopping of the charge carriers between potential barriers.46–48 For numerous ceramics, the conductivity spectra can be investigated based on the Bruce law due to the occurrence of two power-law variations.9 In this case, the appearance of a second power law behavior at higher frequencies, with a frequency exponent higher than the unity, can be due to the motion of the ions that undergo ineffective forward-backward forward hopping, ensuing in a comparable orientational polarization contribution in the materials.9 The aforementioned hopping motion can be envisaged as a competition between two dissimilar relaxation processes (successful and unsuccessful motions of charge carriers). In the present part, the spectroscopic conductivity spectra of the La0.55Ca0.45Mn0.8Nb0.2O3 ceramic are examined over a large frequency and temperature sides. Fig. 4(a and b) shows the frequency dependence of the electrical conductivity in the temperature range from 153 K to 400 K. Each spectrum can be divided into two dissimilar variations exhibiting different microstructural contributions in the studied sample. Thus, the conductivity spectra exhibit a transition from the elevated frequency dispersion (unceasingly increases versus the frequency variation) to the frequency-independent conductivity at the lower frequency range. The transition from the DC conductivity side to the frequency dispersion side (dynamic conductivity) indicates the presence of a conductivity relaxation that moves towards elevated frequency values versus the temperature rises. At low frequencies, the observed DC plateau feature is attributed to the contribution of the grain boundary regions. This frequency plateau can be employed to investigate the electrical behavior of the material. For the studied sample, the electrical conductivity is found to increase against increasing the temperature over the explored temperature interval. This indicates that the sample reveals a semiconductor nature. The aforementioned behavior can be attributed to the presence of hopping conduction mechanisms. Fig. 4(c) represents the evolution of ln(σdc × T) against 1/(kB × T) for the La0.55Ca0.45Mn0.8Nb0.2O3 sample. As observed from Fig. 4(c), we found the presence of three linear regions. The existence of three activation energies can be attributed to the presence of three electrical conduction mechanisms in the studied sample. At high temperatures (R-I), the plotted result is characterized by the presence of a good linear slope with R2 = 0.999. In the literature, this behavior characterizes a feature of a polaronic hopping transport process.49,50 For T > 300 K (R-I), the electrical transport of a polaron charge carrier is determined by an activation energy value of Ea1 = 249 meV. At low-temperature range (R-III), the deduced disorder energy value is Ea3 = 96 meV. Fig. 4(d) shows the evolution of ln(σdc) as a function of T−1/4 for the studied compound. The observed linear variation at low temperatures (R-I) suggests that the electrical conductivity of the material is dominated by the Mott-variable range hopping conduction process. In this temperature range, the estimated value of the characteristic temperature coefficient is T0 = 35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 105 K. According to previous works, the low-temperature range is characterized by the absence of the Coulomb interactions between the mobile charge carriers.6,11 The inset of Fig. 4(d) shows the variation of ln(σdc × T1/2) against T−1/2 for the studied ceramic. In the intermediate temperature side (R-II), the linear evolution with a slope of 227 confirms that the semi-conductor behavior, in the studied sample, is attributed to the contribution of the Shklovskii–Efros variable range hopping (VRH) process on the electrical response of the material. In this case, the investigated contribution is characterized by a strong Coulomb interaction between the charge carriers. Therefore, the deduced value of the characteristic Shklovskii–Efros temperature, from the linear slope, is TSE = 51
105 K. According to previous works, the low-temperature range is characterized by the absence of the Coulomb interactions between the mobile charge carriers.6,11 The inset of Fig. 4(d) shows the variation of ln(σdc × T1/2) against T−1/2 for the studied ceramic. In the intermediate temperature side (R-II), the linear evolution with a slope of 227 confirms that the semi-conductor behavior, in the studied sample, is attributed to the contribution of the Shklovskii–Efros variable range hopping (VRH) process on the electrical response of the material. In this case, the investigated contribution is characterized by a strong Coulomb interaction between the charge carriers. Therefore, the deduced value of the characteristic Shklovskii–Efros temperature, from the linear slope, is TSE = 51![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 530 K. At the high-frequency range, the appearance of dispersion conductivity variation (Fig. 4(a)) is attributed to the microscopic nature of the ceramic materials that contain inhomogeneous domains (grains, grain boundaries, impurities…) and random distribution of energy barriers.30 In the literature, the appearance of dynamic conductivity typically remains up to the phonon frequencies.51 At high temperatures, the reported results from Fig. 4(b) show that the conductivity spectra exhibit a large DC plateau over the studied frequency range. In addition, we found the absence of the conductivity dispersion region. In this case, the absence of the frequency-dependent dispersion region at high temperatures and frequency ranges indicates that the frequency exponent is equal to zero. Therefore, the equality in the DC and AC conductivities confirms that the phonon frequencies are enable to generate new conduction canals. For each measured temperature value, the frequency-dependent conductivity follows a power law. Numerous theoretical conduction models are advanced to examine the origin of power law variation that is observed at high frequencies.10 Equally, the power evolutions are reported with further non-Debye responses like the Cole–Cole and the Nyquist diagrams, the Cole–Davidson, and the Havriliak–Negami representations.52 Accordingly, the electrical conductivity dynamics and power law variations are attributed to the presence of one or several kinds of inhomogeneities in the oxide systems. Each kind of inhomogeneity can be of a macroscopic or microscopic type. However, the focus is most concentrated on the hopping conduction model in which inhomogeneities are expected to be realized on an atomic scale via the energy barriers distribution.53 For hopping formalism, two basic kinds of theories are employed to explain the electrical characteristics of oxide ceramics.53,54 Independent-ionic hopping movements and a broad relaxation times distribution characterize the first transport formalism. The relaxation times distribution can be examined using William Watts's relaxation expression.54 In the second formalism, collective belongings arise such that the hopping of each ion reveals elevated Coulomb interactions with nearby ions.55 According to various studies, the universal Jonscher power law is related to the second transport formalism.7 The frequency exponent “s” appears to describe the deviance from Debye's character and to analyze the inter-ionic Coulomb interaction and the coupling strength. Numerous efforts are conducted in the literature to validate that the power variation of the conductivity derives from both the Coulomb interaction between nearest-neighbor ions and the site energy evolution.56,57 Under the second formalism, Ngai suggested the coupling model, which assumes that the cooperative adjustment of the environment on the ion movements is followed by an enlarged relaxation mechanism to times significantly greater than the original Debye relaxation time for the hopping of non-interacting charge carriers.56,57 Here it is expected that the direct and the alternative current conductivities are attached, increasing stretching exponential relaxation of the type. According to numerous works, the temperature dependence of the exponent “s” reveals the origin of the dynamic conductivity spectra. According to Sidebottom,58 the frequency exponents are correlated to the dimensionality of the transport pathways. As a function of the temperature variation, variations of the exponent “s” are expected and associated with various conduction processes. Sidebottom envisages that a low value of the frequency exponent pertains to a one-dimensional (1D) system of charge carriers conduction while, the frequency exponent is close to one (nearly constant loss), demonstrating the motion of mobile charge carriers and ionic species in asymmetric double-well potentials.59 In the limit of the AC regime, the nature of the conduction process has been confirmed by
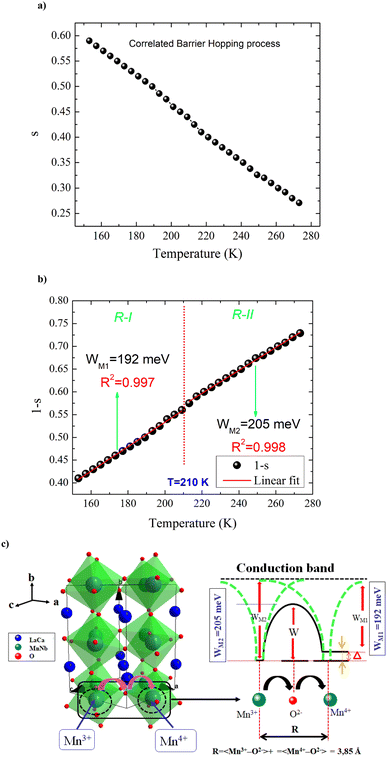
plotting the temperature dependence of the frequency exponent ‘‘s’’ (Fig. 5(a)). From Fig. 5(a) and (b), the frequency exponent increases to unity at low temperatures for the studied sample. This variation confirms that the transport properties are controlled by the hopping of charge carriers (two electrons: bi-polaron) among oppositely charged states (defects) over a potential barrier. Each pair of defect states is expected to constitute a dipole with a potential barrier over which the charge carriers must hop to contribute to the conduction phenomena (Fig. 5(c)). The height of the barrier is associated with the inter-site separation distance by Coulomb interactions, which reasonably accounts for significant features of the alternative current transport in the ceramics systems. As illustrated in Fig. 5(c), the charge carriers (two holes or electrons) make a classic simultaneous hopping, and the barrier height W is associated with the inter-site separation distance (R) and the maximum barrier energy height (WM) by the following relation:
530 K. At the high-frequency range, the appearance of dispersion conductivity variation (Fig. 4(a)) is attributed to the microscopic nature of the ceramic materials that contain inhomogeneous domains (grains, grain boundaries, impurities…) and random distribution of energy barriers.30 In the literature, the appearance of dynamic conductivity typically remains up to the phonon frequencies.51 At high temperatures, the reported results from Fig. 4(b) show that the conductivity spectra exhibit a large DC plateau over the studied frequency range. In addition, we found the absence of the conductivity dispersion region. In this case, the absence of the frequency-dependent dispersion region at high temperatures and frequency ranges indicates that the frequency exponent is equal to zero. Therefore, the equality in the DC and AC conductivities confirms that the phonon frequencies are enable to generate new conduction canals. For each measured temperature value, the frequency-dependent conductivity follows a power law. Numerous theoretical conduction models are advanced to examine the origin of power law variation that is observed at high frequencies.10 Equally, the power evolutions are reported with further non-Debye responses like the Cole–Cole and the Nyquist diagrams, the Cole–Davidson, and the Havriliak–Negami representations.52 Accordingly, the electrical conductivity dynamics and power law variations are attributed to the presence of one or several kinds of inhomogeneities in the oxide systems. Each kind of inhomogeneity can be of a macroscopic or microscopic type. However, the focus is most concentrated on the hopping conduction model in which inhomogeneities are expected to be realized on an atomic scale via the energy barriers distribution.53 For hopping formalism, two basic kinds of theories are employed to explain the electrical characteristics of oxide ceramics.53,54 Independent-ionic hopping movements and a broad relaxation times distribution characterize the first transport formalism. The relaxation times distribution can be examined using William Watts's relaxation expression.54 In the second formalism, collective belongings arise such that the hopping of each ion reveals elevated Coulomb interactions with nearby ions.55 According to various studies, the universal Jonscher power law is related to the second transport formalism.7 The frequency exponent “s” appears to describe the deviance from Debye's character and to analyze the inter-ionic Coulomb interaction and the coupling strength. Numerous efforts are conducted in the literature to validate that the power variation of the conductivity derives from both the Coulomb interaction between nearest-neighbor ions and the site energy evolution.56,57 Under the second formalism, Ngai suggested the coupling model, which assumes that the cooperative adjustment of the environment on the ion movements is followed by an enlarged relaxation mechanism to times significantly greater than the original Debye relaxation time for the hopping of non-interacting charge carriers.56,57 Here it is expected that the direct and the alternative current conductivities are attached, increasing stretching exponential relaxation of the type. According to numerous works, the temperature dependence of the exponent “s” reveals the origin of the dynamic conductivity spectra. According to Sidebottom,58 the frequency exponents are correlated to the dimensionality of the transport pathways. As a function of the temperature variation, variations of the exponent “s” are expected and associated with various conduction processes. Sidebottom envisages that a low value of the frequency exponent pertains to a one-dimensional (1D) system of charge carriers conduction while, the frequency exponent is close to one (nearly constant loss), demonstrating the motion of mobile charge carriers and ionic species in asymmetric double-well potentials.59 In the limit of the AC regime, the nature of the conduction process has been confirmed by
plotting the temperature dependence of the frequency exponent ‘‘s’’ (Fig. 5(a)). From Fig. 5(a) and (b), the frequency exponent increases to unity at low temperatures for the studied sample. This variation confirms that the transport properties are controlled by the hopping of charge carriers (two electrons: bi-polaron) among oppositely charged states (defects) over a potential barrier. Each pair of defect states is expected to constitute a dipole with a potential barrier over which the charge carriers must hop to contribute to the conduction phenomena (Fig. 5(c)). The height of the barrier is associated with the inter-site separation distance by Coulomb interactions, which reasonably accounts for significant features of the alternative current transport in the ceramics systems. As illustrated in Fig. 5(c), the charge carriers (two holes or electrons) make a classic simultaneous hopping, and the barrier height W is associated with the inter-site separation distance (R) and the maximum barrier energy height (WM) by the following relation:
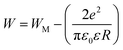 | (3) |
From the reported result in Fig. 5(b) and (c), the deduced barrier energy values are WM1 = 192 meV and WM2 = 205 meV. The activation energy WM2 = 205 meV, when the centers are randomly distributed, turns out to be the extreme of an entire interval of the energy values required to account for the frequency dynamic region. The frequency exponent is bandgap and temperature dependent. When the frequency exponent tends to unity (the bandgap is temperature independent), oppositely charged centers could couple owing to their Coulomb attraction. In this case, it is essential not to invoke an atomic mechanism for the investigation of the electrical conduction properties in the alternative regime.
3.5. Scaling of the electrical conductivity
For the perovskite materials, the alternative current conductivity measurement directly confirms the charge carriers-dynamics that are the focus of profound scientific attention and are a challenging topic. Accordingly, the investigation of the electrical conductivity isotherms permits the application of the time-temperature superposition principle (TTSP) scaling law.60 The aforementioned principle defines the microscopic processes under investigation in numerous electrical materials. For a given compound, the conductivity spectra can be superposed into a single master curve with a suitable scaling model for the frequency and the conductivity isotherms axis via a general scaling expression of the form:
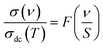 | (4) |
For the case of the Isard scaling approach, S = νH, S = (σdc × T) for the Summerfield formalism, and S = (σdc × T/Tα) in the limit of the corrected Summerfield scaling. Corrections to the Summerfield scaling deviations are suggested in the limit of the random barrier model that accounts for the presence of inhomogeneities produced by the chemical compositions. Baranovskii et al.60 corrected this by introducing a scaling parameter α that shows the nature of the interactions of the charge carriers. When the conductivity arises from non-interacting charge carriers, the parameter, α exhibits negative values.61 Recently, the scaling formalism of the conductivity spectra is investigated through directly accessible parameters like the σdc values, the absolute temperature, the charge carriers concentration (density), the dipolar relaxation loss peak, and dielectric strength (Δε = εs − ε∞) or via the hopping frequency factor (νH).59,60 Numerous disordered ceramics do not have a distinct dielectric loss peak and therefore, the static permittivity or the maximum dielectric loss cannot be acquired through the data of the dielectric spectra. In such conditions, the frequency axis can be scaled using the ωH = 2πνH quantity that spontaneously takes into consideration the dielectric permittivity variation and the correspondence belongings among consecutive hop movements in the disordered lattice. In Jonscher's law, both σdc conductivity and hopping frequency νH of the charge carriers are temperature-assisted hopping mechanisms and follow the same law with identical activation energy values. The hopping frequency scripts the crossover from the long-range translational conduction to the dynamical short-range regime at high frequencies.
According to previous investigations,18 the perovskite oxides are heterogeneous due to the contribution of conducting grains and more resistive grain boundaries to the AC electrical conduction. In this material family, the occurrence of a conductivity relaxation is normally attributed to the effect of the microstructure inhomogeneities (presence of grains and grain-boundary regions) and the electrode-sample interface contributions to the transport phenomena. For the studied compound, the relaxations phenomena and the transport properties are assigned to intrinsic bulk and grain boundary (GB) contributions. Accordingly, the electrical and relaxation properties of materials are strongly dependent upon the role of two main components i.e., grain and grain boundaries. The information about the physical parameters related to these components is vital for understanding the overall characteristics of the oxide compounds. The highly resistive grain boundaries are sandwiched between relatively conductive grains. Grain boundary capacitance exists in parallel combination with the grain boundary resistance. When the electrode-sample polarization is absent, the conductivity spectra of the ceramics indicate the existence of plateau region and dispersion variation due to the contribution from diverse microstructural domains.
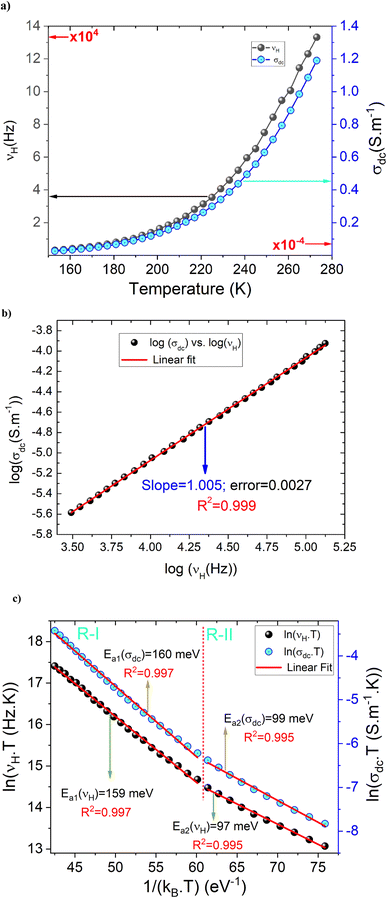
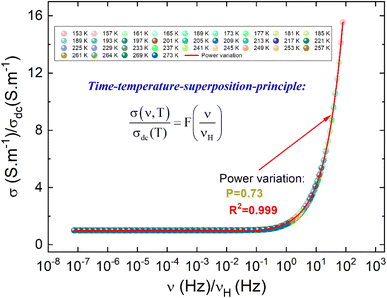
Fig. 6(a) shows the temperature dependence of both σdc and νH curves in the temperature range from 153 to 273 K. By increasing the temperature, the conductivity of the compound is improved due to the hopping motions of the charge carriers through the energy barrier gap. The observed variation indicates the semiconductor behavior of the as-prepared sample. For the investigated ceramic, the strong correlation between the DC and the AC conductivity regimes and the proportionality between σdc and νH parameters are confirmed via the negative linear nature in Fig. 6(b) with a slope of almost −1. Fig. 6(c) displays the evolution of log(σdc) and log(νH) as a function of the reciprocal of the absolute temperature. Over the explored temperature range, the reported results indicate that both σdc conductivity and νH hopping frequency curves are characterized by the presence of linear curves at low and high-temperature regions. In this case, both parameters are governed by the contribution of similar two activated hopping processes. For each mechanism, the deduced energy values are indicated in Fig. 6(c). The activation energy values deduced from the temperature dependence of νH are almost equal to those obtained from the σdc(T) curve. The approximate similarity in the activation energy values of σdc and νH is normally due to the proportionality between σdc and νH.
Based on previous experimental and theoretical investigations,11–13 it is found that the DC electrical properties in numerous classes of perovskites are governed by the contribution of various hopping conduction mechanisms. This hypothesis is usually confirmed based on the Mott approach.12 Accordingly, it is assumed that the electrical conductivity variation and the semiconductor nature at high temperatures are principally linked to the contribution of the small polaron hopping mechanism. In the same context, the electrical properties and the appearance of a semiconductor behavior at low and intermediate temperature ranges are usually explained by the contribution of the variable range hopping mechanism. The VRH model readily describes the aforementioned process, by a hopping of the charge carriers localized by random potential fluctuations.
To gain an appreciated understanding of the dynamics of the charge carriers and the grain and grain boundary responses to the conductivity of the La0.55Ca0.45Mn0.8Nb0.2O3, the scaling formalism of Ghosh and Pan is employed (Fig. 7). At the grain and the grain boundary regions, it is displayed that the scaled isotherms overlap exactly on a master curve. This indicates that the relaxation processes at both grain and grain boundary domains obey the time-temperature superposition principle (TTSP)59 and the Isard approach.22 In this case, the isotherms satisfy the pure universal dielectric relaxation behavior. In addition, the reported result confirms the occurrence of a temperature-independent microscopic transport process in the La0.55Ca0.45Mn0.8Nb0.2O3 ceramic. The temperature variation implies only an evolution in the density of charge carriers without affecting the conduction process. As can be observed from Fig. 7, all the isotherms are fitted using the scaling equation with p being equal to 0.73. As tabulated by Sidebottom,29 the deduced p-value for the La0.55Ca0.45Mn0.8Nb0.2O3 ceramic falls into the class of large numbers of oxide compounds that reveal a frequency exponent of 2/3 ± 0.05. It is confirmed that the exponent depends mainly on the structural dimensionality of the charge carrier's conduction pathways. Accordingly, the decrease of the frequency exponent decreases the dimensionality of the carrier's motion. When the frequency exponent reveals a lower value of p = 0.4 ± 0.1, 1D-motion of charge carriers occurs in the non-communicating channels of the corner. In recent works, we have testified the TTSP conductivity scaling, the Summerfield scaling, and the correction for the Summerfield scaling via the application of the random barrier model (the example of the Baranovskii and Cordes approach60). This is among examples that validate the application of scaling formalisms for materials other than amorphous compounds. For the La0.5Ca0.3Ag0.2MnO3, deviations from the Summerfield scaling are established at T = 220 K < TC = 264 K (TC is the Curie temperature value) which are successfully corrected via the application of the Baranovskii and Cordes scaling approach.15 However, the Summerfield scaling formalism is still disobeyed by numerous systems.61 In the La0.5Ca0.3Ag0.2MnO3 ceramic, the Summerfield deviations are corrected by introducing a function Tα with α = 1.2.15 The positive value of α is attributed to the presence of Coulomb interactions between particles. This behavior is also attributed to the fact that the electrical conductivity follows a modified Jonscher law, demonstrating the presence of several transport and relaxation processes that are unidentified in several crystalline-ordered materials, as opposed to amorphous systems. When α exhibits negative values, the electrical conductivity of materials is related to the important contribution of non-interacting charged particles.62 Fig. 8 shows the conductivity isotherms, at various temperatures, after the application of the Summerfield scaling approach. The superposition of the master curve, for different temperature values, confirms that the dynamic of the charges, which control the microscopic transport at elevated frequencies, is temperature independent.
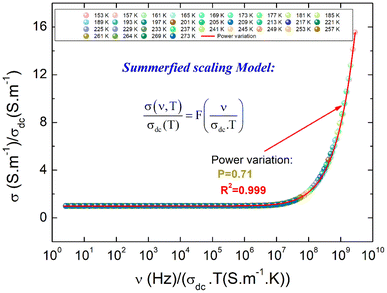 | ||
| Fig. 8 The scaled conductivity spectra after the application of the Summerfield approach for the La0.55Ca0.45Mn0.8Nb0.2O3 compound. | ||
4. Conclusion
In the present work, we have investigated the structural, morphological, and electrical properties of La0.55Ca0.45Mn0.8Nb0.2O3 powder that is prepared by the ball-milling process. La0.55Ca0.45Mn0.8Nb0.2O3 perovskite crystallizes in the orthorhombic crystal structure with the ‘Pnma’ space group. The synthesized compound exhibits semiconductor characteristics throughout a broad temperature range due to charge carriers' hopping mobility between suitable sites. The Jonscher power law and various scaling methodologies are utilized in this study to explore the experimental conductivity spectra. Thus, the appearance of a dispersive conductivity region is attributed to the activation of the correlated barrier hopping conduction mechanism. The superposition of the spectra into a single master curve confirms that the charge transport dynamics and the relaxation processes are temperature-independent. The Summerfield scaling approach is employed successfully to provide more information about the transport dynamics in the studied sample. Finally, we prove that La0.55Ca0.45Mn0.8Nb0.2O3 pursues the universal time-temperature superposition principle established from the scaled conductivity isotherms. The obtained results will motivate further critical studies into the conduction processes with other order-disorder materials.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Authors acknowledged that M. Tarnacka, K. Kamiński, and A. Bajorek support the acquisition of the electrical conductance measurements.References
- A. Žužić, A. Ressler and J. Macan, Ceram. Interfaces, 2023, 48, 27240–27261 CrossRef
.
- A. M. Aliev and A. G. Gamzatov, J. Magn. Magn. Mater., 2022, 553, 169300 CrossRef CAS
.
- F. Guan, Z.-w. Dang, X. Cheng and W. P. Liao, J. Phys. Chem. Solids, 2023, 174, 111120 CrossRef CAS
.
- J. Ramírez-Hernandez, A. M. Torres-Huerta, S. B. Brachetti-Sibaja, M. A. Domínguez-Crespo, D. Palma-Ramírez, A. E. Rodríguez-Salazar and A. Ezeta-Mejia, Ceram. Interfaces, 2022, 48, 21221–21234 CrossRef
.
- Y. Sheng, H. Tan, A. Quintana, M. Villa, J. Gázquez, I. Fina and J. Fontcuberta, Acta Mater., 2023, 245, 118601 CrossRef CAS
.
- Y. Moualhi, M. Smari, H. Rahmouni and K. Khirouni, ACS Appl. Electron. Mater., 2022, 4, 4893–4902 CrossRef CAS
.
- A. K. Jonscher, Nature, 1977, 267, 673–679 CrossRef CAS
.
- A. K. Jonscher, J. Phys. D: Appl. Phys., 1999, 32, R57 CrossRef CAS
.
- P. Bruce, Solid State Ionics, 1985, 15(3), 247–251 CrossRef CAS
.
- A. Ghosh, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 42, 5665 CrossRef CAS PubMed
.
- Y. Moualhi, H. Rahmouni and K. Khirouni, Results Phys., 2020, 19, 103570 CrossRef
.
- N. F. Mott and E. A. Davis, Electronic processes in non-crystalline materials, Oxford University Press, 2012 Search PubMed
.
- Y. Moualhi, H. Rahmouni and K. Khirouni, Phys. B, 2021, 616, 413129 CrossRef CAS
.
- P. V. Jithin, B. Yugandhar, M. P. Manju, V. Ganesan, K. J. Sankaran and J. Kurian, Mater. Chem. Phys., 2023, 301, 127651 CrossRef CAS
.
- Y. Moualhi, H. Rahmouni, M. Gassoumi and K. Khirouni, Ceram. Interfaces, 2020, 46, 24710–24717 CrossRef CAS
.
- Y. B. Saddeek, A. A. El-Maaref, M. G. Moustafa, M. M. El-Okr and A. A. Showahy, J. Mater. Sci.: Mater. Electron., 2018, 29, 9994–10007 CrossRef CAS
.
- Y. Moualhi, R. M'nassri, H. Rahmouni, M. Gassoumi and K. Khirouni, RSC Adv., 2020, 10, 33868–33878 RSC
.
- Y. Moualhi, M. Smari, H. Rahmouni, K. Khirouni and E. Dhahri, J. Alloys Compd., 2022, 898, 162866 CrossRef CAS
.
- D. P. Singh, K. Shahi and K. K. Kar, Solid State Ionics, 2016, 287, 89–96 CrossRef CAS
.
- D. P. Singh, K. Shahi and K. K. Kar, Solid State Ionics, 2013, 231, 102–108 CrossRef CAS
.
- A. Ioanid and A. S. Dafinei, J. Optoelectron. Adv. Mater., 2004, 6, 465–470 CAS
.
- J. O. Isard, J. Non-Cryst. Solids, 1970, 4, 357–365 CrossRef CAS
.
- J. C. Dyre and T. B. Schroder, Rev. Mod. Phys., 2000, 72, 873 CrossRef
.
- S. Summerfield and P. N. Butcher, J. Non-Cryst. Solids, 1985, 77, 135–138 CrossRef
.
- S. Summerfield, Philos. Mag. B, 1985, 52, 9–22 Search PubMed
.
- S. Murugavel and B. Roling, Phys. Rev. Lett., 2002, 89, 195902 CrossRef CAS PubMed
.
- B. Roling, K. Funke, A. Happe and M. D. Ingram, Phys. Rev. Lett., 1997, 78, 2160 CrossRef CAS
.
- B. Roling and C. Martiny, Phys. Rev. Lett., 2000, 85, 1274 CrossRef CAS PubMed
.
- D. L. Sidebottom, Phys. Rev. Lett., 1999, 82, 3653 CrossRef CAS
.
- J. C. Dyre, J. Appl. Phys., 1988, 64, 2456–2468 CrossRef
.
- A. Ghosh and A. Pan, Phys. Rev. Lett., 2000, 84, 2188 CrossRef CAS PubMed
.
- A. Ghosh and M. Sural, J. Chem. Phys., 2001, 114, 3243–3247 CrossRef CAS
.
- G. B. Jensen and O. V. Nielsen, J. Phys. C: Solid State Phys., 1974, 7, 409 CrossRef CAS
.
- M. F. Sunding, K. Hadidi, S. Diplas, O. M. Løvvik, T. E. Norby and A. E. Gunnæs, J. Electron Spectrosc. Relat. Phenom., 2011, 184, 399–409 CrossRef CAS
.
- J. Choi, J. Zhang, S.-H. Liou, P. A. Dowben and E. W. Plummer, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 13453 CrossRef CAS
.
- S. Devaraj and N. Munichandraiah, J. Phys. Chem. C, 2008, 112, 4406–4417 CrossRef CAS
.
- M. Smari, R. Hamdi, S. Slimani, A. Bajorek, D. Peddis, I. Walha, U. Koneva, E. Dhahri and Y. Haik, J. Phys. Chem. C, 2020, 124, 23324–23332 CrossRef CAS
.
- K. Safeen, V. Micheli, R. Bartali, G. Gottardi, A. Safeen, H. Ullah and N. Laidani, Mater. Sci. Semicond. Process., 2017, 66, 74–80 CrossRef CAS
.
- A. Gupta, M. Mittal, M. K. Singh, S. L. Suib and O. P. Pandey, Sci. Rep., 2018, 8, 13597 CrossRef PubMed
.
- L. Malavasia, M. C. Mozzati, C. B. Azzoni, G. Chiodelli and G. Flor, Solid State Commun., 2002, 123, 321–326 CrossRef
.
- Y. Moualhi, R. M'nassri, M. M. Nofal, H. Rahmouni, A. Selmi, M. Gassoumi, N. Chniba-Boudjada, K. Khirouni and A. Cheikrouhou, J. Mater. Sci.: Mater. Electron., 2020, 31, 21046–21058 CrossRef CAS
.
- H. L. Ju, J. Gopalakrishnan, J. L. Peng, Q. Li, G. C. Xiong, T. Venkatesan and R. L. Greene, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 51, 6143 CrossRef CAS PubMed
.
- A. Karmakar, S. Majumdar and S. Giri, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 094406 CrossRef
.
- S. R. Elliott, Adv. Phys., 1987, 36, 135–217 CrossRef CAS
.
- A. R. Long, Adv. Phys., 1982, 31, 553–637 CrossRef CAS
.
- B. Panda, K. L. Routray and D. Behera, Phys. B, 2020, 583, 411967 CrossRef CAS
.
- M. Shah, M. Idrees, M. Nadeem, U. Ghazanfar, M. Atif, F. Alam, A. Asadullah, M. Sultan Irshad, M. M. Abbasi, F. Bukhari and M. Rizwan, J. Magn. Magn. Mater., 2022, 564, 170160 CrossRef CAS
.
- Y. Moualhi, A. Mleiki, H. Rahmouni, K. Khirouni and A. Cheikhrouhou, Mater. Res. Bull., 2022, 155, 111976 CrossRef CAS
.
- M. G. Moustafa, Ceram. Int., 2016, 42, 17723–17730 CrossRef CAS
.
- M. G. Moustafa, H. M. H. Saad and M. H. Ammar, Mater. Res. Bull., 2021, 140, 111323 CrossRef CAS
.
- C. Cramer, K. Funke and T. Saatkamp, Philos. Mag. B, 1995, 71, 701–711 CrossRef CAS
.
- G. Govindaraj and R. Murugaraj, Solid State Ion.: Sci. Tech., 2005, 176, 109–116 CrossRef
.
- R. Murugaraj, J. Mater. Sci., 2007, 42, 10065–10073 CrossRef CAS
.
- G. Williams and D. C. Watts, Trans. Faraday Soc., 1970, 66, 80–85 RSC
.
- P. Maass, J. Petersen, A. Bunde, W. Dieterich and H. E. Roman, Phys. Rev. Lett., 1991, 66, 52 CrossRef PubMed
.
- K. L. Ngai, J. Non-Cryst. Solids, 1999, 248, 194–202 CrossRef CAS
.
- K. L. Ngai, J. Chem. Phys., 1999, 110, 10576–10584 CrossRef CAS
.
- D. L. Sidebottom, Phys. Rev. Lett., 1999, 83, 983 CrossRef CAS
.
- S. Halder, A. Duttab and T. P. Sinhaa, RSC Adv., 2017, 7, 43812–43825 RSC
.
- S. D. Baranovskii and H. Corder, J. Chem. Phys., 1999, 111, 7546–7557 CrossRef CAS
.
- M. M. Kumar and Z.-G. Ye, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 024104 CrossRef
.
- T. B. Schroder and J. C. Dyre, Phys. Rev. Lett., 2000, 84, 310 CrossRef CAS PubMed
.
| This journal is © The Royal Society of Chemistry 2023 |