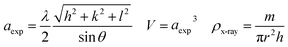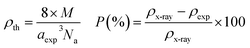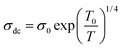Study of the effect of the substitution of Fe by Ti on the microstructure and the physical properties of the perovskite system La_0.67Ca_0.2Ba_0.13Fe_1−xTi_xO₃ with x = 0 and 0.03 at low temperatures

Abstract

La_0.67Ca_0.2Ba_0.13Fe_1−xTi_xO₃ samples (x = 0 and 0.03) were synthesized by the auto-combustion method. Analysis of XRD diffractograms revealed that these compounds crystallize in the cubic system with the space group Pm3̄m. The dielectric properties have been studied in the 10²–10⁶ frequency range and the 120–280 K temperature range. Analysis of AC conductivity shows that the conduction mechanisms are of polaronic origin and that they are co-dominated by the NSPT and OLPT models. The monotonic increase in conductivity with increasing temperature results from the reduction of defect centers and the increase in charge carrier mobility. Such variation is consistent with impedance variation at different frequencies and temperatures indicating semiconductor behavior. Nyquist diagrams are characterized by the appearance of semi-circular arcs. These spectra are modeled in terms of equivalent electrical circuits confirming the contribution of grains (R_g//CPE_g) and grain boundaries (R_gb//CPE_gb). The dielectric analysis showed an evolution of the dielectric constant in accordance with Koop's theory and the phenomenological model of Maxwell–Wagner. The low conductivity and the high values of the real permittivity at low frequency make our compounds potential candidates for energy storage and applications for electronic devices and microwaves.

---

1. Introduction

Nanotechnologies have received considerable attention due to their many applications, such as photocatalysis, environment, disease diagnosis, and energy.^1,2 At a nanometric scale, the materials possess exceptional properties, such as mechanical, optical, magnetic and electrical due to the high surface-to-volume ratio compared to bulk materials.^3,4 Metal oxide nanoparticles have been widely studied and used in different fields.⁵ More recently, iron-based perovskite oxides have attracted increasing interest due to their chemical stability, low price, catalytic activity and exceptional properties. In general, perovskite has the formula ABX₃ where A is usually an alkali or rare earth ion, B is usually a transition metal ion, and X is usually an oxygen or sulfur ion. The B cation occupying the octahedral site is surrounded by six X ions and is called the BX₆ octahedron. The significant factor that defines the structure is the tolerance factor introduced by Goldschmidt as follows:
where r_A, r_B and r_X are the ionic radii of ions A, B and X respectively. The ideal structure of perovskite is cubic. In this structure, the tolerance factor t_G varies between 0.8 and 1.⁶ The properties of these materials such as physical, photochemical, catalytic activity, and redox potential are variable depending on the replacement of positions A and B in these compounds.⁷ The LaFeO₃ compound is a very attractive material due to its thermal stability, excellent catalytic activity, good oxidation power, super conductivity⁸ high dielectric permittivity, chemical stability, low dielectric loss and high electrical resistivity. It exhibits an orthorhombic geometric structure with a Pbnm space group.⁹ This compound offers a wide range of applications in different fields such as photocatalysis, energy production and storage, sensors, environment.^10,11 Even at low temperatures, it is very efficient in converting carbon monoxide to carbon dioxide and has been used as a sensor for detecting CO gas leaks.¹² The hopping process with double/super exchange interaction and the charge transfer mechanism are the basis for the electrical conduction mechanisms of ABO₃ perovskite. In addition, the electronic conductivity of perovskites can be explained by thermally activated small polarons. The charge jumps from one interstitial site to the other via the oxygen ion (B–O–B) depends strongly on the B–O distance and the B–O–B super angle. In the literature, substitution in the A site generates a cationic disorder which influences the structural, magnetic properties and affects the iron valence state, the mobility and the charge density, which modifies the exchange processes and involves a modification of the electrical properties of materials.^13,14 On the other side, B-site substitution leads to changes in magnetocaloric properties and affects relative cooling power.^15,16 Similarly, it modifies the value of the activation energy, which implies a change in the electrical conduction process.¹⁷ Several works have reported that the substitution in sites A and/or B of the La_1−xA_xFe_1−yM_yO₃ system improves the physical properties (optical, electrical and magnetic) giving good candidates for many applications, such as the detection of toxic gases, batteries, solid oxide fuel cells (SOFCS).^18,19 Hudspeth et al.²⁰ and Sun et al.²¹ noticed that the substitution of calcium for a rate of 20% Ca or 10% Ba leads to a mixed oxidation state of iron which causes a considerable increase in conductivity and influences the magnetic properties of these materials. Recent research conducted on La_0.67Ca_0.2Ba_0.13FeO₃ has a valid semiconductor behavior for a wide temperature range.²² The electrical conduction process is attributed to the correlated barrier jump model. The replacement of Fe by a transition ion (Cr, Mn, Ti, Co…) strongly affects the magnetic, optical, catalytic, electrical and dielectric properties and leads to a strong impact on the ferroelectricity and the piezoelectricity of the aforementioned compound.²² According to previous research, the substitution of Ti on the Fe–B sites induces unexpected properties compared to its pure compounds²³ The interest in replacing Fe with Ti in ferrites comes from the fact that Ti ions can exist in the structure in a variety of valence and spin–orbital states, as well as the anticipated wide range of magnetic and electrical phenomena linked to various levels of substitution. Ti⁴⁺ ions with (Ar)3d⁰4s⁰ electronic configuration have an ionic radius (r_Ti⁴⁺ = 0.605 Å) significantly smaller than that of Fe³⁺ (r_Fe³⁺ = 0.645 Å). Substitution by Ti⁴⁺ affects the valence and number of Fe³⁺ ions. This substitution considerably affects the double exchange process leading to the appearance of weak ferromagnetic behavior with an increase in magnetic susceptibility and saturation magnetization.^24,25 Kumar et al. reported that the substitution of Fe³⁺ with Ti⁴⁺ leads to a decrease in leakage current, which may help to improve the ferroelectric and dielectric properties of the doped sample.²⁶ Sasikala et al.²⁷ described that Ti doping (40–60%) on the Fe sites, synthesized via the sol–gel method, increases the optical band gap E_g in the 2.05–2.61 eV range as the Ti content rises. Moreover, the lattice parameters and/or cell volumes are reduced as Ti concentration increase. Lańcucki et al. showed that increasing Ti content results in improved phase stability followed by a decreased crystallite size in three-dimensionally ordered (3 DOM) materials based on LaFe_1−xTi_xO₃ with 0–20 mol% Ti content.²⁸ As a result, we discovered that substituting a small amount of Ti in Fe has an impact on the type of activated conduction mechanism (this allows for the activation of the non-overlapping small polaron tunneling conduction process at low temperature, which improves the studied sample's electrical properties). Additionally, the inter-site distance and activation energy are impacted by the substitution of 3% Ti.

In the present work, the La_0.67Ca_0.2Ba_0.13Fe_1−xTi_xO₃ (x = 0 and 0.03) compounds were synthesized via the auto-combustion method. Therefore, the objective of this work is to study the effect of doping LaCaBaFeO₃ with tetravalent ions (Ti⁴⁺) on the physical properties of a perovskite ferrite. In addition, the present work focuses on structural properties, low-frequency dielectric relaxation behavior and conduction at low temperatures. These measurements allow us to examine the suitability of La_0.67Ca_0.2Ba_0.13Fe_0.97Ti_0.03O₃ for electronic devices and microwaves.

2. Detailed experimentation

To prepare the La_0.67Ca_0.2Ba_0.13Fe_1−xTi_xO₃ compounds with x = 0 and 0.03, we used the auto-combustion technique. In this context, reagents of analytical quality were chosen such as iron nitrate Fe(NO₃)₃·9H₂O, lanthanum nitrate La(NO₃)₃·6H₂O, calcium nitrate Ca(NO₃)₂·4H₂O, barium nitrate Ba(NO₃)₂ and titanium nitrate Ti(NO₃)₃·6H₂O from Sigma Aldrich. First, the metal reagents were diluted in distilled water and stirred thoroughly at room temperature for 1 hour. Then, a quantity of glycine fixed based on a glycine/nitrate ratio = 1.2 was added to the solution (composition rich in fuel so that the combustion reaction is complete). The obtained solution was heated, using a hot plate, to 80 °C with continuous magnetic stirring. The excess water evaporated and the solution turned into a viscous gel when the temperature was increased to 180 °C. An auto-combustion reaction is started at 300 °C. Finally, the obtained powders were sintered at 900 K for 30 min.

The X-ray diffraction (D8 ADVANCE, Bruker) was used to identify the crystal structure of the auto-combustion prepared sample via Cu-K_α1 radiation source (λ = 1.5406 Å) in θ–2θ Bragg–Brentano geometry. Structural acquisition data were reported in the 10–90° range. The XRD patterns were used to determine the lattice parameters of the samples through the Fullprof program by the Rietveld method. The SEM (Scanning Electron Micrographs) analyses were taken using a TESCAN VEGA3 SBH microscope equipped with an EDS detector Bruker XFlagh 410 M. An impedance spectrometer was used to determine the compound's electrical characteristics. The powder was formed into a pellet using a hydraulic press. The powder was mechanically compacted between two parallel platinum plates during the electrical measurement. A Network Analyzer Agilent 4294 with a C_p-R_p setup (capacitance in parallel with resistance) operating between 100 Hz and 1 MHz was used for the measurement in the frequency range of 10²–10⁶ Hz. The compounds were placed in Janis VPF 800-cryostat to vary the temperature parameter between 120–280 K.

3. Results and discussion

3.1. X-ray diffraction study

The recorded X-ray diffractograms are shown in Fig. 1(a and b) for both compounds. One can clearly notice the presence of broad and intense peaks, which indicate the good crystallization of these compounds. The reflections of the atomic planes indexed by the Miller indices confirm the formation of the perovskite phase which crystallizes in the face-cantered cubic structure with the space group Pm3̄m. These diffractograms were refined according to the Rietveld method using FullProf software.²⁹ The superposition of the observed profile and that calculated indicates the effectiveness of this structural refinement, which validates the structural parameters calculated and reported in Table 1. As shown in Fig. 1c we can notice that the introduction of Ti leads to a slight decrease in the intensity of the main peak with a small shift towards the high angles. Also, it can be noted that the substitution of Fe by Ti causes the reduction of the width at half maximum which leads to the increase in the crystallite size. The microstructure parameters such as lattice parameter, volume, densities (theoretical and experimental) and porosity are calculated using the following equations:³⁰

with hkl are the Miller indices, θ is the diffraction angle, m is the mass, r is the radius, h is the thickness, M is the molar mass and N_a is the Avogadro number.

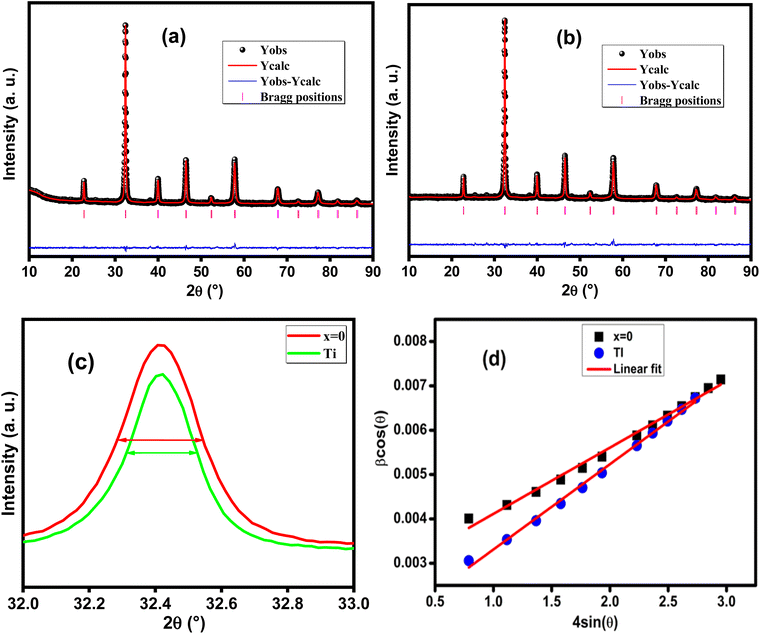Fig. 1 (a and b) X-ray diffractograms refined by the Rietveld method for x = 0 and 0.03 respectively, (c) an enlarged view of the main peak and (d) Williamson–Hall plot.

Table 1 Crystallographic parameters calculated from the Rietveld refinement, X-ray density(ρ_X-ray), theoretical density (ρ_th), specific surface (S) and porosity (P)

	La0.67Ca0.2Ba0.13FeO3	La0.67Ca0.2Ba0.13Fe0.97Ti0.03O3
χ^2	1.57	2.28
aexp (Å)	3.9061	3.9058
Volume (Å^3)	59.5977	59.5841
ρX-ray (g cm^−3)	5.4742	5.1722
ρexp (g cm^−3)	3.0111	2.6641
P (%)	45	48
DSC (nm)	32	39
DW–H (nm)	53	65
ε × 10^−4	14.9	19.2

---

The particle size can be calculated by the Debye–Scherrer formula by the following formula:^31,33

where K is the shape factor (K = 0.96 for the spherical shape), λ is the wavelength and β is the width at half height of the main peak.

However, this formula only takes into account the most intense peak and neglects the local deformation of the lattice, which leads us to use the Williamson–Hall formula expressed by the following relation:³²

where ε is the lattice deformation.

The Williamson–Hall curve (β cos(θ) versus 4 sin θ) is shown in Fig. 1d. The crystallite sizes are shown in Table 1.

The morphology study of the particles within these compounds was carried out by scanning electron microscopy. As shown in Fig. 2(a and b), these grains have irregular shapes and are strongly agglomerated. The cartographic images presented in boxes of these figures reveal a uniform and homogeneous distribution of the constituent elements of these materials. Moreover, in order to verify the chemical composition of these compounds, we have plotted the energy dispersion spectra (EDS) in Fig. 2(c and d). All the peaks are associated with the constituent chemical elements of these samples, which demonstrates the purity of our compounds.

Fig. 2 (a and b) SEM image. (c and d) EDAX elemental analysis of x = 0 and 0.03 respectively.

3.2. Conductivity analysis

The conductivity variation analysis as a function of frequency shown in Fig. 3(a and b), reveals the presence of two different behaviors. At low frequencies, this variation is characterized by a static behavior independent of the frequency increase. It is associated with the low amplitude of the electrical excitation at low frequencies to generate conductivity by long-range charge hopping.³⁴ As the temperature increases, the conductivity increases which indicates the thermal activation of conduction in these materials. Beyond certain particular frequencies, the conductivity begins to move away from its static behavior towards a dispersive behavior. This last behavior can be explained by considering the frequency as a pumping force whose increase improves the extraction of the charges trapped in the structural defects.^35,36 This evolution is described by Jonscher's classical law given by the following formula:³⁷

σ_ac = σ_dc + Aω^s

Where σ_dc represents the steady state conductivity, A is a temperature dependent factor, ω is the angular frequency and s has an important physical significance since it indicates the degree of interaction between moving charges and their environment.³⁸ According to Funke, values of s less than 1 signify a translational motion of charges with a sudden jump, while values greater than 1 signifies a jump of charge carriers between neighboring localized sites.³⁹ In addition, this parameter is used to determine the model that dominates the conduction process. According to the thermal variation of s, several models can intervene in the conduction in two different ways: electronic and/or polaronic. When s decreases with increasing temperature, the barrier-correlated jump model predominates conduction (CBH).⁴⁰ Then when s increases with temperature the conduction mechanisms are governed by the non-overlapping small polaron model (NSPT).⁴¹ However, when s decreases to a minimum value then it increases the charge transport process is done following the model of large overlapping polarons (OLPT) dominates.⁴² Another model of tunneling by quantum mechanics (QMT) will take place when s is insensitive to the variation of the increase in temperature and always remains near 0.81.⁴³

Fig. 3 (a and b) Frequency response of ac conductivity at several temperatures of x = 0 and 0.03 respectively, (c) variation of log(σ_dc) versus temperature, (d) variation of log(σ_dcT) versus 1000/T and (e) variation of log(σ_dc) versus (1/T)^¼.

As shown in the insets of Fig. 3(a and b) the thermal variation of s indicates that the conduction mechanisms are of polaronic origin and that they are co-dominated by the NSPT and OLPT models. The thermal variation of the σ_dc conduction, represented in Fig. 3c, shows a monotonic increase with increasing temperature resulting from the reduction of the centers of the defects and the increase of the mobility of the charge carriers. Such variation is attributed to semiconductor behavior.⁴⁴ To study the different electric transport mechanisms within compounds, two electric transport models can be introduced in this context: the small polaron hopping model (SPH) and the variable distance jump model. In the SPH model, conductivity and temperature are correlated by the following formula:⁴⁵

σ_dcT = σ₀ exp(−E_a/K_BT)

With σ₀ as a pre-exponential factor, E_a represents the conduction activation energy and K_B is the Boltzmann constant.

For this, we have plotted the variation of ln(σ_dcT) as a function of 1000/T in Fig. 3d which presents a linear behavior in the high-temperature region. The values of the activation energies of these compounds are reported in Table 2. Some authors have reported that the activation energy greater than 1 eV is associated with the process of conduction by ion transfer between the different crystallographic sites. While the activation energy around 0.4 eV is associated with conductions by electronic and/or polaronic exchange.³⁰

Table 2 The values of the activation energies (E_a), the Mott temperature (T₀) and the density of charge carriers near the Fermi level (N_EF)

Compounds	La0.67Ca0.2Ba0.13Fe1O3	La0.67Ca0.2Ba0.13Fe0.97Ti0.03O3
Ea (meV)	64.47	92.84
T0 (K) × 10^6	1.8	3.23
N(EF) (eV cm^−3) × 10^20	1.3	2.3

---

On the other side in the variable distance hopping transport model the conductivity is expressed by the following Mott relation:⁴⁶

with T₀ is called the Mott temperature and is determined from the slope of the linear fit in the low-temperature region as shown in Fig. 3e. This temperature is used to determine the density of charge carriers near the Fermi level N(E_F).⁴⁷
where ξ represents the cation–cation distance for the tetrahedral sites, which is the order 3Å.

The values of these parameters are reported in Table 2.

3.3. Impedance analysis

The variation of the real part of impedance (Z′) as a function of the frequency for different temperatures is represented in Fig. 4(a and b). This variation shows the presence of two distinct behaviors depending on the frequency. Initially, this evolution is characterized by a plateau regardless of the increase in frequency. However, for a given frequency, the value of Z′ decreases considerably with increasing temperature. This behavior is in good agreement with that of the continuous variation of conductivity at low frequencies, which confirms the semiconductor behavior of our compounds. In the intermediate frequency zone, the increase in frequency decreases the charges accumulated at the grain boundaries and consequently induces a decrease in Z′. At high frequencies, the spectra of Z′ tend to merge independently of frequency and temperature, which reflects the release of space charges following the reduction of the potential barrier.⁴⁸ This static behavior can be explained by the fact that in this frequency range, the mobile charges reach their relaxation frequencies and can no longer follow the external electrical excitation. The same evolution has been reported for similar compounds.⁴⁹

Fig. 4 (a and b) The frequency dependence of the real parts of impedance at several temperatures for x = 0 and 0.03 respectively and (c and d) The frequency dependence of the imaginary parts of impedance at several temperatures for x = 0 and 0.03 respectively.

The variation of the imaginary part of the impedance Z′′ as a function of the frequency for different temperatures is represented in Fig. 4(c and d). It can be seen for each temperature that each curve is characterized by the existence of a single relaxation peak at a particular frequency. These peaks indicate the change in moving charge dynamics from long range to short range.⁵⁰ We can also notice that with the increase in temperature, these peaks shift towards high frequencies, which underlines that the relaxation process is thermally activated (activation of the dipoles). Also, the increase in temperature is accompanied by a decrease in the maximum of these peaks. Such a result is due to the decrease in the electrical resistance of these compounds. Conduction mechanisms are governed by various contributions from grains, grain boundaries and electrodes. Fig. 5(a and b) represents the impedance curves in the complex plane for x = 0 and 0.03 respectively. This representation is known as the Nyquist diagram and reveals the presence of semi-circular arcs whose maximum decreases with increasing temperature, which confirms the semiconductor nature.⁴² The spectra of each compound are well modeled using Zview software (red line) in terms of two series-connected equivalent electrical circuits representing the contribution of grains and grain boundaries. The configuration of the equivalent circuit is [(R_g//CPE_g) + (R_gb//CPE_gb)] for our two compounds (x = 0 and 0.3). The values of these parameters are collected in Tables 3 and 4 for x = 0 and 0.03 respectively.

Fig. 5 (a and b) Nyquist diagram at several temperatures for x = 0 and 0.03 respectively.

Table 3 The values of the equivalent circuit elements representative of La_0.67Ca_0.2Ba_0.13FeO₃

T for x = 0	Rg ×10^6 (Ω)	CPEg ×10^−11 (F)	αg	Rgb ×10^6 (Ω)	CPEgb ×10^−11 (F)	αgb
120	24.85	2.5288	0.892	216.3	1.0793	0.9426
140	15.19	2.8451	0.885	122.4	1.2342	0.9616
160	0.9613	5.5574	0.882	23.47	2.1275	0.9595
180	0.3294	6.881	0.875	13.22	1.8366	0.9569
200	0.1100	10.482	0.863	9.393	1.8557	0.9598
220	0.0428	20.816	0.833	5.837	1.9427	0.9371
240	0.0201			2.784	1.9455	0.9412
260	0.0032			1.854	2.5949	0.9518
280	0.0017			1.541	2.6312	0.9621

---

Table 4 The values of the equivalent circuit elements representative of La_0.67Ca_0.2Ba_0.13Fe_0.97Ti_0.03O₃

T for x = 0.03	Rg ×10^6 (Ω)	CPEg ×10^−11 (F)	αg	Rgb ×10^6 (Ω)	Cgb ×10^−11 (F)
120	45.7	3.0479	0.91188	169.7	45.224
140	23.82	1.8048	0.90538	55.92	1.0431
160	20	3.4123	0.87312	23.98	1.179
180	7.917	1.0145	0.8212	10.35	1.0849
200	7.622	6.8932	0.83705	12.45	4.591
220	2.232	6.9162	0.85342	7.802	5.4689
240	1.749	6.4998	0.87495	4.095	4.4369
260	0.855	5.6372	0.89484	1.917	3.9508
280	0.382	5.1791	0.90729	0.967	3.6273

---

3.4. Modulus analysis

The variation as a function of the frequency of the real part of the modulus M′ at different temperatures is represented in Fig. 6(a and b). At low temperatures, M′ increases continuously with frequency. At high temperatures, the frequency evolution of M′ begins with a static behavior at low frequencies and then increases to an intermediate frequency where it reaches a saturated value independent of the frequency. This behavior can be associated with the quantum confinement which is at the origin of the change in the dynamics of the charge carriers.⁵¹ The low value of M′ indicates that the polarization of the electrodes is completely negligible.⁵² The variation of the imaginary part of the modulus M′′ as a function of the frequency for different temperatures is represented in Fig. 6(c and d). This figure shows for each temperature, the presence of two relationship peaks. The thermal activation of the mechanisms of this relaxation is approved by the shift of the frequencies of the peaks towards the high frequencies with the increase in temperature.⁵³

Fig. 6 (a and b) The frequency dependence of the real parts of modulus at several temperatures for x = 0 and 0.03 respectively and (c and d) the frequency dependence of the imaginary parts of modulus at several temperatures for x = 0 and 0.03 respectively.

3.5. Permittivity analysis

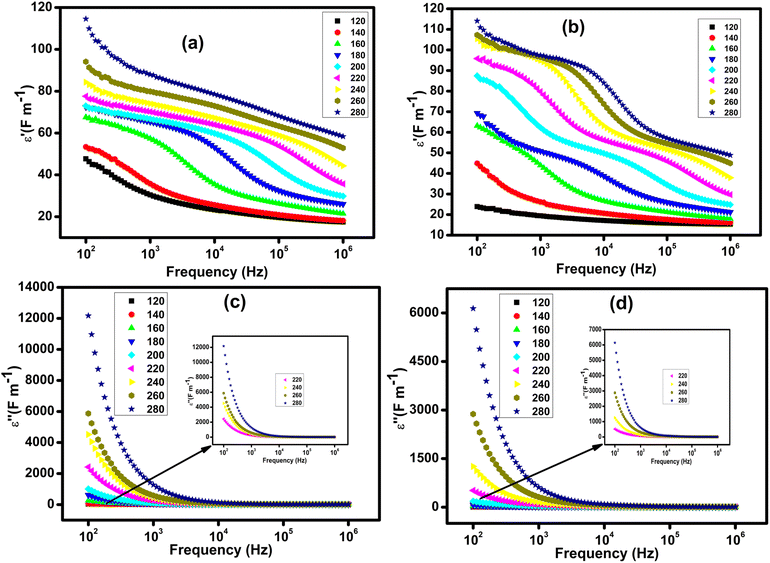
The frequency dependence of the real part of the permittivity at different temperatures is shown in Fig. 7(a and b). At low frequencies, the high value of permittivity is associated with the effect of grain size and the existence of different types of polarization such as ionic, electronic, dipolar and interfacial.⁵⁴ With increasing frequency, the permittivity slowly decreases until it reaches an almost constant low value at high frequencies, suggesting the presence of space charges. The speed of this decrease is uniform for low temperatures, while for high temperatures, ε′ shows a quasi-stability at low frequencies before being rapidly reduced beyond certain frequencies. This evolution can be interpreted by the increase in the density of mobile charges and/or the difficulty encountered by the electric dipoles in following the applied electric excitation. The frequency dependence of the imaginary part of the permittivity at different temperatures is shown in Fig. 7(c and d). With the increase in frequency the values of ε'' decrease rapidly until reaching a minimum value at certain frequencies around 10⁴ Hz and beyond this frequency ε′′ becomes insensitive to the increase in frequency and temperature.⁵⁵ This evolution has been explained by Koop's theory and the Maxwell–Wagner phenomenological model. The dielectric structure of these compounds is formed by grains that have high conductivity and are more effective at high frequencies. These grains are separated by grain boundaries having low conductivity and which are more effective at low frequencies. At low frequencies, the charge carriers are strongly accumulated on the grain boundaries due to their resistive behavior.⁵⁶ At high frequencies, the grains are activated and the charge jump frequency no longer follows the frequency of the AC excitation therefore ε′′ becomes independent of the frequency in this region.^56,57 It is also observed that ε′′ increases with temperature which may be associated with the enhancement of charge carrier jumping and the thermal activation of the conduction process.

Fig. 7 (a and b) The frequency dependence of the real parts of permittivity at several temperatures for x = 0 and 0.03 respectively and (c and d) the frequency dependence of the imaginary parts of permittivity at several temperatures for x = 0 and 0.03 respectively.

4. Conclusion

Analysis of X-ray diffractograms confirmed the formation of the perovskite phase of these compounds which crystallize in a face-cantered cubic structure with the Pm3̄m space group. The variation of the AC conductivity σ_ac in a frequency range from 100 to 10⁶ Hz is well adapted by Jonscher's power law. The increase in temperature from 120 to 200 K is accompanied by a decrease in the electrical resistance indicating that the charge carriers are thermally activated and thus confirming the semiconducting nature of these compounds. The substitution of Fe by Ti in small quantities (3%) does not affect the conduction mechanisms. At low temperatures, for both samples, the appropriate model is the NSPT, while it is the OLPT model at high temperatures. Nyquist diagrams are characterized by the appearance of semi-circular arcs, modeled in terms of an equivalent electrical circuit representing the contribution of grains and grain boundaries.

Data availability

All data obtained or analyzed in this study is included in this paper. Furthermore, the data analyzed during this study is available on request to the corresponding author.

Author contributions

R. Dhahri: wrote the paper, analyzed and interpreted the data. M. A. Valente, P. Graça: conceived and designed the experiments. B. F. O. Costa: performed the experiments.

Conflicts of interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

References

1. I. Elhamdi, F. Mselmi, H. Souissi, S. Kammoun, E. Dhahri, P. Sanguino and B. F. O. Costa, RSC Adv., 2023, 13, 3377–3393.
2. I. S. Smirnova, Phys. B, 1999, 262, 247–261.
3. F. S. dos Santos, F. R. Lago, L. Yokoyama and F. V. Fonseca, J. Mater. Res. Technol., 2017, 6, 178–183.
4. E. M. Abdelrazek, A. M. Abdelghany, S. I. Badr and M. A. Morsi, J. Mater. Res. Technol., 2018, 7, 419–431.
5. M. A. Khan, K. Khan, A. Mahmood, G. Murtaza, M. N. Akhtar, I. Ali, M. Shahid, I. Shakir and M. F. Warsi, Ceram. Int., 2014, 40, 13211–13216.
6. D. Makovec, A. Kodre, I. Arčon and M. Drofenik, J. Nanopart. Res., 2009, 11, 1145–1158.
7. A. Dhahri, A. Zaouali, A. Benali, N. Abdelmoulla, J. Massoudi, K. Nouri, L. Bessais, M. P. F. Graça, M. A. Valente and B. F. O. Costa, J. Mater. Sci.: Mater. Electron., 2021, 32, 7926–7942.
8. S. Farhadi and S. Sepahvand, J. Alloys Compd., 2010, 489, 586–591.
9. S. E. Dann, D. B. Currie, M. T. Weller, M. F. Thomas and A. D. Al-Rawwas, J. Solid State Chem., 1994, 109, 134–144.
10. D. Berger, V. Fruth, I. Jitaru and J. Schoonman, Mater. Lett., 2004, 58, 2418–2422.
11. F. Ling, O. C. Anthony, Q. Xiong, M. Luo, X. Pan, L. Jia, J. Huang, D. Sun and Q. Li, Int. J. Hydrogen Energy, 2016, 41, 6115–6122.
12. J.-C. Ding, H.-Y. Li, Z.-X. Cai, X.-X. Wang and X. Guo, Sens. Actuators, B, 2016, 222, 517–524.
13. A. Benali, M. Bejar, E. Dhahri, M. P. F. Graça, M. A. Valente, E. K. Hlil and B. F. O. Costa, J. Alloys Compd., 2021, 876, 160222.
14. R. Hamdi, A. Tozri, M. Smari, K. Nouri, E. Dhahri and L. Bessais, J. Mol. Struct., 2019, 1175, 844–851.
15. A. Omri, M. Bejar, E. Dhahri, M. Es-Souni, M. A. Valente, M. P. F. Graça and L. C. Costa, J. Alloys Compd., 2012, 536, 173–178.
16. A. Bougoffa, J. Massoudi, M. Smari, E. Dhahri, K. Khirouni and L. Bessais, J. Mater. Sci.: Mater. Electron., 2019, 30, 21018–21031.
17. S. Vadnala, T. D. Rao, P. Pal and S. Asthana, Phys. B, 2014, 448, 277–280.
18. F. B. Abdallah, A. Benali, S. Azizi, M. Triki, E. Dhahri, M. P. F. Graça and M. A. Valente, J. Mater. Sci.: Mater. Electron., 2019, 30, 8457–8470.
19. X.-P. Xiang, L.-H. Zhao, B.-T. Teng, J.-J. Lang, X. Hu, T. Li, Y.-A. Fang, M.-F. Luo and J.-J. Lin, Appl. Surf. Sci., 2013, 276, 328–332.
20. J. M. Hudspeth, G. A. Stewart, A. J. Studer and D. J. Goossens, J. Phys. Chem. Solids, 2011, 72, 1543–1547.
21. L. Sun, H. Qin, K. Wang, M. Zhao and J. Hu, Mater. Chem. Phys., 2011, 125, 305–308.
22. A. Dhahri, Y. Moualhi, C. Henchiri, A. Benali, P. Sanguino, M. P. F. Graça, M. A. Valente, N. Abdelmoula, H. Rahmouni and B. F. O. Costa, Inorg. Chem. Commun., 2022, 140, 109435.
23. U. Hanifah, D. Triyono and D. Y. Jufri, in IOP Conference Series: Materials Science and Engineering, IOP Publishing, 2020, vol. 763, p. 012059.
24. C. Sasikala, G. Suresh, N. Durairaj, I. Baskaran, B. Sathyaseelan, E. Manikandan, R. Srinivasan and M. K. Moodley, J. Supercond. Novel Magn., 2019, 32, 1791–1797.
25. M. M. Arman, M. A. Ahmed and S. I. El-Dek, J. Supercond. Novel Magn., 2018, 31, 1867–1879.
26. G. Kumar, R. K. Kotnala, J. Shah, V. Kumar, A. Kumar, P. Dhiman and M. Singh, Phys. Chem. Chem. Phys., 2017, 19, 16669–16680.
27. C. Sasikala, N. Durairaj, I. Baskaran, B. Sathyaseelan, M. Henini and E. Manikandan, J. Alloys Compd., 2017, 712, 870–877.
28. L. Lańcucki, A. Mizera, A. Lącz, E. Drożdż, M. M. Bućko and P. Pasierb, J. Alloys Compd., 2017, 727, 863–870.
29. S. M. Patange, S. E. Shirsath, G. S. Jangam, K. S. Lohar, S. S. Jadhav and K. M. Jadhav, J. Appl. Phys., 2011, 109, 053909.
30. D. Bouokkeze, J. Massoudi, W. Hzez, M. Smari, A. Bougoffa, K. Khirouni, E. Dhahri and L. Bessais, RSC Adv., 2019, 9, 40940–40955.
31. S. K. Abdel-Aal and A. S. Abdel-Rahman, J. Nanopart. Res., 2020, 22, 1–10.
32. A. V. Humbe, A. C. Nawle, A. B. Shinde and K. M. Jadhav, J. Alloys Compd., 2017, 691, 343–354.
33. E. Oumezzine, S. Hcini, F. I. H. Rhouma and M. Oumezzine, J. Alloys Compd., 2017, 726, 187–194.
34. A. L. Efros and B. I. Shklovskii, Phys. Status Solidi B, 1976, 76, 475–485.
35. S. F. Mansour, F. Al-Hazmi and M. A. Abdo, J. Alloys Compd., 2019, 792, 626–637.
36. M. Srivastava, R. K. Mishra, J. Singh, N. Srivastava, N. H. Kim and J. H. Lee, J. Alloys Compd., 2015, 645, 171–177.
37. A. K. Jonscher, nature, 1977, 267, 673–679.
38. A. K. Jonscher, J. Phys. D: Appl. Phys., 1999, 32, R57.
39. K. Funke, Prog. Solid State Chem., 1993, 22, 111–195.
40. R. B. Said, B. Louati, K. Guidara and S. Kamoun, Ionics, 2014, 20, 1071–1078.
41. A. Ghosh, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 42, 5665.
42. M. F. Kotkata, F. A. Abdel-Wahab and H. M. Maksoud, J. Phys. D: Appl. Phys., 2006, 39, 2059.
43. S. R. Majid and A. K. Arof, Phys. B, 2007, 390, 209–215.
44. L. M. Falicov and J. C. Kimball, Phys. Rev. Lett., 1969, 22, 997.
45. K. P. Padmasree, D. K. Kanchan and A. R. Kulkarni, Solid State Ionics, 2006, 177, 475–482.
46. R. Moussi, A. Bougoffa, A. Trabelsi, E. Dhahri, M. P. F. Graça, M. A. Valente and R. Barille, J. Mater. Sci.: Mater. Electron., 2021, 32, 11453–11466.
47. N. F. Mott and E. A. Davis, Electronic processes in non-crystalline materials, Oxford university press, 2012.
48. J. H. Joshi, G. M. Joshi, M. J. Joshi, H. O. Jethva and K. D. Parikh, New J. Chem., 2018, 42, 17227–17249.
49. Y. Moualhi, R. M'nassri, M. M. Nofal, H. Rahmouni, A. Selmi, M. Gassoumi, N. Chniba-Boudjada, K. Khirouni and A. Cheikhrouhou, J. Mater. Sci.: Mater. Electron., 2020, 31, 21046–21058.
50. K. Abdouli, F. Hassini, W. Cherif, P. R. Prezas, M. P. F. Graça, M. A. Valent, O. Messaoudi, S. Elgharbi, A. Dhahri and L. Manai, RSC Adv., 2022, 12, 16805–16822.
51. B. Behera, P. Nayak and R. N. P. Choudhary, Mater. Chem. Phys., 2007, 106, 193–197.
52. N. H. Vasoya, P. K. Jha, K. G. Saija, S. N. Dolia, K. B. Zankat and K. B. Modi, J. Electron. Mater., 2016, 45, 917–927.
53. T. Badapanda, S. Sarangi, S. Parida, B. Behera, B. Ojha and S. Anwar, J. Mater. Sci.: Mater. Electron., 2015, 26, 3069–3082.
54. S. G. Kakade, Y.-R. Ma, R. S. Devan, Y. D. Kolekar and C. V. Ramana, J. Phys. Chem. C, 2016, 120, 5682–5693.
55. M. B. Mohamed and K. El-Sayed, Mater. Res. Bull., 2013, 48, 1778–1783.
56. M. Nasri, C. Henchiri, R. Dhahri, J. Khelifi, H. Rahmouni, E. Dhahri, L. H. Omari, A. Tozri and M. R. Berber, Mater. Sci. Eng., B, 2021, 272, 115331.
57. H. Chouaibi, J. Khelifi, A. Benali, E. Dhahri and M. A. Valente, J. Alloys Compd., 2020, 839, 155601.

---