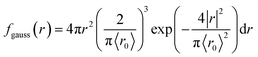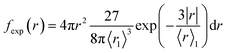Open Access Article
Open Access ArticleFirst-principles simulation of an ejected electron produced by monochromatic deposition energy to water at the femtosecond order
Takeshi Kai *a,
Tomohiro Toigawa
*a,
Tomohiro Toigawa a,
Yusuke Matsuya
a,
Yusuke Matsuya ab,
Yuho Hirata
ab,
Yuho Hirata a,
Tomoya Tezukac,
Hidetsugu Tsuchida
a,
Tomoya Tezukac,
Hidetsugu Tsuchida cd and
Akinari Yokoya
cd and
Akinari Yokoya e
e
aNuclear Science and Engineering Center, Japan Atomic Energy Agency, 2-4 Shirane Shirakata, Tokai-mura, Naka-gun, Ibaraki, 319-1195, Japan
bFaculty of Health Sciences, Hokkaido University, Kita-12 Nishi-5, Kita-ku, Sapporo, Hokkaido 060-0812, Japan
cDepartment of Nuclear Engineering, Kyoto University, Nishikyo-ku, Kyoto 615-8530, Japan
dQuantum Science and Engineering Center, Kyoto University, Gokasho, Uji, Kyoto 611-0011, Japan
eInstitute for Quantum Life Science, National Institutes for Quantum Science and Technology, 4-9-1 Anagawa, Inage-ku, Chiba-shi 263-8555, Japan
First published on 3rd November 2023
Abstract
This study uses a time-dependent first-principles simulation code to investigate the transient dynamics of an ejected electron produced in the monochromatic deposition energy from 11 to 19 eV in water. The energy deposition forms a three-body single spur comprising a hydroxyl radical (OH˙), hydronium ion (H3O+), and hydrated electron (eaq−). The earliest formation involves electron thermalization and delocalization dominated by the molecular excitation of water. Our simulation results show that the transient electron dynamics primarily depends on the amount of deposition energy to water; the thermalization time varies from 200 to 500 fs, and the delocalization varies from 3 to 10 nm in this energy range. These features are crucial for determining the earliest single-spur formation and facilitating a sequential simulation from an energy deposition to a chemical reaction in water photolysis or radiolysis. The spur radius obtained from the simulation correlates reasonably with the experimental-based estimations. Our results should provide universalistic insights for analysing ultrafast phenomena dominated by the molecular excitation of water in the femtosecond order.
Introduction
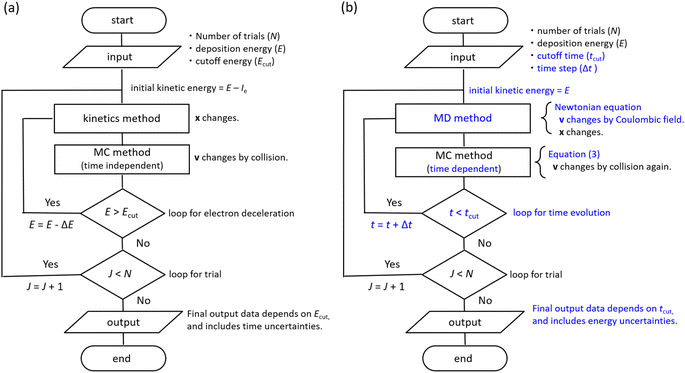
Water photolysis and radiolysis are attractive research fields because of their importance in nuclear reactors, transuranic and high-level mixed waste storage, industrial applications, radiation biology, and medicine.1,2 Water radiolysis3–8 or photolysis9–21 produces various reactive products, such as hydroxyl radicals (OH˙), hydronium ion (H3O+), and hydrated electrons (eaq−) etc., and their thermal diffusions proceed chemical reactions. When monochromatic short-pulse lasers are irradiated into water, extremely low-energy electrons are ejected by photolysis.9–21 Consequently, a three-body single spur comprising OH˙, H3O+, and eaq− is formed. Furthermore, the radiolysis forms a single spur when the deposition energy is <19 eV because the lowest electronic excitation and ionization energies are 8.4 eV and 10.9 eV, respectively.22,23 Previous photolysis experiments at ∼8 eV energy deposition revealed that the ejected electrons, i.e., the prehydrated electrons (epre−), are weakly trapped in the bulk water at ∼100 fs.9–13 The epre− transitions to eaq− by the orientation polarization after several 100 fs.9–13 However, no method has been proposed to directly measure the initial spatial distribution of eaq−, with a mean distance of a spur radius.Three processes classify these radiation-induced phenomena. Ultrafast phenomena, such as radiation transport, energy deposition, and electron ejection, are categorized in the physical process (a few fs). The physicochemical process corresponds to the deceleration, thermalization, delocalization (within a few 100 fs), and hydration (within a few 10 ps) of the ejected electrons. Delocalization indicates the spatial distribution of a few nm of the electrons ejected from the parent cations; the initial chemical species are typically determined in this process. The diffusion and reaction of the chemical species are categorized in the chemical process (after a few 100 ps). In the physical process, the incident and ejected electron trajectories are calculated using Monte Carlo codes (MCCs),2,24–33 such as the Kyushu University Radiobiology Unit Code (KURBUC),2,27,28 the TRACk structure of Electrons in Liquid water (TRACEL),25 TRACELE,26 RITRACKS,29 PARTRAC,30 Geant4-DNA,31 and Particle and Heavy Ion Transport code System (PHITS).32,33 Although Geant4-DNA enabled the electron deceleration calculation down to eV in the latest developments,34–36 MCCs typically need cutoff energy for electron deceleration (7–10 eV).34 Molecular excitations are crucial when the electron deceleration is <7 eV, such as intramolecular and intermolecular vibrations and rotation induced by the low-energy electrons in liquid water. However, the cross-sections of liquid water still need to be determined. When analysing the physicochemical process in water radiolysis based on simulation,2,24–36 the initial spatial distribution of eaq− must be modelled based on experimental evidence.34,37,38 For water photolysis,14–21 the distributions have been reversely predicted from the chemical process calculations for reproducing experimental results (experimental prediction). Therefore, the earliest formation process of a single spur has been unclear.
We developed a dynamic MCC for the physical process (dmcc_phys) to investigate ejected electron thermalization, delocalization, and relocalization in water.39–46 The code simulates physical and physicochemical processes by implementing cross-sections from 1 meV to 1 MeV.45,46 Implementing the molecular excitation cross-sections of liquid water40 allows for a detailed analysis of the physical and physicochemical processes.45,46 Thus, our simulation provides a clue to unravel the unclear earliest single-spur formation. We used the dmcc_phys to investigate the physicochemical nature of ejected electrons produced by water photolysis at 12.4 eV.46 Our results for electron delocalization correlated well with the experimental predictions,19 and some electrons relocalized into parent cations. In other words, the results46 will reproduce successive chemical reactions in water photolysis experiments.19 By connecting our code to the chemical codes,47–50 we should provide a sequential simulation from an energy deposition to a chemical reaction in the three-body single spur without physicochemical models.34,37,38
Several models for low-energy electron range calculations below a few eV have been devised from these backgrounds.34,37,38 However, those models assumed that water irradiates the incident electrons; therefore, they cannot predict the spatial distribution of the electron ejected from the parent cation. This study considered that an incident electron motion was not simulated but only ejected electron motion. Fig. 1 shows the difference between the conventional approach and our approach. A minor spur radius calculation involved in the ejected electron has been reported.43,46 Moreover, it is impossible to measure the spur radius directly; therefore, the time-evolution yields of eaq− are measured under irradiation conditions where the simplest radiolytic unit, a three-body single spur, is formed.14–19 Using a chemical code,14–19 a parameter analysis is performed to evaluate the initial spur radius that reproduces these experimental results.14–19 In this analysis, the only spur radius is an unknown free parameter, so its value strongly reflects the experimental results; therefore, this study calls these values experimental predictions. The experimental predictions are reported from 8 eV to 12.4 eV,14–19 but there are two ionization mechanisms. Ionization from 8 eV to 10.9 eV (ionization energy23) deposition energy occurs due to proton-coupled electron transfer,19 and the deposition energy above the ionization energy produces typical ionization.
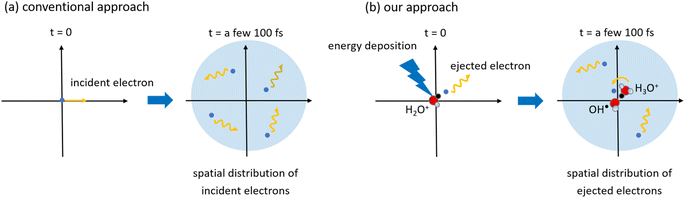 | ||
| Fig. 1 An illustration of the (a) conventional approach and (b) our approach in simulation studies of low-energy electrons. Conventional approaches report several models for the range calculations of low-energy electrons irradiated into water as a function of incident electron energy.34,37,38 In our approach,43,46 we calculated the spatial distribution of ejected electrons generated in water using a first principles simulation. As our code considers the coulombic field of a parent cation, the delocalization and relocalization of ejected electrons can be calculated. When the ejected electrons slow down sufficiently, they hydrate, and a three-body single spur comprising OH˙, H3O+, and eaq− is formed. | ||
This study investigates the ejected electron thermalization, delocalization, and relocalization dominated by the coulombic force of parent cation and the molecular excitation of liquid water at a deposition energy of 11–19 eV to unravel the unclear earliest single-spur formation because our code cannot accurately simulate proton-coupled electron transfer. First, we present the simulation results of the mean ejection distance and kinetic energy of the ejected electrons. Then, we present the simulation results of the kinetic energy and spatial distributions of the ejected electrons. Finally, we evaluate the spur radius and thermalization time at 11–19 eV and compare our evaluation with the experimental predictions and value at 8–12.4 eV.14–21 Therefore, the experimental prediction values in the 11–12.4 eV energy range are helpful for our code validation. We successfully performed an experimental analysis of the photolysis for a deposition energy of 12.4 eV.46 For water radiolysis, various energies are deposited into the water. Our results contribute to a much deeper understanding of the earliest formation process of a three-body single spur formed by water radiolysis.
Methods
The dmcc_phys uses time-dependent first-principles simulation to simulate electron deceleration, thermalization, delocalization, and relocalization in the physicochemical process.39–46 Our code does not require a cutoff energy; a cutoff time is necessary. In the simulation, the dynamical motions of the ejected electrons are calculated using the molecular dynamics (MD) and the time-dependent Monte Carlo (MC) methods.45,46 Our code was developed by implementing MD based on a Newtonian equation into the time-dependent MCC based on the probability theory of collision.45,46 PHITS is a general-purpose MCC that can analyse the radiation kinetics at microscopic and macroscopic scales.32,33 Conversely, the electron track structure mode of PHITS,32,33 corresponding to the MCC, was previously developed by eliminating MD and replacing the time-dependent MC with the time-independent MC in our code.32,33 The dmcc_phys simulates the electron dynamic motion in the coulombic field created by the parent cation.45,46 This coulombic field is shielded along the dielectric response, which is the time evolution of the relative dielectric constant.45,46 The dielectric response simplifies the hydration process.45,46 Our code considers the dielectric response comprising electronic, phonon, and orientation polarizations. Thus, the electron or cation charges in water are gradually shielded.46 Our code could distinguish between the free electrons, epre−, and eaq− via the dielectric response.46 We indicated that the phonon and orientation polarizations contribute to the epre− and eaq− formation, respectively.46 Our code does not consider electron mass change via the dielectric response.46 However, this assumption is acceptable to calculate the electron dynamics after a few 100 fs because the electrons are nearly stopped at the phonon (prehydration) and orientation (hydration) polarization timescales.46 Our previous reports showed a detailed flowchart of our water radiolysis and photolysis code,45,46 clarifying the difference between our code39–46 and the MCCs.2,24–36 Furthermore, we show the flowchart of typical MCCs and dmcc_phys to explain those differences in Fig. 2. The subsections describe the cross-sections, time-dependent MC and MD methods, and spur radius.Cross-sections
The database of the electron collision cross-sections used herein (Fig. 3) is shown in our previous studies,45,46 and the database was implemented into PHITS.32,33 The molecular excitation cross-sections of water differ substantially between the gas and condensed phases. The electron impact cross-sections for elastic scattering, intramolecular and intermolecular vibrations, and rotation excitations are essential to analyse the ejected electron motion. Fig. 3(a) shows the rotation excitation cross-sections;40 for comparison, the rotation excitation cross-section for water vapor51 is also shown. Fig. 3(b) shows the intermolecular vibration excitation cross-sections. In our previous study,40 the data were calculated by an optical approximation using the complex dielectric function of liquid water. However, since the approximation cannot reproduce the resonance structure, the data above 1.7 eV were connected by scaling the amorphous ice data to our data. Fig. 3(c) shows the intramolecular vibrational excitation cross-sections. We used the amorphous ice data to obtain the cross-sections for the condensed phase.52 The data were connected by scaling the water vapor data52 to the amorphous ice data because no data below 1.7 eV has been reported. Fig. 3(d) shows our total molecular excitation cross-sections. For comparison, the cross-sections of rotation excitation for the water vapor,51 total intramolecular vibration excitation for the water vapor,51 and total intermolecular vibration excitation for the amorphous ice52 are shown. In doing so, we excluded water vapor information in developing our cross-section database.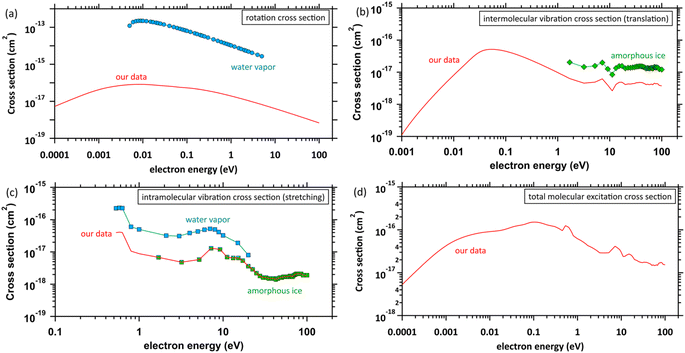 | ||
| Fig. 3 Molecular excitation cross-sections: (a) rotation excitation cross-sections, red solid line: our data (liquid water), ○: other data (water vapor),51 (b) intermolecular vibration excitation cross-sections, red solid line: our data (liquid water), ◇: other data (amorphous ice),52 (c) intramolecular vibration excitation cross-sections, red solid line: our data (amorphous ice base), □: other data (water vapor),51 ◇: other data (amorphous ice),52 and (d) total molecular excitation cross-section, red solid line: our data. | ||
A previous study53 measured dissociative electron attachment (DEA) in low-energy electron irradiation experiments using amorphous water films. In 2000, DNA double-strand breaks triggered by the DEA were measured using DNA films in a vacuum in low-energy electron irradiation experiments.54 DNA damage yields were also quantified in low-energy electron irradiation below 30 eV using hydrated plasmid DNA films.55 From the experimental evidence, the DEA attracted attention as a new elementary DNA damage process; however, the DEA was hardly induced in aqueous solution.56 Geant4-DNA sets the initial G-value of the DEA at 0.02 1/(100 eV) in liquid water.57 The G-value is reasonable because it well reproduces the experimental results of subsequent chemical reactions.57 From the background, DEA induction yields seem to strongly depend on the experimental conditions. Since we are targeting liquid water, this study did not consider the DEA cross-section, but further discussion might be needed.
Moliere's elastic scattering cross-section was used,58 which is much higher than the molecular excitation cross-sections.45,46 Therefore, we assumed that the scattering angle of electrons changes in inducing the elastic scattering in this study. The scattering angle was sampled from the differential cross-section of the elastic scattering.58
When elastic scattering is induced, no energy change occurs in the relative motions of an electron and a water molecule; however, the energy for the motion of the centre-of-mass system changes.54,55 This phenomenon is evaluated using the momentum transfer cross-section σmom obtained from the differential cross-section q(ϑ) of elastic scattering.59,60
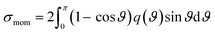 | (1) |
Using the σmom of eqn (1) and integral cross-section of elastic-scattering σelas, the energy transfer is given as45,46,59,60
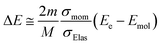 | (2) |
Time-dependent MC and MD method
The general MCCs provide the one-step distance of an electron moving to the next collisional position in the water as Δs = −λ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(k),25 where λ is the mean free path and is obtained from the total cross-section σ and atomic density N (3.318565 × 1022 molecules per cm3) as λ = 1/(σN); k is a uniform random number. This code assumes that collisions between electrons and water are induced if the following conditions are satisfied,45,46
ln(k),25 where λ is the mean free path and is obtained from the total cross-section σ and atomic density N (3.318565 × 1022 molecules per cm3) as λ = 1/(σN); k is a uniform random number. This code assumes that collisions between electrons and water are induced if the following conditions are satisfied,45,46
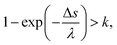 | (3) |
We assumed that the electrons and cations are finite-size particles, a sphere of radius with negative and positive charges (e) uniformly distributed within the sphere (the finite-size particle model).45,46 The particle radius is 0.099 nm to reproduce the ionization energy of 10.9 eV (ref. 23) and a minimum position of the potential energy (−10.9 eV) is allocated at the origin. When the potential of the cation is expressed in the spherical coordinates, it can be presented in eqn (4).
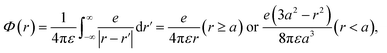 | (4) |
Spur radius
We present the numerical data for electron delocalization, i.e., electron number distribution as a function of radius r in polar coordinates. The r is the distance from the ionic core of the parent cation. The numerical data cannot be reproduced with Gaussian or exponential distributions alone because the ejected electron motion depends on the coulombic field of the parent cation and thermal diffusion in water. Thus, we expect the numerical distribution to be reproduced by Gaussian and exponential distributions, especially in the deposition energy around the ionization energy (10.9 eV (ref. 23)). Therefore, the following equation, which multiplies the volume elements by Gaussian fgauss(r) and exponential fexp(r) distributions, is used to express the electron delocalization distribution f(r) analytically.| f(r) = (Afgauss(r) + Bfexp(r))/C | (5) |
and
where r is the distance from the ionic core of the parent cation, and 〈r0〉 (or 〈r1〉) is the mean distance of the spatial distribution of an electron. H3O+ and OH˙ are near the origin. The spur radius was defined by A〈r0〉 + B〈r1〉. The electron relocalization into the parent cation can be calculated using our code.43–46 However, the functional distribution fitting for the relocalized electrons was challenging; therefore, it was performed to reproduce the distribution more than 1 nm from the origin. When the numerical distribution is integrated over the entire space, it is normalized to 1 but not when integrated over the region above 1 nm, excluding the relocalized electrons. Therefore, a scaling parameter is necessary to reproduce the region above 1 nm by functional fitting. We introduced the parameter C in eqn (4), which corresponds approximately to electron relocalization yield.
Results and discussion
First, the electrons' mean ejection distance and kinetic energy were presented to determine the cutoff time. The kinetic energy distributions of an electron are presented and compared to the Maxwellian of 300 K bulk water to discuss electron thermalization. The spatial distributions of the ejected electron are presented to evaluate the spur radius. From these results, the thermalization and hydration of electrons produced by water photolysis and radiolysis were finally discussed.Mean ejection distance and kinetic energy
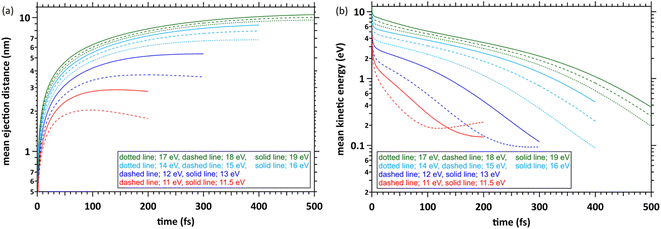
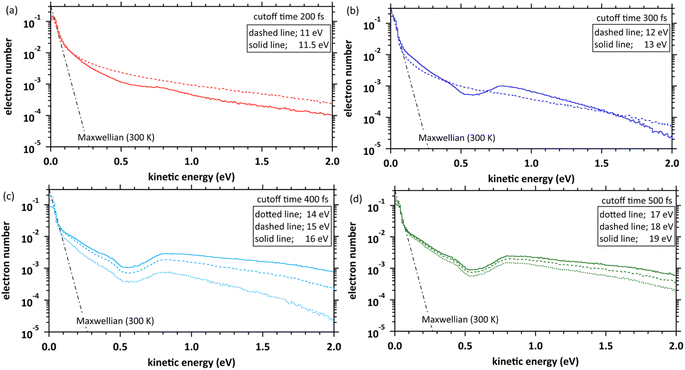
Fig. 4(a) shows the simulation results with the time evolution of the mean ejection distances, defined as a straight line between the starting point (origin) and the position of the ejected electron at each time. When the deposition energies were 11 and 11.5 eV, the mean ejection distances converged at ∼200 fs. When the deposition energies were 12, 13, 14–16, and 17–19 eV, the mean ejection distances converged at 300, 400, and 500 fs, respectively. The epre− formation time has yet to be reported as experimental results, except for the 8 eV deposition energy.9–13 Therefore, defining the cutoff time for all deposition energies is difficult. We defined the cutoff time as the time when the mean energy of the electrons decelerates to roughly a few 100 meV. Then, the mean ejection distances of electrons are well converged. Fig. 4(b) shows the simulation results with time evolution of the mean kinetic energy of the electrons. The cutoff times for each deposition energy were the same as those in Fig. 4(a), and the mean kinetic energy was <1 eV. Previous reports9–13 measured the epre− and eaq− formations using photolysis experiments at ∼8 eV deposition energy, where epre− is formed at ∼100 fs and eaq− at several 100 fs. Although these experimental results are yet to be reported in a deposition energy of 11–19 eV, the epre− and eaq− formation time could be longer than the time reported in the photolysis experiments, i.e., around 8 eV.Kinetic energy distribution of ejected electrons
Fig. 5 shows our simulation results for the electron kinetic energy distributions at each deposition energy (11–19 eV) and the cutoff times. The molecular excitations, the momentum transfer of eqn (2), and the cation potential of eqn (4) dominate these electron kinetic energy distributions.46 These results show that the electron kinetic energy distributions exhibit nonthermal equilibrium distributions because some electrons were relocalized into the parent cations due to the coulombic field. In the extremely low-energy region within 0.1 eV, the kinetic energy distribution of electrons, which escaped from the coulombic field, approaches the Maxwellian of 300 K bulk water. Our results indicate that the electrons were sufficiently decelerated at the cutoff time for each deposition energy. Therefore, the cutoff time used herein was reasonable for discussing the spur radius. When the deposition energy exceeded 13 eV, a depression was observed near the kinetic energy distribution of 0.5 eV. A potential reason is the contribution of intramolecular vibration excitations with resonance structures in the cross-section near several 0.1 eV (see, Fig. 3(c)).Spatial distribution of ejected electrons
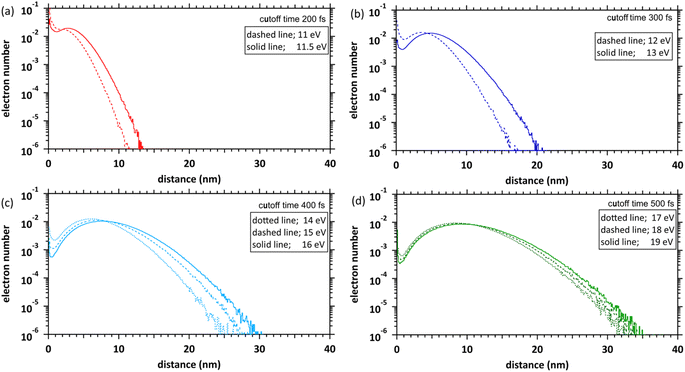
Fig. 6 shows our simulation results of the spatial distributions of the ejected electrons at each deposition energy (11–19 eV) and the cutoff times. The fraction of electrons near the parent cations (within 1 nm) is considerably high at the 11 and 11.5 eV deposition energies near the ionization energy (10.9 eV (ref. 23)). This result indicates that many electrons are relocalized into the parent cations within several 100 fs, even if the deposition energy exceeds the ionization energy. The relocalized electrons will form excited states.20 The fraction of the relocalized electrons decreases with the increasing deposition energy and becomes negligible at deposition energies above 15 eV. The liquid water has some highly excited states at 11–14 eV.22 During several 100 fs, many electrons that transited to the Rydberg (A + B) (excitation energy of 11.26 eV (ref. 22)) or Rydberg (C + D) (excitation energy of 11.93 eV (ref. 22)) were finally relocalized. However, the electrons that transited to the diffuse band (excitation energy of 14.1 eV (ref. 22)) were mostly delocalized. These results become a new universalistic insight for analysing the initial yield of eaq− in water radiolysis.45 The maxima of these distributions shift from 3 nm to 10 nm as the deposition energy increases.Spur radius
We determined the spur radius by obtaining the parameters 〈r0〉, 〈r1〉, A, B, and C in eqn (5) by fitting our results (Fig. 6). Fig. 7(a) shows our results (11–19 eV) and previous experimental predictions14–19 (8–12.4 eV) for the spur radius. The present results, indicated by circles from 11 to 19 eV, reasonably correlate with the previous experimental predictions indicated by squares from 8 to 12.4 eV in Fig. 7(a). Table 1 shows the fitting parameters (〈r0〉, 〈r1〉, A, B, and C). From these results, the distributions shift from the exponential type to the Gaussian type as the deposition energy increases. When the deposition energy is <14 eV, Gaussian and exponential distributions are required to reproduce the spatial distribution of the ejected electrons. However, when the deposition energy is >14 eV, it can be approximately represented by a Gaussian. Electron delocalization in the three-body single spur will be easily reproduced using the data listed in Table 1. These distributions correspond to the initial spatial distribution of eaq−. Although these spur radii were one of the remaining unknown parameters in water photolysis and radiolysis, this study elucidated their values.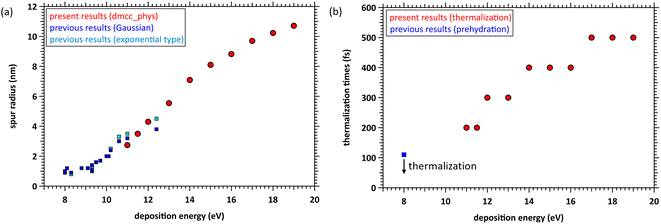 | ||
| Fig. 7 (a) Spur radii of electrons in the deposition energy region of 8–19 eV; □: experimental predictions,14–19 ○: present. (b) Thermalization time at the deposition energy region of 11–19 eV, and prehydration times at 8 eV.10 | ||
| Energy (eV) | A | r0 (nm) | B | r1 (nm) | C | Radius (nm) |
|---|---|---|---|---|---|---|
| 11.0 | 0.2 | 2.5 | 0.8 | 2.8 | 1.70 | 2.74 |
| 11.5 | 0.5 | 3.2 | 0.5 | 3.8 | 1.30 | 3.50 |
| 12.0 | 0.5 | 4.4 | 0.5 | 4.2 | 1.20 | 4.30 |
| 13.0 | 0.8 | 5.8 | 0.2 | 4.5 | 1.05 | 5.54 |
| 14.0 | 0.7 | 6.7 | 0.3 | 8.0 | 1.00 | 7.09 |
| 15.0 | 0.8 | 8.0 | 0.2 | 8.5 | 1.00 | 8.10 |
| 16.0 | 0.9 | 8.8 | 0.1 | 9.0 | 1.00 | 8.82 |
| 17.0 | 0.9 | 9.7 | 0.1 | 9.7 | 1.00 | 9.70 |
| 18.0 | 0.9 | 10.2 | 0.1 | 10.5 | 1.00 | 10.23 |
| 19.0 | 0.9 | 10.7 | 0.1 | 10.8 | 1.00 | 10.72 |
Thermalization and hydration
From the photolysis experiments at 8 eV deposition energy,10 the physicochemical process of water photolysis progresses with electron thermalization, prehydration, and hydration. epre− was formed at ∼110 fs, and epre− transitioned to eaq− at ∼240 fs.10 Although the epre− formation time has been reported as experimental results at 8 eV deposition energy,9–13 proton-coupled electron transfer ionizes the electrons. As our code cannot simulate this mechanism, we show the calculation results for energy deposition above the ionization energy (10.9 eV (ref. 23)). The results in Fig. 4 indicate that the prehydration and hydration times depend on the deposition energy because the thermalization time depends on the deposition energy. Fig. 7(b) shows the thermalization times estimated from the cutoff times herein and the prehydration time reported previously.10 Our simulation results are discrete (Fig. 7(b) shown in circles), but the linearity is roughly preserved in the energy region from 8 to 19 eV. Therefore, we predict that the prehydration and hydration times will exceed 500 fs, at least when the deposition energy exceeds 17 eV. From the energy-loss function of water reported in our recent literature,45 a high-energy incident electron in liquid water primarily imparts an energy of ∼20 eV to water. Thus, the electron thermalization times differ considerably between water photolysis and radiolysis. Our findings for thermalization and delocalization above 17 eV can provide new universalistic insight into the physicochemical process of water radiolysis. We expect new experimental results with deposition energies above 12.4 eV.Future
As shown in Fig. 1, previous studies irradiated low-energy electrons into the water, whereas this study analyses the dynamics of ejected electrons resulting from the energy deposited into the water. Consequently, we simulated the delocalization and relocalization of ejected electrons and elucidated the energy deposition dependence of the spur radius and thermalization time. The electrons cannot induce additional ionization or electronic excitation at the deposition energy of 11–19 eV; therefore, a three-body single spur was formed. As the deposition energy increases, the ejected electrons induce additional ionization and electronic excitation, forming multibody single spurs. In a biological system, this spur formation induces complex DNA lesions, such as double-strand breaks, causing biological effects with a certain probability.61,62 In the future, we will investigate the multibody single-spur formation process in water radiolysis.Conclusions
We investigated the transient dynamics of an ejected electron produced in the range of monochromatic deposition energy into water using dmcc_phys, resulting in the earliest three-body single spur. We found that electron thermalization, delocalization, and relocalization dominated by the molecular excitation of liquid water in the coulombic field created by the parent cation, largely depend on the amount of deposition energy into the water. In other words, physicochemical timescales differ considerably between water photolysis and radiolysis. The estimated spur radius based on the MD and MC reasonably correlates with the experimental prediction values (8–12.4 eV).14–19 We validated our simulation code, including the molecular excitation cross-sections of liquid water.The role of highly excited electrons in water radiolysis is not well understood.1 Liquid water has some highly excited states at a deposition energy of 11–14 eV.22 Many electrons that transited to the highly excited states were finally relocalized. However, the ejected electrons were mostly delocalized at the deposition energy of >14 eV. Electron relocalization produces chemical species, such as OH˙ + H˙ or O + H2, or energy relaxation, originating from electronic excitation, whereas electron delocalization produces chemical species, such as OH˙, H3O+, and eaq−, originating from ionization. The scientific insights proposed by this study should be widely available for the subsequent chemical processes in radiation biology,2 nuclear chemistry,1 and other fields.
Author contributions
T. Kai and T. Toigawa designed this work. T. Kai developed the dynamic Monte Carlo code for the physical process and performed all calculations. Y. Matsuya and Y. Hirata contributed to the discussion for developing the code and radiation physics. H. Tsuchida and T. Tezuka contributed to the discussion of radiation physics. T. Toigawa contributed to the discussion of radiation chemistry. A. Yokoya supervised this study. T. Kai wrote the manuscript. All authors contributed to the discussion of this study and have reviewed the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Dr T. Sato, Dr Y. Iwamoto, Dr T. Furuta, Dr Hashimoto, Dr T. Ogawa, and Dr S. Abe (JAEA) for useful discussions on developing our code. This work was supported by the Japan Society for the Promotion of Science KAKENHI (Grant No. 22K04993, 22K14631, 22H03744, 22K14630, and 22K03549).Notes and references
- B. C. Garrett, et al., Chem. Rev., 2005, 105, 355–390 CrossRef CAS PubMed.
- H. Nikjoo, D. Emfietzoglou, T. Liamsuwan, R. Taleei, D. Liljequist and S. Uehara, Rep. Prog. Phys., 2016, 79, 116601 CrossRef CAS PubMed.
- D. M. Bartels, A. R. Cook, M. Mudaliar and C. D. Jonah, J. Phys. Chem. A, 2000, 104, 1686–1691 CrossRef CAS.
- Y. Muroya, M. Lin, G. Wu, H. Iijima, K. Yoshii, T. Ueda, H. Kudo and Y. Katsumura, Radiat. Phys. Chem., 2005, 72, 169–172 CrossRef CAS.
- J. Yang, T. Kondoh, K. Kan and Y. Yoshida, Nucl. Instrum. Methods Phys. Res., Sect. A, 2011, 629, 6–10 CrossRef CAS.
- G. P. Horne, T. A. Donoclift, H. E. Sims, R. M. Orr and S. M. Pimblott, J. Phys. Chem. B, 2016, 120, 11781–11789 CrossRef CAS PubMed.
- J. Ma, F. Wang, S. A. Denisov, A. Adhikary and M. Mostafavi, Sci. Adv., 2017, 3, e1701669 CrossRef PubMed.
- K. Kitajima, H. Tsuchida, T. Majima and M. Saito, J. Chem. Phys., 2019, 150, 095102 CrossRef PubMed.
- A. Migus, Y. Gauduel, J. L. Martin and A. Antonetti, Phys. Rev. Lett., 1987, 58, 1559–1562 CrossRef CAS PubMed.
- Y. Gauduel, S. Pommeret, A. Migus and A. Antonetti, J. Phys. Chem., 1989, 93, 3880–3882 CrossRef CAS.
- C. Silva, P. K. Walhout, K. Yokoyama and P. F. Barbara, Phys. Rev. Lett., 1998, 80, 1086–1089 CrossRef CAS.
- M. Assel, R. Laenen and A. Laubereau, J. Phys. Chem. A, 1998, 102, 2256–2262 CrossRef CAS.
- A. Thaller, R. Laenen and A. Laubereau, Chem. Phys. Lett., 2004, 398, 459–465 CrossRef CAS.
- M. U. Sander, M. S. Gudiksen, K. Luther and J. Troe, Chem. Phys., 2000, 258, 257–265 CrossRef CAS.
- C. L. Thomsen, D. Madsen, S. R. Keiding, J. Thogersen and O. Christiansen, J. Chem. Phys., 1999, 110, 3453–3462 CrossRef.
- D. Madsen, C. L. Thomsen, J. Thogersen and S. R. Keiding, J. Chem. Phys., 2000, 113, 1126–1134 CrossRef CAS.
- J. A. Kloepfer, V. H. Vilchiz, V. A. Lenchenkov, A. C. Germaine and S. E. Bradforth, J. Chem. Phys., 2000, 113, 6288 CrossRef CAS.
- R. A. Crowell and D. M. Bartels, J. Phys. Chem., 1996, 100, 17940 CrossRef CAS.
- C. G. Elles, A. E. Jailaubekov, R. A. Crowell and S. E. Bradforth, J. Chem. Phys., 2006, 125, 044515 CrossRef PubMed.
- C. G. Elles, I. A. Shkrob, R. A. Crowell and S. E. Bradforth, J. Chem. Phys., 2007, 126, 164503 CrossRef PubMed.
- J. Savolainen, F. Uhlig, S. Ahmed, P. Hamm and P. Jungwirth, Nat. Chem., 2014, 6, 697–701 CrossRef CAS PubMed.
- H. G. Paretzke, D. T. Goodhead, I. G. Kaplan, and M. Terrissol, Track structure quantities, in Atomic and molecular data for radiotherapy and radiation research, IAEA, Vienna, 1995, ch. 9, (IAEA-TECDOC-799) Search PubMed.
- M. Faubel and B. Steiner, Photoelectron spectroscopy at liquid water surfaces, in Linking the gaseous and condensed phases of matter. The behavior of slow electrons, ed. L. G. Christophorou, E. Illenberger and W. F. Schmidt, NATO ASI Series B-326, Plenum Press, New York, 1994, pp. 517–523 Search PubMed.
- S. M. Pimblott and J. A. LaVerne, J. Phys. Chem. A, 1997, 101, 5828–5838 CrossRef CAS.
- H. Tomita, M. Kai, T. Kusama and A. Ito, Radiat. Environ. Biophys., 1997, 36, 105–116 CrossRef CAS PubMed.
- V. Cobut, Y. Frongillo, J. P. Patau, T. Goulet, M.-J. Frasher and J.-P. Jay-Gerin, Radiat. Phys. Chem., 1998, 51, 229–243 CrossRef CAS.
- H. Nikjoo, S. Uehara, D. Emfietzoglou and F. A. Cucinotta, Radiat. Meas., 2006, 41, 1052–1074 CrossRef CAS.
- S. Uehara and H. Nikjoo, J. Radiat. Res., 2006, 47, 69–81 CrossRef CAS PubMed.
- I. Plante and F. A. Cucinotta, New J. Phys., 2009, 11, 063047 CrossRef.
- W. Friedland, M. Dingfelder, P. Kundrát and P. Jacob, Mutat. Res., 2011, 711, 28 CrossRef CAS PubMed.
- S. Incerti, I. Kyriakou, M. C. Bordage, S. Guatelli, V. Ivanchenko and D. Emfietzoglou, J. Appl. Phys., 2019, 125, 104301 CrossRef.
- T. Sato, Y. Iwamoto, S. Hashimoto, T. Ogawa, T. Furuta, S. Abe, T. Kai, P. E. Tsai, N. Matsuda, H. Iwase, N. Shigyo, L. Sihver and K. Niita, J. Nucl. Sci. Technol., 2018, 55, 684–690 CrossRef CAS.
- Y. Matsuya, T. Kai, Y. Yoshii, Y. Yachi, S. Naijo, H. Date and T. Sato, J. Appl. Phys., 2019, 126, 124701 CrossRef.
- I. Kyriakou, D. Sakata, H. N. Tran, Y. Perrot, W.-G. Shin, N. Lampe, S. Zein, M. C. Bordage, S. Guatelli, C. Villagrasa, D. Emfietzoglou and S. Incert, Cancers, 2022, 14, 35 CrossRef CAS PubMed.
- W.-G. Shin, J. Ramos-Mendez, B. Faddegon, H. N. Tran, C. Villagrasa, Y. Perrot, S. Okada, M. Karamitros, D. Emfietzoglou, I. Kyriakou, M. C. Bordage, D. Sakata, S. Guatelli, H. J. Choi, C. H. Min, S. B. Lee and S. Incerti, J. Appl. Phys., 2019, 126, 114301 CrossRef.
- S. Incerti, I. Kyriakou, M. A. Bernal, M. C. Bordage, Z. Francis, S. Guatelli, V. Ivanchenko, M. Karamitros, N. Lampe, S. B. Lee, S. Meylan, C. H. Min, W. G. Shin, P. Nieminen, D. Sakata, N. Tang, C. Villagrasa, H. N. Tran and J. M. C. Brown, Med. Phys., 2018, 45, e722–e739 CrossRef CAS PubMed.
- S. M. Pimblott and A. Mozumder, J. Phys. Chem., 1991, 95, 7291–7300 CrossRef CAS.
- R. H. Ritchie, R. N. Hamm, J. E. Turner, and W. E. Bolch, in Computational Approaches in Molecular Radiation Biology, Basic Life Sciences, ed. M. N. Varma and A. Chatterjee, Plenum Press, New York, 1994, vol. 63, pp. 33–44 Search PubMed.
- T. Kai, A. Yokoya, M. Ukai, K. Fujii, M. Higuchi and R. Watanabe, Radiat. Phys. Chem., 2014, 102, 16–22 CrossRef CAS.
- T. Kai, A. Yokoya, M. Ukai and R. Watanabe, Radiat. Phys. Chem., 2015, 108, 13–17 CrossRef CAS.
- T. Kai, A. Yokoya, M. Ukai, K. Fujii and R. Watanabe, Radiat. Phys. Chem., 2015, 115, 1–5 CrossRef CAS.
- T. Kai, A. Yokoya, M. Ukai, K. Fujii and R. Watanabe, Int. J. Radiat. Biol., 2016, 92, 654–659 CrossRef CAS PubMed.
- T. Kai, A. Yokoya, M. Ukai, K. Fujii and R. Watanabe, J. Phys. Chem. A, 2016, 120, 8228–8233 CrossRef CAS PubMed.
- T. Kai, A. Yokoya, M. Ukai, K. Fujii, T. Toigawa and R. Watanabe, Phys. Chem. Chem. Phys., 2018, 20, 2838–2844 RSC.
- T. Kai, T. Toigawa, Y. Matsuya, Y. Hirata, T. Tezuka, H. Tsucida and A. Yokoya, RSC Adv., 2023, 13, 7076–7086 RSC.
- T. Kai, T. Toigawa, M. Ukai, K. Fujii, R. Watanabe and A. Yokoya, J. Chem. Phys., 2023, 158, 164103 CrossRef CAS PubMed.
- I. A. Plante, Phys. Med. Biol., 2021, 66, 03TR02 CrossRef CAS PubMed.
- W. G. Shin, J. Ramos-Mendez, N. H. Tran, S. Okada, Y. Perrotf, C. Villagrasa and S. Incerti, Phys. Med., 2021, 88, 86–90 CrossRef PubMed.
- P. Clifford, N. J. B. Green, M. J. Oldfield, M. J. Pilling and S. M. Pimblott, J. Chem. Soc., Faraday Trans. 1, 1986, 82, 2673–2689 RSC.
- S. M. Pimblott and J. A. LaVerne, J. Phys. Chem. A, 1998, 102, 2967–2975 CrossRef CAS.
- Y. Itikawa and N. Mason, J. Phys. Chem. Ref. Data, 2005, 34, 1–22 CrossRef CAS.
- M. Michaud, A. Wen and L. Sanche, Radiat. Res., 2003, 159, 3–22 CrossRef CAS PubMed.
- P. Rowntree, L. Parenteau and L. Sanche, J. Chem. Phys., 1991, 94, 8570–8576 CrossRef CAS.
- B. Boudaïffa, P. Cloutier, D. Hunting, M. A. Huels and L. Sanche, Science, 2000, 287, 1658–1660 CrossRef PubMed.
- E. Alizadeh, A. G. Sanz, G. García and L. Sanche, J. Phys. Chem. Lett., 2013, 4, 820–825 CrossRef CAS PubMed.
- C.-R. Wang, J. Nguyen and Q.-B. Lu, J. Am. Chem. Soc., 2009, 131, 11320–11322 CrossRef CAS PubMed.
- W. G. Shin, J. R. Mendez, N. H. Tran, S. Okada, Y. Perrot, C. Villagrasa and S. Incerti, Phys. Med., 2021, 88, 86–90 CrossRef PubMed.
- G. Moliere, Theorie der streuung schneller gelandener teilchen II: Mehrfachund ielfachstreuung, Z. Naturforsch., 1948, 3, 78–97 CrossRef.
- K. Takayanagi, Introduction to electron-molecule collisions, in Electron-Molecule Collisions, ed. I. Shimamura and K. Takayanagi, Plenum Press, New York, 1984, pp. 1–87 Search PubMed.
- I. KrajcarBronić, M. Kimura and M. Inokuti, J. Chem. Phys., 1995, 102, 6552–6558 CrossRef.
- D. T. Goodhead, Int. J. Radiat. Biol., 1994, 65, 7–17 CrossRef CAS PubMed.
- J. F. Ward, Prog. Nucleic Acid Res. Mol. Biol., 1988, 35, 95–125 CAS.
| This journal is © The Royal Society of Chemistry 2023 |