[Cs©C₁₈]⁺ and [Na©C₁₄]⁺: perfect planar alkaline-metal-centered polyynic cyclo[n]carbon complexes with record coordination numbers

Abstract

Searching for the maximum coordination number (CN) in planar species with novel bonding patterns has fascinated chemists for many years. Using the experimentally observed polyynic cyclo[18]carbon D_9h C₁₈ and theoretically predicted polyynic cyclo[14]carbon D_7h C₁₄ as effective ligands and based on extensive first-principles theory calculations, we predict herein their perfect planar alkaline-metal-centered complexes D_9h Cs©C₁₈⁺ (1) and D_7h Na©C₁₄⁺ (4) which as the global minima of the systems possess the record coordination numbers of CN = 18 and 14 in planar polyynic species, respectively. More interestingly, detailed energy decomposition and adaptive natural density partitioning bonding analyses indicate that the hypercoordinate alkaline-metal centers in these complexes exhibit obvious transition metal behaviors, with effective in-plane (π-6s)σ, (π-7p)σ, and (π-5d)σ coordination bonds formed in Cs©C₁₈⁺ (1) and (π-3s)σ, (π-3p)σ, and (π-3d)σ coordination interactions fabricated in Na©C₁₄⁺ (4) to dominate the overall attractive interactions between the metal center and its cyclo[n]carbon ligand. Similarly, alkaline-metal-centered planar C_s Cs©C₁₇B (2), C_2v Cs©C₁₇⁻ (3), C_2v Na©C₁₃B (5), and C_2v Na©C₁₃⁻ (6) have also been obtained with CN = 18, 17, 14, and 13, respectively.

---

1 Introduction

The successive discoveries of fullerenes in 1985,¹ carbon nanotubes in 1991,² and graphene in 2004 ³ which all consist exclusively of 3-coordinate carbon atoms have sparked a new field of synthetic carbon allotropes in chemistry. The recent characterization of polyynic cyclo[18]carbon D_9h C₁₈ with bond length alternation (BLA) in 2019 using high-resolution atomic force microscopy marked the onset of an alternative family of molecular carbon allotropes consisting solely of 2-coordinate carbon atoms in the C_4N+2 cyclo[n]carbon ring series.⁴ Previous gas-phase experiments indicated that cyclo[n]carbon rings as primary precursors may coalescence to form fullerenes and carbon nanotubes.^5,6 Electronic spectroscopic measurements showed that both C₁₈ and C₁₄ possess monocyclic geometries, though these studies did not reveal whether they have cumulantic or polyynic structures.^7,8 High level quantum Monte Carlo (QMC) simulation and coupled cluster methods with single and double excitations (CCSD) investigations indicated that both polyynic D_9h C₁₈ and D_7h C₁₄ are the ground states of the systems due to second-order Jahn-Taller effects, with their cumulantic counterparts with no BLA always behaving as transition states.^9,10 Such perfect monocyclic D_(2N+1)h C_4N+2 polyynic species have aroused considerable interests among chemists and presented viable possibilities to form planar metal-doped cyclo[n]carbon complexes with super-high coordination numbers (CN). A recent theoretical investigation¹¹ suggested that the Li-doped C₁₈ complex may serve as a potential optical switch which transforms between two stable C_s configurations with Li inside (Li@C₁₈ⁱⁿ) and outside the carbon ring (Li@C₁₈^out). However, in the ground state (Li@C₁₈ⁱⁿ) of such an alkaline-metal-doped cyclo[18]carbon complex, the Li atom with the coordination number of CN = 5 appears to be severely off-centered due to the size mismatch between Li and its monocyclic C₁₈ ligand. Similar situation happens in the recently proposed metal-doped M@C₁₆ complexes (M = Ca, Sc, Ti, V, Ce, U) in which the off-centered alkaline-earth, lanthanide, or actinide metal atoms have the coordination numbers between CN = 4 ∼ 6,¹² again due to size effect. A recent first-principles theory investigation by our group indicated that, in the experimentally observed La©C₁₃⁺, the La center with the large atomic radius of r_La = 1.83 Å ¹³ matches the C₁₃ ligand perfectly both geometrically and electronically to form the perfect planar La-centered D_13h La©C₁₃⁺ which has the highest coordination number of CN = 13 in planar species reported to date, demonstrating the unique coordinating capability of cyclo[n]carbon rings as effective ligands to metal centers in chemistry.¹⁴ However, it still remains unknown to date in both experiments and theory whether or not metal-centered hypercoordinate planar cyclo[n]carbon complexes with CN > 13 can be achieved in chemistry. To achieve higher CNs (CN = n ≥ 14) in metal-centered cyclo[n]carbon complexes, it requires in chemical intuition that the metal centers have atomic radii greater than that of La.

Searching for the maximum coordination number in planar species is more than a curiosity, it is to push the limits and ultimately to understand the essential concepts in chemistry.^14,15 To successfully design a metal-centered hyper-coordinate planar complex, the metal center and its ligand must match both geometrically and electronically, i.e., they must have the right geometrical sizes and electronic configurations. The prototypical electron-deficient planar cyclo[n]boron rings have proven to be effective ligands to coordinate transition metal centers. Perfect σ + π dually aromatic wheel-like D_8h Co©B₈⁻, D_9h Ru©B₉⁻, D_9h Rh©B₉⁻, D_9h Ir©B₉⁻, D_10h Ta©B₁₀⁻, and D_10h Nb©B₁₀⁻ with CN = 8, 9, 9, 9, 10, and 10 have been observed in gas phases in recent joint photoelectron spectroscopy and first-principles theory investigations.^15–20 These results present the possibility to form metal-centered hyper-coordinate planar complexes using C_nB_m binary monocyclic rings as effective ligands, as indicated in the cases of the previously reported C_2v Y©B₆C₆⁺ and C_2v Sc©B₅C₆.¹⁴

Alkaline-earth metal centers in their perfect body-centered cubic carbonyl complexes O_h M(CO)₈⁺ (M = Ca, Sr, or Ba) in low-temperature neon matrixes have been confirmed to be honorary transition metals with effective M–(CO)₈ (π) coordination interactions.²¹ Similar M(d_π)–(CO)₈ (π) coordination bonds were predicted to exist in O_h M(CO)₈⁻ complexes (M = K, Rb) in which the alkaline metal centers K and Rb exhibit transition metal behaviours.²² Given the fact that alkaline metals possess the largest atomic radii in the periodical table²³ and have the potential to form complexes with transition metal behaviors, it is possible to form alkaline-metal-doped cyclo[n]carbon complexes (n ≥ 14) or their boron-substituted derivatives with CN ≥ 14 if the alkaline metal center and its ligand are chosen properly to match both geometrically and electronically.

Keeping the inspirations in mind, using the experimentally observed perfect planar ring-like D_9h C₁₈ and theoretically predicted D_7h C₁₄ as ligands and based on extensive global minimum searches augmented with first-principles theory calculations, we predict in this work the perfect planar alkaline-metal-centered D_9h Cs©C₁₈⁺ (1) and D_7h Na©C₁₄⁺ (4) which have the record coordination numbers of CN = 18 and 14 in planar species, respectively. Cs and Na with the atomic radii of r_Cs = 2.65 Å and r_Na = 1.86 Å ¹³ prove to match the D_9h C₁₈ and D_7h C₁₄ ligands perfectly both geometrically and electronically, respectively. Effective in-plane (π-s)σ, (π-p)σ, and (π-d)σ coordination bonds are formed to dominate the attractive interactions in these novel complexes in which the alkaline-metal centers exhibit transition metal behaviors. The iso-chemical shielding surfaces and out-of-plane π and in-plane σ ring current maps of the concerned species are computationally simulated to evidence their σ + π dual aromaticity.

2 Computational details

Extensive global-minimum (GM) searches were performed on Cs©C₁₈⁺, Na©C₁₄⁺, Cs©C₁₇B, Cs©C₁₇⁻, Na©C₁₃B, and Na©C₁₃⁻ using the TGmin2 code²⁴ at DFT level based on the basin-hopping algorithm.²⁵ Over 1000 stationary points were explored for each species at PBE/DZVP level employing the CP2K program.^26,27 The low-lying isomers were then fully optimized at both M06-2X and ωB97XD levels^28,29 with vibrational frequencies checked, with the aug-cc-pvtz basis set for C, B, Na, and K and Stuttgart relativistic small-core pseudopotentials^30,31 for Rb, Cs, and Fr, using the Gaussian16 program.³² The fact that M06-2X produces essentially the same polyynic D_9h C₁₈ and D_7h C₁₄ structures (Fig. S1†) as that obtained at the more accurate QMC and CCSD levels^9,10 evidences the reliability of the optimized geometries depicted in Fig. 1. Natural bond orbital (NBO) analyses were performed using NBO 7.0 program.³³ The energy decomposition analyses (EDA) together with the natural orbitals for chemical valence (NOCV) calculations, denoted as EDA-NOCV,^34–36 were carried out with the ADF program package³⁷ at M06-2X/TZ2P³⁸ level where scalar relativistic effects were considered for Cs using the zero order regular approximation (ZORA).³⁹ The frozen core approximation was not employed in EDA-NOCV computations. The overall interaction energy (ΔE_int) between two fragments is divided into three main terms: the electrostatic interaction energy (ΔE_elstat), Pauli repulsion (ΔE_Pauli), and orbital interaction energy (ΔE_orb) in eqn (1):

ΔE_int = ΔE_elstat + ΔE_Pauli + ΔE_orb. (1)

Fig. 1 Optimized structures of D_9h Cs©C₁₈⁺ (1), C_s Cs©C₁₇B (2), C_2v Cs©C₁₇⁻ (3), D_7h Na©C₁₄⁺ (4), C_2v Na©C₁₃B (5), and C_2v Na©C₁₃⁻ (6) at M06-2X level.

Detailed bonding analyses on D_9h Cs©C₁₈⁺ (1), D_7h Na©C₁₄⁺ (4), and C_s Cs©C₁₇B (2) were implemented using the adaptive natural density partitioning (AdNDP 2.0) approach^40,41 at the M06-2X/6-31G level, with the isosurface maps of the orbitals visualized using the Visual Molecular Dynamics (VMD) software.⁴² The iso-chemical shielding surfaces (ICSSs)^43,44 and isosurfaces of localized orbital locators (LOL)⁴⁵ were obtained with Multiwfn 3.8 code.⁴⁶ The anisotropy of the current-induced density (ACID) analyses were realized by the ACID code,⁴⁷ with the maps finally generated by POV-Ray render.⁴⁸

3 Results and discussions

3.1 Structures and stabilities

The optimized GM structures of D_9h Cs©C₁₈⁺ (1), C_s Cs©C₁₇B (2), C_2v Cs©C₁₇⁻ (3), D_7h Na©C₁₄⁺ (4), C_2v Na©C₁₃B (5), and C_2v Na©C₁₃⁻ (6) are collectively plotted in Fig. 1, with more alternative isomers summarized in Fig. S3–S8.† Fig. S2† depicts the optimized GM structures of (a) the alkaline-metal-centered cyclo[18]carbon complexes M©C₁₈⁺ with M = Li, Na, K, Rb, Cs, and Fr and (b) alkaline-metal-centered cyclo[14]carbon complexes M©C₁₄⁺ with M = Li, Na, and K at M06-2X. It is noticed that the alkaline metal atoms in the GMs are all located inside the cyclo[n]carbon rings, with the alkaline metal atoms severely off-centered in C_2v Li©C₁₈⁺, C_2v Na©C₁₈⁺, C_2v K©C₁₈⁺, and C_2v Li©C₁₄⁺ and slightly off-centered in C_s Rb©C₁₈⁺ and C_s Fr©C₁₈⁺. The K atom in C_7v K©C₁₄⁺ lies about 1.14 Å above the ligand plane along the C₇ molecular axis due to its large atomic radius (r_K = 2.32 Å) which appears to be too big to be hosted inside the C₁₄ ring.

Encouragingly, the Cs center with the NBO net atomic charge of q_Cs = +0.99 |e| proves to have the right atomic radius of r_Cs = 2.65 Å to be coordinated exactly at the center of the D_9h C₁₈ ligand in D_9h Cs©C₁₈⁺ (1) to achieve the highest coordination number of CN = 18 reported to date. As the well-defined GM of the complex (Fig. S3†), Cs©C₁₈⁺ (1) exhibits the alternating bond lengths of r_C–C = 1.343 Å and r_C≡C = 1.224 Å at M06-2X which are well inherited from its parent ligand D_9h C₁₈ ligand with r_C–C = 1.343 Å and r_C≡C = 1.223 Å at the same theoretical level (Fig. S1 and Table S1†).

The large calculated HOMO–LUMO gap of ΔE_gap = 5.38 eV at M06-2X well supports its high chemical stability. The second isomer C_2v Cs©C₁₈⁺ with a Cs⁺ located outside the C₁₈ ring and the seventh isomer C_2v Cs©C₁₈⁺ with a Cs⁺ inserted into the C₁₈ ring appear to be 0.38 eV and 4.79 eV less stable than D_9h GM at M06-2X, respectively (Fig. S3†). The slightly off-centered planar C_s Rb©C₁₈⁺ and C_s Fr©C₁₈⁺ also possess the coordination numbers of CN = 18 (Fig. S2†). Both the planar neutral C_s Cs©C₁₇B (2) which is isoelectronic with Cs©C₁₈⁺ (1) with obviously bond-length alternations and C_2v Cs©C₁₇⁻ (3) with roughly the same averaged bond lengths are the well-defined GMs of the systems with CN = 18 and 17, respectively (Fig. S4 and S5†). However, the severely off-centered C_2v Li©C₁₈⁺, C_2v Na©C₁₈⁺, and C_2v K©C₁₈⁺ with obvious smaller alkaline metal centers Li, Na, and K appear to have much smaller coordination numbers with CN = 4 ∼ 6 (Fig. S2†).

Similarly, the Na center with q_Na = +0.95 |e| appears to have the right atomic radius (r_Na = 1.86 Å) to be hosted exactly at the center of the D_7h C₁₄ ligand to form the perfect planar polyynic D_7h Na©C₁₄⁺ (4) (Fig. S6†) with CN = 14. The second lowest-lying isomer C_s Na©C₁₄⁺ with the Na⁺ center located outside the C₁₄ ring lies only 0.23 eV higher than Na©C₁₄⁺ (4) (Fig. S6†). The two close-lying lowest-lying isomers of Cs©C₁₈⁺ and Na©C₁₄⁺ discussed above (Fig. S3 and S6†) may transform between each other with low energy barriers under certain conditions. Na©C₁₄⁺ (4) as the GM of the system has the alternating bond lengths of r_C–C = 1.326 Å and r_C≡C = 1.240 Å at M06-2X well comparable with the corresponding values of r_C–C = 1.324 Å and r_C≡C = 1.237 Å calculated for D_7h C₁₄ at the same theoretical level (Fig. S1 and Table S1†), while Li with the atomic radius of r_Li = 1.52 Å proves to be too small and K with r_K = 2.32 Å appears to be too big to be hosted at the ring center of the C₁₄ ligand, they form severely off-centered and off-planed structures, respectively (Fig. S2†). With the HOMO–LUMO gap of ΔE_gap = 5.87 eV, Na©C₁₄⁺ (4) is expected to have a high chemical stability. The slightly off-centered planar C_2v Na©C₁₃B (5) with CN = 14 and vibrationally averaged C_2v Na©C₁₃⁻ (6) with CN = 13 with roughly the averaged bond lengths also appear to be the well-defined GMs of the systems (Fig. S7 and S8†).

As expected, the high-symmetry Cs©C₁₈⁺ (1) and Na©C₁₄⁺ (4) exhibit highly characteristic calculated vibrational spectroscopic features as shown in their simulated IR spectra in Fig. S9,† with the former possessing well characterized IR peaks at 513 and 2202 cm⁻¹ and Raman active vibrations at 1792 and 2293 cm⁻¹, respectively, while the latter having two well separated IR peaks at 545 and 2160 cm⁻¹ and one dominant Raman feature at 1252 cm⁻¹. Such well-defined spectral features can help facilitate future experimental characterizations of these species. Their simulated UV-vis spectra are also shown in Fig. S9† with 100 excited states included to better understand their electronic structures.

3.2 EDA-NOCV bonding scheme analyses

To shed insights into the bonding nature of D_9h Cs©C₁₈⁺ (1) and D_7h Na©C₁₄⁺ (4), detailed EDA-NOCV analyses were carried out at M06-2X/TZ2P. The D_3h subgroup was applied to D_9h Cs©C₁₈⁺ (1) because the highest point group supported by ADF program is D_8h. It was found that Cs⁺ and C₁₈ as the most possible reacting fragments give the most favourite orbital interaction energy of ΔE_orb = −13.95 kcal mol⁻¹ for Cs©C₁₈⁺ (1) in different fragmental schemes (Table S2†). They are thus chosen as interacting species to demonstrate the bonding scheme of Cs©C₁₈⁺ (1) in Fig. 2(a). Similarly, Na⁺ and C₁₄ as reacting fragments with ΔE_orb = −22.41 kcal mol⁻¹ are chosen for Na©C₁₄⁺ (4) in Fig. 2(b).

Fig. 2 (a) MO bonding scheme of D_3h Cs©C₁₈⁺ with the fragments of C₁₈ and Cs⁺ as interacting species and (b) MO bonding scheme of D_7h Na©C₁₄⁺ with C₁₄ and Na⁺ as interacting species at M06-2X/TZ2P-ZORA level.

The bonding molecular orbitals (MOs) 15a₁′, 19e₁′ and 20e₁′ of D_3h Cs©C₁₈⁺ representing covalent bonding MOs between Cs⁺ and C₁₈ are connected with the corresponding fragmental orbitals by bold dashed lines in Fig. 2(a), with the orbital compositions tabulated in Table S3.† The non-degenerate 15a₁′ mainly originates from the occupied 8a₁′ of C₁₈ with in-plane π characteristics (abbreviated as π_in) and vacant 6s of Cs⁺ via (π-6s)σ coordination interaction, the doubly degenerate 19e₁′ is composed of the occupied in-plane 13e₁′ (π_in) of C₁₈ with one nodal plane and vacant 7p_x and 7p_y of Cs⁺ via (π-7p)σ coordination, while the doubly degenerate 20e₁′ is composed of the occupied 14e₁′ of C₁₈ with π_in characteristics with two nodal planes and vacant 5d_xy and 5d_x²–y² of Cs⁺ via (π-5d)σ coordination. As detailed in Table 1, EDA analyses demonstrate that the overall interaction energy of ΔE_int = −15.22 kcal mol⁻¹ between the Cs⁺ and C₁₈ in Cs©C₁₈⁺ consists of the Pauli repulsion ΔE_Pauli = 1.89 kcal mol⁻¹, coulombic attraction ΔE_elstat = −3.16 kcal mol⁻¹, and orbital interaction ΔE_orb = −13.95 kcal mol⁻¹, with covalent orbital interaction making a dominating contribution of 81.5% to the overall attraction interaction (−17.11 kcal mol⁻¹), while electrostatic attraction contributing only 18.5%. The decompositions of the orbital interactions ΔE_orb into pairwise contributions between occupied and vacant MOs of the fragments provide quantitative insight into the charge flow. The strongest orbital interaction ΔE_orb(1) (20e₁′, 27.5%) arises mainly from [C₁₈ (π_in)] → [Cs⁺ (5d)] where C₁₈ serves as a π_in-donor to coordinate the 5d_xy and 5d_x²–y² orbitals of the Cs⁺ as σ-acceptors. The orbital interaction ΔE_orb(2) (19e₁′, 16.8%) originates from [C₁₈ (π_in)] → [Cs⁺ (7p)] where the 7p_x and 7p_y orbitals of the Cs⁺ serve as σ-acceptors. The orbital interaction ΔE_orb(3) (15a₁′, 14.1%) originates from [C₁₈ (π_in)] → [Cs⁺ (6s)] where the 6s orbital of the Cs⁺ is a σ-acceptor. Fig. S10† shows the corresponding deformation densities Δρ associated with the pairwise interactions ΔE_orb(1), ΔE_orb(2) and ΔE_orb(3) in Cs©C₁₈⁺, further indicating that C₁₈ serves as a π_in-donor while Cs⁺ is a σ-acceptor in the complex.

Table 1 EDA-NOCV results for Cs©C₁₈⁺ (1) and Na©C₁₄⁺ (4) at the M06-2X/TZ2P-ZORA level, taking C₁₈ with Cs⁺ and C₁₄ with Na⁺ as interacting fragments, respectively. Energy values are given in kcal mol⁻¹

Energy terms	Interaction	Cs^+ + C18	Interaction	Na^+ + C14
a The value in parentheses gives the percentage contribution to the total attractive interactions (ΔEelstat + ΔEorb).b The value in parentheses gives the percentage contribution to the total orbital interaction (ΔEorb).
ΔEint		−15.22		−24.44
ΔEelstat^a		−3.16 (18.5%)		−1.42 (6.0%)
ΔEPauli		1.89		3.45
ΔEorb^a		−13.95 (81.5%)		−22.41 (94.0%)
ΔEorb(1)^b	C18 (πin) donation → [Cs^+ (5d)]	−3.84 (27.5%)	C14 (πin) donation → [Na^+ (3p)]	−5.58 (24.9%)
ΔEorb(2)^b	C18 (πin) donation → [Cs^+ (7p)]	−2.34 (16.8%)	C14 (πin) donation → [Na^+ (3s)]	−4.30 (19.2%)
ΔEorb(3)^b	C18 (πin) donation → [Cs^+ (6s)]	−1.96 (14.1%)	C14 (πin) donation → [Na^+ (3d)]	−4.06 (18.1%)
ΔEorb(rest)^b		−5.81 (41.6%)		−8.47 (37.8%)

---

Detailed EDA-NOCV calculations for D_7h Na©C₁₄⁺ (4) gives a similar trend as shown in Fig. 2(b) and Table 1. The bonding MOs 6a₁′, 6e₁′ and 5e₂′ representing covalent bonding interactions between the Na⁺ and C₁₄ fragmental orbitals are connected by bold dashed lines, with the orbital compositions listed in Table S4.† The 6a₁′ mainly originates from the occupied 4a₁′ of C₁₄ with π_in characteristics and vacant 3s of Na⁺ via (π-3s)σ coordination interaction, the doubly degenerate 6e₁′ is composed of occupied 5e₁′ of C₁₄ with π_in characteristics and vacant 3p_x and 3p_y of Na⁺ via (π-3p)σ coordination, while the 5e₂′ is composed of C₁₄ with π_in characteristics and vacant 3d_xy and 3d_x²–y² of Na⁺ via (π-3d)σ coordination.

EDA analyses (Table 1) indicate that overall attraction interaction is overwhelmingly dominated by covalent orbital contribution (94.0%), while electrostatic attraction makes only a marginal contribution (6.0%). The decompositions of ΔE_orb into pairwise contributions between occupied and vacant MOs of the fragments reveals that the strongest orbital interaction ΔE_orb(1) (24.9%) originates mainly from [C₁₄ (π_in)] → [Na⁺ (3p)], the orbital interaction ΔE_orb(2) (19.2%) arises mainly from [C₁₄ (π_in)] → [Na⁺ (3s)], while the orbital interaction ΔE_orb(3) (18.1%) originates from [C₁₄ (π_in)] → [Na⁺ (3d)]. The corresponding deformation densities Δρ associated with the pairwise interactions ΔE_orb(1), ΔE_orb(2) and ΔE_orb(3) in Na©C₁₄⁺ in Fig. S11† clearly indicate that C₁₄ serves as a π_in-donor while Na⁺ is a σ-acceptor.

The EDA-NOCV results detailed above quantitatively indicate that the cyclo[4N + 2]carbon ligands (N = 4, 3) serve as good π_in-donors to stabilize alkaline metal centers in both Cs©C₁₈⁺ (1) and Na©C₁₄⁺ (4) by donating their π_in valence electrons partially to the vacant s, p, and d orbitals of Cs⁺ and Na⁺ through effective in-plane (π-s)σ, (π-p)σ, and (π-d)σ coordination interactions.

Localized orbital locator (LOL) is an effective space function in revealing the distributions of delocalized electrons on conjugated rings in molecules. We calculated in-plane LOL-σ, in-plane LOL-π_in, and out-of-plane LOL-π_out separately based on the corresponding in-plane σ MOs, in-plane π MOs, and out-of-plane π MOs of the systems, respectively. To better reflect spatial distributions of LOL-σ, LOL-π_in, and LOL-π_out in Cs©C₁₈⁺ (1) and Na©C₁₄⁺ (4), the color-filled maps of LOL-σ on the ring plane, LOL-π_in on the ring plane, and LOL-π_out 1 Å above the ring plane are plotted in Fig. 3(a) and (b) comparatively. By comparing the area colors on the maps, it can be clearly seen that both LOL-π_in and LOL-π_out exhibit heavy density distributions over the short C≡C bonds and light density distributions over the long C–C bonds, well supporting the alternating of triple and single bonds in different bond lengths in both polyynic Cs©C₁₈⁺ (1) and Na©C₁₄⁺ (4).

Fig. 3 Color-filled maps of the localized orbital locator isosurfaces of (a) D_9h Cs©C₁₈⁺ (1) and (b) D_7h Na©C₁₄⁺ (4) and AdNDP bonding patterns of (c) D_9h Cs©C₁₈⁺ (1) and (d) D_7h Na©C₁₄⁺ (4) with the occupation numbers (ON) indicated.

3.3 AdNDP bonding pattern analyses

Detailed AdNDP analyses in Fig. 3(c) and (d) unveil both the localized and delocalized bonds in D_9h Cs©C₁₈⁺ (1) and D_7h Na©C₁₄⁺ (4) more vividly. As expected, out of the 72 valence electrons in Cs©C₁₈⁺ (1), 36 electrons form 18 equivalent 2c–2e C–C peripheral in-plane σ bonds with the occupation numbers of ON = 2.00 |e|. The remaining 36 valence electrons are distributed in two types of chemical bonds, including 9 equivalent in-plane 3c–2e σ bonds on nine CsC₂ triangles with ON = 1.83 |e| and 9 equivalent out-of-plane 2c–2e C–C π bonds with ON = 1.83 |e|, respectively. Such a bonding pattern follows the 4N + 2 aromatic rule for σ aromaticity with N_σ = 4 and π aromaticity with N_π = 4, respectively, making the planar complex σ + π dually aromatic in nature and rendering extra stability to the system, similar to the situation in the previously reported D_9h C₁₈.¹¹

Similarly, as shown in Fig. 3(d), D_7h Na©C₁₄⁺ (4) possesses 7 equivalent 2c–2e C–C periphery in-plane σ bonds, 7 equivalent 3c–2e in-plane σ bonds on seven NaC₂ triangles, and 7 equivalent 2c–2e out-of-plane C–C π electrons, again following the 4N + 2 aromatic rule with N_σ = N_π = 3 for σ + π dual aromaticity. Similar bonding patterns exist in C_s Cs©C₁₇B (2) (Fig. S12†). The dual aromaticities of both Cs©C₁₈⁺ (1) and Na©C₁₄⁺ (4) are also well supported by numbers of their delocalized in-plane σ MOs and delocalized out-of-plane π MOs shown in Fig. S13.†

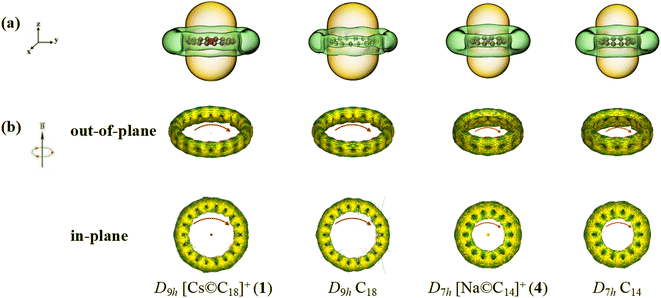
The simulated ICSS isosurfaces of D_9h Cs©C₁₈⁺ (1) and D_7h Na©C₁₄⁺ (4) based on the ZZ components of the calculated nuclear-independent chemical shifts (NICS-ZZ) are presented as Fig. 4(a), in comparison with that of the previously reported σ + π dually aromatic D_9h C₁₈ and D_7h C₁₄. It can be clearly seen that, similar to D_9h C₁₈ and D_7h C₁₄, both D_9h Cs©C₁₈⁺ (1) and D_7h Na©C₁₄⁺ (4) are aromatic in nature, with the spaces inside the cyclo[n]carbon rings and within ∼1.0 Å above the ring planes belonging to chemical shielding areas with negative NICS-ZZ values (highlighted in yellow) and the blet-like regions around the cyclo[n]carbon rings in horizontal direction belonging to chemical deshielding areas with positive NICS-ZZ values (highlighted in green).

Fig. 4 (a) Calculated iso-chemical shielding surfaces (ICSSs) of D_9h Cs©C₁₈⁺ (1), D_9h C₁₈, D_7h Na©C₁₄⁺ (4), and D_7h C₁₄. Yellow and green regions stand for chemical shielding and deshielding areas, respectively. (b) Calculated out-of-plane-π and in-plane-σ ring current maps of D_9h Cs©C₁₈⁺ (1) and D_7h Na©C₁₄⁺ (4), compared with the corresponding ring current maps of D_9h C₁₈ and D_7h C₁₄, respectively. The external magnetic field is perpendicular to the ring plane. The red arrows indicate the directions of the ring currents on the ACID iso-surfaces.

The widely used ACID method can be employed to display graphically the ring currents induced by an external magnetic field in vertical directions perpendicular to the cyclo[n]carbon ring. Fig. 4(b) presents the calculated out-of-plane π and in-plane σ ring currents maps for both D_9h Cs©C₁₈⁺ (1) and D_7h Na©C₁₄⁺ (4), in comparison with the corresponding ring currents obtained for D_9h C₁₈ and D_7h C₁₄ at the same theoretical level, respectively. As clearly indicated in Fig. 4(b), these alkaline-metal-centered polyynic complex monocations do possess intrinsic σ aromaticity and π aromaticity simultaneously, similar to their neutral parent ligands D_9h C₁₈ and D_7h C₁₄ in ring current distributions.

4 Conclusions

In summary, based on extensive first-principles theory calculations, we have predicted in this work a series of alkaline-metal-centered perfect planar complexes Cs©C₁₈⁺ (1), Cs©C₁₇B (2), Cs©C₁₇⁻ (3), Na©C₁₄⁺ (4), Na©C₁₃B (5), and Na©C₁₃⁻ (6) which turn out to be GMs of the systems with the record coordination numbers of CN = 18 ∼ 13 in planar species. These hyper-coordinate planar complexes possess effective in-plane (π-s)σ, (π-p)σ, and (π-d)σ coordination interactions which dominate the attractive interaction between the alkaline metal center as σ-acceptor and its cyclo[n]carbon ligand as in-plane π-donor, evidencing the transition metal behaviors of the alkaline metal centers in them. Similar to the situation in the recently observed alkaline-earth metal carbonyl species,²¹ the proposed perfect planar alkaline-metal-centered polyynic D_(2N+1)h cyclo[4N + 2]carbon complexes with relatively low coordination energies may be produced in gas phases by laser ablation of alkaline-metal-carbon mixed binary targets and characterized by spectroscopic measurements at low temperatures to further push the boundary of coordination chemistry.

Author contributions

S. D. Li, Z. H. Wei, and Q. Chen conceived the project and finalized the manuscript. M. Z. and R. N. Y. did the calculations and prepared the first draft. Y. B. Wu helped analyze the data. All authors approved the final version.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The work was supported by the National Natural Science Foundation of China (21973057, 21720102006 and 22003034) and Natural Science Foundation of Shanxi Province of China (20210302124002).

Notes and references

1. H. W. Kroto, J. R. Heath, S. C. O'Brien, R. F. Curl and R. E. Smalley, Nature, 1985, 318, 162–163.
2. S. Iijima and T. Ichihashi, Nature, 1993, 363, 603–605.
3. K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Science, 2004, 306, 666–669.
4. K. Kaiser, L. M. Scriven, F. Schulz, P. Gawel, L. Gross and H. L. Anderson, Science, 2019, 365, 1299–1301.
5. G. von Helden, N. G. Gotts and M. T. Bowers, Nature, 1993, 363, 60–63.
6. Y. Rubin, M. Kahr, C. B. Knobler, F. Diederich and C. L. Wilkins, J. Am. Chem. Soc., 1991, 113, 495–500.
7. A. E. Boguslavskiy, H. Ding and J. P. Maier, J. Chem. Phys., 2005, 123, 034305.
8. A. E. Boguslavskiy and J. P. Maier, Phys. Chem. Chem. Phys., 2007, 9, 127–130.
9. T. Torelli and L. Mitas, Phys. Rev. Lett., 2000, 85, 1702–1705.
10. S. Arulmozhiraja and T. Ohno, J. Chem. Phys., 2008, 128, 114301.
11. Z. y. Liu, X. Wang, T. Lu, A. h. Yuan and X. f. Yan, Carbon, 2022, 187, 78–85.
12. Y. h. Jiang, Y. b. Wu, J. j. Deng and Z. y Wang, Phys. Chem. Chem. Phys., 2021, 23, 8817–8824.
13. J. A. Dean, Lange's Handbook of Chemistry, McGraw-Hill Book Co., 15th edn, 1999.
14. X. Q. Lu, H. G. Lu and S. D. Li, RSC Adv., 2021, 11, 27193–27198.
15. T. Heine and G. Merino, Angew. Chem., Int. Ed., 2012, 51, 4275–4276.
16. T. R. Galeev, C. Romanescu, W. L. Li, L. S. Wang and A. I. Boldyrev, Angew. Chem., Int. Ed., 2012, 51, 2101–2105.
17. C. Romanescu, T. R. Galeev, W. L. Li, A. I. Boldyrev and L. S. Wang, Angew. Chem., Int. Ed., 2011, 50, 9334–9337.
18. C. Romanescu, T. R. Galeev, W. L. Li, A. I. Boldyrev and L. S. Wang, J. Chem. Phys., 2013, 138, 134315.
19. W. L. Li, C. Romanescu, T. R. Galeev, Z. A. Piazza, A. I. Boldyrev and L. S. Wang, J. Am. Chem. Soc., 2012, 134, 165–168.
20. C. Romanescu, T. R. Galeev, W. L. Li, A. I. Boldyrev and L. S. Wang, Acc. Chem. Res., 2013, 46, 350–358.
21. X. Wu, L. L. Zhao, J. Y. Jin, S. D. Pan, W. Li, X. Y. Jin, G. J. Wang, M. F. Zhou and G. Frenking, Science, 2018, 361, 912–916.
22. H.-R. Li, X.-Q. Lu, Y.-Y. Ma, Y.-W. Mu, H.-G. Lu, Y.-B. Wu and S.-D. Li, J. Clust. Sci., 2019, 30, 621–626.
23. J. A. Dean, Lange's handbook of Chemistry, McGraw-Hill Book Co, 15th edn, 1999.
24. X. Chen, Y.-F. Zhao, Y.-Y. Zhang and J. Li, J. Comput. Chem., 2019, 40, 1105–1112.
25. D. J. Wales and H. A. Scheraga, Science, 1999, 285, 1368–1372.
26. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
27. J. VandeVondele, M. Krack, F. Mohamed, M. Parrinello, T. Chassaing and J. Hutter, Comput. Phys. Commun., 2005, 167, 103–128.
28. Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241.
29. J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615.
30. D. Feller, J. Comput. Chem., 1996, 17, 1571–1586.
31. L. Schuchardt, B. T. Didier, T. Elsethagen, L. Sun, V. Gurumoorthi, J. Chase, J. Li and T. L. Windus, J. Chem. Inf. Model., 2007, 47, 1045–1052.
32. M. J. Frisch, Gaussian 16, Revision A.03, Gaussian Inc., Wallingford, CT, 2016.
33. E. D. Glendening, C. R. Landis and F. Weinhold, J. Comput. Chem., 2019, 40, 2234–2241.
34. T. Ziegler and A. Rauk, Theor. Chim. Acta, 1977, 46, 1–10.
35. M. Mitoraj and A. Michalak, Organometallics, 2007, 26, 6576–6580.
36. M. P. Mitoraj, A. Michalak and T. Ziegler, J. Chem. Theory Comput., 2009, 5, 962–975.
37. G. te Velde, F. M. Bickelhaupt, E. J. Baerends, C. Fonseca Guerra, S. J. A. van Gisbergen, J. G. Snijders and T. Ziegler, J. Comput. Chem., 2001, 22, 931–967.
38. E. Van Lenthe and E. J. Baerends, J. Comput. Chem., 2003, 24, 1142–1156.
39. E. van Lenthe, E. J. Baerends and J. G. Snijders, J. Chem. Phys., 1993, 99, 4597.
40. D. Y. Zubarev and A. I. Boldyrev, Phys. Chem. Chem. Phys., 2008, 10, 5207–5217.
41. N. V. Tkachenko and A. I. Boldyrev, Phys. Chem. Chem. Phys., 2019, 21, 9590–9596.
42. W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graph., 1996, 14, 33–38.
43. S. Klod and E. Kleinpeter, J. Chem. Soc., Perkin Trans., 2001, 2, 1893–1898.
44. E. Kleinpeter, S. Klod and A. Koch, J. Mol. Struct., 2007, 811, 45–60.
45. H. L. Schmider and A. D. Becke, J. Mol. Struct. (THEOCHEM), 2000, 527, 51–61.
46. T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592.
47. D. Geuenich, K. Hess, F. Köhler and R. Herges, Chem. Rev., 2005, 105, 3758–3772.
48. Povray, Persistence of vision raytracer, POV-Ray 3.7, https://www.povray.org/.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ra03930g

---