Open Access Article
Open Access ArticleAnalytical study of gold–DNA nano core–shell cloaking characteristics for drug delivery and cancer therapy
Nahid Osanloo a,
Vahid Ahmadi
a,
Vahid Ahmadi *b,
Mohammad Naser-Moghaddasia and
Elham Darabic
*b,
Mohammad Naser-Moghaddasia and
Elham Darabic
aFaculty of Engineering, Science and Research Branch, Islamic Azad University, Tehran, Iran
bDepartment of Electrical and Computer Engineering, Tarbiat Modares University, Tehran, Iran. E-mail: v_ahmadi@modares.ac.ir
cPlasma Physics Research Center, Science and Research Branch, Islamic Azad University, Tehran, Iran
First published on 1st August 2023
Abstract
The cloaking characteristics of biocells can be considered as a factor to determine drug absorption by the tissues. The metal–organic core–shell structure can act as a cloak around the molecules of tissue and can be used as a nanomachine for drug delivery. Thus, we define a ratio of drug absorption based on frequency red-shift and the effective permittivity in the optical spectrum. Here, a cylinder of molecules coated by plasmonic nano core–shells is proposed for measuring the cloaking characteristics of biocells. The overall bandwidth of the proposed cloak for reflectance less than −10 dB is 36%. We check the effect of the filling factors of nanoparticles on the reflection and the frequency response of the tissue. Besides the frequency red-shift and change in the level of reflection, the phase and impedance are extracted. We could obtain the normalized scattering cross-section of 5 dB lower than the cylinder without cloak for the cylinder with a gold–DNA core–shell cloak. Here, we modify the Maxwell-Garnett equation for a cylindrical structure to obtain the effective value of the permittivity for cancer and normal tissues. The results show that obtained permittivity from the simulation has a good match with the calculated permittivity from the Maxwell-Garnet equation. Therefore, this approach can be considered as an efficient method for drug absorption and diagnosis of cancer cells from normal cells.
Introduction
A metamaterial is known as a macroscopic composite with a periodic or non-periodic structure, and possesses unique characteristics that is not found in nature, such as negative permittivity and permeability and negative refractive index.1,2 The advancement in metamaterial science and technology has given rise to some interesting applications such as invisibility cloaks.3,4Invisibility cloaks can manipulate the interaction between electromagnetic fields and matter, redirecting electromagnetic waves around the cloaked object,5 so that the total scattering cross-section of the cloaked object is reduced.6 Numerous techniques and formations have been noticed to suppress or divert the scattering of objects and improve the cloaking quality and bandwidth in different frequency regions, including microwave7 and terahertz (THz) regions,8 infrared, optics, acoustics, etc.9
For instance, Schurig et al. developed the split ring resonator for microwave applications,10 a method later expanded by Wang et al. to exhibit dual-band characteristics.11 Additionally, other structures such as photonic band-gap structures have been employed in microwave applications.12
The cloaks have been developed in the optical spectrum where the nanoparticles in several shapes have been noticed based on plasmonic attributes.13,14 Recently plasmonic spherical15 and plasmonic Rods16 have been studied for reducing the radar cross-section by various placements of the nanoparticles. In addition, the composition and disposition of the nanoparticle in the PMMA layer were suggested for the design of the cylindrical cloak.17
When the light is incident to metal in the optical spectrum, the light photon energy is absorbed by the electron of the metal.18,19 In this case, the electron has a charge and energy named polaritons. These polaritons propagate at the interface between the metal and air or metal and dielectric and cause oscillations of the metal's plasma.20 Surface plasmon polaritons (SPPs) waves are the surface waves that result from the interaction of incident field and subwavelength metal at the optical regime.21 Polaritons which are free electrons of metal have absorbed the energy of the incident photon and propagate at the metal–dielectric or metal–air interface. These polaritons cause oscillations of the metal's plasma, and the metal is modeled by Palik and Johnson.22 The surface charge density oscillations due to surface plasmons can cause to enhance optical near-fields strongly in the space above the surface. This characteristic is noticed in designing optical subwavelength devices such as nano-antenna,23 optical nano filter,24 and optical coupler.25
Plasmonic nanoparticles can confine the light, so the absorption of light is increased. Therefore, they are noticeable for perfect absorbers based on metamaterials that have attracted considerable interest.26 Perfect absorbers can eliminate multipath reflections due to different interfaces and enhance absorption, reradiating an out-of-phase wave from surface currents.27 One of the applications of absorbers is in radar-absorbing coatings28 to reduce the reflectance and scatter the radar signals away.29
THz metamaterial based gold–DNA nano core–shells cloaking can be used as a very promising technique in the field of bionanotechnology. This new method can be employed in various applications such as drug delivery and optical imaging. The gold–DNA nano core–shells can act as a highly efficient targeted drug delivery system. The protein coating acts as a protective layer on the gold nanosphere and increases its stability and biofriendliness. These nanospheres are able to accurately carry drugs to the target cells in the body. This method allows the controlled release of the drug at the stimulated site and makes available the improvement of various treatment methods. Also, these nanoparticles with extremely small sizes are suitable for molecular imaging. They can target specific molecules or tissues of interest and emit signals that make them promising for the enhancement of molecular imaging.
Analytical study of phase and impedance, along with frequency change, reflection level, and electrical permittivity, are used as criteria to determine the amount of drug absorption and distinguish healthy cells from cancer in optical imaging. One of the advantages of this work compared to previous researches is that we have focused on the study of the effect of the coating ratio on the absorption rate, and this can have a significant improvement in the efficiency and control of the drug used. Also, in the past researches, mostly gold nanoparticles have been used as a hiding agent, but our examination of the advantages in this field shows that the use of gold nanospheres with protein coating has the ability to absorb and emit light. These properties allow us to utilize these nanospheres as optical contrast agents in vector images. This innovation can lead to significant improvements in detection accuracy and advancements in light-based imaging technologies.
By acting as a cloak, the gold–DNA nano core–shells are designed to protect and deliver therapeutic agents such as drugs to specific targets, while providing real-time information about the treatment response. These simultaneous capabilities enhance the overall efficiency of nano-theranostics. This integrated approach of combining diagnostics and therapeutics into a single system holds great promise for targeted drug delivery, allowing for more precise and effective treatments such as the determination of drug absorption ratio.
Recently, drug delivery methods have been developed for treating cancer tissue based on nanoparticles.30,31 Many researches have been done about nanoparticle shape32 and their effect on the spectroscopy response based on different factors such as nanoparticle size.33,34 Various techniques have been studied to realize the ratio of absorption of the drugs by the cancer tissue in the microwave35 and optical spectrum based on impedance.36,37
Based on the transformation optics technique, a special coat can manipulate the electromagnetic wave. So, this behavior can be considered for measuring drug absorption by tissues. Here, we present a coat for the cylindrical object and examine the effect of the coat's permittivity on reflection for both TE and TM modes. In TE (Transverse Electric) mode, all the electric field lines are perpendicular to the plane of the incident wave and the magnetic field is zero. In TM (Transverse Magnetic) mode, all the magnetic field lines are perpendicular to the plane of the incident wave and the electric field is zero.
The coat's permittivity impacts both reflection level and frequency. Thus, this coat can be designed by nanoparticles at the optical spectrum using the plasmonic characteristic as discussed by Alu et al.38–40 The cancer cells or organic elements in the human body can be assumed as cylindrical object as shown in this paper. The nanoparticles with the organic coat can be supposed as nanomachines for drug delivery.41 So, the absorption of this organic coat is assumed to correspond to drug absorption. The absorption and reflection of the object can be changed by the size of the nanoparticles or the number of these nanoparticles. Therefore, the filling factor can impact permittivity based on the Maxwell-Garnet equation and we can recognize how much the drugs are absorbed by the tissue. In addition, based on the transmission and reflection, the impedance of the coated element can be obtained which shows the ratio of the absorption of the drug. Also, the phase variation is checked for structures to increase recognition accuracy. So, the simulations prove that the filling factor's effects on frequency shift and absorption are more than the arrangement of the nanoparticle, and this nanoparticle placement are selected randomly and studied for TE and TM modes. In short, these studies reveal the drug delivery relation with cloaking which is important for accurately detecting and treating cancer cells.
Theory of optical cloaking
Transformation method for cylindrical objects
The optical transformation method for the cylindrical coordinates is used for designing the homogeneous cylindrical cloak as described by.42,43 Maxwell's equations in the original space are
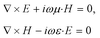 | (1) |
| x′ = x′(x) | (2) |
Maxwell's equations in the new coordinate system become
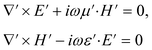 | (3) |
| E′(x′) = (ΛT)−1E(x); H′(x′) = (ΛT)−1H(x) | (4) |
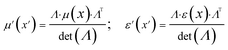 | (5) |
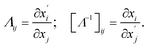 | (6) |
The transformation matrix has been presented for the cylindrical cloak. It is in the two dimensions normal to the cylinder's axis and has been oriented from Jacobian transformation based on converting virtual and physical spaces. The transformation for a cylindrical cloak is an identity along the z-axis; hence the coordinate transformation is in the xoy plane. Spatial transformation in the Cartesian coordinates is
 | (7) |
Then the transformation matrix oriented from Jacobian based on converting virtual and physical spaces is
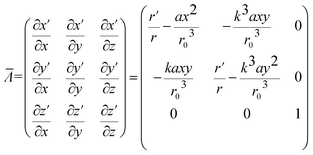 | (8) |
 ,
,  . Or written in a closed-form expression:
. Or written in a closed-form expression:
 | (9) |
Therefore relative permittivity and permeability tensors for the cloaking shell can be obtained by eqn (5) and (8).
 | (10) |
The material parameters are43
 | (11) |
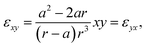 | (12) |
 | (13) |
 | (14) |
Plasmonic material
For determining the localized surface plasmon resonance (LSPR), the Drude model can be used as
 | (15) |
In this research, plasmonic gold nanoparticles are considered as nanoelectronic materials for their superior features. Gold nanoparticles, because of their biocompatibility, chemical stability, sharp plasmonic resonance frequency, and favorable dielectric function can be used in optical imaging, and therapeutic applications, for example, in some hyperthermia methods or cancer treatment.
Simulation and the results
Simulation method
Various types of core–shell structures in previous studies have been examined based on the shell of DNA rods. The main problem with the core–shell structures is that they are analyzed in the fluid phase. However, DNA-based core–shells have the ability to crystallize, and on the other hand, DNA rods around the sphere structure prevent the spaces from being empty and the physical contact of the spheres. We determine the effect of DNA filling space on permittivity and investigate the effect of different percentages of filling and arrangement geometry on conductivity. We investigate the effect of DNA for different filling factors, on the frequency response. We use the Maxwell-Garnett model to compare with the simulation results.The arrays of gold–DNA core–shells can be used for cloaking. We analyze the structures using two ports model in the CST Microwave Studio software in the time domain solver with hexahedral mesh. Finite Integration Technique (FIT) in CST has high analysis speed. Due to the more accurate mesh generation, the FIT method is used to solve Maxwell's equations efficiently and fast. This technique is very efficient, especially in small dimensions and curved objects, and analyzes complex models optimally and quickly. Here, a waveguide port is used for excitation on both sides of the nanosphere. Boundary conditions are assumed to be perfect conductive (PEC) in the X-direction and fully magnetic conductive (PMC) in the Y-direction, and in the Z-direction, we use open and space conditions.
Nanosphere without coat
Fig. 1 shows how much the permittivity can be controlled by changing the radius, and this helps us to design broadband structures and modify the nanosphere for cloak layers. In Fig. 1(a) the nanosphere is excited by using two-port excitation. As Fig. 1(b) shows, radius variations cause a change in the frequency response. At a radius of 50 nm, the maximum permittivity will be about 30. As can be seen, increasing the radius reduces the resonance frequency. These variations help to adjust the resonance frequency in the designs. So that for a maximum radius of 45 nm, it is at 240 THz but for 60 nm it is at 170 THz. | ||
| Fig. 1 (a) The nanosphere excited by using two-port excitation (b) the effect of the radius of the nanosphere on permittivity. | ||
Nanosphere with DNA coat
In the second part, we assume a thin rod of DNA with a height of 20 nm and a radius of 2.5 nm in the crystal form as a coat on the nanosphere (Fig. 2(a)). For DNA, we considered two factors, electrical conductivity, and permittivity, and studied their variation effect on the effective permittivity. In the optical spectrum, the permittivity of the DNA rods can be assumed 1 to 1.2,45 and we assume 1.1 in the final analysis. And in Fig. 2(b) a comparison of different permittivity shows that it has no particular effect on the effective permittivity frequency response. The second parameter is considered to be conductivity. DNA conductivity can be controlled by the amount of silver and gold combined with DNA rods, and different values have been reported in previous research.46 Therefore, in Fig. 2(c) we examined the proposed structure for different conductivities of 10, 100, 1000, and 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000. As shown in Fig. 2(c) the results for 10, 100, and 1000 are very close to each other, but when the value 100
000. As shown in Fig. 2(c) the results for 10, 100, and 1000 are very close to each other, but when the value 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 is selected, the switching mode is visible in the structure. Here we consider the on or low impedance state to be 1000 and the off or high impedance state to be 100
000 is selected, the switching mode is visible in the structure. Here we consider the on or low impedance state to be 1000 and the off or high impedance state to be 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000, which is usually reported for DNA structures with an impedance ratio in the range of a few hundred.47
000, which is usually reported for DNA structures with an impedance ratio in the range of a few hundred.47
Design of plasmonic cloak
In this section, the nanosphere array and the coated nanosphere are used for cloaking, and the goal is to use the cylindrical cloak around the dielectric cylinder structure in the previous research on silica rods with a permittivity of 2.1.39 In addition, nanorods of polymer with various lengths have been used for detecting and trapping breast cancer cells. Thus, in the first simulations, the refractive index of the rod is assumed to be 2 which is near to the refractive index of polymer and finally the rod is replaced with normal and cancer tissues. Fig. 3 shows the three structures of the object without a cloak, an object with a nanosphere cloak, and finally the object with the gold–DNA core–shell cloak.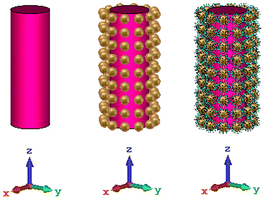 | ||
| Fig. 3 The object (a) without a cloak, (b) with a gold nanosphere cloak and (c) with gold–DNA core–shell cloak. | ||
The proposed structure with nanosphere coat and nanosphere with DNA coat is examined for two modes of TM and TE, and results are shown in Fig. 4(a–d). For TM mode in Fig. 4(a), the reflection for the structure with the nanosphere coat shows dual band characteristics at 147.8 and 177.2 THz. But, the structure with core–shell cloak has only one resonance at 160.3 THz. In addition, the core–shell structure provides lower reflection from the object in comparison with the nanosphere coat and this value is about −6 dB. The bandwidth below −10 dB is about 35% (from 132 to 189 THz). For the TE mode in Fig. 4(b), the reflection has one resonance at 173.4 THz. In this mode, the bandwidth below −10 dB is about 36% (from 141 to 205 THz) for the gold–DNA core–shell coat.
Transmission of simple object, object with nanosphere coat, and with gold–DNA core–shell coat in their resonance frequencies in TM and TE modes are compared in Fig. 4(c) and (d), respectively. As can be seen, the transmission of the object with nanosphere coat and with gold–DNA core–shell coat in their resonance frequencies increases nearly to 0 dB. This transmission increment besides the reflection decrement shows that these coats decrease the absorption according to the relation of A = 1 − T − R where R is reflection, T transmission, and A absorption. This absorption of near zero can cloak the object coated with gold–DNA core–shell.
In Fig. 5(a) and (b), the reflections are examined for object covered with nanosphere cloak for various filling factors for TM and TE modes, respectively. As shown in Fig. 5(a), by increasing the number of nanosphere in the coating layer, the resonance shifts to a lower frequency. This resonance red-shift can be attributed to the increase of capacitance due to the presence of more nanosphere in the coat of structure in TM mode. For lower filling factor structure which there is the possibility of different orientations of nanospheres, we observe that there are different resonance frequencies for the nanosphere coat (as can be seen for the 66% structures). However, when we use gold–DNA core–shells there is no difference between the resonance frequency of different 66% types (as can be seen in Fig. 6(a) and (b)). In Fig. 6, the reflections are examined for the object covered with gold–DNA core–shell cloak for various filling factors for TM and TE modes, respectively. Therefore, the resonance frequency of the gold–DNA core–shell cloak in these structures is independent of the nano core–shells arrangement.
 | ||
| Fig. 5 Reflection of the object covered with nanosphere cloak for various filling factors for two modes (a) TM and (b) TE mode. | ||
 | ||
| Fig. 6 Reflection of the object covered with core–shell cloak for various filling factors for two modes (a) TM and (b) TE (c) two different types for filing factor of 66% (type 1 and type 2). | ||
Fig. 7 compares power flow distribution for the bare structure without and with 100% nanosphere cloak and with 100% core–shell cloak at 173.4 THz. As shown in Fig. 7(a), the bare cylinder disrupts the flow in the absence of the cloak layer. However, by using the cloak structure, this drawback has been eliminated and the comparison of Fig. 7(b) and (c) shows us that the structure with gold–DNA core–shell has helped to improve the uniformity of the power flow distribution, especially in corners that are sensitive. There is a strong backscattering for bare cylinder. However, for the cloaked cylinder, this backscattering is reduced properly. So, we consider the object covered with gold–DNA core–shell cloak as the selected cloak structure.
 | ||
| Fig. 7 The power flow for (a) the object without cloak layer (b) the object with nanosphere cloak (c) the object with core–shell cloak. | ||
To further confirm the selected gold–DNA core–shell cloak, the scattering cross-section for the proposed cylinder is examined and compared with a bare cylinder. The results are presented in Fig. 8. In this case the structure is illuminated by a TMz-polarized plane wave. As can be observed, at the resonance frequency of 177.2 THz, the cloak has reduced the normalized scattering cross-section by about 5 dB.
Application for medical sensing
For detecting the cancer cells from the normal cells typically the frequency shift can be considered and this frequency shift also can be used for various types of viruses such as Flu.48 Moreover, we can use this property for photothermal therapy of cancer tissue. By cloaking the normal tissue at its resonance frequency and illuminating the laser on the whole tissue, only the cancer cells will absorb the wave and will be treated by the laser tuned at this frequency. In addition, as mentioned in49, the phase of the cancer cells is different from the normal tissue. So, the phase variation can also be checked for different tissue with various amounts of absorption of the drugs. These analytical studies are used for the determination of the ratio absorbed drug with gold nanosphere by the normal and cancer cells. The conventional pathology techniques for determining the progress of cancer is time-taking and other techniques of imaging such as PET scan are not practical in every case. The DNA-coated gold nanoparticles can be supposed as nanomachines for drug delivery.41 So, absorption of this organic coat is assumed to be equivalent to absorption of drugs. Thus, by using the DNA-coated gold nanoparticles in the process of sampling, detecting, and treating the cancer tumor, we can distinguish the cancer and normal tissues and also we can predict the ratio of the drug absorption in normal and cancer tissues. For this purpose, we can use the magnetic surface impedance defined as:
 | (16) |
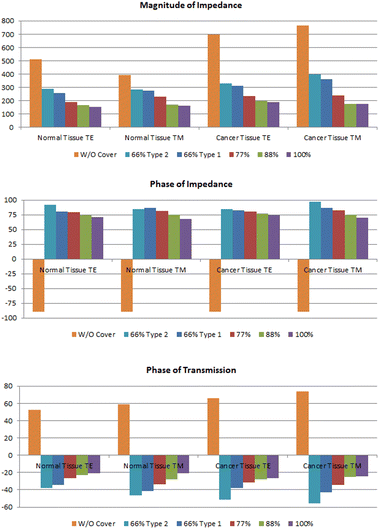
The values of |ZTE|, |ZTM|, 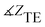 ,
,  and the phase of transmission for TM and TE modes are presented in Table 1. As can be seen, for TE and TM modes, |ZTE|, |ZTM|, φTE and φTM of cancer and normal tissues have different values without drug absorption. Increasing the filling factors of core–shell nanoparticles corresponds to the absorption rate of the drugs. We compare the results of Table 1 in Fig. 9. As shown in Fig. 9(a and b), By increasing the percent of absorption of drugs, both cancer and normal tissues have descending trend for |ZTE|, |ZTM|,
and the phase of transmission for TM and TE modes are presented in Table 1. As can be seen, for TE and TM modes, |ZTE|, |ZTM|, φTE and φTM of cancer and normal tissues have different values without drug absorption. Increasing the filling factors of core–shell nanoparticles corresponds to the absorption rate of the drugs. We compare the results of Table 1 in Fig. 9. As shown in Fig. 9(a and b), By increasing the percent of absorption of drugs, both cancer and normal tissues have descending trend for |ZTE|, |ZTM|, 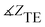 and
and  (for the same type of the structure). The transmission phase variation (φTE and φTM) can be used to obtain the type of tissue and percentage of absorption. The results of transmission phase variation are shown in Fig. 9(c). The object transmission phase changes proportionally with increasing the percentages of the drug. This form of variation can be seen for TE and TM modes in both normal and cancer tissues. We can analyze the tissue for various percentages of drug absorption in TE and TM modes. By analyzing the impedance and transmission phase and combining the results we can correct unexpected errors in experimental measurement.
(for the same type of the structure). The transmission phase variation (φTE and φTM) can be used to obtain the type of tissue and percentage of absorption. The results of transmission phase variation are shown in Fig. 9(c). The object transmission phase changes proportionally with increasing the percentages of the drug. This form of variation can be seen for TE and TM modes in both normal and cancer tissues. We can analyze the tissue for various percentages of drug absorption in TE and TM modes. By analyzing the impedance and transmission phase and combining the results we can correct unexpected errors in experimental measurement.
The results show that changes in the percentage of nanospheres affect the effective throughput and we can analyze the data from the Maxwell-Garnett equation based on the filling coefficient. Maxwell-Garnett equations are a theoretical method used to calculate the effective electrical permittivity in composite materials. Using the Maxwell-Garnett equation and considering the electrical permittivity of each nanomaterial component and their relative volumes in the composite, it is possible to calculate the effective electrical permittivity of composite materials.
The effective permittivity can be obtained by the Maxwell-Garnett equation as52
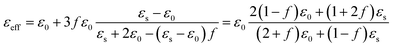 | (17) |
Since the Maxwell-Garnett equation is defined for cubic volume, some coefficients are needed to modify this equation for the curved surface of the cylinder.
The εeff is the complex permittivity of the composite and the f is the fraction ratio. The εs is the permittivity of the Au (gold) nanosphere which is extracted from Fig. 1(b) in the desired radius of the nanosphere and ε0 is the air permittivity for our model. The fraction ratio contains two main parts. One part is the ratio of the nanosphere volume to that of a cube which the nanosphere exactly fits inside this cube is obtained as 0.52. The second part is the percentage of the nanosphere in the arrangement which coats the organic cell, called fS in the relation. Then the modified Maxwell-Garnett for the composite of environment and filling nanospheres will be as
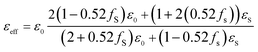 | (18) |
The total permittivity, ignoring some other effect such as the imaginary part of the permittivity and reflection between surfaces can be obtained by
| εT = ε1 + ε2 = ε1 + 2εeff | (19) |
The permittivity of the cylindrical tissue ε1cylindircal can be obtained by the ratio of the circular volume to the rectangular one as
| ε1cylindircal = (πr2h/4r2h)ε1slab = (π/4)ε1slab | (20) |
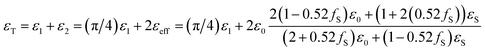 | (21) |
The permittivity for normal and cancer tissues with various absorption ratios based on eqn (21) for the TE mode is obtained for cylindrical element in Table 2. The results show obtained permittivity from the simulation is matched with the calculated permittivity from Maxwell-Garnet, properly. So, the obtained permittivity in the test can be supposed as another factor for determining the type of tissue and ratio of drug absorption besides the impedance and transmission phase of the sample. Moreover, the effect of the percentage of nanoparticles on permittivity is an important factor. The value of permittivity is reduced for smaller filling factors. Furthermore, as shown in Table 2, the permittivity of the cancer tissue is higher than normal tissue.
| 100% | 88% | 77% | 66% type 1 | 66% type 2 | ||
|---|---|---|---|---|---|---|
| Normal tissue | εeff,calculation | 4.42 | 4.33 | 4.25 | 4.14 | 4.17 |
| εeff,simulation | 4.41 | 4.29 | 4.11 | 4.12 | 4.05 | |
| Frequency (THz) | 162.6 | 166 | 170.2 | 175.2 | 177 | |
| Cancer tissue | εeff,calculation | 4.67 | 4.57 | 4.48 | 4.44 | 4.41 |
| εeff,simulation | 4.58 | 4.34 | 4.16 | 4.14 | 4.11 | |
| Frequency (THz) | 163.8 | 167.2 | 171.6 | 177.5 | 179.2 | |
In brief, the study of the transmission phase, and impedances reveal the ratio of the nanomachine absorption as core–shell biomaterial by cancer or healthy tissue and the result shows the percentage of material absorption by tissue impacts on the operation frequency, phase and impedance. We can examine suspected tissue for cancer by comparing it with conventional healthy tissue. Taking new sample after receiving the drug can give information about the ratio of drug absorption by the tissue.
Conclusions
Having analytical data on the ratio of drug absorption can help us to understand how much a drug is absorbed by cancer and normal tissues. With the small sampling of patients, we can determine the type of tissue and drug absorption. In this paper, we focused on the cloaking characteristics of nanoparticles in the optical range (100 to 200 THz) to differentiate between cancerous and normal tissues based on drug absorption. The nanosphere with DNA coat can impact on phase and impedance of the environment. The effective permittivity and conductivity besides the effective length play an important role in phase and impedance controlling. It means there is a relation between the absorbed drug ratio and the phase or impedance of the sample. Here, the results revealed that for the smaller values of absorbed drug ratio, the phase and impedance value is reduced for both TE and TM modes. As a matter of fact, by TE and TM analysis for impedance and phase, we have made four degrees of freedom. We can minimize the measurement errors of the cancer tissue. Furthermore, the Maxwell-Garnett equation was modified for this structure to obtain the effective value of the permittivity for cancer and normal tissue for TE mode which was examined for the cylindrical object. The results show obtained permittivity from the simulation is matched with the calculated permittivity from the modified Maxwell-Garnet equation, properly. With these analyses, the behavior of the tissue and absorbed material effects on phase, impedance, and permittivity can be discussed clearly.Conflicts of interest
The authors declare no conflict of interest.Notes and references
- S. Agarwal and Y. K. Prajapati, Multifunctional metamaterial surface for absorbing and sensing applications, Opt. Commun., 2019, 439, 304–307 CrossRef CAS.
- Y. Cheng, H. Chen, J. Zhao, X. Mao and Z. Cheng, Chiral metamaterial absorber with high selectivity for terahertz circular polarization waves, Opt. Mater. Express, 2018, 8(5), 1399–1409 CrossRef CAS.
- Y. X. Li, M. K. Fan, L. Kang and H. W. Zhuang, Plasmonic cloak using graphene at infrared frequencies, Opt. Commun., 2015, 354, 154–157 CrossRef CAS.
- H. F. Ma and T. J. Cui, Three-dimensional broadband ground-plane cloak made of metamaterials, Nat. Commun., 2010, 1, 21 CrossRef PubMed.
- J. B. Pendry, D. Schurig and D. R. Smith, Controlling electromagnetic fields, Science, 2006, 312(5781), 1780–1782 CrossRef CAS.
- W. Kan, B. Liang, R. Li, X. Jiang, X.-Y. Zou, L.-L. Yin and J. Cheng, Three-dimensional broadband acoustic illusion cloak for sound-hard boundaries of curved geometry, Sci. Rep., 2016, 6, 36936 CrossRef CAS.
- S. S. Islam, M. R. I. Faruque and M. T. Islam, An object-independent ENZ metamaterial-based wideband electromagnetic cloak, Sci. Rep., 2016, 6(1), 33624 CrossRef CAS PubMed.
- B. Orazbayev, N. Mohammadi Estakhri, M. Beruete and A. Alù, Terahertz carpet cloak based on a ring resonator metasurface, Phys. Rev. B, 2015, 91(19), 195444 CrossRef.
- M. D. Guild, M. R. Haberman and A. Andrea, Plasmonic cloaking and scattering cancelation for electromagnetic and acoustic waves, Wave Motion, 2011, 48(6), 468–482 CrossRef.
- D. Schurig, J. J. Mock, B. J. Justice, S. A. Cummer, J. B. Pendry, A. F. Starr and D. R. Smith, Metamaterial electromagnetic cloak at microwave frequencies, Science, 2006, 314(5801), 977–980 CrossRef CAS PubMed.
- J. Wang, S. Qu, Z. Xu, A. Zhang, H. Ma, J. Zhang, H. Chen and M. Feng, Multifrequency super-thin cloaks, Photonics Nanostructures – Fundam. Appl., 2014, 12(2), 130–137 CrossRef.
- E. Semouchkina, R. Duan, N. P. Gandji, J. Saeid, S. George and P. Ravi, Superluminal media formed by photonic crystals for transformation optics-based invisibility cloaks, J. Opt., 2016, 18(4), 044007 CrossRef.
- W. J. M. Kort-Kamp, F. S. S. Rosa, F. A. Pinheiro and C. Farina, Tuning plasmonic cloaks with an external magnetic field, Phys. Rev. Lett., 2013, 111(21), 215504 CrossRef CAS PubMed.
- X. C. Jiang, Y. W. Zhou, D. L. Gao, Y. Huang and L. Gao, Realizing optical bistability and tristability in plasmonic coated nanoparticles with radial-anisotropy and Kerr-nonlinearity, Opt. Express, 2020, 28(12), 17384–17394 CrossRef CAS PubMed.
- M. Farhat, C. Rockstuhl and H. Bağcı, A 3D tunable and multi-frequency graphene plasmonic cloak, Opt. Express, 2013, 21(10), 12592–12603 CrossRef CAS PubMed.
- K. Hansen, A. Dutta, M. Cardona and C. Yang, Zirconium Nitride for Plasmonic Cloaking of Visible Nanowire Photodetectors, Plasmonics, 2020, 1–11 Search PubMed.
- D. Diedrich, A. Rottler, D. Heitmann and S. Mendach, Metal–dielectric metamaterials for transformation-optics and gradient-index devices in the visible regime, New J. Phys., 2012, 14(5), 053042 CrossRef.
- S. Ebrahimi, Optical absorber based on self-similar cylindrical element for detecting optical material, Opt. Quantum Electron., 2020, 52(no. 2), 87 CrossRef CAS.
- B. Zhang, C. Zhang, J. Wang and Y. Peng, Modeling and analysis of surface plasmon microscopy with radial polarization, Opt. Commun., 2018, 427, 369–373 CrossRef CAS.
- L. Hu, S. Gong, M. Hu, R. Zhong, T. Zhao and S. Liu, Enhanced dielectric waveguide mode from the coupling of surface plasmon polaritons excited by a parallel electron beam, Opt. Commun., 2019, 433, 195–199 CrossRef CAS.
- A. Bahari and S. Mohsen Gahremani, Investigation of optical properties by localized surface plasmon excitation of nanoparticle arrays in photodetectors, Opt. Commun., 2018, 427, 567–572 CrossRef CAS.
- F. Ghodsi, H. Dashti and J. Ahmadi Shokouh, Design of a multilayer nano antenna as a hyperbolic metamaterial with Fano response for optical sensing, Opt. Quantum Electron., 2020, 52, 316 CrossRef CAS.
- A. Ahmadivand, R. Sinha and N. Pala, Hybridized plasmon resonant modes in molecular metallodielectric quad-triangles nanoantenna, Opt. Commun., 2015, 355, 103–108 CrossRef CAS.
- R. Kotb, Y. Ismail and M. A. Swillam, Nonlinear tuning techniques of plasmonic nano-filters, Opt. Commun., 2015, 336, 306–314 CrossRef CAS.
- N. Nozhat and N. Granpayeh, Switching power reduction in the ultra-compact Kerr nonlinear plasmonic directional coupler, Opt. Commun., 2012, 285(6), 1555–1559 CrossRef CAS.
- M. Zhang, J. Fang, F. Zhang, J. Chen and H. Yu, Ultra-narrow band perfect absorbers based on Fano resonance in MIM metamaterials, Opt. Commun., 2017, 405, 216–221 CrossRef CAS.
- W. Withayachumnankul, S. Charan Manish, C. Fumeaux, B. S.-Y. Ung, W. J. Padilla, M. Bhaskaran, D. Abbott and S. Sriram, Plasmonic resonance toward terahertz perfect absorbers, ACS Photonics, 2014, 1(7), 625–630 CrossRef CAS.
- N. Liu, M. Mesch, T. Weiss, M. Hentschel and H. Giessen, Infrared perfect absorber and its application as plasmonic sensor, Nano Lett., 2010, 10(7), 2342–2348 CrossRef CAS PubMed.
- M. G. Silveirinha, A. Andrea and N. Engheta, Cloaking mechanism with antiphase plasmonic satellites, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78(20), 205109 CrossRef.
- S. Siddique and J. C. L. Chow, Gold nanoparticles for drug delivery and cancer therapy, Appl. Sci., 2020, 10(11), 3824 CrossRef CAS.
- N. Zhang, L. Minghui, S. Xuetan, J. Huizhen and L. Wenguang, NIR-responsive cancer cytomembrane-cloaked carrier-free nanosystems for highly efficient and self-targeted tumor drug delivery, Biomaterials, 2018, 159, 25–36 CrossRef CAS PubMed.
- A. Tomitaka, H. Arami, A. Ahmadivand, N. Pala and J. Anthony, McGoron, Yasushi Takemura, Marcelo Febo, and Madhavan Nair. Magneto-plasmonic nanostars for image-guided and NIR-triggered drug delivery, Sci. Rep., 2020, 10(1), 1–10 CrossRef PubMed.
- J. Song, J. Xie, C. Li, J.-H. Lu, Q.-F. Meng, Z. Yang, R. J. Lee, Di Wang and T. Le-Sheng, Near infrared spectroscopic (NIRS) analysis of drug-loading rate and particle size of risperidone microspheres by improved chemometric model, Int. J. Pharm., 2014, 472(1–2), 296–303 CrossRef CAS.
- C. Y. Chain, D. M. María Antonieta, C. José Sebastián, E. Alejandro Ramirez and M. Elena Vela, Surface Plasmon Resonance as a Characterization Tool for Lipid Nanoparticles Used in Drug Delivery, Front. Chem., 2021, 1225 Search PubMed.
- P. Arpaia, U. Cesaro and N. Moccaldi, Noninvasive measurement of transdermal drug delivery by impedance spectroscopy, Sci. Rep., 2017, 7, 44647 CrossRef CAS PubMed.
- Y.-J. Kim, B. Kim, J. W. Kim, G. Nam, H.-S. Jang, S.-W. Kang and U. Jeong, Combination of nanoparticles with photothermal effects and phase-change material enhances the non-invasive transdermal delivery of drugs, Colloids Surf., B, 2015, 135, 324–331 CrossRef CAS PubMed.
- K. B. Male, B. Lachance, S. Hrapovic, G. Sunahara and J. H. T. Luong, Assessment of cytotoxicity of quantum dots and gold nanoparticles using cell-based impedance spectroscopy, Anal. Chem., 2008, 80(14), 5487–5493 CrossRef CAS PubMed.
- A. Monti, A. Andrea, A. Toscano and F. Bilotti, Optical invisibility through metasurfaces made of plasmonic nanoparticles, J. Appl. Phys., 2015, 117(12), 123103 CrossRef.
- P.-Y. Chen, J. Soric and A. Andrea, Invisibility and cloaking based on scattering cancellation, Adv. Mater., 2012, 24(44), OP281–OP304 CrossRef CAS.
- A. Alù and N. Engheta, Multifrequency optical invisibility cloak with layered plasmonic shells, Phys. Rev. Lett., 2008, 100(11), 113901 CrossRef.
- H. Park, J. Kim, S. Jung and W. J. Kim, DNA-Au nanomachine equipped with i-motif and G-quadruplex for triple combinatorial anti-tumor therapy, Adv. Funct. Mater., 2018, 28(5), 1705416 CrossRef.
- D. Schurig, J. B. Pendry and D. R. Smith, Calculation of material properties and ray tracing in transformation media, Opt. Express, 2006, 14(21), 9794–9804 CrossRef CAS PubMed.
- T. J. Cui, D. R. Smith and R. Liu, Metamaterials, Boston, MA, USA, Springer, 2010 Search PubMed.
- B. B. Yousif and A. S. Samra, Optical responses of plasmonic gold nanoantennas through numerical simulation, J. Nanopart. Res., 2013, 15(1), 1–15 CrossRef.
- F. El-Diasty and F. Abdel-Wahab, Optoelectronic studies on heterocyclic bases of deoxyribonucleic acid for DNA photonics, Mater. Sci. Eng., C, 2015, 55, 524–529 CrossRef CAS .
- J. Richter, M. Mertig, W. Pompe, I. Mönch and H. K. Schackert, Construction of highly conductive nanowires on a DNA template, Appl. Phys. Lett., 2001, 78(4), 536–538 CrossRef CAS.
- N. Osanloo, V. Ahmadi, M. Naser-Moghaddasi and E. Darabi, Engineered nano-sphere array of gold-DNA core–shells and junctions as opto-plasmonic sensors for biodetection, RSC Adv., 2021, 11(44), 27215–27225 RSC.
- A. Dalal, H. Mohan, M. Prasad and C. S. Pundir, Detection methods for influenza A H1N1 virus with special reference to biosensors: a review, Biosci. Rep., 2020, 40(2), BSR20193852 CrossRef.
- W. J. Choi, D. I. Jeon, S.-G. Ahn, J.-H. Yoon, S. Kim and B. Ha Lee, Full-field optical coherence microscopy for identifying live cancer cells by quantitative measurement of refractive index distribution, Opt. Express, 2010, 18(22), 23285–23295 CrossRef CAS.
- L. W. Wu, H. F. Ma, Y. Gou, R. Y. Wu, Z. X. Wang, M. Wang, X. Gao and T. J. Cui, High-transmission ultrathin huygens' metasurface with 360 phase control by using double-layer transmitarray elements, Phys. Rev. Appl., 2019, 12(2), 024012 CrossRef CAS.
- C. Pfeiffer and A. Grbic, Metamaterial Huygens' surfaces: tailoring wave fronts with reflectionless sheets, Phys. Rev. Lett., 2013, 110(19), 197401 CrossRef PubMed .
- V. A. Markel, Introduction to the Maxwell Garnett approximation: tutorial, J. Opt. Soc. Am. A, 2016, 33(7), 1244–1256 CrossRef.
| This journal is © The Royal Society of Chemistry 2023 |