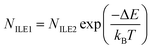Twist-angle-dependent momentum-space direct and indirect interlayer excitons in WSe₂/WS₂ heterostructure

Abstract

Interlayer excitons (ILEs) in the van der Waals (vdW) heterostructures of type-II band alignment transition metal dichalcogenides (TMDCs) have attracted significant interest owing to their unique exciton properties and potential in quantum information applications. However, the new dimension that emerges with the stacking of structures with a twist angle leads to a more complex fine structure of ILEs, presenting both an opportunity and a challenge for the regulation of the interlayer excitons. In this study, we report the evolution of interlayer excitons with the twist angle in the WSe₂/WS₂ heterostructure and identify the direct (indirect) interlayer excitons by combining photoluminescence (PL) and density functional theory (DFT) calculations. Two interlayer excitons with opposite circular polarization assigned to the different transition paths of K–K and Q–K were observed. The nature of the direct (indirect) interlayer exciton was confirmed by circular polarization PL measurement, excitation power-dependent PL measurement and DFT calculations. Furthermore, by applying an external electric field to regulate the band structure of the WSe₂/WS₂ heterostructure and control the transition path of the interlayer excitons, we could successfully realize the regulation of interlayer exciton emission. This study provides more evidence for the twist-angle-based control of heterostructure properties.

---

1. Introduction

As semiconductor materials, monolayer transition metal dichalcogenides (TMDCs) have recently attracted significant interest as they exhibit a strong Coulomb confinement effect, and the unique exciton characteristics brought about by spin-valley coupling provide a new platform for the study of excitonic phenomena.^1–6 van der Waals (vdW) heterostructures formed by stacking different TMDCs have further emerged as a new powerful tool for exploring new excitonic phenomena with designed functionalities, especially in the so-called type-II band alignment, wherein the conduction band minimum (CBM) and the valence band maximum (VBM) are in different layers.^7–12 In the vdW heterostructures with type-II band alignment, spatially indirect interlayer excitons can be formed with electrons and holes localized in different TMDC layers with much longer lifetimes and^13,14 valley depolarization time¹⁵ than those of spatially direct intralayer excitons, thereby allowing ultrafast charge transfer^16–18 and ultra-long-range exciton diffusion.¹⁹ Meanwhile, the lattice mismatch and rotational misalignment in the heterostructure are predicted to strongly influence interlayer coupling,^12,20–24 which suggests the possibility of regulating the interlayer excitons by simply varying the twist angles.

However, the twist angle and lattice mismatch between the two layers in the heterostructure influence the overlap of electron clouds between the two components and generate moire superlattice potential, which makes the structure of the interlayer exciton more complex and fine.^25–27 For example, similar to monolayer TMDC materials, neutral excitons and trions are also observed in the interlayer excitons of MoSe₂/WSe₂ heterostructures.²⁸ Meanwhile, considering spin–orbit coupling, band splitting enables the formation of two indirect interlayer excitons, which hold opposite circular polarization. Moreover, unlike the excitons in monolayer TMDCs, the breaking of the out-of-plane mirror symmetry in the TMDC heterostructures allows spin–flip transition dipole coupling with both in-plane and out-of-plane light.²⁹ As a result, spin-singlet and spin-triplet interlayer excitons can be observed in TMDC heterostructures without any special configurations, such as a magnetic field and out-of-plane light.^30–32 Indeed, although there are many reports on the fine structure of interlayer excitons, the energies of the interlayer excitons are very close, which also leads to many deficiencies in the understanding of interlayer excitons, especially in the twisted structure. On the other hand, the study of momentum-space direct and indirect interlayers, which can provide information on different energy valleys, is still insufficient, due to which the regulation of the momentum-space direct and indirect interlayers remains a challenge.

In this work, we report the evolution of the interlayer exciton with the twist angle in the WSe₂/WS₂ heterostructure and precisely identify the direct (indirect) interlayer excitons by combining photoluminescence (PL) and density functional theory (DFT) calculations. The twist angle between two layers shows a strong modulatory effect on the interlayer excitons. The PL of the interlayer excitons was enhanced only when the twist angle was close to 0° and 60°. Moreover, the interlayer excitons could be resolved into two components ILE1 and ILE2, corresponding to the direct transition of K–K and indirect transition of Q–K, respectively. The nature of the direct (indirect) interlayer exciton was confirmed by circularly polarized PL measurement, excitation power-dependent PL measurement, and DFT calculations. In addition, by applying an external electric field to regulate the band structure of the WSe₂/WS₂ heterostructure and control the transition path of the interlayer excitons, we could successfully realize the regulation of interlayer exciton emission, and the results were also confirmed by the DFT calculations. Our results provide a simple solution for regulating interlayer excitons and more possibilities for optoelectronic devices based on twisted angle heterostructures.

2. Experimental details

2.1 The growth of monolayer WS₂ and WSe₂

Monolayer WS₂ and WSe₂ were grown on a sapphire substrate by using the method reported in ref. 25. In detail, a 5 nm W source was coated onto a sacrificial substrate by thermal evaporation. After that, the sapphire substrate was placed on the sacrificial substrate face-to-face and placed in the high-temperature zone of a furnace. 200 mg X (S or Se) powder was placed in the low-temperature zone of the furnace. The two zones were heated to the target temperature (950 °C for the high-temperature zone and 300 °C for the low-temperature zone) at the same time and maintained at the growth temperature for 20 min. Argon gas at a flow rate of 100 sccm was employed as the carrier gas during the whole process. After the growth of the monolayers, the furnace was cooled down to room temperature naturally.

2.2 Fabrication of the heterostructures

The mechanically exfoliated samples were transferred by the dry transfer method. Each sample was exfoliated onto the PDMS polymer, which was pre-deposited on quartz glass first. After that, the samples were released onto the target substrate by using a micromanipulator system. The CVD-grown materials were transferred by combining the wet and dry transfer methods. Firstly, the PDMS polymer was coated onto the materials on the sapphire substrate. Secondly, the samples were etched at 90 °C in a NaOH solution (2 mol L⁻¹) for 4 min. Thirdly, the samples were placed in deionized (DI) water, and consequently, the materials detached from the sapphire substrate and transferred onto the PDMS polymer because of the hydrophilic surface of sapphires. Finally, the materials were transferred onto the target substrate by using the dry transfer method, as mentioned above.

Notably, to remove the residues and enhance contact between the layers, after each layer was transferred, the sample was annealed at 300 °C in a vacuum chamber for 2 h.

2.3 Optical measurements

The Raman and PL measurements were performed using a confocal Raman microscopy system (WITec Alpha 300R) with a 532 nm continuous wavelength (CW) laser as the excitation source. For room-temperature measurements, the Raman and PL spectra were collected using a 100× (Zeiss, N.A. = 0.9) objective lens. For temperature-dependent PL measurements, each sample was mounted inside the chamber of a high-vacuum multifunctional system with liquid helium refrigeration (CRYO Industries of America, Inc), and the signal was collected using a 50× (Zeiss, N.A. = 0.8) objective lens. The SHG measurement was also performed using this system but with a 1064 nm picosecond laser for excitation.

2.4 DFT calculations

The DFT calculations were performed using the Vienna ab initio simulation package (VASP). The generalized gradient approximation (GGA) of Perdew–Burke–Ernzerhof (PBE) parametrization was selected to treat the exchange–correlation interaction with a plane-wave cutoff energy of 500 eV. The semi-empirical correction scheme of Grimme (DFT-D2) was selected to evaluate the effects of vdW interactions on the electronic properties of the WSe₂/WS₂ heterostructure. Different WSe₂/WS₂ heterostructure configurations with twist angles equal to 0°, 27.8°, 38.2°, and 60° were constructed with a vacuum layer larger than 14 Å to avoid interactions between the periodic images along the c axis. The convergence condition for energy was chosen as 10⁻⁵ eV, and the forces on each atom converged to less than 0.01 eV Å⁻¹. The Monkhorst–Pack grid was employed to sample the Brillouin zone with a mesh of 15 × 15 × 1 for the full relaxation and self-consistent calculations of both 0° and 60° twisted WSe₂/WS₂ heterostructures, respectively, while a mesh of 5 × 5 × 1 was adopted for the 27.8° and 38.2° twisted structures. The spin–orbit coupling (SOC) effect was considered in the calculation for investigating the effect of the electric field on the band structure of the heterostructure with 0° twisted stacking.

3. Results and discussion

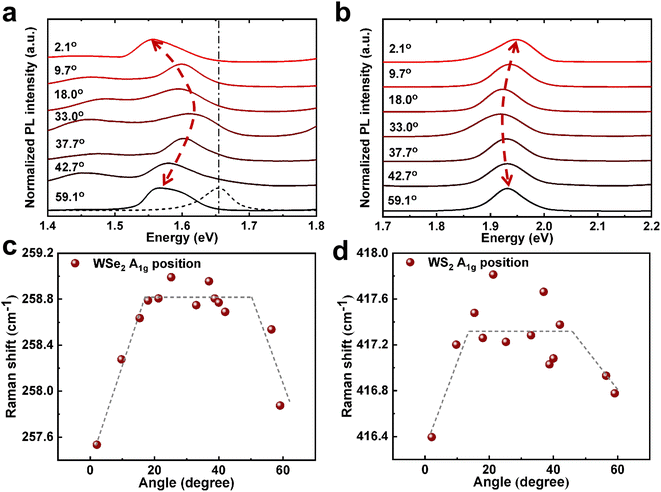
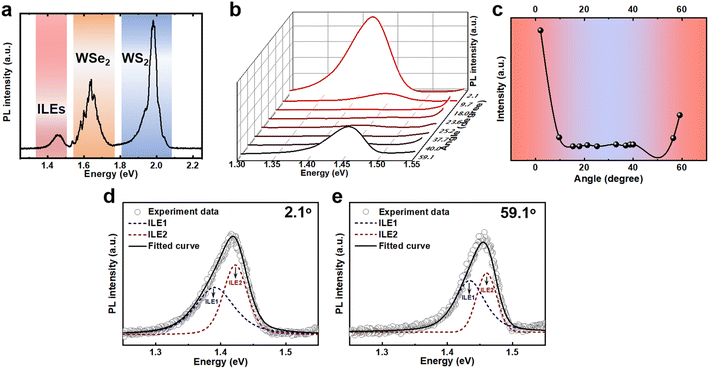
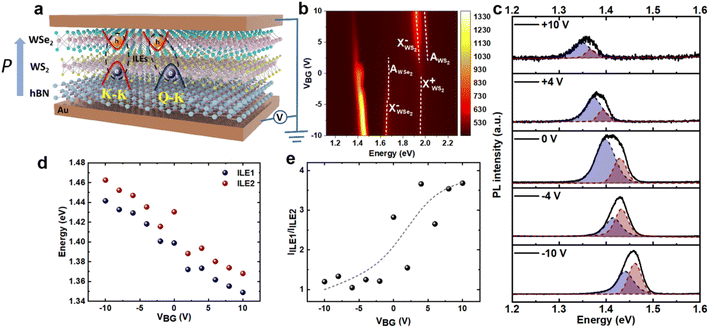
The WSe₂/WS₂ heterostructures with different twist angles were fabricated by the dry transfer approach. High-density WS₂ was directly grown on the SiO₂/Si substrate by a chemical vapor deposition (CVD) process (see method section).³³ Since most of the samples grown by CVD possessed the regular shape of a triangle, it enables us to preliminarily control the twist angle. In order to better control the angle between WS₂ and WSe₂ and reduce the influence of material non-uniformity on the results, a large WSe₂ monolayer exfoliated from a single crystal was stacked on top of WS₂ by dry transfer (as shown in Fig. S1†).³⁴ The precise twist angle between the two layers was decided by the optical second-harmonic generation (SHG) (Fig. S2†). To reveal the evolution of interlayer coupling in the WSe₂/WS₂ heterostructure at different twist angles, we performed PL measurements at room temperature, and the results are shown in Fig. 1a and b. Obviously, when the twist angle was switched from 0° to 60°, the neutral exciton of WSe₂ (A_WSe2) and WS₂ (A_WS2) showed a periodic but opposite evolution. These interesting behaviors indicate that the strength of interlayer coupling periodically changes with the twist angle of the heterostructure. When the twist angle was near 0° or 60° corresponding to AA and AB stacking, respectively, A_WSe2 showed a red shift, but A_WS2 showed a slight blue shift, which may be because the smaller distance between the two layers increases the overlap of the electron and hole wavefunctions and facilitates charge transfer between the two layers. The type II band alignment of the WSe₂/WS₂ heterostructure allows the electrons to transfer into the WSe₂ layer and cause n-type doping.^35,36 Meanwhile, the holes transferred into the WS₂ layer lead to p-type doping behavior and lead to the renormalization of the bandgap in WS₂, which may enlarge the bandgap.^37,38 These behaviors also were evidenced by the variety of Raman signals (Fig. S1e†) at the peak position of the out-of-plane mode A_1g of WSe₂ and WS₂, which are sensitive to doping and interlayer coupling, as shown in Fig. 1c and d, respectively. The A_1g of WSe₂ showed a red shift when the twist angle was near 0° or 60°, which may stem from the increase in electron density and enhanced carrier–phonon interaction.³⁹ However, the A_1g of the WS₂ also showed a red shift when the twist angle was near 0° or 60°, and this phenomenon was unexpected. Since more electrons from WS₂ are transferred into the WSe₂ layer with the enhancement of interlayer coupling, the decrease in electron density stiffens the A_1g mode, as reported previously.⁴⁰ We deduce two possible reasons for this phenomenon; one is that WS₂ lies in the bottom layer, thus its strong coupling with the substrate makes the A_1g mode insensitive to charge transfer.^41–43 Another reason is the layer decoupling effect caused by laser resonance.³⁹

Fig. 1 PL and Raman measurements of the WSe₂/WS₂ heterostructures with different twist angles. (a) and (b) Display the PL of the A excitons of WSe₂ and WS₂ in WSe₂/WS₂ heterostructures with different twist angles; the dashed spectrum is the PL of monolayer WSe₂. (c) and (d) Present the variation of the peak frequencies of the A_1g Raman mode of WSe₂ and WS₂ in the WSe₂/WS₂ heterostructures with different twist angles.

We then studied the effect of the twist angle on the WSe₂/WS₂ heterostructure by PL measurement at 7 K. Fig. 2a shows the PL spectrum of the WSe₂/WS₂ heterostructure; the emerging peak located at ∼1.4 eV corresponds to the interlayer exciton, which is another strong evidence of strong interlayer coupling in the type II band alignment heterostructure.^35,36 PL mapping (shown in Fig. S3†) showed that this peak exists only in the heterostructure region, which also confirms the nature of the interlayer exciton rather than the defect-trapped state.^44,45 Fig. 2b shows the specific PL spectra of the WSe₂/WS₂ heterostructures with different twist angles. The evolution of the integrated intensity of the interlayer exciton with the twist angle is shown in Fig. 2c. Although all these spectra are acquired under the same condition, the interlayer exciton is enhanced obviously when the twist angle is near 0° or 60° but almost disappears when the twist angle approaches 30°. This periodic change in strength behavior can be attributed to the different distances between the two layers at different twist angles, which strongly affects interlayer coupling. Then, we focused on the emission properties of the WSe₂/WS₂ heterostructures with a twist angle near 0° or 60° and stronger interlayer coupling. Fig. 2d and e show the interlayer exciton emission peaks of the heterostructures with twist angles of 2.1° and 59.1°, respectively. The peak located at ∼1.4 eV could be resolved into two peaks at ∼1.390 eV (ILE1) and ∼1.423 eV (ILE2) at a twist angle of 2.1°, as shown in Fig. 2d, which may be assigned to the direct transition path of K–K and indirect transition path of Q–K, respectively. However, when the twist angle was 59.1°, ILE1 and ILE2 were shifted to ∼1.433 eV and ∼1.460 eV, respectively. This phenomenon results from the difference in the strength of interlayer coupling when the twist angle is near 0° and 60° (the details are discussed later).

Fig. 2 The PL measurements of the WSe₂/WS₂ heterostructures with different twist angles at 7 K. (a) The typical PL spectrum of the WSe₂/WS₂ heterostructure at 7 K. (b) The PL spectra of interlayer excitons in the WSe₂/WS₂ heterostructures with different twist angles. The variation of the intensity of the interlayer exciton with the twist angle is shown in (c). (d) and (e) are the Gaussian-line-shape compositions of the interlayer exciton in the WSe₂/WS₂ heterostructures with twist angles of 2.1° and 59.1°, respectively.

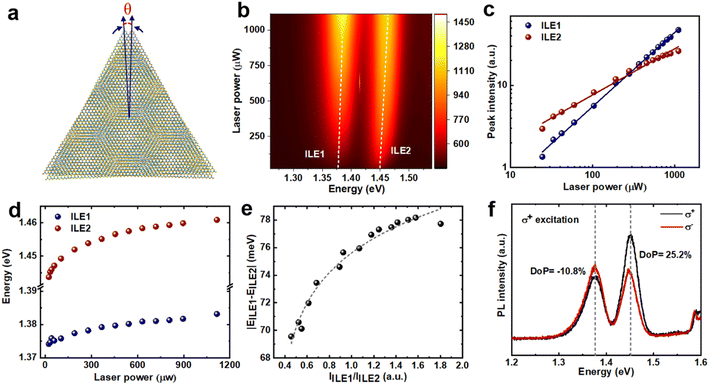
To reveal the nature of ILE1 and ILE2, another WSe₂/WS₂ heterostructure was fabricated using a CVD-grown sample with a twist angle of ∼1.8° and encapsulated in hBN, as shown in Fig. 3a (see methods). The emission of the interlayer excitons is the result of the recombination of the electrons from the WS₂ layer and the holes from the WSe₂ layer, which can be strongly affected by the carrier density. In view of this, excitation-power-dependent PL measurement was applied on the hBN-encapsulated WSe₂/WS₂ heterostructure to regulate the carrier density; the color plot of the PL intensity as a function of excitation power is shown in Fig. 3b. Fig. 3c displays the variation of PL intensity with excitation power, and the linear increase of the integrated intensity with increasing excitation power eliminates the possibility of the ILEs originating from the defect-bound state. Meanwhile, with increasing excitation power, both ILE1 and ILE2 showed blue shifts, as seen in Fig. 3d. This phenomenon is attributed to the dipole–dipole repulsive effect, which increases the exciton energy.^46,47 With the increase of carrier density, more interlayer excitons are formed and enhance the repulsive effect. Fig. 3e shows the energy difference between ILE1 and ILE2 (E_ILE1 − E_ILE2) versus the ratio of the integrated intensities of ILE1 and ILE2 (I_ILE1/I_ILE2). We analyzed the interlayer exciton emission intensity in a simple two-level system. At thermal equilibrium, the population of excitons in the two interlayer states follow the Boltzmann distribution:⁴⁸

where N_ILE1 and N_ILE2 are the populations of the ILE1 and ILE2 excitons, respectively, ΔE = E_ILE1 − E_ILE2 is the energy difference between the ILE1 and ILE2 exciton states, and K_B is the Boltzmann constant. The good fit of our experimental data confirms the direct transition of ILE1 and the indirect transition of ILE2. The circularly polarized PL measurement was applied to further reveal the origin of the two interlayer excitons, as shown in Fig. 3f. We excited the hBN encapsulated WSe₂/WS₂ heterostructure with positive helicity (σ⁺) and detected the emission signals with the same (σ⁺) or opposite helicity (σ⁻). 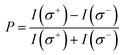The degree of polarization (DoP) is defined as , where I(σ^±) is the integrated PL intensity of the same helicity (σ⁺) and the opposite helicity (σ⁻). Notably, the two interlayer excitons showed opposite circular polarization; ILE1 had a DoP of −10.8%, and ILE2 had a DoP of 25.2%. This behavior denotes emission from the direct transition path K–K and the indirect transition path Q–K, which possess opposite spin directions of the states at these two points.

Fig. 3 PL measurements of the hBN-encapsulated WSe₂/WS₂ heterostructure. (a) The schematic of the WSe₂/WS₂ heterostructure fabricated using the CVD-grown samples. (b) The excitation-power-dependent PL measurements of the WSe₂/WS₂ heterostructure. (c) and (d) Depict the PL intensity and PL energy as a function of excitation power, respectively. (e) The fitting results of the energy difference vs. intensity ratio of the two interlayer excitons. (f) The circular polarized PL measurement of the WSe₂/WS₂ heterostructure with an excitation source energy of 2.33 eV.

To further reveal the nature of the two emergent interlayer excitons, we performed gate-voltage-dependent PL measurements at 7 K (Fig. 4a). Fig. 4b shows the color plot of the PL intensity versus gate voltage; it can be seen that the gate voltage effectively modifies the optical signatures of the WSe₂/WS₂ heterostructure. First, we focused on the emission of the intralayer excitons from the WSe₂ and WS₂ layers. In the electron doping region (V_BG > 0), the intensity of the excitonic states of WS₂, including the neutral exciton (A_WS2) and negatively-charged exciton (X_WS2⁻), enhanced with the increase in V_BG. However, for WSe₂, the emission of the neutral exciton A_WSe2 decreased immediately. This phenomenon can be explained by the charge transfer between the WSe₂ layer and the WS₂ layer. In detail, the external electric field V_BG results in the transfer of electrons from WSe₂ to WS₂ and holes transfer from WS₂ to WSe₂, which induce p-doping of WSe₂ and n-doping of WS₂. The increase (decrease) in electrons leads to the enhancement (decrease) of excitons and charged exciton emission in WS₂ (WSe₂). On the contrary, in the hole doping region (V_BG < 0), the electrons from WS₂ are transferred to the WSe₂ layer and result in the disappearance of the emission peaks of A_WS2 and X_WS2⁻ and the appearance of the emission peak of the positively-charged exciton (X_WS2⁺). In WSe₂, the excessive electrons injected because of the external electric field facilitated the formation of the negatively-charged exciton (X_WSe2⁻).

Fig. 4 Gate-voltage-dependent PL measurement of the WSe₂/WS₂ heterostructure at 7 K. (a) The schematic of the setup used for the gate-voltage-dependent PL measurements. (b) The color plot of the PL intensity as a function of gate voltage. (c) PL spectra at the gate voltages of −10, −4, 0, +4, and +10 V. (d) The peak positions of ILE1 and ILE2 as functions of the gate voltage. (e) The ratio of the integrated peak intensities (I_ILE1/I_ILE2) as a function of gate voltage.

The external electric field also strongly modified the emission of the interlayer exciton. Fig. 4c shows the PL spectrum at five specific gate voltages. Obviously, with the gate voltage increasing from −10 V to 10 V, both ILE1 and ILE2 showed significant red shifts. This phenomenon may be attributed to the interaction between the external electric field and the dipole of the interlayer exciton, which can be briefly described as ΔU = |P·EE|, where, P is the dipole (as shown in Fig. 4a), and E is the direction of the external electric field. When E is antiparallel (parallel) to the direction of dipole P, the energy of the interlayer exciton should blue shift (red shift). The variation of peak position versus gate voltage is shown in Fig. 4d, the ratios of the peak position and gate voltage were ∼4.9 meV V⁻¹ (ILE1) and ∼5.0 meV V⁻¹ (ILE2). Such similarity also confirms that the two interlayer emissions feature excitons rather than the interlayer trion because the variation of energy in the electric field would be different for interlayer trions and interlayer excitons due to the different types of charges carried by them, leading to differences in the dipole.^49,50 The intensity of the interlayer exciton also changed with the gate voltage (as shown in Fig. 4b). Obviously, as the gate voltage was decreased from 10 V to −10 V, the intensity of the interlayer exciton was strongly enhanced. This phenomenon may be ascribed to the interaction between the interlayer exciton with the external electric field; when V_g < 0 V, the direction of the external electric field is the same as that of exciton recombination (electron transition from WS₂ to WSe₂), which strongly enhances the recombination of the interlayer exciton, and vice versa. However, when an external electric field is applied, the extraction and injection of electrons from the heterostructure due to the electrode may also lead to this phenomenon. In order to eliminate this possibility as much as possible, we used hBN to shield the influence of the electrode in the heterostructure (details shown in Fig. S5†); however, the interlayer exciton shows the same trend with the change in voltage, which further confirms that the enhancement of interlayer excitons results from the interaction between the interlayer excitons and the external electric field. Notably, in addition to the overall intensity change of the interlayer exciton, the relative intensity of ILE1 and ILE2 also changed with changes in the external electric field (as shown in Fig. 4c). Fig. 4e shows the variation of the ratio of the ILE1 and ILE2 intensities (I_ILE1/I_ILE2) with the gate voltage. It can be seen that with the gate voltage increasing from −10 V to 10 V, the intensities of ILE1 and ILE2 displayed an interesting reversal phenomenon, and the ratio I_ILE1/I_ILE2 increased.

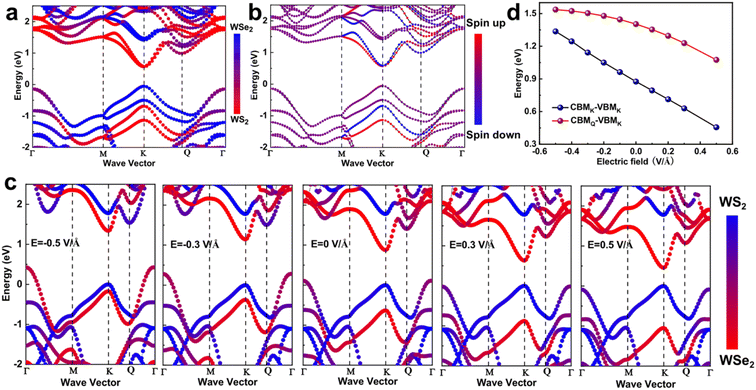
In order to understand the behavior of the interlayer excitons, the band structure of the WSe₂/WS₂ heterostructures with twist angles of 0°, 27.8°, 38.2° and 60° (Their side-views and top-views are shown in Fig. S6.†) were calculated by using the density functional theory (DFT), as shown in Fig. 5, where the color-coding indicates the contribution of each layer. In particular, when the twist angle approached 0° and 60°, the conduction band showed two valleys at the K point and the Q point, respectively. The valence band maximum (VBM_K) and conduction band minimum (CBM_K) located at K and K′ are entirely contributed by WSe₂ and WS₂ respectively, but the CBM_Q located at Q is contributed by both WS₂ and WSe₂. Notably, the energy difference between CBM_K − VBM_K and CBM_Q − VBM_K varied between the WSe₂/WS₂ heterostructures with twist angles of 0° and 60°, which is consistent with our experimental results that the energies of their interlayer excitons are different. To further understand this phenomenon, the differential charge densities were calculated (as shown in Fig. S7†). Obviously, charge transfer in the WSe₂/WS₂ heterostructures with twist angles of 0° and 60° were higher than that in the WSe₂/WS₂ heterostructure with the twist angle close to 30°, which is consistent with our findings from the experimental results that interlayer excitons are strongly enhanced when the twist angle is close to 0° or 60°.

Fig. 5 The DFT calculations of the WSe₂/WS₂ heterostructures with different twist angles. (a)–(d) Depict the band structures of the WSe₂/WS₂ heterostructure with twist angles of 0°, 27.8°, 38.2° and 60°, respectively.

Further, considering spin–orbit coupling in the WSe₂/WS₂ heterostructure with a twist angle of 0°, Fig. 6a and b show the spin-resolved band structure. Obviously, CBM_K demonstrated very small splitting, which would make the electron more likely to spin-flip and result in a smaller DoP for ILE1 (as shown in Fig. 3f). However, the CBM_Q band is entirely contributed by the spin-down state, which leads to the higher DoP of ILE2. Meanwhile, the CBM_K and CBM_Q show opposite spin directions, which results in the opposite DoP of ILE1 and ILE2. These results also confirm the nature of the K–K (Q–K) transition of the ILE2 (ILE1). Furthermore, we also calculated the behavior of the band structure under an electric field. Fig. 6c shows the band structure under the electric fields of ±0.5, ±0.3, and 0 V Å⁻¹. Similar to the experimental findings, the direction of the electric field was from the WS₂ layer to the WSe₂ layer. The conduction band showed an obvious shift with the variation of the electric field from −0.5 V Å⁻¹ to 0.5 V Å⁻¹. Both CBM_K and CBM_Q became closer to the valence band, and the energy differences between K and Q are summarized in Fig. 6d. This phenomenon is consistent with our experimental results, in which the ILEs show a significant red shift with the increase of the electric field. Meanwhile, with an increasing electric field, the energy difference between CBM_K and CBM_Q increased; this behavior supports the fact that the electrons in CBM_Q tend to relax to CBM_K and suppress the transition path of Q–K. This is also the reason for the increase in the ratio of ILE1/ILE2 with an increase in gate voltage in the experiments (as shown in Fig. 4e).

Fig. 6 DFT calculations of the WSe₂/WS₂ heterostructure with a twist angle of 0°. (a) The component-resolved band structure of the WSe₂/WS₂ heterostructure with a twist angle of 0°. (b) The spin-resolved band structure of the WSe₂/WS₂ heterostructure with a twist angle of 0°. (c) The band structure as a function of gate voltage. (d) The energy of CBM_K–VBM_K and CBM_Q–VBM_K as a function of gate voltage.

4. Conclusions

In summary, we have studied the evolution of the interlayer excitons with the twist angle in TMDC heterostructures by combining PL measurements and DFT calculations. Two strong interlayer excitons were observed when the twist angles were near 0° and 60° due to the enhancement of interlayer coupling. Furthermore, two interlayer excitons were identified as the direct and indirect interlayer excitons based on the gate-, excitation-power-, and helicity-dependent PL measurements. Helicity-resolved PL shows that the two interlayer excitons hold opposite DoP. By comparing these results with the DFT calculations, we could assign two interlayer excitons to the direct transition of K–K and the indirect transition of Q–K, respectively. Finally, the emission properties of the interlayer excitons were further regulated by applying an electric field, and their emission energy and intensity show great adjustability under the influence of the electric field. Our results show great potential in the field of twist-angle optoelectronic-dependent devices in the future.

Author contributions

Chunxiao Cong directed the research work. Chunxiao Cong, Jiajun Chen and Xiaofei Yue conceived and designed the experiments. Jiajun Chen fabricated the samples and implements the project. Jiajun Chen, Xiaofei Yue, Yabing Shan, Huishan Wang, Jinkun Han, conducted the experiments. Weihuang Yang perform the DFT calculations. Chunxiao Cong, Jiajun Chen, Xiaofei Yue, Weihuang Yang and Zhi-Jun Qiu analyzed the data. Chunxiao Cong and Jiajun Chen co-wrote the manuscript. All authors discussed the results and commented on the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work is supported by the National Key R&D Program of China (Grant No. 2018YFA0703700, Grant No. 2017YFF0206106), the Shanghai Municipal Science and Technology Commission (Grant No. 20ZR1403200), the National Natural Science Foundation of China (Grant No. 61774040, 61774042), the Strategic Priority Research Program of Chinese Academy of Sciences (Grant No. XDB30000000), and the National Young 1000 Talent Plan of China.

Notes and references

1. D. Xiao, G. B. Liu, W. Feng, X. Xu and W. Yao, Phys. Rev. Lett., 2012, 108, 196802.
2. H. Zeng, J. Dai, W. Yao, D. Xiao and X. Cui, Nat. Nanotechnol., 2012, 7, 490–493.
3. K. F. Mak, K. He, C. Lee, G. H. Lee, J. Hone, T. F. Heinz and J. Shan, Nat. Mater., 2013, 12, 207–211.
4. Y. Lin, X. Ling, L. Yu, S. Huang, A. L. Hsu, Y. H. Lee, J. Kong, M. S. Dresselhaus and T. Palacios, Nano Lett., 2014, 14, 5569–5576.
5. Y. You, X. X. Zhang, T. C. Berkelbach, M. S. Hybertsen, D. R. Reichman and T. F. Heinz, Nat. Phys., 2015, 11, 477–481.
6. J. X. Li, W. Q. Li, S.-H. Hung, P. L. Chen, Y. C. Yang, T. Y. Chang, P. W. Chiu, H. T. Jeng and C. H. Liu, Nat. Nanotechnol., 2022, 17, 721–728.
7. C. Gong, H. Zhang, W. Wang, L. Colombo, R. M. Wallace and K. Cho, Appl. Phys. Lett., 2013, 103, 053513.
8. V. O. Özçelik, J. G. Azadani, C. Yang, S. J. Koester and T. Low, Phys. Rev. B, 2016, 94, 035125.
9. H. M. Hill, A. F. Rigosi, K. T. Rim, G. W. Flynn and T. F. Heinz, Nano Lett., 2016, 16, 4831–4837.
10. N. R. Wilson, P. V. Nguyen, K. Seyler, P. Rivera, A. J. Marsden, Z. P. Laker, G. C. Constantinescu, V. Kandyba, A. Barinov and N. D. Hine, Sci. Adv., 2017, 3, e1601832.
11. E. Barré, O. Karni, E. Liu, A. L. O'Beirne, X. Chen, H. B. Ribeiro, L. Yu, B. Kim, K. Watanabe, T. Taniguchi, K. Barmak, C. H. Lui, S. Refaely-Abramson, F. H. da Jornada and T. F. Heinz, Science, 2022, 376, 406–410.
12. J. Peng, C. Ren, W. Zhang, H. Chen, X. Pan, H. Bai, F. Jing, H. Qiu, H. Liu and Z. Hu, ACS Nano, 2022, 16, 21600–21608.
13. C. Jin, J. Kim, M. I. B. Utama, E. C. Regan, H. Kleemann, H. Cai, Y. Shen, M. J. Shinner, A. Sengupta and K. Watanabe, Science, 2018, 360, 893–896.
14. P. Rivera, J. R. Schaibley, A. M. Jones, J. S. Ross, S. Wu, G. Aivazian, P. Klement, K. Seyler, G. Clark and N. J. Ghimire, Nat. Commun., 2015, 6, 1–6.
15. P. Rivera, K. L. Seyler, H. Yu, J. R. Schaibley, J. Yan, D. G. Mandrus, W. Yao and X. Xu, Science, 2016, 351, 688–691.
16. X. Zhu, N. R. Monahan, Z. Gong, H. Zhu, K. W. Williams and C. A. Nelson, J. Am. Chem. Soc., 2015, 137, 8313–8320.
17. Y. Yoon, Z. Zhang, R. Qi, A. Y. Joe, R. Sailus, K. Watanabe, T. Taniguchi, S. Tongay and F. Wang, Nano Lett., 2022, 22, 10140–10146.
18. J. E. Zimmermann, Y. D. Kim, J. C. Hone, U. Höfer and G. Mette, Nanoscale Horiz., 2020, 5, 1603–1609.
19. L. Yuan, B. Zheng, J. Kunstmann, T. Brumme, A. B. Kuc, C. Ma, S. Deng, D. Blach, A. Pan and L. Huang, Nat. Mater., 2020, 19, 617–623.
20. C. Zhang, C. P. Chuu, X. Ren, M.-Y. Li, L. J. Li, C. Jin, M. Y. Chou and C. K. Shih, Sci. Adv., 2017, 3, e1601459.
21. H. Yu, G. B. Liu, J. Tang, X. Xu and W. Yao, Sci. Adv., 2017, 3, e1701696.
22. R. Xiong, J. H. Nie, S. L. Brantly, P. Hays, R. Sailus, K. Watanabe, T. Taniguchi, S. Tongay and C. Jin, Science, 2023, eadd5574.
23. H.-J. Chuang, M. Phillips, K. M. McCreary, D. Wickramaratne, M. R. Rosenberger, V. P. Oleshko, N. V. Proscia, M. Lohmann, D. J. O'Hara, P. D. Cunningham, C. S. Hellberg and B. T. Jonker, ACS Nano, 2022, 16, 16260–16270.
24. O. Karni, E. Barré, V. Pareek, J. D. Georgaras, M. K. L. Man, C. Sahoo, D. R. Bacon, X. Zhu, H. B. Ribeiro, A. L. O'Beirne, J. Hu, A. Al-Mahboob, M. M. M. Abdelrasoul, N. S. Chan, A. Karmakar, A. J. Winchester, B. Kim, K. Watanabe, T. Taniguchi, K. Barmak, J. Madéo, F. H. da Jornada, T. F. Heinz and K. M. Dani, Nature, 2022, 603, 247–252.
25. E. M. Alexeev, D. A. Ruiz-Tijerina, M. Danovich, M. J. Hamer, D. J. Terry, P. K. Nayak, S. Ahn, S. Pak, J. Lee and J. I. Sohn, Nature, 2019, 567, 81–86.
26. Z. Ji, H. Hong, J. Zhang, Q. Zhang, W. Huang, T. Cao, R. Qiao, C. Liu, J. Liang and C. Jin, ACS Nano, 2017, 11, 12020–12026.
27. P. K. Nayak, Y. Horbatenko, S. Ahn, G. Kim, J. U. Lee, K. Y. Ma, A.-R. Jang, H. Lim, D. Kim and S. Ryu, ACS Nano, 2017, 11, 4041–4050.
28. E. Calman, L. Fowler-Gerace, D. Choksy, L. Butov, D. Nikonov, I. Young, S. Hu, A. Mishchenko and A. Geim, Nano Lett., 2020, 20, 1869–1875.
29. H. Yu, G. B. Liu and W. Yao, 2D Mater., 2018, 5, 035021.
30. M. Long, P. Wang, H. Fang and W. Hu, Adv. Funct. Mater., 2019, 29, 1803807.
31. Y. Tang, K. F. Mak and J. Shan, Nat. Commun., 2019, 10, 1–7.
32. Y. Zhou, G. Scuri, D. S. Wild, A. A. High, A. Dibos, L. A. Jauregui, C. Shu, K. De Greve, K. Pistunova and A. Y. Joe, Nat. Nanotechnol., 2017, 12, 856–860.
33. J. Chen, K. Shao, W. Yang, W. Tang, J. Zhou, Q. He, Y. Wu, C. Zhang, X. Li, X. Yang, Z. Wu and J. Kang, ACS Appl. Mater. Interfaces, 2019, 11, 19381–19387.
34. G. Cheng, B. Li, C. Zhao, X. Yan, H. Wang, K. M. Lau and J. Wang, Nano Lett., 2018, 18, 5640–5645.
35. K. Wang, B. Huang, M. Tian, F. Ceballos, M.-W. Lin, M. Mahjouri-Samani, A. Boulesbaa, A. A. Puretzky, C. M. Rouleau and M. Yoon, ACS Nano, 2016, 10, 6612–6622.
36. C. Jin, E. C. Regan, A. Yan, M. Iqbal Bakti Utama, D. Wang, S. Zhao, Y. Qin, S. Yang, Z. Zheng and S. Shi, Nature, 2019, 567, 76–80.
37. S. Zhang, H. M. Hill, K. Moudgil, C. A. Richter, A. R. Hight Walker, S. Barlow, S. R. Marder, C. A. Hacker and S. J. Pookpanratana, Adv. Mater., 2018, 30, 1802991.
38. A. Chernikov, A. M. Van Der Zande, H. M. Hill, A. F. Rigosi, A. Velauthapillai, J. Hone and T. F. Heinz, Phys. Rev. Lett., 2015, 115, 126802.
39. X. Lu, M. Utama, X. Wang, W. Xu, W. Zhao, M. H. S. Owen and Q. Xiong, Small, 2017, 13, 1701039.
40. L. Wu, C. Cong, J. Shang, W. Yang, Y. Chen, J. Zhou, W. Ai, Y. Wang, S. Feng and H. Zhang, Nano Res., 2021, 14, 2215–2223.
41. S. Tongay, W. Fan, J. Kang, J. Park, U. Koldemir, J. Suh, D. S. Narang, K. Liu, J. Ji and J. Li, Nano Lett., 2014, 14, 3185–3190.
42. N. Peimyoo, J. Shang, W. Yang, Y. Wang, C. Cong and T. Yu, Nano Res., 2015, 8, 1210–1221.
43. J. T. Mlack, P. Masih Das, G. Danda, Y. C. Chou, C. H. Naylor, Z. Lin, N. P. López, T. Zhang, M. Terrones, A. T. C. Johnson and M. Drndić, Sci. Rep., 2017, 7, 43037.
44. M. Kremser, M. Brotons-Gisbert, J. Knörzer, J. Gückelhorn, M. Meyer, M. Barbone, A. V. Stier, B. D. Gerardot, K. Müller and J. J. Finley, npj 2D Mater. Appl., 2020, 4, 1–6.
45. A. Branny, G. Wang, S. Kumar, C. Robert, B. Lassagne, X. Marie, B. D. Gerardot and B. Urbaszek, Appl. Phys. Lett., 2016, 108, 142101.
46. B. Laikhtman and R. Rapaport, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 195313.
47. L. Butov, A. Shashkin, V. Dolgopolov, K. Campman and A. Gossard, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 60, 8753.
48. W. T. Hsu, L. S. Lu, D. Wang, J. K. Huang, M. Y. Li, T. R. Chang, Y. C. Chou, Z. Y. Juang, H. T. Jeng and L. J. Li, Nat. Commun., 2017, 8, 1–7.
49. J. Shang, X. Shen, C. Cong, N. Peimyoo, B. Cao, M. Eginligil and T. Yu, ACS Nano, 2015, 9, 647–655.
50. E. Liu, E. Barré, J. van Baren, M. Wilson, T. Taniguchi, K. Watanabe, Y. T. Cui, N. M. Gabor, T. F. Heinz, Y. C. Chang and C. H. Lui, Nature, 2021, 594, 46–50.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ra02952b

‡ These authors contributed equally to this work.

---