Graphene nanoplatelets (GNPs): a source to bring change in the properties of Co–Ni–Gd-ferrite/GNP nanocomposites

Abstract

The nanocomposites of Co_0.5Ni_0.5Gd_0.03Fe_1.97O₄/graphene nanoplatelets (CNGF/GNPs) were synthesized by a cost-effective sol–gel auto combustion (SGAC) route. The X-ray diffraction analysis confirmed the cubic structure of the as-prepared nanocomposites, and a crystallite size of 32.28 nm was observed for the 7.5 wt% GNPs. Irregular and unique nanoparticles consisting of short stacks of graphene sheets having a platelet shape were confirmed by the morphological analysis of the as-prepared nanocomposites. Raman analysis revealed a spinel crystal structure along with a new vibrational mode due to the GNPs. The energy bandgap was 3.98 eV for the composite with 7.5 wt% GNP concentration. It was observed that the percentage temperature coefficient of resistance (TCR%) rapidly decreased with an increase in temperature both in low- and high-temperature ranges. Dielectric studies carried out in the frequency range 10⁴–10⁷ Hz confirmed that the graphene-added composites had high values for both the real and imaginary parts of permittivity at low frequencies. A decrease in saturation magnetization with an increase in GNP concentration was observed compared with the pure CNGF samples. Hence, the as-prepared composites are useful for application in high-frequency devices as well as spintronics.

---

1. Introduction

The incorporation of nano-sized particles into the matrix of a standard material results in a nanocomposite, which exhibits drastic improvement in several properties, such as mechanical strength and magnetic, optical, electrical, and thermal conductivities. An excellent example of the nanocomposites is graphene with soft ferrites, which show tremendous changes and enhancement in properties and hence are successfully used in various fields, such as wastewater treatment, improvement of broadband absorption in gigahertz frequencies and microwave absorption, and energy storage sensors.^1–4 The structure of graphene is capable of modifying the different properties of soft ferrites, such as non-conductivity to conductivity, thereby intensifying their magnetism and improving the structural and mechanical parameters. Moreover, it can also improve the thermal and dielectric properties of the nanocomposites. These promising structural, electrical, optical, magnetic, mechanical, and thermal properties of graphene have opened new avenues for learning materials science.^5,6 Compared with other nanomaterials, soft ferrites are less expensive, reliably stable, and easy to prepare. Their high permeability at radio frequencies, high Curie temperature, high electrical resistivity, low eddy current loss, fine environmental stability, and mechanical hardness make them suitable for application in many devices, such as microwave apparatus, inductors, choke coils, transformers, and electromagnetic interface (EMI) suppressors. One class of soft ferrites is cubic spinel ferrites (SFs) with MFe₂O₄, where M is a divalent ion, such as Mn²⁺, Ni²⁺, Fe²⁺, Co²⁺, or Mg²⁺. A lot of studies and research have been done on cubic ferrites and many mixed ferrites. Saqib et al. studied the structural, electrical, and magnetic properties of Mg-doped ZnFe₂O₄ ferrites.⁷ Different ferrites are considered unique for different properties; cobalt ferrite has special magnetic properties^8–10 and outstanding chemical and structural stability.^11–13 The substitution of Fe³⁺ ions with rare earth metals with larger ionic radii than Fe³⁺ into the spinel structure alters the electromagnetic properties of ferrites. Consequently, the inconsistent behavior of doped nickel ferrites is observed.^14–16

The preparation techniques used for cubic ferrites with different concentrations and the distribution of different cations at the tetrahedral (A-) and octahedral (B-) sites of the sample lattice play a vital role in tuning the properties. Thus, any addition and alteration in the distribution and ratio of these cations can change their magnetic behavior. Satalkar et al. prepared Zn_0.7−xNi_xMg_0.2Cu_0.1Fe₂O₄ (x = 0.0–0.7) ferrites by a sol–gel auto-combustion (SGAC) method. They found that Ni²⁺ addition plays a part in determining the magnetic properties and changes the cationic distribution.¹⁷ Therefore, the usage of suitable additives plays a vital role in gaining high-performance ferrites.

Tremendous work has been done on the addition of rare earth metals to soft ferrites at varying concentrations by using a variety of mechanical and chemical procedures, such as sol–gel, hydrothermal, and traditional ceramic technology. Elements of the lanthanide series, such as gadolinium, neodymium, cerium, and yttrium, are added to different ferrites due to their special characteristics. These elements are frequently used with ferrite combinations at different concentrations in many applications as they enhance optical, structural, magnetic, electrical, and morphological properties. Pawar et al. reported that Gd³⁺ substitution in the Co–Zn ferrite increases the saturation magnetization and coercivity. Consequently, these Gd³⁺-substituted materials are appropriate for use in permanent magnets and magnetic recording media.¹⁸ The properties of cubic ferrites are enhanced when rare earth metals with higher ionic radii are substituted for Fe³⁺. The concentration of rare earth metals plays a pivotal role in determining the properties of the cubic ferrites.¹⁹ Poudel et al. studied that the concentration of Gd³⁺ in Ni ferrite enriched its properties.¹⁶ Hossain, M. D., et al. studied the properties tailored by Gd³⁺ substitution at the B sites, replacing the Fe³⁺ ions of the Ni–Zn–Co ferrite. Due to substitution with gadolinium, they found changes in the structural properties, as well as electrical properties.²⁰ It is worth mentioning that the content of graphene plays an important, leading role in defining the dielectric behavior of carbon materials along with their magnetic anisotropy. This subsequently would impact the microwave weakening behavior.

In this work, we followed the sol–gel auto-combustion route to prepare Ni-doped cobalt ferrites with a stoichiometric formula of Co_0.5Ni_0.5Gd_0.03Fe_1.97O₄ (CNGF) and loaded them on the surface of graphene nanoplatelets (GNP) using a sonochemical approach. Therefore, this work aims to investigate the impact of graphene nanoplatelets (GNPs) on the spectral, electrical, magnetic, and dielectric properties of the CNGF composites prepared via the sol–gel auto combustion (SGAC) process.

2. Materials and methods

2.1 Materials

The following chemicals were used for the synthesis of the Co_0.5Ni_0.5Gd_0.03Fe_1.97O₄ (CNGF) sample and the CNGF/GNP composites. Iron nitrate nonahydrate [(Fe(NO₃)₂·9H₂O), nickel nitrate hexahydrate [(Ni(NO₃)₂·6H₂O), aqueous ammonia [(NH₄OH), cobalt nitrate hexahydrate [(Co(NO₃)₂·6H₂O), gadolinium nitrate hexahydrate [Gd(NO₃)₂·6H₂O], citric acid (C₆H₈O₇), and graphene nanoplatelets (GNP).

2.2 Synthesis of CNGF sample

The CHNF sample was prepared by the sol–gel auto-combustion (SGAC) method. All chemicals at proper stoichiometric proportions were sonicated individually for 10 min at 353 K to make their homogenous solutions in distilled water. All prepared solutions were mixed again by using a magnetic stirrer for up to 15 minutes until well combined, followed by the addition of the citric acid solution. NH₄OH was added dropwise to maintain the pH of the solution at 7 and stirring was further continued for 20 minutes. The samples were heated at 523 K until a gel was formed, after which the magnetic stirrer was turned off while heating was continued, which further led to self-combustion, and the solution turned into ash. It was mechanically ground by using a mortar and pestle to make a fine powder, which was calcined at 1123 K for 5 h. The calcined samples were again ground to obtain their powder form.

2.3 Synthesis of CNGF/GNP nanocomposites

The sonochemical approach was used to prepare the CNGF/GNP nanocomposites by keeping the stoichiometric quantities of GNP at 2.5 wt%, 5 wt%, and 7.5 wt% of the total metal nitrate salts. The required amount of GNP was dissolved in distilled water, and the mixture was sonicated for half an hour to get a homogeneous dispersion. All the metal nitrate salts dissolved in distilled water were separately added in dispersed GNP, and each mixture was again sonicated for 20 minutes. A calculated amount of citric acid dissolved in distilled water was added to the metal nitrate salts -GNP mixture and sonicated further for 10 minutes. This mixture was placed on a magnetic stirrer for thorough mixing, and this was followed by the SGAC method to get ash, which was ground into a fine powder and then calcined at 1123 K for 5 h. Fig. 1 illustrates the step-by-step fabrication process.

Fig. 1 A schematic representation of the synthesis of NCGF/GNP nanocomposites.

2.4 Characterization techniques used

The structural properties and phase confirmation of the prepared samples were studied by X-ray diffraction (XRD) analysis using a Bruker D8 Advanced X-ray diffractometer (XRD) using Cu-Kα source with a wavelength of 1.54 (Å). To inspect the surface morphology, scanning electron microscopic (SEM) images were captured using a Nova Nano SEM series 450. Raman analysis was used to confirm the lattice structure of the ferrites along with Gd³⁺ substitution of and addition of GNP by using laser excitation at 532 and 780 nm in the range of 200–1800 cm⁻¹. The energy bandgap (E_g) of the as-prepared samples was determined through UV-visible spectroscopy. Current–voltage (I–V) measurements and hence resistivity were calculated by using the two-probe technique on an electric meter KEITHLEY Model 2401. The dielectric behavior was studied using an LCR Meter (IM3533 series) in the frequency range of 4 Hz to 8 MHz at room temperature. The magnetic properties were investigated by studying the M–H loop at 303 K by using a vibrating sample magnetometer (VSM-175).

3. Results and discussion

3.1 Structural properties

To discuss the effect of GNP on the structure of the CNGF nanoparticles, XRD analysis and Raman spectroscopy were used, while the effect of GNP on the surface morphology was studied using the micrographs obtained from SEM.

3.1.1 X-Ray diffraction analysis. XRD spectra were used to understand the structural changes in the CNGF crystals after the addition of GNP, as shown in Fig. 2. GNP showed diffraction peaks (as shown in Fig. 2) at a 2θ value of 26.38°, which denotes the (002) crystal plane.²¹ In addition to that, the CNGF/GNP nanocomposites revealed diffraction peaks at 2θ of 30.2°, 35.6°, 37.2°, 43.3^°, 53.3° and 57.3°, corresponding to the (220), (311), (222), (400), (422), and (511) planes, respectively.²² Further, using Braggs equation: 2d sin θ= nλ, the d-spacing for pure GNP calculated based on 2θ = 26.8° corresponding to the (002) plane was 3.38 Å, which is larger than the values of the CNGF nanoparticles and CNFG/GNP nanocomposites, as shown in Table 1. Being a cubic crystal structure, the three lattice constants are the same a = b = c, and their value was calculated using the formula; a = d_hkl[h² + k² + l²]^1/2, where h, k, and l Miller indices of the high-intensity peak (311)were used to calculate the value of the lattice constants as listed in Table 1. The values of unit cell volume (V = a³) were calculated by using the value of the lattice constant. The lattice constant and unit cell volume of the CNGF/GNP nanocomposites did not change significantly. This may be due to the incorporation of GNP in the CNGF nanoparticle spinel lattice. The crystalline size (D) of the as-synthesized nanocomposites was calculated using the Scherrer equation; D = 0.94λ/β cos θ, where β is the full width at half maxima (FWHM) of the highest intensity peak of the samples, λ = 1.5406 Å is the wavelength of the used Cu K_α radiation source, and” represents the Braggs reflection angle. The smaller crystallite size of the CNGF/GNP nanocomposites compared with the pure CNGF sample may be due to the incorporation of GNP in the CNGF lattice (as shown in Table 1). The dislocation density (δ = 1/D²) is a measure of the number of dislocations per unit volume of a crystalline material and follows the opposite trend to crystallite size i.e. when the crystallite size of the material is the maximum, the dislocation line density is minimum and vice versa. The crystallite size was minimum for the CNGF/2.5wt% GNP nanocomposite and it had the maximum dislocation line density, as shown in Table 1. It is clear from Table 1 that the packing factor (p) also was smaller for the CNGF/GNP nanocomposites compared with the CNGF nanoparticles. The increase in the values of microstrain (ε) of the CNGF/GNP nanocomposites to that of the CNGF nanoparticles, along with a deteriorating trend of crystalline size, suggests their enhanced electrocatalytic activity.²³

Fig. 2 The XRD spectra of the CNGF nanoparticles and CNGF/GNP nanocomposites.

Table 1 The structural parameters of the CNFG nanoparticles and CNFG/GNP nanocomposites

Samples	a (Å)	D (nm)	V (Å)^3	d (Å)	δ × 10^−4 (nm^−2)	ε	p
CNGF	8.345	40.18	581.21	2.518	6.193	0.00294	159.69
CNGF/2.5wt%GNP	8.335	28.76	579.18	2.515	12.131	0.00411	114.44
CNGF/5wt%GNP	8.343	36.38	580.88	2.459	7.552	0.00325	144.64
CNGF/7.5wt%GNP	8.344	32.80	581.05	2.518	9.292	0.00361	130.38

---

3.1.2 Scanning electron microscopy analysis. SEM images were used to analyze the morphology of the CNGF nanoparticles and CNGF/GNP nanocomposites, as shown in Fig. 3(a–d). Irregular particle morphology was observed in the nanoparticles, as seen in Fig. 3(a). The reported morphology of GNP is flake-like; moreover, graphene nanoplatelets are unique nanoparticles consisting of short stacks of graphene sheets having a platelet shape.²⁴ The SEM images of the as-prepared CNGF/GNP nanocomposites in Fig. 3(a–d) indicate that the GNP was densely covered with the CNGF nanoparticles. This indicates that the mechanism of electrostatic attraction between the nanoparticles and graphene²⁵ gives rise to the agglomeration of nanoparticles in the flake-like structure of GNP due to weak van der Waals, electrostatic, and capillary forces, which are responsible for producing magnetic interactions between the particles. The SEM images showed that samples with graphene were thicker than CNGF, which is due to the presence of different functional groups like carboxyl and carbonyl and some traces of oxygen, while, in the absence of graphene, the nanoparticles showed scattered behavior (as shown in Fig. 3(a)).²⁴

Fig. 3 The SEM images of the (a) CNGF nanoparticles, (b) CNGF/2.5wt%GNP nanocomposite, (c) CNGF/5wt%GNP nanocomposite, and (d) CNGF/7.5wt%GNP nanocomposite.

3.1.3 Raman spectroscopy analysis. Fig. 4 reveals the Raman spectra of pure GNP, the CNGF sample, and the CNGF/GNP composites. Pure GNP showed two vibrational bands around 1343 cm⁻¹ and 1621 cm⁻¹ corresponding to the D-band and G-band, respectively. The characteristic peaks at 689.1 cm⁻¹, 545.6 cm⁻¹, 471.6 cm⁻¹, 316.8 cm⁻¹, and 370.1 cm⁻¹ of the SFs corresponded with five active Raman modes A_1g (R), 3 T_2g (R) and E_g respectively, where A, E, and T denote one-, two- and three-dimensional display of the SFs, respectively, and g denotes symmetry at the center of inversion.²⁶ Raman spectra of the samples containing GNP at concentrations 2.5%, 5%, and 7.5% are shown in Fig. 4, showing slight changes in the first five active modes: the A_1g (1) mode of vibration at around 689.1 cm⁻¹ changed to 686.6 cm⁻¹ due to GNP addition due to the symmetric stretching of the oxygen atoms between Fe–O and metal ions at the tetrahedral (A-) site. T_2g (3), which is assigned to the asymmetric bending of oxygen at the octahedral (B-) site relative to Fe, changed from 545.6 to 543.3 cm⁻¹ due to the insertion of GNP. T_2g (2), which is responsible for the asymmetric stretching of the Fe–O bond at the B-site, was originally found at 471.6 cm⁻¹ but shifted to 467.7 cm⁻¹ due to the addition of GNP. A low-intensity peak at 370.2 cm⁻¹ representing the E_g mode, which is responsible for the symmetric bending of the oxygen ions with respect to iron, moved to 365.8 cm⁻¹ in the CNGF/GNP composites. The T_2g (1) peak assigned to the translational motion of the complete tetrahedron (Fe–O₄) was present at 316.8 cm⁻¹ and moved to 314.5 cm^−127,28

Fig. 4 The Raman spectra of GNP (inset), CNGF, and CNGF/GNP composites.

3.2 Optical studies by UV-vis analysis

The optical transition nature and energy bandgap of the as-prepared CNGF sample and CNGF/GNP composites were measured by using the Tauc plot method. SFs and their composites have a direct energy bandgap.²⁹ The Tauc plot equation is given as:²⁶ (αhv)² = K(hv − E_g), where “2” is for direct allowed transitions, the absorption coefficient (α) was determined by employing the following equation:²⁶ α = 2.303 log(A)/l, where A indicates the absorbance, and l is the path length of light along which absorbance takes place, and the energy bandgap (E_g) was calculated by extrapolating the linear part of the curves in Fig. 5(a–d). The E_g values were 4.14 eV, 3.99 eV, 3.88 eV, and 3.94 eV for CNGF, CNGF/2.5wt%GNP, CNGF/5wt%GNP, and CNGF/7.5wt%GNP, respectively. The E_g of the CNGF sample is the widest due to the interaction between the O²⁻p and Fe-3d energy states, resulting in orbital overlap, while the change in energy bandgap is due to the insertion of GNP in the host CNGF sample.

Fig. 5 (a–d) The Tauc plots for the CNGF sample and CNGF/GNP composites.

3.3 I–V measurements analysis

The two-probe method was used to determine the DC resistivity of the CNFG nanoparticles and CNGF-GNP (2.5%, 5%, and 7.5%) nanocomposites. The resultant measured resistivity values of each given sample are summarized in Table 2. The calculated resistivity of the integrated CNGF nanoparticle was 2.44 × 10⁹ Ω cm at room temperature. The general behavior of ferrite nanoparticles is more insulating, but they can conduct due to the temperature dependency of the electrons, which causes the transfer of the electrons between the ferrous (Fe²⁺) and ferric (Fe³⁺) ions at the octahedral B-lattice sites and transfer of holes between the Ni²⁺ and Ni³⁺ ions.³⁰ The log ρ vs. 1000/T (Arrhenius plots) graphs are shown in Fig. 6 at different temperatures ranging from 313 K to 673 K. Based on the variation in the slope of the curve, the resistivity curve can be split into two regions, namely the ferromagnetic region and paramagnetic region. The change in resistivity is in line with a specific temperature at which the log values show a transformation; this is described as the Curie temperature or the transition temperature and is denoted as (T_C). This process or mechanism also causes the transformation of magnetic collation from ferromagnetic to paramagnetic, thus forming two distinct regions in the plots. It is worth noting here that the region below T_C is called the ferromagnetic region, whilst the region above the T_C is referred to as the paramagnetic region.³¹

Table 2 The DC electrical resistance and resistivity of the CNFG nanoparticles and CNFG-GNP nanocomposites

Samples	CNGF	CNGF-GNP (2.5%)	CNGF-GNP (5%)	CNGF-GNP (7.5%)
Resistance (Ω)	1.36 × 10^9	5.85 × 10^7	1.23 × 10^8	4.41 × 10^7
Resistivity (Ω cm)	2.44 × 10^9	1.05 × 10^8	2.21 × 10^8	7.89 × 10^7

---

Fig. 6 Arrhenius plots of all the samples.

On the contrary, the resistivity of graphene is poor, and hence it is found to be a good conductor with a pristine surface containing encapsulated sp²-hybridized carbon atoms inside the hexagonal lattice with certain constraints. This is because of the availability of functional groups like ethers, carboxyl, and hydroxyls, which can react with atmospheric humidity to form acids and other compounds. It is worth noting here that the oxidation level has been shown to directly resist the electrical properties of graphene nanoplatelets due to the quasi-ID active bonding between the carbon sheets with a conducting nature and the defects, according to the variable range hopping model.³² The temperature dependency of the resistivity of the fabricated samples is shown in Fig. 7(a–c), which reveals that in the low-temperature range, the resistivity of CNGF increases with the increase in temperature, but in the medium- and high-temperature ranges, resistivity increases when temperature decreases, confirming the semiconducting nature of the gadolinium-doped ferrites. The same trend is found when GNPs are added to CNGF but with less diversity.²⁰ These reveal that lesser ferrite particles could get into the honeycomb or hexagonal structures of GNP, causing a rise in the density of functional groups that act as charge carriers. Therefore, the conductivity of graphene remains supreme, and the resistivity of the composites deteriorates with different concentrations of GNP, as shown in Fig. 7(a–c). The resistivity of the CNGF-GNP nanocomposites is less compared with the gadolinium-doped cobalt nickel ferrite nanoparticles. It is, therefore, comprehended that the CNGF-GNP composites have changed the resistivity of the ferrite nanoparticles, and they can be used in the preparation of supercapacitors.³³ TCR% is the percentage of the relative change in resistivity per degree temperature change. TCR is a valuable resistor performance stability indicator. TCR% is essential for estimating the relationship of resistivity with ambient temperature variations, both at low and high operating temperatures. TCR% is calculated from resistivity using the formula:⁴² TCR (%) = [(1/ρ) × (dρ/dT)] × 100%. The TCR% values were calculated for all samples from 313 K to 673 K and plotted against temperature, as shown in Fig. 8(a). The TCR% decreased rapidly with an increase in temperature both in the low-temperature range and high-temperature range, as shown in Fig. 8(b). The CNGF sample without graphene nanoplatelets showed the maximum value of 3.70 K⁻¹ at a temperature of 313 K, while the composites with graphene nanoplatelets showed lesser values at 313 K due to the carbon in graphene. The peak values of TCR% were −2.43% K⁻¹ at 373 K, −2.62% K⁻¹ at 368 K, −2.71% K⁻¹ at 341 K, and −2.45% K⁻¹ at 368 K for CNGF, CNGF-GNP 2.5%, CNGF-GNP 5% and CNGF-GNP 7.5% respectively. Materials with temperature-dependent electrical resistance can be used as a source of radiant heat and are used in many applications, such as bolometric devices for microwave measurements, astronomy, and thermal cameras.²⁷

Fig. 7 The temperature-dependent DC resistivity (ρ_DC) of the CNGF nano particles and CNGF-graphene nanoplatelet composites in the (a) lower temperature range (b) medium temperature range and (c) elevated temperature range.

Fig. 8 (a) Temperature versus the temperature coefficient of resistance percentage for all the samples; (b) T versus TCR% for each sample.

3.4 Dielectric studies

The term permittivity or dielectric constant refers to the measure of capacitance observed during the formation of an electric field.³⁴ The electronic distribution of the synthesized samples was predicted by measuring their polarizations through dielectric analysis.²⁰ The values of dielectric constant (ε′) and dielectric constant loss (ε′′) were plotted as functions log of frequency (10⁴ Hz to 10⁷ Hz) at room temperature, as shown in Fig. 9(a) and (b), respectively. The dielectric constant and loss initially decreased due to the reduction in the space charge polarization effect. Then, it remained approximately constant. On the other hand, a high dielectric constant was observed at low frequencies. This is because a potential barrier is created at the grain boundaries by space charge polarization. Subsequently, there is an accumulation of charge at the grain boundary, resulting in an increase in the real and imaginary parts of the permittivity values. The dielectric dispersion can be explained by the dominance of the impact of grain boundaries rather than the grains. Koop's phenomenological theory attributes this to the Maxwell–Wagner kind of interfacial polarization. Both ε′ and ε′′ show maximum values when the frequency is low because of interfacial and dipole polarization.³⁵ The CNGF nanoparticles showed lower values of dielectric constant and dielectric constant loss, while the CNGF/GNP nanocomposites showed higher values of both at low frequencies, proving the graphene and ferrite interactions and the presence of better polarization due to graphene. Moreover, the CNGF/5wt%GNP nanocomposite exhibited higher values of the real and imaginary parts of the dielectric constant than those of the CNGF nanoparticles. As the frequency was increased, the values of ε′ and ε′' remained constant for all the samples. At higher frequencies, due to fast variation in the applied field, the dipoles cannot follow the exact variation speedily, and the response of the permanent dipoles along with the contribution of charge carriers decreases, leading to a decrease in the dielectric constants. Graphene enhances the dielectric constant at lower frequencies, making it a significant factor in the development of high-temperature ceramic supercapacitors.³⁶ The values of dielectric constant and dielectric constant loss increased when graphene nanoparticles were added.³⁷ In CNGF, the net polarization is due to two types of charges: (1) due to electron transfer at the octahedral site between Fe²⁺ and Fe³⁺, and (2) due to p-type charge carriers, namely Ni³⁺/Ni²⁺ and Co³⁺/Co²⁺, at the B-site. At higher frequencies, the dielectric constant is not dependent on the frequency, so polarization remains unchanged at these frequencies; this shows that polarization depends on the variation in the frequency range. Moreover, due to the insertion of doped ferrites into graphene nanoplatelets, an interface is produced, and charges accumulate at this interface with different relaxation times when current is passed through the sample, which can be well-described by the Maxwell–Wagner (MW) effect.³⁸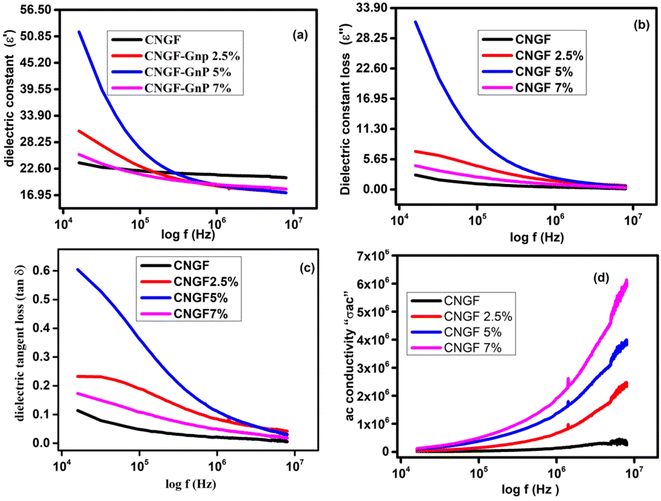

Fig. 9 The plots of (a) ε′ versus frequency, (b) ε′′ versus frequency, (c) tan δ versus frequency, and (d) σ ac versus frequency.

The dielectric loss tangent (tan δ = ε′′/ε′) illustrates its dependence on the energy dissipation frequency.³⁹ Energy dissipation in the samples due to conduction (electrical) and resonance occurring at the domain wall is described by calculating the dielectric loss tangent. The plot of tan δ and frequency is shown in Fig. 9(c), indicating its dependency on the frequency i.e., at a higher frequency, the dielectric loss tangent has the lowest value.³² One of the characteristics of nanocomposites is that, with a change in frequency, the ac conductivity changes, as noticed in Fig. 9(d), and this behavior can be well-explained by Koop's theory, according to which conductivity shows variation/dispersion in the higher frequency range (>10⁵ Hz). At room temperature, transitions between Fe²⁺ to Fe³⁺ at the B-site increase (a hopping mechanism) and lessen the effect of oxygen ions, thus forming well-conducting grains and poor-conducting grain boundaries.⁴⁰ Firstly, the presence of multiple interfaces between the graphene nanoplatelets and the modified magnetic materials leads to increased interfacial polarization and the subsequent relaxation process. This phenomenon contributes to the enhancement of dielectric loss. Moreover, recent research findings indicate that charges can be transferred across the interface of a graphene-ferrite heterostructure due to the distinct physical properties of these materials. Hence, in this study, it is reasonable to expect a charge transfer process to take place at the interface between the GNPs and the CNGF sample. This would result in the introduction of free carriers from ferrite into graphene, leading to electric polarization in the as-prepared composites. This process significantly contributes to the increase in dielectric loss.⁴¹

The electrical performance of the synthesized sample was calculated by studying the Q factor as a function of frequency. As the Q factor reveals the association of stored energy with waste (thermal) energy, it is useful to describe the efficiency of the material in terms of storing energy. The Q factor versus frequency graphs of all samples are shown in Fig. 10, which clearly demonstrate that the samples with graphene nanoplatelets have lower values of Q-factor than CNGF. The Q factor values increase as the frequency increases due to the AC frequency and skin effect.⁴²

Fig. 10 Q factor variation versus frequency.

The samples were also analyzed by studying complex impedance, which in turn constitutes a real Z′ and an imaginary part Z′′ and measures the opposition caused by the material when current is passed through it. Fig. 11 shows the variation in Z′ with frequency for all four samples: without (CNGF) and with graphene (CNGF-GNP 2.5%, 5%, and 7%). All the curves show high impedance at low frequencies; the values decrease when the frequency is increased up to 10⁷ Hz, and then the impedance remains at a constant value even when the frequency is increased further. The high value of impedance at low frequencies is due to high dipole polarization and interfacial polarization, which in turn are due to the grain boundaries present in the crystal structure and electrode contribution, respectively. CNGF had the maximum impedance, while the CNGF-graphene nanocomposites showed lesser values, which reveals that the crystal grain boundary defects are lessened due to the addition of graphene. Further, the XRD results prove the reduction in crystal size due to graphene, and hence the CNGF-GNP nanocomposites have low impedance.⁴³

Fig. 11 The variation of the real part of complex impedance with frequency.

When the frequency is increased, the effect of dipole polarization and space charge participation reduces due to their inability to respond at these high frequencies; thus, impedance decreases, leading to a constant value at which conduction becomes prominent due to the hopping of electrons. The imaginary part of the impedance is plotted against frequency for all the prepared samples in Fig. 12, which shows high values at low frequencies, a decrease in value as the frequency rises, and then reaching stability at high values of frequency; this is in agreement with the fact that polarization is compatible at low frequencies but lags at high frequencies, and thus due to the transfer of electrons, conduction is possible at high frequencies.

Fig. 12 The variation of the imaginary part of complex impedance with frequency.

The physical interpretation of the imaginary part is represented as the energy storage component, and the results revealed that graphene-added composites had higher values for the imaginary part of impedance than the bare spinel ferrite. The relationship between the imaginary parts and real parts of impedance was plotted based on the Nyquist theorem. All the curves showed incomplete semi-circles, thus demonstrating dependence on one dielectric relaxation (Fig. 13(a–d)).

Fig. 13 Nyquist plots showing the variations between the imaginary and real parts of the impedance of the (a) CNGF nanoparticles, (b) CNGF-GNP 2.5% composites, (c) CNGF-GNP 5% composites, and (d) CNGF-GNP 7.5% composites.

3.5 Magnetic studies

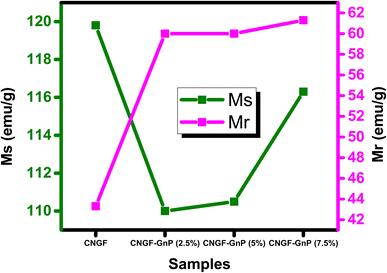
Experimental evidence demonstrates that pure CNGF exhibits characteristic soft ferromagnetic behavior, accompanied by a small coercivity.⁴⁴ To investigate the effect of GNP on the magnetic properties of the CNGF sample, the magnetization versus applied field (M–H) loops were recorded at room temperature, as shown in Fig. 14. It is clear from Fig. 14 that the saturation magnetization (M_S) of the CNGF sample was the greatest, while it decreased with the insertion of GNP in the CNGF sample, indicating that GNP has poor ferromagnetic properties, while ferrites are good, and their combination results in weak magnetization due to the formation of a single domain rather than domain walls. Furthermore, it has also been observed from the XRD analysis that the sizes of CNGF-GNPs nanocomposites are reduced due to the formation of a domain.⁴⁵ The combined magnetization graphs of the samples plotted against the applied field are shown in Fig. 14. The trends of M_s and M_r are shown in Fig. 15. The values of maximum saturation magnetization, remanence, squareness ratio, and coercivity are tabulated in Table 3. The Hc values are also shown in Table 3, which reveals the maximum value for graphene, while the minimum value was recorded for the CNGF nanoparticles. Coercivity values depend on anisotropy, and hence, the magneto-crystalline anisotropic parameters K were calculated by using M_s and H_c and are tabulated in Table 3. The CNGF nanoparticles had the minimum anisotropic constant value, while it was increased for the samples with GNPs. The change in coercivity value is due to the change in magnetocrystalline anisotropy as a consequence of the material added in the Nickel ferrites to replace the Ni ions at the octahedral sites.⁴⁵ The squareness ratio was calculated for each sample, as tabulated in Table 3. Moreover, the squareness ratio and coercivity values of the samples are plotted in Fig. 16.

Fig. 14 The M–H loops for all the as-prepared composites.

Fig. 15 Variation in the Hc and SQ ratios versus the samples.

Table 3 The magnetic parameters of the CNFG nanoparticles and CNFG-GNP nanocomposites

Parameters	CNGF	CNGF/2.5wt%GNP	CNGF/5wt%GNP	CNGF/7.5wt%GNP
MS (emu g^−1)	119.8	110.5	110	116.3
Mr (emu g^−1)	43.3	60	60	61.3
HC (Oe)	361.1	784	805	657
K (erg cm^−3)	45 062	90 241.6	92 239.5	76 409.1
SQ	0.36	0.54	0.55	0.53

---

Fig. 16 The M_s and M_r trend of the samples.

The saturation magnetization decreased when GNPs were added to the spinel ferrites. It was also obvious that an increase in the GNP ratio led to an increase in the M_s value of the CNGF-GNP nanocomposites, while the anisotropic constant increased when GNPs were added. A further change in the weight ratio of GNPs led to a decrease in K values. Previous studies have revealed that graphene has a diamagnetic nature, so its momentum is in the opposite direction to the applied external magnetic field. However, our present findings show that the CNGF-GNP nanocomposites have different magnetic behavior from that of their constituents i.e., spinel ferrites, which are ferromagnetic, and graphene, which is diamagnetic. Therefore, it can be hypothesized that in the presence of an applied external field, the exchange coupling phenomenon exists between them due to which the synthesized neoteric nanocomposites have wide and shifted hysteresis loops as the momentums of CNGF and GNPs interact.⁴⁶ Hence, it can be stated that the CNGF nanoparticles attached to the layers of GNPs act as functionalizing agents. Accordingly, it can be concluded that the magnetic properties of as-prepared Co_0.5 Ni_0.5 Fe_2−xGd_xO₄-GnP can be tuned by adjusting the ratio of GNPs. Such graphene-based spinel ferrites can be used in semiconductor applications, such as spintronics.⁴⁷

4. Conclusion

The structural, dielectric, electrical, optical, and magnetic properties of CNGF nanoparticles and changes in these properties due to graphene nanoplatelets are reported in this study by fabricating CNGF-GNP nanocomposites with varying GNP concentrations via a sol–gel auto-combustion route. It was observed that crystalline size D decreased from 40.1817 nm to 28.76267 nm due to the addition of the graphene nanoplatelets, besides providing the confirmation of GNP in the crystal structure. The SEM images revealed that samples with graphene were thicker than CNGF. The Raman spectra also showed the substitution of GNPs in the CNGF lattice. The TCR% decreased rapidly with an increase in temperature both in the low-temperature range and high-temperature range; moreover, the peak values of TCR% were −2.43% K⁻¹ at 373 K, −2.62% K⁻¹ at 368 K, −2.71% K⁻¹ at 341 K and −2.45% K⁻¹ at 368 K for CNGF, CNGF-GNP 2.5%, CNGF-GNP 5wt% and CNGF-GNP 7.5wt%, respectively. With the change in frequency, the variations in permittivity and conductivity were observed. Moreover, at higher frequencies, the external alternating field vibrated so rapidly that the dipole of the materials remained stationary giving no polarization, while the ε′′ intercept presented a higher value at low frequencies due to the addition of the graphene nanoplatelets, which provided more ions to jump in the direction of the field at low frequencies. CNGF had the maximum impedance, while the CNGF-GNPs nanocomposites showed lower values. The saturation magnetization (M_s) value of the CNGF nanoparticles was higher, while it decreased when graphene nanoplatelets were added, reaching the minima when GNP was at 2.5% and 5%. Meanwhile, the squareness ratio increased from 0.36 for CNGF to 0.55 for the GNGF-GNP nanocomposites.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors extend their appreciation to the Deanship of Scientific Research at King Khalid University, Abha, Saudi Arabia, for funding this work through the Research Groups Program, under grant no. RGP.2-259-44.

References

1. M. Zahid, N. Nadeem, M. A. Hanif, I. A. Bhatti, H. N. Bhatti and G. Mustafa, Metal ferrites and their graphene-based nanocomposites: synthesis, characterization, and applications in wastewater treatment, Magnetic Nanostructures: Environmental and Agricultural Applications, 2019, 181–212.
2. R. Bhattacharyya, O. Prakash, S. Roy, A. P. Singh, T. K. Bhattacharya, P. Maiti, S. Bhattacharyya and S. Das, Graphene oxide-ferrite hybrid framework as enhanced broadband absorption in gigahertz frequencies, Sci. Rep., 2019, 9, 12111.
3. R. Shu, G. Zhang, J. Zhang, X. Wang, M. Wang, Y. Gan, J. Shi and J. He, Fabrication of reduced graphene oxide/multi-walled carbon nanotubes/zinc ferrite hybrid composites as high-performance microwave absorbers, J. Alloys Compd., 2018, 736, 1–11.
4. A. U. Rehman, F. Afzal, M. T. Ansar, A. Sajjad and M. A. Munir, Introduction and Applications of 2D Nanomaterials, 2D Functional Nanomaterials: Synthesis, Characterization Applications, John Wiley & Sons, Ltd, 2021, ch. 21, pp. 369–382.
5. F. S. Alruwashid, M. A. Dar, N. H. Alharthi and H. S. Abdo, Effect of graphene concentration on the electrochemical properties of cobalt ferrite nanocomposite materials, Nanomaterials, 2021, 11, 2523.
6. T. Kuilla, S. Bhadra, D. Yao, N. H. Kim, S. Bose and J. H. Lee, Recent advances in graphene based polymer composites, Prog. Polym. Sci., 2010, 35, 1350–1375.
7. H. Saqib, S. Rahman, R. Susilo, B. Chen and N. Dai, Structural, vibrational, electrical, and magnetic properties of mixed spinel ferrites Mg_1−xZn_xFe₂O₄ nanoparticles prepared by co-precipitation, AIP Adv., 2019, 9, 055306.
8. C. Feng, X. Liu, S. W. Or and S. L. Ho, Exchange coupling and microwave absorption in core/shell-structured hard/soft ferrite-based CoFe₂O₄/NiFe₂O₄ nanocapsules, AIP Adv., 2017, 7, 056403.
9. A. U. Rehman, S. Sharif, H. Hegazy, N. Morley, N. Amin, M. Akhtar, M. I. Arshad, Z. Farooq, Z. Munir and T. Munir, Low dielectric loss, and enhanced magneto-dielectric properties of Cu_0.5Cd_0.5−xCo_xFe₂O₄ ferrites via Co²⁺ substitution, Mater. Today Commun., 2023, 105371.
10. A. Aslam, A. Razzaq, S. Naz, N. Amin, M. I. Arshad, M. A. U. Nabi, A. Nawaz, K. Mahmood, A. Bibi and F. Iqbal, Impact of lanthanum-doping on the physical and electrical properties of cobalt ferrites, J. Supercond. Novel Magn., 2021, 1–10.
11. A. U. Rehman, G. Abbas, B. Ayoub, N. Amin, M. A. un Nabi, N. A. Morley, M. Akhtar, M. I. Arshad, M. U. Khalid and M. Afzaal, Impact of Ni²⁺ on the structural, optical, electrical, and dielectric properties of Cu_0.25Co_0.25Mg_0.5−xNi_xCe_0.03Fe_1.97O₄ spinel ferrites synthesized via sol–gel auto combustion (SGAC) route, J. Mater. Sci. Eng. B, 2023, 291, 116407.
12. A. U. Rehman, N. Morley, N. Amin, M. I. Arshad, M. A. un Nabi, K. Mahmood, A. Ali, A. Aslam, A. Bibi and M. Z. Iqbal, Controllable synthesis of La³⁺ doped Zn_0.5Co_0.25Cu_0.25Fe_2−xLa_xO₄ (x = 0.0, 0.0125, 0.025, 0.0375, 0.05) nano-ferrites by sol–gel auto-combustion route, Ceram. Int., 2020, 46, 29297–29308.
13. K. Hussain, N. Amin and M. I. Arshad, Evaluation of structural, optical, dielectric, electrical, and magnetic properties of Ce³⁺ doped Cu_0.5Cd_0.25Co_0.25Fe_2-xO₄ spinel nano-ferrites, Ceram. Int., 2021, 47(3), 3401–3410.
14. K. Kamala Bharathi and G. Markandeyulu, Ferroelectric and ferromagnetic properties of Gd substituted nickel ferrite, J. Appl. Phys., 2008, 103, 07E309.
15. K. Tanbir, M. P. Ghosh, R. K. Singh, M. Kar and S. Mukherjee, Effect of doping different rare earth ions on microstructural, optical, and magnetic properties of nickel–cobalt ferrite nanoparticles, J. Mater. Sci.: Mater. Electron., 2020, 31, 435–443.
16. T. Poudel, B. Rai, S. Yoon, D. Guragain, D. Neupane and S. Mishra, The effect of gadolinium substitution in inverse spinel nickel ferrite: structural, Magnetic, and Mössbauer study, J. Alloys Compd., 2019, 802, 609–619.
17. M. Satalkar, S. Kane, M. Kumaresavanji and J. Araujo, On the role of cationic distribution in determining magnetic properties of Zn_0.7−xNi_xMg_0.2Cu_0.1Fe₂O₄ nano ferrite, Mater. Res. Bull., 2017, 91, 14–21.
18. R. Pawar, S. M. Patange, A. Shitre, S. Gore, S. Jadhav and S. E. Shirsath, Crystal chemistry and single-phase synthesis of Gd³⁺ substituted Co–Zn ferrite nanoparticles for enhanced magnetic properties, RSC Adv., 2018, 8, 25258–25267.
19. X. Zhong, X. Guo, S. Zou, H. Yu, Z. Liu, Y. Zhang and K. Wang, Improving soft magnetic properties of Mn-Zn ferrite by rare earth ions doping, AIP Adv., 2018, 8, 047807.
20. M. Hossain, A. Jamil, M. S. Hossain, S. Ahmed, H. Das, R. Rashid, M. Hakim and M. Khan, Investigation on structure, thermodynamic and multifunctional properties of Ni–Zn–Co ferrite for Gd 3+ substitution, RSC Adv., 2022, 12, 4656–4671.
21. G. Wang, J. Yang, J. Park, X. Gou, B. Wang, H. Liu and J. Yao, Facile synthesis and characterization of graphene nanosheets, J. Phys. Chem. C, 2008, 112, 8192–8195.
22. K. Mehmood, A. U. Rehman, N. Amin, N. Morley and M. I. Arshad, Graphene nanoplatelets/Ni–Co–Nd spinel ferrite composites with improving dielectric properties, J. Alloys Compd., 2023, 930, 167335.
23. R. Nivetha and A. N. Grace, Manganese and zinc ferrite based graphene nanocomposites for electrochemical hydrogen evolution reaction, J. Alloys Compd., 2019, 796, 185–195.
24. A. A. Kadhem and A. Al-Nayili, Dehydrogenation of formic acid in liquid phase over Pd nanoparticles supported on reduced graphene oxide sheets, Catal. Surv. Asia, 2021, 25, 324–333.
25. M. D. Ali, A. Aslam, T. Zeeshan, R. Mubaraka, S. A. Bukhari, M. Shoaib, M. Amami, I. ben Farhat, S. ben Ahmed and J. Abdelhak, Robust effectiveness behavior of synthesized cobalt doped Prussian blue graphene oxide ferrite against EMI shielding, Inorg. Chem. Commun., 2022, 137, 109204.
26. M. I. Arshad, M. Hasan, A. U. Rehman, M. Akhtar, N. Amin, K. Mahmood, A. Ali, T. Trakoolwilaiwan and N. T. K. Thanh, Structural, optical, electrical, dielectric, molecular vibrational and magnetic properties of La³⁺ doped Mg–Cd–Cu ferrites prepared by Co-precipitation technique, Ceram. Int., 2022, 48, 14246–14260.
27. J. Massoudi, M. Smari, K. Nouri, E. Dhahri, K. Khirouni, S. Bertaina and L. Bessais, Magnetic and spectroscopic properties of Ni–Zn–Al ferrite spinel: from the nanoscale to microscale, RSC Adv., 2020, 10, 34556–34580.
28. G. Datt, M. S. Bishwas, M. M. Raja and A. Abhyankar, Observation of magnetic anomalies in one-step solvothermally synthesized nickel–cobalt ferrite nanoparticles, Nanoscale, 2016, 8, 5200–5213.
29. A. Manikandan, J. J. Vijaya, M. Sundararajan, C. Meganathan, L. J. Kennedy and M. Bououdina, Optical and magnetic properties of Mg-doped ZnFe₂O₄ nanoparticles prepared by rapid microwave combustion method, Superlattices Microstruct., 2013, 64, 118–131.
30. A. Anwar, M. A. Yousuf, B. Tahir, M. Shahid, M. Imran, M. A. Khan, M. Sher and M. F. Warsi, New Er³⁺-substituted NiFe₂O₄ nanoparticles and their nano-heterostructures with graphene for visible light-driven photo-catalysis and other potential applications, Curr. Nanosci., 2019, 15, 267–278.
31. A. U. Rehman, N. Amin, M. B. Tahir, M. A. un Nabi, N. Morley, M. Alzaid, M. Amami, M. Akhtar and M. I. Arshad, Evaluation of spectral, optoelectrical, dielectric, magnetic, and morphological properties of RE³⁺ (La³⁺, and Ce³⁺) and Co²⁺ co-doped Zn_0.75Cu_0.25Fe₂O₄ ferrites, Mater. Chem. Phys., 2022, 275, 125301.
32. M. Nawaz, M. Islam, M. A. Nazir, I. Bano, I. Gul and M. Ajmal, Transport properties in spinel ferrite/graphene oxide nanocomposites for electromagnetic shielding, Ceram. Int., 2021, 47, 25505–25513.
33. S. Malik, I. H. Gul and M. M. Baig, Hierarchical MnNiCo ternary metal oxide/graphene nanoplatelets composites as high rated electrode material for supercapacitors, Ceram. Int., 2021, 47, 17008–17014.
34. P. Liu, Z. Yao, V. M. H. Ng, J. Zhou, L. B. Kong and K. Yue, Facile synthesis of ultrasmall Fe₃O₄ nanoparticles on MXenes for high microwave absorption performance, Composites, Part A, 2018, 115, 371–382.
35. C. Rayssi, S. E. Kossi, J. Dhahri and K. Khirouni, Frequency and temperature-dependence of dielectric permittivity and electric modulus studies of the solid solution Ca_0.85Er_0.1Ti_1−xCo_4x/3O₃ (0 ≤ x ≤ 0.1), RSC Adv., 2018, 8, 17139–17150.
36. S. A. Habib, S. A. Saafan, T. M. Meaz, M. A. Darwish, D. Zhou, M. U. Khandaker, M. A. Islam, H. Mohafez, A. V. Trukhanov and S. Trukhanov, Structural, magnetic, and AC measurements of nanoferrites/graphene composites, Nanomaterials, 2022, 12, 931.
37. N. A. Kumar, V. Ravibabu, A. Ashokbabu and P. Thomas, Effect of Graphene Nanoplatelets (GNP) on the Dielectric and Thermal Properties of Polystyrene (PS)/Polyvinylidenedifluoride (PVDF) Blends, in 2021 IEEE International Conference on the Properties and Applications of Dielectric Materials (ICPADM), IEEE, 2021, pp. 354–357.
38. R. Tamura, E. Lim, T. Manaka and M. Iwamoto, Analysis of pentacene field effect transistor as a Maxwell-Wagner effect element, J. Appl. Phys., 2006, 100(11), 114515.
39. P. Liu, V. M. H. Ng, Z. Yao, J. Zhou, Y. Lei, Z. Yang, H. Lv and L. B. Kong, Facile synthesis and hierarchical assembly of flowerlike NiO structures with enhanced dielectric and microwave absorption properties, ACS Appl. Mater. Interfaces, 2017, 9, 16404–16416.
40. A. Radoń, D. Łukowiec, M. Kremzer, J. Mikuła and P. Włodarczyk, Electrical conduction mechanism and dielectric properties of spherical shaped Fe₃O₄ nanoparticles synthesized by co-precipitation method, Materials, 2018, 11, 735.
41. P. Liu, Z. Yao and J. Zhou, Controllable synthesis and enhanced microwave absorption properties of silane-modified Ni_0.4Zn_0.4Co_0.2Fe₂O₄ nanocomposites covered with reduced graphene oxide, RSC Adv., 2015, 5, 93739–93748.
42. F. Salman, R. Khalil and H. Hazaa, Dielectric Studies and Cole-Cole plot Analysis of Silver-ion conducting glasses, Advance Journal of Physical Science, 2014, 3, 1–9.
43. S. Saha, N. Das, P. Chakra, K. L. Routray and D. Behera, Role of graphene on structural, dielectric and magnetic properties of CoFe₂O₄ nanoparticles, J. Mater. Sci.: Mater. Electron., 2019, 30, 14464–14479.
44. P. Liu, Z. Yao, J. Zhou, Z. Yang and L. B. Kong, Small magnetic Co-doped NiZn ferrite/graphene nanocomposites and their dual-region microwave absorption performance, J. Mater. Chem. C, 2016, 4, 9738–9749.
45. X. Chen, C. Hou, Q. Zhang, Y. Li and H. Wang, One-step synthesis of Co–Ni ferrite/graphene nanocomposites with controllable magnetic and electrical properties, J. Mater. Sci. Eng. B, 2012, 177, 1067–1072.
46. A. Mishra, V. Sharma, T. Mohanty and B. K. Kuanr, Microstructural and magnetic properties of rGO/MnFe₂O₄ nanocomposites; relaxation dynamics, J. Alloys Compd., 2019, 790, 983–991.
47. E. K. Heidari, A. Ataie, M. H. Sohi and J.-K. Kim, NiFe₂O₄/graphene nanocomposites with tunable magnetic properties, J. Magn. Magn. Mater., 2015, 379, 95–101.

---