Synthesis, structures and reactions of acylsulfenyl iodides with theoretical investigations

Abstract

A series of acylsulfenyl iodides (RCOSI) were synthesized by the reactions of carbothioic acid group 11–16 element derivatives with iodine or N-iodosuccinimides in moderate to good yields. The structure of the PhCOSI was nearly square planar based on the X-ray analysis, where the C=O⋯I distance (3.153(5) Å) was significantly shorter than the sum of the van der Waals radii of the atoms (Σr_vdW), indicating close contact within the molecule. The distances between an iodine atom and the neighbouring two iodine atoms were also less than Σr_vdW, perhaps due to the energy lowering effect of the interactions. The acylsulfenyl iodides readily reacted with alkenes and alkynes to give the expected addition products in moderate to good yields at approximately 0 °C. A new synthesis of acylated sulfines, sulfenamides and sulfenochalcogenides using acylsulfenyl iodides is also described. Theoretical calculations were performed on PhCOSI with the Sapporo-TZP(+1s1p) basis sets at the MP2 level, which perfectly reproduced the observed structures. Similar calculations were performed on the reactions, exemplified by those of MeCOSI and CH₂=CH₂, together with those of MeSI and CH₂=CH₂. Mechanisms for both reactions were proposed, which were very similar. The proposed mechanism for the former was understood based on that of the latter. For both mechanisms, the episulfuranes and episulfonium ions played an important role. The dynamic and static nature of the bonds in the COSI group of PhCOSI and MeCOSI were elucidated based on QTAIM dual functional analysis.

---

1 Introduction

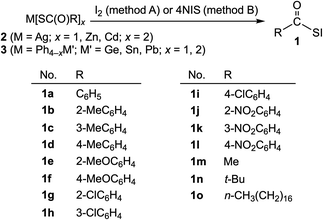
Acylsufenyl halides were first synthesized in 1952 by Böhme and Clement, who isolated acetylsulfenyl chloride in the reaction of ethanecarbothioic acid with chlorine.¹ There have been no reports of the synthesis of other acylsulfenyl halides, to the best of our knowledge, most likely due to their instability and difficulty with purification. In 1982, we described a convenient synthesis of aroylsulfenyl iodides from the reaction of PhHg(SC(O)R) with iodine.² Sulfenyl iodides (iodosulfanes) have been considered to be important intermediates in thyroid biochemistry since there is evidence to support thyroxine activation, not only by clarifying the mechanism of Graves' disease (hyperthyroidism) but also for the development of antithyroidal agents.³ In general, sulfenyl iodides are labile towards oxygen and thermally and readily undergo disproportionation [D_H value (−4.30 kcal mol⁻¹) during the reaction of RSI → 1/2RSSR + 1/2I₂].^3–5

This paper presents a more convenient synthesis of acylsulfenyl iodides (1), together with the reactions. Scheme 1 shows the structures of 1 (1a–1o) synthesized by the reactions of a variety of carbothioic acid derivatives (2 and 3) with iodine and N-iodosuccinimide (hereafter referred to NIS). The structure of 1a was determined by X-ray crystallographic analysis, and the fine details of the structure were clarified.

Scheme 1 Synthesis of RCOSI 1 from carbothioic acid derivatives 2 and 3.

The reactivity of compound 1 must be of great interest. The addition reactions of 1 to olefines were carefully examined after the addition of alkyl/arylsulfenyl chlorides to olefines. It is well known that alkyl/arylsulfenyl chlorides react with alkenes to afford the corresponding addition products. The addition reactions of alkyl/arylsulfenyl chlorides (RSCl) and bromides (RSBr) have been extensively studied experimentally and theoretically.^6–13 Such reactions proceed with both regio- and stereoselectivity at low temperatures, where the intermediacy of episulfonium ions has been proposed, followed by nucleophilic trans attack by chloride or bromide ions. The easy isomerization of the products proceeded through the ions as observed. However, to the best of our knowledge, there have been no reports on the reactions of alkyl/arylsulfenyl iodides (RSI) with alkenes.

In this paper, we also describe new syntheses of S-acylsulfenoxides and amides and S-acylated sulfenochalcogenides, together with the addition reactions of 1 to olefins and related species. The mechanism for the reaction of RCOSI and olefins is proposed, which is expected to be similar to that for RSI with olefins (see Scheme 5).

Theoretical calculations are performed to reveal the reason for the fine details of the structures and the reactivity of 1, together with the nature of the interactions. The results are verified by theoretical calculations. The quantum theory of atoms-in-molecules dual functional analysis (QTAIM-DFA) is also applied to elucidate the nature of the interactions in question.^14–19

2 Results and discussion

2.1 Synthesis of acylsulfenyl iodides (1)

Varieties of acylsulfenyl iodides RCOSI (1a–1o) were synthesized through the reactions of various carbothioic acid groups 11, 12 and 14 element derivatives (2 and 3) with iodine (method A) and NIS (method B), as shown in Scheme 1. The reactions were examined carefully. The S-iodinations of 2 and 3 proceeded at −15–0 °C in dichloromethane or chloroform to give the expected acylsulfenyl iodides 1 (1a–1o) in moderate to good yields (40–90%). The results for the individual reactions and the reaction conditions are summarized in Tables S1–S6 of the ESI.† The spectroscopic data for the products are collected in Table S7 of the ESI.†

It is usually troublesome to remove the byproducts, such as metal halides and succinimides and solvents, in this case, for the efficient purification of the target products in the synthesis. In this study, we demonstrated that the use of M(SC(O)R)_x (M = Ag, Zn, Cd, Ph₃Ge, Ph₂Ge Ph₃Sn, Ph₂Sn, Ph₃Pb and Ph₂Pb; x = 1, 2) in 2 and 3 as thioacylating agents, with NIS as the S-iodination agent, among the reagents shown in Scheme 1, was more favourable than the use of iodine as the S-iodination agent, although a large excess of NIS was necessary. Very low yields of none of the desired products were obtained after several attempts if the aliphatic derivatives of triphenyltin carbothioates 3c and diphenyltin carbothioates 3d (R = alkyl) were employed for the reaction.

The obtained aroylsulfenyl iodides 1 were relatively stable in the solid-state below 0 °C. For example, crystals of 4-methylbenzoylsulfenyl iodide 1d were stored in a refrigerator (ca. −15 °C) for over one week without any appreciable change under an argon atmosphere. However, they gradually oxidized to give diacyl disulfide at approximately room temperature. Notably, the corresponding acyl iodide was formed. Scheme 2 explains the decomposition of 1a.

Scheme 2 Possible route for the decomposition of 1a at approximately room temperature.

2.2 Structure of acylsulfenyl iodide

High-quality crystals of benzoylsulfenyl iodide 1a were obtained by crystallization from ether/petroleum ether, and X-ray crystallographic analysis was performed on one of the crystals. Fig. 1 shows the ORTEP drawing of 1a (Deposition No. 2121145). The final atomic position parameters and selected geometric parameters are listed in Tables S8 and S9 of the ESI,† respectively.

Fig. 1 ORTEP drawing of 1a with the thermal ellipsoid drawn at 50% probability. ϕ(O1–C1–S1–I1) = 4.8(6)°, ϕ(C3–C2–C1–O1) = 15.0(9)°, and f(C7–C2–C1–S1) = 16.3(8)°.

The bond lengths of C1–O1 [1.207(7) Å] and C1–S1 [1.799(7) Å] corresponded to those of C=O double and C–S single bonds,²⁰ respectively. The bond length of S1–I1 [2.3653(17) Å] indicated that of the S–I single bond [typically, 2.386 ²⁰ to 2.416 ²¹ Å]. The distance between the carbonyl oxygen O1 and iodine I1 was 3.153(5) Å, which was significantly shorter than the sum of the van der Waals radii (vdW) of both atoms (Σr_vdW = 3.50 Å). The value strongly indicated intramolecular contact. The torsional angle of O1–C1–S1–I1 (= ϕ(O1–C1–S1–I1) was 4.8(6)°, with ϕ(C7–C2–C1–S1) = 16.3(8)° and ϕ(C3–C2–C1–O1) = 15.0(9)°, which indicated a nearly planar molecule for 1a.²² The nearly planar four-membered O1–C1–S1–I1 ring with the unexpectedly short O1–I1 distance reminded us of the stability through the cyclic 6p electron interactions in the four-membered ring constructed by the different kinds of four atoms.

2.3 Intermolecular close contacts and molecular arrangement

Fig. 2 illustrates the molecular arrangements of 1a. Various intermolecular short contacts were present in the crystal of 1a, which are shown in Fig. 2. As shown in Fig. 2a, it appeared that the S atom in 1a was not in close contact with the atoms in the neighbouring molecules. Instead, the distances between I1 and I1′ or I1′′ atoms in the neighbouring molecules (3.7630(9) Å) were significantly shorter than the sum of the vdW radii²³ of both atoms (Σr_vdW = 3.96 Å) (see Fig. 2a). The distances between O1 and I1′ atoms (3.289(5) Å) were also significantly shorter than the Σr_vdW value of 3.50 Å. The S1–I1–I1′ angle (= ∠S1–I1–I1′) was nearly a right angle (94.62(5)°), while the ∠S1–I1–I1′′ value was 160.37(5)°, which was close to linear. The distance between the carbonyl oxygen (O1) and the phenyl ortho-hydrogen of a neighbouring molecule (H5′) (2.40398(7) Å) was much shorter than the Σr_vdW value of 2.72 Å (between O and H′), which underwent hydrogen bonding of the C=O⋯H–C(Ph) type, as shown in Fig. 2a. The hydrogen bonding together with the intermolecular I1⋯I1′′ and O1⋯I1′ interaction arranged the molecules into a planar sheet, while the π⋯π interactions (3.253 Å, Σr_vdW value of 3.54 Å) between the phenyl rings and the intermolecular I1⋯I1′ and O1⋯I1′ interactions formed a column of molecules as shown in Fig. 2b. The sheets are stacked vertically to form 3-D networks by intermolecular interactions. Halogen bonding by the iodine moiety must contribute to the formation of planar sheets and columns (Fig. 2b and c). The four iodine atoms in the four neighbouring molecules formed a zig–zag chain but not a planar rectangle, as shown in Fig. 2c. The formation of infinite linear zig–zag chains by the intermolecular I⋯I close contacts, shown in Fig. 2d, was the first example for organo-iodine compounds, to the best of our knowledge.

Fig. 2 Intermolecular close contacts and molecular arrangement of 1a. Purple, yellow, red, grey, and white balls represent iodine, sulphur, oxygen, carbon and hydrogen atoms, respectively. Red–purple, green, and blue dotted lines show the intermolecular weak bonding in (a). A 3-D arrangement was formed by the stacking of the sheets, as shown in (b). Almost linear molecular chains were formed by short contacts between carbonyl oxygen and ortho-hydrogen atoms and between the I1⋯I1′, I1⋯I1′′, and O1⋯I1′ atoms, as shown in (c). An infinite zig–zag chain formed by the I⋯I short contacts (d).

2.4 Reactions of acylsulfenyl iodides 1

2.4.1 Reactions of compound 1 with alkenes and alkynes. The reaction of 1 with various alkenes 4 and alkynes 5 were carefully examined in dichloromethane or chloroform at −15–0 °C. The low temperature prevented the decomposition of 1. A large excess of alkenes (usually over 5 equivalents) was used for the reaction, and the reaction was rounded up in a relatively short time (usually less than 60 min). A typical procedure of the desirable conditions for the reactions was as follows: alkene 4 (6 mol) was added dropwise to a solution of acylsulfenyl iodide 1 in dichloromethane below −15 °C and stirred at 0 °C for 60 min. The corresponding addition products 6 and 7 were obtained as colourless to pale yellow crystals or oil by preparative thin layer chromatography (PTLC) of the resulting residue after removal of the solvent and excess alkene under reduced pressure. O-Thioacylated adducts (RC(S)OCH₂(CH₂)₃I) and acyl 4-iodobutyl disulfides (RC(O)SSCH₂(CH₂)₃I) to 1-butene 4a were not detected in the reactions. The notations 6xy and/or 7xy were used for the products when 1x was reacted with 4y (x, y = a, b, c, …). The structures of 6 and 7 are shown in Table 1. Structures of 6 and 7 often stand for the Markovnikov and anti-Markovnikov adducts, respectively, although they change case by case. Table 1 summarizes the reaction conditions and the structures of the addition products 6 and 7 with the yields. The spectral data are collected in Tables S10–S17 of the ESI.†

Table 1 Reactions of acylsulfenyl iodides 1 with alkenes

Entry	R in 1x	Alkene 4y	Molar ratio (1 : 4)	Solvent	Temp. (°C)	Time (min)	Products
							6xy and/or 7xy	Yield (%)	Ratio (6 : 7)
1	Ph (1a)	CH3(CH2)3CH=CH2 (4a)	1 : 6	CH2Cl2	−15–0	60	6aa : 7aa	22	64 : 36
2	Ph (1a)	cyclo-Pentane (4b)	1 : 6	CH2Cl2	−15–0	60	6ab	56
3	Ph (1a)	cyclo-Hexene (4c)	1 : 6	CH2Cl2	−15–0	60	6ac	56
4	4-MeC6H4 (1d)	cyclo-hexene (4c)	1 : 6	CH2Cl2	−15–0	60	6dc	74
5	Ph (1a)	(CH3)2CH=CH2 (4d)	1 : 6	CH2Cl2	−15–0	60	6ad	10
6	Ph (1a)	(CH3)2CH=CHCH3 (4e)	1 : 6	CH2Cl2	−15–0	60	6ae	64
7	4-MeC6H4 (1d)	(CH3)2CH=CHCH3 (4e)	1 : 6	CH2Cl2	−15–0	60	6de	55
8	4-ClC6H4 (1i)	(CH3)2CH=CHCH3 (4e)	1 : 6	CH2Cl2	−15–0	60	6ie	50
9	Ph (1a)	(CH3)3CCH=CH2 (4f)	1 : 6	CH2Cl2	−15–0	60	6af : 7af	64	30 : 70
10	Ph (1a)	Z-CH3CH=CHCH3 (4gZ)	1 : 6	Hexane	0	60	6agth : 7ager	10	50 : 50
11	Ph (1a)	Z-CH3CH=CHCH3 (4gZ)	1 : 6	CH2Cl2	0	60	6agth : 7ager	77	68 : 32
12	Ph (1a)	Z-CH3CH=CHCH3 (4gZ)	1 : 6	CH3CN	0	60	6agth : 7ager	54	100 : 0
13	4-MeC6H4 (1d)	Z-CH3CH=CHCH3 (4gZ)	1 : 6	CH2Cl2	0	60	6dgth : 7dger	68	87 : 13
14	4-ClC6H4 (1i)	Z-CH3CH=CHCH3 (4gZ)	1 : 6	CH2Cl2	0	60	6igth : 7iger	59	95 : trace
15	Ph (1a)	E-CH3CH=CHCH3 (4gE)	1 : 6	CH2Cl2	0	60	6agth : 7ager	9	50 : 50
16	Ph (1a)	E-CH3CH=CHCH3 (4gE)	1 : 6	CH2Cl2	0	60	6agth : 7ager	74	48 : 52
17	Ph (1a)	E-CH3CH=CHCH3 (4gE)	1 : 6	CH3CN	0	60	6agth : 7ager	69	46 : 54
18	Ph (1a)	CH2 = CHCH=CH2 (4h)	1 : 6	CH2Cl2	−15–0	60	6ah	33

---

As shown in Table 1, benzoylsulfenyl iodide 1a reacted with 1-hexene 4a to give a mixture of 2-iodohexyl benzoyl sulfide 6aa and 1-iodomethylpenthyl benzoyl sulfide 7aa in 22% yield (entry 1). The methine proton on the carbon atom attached to a benzenecarbothioate group (δ 4.43) appeared at a lower field than the proton on the carbon bonded to the iodine atom (δ 3.98). Furthermore, the methylene protons at the 1-position in 6aa and 7aa showed characteristic geminal coupling constants of 13.9 and 9.9 Hz, respectively, due to the asymmetric carbon at the 2-position.²⁴ Indeed, the structural determination of such adducts based on the δ_H values had been established, exemplified by the addition products of benzenesulfenyl chloride to 2-methylpropene,²⁵ but it was necessary to consider the differences between Cl and I in the assignments. However, only one product (6ab or 6ac) was obtained through trans-addition in the reaction of 1a with each of the cyclic alkenes, such as cyclo-pentene 4b or cyclo-hexene 4c, respectively (entries 2 and 3). The methyl derivative of 1a (1d) similarly gave 6dc in the reaction with 4c (entry 4). The yields were rather good.

The reactions of 1a with trans-2-butene 4g_E were examined in the presence of phenol, which would have acted as a radical inhibitor. The yields of the adducts of threo-isomer 6ag_th and erythro-isomer 7ag_er and the ratio of 6ag_th/7ag_er were very similar when the reaction proceeded in the presence or absence of phenol. Therefore, the radical mechanism seemed unlikely in this case, although the mechanism should be examined carefully.

The reactions were examined starting with regioselectivity.

2.4.2 Regioselectivity. The products 6aa and 7aa from the reaction of 1a with 4a corresponded to the Markovnikov- and anti-Markovnikov adducts, respectively, of which isomer ratio (6aa/7aa) was 64 : 36 (entry 1). However, the reactions of 1a with 2-methylpropene 4d and 2-methyl-2-butene 4e gave Markovnikov adducts 6ad and 6ae, respectively, without the formation of anti-Markovnikov adducts (entries 5 and 6). Similarly, 4-Me- and 4-Cl-derivatives of 1a (1d and 1i, respectively) gave only Markovnikov adducts of 6de and 6ie, respectively, in the reaction with 4e (entries 7 and 8). It should be noted that the addition of 1 to alkenes 4 proceeded to yield Markovnikov-oriented adducts prior to the anti-Markovnikov-oriented adducts.

The effect of the sterically hindered tert-butyl group in 3,3-dimethyl-1-butene 4f on the reaction is of interest. Under similar conditions, 1a reacted with 4f to give a mixture of 2-iodo-3,3-dimethylbutyl benzoyl sulfide 6af (Markovnikov adduct) and 1-iodomethyl-2,2-dimethylpropyl benzoyl sulfide 7af (anti-Markovnikov adduct) in 64% yield. The ratio of the isomers 6af/7af was 30 : 70, of which the coupling constants were J_ab = 11.4 and 14.4 and J_g = 2.4 Hz for 6af and J_ab = 10.6 and 14.5 Hz and J_g = 3.2 Hz for 7af, respectively (entry 9). The steric hindrance around the reaction area in the alkene should also be considered.

The stereochemistry of the addition reaction was examined, exemplified by the reaction of 1 with 2-butene (4g). The results are discussed next.

2.4.3 Stereochemistry. The reactions of 1a with cis-2-butene 4g_Z and trans-2-butene 4g_E gave two products (entries 10–17). The results contrasted sharply to the reactions with cyclic alkenes, where only trans-formed adducts were obtained (entries 2–4). The addition of acylsulfenyl iodides 1 to 4g_E and 4g_Z led to the formation of both threo- and erythro-isomers (6g_th and 7g_er, respectively) (entries 10–17). The notation x in 6xg_th and 7xg_er is sometimes omitted when x in 1x is not shown, where 1 stands for various acylsulfenyl iodides. 4-Methylbenzoyl- and 4-chlorobenzoylsulfenyl iodides (1d and 1i, respectively) reacted similarly with 4g_Z to produce mixtures of (6dg_th, 7dg_er) and (6ig_th, 7ig_er), respectively (entries 13 and 14). The reactions of 1a, 1d and 1i with 4g_Z produced mainly the threo-isomers (6ag_th, 6dg_th and 6ig_th, respectively) via the trans-addition mechanism rather than the erythro-isomers (7ag_er, 7dg_er and 7ig_er, respectively) via the cis-addition mechanism, although formally, in CH₂Cl₂ and CH₃CN. Namely, the formation of the former was superior to that of the latter in this case. Similarly, the reaction of 1a with 4g_E yielded 6ag_th and 7ag_er. The ratios of threo-versus erythro-isomers (6ag_th/7ag_er) were 0.74, 0.60 and 0.59 in CH₂Cl₂, CH₂Cl₂ and CH₃CN, respectively. The threo/erythro isomer ratios for adducts with 4g_E were essentially the same, which was in contrast with the case with 4g_Z. However, the yield of threo-isomer 6ig_th was much larger than that of erythro-isomer 7ig_er in the reaction of 4-chloro derivative 1i (6ig_th: 7ig_er = 95: trace, see entry 14). No rearrangements were observed between 6id_th and 7id_er in this case.

1,3-Butadiene 4h reacted with 1a to give trans-4-iodo-2-butenyl benzoyl sulfide 6ah in 33% yield (entry 18). The ¹H NMR spectrum of 6ah shows two doublet peaks at δ 3.70 and δ 3.86 due to the methylene protons and two doublets of triplet peaks at δ 5.77 and δ 6.01 due to a vinylic proton, and the adjacent vicinal proton spin–spin coupling constant was 15 Hz.

2.4.4 Solvent effect. The addition reactions of 1a to 4gZ and 4gE were performed in hexane, dichloromethane and acetonitrile. Table 1 collects the results (entries 10–12 and 15–17, see also entries 13 and 14). As shown in the table, the addition reactions of 1a to 4gZ and 4gE seemed to proceed regiospecifically and stereospecifically in the solvents. The desirable conditions for the reaction occurred at approximately below 0 °C in dichloromethane, and the reaction period was less than 60 min. In the reaction with 4gZ, the formation of threo-isomer 6agth increased as the polarity of the solvents increased relative to erythro-isomer 7ager, whereas the 6agth/7ager ratios were almost constant in the reaction with 4gE under the same conditions. The addition reactions in hexane resulted in very low yields of both adducts to 4gZ and 4gE, although the ratios of 6agth/7ager were almost the same. Such solvent dependency in the reaction may be explained by the enhanced polarity of the S–I bond due to the solvent polarity, where the S–I bond must also be greatly affected by the very polar C=O group attached directly to S.

The effect of the iodide and iodine ions on the addition of 1 to 4 was also examined. A remarkable increase in the trans-addition products was observed in the presence of iodine in the reaction of 1a with 4gZ and 4gE. In particular, the reaction with 4gZ exclusively yielded trans-adducts in over 65% yields. The (proposed) mechanism should reasonably explain the observed results.

2.4.5 Mechanism for addition reactions of 1 to alkenes. Scheme 3 shows a postulated mechanism for the addition reaction of acylsulfenyl iodides 1 to alkenes 4 that produces the corresponding products IIIA and IIIB. It is necessary to examine the following three routes: the intermediacy of episulfonium ions II (II⁺ + I⁻) via episulfuranes I (route A), the direct intermediacy of episulfuranes I (route B), and the direct cis-addition from episulfuranes I (route C). Details of the mechanisms are discussed after the calculations for the mechanisms. A carbocation intermediary would be plausible; however, the carbocation centre would be coordinated strongly by the neighbouring S atom. The structure should be called an episulfonium ion. However, such carbocation would appear as a TS on the interconversion of I and the topological isomer.

Scheme 3 Postulated mechanism for the reaction of 1 with olefin 4.

Only a few reports have been found for the reactions of 1 with alkynes 5, enamines, and trialkylsiloxyalkenenes, to the best of our knowledge, although phenylsufenyl chloride reacts with silylenol ethers to produce α-phenylsulfenyl ketones.²² No reaction was observed between 1a and ethynylbenzene; therefore, the reactions of 1 with 5 is be discussed further in this paper. The reactions of 1a with enamines and trialkylsiloxyalkenenes are discussed next.

2.5 Reactions of 1 with silylenol ethers and enamines

Benzoylsulfenyl iodide 1a reacted with 1-morpholino-1-cyclopentene 4i and cyclohexene 4j to give 2-benzoyl- and 2,6-dibenzoylcycopentaxanones (6ai and 7ai, respectively) and 2-benzoyl and 2,6-dibenzoyl cyclohexanones (6aj and 7aj, respectively) in moderate to low yields, respectively, at 20–26 °C (entries 19 and 20 in Table 2, respectively). Table 2 summarizes the results of the reactions. Under similar conditions, the reaction of 1a with 2-methylpropenylmolpholine 4k gave 2-benzoylsulfenylated aldehyde 6ak with a very small amount of (PhCOS)₂ (7′ak) (entry 21), while 3,3-dimethyl-2-molpholyl-1-butene 4l afforded 1-benzoylsulfenyl-3,3-dimethyl-2-butanone 6al (entry 22). The reaction of 1a and 2-trimethysiloxy butene 4m produced the corresponding 4-benzoylsulfenyl-2-pentanone 6am, but the yield was very low (<2%) (entry 23). Table 2 summarizes the results of the reactions. The spectral data of products 6 and 7 are collected in Tables S10–S17 of the ESI.†

Table 2 Reactions of acylsulfenyl iodides 1 with alkenes

Entry	R in 1x	Alkene	Molar ratio (1 : 4)	Solvent	Temp. (°C)	Time (min)	Products
							6xy and/or 7xy (yield: %)
19	Ph (1a)	4i	1 : 1	Et2O	20	30	6ai (25); 7ai (12)
20	Ph (1a)	4j	1 : 1	Et2O	24	30	6aj (22); 7aj (8)
21	Ph (1a)	4k	1 : 1	Et2O	20	30	6ak (44); 7′ak (≪1)
22	Ph (1a)	4l	1 : 1	Et2O	26	30	6al (15)
23	Ph (1a)	4m	1 : 1	Et2O	26	30	6am (<2)

---

2.6 Reactions of 1 with alcohols, thiols, amines, carboselenoic acids, diaroyl diselenides, diacyl ditellurides and related species

The reactions of 1 were also examined for alcohols, thiols [RSH, R′C(O)SH and R′C(S)SH], amines, carboselenoic acids and their potassium salts, diaroyl diselenides and diacyl ditellurides. Scheme 4 summarizes the products of the reactions, the reaction conditions, and the yields.

Scheme 4 Reactions of acylsulfenyl iodides 1 with various species.

As shown in Scheme 4, alcohols, thiols, carbothioic acids, and alkali and ammonium salts were found to react with 1 at −15–0 °C to give corresponding sulfenates 8 (Table S18 of the ESI†) and unsymmetrical disulfides 9 (Table S21 of the ESI†) and 10 (Table S23 of the ESI†),²⁶ respectively.

We previously reported a method for the synthesis of Se-aryl (aryl)oxomethanesulfenoselenoates 11 by the reaction of acylsulfenyl bromides with sodium benzeneselenolate, along with carbothioic acid and its alkali metal, peridinium and zinc salts with diphenyl diselenide or sodium benzeneselenolate.²⁷ The preparation of 11 using 1 was examined here. Compound 1 reacted readily with alkali metal benzeneselenolates to give compound 11 in the 23–76%, as expected (Table S25 of the ESI†). The reaction of acylsulfenyl iodides 1 with sodium phenyltellurate gave Te-aryl acyloxymethanesulfenotelluroates 12 in moderate yields; however, the reactions of 1 with diphenyl ditelluride did not give 12 (Table S27 of the ESI†). Under similar conditions, the reaction of 1 with primary and secondary amines led to the expected sulfenamides 13, except for bulky tert-butyl compound 13ag (73%) in 43–73% yield (Tables S29 and S30 of the ESI†). In the reaction of two molar amounts of 4-methylbenzoylsulfenyl iodide 1d with ethylamine, a trace of (benzoylsulfenyl)-1-propylamide 13d was detected along with di(benzoylsulfenyl)-1-propylamide 13d′, indicating the process via mono acylsulfenated compound 13d. The spectral data of products 8–13 are collected in Tables S19, S20, S22, S24, S26, S28 and S31–S33 of the ESI, respectively.

2.7 Theoretical investigations

2.7.1 Optimizations of 1. Theoretical calculations were performed on 1 (RCOSI) with MP2/S-TZPsp, exemplified by 1a (R = Ph) and 1m (R = Me). The syn-conformers of the C₁ and C_s symmetries and anti-conformer of the C₁ symmetry were optimized for 1a (R = Ph), and the syn-conformers of the C₁ and C_s symmetries and anti-conformer the C_s symmetry were optimized for 1m (R = Me). The syn-conformers of the C₁ symmetry (syn-C₁) were the global minima for both. The energy differences between the two conformers ΔE (= E − E_syn-C1) were also calculated. Table 3 collects the selected structural data for the optimized structures of 1a and 1m, together with the ΔE values. Table 3 contains some observed structural data of 1a. If the reason for the observed fine details of the syn-structure of 1a with the significantly short intramolecular O⋯I interaction distance can be clarified based on the theoretical background, then it would be very instructive.

Table 3 Selected data for the optimized structures and the ΔE values for the syn- and anti-conformers of PhCOSI (1a) and MeCOSI (1m)^a,b,c

Species	ϕ(OCSI) (°)	ϕ(OCCiCo) (°)	r(O, C) (Å)	r(C, S) (Å)	r(S, I) (Å)	r(I, O) (Å)	ΔE (kJ mol^−1)	n^d
a Calculated without considering the solvent effect under MP2/S-TZPsp.b The calculated syn- and anti-conformers and the observed structure of 1a are shown by 1asyn, 1aanti and 1asyn-obsd, respectively, for example.c The Esyn and Eanti values are collected in Table S44 of the ESI.d Number of imaginary vibrations.
1asyn-C1	4.5	22.5	1.211	1.816	2.355	3.184	As 0.0	0
1asyn-Cs	0.0	0.0	1.211	1.819	2.353	3.160	0.6	1
1aanti-C1	−156.5	45.5	1.212	1.820	2.373	4.476	15.9	0
1asyn-obsd	4.8	15.0	1.207	1.799	2.365	3.153	—	—
1msyn-C1	−1.0	9.1	1.206	1.808	2.354	3.226	As 0.0	0
1msyn-Cs	0.0	0.0	1.206	1.816	2.354	3.217	1.0	1
1manti-Cs	180.0	0.0	1.211	1.813	2.374	4.527	8.6	0

---

As shown in Table 3, the fully optimized syn-conformer of 1a (1a_syn-C1) with MP2/S-TZPsp excellently reproduced the observed structure, especially for the bond lengths around the COSI group, although the ϕ(OCC_iC_o) value seemed slightly different.^4,6 The torsional angles would be greatly affected by the crystal packing. To examine the behaviour of the torsional angles, 1a was further optimized assuming the planar structure around the COSI group, which is denoted by 1a_syn-Cs. One imaginary frequency was detected in 1a_syn-Cs, of which motion corresponded to the rotation around the C_C=O–C_i bond. Namely, the planar structure was not the minimum, where the differences in ϕ(OCC_iC_o) (= 22.5°) and ϕ(OCSI) (= 4.5°) seemed reasonable. It was noteworthy that the observed r(I, O) value (3.153 Å)^4,6 was close to those of 1a_syn-C1 (3.184 Å) and 1a_syn-Cs (3.160 Å), irrespective of the ϕ(OCSI) and ϕ(OCC_iC_o) values.¹¹ The bond lengths in 1a_anti-C1 were also very similar to the corresponding values of 1a_syn, except for r(I, O). 1a_syn-C1 and 1a_syn-Cs were predicted to be more stable than 1a_anti-C1 by approximately 15–16 kJ mol⁻¹. The energy lowering effect by the cyclic interaction containing I⋯O may have led to the results. The dihedral angles in 1a seemed to change rather widely between the conformers; however, the effect from the phenyl group seemed less severe on the stabilization of 1a. It was also predicted that 1m_syn-C1 and 1m_syn-Cs seemed more stable than 1m_anti-Cs by 8–9 kJ mol⁻¹, possibly due to the cyclic I⋯O interaction. The behaviour of the methyl derivatives of 1m_syn and 1m_anti can be understood similarly to that of the phenyl derivatives.

2.8 Analysis of the reaction of 1 with CH₂=CH₂

The mechanism for the reaction of acylsulfenyl iodides 1 with alkenes 4 was clarified. The mechanism was expected to be similar to that of RSI (14) with 4. Various mechanisms have been proposed to explain the reactions of RSX (X = Cl and Br) with 4. However, there seem to be no reports on the reactions of 14 with 4, and to the best of our knowledge, the reactions of 1 with 4 are rare. As a result, the mechanism for the reaction of 14 with 4 was clarified before considering the mechanism of the main reaction of 1 with 4. The mechanisms for the reaction of 14 with 4 were investigated based on the theoretical background, exemplified by the addition of 14m to CH₂=CH₂. Theoretical calculations were performed on the reaction processes predicted in Scheme 3 and those expected as a guideline. Theoretical calculations on the reaction of 1m with CH₂=CH₂ were performed, employing the results for the calculations on 14m with CH₂=CH₂ as the guideline.

As the first step of the investigations, calculations were performed without considering the solvent effect. The results for MeCOSI (1m) and MeSI (14m) with CH₂=CH₂ are shown in Fig. S1 and S2 of the ESI,†, respectively, and the values are collected in Table S44 of the ESI,† the relative energies (E_rel) for (MeS⁺(CH₂)₂ + I⁻ (II)) from (14m + CH₂=CH₂)) and (MeCOS⁺(CH₂)₂ + I⁻ (II)) from (1m + CH₂=CH₂) were evaluated to be 454 and 474 kJ mol⁻¹, respectively, on the energy surfaces, for instance. Such unexpectedly high energies for the ionic species relative to the neutral species must be predicted due to the calculations without considering the solvent effect. Calculations considering the solvent effect were necessary for the reactions since the reaction processes contain many ionic species and/or polar bonds. Then, the calculations were performed under the solvent effect of acetonitrile with SCRF method (PCM (polarizable continuum model)²⁸ starting from the structures optimized without considering the solvent effect, if possible. The E_rel values for (MeS⁺(CH₂)₂ + I⁻) from (14m + CH₂=CH₂) and (MeCOS⁺(CH₂)₂ + I⁻) from (1m + CH₂=CH₂) were much improved to −4 and 32 kJ mol⁻¹, respectively. Based on this result, all species and processes containing transition states (TSs) were reoptimized under the solvent effect of acetonitrile. The results are collected in Table S45 of the ESI†. Scheme 5 shows the proposed mechanisms for the reactions of 1 with 4 and 14 with 4, exemplified by 1m with C₂H₄ and 14m with C₂H₄, respectively.

Scheme 5 Proposed mechanisms for the reactions of R′COSI and R′SI with olefins, where (R′, ¹R, ²R) = (Me, H, H) were selected for the calculations. As a result, IIIB was equal to IIIA in the figure. The contributions of the equilibrium structures would be larger for R′SI relative to the case of R′COSI, although the interconversion between IIIA and IIIA' occurred through free rotation around the C–C bond.

Fig. 3 shows the displacements of atoms using arrows corresponding to the imaginary frequency in each TS for a better understanding of the proposed mechanism based on the calculations. The displacements in each TS rationalized the process connecting the two minima shown in Scheme 5, although the intrinsic reaction coordinate (IRC) analysis was necessary for a detailed discussion. Fig. 4 and 5 illustrate the energy profiles for the reactions of 14m with C₂H₄ and 1m with C₂H₄, respectively.

Fig. 3 The motion for the imaginary frequency of each TS. The total displacements of atoms in each TS were determined when the centre of gravity was unchanged, based on the total momentum. As a result, the displacement of I was approximately one tenth of C in the figure.

Fig. 4 Energy profile for the reaction of 14m and CH₂=CH₂, calculated under the solvent effect of acetonitrile with MP2/S-TZPsp.

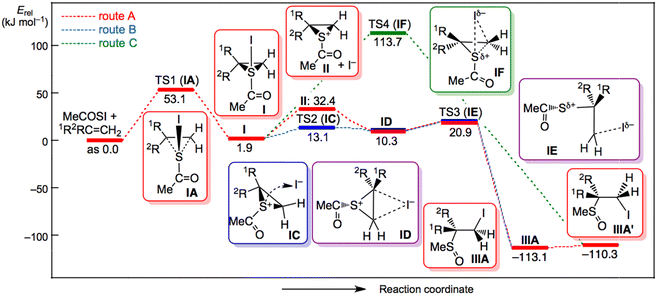Fig. 5 Energy profile for the reaction of 1m with CH₂=CH₂, calculated under the solvent effect of acetonitrile with MP2/S-TZPsp.

The results of the calculations for the reaction of 14m with C₂H₄ under the solvent effect of acetonitrile are discussed first. Episulfurane (I) formed from the reaction of 14m and C₂H₄ exothermically by 35 kJ mol⁻¹. The activation energy (ΔE^‡) for the TS (TS1 : IA) was 34 kJ mol⁻¹ (see Scheme 5 and Fig. 4). I ionized to episulfonium ions (II⁺) and I⁻ endothermically by 30 kJ mol⁻¹, although II⁺ + I⁻ was predicted to be more stable than 14m and C₂H₄ by 4.2 kJ mol⁻¹ in acetonitrile. A species IB in Scheme 5 was postulated for the ionization process. The energy of IB became monotonically higher as the S⋯I distance increased; therefore, the process for IB did not contain a TS (transition state). It was necessary for I⁻ to move to the other side of S of II⁺ for the reaction to give the final products of IIIA and IIIB. An ion pair, named ID, was optimized to be minimum, which would be easily produced after ionization, since the free I⁻ could move easily to the backside. This route corresponded to route A in Scheme 3. However, the theoretical calculations predicted another route to ID from I that corresponded to route B in Scheme 3. In route B, I⁻ moved along the molecular surface of I to reach ID via TS2 of IC. The ΔE^‡ value of TS2 (IC) from I was calculated to be 11.2 kJ mol⁻¹. In route B, the I⁻ would move not thus far from the cationic sulphur (and on the molecular surface) throughout the process, which would result in the very low ΔE^‡ value for TS2 (IC). The ion pair ID gave the final products IIIA via the TS3 of IE, where ID was more stable than IE by 25 kJ mol⁻¹. TB3 of IE corresponded to the TS optimized for the S_N2 reactions in the process from ID to IIIA. The C⋯I distances in ID, IE and IIIA were 3.578, 2.770, and 2.149 Å, respectively. The behaviour of I⁻ in this process is of interest. If I⁻ was placed approximately 7 Å from the C atom in ID, the given structure converged to ID.

Namely, I⁻ approached to a carbon atom of ID but never gave IIIA in this calculation. The I⁻ stayed at the C⋯I distance of 3.578 Å. The intramolecular route from I to ID via IC seemed superior to that via II⁺ and I⁻‘’ (by 23 kJ mol⁻¹); however, we were careful since many energetic processes would be present between those via IC and (II⁺ and I⁻), since the II⁺⋯I⁻ distance was assumed to be infinite. The TS3 of ID may play an important role in determining the product distributions, such as [IIIA]/[IIIB], as the initial stage. The direct cis-addition process from I waws expected to give a final product of IIIA′ corresponding to route C in Scheme 3. Indeed, transition state TS4 of IF was optimized for the direct cis-addition process from I; however, the predicted ΔE^‡ value of 140 kJ mol⁻¹ was very high. Therefore, the direct cis-addition process from I to IIIA′ via IF truly existed, but the process did not operate due to the very high activation energy.

The mechanism for the reaction of 1 with 4 seemed very similar to that for 14 with 4. The mechanism was explained by the reaction of 1m with C₂H₄ calculated under the solvent effect of acetonitrile. Episulfurane (I) was formed slightly endothermically by 2 kJ mol⁻¹ relative to 1m and C₂H₄. The ΔE^‡ value was 53 kJ mol⁻¹ for the TS1 of IA (see Scheme 5 and Fig. 5). I ionized endothermically (30 kJ mol⁻¹) to give episulfonium ions (II⁺) and I⁻, where II⁺ + I⁻ was less stable than 1m + C₂H₄ by 32 kJ mol⁻¹. The final products of IIIA and IIIB formed from II⁺ + I⁻ via the ion pair (ID) and TS3 (IE) in route A. However, another mechanism was predicted by the theoretical calculations (route B). The ion pair (ID) directly formed via TS2 of IC where I⁻ moved along the molecular surface of I, similar to the case of 14m with C₂H₄. The ΔE^‡ value from I to IC was 11 kJ mol⁻¹, where IC was less stable than 1m and C₂H₄ by 13 kJ mol⁻¹.

The ion pair ID was more stable than IC by 3 kJ mol⁻¹ but less stable than 1m with C₂H₄ by 10 kJ mol⁻¹. The final product was obtained from ID via TS3 of IE. The ΔE^‡ value of IE from ID was 11 kJ mol⁻¹, where IE was less stable than 1m and C₂H₄ by 21 kJ mol⁻¹. IC was more stable than (II⁺ and I⁻) by 19 kJ mol⁻¹. Therefore, the intramolecular route from I to ID via IC seemed superior to that via II⁺ and I⁻ (by 19 kJ mol⁻¹). However, the distance was assumed to be infinite because in terms of energy, there are many processes between those via IC and via (II⁺ and I⁻). The IE (TS3) may play an important role in determining the product distributions, such as [IIIA]/[IIIB], as the initial stage. The direct cis-addition from I (route C) was also optimized to directly yield the final products. Indeed, the TS4 of IF corresponding to the direct cis-addition process was optimized again, but the ΔE^‡ value from I to IF was predicted to be very large, 112 kJ mol⁻¹. The direct cis-addition process is precluded by the very high activation energy, irrespective of the optimized results.

What is the role of the carbocations in the reactions of 1 and 14 with olefins? As mentioned above, if the carbocations are formed in the reactions, they are stabilized through coordination by the neighbouring divalent sulphur. In this case, the nonbonding orbitals of S, which are filled with electrons, play an important role in the stabilization since a carbocation has a vacant orbital on C⁺. The vacant orbital of C⁺ shares the electrons in the nonbonding orbital on S, especially the p-type orbital.

As shown in Fig. 6, the activation energies for the TSs on the C–C bond rotations in MeS⁺C₂H₄ and MeCOS⁺C₂H₄ were calculated to be 208 and 173 kJ mol⁻¹, respectively. The ΔE^‡ value for the latter was smaller than that for the former by 35 kJ mol⁻¹, which may result from the weaker electron donation ability of S in SCOMe relative to that in SMe. Namely, the C–S bonds of MeCOS⁺C₂H₄ would be less stable than those in MeS⁺C₂H₄. Nevertheless, the ΔE^‡ values of 173–208 kJ mol⁻¹ seemed too high to contribute to the reactions as carbocations in reality. In the case of the episulfonium MeS⁺C₂H₂Me₂ and MeCOS⁺C₂H₂Me₂ ions, the E-types were evaluated to be less stable than the Z-types, although E-MeCH = CHMe was slightly more stable than Z-MeCH = CHMe (see Fig. 6). The ΔE^‡ values for the site change processes were similarly calculated to be 165 and 103 kJ mol⁻¹ relative to the Z forms of the episulfonium MeS⁺C₂H₂Me₂ and MeCOS⁺C₂H₂Me₂ ions, respectively. The difference in the activation energies again came from that of the donating ability of S in MeS and MeCOS. The difference in the ΔE^‡ values of the C₂H₂Me₂ adducts was larger than those of the C₂H₄ adducts. The two Me groups in the sulfonium ions contributed to decreasing the ΔE^‡ values by stabilizing electronically but destabilizing sterically, which were predicted to be stabilized totally by 43–70 kJ mol⁻¹. The ΔE^‡ values of 103–165 kJ mol⁻¹ seemed too high for the free carbocations to contribute to the site exchange processes, again, in spite of the stabilization of the TSs by the Me groups.

Fig. 6 The transition states for the C–C rotation in the S⁺C₂ three-membered rings of episulfonium ions. The motion for the imaginary frequency of each TS. The total displacements of atoms in each TS were determined with the centre of gravity unchanged, based on the total momentum.

It seems necessary to rotate around the C–C bond for the interconversion of the threo- and erythro-isomers. The direct C–C bond rotation in episulfonium ions seems difficult judging from the predicted high activation energies. Indeed, the episulfonium ions are stabilized in polar solvents, but the free carbonium ions should also be stabilized. Therefore, the interconversion between the threo- and erythro-isomers would not be greatly decelerated in polar solvents. The interconversion mechanism should be clarified theoretically. The differences between the experimental and calculation conditions should also be considered carefully. The next issue was to verify the interconversion processes based on the theoretical background.

2.9 Nature of the bonds in the COSI group of 1

What are the nature of the bonds and/or interactions in the COSI group of 1a and 1m, discussed in Table 3? It is instructive to visualize the nature of the bonds and/or interactions in question. Fig. 7 shows the optimized structures of 1a_syn-C1 and 1m_syn-C1. QTAIM-DFA was applied to analysis of 1. The basic concept of the QTAIM-DFA approach was explained in the appendix of the ESI using Schemes SA1–SA3, Fig. SA1 and SA2, Table SA1 and eqn (SA1)–(SA7).† The details of the calculation method are also described in “Methodological details in calculations” of the experimental section. The QTAIM functions^14–19 were calculated at the bond critical points (BCPs) on the bond paths (BPs), corresponding to the bonds in question containing the C_CO-*-C_R bond, as a typical example. QTAIM functions are designated as charge density (ρ_b(r_c)), total electron energy densities H_b(r_c), potential energy densities V_b(r_c), kinetic energy densities G_b(r_c), and k_b(r_c) (= V_b(r_c)/G_b(r_c)) at BCPs. Table 4 collects the ρ_b(r_c), H_b(r_c), and H_b(r_c) − V_b(r_c)/2 (=(ћ²/8m)∇²ρ_b(r_c)) values for the bonds in 1a_syn-C1 and 1m_syn-C1 along with 1a_obsd; they were calculated without considering the solvent effect under MP2/S-TZPsp. Fig. 8 shows the QTAIM-DFA plots of H_b(r_c) versus H_b(r_c) − V_b(r_c)/2 for the interactions in 1a_syn-C1, 1m_syn-C1 and 1a_obsd. The QTAIM-DFA parameters of (R, θ) and/or (θ_p, κ_p) were calculated by analysing the plots in Fig. 8 according to eqn (SA1)–(SA6) of the appendix in the ESI.† Table 4 collects the (R, θ), (θ_p, κ_p) and/or C_ii values for the bonds in question. The definitions of (R, θ) and (θ_p, κ_p) are also found in the footnotes of Table 4. The parameters are illustrated in Fig. 8, exemplified by 1m_syn-C1 : C₁-*-C₂.

Fig. 7 Molecular graphs with contour maps of r_b(r_c) of 1a_syn-C1 (a) and 1m_syn-Cs (b), evaluated with MP2/S-TZPsp. BCPs are denoted by red dots, RCPs (ring critical points) by yellow dots and BPs by pink lines. Carbon atoms are shown in black, and hydrogen atoms are in grey, with oxygen, sulfur and iodine atoms in red, yellow and purple, respectively. Contour plots are drawn on the OCI planes of the species.

Table 4 QTAIM functions and QTAIM-DFA parameters for the bonds/interactions in the COSI four-membered rings in 1a and 1m calculated with MP2/Spr-TZPsp^a

Species X-*-Y	ρb(rc) (eao^−3)	c∇^2ρb(rc)^b (au)	Hb(rc) (au)	R^c (au)	θ^d (°)	Cii^e (Å mdyn^−1)	θp^f (°)	κp^g (au^−1)	Predicted nature
a Data are given at BCPs.b c∇^2ρb(rc) = Hb(rc) − Vb(rc)/2, where c = ћ^2/8m.c R = (x^2 + y^2)^1/2, where (x, y) = (Hb(rc) − Vb(rc)/2, Hb(rc)).d θ = 90° − tan^−1 (y/x).e Diagonal elements of the compliance constant.f θp = 90° − tan^−1 (dy/dx).g κp = |dy^2/dx^2|/[1 + (dy/dx)^2]^3/2.
1asyn-C1
C1-*-O	0.4099	−0.0626	−0.7298	0.7325	184.9	0.089	165.2	1.9	SS/Cov-s
C1-*-S	0.1801	−0.0307	−0.1215	0.1253	194.2	0.490	200.2	0.1	SS/Cov-w
S-*-I	0.1070	−0.0033	−0.0533	0.0534	183.6	0.421	183.9	11.1	SS/Cov-w
C1-*-Ci	0.2628	−0.0862	−0.2438	0.2586	199.5	0.233	201.7	0.1	SS/Cov-s
1aobsd
C1-*-O	0.4138	−0.0608	−0.7411	0.7436	184.7				SS/Cov-s
C1-*-S	0.1860	−0.0341	−0.1304	0.1348	194.6				SS/Cov-w
S-*-I	0.1052	−0.0032	−0.0516	0.0517	183.5				SS/Cov-w
C1-*-Ci	0.2611	−0.0851	−0.2410	0.2555	199.4				SS/Cov-s
1msyn-C1
C1-*-O	0.4140	−0.0603	−0.7414	0.7438	184.6	0.086	164.3	1.9	SS/Cov-s
C1-*-S	0.1830	−0.0321	−0.1255	0.1295	194.3	0.479	200.2	0.1	SS/Cov-w
S-*-I	0.1073	−0.0034	−0.0535	0.0536	183.7	0.417	184.1	10.7	SS/Cov-w
C1-*-CMe	0.2502	−0.0779	−0.2234	0.2366	199.2	0.250	201.7	0.1	SS/Cov-s

---

Fig. 8 QTAIM-DFA plot of H_b(r_c) versus H_b(r_c) − V_b(r_c)/2 for the bonds in the COSI group of 1a and 1m evaluated with MP2/S-TZPsp, where the perturbed structures were generated with CIV. Whole picture of the plots (a) and (b) the partial one (b).

The θ values were larger than 180° (H_b(r_c) − V_b(r_c)/2 < 0) for all interactions shown in Table 4. Such interactions are called shared shell (SS) interactions, which correspond to classical covalent (Cov) bonds. The Cov bonds of SS are called strong (Cov-s) when R > 0.15 au and weak (Cov-w) when R < 0.15 au (tentative). The (R, θ) values were (0.237–0.259 au, 199.2–199.5°) for C_C=O-*-C_R in 1a_syn-C1, 1a_obsd and 1m_syn-C1, which were typical examples of the classical strong covalent (single) bond that appeared in the SS region, according to the above criteria, and denoted by SS/Cov-s. The (R, θ) values were (0.733–0.744 au, 184.6–184.9°) for O-*-C, (0.125–0.135 au, 194.2–194.6°) for C-*-S and (0.052–0.054 au, 183.5–183.7°) for S-*-I in 1a_syn-C1, 1a_obsd and 1m_syn-C1. Consequently, the O-*-C, C-*-S and S-*-I bonds were predicted to have SS/Cov-s, SS/Cov-w and SS/Cov-w nature, respectively. The θ values of 194.2–194.6° for C-*-S were largest among the three bonds in the COSI group, but the R values of 0.125–0.135 au seemed close to the borderline value of 0.15 au. The values may change somewhat depending on the basis sets employed for the calculations.²⁹ The C-*-S bonds may be better recognized to have SS/Cov-s nature.

We used another set of criteria, which are more commonly used. The set of criteria employs the (θ, θ_p) values, where 45° < θ < 206.6° and 45° < θ_p < 206.6°.¹⁶ While θ classifies the interactions, θ_p characterizes them. It has been established that the (θ, θ_p) values of (75°, 90°), (90°, 125°), (115°, 150°), (150°, 180°) and (180°, 190°) correspond to the borderlines between the nature of the interactions for vdW/t-HB_nc (typical hydrogen bonds with no covalency), t-HB_nc/t-HB_wc (typical HBs with covalency), t-HB_wc/CT-MC (interactions in molecular complexes through charge transfer), CT-MC/CT-TBP (interactions in trigonal bipyramidal adducts through CT) and CT-TBP/Cov-w (weak covalent bonds). The parameters described in bold were superior to the tentative parameters in the classification and/or characterization of interactions.

The nature of the three bonds (C₁-*-C_R, C₁-*-S and S-*-I) were re-examined based on this set of criteria, together with (θ, θ_p) = (199.2–199.5°, 201.7°) for the typical classical single bond of C₁-*-C_R (SS/Cov-s), as guidance. The C-*-S bonds are typically predicted to have SS/Cov-s nature, based on the (θ, θ_p) values of (194.2–194.3°, 200.2°) irrespective of R values.

The (θ, θ_p) values were (183.6–183.7°, 183.9–184.1°) for S-*-I, which predicted the SS/Cov-w nature for the bond. The nature derived from the (θ, θ_p) values seemed in good agreement with those based on the (R, θ) values for the three bonds. However, the (θ, θ_p) values were (184.6–184.9°, 164.3–165.2°) for C₁-*-O, where the θ_p values of 164.3–165.2° corresponded to the CT-MC nature irrespective of the R values. The results may show abnormal character for C₁-*-O, which would be affected by the I⋯O interaction. Indeed, such character was not detected in S-*-I, but the (θ, θ_p) values for S-*-I would be somewhat curious. The θ_p values seemed very close to the θ values in 1a_syn-C1 and 1m_syn-C1, although the θ_p values were substantially larger than θ for the standard interactions. Such discrepancies in the parameters for the bonds seemed to originate from the abnormal characteristics of the bonds in the species (see Table 4). The discrepancies seemed large for C₁-*-O and S-*-I but not C-*-S (and C₁-*-C_R). Abnormal characteristics were also found in the complicated plots (curves) for the former, as shown in Fig. 8.

The character of the O-*-C₁-*-S-*-I bonds in 1 would be clarified more if the I-*-O interactions could be analysed. The COSI four-membered ring with the 6p electrons in 1 were reminiscent of the stabilization of the system by the aromatic character. However, further insight into the issue was not attempted since BPs with BCPs corresponding to I-*-O were unfortunately not detected, while the bonds were significantly shorter than those expected. It was noteworthy that from the appearance to the disappearance of the BPs with BCPs corresponding to I-*-O of 1a_syn-C1 and 1m_syn-Cs, the bonds seemed near the borderline, judging from the contour maps of ρ_b(r_c) shown in Fig. 7, although the appearance and disappearance of the BPs were very complex and difficult to analyse in the context of this study. A detailed analysis of the I⋯O interactions without BPs would be beyond the scope of this study.

3 Conclusions

A series of acylsulfenyl iodides 1 were synthesized through the reaction of carbothioic acid group 11–16 element derivatives with iodine or NIS in moderate to good yields. The structure of benzoylsulfenyl iodide 1a was clarified to be nearly square planar, where the C=O⋯I distance (3.153(7) Å) was significantly shorter than the sum of the vdW radii of both atoms (Σr_vdW), indicating intramolecular close contact. In addition, the intermolecular distances between the iodine atom and two neighbouring iodine atoms were shorter than the Σr_vdW value, possibly due to the energy lowering effect of the interactions. The planar structure of 1a was reminiscent of the similar planar structures of 1, other than 1a, together with the corresponding benzoylsulfenyl halides of PhCOSX (X = F, Cl and Br). Alkenes and alkynes readily reacted with 1 at 0 °C to give the expected addition products (RCOSCH₂CH₂I) in moderate to good yields, along with disulfides (RCOSSCH₂CH₂I), as do alcohols and amines, affording new types of S-acylated-sulfines and -sulfenamides in moderate to good yields.

The theoretical calculations performed on 1a with MP2/S-TZPsp perfectly reproduced the observed results. Mechanisms for the reactions were proposed based on the theoretical calculations performed on the reactions of MeCOSI (1m) and CH₂=CH₂ with MP2/S-TZPsp. The mechanisms were also investigated for the reactions of alkane sulfenyl iodides with olefins, which are seldom encountered, as exemplified by methane sulfenyl iodide 14m and CH₂=CH₂ with MP2/S-TZPsp. The proposed mechanisms for both reactions seemed very similar. Episulfurans played an important role in the reactions as intermediates, especially in the initial stages. The dynamic and static nature of the interactions in question were also predicted based on QTAIM-DFA.

The structure and reactivity of acylsulfenyl iodides 1 must shed light on the anti-thyroidal activity and tyrosine residue of thyroglobulin and the related area. Such investigations are in progress.

4 Experimental

The melting points were measured by a Yanako micro-melting point apparatus and uncorrected. The IR spectra were measured on a PerkinElmer FT-IR 1640 and a JASCO grating IR spectrophotometer IR-G. The ¹H-NMR spectra were recorded on JEOL R-22 (90 MHz) and JEOL JNM-GX-270 (270 MHz) instruments. ¹³C-NMR spectra were recorded on a JEOL JNM-GX-270 (67.5 MHz) and JEOL JNM-α400 (100 MHz) instruments. ⁷⁷Se and ²⁵Te NMR spectra were recorded on a JEOL JNM-α400 at 76.2 and 126 MHz, respectively. For the NMR measurements, CDCl₃ was used as the solvent. As the internal standard, Me₄Si was used for ¹H and ¹³C NMR, while the external standards Me₂Se and Me₂Te were used for ⁷⁷Se NMR and ¹²⁵Te NMR, respectively. The following abbreviations were used: singlet = s, doublet = d, doublet of doublets = dd, triplet = t, quartet = q, quintet = quin, sextet = sex, septet = sep, doublet of triplets = dt, multiplet = m, germinal = g. Electron spectra were measured on a JASCO U-Best 55. The mass spectra (H.R.M.S.) were recorded on Shimadzu GCMS QP1000 (A) (EI/CI, model) and GCMS 9020DF high resolution mass spectrometers and on a Hitachi RMU-6 (20 eV) high resolution mass spectrometer. Elemental analyses were performed by the Elemental Analysis Center of Kyoto University and Gifu Pharmaceutical University.

4.1 Materials

Diethylamine, n-propyl and iso-propylamines, 1-butyl, iso-butyl and tert-butylamines and phenyl- and diphenylamines, pirolidine, piperidine and morphorine, cyclohexene, 3,3-dimethylbutene, 1-hexene, 2-methyl-2-butene, 2-norbornene and benzoyl chloride were obtained from Nacalai Tesque. 2-Methylpropene (>99%), cis- and trans-2-butene (>99%), 1,3-butadiene and cyclopentene (>96%) were obtained from Aldrich. Iodine, potassium 1,1-dimethylethoxide, ethyl-, propyl-, butyl- and phenylmercaptanes, and phenol, iodine and N-iodosuccinimide (NIS) (98%) were purchased from Tokyo Kasei and used without further purification. Ether, tetrahydrofuran (THF) and hexane were dried over sodium benzophenone and distilled before use. Dichloromethane and chloroform were dried on phosphorus pentoxide and distilled before use. Silica gel for the preparative thin layer chromatography (PTLC) was Wako gel B-5F of Wako Pure Chemical Industry, Ltd. Carbothioic acids and their potassium³⁰ and piperidinium salts³¹ were prepared according to previous reports. Silver carbothioates,³² zinc and cadmium di(carbothioates) were prepared by the reaction of the corresponding metal chlorides, acetates or nitrates with carbothioic acids and their potassium or piperidinium salts, respectively.³³ Their yields and spectral data are shown in Tables 34–36 of the ESI.† The yields, physical properties and spectral data of compounds 1a–1o are shown in Tables S1–S7 of the ESI.†

S-Triphenylgermenium carbothioates,^34,35 S-diphenylgermenium di(carbothioates),^34,35 S-triphenyltin carbothioates,^34,35 S-diphenyltin di(carbothioates),^34,35 S-triphenyllead carbothioates,³⁵ and S-diphenyllead di(carbothioates)³⁵ were prepared according to the literature (Scheme S1 of the ESI†). Their yields, physical properties and spectral data are shown in Tables 37–42 and the procedures in Exp. S2 of the ESI.†

4.2 Preparation of acylsulfenyl iodides 1

The preparation methods of acylsulfenyl iodides (1a–1o) from the reactions of silver carbothioates, zinc and cadomium di(carbothioates) and S-diphenylgermanium di(carbothioates), S-triphenylgermanium carbothioates, S-diphenyltin di(carbothioates), S-triphenyltin carbothioates, S-diphenylead di(carbothioates), and S-triphenyllead carbothioate with iodine or N-iodosuccinimide are shown as typical procedures (Exp. S1 of the ESI).† Their yields, physical properties and spectral data are shown in Tables S1–S7 of the ESI.† Recrystallized solvents for 1a–1h were dichloromethane and hexane, while that for 1i–1o was hot hexane.

4.3 Benzoylsulfenyl iodide 1a by the reaction of Ag(RCOS) with I₂ (method A)

A solution of iodine (0.762 g, 3.0 mmol) in dichloromethane (20 mL) was added to a suspension of silver benzenecarbothioate 2a (0.740 g, 3.0 mmol) in dichloromethane/methanol (7 : 3, 20 mL) and stirred at 0 °C for 10 min. After removal of solids (AgI), the solvents were evaporated under reduced pressure below 10 °C. Recrystallization of the resulting residue from hexane gave benzoylsulfenyl iodide 1a as orange crystals; yield: 0.364 g (46%); mp 45–48 °C (decomp.); found, C, 31.74; H, 1.95; S, 12.15%; calc. for C₇H₅IOS (264.08) requires C, 31.84; H, 1.91; S, 12.14; i.r. n_max (KBr)/cm⁻¹ 1667 (C=O); δ_H (90 MHz, CDCl₃/TMS) 7.02–7.78 (m, 5H, arom); δ_C (100 MHz, CDCl₃/TMS): 184.4 (C=O); 109.1–133.5; m/z (EIS, 20 eV); found: M⁺ 263.91021; calc. for C₇H₅IOS requires 263.91058.

4.4 X-ray measurements of 1a

The measurement was performed on a Rigaku AFC7R four-circle diffractometer with graphite-monochromated Mo Kα radiation (λ = 0.71069 Å). All structures were solved and refined using the teXsan crystallographic software package³⁶ on an IRIS Indigo computer. The X-ray quality crystals of compound 1a (Deposition No. 2121145) were obtained by crystallization from ether/petroleum ether. These crystals were cut and coated with an epoxy resin and mounted on a glass fibre. The cell dimensions were determined from a least-squares refinement of the setting diffractometer angles for 25 automatically centred reflections. Lorentz and polarization corrections were applied to the data, and empirical absorption corrections (ψ-scans³⁷) were also applied. The structures were solved by the direct method using SHELXL-97 ³⁸ and expanded using DIRDIF92.³⁹ Scattering factors for neutral atoms were from Cromer and Waber⁴⁰ and anomalous dispersion⁴¹ was used. The function minimized was Σw(IF_oI − IF_cI)², and the weighting scheme employed was w = [σ²(F_o) + p²(F_o)²/4]⁻¹. A full-matrix least-squares refinement was executed with nonhydrogen atoms being anisotropic. The final least–square cycle included fixed hydrogen atoms at calculated positions; each isotropic thermal parameter was set to 1.2 times that of the connecting atom.

4.5 Methodological details in calculations

Calculations were performed using the Gaussian 09 software package⁴² under nonrelativistic conditions. The basis sets of the (7433211/743111/7411/2+1s1p) form for I, the (63211/6111/31/2+1s1p) form for S and the (6211/311/21/2+1s1p) form for C and O with the (211/21/2) form for H were used for the calculations, as implemented in the Sapporo Basis Set Factory.⁴³ The forms correspond to the Sapporo-TZP basis sets with the 1s1p diffusion functions, which are abbreviated by S-TZPsp, in this study. The Møller–Plesset second-order energy correlation (MP2) level⁴⁴ was applied for the calculations (MP2/S-TZPsp). The species in question were optimized, and the optimized structures were confirmed by frequency analysis. An optimized structure containing only one imaginary frequency was assigned to a transition state (TS), while that with all real (positive) frequencies was assigned to the minimum structure. The calculations were performed under the solvent effect of acetonitrile with SCRF method (PCM (polarizable continuum model))²⁸ starting from the structures optimized without considering the solvent effect. The QTAIM functions were calculated using the same method as that used for the optimizations. The AIM2000 ⁴⁵ and AIMAll⁴⁶ programs were used to analyse and visualize the results.

QTAIM-DFA^14–19 was developed by applying the QTAIM approach and is explained in the appendix of ESI using Schemes SA1–SA3, Fig. SA1 and SA2, Table SA1 and eqn (SA1)–(SA7).† H_b(r_c) was plotted versus H_b(r_c) − V_b(r_c)/2 (= (ћ²/8m)∇²ρ_b(r_c)) (QTAIM-DFA plot). Data from the fully optimized structures were analysed using the polar coordinate (R, θ) representation, while those from both perturbed and fully optimized structures were expressed by (θ_p, κ_p), where θ_p and κ_p corresponded to the tangent line of the curvature, respectively, in the plot. The definitions of the QTAIM parameters of (R, θ) and (θ_p, κ_p) were also found in the footnotes of Table 4 and Fig. 8.

It is necessary to establish a reliable method to generate the perturbed structures for the effective analysis with QTAIM-DFA. We recently proposed a highly reliable method to generate the perturbed structures for QTAIM-DFA.⁴⁷ The method is named CIV and employs the coordinates derived from the compliance constants C_ii for the internal vibrations. Eqn (1) defines C_ij, as the partial second derivatives of the potential energy due to an external force, where i and j refer to internal coordinates, and the force constants f_i and f_j correspond to i and j, respectively. While the off-diagonal elements C_ij (i ≠ j) in eqn (1) correspond to the compliance coupling constants, the diagonal elements C_ii represent the compliance constants for an internal coordinate i. The C_ii values and coordinates corresponding to C_ii were calculated using the Compliance 3.0.2 program⁴⁸ released by Grunenberg and Brandhorst.^49–53

Eqn (2) explains the method to generate the perturbed structures with CIV. The k-th perturbed structure in question (S_kw) was generated by the addition of the coordinates of the k-th internal vibration (C_k) in question to the standard orientation of a fully optimized structure (S_o) in the matrix representation. The coefficient f_kw in eqn (2) controlled the difference in the structures between S_kw and S_o; f_kw was determined to satisfy eqn (3) for an interaction in question, where r and r_o stand for the distances in question in the perturbed and optimized structures, respectively, with a_o equal to the Bohr radius (0.52918 Å). Five data points for w = 0, ±0.05 and ±0.1 in eqn (3) were typically used in the QTAIM-DFA plots. Each plot was analysed using a regression curve of the cubic function, as shown in eqn (4), where (x, y) = (H_b(r_c) − V_b(r_c)/2, H_b(r_c)) (R_c² > 0.99999 in usual).¹⁶

C_ij = ∂²E/∂f_i∂f_j (1)

S_kw = S_o + f_kw·C_k (2)

r = r_o + wa_o (w = (0), ±0.05, ±0.1; a_o = 0.52918 Å) (3)

y = c_o + c₁x + c₂x² + c₃x³ (4)

R_c²: square of correlation coefficient.

Conflicts of interest

The authors declare no conflict of interest.

Acknowledgements

S. K. thanks Messrs. Motohiro Oguri, Kazuyasu Tani, Yoshinari Deguchi and Noriyuki Sugiura for their synthesis of the starting compounds and Professor Hideharu Ishihara for mass spectra and ¹³C, ⁷⁷Se and ¹²⁵Te NMR spectra measurements.

References

1. H. Böhme and G. Zinner, Justus Liebigs Ann. Chem., 1954, 585, 142–149.
2. S. Kato, E. Hattori, M. Mizuta and M. Ishida, Angew. Chem., 1982, 94, 148; S. Kato, E. Hattori, M. Mizuta and M. Ishida, Angew. Chem. Int. Ed. Engl., 1982, 21, 150.
3. J. P. Johnson, M. P. Murchie, J. Passmore, M. Tajik, P. S. White and C.-M. Wong, Can. J. Chem., 1987, 65, 2744–2749.
4. R. Minkwitz, H. Preut and J. Sawatzki, Z. Naturforsch., B: Anorg. Chem., Org. Chem., 1988, 43, 399–402.
5. R. Minkwitz and J. Sawatzki, Z. Naturforsch., B: Anorg. Chem., Org. Chem., 1988, 566, 151–159.
6. G. K. Helmkamp and D. J. Pettitt, J. Org. Chem., 1960, 25, 1754–1755.
7. G. K. Helmkamp and D. J. Pettitt, J. Org. Chem., 1962, 27, 2942–2943.
8. T. Warren, J. Org. Chem., 1969, 34, 871–874.
9. W. H. Mueller, Angew. Chem., 1969, 8, 475–484; W. H. Mueller, Angew. Chem. Int. Ed. Engl., 1969, 8, 482–492.
10. L. Vektariene, Pharm. Chem. J., 1998, 32, 629–632.
11. D. B. Johnson and B. M. Pinto, J. Org. Chem., 2000, 65, 4607–4610.
12. C. Baldwin, B. M. Pinto, M. D. Eastgate, D. J. Fox and S. Warren, Org. Lett., 2002, 4, 4381–4384.
13. P. Bird, J. Eames, A. G. Fallis, R. V. H. Jones, M. Roddis, C. F. Sturino, S. O. Sullivan, S. Warren, M. S. Westwell and J. Worrall, Tetrahedron Lett., 1995, 36, 1909–1912.
14. W. Nakanishi, S. Hayashi and K. Narahara, J. Phys. Chem. A, 2009, 113, 10050–10057.
15. W. Nakanishi and S. Hayashi, Current Org. Chem., 2010, 14, 181–197.
16. W. Nakanishi and S. Hayashi, J. Phys. Chem. A, 2010, 114, 7423–7430.
17. W. Nakanishi, S. Hayashi, K. Matsuiwa and M. Kitamoto, Bull. Chem. Soc. Jpn., 2012, 85, 1293–1305.
18. W. Nakanishi and S. Hayashi, J. Phys. Chem. A, 2013, 117, 1795–1803.
19. S. Hayashi, K. Matsuiwa, M. Kitamoto and W. Nakanishi, J. Phys. Chem. A, 2013, 117, 1804–1816.
20. K. Goto, M. Holler and R. Okazaki, Chem. Commun., 1998, 1915–1916.
21. C. Wismach, P. G. Jones, W.-W. duMont, G. Mugesh, U. Papke, H. B. Linden, M. Arca and V. Lippolis, Eur. J. Inorg. Chem., 2014, 1399–1406.
22. https://www.ccdc.cam.ac.uk/products/csd/radii/table.php4, accessed on 6 January 2023.
23. A. Bondi, J. Phys. Chem., 1964, 68, 441–451.
24. A. Vektariene, G. Vektaris and D. W. H. Rankin, Heteroatom Chem., 2007, 18, 695–703,  DOI:10.1002/hc.20378.
25. M. Oki, W. Nakanishi, M. Fukunaga, G. D. Smith, W. L. Duax and S. Osawa, Chem. Lett., 1975, 1277–1280.
26. M. Mizuta, T. Katada, E. Itoh and S. Kato, Synthesis, 1980, 721–722.
27. G. K. Hepke, J. Martence, K. Praefke and H. Simon, Angew. Chem., 1977, 89, 328; G. K. Hepke, J. Martence, K. Praefke and H. Simon, Angew. Chem. Int. Ed. Engl., 1977, 16, 318; T. G. Back, S. Collins and R. G. Kerr, J. Org. Chem., 1981, 46, 1564–1570; P. A. Grieco, Y. Yokoyama and E. Williams, J. Org. Chem., 1978, 43, 1238–1246; S. Kato, H. Kabuto, M. Kimura, H. Ishihara and T. Murai, Synthesis, 1985, 519–520; S. Kato, H. Kabuto, M. Kimura, H. Ishihara and T. Murai, Synthesis, 1985, 520–522.
28. (a) M. T. Cancès, B. Mennucci and J. Tomasi, J. Chem. Phys., 1997, 107, 3032–3041; (b) M. Cossi, V. Barone, B. Mennucci and J. Tomasi, Chem. Phys. Lett., 1998, 286, 253–260; (c) B. Mennucci and J. Tomasi, J. Chem. Phys., 1997, 106, 5151–5158.
29. The R values of 0.15 au is determined under MP2/6-311++(3df,3pd). See ref. 15.
30. P. Noble Jr and D. S. Tabell, Org. Synth., 1963, 924; S. Kato, M. Oguri and M. Ishida, Z. Naturforsch. B, 1983, 38, 1585–1590.
31. S. Kato, W. Akada and M. Mizuta, Int. J. Sulfur Chem., Part A, 1972, 2, 279–282.
32. S. Kato, Y. Komatsu, K. Miyagawa and M. Ishida, Synthesis, 1983, 552–553.
33. Zinc and cadmium di(carbothioates) were prepared by the reactions of the corresponding metal chlorides or acetates with carbothioic acids. See Tables S35 and S36 of the ESI.†.
34. S. Kato, W. Akada, M. Mizuta and Y. Ishii, Bull. Chem. Soc. Jpn., 1973, 46, 244–248; O. Niyomura, S. Kato and T. Kanda, Inorg. Chem., 1999, 38, 507–518.
35. K. Tani, Master thesis, Gifu University, 1999.
36. teXsan, Crystal Structure Analysis Package, Molecular Structure Corporation, 1992.
37. A. C. T. North, D. C. Phillips and F. S. Mathews, Acta Crystallogr., Sect. A: Found. Crystallogr., 1968, 24, 351.
38. M. Sheldrick, Crystallographic Computing 3; SHELXL97 Program for the Refinement of Crystal Structure, University of Göttingen, Germany, 1997.
39. P. T. Beukskens, G. Admiraal, G. Beurskiens, W. P. Bosman, S. Garcia-Granda, R. O. Gould, J. M. M. Smits and C. Smykalla, Technical Report of the Crystallography Laboratory, University of Nijmegen, The Netherlands, 1992.
40. D. T. Cromer and J. T. Waber, International Tables for X-ray Crystallography, the Kynoch Press: Birmingham, UK, 1974, vol. 4, Table 2.2A.
41. (a) M. Fachini, V. Luchini, G. Modena, M. Pasi and L. Pasquato, J. Am. Chem. Soc., 1999, 121, 3944–3950; (b) A. Vektariene and G. Vktaris, Arkivoc, 2006, 16, 23–34.
42. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision D.01, Gaussian, Inc., Wallingford CT, 2009.
43. T. Noro, M. Sekiya and T. Koga, Theoret. Chem. Acc., 2012, 131, 1–8.
44. (a) C. Møller and M. S. Plesset, Phys. Rev., 1934, 46, 618–622; (b) J. Gauss, J. Chem. Phys., 1993, 99, 3629–3643; (c) J. Gauss, Ber. Bunsen-Ges. Phys. Chem., 1995, 99, 1001–1008.
45. F. Biegler-König, The AIM2000 program (Version 2.0) is employed to analyze and visualize atoms-in-molecules, J. Comput. Chem., 2000, 21, 1040–1048.
46. T. A. Keith, AIMAll (Version 17.11.14), TK Gristmill Software, Overland Park, KS 2017, https://www.aim.tkgristmill.com, accessed on 5 April 2023.
47. W. Nakanishi and S. Hayashi, Int. J. Quantum Chem., 2018, 118, 255900,  DOI:10.1002/qua.25590.
48. The C_ii values and the coordinates corresponding to C_ij were calculated by using the Compliance 3.0.2 program released by J. Grunenberg, K. Brandhorst, available online: https://www.oc.tu–bs.de/Grunenberg/compliance.html, accessed on 5 April 2023.
49. K. Brandhorst and J. Grunenberg, J. Chem. Phys., 2010, 132, 184101–184107.
50. K. Brandhorst and J. Grunenberg, Chem. Soc. Rev., 2008, 37, 1558–1567.
51. J. Grunenberg, Chem. Sci., 2015, 6, 4086–4088.
52. J. Grunenberg, J. Am. Chem. Soc., 2004, 126, 16310–16311.
53. J. Grunenberg and G. Barone, RSC Adv., 2013, 3, 4757–4762.

---

Footnotes

† Electronic supplementary information (ESI) available: Experimental data, QTAIM-DFA approach, and computational data. CCDC 2121145. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d3ra00646h

‡ Present address: Maruno-uchi 2-14-32, Lions-City Maruno-uchi 1105, Naka-ku, Nagoya 460-0002, Japan.

---