Hydrogen evolution reaction following the Slater–Pauling curve: acceleration of rate processes induced from dipole interaction between protons and ferromagnetic catalysts

Abstract

Developing new concepts to design noble-metal-free catalysts is necessary to achieve the hydrogen economy and reduce global CO₂ emissions. Here, we provide novel insights into the design of catalysts with internal magnetic fields by investigating the relationship between the hydrogen evolution reaction (HER) and the Slater–Pauling rule. This rule states that adding an element to a metal reduces the alloy's saturation magnetization by an amount proportional to the number of valence electrons outside the d shell of the added element. We observed that rapid hydrogen evolution occurred when the magnetic moment of the catalyst was high, as predicted by the Slater–Pauling rule. Numerical simulation of the dipole interaction revealed a critical distance, r_C, at which the proton trajectory changes from a Brownian random walk to a close-approach orbit towards the ferromagnetic catalyst. The calculated r_C was proportional to the magnetic moment, consistent with the experimental data. Interestingly, r_C was proportional to the number of protons contributing to the HER and accurately reflected the migration length for the proton dissociation and hydration and the O–H bond length in water. The magnetic dipole interaction between the nuclear spin of the proton and the electronic spin of the magnetic catalyst is verified for the first time. The findings of this study will open a new direction in catalyst design aided by an internal magnetic field.

---

Introduction

To reduce CO₂ emissions, the production of hydrogen fuel instead of fossil fuels is critical.¹ Although Pt-based catalysts are being widely used for hydrogen production,^2–8 Pt is one of the most expensive noble metals. One strategy to achieve the hydrogen economy is to develop inexpensive catalysts with pertinent activity to replace Pt. In 1845, Faraday⁹ had an insight that magnetic forces affect electrolytes. However, his insight was greatly overlooked for the next 150 years. Recently, the use of magnetic fields has been highlighted as an effective strategy for improving the performance of catalysts for the oxygen evolution reaction (OER)^10–16 and hydrogen evolution reaction (HER)^17–21 during water splitting,^{10–15,17–21} and for enhancing power generation with fuel cells.¹⁶

The oxygen molecule, O₂(g), has a triplet spin configuration. Catalysts with spin selectivity²² are known to improve OER efficiency by effectively inducing a triplet spin configuration, thereby decreasing the OER overpotential.^10–15 The spin-selective reaction that accelerates OER consists of the following three steps:^10–16 (I) spin-selective conduction in the catalyst acting as a spin filter;^11–15 (II) spin transport from the catalyst to O₂(g) to configure the triplet spin state;^12–16 and (III) dissociation of triplet O₂(g).¹⁰

Step (I) has been validated experimentally.^11–15 TiO₂ electrodes coated with self-assembled DNA,¹¹ chiral paramagnetic CoO_x films,¹⁴ and ferrite oxides¹³ were shown to act as spin filters for OER. Concerning step (II), Gracia¹² used transition theory to describe the tunnelling phenomenon as the mechanism of catalyst-to-O₂(g) spin transport required to reach the spin-parallel triplet state. In addition, the spin-selective emission of β rays (i.e., electron beams) was observed during the β decay of radionuclide ⁶⁰Co.²³ Regarding step (III), first-principles calculations verified that the triplet spin state is advantageous for the dissociation process.¹⁰

Exposure to an external magnetic field is found to increase the electric current generated during the HER.^17–21 Water is composed of the diamagnetic H₂O(l) molecule and charged ions, i.e., proton (H⁺(aq)), hydroxide (OH⁻(aq)), and hydronium (H₃O⁺(aq)) ions. Under an external magnetic field, as is well-known in the field of magnetohydrodynamics (MHD), an increase in the hydrogen evolution rate results from convection due to the Lorenz force^17–21 and from enhanced electrical conductance due to the magneto-resistive effect.^20,21 Nonetheless, the interaction between the nuclear spin of the proton and the electronic spin of the metal catalyst remains unclear.^9–22

Tungsten carbide (WC) has 10 valence electrons, 5d⁶ from W and 2p⁴ from C, making it similar to Pt (5d¹⁰). In 1973, Levy and Boudart²⁴ proposed that WC exhibited singular catalytic activity similar to Pt. Since then, many researchers have investigated this theory using spectroscopy,^25–27 first principles calculations,^28,29 and experiments to measure catalytic activity.^24,30–35 The catalytic activities of WC and its composites have only been observed under applied external voltage,^30–35 and the predicted intrinsic catalytic activity of mono-WC under voltage-free operation has not yet been verified.

Bennett et al.²⁵ reported that magnetic properties are one of the intrinsic differences between WC and Pt. WC is non-magnetic, whereas Pt exhibits high magnetic susceptibility. In our previous study,³⁶ an HER catalyst was developed by doping tungsten carbide (WC) lattice with ferromagnetic Co nanocrystals. The resulting alloy was used for the catalytic hydrolysis of ammonium borane (NH₃BH₃), a material known as a high-capacity hydrogen-storage compound.^37–43 The activity of the novel carbide was 30% higher than Pt nanoparticles under the same conditions. We hypothesised that the enhanced catalytic activity was attributed to the synergistic effect of the WC matrix promoting hydrolytic cleavage of NH₃BH₃ and the ferromagnetic Co crystals interacting with the nucleus spin of the protons. In the present study, we aimed to verify the interaction between the nucleus proton and magnetic substances from both experimentation and numerical simulation. The relationship between the rate of HER and the magnetic moment of a catalyst was investigated considering the Slater–Pauling rule.^44,45 This rule states that adding an element to a metal reduces the alloy's saturation magnetization by an amount proportional to the number of valence electrons outside the d shell of the added element. To understand the relationship between HER and the Slater–Pauling rule,^44,45 the dipole interaction⁴⁴ between the proton nucleus spin and magnetic substances was simulated based on the electromagnetism for the first time.

An application of HER catalysts is the generation of hydrogen fuel from NH₃BH_3. In its stable crystal form, NH₃BH₃ contains 19.6 wt% hydrogen,^37–43 and is being investigated for efficient transportation of hydrogen-based fuel for portable fuel-cell systems. Previous studies investigated the HER by hydrolysis over 10 wt% Co (ref. 39) or 2 wt% Pt (ref. 40) (both supported by Al₂O₃) and found that the HER in the latter was significantly faster than that in the former. A similar HER in NH₃BH₃(aq) catalysed by Ni nanoparticles (NPs) supported by a zeolite molecular sieve was observed.⁴² The atomic configuration in the AB molecule was investigated by neutron diffraction.³⁸ The chemical bonding states for AB were investigated by first principles calculations⁴¹ and soft X-ray adsorption spectroscopy.⁴³ The standard enthalpy of formation, 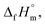at 298.15 K was determined by combustion calorimetry.³⁷ The catalytic design of selecting metals and alloys based on thermodynamic cycles for hydrolysis of AB have not previously been investigated. In the present study, a new strategy was developed to enhance catalytic performance and investigate the effect of an internal magnetic field on the thermodynamic mechanism of the hydrolysis of AB.

Methods

Sample preparation

Cobalt(II) acetate tetrahydrate [Co(C₂H₃O₂)₂·4H₂O, 99%, Kojundo Chemical Laboratory Co., Ltd., Saitama], iron(III) nitrate nonahydrate [Fe(NO₃)₂·9H₂O, 99.9%, Kojundo Chemical Laboratory Co., Ltd., Saitama], and nickel(II) acetate tetrahydrate [Ni(C₂H₃O₂)₂·4H₂O, 99%, Kanto Chemical Co., Inc., Tokyo], were used as the starting materials. Thirteen catalyst compositions were prepared with various compositions using the following procedure. For each sample, the requisite amount of Co(C₂H₃O₂)₂·4H₂O, Fe(NO₃)₂·9H₂O, and Ni(C₂H₃O₂)₂·4H₂O were separately dissolved in 100 ml deionized water at 363 K contained in alumina crucibles.

For all samples (except 1, 7, and 13), the corresponding precursor solutions were mixed to form homogeneous aqueous solutions with a total volume of 200 ml. The homogeneous mixtures of metal complexes were prepared by calcination at about 500 K. These mixtures were then thermally decomposed under O₂ at 773 K for 2 h to obtain homogeneous oxide-containing components. After thermal decomposition, powder samples were produced by reducing oxide-containing components with H₂ at 1073 K for 2 h followed by cooling with 20 K min⁻¹. Using an electron probe microanalysis system (JXA-8530FPlus, Co., JOEL Ltd, Tokyo) with a 15 kV accelerating voltage, the homogeneous chemical compositions of the samples were confirmed via X-ray images. Particle sizes and morphologies were compared by scanning electron microscopy (SEM).

The SA of the samples was determined by the Brunauer–Emmett–Teller method using nitrogen physisorption isotherms at 77 K, obtained with a sorption and porosity analyzer (BELSORP mini, MicrotracBEL Corp). The SA of the sample powders was about 2 m² g⁻¹, as shown in Table 1.

Table 1 Composition, electron concentration (E_conc), magnetic moment (M_Ferro),^44,45 specific surface area (SSA), structure determined from XRD, average electron-vacancy number, N_v,⁵⁴ and the d level of alloying element, M_d⁵⁵

Sample	Co/mol%	Fe/mol%	Ni/mol%	Econc^a	MFerro/μB^b	SSA/(m^2 g^−1)	Structure	Nv	Md/eV
a The Econc values for Fe (3d^6 and 4s^2), Co (3d^7 and 4s^2), and Ni (3d^8 and 4s^2) are 8, 9, and 10, respectively. The Slater–Pauling rule^44,45 was used to calculate the Econc of alloys by averaging the Econc of the elemental components.b The MFerro values for the samples (except 1, 7, and 13) were estimated by interpolating the Slater–Pauling curve.c Two phase equilibrium region composed of fcc and bcc solid solutions in the Co–Fe binary system.^46d Single phase region composed of hcp solid solutions in the Co–Fe binary system.^46e Single phase region composed of hcp solid solutions in the Co–Ni binary system.^46
1	0	100	0	8.00	2.20	2.01	bcc	2.66	0.81
2	50	50	0	8.50	2.29	1.92	bcc	2.19	0.43
3	65	35	0	8.65	2.23	2.27	bcc	2.04	0.32
4	85	15	0	8.85	1.87	1.71	fcc^c	1.85	0.17
5	92	8	0	8.92	1.82	1.94	fcc	1.79	0.12
6	96	4	0	8.96	1.76	1.94	fcc^d	1.75	0.09
7	100	0	0	9.00	1.70	1.93	hcp	1.71	0.06
8	96	0	4	9.04	1.66	1.92	hcp + fcc^e	1.67	0.09
9	92	0	8	9.08	1.59	1.86	hcp + fcc^e	1.63	0.13
10	85	0	15	9.15	1.55	1.91	hcp + fcc^e	1.55	0.18
11	65	0	35	9.35	1.37	1.85	fcc	1.28	0.27
12	50	0	50	9.50	1.18	1.47	fcc	1.19	0.48
13	0	0	100	10.0	0.60	1.93	fcc	0.66	0.89

---

HER analysis

For HER tests, 20 mg of each sample was placed in a glass test tube containing 1 ml of H₂O. Separately, solutions of NH₃BH₃(aq) were made by dissolving 0.5 mmol NH₃BH₃(cr) in 1.5 ml H₂O. This solution was then mixed with each sample to initiate hydrolysis and hydrogen evolution. The volume of evolved hydrogen (V_HER) was measured as a function of time t, and the hydrogen evolution rate (R_HER) was determined from the slope of the V_HER vs. t curve. From this, it was determined that V_HER increased linearly while excess unreacted NH₃BH₃(aq) remained. The used aqueous solution was decanted after the first V_HER measurement, while the ferromagnetic samples were held back inside the test tube with an external magnet placed outside the glass test tube. After draining, the second and third V_HER measurements were conducted similarly to the first. After completing the third measurement, fresh water was added to the ferromagnetic samples, which were then drained. After drying the samples in a dryer overnight, a fourth measurement was performed in the same way. The fourth V_HER measurement was similar to the first three. Because the produced hydrogen gas appeared to reduce the sample surface, the V_HER obtained in all four was averaged and used as the total V_HER. During the HER test, the AB solution was stirred with a rotating magnetic stirrer.

Results and discussion

Hydrogen evolution following the Slater–Pauling magnetic rule

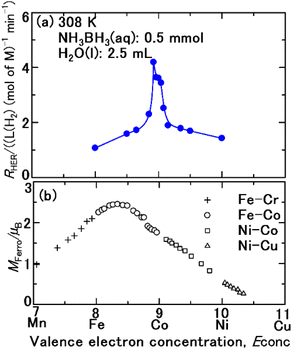
The structures of the samples determined from XRD are summarized in Table 1. The phases were consistent with the phase diagrams⁴⁶ of the Co–Fe and Co–Ni binary systems. However, the phases composed in 85 mol% Co–15 mol% Fe (no. 4), 96 mol% Co–4 mol% Fe (no. 6), 96 mol% Co–4 mol% Ni (no. 8), 96 mol% Co–8 mol% Ni (no. 9), 85 mol% Co–15 mol% Ni (no. 10) were different from the equilibrium phase diagrams⁴⁶ as shown in Fig. S1–S5 (ESI†). In no. 4, the high temperature fcc solid solution⁴⁷ was only formed due to rapid cooling (20 K min⁻¹), which prevented the formation of the equilibrium bcc solid solution.⁴⁶ In no. 6, the high temperature fcc solid solution⁴⁷ remained due to rapid cooling, which prevented the formation of the equilibrium hcp solid solution.⁴⁸ In no. 8–10, the high fcc solid solution⁴⁷ remained partly mixed with the equilibrium hcp solid solution⁴⁸ resulting from rapid cooling. However, the meta stable fcc solid solutions were in the ferromagnetic phase.

Fig. 1a and b compare the plots of R_HER for the hydrolysis of ammonium borane (NH₃BH₃)³⁶ as a function of the valence electron concentration E_conc, of the catalyst and the Slater–Pauling curve.^44,45 The composition, E_conc, magnetic moment, SSA, and crystal structure of Fe, Co, Ni, and their binary alloys are shown in Table 1. The perpendicular axis of the Slater–Pauling curve^44,45 is the magnetic moment M_Ferro with the units of Bohr magneton. The M_Ferro of pure Fe, Co, and Ni, as well as their alloys, varies with E_conc. The Co–Fe alloy, with an E_conc of 8.33, has the highest M_Ferro. The R_HER increases with E_conc, beginning with Fe (E_conc = 8), and reaching a maximum for the 92Co–8Fe (mol%) alloy with E_conc = 8.92. As E_conc continues to increase, R_HER decreases. Specifically, R_HER varies according to the Slater–Pauling curve, and a magnetic-moment-induced increase in R_HER is observed.

Fig. 1 (a) Hydrogen evolution rate R_HER for NH₃BH₃(aq) over pristine Fe, Co, and Ni, and their alloys as a function of the valence electron concentration, E_conc. (b) Slater–Pauling curve showing the relationship between the magnetic moment M_Ferro of pristine metals or their alloys and E_conc.

To clarify the reason for that the magnetic-moment increase in R_HER, the first of all, the thermodynamic cycle of hydrolysis of AB was discussed. Table 2 shows the thermodynamic cycle of the hydrolysis of AB where the standard enthalpies of formation, at 298.15 K of the standard substances of NH₃BH₃(cr),³⁷ H₂O(l),⁴⁹ orthoboric acid (B(OH)₃(aq)),⁴⁹ ammonium (NH⁴⁺(aq)),⁴⁹ metaboric acid (BO₂⁻(aq)),⁵⁰ and H₂(g)⁴⁹ are summarised in Table S1.† Eqn (I) shows the hydration reaction of NH₃BH₃(cr), where the thermodynamic value is unknown. Eqn (II) shows the HER of the hydrolysis of NH₃BH₃(aq). Eqn (III), rewritten as the sum of eqn (I) and (II), indicates the HER from the initial substance of NH₃BH₃(cr). Eqn (IV) shows the formation of NH⁴⁺(aq). Eqn (V) shows the formation of BO₂⁻(aq). Finally, eqn (VI), rewritten as the sum of eqn (III)–(V), shows the final state of the hydrolysis Since eqn (IV)–(VI) are spontaneous reactions, the HER is given by eqn (III). As the standard entropy, of NH₃BH₃(cr) has not yet been measured, the standard entropy of reaction, Δ_rS^°, and the standard Gibbs energy of reaction, Δ_rG^°, are unknown. However, Δ_rG^° is more negative than Δ_rH^° as the HER increases Δ_rS^°. Therefore, when a driving energy is applied corresponding to the hydrogen overpotential of metals, the HER reaches equilibrium, as defined by eqn (VI) via eqn (III).

Table 2 Thermodynamic cycle of hydrolysis of ammonium borane, NH₃BH₃

---

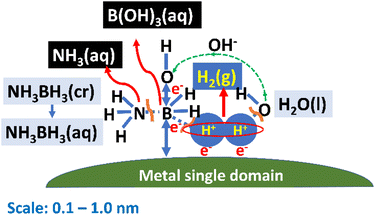
Next, we sought to understand the HER mechanism using the Slater–Pauling rule.^44,45 Fig. 2 depicts a schematic illustration of the catalytic HER over a magnetic metal single domain, which is relevant for Fe, Co, and Ni pure metals and their alloys. The HER is carried out through the following steps: (1) NH₃BH₃ molecules collide during Brownian motion⁵¹ and are adsorbed on the single domain. (2) The B–N bonds in NH₃BH₃(aq) are broken to form the stable NH₃(aq) molecule and transition-state species BH₃(aq) to reach equilibrium. (3) Short-lived BH₃(aq) releases three quasi-stable protons, and the B atom coordinates the three OH⁻(aq) ions released from the surrounding H₂O(l) molecule to form a stable B(OH)₃ molecule. H₂O(l) also releases three protons. (4) A sufficient number of protons from BH₃(aq) and H₂O(l) assemble at the single domain owing to the magnetic interaction between their nuclear spins and the electronic spin of the single domain. (5) Hydrogen molecules are produced when protons accept electrons (e⁻). (6) One e⁻ is released, along with a proton, during the decomposition of BH₃, while the other e⁻ is released from OH⁻(aq) during coordination to form B(OH)₃(aq). In other words, the source of charge transfer is the B atom adsorbed on the metal single domain. It is likely that an attractive dipole interaction⁴⁴ occurs directly between a proton and ferromagnetic single domain when the nuclear and electronic spins of the catalyst are aligned in parallel. As a result, the magnetic force of a ferromagnetic material interacts with protons followed by H₂ (g) evolution. An attractive dipole interaction⁴⁴ was studied by a numerical simulation in the next section.

Fig. 2 Schematic of hydrogen evolution via the hydrolysis of NH₃BH₃(aq) over a magnetic metal single domain. A sufficient number of protons from BH₃(aq) and H₂O(l) assemble at the single domain owing to the magnetic interaction between their nuclear spins and the electronic spin of the single domain.

The thermodynamic cycle shown in Table 2 can be re-written as an electrochemical cycle, given by

Anode: NH₃NH₃(aq) + 3H₂O(l) = NH₃(aq) + B(OH)₃(aq) + 6H⁺(aq) + 6e⁻ (1)

Cathode: 6H⁺(aq) + 6e⁻ = 3H₂(g) (2)

Therefore, the cathodic protection mechanism prevents the surface of the sample from corrosion, which is further evidence for HER following the Slater–Pauling magnetic rule.⁴⁴

The maximum M_Ferro in the Slater–Pauling curve is at E_conc = 8.33, whereas the maximum R_HER is at E_conc = 8.92. That is, the HER drop was observed in the samples including 15 mol% Fe (no. 4), 35 mol% Fe (no. 3), 50 mol% Fe (no. 2), and pristine Fe (no. 1). The cause of the HER drop was examined. The NH₃BH₃(aq) solution was alkaline (pH 8.53). The electric potential (E_h)–pH diagram⁵² indicates that Fe₂O₃(cr) is stable. Therefore, the aqueous ion equilibrated with Fe₂O₃(cr) is ferric hydroxide ion Fe³⁺(aq), which appears with an orange colour. Fig. 3 shows the aqueous solution after first series of the hydrolysis of AB over the sample 85 mol%–15 mol% Fe (no. 4). Orange colour development was clearly observed. The same colour development occurred with other samples including 35 mol% Fe (no. 3), 50 mol% Fe (no. 2), and pristine Fe (no. 1). Consequently, the corrosion of samples with over 15 mol% Fe resulted in overriding of the cathodic protection (eqn (2)).

Fig. 3 Appearance of 85 mol% Co–15 mol% Fe sample after hydrolysis of ammonia borane. The aqueous solution shows orange colour indicating that Fe³⁺ aqueous ion was formed.

It is well known that d-electron vacancies⁵³ have control on the corrosion of transition metals and alloys. d-electron vacancies⁵³ capture the electrons of OH⁻(aq), resulting in adsorption of the radical oxygen atoms. The alloys with high Fe content have many electron vacancies in the 3d band. The samples with over 15 mol% Fe (no. 1–4) had many d-electron vacancies, which adsorb the radical oxygen atoms to form a carrion product, Fe₂O₃. This product overrides the cathodic protection (eqn (2)) during the hydrolysis of AB, which was concluded to be the reason for the HER drop.

The quantitative contents of the d-electron vacancies⁵³ were defined as the N_v values.⁵⁴ The phase stabilities of the super heat resistant alloys are estimated in terms of the N_v values. The alloys with excess N_v values form harmful σ phases, as was determined by multiple regression analysis⁵⁴ of the experimental data. The optimum alloy compositions are simulated to be less than the critical N_v value, known as PHACOMP (Phase Computation).⁵⁴ The d-orbital level parameter, M_d, was suggested based on the molecular orbital calculations to update the N_v values considering the alloying effect.⁵⁵ The N_v (ref. 54) and M_d (ref. 55) values for the samples are shown in Table 1.^54,55 The critical value of N_v was 1.85 and M_d was 0.17 eV for 85 mol% Co–8 mol% Fe (no. 4), which was determined to prevent corrosion. When values less than the critical values are used, HER is actively caused by the cathodic protection of the surface from corrosion.

Numerical simulation of the dipole interaction between proton and magnetic catalyst

A hypothesis that an attractive dipole interaction occurs directly between a proton and ferromagnetic single domain when its nuclear and the electronic spin of the catalyst are aligned in parallel based on that HER follows the Slater–Pauling rule. In this section, the dipole interaction⁴⁴ was directly investigated by numerical simulation.

Fig. 4 depicts a schematic of the most fundamental model.⁴⁴ The potential energy resulting from this magnetic dipole interaction U_mag, is defined as follows.

where M_Ferro and M_P are the magnetic moments of the nano sphere single domain,^56–59 and the proton, respectively, μ₀ is the permeability of free space, 4π × 10⁻⁷ (H m⁻¹).⁴⁴ The r datum is the distance between the N and S, or S and N poles of them. Accordingly, the magnetic force, F, exerted by the ferromagnetic single domain to the proton is defined as follows.

Fig. 4 Schematic of the dipole interaction between a proton and ferromagnetic nano sphere single domain.^56–59

The acceleration, a, of the proton is determined by dividing F by the mass of the proton m_P (1.67262171 × 10⁻²⁷ kg).⁶⁰

The present model includes a Co single domain sphere with an assumed diameter, d, of 60 nm to correlate it with the same domain in the WC lattice used in our previous study.³⁶ The magnetic moment per Co atom^44,45 is 1.7μ_B, and the number of moles, n, in this Co single domain is 1.6945 × 10⁻¹⁷ based on the density of hcp Co (8.9 Mg m⁻³).⁶¹ Therefore, the number of atoms, N, is 1.0205 × 10⁷. The magnetic moment of the Co single domain is N × 1.7μ_B per Co atom;^44,45 hence, M_Ferro equals 2.0211 × 10⁻²² Wb m. The M_P of a proton⁴⁴ is 6.33 × 10⁻³³ Wb m.

These M_Ferro and M_P values were used in eqn (3) to simulate a as a function of r, and the resulting plot is shown in Fig. 5. When r is 2.33375 μm, a is 9.807 ms⁻², consistent with the gravitational acceleration, g.⁶⁰ Because g was obtained at the appropriate distance, the present simulation accurately estimated the magnetic dipole interaction.

Fig. 5 Acceleration, a, acting on a proton as a function of the distance r from a Co single domain with a diameter of 60 nm under the magnetic potential energy U_mag acting on a proton.

To confirm that the proton is attracted to the magnetic force of the ferromagnetic single domain, its hydration was subsequently investigated. The hydration enthalpy ΔH⁺_ad is −260.7 ± 2.5 (kcal mol⁻¹),^62,63 i.e., −1.811 [aJ (H⁺_ad)⁻¹]^62,63 per proton. With the Brownian motion,²⁹ a proton dissociates from H₃O⁺(aq) and is then hydrated by another H₂O(l) molecule.^64–66 Fig. 6 shows schematic structures for H₃O⁺(aq) and H₂O(l) molecules, and a proton migrating between them. The migration length l_m of the dissociation and hydration is 0.03–0.08 nm.⁶⁴ Moreover, the O–H bond length in the H₂O(l) molecule is 0.097 nm.⁶⁴

Fig. 6 Schematic of the structures of hydronium ion, H₃O⁺(aq), and H₂O(l) molecules, and migration length of proton between them.^62–64

Fig. 7 shows the effect of U_mag of a Co single domain on a proton as a function of r (in the range of 0.03–0.06 nm) as described by eqn (3). With decreasing r, U_mag shifts to negative values. Remarkably, at 0.044725 nm, U_mag becomes equal to −1.811 [aJ (H⁺_ad)⁻¹],^62,63 which is the ΔH⁺_ad. The r value at which U_mag is equal to ΔH⁺_ad is the critical distance r_c, exactly. Therefore, as shown in Fig. 7, when r < r_c (0.044725 nm), U_mag becomes deeper than ΔH⁺_ad, causing a proton to be attracted to the Co single domain. Specifically, protons assemble on the Co single domain, and hydrogen gas rapidly evolves. (A) Initially, a proton accepts an electron to form a hydrogen atom, followed by adsorption (Volmer mechanism^2,3). (B) Subsequently, another proton accepts another electron and aggregates with a hydrogen atom to form a dimer molecule, and a hydrogen gas molecule H₂(g) desorbs (Heyrovsky mechanism^2,4). (C) Selectively, two hydrogen atoms aggregate to form a dimer molecule, and a hydrogen gas molecule H₂(g) dissociates (Tafel mechanism^5,6).

Fig. 7 U_mag acting on a proton as a function of r from a Co single domain with a diameter of 60 nm. r_c is the critical distance at which the proton, hydrated by a H₂O molecule as H₃O⁺(aq), changes its path from a Brownian random walking trajectory to a close-approach orbit towards the ferromagnetic single domain.

In contrast, when r is greater than r_c, U_mag becomes shallower than ΔH⁺_ad, causing a proton to move towards an H₂O molecule and form H₃O⁺(aq) in Brownian motion. In conclusion, r_c is the exact distance at which the trajectory of a proton changes from a random walk caused by Brownian motion to an approach orbit towards the Co single domain. Moreover, the calculated r_c value (0.044725 nm) is within the range of l_m of proton dehydration and rehydration (0.03–0.08 nm^64,66) and the O–H bond length (0.097 nm (ref. 62) in water. The effective particle number, N_eff, of the proton, of which diameter, l_P, is 8.751 × 10⁻⁷ nm,⁶⁷ contributing to the frequency factor, A, in the Arrhenius equation⁶⁸ is likely to be proportional to r_c.

The r_c values for other single domains with the same compositions as the samples (Table 1) were calculated in the same way. Additionally, the M_Ferro values were estimated by interpolating the Slater–Pauling curve. Fig. 8 depicts the calculated r_c as a function of E_conc, which shows that E_conc is optimal when r_c is 8.5. Theoretically, the contribution of N_eff to R_HER is the highest at E_conc = 8.5. However, as shown in Fig. 1, the maximum R_HER is obtained when E_conc is 8.92. Due to excess Fe, the formation of Fe₂O₃, resulting from excess 3d electron vacancies as above described, inhibited by the Heyrovsky^2,4 and Tafel mechanisms,^5,6 which are mediated by the Volmer mechanism.^2,3

Fig. 8 Critical distance r_c as a function of the valence electron concentration E_conc. r_c is the distance at which a proton changes its path from a Brownian random walk trajectory to a close-approach orbit towards a single domain while hydrated by an H₂O molecule as H₃O⁺(aq). The diameter of each single domain is assumed to be 60 nm.

The auxiliary data for the present numerical simulation were summarized in Table 3.

Table 3 Auxiliary data of the permeability of free space (μ₀), mass (m_p) and diameter (l_P) of the proton, magnetic moment of a Co atom (β), densities (ρ) of Co and WC, magnetic moment, (M_P) of a proton, hydration enthalpy (ΔH⁺_ad), gravitational acceleration (g), the adopted data of numbers of moles (n), and Co atoms (N), magnetic moment (M_Ferro), in the 60 nm sphere Co single domain for the present study

---

The singular catalytic activity of the Co nanocrystal doped WC in our previous study³⁶ was discussed. The valence electron number of WC and Pt are the same. However, their magnetic properties are different and Pt has a higher magnetic susceptibility because WC is non-magnetic. Singular WC does not show catalytic activity. In our previous study,³⁶ WC was doped with 60 nm diameter ferro-magnetic Co crystals to introduce an ordered-spin configuration, which showed a R_HER value even higher than that of the Pt nanoparticles during the hydrolysis of AB. A hypothesis for the enhanced catalytic activity was attributed to the synergistic effect of the WC matrix promoting hydrolytic cleavage of NH₃BH₃ and the ferromagnetic Co crystals interacting with the nucleus spin of the protons. The present verified attractive dipole interaction between protons and Co is evidence for the hypothesis of singular catalytic activity of WC arising from an internal magnetic field.

It was previously hypothesised that a synergetic effect of WC breaking NH₃BH₃(aq) to form protons and the antiparallel alignment of the nuclear spins of protons and electronic spins in a single domain to increase the magnetic entropy.^36,69,70 Therefore, the 1s electronic spin of the hydrogen atoms absorbed by Pd (ref. 71) and adsorbed on Gd (ref. 72) induce disorder of their electron spin polarisation, thereby increasing the entropy of the system. By the above-described mechanism for HER, it is concluded the dipole attractive interaction between proton and magnetic catalyst enhances HER. After donating electrons by the Volmer mechanism,^2,3 electronic spins of that hydrogen atoms are likely to be aligned against spins of Co. This problem should be further investigated by molecular orbital calculations.

AB is hopeful hydrogen fuel.^37–43 The HER by hydrolysis over the 10 wt% Co nano particle supported on the SiO₂ nano particle (Co/SiO₂) was investigated by Xu and Chandra.³⁹ In order to compare HER property of the Co particle obtained in the present study with one of Co/SiO₂ by Xu and Chandra,³⁹ their normalised hydrogen evolution rate per unit area (m⁻²), R^N_HER, was evaluated. Table 4 shows their R^N_HER data. The experimental conditions for Co/SiO₂ were 50 percent more conc. in the concentration of AB, 25 times larger in SSA (=52 m⁻² g⁻¹), and 83 percent smaller in mass (3.4 mg) than ones for the present Co particle. Considering difference in the experimental conditions, the intrinsic R^N_HER data appears to be similar.

Table 4 Normalised hydrogen evolution rate per unit area, R^N_HER, of the Co particle in the present study, compared with the Co nano-crystal in WC matrix,³⁶ and the 10 wt% Co nano particle supported on γ-Al₂O₃ nano particle.³⁹

	R^NHER/(H2 mmol min^−1 m^−2)	n(AB)/mmol	V(H2O)/mL	Remarks
a SSA of the Co nano was 52 m^−2 g^−1, and its mass was 3.4 mg.b SSA was hypothetically estimated as volume ratio of the Co nano-crystal against WC matrix.
Co particle	1.28	0.5	2.5	This study
Co(cr)/SiO2	0.70^a	3.2	10	Ref. 39
Co(cr) in WC	31.9^b	0.5	2.5	Ref. 36

---

The atomic configuration in the AB molecule was investigated by the neutron diffraction by Klooster et al.³⁸ The chemical bonding states for AB were investigated by the first principles calculation by Banu et al.,⁴¹ and soft X-ray adsorption spectroscopy by Niibe et al.⁴³ The datum at 298.15 K was determined by the combustion calorimetry by Shaulov.³⁷ The effect of an internal magnetic field cooperating the cathodic protection on the thermodynamic mechanism of the hydrolysis of AB has been suggested in the present study for the first time.

In our previous study for the Co doped WC,³⁶ the activation energy determined by the Arrhenius plots was found to be well consistent with the electrochemical hydrogen over potential of Co.⁷³ This means hydrogen gas H₂(g) is evolved over the Co crystals via Heyrovsky^2,4 and Tafel mechanisms.^5,6 The R^N_HER datum of the Co crystals in the WC matrix was compared with that of the Co particle in the present study. Where the ratio of SSA of the fcc Co³⁶ nanocrystals against the WC matrix were hypothetically assumed to be as same as the ratio of their volumes.^61,74 Their volumes were calculated from their densities (Table 3). Table 4 shows their R^N_HER data. The R^N_HER of the Co crystal was found to be 25 times higher than that of the Co particle in the present study. This means that WC, of which electrons density of states are similar to Pt, adsorbs much amount of AB followed by decomposing the B–N bonding, and makes much protons dissociating from AB. Much protons are aligned on the Co crystals by the attractive dipole interaction, and 25 times higher R^N_HER is concluded to be caused.

The parameters used in the present simulation are an extremely small scale power functions as, e.g., M_Ferro/(Wb m) = 2.0211 × 10⁻²², and M_P/(Wb m) = 6.33 × 10⁻³³ (Table 3) ⁴⁴ the obtained r_c datum reflects the structure parameters for H₃O⁺(aq) and H₂O(l) molecules, and a proton migration (Fig. 6), indicating that the present numerical simulation was done with highly accuracy. Although a very fundamental model based on the sphere single domain magnetic structure^64–66 was adopted, this is a novel finding and likely to give impact to general science due to that proton in aqueous solution are associated with various phenomena in nature. In the future, the dipole interactions in the complicated magnetic force lines from the magnetic substances composed of the multi domain should be investigated.

Conclusions

The current study clarified the magnetic dipole interactions between the nuclear spin of a proton and the electronic spin of a magnetic catalyst for the first time. The conclusions are as follows: (1) the HER rate varied in accordance with the Slater–Pauling rule, resulting in a rapid rate of hydrogen evolution for catalysts with a high magnetic moment. (2) Numerical simulation of the magnetic dipole interaction revealed a critical distance at which the proton, as H₃O⁺(aq), changes its path from a Brownian random walk trajectory to a close-approach orbit towards the ferromagnetic catalyst, in the same order as the migration length of the dissociation and hydration of the proton and O–H bond length in water. Consequently, this study provides novel insights into noble-metal-free catalyst design from the viewpoint of the internal magnetic field.

Conflicts of interest

There are no conflicts to declare.

Author contributions

M. M. conceived the idea and wrote the paper; Y. O. and R. F. synthesized the materials and conducted the hydrogen evolution tests and SA measurements; H. Y. reviewed and validated the work shown in the paper; and H. Y. rendered helpful discussions.

Acknowledgements

This work was supported by an academic research grant from the Hyogo Science and Technology Association and special research grant for hydrogen energy from the University of Hyogo.

References

1. International Energy Agency, Global Hydrogen Review 2022, https://www.iea.org/reports/global-hydrogen-review-2022, September 2022.
2. N. M. Marković, B. N. Grgur and P. N. Ross, Temperature-dependent hydrogen electrochemistry on platinum low-index single-crystal surfaces in acid solutions, J. Phys. Chem. B, 1997, 101, 5405–5413.
3. N. M. Marković and P. N. Ross Jr, Surface science studies of model fuel cell electrocatalysts, Surf. Sci. Rep., 2002, 45, 117–229.
4. M. C. Tavares, S. A. S. Machado and L. H. Mazo, Study of hydrogen evolution reaction in acid medium on Pt microelectrodes, Electrochim. Acta, 2001, 46, 4359–4369.
5. J. Barber, S. Morin and B. E. Conway, Specificity of the kinetics of H₂ evolution to the structure of single-crystal Pt surfaces, and the relation between opd and upd H, J. Electroanal. Chem., 1998, 446, 125–138.
6. K. Kunimatsu, T. Senzaki, M. Tsushima and M. Osawa, A combined surface-enhanced infrared and electrochemical kinetics study of hydrogen adsorption and evolution on a Pt electrode, Chem. Phys. Lett., 2005, 401, 451–454.
7. I. Hamada and O. Sugino, Towards first-principles understanding of hydrogen evolution reaction at the platinum electrode, J. Surf. Sci. Soc. Jpn., 2013, 34, 638–643.
8. W. Karim, C. Spreafico, A. Kleibert, J. Gobrecht, J. VandeVondele, Y. Ekinci and J. A. V. Bokhoven, Catalyst support effects on hydrogen spillover, Nature, 2017, 541, 68–71.
9. M. Faraday, Faraday's Diary, Bell and Sons, London, 2018, vol. IV, pp. 288–290.
10. S. Chrétien and H. Metiu, O₂ evolution on a clean partially reduced rutile TiO₂ (110) surface and on the same surface precovered with Au₁ and Au₂: the importance of spin conservation, J. Chem. Phys., 2008, 129, 074705.
11. W. Mtangi, V. Kiran, C. Fontanesi and R. Naaman, Role of the electron spin polarization in water splitting, J. Phys. Chem. Lett., 2015, 6, 4916–4922.
12. J. Gracia, Spin dependent interactions catalyse the oxygen electrochemistry, Phys. Chem. Chem. Phys., 2017, 19, 20451–20456.
13. F. A. Garcés-Pineda, M. Blasco-Ahicart, D. Nieto-Castro, N. López and J. R. Galán-Mascarós, Direct magnetic enhancement of electrocatalytic water oxidation in alkaline media, Nat. Energy, 2019, 4, 519–525.
14. S. Ghosh, B. P. Bloom, Y. Lu, D. Lamont and D. H. Waldeck, Increasing the efficiency of water splitting through spin polarization using cobalt oxide thin film catalysts, J. Phys. Chem. C, 2020, 124, 22610–22618.
15. Z. Bian, K. Kato, T. Ogoshi, Z. Cui, B. Sa, Y. Tsutsui, S. Seki and M. Suda, Hybrid chiral MoS₂ layers for spin-polarized charge transport and spin-dependent electrocatalytic applications, Adv. Sci., 2022, 9, 2201063.
16. C. Biz, M. Fianchini and J. Gracia, Catalysis meets spintronics; spin potentials associated with open-shell orbital configurations enhance the activity of Pt₃Co nanostructures for oxygen reduction: a density functional theory study, ACS Appl. Nano Mater., 2020, 3, 506–515.
17. O. Lioubashevski, E. Katz and I. Willner, Magnetic field effects on electrochemical processes: a theoretical hydrodynamic model, J. Phys. Chem. B, 2004, 108, 5778–5784.
18. L. Elias and A. C. Hegde, Effect of magnetic field on HER of water electrolysis on Ni–W alloy, Electrocatalysis, 2017, 8, 375–382.
19. N. Bidin, S. Azni, S. Islam, M. Abdullah, M. F. S. Ahmad, G. Krishnan, A. R. Johari, M. A. A. Bakar, N. S. Sahidan, N. Musa, N. M. Salebi, N. Razali and M. Sanagi, The effect of magnetic and optic field in water electrolysis, Int. J. Hydrogen Energy, 2017, 42, 16325–16332.
20. W. Zhou, M. Chen, M. Guo, A. Hong, T. Yu, X. Luo, C. Yuan, W. Lei and S. Wang, Magnetic enhancement for hydrogen evolution reaction on ferromagnetic MoS₂ catalyst, Nano Lett., 2020, 20, 2923–2930.
21. J. Saha, R. Ball and C. Subramaniam, Premagnetized carbon-catalyst interface delivering 650% enhancement in electrocatalytic kinetics of hydrogen evolution reaction, ACS Sustainable Chem. Eng., 2021, 9, 7792–7802.
22. R. Naaman and D. H. Waldeck, Chiral-induced spin selectivity effect, J. Phys. Chem. Lett., 2012, 3, 2178–2187.
23. C. S. Wu, E. Ambler, R. W. Hayward, R. D. D. Hoppes and R. P. Hudson, Experimental test of parity conservation in beta decay, Phys. Rev., 1957, 105, 1413–1415.
24. R. B. Levy and M. Boudart, Platinum-like behavior of tungsten carbide in surface catalysis, Science, 1973, 181, 547–549.
25. L. H. Bennett, J. R. Cuthill, A. J. McAlister and N. E. Erickson, Electronic structure and catalytic behavior of tungsten carbide, Science, 1974, 184, 563–565.
26. J. E. Houston, G. E. Laramore and R. L. Park, Surface electronic properties of tungsten, tungsten carbide, and platinum, Science, 1974, 185, 258–260.
27. L. H. Bennett, J. R. Cuthill, A. J. McAlister and N. E. Erickson, Electronic and catalytic properties of tungsten carbide, Science, 1975, 187, 858–859.
28. L. F. Mattheiss and D. R. Hamann, Bulk and surface electronic structure of hexagonal WC, Phys. Rev. B, 1984, 15, 1731–1738.
29. X. Zhang, B. Grabowski, C. Freysoldt, F. Körmann and J. Neugebauer, Accurate electronic free energies of the 3d, 4d, and 5d transition metals at high temperature, Phys. Rev. B, 2017, 95, 165126.
30. D. V. Esposite, S. T. Hunt, A. L. Stottlemyer, K. D. Dobson, B. E. McCandless, R. W. Birkmire and J. G. Chen, Low-cost hydrogen-evolution catalysts based on monolayer platinum on tungsten monocarbide substrates, Angew. Chem., Int. Ed., 2010, 49, 9859–9862.
31. J. Zhang, J. Chen, Y. Jiang, F. Zhou, G. Wang, R. Wang and R. Wang, Tungsten carbide encapsulated in nitrogen-doped carbon with iron/cobalt electrocatalyst for oxygen reduction reaction, Appl. Surf. Sci., 2016, 389, 157–164.
32. D. J. Ham, R. Ganesan and J. S. Lee, Tungsten carbide microsphere as an electrode for cathodic hydrogen evolution from water, Int. J. Hydrogen Energy, 2008, 33, 6865–6873.
33. W. Zheng, L. Wang, F. Deng, S. A. Stephen, A. Gilles, A. K. Prasad, S. G. Advani, Y. Yan and D. G. Vlachos, Durable and self-hydrating tungsten carbide-based composite polymer electrolyte membrane fuel cells, Nat. Commun., 2017, 8, 418.
34. C. Ma, J. Sheng, N. Brandon, C. Zhang and G. Li, Preparation of tungsten carbide-supported nano Platinum catalyst and its electrocatalytic activity for hydrogen evolution, Int. J. Hydrogen Energy, 2007, 32, 2824–2829.
35. P. Xiao, X. Ge, H. Wang, A. Liu, A. Fisher and X. Wang, Novel molybdenum carbide-tungsten carbide composite nanowires and their electrochemical activation for efficient and stable hydrogen evolution, Adv. Funct. Mater., 2015, 25, 1520–1526.
36. M. Morishita, A. Nozaki, H. Yamamoto, N. Fukumuro, M. Mori, K. Araki, F. Sakamoto, A. Nakamura and H. Yanagita, Catalytic activity of Co-nanocrystal-doped tungsten carbide arising from an internal magnetic field, RSC Adv., 2021, 11, 14063–14070.
37. Y. K. Shaulov, G. O. Shmyreva and S. Tubyanskaya, Heat of combustion of ammonia borane, Zh. Fiz. Khim., 1966, 40, 122–124.
38. W. T. Klooster, T. F. Koetzle, P. E. M. Siegbahn, T. B. Richardson and R. H. Crabtree, Study of the N−H⋯H−B Dihydrogen Bond Including the Crystal Structure of BH3_NH3 by Neutron Diffraction, J. Am. Chem. Soc., 1999, 121, 6337–6343.
39. Q. Xu and M. Chandra, Catalytic activities of non-noble metals for hydrogen generation from aqueous ammonia-borane at room temperature, J. Power Sources, 2006, 163, 364–370.
40. M. Chandra and Q. Xu, Room temperature hydrogen generation from aqueous ammonia-borane using noble metal nano-clusters as highly active catalysts, J. Power Sources, 2007, 168, 135–142.
41. T. Banu, T. Debnath, T. Ash and A. K. Das, Hydrolysis of ammonia borane and metal amidoboranes: a comparative study, J. Chem. Phys., 2015, 143, 194305.
42. C. Wang, J. Tuninetti, Z. Wang, C. Zheng, R. Ciganda, L. Salmon, S. Moya, J. Ruiz and D. Astruc, Hydrolysis of ammonia-borane over Bi/ZIF-8 nanocatalyst: high efficiency, mechanism, and controlled hydrogen release, J. Am. Chem. Soc., 2017, 139, 11610–11615.
43. M. Niibe, Y. Haruyama, A. Heya and S. Ito, Soft X-ray Absorption/Emission Spectroscopy and Atomic Hydrogen Irradiation Effect of AmmoniaBorane, e-J. Surf. Sci. Nanotechnol., 2022, 20, 226–231.
44. S. Chikazumi, Physics of Magnetism, John Wiley & Sons, Inc., New York, 1964, pp. 5–73.
45. C. Kittel, Introduction to Solid State Physics, John Wiley & Sons, Inc., New York, 1986, p. 597.
46. In Binary Alloy Phase Diagrams, ed. T. B. Massalski, H. Okamoto, P. R. Subramanian and L. Kacprzak, ASM International, 1990, p. 1186.
47. L. Marick, Variation of Resistance and Structure of Cobalt with Temperature and a discussion of its photoelectric emission, Phys. Rev., 1936, 49, 831–839.
48. A. Taylor and R. W. Floyd, Prediction Measurements of Lattice Parameters of Non-Cubic Crystals, Acta Crystallogr., 1950, 13, 285–289.
49. H. Gamsjäger, J. Bugajski, T. Gajda, R. J. Lemire and W. Preis, Chemical Thermodynamics of Nickel, Nuclear Energy Agency, Organization for Economic Co-operation, Development, in Chemical Thermodynamics, North Holland Elsevier Science Publisher B. V., Amsterdam, The Netherlands, 2005, vol. 6, pp. 43–52.
50. D. D. Wagman, W. H. Evans, V. B. Parker, R. H. Schumm, I. Halow, S. M. Bailey, K. L. Churney and R. L. Nuttall, The NBS tables of chemical thermodynamic properties: selected values for inorganic and C₁ and C₂ organic substances in SI units, J. Phys. Chem. Ref. Data, 1982, 11(suppl. 2), 123.
51. A. Einstein, Zur Theorie der Brownschen Bewegung, Ann. Phys., 1905, 17, 371–381.
52. N. Takeno, Atlas of Eh-pH Diagrams, https://www.gsj.jp/data/openfile/no0419/openfile419j.pdf, 2005.
53. R. W. Revie and H. H. Uhlig, Corrosion and Corrosion Control: An Introduction to Corrosion Science and Engineering, Wiley Interscience, Inc., Hoboken New Jersey, 4th edn, 2008, pp. 102–108.
54. R. G. Barrows and J. B. Newkirk, A modified system for predicting σ formation, Metall. Mater. Trans. B, 1972, 3, 2889–2893.
55. M. Morinaga, A Quantum Approach to Alloy Design: An Exploration of Material Design and Development Based Upon Alloy Design Theory and Atomization Energy Method, Elsevier Inc., Amsterdam, 2019, 23, 50.
56. J. Frenkel and J. Dorfman, Spontaneous and Induced Magnetisation in Ferromagnetic Bodies, Nature, 1930, 126, 274–275.
57. C. Kittel, Theory of the Structure of Ferromagnetic Domains in Films and Small Particles, Phys. Rev., 1946, 70, 965–971.
58. L. Neél, Properties for Ferromagnetic Cubic Grains, Compt. Rend., 1947, 224, 1488–1490.
59. E. C. Stoner and E. P. Wohlfarth, Interpretation of High Coercivity in Ferromagnetic Materials, Nature, 1947, 160, 650–651.
60. In Chronological Scientific Tables, National Astronomical Observatory, Jpn., 2007354–356.
61. S. Nagasaki, Metals Handbook, Japan Institute of Metals, 1993, p. 10.
62. H. F. Halliwell and S. C. Nyburg, Enthalpy of hydration of the proton, Trans. Faraday Soc., 1963, 59, 1126–1140.
63. H. Ohtaki and M. Tanaka, Thermodynamics and rate theory for analytical chemist II, Jpn. Anal., 1969, 18, 400–414.
64. B. E. Conway, J. O. Bockris and H. Linton, Proton conductance and the existence of the H₃O^• ion, J. Chem. Phys., 1956, 24, 834–850.
65. M. D. Newton, Ab initio studies of the hydrated H₃O⁺ ion. II. The energetics of proton motion in higher hydrates (n = 3–5), J. Chem. Phys., 1977, 67, 5535–5546.
66. K. Ando and J. T. Hynes, Molecular mechanism of HCl acid ionization in water: ab initio potential energy surfaces and Monte Carlo simulations, J. Phys. Chem. B, 1997, 101, 10464–10478.
67. CODATA Value: proton rms charge radius (nist.gov), https://physics.nist.gov/cgi-bin/cuu/Value?rp|search_for=radius+proton.
68. D. Kondepudi, Introduction to Modern Thermodynamics, Wiley, West Sussex, 2008, pp. 266–269.
69. M. Morishita, T. Abe, A. Nozaki, I. Ohnuma and K. Kamon, Calorimetric study of Nd₂Fe₁₄B: heat capacity, standard Gibbs energy of formation and magnetic entropy, Thermochim. Acta, 2020, 690, 178672.
70. M. Morishita, T. Abe, H. Yamamoto, A. Nozaki and S. Kimura, Thermodynamic and Magnetic Properties for Dy₂Fe₁₄B Determined by Heat Capacity Measurement from Very Low to High Temperatures and Solution Calorimetry, Thermochim. Acta, 2023, 721, 179410.
71. R. J. Miller and C. B. Satterthwaite, Electronic model for the reverse isotope effect in superconducting Pd-H(D), Phys. Rev. Lett., 1975, 34, 144–148.
72. A. Cerri, D. Mauri and M. Landolt, Surface magnetization and hydrogen chemisorption on Gd: a spin-polarized photoemission study, Phys. Rev. B, 1983, 27, 6526–6529.
73. H. Ezaki, M. Morinaga and S. Watanabe, Hydrogen overpotential for transition metal and alloys, and its interpretation using an electronic model, Electrochim. Acta, 1993, 38, 557–564.
74. Encyclopedia Chimica, Kyoritsu Shippan Co., LTD, Tokyo, 1975, vol. 5, p. 699.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2ra07865a

---