Theoretical study on structural and mechanical properties of Si-containing ternary transition metal nitrides M_0.5Si_0.5N (M = Ti, Zr, Hf)

Abstract

Si-containing transition-metal nitrides Ti_0.5Si_0.5N, Zr_0.5Si_0.5N and Hf_0.5Si_0.5N with conventional rock salt B1 structure exhibit superior hardness, strength and oxidation resistance. However, the potential phases of the ternary systems at various pressures remain unexplored. In this work, we firstly studied the potential structures of Ti_0.5Si_0.5N, Zr_0.5Si_0.5N and Hf_0.5Si_0.5N in pressures of 0–100 GPa. A hexagonal phase with P6₃/mmc symmetry was uncovered and verified to be quenchable in the ambient conditions. The structural, mechanical and electronic properties were systematically studied and compared with the well-known ordered B1 structure. We surprisingly found that Ti_0.5Si_0.5N within this hexagonal phase displayed much improved ideal indentation shear strength from about 10 GPa for a B1 structure to 30 GPa. The estimated hardness based on the empirical formula is up to 38 GPa, greatly exceeding that of the B1 structure. By the detailed electronic analysis, the underlying atomic mechanism for the outstanding mechanical properties was also studied.

---

1. Introduction

Binary transition metal (TM) nitrides such as TiN, ZrN, TaN, VN, etc. are widely used as protective coatings for cutting tools.¹ However, these nitrides have poor oxidation resistance in oxygen or air when the temperature is beyond 500 °C.^2,3 In cutting applications such as high speed milling, the temperature can be easily improved to exceed 800 °C.⁴ To address this problem, an effective design strategy to enhance the oxidation resistance and mechanical properties is introducing a third element Al or Si into the TM nitrides to form ternary or quaternary systems like TiAlN, TiSiN, TiAlCrN, TiAlCN, etc.^5–10 These aluminum or silicon nitrides have a distinct improvement of oxidation resistance. Furthermore, the introduction of the third element also induces the formation of a nanocomposite structure containing a non-miscible nanocrystalline or amorphous structures and results in high hardness.¹¹

As is known, these binary or ternary TM nitrides adopt the metastable NaCl-type B1 structure at room temperature thanks to the stabilization of the anharmonic effect.¹² This B1 structure can't sustain its dynamic stability when the temperature descends to 0 K due to the appearance of unphysical longitudinal acoustic phonon energy.¹² Most of these ternary B1 nitrides containing two TM elements often have a disordered occupation of TM atoms in the cation locations. As a result of this disordered occupation, the mechanical anisotropy is further improved on the basis of the ordered metastable B1 structure, which is not favorable in engineering application. Additionally, though the cubic B1 structure has relatively high crystal symmetry, the mechanical anisotropy is strong and this has been verified in our previous work for ternary VAlN and quaternary VWCN systems.^13,14 However, these TM nitrides within hexagonal structure often behave less mechanical anisotropy, which can be ascribed to the better distribution of the bonds between TM and nitrogen atoms. Meanwhile, the electronic structure analysis shows the “pseudo-gap” separating the bonding and antibonding states is present in the most B1-structure compounds and the E_F often lies in the antibonding region, which improves the formation enthalpy of the systems and induces the metastability. The occupition of d–d antibonding states also weakens the p–d hybridization between TM and light elements. However, this p–d hybridization is indispensable in determining the anti-shear properties and macroscopic hardness for this type of compounds. Thus, the hardness of these B1 structure TM nitrides is mostly in the range of 10–30 GPa much less than the threshold of the superhard standard (40 GPa).^15,16 For the Si-containing ternary TM nitrides within B1 structure, Si atoms are introduced for replacing partial TM atoms. This replacement can't prominently tune the E_F position due to the structural limitation. Thus, it also can't significantly improve the mechanical properties. Therefore, it is greatly meaningful to search new configuration for these Si-containing nitrides with tuned E_F position and enhanced mechanical properties.

In this work, we systematically explored structural, mechanical and electronic properties of the ternary Ti_0.5Si_0.5N, Zr_0.5Si_0.5N and Hf_0.5Si_0.5N systems using the first-principle and structure searching methods implemented in the CALYPSO code^17,18 in the pressure of 0–100 GPa. The hexagonal P6₃/mmc phase was firstly uncovered. To clarify the structural effects on hardness, strengths, mechanical anisotropies and crystal stability of these three systems within P6₃/mmc and B1 structures, we simulated the uniaxial and biaxial stains to obtain the corresponding stress and analyzed the thermal and dynamic stabilities as well as electronic structures.

2. Calculation methods and details

The structure searching process for Ti_0.5Si_0.5N, Zr_0.5Si_0.5N and Hf_0.5Si_0.5N systems was performed in the pressure of 0–100 GPa, by the method of CALYPSO,^17,18 which has been fully confirmed as an reliable and effective structural searching approach.^19–25 We adopted 0, 30, 50 and 100 GPa as the searching pressure points. The crystal cell containing 1–4 formula units (f.u.) was used in the searching process. All the calculations were carried out by the first-principle density functional theory (DFT) method implemented in the Vienna ab initio simulation package (VASP).²⁶ The generalized gradient approximation (GGA) was used in calculating elastic and structural properties.²⁷ The exchange correlation potential within the GGA proposed by Perdew, Burke and Ernzerhoff (PBE) with projector augmented wave (PAW) method^28,29 was used in all the calculations. The kinetic cutoff energy was set as 600 eV during the optimization process of all the structures. The convergence criteria of the total energy in all the structural relaxations were set as 10⁻⁵ eV. The 7 × 7 × 7 and 12 × 12 × 3 k-point meshs in Monkhorst Pack scheme and Gamma centered grid³⁰ were used for ordered pseudo-B1 and P6₃/mmc sturcutes, respectively. The ternary disordered B1 systems were calculated with 4 × 4 × 4 k-point meshs and 64 atoms supercells using the special quasi-random structure (SQS) method.^31,32 The SQS structure was constructed for ternary Ti_0.5Si_0.5N system using unit cells containing 32 cations and 32 anions within fcc structure. The 2 × 2 × 2 supercell containing 64 atoms was generated. The evaluation of the generated model was performed by the objective function provided by the SQS approach. The simulated SQS model as well as the predicted structures were set in the ESI data.† The phonon spectra were calculated by the density functional perturbation theory (DFPT) approach implemented in the PHONOPY code.³³ The elastic constants C_ij were calculated by applying a small strain onto the crystal structures with a finite variation. All the elastic moduli were calculated according to the Voigt–Reuss–Hill approximation.³⁴ The 3D and 2D distributions of elastic moduli were investigated by calculating the directional Young's and shear moduli, which were obtained by calculating the Young's and shear moduli along various crystal directions based on the formulas provided by the literature³⁵ using the elastic constants. The Chen empirical formula was adopted in assessing the Vickers hardness.³⁶ The electron localization function (ELF)³⁷ is also calculated to further analyze the bonding nature.

3. Results and discussions

3.1. Structure, property and stability

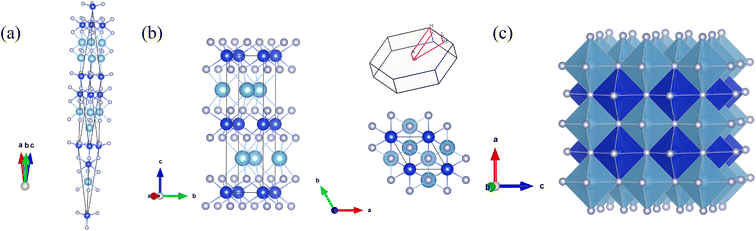
The CALYPSO method was employed to searching potential structures at the pressure points of 0, 30, 50 and 100 GPa, respectively. A trigonal structure with the space group of R3m (No. 160) was confirmed to be the ground-state phase of these three Si-containing ternary systems. However, this phase cannot sustain its thermal stability when the pressure ascends up to 30 GPa. At the pressures of 30, 50 and 100 GPa, the results of the structure searches showed the most favorable structure of these systems tuned to be the hexagonal P6₃/mmc (No.194) phase, which is displayed in Fig. 1. The TM and Si atoms have an alternate layered distribution. As a comparison, the ordered B1 structure was also exhibited in the figure. It can be seen there are six light element N atoms surrounding the TM and Si atoms, which is consistent with the B1 structure. The difference is the bond angles and lengths of the TM-N and Si–N bonds have some variations. Here, we take Ti_0.5Si_0.5N as an example. It is clearly seen the bond angle of all the adjacent Ti–N and Si–N bonds is 90° in the B1 structure. After full relaxation of both lattice constants and the positions of intra atoms, the obtained bond angles are 77.6°, 87.2° for N–Ti–N and 94.0°, 86.0° for N–Si–N. The bond lengths of Ti–N and Si–N are 2.227 Å and 1.909 Å, respectively, which are all different from those of ordered B1 structure. The Wyckoff sites of Ti, Si and N are 2d (0.667, 0.333, 0.25), 2a (0, 0, 0) and 4f (0.333, 0.667, 0.100) respectively. As listed in Table 1, these three ternary systems within the same structures have approximately identical lattice constants. The lattice constants of hexagonal Ti_0.5Si_0.5N are a = b = 2.793 Å and c = 10.236 Å. The evaluated density is 3.007 × 10³ kg m⁻³, larger than the ordered B1 structure (2.726 × 10³ kg m⁻³) and the trigonal structure (2.705 × 10³ kg m⁻³) presented in Table 1. Thus, the average TM–N and Si–N bond lengths are smaller than B1 structure and the trigonal structure. For other two Zr_0.5Si_0.5N and Hf_0.5Si_0.5N systems, the structural properties are similar to the Ti_0.5Si_0.5N system.

Fig. 1 Crystal structures of (a) trigonal R3m, (b) side and top views of hexagonal P6₃/mmc as well as the corresponding first Brillouin zone and (c) ordered B1 structures of Ti_0.5Si_0.5N. The large cyan, blue and small silvery spheres represent Ti, Si and N atoms respectively.

Table 1 Calculated lattice constants, M–N bond lengths (Å), formation enthalpies (eV/f.u.), and densities (kg m⁻³)

	Symmetry	Source	a	c	M–N	Si–N	Hf	Density
Ti0.5Si0.5N	R3m	This work	10.449				−2.092	2.705 × 10^3
	P63/mmc	This work	2.793	10.236	2.227	1.909	−1.918	3.007 × 10^3
	B1	This work	4.230		2.151	2.105	−1.172	2.726 × 10^3
Zr0.5Si0.5N	R3m	This work	10.820				−1.846	3.375 × 10^3
	P63/mmc	This work	2.898	10.891	2.397	1.953	−1.666	3.720 × 10^3
	B1	This work	4.524		2.243	2.281	−1.050	3.210 × 10^3
Hf0.5Si0.5N	R3m	This work	10.709				−1.866	5.494 × 10^3
	P63/mmc	This work	2.878	10.861	2.378	1.946	−1.596	6.021 × 10^3
	B1	This work	4.521		2.226	2.226	−1.104	5.237 × 10^3

---

To verify the thermal stability, we calculated the formation enthalpy using the following formula: 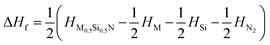, (M = Ti, Zr, Hf), where H_M0.5Si0.5N, H_M, H_Si, and H_N2 are the enthalpies per f.u. of M_0.5Si_0.5N, pure hcp-Ti/Zr/Hf, diomand-type Si and α-N₂. The calculated results are −1.918, −1.666 and −1.596 eV/f.u. for hexagonal Ti_0.5Si_0.5N, Zr_0.5Si_0.5N and Hf_0.5Si_0.5N systems respectively. For trigonal R3m structure, the formation enthalpies are −2.092, −1.846 and −1.866 eV/f.u. respectively. As a contrast, the formation enthalpies of them within ordered B1 structure are −1.172, −1.050 and −1.104 eV/f.u., respectively, indicating the trigonal phases are more thermodynamically stable than the hexagonal and ordered B1 phases in principle at ambient condition. Fig. 2 displays the calculated results of enthalpy differences of these three systems within B1 and R3m structures relative to the hexagonal P6₃/mmc structure as a function of pressure. It is clearly seen that with the pressure ascending beyond 15 15 and 25 GPa, P6₃/mmc structure transforms to be the most energetically favourable phase for them, as it has the lowest total enthalpy. Meanwhile, the enthalpy differences have an increasing tendency with pressure, implying the thermodynamic stability of P6₃/mmc structure can be maintained up to 100 GPa.

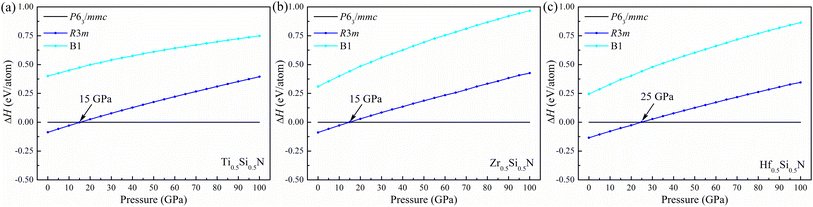Fig. 2 Enthalpy difference of (a) Ti_0.5Si_0.5N, (b) Zr_0.5Si_0.5N and (c) Hf_0.5Si_0.5N within P6₃/mmc structure relative to R3m and B1 structures as a function of pressure.

To further check the stability and the possibility of artificial synthesis of these systems with new uncovered hexagonal structure, the study of dynamic properties are necessary. Therefore, using the DFPT method which is implemented in the PHONOPY code, the phonon spectra as well as the corresponding projected density of states (PDOS) are calculated by simulating the 3 × 3 × 1 supercells for hexagonal Ti_0.5Si_0.5N, Zr_0.5Si_0.5N and Hf_0.5Si_0.5N systems. As is plotted in Fig. 3, there are no imaginary modes in the whole Brillouin zone for all of them, confirming their dynamic stability at ambient condition. For the primitive cell of uncovered hexagonal structure contains 8 atoms, the corresponding phonon spectra have 24 modes for each wave vector q. There are 3 acoustic and 21 optical branches in the spectra. It is obviously seen that the frequency distributions of these three systems are different with each other. The highest frequency of the atomic vibrations is up to near 25 THz for Ti_0.5Si_0.5N, exceeding those of Zr_0.5Si_0.5N and Hf_0.5Si_0.5N. Thus, it can be concluded the atomic interactions of Ti_0.5Si_0.5N are the strongest in them, implying this type of Ti_0.5Si_0.5N has better mechanical property and stability. The PDOS plots provide the information of frequency distributions of each element contained in the systems. One can see for these three Si-containing systems, the vibrations of Si and TM atoms dominate the lower frequency regions and the N atoms mainly supplies the higher frequency ranges.

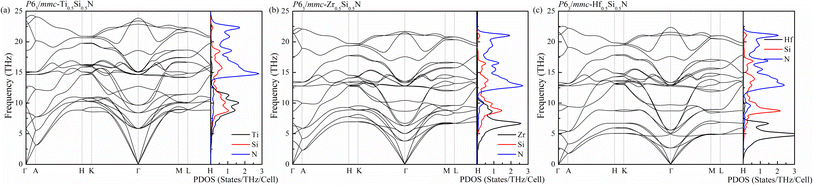Fig. 3 Phonon spectra of Ti_0.5Si_0.5N (a), Zr_0.5Si_0.5N (b) and Hf_0.5Si_0.5N (c) within P6₃/mmc structure at ambient pressure.

3.2. Mechanical property

Let's focus our attention on the mechanical properties of these three ternary Si-containing systems in this section. As is known, ideal strength is an important mechanical property in definiting the macro physical natures of the materials such as hardness, toughness, brittleness and ductility etc. By applying tensile/compressive strains along certain directions while relaxing the crystal along the rest four orientations, the tensile/compressive stress–strain relations can be obtained. In stress–strain curves, the corresponding stress value of the yield point is defined as the ideal strength in this direction. Due to the hexagonal crystal symmetry, stress–strain relations in three directions ([0001],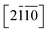 and 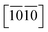) are necessary and plotted in Fig. 4a–c. Here, the tensile/compressive stress is denoted as σ_zz. It can be seen the nonlinear tensile/compressive stress occurs at the strains of about 0.04 and all these three Si-containing systems have the largest/smallest tensile strengths along [0001]/ 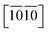directions, reflecting their strongest and weakest stress response are along [0001] and 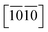directions as shown in Fig. S1,† respectively. The ideal tensile strengths along [0001]/ 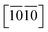directions are 71.7/34.5 GPa, 61.3/23.4 GPa and 63.5/25.9 GPa on the strains of 0.212/0.111, 0.194/0.089 and 0.206/0.089 for Ti_0.5Si_0.5N, Zr_0.5Si_0.5N and Hf_0.5Si_0.5N systems respectively. The compressive strengths are all beyond 75 GPa for them in all these three directions, confirming they all have ultraincompressibility. The fracture is present near the yield points upon tensile strains and the plastic deformation is absent for all of them, implying they all behave brittleness. Because of the longest tensile curves for Ti_0.5Si_0.5N, that means it has the largest toughness nature relative to the rest two. By comparing the largest and the smallest strengths (denoted as σ_max and σ_min), the strength anisotropies can also be assessed by the ratios of σ_max and σ_min. The calculated tensile σ_max/σ_min values are 2.1, 2.6 and 2.5 for Ti_0.5Si_0.5N, Zr_0.5Si_0.5N and Hf_0.5Si_0.5N systems respectively, suggesting Ti_0.5Si_0.5N has the smallest strength anisotropy.

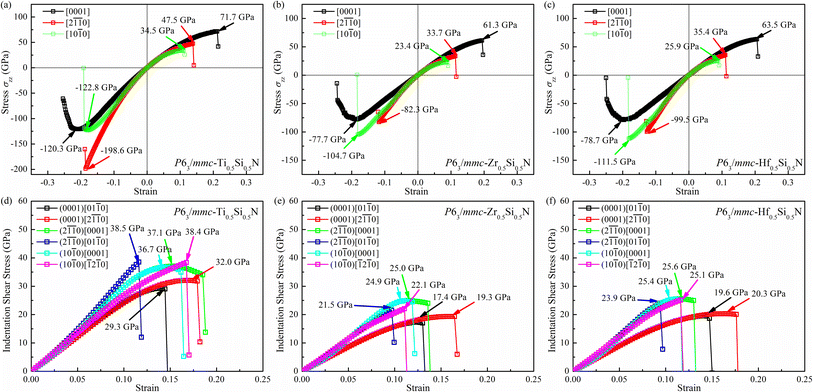Fig. 4 Tensile/compressive (a–c) and indentation shear (d–f) stress–strain curves for Ti_0.5Si_0.5N, Zr_0.5Si_0.5N and Hf_0.5Si_0.5N.

By simulating the real experimental measuring process of Vickers hardness, we also evaluated the values of hardness for these three systems. According to the measuring process, a biaxial strain field containing two stress components (shear σ_zx and compressive σ_zz) forms in the tested materials. The relation of the two stress components obeys the formula: σ_zx = σ_zz tan φ, where φ (=68°) denotes the face-to-centerline angle of the diamond indenter.³⁸ Using this method, the Vickers hardness of them should be well assessed. The calculated results of indentation shear stress–strain relations are plotted in Fig. 4d–f. In accord with the tensile strength, the weakest stress response occurs in the (0001) for all of these three systems, suggesting the (0001) plane can be viewed as their first cleavage plane. To obtain the indentation shear strength along as many crystal directions as possible, three typical planes along six slip directions were adopted to calculate the indentation shear strength. The largest/smallest strengths are 38.5/30.0, 25.0/17.4 and 25.6/19.6 on the strains of 0.116/0.139, 0.113/0.122 and 0.116/0.141 for Ti_0.5Si_0.5N, Zr_0.5Si_0.5N and Hf_0.5Si_0.5N systems respectively. Correspondingly, the indentation shear σ_max/σ_min values are about 1.28, 1.44 and 1.31 respectively, meaning Ti_0.5Si_0.5N has the best shear strength anisotropy again. To be noted that this ideal strength calculations don't take the defect and impurity inside the real crystals into consideration. However, it is effective to assess the Vickers hardness for the ideal crystalline materials. Thus, it can be concluded that this hexagonal P6₃/mmc Ti_0.5Si_0.5N possesses high Vickers hardness up to 38.5 GPa under real experimental conditions in principle, very close to the threshold of superhard bound (40 GPa). Meanwhile, Ti_0.5Si_0.5N, Zr_0.5Si_0.5N and Hf_0.5Si_0.5N systems all have larger tensile/compressive strengths in various directions relative to their shear strengths, indicating the failure modes of them are mainly induced by the shear loadings in the future engineering applications.

In comparison, the tensile strengths of Ti_0.5Si_0.5N in ordered B1 and disordered SQS-B1 structures are also studied. As is plotted in Fig. S2,† it can be obviously seen both of them exhibit much weaker tensile and compressive strengths relative to those of hexagonal phase. The largest/smallest strengths are 13.6/6.5 GPa and 12.4/6.4 GPa for ordered and disordered structures respectively, which are very close to each other, implying there is little effect on the mechanical strengths for the occupations of the TM and Si atoms. However, most experimental hardness values of this B1–Ti_0.5Si_0.5N are up to beyond 20 GPa, which is mainly ascribed to the hardening effect of superlattice formed as nanocomposite.

Calculated elastic constants C_ij, corresponding elastic moduli and the assessed Vickers hardness are given in Table 2. The hexagonal P6₃/mmc structure has five independent elastic constants (C₁₁, C₃₃, C₄₄, C₁₂ and C₁₃) and the cubic B1 has three (C₁₁, C₁₂ and C₄₄). However, this ternary systems have three elements with different radii, thus, the ordered B1 structure have different lattice constants of a and b due to the layered and alternated distribution of TM and Si atoms. Thus, the cubic B1 structure degenerates to be the tetragonal phase, correlating to the six independent elastic constants. For the firstly uncovered P6₃/mmc structure, the mechanical stability was checked using the criteria:³⁴ C₄₄ > 0, C₁₁ > |C₁₂|, (C₁₁ + 2C₁₂)C₃₃ > 2C²₁₃. All these three Si-containing systems well satisfy the criteria, suggesting their mechanical stabilities. As is seen in Table 2, the present calculated three elastic constants for binary TiN are excellently agreement with the previous theoretical and experimental results, confirming the high reliability of our calculations. For the hexagonal ternary systems, the firstly calculated elastic constants can be used as good references for future theoretical or experimental study. Notably, with the addition of Si element, there is a decreasing trend of bulk modulus, which is attributed to the reduction of electron concentrations. However, due to the enhanced p–d hybridization and weakened d–d metallic states between TM and N atoms, the shear moduli are maintained or improved at large values, leading to larger G/B values for them. Thus, these three ternary systems all behave brittle nature (G/B > 0.57).^39,40 Meanwhile, based on the elastic moduli, the Vickers hardness is calculated using the Chen formula.³⁵ Their hardness values are 38.1, 27.3 and 30.2 GPa for Ti_0.5Si_0.5N, Zr_0.5Si_0.5N and Hf_0.5Si_0.5N respectively. Remarkably, despite the fact that these hardness values are evaluated in the elastic limit of the crystals, they are highly consistent with our results using the indentation shear stress–strain method above. Such high hardness supports they can be viewed as potential superhard materials. Also, it can be seen the hardness of B1 structure of Ti_0.5Si_0.5N is much smaller, though it was reported to possess the high hardness up to 30 GPa. The reason of the deviation can be mainly ascribed to the superlattice effect in the experimental condition. Additionally, it can be seen the mechanical properties of these three ternary systems such as the G/B values, hardness as well as strengths are not linear while going from Ti_0.5Si_0.5N to Zr_0.5Si_0.5N to Hf_0.5Si_0.5N. The hardness of the hexagonal Hf_0.5Si_0.5N is slightly higher than Zr_0.5Si_0.5N while Ti_0.5Si_0.5N has the largest value. Similar results can be seen in the “indentation shear” strengths. This seeming irregularity may be ascribed to the nonlinear distribution of the atomic radii from Ti to Zr to Hf. Zr has the largest atomic radius resulting in the largest lengths of Zr–N bonds which leads to the weaker bond strength. Thus, Zr_0.5Si_0.5N has the smallest hardness and lowest strengths.

Table 2 Calculated elastic constants (C_ij, GPa), bulk modulus (B, GPa), shear modulus (G, GPa), Young's modulus (E, GPa), Poisson's ratio ν, G/B ratio and the Vickers hardness (H_v, GPa)

	Symmetry	Source	C11	C22	C33	C44	C55	C66	C12	C13	C23	B	G	E	ν	G/B	Hv
a Ref. 41.b Ref. 42.c Ref. 43.d Ref. 44.
Ti0.5Si0.5N	P63/mmc	This work	640		570	223		251	137	101		280	240	559	0.17	0.86	38.1
	B1	This work	316	399		156	47		129		101	203	89	232	0.31	0.44	7.5
	B1	Exp^a												260			25
	B1	Exp^b												334			26
Zr0.5Si0.5N	P63/mmc	This work	528		469	168		197	134	107		246	185	443	0.20	0.75	27.3
Hf0.5Si0.5N	P63/mmc	This work	568		477	174		216	136	96		251	197	468	0.19	0.79	30.2
TiN	B1	This work	598			155			144			295	181	451	0.25	0.61	20.6
	B1	Theory^c	590			169			145			294	189	466	0.24	0.51	22.6
	B1	Exp^d	625			163			165			320					23

---

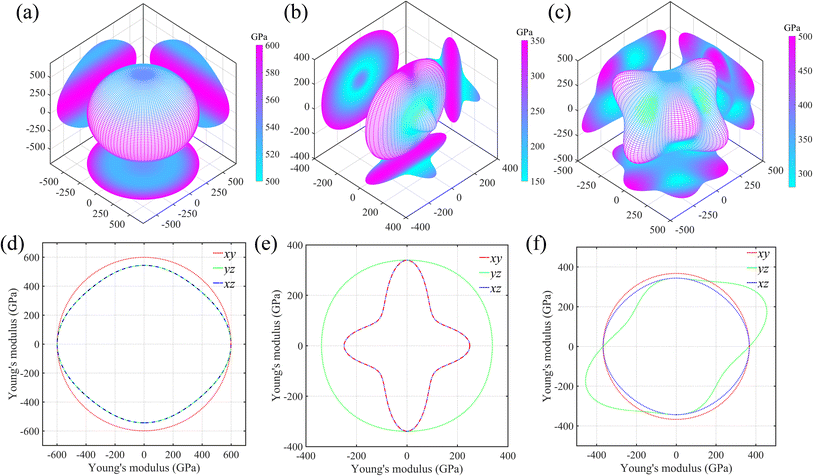
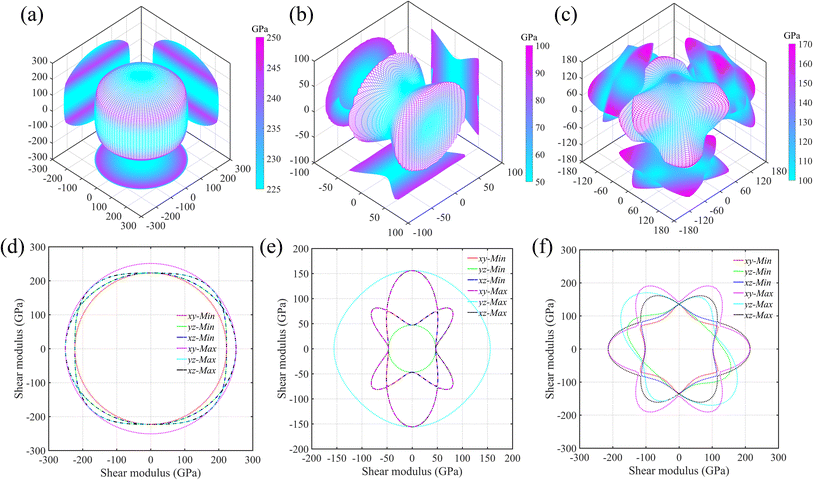
As is known, the elastic properties are achieved by estimating the stress response of the crystals under micro strains. Normally, there is elastic anisotropy depending on the crystal symmetry and the bond distributions in the materials. Here, we adopt Ti_0.5Si_0.5N as the representative to further compare the elastic anisotropies of hexagonal P6₃/mmc, B1 and trigonal R3m structures through calculating the Young's (E) and shear (G) moduli in various directions based on the formulas provided by the literature.³⁵ The results are displayed in Fig. 5 (Young's modulus E) and Fig. 6 (shear modulus G) using the three-dimensional (3D) surface representations and two-dimensional (2D) projections on xy, xz and yz crystal planes. Here, we use the distance from the coordinate origin to the 3D surface denote the directional modulus E/G. Thus, if a material behaves isotropic elastic properties, the 3D plots would be a perfect sphere. The deviation from the sphere can reflect the elastic anisotropy. It is obviously deduced the P6₃/mmc structure possesses the best isotropic elastic properties thanks to the smallest deviation from the perfect sphere. This is in accordance with the calculated tensile/compressive stress–strain curves, in which the curve slopes of those three typical crystal directions near the coordinate origin are close with each other. The largest/smallest Young's moduli (E_max/E_min) for P6₃/mmc, B1 and R3m structures are 599/528 GPa, 348/152 GPa and 500/277 GPa, respectively. The quantitative elastic anisotropies can be compared by the ratios of E_max and E_min. The E_max/E_min values of them are 1.13, 2.29 and 1.81, meaning the P6₃/mmc structure has the best elastic isotropy. Also, 3D and 2D directional dependence of the shear modulus (G) are plotted in Fig. 6. Notably, the shear modulus is different from the Young's modulus, because the G value varies with the slipping direction for a given crystal plane. Therefore, each crystal plane has minimum and maximum G values (G_min and G_max). Here, the 3D directional dependence of G_min are plotted in Fig. 6a–c and the 2D projections of G_min and G_max on xy, xz and yz planes are plotted in Fig. 6d–f. Obviously, P6₃/mmc structure exhibits the best shear anisotropy due to the fact that its 3D plot is close to a perfect sphere. The ratios of G_max/G_min are 251 GPa/223 GPa ≈ 1.13 (P6₃/mmc), 156 GPa/47 GPa ≈ 3.32 (B1) and 216 GPa/105 GPa ≈ 2.06 (R3m). It can be seen the ordered B1 structure has large shear anisotropy. For the Zr_0.5Si_0.5N and Hf_0.5Si_0.5N systems within these three structures, the results of the strength and elastic anisotropies are similar to the Ti_0.5Si_0.5N. Hence, they are not repetitively discussed here.

Fig. 5 Three-dimensional (3D) surface representations of Young's moduli for Ti_0.5Si_0.5N within P6₃/mmc (a), B1 (b) and R3m (c) structures and two-dimensional (2D) projections (d–f) of the Young's moduli on the xy, yz and xz planes.

Fig. 6 Three-dimensional (3D) surface representations of shear moduli for Ti_0.5Si_0.5N within P6₃/mmc (a), B1 (b) and R3m (c) structures and two-dimensional (2D) projections (d–f) of the shear moduli on the xy, yz and xz planes.

3.3. Electronic properties

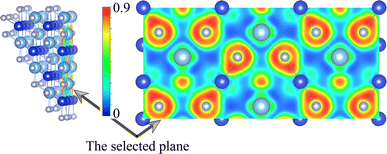
We now turn to discuss the electronic properties of these Si-containing ternary systems. Due to the same valence electrons for Ti, Zr and Hf elements, the electronic structures of Ti_0.5Si_0.5N, Zr_0.5Si_0.5N and Hf_0.5Si_0.5N systems are similar with each other in the same structures. Fig. 7 shows the calculated projected band structures and partial density of states (PDOS) of Ti_0.5Si_0.5N, Zr_0.5Si_0.5N and Hf_0.5Si_0.5N within P6₃/mmc structure. It can be seen their band structures are analogous with each other. The band gaps are absent for all of them, indicating their metallic nature. In particular, it can be seen the conduction bands are mainly dominated by the M–d orbitals, the valence bands by partial M–d and N–p orbitals. The p–d hybridization can be obviously observed near the E_F. Meanwhile, one can see the difference of crystal structure enormously impact the band structures. As shown in Fig. S3(a),† for Ti_0.5Si_0.5N within B1 phase, the E_F lies at the antibonding regions, in contrast, it is modified effectively at the overlap of valence band top and conduction band bottom for P6₃/mmc structure, leading to the enhanced electronic stability and mechanical property. In comparison, TiN and SiN within hexagonal P6₃/mmc structure are also simulated to study the difference of the band structure from the ternary system. As seen in Fig. S3(b and c),† it can be seen some conduction bands descend below the E_F for TiN, as a contrast, the valence bands spread through the E_F for SiN. That means the ternary hexagonal phase possesses the best electronic stability and the maximized covalent p–d hybridization, inducing the enhanced anti-shear property. The PDOS plots show that the pseudo-gaps near the E_F separating the bonding and antibonding states can be obviously seen for Ti_0.5Si_0.5N within P6₃/mmc and B1 structures. However, thanks to the introduction of Si element, the E_F is exactly modulated at the valley of the pseudo-gap for P6₃/mmc structure. It suggests the bonding states are fully occupied, whereas the antibonding states are not. The p–d hybridization can be seen in the energy range of 0 to −5 eV for Ti_0.5Si_0.5N. B1 structure exhibits the obvious occupation of d–d states near the E_F, resulting in the improved total formation enthalpy and the metallic nature, which is not favorable for the mechanical properties of compounds. Though the Si element induces the modulated electronic structure, it has weaker interactions with N element due to its small contributions to the bonding states for both s-orbitals and p-orbitals in the related energy range. The plot of calculated ELF is presented in Fig. 8. To clearly exhibit the Ti–N and Si–N bonding nature, herein, we selected a crystal plane holding the Ti, Si and N atoms within a common plane. The ELF value is dimensionless and it has a range of 0–1. ELF = 1/ELF = 0 have the meaning of highly localized/lack of electrons. Hence, the bonding nature can be evaluated by discerning the color of the region among the atoms in the plot. It can be seen the electrons are highly localized between Si and N atoms, suggesting the covalent Si–N bonding. Thanks to the highly p–d coupling, the Ti–N bonds also exhibit strong covalent feature, though comprising some of metallic component.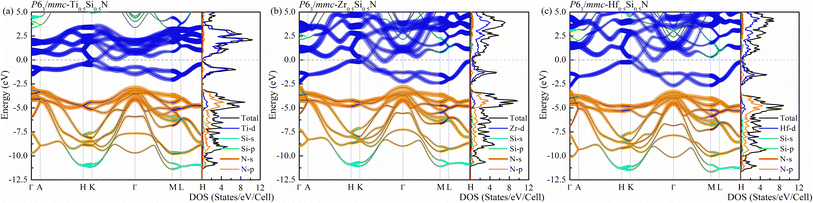

Fig. 7 Projected band structures and projected density of states (PDOS) for (a) Ti_0.5Si_0.5N, (b) Zr_0.5Si_0.5N and (c) Hf_0.5Si_0.5N within P6₃/mmc structure.

Fig. 8 Calculated ELF slice of the selected plane of P6₃/mmc-Ti_0.5Si_0.5N.

4. Conclusions

In summary, the structure diversity of Ti_0.5Si_0.5N, Zr_0.5Si_0.5N and Hf_0.5Si_0.5N systems under the pressure of 0–100 GPa are firstly explored using the developed crystal structure searching method combined with the first-principle calculations. Theoretical explorations on their structural stability, electronic and mechanical properties were systematically performed by first-principle calculations. Our results confirmed that the P6₃/mmc structure of these three Si-containing ternary systems has surprisingly enhanced ideal strengths and larger hardness up to 38.1 GPa, as well as better mechanical isotropy relative to the ordered B1 structure. Electronic analysis in depth was also carried out to further study the mechanism of the hardening inducement. For this new hexagonal P6₃/mmc structure, the addition of Si element well tuned the electronic structure to make the E_F position optimized and maximized the p–d hybridization and minimized the occupation of antibonding d–d states. Meanwhile, the structural stability was also improved by this electronic adjust. All these findings would be expected to stimulate further experimental and theoretical works on these Si-containing systems and provide effective strategy in designing new type of hard materials with composite combination of beneficial properties.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by State Key Laboratory of Precision Blasting and Hubei Key Laboratory of Blasting Engineering, Jianghan University (No. PBSKL2022D03), the Natural Science Foundation of China (Grant Nos. 51808554), the Natural Science Basic Research plan in Shaanxi Province of China (Grant No. 2020JQ-892).

References

1. R. F. Bunshah, Handbook of Hard Coatings, William Andrew Publishing, New York, 2002.
2. J. H. Hsieh, A. L. K. Tan and X. T. Zeng, Oxidation and wear behaviors of Ti-based thin films, Surf. Coat. Technol., 2006, 201, 4094–4098.
3. M. Wittmer, J. Noser and H. Melchior, Oxidation kinetics of TiN thin films, J. Appl. Phys., 1981, 52, 6659.
4. T. Altan, Process simulation using finite element method-prediction of cutting forces, tool stresses and temperatures in high-speed flat end milling, Int. J. Mach. Tools Manuf., 2000, 40, 713–738.
5. B. D. Beake, L. Isern, J. L. Endrino and G. S. Fox-Rabinovich, Micro-impact testing of AlTiN and TiAlCrN coatings, Wear, 2019, 418–419, 102–110.
6. G. S. Fox-Rabinovich, A. I. Kovalev, M. H. Aguirre, B. D. Beake, K. Yamamoto, S. C. Veldhuis, J. L. Endrino, D. L. Wainstein and A. Y. Rashkovskiy, Design and performance of AlTiN and TiAlCrN PVD coatings for machining of hard to cut materials, Surf. Coat. Technol., 2009, 204(4), 489–496.
7. D. G. Sangiovanni, V. Chirita and L. Hultman, Toughness enhancement in TiAlN-based quarternary alloys, Thin Solid Films, 2012, 520(11), 4080–4088.
8. D. Becker, Wear of nanostructured composite tool coatings, Wear, 2013, 304, 88–95.
9. G. Greczynski, S. Mráz, M. Hans, D. Primetzhofer, J. Lu, L. Hultman and J. M. Schneider, Unprecedented Al supersaturation in single-phase rock salt structure VAlN films by Al+ subplantation, J. Appl. Phys., 2017, 121(17), 171907.
10. I. Endler, M. Höhn, J. Schmidt, S. Scholz, M. Herrmann and M. Knaut, Ternary and quarternary TiSiN and TiSiCN nanocomposite coatings obtained by Chemical Vapor Deposition, Surf. Coat. Technol., 2013, 215, 133–140.
11. S. Vepřek and S. Vepr, The search for novel, superhard materials, J. Vac. Sci. Technol., A, 1999, 17, 2401.
12. A. B. Mei, O. Hellman, N. Wireklint, C. M. Schlepütz, D. G. Sangiovanni, B. Alling, A. Rockett, L. Hultman, I. Petrov and J. E. Greene, Dynamic and structural stability of cubic vanadium nitride, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91(5), 054101.
13. L. Chen, J. Xu, M. Zhang, T. Rong, Z. Jiang and P. Li, Systematic study on mechanical and electronic properties of ternary VAlN, TiAlN and WAlN systems by first-principles calculations, Ceram. Int., 2021, 47(6), 7511–7520.
14. L. Chen and Z. Jiang, First-principles study on a new type of quaternary carbonitride VWCN with outstanding mechanical properties, Int. J. Refract. Met. Hard Mater., 2020, 92, 105319.
15. Y. Tian, B. Xu and Z. Zhao, Microscopic theory of hardness and design of novel superhard crystals, Int. J. Refract. Met. Hard Mater., 2012, 33, 93–106.
16. X. Guo, L. Li, Z. Liu, D. Yu, J. He, R. Liu, B. Xu, Y. Tian and H. T. Wang, Hardness of covalent compounds Roles of metallic component and d valence electrons, J. Appl. Phys., 2008, 104, 023503.
17. Y. Wang, J. Lv, L. Zhu and Y. Ma, Crystal structure prediction via particle-swarm optimization, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82(9), 1–8.
18. Y. Wang, J. Lv, L. Zhu and Y. Ma, CALYPSO: A method for crystal structure prediction, Comput. Phys. Commun., 2012, 183, 2063–2070.
19. M. Zhang, H. Yan and Q. Wei, Unexpected ground-state crystal structures and mechanical properties of transition metal pernitrides MN₂ (M= Ti, Zr, and Hf), J. Alloys Compd., 2019, 774, 918–925.
20. Q. Wei, W. Tong, B. Wei, M. Zhang and X. Peng, Six new silicon phases with direct band gaps, Phys. Chem. Chem., 2019, 21, 19963–19968.
21. L. Chen, J. Xu, M. Zhang, Z. Wen and Z. Jiang, Structural , mechanical and electronic properties study on group 5 transition metals ternary mononitrides from first-principles calculations, J. Alloys Compd., 2020, 813, 152246.
22. L. Chen, M. Zhang, J. Chang and Z. Jiang, Theoretical investigation on vanadium dinitrides from first-principles calculations, Ceram. Int., 2018, 45(2), 2457–2465.
23. Y. R. Zhao, T. T. Bai, L. N. Jia, W. Xin, Y. F. Hu, X. S. Zheng and S. T. Hou, Probing the Structural and Electronic Properties of Neutral and Anionic Lanthanum-Doped Silicon Clusters, J. Phys. Chem. C, 2019, 123(47), 28561–28568.
24. L. Chen, J. Xu, M. Zhang and Y. Zhang, Theoretical study on structural, mechanical and electronic properties of ternary mononitride Ti_0.5W_0.5N from first-principles calculations, Mater. Chem. Phys., 2020, 242, 122476.
25. L. Chen, J. Xu, M. Zhang, G. Zhang, Y. Zhao and Y. Zhang, Theoretical study on novel orthorhombic ternary monocarbides M_0.5Re_0.5C (M = V, Nb, Ta) from first-principles calculations, Ceram. Int., 2020, 46(15), 24624–24634.
26. G. Kresse and J. Furthmüller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54(16), 11169–11186.
27. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865–3868.
28. P. E. Blöchl, Projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
29. G. Kresse and D. Joubert, From ultrasoft pseudopotentials to the projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59(3), 1758–1775.
30. H. J. Monkhorst and J. D. Pack, Special points for Brillonin-zone integrations, Phys. Rev. B: Solid State, 1976, 13, 5188–5192.
31. S. H. Wei, L. G. Ferreira, J. E. Bernard and A. Zunger, Electronic properties of random alloys: Special quasirandom structures, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 42(15), 9622–9649.
32. S. H. W. A. Zunger, L. G. Ferreira and J. E. Bernard, Special Quasirandom Structures, Phys. Rev. Lett., 2012, 65(3), 353–356.
33. A. Togo and I. Tanaka, First principles phonon calculations in materials science, Scr. Mater., 2015, 108, 1–5.
34. K. H. M. Born, Dynamical Theory of Crystal Lattices, Oxford University Press, Inc., London, 1954.
35. T. C. T. Ting, Anisotropic Elasticity Theory and Applications, Oxford University Press, Inc., 1996.
36. X.-q. Chen, H. Niu, D. Li and Y. Li, Intermetallics Modeling hardness of polycrystalline materials and bulk metallic glasses, Intermetallics, 2011, 19(9), 1275–1281.
37. A. S. B. Silvi, Classification of chemical bonds based on topological analysis of electron localization functions, Nature, 1994, 371, 683–686.
38. C. Zang, H. Sun, J. S. Tse and C. Chen, Indentation strength of ultraincompressible rhenium boride , carbide , and nitride from first-principles calculations, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 014108.
39. S. F. Pugh, XCII. Relations between the elastic moduli and the plastic properties of polycrystalline pure metals, Philos. Mag., 1954, 45, 823–843.
40. H. Yan, Z. Wei, M. Zhang and Q. Wei, Exploration of stable stoichiometries, ground-state structures, and mechanical properties of the W–Si system, Ceram. Int., 2020, 46(10), 17034–17043.
41. G. Greczynski, B. Bakhit, L. Hultman and M. Odén, High Si content TiSiN films with superior oxidation resistance, Surf. Coat. Technol., 2020, 398, 126087.
42. A. Al-rjoub, A. Cavaleiro and F. Fernandes, Influence of Ag alloying on the morphology, structure, mechanical properties, thermal stability and oxidation resistance of multilayered TiSiN/Ti(Ag)N films, Mater. Des., 2020, 192, 108703.
43. S. Yu, Q. Zeng, A. R. Oganov, G. Frapper and L. Zhang, Phase stability, chemical bonding and mechanical study, Phys. Chem. Chem. Phys., 2015, 17, 11763–11769.
44. R. Ahuja, O. Eriksson and J. Wills, Structural, elastic, and high-pressure properties of cubic TiC, TiN, and TiO, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 53(6), 3072–3079.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2ra06423e

---