Strong anisotropic second-order nonlinear optical responses in 0D lead-free chiral perovskite single-crystalline microwire arrays†
Meiqiu
Dong
a,
Binshuai
Wang
f,
Ziwei
Yu
a,
Jinjin
Zhao
de,
Xinyi
Li
a,
Yue
Fu
a,
Yangwu
Guo
 *a,
Yingjie
Zhao
*c,
Hanfei
Gao
*a,
Yingjie
Zhao
*c,
Hanfei
Gao
 *a,
Lei
Jiang
*a,
Lei
Jiang
 ab and
Yuchen
Wu
ab and
Yuchen
Wu
 ab
ab
aJi Hua Laboratory, Foshan, Guangdong 528000, P.R. China. E-mail: guoyangwu15@mails.ucas.ac.cn; gaohanfei15@mails.ucas.ac.cn
bCAS Key Laboratory of Bio-inspired Materials and Interfacial Science, Technical Institute of Physics and Chemistry, Chinese Academy of Sciences, Beijing, 100190, P.R. China
cCollege of Chemistry, Zhengzhou University, Zhengzhou 450001, P.R. China. E-mail: zhaoyingjie5@zzu.edu.cn
dDepartment of Physics, Shanxi Datong University, Datong, 037009, P.R. China
eShanxi Province Key Laboratory of Microstructure Functional Materials Institute of Solid State Physics, Shanxi Datong University, Datong, 037009, P.R. China
fDepartment of Urology, Peking University Third Hospital, Beijing, 100191, P.R. China
First published on 24th March 2023
Abstract
Low-dimensional hybrid organic–inorganic chiral perovskites with intrinsic non-centrosymmetric structures have shown promising potential for second-order nonlinear optical applications due to their structural diversity and large lattice distortions. Simultaneously, “structure-level” low-dimensional single crystal perovskites have attracted wide attention to meet the increasing demand of on-chip integrated nonlinear optical devices. Herein, we synthesized two new chiral hybrid 0D perovskites (R/S-MBA)4Bi2Cl10 based on the non-toxic element bismuth by introducing chiral R/S-MBA as the organic component. The highly ordered assembly microwire arrays were further prepared using a capillary-bridge confined technique. These high-crystallinity chiral perovskite microwire arrays preserve their structures with high distortion levels and achieve high-efficiency frequency conversion across a wide range of bands and different polarization states with a high polarization ratio of up to 0.992, which is superior to those of the corresponding polycrystalline films that cause undesirable light scattering. Such non-toxic Bi-based low-dimensional chiral perovskite single-crystalline microwire arrays with excellent NLO performances might provide a strategy for NLO-integrated applications in advancing photonic devices.
1. Introduction
Nonlinear optics (NLO) is the branch of science concerned with the nonlinear regime of the interaction between intense lasers and matter, which is of great significance in the development of laser technology and spectroscopy.1,2 As a typical second-order NLO response, second-harmonic generation (SHG) refers to a nonlinear process of converting two photons with the same frequency into one with twice the frequency based on the asymmetric structure, boosting a series of advanced applications ranging from laser manufacturing and engineering, biological microscopic imaging, to telecommunication and military technology.3–7 At present, most commercial SHG materials are inorganic materials due to their relatively high second-order NLO susceptibility, high mechanical strength, and good physicochemical stability.8–10 However, the inherent shortcomings of inorganic materials, such as the incompatibility of flexible substrates and processing difficulties, significantly hinder their potential application in flexible, miniaturized, and integrated NLO devices. Thus, it is imperative to develop novel NLO materials to promote the advancement of NLO fields.A hybrid halide perovskite with abundant chemical structures and optical-electrical properties has emerged as a promising material for optoelectronic applications, such as light-emitting diodes, photodetectors, field-effect transistors, solar cells, etc.11–19 Recently, the introduction of chiral cations has bolstered multiple exotic optical, electrical, and spintronic properties of perovskites. Particularly, the breaking of lattice inversion symmetry induced by chiral cations opens a new avenue for chiral halide perovskites in the field of NLO.20–24 Compared to their three-dimensional counterparts, low-dimensional perovskite materials ranging from two, one, to zero dimensions (0D) exhibit a more pronounced NLO responses due to the light–matter interaction, various excitonic effects, structural diversity, and large lattice distortions.25–32 Meanwhile, the large bandgap of these low-dimensional perovskites leads to their transparency over a broader spectral range, providing a wide wavelength window for SHG applications.26,27 However, most low-dimensional chiral perovskites contain toxic Pb2+, seriously impeding their future commercialization and industrialization for NLO devices. The adjacent VA group cation Bi3+, which possesses a similar ionic radius and electronegativity but less toxicity compared to the toxic Pb2+, has been recently developed as an isoelectronic alternative to Pb2+.33–36 The introduction of Bi3+ can also promote the formation of low-dimensional perovskite structures to further improve the stability.35,36 Thus, the non-toxic Bi-based low-dimensional perovskites will become the new and important explored sector of perovskite application accelerating the development of integrated NLO devices.
Besides the “material-level” low dimension, the “structure-level” low dimension, emphasizing the morphology, especially the array patterning, is also an essential step toward integrated nonlinear optical devices.31,32,37–43 Long-range ordered perovskite single-crystalline arrays with unique optical anisotropy and cleavage surface necessary for nonlinear optics can compensate for the defects, such as scattering of light in films and inherently dispersive refractive indices of bulk crystals, attracting more attention for compact integrated devices to meet the increasing demand of integrated photonic circuits and on-chip nanophotonics.43–45 However, the controllable manufacturing and patterning of high-quality NLO perovskite single-crystal arrays have become one of the key bottlenecks in the next generation of nanophotonic devices.
In this work, we report the synthesis of two new 0D chiral non-toxic Bi-based perovskites, (R/S-MBA)4Bi2Cl10, featuring an intrinsic non-centrosymmetric polar crystal structure, and the observation of efficient second-order NLO responses from their high crystallinity and pure crystallographic orientation microwire arrays assembled by capillary-bridge confined techniques. The systematic study of power-, wavelength-, and polarization-dependent SHG responses demonstrates the excellent second-order NLO performance of those chiral perovskite microwire arrays with a wide transparent region. In contrast to the polycrystalline film counterparts, (R/S-MBA)4Bi2Cl10 single-crystalline microwire arrays exhibit excellent NLO performances, such as a stronger SHG response and a higher polarization ratio of up to 0.992. This work suggests the potential applications of low-dimensional lead-free chiral perovskites in NLO applications and will vigorously accelerate the development of integrated optical devices.
2. Experimental section
2.1. Synthesis of perovskite crystals
Bi2O3 (466 mg, 1 mmol) and R-(+)- or S-(−)-α-methylbenzylamine (485 mg, 4 mmol) were added into aqueous HCl solution (20 mL) with magnetic stirring. The solution was heated to 150 °C for 5 h until it is clear and then was slowly cooled to room temperature. Colorless perovskite crystals were obtained after 2 h, which were filtered, washed with chlorobenzene, and dried in a vacuum oven for purification.2.2. Fabrication of microwire arrays and films
The synthesized crystals were dissolved in anhydrous dimethylsulfoxide (DMSO) or N,N-dimethylformamide (DMF) to prepare perovskite precursor solution with different concentrations. The perovskite precursor solution (10 μL, 30 mg mL−1, DMSO) was first added to a silicon micropillar template with asymmetric wettability. Then a cleaned Si or quartz glass substrate was pressed on it to form a sandwiched assembly system, which was moved to a vacuum oven at 75 °C for 24 h until the solution evaporated completely. On peeling off the micropillar template, the perovskite single-crystalline microwire arrays on the target substrate can be obtained. To prepare polycrystalline films, the perovskite precursor solution (50 μL, 200 mg mL−1, DMF) was firstly spin-coated onto the substrate (3000 rpm, 45 s), and then transferred to a hot plate at 70 °C for 10 min.2.3. Characterization
Single-crystal X-ray diffraction (SCXRD) analyses were performed on a Bruker SMART APEX II CCD diffractometer with Mo Kα (λ = 0.71073 Å) radiation at 170 K. The crystal structure was solved by direct methods using SHELXs and refined on F2 by full-matrix least-squares techniques using the program SHELXTL within the Olex2 crystallographic package. The XRD patterns were measured on an X-ray diffractometer (Bruker, D8 focus, Germany) with monochromatized Cu Kα radiation (λ = 1.5406 Å). Rocking curves were recorded using a high-resolution X-ray diffractometer (Rigaku Corporation, SmartLab, Japan). The ultraviolet–visible-near infrared ray (UV-vis-NIR) transmittance spectrum was collected on a UV-vis-NIR spectrophotometer (Agilent, Cary 7000, USA) and a Fourier transform infrared spectrometer (Varian, Excalibur 3100, USA). The circular dichroism (CD) spectra were recorded using a circular dichroism spectrometer (JASCO, J-815, Japan). The morphology and elemental distribution were characterized using a scanning electron microscope (Hitachi, S-4800, Japan). The chemical state of elements was investigated using an X-ray photoelectron spectroscope (Thermo Fisher, ESCALAB 250Xi, UK). Thickness measurements were performed on an atomic force microscope (Bruker, ICON2-SYS, Germany). Transmission electron microscopy (TEM) and selected area electron diffraction (SAED) characterization was carried out using a transmission electron microscope (JEOL, 2100, Japan). The grazing-incidence wide-angle X-ray scattering (GIWAXS) patterns were measured using a WZX-SAXS/WAXS system (Xenocs, XEUSS, France). The static CA was investigated using a contact angle system (Dataphysics, OCA20, Germany).2.4. Calculation details
The Vienna ab initio simulation package (VASP) was employed to perform the density functional theory (DFT) calculations based on the frozen-core all-electron projector augmented wave (PAW) method. The generalized gradient approximation (GGA) of the Perdew–Burke–Ernzerhof (PBE) formulation was selected to describe the exchange–correlation energy. For the plane wave, a 400 eV kinetic energy cutoff with a Gaussian smearing of 0.1 eV in width was adopted. For structural optimization, the Monkhorst–Pack k-point grid with a resolution of 0.2 Å−1 was selected to sample the reciprocal space. Considering the van der Waals (vdW) interactions, the DFT-D3 correction with Becke–Johnson damping was adopted during calculations. For electronic properties, the convergence criterion was set to 1.0 × 10−6 eV in energy and 0.005 eV Å−1 in force.2.5. Nonlinear optical measurements
Powder second-order NLO properties were examined using the Kurtz–Perry method under 2090 nm Q-switched laser irradiation. The SHG intensities were semi-quantitatively determined by using AgGaS2 with the same sieved particle size as the reference. The SHG measurements of microwires and films were performed using a confocal microscope with a Ti:sapphire femtosecond pump (Spectra physics Mai Tai, <150 fs, 80 MHz, 740–900 nm). A 50× objective lens (NA = 0.80) was used to focus the laser onto a spot with a diameter of about 4 μm. SHG mapping was performed using an MStarter 100 confocal microscope (Metatest Optoelectronic). The linear polarization direction of the incident pump was tuned with a half-wave plate.3. Results and discussion
3.1. Crystal structure analysis
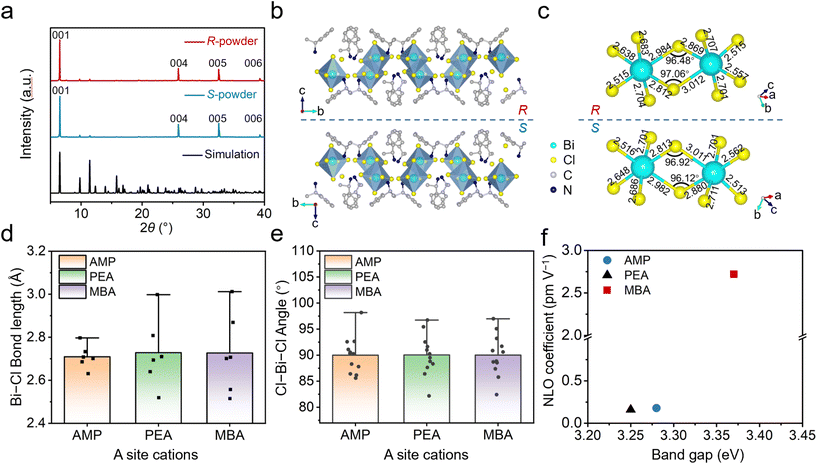
To obtain the symmetry-breaking perovskite structure required for SHG, colorless plate crystals of 0D chiral perovskites (R/S-MBA)4Bi2Cl10 were synthesized by a temperature-lowering crystallization method (see the Experimental section and Fig. S1†). Briefly, chiral R-(+)- or S-(−)-α-methylbenzylamine (R- or S-MBA) and Bi2O3 with a 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 stoichiometry were dissolved in aqueous HCl solution, and then the crystal precipitated with the decrease of temperature. To reveal the chiral crystal structure, SCXRD was performed, and the crystallographic data are listed in Tables S1–3.† The powder XRD patterns of (R/S-MBA)4Bi2Cl10 were consistent with the simulated ones and proved the high-phase purity, as presented in Fig. 1a. Both (R/S-MBA)4Bi2Cl10 crystallize in the Sohncke space group of monoclinic P21 with identical unit cell parameters, suggesting non-centrosymmetric and polar crystal structures. Scanning electron microscopy (SEM) images of the exfoliated crystal show smooth surfaces, confirming the high crystallinity of the as-prepared perovskite crystals (Fig. S1†). Fig. 1b, c and Fig. S2† present the crystal structures of (R/S-MBA)4Bi2Cl10. Obviously, these two enantiomers are a mirror image of each other (Fig. 1b). With the introduction of large MBA+ cations, these two 0D perovskites are composed of isolated [Bi2Cl10]4− edge-sharing dimers, maintaining the electrical neutrality of the system. The –NH3+ groups of the chiral MBA+ cations around the [Bi2Cl10]4− building blocks interact with Cl− ligands by the N–H⋯Cl–Bi hydrogen bond to stabilize the structure (Fig. S3†), resulting in chirality transfer and the asymmetric tilt and distortion of BiCl6 octahedra. The inhomogeneous Bi–Cl bond lengths and Bi–Cl–Bi bond angles observed in those distorted octahedra are 2.515–3.012 Å and 96.48–97.06° for (R-MBA)4Bi2Cl10, and 2.513–3.011 Å and 96.12–96.92° for (S-MBA)4Bi2Cl10, respectively (Fig. 1e and f). It has been reported that the A-site cations have a significant effect on the structure, properties, and device performance.46 The subtle distortions from one structure to the next could be behind the observed differences in optical properties. To characterize the effects of A-site cations on the deformation of octahedra, we compared the metal–halide (Bi–Cl) bond lengths and halide–metal–halide (Cl–Bi–Cl) bond angles in the octahedra of 0D perovskite structures with different A-site cations, 2-picolylamine (AMP),35R-1-(4-fluoro)phenylethylamine (PEA),47 and R-MBA (MBA) in our system, as presented in Fig. 1d, e and Fig. S4.† Obviously, the average values of Bi–Cl bond lengths and Cl–Bi–Cl bond angles tend to be uniform in three octahedra, while the value distribution of MBA octahedra is more dispersed and more deviated from that of the perfect octahedron. Axial Cl–Bi–Cl angles follow the same distribution rule (Fig. S5†). All these indicate that the MBA-octahedra have the largest distortion level, which is more conducive to the enhancement of nonlinear optical effects. As expected, the perovskite with the MBA spacer in our work exhibits a higher band gap and NLO coefficient discussed in detail below (Fig. 1f). Additionally, we further calculated the degree of octahedral distortion which can be quantified using the following formulas:
1 stoichiometry were dissolved in aqueous HCl solution, and then the crystal precipitated with the decrease of temperature. To reveal the chiral crystal structure, SCXRD was performed, and the crystallographic data are listed in Tables S1–3.† The powder XRD patterns of (R/S-MBA)4Bi2Cl10 were consistent with the simulated ones and proved the high-phase purity, as presented in Fig. 1a. Both (R/S-MBA)4Bi2Cl10 crystallize in the Sohncke space group of monoclinic P21 with identical unit cell parameters, suggesting non-centrosymmetric and polar crystal structures. Scanning electron microscopy (SEM) images of the exfoliated crystal show smooth surfaces, confirming the high crystallinity of the as-prepared perovskite crystals (Fig. S1†). Fig. 1b, c and Fig. S2† present the crystal structures of (R/S-MBA)4Bi2Cl10. Obviously, these two enantiomers are a mirror image of each other (Fig. 1b). With the introduction of large MBA+ cations, these two 0D perovskites are composed of isolated [Bi2Cl10]4− edge-sharing dimers, maintaining the electrical neutrality of the system. The –NH3+ groups of the chiral MBA+ cations around the [Bi2Cl10]4− building blocks interact with Cl− ligands by the N–H⋯Cl–Bi hydrogen bond to stabilize the structure (Fig. S3†), resulting in chirality transfer and the asymmetric tilt and distortion of BiCl6 octahedra. The inhomogeneous Bi–Cl bond lengths and Bi–Cl–Bi bond angles observed in those distorted octahedra are 2.515–3.012 Å and 96.48–97.06° for (R-MBA)4Bi2Cl10, and 2.513–3.011 Å and 96.12–96.92° for (S-MBA)4Bi2Cl10, respectively (Fig. 1e and f). It has been reported that the A-site cations have a significant effect on the structure, properties, and device performance.46 The subtle distortions from one structure to the next could be behind the observed differences in optical properties. To characterize the effects of A-site cations on the deformation of octahedra, we compared the metal–halide (Bi–Cl) bond lengths and halide–metal–halide (Cl–Bi–Cl) bond angles in the octahedra of 0D perovskite structures with different A-site cations, 2-picolylamine (AMP),35R-1-(4-fluoro)phenylethylamine (PEA),47 and R-MBA (MBA) in our system, as presented in Fig. 1d, e and Fig. S4.† Obviously, the average values of Bi–Cl bond lengths and Cl–Bi–Cl bond angles tend to be uniform in three octahedra, while the value distribution of MBA octahedra is more dispersed and more deviated from that of the perfect octahedron. Axial Cl–Bi–Cl angles follow the same distribution rule (Fig. S5†). All these indicate that the MBA-octahedra have the largest distortion level, which is more conducive to the enhancement of nonlinear optical effects. As expected, the perovskite with the MBA spacer in our work exhibits a higher band gap and NLO coefficient discussed in detail below (Fig. 1f). Additionally, we further calculated the degree of octahedral distortion which can be quantified using the following formulas: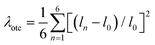 | (1) |
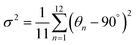 | (2) |
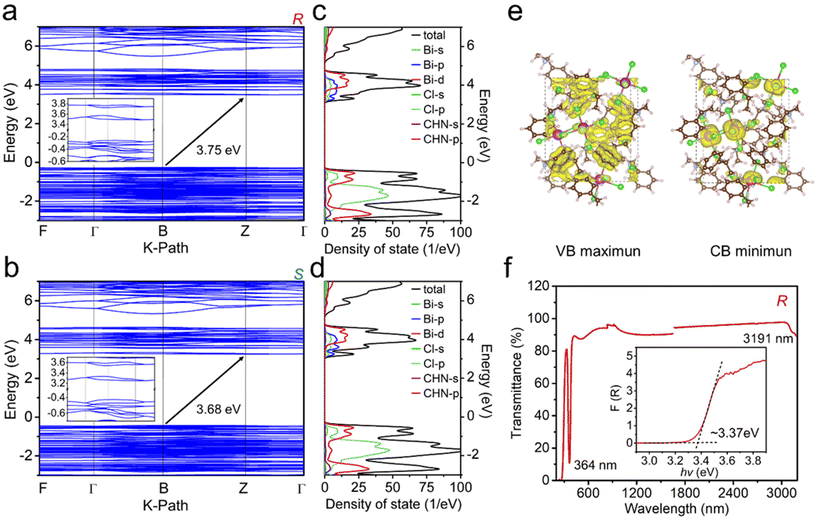
To further reveal the electronic properties of the (R/S-MBA)4Bi2Cl10 chiral perovskite, the band structures and partial densities of states (PDOS) have been calculated based on DFT. As shown in Fig. 2a and b, the valence band (VB) maximum is located at B points of the Brillouin zone, while the conduction band (CB) minimum is located at the Z points, indicating an indirect bandgap characteristic of both (R/S-MBA)4Bi2Cl10. The calculated bandgap energies of (R-MBA)4Bi2Cl10 and (S-MBA)4Bi2Cl10 are 3.75 eV and 3.68 eV, respectively, which are slightly higher than the experimentally measured value of 3.37 eV for both (R/S-MBA)4Bi2Cl10 based on the Tauc plot (Fig. 2f and Fig. S6†), which is probably due to the exclusion of the spin–orbit coupling effect in the self-consistent field (SCF) calculations.49 The PDOS around the Fermi levels in Fig. 2c and d reveals that the VB maximum is primarily composed of the CHN-p orbital, while the CB minimum is mainly contributed by the Bi-p and Cl-s orbitals. It means that both anionic [Bi2Cl10]4− groups and R/S-MBA organic cations have a significant influence on the band gap energy, as well as the optical properties of (R/S-MBA)4Bi2Cl10. Moreover, the isosurface plot of the wave functions of the VB maximum also shows that the charge density is mainly distributed on R/S-MBA organic cations, while the CB minimum is mainly distributed on [Bi2Cl10]4− groups (Fig. 2e and Fig. S7†). The UV-vis-NIR transmittance spectra of (R/S-MBA)4Bi2Cl10 show a very wide window with a high transparency range from 364 nm to 3191 nm, indicating that it could be effectively pumped and applied from the visible light to near-infrared region (Fig. 2f and Fig. S6†).
3.2. Fabrication and characterization of chiral perovskite single-crystalline microwire arrays
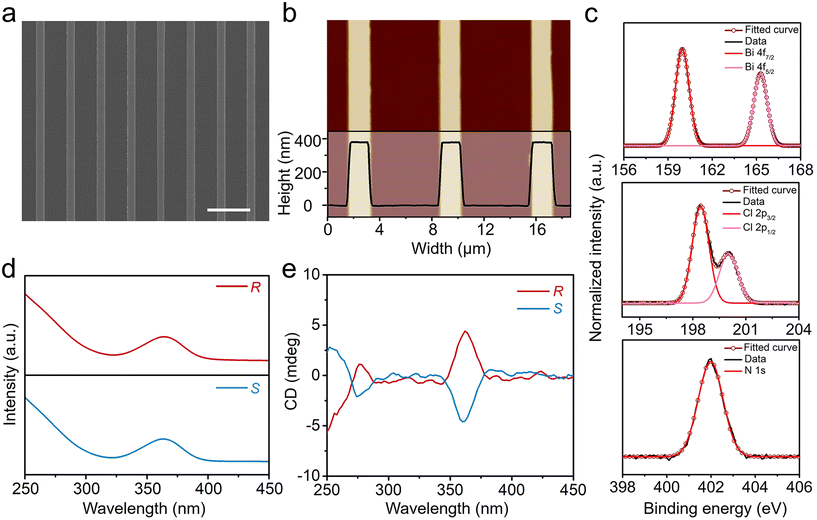
To achieve reliable processing technology to meet the large-scale integration of NLO devices, we employed a capillary-bridge confined technique to manipulate the nucleation and growth of perovskite crystals, patterning highly ordered assembly microwire arrays with high crystallinity (see the Experimental section and Fig. S8†). Briefly, by introducing the asymmetric-wettability micropillar templates with hydrophilic tops and hydrophobic sidewalls (Fig. S9†), the perovskite precursors will be confined between the hydrophilic pillar tops and the substrate to form a sandwiched assembly system; thus the nucleation site can be precisely controlled. Simultaneously, the asymmetric modification steers a directional dewetting process, determining the directional growth of the assembly of microwire arrays. As the solvent evaporated completely, the lead-free chiral perovskite microwire arrays of (R/S-MBA)4Bi2Cl10 with high crystallinity and a pure crystallographic orientation were fabricated.To study the morphology and surface roughness of the as-fabricated chiral perovskite NLO microwire arrays, SEM and atomic force microscopy (AFM) were performed. As shown in Fig. 3a and Fig. S10,† the SEM images present high-quality perovskite microwire arrays with a precise location, a strictly isometric arrangement, and homogeneous size over a large area. AFM images further illustrate the smooth surface and uniform size of microwires with a height of about 370 nm, a width of about 1.9 μm, and an adjacent distance of about 5.1 μm (Fig. 3b and Fig. S11†). The elemental components and distribution of the chiral perovskite microwires were analyzed by X-ray photoelectron spectroscopy (XPS) and energy dispersive spectroscopy (EDS). The XPS results exhibit two characteristic peaks in the Bi 4f region with binding energies of 160.0 eV for 4f7/2 and 165.3 eV for 4f5/2, two characteristic peaks in the Cl 2p region with binding energies of 198.4 eV for 2p3/2 and 200.0 eV for 2p1/2, and one characteristic peak in the N 1s region with a binding energy of 402.0 eV, revealing the stable chemical state of those elements within microwires (Fig. 3c and Fig. S12†). EDS elemental mappings in Fig. S13† further confirm the presence of Bi, Cl, C, and N elements, which are uniformly distributed in those microwires. The EDS result shows that the atomic ratio of Bi/Cl is 1/4.97, which is consistent with the stoichiometry of (R-MBA)4Bi2Cl10 (Bi/Cl, 1/5). We also studied the optical and chiroptical properties of the chiral perovskite microwire arrays. As shown in Fig. 3d, the UV-vis absorption of both (R/S-MBA)4Bi2Cl10 microwire arrays shows an absorption peak at 364 nm. The CD spectrum of the (R/S-MBA)4Bi2Cl10 microwire arrays in Fig. 3e exhibits obvious CD signals with bisignated features different from those of the corresponding chiral R/S-MBA precursors,50 which confirms the intrinsic chirality and non-centrosymmetric polar crystal structures of the (R/S-MBA)4Bi2Cl10 microwire arrays.
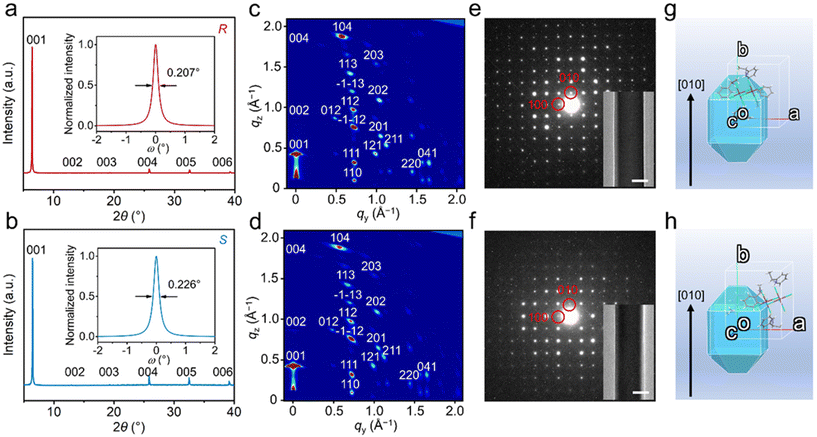
As the NLO response depends on the anisotropy structure and crystallinity of the perovskite crystals,51 we further carried out XRD, GIWAXS, TEM, and SAED measurements to clarify the crystallinity and crystallographic orientation of (R/S-MBA)4Bi2Cl10 microwire arrays. The XRD patterns of the microwire arrays are presented in Fig. 4a, b and Fig. S14†; they show periodic sharp diffraction peaks that can be assigned to the (00l) planes, reflecting that the (001) plane is parallel to the substrate. As shown in the insets, the rocking curves of (001) peaks show a sharp arc-like feature with the full width at half maximum (FWHM) as low as 0.2°, indicating the high crystallinity of the microwire arrays. The GIWAXS patterns in Fig. 4c and d show sharp discrete diffraction spots, further confirming the high-crystallinity (001)-oriented (R/S-MBA)4Bi2Cl10 microwires along the out-of-plane direction. TEM images illustrate that the microwires are well-shaped with sharp edges and smooth surfaces, and the corresponding SAED patterns exhibit sharp diffraction spots, verifying the single crystallinity and the preferential growth along the (010) direction of those chiral perovskite microwires (Fig. 4e and f). The predicted (R/S-MBA)4Bi2Cl10 crystal morphology based on Bravais–Friedel–Donnay–Harker (BFDH) calculations is presented in Fig. 4g and h, revealing the dominant growth direction along the [010] zone axis, which is in line with the SAED results.
3.3. The second-order nonlinear optical properties
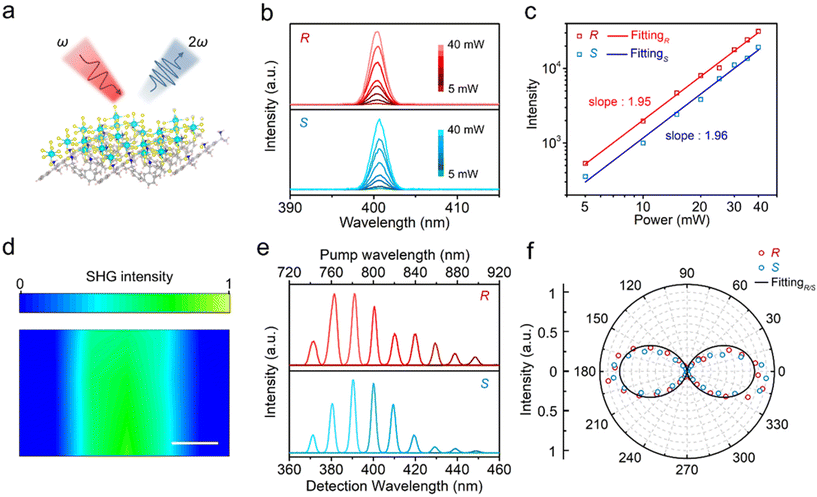
To assess the nonlinear optical properties of the chiral perovskites featuring a non-centrosymmetric structure, we preliminarily evaluated the SHG signals of polycrystalline powder samples using the Kurtz–Perry method with a pump wavelength of 2090 nm, and the sieved AgGaS2 crystals serve as references. As shown in Fig. S15,† (R/S-MBA)4Bi2Cl10 polycrystalline samples exhibit remarkable SHG responses, which are estimated to be 0.04 × AgGaS2 with the particle size ranging from 150 to 200 μm. Since the intensity of the SHG response is proportional to the square of the second-order NLO coefficient, it can be estimated that the effective NLO coefficient of the title compound is approximately 2.72 pm V−1 under a 2090 nm laser. This value is larger than those of most of the similar organic–inorganic hybrid perovskites reported recently, demonstrating its potential applications in the field of infrared nonlinear optics (Table S4†).27,28,31 Then we studied the second-order NLO properties of the as-fabricated chiral perovskite single-crystalline microwire arrays in detail utilizing a home-built femtosecond laser setup (Fig. S16†). Fig. 5a illustrates a diagram of the SHG process in those perovskite microwires. As shown in Fig. 5b, under laser irradiation with a wavelength of 800 nm, a clear set of response signals with a central wavelength of half the pump wavelength can be observed, corresponding to the expected second-order nonlinear process. The power-dependent SHG signals in Fig. 5b can be well fitted linearly on a logarithmic scale with slopes of 1.95 for (R-MBA)4Bi2Cl10 and 1.96 for (S-MBA)4Bi2Cl10 (Fig. 5c), displaying a quadratic relationship between the SHG intensity and the incident laser power, which confirms that the strong visible signals are generated from the second-order NLO process. Fig. 5d depicts the SHG intensity mapping image of an individual (R-MBA)4Bi2Cl10 microwire, which clearly demonstrates the high quality and homogeneity of the as-fabricated single-crystalline microwire arrays. To evaluate the stability of the as-prepared microwire arrays, SHG spectra of the (R-MBA)4Bi2Cl10 microwire were collected every minute with laser on. No obvious degradation was observed after continuous radiation, indicating the high stability of the perovskite microwire arrays (Fig. S17†). To verify the high-efficiency SHG based on the microwire arrays, we also performed power-dependent SHG measurements on their polycrystalline film counterpart. As expected, the (R-MBA)4Bi2Cl10 film shows a weaker SHG response compared to the single-crystalline microwire under the same excitation conditions (Fig. S18a–c†). The formula for SHG conversion efficiency η2ω is shown below:| η2ω = P2ω/Pω2 | (3) |
The wavelength-dependent SHG intensity of (R/S-MBA)4Bi2Cl10 microwires measured in the tuning pump wavelength range from 740 to 900 nm with a step of 20 nm is presented in Fig. 5e, showing the strong SHG signals at the second harmonic wavelength from 370 to 450 nm. Both (R/S-MBA)4Bi2Cl10 microwires show no difference in the SHG signal changes at different second-harmonic wavelengths and exhibit the highest SHG intensity at 390 nm, which is mainly due to the strong self-absorption and phase mismatch.25,31 Since the inherent structural asymmetry usually implies an anisotropic SHG response, we further investigate the linear polarization-resolved SHG intensity of (R/S-MBA)4Bi2Cl10 microwires. The polarization direction of the incident laser can be changed with the azimuthal angle from 0° to 360° by tuning the half-wave plate, where 0° corresponds to that the polarization direction of the incident laser is parallel to the long axis microwire, the crystallographic b-axis. Fig. 5f presents the polarization-dependent SHG intensity of (R/S-MBA)4Bi2Cl10 microwires, which was fitted with a cos4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ function, showing distinct anisotropy characteristics. The SHG signals exhibit a typical twofold pattern, with maximum intensity observed in the parallel direction (0°) and minimum intensity observed in the vertical direction (90°). The polarization ratio is calculated using the following formula:
θ function, showing distinct anisotropy characteristics. The SHG signals exhibit a typical twofold pattern, with maximum intensity observed in the parallel direction (0°) and minimum intensity observed in the vertical direction (90°). The polarization ratio is calculated using the following formula:
| ρ = (Imax − Imin)/(Imax + Imin) | (4) |
4. Conclusions
In summary, we synthesized lead-free chiral 0D perovskites (R/S-MBA)4Bi2Cl10 with high distortion levels and successfully constructed high-quality single-crystalline microwire arrays by employing the capillary-bridge confined techniques. The as-prepared chiral (R/S-MBA)4Bi2Cl10 single-crystalline microwire arrays feature an intrinsic non-centrosymmetric polar crystal structure and exhibit a wide transparent region, excellent SHG conversion efficiency and high polarization ratio of up to 0.992. The simultaneous realization of large nonlinear anisotropy and high-efficiency SHG responses with a broadband transparency window in (R/S-MBA)4Bi2Cl10 single-crystalline microwire arrays would pave the way toward the engineering and development of advanced technological applications in nanophononics and optoelectronics.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Ji Hua Laboratory Science Program (grant no. X190251UZ190), the National Natural Science Foundation of China (22205077, 52173190, and 21988102), the Ministry of Science and Technology (MOST) of China (2018YFA0208502, and 2018YFA0704803), the project funded by the China Postdoctoral Science Foundation (2021M701401), and the Youth Innovation Promotion Association CAS (2018034).References
- R. W. Boyd, Nonlinear optics, Academic Press, New York, 2007 Search PubMed.
- A. Autere, H. Jussila, Y. Y. Dai, Y. D. Wang, H. Lipsanen and Z. P. Sun, Nonlinear optics with 2D layered materials, Adv. Mater., 2018, 30, 1705963 CrossRef PubMed.
- Y. Zhang, F. Wang, X. Feng, Z. D. Sun, J. W. Su, M. Zhao, S. Z. Wang, X. Z. Hu and T. Y. Zhai, Inversion symmetry broken 2D SnP2S6 with strong nonlinear optical response, Nano Res., 2022, 15, 2391–2398 CrossRef CAS.
- T. Schmitt, S. Bourelle, N. Tye, G. Soavi, A. D. Bond, S. Feldmann, B. Traore, C. Katan, J. Even, S. E. Dutton and F. Deschler, Control of crystal symmetry breaking with halogen-substituted benzylammonium in layered hybrid metal-halide perovskites, J. Am. Chem. Soc., 2020, 142, 5060–5067 CrossRef CAS PubMed.
- W. Q. Liao, Y. Zhang, C. L. Hu, J. G. Mao, H. Y. Ye, P. F. Li, S. P. D. Huang and R. G. Xiong, A lead-halide perovskite molecular ferroelectric semiconductor, Nat. Commun., 2015, 6, 7338 CrossRef PubMed.
- P. A. Franken, A. E. Hill, C. W. Peters and G. Weinreich, Generation of optical harmonics, Phys. Rev. Lett., 1961, 7, 118–119 CrossRef.
- L. Menne, M. M. Furchi, S. Wachter, M. Paur, D. K. Polyushkin and T. Mueller, Optical imaging of strain in two-dimensional crystals, Nat. Commun., 2018, 9, 516 CrossRef PubMed.
- M. Aoyama, T. Harimoto, J. Ma, Y. Akahane and K. Yamakawa, Second-harmonic generation of ultra-high intensity femtosecond pulses with a KDP crystal, Opt. Express, 2001, 9, 579–585 CrossRef CAS PubMed.
- D. F. Eaton, Nonlinear optical materials, Science, 1991, 253, 281–287 CrossRef CAS PubMed.
- D. N. Nikogosyan, Nonlinear optical crystals: a complete survey, Springer Science+Business Media, Inc., New York, 2005 Search PubMed.
- Y. Lin, Y. J. Fang, J. J. Zhao, Y. C. Shao, S. J. Stuard, M. M. Nahid, H. Ade, Q. Wang, J. E. Shield, N. H. Zhou, A. M. Moran and J. S. Huang, Unveiling the operation mechanism of layered perovskite solar cells, Nat. Commun., 2019, 10, 1008 CrossRef PubMed.
- C. C. Stoumpos, D. H. Cao, D. J. Clark, J. Young, J. M. Rondinelli, J. I. Jang, J. T. Hupp and M. G. Kanatzidis, Ruddlesden–popper hybrid lead iodide perovskite 2D homologous semiconductors, Chem. Mater., 2016, 28, 2852–2867 CrossRef CAS.
- P. J. Huang, K. Taniguchi and H. Miyasaka, Bulk photovoltaic effect in a pair of chiral-polar layered perovskite-type lead iodides altered by chirality of organic cations, J. Am. Chem. Soc., 2019, 141, 14520–14523 CrossRef CAS PubMed.
- N. N. Wang, L. Cheng, R. Ge, S. T. Zhang, Y. F. Miao, W. Zou, C. Yi, Y. Sun, Y. Cao, R. Yang, Y. Q. Wei, Q. Guo, Y. Ke, M. T. Yu, Y. Z. Jin, Y. Liu, Q. Q. Ding, D. W. Di, L. Yang, G. C. Xing, H. Tian, C. H. Jin, F. Gao, R. H. Friend, J. P. Wang and W. Huang, Perovskite light-emitting diodes based on solution-processed self-organized multiple quantum wells, Nat. Photonics, 2016, 10, 699–704 CrossRef CAS.
- C. Chen, L. Gao, W. R. Gao, C. Ge, X. Y. Du, Z. Li, Y. Yang, G. D. Niu and J. Tang, Circularly polarized light detection using chiral hybrid perovskite, Nat. Commun., 2019, 10, 1927 CrossRef PubMed.
- Y. C. Liu, Y. X. Zhang, Z. Yang, H. C. Ye, J. S. Feng, Z. Xu, X. Zhang, R. Munir, J. Liu, P. Zuo, Q. X. Li, M. X. Hu, L. N. Meng, K. Wang, D. M. Smilgies, G. T. Zhao, H. Xu, Z. P. Yang, A. Amassian, J. W. Li, K. Zhao and S. Z. Liu, Multi-inch single-crystalline perovskite membrane for high-detectivity flexible photosensors, Nat. Commun., 2018, 9, 5302 CrossRef CAS PubMed.
- J. C. Blancon, H. Tsai, W. Nie, C. C. Stoumpos, L. Pedesseau, C. Katan, M. Kepenekian, C. M. M. Soe, K. Appavoo, M. Y. Sfeir, S. Tretiak, P. M. Ajayan, M. G. Kanatzidis, J. Even, J. J. Crochet and A. D. Mohite, Extremely efficient internal exciton dissociation through edge states in layered 2D perovskites, Science, 2017, 355, 1288–1292 CrossRef CAS PubMed.
- D. D. Nuzzo, L. S. Cui, J. L. Greenfield, B. D. Zhao, R. H. Friend and S. C. J. Meskers, Circularly polarized photoluminescence from chiral perovskite thin films at room temperature, ACS Nano, 2020, 14, 7610–7616 CrossRef PubMed.
- W. Weng, Q. Chen, Y. Fan, Z. Li, H. Huang, H. Wu, C. Ji and W. Lin, A lead-free halide hybrid perovskite (TMHD)BiCl5 for ultraviolet photodetection, Inorg. Chem. Front., 2022, 9, 4876–4880 RSC.
- J. L. Xu, X. Y. Li, J. B. Xiong, C. Q. Yuan, S. Semin, T. Rasing and X. H. Bu, Halide perovskites for nonlinear optics, Adv. Mater., 2020, 32, 1806736 CrossRef CAS PubMed.
- Y. X. Zhou, Y. Y. Huang, X. L. Xu, Z. Y. Fan, J. B. Khurgin and Q. H. Xiong, Nonlinear optical properties of halide perovskites and their applications, Appl. Phys. Rev., 2020, 7, 041313 CAS.
- M. K. Jana, R. Song, H. Liu, D. R. Khanal, S. M. Janke, R. Zhao, C. Liu, Z. V. Vardeny, V. Blum and D. B. Mitzi, Organic-to-inorganic structural chirality transfer in a 2D hybrid perovskite and impact on Rashba-Dresselhaus spin-orbit coupling, Nat. Commun., 2020, 11, 4699 CrossRef CAS PubMed.
- Y. Y. Dang, X. L. Liu, B. Q. Cao and X. T. Tao, Chiral halide perovskite crystals for optoelectronic applications, Matter, 2021, 4, 794–820 CrossRef CAS.
- G. K. Long, R. Sabatini, M. I. Saidaminov, G. Lakhwani, A. Rasmita, X. G. Liu, E. H. Sargent and W. Gao, Chiral-perovskite optoelectronics, Nat. Rev. Mater., 2020, 5, 423–439 CrossRef.
- G. Wang, S. L. Mei, J. F. Liao, W. Wang, Y. X. Tang, Q. Zhang, Z. K. Tang, B. Wu and G. C. Xing, Advances of nonlinear photonics in low–dimensional halide perovskites, Small, 2021, 17, 2100809 CrossRef CAS PubMed.
- F. Ge, B. H. Li, P. X. Cheng, G. Li, Z. F. Ren, J. L. Xu and X. H. Bu, Chiral hybrid copper(I) halides for high efficiency second harmonic generation with a broadband transparency window, Angew. Chem., Int. Ed., 2022, 61, e202115024 CAS.
- Y. K. Zhou, W. N. Li, X. M. Chen, X. Z. Li, X. J. Wang, B. F. Bai, Y. Chen and H. H. Fang, Efficient second-order nonlinear response and upconversion emission from wide-bandgap quasi-1D lead bromide perovskite, J. Mater. Chem. C, 2022, 10, 15424–15430 RSC.
- Z. H. Guo, J. Z. Li, J. C. Liang, C. S. Wang, X. Zhu and T. C. He, Regulating optical activity and anisotropic second-harmonic generation in zero-dimensional hybrid copper halides, Nano Lett., 2022, 22, 846–852 CrossRef CAS PubMed.
- L. Yao, Z. X. S. Zeng, C. K. Cai, P. Xu, H. G. Gu, L. Gao, J. B. Han, X. W. Zhang, X. Wang, X. Wang, A. L. Pan, J. Wang, W. X. Liang, S. Y. Liu, C. Chen and J. Tang, Strong second- and third-harmonic generation in 1D chiral hybrid bismuth halides, J. Am. Chem. Soc., 2021, 143, 16095–16104 CrossRef CAS PubMed.
- D. Y. Fu, J. L. Xin, Y. Y. He, S. C. Wu, X. Y. Zhang, X. M. Zhang and J. H. Luo, Chirality-dependent second-order nonlinear optical effect in 1D organic–inorganic hybrid perovskite bulk single crystal, Angew. Chem., Int. Ed., 2021, 60, 20021–20026 CrossRef CAS PubMed.
- C. Q. Yuan, X. Y. Li, S. Semin, Y. Q. Feng, T. Rasing and J. L. Xu, Chiral lead halide perovskite nanowires for second-order nonlinear optics, Nano Lett., 2018, 18, 5411–5417 CrossRef CAS PubMed.
- Y. S. Zheng, J. L. Xu and X. H. Bu, 1D chiral lead halide perovskites with superior second–order optical, Adv. Opt. Mater., 2022, 10, 2101545 CrossRef CAS.
- W. C. Zhang, K. W. Tao, C. M. Ji, Z. H. Sun, S. G. Han, J. Zhang, Z. Y. Wu and J. H. Luo, (C6H13N)2BiI5: a one-dimensional lead-free perovskite-derivative photoconductive light absorber, Inorg. Chem., 2018, 57, 4239–4243 CrossRef CAS PubMed.
- M. Lyu, J. H. Yun, M. L. Cai, Y. L. Jiao, P. V. Bernhardt, M. Zhang, Q. Wang, A. J. Du, H. X. Wang, G. Liu and L. Z. Wang, Organic–inorganic bismuth(III)-based material: a lead-free, air-stable and solution-processable light-absorber beyond organolead perovskites, Nano Res., 2016, 9, 692–702 CrossRef CAS.
- D. F. Sun, D. L. Wang, H. Z. Chen, R. X. Hou, Y. Y. Dang, K. Wu, J. Y. Wang and C. Y. Shen, New low-dimensional lead-free perovskite (2-AMP)2BiX7.H2O (X = Cl, Br) crystals: synthesis, stability, and nonlinear optical properties, Inorg. Chem., 2022, 61, 15247–15255 CrossRef CAS PubMed.
- A. A. Babaryk, Y. Pérez, M. Martínez, M. E. G. Mosquera, M. H. Zehender, S. A. Svatek, E. Antolín and P. Horcajada, Reversible dehydration–hydration process in stable bismuth-based hybrid perovskites, J. Mater. Chem. C, 2021, 9, 11358–11367 RSC.
- H. He, X. Q. Zhang, X. Yan, L. L. Huang, C. L. Gu, M. l. Hu, X. Zhang, X. M. Ren and C. Y. Wang, Broadband second harmonic generation in GaAs nanowires by femtosecond laser sources, Appl. Phys. Lett., 2013, 103, 143110 CrossRef.
- X. Y. Lu, G. Moille, A. Rao, D. A. Westly and K. Srinivasan, Efficient photoinduced second-harmonic generation in silicon nitride photonics, Nat. Photonics, 2021, 15, 131–136 CrossRef CAS.
- J. Shi, P. Yu, F. C. Liu, P. He, R. Wang, L. Qin, J. B. Zhou, X. Li, J. D. Zhou, X. Y. Sui, S. Zhang, Y. F. Zhang, Q. Zhang, T. C. Sum, X. H. Qiu, Z. Liu and X. F. Liu, 3R MoS2 with broken inversion symmetry: a promising ultrathin nonlinear optical device, Adv. Mater., 2017, 29, 1701486 CrossRef PubMed.
- C. Lee, E. Z. Xu, Y. W. Liu, A. Teitelboim, K. Y. Yao, A. F. Bravo, A. M. Kotulska, S. H. Nam, Y. D. Suh, A. Bednarkiewicz, B. E. Cohen, E. M. Chan and P. J. Schuck, Giant nonlinear optical responses from photon-avalanching nanoparticles, Nature, 2021, 589, 230–237 CrossRef CAS PubMed.
- S. Klimmer, O. Ghaebi, Z. Y. Gan, A. George, A. Turchanin, G. Cerullo and G. Soavi, All-optical polarization and amplitude modulation of second-harmonic generation in atomically thin semiconductors, Nat. Photonics, 2021, 15, 837–842 CrossRef CAS.
- K. Koshelev, S. Kruk, E. M. Gaykazyan, J. H. Choi, A. Bogdanov, H. G. Park and Y. Kivshar, Subwavelength dielectric resonators for nonlinear nanophotonics, Science, 2020, 367, 288–292 CrossRef CAS PubMed.
- J. J. Zhao, Y. J. Zhao, Y. W. Guo, X. Q. Zhan, J. G. Feng, Y. Geng, M. Yuan, X. Fan, H. F. Gao, L. Jiang, Y. L. Yan and Y. C. Wu, Layered metal–halide perovskite single–crystalline microwire arrays for anisotropic nonlinear optics, Adv. Funct. Mater., 2021, 31, 2105855 CrossRef CAS.
- H. Zhou, X. X. Wang, X. J. Zhuang and A. L. Pan, Second harmonic generation and waveguide properties in perovskite Na0.5Bi0.5TiO3 nanowires, Opt. Lett., 2016, 41, 3803–3805 CrossRef CAS PubMed.
- W. J. Wei, X. X. Jiang, L. Y. Dong, W. W. Liu, X. B. Han, Y. Qin, K. Li, W. Li, Z. S. Lin, X. H. Bu and P. X. Lu, Regulating second-harmonic generation by van der Waals interactions in two-dimensional lead halide perovskite nanosheets, J. Am. Chem. Soc., 2019, 141, 9134–9139 CrossRef CAS PubMed.
- X. T. Li, J. M. Hoffman and M. G. Kanatzidis, The 2D halide perovskite rulebook: how the spacer influences everything from the structure to optoelectronic device efficiency, Chem. Rev., 2021, 121, 2230–2291 CrossRef CAS PubMed.
- N. Dehnhardt, M. Axt, J. Zimmermann, M. Yang, G. Mette and J. Heine, Band gap-tunable, chiral hybrid metal halides displaying second-harmonic generation, Chem. Mater., 2020, 32, 4801–4807 CrossRef CAS.
- D. Chen, S. Q. Hao, L. B. Fan, Y. W. Guo, J. Y. Yao, C. Wolverton, M. G. Kanatzidis, J. Zhao and Q. L. Liu, Broad photoluminescence and second-harmonic generation in the noncentrosymmetric organic–inorganic hybrid halide (C6H5(CH2)4NH3)4MX7·H2O (M = Bi, In, X = Br or I), Chem. Mater., 2021, 33, 8106–8111 CrossRef CAS.
- T. H. Moon, S. J. Oh and K. M. Ok, [((R)-C8H12N)4][Bi2Br10] and [((S)-C8H12N)4][Bi2Br10]: chiral hybrid bismuth bromides templated by chiral organic cations, ACS Omega, 2018, 3, 17895–17903 CrossRef CAS PubMed.
- G. K. Long, C. Y. Jiang, R. Sabatini, Z. Y. Yang, M. Y. Wei, L. N. Quan, Q. M. Liang, A. Rasmita, M. Askerka, G. Walters, X. W. Gong, J. Xing, X. L. Wen, R. Q. Bermudez, H. F. Yuan, G. C. Xing, X. R. Wang, D. D. Song, O. Voznyy, M. T. Zhang, S. Hoogland, W. B. Gao, Q. H. Xiong and E. H. Sargent, Spin control in reduced-dimensional chiral perovskites, Nat. Photonics, 2018, 12, 528–533 CrossRef CAS.
- X. Y. Xu, C. Trovatello, F. Mooshammer, Y. M. Shao, S. Zhang, K. Y. Yao, D. N. Basov, G. Cerullo and P. J. Schuck, Towards compact phase-matched and waveguided nonlinear optics in atomically layered semiconductors, Nat. Photonics, 2022, 16, 698–706 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Details of crystallographic data, spectral data, SHG data, etc. CCDC 2233314 and 2233315. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d2qi02783f |
| This journal is © the Partner Organisations 2023 |