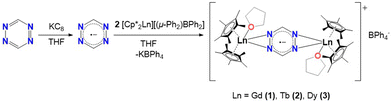
New members of radical bridged Ln₂ metallocene single-molecule magnets based on the unsubstituted 1,2,4,5-tetrazine ligand

Abstract

Magnetic coupling plays a critical role in the overall magnetic behaviour of a single-molecule magnet (SMM). Through a careful design strategy that employs the highly delocalized 1,2,4,5-tetrazinyl (tz) radical anion with lanthanide metallocenes, a new family of dinuclear complexes was isolated; [(Cp*₂Ln^III)₂(tz˙⁻)(THF)₂](BPh₄), (Ln = Gd (1), Tb (2), Dy (3); THF = tetrahydrofuran; Cp* = pentamethylcyclopentadienyl). The strong magnetic exchange coupling of J_Gd–rad = −7.2 cm⁻¹ observed in 1, was probed through SQUID magnetometry as well as computational studies. This, combined with the highly anisotropic Tb^III and Dy^III ions in 2 and 3, respectively, leads to zero-field SMM behaviour and slow relaxation of the magnetization through thermally activated processes. These dinuclear complexes serve as ideal models for understanding the magnetic interactions between 4f elements.

---

Introduction

For more than thirty years, single-molecule magnets (SMMs) have been anticipated to be viable candidates for next-generation molecular devices for information storage in spin-based electronics.^1–3 Although the field of SMMs started from the study of 3d-based molecular systems,⁴ it flourished upon switching towards 4f-based molecular systems due to the bistability of their magnetic ground state in addition to their large inherent anisotropy.^5,6 Lanthanide-based SMMs have been known to yield longer relaxation times of their magnetization, stemming from considerable thermal barriers to spin reversal (U_eff) and magnetic remanence at higher temperatures (T_B).^7–9 Over the past decade, the targeted design of Ln systems for achieving superior SMM behaviour, such as increasing the axiality of the crystal field (CF) around the metal centres, has enabled critical scientific breakthroughs.¹⁰ In particular, it is well established that increasing the axiality of the crystal field in oblate Tb^III and Dy^III ions can lead to larger thermal barriers.^5,6,11 While these features, such as high blocking temperatures, could lead to spin-based information storage, research has mostly focused on mononuclear SMMs.^9,12 Consequently, the switch towards the synthesis of polynuclear Ln-complexes with enhanced magnetic properties requires careful selection of multidentate bridging ligands.

In addition to the aforementioned design principle, through-barrier relaxation of the magnetization needs to be minimized (such as quantum tunnelling of the magnetization – QTM, Raman and direct mechanisms).³ Lanthanide SMMs are often plagued by such through-barrier relaxation. Recent studies show that the strong magnetic coupling between the Ln centres can alleviate these issues leading to high-performing SMMs. The importance of magnetic coupling in the form of a metal–metal bond was recently reported by Gould et al. in (Cp^iPr5)₂Ln₂I₃ (Ln = Gd, Tb, Dy; Cp^iPr5 = pentaisopropylcyclopentadienyl), which exhibited an enormous coercive field (>14 T) at temperatures as high as 60 K.¹³ However, rationally targeting metal–metal bonded systems is not easy to control. A promising alternative to this relies on the exploitation of open shell ligands, which benefits from the magnetic Ln–rad coupling. Given that the latter is strong enough, the successful suppression of QTM can be achieved. Indeed, this approach has led to increased magnetic performance in complexes exhibiting strong Ln–radical coupling, which have shown high blocking temperatures of the magnetization (up to 20 K) and significant magnetic hardness (H_c = 7.9 T).¹⁴ Strong exchange coupling between the diffuse spin of the radicals and the lanthanide centres gives rise to a high angular momentum ground state by minimizing single-ion effects (i.e., QTM). To this day, several attempts in this direction have been made,^15–18 with the N₂˙³⁻-based family having the best magnetic performance for a radical bridged system, yet reported.^14,19 With that said, the isolation of N₂˙³⁻ radical bridged complexes is a synthetic challenge as it cannot, rationally, be incorporated into complexes, and it offers no room for structural modification.

Recently, we demonstrated that the incorporation of the 1,2,4,5-tetrazine radical anion (tz˙⁻) into tetranuclear “Ln₄” metallocenes ([(Cp*₂Ln)₄(tz˙⁻)₄]·3(C₆H₆), where Ln = Dy and Gd; Cp* = pentamethylcyclopentadienyl), can lead to strong magnetic coupling and significant magnetic hardness (H_c = 3 T).²⁰ Apart from the synthetic advances over the N₂˙³⁻ radical bridge, the very low-lying π* LUMO of the tz ring can easily undergo one e⁻ reduction, forming the tz˙⁻ radical anion.²¹ The diffuse nature of the spin orbitals of tz˙⁻-based radicals are ideally suited to penetrate the shielded 4f orbitals, promoting strong coupling.²²

As such, we aimed to isolate a dinuclear building block to understand the role of the bridging ligand in the overall magnetic coupling in Ln systems. With these in mind, our efforts involve the use of the tz˙⁻ to connect two [Cp*₂Ln^III]⁺ moieties, which are characterized by significant magnetic axiality. Herein, we report the employment of the unsubstituted tz˙⁻ for the first time in dinuclear lanthanide metallocene complexes, yielding: [(Cp*₂Ln^III)₂(tz˙⁻)(THF)₂](BPh₄), (Ln = Gd (1), Tb (2), Dy (3); THF = tetrahydrofuran). Strong antiferromagnetic coupling between the tz˙⁻ and the Ln^III centres is observed for all three complexes, yielding zero-field SMM behaviour with slow relaxation of the magnetization and magnetic hysteresis for 2 and 3. Based on ab initio calculations, the strong antiferromagnetic Ln–rad coupling is probed, verifying that their magnetic state can be interpreted as a giant-spin where the relaxation of the magnetization is related to changes in the magnetic state of the overall exchange-coupled system.

Results and discussion

Synthetic procedure and structural description

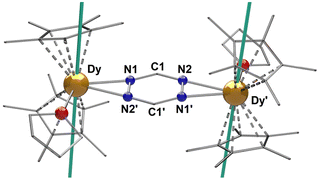
The first step, in the synthesis of 1–3, involves the equimolar reduction of the tz ligand with potassium graphite (KC₈) in THF (Scheme 1). The dark grey coloured mixture is slowly added to a solution of two equivalents of [Cp*₂Ln^III][(μ-Ph₂)BPh₂] (where Ln = Gd (1), Tb (2), Dy (3)) in THF. The resulting dark red solution was stirred overnight, filtered and placed in an Et₂O bath. After two days, dark red crystals of [(Cp*₂Ln^III)₂(tz˙⁻)(THF)₂](BPh₄), (Ln = Gd (1), Tb (2), Dy (3)) were obtained (Fig. S1†).

Scheme 1 Synthesis of the radical-bridged dinuclear compounds (1–3).

Single-crystal X-ray diffraction (SCXRD) analysis reveals that 1–3 crystallize in the monoclinic I2/a space group as centrosymmetric dinuclear complexes, with one crystallographically independent Ln^III center. Selected bond distances and angles along with X-ray data of all complexes are summarized in Tables S1 and S2.† The three cationic complexes are isomorphous (Fig. S2†) and therefore, only 3 is presented in Fig. 1. The complexes consist of two [Cp*₂Ln^III]⁺ moieties, bridged by a μ-tz˙⁻ ligand. The coordination sphere of each Ln^III centre is completed by one THF molecule (av. Ln–O_THF: 2.389(2) Å). To stabilize the cationic complex, one BPh₄⁻ is found in the crystal lattice. The average Ln–C_Cp* bond distances are 2.707(1), 2.687(2) and 2.678(1) Å for complexes 1–3, respectively, while the Cp*_cent–Ln–Cp*_cent angles are 136.3(2)°, 136.4(2)° and 136.6(2)°. These bond distances and angles highlight the fact that the axiality imposed by the Cp* ligands is increasing along the lanthanide series, which is a consequence of the effect of the lanthanide contraction. These values are similar to those reported for other radical bridged SMMs containing [Cp*₂Ln]⁺ moieties, which usually display high single-ion anisotropy.^18,23,24 The average Ln–Cp*_cent distances (2.427(5), 2.405(5) and 2.395(5) Å for 1–3, respectively) and Ln–N_tz bond distances (2.485(3), 2.469(2) and 2.460(2) Å for 1–3, respectively) are close to the respective distances for the reported “Ln₄” complexes (av. Ln–Cp*_cent: 2.403(1) Å and av. Ln–N_tz: 2.601(4) Å).²⁰ These Ln–N_tz bond distances are also similar to those observed for bipyrimidyl radical-bridged complexes (2.424(6)–2.440(6) Å),^18,25 but, as expected, they are larger upon comparison to the N₂˙³⁻ systems (2.234(1) Å).^14,19 The reduction of the tz ligand is confirmed through charge balance considerations, as well as the elongation of the N–N bonds of the tetrazine ring which is significant when compared to the free ligand.²⁶ The average N1–N2′ bond distance in 1–3 range from 1.391(3) to 1.394(3) Å. Such N–N bond elongations have been previously reported for tz˙⁻-based ligands.^20,27

Fig. 1 Molecular structure of 3. Partial labelling and omission of the BPh₄⁻ moiety and H-atoms have been employed for clarity. The solid teal lines represent the orientation of the principal magnetic axes of the ground Kramers doublet. Colour code: C: light grey; N: blue; O: red; Dy: orange.

Inspection of the packing arrangement of all three compounds reveals that these dimers are in relatively close proximity (Fig. S3†). A thorough study of the supramolecular organization of the Ln₂ units via Hirshfeld surface analysis²⁸ is given in the ESI (Fig. S3 and S4†). The absence of strong hydrogen bonding donors or acceptors in both the main residue and solvent area of 1, 2 and 3 leads mostly to close packing interactions such as C⋯H/H⋯C and H⋯H interactions with total percentages of 12% and 88%, respectively, as revealed by the 2D fingerprint plots of all interatomic interactions (Fig. S4†). Notably, the average shortest intermolecular Ln⋯Ln distance is 9.505(6) Å, while the respective average intramolecular distance is 7.099(5) Å (Fig. S5†).

Magnetic properties

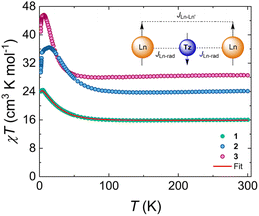
To probe the magnetic behaviour of 1–3, direct current (dc) and alternating current (ac) magnetic susceptibility studies were undertaken. The dc magnetic susceptibilities of all complexes were measured between 300 and 1.8 K at 1000 Oe (Fig. 2). At room temperature, the χT products are 16.11 cm³ K mol⁻¹, 23.96 cm³ K mol⁻¹ and 28.58 cm³ K mol⁻¹ for 1–3, respectively. These are consistent with the theoretical values of 16.13 cm³ K mol⁻¹, 24.01 cm³ K mol⁻¹ and 28.71 cm³ K mol⁻¹ for 1–3, respectively, for two Ln^III ions (Gd: S = 7/2, ⁸S_7/2, g = 2, C = 7.88 cm³ K mol⁻¹; Tb: S = 3, L = 3, ⁷F₆, g = 3/2, C = 11.82 cm³ K mol⁻¹; Dy: S = 5/2, L = 5, ⁶H_15/2, g = 4/3, C = 14.17 cm³ K mol⁻¹) and one radical moiety (S = 1/2, C = 0.37 cm³ K mol⁻¹). Upon lowering of the temperature, the χT product slightly decreases until ∼145 K for 1, ∼150 K for 2 and ∼90 K for 3 reaching a shallow minimum (15.85 cm³ K mol⁻¹, 23.4 cm³ K mol⁻¹ and 27.97 cm³ K mol⁻¹, for 1–3 respectively). Above that temperature, it starts to increase rapidly upon further lowering of the temperature, until it reaches a maximum of 24.43 cm³ K mol⁻¹ at 5 K for 1, 35.83 cm³ K mol⁻¹ at 14 K for 2 and 45.6 cm³ K mol⁻¹ at 6.5 K for 3. This behaviour can be attributed to the spin alignment of the Ln ions which is caused by the strong antiferromagnetic interactions between the metal centres and the tz˙⁻ ligand (Fig. 2, insert).^20,23,25 In other words, the antiferromagnetic metal–radical coupling leads to a ferrimagnetic ground state where the magnetic moments of the lanthanides are aligned in the same direction, leading to an increase in the susceptibility at low temperatures. Bellow this temperature, the χT value decreases slowly for 1 and rapidly for 2 and 3 with the temperature drop until it reaches a value of 24.02 cm³ K mol⁻¹, 29.15 cm³ K mol⁻¹ and 40.93 cm³ K mol⁻¹ at 1.8 K, respectively. For 2 and 3, this steep downturn in the lower temperature region is attributed to magnetic blocking as observed for similar lanthanide systems.²⁵

Fig. 2 Variable temperature dc susceptibility of 1 (teal circles), 2 (blue circles) and 3 (magenta circles) under an applied field of 1000 Oe. The solid red line represents the fit as determined from the application of the −2J formalism. Insert: simplified illustration of the two J-model which was used to fit the data highlighting the antiparallel spin alignment of the Ln^III ions with respect to the tz˙⁻ ligand. Colour code: Ln^III: orange spheres; tz˙⁻: blue sphere.

To validate the presence of magnetic blocking, zero-field-cooled/field-cooled (ZFC/FC) magnetic susceptibility measurements were performed for 2 and 3. For both complexes, the divergence of the two data sets, at 3.4 K for 2 and 2.2 K for 3, confirms the pinning of the magnetic moment below these temperature regions (Fig. S7†). Field-dependence of the magnetization (up to 70 kOe) at different temperatures (1.9 to 7 K) was measured for all three complexes. For 2 and 3, distinct s-shape curves were observed in the isotemperature lines at 1.9 and 3 K for 2 and 1.9 K for 3 (Fig. S8†), suggesting the presence of magnetic blocking. Consequently, magnetic hysteresis measurements were performed for 2 and 3 to confirm the observed trends for both complexes. Using an average sweep rate of 31 Oe s⁻¹, the magnetic hysteresis was measured between 70 to −70 kOe in the temperature range of 1.8 to 3.8 K for 2 and 1.8 to 3.5 K for 3 (Fig. S9†). The butterfly-shaped hysteresis loops are waist-restricted for both complexes at 1.8 K and zero field. This crossing at H_dc = 0 Oe is often attributed to QTM, which is also expected to be present in the ac magnetic susceptibility of 2 but not for 3 (non-Kramers vs. Kramers ion). Upon increase of the field, the opening of the loops is observed. The loops remain open until 3.8 K for 2 and 3.5 K for 3, above which they are no longer open.

As already mentioned, blocking of the magnetization can result from a high-angular momentum ground state arising from the strong antiferromagnetic coupling between the radical bridging ligand and the lanthanide ions. The isotropic nature of the 4f ⁷ electron configuration of the Gd^III centres in 1 allows for the quantification of the magnetic exchange coupling. The dc magnetic susceptibility data of 1 were fit with the PHI software,²⁹ to the spin-only Hamiltonian: Ĥ = −2J_Gd–radŜ_rad(Ŝ_Gd + Ŝ_Gd′) −2J_Gd–Gd′Ŝ_GdŜ_Gd′, where J_Gd–rad represents the Gd^III–radical exchange coupling, J_Gd–Gd′ represents the intramolecular Gd^III–Gd^III exchange coupling and Ŝ_i are the spin operators for each paramagnetic centre. The best fit afforded J_Gd–rad = −7.2 cm⁻¹, confirming the anticipated antiferromagnetic Gd^III–radical coupling. Surprisingly, this value is comparable to some dinitrogen-bridged complexes with similar exchange strengths (−7.2 and −7.3 cm⁻¹).¹⁴ Since similar trends were observed in the temperature-dependence of the χT data for 2 and 3 (vide supra) it can be assumed that they also exhibit strong antiferromagnetic Ln^III-tz˙⁻ coupling (vide infra). Additionally, due to the strong antiferromagnetic alignment of the Ln spins with the radical, the best fit yielded J_Gd–Gd′ = 0.32 cm⁻¹, indicating ferromagnetic coupling between the Ln^III centres. This is further validated by the field-dependent magnetization measurements for 1 at low temperatures. The magnetization plot (M vs. H, Fig. S8†) shows field-dependence, as it increases rapidly upon increasing the field, reaching a value of 13.84 Nμ_B at 1.9 K and 70 kOe.

To probe the potential SMM behaviour, ac magnetic susceptibility measurements for 2 and 3 were undertaken. For both complexes, a temperature-dependent ac susceptibility signal was observed in the absence of a static magnetic field (H_dc = 0 Oe) in the frequency range of 0.1 to 1500 Hz. For 2, both the in-phase (χ′) (Fig. S10†) and out-of-phase (χ′′) (Fig. 3A) ac susceptibilities show frequency-dependent behaviour between 8 and ∼4.2 K, which is indicative of a thermally activated relaxation mechanism. Below that temperature (4 to 1.8 K), the overlap of the χ′′ signal, and the small frequency-dependence of the peak of the susceptibility, suggest that QTM effects dominate the relaxation of the magnetization in the low temperature region. Fitting of the ac susceptibility data for 2 (when H_dc = 0 Oe) using CCFit-2 software³⁰ (Fig. 3B) to a generalized Debye model, afforded the relaxation times (τ) (Table S3†). Insight into the magnetic relaxation dynamics of 2 in the absence of a static dc field, was gained by the analysis and fitting of the τ vs. T plots (Fig. 3C). A combination of QTM and Orbach mechanisms was used to accurately fit the relaxation times for 2, using eqn (1):

τ⁻¹ = τ_QTM⁻¹ + τ₀⁻¹ exp(−U_eff/k_BT) (1)

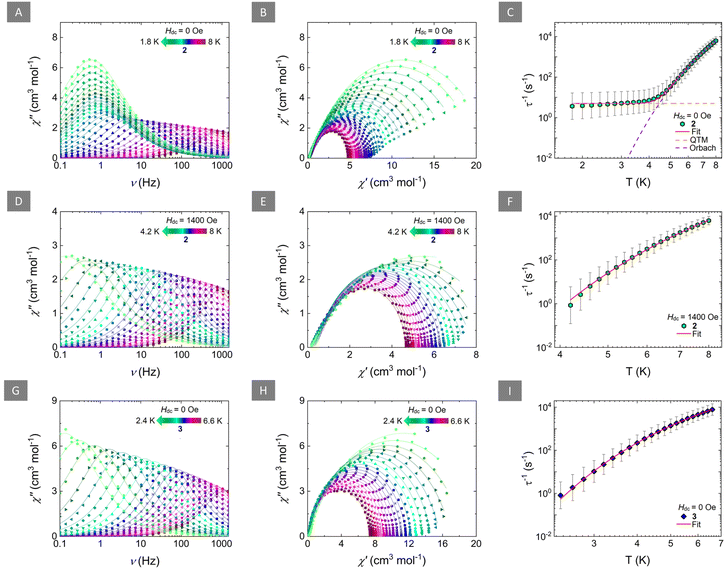Fig. 3 Left: frequency-dependence of the out-of-phase magnetic susceptibility (χ′′) for 2 (H_dc = 0 Oe; (A); H_dc = 1400 Oe; (D)) and 3 (H_dc = 0 Oe; (G)) at the respective temperature regions. Solid lines represent fits to the generalized Debye model. Middle: Cole–Cole plots for 2 (H_dc = 0 Oe; (B); H_dc = 1400 Oe; (E)) and 3 (H_dc = 0 Oe; (H)) at the respective temperature regions. Solid lines represent fits to the generalized Debye model. Fitting parameters for the generalized Debye fit of the ac susceptibilities are summarized in Tables S3, S5 and S6,† respectively. Right: temperature-dependence of the relaxation times (τ) for 2 (H_dc = 0 Oe; (C); H_dc = 1400 Oe; (F)) and 3 (H_dc = 0 Oe; (I)) with the respective estimated standard deviations (gray bars). The estimated standard deviations of the τ were calculated from the α-parameters of the generalized Debye fits and the log–normal distribution as described in ref. 30. The solid red lines represent the best-fit based on eqn (1) for (C) and eqn (2) for (F) and (I), while the dashed orange and purple lines in (C) represent the individual components of the magnetic relaxation for QTM and Orbach processes, respectively.

The best fit for 2 yielded τ_QTM = 0.20 s, τ₀ = 2.33 × 10⁻⁸ s and U_eff = 49.2 cm⁻¹. A term accounting for Raman relaxation was also investigated without improving the fit or providing any physically meaningful parameters and was therefore omitted.

To probe the effect of an applied static field in the relaxation process of 2, ac measurements were undertaken at various static fields (0–3000 Oe). At a constant temperature of 4.5 K, a field-dependent signal of the χ′′ of 2 was observed (Fig. S11†). Fitting of the χ′′ via a generalized Debye model yielded the field-dependent relaxation times of 2 (Table S4†). As evident by Fig. S12,† the relaxation times increase with the increase of the applied static field between 0 and 1400 Oe. At higher fields, the relaxation times become field-independent, indicating that beyond this field, QTM has been successfully suppressed and the relaxation of the magnetization is indeed mediated via the thermally activated pathway.

Since the presence of a static field can lead to effective suppression of QTM in 2, ac susceptibility measurements at 1400 Oe between 8 and 4.2 K were performed (Fig. 3D, E and S13†). Fitting of the ac susceptibility for 2 (when H_dc = 1400 Oe) via a generalized Debye model, yielded longer relaxation times (Table S5†). As expected, the peaks of the susceptibility showed an exponential increase upon lowering of the temperature, indicative of a thermally activated relaxation process, i.e., Orbach mechanism. As such, the relaxation times were fitted, using eqn (2) (Fig. 3F):

τ⁻¹ = τ₀⁻¹ exp(−U_eff/k_BT) (2)

The best-fit parameters were τ₀ = 1.35 × 10⁻⁸ s and U_eff = 51.9 cm⁻¹. Accordingly, the Arrhenius plot of the ln(τ) vs. T⁻¹ was constructed to verify these findings were a linear trend of the τ was observed, as expected (Fig. S14†).

Comparatively, the ac susceptibility for 3 in the absence of a static dc field (H_dc = 0 Oe) showed frequency-dependence in a smaller temperature region (6.6 to 2.4 K) (Fig. 3G and S15†). Fitting of the ac susceptibility data for 3 (Fig. 3H) afforded the τ (Table S6†) which were further analyzed and fit using eqn (2) (Fig. 3I and Fig. S16†). The best-fit for 3, yielded τ₀ = 5.61 × 10⁻⁷ s and a smaller U_eff = 25.0 cm⁻¹.

Contrary to 2, the field-dependence of the χ′′ susceptibility of 3 (Fig. S17†), upon fitting with a generalized Debye model (Table S7†), yielded, relatively constant relaxation times which were, as expected, altogether not affected by the variation of the applied static field (Fig. S18†). The superposition of the field-dependent ac susceptibility and the non-improvement of the signal with the increase of the applied field further confirms the presence of an Orbach-only mediated magnetic relaxation which is expected to be extremely weak field-dependent.

The U_eff that were obtained for 2 and 3 (Table S8†) are higher compared to other tetrazine-based radical bridged lanthanide systems^15,16,27 but are modest in comparison to the “Ln₄” tetranuclear tz˙-bridged system²⁰ or other radical bridged systems.^14,18,19 This is probably attributed to the presence of the coordinated THF. The Ln–O_THF distances (2.388(2)–2.376(2) Å) are comparable to the Ln–N_tz distances (2.453(2)–2.445(2) Å). These equatorial contributions are significant enough to compete with the axiality imposed by the Cp* ligands, thus lowering the overall SMM performance. As such, removing these coordinated solvents is expected to enhance the SMM properties. However, efforts to remove the coordinated THF solvent molecules were not successful as the complexes were not preserved and, thus, the THF-free dimers could not be isolated.

Computational studies

To validate the observed magnetic behaviour of 1–3, the metal–radical exchange interaction was studied by computational methods. The isotropic exchange coupling parameters in 1 were calculated by broken-symmetry density functional theory (BS-DFT)^31–36 using the CAM-B3LYP function^37–39 as implemented in the Orca code.^40–42 The Gd–radical and Gd–Gd′ exchange couplings were calculated as J_Gd–rad = –5.4 cm⁻¹ and J_Gd–Gd′ = –3.8 cm⁻¹, respectively. While the Gd–radical exchange is in reasonable agreement with the value obtained from the fit (J_Gd–rad = –7.2 cm⁻¹, J_Gd–Gd′ = 0.32 cm⁻¹, vide supra), the Gd–Gd′ interaction is unreasonably large. The origin of this discrepancy could not be determined but based on various test calculations, it was not a functional-dependent effect. In order to get a more reliable computational estimate of the exchange interaction, the metal–radical exchange parameter was also calculated at NEVPT2//SA-CASSCF(13,13) level (see the ESI for further details†).^40–48 The calculated value is J_Gd–rad = –6.2 cm⁻¹, which is in reasonable agreement with the fitted value although slightly underestimated. It is typical that SA-CASSCF calculations underestimate the kinetic exchange contribution to the exchange interaction and therefore underestimate the strength of antiferromagnetic coupling.

The strong magnetic anisotropy arising from the first-order orbital contribution to the magnetic moment in 2 and 3 makes analysis of the exchange coupling considerably more difficult. The energy spectrum of the Hamiltonian of the full complex was constructed from NEVPT2//SA-CASSCF//QDPT calculations^40–50 treating one metal–radical interaction while the other metal ion was replaced by the diamagnetic Y^III ion. The procedure is based on mapping the ab initio states to pseudospin states and on the construction of a pseudospin Hamiltonian.⁵¹ Unlike the commonly used Lines model that is valid only at the weak exchange limit,⁵² the present model utilizes the full exchange tensor that is valid also for strong exchange interaction.⁵¹ The present approach differs from earlier ab initio treatments of the full lanthanide–radical exchange interaction^53–55 in that it is completely based on multireference calculations and does not require any fitted or DFT-based parameters. The disadvantage of the approach is that in its present form it does not give direct access to the different components of the exchange tensor. Details of the process are given in the ESI.† The magnetic susceptibilities calculated using the pseudospin Hamiltonian are in reasonable agreement with the experimentally observed susceptibilities (Fig. S19†). This along with the agreement between the calculated and fitted exchange coupling constants for 1 show that the model is reliable.

The energies and properties of the four lowest Kramers doublets of 2 and 3 are described in Tables S11 and S12.† The energies of the first excited KDs of both 2 and 3 (38 cm⁻¹ and 21 cm⁻¹, respectively) are in reasonable agreement with the observed barrier heights (49 cm⁻¹, 25 cm⁻¹). The values are slightly lower due to the slight underestimation of the strength of the antiferromagnetic exchange as is the case of 1. Thus, the relaxation of magnetization most likely proceeds via the first excited KDs. The calculated transition magnetic moment matrix elements⁵⁶ show that in the case of 2, the barrier crossing takes place earliest at the first excited KD and the latest at the second excited KD (Fig. S20†). In the case of 3, the barrier could not be reliably reproduced. The discrepancies in the calculated barriers most likely originate from numerical inaccuracies. Analysis of the g tensors shows that the ground KD corresponds to an Ising-type ferrimagnetic spin configuration where the metal magnetic momenta are aligned in the same direction and the radical moment in the opposite direction. The first excited KD corresponds to a situation where one of the metal moments has flipped so that the metal moments lie in opposite directions. Therefore, the magnetic relaxation is related to changes in the magnetic state of the overall exchange-coupled system and not just the individual lanthanide ions, consistent with a giant-spin interpretation of the magnetic state.

Conclusions

In summary, the use of the tz˙⁻ as a bridging ligand of [Cp*₂Dy^III]⁺ moieties led to the isolation of a new family of radical bridged dinuclear metallocenes. This family of complexes is only the second example of the radical form of the 1,2,4,5-tetrazine in the literature. Strong antiferromagnetic coupling between the Ln^III ions and the tz˙⁻, mediated by the diffuse π* orbitals of the tetrazinyl ring, yielded a strong J_Gd–rad of −7.2 cm⁻¹ in 1, which is comparable to some dinitrogen-bridged complexes with similar exchange strengths (−7.2 and −7.3 cm⁻¹).¹⁴ For 2 and 3, ac magnetic susceptibility measurements revealed that these SMMs relax slowly via thermally activated processes, through the first excited KDs. Using computational studies, it was found that these KDs correspond to an Ising-type ferrimagnetic spin configuration where the magnetic moments of the Ln^III ions are co-aligned while the magnetic moment of the radical points to the opposite direction, supporting the proposed J model. As such, 2 and 3 relax as a magnetic entity rather than weakly coupled individual spins. The U_eff that were obtained for 2 and 3 are higher compared to other tetrazine-based radical bridged Ln systems proving that the unexplored unsubstituted tz˙⁻ ligand can provide new aspects in molecular magnetism towards the synthesis of new strongly-coupled zero field SMMs.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors thank the University of Ottawa, the Canada Foundation for Innovation (CFI) and Natural Sciences and Engineering Research Council of Canada (NSERC) for the financial support of this work. N. M. acknowledges the University of Ottawa and the Stavros Niarchos Foundation for financial support through scholarships. A. M. acknowledges funding provided by the Academy of Finland (grant no. 332294) and the University of Oulu (Kvantum Institute). Computational resources were provided by CSC-IT Center for Science in Finland and the Finnish Grid and Cloud Infrastructure (persistent identifier urn:nbn:fi:research-infras-2016072533).

References

1. E. Coronado, Molecular magnetism: from chemical design to spin control in molecules, materials and devices, Nat. Rev. Mater., 2020, 5, 87–104.
2. N. F. Chilton, Molecular Magnetism, Annu. Rev. Mater. Res., 2022, 52, 79–101.
3. K. L. M. Harriman, D. Errulat and M. Murugesu, Magnetic Axiality: Design Principles from Molecules to Materials, Trends Chem., 2019, 1, 425–439.
4. C. J. Milios, A. Vinslava, W. Wernsdorfer, S. Moggach, S. Parsons, S. P. Perlepes, G. Christou and E. K. Brechin, A Record Anisotropy Barrier for a Single-Molecule Magnet, J. Am. Chem. Soc., 2007, 129, 2754–2755.
5. P. Kumar, S. Biswas, A. Swain, J. Acharya, V. Kumar, P. Kalita, J. F. Gonzalez, O. Cador, F. Pointillart, G. Rajaraman and V. Chandrasekhar, Azide-Coordination in Homometallic Dinuclear Lanthanide(III) Complexes Containing Nonequivalent Lanthanide Metal Ions: Zero-Field SMM Behavior in the Dysprosium Analogue, Inorg. Chem., 2021, 60, 8530–8545.
6. N. Ishikawa, M. Sugita, T. Ishikawa, S. Koshihara and Y. Kaizu, Lanthanide Double-Decker Complexes Functioning as Magnets at the Single-Molecular Level, J. Am. Chem. Soc., 2003, 125, 8694–8695.
7. C. A. P. Goodwin, F. Ortu, D. Reta, N. F. Chilton and D. P. Mills, Molecular magnetic hysteresis at 60 kelvin in dysprosocenium, Nature, 2017, 548, 439–442.
8. F.-S. Guo, B. M. Day, Y.-C. Chen, M.-L. Tong, A. Mansikkamäki and R. A. Layfield, A Dysprosium Metallocene Single–Molecule Magnet Functioning at the Axial Limit, Angew. Chem., Int. Ed., 2017, 5.
9. J. Liu, Y.-C. Chen, J.-L. Liu, V. Vieru, L. Ungur, J.-H. Jia, L. F. Chibotaru, Y. Lan, W. Wernsdorfer, S. Gao, X.-M. Chen and M.-L. Tong, A Stable Pentagonal Bipyramidal Dy(III) Single-Ion Magnet with a Record Magnetization Reversal Barrier over 1000 K, J. Am. Chem. Soc., 2016, 138, 5441–5450.
10. F.-S. Guo, B. M. Day, Y.-C. Chen, M.-L. Tong, A. Mansikkamäki and R. A. Layfield, Magnetic hysteresis up to 80 kelvin in a dysprosium metallocene single-molecule magnet, Science, 2018, 362, 1400–1403.
11. A. B. Canaj, S. Dey, E. R. Martí, C. Wilson, G. Rajaraman and M. Murrie, Insight into D6 h Symmetry: Targeting Strong Axiality in Stable Dysprosium(III) Hexagonal Bipyramidal Single-Ion Magnets, Angew. Chem., Int. Ed., 2019, 58, 14146–14151.
12. S. K. Gupta, T. Rajeshkumar, G. Rajaraman and R. Murugavel, An air-stable Dy(III) single-ion magnet with high anisotropy barrier and blocking temperature, Chem. Sci., 2016, 7, 5181–5191.
13. C. A. Gould, K. R. McClain, D. Reta, J. G. C. Kragskow, D. A. Marchiori, E. Lachman, E.-S. Choi, J. G. Analytis, R. D. Britt, N. F. Chilton, B. G. Harvey and J. R. Long, Ultrahard magnetism from mixed-valence dilanthanide complexes with metal-metal bonding, Science, 2022, 375, 198–202.
14. S. Demir, M. I. Gonzalez, L. E. Darago, W. J. Evans and J. R. Long, Giant coercivity and high magnetic blocking temperatures for N 2 3− radical-bridged dilanthanide complexes upon ligand dissociation, Nat. Commun., 2017, 8, 2144.
15. B. S. Dolinar, D. I. Alexandropoulos, K. R. Vignesh, T. James and K. R. Dunbar, Lanthanide Triangles Supported by Radical Bridging Ligands, J. Am. Chem. Soc., 2018, 140, 908–911.
16. B. S. Dolinar, S. Gómez-Coca, D. I. Alexandropoulos and K. R. Dunbar, An air stable radical-bridged dysprosium single molecule magnet and its neutral counterpart: redox switching of magnetic relaxation dynamics, Chem. Commun., 2017, 53, 2283–2286.
17. P. Zhang, M. Perfetti, M. Kern, P. P. Hallmen, L. Ungur, S. Lenz, M. R. Ringenberg, W. Frey, H. Stoll, G. Rauhut and J. van Slageren, Exchange coupling and single molecule magnetism in redox-active tetraoxolene-bridged dilanthanide complexes, Chem. Sci., 2018, 9, 1221–1230.
18. C. A. Gould, E. Mu, V. Vieru, L. E. Darago, K. Chakarawet, M. I. Gonzalez, S. Demir and J. R. Long, Substituent Effects on Exchange Coupling and Magnetic Relaxation in 2,2′-Bipyrimidine Radical-Bridged Dilanthanide Complexes, J. Am. Chem. Soc., 2020, 142, 21197–21209.
19. J. D. Rinehart, M. Fang, W. J. Evans and J. R. Long, Strong exchange and magnetic blocking in N23−-radical-bridged lanthanide complexes, Nat. Chem., 2011, 3, 538–542.
20. N. Mavragani, D. Errulat, D. A. Gálico, A. A. Kitos, A. Mansikkamäki and M. Murugesu, Radical-Bridged Ln4 Metallocene Complexes with Strong Magnetic Coupling and a Large Coercive Field, Angew. Chem., Int. Ed., 2021, 60, 24206–24213.
21. O. Stetsiuk, A. Abhervé and N. Avarvari, 1,2,4,5-Tetrazine based ligands and complexes, Dalton Trans., 2020, 49, 5759–5777.
22. N. Mavragani, A. A. Kitos, J. L. Brusso and M. Murugesu, Enhancing Magnetic Communication between Metal Centres: The Role of s-Tetrazine Based Radicals as Ligands, Chem. – Eur. J., 2021, 27, 5091–5106.
23. C. A. Gould, L. E. Darago, M. I. Gonzalez, S. Demir and J. R. Long, A Trinuclear Radical-Bridged Lanthanide Single-Molecule Magnet, Angew. Chem., Int. Ed., 2017, 56, 10103–10107.
24. S. Demir, M. Nippe, M. I. Gonzalez and J. R. Long, Exchange coupling and magnetic blocking in dilanthanide complexes bridged by the multi-electron redox-active ligand 2,3,5,6-tetra(2-pyridyl)pyrazine, Chem. Sci., 2014, 5, 4701–4711.
25. S. Demir, J. M. Zadrozny, M. Nippe and J. R. Long, Exchange Coupling and Magnetic Blocking in Bipyrimidyl Radical-Bridged Dilanthanide Complexes, J. Am. Chem. Soc., 2012, 134, 18546–18549.
26. F. Bertinotti, C. Giacomello and A. M. Liquori, The structure of heterocyclic compounds containing nitrogen. I. Crystal and molecular structure of s-tetrazine, Acta Crystallogr., 1956, 9, 510–514.
27. G. Brunet, M. Hamwi, M. A. Lemes, B. Gabidullin and M. Murugesu, A tunable lanthanide cubane platform incorporating air-stable radical ligands for enhanced magnetic communication, Commun. Chem., 2018, 1, 1–6.
28. J. J. McKinnon, A. S. Mitchell and M. A. Spackman, Hirshfeld Surfaces: A New Tool for Visualising and Exploring Molecular Crystals, Chem. – Eur. J., 1998, 4, 2136–2141.
29. N. F. Chilton, R. P. Anderson, L. D. Turner, A. Soncini and K. S. Murray, PHI: A powerful new program for the analysis of anisotropic monomeric and exchange-coupled polynuclear d- and f-block complexes, J. Comput. Chem., 2013, 34, 1164–1175.
30. D. Reta and N. F. Chilton, Uncertainty estimates for magnetic relaxation times and magnetic relaxation parameters, Phys. Chem. Chem. Phys., 2019, 21, 23567–23575.
31. L. Noodleman, Valence bond description of antiferromagnetic coupling in transition metal dimers, J. Chem. Phys., 1981, 74, 5737–5743.
32. G. Jonkers, C. A. de Lange, L. Noodleman and E. J. Baerends, Broken symmetry effects in the He(I) valence photoelectron spectrum of Se(CN)2, Mol. Phys., 1982, 46, 609–620.
33. L. Noodleman, J. G. Norman, J. H. Osborne, A. Aizman and D. A. Case, Models for ferredoxins: electronic structures of iron-sulfur clusters with one, two, and four iron atoms, J. Am. Chem. Soc., 1985, 107, 3418–3426.
34. L. Noodleman and E. R. Davidson, Ligand spin polarization and antiferromagnetic coupling in transition metal dimers, Chem. Phys., 1986, 109, 131–143.
35. I. d. P. R. Moreira and F. Illas, A unified view of the theoretical description of magnetic coupling in molecular chemistry and solid state physics, Phys. Chem. Chem. Phys., 2006, 8, 1645–1659.
36. H. Xiang, C. Lee, H.-J. Koo, X. Gong and M.-H. Whangbo, Magnetic properties and energy-mapping analysis, Dalton Trans., 2013, 42, 823–853.
37. T. Yanai, D. P. Tew and N. C. Handy, A new hybrid exchange–correlation functional using the Coulomb-attenuating method (CAM-B3LYP), Chem. Phys. Lett., 2004, 393, 51–57.
38. A. D. Becke, Density-functional exchange-energy approximation with correct asymptotic behavior, Phys. Rev. A, 1988, 38, 3098–3100.
39. C. Lee, W. Yang and R. G. Parr, Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789.
40. F. Neese, Software update: the ORCA program system, version 4.0, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1327.
41. F. Neese, F. Wennmohs, U. Becker and C. Riplinger, The ORCA quantum chemistry program package, J. Chem. Phys., 2020, 152, 224108.
42. F. Neese, The SHARK integral generation and digestion system, J. Comput. Chem., 2022, 1 DOI:10.1002/jcc.26942 , in press.
43. (a) B. O. Roos, in Advances in Chemical Physics, Ab Initio Methods in Quantum Chemistry II, ed. K. P. Lawley, Wiley, New York, 1987, vol. 69, pp. 399–455; (b) P. Siegbahn, A. Heiberg, B. Roos and B. Levy, A Comparison of the Super-CI and the Newton-Raphson Scheme in the Complete Active Space SCF Method, Phys. Scr., 1980, 21, 323–327.
44. B. O. Roos, P. R. Taylor and P. E. M. Sigbahn, A complete active space SCF method (CASSCF) using a density matrix formulated super-CI approach, Chem. Phys., 1980, 48, 157–173.
45. (a) P. E. M. Siegbahn, J. Almlöf, A. Heiberg and B. O. Roos, The complete active space SCF (CASSCF) method in a Newton–Raphson formulation with application to the HNO molecule, J. Chem. Phys., 1981, 74, 2384–2396; (b) B. O. Roos, R. Lindh, P.Å Malmqvist, V. Veryazov and P.-O. Widmark, Multiconfigurational Quantum Chemistry, Wiley, Hoboken, NJ, 2016.
46. C. Angeli, R. Cimiraglia, S. Evangelisti, T. Leininger and J.-P. Malrieu, Introduction of n-electron valence states for multireference perturbation theory, J. Chem. Phys., 2001, 114, 10252–10264.
47. C. Angeli, R. Cimiraglia and J.-P. Malrieu, N-electron valence state perturbation theory: a fast implementation of the strongly contracted variant, Chem. Phys. Lett., 2001, 350, 297–305.
48. C. Angeli, R. Cimiraglia and J.-P. Malrieu, n-electron valence state perturbation theory: A spinless formulation and an efficient implementation of the strongly contracted and of the partially contracted variants, J. Chem. Phys., 2002, 117, 9138–9153.
49. F. Neese, T. Petrenko, D. Ganyushin and G. Olbrich, Advanced aspects of ab initio theoretical optical spectroscopy of transition metal complexes: Multiplets, spin-orbit coupling and resonance Raman intensities, Coord. Chem. Rev., 2007, 251, 288–327.
50. M. Atanasov, D. Aravena, E. Suturina, E. Bill, D. Maganas and F. Neese, First principles approach to the electronic structure, magnetic anisotropy and spin relaxation in mononuclear 3d-transition metal single molecule magnets, Coord. Chem. Rev., 2015, 289, 177–214.
51. (a) N. Iwahara and L. F. Chibotaru, Exchange interaction between $J$ multiplets, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 174438; (b) L. F. Chibotaru in Advances in Chemical Physics, ed. S. A. Rice and A. R. Dinner, Wiley, 2013, vol. 153, pp. 397–519.
52. (a) M. E. Lines, Orbital Angular Momentum in the Theory of Paramagnetic Clusters, J. Chem. Phys., 1971, 55, 2977–2984; (b) L. Ungur and L. F. Chibotaru, Computational Modelling of Magnetic Properties of Lanthanide Compounds, in Lanthanide and Actinides in Molecular Magnetism, ed. R. A. Layfield and M. Murugesu, Wiley,-VHC, Weinheim, Germany, 2015.
53. V. Vieru, N. Iwahara, L. Ungur and L. F. Chibotaru, Giant exchange interaction in mixed lanthanides, Sci. Rep., 2016, 6, 24046.
54. G. T. Nguyen and L. Ungur, Understanding the magnetization blocking mechanism in N ₂³⁻ -radical-bridged dilanthanide single-molecule magnets, Phys. Chem. Chem. Phys., 2021, 23, 10303–10310.
55. G. T. Nguyen and L. Ungur, The Role of Radical Bridges in Polynuclear Single-Molecule Magnets, Chem. – Eur. J., 2022, 28, e202200227.
56. L. Ungur, M. Thewissen, J.-P. Costes, W. Wernsdorfer and L. F. Chibotaru, Interplay of Strongly Anisotropic Metal Ions in Magnetic Blocking of Complexes, Inorg. Chem., 2013, 52, 6328–6337.

---

Footnote

† Electronic supplementary information (ESI) available: Synthetic procedures, single-crystal X-ray diffraction data, additional magnetic and computational data. CCDC 2202463–2202465. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d2qi02164a

---