Revealing the interaction between peptide drugs and permeation enhancers in the presence of intestinal bile salts

Abstract

Permeability enhancer-based formulations offer a promising approach to enhance the oral bioavailability of peptides. We used all-atom molecular dynamics simulations to investigate the interaction between two permeability enhancers (sodium caprate, and SNAC), and four different peptides (octreotide, hexarelin, degarelix, and insulin), in the presence of taurocholate, an intestinal bile salt. The permeability enhancers exhibited distinct effects on peptide release based on their properties, promoting hydrophobic peptide release while inhibiting water-soluble peptide release. Lowering peptide concentrations in the simulations reduced peptide–peptide interactions but increased their interactions with the enhancers and taurocholates. Introducing peptides randomly with enhancer and taurocholate molecules yielded dynamic molecular aggregation, and reduced peptide–peptide interactions and hydrogen bond formation compared to peptide-only systems. The simulations provided insights into molecular-level interactions, highlighting the specific contacts between peptide residues responsible for aggregation, and the interactions between peptide residues and permeability enhancers/taurocholates that are crucial within the mixed colloids. Therefore, our results can provide insights into how modifications of these critical contacts can be made to alter drug release profiles from peptide-only or mixed peptide–PE–taurocholate aggregates. To further probe the molecular nature of permeability enhancers and peptide interactions, we also analyzed insulin secondary structures using Fourier transform infrared spectroscopy. The presence of SNAC led to an increase in β-sheet formation in insulin. In contrast, both in the absence and presence of caprate, α-helices, and random structures dominated. These molecular-level insights can guide the design of improved permeability enhancer-based dosage forms, allowing for precise control of peptide release profiles near the intended absorption site.

---

Introduction

Peptide drugs constitute an increasingly significant portion of the pharmaceutical market, with projected worldwide sales expected to double within the next decade. This class of therapeutic molecules plays a crucial role in effectively treating several critical diseases, including cancer, diabetes, and hypercholesterolemia, the latter of which is closely linked to the development of coronary heart disease.¹ Compared to small molecules, peptide drugs offer higher specificity and a relatively larger surface area for inhibiting e.g. protein–protein interactions.^1,2 Furthermore, they have lower production costs compared to larger biological drugs, such as proteins and antibodies. However, peptide drugs face challenges related to in vivo stability due to the susceptibility of amide bonds to hydrolysis.¹ This vulnerability can impact their therapeutic efficacy. Additionally, the relatively larger size and hydrophilicity of peptides present obstacles in terms of permeating the intestinal epithelium, thereby affecting their oral bioavailability.

In response to these challenges, the utilization of permeability enhancer (PE)-based formulations has emerged as a promising approach for enhancing the oral bioavailability of peptides. Notably, the Food and Drug Administration (FDA) recently granted approval to two oral formulations, namely semaglutide tablets (Rybelsus) and octreotide capsules (Mycapssa), which incorporate PEs to enhance peptide absorption. This approval highlights the growing recognition of the potential of PE-based formulations in optimizing peptide delivery via the oral route. Furthermore, there is an ongoing clinical trial involving an oral macrocyclic peptide called MK-0616, formulated with the medium-chain fatty acid sodium caprate as the permeation enhancer.^3,4 MK-0616 functions as a proprotein convertase subtilisin/kexin-type 9 (PCSK9) inhibitor and holds promise for effectively treating hypercholesterolemia and coronary artery disease.

Aside from the MK-0616 example, despite being a simple, straightforward, and cost-effective formulation strategy, still, only a limited number of PE-based dosage forms have progressed to clinical trials.⁵ One of the key reasons for the underperformance of PE-based formulations is the lack of fundamental understanding regarding the solubilization of peptides within these formulations. Specifically, the interactions between peptides and the colloidal nanostructures formed by the PE molecules remain poorly understood, posing a significant challenge to rational formulation design. Additionally, the presence of different concentrations of bile salts in the intestine introduces further complexities. These bile salts have the potential to induce self-aggregation or interact with the colloidal structures present in PE-based formulations, affecting their stability and performance. Previous studies have demonstrated that the absorption of drug molecules when combined with various permeability enhancers is lower in the presence of fed-state simulated intestinal fluids (FeSSIF) compared to fasted-state simulated intestinal fluids (FaSSIF). This observation holds true for both in vitro and in vivo experiments.^6,7 Notably, the concentration of bile salts in FeSSIF is approximately 5–6 times higher than in FaSSIF. These findings highlight the impact of the physiological state of the gastrointestinal tract on the performance of drug molecules when used in conjunction with PEs.

Several biophysical experimental techniques have been employed to investigate and explore the interactions between peptides and permeability enhancers, as well as bile salt molecules and/or micelles. These techniques have shed light on certain aspects, such as the diffusion coefficient of molecules and the hydrodynamic radii of mixed micelles containing peptides, PEs, and bile salts.⁸ However, most experimental techniques have limitations in providing a comprehensive molecular-level understanding of the relevant interactions between peptides and other formulation components. Nevertheless, achieving this molecular-level understanding is crucial for identifying optimal peptide–PE combinations. An illustrative example of this is the case of the semaglutide formulation, where the use of o-SNAC as a PE resulted in lower permeability of semaglutide compared to SNAC.⁹ Notably, the only difference between o-SNAC and SNAC is the position of a single hydroxyl group. This subtle alteration in chemical structure significantly impacted the permeation characteristics of semaglutide, highlighting the importance of even minor modifications in PE design. Similarly, Lamson et al. demonstrated that pelargonidin (a type of plant pigment), selectively enhances the permeation of insulin (in both in vitro and in vivo studies) in its aglycone form.¹⁰ Finally, in vitro studies have shown that SNAC has the ability to enhance insulin permeability.¹¹ This effect is achieved by the formation of a complex between SNAC and insulin, facilitated by the negatively charged carboxylate group of SNAC, particularly at higher pH levels (≥6.8). However, at lower pH levels, the presence of SNAC did not lead to an increase in the cellular uptake of insulin. This finding confirms the necessity of a specific interaction between insulin and SNAC for the enhanced permeability effect. These examples highlight the significance of understanding precise molecular interactions in determining the efficacy of peptide–PE combinations.

All-atom molecular dynamics (AA-MD) simulations have proven to be a valuable tool for gaining insights into the molecular-level interactions between different molecules. For instance, Pabois et al. conducted AA-MD simulations to study the aggregation behavior of different bile salts, confirming their self-assembly driven by the hydrophobic steroid region.¹² The simulations revealed that the ionic chain and hydroxyl groups of bile salts predominantly interact with the bulk water. Several studies have also utilized AA-MD simulations to investigate the aggregation behavior of diverse peptide molecules. Examples include amyloid-β peptide variants (Aβ40 and Aβ42) as well as shorter fragments of this, and peptides analogous to gonadotropin-releasing hormone (GnRH) such as cetrorelix, ozarelix, and D-Phe-GnRH.^13–16 These simulations accurately predicted the aggregation propensities of peptides by accounting for variations in the number of residues within the peptide sequence, their charge states, and their degree of hydrophobicity. The simulations revealed that the oligomerization process of Aβ42 involves a transition from random coil to β-sheet conformation in an aqueous environment.¹⁶ The transition of Aβ42 from a random coil to a β-sheet can be restricted, however, by the sugar groups of gangliosides present in the lipid membrane, consequently inhibiting Aβ42 oligomerization.¹⁶

Additionally, AA-MD simulations identified key hydrophobic residues and the formation of hydrogen bonds responsible for influencing the aggregation propensities of structurally similar decapeptides.¹⁵ The interactions between human insulin and different ions (such as sulfate, chloride, and perchlorate) at various concentrations were investigated using AA-MD simulations, revealing that human insulin stability is impacted by specific ions and ionic concentration.¹⁷ However, extensive exploration of molecular-level interactions involving PEs, peptides, and bile salts remains limited. In vitro diffusion studies have demonstrated that the interaction between peptides and bile salts or PEs can lead to a reduction in the availability of free peptide monomers. These findings highlight the complex interplay between peptide–colloid interactions and peptide stability, all of which ultimately affect peptide absorption and bioavailability.^8,18 Thus, it is imperative to gain molecular-level insights into peptide–PE interactions in the presence of bile salts, and AA-MD simulations provide a suitable approach for this purpose.

In this study, we have conducted an investigation into the interaction patterns between four different peptides (degarelix, octreotide, hexarelin, and insulin) and two different permeability enhancers (sodium caprate and SNAC). We specifically examined these interactions in the presence of varying concentrations of peptides and taurocholate, a bile salt compound. Our goal was to gain insights into the molecular aggregation pathways of the peptides in the presence and absence of PEs and taurocholates. Additionally, we examined the release behavior of degarelix, octreotide, and hexarelin from mixed colloids composed of peptides, PEs, and taurocholate. To comprehensively understand this process, we initiated the release simulations from two different initial configurations. In addition to molecular dynamics simulations, we have also employed Fourier transform infrared spectroscopy (FTIR) to investigate the impact of the PEs on changes in the secondary structures of insulin. By comparing the results obtained from FTIR experiments with the findings from the simulations, we aimed to validate the simulation outcomes and enhance our understanding of the impact of PEs on the secondary structure of insulin.

Methods

System description

We performed simulations involving various combinations of peptides and PEs in the presence of taurocholates. Information on peptide concentration in oral dosage forms is limited in the literature. Berg et al. studied a solid oral dosage form containing 18 mg of octreotide.¹⁹ This amount of peptide can yield approximately 0.35 mM to 3.5 mM of peptide in an intestinal water pocket, assuming the release of the dosage occurs within 1–5 pockets with a volume of approximately 5–10 mL. In this study, we employed two distinct peptide concentrations (3.3 mM and 10 mM) in the simulations, closely corresponding to therapeutically relevant concentrations. The concentration of permeability enhancers was set at 50 mM, a level observed to enhance the absorption of therapeutic peptides and proteins in vivo.²⁰ The concentration of taurocholate was either 3 mM or 15 mM, representing the intestinal fluid in the fasted and fed state. Half of the PE molecules were negatively charged, while the other half remained in a neutral state. This is an effort to account for the increase in the pKa (and therefore changed ionization state) of the fatty acids as a consequence of them being incorporated into micelles.²¹

As a means to unbias the results of our simulations from the initial starting configurations, we also examined two different starting placements of the molecules for the simulations containing 10 mM peptides. In one case, all molecules, including the peptides, were randomly placed in the simulation box at the beginning of the simulations. In the other case, PEs and taurocholate (Taur) were randomly added in the presence of pre-formed peptide aggregates. For a detailed description of the simulated systems, please refer to Table 1.

Table 1 Description of the simulated systems investigated in this study

Systems	Components	Starting configuration	Number of peptides, PEs and taurocholates
1	Peptide only (10 mM)	All the molecules placed randomly in the box	Peptide: 6
2	Peptide (10 mM), C10 (50 mM), Taur (3 mM)		Peptide: 6, C10: 32, Taur: 2
3	Peptide (10 mM), C10 (50 mM), Taur (15 mM)		Peptide: 6, C10: 32, Taur: 10
4	Peptide (10 mM), SNAC (50 mM), Taur (3 mM)		Peptide: 6, SNAC: 32, Taur: 2
5	Peptide (10 mM), SNAC (50 mM), Taur (15 mM)		Peptide: 6, SNAC: 32, Taur: 10
6	Peptide (10 mM), C10 (50 mM), Taur (3 mM)	Pre-formed peptide aggregates, PEs, and Taur molecules added randomly	Peptide: 6, C10: 32, Taur: 2
7	Peptide (10 mM), C10 (50 mM), Taur (15 mM)		Peptide: 6, C10: 32, Taur: 10
8	Peptide (10 mM), SNAC (50 mM), Taur (3 mM)		Peptide: 6, SNAC: 32, Taur: 2
9	Peptide (10 mM), SNAC (50 mM), Taur (15 mM)		Peptide: 6, SNAC: 32, Taur: 10
10	Peptide only (2 mM)	All the molecules placed randomly in the box	Peptide: 2
11	Peptide (2 mM), C10 (50 mM), Taur (3 mM)		Peptide: 2, C10: 32, Taur: 2
12	Peptide (2 mM), C10 (50 mM), Taur (15 mM)		Peptide: 2, C10: 32, Taur: 10
13	Peptide (2 mM), SNAC (50 mM), Taur (3 mM)		Peptide: 2, SNAC: 32, Taur: 2
14	Peptide (2 mM), SNAC (50 mM), Taur (15 mM)		Peptide: 2, SNAC: 32, Taur: 10

---

All-atom molecular dynamics simulations

All simulations were performed using Gromacs 2018 and 2021, employing the Charmm36 force field.^22,23 Molecular topologies for sodium caprate (neutral and charged) were obtained directly from Charmm36 force field files. The SNAC topology was the same as in our previous study, where the molecule was parameterized using the Charmm General Force Field (CGenFF) 1.0.0 program and subsequently refined with the fftk toolkit in VMD.^24–26 Taurocholate topologies were also adopted from our previous study.²⁷

All non-standard residues were parameterized either by analogy with existing Charmm36 force field parameters, or using CGenFF (v. 1.0.0), with low penalty values (<10) throughout.^24,25,28 The initial structure file for insulin was sourced from the Protein Data Bank (ID 2G4M), and had a total molecular weight of 5.79 kDa. The molecular structures and amino acid sequence of the investigated peptides are presented in ESI Fig. 1.† In the simulations, octreotide and hexarelin carried a net charge of +2, degarelix had a net charge of +1, and insulin possessed a negative charge of −2.

In order to study peptide aggregation, we placed 6 peptides (equivalent to a concentration of 10 mM) and 2 peptides (equivalent to a concentration of 3.3 mM) inside a cubic box with a side length of 10 nm. To create the mixed systems consisting of 10 mM peptides, PEs, and taurocholate, we employed the two different starting configurations mentioned earlier. All systems were prepared in a cubic box with a side length of 10 nm. The specific number of molecules added to each system can be found in Table 1. Each system underwent energy minimization using the steepest descent algorithm for 10 000 steps, followed by equilibration of density and pressure for 100 ps. Final production runs were conducted for 500 ns for each system, employing periodic boundary conditions. To maintain isotropic pressure coupling, the Parrinello-Rahman coupling method was employed, with a reference pressure of 1 bar.²⁹ The time step was 2 fs, and the system temperature was maintained at 37 °C using the velocity rescale thermostat.³⁰ Electrostatic interactions were calculated using the Particle Mesh Ewald method, while van der Waals interactions were evaluated with a force-switch ranging between 1.0 and 1.2 nm.³¹

Simulation analysis

The transition networks were constructed by considering all pairwise transitions between aggregate states, following the methodology described in ref. 13 and 15. At each snapshot, the aggregate state of each peptide was determined based on the number of peptides in an aggregate. A distance cut-off of 0.5 nm was applied to determine if two molecules were considered part of the same aggregate, and changes in the aggregate states of each peptide were tracked over time. Once all the aggregate states and the corresponding transitions of peptides between these states across subsequent snapshots were identified, we generated a transition matrix. This matrix captures the total number of transitions between different states but also allows the occurrence of specific states throughout the simulation period to be estimated. The transition network plots were then created using the Cytoscape v. 3.9.1.³²

Hydrogen bond analysis used the gmx hbond module in Gromacs. To create the peptide residue-residue contact map, a contact was defined between two residues if the distance between any pair of atoms from the respective residues was less than 0.5 nm. The same distance cut-off was employed to determine contacts between the peptide and PEs, as well as taurocholate molecules. The solvent-accessible surface areas (SASA) were calculated using the gmx sasa module. The secondary structure analysis was done using gmx dssp.^33,34 Snapshot images were generated using VMD.³⁵

Umbrella sampling (US) simulations

To investigate the release of octreotide, hexarelin, and degarelix from either a homogenous peptide aggregate or the mixed colloids consisting of peptides, PEs, and taurocholate, we employed umbrella sampling (US) simulations to compute the potential of mean force (PMF) profiles. The simulations focused on the expulsion of a single peptide molecule from an aggregate into the water phase. To perform the US simulations, we generated a series of configurations along the reaction coordinate (in this case the distance from the aggregate surface to the bulk water phase). The configurations were spaced at intervals of 0.2 nm along this reaction coordinate. Before the US simulations, energy minimization and equilibration for 100 ps was performed for each window, followed by production runs of 12 ns. To extract the potential of mean force (PMF) along the reaction coordinate from the US simulations, we utilized the weighted histogram analysis method (WHAM),³¹ implemented in Gromacs in gmx wham.

Chemicals (used for FTIR experiments)

Human insulin, CAS-no: 11061-68-0, I2643, >98%, Sigma, Merck Life Science AB. Salcaprozate sodium (SNAC), CAS-no: 203787-91-1, HY-114299, 99.72%, MedChemExpress, USA. Sodium taurocholate hydrate, CAS-no: 345909-26-4, 86339, ≥97.0%, Sigma, Merck Life Science AB, Sodium decanoate (caprate acid sodium) CAS-no: 1002-62-6, C4151, >98%, Sigma, Merck Life Science AB. Sodium chloride, CAS-no: 7647-14-5, 99-5-100.5%, VWR Chemicals. Sodium hydroxide, CAS-no: 1310-73-2, and Hydrochloric acid, CAS-no: 7647-01-0, Sigma, Merck Life Science AB.

Sample preparation for FTIR experiments

To investigate the secondary structure of insulin in the presence of NaCl, we prepared six samples: three at pH 2 and three at pH 6. Insulin powder was dissolved in NaCl solutions of 100 mM, 250 mM, and 500 mM, respectively, to achieve an insulin concentration of 5 mg mL⁻¹ in each sample. The pH was adjusted to 2 (2.16 ± 0.04) by adding 0.1 M HCl, and to 6 (6.13 ± 0.07) by adding 0.2 M NaOH.

In addition, we prepared samples to investigate the secondary structure of insulin in the presence of PEs and taurocholate. These samples were created by dissolving insulin powder in 50 mM PEs (either sodium caprate or SNAC) and taurocholate (either 3 mM or 15 mM). The concentration of insulin in these samples was 5 mg mL⁻¹. A sample containing only insulin was also prepared. The pH of these samples was adjusted to 6 by adding 0.2 M NaOH. All samples were filtered through a preconditioned polyamide filter membrane with a 0.2 μm pore size and a 25 mm membrane diameter (Chromafil xtra, MACHEREY-NAGEL), then heated at 65 °C and shaken at 350 RPM for 22 hours using a thermoshaker (Thermoshaker PHMT-PSC24N, Grant bio Instruments).

Collection of FTIR spectra

The samples were freeze-dried for at least 30 hours. The spectra of the freeze-dried samples were collected in transmission mode with 256 scans, 4 cm⁻¹ in resolution in the 4000–600 cm⁻¹ region at room temperature using an Alpha II FTIR spectrometer (Bruker, USA). A second-order derivative with 9 points was applied to the obtained spectra, which were then area-normalized in the amide I region.

Results and discussion

Molecular dynamics simulations can predict the aggregation tendencies of various peptides

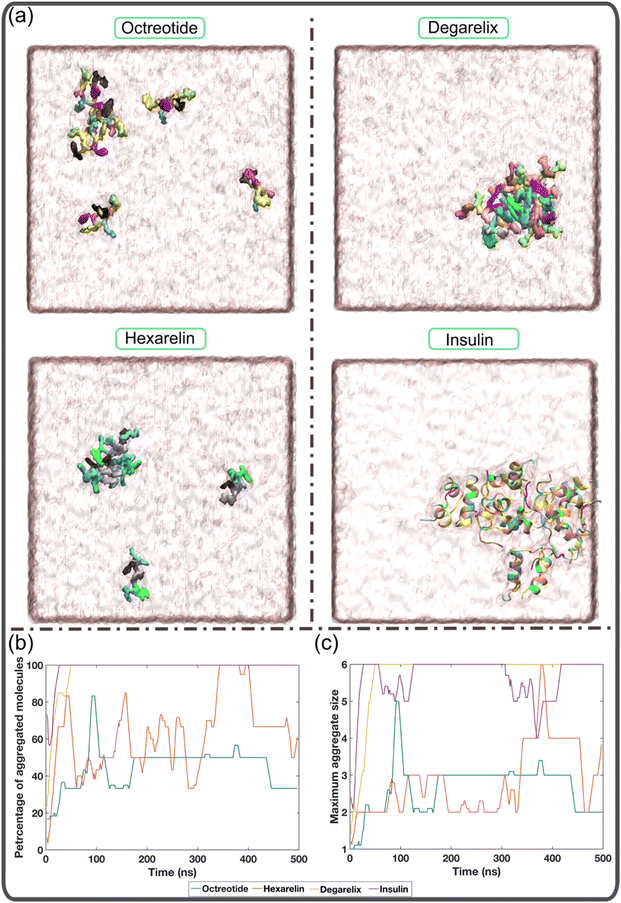
In this study, we investigated the aggregation behavior of four different peptides: degarelix, octreotide, hexarelin, and insulin. Fig. 1a shows snapshots at the end of the simulations (500 ns) for each peptide. It is evident that octreotide and hexarelin exhibit a dynamic coexistence as both aggregated species and free monomers in the solution. In contrast, degarelix and insulin molecules were present exclusively as aggregates. Since all peptides carried an overall charge, these differences in aggregation propensity between the peptides cannot be explained only by electrostatic effects.

Fig. 1 Aggregation tendencies of different peptides. (a) Representative snapshots of each peptide at the end of the simulation (500 ns). The octreotide, hexarelin, and degarelix peptides are shown with a surface representation, and insulin is presented as a cartoon. Panels (b) and (c) show the variation in the percentage of aggregated molecules as well as the maximum aggregate size with time for each peptide.

Fig. 1b illustrates the temporal evolution of the percentage of aggregated molecules in each system. The simulations demonstrate that all degarelix and insulin molecules rapidly aggregated within the first 50 ns and remained in this aggregated state throughout the simulation. In the case of octreotide and hexarelin, the profiles of maximum aggregate size vs. time (Fig. 1c), reveal that trimers and tetramers, respectively, represent the most prevalent aggregate size. However, the profiles of the percentage of aggregated molecules also varied with time for these two peptides (Fig. 1b). This suggests that the octreotide and hexarelin aggregates were not stable throughout the simulations because of insertions or expulsions of peptide monomers from the aggregates. Octreotide and hexarelin are predominantly water-soluble and possess two positively charged residues that work against the formation of stable aggregates.

In contrast, degarelix, which has a critical aggregation concentration of approximately 1 mM, exhibits a higher aggregation tendency.¹⁵ Insulin also shows a greater aggregation tendency, compatible with it being observed to form aggregates or fibrils within a pH range of 1.6 to 7.4 and at very low concentrations (0.17 mg mL⁻¹).^36–38 Overall, Fig. 1 suggests that the MD simulations successfully capture the aggregation behavior of both typical water-soluble peptides, such as octreotide and hexarelin, and peptides with higher aggregation tendencies, such as degarelix and insulin.

Transition networks can elucidate the molecular aggregation pathways of the peptides under different conditions including the presence or absence of PEs and taurocholates

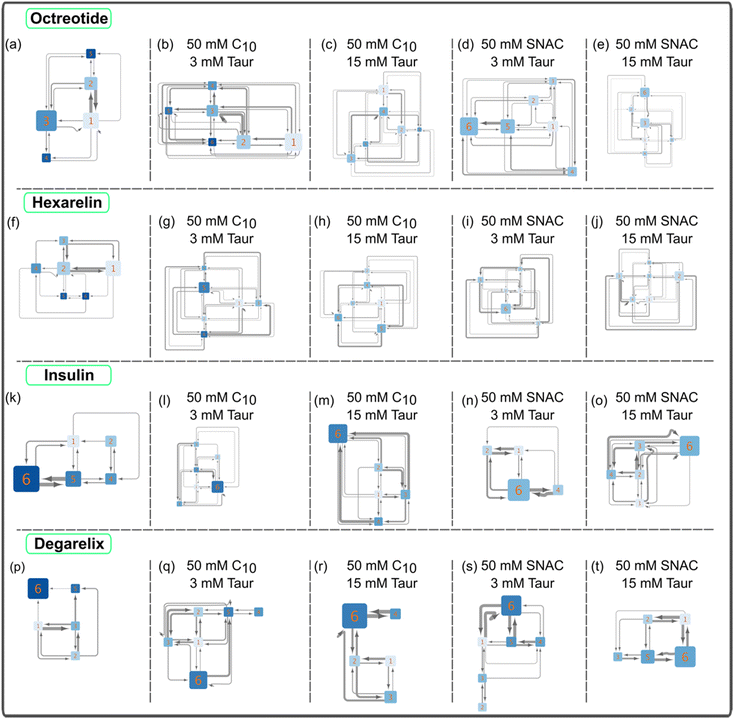
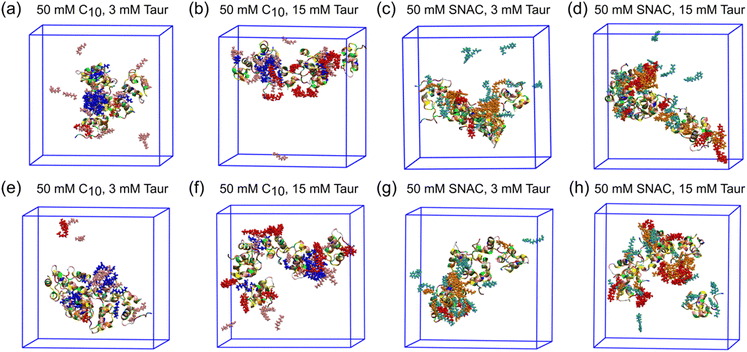
Fig. 2 shows the resulting transition networks for the octreotide, hexarelin, degarelix, and insulin systems at the 10 mM peptide concentration and a random starting configuration for all the molecules within the simulation box. Similar to Fig. 1, the transition networks obtained from the simulations revealed that in the system containing only octreotide, the dominant aggregate size was a trimer (Fig. 2a), and in the system containing only hexarelin the dominant aggregate size was a tetramer, coexisting with monomers and dimers (Fig. 2f). In contrast, aggregates containing more peptide molecules (up to the maximum of 6) were formed more frequently in the presence of PEs and taurocholate (Fig. 2b–e and g–j). This can be attributed to the formation of mixed colloids consisting of peptides as well as PEs and taurocholate when these additives are present.

Fig. 2 Illustrations of peptide aggregation transition networks for systems containing 10 mM peptides, including octreotide (panels a–e), hexarelin (f–j), insulin (k–o), and degarelix (p–t). The simulations’ initial setup featured a starting configuration where all molecules, including the peptides, were randomly placed within the simulation box. These networks depict the aggregation patterns and transitions between different aggregate sizes for each peptide. In panels a, f, k, and p, transition networks for systems with peptides alone are displayed. The numbers on each node represent the number of peptide molecules in that aggregate state. The node size corresponds to the probability of observing that specific aggregate state during the simulation. The thickness of the arrows signifies the number of transitions between pairs of nodes. Additionally, the color of the nodes reflects the number of peptide–peptide contacts normalized by the aggregate size; a darker color indicates a higher number of contacts.

Fig. 3 and ESI Fig. 2–4† show representative snapshots of these mixed colloids for the different peptides. It should be noted that peptide aggregates refer to cases where peptides come into contact with each other. In a mixed colloid, if two peptides are not in contact with each other, they are not considered part of the same peptide aggregate, even though they are part of the same mixed colloid. Peptides need to come into contact based on the cutoff distance mentioned in the method section to be considered as a specific peptide aggregate state shown in the transition networks.

Fig. 3 Representative snapshots at the end of the simulations for different systems containing Insulin. Panels (a–d) represent the starting configuration where all the molecules (including the peptides) were randomly placed in the simulation box, and panels (e–h) represent the starting configuration where the peptides are in a pre-aggregated state, but with PE and taurocholate molecules placed randomly. Peptides are shown by the cartoon representation. Caprate, SNAC, and taurocholate molecules are presented by CPK. The neutral and negatively charged caprates are represented by blue and pink, respectively. The neutral and negatively charged SNAC are represented by orange and cyan, respectively. Taurocholate molecules are represented by red color.

We also examined whether the 10 mM peptide systems (with PEs and taurocholate) reached equilibrium within the 500 ns simulation period. We monitored the temporal evolution of the percentage of aggregated peptide molecules in each system, as presented in ESI Fig. 5.† The results revealed that, in all systems, the percentage of aggregated peptides comes to between 60 to 80% within 100–250 ns, and then oscillates for the remainder of the simulations. Octreotide and hexarelin profiles displayed higher oscillations, whereas degarelix and insulin profiles showed nearly 100% aggregated molecules for the last 200–300 ns. Notably, during the final 200–300 ns of the simulations, all peptides were part of the mixed colloids. Therefore, we concluded that the simulation duration was sufficient for studying the transition network of peptide aggregates and the interactions between peptides within the mixed colloids.

The transition network for systems with 10 mM peptide and starting configuration where peptides in an already pre-formed, aggregated state are presented in ESI Fig. 6.† The transition networks of the octreotide and hexarelin systems were minimally affected by the two starting configurations (comparing Fig. 2b–e and ESI Fig. 6a–d,† and Fig. 2g–j and ESI Fig. 6e–h†). The presence of PEs (either sodium caprate or SNAC), or different taurocholate concentrations also did not significantly affect the transition networks of octreotide and hexarelin.

In contrast to hexarelin and octreotide, notable differences were observed between the two starting configurations for degarelix and insulin. In the case of degarelix, when PEs and taurocholate were introduced into the already aggregated peptides, these remained unchanged throughout the simulation. Therefore, no transition network was possible to obtain in this case. This suggests that the hydrophobic interactions between degarelix molecules were robust enough to prevent disruption of the initial hexameric state by PE (or taurocholate) molecules. When all molecules (peptides, PEs, and taurocholate) are placed randomly in the simulation box initially, hexamer was the dominant aggregate size, both in the absence (Fig. 2p) and the presence (Fig. 2q–t) of PEs and taurocholate. However, the presence of smaller aggregates (<6) was also evident from the transition network.

For insulin, the transition network also showed a fewer number of transitions between different aggregate states when PEs and taurocholate were introduced into the aggregated peptides compared to the starting configuration when all molecules were placed randomly in the simulation box initially. This suggest that the presence of PEs or taurocholates has a somewhat disruptive effect on the insulin hexamer in the simulations. The snapshot of the mixed colloid containing insulin (Fig. 3) suggests that the size of the insulin molecules might pose a barrier for the PEs and taurocholate molecules to disturb insulin aggregates. However, in a few cases, PEs were able to separate insulin molecules from their aggregated state (Fig. 3h).

The molecular dynamics simulations provided valuable insights into the behavior of peptide molecules in the presence of PEs and taurocholate. The simulations demonstrated the formation of mixed colloids, wherein PEs and taurocholate molecules interacted with peptides present in the system. The formation of mixed colloids results in a decrease in the amount of free peptide monomers in the aqueous phase. Such a reduction in the concentration of water-soluble free monomers in solution upon the addition of PEs and taurocholate was also observed experimentally for octreotide.⁸ The peptide aggregation transition networks generally provided insights into the impact of PEs and taurocholate on the peptide aggregation behavior. The addition of PEs and taurocholate resulted in larger peptide aggregates in the case of water-soluble peptides (octreotide and hexarelin). However, for degarelix and insulin, although the hexamer was the most prevalent aggregate state in both systems, at least for the case with the initial starting configuration being all molecules randomly placed into the simulation box, more dynamic molecular aggregation pathways were observed. There was a tendency for the peptides to monomerize, compatible with how SNAC is suggested to induce monomerization for semaglutide.⁹

PEs and taurocholate were found to influence peptide–peptide contact interactions

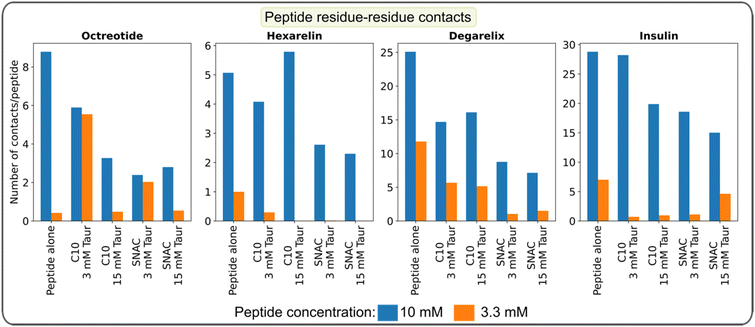
In the transition networks presented in Fig. 2, the color of the nodes represents the number of peptide–peptide contacts normalized by the aggregate size. Darker colors indicate a higher number of contacts. The presence of PEs and taurocholate resulted in a decrease in the average number of contacts for a given aggregate size compared to pure peptide aggregates of corresponding sizes. This observation suggests that while PEs and taurocholate promote the formation of larger aggregates through the mixed colloids, the number of peptide–peptide contacts is reduced when the simulations were initiated by randomly placing all molecules in the box, as opposite to peptide-only systems. Furthermore, in the presence of SNAC, the number of peptide–peptide contacts appeared to be slightly lower than that in systems containing sodium caprate. For instance, a lighter color was observed in the nodes of the hexamer, as shown in Fig. 2d, compared with Fig. 2b.

We then calculated the average number of peptide residue-residue contact per peptide for each system (Fig. 4). From this, the conclusion that the presence of PEs and taurocholates reduces the peptide–peptide interaction within the mixed colloids largely remains (the exception being the system containing 10 mM hexarelin, 50 mM caprate and 15 mM taurocholate). The systems containing SNAC exhibited a lower number of contacts per peptide compared to the systems containing caprate as the PEs. Concentration dependent effects can also be seen: reducing the peptide concentration from 10 mM to 3.3 mM significantly decreased the number of peptide–peptide contacts within the mixed colloid. However, for octreotide, the number of peptide–peptide interactions were greater compared to systems with 3.3 mM octreotide alone. It's important to note that in systems with a 3.3 mM peptide concentration, peptides also became part of the mixed colloid within 200–300 ns.

Fig. 4 Average number of peptide residue-residue contacts per peptide calculated over the final 100 ns of the simulation. The data represents the systems initiated with a starting configuration where all molecules, including the peptides, were randomly placed within the simulation box.

The peptide residue-residue contact maps, presented in ESI Fig. 7–10,† provide additional evidence that the presence of PEs and taurocholate reduces peptide residue-residue contacts, especially when simulations begin with the random placement of all molecules. When simulations started from pre-formed peptide aggregate states, peptide residue-residue contacts in the presence of PEs and taurocholates appeared to increase compared to systems with peptides alone. This trend became more apparent when comparing the average number of peptide residue-residue contacts per peptide for systems with different starting configurations and 10 mM peptides (see ESI Fig. 11†).

The intermolecular hydrogen bond maps presented in ESI Fig. 12–15† provide additional insights into the interactions between peptide molecules. When the peptides were initially placed randomly in the simulation box, the presence of PEs and taurocholates resulted in a reduction in the formation of hydrogen bonds. Specifically, for degarelix, the results indicated that PEs and taurocholate can restrict the formation of hydrogen bonds between the 4-S-Phe and 4-D-Phe residues, which play a dominant role in the formation of degarelix aggregates (ESI Fig. 14a†). Similarly, in the case of hexarelin, the formation of hydrogen bonds between tryptophan moieties, which play a crucial role in hexarelin aggregate formation, is restricted in the presence of taurocholate and PEs, particularly SNAC (ESI Fig. 13b–e†).

In the absence of PEs and taurocholates, the intermolecular hydrogen bond map of insulin showed that the Tyr and Glu residues in chain A and Phe, Val, Gln, Glu, and Lys in chain B play a dominant role in insulin aggregate formation (ESI Fig. 15a†). These residues are known to be major contributors to nucleus formation and insulin aggregation through hydrogen bonding and hydrophobic contacts.³⁹ Interestingly, the presence of PEs and taurocholate did not significantly impact the formation of hydrogen bonds between these key insulin residues.

We also computed the average number of residue-residue hydrogen bonds per peptide and compared systems with two different peptide concentrations (see ESI Fig. 16†) and two different starting configurations (see ESI Fig. 17†). Similar to the average number of contacts per peptide, the number of hydrogen bonds per peptide significantly decreased when the peptide concentration was reduced from 10 mM to 3.3 mM. Conversely, the number of H-bonds per peptide increased when simulations began from a pre-formed aggregate state compared to the random placement of peptide molecules.

The comprehensive analysis of transition networks, residue-residue contact maps, and hydrogen bond formation provides valuable insights into the influence of PEs and taurocholate on peptide aggregation behavior. The results suggest that higher peptide concentrations in the system result, rather unsupringsly, in increased peptide–peptide interactions, both in the presence and absence of PEs and taurocholates. However, at higher peptide concentrations (10 mM), PEs and taurocholate can also effectively limit peptide–peptide contact interactions within the mixed colloids. This suggests that the presence of these additives reduces the propensity of peptides to interact with each other. SNAC appears to be slightly more effective than caprate in restricting peptide–peptide contacts as well as the formation of certain key interpeptide hydrogen bonds. With its larger size compared to sodium caprate, from the presence of an aromatic ring at the end of the aliphatic chain, SNAC may more efficiently prevent contact between peptide molecules within the mixed colloids.

Hydrophobic interactions play a dominant role in the interaction of PEs and taurocholate with peptides

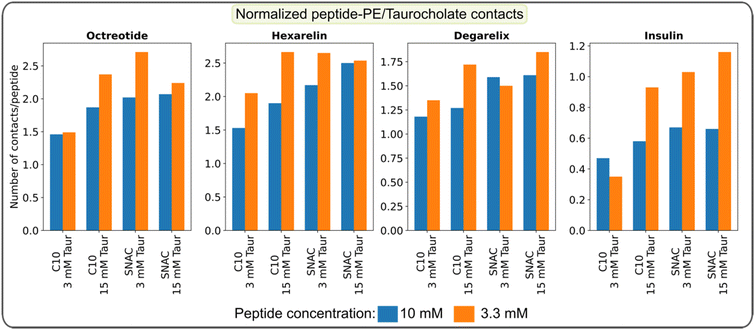
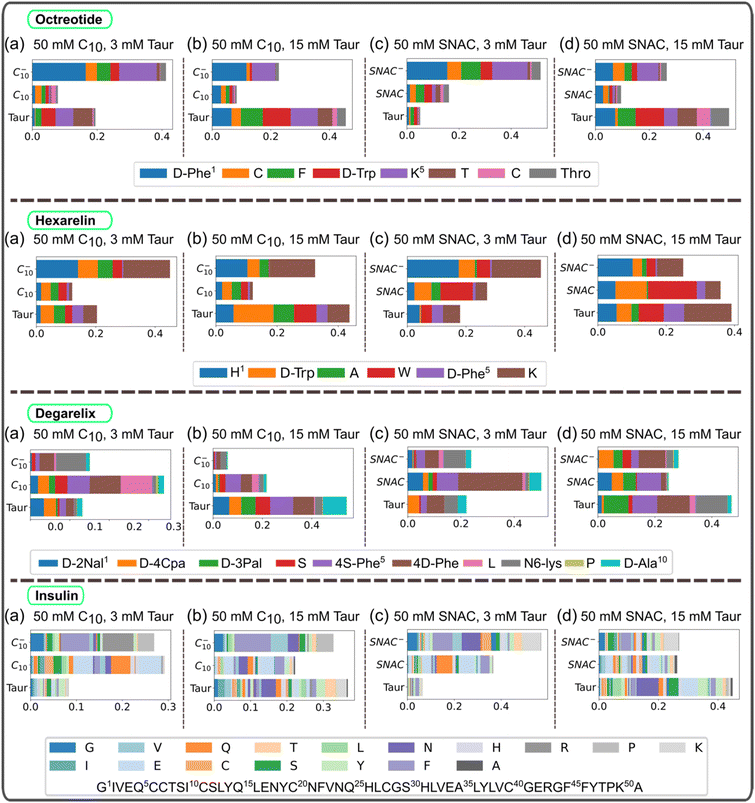
We initially computed the time evolution of the average number of contacts between the peptides and PEs/taurocholates in systems containing 10 mM peptides, with the peptides initially positioned randomly. The results, presented in ESI Fig. 18,† demonstrate an initial increase in the number of contacts up to 100–250 ns, followed by a plateau with slight oscillations. These findings indicate that the systems reached an equilibrium state within 250 ns. Moreover, the overall simulation time is sufficient for conducting a detailed analysis of the peptides’ interaction with PEs and taurocholates.

We calculated then the number of contacts between peptide residues and PEs/taurocholates, as shown in Fig. 5. Each peptide contains positively charged residues, such as D-Phe and Lys in octreotide, His and Lys in hexarelin, N6-Lys in degarelix, and Arg and Lys in insulin. Intuitively, one would expect these positively charged residues to interact more with the negatively charged PEs and taurocholate. However, the contact maps in Fig. 5 suggest that interactions between hydrophobic amino acid residues play a more prominent role. For example, in octreotide, hydrophobic residues such as D-Phe, Phe, and D-Trp show significant contact with the PEs and taurocholate. Similarly, in hexarelin, hydrophobic residues like D-Trp, Trp, and D-Phe play a dominant role in the interaction. In degarelix, hydrophobic residues such as D-2Nal, D-4Cpa, and 4S-Phe are involved in substantial contacts. In insulin, hydrophobic residues including Leu, Phe, Val, and Ile contribute significantly to the interaction with PEs/taurocholates. Interestingly, the contact maps also highlight that neutral caprate and SNAC molecules exhibit more contact with peptide residues compared to their charged counterparts.

Fig. 5 Normalized contact between peptide residues, PEs, and taurocholates for different systems containing 10 mM of octreotide, hexarelin, degarelix and insulin. For each system, the contact values are normalized using the maximum number of contacts found in each case. The data here represents the starting configuration where all the molecules including the peptides were randomly placed in the box. C₁₀ and C₁₀⁻ represent neutral and negatively charged sodium caprate molecules, and SNAC and SNAC⁻ represent neutral and negatively charged SNAC molecules. Taur represents taurocholate molecules.

Furthermore, the contact maps in Fig. 5 demonstrate that increasing the concentration of taurocholate enhances the interaction between peptides and taurocholate. Typically, the concentration of taurocholate increases at the fed state (after food intake) which impacts the colloid structure and interaction pattern between taurocholates and peptides. Additionally, the hydrophobic residues of the peptides showed more contact with SNAC than with the sodium caprate molecules. This observation aligns with the fact that SNAC typically reduces peptide–peptide interactions to a greater extent compared to sodium caprate.

We also quantified the average number of contacts between peptides and PEs/taurocholates, as illustrated in Fig. 6. The results confirm that SNAC exhibits a higher number of contacts with peptides compared to caprate. Additionally, systems with higher taurocholate concentrations exhibit more contacts per peptide. Comparing different peptide concentrations revealed that systems with lower peptide concentrations had a higher number of contacts per peptide (matching the reduction in peptide–peptide contacts, Fig. 4). Furthermore, comparing the two different starting configurations (ESI Fig. 19†), we observed that systems starting from pre-formed peptide aggregates had fewer contacts compared to those starting from random peptide positions. We also plotted contacts between peptide residues and PEs/taurocholates for the systems containing 3.3 mM peptide, as shown in ESI Fig. 20.† These results indicated similar interaction patterns, emphasizing the significant role of hydrophobic residues in the interactions between peptides and PEs/taurocholates.

Fig. 6 Average number of contacts between peptides and PEs/taurocholates per peptide calculated over the final 100 ns of the simulation and normalized by the number of atoms for each peptide. The data represents the systems initiated with a starting configuration where all molecules, including the peptides, were randomly placed within the simulation box.

Overall, the simulations offered insights into the interactions between peptide residues, permeability enhancers, and taurocholate. The simulations also enable predictions about the extent of these interactions based on the initial configuration and concentrations.

The hydrogen bonds formed between peptide residues and PEs, as well as taurocholate were also analyzed and are presented in Fig. 7. The results indicate that charged PEs form a higher number of hydrogen bonds with the peptides compared to neutral PEs, particularly with the positively charged residues of the peptides. The number of hydrogen bonds formed between peptides and taurocholate increased as the concentration of taurocholate increased. Note that the number of hydrogen bonds formed between peptides and PEs is typically only a fraction of the total number of peptide–PE contacts. Therefore, although the charge state of the molecules plays an important role in the formation of peptide–PE and peptide–taurocholate hydrogen bonds, the hydrophobic peptide residues play a dominant role in the formation of mixed colloids consisting of peptides, PEs, and taurocholates.

Fig. 7 Hydrogen bonds between peptide residues, PEs, and taurocholates for different systems containing (a) 50 mM C₁₀, 3 mM Taur, (b) 50 mM C₁₀, 15 mM Taur, (c) 50 mM SNAC, 3 mM Taur, (d) 50 mM SNAC, 15 mM Taur, and 10 mM peptides. For systems containing a specific peptide, the number of hydrogen bonds was normalized based on the maximum number of hydrogen bonds. The figures here represent the starting configuration, where all the molecules including the peptides were randomly placed in the box. C₁₀ and C₁₀⁻ represent neutral and negatively charged caprate molecules, respectively, and SNAC and SNAC⁻ represent neutral and negatively charged SNAC molecules. Taur represents taurocholate molecules.

PEs and taurocholates can influence the release of both hydrophobic and water-soluble peptide monomers into an aqueous phase

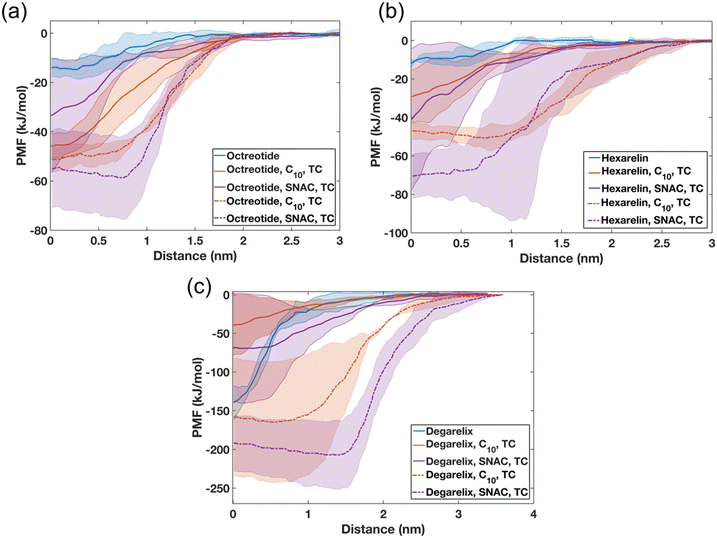
To investigate the impact of colloid composition on peptide release/expulsion, umbrella sampling (US) simulations were performed to calculate the potential of mean force (PMF). The PMF analysis involved measuring the free energy required to move a peptide molecule from either a homogenous peptide aggregate or mixed colloids to the water phase, thus simulating an expulsion/release event. The PMF profiles will be highly dependent on the particular peptide conformation, the overall structure of the aggregate, and the location of the peptide within the aggregate. Therefore, for each case, we have replicated the simulations three times by selecting different peptides each time within the aggregate.

The PMF profiles presented in Fig. 8 exhibit distinct patterns for water-soluble and hydrophobic peptides. Specifically, for octreotide and hexarelin, the results demonstrate that the process of separating a peptide molecule from a mixed colloid requires two to five times more energy than separating it from a pure peptide aggregate. The estimated free energy difference (ΔG) for separating octreotide and hexarelin molecules from mixed colloids for the starting configuration in which peptide molecules were randomly added initially were within the range of 30–50 kJ mol⁻¹. It is worth noting that significant differences are found between the two starting conditions, with higher energy requirements observed when PEs and taurocholate were introduced with pre-formed peptide aggregates. These findings suggest that PEs and taurocholate can reduce the release of water-soluble peptides such as octreotide and hexarelin, consequently reducing the number of free monomers in the aqueous phase. This decline in the fraction of free peptide is also evident in transition network analysis and was also observed experimentally for octreotide.⁸

Fig. 8 Potential mean force (PMF) profiles observed when pulling a peptide molecule from pure peptide or mixed colloids composed of 10 mM peptides, 50 mM PEs (either caprate or SNAC), and 15 mM TC. PMF profiles depicting the energy required to pull (a) one octreotide, (b) hexarelin, and (c) degarelix molecule from the aggregate surface into the aqueous phase. In the PMF profiles, the lines and shaded regions represent the means and standard deviations, respectively (n = 3). The legend describes the constituent components of the aggregate. Solid lines represent the starting configuration, where peptide, PE, and TC molecules were added randomly. The dashed lines represent the starting configuration where PEs and TCs were added randomly, and the peptides were aggregated. Abbreviations: C₁₀, caprate, TC, taurocholate.

The decreased availability of free peptides due to their interaction with PEs and taurocholate may have implications for their absorption rate across the intestinal epithelium. When peptides are strongly bound within mixed colloids, their release into the aqueous environment becomes more challenging, potentially reducing their absorption efficiency. However, this stronger interaction between peptides, the PEs, and taurocholate in the mixed colloids can also serve a beneficial role by protecting the peptides from enzymatic degradation. This reduced enzymatic degradation increases the overall availability of intact peptides for absorption in the intestine.

Also, for degarelix, the PMF profiles indicate that higher energy is required to separate peptide molecules from the mixed colloids when PEs and taurocholates were introduced to the peptide aggregates, compared to the pure peptide aggregates (Fig. 8c). The ΔG required to separate a degarelix molecule from the pure degarelix aggregate was approximately 140 kJ mol⁻¹, which is nearly nine times higher than the ΔG required to separate octreotide and hexarelin molecules from similar pure peptide aggregates. However, the opposite trend was observed for the other starting configuration (peptides molecules added randomly). In this starting configuration, the ΔG values required to separate a degarelix molecule decreased to 40 and 68 kJ mol⁻¹ for the mixed colloids containing caprate and SNAC, respectively. This suggests that the PEs and taurocholate can increase the release rate of degarelix, which is a highly hydrophobic peptide, and highlight the importance of understanding and controlling the release conditions of the peptide from the dosage form.

The FTIR spectra suggest that SNAC can induce insulin fibrillation at pH 6

Finally, we looked a little closer at the behavior of insulin, since any insights into how the oral bioavailability of insulin can be increased would have tremendous therapeutic benefit. Insulin is prone to fibrillation under various physiological conditions, such as elevated temperature, different ionic strengths, and low pH.^38,40 The fibril formation of insulin is typically characterized by the presence of β-sheet-rich structures. Using FTIR, Chaaban et al. investigated the secondary structure of insulin in the presence of various concentrations of NaCl at pH 2 and observed a broad peak around 1620–1625 cm⁻¹ in the spectra, which corresponded to β-sheet-rich structures.⁴¹ Compatible with this, we detected a peak at approximately 1632 cm⁻¹ in the FTIR spectra when different concentrations of NaCl were present at pH 2 (see ESI Fig. 21a†). It is worth noting that peaks corresponding to β-sheet structures have been observed in the range of 1620 cm⁻¹ to 1637 cm⁻¹ in various studies.^42–45

We then investigated the variation in the secondary structure of insulin in the presence of various NaCl concentrations at pH 6 (this value was chosen to mimic conditions in the duodenum⁴⁶), and observed a peak at approximately 1658 cm⁻¹ in the FTIR spectra (ESI Fig. 21b†). FTIR-spectra peaks within the range of 1645 cm⁻¹ to 1660 cm⁻¹ typically correspond to α-helical and random structures, which are observed in native insulin and systems with relatively higher pH.^40–42

We further investigated the impact of PEs and taurocholate on the secondary structure of insulin (again at pH 6) (ESI Fig. 22†). In line with native insulin and systems with a relatively higher pH, the FTIR spectra exhibited a broad peak around 1650 cm⁻¹ for the systems containing insulin only, as well as for the combination of insulin with sodium caprate and taurocholate. However, in the systems that included SNAC, a shift in the FTIR spectra peaks occurred, from approximately 1650 cm⁻¹ to 1637 cm⁻¹. This suggests an increase in the β-sheet-rich structural region and would indicate fibrillation of insulin in the presence of SNAC. However, the position of the β-sheet peak in these SNAC systems at pH 6 was slightly upshifted compared with that of the samples at pH 2 (ESI Fig. 21a†). This upshift is associated with the weakening of hydrogen bonding and more loosely packed β-sheet structures. Similar results were also observed by Iannuzzi et al. for insulin at pH 7.⁴⁷

Finally, we conducted a DSSP analysis of the insulin-containing systems. Across all systems, a higher percentage of α-helices (approximately 50%) and random structures (approximately 45–47%) was observed, while the percentage of β-sheet structures was relatively lower (approximately 3–5%), as shown in ESI Fig. 23.† These values align well with the peaks observed in the FTIR spectra of native insulin and systems with higher pH, indicating the prevalence of α-helix and random structures.^40–42 Thus, the DSSP results suggest minimal structural rearrangements in the insulin molecules during the simulations, indicating that the timescale for insulin aggregation or fibrillation (in the presence of PEs such as SNAC) is longer than what was simulated. It is worth noting though that the results indicated a slightly higher percentage of β-sheet structures when simulations were initiated from the aggregated state of insulin.

Conclusions

In this study, we employed AAMD simulations to investigate the interaction patterns between different peptides and two different permeability enhancers in the presence of varying concentrations of taurocholate, a bile salt compound. AAMD simulations can accurately predict the aggregation tendencies of both water-soluble peptides such as octreotide and hexarelin, and peptides with higher aggregation tendencies, such as degarelix and insulin. The simulation also showed the formation of mixed colloids when PEs and taurocholates were added to the simulation box with peptides.

PEs and taurocholates were capable of reducing the peptide–peptide contact interactions and key hydrogen bond formations, which are the main driving elements in peptide aggregation. We also found that SNAC is relatively more effective in restricting the peptide–peptide interactions compared to caprate, likely due to its larger size. Lowering the peptide concentration also reduces the amount of peptide–peptide interactions and increases the interaction of peptides with PEs and taurocholates. We also demonstrated the importance of considering different starting configurations in the simulations to better understand the impact of the initial state of the peptide aggregates on the molecular interaction pattern among peptides, PEs, and taurocholate. For instance, when the peptides were randomly placed in the simulation box initially, we observed more dynamic molecular aggregation pathways for the peptides in the presence of PEs and taurocholate compared to the peptide-only systems.

We showed that US simulations can provide valuable information about the release of peptide molecules from mixed colloids. PEs and taurocholate were found to decrease the release rate of water-soluble peptides such as octreotide and hexarelin in the aqueous phase. However, the release of the highly hydrophobic degarelix can be enhanced in the presence of PEs and taurocholate. The unrestrained simulation also highlighted key interactions between peptide residues leading to aggregation and interactions with peptides and PEs/taurocholates within the mixed colloids. Any means of changing or adjusting these crucial interactions, would potentially allow the peptide release profiles to be modified. Furthermore, the simulation provides a means to quantify and adjust interactions among the components in this study by altering their concentrations. Changes in the components and the concentrations in the constituent components in the systems might obviously impact the overall interaction patterns.

The FTIR spectra showed the prevalence of α-helices and random structures in the insulin at pH 6. The inclusion of caprate and taurocholate showed similar results. However, peaks of the FTIR spectra indicate an increase in the β-sheet-rich structural region in the presence of SNAC. Overall, our study revealed important molecular-level interaction patterns among the peptides, PEs, and taurocholates, which will be crucial for designing PE-based dosage forms with desired release profiles for specific peptides. Achieving a more controlled release profile near the absorption site will significantly improve the bioavailability of peptide drugs.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The computations/data handling were/was enabled by resources provided by the National Academic Infrastructure for Supercomputing in Sweden (NAISS) and the Swedish National Infrastructure for Computing (SNIC) at the Uppsala Multidisciplinary Center for Advanced Computational Science (UPPMAX), the Center for High-Performance Computing (PDC), and the High-Performance Computing Center North (HPC2N) partially funded by the Swedish Research Council through grant agreements no. 2022-06725 and no. 2018-05973. Financial support from VINNOVA (2019-00048) for the Swedish Drug Delivery Center (SweDeliver) is gratefully acknowledged.

References

1. L. Wang, N. Wang, W. Zhang, X. Cheng, Z. Yan, G. Shao, X. Wang, R. Wang and C. Fu, Therapeutic Peptides: Current Applications and Future Directions, Signal Transduction Targeted Ther., 2022, 7, 48,  DOI:10.1038/s41392-022-00904-4.
2. M. C. Smith and J. E. Gestwicki, Features of Protein–Protein Interactions That Translate into Potent Inhibitors: Topology, Surface Area and Affinity, Expert Rev. Mol. Med., 2012, 14, e16,  DOI:10.1017/erm.2012.10.
3. T. J. Tucker, M. W. Embrey, C. Alleyne, R. P. Amin, A. Bass, B. Bhatt, E. Bianchi, D. Branca, T. Bueters, N. Buist, S. N. Ha, M. Hafey, H. He, J. Higgins, D. G. Johns, A. D. Kerekes, K. A. Koeplinger, J. T. Kuethe, N. Li, B. Murphy, P. Orth, S. Salowe, A. Shahripour, R. Tracy, W. Wang, C. Wu, Y. Xiong, H. J. Zokian, H. B. Wood and A. Walji, A Series of Novel, Highly Potent, and Orally Bioavailable Next-Generation Tricyclic Peptide PCSK9 Inhibitors, J. Med. Chem., 2021, 64(22), 16770–16800,  DOI:10.1021/acs.jmedchem.1c01599.
4. C. M. Ballantyne, P. Banka, G. Mendez, R. Garcia, J. Rosenstock, A. Rodgers, G. Mendizabal, Y. Mitchel and A. L. Catapano, Phase 2b Randomized Trial of the Oral PCSK9 Inhibitor MK-0616, J. Am. Coll. Cardiol., 2023, 81(16), 1553–1564,  DOI:10.1016/j.jacc.2023.02.018.
5. S. Berg, H. Edlund, W. R. F. Goundry, C. A. S. Bergström and N. M. Davies, Considerations in the Developability of Peptides for Oral Administration When Formulated Together with Transient Permeation Enhancers, Int. J. Pharm., 2022, 628, 122238,  DOI:10.1016/j.ijpharm.2022.122238.
6. C. Roos, D. Dahlgren, E. Sjögren, M. Sjöblom, M. Hedeland and H. Lennernäs, Effects of Absorption-Modifying Excipients on Jejunal Drug Absorption in Simulated Fasted and Fed Luminal Conditions, Eur. J. Pharm. Biopharm., 2019, 142, 387–395,  DOI:10.1016/j.ejpb.2019.07.012.
7. K. Gradauer, A. Nishiumi, K. Unrinin, H. Higashino, M. Kataoka, B. L. Pedersen, S. T. Buckley and S. Yamashita, Interaction with Mixed Micelles in the Intestine Attenuates the Permeation Enhancing Potential of Alkyl-Maltosides, Mol. Pharm., 2015, 12(7), 2245–2253,  DOI:10.1021/mp500776a.
8. T. J. Dening, J. T. Douglas and M. J. Hageman, Do Macrocyclic Peptide Drugs Interact with Bile Salts under Simulated Gastrointestinal Conditions?, Mol. Pharm., 2021, 18(8), 3086–3098,  DOI:10.1021/acs.molpharmaceut.1c00309.
9. S. T. Buckley, T. A. Bækdal, A. Vegge, S. J. Maarbjerg, C. Pyke, J. Ahnfelt-Rønne, K. G. Madsen, S. G. Schéele, T. Alanentalo and R. K. Kirk, Transcellular Stomach Absorption of a Derivatized Glucagon-like Peptide-1 Receptor Agonist, Sci. Transl. Med., 2018, 10(467), eaar7047,  DOI:10.1126/scitranslmed.aar7047.
10. N. G. Lamson, K. C. Fein, J. P. Gleeson, A. N. Newby, S. Xian, K. Cochran, N. Chaudhary, J. R. Melamed, R. L. Ball, K. Suri, V. Ahuja, A. Zhang, A. Berger, D. Kolodieznyi, B. F. Schmidt, G. L. Silva and K. A. Whitehead, The strawberry-derived permeation enhancer pelargonidin enables oral protein delivery, Proc. Natl. Acad. Sci. U. S. A., 2022, 119(33), e2207829119,  DOI:10.1073/pnas.2207829119.
11. H. Weng, L. Hu, L. Hu, Y. Zhou, A. Wang, N. Wang, W. Li, C. Zhu, S. Guo, M. Yu and Y. Gan, The Complexation of Insulin with Sodium N–[8−(2−hydroxybenzoyl)Amino]–caprylate for Enhanced Oral Delivery: Effects of Concentration, Ratio, and PH, Chin. Chem. Lett., 2022, 33(4), 1889–1894,  DOI:10.1016/j.cclet.2021.10.023.
12. O. Pabois, R. M. Ziolek, C. D. Lorenz, S. Prévost, N. Mahmoudi, M. W. A. Skoda, R. J. L. Welbourn, M. Valero, R. D. Harvey, M. M. L. Grundy, P. J. Wilde, I. Grillo, Y. Gerelli and C. A. Dreiss, Morphology of Bile Salts Micelles and Mixed Micelles with Lipolysis Products, from Scattering Techniques and Atomistic Simulations, J. Colloid Interface Sci., 2021, 587, 522–537,  DOI:10.1016/j.jcis.2020.10.101.
13. B. Barz, Q. Liao and B. Strodel, Pathways of Amyloid-β Aggregation Depend on Oligomer Shape, J. Am. Chem. Soc., 2018, 140(1), 319–327,  DOI:10.1021/jacs.7b10343.
14. B. Barz, D. J. Wales and B. Strodel, A Kinetic Approach to the Sequence-Aggregation Relationship in Disease-Related Protein Assembly, J. Phys. Chem. B, 2014, 118(4), 1003–1011,  DOI:10.1021/jp412648u.
15. J. Hjalte, S. Hossain, A. Hugerth, H. Sjögren, M. Wahlgren, P. Larsson and D. Lundberg, Aggregation Behavior of Structurally Similar Therapeutic Peptides Investigated by ¹H NMR and All-Atom Molecular Dynamics Simulations, Mol. Pharm., 2022, 19(3), 904–917,  DOI:10.1021/acs.molpharmaceut.1c00883.
16. H. Fatafta, M. Khaled, M. C. Owen, A. Sayyed-Ahmad, B. Strodel and G. Hummer, Amyloid-β Peptide Dimers Undergo a Random Coil to β-Sheet Transition in the Aqueous Phase but Not at the Neuronal Membrane, Proc. Natl. Acad. Sci. U. S. A., 2021, 118(39) DOI:10.1073/pnas.2106210118.
17. C. Hussein, Effect of Hofmeister Ions on Protein Stability and Amyloid Aggregation. PhD thesis, University of Copenhagen, Copenhagen, 2022.
18. P. Gadgil, C. Alleyne, K.-I. Feng, M. Hu, M. Gindy, A. V. Buevich, S. Fauty, G. Salituro, J. Wen, Y. Li, R. Nofsinger, T. K. Sawyer and N. Buist, Assessing the Utility of In Vitro Screening Tools for Predicting Bio-Performance of Oral Peptide Delivery, Pharm. Res., 2019, 36(10), 151,  DOI:10.1007/s11095-019-2682-8.
19. S. Berg, J. Krause, A. Björkbom, K. Walter, S. Harun, A. Granfeldt, D. Janzén, S. F. Nunes, M. Antonsson, N. Van Zuydam, S. Skrtic, A. Hugerth, W. Weitschies, N. Davies, B. Abrahamsson and C. A. S. Bergström, In Vitro and In Vivo Evaluation of 3D Printed Capsules with Pressure Triggered Release Mechanism for Oral Peptide Delivery, J. Pharm. Sci., 2021, 110(1), 228–238,  DOI:10.1016/j.xphs.2020.10.066.
20. S. Berg, D. Suljovic, L. Kärrberg, M. Englund, H. Bönisch, I. Karlberg, N. Van Zuydam, B. Abrahamsson, A. Martin Hugerth, N. Davies and C. A. S. Bergström, Intestinal Absorption of FITC-Dextrans and Macromolecular Model Drugs in the Rat Intestinal Instillation Model, Mol. Pharm., 2022, 19(7), 2564–2572,  DOI:10.1021/acs.molpharmaceut.2c00261.
21. J. R. Kanicky and D. O. Shah, Effect of Premicellar Aggregation on the PKa of Fatty Acid Soap Solutions, Langmuir, 2003, 19(6), 2034–2038,  DOI:10.1021/la020672y.
22. M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindah, Gromacs: High Performance Molecular Simulations through Multi-Level Parallelism from Laptops to Supercomputers, SoftwareX, 2015, 1–2, 19–25,  DOI:10.1016/j.softx.2015.06.001.
23. J. Huang and A. D. Mackerell, CHARMM36 All-Atom Additive Protein Force Field: Validation Based on Comparison to NMR Data, J. Comput. Chem., 2013, 34(25), 2135–2145,  DOI:10.1002/jcc.23354.
24. K. Vanommeslaeghe and A. D. J. MacKerell, Automation of the CHARMM General Force Field (CGenFF) I: Bond Perception and Atom Typing, J. Chem. Inf. Model., 2012, 52(12), 3144–3154,  DOI:10.1021/ci300363c.
25. K. Vanommeslaeghe, E. Prabhu Raman and A. D. MacKerell Jr., Automation of the CHARMM General Force Field (CGenFF) II: Assignment of Bonded Parameters and Partial Atomic Charges, J. Chem. Inf. Model., 2012, 52(12), 3155–3168,  DOI:10.1021/ci3003649.
26. C. G. Mayne, J. Saam, K. Schulten, E. Tajkhorshid and J. C. Gumbart, Rapid Parameterization of Small Molecules Using the Force Field Toolkit, J. Comput. Chem., 2013, 34(32), 2757–2770,  DOI:10.1002/jcc.23422.
27. S. Hossain, A. Parrow, A. Kabedev, R. C. Kneiszl, Y. Leng and P. Larsson, Explicit-Ph Coarse-Grained Molecular Dynamics Simulations Enable Insights into Restructuring of Intestinal Colloidal Aggregates with Permeation Enhancers, Processes, 2022, 10(1) DOI:10.3390/pr10010029.
28. A. Croitoru, S.-J. Park, A. Kumar, J. Lee, W. Im, A. D. MacKerell Jr. and A. Aleksandrov, Additive CHARMM36 Force Field for Nonstandard Amino Acids, J. Chem. Theory Comput., 2021, 17(6), 3554–3570,  DOI:10.1021/acs.jctc.1c00254.
29. M. Parrinello and A. Rahman, Polymorphic Transitions in Single Crystals: A New Molecular Dynamics Method, J. Appl. Phys., 1981, 52(12), 7182–7190,  DOI:10.1063/1.328693.
30. G. Bussi, D. Donadio and M. Parrinello, Canonical Sampling through Velocity Rescaling, J. Chem. Phys., 2007, 126(1) DOI:10.1063/1.2408420.
31. T. Darden, D. York and L. Pedersen, Particle Mesh Ewald: An N·log(N) Method for Ewald Sums in Large Systems, J. Chem. Phys., 1993, 98(12), 10089–10092,  DOI:10.1063/1.464397.
32. P. Shannon, A. Markiel, O. Ozier, N. S. Baliga, J. T. Wang, D. Ramage, N. Amin, B. Schwikowski and T. Ideker, Cytoscape: A Software Environment for Integrated Models of Biomolecular Interaction Networks, Genome Res., 2003, 13(11), 2498–2504,  DOI:10.1101/gr.1239303.
33. W. Kabsch and C. Sander, Dictionary of Protein Secondary Structure: Pattern Recognition of Hydrogen-Bonded and Geometrical Features, Biopolymers, 1983, 22(12), 2577–2637,  DOI:10.1002/bip.360221211.
34. W. G. Touw, C. Baakman, J. Black, T. A. H. te Beek, E. Krieger, R. P. Joosten and G. Vriend, A Series of PDB-Related Databanks for Everyday Needs, Nucleic Acids Res., 2015, 43(D1), D364–D368,  DOI:10.1093/nar/gku1028.
35. W. Humphrey, A. Dalke and K. Schulten, VMD: Visual Molecular Dynamics, J. Mol. Graphics, 1996, 14, 33–38,  DOI:10.1016/0263-7855(96)00018-5.
36. W. D. Lougheed, H. Woulfe-Flanagan, J. R. Clement and A. M. Albisser, Insulin Aggregation in Artificial Delivery Systems, Diabetologia, 1980, 19(1), 1–9,  DOI:10.1007/BF00258302.
37. A. H. Pekar and B. H. Frank, Conformation of Proinsulin. Comparison of Insulin and Proinsulin Self-Association at Neutral PH, Biochemistry, 1972, 11(22), 4013–4016,  DOI:10.1021/bi00772a001.
38. S.-H. Wang, X.-Y. Dong and Y. Sun, Effect of (−)-Epigallocatechin-3-Gallate on Human Insulin Fibrillation/Aggregation Kinetics, Biochem. Eng. J., 2012, 63, 38–49,  DOI:10.1016/j.bej.2012.02.002.
39. A. Das, M. Shah and I. Saraogi, Molecular Aspects of Insulin Aggregation and Various Therapeutic Interventions, ACS Bio Med Chem Au, 2022, 2(3), 205–221,  DOI:10.1021/acsbiomedchemau.1c00054.
40. M. Manno, E. F. Craparo, A. Podestà, D. Bulone, R. Carrotta, V. Martorana, G. Tiana and P. L. San Biagio, Kinetics of Different Processes in Human Insulin Amyloid Formation, J. Mol. Biol., 2007, 366(1), 258–274,  DOI:10.1016/j.jmb.2006.11.008.
41. H. Chaaban, J. J. Vallooran, M. Van De Weert and V. Foderà, Ion-Mediated Morphological Diversity in Protein Amyloid Systems, J. Phys. Chem. Lett., 2022, 13(16), 3586–3593,  DOI:10.1021/acs.jpclett.2c00182.
42. L. Nielsen, S. Frokjaer, J. F. Carpenter and J. Brange, Studies of the Structure of Insulin Fibrils by Fourier Transform Infrared (FTIR) Spectroscopy and Electron Microscopy, J. Pharm. Sci., 2001, 90(1), 29–37,  DOI:10.1002/1520-6017(200101)90:1<29::AID-JPS4>3.0.CO;2-4.
43. E. J. Ambrose, A. Elliott and A. H. Wilson, Infra-Red Spectroscopic Studies of Globular Protein Structure, Proc. R. Soc. London, Ser. A, 1951, 208(1092), 75–90,  DOI:10.1098/rspa.1951.0145.
44. S. N. Timashef, H. Susi and L. Stevens, Infrared Spectra and Protein Conformations in Aqueous Solutions: II. Survey of Globular Proteins, J. Biol. Chem., 1967, 242(23), 5467–5473,  DOI:10.1016/S0021-9258(18)99382-8.
45. M. J. Pikal and D. R. Rigsbee, The Stability of Insulin in Crystalline and Amorphous Solids: Observation of Greater Stability for the Amorphous Form, Pharm. Res., 1997, 14(10), 1379–1387,  DOI:10.1023/A:1012164520429.
46. J. Fallingborg, Intraluminal PH of the Human Gastrointestinal Tract, Dan. Med. Bull., 1999, 46(3), 183–196.
47. C. Iannuzzi, M. Borriello, M. Portaccio, G. Irace and I. Sirangelo, Insights into Insulin Fibril Assembly at Physiological and Acidic PH and Related Amyloid Intrinsic Fluorescence, Int. J. Mol. Sci., 2017, 18(12), 2551,  DOI:10.3390/ijms18122551.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3nr05571j

---