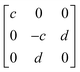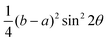Anisotropy and thermal properties in GeTe semiconductor by Raman analysis†
Shuai
Yang
 ,
Fengrui
Sui
,
Yucheng
Liu
,
Fengrui
Sui
,
Yucheng
Liu
 ,
Ruijuan
Qi
*,
Xiaoyu
Feng
,
Shangwei
Dong
,
Ruijuan
Qi
*,
Xiaoyu
Feng
,
Shangwei
Dong
 ,
Pingxiong
Yang
and
Fangyu
Yue
*
,
Pingxiong
Yang
and
Fangyu
Yue
*
Key Laboratory of Polar Materials and Devices (MOE), Department of Electronics, East China Normal University, Shanghai 200241, China. E-mail: fyyue@ee.ecnu.edu.cn; rjqi@ee.ecnu.edu.cn
First published on 25th July 2023
Abstract
Low-symmetric GeTe semiconductors have attracted wide-ranging attention due to their excellent optical and thermal properties, but only a few research studies are available on their in-plane optical anisotropic nature that is crucial for their applications in optoelectronic and thermoelectric devices. Here, we investigate the optical interactions of anisotropy in GeTe using polarization-resolved Raman spectroscopy and first-principles calculations. After determining both armchair and zigzag directions in GeTe crystals by transmission electron microscopy, we found that the Raman intensity of the two main vibrational modes had a strong in-plane anisotropic nature; the one at ∼88.1 cm−1 can be used to determine the crystal orientation, and the other at ∼124.6 cm−1 can reveal a series of temperature-dependent phase transitions. These results provide a general approach for the investigation of the anisotropy of light–matter interactions in low-symmetric layered materials, benefiting the design and application of optoelectronic, anisotropic thermoelectric, and phase-transition memory devices based on bulk GeTe.
1. Introduction
Low-symmetric two-dimensional (2D) layered materials present intriguing in-plane anisotropy.1–4 For instance, GaTe, GeSe, GeAs, and black phosphorus have been reported to have significant directional dependence of their photoemission, thermoelectricity, and mobility properties, mainly due to the anisotropic light–matter interactions, such as the electron–photon and electron–phonon couplings.1,2,4–8 As a typical binary IV–VI chalcogenide with a rhombohedral (α-phase; or pseudo-cubic) crystal structure at room temperature that is formed by distortion at high-temperature of the cubic phase,9,10 GeTe (R3m-C3v space group) has advantages for application in thermal-/opto-electronic devices, e.g., with a maximum thermoelectric figure-of-merit (ZT) value of ∼0.8 that can be improved up to the currently known 2.7 at 750 K (ref. 11) by elemental doping, as well as substitution or alloying with other compounds.12–16 Based on the successful realization of the electrical control of the electronic spin states, GeTe can be used to prepare spin and photovoltaic devices due to its giant bulk Rashba spin–orbit coupling,17–19 strong ferroelectric polarization (64–70 μC cm−2), and high ferroelectric transition temperature.20,21 Simultaneously, GeTe has been widely used in phase-change memory devices and phase-change switches because of its reversible phase change (e.g., α and β phases), rapid crystallization, and a great difference among the optical and electrical properties of amorphous and crystalline states.22–27 More importantly, as a member of the family of low-symmetric layered materials, GeTe has a narrow bandgap (Eg) of ∼0.7 eV, which is rather useful for infrared optoelectronic devices, including light-emission and light-detection.28,29 For example, Zhao et al. reported a prototype photodetector based on GeTe films with a high responsivity of 102 A W−1 and a detectivity of 1013 Jones under irradiation with an 850 nm laser.30 These suggest that, being a low-symmetric laminate material with strong anisotropic nature, GeTe has the potential to be a promising material for use in polarization-dependent optothermal or optoelectrical devices. However, only a few studies have focused on its in-plane anisotropy and no unified consensus is found on the study of its vibrational modes and the phase transition relationships.In this work, we investigate the in-plane anisotropy of low-symmetric rhombohedral GeTe crystals using high-angle annular dark-field scanning transmission electron microscopy (HAADF-STEM), Raman spectroscopy, and first-principles calculations. By analyzing the vibrational modes via the polarization- and temperature-dependent Raman results under parallel and cross configurations, we observed up to four Raman active modes. Based on this, the crystal orientation could be determined and the symmetry of the crystal structure could be understood. Furthermore, a strong four-phonon coupling process was analyzed during the change in temperature and the temperature-induced phase transitions between the α, γ, and β phases could be determined in GeTe.
2. Experimental and theoretical details
Single-crystalline rhombohedral (R) GeTe (α-phase) was purchased from 2D semiconductors. GeTe crystal with a thickness of less than ∼5 mm was used in this work. Crystal X-ray diffractions (XRD) were performed at 300 K (Bruker D8 VENTURE) using Mo-Kα radiation (λ = 0.711 Å). Integration and scaling of intensity data were performed using the SAINT program. Data were corrected for the effects of absorption using SADABS. The cross-sectional TEM lamellae were fabricated on a dual-beam focused ion beam system (Helios G4 UX, FEI, USA) using Ga-ion accelerating voltages ranging from 2 to 30 kV. The (HAADF-STEM) images were acquired on a Cs-TEM (JEOL Grand ARM300) by an annular dark-field image detector with the inner semi-angle larger than 64 mrad. Raman measurements were performed on the inVia Reflex confocal micro-Raman spectrometer (Renishaw) equipped with a 532 nm excitation source from a solid-state laser and a 50× objective. For the polarization-dependent Raman measurement, a linear polarizer (or together with a waveplate) was placed before the detector to achieve parallel or cross configurations between the scattering and incident lights. During measurements, the sample was rotated with a step of 15°.The electronic structure of bulk GeTe was calculated using the Kohn–Sham density functional theory (KS-DFT).31 The real space electronic structure calculator (RESCU) was used to calculate the phonon modes and the phonon scattering relationship for bulk GeTe.32,33 The exchange–correlation potential was described by the generalized gradient approximation (GGA) of the Perdew–Burke–Ernzerhof functional (PBE).34 The Monkhorst–Pack scheme with 7 × 7 × 7 mesh was used to sample k-points of the Brillouin zone of bulk GeTe. The physical quantities were expanded using the real space lattice method, and the self-consistent field procedure was performed until the global charge variation was less than 10−5. Lattice-dynamical properties were obtained for the Γ-point using the direct-force constant approach.
3. Results and discussion
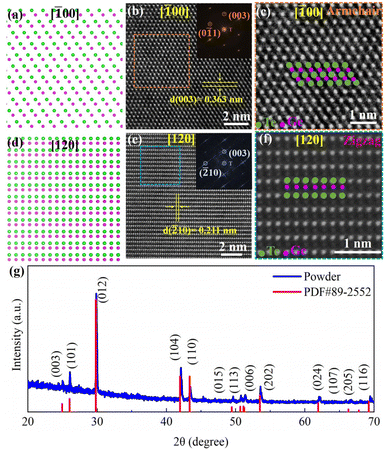
Bulk α-GeTe belongs to a trigonal R3m space group, consisting of three Ge and three Te atoms in the unit cell. Ge2+ (Te2−) is bonded to six equivalent Te2− (Ge2+) atoms to form a mixture of edge and corner-sharing GeTe6 (TeGe6) octahedra. The corner-sharing octahedral tilt angles are 10°. There are three shorter (2.86 Å) and three longer (3.25 Å) Ge–Te bonds. Fig. 1b and e show the representative HAADF-STEM images and the corresponding FFT patterns taken along [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 00]R and [120]R zone axes; these show the regular atomic arrangements of the armchair (AC) and zigzag (ZZ) directions, which are in line with the simulated structure of α-GeTe (Fig. 1a and d). The crystal plane spacing of (
00]R and [120]R zone axes; these show the regular atomic arrangements of the armchair (AC) and zigzag (ZZ) directions, which are in line with the simulated structure of α-GeTe (Fig. 1a and d). The crystal plane spacing of (![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 10) and (003) is 0.211 nm and 0.363 nm, respectively. The zoom-in HAADF images in Fig. 1c and f show clear atomic configurations for both the AC and ZZ directions for R-phase GeTe with brighter spots representing Te columns and smaller ones for Ge columns. To get accurate phase information by using the powder XRD technique, we ground GeTe crystal into powders, so that we could obtain all the related diffraction peaks. As shown in Fig. 1g, together with the standard card of PDF#89-2552, all diffraction peaks could be indexed to an R-phase structure of the GeTe crystal with lattice parameters a = b = 4.230 Å and c = 10.889 Å, which is in agreement with previous reports.11,35
10) and (003) is 0.211 nm and 0.363 nm, respectively. The zoom-in HAADF images in Fig. 1c and f show clear atomic configurations for both the AC and ZZ directions for R-phase GeTe with brighter spots representing Te columns and smaller ones for Ge columns. To get accurate phase information by using the powder XRD technique, we ground GeTe crystal into powders, so that we could obtain all the related diffraction peaks. As shown in Fig. 1g, together with the standard card of PDF#89-2552, all diffraction peaks could be indexed to an R-phase structure of the GeTe crystal with lattice parameters a = b = 4.230 Å and c = 10.889 Å, which is in agreement with previous reports.11,35
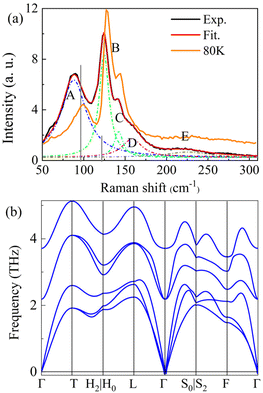
We performed Raman measurements on the GeTe crystal at different temperatures. Fig. 2a shows the Raman spectra of bulk GeTe at 300 K and ∼80 K (more details in Fig. S3†) with a similar curve shape. A fit procedure on the curve of 300 K roughly presented five peaks, which were denoted as A, B, C, D, and E at 88.1 cm−1, 124.6 cm−1, 142.2 cm−1, 158.4 cm−1, and 225.5 cm−1, respectively. The two characteristic peaks, A and B, originated from the Ge–Te vibration; the former among these is the double-degenerate E symmetry transverse/longitudinal optical modes, and the latter is the A1 symmetry transverse optical mode.36–39 Peak C is due to the long-range interactions between crystalline Te, and peak D is triggered by the vibrational density of states of the long Te chains in disorder.37,40 Peak E may be assigned to the antisymmetric stretching mode of the GeTe4 tetrahedra.41 The calculated Raman peaks by the density functional perturbation theory (DFPT)42 are also shown with black vertical lines in Fig. 2a. Fig. 2b depicts the calculated phonon dispersion results. There are three acoustic waves with zero frequency at the Γ point, and the rest are optical waves. The phonon spectrum has negligible tiny virtual frequencies near the Γ point, indicating good dynamical stability of the model structure. Based on the group theory, GeTe has a total of two phonon modes, E (96.3 cm−1) and A1 (121.8 cm−1), and both are Raman- and infrared-active. By comparing with the theoretical and experimental (at ∼80 K) values in Fig. 2a, where the values of E and A1 modes are experimentally 99 and 127 cm−1, respectively, we can find a frequency difference in the two main modes, i.e., ∼2.7 and ∼5.2 cm−1 blue shifts of E and A1 modes, respectively. Inconsistency was also observed in low-symmetric ReSe2,43 whose reason was ascribed to the weak interlayer interaction due to the presence of both in-plane and out-of-plane components in their Ag vibrational modes. Therefore, the frequency shift in the A1 mode may be understood as a competition between the interlayer coupling and the dielectric shielding. However, the maximum frequency shift of only 4 cm−1 in ReSe2 was significantly different from that observed with the E mode. This suggests that other potential influences may be involved here, e.g., the effect of temperature.44 Notice that according to the DFT calculation (Fig. S1†), the direct Eg transition for bulk GeTe is located at the L point (Eg = 0.71 eV), and a slightly larger Eg can be seen at the T point (0.88 eV). The highest valence band (VB) and the lowest conduction band (CB) are dominated by the 4p orbital of Ge and the 5p orbital of Te, respectively. These observations are consistent with previous work28 and verify the reliability and accuracy of the calculated results.
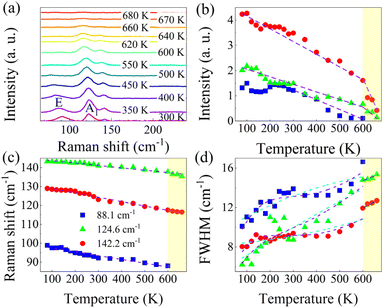
Polarization-resolved Raman measurements were further performed. Fig. 3a–d show the polar plot of the Raman intensity for the two Raman modes, E (88.1 cm−1) and A1 (124.6 cm−1). The results for other modes are shown in Fig. S2;† the Raman modes exhibit different degrees of anisotropy. The E mode exhibits strong anisotropy in both cross (Fig. 3a) and parallel (Fig. 3c) configurations with a period of 90°, but with an angular difference of ∼45° for the intensity maximum and minimum values. The mode of A1 exhibits a two-lobe shape only in the cross configuration (Fig. 3b) with a period of 180°. While the behavior in the parallel configuration exhibits an asymmetric case (Fig. 3d), the poles correspond to the same angles as in the cross configuration. One of the reasons for this phenomenon may be the non-normal incident of the laser onto the surface of GeTe.
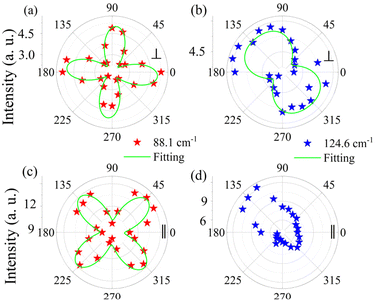 | ||
| Fig. 3 (a)–(d) Polar plots of the peak intensity of E and A1 modes under the polarization configurations (parallel or cross). Stars – experimental values; green curves – fit results. | ||
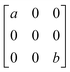
To better understand the results of polarization-resolved Raman spectroscopy of GeTe, the second-order Raman tensor for the Raman mode is taken into account. According to the classical Placzek approximation,45 the Raman intensity can be written as,
| I ∝ |ei·R·es|2 | (1) |
In the current geometrical configuration, ei and es are in the x–z plane. Thus, the incident polarization angle of θ is set to the crystal axis, ei = (cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ, 0, sin
θ, 0, sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ), while es = (cos
θ), while es = (cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ, 0, sin
θ, 0, sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ)T (parallel polarization configuration) and (−sin
θ)T (parallel polarization configuration) and (−sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ, 0, cos
θ, 0, cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ)T (cross-polarization configuration). Table 2 shows the derived intensity for A1 and E modes in parallel and cross-polarization configurations obtained from eqn (1). The measured data for E (88.1 cm−1) mode exhibited a tetrad shape, which could be traced well by the equation listed in the table; also see Fig. 3a and c. However, the modes of 124.6 cm−1 (and 142.2 cm−1) are poorly fitted, which may be due to the light absorption and birefringence effects mentioned above. There was no obvious rule for the 158.4 cm−1 mode, probably due to the vibration of disordered long Te chains. The period of 225.5 cm−1 in both configurations is 90°, which is the same as that of 88.1 cm−1 corresponding to the antisymmetric stretching mode of the GeTe4 tetrahedron. Thus, for GeTe, the maxima of the E Raman intensity can be aligned along 0° in the parallel polarization configuration. This indicates that 0 or 90° corresponds to either the x- or y-axis of the GeTe crystal, indicating the crystal orientation.
θ)T (cross-polarization configuration). Table 2 shows the derived intensity for A1 and E modes in parallel and cross-polarization configurations obtained from eqn (1). The measured data for E (88.1 cm−1) mode exhibited a tetrad shape, which could be traced well by the equation listed in the table; also see Fig. 3a and c. However, the modes of 124.6 cm−1 (and 142.2 cm−1) are poorly fitted, which may be due to the light absorption and birefringence effects mentioned above. There was no obvious rule for the 158.4 cm−1 mode, probably due to the vibration of disordered long Te chains. The period of 225.5 cm−1 in both configurations is 90°, which is the same as that of 88.1 cm−1 corresponding to the antisymmetric stretching mode of the GeTe4 tetrahedron. Thus, for GeTe, the maxima of the E Raman intensity can be aligned along 0° in the parallel polarization configuration. This indicates that 0 or 90° corresponds to either the x- or y-axis of the GeTe crystal, indicating the crystal orientation.
Fig. 4a shows the Raman spectra of GeTe during the temperature range of 300–680 K (see Fig. S3† for results at low temperature). With the increase in temperature, the Raman peaks of the three strong modes showed different red-shifts and broadenings, which were generally related to anharmonic phonon interactions, electron–phonon coupling, or thermal expansion.46 For clarity, Fig. 4b–d depict the temperature dependence of the peak intensity, position, and full-width at half-maximum (FWHM) of the three Raman modes. From Fig. 4b, we can see that the 88.1 cm−1 mode disappears beyond ∼600 K, and the modes at 124.6 cm−1 and 142.2 cm−1 were not visible after 670 K; in addition, the clear inflection points (different slopes or disappearing) can be seen at 600 or 670 K (shadow zone), which may suggest that the GeTe undergoes different temperature-induced phase transitions. In Fig. 4c, all three modes were almost linearly red-shifted with an increase in temperature, which could be fitted with the following expression,
| ω(T) = ω0 + χT | (2) |
Simultaneously, as shown in Fig. 4d, the FWHM of three modes shows different trends with increasing temperature, where the FWHM of 88.1 and 124.6 cm−1 modes shows a similar temperature-dependent trend but with a slight decrease in the temperature range of 300–450 K. It is well known that the smaller the FWHM is, the more regular the crystal vibration is and the more stable the crystal structure is. On the contrary, after 450 K the FWHM increases significantly, and the crystal structure starts to become unstable; additionally, the E and A1 modes start to present thermal-related broadening. The 142.2 cm−1 mode showed an approximately linear evolution with the temperature here, which is mainly due to the presence of the homopolar bonding of Te–Te, a trend that is prevalent in Te compounds, such as BiTe.51 When the temperature reaches 600 K, the E mode at 88.1 cm−1 disappears, and the A1 mode at 124.6 cm−1 maintains a slightly linear increase till the temperature is beyond 670 K, where the Raman pattern approaches a curve with a very low signal-to-noise ratio without the appearance of evident peaks. A comparison with the results of Raman intensity and shift shows that these behaviors are consistent with the three key parameters.
It has been reported that GeTe can spontaneously transit between the polar α-phase (rhombohedral, low-temperature phase) and the β-phase (cubic, high-temperature phase) at the Curie temperature of ∼625 K,52 and the phase transition temperature of GeTe is highly influenced by its stoichiometric ratio. For instance, Rinaldi et al. found that the tendency of Te to detach from GeTe at high temperatures leads to a change in its stoichiometric ratio.17 Therefore, we believe that the GeTe has started to undergo a phase change, when the temperature is close to ∼600 K, and may complete the phase transition process after ∼670 K by referring to the similar temperature-dependent way and the almost simultaneous disappearance of the modes of 124.6 and 142.2 cm−1. Thus, by combining with the phase diagram involving the composition ratio-dependent phase transition dynamics of GeTe,10 we suggest that in the temperature range of 600–670 K, the status of GeTe comprises mixed α, γ, and β phases, i.e., first from α phase to γ phase and then to β phase with the increase in temperature. For the high-temperature stable β phase with a sodium chloride structure, the previous report gave a phase transition temperature of 670 K,53 and a close phase transition temperature of 673 K was also reported.10
Notice that the FWHM broadening of the Raman peaks can be fitted with the higher-order phonon scattering model proposed by Balkanski et al.:54
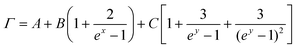 | (3) |
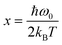 ; y = ħω0/3kBT; kB is the Boltzmann constant; and ħω0 is the specific vibration energy of a mode at 0 K. The constant (A) is the FWHM change caused by the phonon confinement effect and non-uniform strain; the constants B and C are the effects of three-phonon and four-phonon processes on the FWHM, i.e., the excited optical phonon by photons decaying into two or three phonons, respectively, due to the non-harmonic effect when the material absorbs a photon. The fit curves (cyan) are shown in Fig. 4d, and the fitted (below 600 K) results by eqn (3) are given in Table 3. It shows that the A-values are roughly the same order of magnitude, but the B- and C-values vary significantly for different peaks. The 124 and 142 cm−1 modes, where both B- and C-values are positive, indicate that both three-phonon and four-phonon processes have positive effects on the FWHM. However, in the 88 cm−1 mode, the B is positive, and the C is negative, suggesting the opposite effects of three-phonon and four-phonon processes on the FWHM. Surprisingly, although the C-value is extremely small, it is still non-negligible during the fit procedure, indicating the presence of a four-phonon coupling process in GeTe during the temperature change.
; y = ħω0/3kBT; kB is the Boltzmann constant; and ħω0 is the specific vibration energy of a mode at 0 K. The constant (A) is the FWHM change caused by the phonon confinement effect and non-uniform strain; the constants B and C are the effects of three-phonon and four-phonon processes on the FWHM, i.e., the excited optical phonon by photons decaying into two or three phonons, respectively, due to the non-harmonic effect when the material absorbs a photon. The fit curves (cyan) are shown in Fig. 4d, and the fitted (below 600 K) results by eqn (3) are given in Table 3. It shows that the A-values are roughly the same order of magnitude, but the B- and C-values vary significantly for different peaks. The 124 and 142 cm−1 modes, where both B- and C-values are positive, indicate that both three-phonon and four-phonon processes have positive effects on the FWHM. However, in the 88 cm−1 mode, the B is positive, and the C is negative, suggesting the opposite effects of three-phonon and four-phonon processes on the FWHM. Surprisingly, although the C-value is extremely small, it is still non-negligible during the fit procedure, indicating the presence of a four-phonon coupling process in GeTe during the temperature change.
| Raman shift (cm−1) | A (cm−1) | B (cm−1) | C (cm−1) |
|---|---|---|---|
| 88 (E mode) | 9.78 | 3.64 × 10−12 | −3.27 × 10−25 |
| 124 (A1 mode) | 8.25 | 3.99 × 10−13 | 1.87 × 10−25 |
| 142 (Te–Te) | 5.72 | 3.91 × 10−12 | 5.06 × 10−25 |
Due to the lack of well-fitted data using the higher-order phonon scattering model, for phase-change materials, the temperature dependence of the FWHM of Raman peaks can be investigated by the model proposed by F. Jebari et al.,55
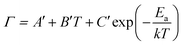 | (4) |
| Parameters | 88 (cm−1) | 124 (cm−1) | 142 (cm−1) |
|---|---|---|---|
| A′ | 6.41 | 5.14 | 3.79 |
| B′ | 4.29 × 10−2 | 3.01 × 10−2 | 3.22 × 10−2 |
| C′ | −44.45 | −30.36 | −22.81 |
| E a (kJ mol−1) | 8.19 | 7.46 | 7.75 |
Based on the FWHM of Raman peaks at different temperatures, we can semi-quantitatively estimate the thermal conductivity (K) of GeTe.58
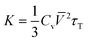 | (5) |
Where Cv, ![[V with combining macron]](https://www.rsc.org/images/entities/i_char_0056_0304.gif) , and τT are heat capacity under constant volume, averaged acoustic phonon velocity, and the thermal transport relaxation time, respectively. Under the assumed conditions, where Cv is 2kB and
, and τT are heat capacity under constant volume, averaged acoustic phonon velocity, and the thermal transport relaxation time, respectively. Under the assumed conditions, where Cv is 2kB and ![[V with combining macron]](https://www.rsc.org/images/entities/i_char_0056_0304.gif) is 5 km s−1,4,59 the thermal transport relaxation time can be approximated as the quasi-particle lifetime of the Raman optical phonon τ,
is 5 km s−1,4,59 the thermal transport relaxation time can be approximated as the quasi-particle lifetime of the Raman optical phonon τ, 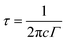 . By referring to the FWHM (Γ) value in the range of 8–16 cm−1, τ ranges from 0.33–0.66 ps. The range of the K value from eqn (5) can then be 5.5–11.0 W m−1 K−1, of which the mean value is ∼8.25 W m−1 K−1, which is extremely close to the previously-reported experimental value of 8.3 W m−1 K−1.60
. By referring to the FWHM (Γ) value in the range of 8–16 cm−1, τ ranges from 0.33–0.66 ps. The range of the K value from eqn (5) can then be 5.5–11.0 W m−1 K−1, of which the mean value is ∼8.25 W m−1 K−1, which is extremely close to the previously-reported experimental value of 8.3 W m−1 K−1.60
4. Conclusions
In summary, we present the first indication and interpretation of the vibrational modes of GeTe by combining observations with the experimental and theoretical Raman analysis; we provide an initial determination of in-plane anisotropy by polarization-resolved Raman spectroscopy, which can provide meaningful guidance to efficient thermoelectric studies due to the close relationship between structural anisotropy and the lattice thermal conductivity anisotropy. The crystal orientation of GeTe can be determined by the E mode; there is a strong four-phonon coupling process in the variable temperature process, which demonstrates a series of phase transitions starting at ∼600 K and ending at ∼670 K, which is close to previous reports. Based on the temperature-dependent FWHM of the Raman peaks, we can estimate not only the phase transition temperature and activation energy, but also the thermal parameters, including the thermal transport relaxation time and thermal conductivity. Our work may provide a useful guide to exploring the application of GeTe in thermoelectric, optoelectronic, and phase change memory devices.Author contributions
F. Y. conceived this project. S. Y., F. S., and R. Q. prepared the samples. S. Y., F. S., R. Q., Y. L., S. D., and X. F. conducted the investigations and characterizations. F. Y. and R. Q. analyzed the data. S. Y. and F. Y. drafted the original manuscript. R. Q. and P. X. reviewed and edited the manuscript with contributions from all authors. We gratefully acknowledge HZWTECH for providing computation facilities.Conflicts of interest
The authors declare that they have no competing interests.Acknowledgements
This work is supported by the National Key Research Project (2022YFA1402902), the National Natural Science Foundation of China (12134003, 62274061, 61874043, 61790583), Shanghai Science and Technology Innovation Action Plan (21JC1402000).References
- F. Xia, H. Wang and Y. Jia, Nat. Commun., 2014, 5, 4458 CrossRef CAS PubMed.
- Z. Luo, J. Maassen, Y. Deng, Y. Du, R. P. Garrelts, M. S. Lundstrom, P. D. Ye and X. Xu, Nat. Commun., 2015, 6, 8572 CrossRef CAS PubMed.
- F. Sui, M. Jin, Y. Zhang, R. Qi, Y. N. Wu, R. Huang, F. Yue and J. Chu, Nat. Commun., 2023, 14, 36 CrossRef CAS PubMed.
- Y. Liu, S. Yang, F. Sui, R. Qi, S. Dong, P. Yang and F. Yue, Phys. Chem. Chem. Phys., 2023, 25, 3745–3751 RSC.
- S. Huang, Y. Tatsumi, X. Ling, H. Guo, Z. Wang, G. Watson, A. A. Puretzky, D. B. Geohegan, J. Kong, J. Li, T. Yang, R. Saito and M. S. Dresselhaus, ACS Nano, 2016, 10, 8964–8972 CrossRef CAS PubMed.
- X. Li, Y. Machida, A. Subedi, Z. Zhu, L. Li and K. Behnia, Nat. Commun., 2023, 14, 1027 CrossRef CAS PubMed.
- J. Wang, W. Liu and C. Wang, Adv. Electron. Mater., 2023, 9, 2201126 CrossRef CAS.
- Z. Zhou, T. Shen, P. Wang, Q. Guo, Q. Wang, C. Ma, K. Xin, K. Zhao, Y. Yu, B. Qin, Y. Y. Liu, J. Yang, H. Hong, K. Liu, C. Liu, H. X. Deng and Z. Wei, Sci. Bull., 2023, 68, 173–179 CrossRef CAS PubMed.
- A. Giussani, K. Perumal, M. Hanke, P. Rodenbach, H. Riechert and R. Calarco, Phys. Status Solidi B, 2012, 249, 1939–1944 CrossRef CAS.
- H. Okamoto, J. Phase Equilib., 2000, 21, 496–496 CrossRef.
- B. B. Jiang, W. Wang, S. X. Liu, Y. Wang, C. F. Wang, Y. N. Chen, L. Xie, M. Y. Huang and J. Q. He, Science, 2022, 377, 208 CrossRef CAS PubMed.
- S. Perumal, S. Roychowdhury, D. S. Negi, R. Datta and K. Biswas, Chem. Mater., 2015, 27, 7171–7178 CrossRef CAS.
- S. Perumal, S. Roychowdhury and K. Biswas, J. Mater. Chem. C, 2016, 4, 7520–7536 RSC.
- M. Hong, Z. G. Chen, L. Yang, Y. C. Zou, M. S. Dargusch, H. Wang and J. Zou, Adv. Mater., 2018, 30, 1705942 CrossRef PubMed.
- J. Li, X. Zhang, Z. Chen, S. Lin, W. Li, J. Shen, I. T. Witting, A. Faghaninia, Y. Chen, A. Jain, L. Chen, G. J. Snyder and Y. Pei, Joule, 2018, 2, 976–987 CrossRef CAS.
- X. Y. Tan, J.-F. Dong, N. Jia, H.-X. Zhang, R. Ji, A. Suwardi, Z.-L. Li, Q. Zhu, J.-W. Xu and Q.-Y. Yan, Rare Met., 2022, 41, 3027–3034 CrossRef CAS.
- C. Rinaldi, S. Varotto, M. Asa, J. Slawinska, J. Fujii, G. Vinai, S. Cecchi, D. Di Sante, R. Calarco, I. Vobornik, G. Panaccione, S. Picozzi and R. Bertacco, Nano Lett., 2018, 18, 2751–2758 CrossRef CAS PubMed.
- Y. Yao, H. F. Huang, Y. J. Dong, H. Gu, J. L. Zhong, X. Hao and Y. Z. Wu, Ann. Phys., 2022, 534, 2100603 CrossRef CAS.
- S. W. Cho, Y. W. Lee, S. H. Kim, S. Han, I. Kim, J.-K. Park, J. Y. Kwak, J. Kim, Y. Jeong, G. W. Hwang, K. S. Lee, S. Park and S. Lee, J. Alloys Compd., 2023, 957, 170444 CrossRef CAS.
- D. Di Sante, P. Barone, R. Bertacco and S. Picozzi, Adv. Mater., 2013, 25, 509–513 CrossRef CAS PubMed.
- J. Krempaský, S. Muff, J. Minár, N. Pilet, M. Fanciulli, A. P. Weber, E. B. Guedes, M. Caputo, E. Müller, V. V. Volobuev, M. Gmitra, C. A. F. Vaz, V. Scagnoli, G. Springholz and J. H. Dil, Phys. Rev. X, 2018, 8, 021067 Search PubMed.
- B. J. Kooi and J. Momand, Phys. Status Solidi RRL, 2019, 13, 1800562 CrossRef.
- P. Guo, A. Sarangan and I. Agha, Appl. Sci., 2019, 9, 530 CrossRef CAS.
- W. Zhang, R. Mazzarello, M. Wuttig and E. Ma, Nat. Rev. Mater., 2019, 4, 150–168 CrossRef CAS.
- K. Ren, M. Zhu, W. Song, S. Lv, M. Xia, Y. Wang, Y. Lu, Z. Ji and Z. Song, Nanoscale, 2019, 11, 1595–1603 RSC.
- J. Wang, L. Gao, S. Qu, H. Chen and J. Zhang, Vacuum, 2022, 200, 111015 CrossRef CAS.
- S. Guo, Y. Wang, X. Zhang, B. Wang and J. Zhang, Mater. Lett., 2022, 329, 133199 CrossRef CAS.
- L. Vadkhiya, G. Arora, A. Rathor and B. L. Ahuja, Radiat. Phys. Chem., 2011, 80, 1316–1322 CrossRef CAS.
- A. Edwards, A. Pineda, P. Schultz, M. Martin, A. Thompson, H. Hjalmarson and C. Umrigar, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 045210–045213 CrossRef.
- Y. Zhao, L. Tang, S. Yang, K. Seng Teng and S. Ping Lau, Opt. Lett., 2020, 45, 1108–1111 CrossRef CAS PubMed.
- V. Michaud-Rioux, L. Zhang and H. Guo, J. Comput. Phys., 2016, 307, 593–613 CrossRef CAS.
- P. Kang, W.-T. Zhang, V. Michaud-Rioux, X.-H. Kong, C. Hu, G.-H. Yu and H. Guo, Phys. Rev. B, 2017, 96, 195406–195408 CrossRef.
- D. Liu, X. Chen, Y. Hu, T. Sun, Z. Song, Y. Zheng, Y. Cao, Z. Cai, M. Cao, L. Peng, Y. Huang, L. Du, W. Yang, G. Chen, D. Wei, A. T. S. Wee and D. Wei, Nat. Commun., 2018, 9, 193 CrossRef PubMed.
- J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke, Phys. Rev. Lett., 2008, 100, 136406 CrossRef PubMed.
- D. Wu, L. D. Zhao, S. Hao, Q. Jiang, F. Zheng, J. W. Doak, H. Wu, H. Chi, Y. Gelbstein, C. Uher, C. Wolverton, M. Kanatzidis and J. He, J. Am. Chem. Soc., 2014, 136, 11412–11419 CrossRef CAS PubMed.
- M. J. Polking, J. J. Urban, D. J. Milliron, H. Zheng, E. Chan, M. A. Caldwell, S. Raoux, C. F. Kisielowski, J. W. Ager, R. Ramesh and A. P. Alivisatos, Nano Lett., 2011, 11, 1147–1152 CrossRef CAS PubMed.
- X. Zhang, F. Zhao, Y. Wang, X. Liang, Z. Zhang, Y. Feng, Y. Li, L. Tang and W. Feng, ACS Appl. Mater. Interfaces, 2020, 12, 37108–37115 CrossRef CAS PubMed.
- D. Sarkar, G. Sanjeev and M. G. Mahesha, Appl. Phys. A, 2015, 119, 49–54 CrossRef CAS.
- K. S. Andrikopoulos, S. N. Yannopoulos, A. V. Kolobov, P. Fons and J. Tominaga, J. Phys. Chem. Solids, 2007, 68, 1074–1078 CrossRef CAS.
- R. De Bastiani, E. Carria, S. Gibilisco, M. G. Grimaldi, A. R. Pennisi, A. Gotti, A. Pirovano, R. Bez and E. Rimini, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 245205–245206 CrossRef.
- K. S. Andrikopoulos, S. N. Yannopoulos, G. A. Voyiatzis, A. V. Kolobov, M. Ribes and J. Tominaga, J. Phys.: Condens. Matter, 2006, 18, 965–979 CrossRef CAS.
- S. Baroni, C. A. Dal, P. Giannozzi and G. S. De, Rev. Mod. Phys., 2001, 73, 515–562 CrossRef CAS.
- G. C. Resende, G. A. S. Ribeiro, O. J. Silveira, J. S. Lemos, D. Rhodes, L. Balicas, M. Terrones, M. S. C. Mazzoni, C. Fantini, B. R. Carvalho and M. A. Pimenta, J. Raman Spectrosc., 2021, 52, 2068–2080 CrossRef CAS.
- Y. El Mendili, B. Minisini, A. Abdelouas and J. F. Bardeau, RSC Adv., 2014, 4, 25827–25834 RSC.
- R. Loudon, Adv. Phys., 1964, 13, 423–482 CrossRef CAS.
- S. Luo, X. Qi, H. Yao, X. Ren, Q. Chen and J. Zhong, J. Phys. Chem. C, 2017, 121, 4674–4679 CrossRef CAS.
- J. Xia, X. Z. Li, X. Huang, N. Mao, D. D. Zhu, L. Wang, H. Xu and X. M. Meng, Nanoscale, 2016, 8, 2063–2070 RSC.
- A. Łapińska, A. Taube, J. Judek and M. Zdrojek, J. Phys. Chem. C, 2016, 120, 5265–5270 CrossRef.
- L. Pi, L. Li, X. Hu, S. Zhou, H. Li and T. Zhai, Nanotechnology, 2018, 29, 505709 CrossRef PubMed.
- X. Zhou, X. Hu, B. Jin, J. Yu, K. Liu, H. Li and T. Zhai, Adv. Sci., 2018, 5, 1800478 CrossRef PubMed.
- P. Mal, G. Bera, G. R. Turpu, S. K. Srivastava, A. Gangan, B. Chakraborty, B. Das and P. Das, Phys. Chem. Chem. Phys., 2019, 21, 15030–15039 RSC.
- M. J. Polking, M. G. Han, A. Yourdkhani, V. Petkov, C. F. Kisielowski, V. V. Volkov, Y. Zhu, G. Caruntu, A. P. Alivisatos and R. Ramesh, Nat. Mater., 2012, 11, 700–709 CrossRef CAS PubMed.
- G. S. Pawley, W. Cochran, R. A. Cowley and G. Dolling, Phys. Rev. Lett., 1966, 17, 753–755 CrossRef CAS.
- M. Balkanski, R. F. Wallis and E. Haro, Phys. Rev. B: Condens. Matter Mater. Phys., 1983, 28, 1928–1934 CrossRef CAS.
- F. Jebari, P. Becker and C. Carabatos-Nédelec, J. Raman Spectrosc., 1994, 25, 261–265 CrossRef CAS.
- M. Ben Gzaiel, A. Oueslati, J. Lhoste, M. Gargouri and A. Bulou, J. Mol. Struct., 2015, 1089, 153–160 CrossRef CAS.
- I. Gharbi, A. Oueslati, A. Bulou and M. Gargouri, Mater. Res. Bull., 2021, 139, 111250 CrossRef CAS.
- G. D. Mahan, Condensed Matter in a Nutshell, Princeton University Press, Princeton, 2011 Search PubMed.
- B. Marfoua, Y. S. Lim and J. Hong, Phys. Chem. Chem. Phys., 2020, 22, 12273–12280 RSC.
- S. Perunnal, S. Roychowdhury, D. S. Negi, R. Datta and K. Biswas, Chem. Mater., 2015, 27, 7171–7178 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3nr02678g |
| This journal is © The Royal Society of Chemistry 2023 |