Preferential perovskite surface-termination induced high piezoresponse in lead-free in situ fabricated Cs3Bi2Br9-PVDF nanocomposites promotes biomechanical energy harvesting†
Abstract
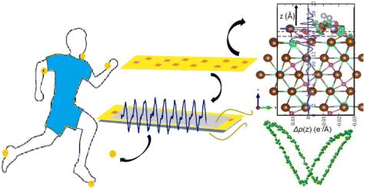
Lead-free halide perovskites have gained immense popularity in photovoltaic and energy harvesting applications because of their excellent optical and electrical attributes with minimal toxicity. We synthesized composite films of lead-free Cs3Bi2Br9 perovskite embedded in the polyvinylidene fluoride (PVDF) matrix and have investigated their piezoelectric energy harvesting. Five PVDF@Cs3Bi2Br9 composite films were fabricated with varying wt% of the perovskite in the PVDF. The composite with a 4 wt% of the perovskite shows 85% activation of the electroactive β-phase of PVDF. Additionally, this composite exhibits a maximum polarisation of ∼0.1 μC cm−2 and the best energy storage density of ∼0.8 mJ cm−3 at an applied field of ∼16 kV cm−1 among all the synthesized composites. A nanogenerator fabricated using 4 wt% loading in the composite film produced an instantaneous output voltage of ∼40 V, an instantaneous current of ∼4.1 μA, and a power density of ∼17.8 μW cm−2 across 10 MΩ resistance when repeatedly hammered by the human hand. The nanogenerator is further employed to light up several LEDs and to charge capacitors with a small active area demonstrating significant promise for prospective wearables and portable devices and paving the way for high-performance nanogenerators using lead-free halide perovskites. Density functional theory calculations were performed to understand the interaction of the electroactive phase of the PVDF with different perovskite surface terminations to unravel the various interaction mechanisms and their ensuing charge transfer properties.
- This article is part of the themed collection: Celebrating International Women’s day 2024: Women in Nanoscience


 Please wait while we load your content...
Please wait while we load your content...