Estimating the heating of complex nanoparticle aggregates for magnetic hyperthermia

Abstract

Understanding and predicting the heat released by magnetic nanoparticles is central to magnetic hyperthermia treatment planning. In most cases, nanoparticles form aggregates when injected in living tissues, thereby altering their response to the applied alternating magnetic field and preventing the accurate prediction of the released heat. We performed a computational analysis to investigate the heat released by nanoparticle aggregates featuring different sizes and fractal geometry factors. By digitally mirroring aggregates seen in biological tissues, we found that the average heat released per particle stabilizes starting from moderately small aggregates, thereby facilitating making estimates for their larger counterparts. Additionally, we studied the heating performance of particle aggregates over a wide range of fractal parameters. We compared this result with the heat released by non-interacting nanoparticles to quantify the reduction of heating power after being instilled into tissues. This set of results can be used to estimate the expected heating in vivo based on the experimentally determined nanoparticle properties.

---

1 Introduction

The localized heat produced upon applying an alternating magnetic field (AMF) to magnetic nanoparticles can be harnessed in oncology as either a monotherapy or an adjuvant to other first line treatments, giving rise to a modality that is broadly known as magnetic hyperthermia.^1,2 Over the last few years, the main components of this therapy – namely biocompatible magnetic nanoparticles and AMF applicators – have experienced notable advancements,^3,4 contributing to improving its nominal effectiveness and increasing the likelihood of a wider clinical adoption. Thanks to these advancements, and together with the specification of new ISO standards,⁵ the use of magnetic hyperthermia is spreading worldwide, which in turn contributes towards its clinical implementation.⁶ Given the strict requirements to approve medical devices, drugs and combination products,^7,8 ensuring the safety of clinical magnetic hyperthermia by controlling the elements that make up the procedure itself still constitutes one of the biggest challenges to overcome.^9–11 In this sense, understanding the physical properties of nanoparticles and their response to the applied AMF, mainly the dynamics involved in heat generation and exchange at the nanoscale, is a critical step in determining the best possible treatment for a particular tumor. In this field, some seminal in silico analyses were performed to simulate in vivo nanoparticle heat exchange on the millimeter length scale.^12,13 However, these methods lack single particle information, and therefore require additional input data to correctly model the generated heat at each location. Providing accurate estimates of this heat is hampered by the fact that nanoparticles form complex aggregates after cell uptake in biological tissues, i.a., due to the interactions with proteins.¹⁴The local heating achieved at the tumor site is not only determined by the local average iron concentration,¹⁵ but also by the intratumoral three-dimensional distribution of nanoparticles within the aggregates, which has been the subject of numerous in vivo studies.^16–18 The inherent difficulty in precisely determining the structure and distribution of these aggregates has led to the search for indirect methods of monitoring them after the injection of nanoparticles – mainly intratumourally, such as the use of infrared thermal imaging¹⁹ or magnetic particle imaging (MPI).^20,21 There is only limited understanding of single particle heating within such aggregates, which is especially problematic because it is known that this aggregation greatly affects the released heat. As shown by Etheridge et al.²² and Dähring et al.,¹⁷ there are significant differences in heating for various clusters in in vivo experiments compared to in vitro measurements. Therefore, using in silico analysis to study the amount and location of the generated heat within aggregates can lead to a better understanding of the heating phenomena at the macroscale. The work done by Carrey et al.,²³ Gavilán et al.²⁴ Raikher and Stepanov²⁵ and Muñoz-Menendez et al.²⁶ shows several micromagnetic and Monte Carlo models to estimate and optimize single particle heating. However, because of the field and thermally induced switching due to which the nanoparticle heating behavior in aggregates is strongly affected by interparticle interactions, these models are not directly applicable to estimate the heat generated by nanoparticle clusters. Based on the work by Muñoz-Menendez et al.,²⁷ Leliaert et al.²⁸ have developed the necessary methodology to address this challenge, allowing us to calculate the heat dissipated by individual, interacting, particles due to the field and thermally induced switching. Building upon this new methodology, the present work aims to close the gap between single- and multiple-particle simulations by studying the average heating per nanoparticle in clusters. We show that it is possible to infer the heat released by large aggregates of nanoparticles from that released by their smaller counterparts.

2 Methods

The magnetization dynamics, and consequently the heat released by magnetic nanoparticles, will be studied within the micromagnetic framework. This allows us to include all relevant effects in a bottom-up way, such that particle switching emerges organically, without imposing a predefined switching rate. The nanoparticles used in magnetic hyperthermia typically have a size of a few tens of nanometers,^29–31 which is comparable to the exchange length for materials commonly considered (such as ferrimagnetic iron oxides). The particles therefore are uniformly magnetized,³²i.e., a single domain state, and can be approximated using a single macrospin. In micromagnetism, the magnetization dynamics are described by the Landau–Lifshitz–Gilbert equation, eqn (1):

In this equation, γ denotes the gyromagnetic ratio and α is the Gilbert damping constant. It describes the time evolution of the magnetization m as a function of the effective field B_eff, comprising an externally applied field; the anisotropy field 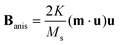, where K and u denote the strength and direction of the uniaxial anisotropy, respectively, and M_s is the saturation magnetization; the dipolar field B_int, which accounts for interparticle interactions; and the stochastic thermal field B_th, which accounts for the effects of thermal fluctuations at nonzero temperatures.^33–35

All simulations were performed using the macrospin simulation tool Vinamax,³⁶ where the differential LLG equation was solved using a Runge–Kutta solver. The heat released by each of the particles was determined by integrating the following equation:²⁸

In biological tissues, nanoparticles tend to form aggregates that can be accurately described as fractals,^37–39 characterized by the fractal equation,^40,41eqn (3):

where n_p and r_p represent the number of particles in the cluster and their radius, R_g is the radius of gyration and D_f and k_f are the fractal dimension and fractal prefactor, respectively. The fractal dimension contains most of the information on the cluster shape and ranges between 1 and 3, with 1 corresponding to a straight line and 3 to a perfectly spherical cluster. Most fractals found in biological tissues have a dimension ranging from 1.6 to 2.5.^22,42 The physical meaning of the fractal prefactor k_f and its numerical value are still under discussion.^43,44 For instance, Woźniak et al.⁴⁵ reported values from 1.23 to 3.5, while Jeon et al.⁴² and Etheridge et al.²² reported values from 1.2 to 2, and Pratsinis⁴⁶ even suggested values as low as 0.41. In this work, we will consider values between 0.5 and 1.9. To generate a fractal geometry with the desired number of particles, size and fractal dimension, we used FracVal.⁴⁷ It uses a cluster–cluster aggregation algorithm, which preserves the fractal parameters in each step by calculating the radius of gyration directly from the fractal equation. For two different subclusters, it calculates the radius of gyration, the distance between their centers of mass and subsequently adds them together. The algorithm will repeat until the desired cluster size is reached. This tool allowed us to generate aggregates for D_f between 1 and 3, which were subsequently used as input for micromagnetic simulations.

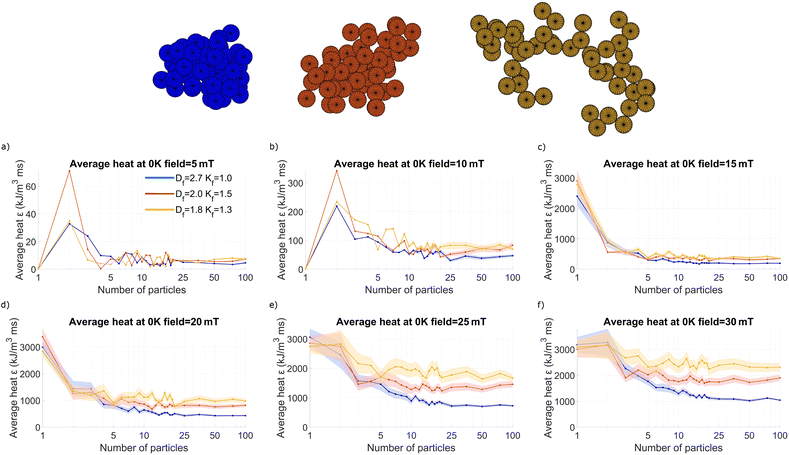
To study how the generated heat depends on the number of particles in the aggregate, we simulated different fractals with n_p ranging between 1 and 100. In particular, we considered three different sets of fractal parameters close to the values reported by Etheridge et al.²², which are based on the measurements of real particle aggregates in cells: D_f = 2.7, k_f = 1.0; D_f = 2.0, k_f = 1.5; and D_f = 1.8, k_f = 1.3.

Each of these sets of parameters was used to generate a hundred different clusters, thereby accounting for the different orientations and configurations the particles can present and which may affect the generated heat. Simulations were performed using monodisperse spherical particles with a diameter equal to 22 nm, which is approximately the size range suggested as optimum for iron oxides as hyperthermia mediators.⁴⁸ The material parameters are as follows: α = 0.5, M_s = 446 kA m⁻¹, and K_anis = 5 kJ m⁻³, with the uniaxial anisotropy axis randomly oriented in each particle. These parameters are close to those reported for maghemite,⁴⁹ whereas the magnetocrystalline anisotropy constant for bulk magnetite is about twice higher. However, for magnetite nanoparticles, values between 3 and 6 kJ m⁻³ are reported,^50–52 so our simulations are representative for both maghemite and magnetite nanoparticles. We performed simulations at both temperatures of 0 K and 300 K, using a sinusoidally varying field with intensities of 5, 10, 15, 20, 25 and 30 mT, and a frequency of 300 kHz.

These simulations allowed us to define a cluster size – containing about 20 particles – above which the average heat per particle stagnates.

Subsequently, we investigated how the heating is affected by the fractal parameters by expanding the number of considered parameters D_f and k_f. A total to 31 different geometries, whose parameters can be seen in Fig. 4, were studied using the same material parameters mentioned above under the application of a 25 mT field. In this study, we used clusters comprising 50 particles, for which we established that the heat per particle is independent of the number of particles, meaning that the results are also representative for larger clusters, as found in biological samples.

3 Results and discussion

3.1 Average heat per particle as a function of cluster size

We investigated cluster heating as a function of cluster size at both 0 K (the athermal case) and 300 K, thereby including thermal switching, similar to what happens in any real world application. The athermal case is also included in our analysis because it gives additional insight into the energy barriers and allows us to gain a deeper understanding of what happens at nonzero temperatures. The results are presented in Fig. 1 (0 K) and Fig. 3 (300 K). Panels (a–f) show the results obtained for different field intensities while the clusters (shown at the top of the figure) were generated using the different (color-coded) sets of fractal parameters.

Fig. 1 Average generated heat per particle, and the uncertainty on this value (shaded regions), released by different color-coded clusters (colored lines) as a function of the number of particles at 0 K in the presence of a sinusoidally varying applied field with a frequency of 300 kHz and amplitudes of 5 mT (a), 10 mT (b), 15 mT (c), 20 mT (d), 25 mT (e) and 30 mT (f). Three different sets of fractal parameters are shown: D_f = 2.7 k_f = 1 (blue); D_f = 2 k_f = 1.5 (red); and D_f = 1.8 k_f = 1.3 (yellow).

3.1.1 Athermal case. We can see in Fig. 1 that for lower field intensities of 5 mT and 10 mT [panels (a) and (b)], the particles release very little heat as the field generally is not sufficiently strong to help the magnetization overcome the anisotropy barriers and induce magnetic switching. As a consequence, single particle “clusters” do not release any noticeable heat. In contrast, for clusters containing more than one particle, interparticle interactions do result in some heating, with a peak for 2-particle clusters, followed by a gradual decline for larger clusters. It is deceptive to consider this peak as a proper increase in heating (compared to single particles, which do not display any heating at all) because out of all the possible anisotropy configurations in 2-particle clusters, only a very few result in an energy landscape with sufficient reduction of the switching energy barrier to produce some heat. Note that for 2-particle clusters the three considered cluster geometries are identical (a 2-particle chain) and the seemingly larger peak for the cluster with D_f = 2.0 (in red) compared to the others is an artefact only visible due to the very low amount of produced heat.

Once the field is sufficiently large, at 15, 20, 25, and 30 mT [Panels (c), (d), (e), and (f)], the particles start releasing heat. The heat released by single particle clusters equals about 3000 kJ m⁻³ ms⁻¹,† which is consistent with the value expected from the Stoner–Wohlfarth model (see the appendix) as about 1/4th of the value given by 4M_sB_c = 40 kJ m⁻³ with . Using f = 300 kHz, this means that a heat of about 3000 kJ m⁻³ ms⁻¹ is produced.

The three differently colored lines correspond to clusters with different fractal parameters, displaying differences in heating. However, before looking into these differences, we remark that these figures display a few common trends: at 15 mT and 20 mT, the heating of 2-particle clusters is less than that of single particles, whereas at 25 mT and 30 mT, the heating is more or less equal to that of the one-particle case. In all cases, the heat generation then decreases as a function of the number of particles and reaches a more or less constant value for clusters containing about 20 particles. This trend can be explained as follows: for most 2-particle configurations, the magnetostatic interaction causes the switching energy barrier to be larger than that for the single-particle case, therefore resulting in less heating at low fields. However, when these barriers can be overcome at larger fields, a larger amount of heat can be generated than that from single particles. For larger clusters, containing as few as 3 particles, the interactions result in a more isotropic contribution to the magnetic energy landscape, therefore progressively flattening out these large energy barriers and resulting in a decrease in the heating.

This interpretation of the data is confirmed by the hysteresis loop shown in Fig. 2(a). For single particles, the hysteresis loop already closes slightly below 20 mT, and larger fields will not result in any additional heating. The other loops do not display this behavior, because irreversible switches still occur at these larger fields, indicating the presence of higher energy barriers.

Fig. 2 Hysteresis loops obtained from 1, 2 and 3 particles (the latter with fractal parameters D_f = 2.7, k_f = 1 and D_f = 1.8, k_f = 1.3) at 30 mT field intensity and at 0 K (a) and 300 K (b).

A cluster size of 20 particles is already sufficient for each of the particles to feel the same local environment due to the interactions with their neighbours, such that the average heat released per particle reaches a constant value. This is one of the main conclusions of this work, as it allows the estimation of the heating of very large clusters based on a modestly sized simulation, provided that the fractal dimensions of the cluster under study are known.

Indeed, the heat released presents important variations depending on the fractal dimensions. Specifically, the compact cluster represented by the blue line releases less heat than the most elongated one, represented by the yellow line. This is readily understood because the particles in the compact, spherical, clusters are influenced by neighbours in all directions, which leads to an isotropic energy landscape and consequently a decrease of the switching energy barriers, and less heating. The elongated, chain-like, clusters, on the other hand, mostly have neighbours in one direction, such that their interactions give rise to a shape anisotropy, which increases the energy barriers and thus results in more heating than that for their compact counterparts. These conclusions are also supported by the hysteresis loops shown in Fig. 2(a), in which the narrowest loop corresponds to the most compact cluster geometry and the widest loop (except for the single particle case) corresponds to the most elongated clusters. The influence of fractal parameters on the heating of the clusters is further investigated in section 3.2.

3.1.2 Nonzero temperatures. By investigating the athermal case, we were able to determine a clear picture of the energy landscapes, which will allow us to understand the heat generation in the presence of thermal switching, which is the topic of this section. The results of the simulations obtained at 300 K are shown in Fig. 2(b) and 3.

Fig. 3 Average generated heat per particle, and the uncertainty on this value (shaded regions), released by different color-coded clusters (colored lines) as a function of the number of particles at 300 K in the presence of a sinusoidally varying applied field with a frequency of 300 kHz and amplitudes of 5 mT (a), 10 mT (b), 15 mT (c), 20 mT (d), 25 mT (e) and 30 mT (f). Three different sets of fractal parameters are shown: D_f = 2.7 k_f = 1 (blue); D_f = 2 k_f = 1.5 (red); and D_f = 1.8 k_f = 1.3 (yellow).

For the particles under study, the Néel relaxation time is estimated at about 1 μs, which means that we expect substantial thermal switching on the timescale of our 300 kHz excitation field, and therefore a much lower heating than the one obtained at 0 K. Indeed, although the single particle heating saturates at about 3000 kJ m⁻³ ms⁻¹ at 0 K, it already saturates at 500 kJ m⁻³ ms⁻¹ at 300 K, as also clearly visible in the single particles’ hysteresis loop. Note that this effect is very pronounced for the particles under study here but strongly diminishes for larger particles, with longer Néel relaxation times. Nonetheless, in the presence of thermally assisted switching, the generated heat is almost always lower than that in the athermal case, except when the excitation field strength was insufficient to overcome the switching barriers, i.e., it was lower than the coercivity of the clusters. In the hysteresis loops, this is clearly visible as all loops display a lower coercivity at 300 K than at 0 K, and all loops close already around 20 mT, indicating that higher fields will not necessarily result in additional heating. This effect is confirmed in panels (e) and (f) where the heat release is similar for both cases.

Using the same picture of the energy barriers that we deduced in the athermal case, the larger energy barriers for the 2-particle clusters hamper the (premature) thermal switching, allowing the field to reach higher values before a switching event takes place, resulting in hysteresis loops with a coercive field that is almost twice as large as that of the single-particle case, and consequently results in increased heat generation. The fact that particle dimers release the maximum heat has been already described by Gavilán et al.,⁵⁴ where increases in the SLP for assemblies containing a low number of particles in a chain-like structure have been reported, specifically, for dimers and trimers. Qualitatively, the shape of these images, and their underlying physics, is therefore more similar to the ones obtained at the highest field intensities in the athermal case.

The differences between the compact and more elongated clusters are qualitatively similar, again with elongated clusters generating more heat than the compact ones. However, because of the exponential dependence of the thermally assisted switching on the height of the energy barriers, the fractal dimension plays a larger role here. This is reflected in a larger difference in the shape of the hysteresis loops corresponding to the compact and elongated clusters, already visible for clusters containing as few as 3 particles. This effect is most notable when the applied field has an intensity similar to that of the coercive field, , as seen by comparing panels (c) and (d) in Fig. 1 and 3.

Additionally, it is important to notice that, again, the average released heat is approximately constant for aggregates containing more than 20 particles, reasserting the conclusions found in the previous section.

3.2 Average heat per particle as a function of fractal parameters

As we have just discussed, the average heat per particle stabilizes with respect to the cluster size, and from about 20 particles onward reaches a value that becomes independent of cluster size. Instead, it only depends on the specific configuration and orientation of each cluster, which allows us to extrapolate these results to bigger clusters. To investigate the dependence on the fractal parameters in detail, we simulated a larger set of parameters at 300 K using 100 realizations of aggregate geometries containing 50 particles to ensure a stable heating. Using the Matlab Curve Fitting Toolbox™⁵⁵ we fitted an equation to find the average heat per particle as a function of the fractal parameters D_f and k_f. We found that the heating Q is described well by a plane, defined by linear dependencies on both D_f and k_f:

Q(D_f, k_f) = AD_f + Bk_f + C (4)

with prefactors A = −118.5 ± 18.6 kJ m⁻³ ms⁻¹, B = −54.52 ± 16.93 kJ m⁻³ ms⁻¹, and an offset C of 4601 ± 579 kJ m⁻³ ms⁻¹.

The results of the simulations and the fit are presented in Fig. 4. The data points highlighted in blue, red and yellow correspond to the clusters depicted in both Fig. 1 and 3, with parameters extracted from clusters found in biological samples.²² This figure further confirms that the cluster shape strongly affects the heating, being driven by both the fractal dimension and the fractal prefactor, which together define the fractal shape. Both values are inversely related to the heating, in agreement with the literature.⁴⁵ More specifically, the most elongated geometries present a higher shape anisotropy that leads to an increase in released heat, in accordance to Gavilán et al.²⁴ Additionally, different sets of parameters can give rise to similarly looking clusters, which also release similar amounts of heat. As an example, the three data points highlighted in black are displayed in more detail in Table 1, and all display the same heating.

Fig. 4 Average heat per particle as a function of the fractal dimensions D_f and k_f at 300 K. The three points highlighted in blue, red and yellow match the exemplary aggregates studied in the previous section, as shown on top of Fig. 1 and 3. Highlighted black points represent aggregates that dissipate similar amounts of heat while having different parameters, which can be visualized in Table 1.

Table 1 Example of 3 different clusters with different fractal parameters k_f and D_f, which result in visually similar clusters and almost identical heat generation

k f	1.7	1.1	0.5
D f	1.7	2.1	2.5
Cluster

---

From this observation we conclude that when extracting the fractal parameters from experimental data, D_f and k_f are not independent parameters. From a practical point of view, an entire range of good fits can be made, thus allowing us to fix the value of k_f and only fitting the fractal dimension. A common value for k_f is 1.593, corresponding to an infinitely large hexagonal close-packed aggregate of monodisperse hard spheres in contact.⁴⁵

3.3 Final remarks

Factors such as intra-cluster particle size (or simply “core size”) and particle composition may represent an interesting avenue for future research that complements the work presented here. Blanco-Andujar et al.⁵⁶ experimentally found for randomly-shaped multi-core clusters of iron oxide nanoparticles that an increase in core size led to a cluster containing fewer cores and hence lower hydrodynamic sizes. This resulted in a decrease in the demagnetizing interactions between cores and finally an increase in the SLP. Although the influence of the core size for a given cluster size was not studied, similar to our findings, for few-core clusters a decrease in SLP with cluster size was already observed. We therefore anticipate that while the exact values will differ for particles of different sizes, the overall trends reported in our work will remain unchanged for different core sizes.

In terms of particle composition, iron oxide samples can consist of either a single phase—maghemite or magnetite—or a mixture of both. In general, the expected trends of the collective magnetic behavior will not change much when comparing both oxides (or any mixture of the two in the corresponding proportions) because, as described above, their material parameters are very similar for nanoscale samples. For other materials, the magnetic agglomeration threshold (where the Néel relaxation time exceeds the diffusion time, making particle agglomeration more likely) may shift downward or upward due to the changes in the magnetocrystalline anisotropy constant, as previously established in other studies.^57,58 Another example is that changes in the magnetocrystalline anisotropy constant will result in changes in the coercive field of the aggregates, as well as in the threshold values for the external field separating the viscous and magnetic magnetization oscillation modes proposed by Usov and Liubimov⁵⁹ to explain the expected heat dissipation. In summary, for aggregates composed of different materials or particle sizes, we will enter regimes where the thermal switching of the particles becomes either too fast or too slow, resulting in a clear deterioration of heat generation under biomedically relevant field conditions, but the relative trends reported here will not considerably change.

4 Conclusions

In this manuscript, we investigated the average heat released per particle in clusters of nanoparticles described by a fractal structure, as they appear in biological samples. These clusters were subjected to a temperature of 300 K and were excited by a sinusoidally varying field. We investigated the dependence of the released heat on the size and the fractal parameters of the clusters.

Our main conclusions are that already starting from relatively small clusters of about 20 particles, the heat released per particle stagnates. This result suggests that the heat emitted by large clusters can be predicted from simulations of moderately sized clusters with the same geometrical and magnetic parameters. The most important application of these findings is in magnetic hyperthermia treatment planning, since one of the major problems currently faced is the estimation of the heat produced by an indefinite aggregate of nanoparticles after injection.

Furthermore, we showed that the heat release is strongly affected by the shape of the clusters. Using the value of the heat released by single Stoner–Wohlfarth particles at 0 K as a reference, we found that for the parameters used in this study, the most elongated chain-like clusters display about half as much heating for large excitation, whereas the most compact clusters display about one fifth of this value. Even though the exact numbers will depend on the details of the excitation amplitude and frequency, particle size (distribution), and material composition, these values can be used as a rule of thumb in heating estimates. It is important to note that the heating values obtained from the methodology presented here should be considered an upper limit, as adverse chemical and biochemical processes may occur over time upon nanoparticle injection, such as partial degradation of the nanoparticles or their surface coating.

Conflicts of interest

The authors declare no conflicts of interest.

Appendix

Because our model considers single-domain particles, we can use the Stoner–Wohlfarth model⁶⁰ to estimate the expected heating for “clusters” containing only a single particle.

The coercive field that needs to be overcome for a particle to switch depends on the angle θ between the anisotropy axis and the externally applied field, and reaches a maximum of for θ = 0° (i.e. with the field parallel to the anisotropy axis), and a minimum of H_c/2 for θ = 45°, as shown in Fig. 5(a).

Fig. 5 (a) The coercive field of a Stoner–Wohlfarth particle as a function of the angle θ between the applied field and the anisotropy axis. (b) The heat dissipated in a single hysteresis cycle as a function of θ of a single Stoner–Wohlfarth particle.

The heat dissipated in a single hysteresis cycle strongly depends on this angle as well, and quickly reduces to half of its maximum value of 4 H_cM_s for θ as small as 25°, as shown in Fig. 5(b). As we consider ensembles with an anisotropy direction that is randomly, but uniformly, distributed on the unit sphere, large θ values are more prevalent than small ones (with a proportionality ∝ sin(θ)). This results in an average heat per hysteresis cycle that is only about 1/4th of the maximum value, i.e., ∼H_cM_s (and a variation that is about equally large).

When considering heating as a function of field amplitude, we again turn our attention to Fig. 5(a), which shows the coercive field as a function of the angle between the anisotropy and the externally applied field, as given by

with , as analytically determined by Stoner and Wohlfarth.⁶⁰

From this figure, we learn that as soon as the external field is a bit larger than H_c/2, already a broad range of particles (with angles distributed symmetrically around 45°) can switch, while the external field needs to reach the full value of H_c for all particles to switch. However, as there are very few particles with θ = 0°, and the ones with θ = 0° do not contribute to the heating at all, the average heat as a function of field amplitude reaches its maximum value quite soon for field strengths above H_c/2 and only slightly increases further for fields equal to or larger than H_c. This is confirmed in section 1, in which H_c/2 ≈ 12 mT, and the total heating observed for one-particle clusters is zero for fields of 0 and 5 mT, and remains about constant for fields larger than 15 mT.

Acknowledgements

J. L. was supported by the Fonds Wetenschappelijk Onderzoek (FWO-Vlaanderen) with postdoctoral fellowship No. 12W7622N. Part of the computational resources (Stevin Supercomputer Infrastructure) and services used in this work were provided by the VSC (Flemish Supercomputer Center), funded by Ghent University, FWO, and the Flemish Government – department EWI. This work was also supported by the NoCanTher project, which has received funding from the European Union's Horizon 2020 Research and Innovation Programme under Grant Agreement No. 685795. The authors acknowledge support from the COST Association through the COST action “MyWAVE” (CA17115). D. O. and J. O. J. are thankful for funding support from the Spanish Ministry of Science, Innovation under Contract No. PEJ2018-004866-A, and support under Grant PID2020-117544RB-I00, CEX2020-001039-S, RED2018-102626-T and MAT2017-85617-R funded by MCIN/AEI/10.13039/501100011033, and grant RYC2018-025253-I funded by MCIN/AEI/10.13039/501100011033 and by “FEDER A way of making Europe”. We would also like to thank the Systems Unit of the Information Systems Area of the University of Cádiz for computer resources and technical support.

References

1. D. Ortega and Q. A. Pankhurst, Nanoscience: Volume 1: Nanostructures through Chemistry, The Royal Society of Chemistry, 2013, pp. 60–88.
2. A. Espinosa, R. Di Corato, J. Kolosnjaj-Tabi, P. Flaud, T. Pellegrino and C. Wilhelm, ACS Nano, 2016, 10, 2436–2446.
3. D. Cabrera, I. Rubia-Rodríguez, E. Garaio, F. Plazaola, L. Dupré, N. Farrow, F. J. Terán and D. Ortega, Nanomaterials for Magnetic and Optical Hyperthermia Applications, Elsevier, 2019, ch. 5, pp. 111–138.
4. N. Silvestri, H. Gavilán, P. Guardia, R. Brescia, S. Fernandes, A. C. S. Samia, F. J. Teran and T. Pellegrino, Nanoscale, 2021, 13, 13665–13680.
5. International Organisation for Standardisation: Geneva, Switzerland, ISO/TS 19807-1:2019 Nanotechnologies—Magnetic nanomaterials—Part 1: Specification of characteristics and measurements for magnetic nanosuspensions, 2019, https://www.iso.org/standard/66237.html.
6. I. Rubia-Rodríguez, A. Santana-Otero, S. Spassov, E. Tombácz, C. Johansson, P. D. L. Presa, F. J. Teran, M. D. Puerto, S. Veintemillas-Verdaguer, N. T. K. Thanh, M. O. Besenhard, C. Wilhelm, F. Gazeau, Q. Harmer, E. Mayes, B. B. Manshian, S. J. Soenen, Y. Gu, A. Millán, E. K. Efthimiadou, J. Gaudet, P. Goodwill, J. Mansfield, U. Steinhoff, J. Wells, F. Wiekhorst and D. Ortega, Materials, 2021, 14, 706.
7. European Parliament and the council of the European Union, Regulation (EU) 2017/745 on medical devices, amending Directive 2001/83/EC, Regulation (EC) No 178/2002 and Regulation (EC) No 1223/2009 and repealing Council Directives 90/385/EEC and 93/42/EEC, 2017, https://data.europa.eu/eli/reg/2017/745/oj.
8. FDA guidance, Classification of Products as Drugs and Devices and Additional Product Classification Issues: Guidance for Industry and FDA Staff, 2018, https://www.fda.gov/regulatory-information/search-fda-guidance-documents/classification-products-drugs-and-devices-and-additionalproduct-classification-issues.
9. I. Rubia-Rodríguez, L. Zilberti, A. Arduino, O. Bottauscio, M. Chiampi and D. Ortega, Int. J. Hyperthermia, 2021, 38, 846–861.
10. B. Herrero de la Parte, I. Rodrigo, J. Gutiérrez-Basoa, S. Iturrizaga Correcher, C. Mar Medina, J. J. Echevarría-Uraga, J. A. Garcia, F. Plazaola and I. García-Alonso, Cancers, 2022, 14, 3084.
11. F. L. Tansi, W. O. Maduabuchi, M. Hirsch, P. Southern, S. Hattersley, R. Quaas, U. Teichgräber, Q. A. Pankhurst and I. Hilger, Int. J. Hyperthermia, 2021, 38, 743–754.
12. J. Gellermann, P. Wust, D. Stalling, M. Seebass, J. Nadobny, R. Beck, H. Hege, P. Deuflhard and R. Felix, Int. J. Radiat. Oncol., Biol., Phys., 2000, 47, 1145–1156.
13. G. Sreenivasa, J. Gellermann, B. Rau, J. Nadobny, P. Schlag, P. Deuflhard, R. Felix and P. Wust, Int. J. Radiat. Oncol., Biol., Phys., 2003, 55, 407–419.
14. P. Aggarwal, J. B. Hall, C. B. McLeland, M. A. Dobrovolskaia and S. E. McNeil, Adv. Drug Delivery Rev., 2009, 61, 428–437.
15. P. Southern and Q. A. Pankhurst, Int. J. Hyperthermia, 2018, 34, 671–686.
16. P. L. Zadnik, C. A. Molina, R. Sarabia-Estrada, M. L. Groves, M. Wabler, J. Mihalic, E. F. McCarthy, Z. L. Gokaslan, R. Ivkov and D. Sciubba, J. Neurosurg., 2014, 20, 740–750.
17. H. Dähring, J. Grandke, U. Teichgräber and I. Hilger, Mol. Imaging Biol., 2015, 1, 763–769.
18. F. L. Tansi, F. Fröbel, W. O. Maduabuchi, F. Steiniger, M. Westermann, R. Quaas, U. K. Teichgräber and I. Hilger, Nanomaterials, 2021, 11, 438.
19. T. Kuboyabu, I. Yabata, M. Aoki, N. Banura, K. Nishimoto, A. Mimura and K. Murase, Open J. Med. Imaging, 2016, 06, 1–15.
20. A. Coene and J. Leliaert, J. Appl. Phys., 2022, 131, 160902.
21. S. Harvell-Smith, L. D. Tung and N. T. K. Thanh, Nanoscale, 2022, 14, 3658–3697.
22. M. L. Etheridge, K. R. Hurley, J. Zhang, S. Jeon, H. L. Ring, C. Hogan, C. L. Haynes, M. Garwood and J. C. Bischof, Technology, 2014, 2, 214–228.
23. J. Carrey, B. Mehdaoui and M. Respaud, J. Appl. Phys., 2011, 109, 083921.
24. H. Gavilán, K. Simeonidis, E. Myrovali, E. Mazarío, O. Chubykalo-Fesenko, R. Chantrell, L. Balcells, M. Angelakeris, M. P. Morales and D. Serantes, Nanoscale, 2021, 13, 15631–15646.
25. Y. Raikher and V. Stepanov, J. Magn. Magn. Mater., 2014, 368, 421–427.
26. C. Muñoz-Menendez, I. Conde-Leboran, D. Baldomir, O. Chubykalo-Fesenko and D. Serantes, Phys. Chem. Chem. Phys., 2015, 17, 27812–27820.
27. C. Muñoz-Menendez, D. Serantes, O. Chubykalo-Fesenko, S. Ruta, O. Hovorka, P. Nieves, K. Livesey, D. Baldomir and R. Chantrell, Phys. Rev. B: Condens. Matter Mater. Phys., 2020, 102, 214412.
28. J. Leliaert, J. Ortega-Julia and D. Ortega, Nanoscale, 2021, 13, 14734–14744.
29. Q. A. Pankhurst, J. Connolly, S. K. Jones and J. Dobson, J. Phys. D: Appl. Phys., 2003, 36, R167.
30. G. Cotin, C. Blanco-Andujar, F. Perton, L. Asín, J. M. de la Fuente, W. Reichardt, D. Schaffner, D.-V. Ngyen, D. Mertz, C. Kiefer, F. Meyer, S. Spassov, O. Ersen, M. Chatzidakis, G. A. Botton, C. Hénoumont, S. Laurent, J.-M. Greneche, F. J. Teran, D. Ortega, D. Felder-Flesch and S. Begin-Colin, Nanoscale, 2021, 13, 14552–14571.
31. G. Antonaropoulos, M. Vasilakaki, K. N. Trohidou, V. Iannotti, G. Ausanio, M. Abeykoon, E. S. Bozin and A. Lappas, Nanoscale, 2022, 14, 382–401.
32. S. Tong, H. Zhu and G. Bao, Mater. Today, 2019, 31, 86–99.
33. J. Leliaert, J. Mulkers, J. De Clercq, A. Coene, M. Dvornik and B. Van Waeyenberge, AIP Advances, 2017, 7, 125010.
34. A. Lyberatos, D. V. Berkov and R. W. Chantrell, J. Phys.: Condens. Matter, 1993, 5, 8911.
35. W. F. Brown Jr., Phys. Rev., 1963, 130, 1677.
36. J. Leliaert, A. Vansteenkiste, A. Coene, L. Dupré and B. Van Waeyenberge, Med. Biol. Eng. Comput., 2015, 53, 309–317.
37. J. Cai, X. Hu, B. Xiao, Y. Zhou and W. Wei, Int. J. Heat Mass Transfer, 2017, 105, 623–637.
38. R. Prasher, E. P. Phelan and P. Bhattacharya, Nano Lett., 2006, 6, 1529–1534.
39. O. Hovorka, J. Phys. D: Appl. Phys., 2017, 50, 044004.
40. S. R. Forrest and T. A. Witten, J. Phys. A: Math. Gen., 1979, 12, L109–L117.
41. A. Filippov, M. Zurita and D. E. Rosner, J. Colloid Interface Sci., 2000, 229, 261–273.
42. S. Jeon, K. R. Hurley, J. C. Bischof, C. L. Haynes and C. J. Hogan, Nanoscale, 2016, 8, 16053–16064.
43. J. Cai, N. Lu and C. M. Sorensen, J. Colloid Interface Sci., 1995, 171, 470–473.
44. S. Bau, O. Witschger, F. Gensdarmes, O. Rastoix and D. Thomas, Powder Technol., 2010, 200, 190–201.
45. M. Woźniak, Ph.D. thesis, Aix-Marseille Université, 2012.
46. M. L. Eggersdorfer and S. E. Pratsinis, Aerosol Sci. Technol., 2012, 46, 347–353.
47. J. Morán, A. Fuentes, F. Liu and J. Yon, Comput. Phys. Commun., 2019, 239, 225–237.
48. I. Rodrigo, I. Castellanos-Rubio, E. Garaio, O. K. Arriortua, M. Insausti, I. n. Orue, J. A. García and F. Plazaola, Int. J. Hyperthermia, 2020, 37, 976–991.
49. J. M. D. Coey, Magnetism and Magnetic Materials, Cambridge Univ. Press, 2001.
50. R. Dudric, G. Souca, Á. Szatmári, T. Szilárd, S. Nitica, C. Iacovita, A. I. Moldovan, R. Stiufiuc, R. Tetean and E. Burzo, AIP Conf. Proc., 2020, 2218, 030014.
51. S. A. Shah, D. B. Reeves, R. M. Ferguson, J. B. Weaver and K. M. Krishnan, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 094438.
52. F. Ludwig, H. Remmer, C. Kuhlmann, T. Wawrzik, H. Arami, R. M. Ferguson and K. M. Krishnan, J. Magn. Magn. Mater., 2014, 360, 169–173.
53. Y. Rabin, Int. J. Hyperthermia, 2002, 18, 194–202.
54. H. Gavilán, S. K. Avugadda, T. Fernández-Cabada, N. Soni, M. Cassani, B. T. Mai, R. Chantrell and T. Pellegrino, Chem. Soc. Rev., 2021, 50, 11614–11667.
55. Curve Fitting Toolbox, The MathWorks, Inc., Natick, Massachusetts, United State, 2020.
56. C. Blanco-Andujar, D. Ortega, P. Southern, Q. A. Pankhurst and N. T. K. Thanh, Nanoscale, 2015, 7, 1768–1775.
57. D. Serantes and D. Baldomir, Nanomaterials, 2021, 11, 2786.
58. P. B. Balakrishnan, N. Silvestri, T. Fernandez-Cabada, F. Marinaro, S. Fernandes, S. Fiorito, M. Miscuglio, D. Serantes, S. Ruta, K. Livesey, O. Hovorka, R. Chantrell and T. Pellegrino, Adv. Mater., 2020, 32, 2003712.
59. N. A. Usov and B. Y. Liubimov, J. Appl. Phys., 2012, 112, 023901.
60. E. C. Stoner and E. Wohlfarth, Philos. Trans. R. Soc., A, 1948, 240, 599–642.

---

Footnote

† A note on the units used: we report the particle heating in units of kJ m⁻³ ms⁻¹, meaning that this is the amount of energy (in kilojoules) that gets dissipated as heat per cubic meter of the magnetic material per millisecond. This heating metric in itself gives no indication of the temperature reached as it is determined by the heat exchange with the surrounding cells or tissues.⁵³ However, it does give a good estimate of the amount of thermal energy that gets added at a certain location to the body, from which the temperature increase can be estimated in the next step.

---