Promising ultra-short channel transistors based on OM2S (M = Ga, In) monolayers for high performance and low power consumption†
Xueping
Li
 ab,
Peize
Yuan
a,
Lin
Li
b,
Ting
Liu
b,
Chenhai
Shen
b,
Yurong
Jiang
ab,
Peize
Yuan
a,
Lin
Li
b,
Ting
Liu
b,
Chenhai
Shen
b,
Yurong
Jiang
 b,
Xiaohui
Song
b,
Jingbo
Li
c and
Congxin
Xia
b,
Xiaohui
Song
b,
Jingbo
Li
c and
Congxin
Xia
 *b
*b
aCollege of Electronic and Electrical Engineering, Henan Normal University, Xinxiang, Henan 453007, China
bDepartment of physics, Henan Normal University, Xinxiang 453007, China. E-mail: xiacongxin@htu.edu.cn
cInstitute of Semiconductors, South China Normal University, Guangzhou 510631, China
First published on 23rd November 2022
Abstract
It is hoped that two-dimensional (2D) semiconductors overcome the short channel effect and continue Moore's law. However, 2D material-based ultra-short channel devices still face the challenge of simultaneously achieving high-performance (HP) and low-power (LP) consumption. Here, we theoretically designed monolayer OM2S (M = Ga, In)-based metal–oxide–semiconductor field-effect transistors (MOSFETs), considering the gate length from 1 to 5 nm, doping concentration and underlap structure. We found that in HP (LP) applications, the on-state current exceeds 1000 (500) μA μm−1 under a 1 nm (2 nm) gate length, surpassing the needs of the International Technology Roadmap for Semiconductors (ITRS) in 2028. The subthreshold swing is close to the Boltzmann tyranny (60 mV dec−1) even as the gate length shrinks to 2 nm. The energy-delay product is two orders lower than 1.02 × 10−28 J s μm−1, indicating extraordinary high-speed manipulation and low-energy expending. Therefore, monolayer OM2S has great application in ultra-short scale devices with HP and LP consumption, and can be taken as a candidate to extend Moore's Law.
1. Introduction
Currently, the size of an electronic device is constantly reduced to meet the needs of miniaturization and highly integrated development. However, the short channel effects and high power consumption restrict the downscaling of traditional device dimensions.1–3 Thus, it is pivotal to probe promising channel materials for further continuation of Moore's Law. Recently, it is hoped that two-dimensional (2D) materials replace silicon for highly integrated devices because of their particular intrinsic characteristics, such as atomic thickness, dangling bonds-free surfaces, and high carrier mobility.4–8Group-III chalcogenides possess remarkable electrical and optical features, which can be broadly used in field-effect transistors (FETs), photodetectors and gas sensors.9–13 For example, the responsivity and on/off ratio of back-gated GaS-based FETs are ∼6.4 A W−1 and ∼170, respectively.14 The carrier mobilities of atomically thin InSe were discovered to outnumber 103 cm2 V−1 s−1 (at room temperature) and 104 cm2 V−1 s−1 (at liquid-helium temperature), respectively.15 InS-based devices demonstrate native n-type performance, accompanied by a high on/off current ratio (103).16 Zhang et al. used the chemical vapour deposition (CVD) method to fabricate a Janus MoSSe monolayer, and its atomic layers are arranged as S–Mo–Se, which induces an intrinsic piezoelectric response and a high catalytic activity for the hydrogen evolution reaction.17 Motivated by this study, 2D Janus materials and their performance have also been studied extensively.18–30 Among them, the Janus monochalcogenides have received much attention, such as Ga2SSe, GaInS2, In2SSe, Sn2SeS and SnGeS2.25–29,31 Different from Janus transition metal dichalcogenides, Janus monochalcogenides based on GaS include GaInS2, Ga2SSe and GaInSSe, which consist of double Ga–Ga (In) metal layers sandwiched between S and S (Se) chalcogen layers.25,31 For example, Kandemir et al. found that the Janus In2SSe is a robust direct gap semiconductor under tolerable strain.26 Janus Sn2SeS inherits the orthorhombic structure of the SnS monolayer and has large piezoelectric properties and high carrier mobility, especially the in-plane piezoelectric coefficient (up to 179.37 pm V−1) is many times higher than that of MoS2 (3.73 pm V−1).30
More recently, gallium- or indium-based Janus monochalcogenides have been studied.28,32–34 Liu et al. proposed a class of Janus group-III monochalcogenide OM2S (M = Ga, In) monolayers and reported that they are thermally, dynamically, and mechanically stable 2D materials.32 Moreover, the electron mobility of monolayer OIn2S exceeds 3 × 103 cm2 V−1 s−1, which is higher than those of InSSe (884.8 cm2 V−1 s−1), InSe (943.3 cm2 V−1 s−1), MoSSe (52.27 cm2 V−1 s−1) and WSSe (120.88 cm2 V−1 s−1).23,33 Monolayer OGa2S possesses a direct band structure and strong optical absorption.34 We would like to point out that gallium-based or indium-based monochalcogenides have not been synthesized to date. OM2S monolayers have good stability, high electron mobility and suitable direct band gaps, which make them promising channel material candidates for further continuation of Moore's law. However, the investigation of ternary group-III chalcogenides is mainly concentrated on their electronic, optical, and magnetic characteristics.25,26,35–37 Therefore, the transport properties of monolayer ultra-short scale OM2S devices are still worth studying.
Here, the transport characteristics of ultra-short-channel OM2S metal–oxide–semiconductor field-effect transistors (MOSFETs) were systematically investigated. To further expand the application of devices in high-performance (HP) and low-power (LP) consumption, the doping concentration of the electrode region is adjusted and the underlap length is scaled. The calculation results reveal that the on-state current for a 1 nm OM2S device reaches 1000 μA μm−1, which exceeds the standard of HP applications (900 μA μm−1). Moreover, the on-state current for an OM2S device with a 2 nm gate length is about two times higher than that for the LP standard, which is 295 μA μm−1. This work is expected to provide a new opportunity for realizing ultra-short scale electronic devices with HP and LP consumption simultaneously.
2. Methods
Geometric optimization, band structure, and band-decomposed charge-density analyses were carried out using the Vienna ab initio simulation package (VASP) based on density functional theory (DFT).38 The plane-wave cutoff was set as 550 eV. The energy and force convergence tolerances were set to 10−5 eV and 0.01 eV Å−1, respectively. A 13 × 13 × 1 k-point mesh was used for the sampling in the reciprocal space.The transfer characteristics, densities of states, transmission spectra, and local density of states were determined by the combination of DFT and the non-equilibrium Green's function, which was implemented in the Atomistix ToolKit (ATK).39 According to the formula of Landauer–Bűttiker, the drain current (Ids) can be computed as:
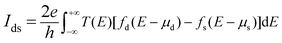 | (1) |
For self-consistency of the electronic structure, we set a real space mesh cutoff of 135 Ha and Monkhorst–Pack k meshes for OGa2S and OIn2S MOSFETs of 1 × 21 × 162 and 1 × 21 × 148, respectively. The temperature was set as 300 K. PseudoDojo optimized norm-conserving pseudopotentials and a medium basis set were used. In addition, the Neumann, periodic, and Dirichlet boundary conditions were applied in the directions of x, y, and z, respectively. In addition, the exchange–correlation interaction was performed using the generalized gradient approximation and the Perdew–Burke–Ernzerhof functional.40,41
3. Results and discussion
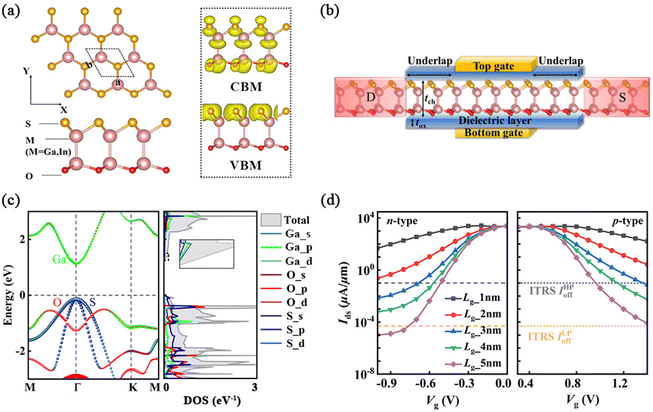
The geometric and electronic characteristics of monolayer OM2S (M = Ga, In) are shown in Fig. 1. These optimized lattice parameters are a = b = 3.375 Å and a = b = 3.688 Å for monolayer OGa2S and OIn2S, respectively. This is very consistent with the previous reports.32 In Fig. 1(a), monolayer OM2S is a sandwich structure with the S and O atoms locating both the side layer and two M atoms as the middle layer. The difference between the upper and lower layers demonstrates that OM2S is a ternary structure. Moreover, the M–S, M–O, and M–M bonds are all connected in the form of covalent bonds. Monolayer OGa2S and OIn2S have similar band-decomposed charge-density distributions, which are relevant to the conduction band minimum (CBM) and the valence band maximum (VBM). The electron wave function is located at the vicinity of O, S, and M atoms at the CBM. The hole wave function is mostly located near the S atom. The band-decomposed charge density distributions of OM2S are shown in Fig. S1 of the ESI.†Fig. 1(c) and Fig. S1(a) of the ESI† show the band structures of monolayer OGa2S and OIn2S, both of them are direct bandgap semiconductors. The bandgap (Eg) of OGa2S and OIn2S is 1.27 eV and 1.05 eV, respectively. Both the CBM and VBM of them are situated at Γ. Moreover, we can know from ESI Fig. S2† that the states around the CBM of OM2S are mostly devoted to M_s, M_p, and S_p orbitals. The VBM of OGa2S is mainly offered by S_p orbitals and a little by Ga_p orbitals, but the VBM of OIn2S is provided by S_p orbitals. It is worthy to note that the CBM and VBM of OM2S have similar energy dispersion relationships along the armchair and zigzag directions, and this work only uses the armchair direction as the transport direction for brevity.
Fig. 1(b) shows the constructed double-gate (DG) monolayer OM2S MOSFETs. The transfer characteristics of the DG and single-gate (SG) OGa2S MOSFETs are shown in Fig. S3 and elaborated in the ESI.† Considering that OGa2S has two different chalcogen surfaces, we constructed two SG devices, where SG_O and SG_S represent the cases where the gate is added to the oxygen and sulfur terminals, respectively. The off-state current (Ioff) of the SG_O device is difficult to meet the high-performance (HP) requirement of the ITRS 2028 level. The LP on-state current (Ion) of the DG device (1300.2 μA μm−1) is about 10 times larger than that of the SG_S configuration. In addition, the subthreshold swing (SS) of the DG OGa2S MOSFET (63.6 mV dec−1) is smaller than that of its SG counterpart (73.0 mV dec−1). Since the DG monolayer OGa2S MOSFETs have better gate control capability, the transport performances are better than that of the SG configuration, so we used the dual-gate configuration instead of the SG model in this work. The intrinsic and doped OM2S monolayers act as channels and electrodes, respectively. In previous theoretical reports, similar electrode structures have been widely used to study the performance of devices including GeSe, BiN, β-TeO2 and GaN MOSFETs.3,42–49 For example, Wang et al. studied the performance limit of the transport characteristics of monolayer planar GaN transistors with the heavy doping hypothesis as the electrodes, and demonstrated the feasibility of the design of the electrode structure by studying the contact characteristics of the active region.49
To prevent the interactions among neighboring units, the vacuum regions of OGa2S and OIn2S normal to the surface are found greater than 20 Å. The equivalent dielectric layer thickness is 0.41 nm and the bias voltage (Vds) of sub-5 nm devices is 0.64 V. On the basis of HP and LP standards for ITRS 2028 horizon, the Ioff should be 0.1 μA μm−1 and 5 × 10−5 μA μm−1, respectively. Ion corresponds to the drain current with the on-state gate voltage (Vg,on). Vg,on can be calculated using the following formula: Vg,on = Vg,off ± Vds,46 where Vg,off is the off-state voltage. The underlap (UL) stands for the undoped channel zone between the source and gate or the drain and gate. In this work, the symmetric length of underlap (LUL) is used. Therefore, the channel length (Lch) can be defined as Lch = Lg + 2LUL, where Lg is the gate length. We would like to point out that this work is only intended to predict the performance limit of OM2S MOSFETs with an ultra-short channel. Considering the computational cost and resources, the transport properties of the electron–phonon interaction are not considered.
The transfer characteristics of n-type and p-type OM2S MOSFETs under various gate lengths are shown in Fig. 1(d) and ESI Fig. S4.† OGa2S MOSFETs possess larger Ids than that of OIn2S MOSFETs. With the increase of gate length both n-type and p-type MOSFETs demonstrate the retention of saturation current (Isat), but the leakage current decreases gradually. In addition, when the gate length is 5 nm, n-type OM2S and p-type OIn2S devices can satisfy the Ioff standard of ITRS in LP applications. For n-type MOSFETs, OIn2S can fulfill the Ioff needs for ITRS 2028 horizon in HP devices when the gate length shrinks to 2 nm. However, the minimum gate length for satisfying this standard is 3 nm for OGa2S n-MOSFETs. More strikingly, the Ion values of these two n-type devices with 3 nm and 5 nm gate lengths are more than 2000 μA μm−1 and 1000 μA μm−1, respectively, far exceeding HP and LP standards. The Ids of 5 nm OGa2S p-MOSFETs approaches the Ioff standards of LP devices at a gate voltage of 1.4 V. The maximum Ids of sub-5 nm OIn2S p-MOSFETs is below 1 × 103 μA μm−1 as the gate voltage ranges 0.5–1.4 V. Although OGa2S has higher Ids, its leakage current is larger than that of OIn2S. Therefore, it is necessary to find a way to reduce the leakage current while maintaining other excellent performances. For simplicity, we take OGa2S MOSFETs as an example for the following study, and the results of OIn2S MOSFETs are presented in the ESI.† Moreover, considering the excellent performance of n-type MOSFETs, we focus on the case of n-type OM2S.
One of the critical factors affecting the transport properties of devices is the doping concentration, which determines the concentration of injected carriers. Therefore, it is necessary to explore the doping concentration influence in the electrode region. The Ids values of OGa2S MOSFETs with gate lengths of 1 nm, 3 nm, and 5 nm changing with the doping concentration and gate voltage are shown in Fig. 2(a). Compared with the cases of 3 nm and 5 nm Lg, it is more difficult to restrain the leakage current of 1 nm OGa2S MOSFETs owing to their severe short channel effect. When the doping concentration is lower than 8 × 1013 e cm−2, the OGa2S MOSFETs with 3 nm gate length can satisfy the Ioff standard for HP applications. For the OGa2S case with 5 nm Lg, the HP (LP) off-state current standard can be satisfied when the doping concentration ranges from 1 × 1013 to 1 × 1014 (5 × 1013) e cm−2. Vg,off increases gradually with the doping concentration increases, which is the result of the enhancement of carrier concentration.
To further assess the influence of doping concentration variation on the gate controllability of the OGa2S MOSFETs with different gate lengths, the subthreshold swing (SS) and transconductance (gm) are extracted from the transfer characteristics (see Fig. S5 of the ESI†). SS can be obtained from the following formula:  ,47 representing the gate voltage required by each order of magnitude change for the current in the subthreshold region. Small SS corresponds to a strong gate control capability.47Fig. 2(b) shows that SS decreases sharply with the decrease of doping concentration when Lg is less than 3 nm. The SS of OGa2S MOSFETs with 1 nm Lg is decreased by more than 500 mV dec−1 when the doping concentration decreases from 1 × 1014 to 5 × 1012 e cm−2. However, it only decreases from 65.9 to 61.7 mV dec−1 for the 5 nm OGa2S MOSFETs. On the other hand, for the superthreshold region, the gate control capability can be characterized by gm (gm = dIds/dVg). A larger gm corresponds to a larger current value, which is advantageous to obtain a large on-state current.50Fig. 2(b) also shows that the gm of devices with different gate lengths exhibits a similar increasing trend. For example, the gm values of 1 nm and 5 nm devices are 1.55 × 103–1.46 × 104 μS μm−1 and 2.04 × 103–2.04 × 104 μS μm−1, respectively. The above analysis shows that SS and gm should be a trade-off in the selection of doping concentration.
,47 representing the gate voltage required by each order of magnitude change for the current in the subthreshold region. Small SS corresponds to a strong gate control capability.47Fig. 2(b) shows that SS decreases sharply with the decrease of doping concentration when Lg is less than 3 nm. The SS of OGa2S MOSFETs with 1 nm Lg is decreased by more than 500 mV dec−1 when the doping concentration decreases from 1 × 1014 to 5 × 1012 e cm−2. However, it only decreases from 65.9 to 61.7 mV dec−1 for the 5 nm OGa2S MOSFETs. On the other hand, for the superthreshold region, the gate control capability can be characterized by gm (gm = dIds/dVg). A larger gm corresponds to a larger current value, which is advantageous to obtain a large on-state current.50Fig. 2(b) also shows that the gm of devices with different gate lengths exhibits a similar increasing trend. For example, the gm values of 1 nm and 5 nm devices are 1.55 × 103–1.46 × 104 μS μm−1 and 2.04 × 103–2.04 × 104 μS μm−1, respectively. The above analysis shows that SS and gm should be a trade-off in the selection of doping concentration.
To reveal the influence mechanism of the doping concentration on gate modulation, the density of states (DOS) and transmission spectra are shown in Fig. 2(c) and (d). The DOS and transmission spectra exhibit an increasing behavior with the increase of doping concentration. The large DOS in the bias window proves that there are a large number of electrons in the channel. On the basis of the above Landauer–Bűttiker formula, the current can be obtained by integrating the transmission spectrum coefficient inside the bias window. A larger transmission corresponds to a higher current. Thus, the gm of the device with a 1 × 1014 e cm−2 doping concentration is larger than those of other doping concentrations, which can be attributed to the large transmission spectrum. To further explain the mechanism of SS changes with the doping concentration, Fig. S6 and S7 of the ESI† show the transmission spectra and spectral current of the 2 nm and 3 nm OGa2S MOSFETs with different doping concentrations. At Vg = −0.6 V, the 3 nm OGa2S MOSFETs show a lower transmission possibility within the bias window than that of 2 nm devices, thus it is easier for the former to approach the off-state. Fig. S7† shows that compared with the 2 nm devices, the 3 nm OGa2S MOSFETs have a larger difference in the spectral current, resulting in a lower SS. Moreover, with the decrease of doping concentration, the difference of spectral current increases gradually and thus SS decreases.
In addition, adding UL structures is another effective way to reduce leakage current. The reason is that the transmission possibility (T(E)) is reduced by increasing the channel barrier width (Λ).51 Thus, the effect of UL length on the characteristics of devices with different gate lengths is systematically shown in Fig. 3. As known from Fig. 3(a), with an increase in Lg, the effect of UL on the transfer characteristics decreases. At the same value of Lg, the leakage current is suppressed to some extent with the increase of UL. For Lg = 1 nm, the leakage current is significantly decreased by utilizing the strategy of UL. When LUL is larger than 1 nm, the value of Ioff can approach the HP standard of ITRS in 2028. However, for the device with 3 nm Lg, Ioff reaches the LP standard of ITRS in 2028 using 1 nm UL. Moreover, as the increase of LUL, Vg,off is almost constant for the MOSFETs possessing a gate length of 5 nm. To intuitively evaluate the influence of LUL and Lg on device transport characteristics, Fig. 3(b) shows SS and Ion, which are extracted from the transfer characteristics (see Fig. S8 of the ESI†). The results show that SS is mainly localized between 60 and 80 mV dec−1. For the HP (LP) applications, Ion ranges from 299.3 (68.2) μA μm−1 to 2618.0 (1587.6) μA μm−1. The UL length less than 2 nm is beneficial for sub-5 nm OGa2S MOSFETs to achieve higher Ion. For instance, the Ion values of 1 nm OGa2S MOSFETs with 2 nm and 3 nm UL lengths are 1032.8 and 694.1 μA μm−1, respectively. The SS of the device with 2 nm Lg is 68.5 mV dec−1 when the LUL is equal to 4 nm, which is lower than that of 1 nm UL (106 mV dec−1). Therefore, the gate capability of the subthreshold region can be improved by increasing the UL length.
To drill deeper into the modulation mechanism of UL, Fig. 3(c) and (d) show the on- and off-state local DOSs of a 3 nm gate-length OGa2S device without/with UL configuration. The channel barrier (ΦB) is delimited as the vertical dimension between the lowest location energy of the conduction band and the Fermi energy of the source. In the off-state, the drain current can be mainly composed of the tunnel current (Itunnel), which is defined as:46
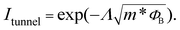 | (2) |
Thus, the large ΦB and Λ are key factors to obtain a small Itunnel. In Fig. 3(c), we can know that the ΦB of the device without UL is 0.26 eV. The device with 1 nm UL possesses lower ΦB (0.18 eV), which is not conducive to inhibiting the leakage current. However, the Λ of the device with 1 nm UL is wider, easy to obtain a lower leakage current. With the increase of gate voltage, both the conduction band and valence band move down, resulting in a decrease of ΦB. In Fig. 3(d), the ΦB of the device without/with UL configuration for the on-state can be reduced to 0 eV, demonstrating large Ids. However, the device with 1 nm UL has more electrical states in the bias window than the device without UL. Therefore, Ion increases when 1 nm UL is used.
As mentioned above, the LP devices have higher requirements for Ioff than that of HP devices. For the sub-3 nm devices with large leakage current, we used a doping concentration of 1 × 1013 e cm−2 to improve the performance of LP applications. In Fig. 4, compared with the 3 × 1013 e cm−2 doping concentration, the devices with a 1 × 1013 e cm−2 doping concentration has higher Ion and lower SS under the same Lg and LUL. For example, when Lg and LUL are equal to 3 nm and 2 nm, the Ion values of the OGa2S (OIn2S) MOSFETs with 3 × 1013 and 1 × 1013 e cm−2 doping concentrations are 632.1 (702.61) and 805.2 (865.3) μA μm−1, respectively. With the increase of LUL, Ion first increases and then decreases, which is mainly because of the degradation of gate control capability in the superthreshold zone. For devices with a gate length of 2 nm, the maximum on-state current is reached when LUL is equal to 2 nm. It is worthy to note that both OGa2S and OIn2S MOSFETs can approach the Ion standard of ITRS low-power applications when Lg is scaled to 2 nm. Moreover, the maximum on-state current for the OM2S device with a 2 nm gate length can exceed 500 μA μm−1 and the value is two times higher than that of the LP standard.
In the following, we study the performance of switching speed and energy consumption for the ultra-short-channel OM2S MOSFETs. It is known that the intrinsic delay time (τ) can be taken as a critical parameter to characterize the conversion speed of logic devices, which can be described as  ,52 where Qon and Qoff represent the Mulliken charge of the channel at the on-state and off-state, respectively, and W is the width of the channel. Fig. 5(a) shows that the τ values of sub-5 nm OGa2S and OIn2S MOSFETs are within the range of 0.027–0.039 ps, lower than the requirement of ITRS in 2028 for the HP (0.423 ps) applications. In Fig. 5(b), the sub-5 nm OGa2S and OIn2S MOSFETs exhibit ultra-low τ values of 0.04 and 0.119 ps, which are far below the LP applications standard (1.497 ps). This feature indicates that the sub-5 nm OM2S MOSFETs have the advantage of fast switching speed.
,52 where Qon and Qoff represent the Mulliken charge of the channel at the on-state and off-state, respectively, and W is the width of the channel. Fig. 5(a) shows that the τ values of sub-5 nm OGa2S and OIn2S MOSFETs are within the range of 0.027–0.039 ps, lower than the requirement of ITRS in 2028 for the HP (0.423 ps) applications. In Fig. 5(b), the sub-5 nm OGa2S and OIn2S MOSFETs exhibit ultra-low τ values of 0.04 and 0.119 ps, which are far below the LP applications standard (1.497 ps). This feature indicates that the sub-5 nm OM2S MOSFETs have the advantage of fast switching speed.
 | ||
| Fig. 5 PDP and Ion for monolayer OM2S and other 2D n-MOSFETs49,53–58 as functions of τ in HP (a) and LP (b) applications. The black dotted line represents the energy-delay product (EDP) standard of the ITRS 2028 horizon (1.02 × 10−28 J s μm−1 for HP and 4.18 × 10−28 J s μm−1 for LP). | ||
The energy consumption characteristics can be evaluated by the switching-energy cost of power dissipation (PDP), which is calculated as 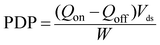 .52 In Fig. 5, the PDP values of sub-5 nm OGa2S (0.026–0.06 fJ μm−1) and OIn2S (0.023–0.057 fJ μm−1) MOSFETs fulfill the ITRS needs for HP (0.24 fJ μm−1) applications. The OGa2S and OIn2S MOSFETs present lower PDP values of 0.013–0.048 fJ μm−1 and 0.017–0.054 fJ μm−1 compared with the target of LP (0.28 fJ μm−1) applications, demonstrating an extremely low switching-energy cost for the OM2S MOSFETs.
.52 In Fig. 5, the PDP values of sub-5 nm OGa2S (0.026–0.06 fJ μm−1) and OIn2S (0.023–0.057 fJ μm−1) MOSFETs fulfill the ITRS needs for HP (0.24 fJ μm−1) applications. The OGa2S and OIn2S MOSFETs present lower PDP values of 0.013–0.048 fJ μm−1 and 0.017–0.054 fJ μm−1 compared with the target of LP (0.28 fJ μm−1) applications, demonstrating an extremely low switching-energy cost for the OM2S MOSFETs.
To express the relationship between τ and PDP, we calculated the energy-delay product (EDP) defined as the expression EDP = τ × PDP.44 The EDP of the sub-5 nm OM2S MOSFETs is varied from 8.28 × 10−31 to 2.22 × 10−30 J s μm−1 in HP applications and 8.8 × 10−31 to 3.22 × 10−30 J s μm−1 in LP applications. The detailed comparations with other sub-5 nm n-type MOSFETs are listed in Fig. 5. It can be found that monolayer OM2S MOSFETs possess lower EDP for HP and LP applications than those of MoS2,53 MoSi2N4,54 InP,55 MoTe2,56 and GaN.49 For example, in HP applications, the EDP value of OGa2S MOSFETs with 3 nm Lg can be 1.22 × 10−30 J s μm−1, less than those of MoS2 (5.77 × 10−29 J s μm−1), MoSi2N4 (1.63 × 10−29 J s μm−1), and GaN (3.19 × 10−28 J s μm−1). In the LP applications, when Lg is 1 nm, the EDP values of OGa2S and OIn2S MOSFETs are 1.38 × 10−30 and 2.02 × 10−30 J s μm−1, respectively, lower than those of MoS2 and MoSi2N4. Although the EDP of OM2S is slightly inferior to those of As,57 Sb,57 and InSe58 cases, the Ion of OM2S is significantly superior to the latter. Therefore, both OGa2S and OIn2S MOSFETs possess extraordinary high-speed manipulation and low-energy expending, which are beneficial for the HP and LP applications.
4. Discussion
To check whether our devices meet IRDS standards, we took the 12 nm n-type OGa2S MOSFETs as an example to further assess the performance of OM2S MOSFETs with a Vds value of 0.65 V, and the Ioff value is specified to 0.01 μA μm−1 for HP and 1 × 10−4 μA μm−1 for LP. Fig. S9 and Table S1† show that the OGa2S MOSFETs possess high Ion (2570.7 μA μm−1 for HP and 2279.8 μA μm−1 for LP), far exceeding the required current criteria (1979 μA μm−1 for HP and 1336 μA μm−1 for LP) of IRDS in 2028. Moreover, other performance parameters of OGa2S MOSFETs, including SS, τ and PDP, also meet IRDS standards.5. Conclusion
In summary, we designed an ultra-short-channel double-gate OM2S MOSFETs and systematically investigated the effect of doping concentrations and UL length modulations on the transport properties. The n-type OM2S MOSFETs have a larger saturation current and a smaller leakage current than those of the p-type OM2S MOSFETs. The drain current of the OGa2S case was higher than that of the OIn2S case. Moreover, for the OM2S MOSFETs with 1 nm gate length, the on-state current can reach 1000 μA μm−1, exceeding the standard of HP applications. Furthermore, the on-state current of OM2S MOSFETs with 2 nm gate length is about two times higher than that of the LP standard. The EDP value of the sub-5 nm OM2S MOSFETs can vary from 8.28 × 10−31 to 2.22 × 10−30 J s μm−1 (8.8 × 10−31 to 3.22 × 10−30 J s μm−1) and the value is two orders lower than the standard of HP (LP) applications, resulting in high-speed manipulation and low-energy expending. The subthreshold swing approaches the limit of MOSFETs at room temperature even as the gate length shrinks to 2 nm. This work is expected to provide new opportunities to realize the ultra-short channel electron devices with high performance and low power consumption in the future by utilizing monolayer OGa2S and OIn2S semiconductor materials.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Natural Science Foundation of China (Grant No. 11904085 and 12074103), the Excellent Youth Foundation of Henan Scientific Committee (Grant No. 202300410221), and the Henan Normal University Innovative Science and Technology Team (Grant No. 20200185). The calculations were also supported by the High Performance Computing Center of Henan Normal University.References
- G. Pizzi, M. Gibertini, E. Dib, N. Marzari, G. Iannaccone and G. Fiori, Nat. Commun., 2016, 7, 12585 CrossRef PubMed.
- I. Ferain, C. A. Colinge and J. P. Colinge, Nature, 2011, 479, 310–316 CrossRef PubMed.
- R. G. Quhe, L. Xu, S. Q. Liu, C. Yang, Y. Y. Wang, H. Li, J. Yang, Q. H. Li, B. W. Shi, Y. Li, Y. Y. Pan, X. T. Sun, J. Z. Li, M. Y. Weng, H. Zhang, Y. Guo, L. Q. Xu, H. Tang, J. C. Dong, J. B. Yang, Z. Y. Zhang, M. Lei, F. Pan and J. Lu, Phys. Rep., 2021, 938, 1–72 CrossRef.
- M. Y. Li, S. K. Su, H. P. Wong and L. J. Li, Nature, 2019, 567, 169–170 CrossRef PubMed.
- S. B. Desai, S. R. Madhvapathy, A. B. Sachid, J. P. Llinas, Q. Wang, G. H. Ahn, G. Pitner, M. J. Kim, J. Bokor, C. Hu, H. P. Wong and A. Javey, Science, 2016, 354, 99–102 CrossRef PubMed.
- J. Ji, X. Song, J. Liu, Z. Yan, C. Huo, S. Zhang, M. Su, L. Liao, W. Wang, Z. Ni, Y. Hao and H. Zeng, Nat. Commun., 2016, 7, 13352 CrossRef CAS PubMed.
- M. Chhowalla, D. Jena and H. Zhang, Nat. Rev. Mater., 2016, 1, 16052 CrossRef CAS.
- E. G. Marin, D. Marian, M. Perucchini, G. Fiori and G. Iannaccone, ACS Nano, 2020, 14, 1982–1989 CrossRef CAS.
- Z. Liu, J. Wang, B. Chen, Y. Wei, W. Liu and J. Liu, Nano Lett., 2021, 21, 7405–7410 CrossRef CAS PubMed.
- D. J. Late, B. Liu, J. Luo, A. Yan, H. S. Matte, M. Grayson, C. N. Rao and V. P. Dravid, Adv. Mater., 2012, 24, 3549–3554 CrossRef PubMed.
- H. Du, M. Tu, S. Luo, Y. Liu, X. Qiu, H. Lu, S. Li, S. Yuan, W. Huang, W. Jie and J. Hao, Appl. Phys. Lett., 2020, 116, 253102 CrossRef.
- S. Lei, F. Wen, L. Ge, S. Najmaei, A. George, Y. Gong, W. Gao, Z. Jin, B. Li, J. Lou, J. Kono, R. Vajtai, P. Ajayan and N. J. Halas, Nano Lett., 2015, 15, 3048–3055 CrossRef PubMed.
- X. Li, P. Yuan, L. Li, M. He, J. Li and C. Xia, Phys. Rev. Appl., 2022, 18, 044012 CrossRef.
- B. J. Carey, J. Z. Ou, R. M. Clark, K. J. Berean, A. Zavabeti, A. S. Chesman, S. P. Russo, D. W. Lau, Z. Q. Xu, Q. Bao, O. Kevehei, B. C. Gibson, M. D. Dickey, R. B. Kaner, T. Daeneke and K. Kalantar-Zadeh, Nat. Commun., 2017, 8, 14482 CrossRef.
- D. A. Bandurin, A. V. Tyurnina, G. L. Yu, A. Mishchenko, V. Zolyomi, S. V. Morozov, R. K. Kumar, R. V. Gorbachev, Z. R. Kudrynskyi, S. Pezzini, Z. D. Kovalyuk, U. Zeitler, K. S. Novoselov, A. Patane, L. Eaves, I. V. Grigorieva, V. I. Fal'ko, A. K. Geim and Y. Cao, Nat. Nanotechnol., 2017, 12, 223–227 CrossRef CAS PubMed.
- C. L. Tu, K. I. Lin, J. Pu, T. F. Chung, C. N. Hsiao, A. C. Huang, J. R. Yang, T. Takenobu and C. H. Chen, Nanoscale, 2020, 12, 9366–9374 RSC.
- J. Zhang, S. Jia, I. Kholmanov, L. Dong, D. Er, W. Chen, H. Guo, Z. Jin, V. B. Shenoy, L. Shi and J. Lou, ACS Nano, 2017, 11, 8192–8198 CrossRef.
- H. Li, Y. Qin, B. Ko, D. B. Trivedi, D. Hajra, M. Y. Sayyad, L. Liu, S. H. Shim, H. Zhuang and S. Tongay, Adv. Mater., 2020, 32, e2002401 CrossRef.
- X. Wan, E. Chen, J. Yao, M. Gao, X. Miao, S. Wang, Y. Gu, S. Xiao, R. Zhan, K. Chen, Z. Chen, X. Zeng, X. Gu and J. Xu, ACS Nano, 2021, 15, 20319–20331 CrossRef PubMed.
- A. Y. Lu, H. Zhu, J. Xiao, C. P. Chuu, Y. Han, M. H. Chiu, C. C. Cheng, C. W. Yang, K. H. Wei, Y. Yang, Y. Wang, D. Sokaras, D. Nordlund, P. Yang, D. A. Muller, M. Y. Chou, X. Zhang and L. J. Li, Nat. Nanotechnol., 2017, 12, 744–749 CrossRef PubMed.
- M. Y. Liu, L. Gong, Y. He and C. Cao, Phys. Rev. B, 2021, 103, 075421 CrossRef.
- M. J. Varjovi, M. Yagmurcukardes, F. M. Peeters and E. Durgun, Phys. Rev. B, 2021, 103, 195438 CrossRef.
- C. Xia, W. Xiong, J. Du, T. Wang, Y. Peng and J. Li, Phys. Rev. B, 2018, 98, 165424 CrossRef.
- M. Y. Liu, L. Gong, Y. He and C. Cao, Phys. Rev. B, 2021, 104, 035409 CrossRef.
- Y. Guo, S. Zhou, Y. Bai and J. Zhao, Appl. Phys. Lett., 2017, 110, 163102 CrossRef.
- A. Kandemir and H. Sahin, Phys. Rev. B, 2018, 97, 155410 CrossRef.
- L. Seixas, J. Appl. Phys., 2020, 128, 045115 CrossRef.
- T. V. Vu, V. T. T. Vi, H. V. Phuc, A. I. Kartamyshev and N. N. Hieu, Phys. Rev. B, 2021, 104, 115410 CrossRef.
- M. Demirtas, M. J. Varjovi, M. M. Cicek and E. Durgun, Phys. Rev. Mater., 2020, 4, 114003 CrossRef.
- J. Qiu, F. Zhang, H. Li, X. Chen, B. Zhu, H. Guo, Z. Ding, J. Bao and J. Yu, IEEE Electron Device Lett., 2021, 42, 561–564 Search PubMed.
- P. Wang, Y. Zong, H. Liu, H. Wen, H. B. Wu and J. B. Xia, J. Mater. Chem. C, 2021, 9, 4989–4999 RSC.
- M. Y. Liu, Y. He, Y. Mao and K. Xiong, Phys. Rev. B, 2022, 105, 035418 CrossRef.
- T. V. Vu, C. V. Nguyen, H. V. Phuc, A. A. Lavrentyev, O. Y. Khyzhun, N. V. Hieu, M. M. Obeid, D. P. Rai, H. D. Tong and N. N. Hieu, Phys. Rev. B, 2021, 103, 085422 CrossRef.
- M. Demirtas, B. Ozdemir, Y. Mogulkoc and E. Durgun, Phys. Rev. B, 2020, 101, 075423 CrossRef.
- Y. Bai, Q. Zhang, N. Xu, K. Deng and E. Kan, Appl. Surf. Sci., 2019, 478, 522–531 CrossRef.
- R. Li, Y. Cheng and W. Huang, Small, 2018, 14, e1802091 CrossRef.
- X. Li, T. Liu, L. Li, M. He, C. Shen, J. Li and C. Xia, Phys. Rev. B, 2022, 106, 125306 CrossRef.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef.
- M. Brandbyge, J. L. Mozos, P. Ordejón, J. Taylor and K. Stokbro, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 165401 CrossRef.
- D. R. Hamann, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 085117 CrossRef.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS.
- S. Liu, J. Yang, L. Xu, J. Li, C. Yang, Y. Li, B. Shi, Y. Pan, L. Xu, J. Ma, J. Yang and J. Lu, Nanoscale, 2021, 13, 5536–5544 RSC.
- Y. Guo, F. Pan, G. Zhao, Y. Ren, B. Yao, H. Li and J. Lu, Nanoscale, 2020, 12, 15443–15452 RSC.
- W. Zhou, S. Zhang, S. Guo, H. Qu, B. Cai, X. Chen and H. Zeng, Nanoscale, 2020, 12, 18931–18937 RSC.
- W. H. Zhou, S. L. Zhang, S. Y. Guo, Y. Y. Wang, J. Lu, X. Ming, Z. Li, H. Z. Qu and H. B. Zeng, Phys. Rev. Appl., 2020, 13, 044066 CrossRef.
- J. S. Huang, P. Li, X. X. Ren and Z. X. Guo, Phys. Rev. Appl., 2021, 16, 044022 CrossRef.
- S. Y. Guo, Y. Y. Wang, X. M. Hu, S. L. Zhang, H. Z. Qu, W. H. Zhou, Z. H. Wu, X. H. Liu and H. B. Zeng, Phys. Rev. Appl., 2020, 14, 044031 CrossRef.
- S. Guo, H. Qu, W. Zhou, S. A. Yang, Y. S. Ang, J. Lu, H. Zeng and S. Zhang, Phys. Rev. Appl., 2022, 17, 064010 CrossRef CAS.
- B. Wang, J. Ning, J. Zhang, D. Wang, X. Yang, Y. Jia, C. Zhang, Y. Zeng and Y. Hao, Appl. Phys. Lett., 2021, 119, 163504 CrossRef CAS.
- D. Yin and Y. Yoon, IEEE Trans. Electron Devices, 2021, 68, 3649–3657 CAS.
- R. G. Quhe, Q. H. Li, Q. X. Zhang, Y. Y. Wang, H. Zhang, J. Z. Li, X. Y. Zhang, D. X. Chen, K. H. Liu, Y. Ye, L. Dai, F. Pan, M. Lei and J. Lu, Phys. Rev. Appl., 2018, 10, 024022 CrossRef CAS.
- H. Li, P. Xu and J. Lu, Nanoscale, 2019, 11, 23392–23401 RSC.
- H. Zhang, B. Shi, L. Xu, J. Yan, W. Zhao, Z. Zhang, Z. Zhang and J. Lu, ACS Appl. Electron. Mater., 2021, 3, 1560–1571 CrossRef CAS.
- X. Sun, Z. Song, N. Huo, S. Liu, C. Yang, J. Yang, W. Wang and J. Lu, J. Mater. Chem. C, 2021, 9, 14683–14698 RSC.
- L. Xu, R. Quhe, Q. Li, S. Liu, J. Yang, C. Yang, B. Shi, H. Tang, Y. Li, X. Sun, J. Yang and J. Lu, J. Mater. Chem. C, 2022, 10, 2223–2235 RSC.
- Q. Li, J. Yang, Q. Li, S. Liu, L. Xu, C. Yang, L. Xu, Y. Li, X. Sun, J. Yang and J. Lu, J. Phys. Chem. C, 2021, 125, 19394–19404 CrossRef.
- X. Sun, Z. Song, S. Liu, Y. Wang, Y. Li, W. Wang and J. Lu, ACS Appl. Mater. Interfaces, 2018, 10, 22363–22371 CrossRef CAS.
- Y. Y. Wang, R. X. Fei, R. Quhe, J. Z. Li, H. Zhang, X. Y. Zhang, B. W. Shi, L. Xiao, Z. G. Song, J. B. Yang, J. J. Shi, F. Pan and J. Lu, ACS Appl. Mater. Interfaces, 2018, 10, 23344–23352 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2nr04840j |
| This journal is © The Royal Society of Chemistry 2023 |