Cucurbit[8]uril forms tight inclusion complexes with cationic triamantanes

Abstract

We report the synthesis of quaternary (di)cationic triamantane derivatives G1 and G3 by the permethylation of the corresponding primary ammonium ions G2 and G4. The complexation behaviors of G1–G4 toward CB[7] and CB[8] were examined by ¹H NMR spectroscopy, which reveals that CB[8] is capable of fully encapsulating G1–G4 whereas CB[7] forms inclusion complexes with G1, G2, and G4 but cannot fully encapsulate the central hydrophobic core of the bis-quaternary ammonium ion G3. The geometries of the CB[n]-guest complexes were determined by analyzing the complexation induced changes in chemical shifts and were further confirmed by molecular modelling using the Conformer–Rotamer Ensemble Sampling Tool (CREST) based on the GFN methods. Finally, the complexation thermodynamics were determined by a combination of ¹H NMR competitive experiments, direct isothermal titration calorimetry (ITC) measurements, and competitive ITC titrations using a tight binding ternary complex as a competitor.

---

Introduction

The synthesis and molecular recognition properties of the cucurbit[n]uril (CB[n]) family of molecular container compounds has undergone rapid development since the turn of the millennium.¹Fig. 1 shows the molecular structure of CB[n] which is composed of n glycoluril units connected by 2n methylene bridges that form a barrel shaped macrocycle with two electron rich ureidyl carbonyl fringed portals and a central hydrophobic cavity. Accordingly, CB[n] hosts bind strongly to guests that feature a central hydrophobic moiety that is flanked by two cationic groups. For example, Mock and co-workers showed that CB[6] binds strongly to alkanediammonium ions in aqueous formic acid solution with selectivity for pentane- and hexanediammonium ions (1 and 2);² the CB[6]-spermine (3) complex achieved K_a = 1.3 × 10⁷ M⁻¹ (K_d = 76 nM). Later studies by Kim, Inoue, and co-workers demonstrated that even higher binding affinity could be achieved by working in the less competitive environment of pure water.³

Fig. 1 Structure of ultratight binding hosts CB[n] (n = 6, 7, 8) and selected guests.

Clues from CB[n] derived self-sorting systems⁴ led us to measure the binding constants of CB[n] (n = 6, 7, 8) toward a panel of ammonium ions in pH 4.74 acetate buffered water and discover the ultratight binding affinity of the CB[7]·adamantane ammonium (4) ion (K_a = 4.2 × 10¹² M⁻¹) using ¹H NMR competitive experiments.⁵ The hydrophobic adamantane skeleton contains ten carbon atoms. Contemporaneously, Kim, Inoue, and Kaifer published the binding affinity of the CB[7]·trimethylaminomethyl ferrocene (5; hydrophobic core: ten C-atoms + Fe) complex (K_a = 4 × 10¹² M⁻¹) in pure water.⁶ In the follow up work, the Kim, Kaifer, Isaacs, Gilson and Inoue group collaboratively explored the CB[7]·(bis)trimethylaminomethyl ferrocene (6) complex and determined K_a = 2.9 × 10¹⁵ M⁻¹ in pure water by competitive ITC titrations.⁷ The potential of [2.2.2]bicyclooctane as a hydrophobic core (eight C-atoms) (e.g., 7) to construct ultratight binding complexes was subsequently reported by the Kim, Inoue, and Gilson team.⁸ The high affinity of CB[n]·guest complexes has been traced, in part, to the presence of intracavity “high energy” water molecules that lack a full complement of H-bonds and that are released upon complexation as shown by DeSimone, Scherman, and Nau.⁹ The K_a values for CB[n]·guest complexes have been featured prominently in a series of blinded challenges (SAMPL and Hydrophobe) that aim to improve computational approaches to free energy computations in water.¹⁰ As illustrated in Fig. 2, the changes in aqueous solvation of both the CB[n] host and the hydrophobic guest contribute to the thermodynamics of complexation.^9b

Fig. 2 Illustration of the changes in the solvation of the host and the guest that occur during the formation of CB[n]·guest complexes. Aqua spheres, bulk water; Blue spheres, intracavity “high energy” water.

More recently, in collaboration with Glaser and Mlinarić-Majerski, we have explored various cationic guests featuring diamantane (14 C-atoms) as the hydrophobic core and demonstrated the attomolar binding affinity of the CB[7]·diamantane-bis(trimethylammonium) ion (8) in pure water (K_a = 7.2 × 10¹⁷ M⁻¹).¹¹ The 10 000-fold weaker binding affinity of the CB[7]·9 complex illustrates that the nature of the ammonium (1° versus 4°) can be a very important factor in some but not all situations.^11,12 In the CB[8] series, using the CB[8]·10 complex K_a = 5.7 × 10¹⁴ M⁻¹ was achieved in 50 mM acetate buffered water (pH = 4.74).¹³ CB[n]·guest complexes have also been shown to be highly responsive to suitable stimuli (e.g., photochemical, electrochemical, chemical, and pH).¹⁴ These high affinity, highly selective, and stimuli responsive binding events render CB[n]·guest complexes useful as a supramolecular latching and switching element in a variety of complex systems. Accordingly, macrocyclic CB[n] have found numerous uses including as a component of (bio)sensing and imaging ensembles,¹⁵ for drug formulation, delivery and sequestration,¹⁶ creating supramolecular organic frameworks,¹⁷ and performing supramolecular catalysis.^9d In this paper, we further investigate into cationic CB[n]·diamondoid complexation events by progressing from C14 diamantane to the larger and more hydrophobic C18 triamantane skeleton. Very recently, Biedermann and co-workers have studied the binding of CB[n] toward diamondoid (adamantane, diamantane, and triamantane) alcohols using a combination of calorimetry and chemical computations.¹⁸ Among other results, Biedermann and co-workers found that CB[8] binds with 3,9-dihydroxytriamantane with log K_a = 7.0 in deionized water which represents the first example of triamantane complexation with CB[n]. Overall, Biedermann's work showed that peculiar host solvation – rather than London dispersion interactions, electronic energies, or entropic factors – is largely responsible for the ultratight binding exhibited by CB[n] hosts.

Results and discussion

This results and discussion section is organized as follows. First, we describe the selection, synthesis, and characterization of guests G1–G4. Next, we investigate the complexation of G1–G4 by complexation induced changes in ¹H NMR chemical shifts along with molecular modelling to glean information about the geometry of the CB[n]·G complexes. Subsequently, we measure the binding constants for the CB[n]·G complexes by direct isothermal titration calorimetry (ITC), ¹H NMR competitive experiments, and competitive ITC titrations as appropriate. Finally, we discuss the data and provide conclusions.

Selection, synthesis, and characterization of G1–G4

As described above, the Isaacs group has a longstanding interest in the design and discovery of tight binding host–guest complexes with an emphasis on CB[n]·cationic diamondoid systems. Previous investigations focused on (di)cationic adamantane (C10) and diamantane (C14) derived guests and showed that both ion–dipole (C=O⋯ammonium) interactions and the hydrophobicity of the diamondoid skeleton play significant roles in determining host–guest binding affinity.^5,13,19 As the next logical step toward the creation of even tighter binding guests for CB[n], we decided to investigate cationic derivatives of triamantane (C18) which is the next larger diamondoid homologue. Accordingly, we synthesized hydrochloride salts G2 and G4 (Fig. 3) from triamantane by three step procedures (hydroxylation, modified Ritter reaction with chloroacetonitrile, and cleavage of the formed chloroacetamide to the corresponding amine) described in the literature.²⁰ The separate permethylation reactions of G2 and G4 with an excess of MeI (15 equiv.) and NaHCO₃ (10 equiv.) were conducted in hot (60 °C) MeOH for 48 h which delivered quaternary ammonium salts G1 and G3 in 47 and 62% yields, respectively. High resolution mass spectrometry showed ions for G1 at 298.2536 (calc. for C₂₁H₃₂N: 298.2535) and G3 at 379.3100 (calc. for C₂₄H₄₀N₂Na: 379.8089) which are in accord with the depicted molecular formulas. Please note that G1 and G3 are prepared and used as iodide salts whereas G2 and G4 are hydrochlorides; we do not consider the influence of counterions in this paper. C_s-symmetric guests G1 and G2 feature a single mirror plane whereas guests G3 and G4 possess two mirror planes and are therefore C_2v-symmetric. In accord with symmetry considerations, the ¹³C NMR spectrum of G1 and G3 recorded in CDCl₃/CD₃OD consist of 14 and 9 resonances, respectively (ESI,† Fig. S2 and S4). While the ¹H NMR spectrum of G1 suffers from spectral overlap, the spectrum for C_s-symmetric G3 (ESI,† Fig. S3) is more diagnostic and displays seven resonances in an 18 : 4 : 4 : 4 : 6 : 2 : 2 ratio; the resonance at 1.79 pm with an integral of six is caused by the accidental overlap of two resonances (4H and 2H).

Fig. 3 Structures of cationic guests G1–G4, competitors C1–C3, and comparison compounds C4–C10 used in this study.

Investigation of host–guest complexation by ¹H NMR spectroscopy

After having synthesized and fully characterized guests G1–G4, we decided to perform a qualitative investigation of the host–guest binding of CB[7] and CB[8] toward guests G1–G4 by ¹H NMR spectroscopy (ESI,† Fig. S5–S16). For example, Fig. 4c shows the ¹H NMR spectra recorded for G4 along with the assignments of the resonances. Because H_b and H_c are diastereotopic they appear as a pair of coupled doublets. The resonances for H_a, H_b, and H_c appear downfield of the other resonances due to the electron withdrawing effect of the adjacent NH₃⁺ group. The ¹H NMR spectra separately recorded for 1 : 1 mixtures of G4 with CB[8] and CB[7] are shown in Fig. 4b and d, respectively. As expected, all of the resonances for guest G4 shift upfield upon formation of CB[7]·G4 and CB[8]·G4 complexes indicating that guest G4 is bound within the magnetically shielding environment of the CB[n] cavity.^1a,2 At 1 : 2 CB[n] : G4 ratio (Fig. 4a and e), we observe separate resonances for free G4 and the CB[n]·G4 complex which evidences the slow kinetics of guest exchange on the ¹H NMR timescale which is typical for ultratight CB[n] guest complexes.⁵ The ¹H NMR spectrum of D_nh-symmetric CB[n] hosts shows one set of diastereotopic resonances (H_x and H_y) for the methylene bridges. In the CB[n]·G4 complex we still observe one set of doublets for H_x and H_y which indicates that its time averaged geometry has a mirror plane passing through the equator of the complex. The magnitude of the complexation induced changes in the chemical shift is presented in Fig. 4b and d. Protons H_a, H_d, and H_g undergo substantial upfield shifts (Δδ from −0.68 to −0.86 ppm) whereas H_b, H_c, and H_e undergo smaller shifts (Δδ from −0.16 to −0.51 ppm) which reflects their position with respect to the magnetically shielding CB[n] cavity (vide infra). To the best of our knowledge, the inclusion of the 18 carbon triamantane skeleton inside the CB[7] cavity is the largest number of heavy (non-hydrogen) atoms incorporated to date. Recently, Biedermann et al. studied the binding of CB[7] toward 3,9-dihydroxytriamantane and 9,15-dihydroxytriamantane and concluded that “the experimental evidence ruled out the positioning of the guest in the hosts’ cavity”.¹⁸ Accordingly, we conclude that the presence of the cationic groups on G4 provides sufficient ion–dipole interactions to drive the formation of the otherwise unfavorable inclusion of the triamantane framework inside CB[7]. Similar ¹H NMR measurements were performed for CB[7]·G1, CB[8]·G1, CB[7]·G2, CB[8]·G2, and CB[8]·G3 complexes which indicate the inclusion of the triamantane skeleton in the CB[n] cavity (ESI,† Fig. S5–S12). In contrast, the ¹H NMR spectra recorded for mixtures of CB[7] and G3 show small upfield shifts for the NMe₃⁺, H_b, and H_c resonances (ESI,† Fig. S9–S10) which suggests that CB[7]·G3 forms an exclusion complex where only one NMe₃⁺ group enters the CB[7] cavity and the other NMe₃⁺ group is outside the cavity (ESI,† Fig. S57). Such exclusion complexes are typically weak. In contrast, ¹H NMR results for CB[7]·G1, CB[8]·G1, CB[7]·G2, CB[8]·G2, and CB[8]·G3 (ESI,† Fig. S5–S12) show that the resonances for the triamantane frameworks of G1, G2, and G3 undergo complexation induced upfield changes in the chemical shift which is indicative of cavity binding. In addition, separate ¹H NMR resonances for free and complexed guests are present at 1 : 2 CB[n]·guest stoichiometry for CB[7]·G1, CB[8]·G1, CB[7]·G2, CB[8]·G2, and CB[8]·G3 which indicates that the kinetics of guest exchange are slow on the chemical shift timescale. For the C_s-symmetric guest G1 we observe a slight downfield shift of the NMe₃⁺ resonance which indicates that the NMe₃⁺ group is located in the deshielding region just outside the C=O portals.^1a,2 In addition, upon formation of the CB[7]·G1, CB[7]·G2, and CB[8]·G2 complexes we observe two sets of resonances for the diastereotopic methylenes of CB[n] (H_x, H_y) which is due to the top-bottom C=O portal dissymmetry induced by the C_s-symmetric guests.

Fig. 4 ¹H NMR spectra recorded (600 MHz, D₂O) for (a) a mixture of G4 (2 mM) and CB[8] (1 mM), (b) a mixture of G4 (1 mM) and CB[8] (1 mM), (c) G4 (1 mM), (d) a mixture of G4 (1 mM) and CB[7] (1 mM), and (e) a mixture of G4 (2 mM) and CB[7] (1 mM). Resonances marked with primes (′) arise from the host·G4 complex.

Molecular modelling

To gain further insight into the geometry characteristics of the CB[n]·G4 complexes we performed molecular modelling. The search for favorable complex geometries was done using the Conformer–Rotamer Ensemble Sampling Tool (CREST) based on the GFN methods²¹ by applying iterative meta-dynamic sampling for non-covalently bound complexes, clusters or aggregates (NCI-iMTD mode). The analytical linearized Poisson–Boltzmann (ALPB) solvation model was used to account for the implicit influence of water in xTB computations. Fig. 5 shows the top and side of the found geometries of the CB[7]·G4 and CB[8]·G4 complexes. Minimized molecular models of the CB[7]·G1–CB[7]·G3 and CB[8]·G1–CB[8]·G3 complexes are shown in the ESI† (Fig. S55–S57). In accordance with the analysis of the complexation induced changes in chemical shifts described above, the molecular models show the encapsulation of the hydrophobic triamantane skeleton in the center of the CB[n] cavity. The average distances of cage H-atoms from the mean equatorial plane defined by the glycoluril methine C-atoms are as follows for CB[7]·G4: H_a, 1.26; H_b, 3.37; H_c, 2.55; H_d, 1.26; H_e, 2.13; H_f, 0.07; H_g 0.19 Å and for CB[8]·G4: H_a, 1.20; H_b, 3.25; H_c, 2.41; H_d, 1.22; H_e, 2.05; H_f, 0.50; H_g, 0.61 Å. As shown in Fig. 4b and d for CB[7]·G4 and CB[8]·G4, H_a, H_d, H_f, and H_g, which undergo substantial upfield shifts in the NMR spectrum, reside closer to the equatorial plane running through the center of the CB[n] cavity. In contrast, the diastereotopic methylene resonance for H_b – which shows the smallest upfield shift for both CB[7]·G4 and CB[8]·G4 – is the farthest from the equator. The average distance between the O-atoms on a single glycoluril ranges from 5.95 to 6.20 Å for CB[7]·G4 and from 5.77 to 5.95 Å for CB[8]·G4 with averages of 6.05 and 5.87 Å, respectively. This is consistent with the expected buttressing effect of the sterically demanding G3 guest against the C=O portals more significantly for CB[7] than CB[8]. Each NH₃⁺ group in CB[7]·G4 forms two H-bonds to the ureidyl C = O groups of CB[7] with the following NH⋯O=C distances (2.00 Å; 1.90 Å), N⋯O=C distances (2.89 Å; 2.76 Å) and NH⋯O=C angles (157.9°; 127.7°). The guests’ N-atoms reside slightly outside the cavity (0.68 Å) in CB[7]·G4 as defined by the distance to the mean plane of the ureidyl O-atoms. The H-bonding metrics for CB[8]·G4 are NH⋯O=C distances (1.77 and 1.80 Å; 1.98 and 2.02 Å), N⋯O=C distances (2.80 and 2.83 Å; 2.87 and 2.91 Å) and NH⋯O=C angles (168.3° and 168.4°; 143.4° and 142.4°). The guests’ N-atoms reside slightly outside the cavity (0.48 Å; 0.76 Å) in CB[8]·G4 as defined by the distance to the mean plane of the ureidyl O-atoms. The distance of CB[7]·G4 (CB[8]·G4) from the centroid of the equatorial methine C-atoms to those methine C-atoms averages 5.84 Å (6.58 Å) whereas the distance from the centroid of the ureidyl O-atoms back to the ureidyl O-atoms averages 4.22 Å (4.80 Å) which defines the width of the cavity and portals, respectively. Note that our modelling results also point towards the preferential formation of the CB[7]·G3 exclusion complex since the geometry where only one NMe₃⁺ group is inside the host cavity (ESI,† Fig. S25) is energetically much more favorable than the hypothetical structure where full inclusion is realized (ESI,† Table S1).

Fig. 5 Side and top views of the energy-minimized geometries of (a) CB[7]·G4 and (b) CB[8]·G4. Color codes: C, gray; H, white; O, red; and N, blue.

Measurement and discussion of the thermodynamic parameters of complex formation

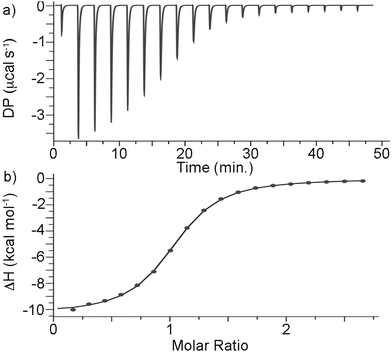
The measurement of all binding constants in this paper was performed in 50 mM NaOAc buffered water at pH = 4.74 to allow comparison with binding constants for cationic adamantane and diamantane derivatives measured previously.^5,13,19a,22 Given the bulkiness of guests G1–G4 which feature the C18 triamantane skeleton and the fast kinetics of guest exchange observed for CB[7]·G3 we suspected that the CB[7] complexes with these guests would be weak. Accordingly, we performed direct isothermal calorimetric titrations for CB[7]·G1, CB[7]·G2, and CB[7]·G4 (ESI,† Fig. S17–S19). Fig. 6a shows the thermogram recorded when a solution of CB[7] (145 μM) in the cell was titrated with a solution of G1 in the syringe. The direct titration data were processed and analyzed using the PEAQ ITC data analysis software. Fig. 6b shows a plot of the integrated heat versus CB[7] : G1 molar ratio fitted to a 1 : 1 binding model that was used to determine the K_a = (1.6 ± 0.1) × 10⁵ M⁻¹ and ΔH = –10.4 ± 0.076 kcal mol⁻¹ values (Table 1). The K_a and ΔH values of CB[7]·G2 and CB[7]·G4 were determined similarly and are presented in Table 1 along with data for selected comparison compounds C4–C10 drawn from the literature.^5,13,19a We performed ¹H NMR competitive experiments using the protocols described previously^{5,13,19a,b,23} to measure the K_a value for CB[7]·G3 (K_a = (3.0 ± 0.5) × 10⁵ M⁻¹) using C1 (K_a = (2.5 ± 0.4) × 10⁴ M⁻¹) as a competitor of known affinity (ESI,† Fig. S21).⁵

Fig. 6 (a) ITC thermogram recorded during the titration of CB[7] (145 μM) in the cell with guest G1 in the syringe, (b) Fitting of the data to a 1 : 1 binding model with K_a = (1.6 ± 0.1) × 10⁵ M⁻¹ and ΔH = –10.4 ± 0.076 kcal mol⁻¹.

Table 1 Binding constants (K_a, M⁻¹) and binding enthalpies (ΔH, kcal mol⁻¹) measured for the complexes between hosts CB[7] or CB[8] with guests G1–G4 and C1–C9. Conditions: 50 mM NaOAc buffered H₂O or D₂O, 298 K, pH 4.74)

G	CB[7]	CB[8]
a Measured by direct ITC titration. b Literature values.^5,13,19a c Measured by ^1H NMR competitive experiments with C1 as a competitor. d CB[8]·G2 complex is insoluble at room temperature. e Measured by ^1H NMR competitive experiments with C2 as a competitor. f Measured by ITC competitive experiments using C3 as a competitor.
G1	(1.6 ± 0.1) × 10^5 ^a	(2.1 ± 0.1) × 10^14 ^c
	–10.4 ± 0.076
G2	(7.5 ± 0.2) × 10^4 ^a	n.d. ^d
	–4.98 ± 0.034
G3	(3.0 ± 0.5) × 10^5 ^c	(1.15 ± 0.17) × 10^13 ^f
		–10.1 ± 0.0
G4	(6.73 ± 1.41) × 10^5 ^a	(1.1 ± 0.3) × 10^14 ^e
	–3.79 ± 0.10	(1.14 ± 0.21) × 10^14 ^f
		–11.5 ± 0.1
C1	(2.5 ± 0.4) × 10^4 ^b	(4.3 ± 1.1) × 10^11 ^b
C2	2030 ^b	(3.3 ± 0.8) × 10^13 ^b
C3	—	(2.67 ± 0.32) × 10^7 (1 : 1)
		–9.23 ± 0.04
		(7.47 ± 1.75) × 10^6 (1 : 2)
		–8.28 ± 0.06
C4	(1.3 ± 0.3) × 10^11 ^b	(8.3 ± 2.3) × 10^11 ^b
C5	(1.9 ± 0.4) × 10^15 ^b	(2.0 ± 0.6) × 10^12 ^b
C6	(8.0 ± 1.9) × 10^11 ^b	(2.7 ± 0.7) × 10^12 ^b
C7	686 ^b	(5.7 ± 1.5) × 10^14 ^b
C8	643 ^b	(7.8 ± 0.8) × 10^13 ^b
C9	(4.2 ± 1.0) × 10^12 ^b	(8.2 ± 1.8) × 10^8 ^b

---

We expected the binding constants of the cationic triamantanes toward CB[8] to far exceed the range that can be measured by direct titrations, so we elected to perform competitive titrations monitored by ¹H NMR or ITC. The literature K_a values of CB[8]-C1 and CB[8]-C2 are given in Table 1. Initially, we performed ¹H NMR competitive studies for CB[8]·G1 using C1 (K_a = 4.3 × 10¹¹ M⁻¹) as a competitor. Experimentally, we prepared a solution of CB[8] (0.100 mM) and C1 (16.5 mM) and then added G1 (0.110 mM) and monitored the equilibration process by ¹H NMR spectroscopy (ESI,† Fig. S20). Specifically, we monitor the two separate H_z resonances for CB[8]·C1 and CB[8]·G1 at ≈ 5.5 ppm until equilibrium is reached. Integration of the resonances by spectral deconvolution, followed by application of the equilibrium and mass balance equations as described previously^{5,13,19b,19a,23} allowed the calculation of K_a = (2.12 ± 0.1) × 10¹⁴ M⁻¹ for CB[8]·G1. Separate experiments that approached equilibrium from the other direction (e.g., starting with CB[8]·G1 and adding C1) gave identical results. The binding constant for CB[8]·G4 ((K_a = (1.1 ± 0.3) × 10¹⁴ M⁻¹), ESI,† Fig. S22) was similarly measured by competitive ¹H NMR assays using C2 as a competitor. Unfortunately, we were not able to measure the binding constant for CB[8]·G3 by ¹H NMR competitive assays because equilibration was extraordinarily slow and complicated by extraneous resonances due to unknown guest decomposition products.

Given the difficulties in measuring K_a for CB[8]·G3 by ¹H NMR competitive assays, we turned to ITC competitive experiments.²⁴ Biedermann et al. have previously suggested a cationic cyclophane as a tight binding competitor for CB[8],²⁵ but because this compound was not commercially available we were unable to test this approach. To avoid problems of slow kinetics which plagued ¹H NMR competitive assays, after much experimentation, we selected the tight binding CB[8]·C3₂ ternary complex as the competitive complex.²⁶Fig. 7a depicts the equilibrium binding model governing this system. Initially, we performed a concatenated series of three direct ITC titrations of a solution of CB[8] (5 μM) in the cell with a solution of C3 (40 μM) from the syringe (Fig. 7b). Fig. 7c shows a plot of the integrated heat data versus molar ratio fitted to the stepwise binding model shown (Fig. 7a) using the Affinimeter^TM software package to deliver the thermodynamic parameters for the formation of the CB[8]·C3 and CB[8]·C3₂ complexes. Affinimeter^TM was used because the PEAQ ITC data analysis software cannot implement the model shown in Fig. 7a. Subsequently, we performed the competitive ITC titration of a solution of CB[8] (30 μM) and C3 (175 μM) in the cell with a solution of G3 (100 μM) from the syringe (Fig. 7d). The DP versus time data were exported to Affinimeter^TM and then integrated to create the plot of ΔH versus molar ratio shown in Fig. 7e. The solid line represents the best global fit of the data to the binding model given in Fig. 7a to calculate the K_a value for CB[8]·G3 (K_a = (1.15 ± 0.17) × 10¹³ M⁻¹). The complete Affinimeter^TM reports are given in the ESI† (Fig. S23–S54). Given that this strategy of using a tight CB[8]·C3₂ ternary complex as a competitor is new and uses a new analysis package (Affinimeter^TM) we decided to further validate our results by performing related competitive titration of CB[8]·C3₂ with G4 which was measured above by ¹H NMR competitive experiments. Gratifyingly, the K_a value measured for CB[8]·G4 by competitive ITC titration (K_a = (1.1 ± 0.3) × 10¹⁴ M⁻¹) is the same as that measured by ¹H NMR competitive experiments (K_a = (1.14 ± 0.21) × 10¹⁴ M⁻¹).

Fig. 7 (a) Schematic representation of binding models implemented in Affinimeter^TM to determine the K_a values for the formation of CB[8]·C3 and CB[8]·C3₂ in the direct titration of CB[8] with C3 and the competitive binding model used to determine the K_a value for CB[8]·G3 during the titration of a mixture of CB[8] and C3 with G3. (b) Thermogram from the direct titration of CB[8] (5 μM) with C3 (40 μM) in the syringe. Three successive titrations were concatenated. (c) Plot of ΔH versus molar ratio. The solid line represents the best fit of the data to the stepwise binding model performed using Affinimeter^TM. (d) Thermogram from the competitive ITC titration of a solution of CB[8] (30 μM) and C3 (175 μM) in the cell with a solution of G3 (100 μM) in the syringe. (e) Plot of ΔH versus molar ratio. The solid line represents the best fit of the data to the stepwise binding model performed using Affinimeter^TM.

With a complete dataset of CB[n]·G thermodynamic parameters in hand, some discussion of the trends in the data is warranted. The magnitude of the binding constants of G1–G4 toward CB[7] (7.5 × 10⁴ to 6.7 × 10⁵ M⁻¹) is dramatically different than that toward CB[8] (1.15 × 10¹³ to 2.1 × 10¹⁴ M⁻¹). Related effects were seen previously in the binding constants of C1, C7, and C8) toward CB[7] and CB[8] which differ dramatically (C1 : 10⁷, C7 : 10¹², C8 : 10¹¹).⁵ We attribute this effect to the fact that the triamantane skeleton (254 ų, PM3 calculation) is too voluminous to be comfortably encapsulated inside CB[7] (volumes: expanded, 272; inner, 242; truncated 158 ų)^9a with a packing coefficient over 100% of the inner cavity whereas triamantane can be easily encapsulated inside CB[8] (volumes: expanded, 479; inner, 367; truncated 263 ų) with a packing coefficient of 69% which is in line with other tight binding CB[n]·diamondoid complexes.¹⁸ For comparison, the calculated volume of diamantane is 206 ų (PM3) which is known to display high affinity toward both CB[7] (packing coefficient 85%) and CB[8].^13,18,19a The observation of inclusion complexes for CB[7]·G1, CB[7]·G2, and CB[7]·G4 demonstrates that the binding free energies of G1, G2, and G4 are sufficiently large to pay the energetic cost to overstuff the cavity of CB[7]. This, coupled with the observation that CB[7]·G3 forms an exclusion complex explains the overall modest binding affinities of CB[7] toward G1–G4. In the CB[7] complexes there is little difference in the binding affinity of the primary ammonium G2 relative to the quaternary ammonium G1. Somewhat surprisingly, amongst the CB[8] complexes, the quaternary ammonium guest G1 binds 18-fold stronger than the quaternary diammonium guest G3 and two-fold more strongly than the primary diammonium guest G4. Unfortunately, the strongest binding achieved among G1–G4 toward CB[8] was for CB[8]·G1 (K_a = 2.21 × 10¹⁴ M⁻¹) which is lower than the diamantane diammonium compounds (e.g., C7) measured previously.¹³ Informative comparisons can also be made across homologous series of guests and comparators (e.g., adamantane vs. diamantane vs. triamantane) to tease out the effect of enlarging the hydrophobic framework. For example, the binding of mono trimethylammonium ions C10, C6, and G1 toward CB[7] decrease in magnitude as the size of the hydrophobic skeleton increases due to the overstuffing of the CB[7] cavity as described above. Conversely, the binding constants of C10, C6, and G1 toward CB[8] increase by three orders of magnitude as the hydrophobic skeleton is increased from 10 to 14 to 18 C-atoms, which reflects the enhanced hydrophobic effect associated with desolvation of the larger hydrophobic residue. In a similar way, CB[8] prefers to bind to the primary diammonium triamantane G4 over the diamantane C4 by a factor of 137-fold which once again reflects the influence of the larger hydrophobic residue. Conversely, CB[7] prefers C4 over G4 by over five orders of magnitude because the packing coefficient of the triamantane derivative G4 is too high for CB[7]. Related trends are seen when comparing the binding constants for quaternary triamantane and diamantane diammonium ions G3 and C5 toward CB[n]. CB[7] prefers the smaller diamantane C5 by nearly ten orders of magnitude whereas the larger CB[8] binds six-fold more strongly to the larger triamantane derivative G3.

Conclusions

We report the preparation and characterization of cationic triamantane derivatives G1–G4 which differ in overall charge (mono- and dication) and in the degree of nitrogen substitution (primary and quaternary). The binding behavior of G1–G4 toward CB[7] and CB[8] was studied by a combination of ¹H NMR spectroscopy, analysis of complexation induced changes in chemical shift, and molecular modelling. Remarkably, CB[7] forms inclusion complexes with triamantanes G1, G2, and G4 which exhibit slow kinetics of exchange on the ¹H NMR timescale. To the best of our knowledge, the encapsulation of 18 heavy (non-hydrogen) atoms inside CB[7] is the highest number observed to date. The binding constants of CB[7] and CB[8] toward triamantane guests G1–G4 were determined by ¹H NMR competitive experiments, direct ITC titrations, and competitive ITC titrations as appropriate based on the magnitude of the binding constants and the kinetics of guest exchange. The use of an ultratight binding ternary complex (CB[8]·C3₂) with fast kinetics of guest exchange represents a new method to measure ultratight CB[8]·guest complexes. This new method capitalized on the ability of Affinimeter^TM to implement this complex binding model and perform global fits of the binding data. Comparisons of the binding data of the homologous series of guests (e.g., adamantane to diamantane to triamantane) showed that the larger C-18 triamantane skeleton delivered enhanced binding affinity toward CB[8] whereas the smaller CB[7] cavity could not accommodate the triamantane framework without incurring substantial energetic penalties due to over-packing. Overall, this work extends our knowledge of the importance of the hydrophobic residue on the binding affinity of cationic diamondoids toward CB[n] and delivers a new competitive ITC method via an ultratight but fast exchanging ternary complex CB[8]·C3₂ to measure ultratight CB[8]·guest complex affinity.

Experimental

General experimental

¹H and ¹³C NMR spectra were recorded with Bruker AV-300, AV-400 or AV-600 NMR spectrometers and the NMR spectra were referenced to tetramethylsilane as an internal standard. The spectral reference for spectra recorded in D₂O was one drop of dioxane-d₈ added after recording the original spectrum. IR spectra were recorded with an FT-IR ABB Bomem MB 102 or FT IR-ATR PerkinElmer UATR Two spectrometer. MALDI-TOF MS spectra were obtained in reflectron mode with an Applied Biosystems Voyager DE STR instrument (Foster City, CA). GC-MS analyses were performed using an Agilent 7890B/5977B GC/MSD instrument equipped with an HP-5ms column. Melting points were obtained by using Original Kofler Mikroheitztisch apparatus (Reichert, Wien). All solvents were obtained from commercial sources and used without further purification. Aminotriamantanes G2 and G4 were prepared according to the previously published procedures²⁰ and their permethylation afforded salts G1·I⁻ and G3·2I⁻, respectively.

General procedure for the permethylation reactions

A mixture of the respective amine (1 equivalent), excess methyl iodide (15 equivalents) and NaHCO₃ (10 equivalents) in methanol (10 mL) was heated in a sealed tube for 48 h at 60 °C.¹¹ The mixture was cooled, the solvent was evaporated, and the crude product was washed with a suitable solvent mixture to afford the corresponding permethylated salt.

N,N,N-Trimethyltriamantane-9-aminium iodide (G1·I⁻)

Permethylation of 9-aminotriamantane hydrochloride (G2·Cl⁻) (146 mg, 0.5 mmol) afforded a solid that was washed with CH₂Cl₂ (20 mL). Evaporation of CH₂Cl₂ gave the crude product which was dissolved in a minimal amount of MeOH and then an excess of Et₂O (20 mL) was added. The solvent was decanted and the washing was repeated two more times, finally yielding the quaternary ammonium salt G1·I⁻ as a white solid (100 mg, 47%). M.p. 296–297 °C. IR (KBr, cm⁻¹): 3473 (br), 3006 (w), 2905 (s), 2874 (s), 2854 (s), 1635 (w), 1480 (m), 1441 (m), 1418 (m), 1341 (w), 1233 (w), 1136 (w), 945 (w), 847 (m). ¹H NMR (CDCl₃ + few drops of CD₃OD, 400 MHz): 1.47 (br. s, 2H), 1.52 (br. s, 2H), 1.64 (s, 2H), 1.67–1.83 (m, 10H), 1.90 (br. s, 1H), 1.99-2.05 (m, 2H), 2.06–2.14 (m, 4H), 3.04 (s, 9H, Me). ¹³C NMR (CDCl₃ + few drops of CD₃OD, 100 MHz): 26.3 (CH, 1C), 32.2 (CH, 1C), 33.5 (CH, 1C), 34.2 (CH₂, 2C), 34.8 (C, 1C), 35.8 (CH₂, 1C), 36.1 (CH, 2C), 36.5 (CH₂, 2C), 38.8 (CH, 2C), 40.9 (CH₂, 1C), 43.7 (CH₂, 1C), 43.8 (CH, 2C), 47.0 (CH₃, 3C, Me), 71.8 (C, 1C, C-N). HR-MS: calcd for [C₂₁H₃₂N]⁺ 298.2535; found 298.2536.

N,N,N,N′,N′,N′-Hexamethyltriamantane-9,15-diaminium diiodide (G3·2I⁻)

Permethylation of 9,15-diaminotriamantane dihydrochloride (G4·2Cl⁻) (137 mg, 0.40 mmol) afforded a solid that was washed with CH₂Cl₂ (20 mL). Evaporation of CH₂Cl₂ gave the crude product which was washed with a MeOH/CH₂Cl₂/ether (0.1 : 1.9 : 8 v : v : v ratio, 100 mL) mixture, yielding the quaternary ammonium salt G3·2I⁻ as a white solid (152 mg, 62%). M.p. >350 °C. IR (neat, cm⁻¹): 3421 (br), 3210 (m), 1621 (m), 1604 (s), 1045 (w), 560 (w). ¹H NMR (600 MHz, D₂O): 1.55 (s, 2H), 1.73 (s, 2H), 1.79 (s, 6H), 2.02-2.07 (m, 4H), 2.10–2.16 (m, 4H), 2.21 (s, 4H), 3.03 (s, Me, 18H) ppm. ¹³C NMR (75 MHz, CD₃OD), δ: 33.5 (CH, 2C), 35.8 (CH₂, 4C), 36.2 (CH₂, 1C), 39.5 (C, 1C), 39.6 (CH, 4C), 42.0 (CH₂, 2C), 43.4 (CH, 2C), 49.4 (CH₃, Me, 6C), 73.3 (C-N, 2C) ppm. HR-MS: calcd for [C₂₄H₄₀N₂ + Na]⁺ 379.3089; found 379.3100.

Conflicts of interest

The authors have no competing interests to declare.

Acknowledgements

We thank the National Science Foundation (CHE-1807486 to L.I.) and the Croatian Science Foundation (project UIP-2017-05-9653 to M.Š.) for financial support. S.M. thanks the Department of Education for a GAANN fellowship (P200A150033) and the University of Maryland for summer research and Wylie dissertation fellowships. The computations were performed using the resources of the computer cluster Isabella based in SRCE – the University of Zagreb, University Computing Centre.

Notes and references

1. (a) E. Masson, X. Ling, R. Joseph, L. Kyeremeh-Mensah and X. Lu, RSC Adv., 2012, 2, 1213–1247; (b) S. J. Barrow, S. Kasera, M. J. Rowland, J. del Barrio and O. A. Scherman, Chem. Rev., 2015, 115, 12320–12406; (c) D. Shetty, J. K. Khedkar, K. M. Park and K. Kim, Chem. Soc. Rev., 2015, 44, 8747–8761; (d) S. Ganapati and L. Isaacs, Isr. J. Chem., 2018, 58, 250–263.
2. W. L. Mock and N.-Y. Shih, J. Org. Chem., 1986, 51, 4440–4446.
3. Y. Kim, H. KIm, Y. H. Ko, N. Selvapalam, M. Rekharsky, Y. Inoue and K. Kim, Chem. – Eur. J., 2009, 15, 6143–6151.
4. P. Mukhopadhyay, A. Wu and L. Isaacs, J. Org. Chem., 2004, 69, 6157–6164.
5. S. Liu, C. Ruspic, P. Mukhopadhyay, S. Chakrabarti, P. Y. Zavalij and L. Isaacs, J. Am. Chem. Soc., 2005, 127, 15959–15967.
6. W. S. Jeon, K. Moon, S. H. Park, H. Chun, Y. H. Ko, J. Y. Lee, E. S. Lee, S. Samal, N. Selvapalam, M. V. Rekharsky, V. Sindelar, D. Sobransingh, Y. Inoue, A. E. Kaifer and K. Kim, J. Am. Chem. Soc., 2005, 127, 12984–12989.
7. M. V. Rekharsky, T. Mori, C. Yang, Y. H. Ko, N. Selvapalam, H. Kim, D. Sobransingh, A. E. Kaifer, S. Liu, L. Isaacs, W. Chen, S. Moghaddam, M. K. Gilson, K. Kim and Y. Inoue, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 20737–20742.
8. S. Moghaddam, C. Yang, M. Rekharsky, Y. H. Ko, K. Kim, Y. Inoue and M. K. Gilson, J. Am. Chem. Soc., 2011, 133, 3570–3581.
9. (a) W. M. Nau, M. Florea and K. I. Assaf, Isr. J. Chem., 2011, 51, 559–577; (b) F. Biedermann, V. D. Uzunova, O. A. Scherman, W. M. Nau and A. De Simone, J. Am. Chem. Soc., 2012, 134, 15318–15323; (c) F. Biedermann, W. M. Nau and H.-J. Schneider, Angew. Chem., Int. Ed., 2014, 53, 11158–11171; (d) K. I. Assaf and W. M. Nau, Chem. Soc. Rev., 2015, 44, 394–418.
10. (a) H. S. Muddana, C. Daniel Varnado, C. W. Bielawski, A. R. Urbach, L. Isaacs, M. T. Geballe and M. K. Gilson, J. Comput.-Aided Mol. Des., 2012, 26, 475–487; (b) K. I. Assaf, M. Florea, J. Antony, N. M. Henrikson, J. Yin, A. Hansen, Z.-W. Qu, R. Sure, D. Klapstein, M. K. Gilson, S. Grimme and W. M. Nau, J. Phys. Chem. B, 2017, 121, 11144–11162; (c) A. Rizzi, S. Murkli, J. N. McNeill, W. Yao, M. Sullivan, M. K. Gilson, M. W. Chiu, L. Isaacs, B. C. Gibb, D. L. Mobley and J. D. Chodera, J. Comput.-Aided Mol. Des., 2018, 32, 937–963.
11. M. Šekutor, K. Molčanov, L. Cao, L. Isaacs, R. Glaser and K. Mlinarić-Majerski, Eur. J. Org. Chem., 2014, 2533–2542.
12. E. Masson, Y. M. Shaker, J.-P. Masson, M. E. Kordesch and C. Yuwono, Org. Lett., 2011, 13, 3872–3875.
13. D. Sigwalt, M. Sekutor, L. Cao, P. Y. Zavalij, J. Hostas, H. Ajani, P. Hobza, K. Mlinaric-Majerski, R. Glaser and L. Isaacs, J. Am. Chem. Soc., 2017, 139, 3249–3258.
14. (a) W. L. Mock and J. Pierpont, J. Chem. Soc., Chem. Commun., 1990, 1509–1511; (b) Y. H. Ko, E. Kim, I. Hwang and K. Kim, Chem. Commun., 2007, 1305–1315; (c) N. Saleh, A. L. Koner and W. M. Nau, Angew. Chem., Int. Ed., 2008, 47, 5398–5401; (d) J. Del Barrio, P. Horton, D. Lairez, G. Lloyd, C. Toprakcioglu and O. Scherman, J. Am. Chem. Soc., 2013, 135, 11760–11763; (e) L. Isaacs, Acc. Chem. Res., 2014, 47, 2052–2062.
15. (a) G. Ghale and W. M. Nau, Acc. Chem. Res., 2014, 47, 2150–2159; (b) A. T. Bockus, L. C. Smith, A. G. Grice, O. A. Ali, C. C. Young, W. Mobley, A. Leek, J. L. Roberts, B. Vinciguerra, L. Isaacs and A. R. Urbach, J. Am. Chem. Soc., 2016, 138, 16549–16552; (c) E. G. Shcherbakova, B. Zhang, S. Gozem, T. Minami, P. Y. Zavalij, M. Pushina, L. D. Isaacs and P. Anzenbacher, J. Am. Chem. Soc., 2017, 139, 14954–14960.
16. (a) W. Li, A. T. Bockus, B. Vinciguerra, L. Isaacs and A. R. Urbach, Chem. Commun., 2016, 52, 8537–8540; (b) H. Yin and R. Wang, Isr. J. Chem., 2017, 58, 188–198; (c) X. Zhang, X. Xu, S. Li, L. Li, J. Zhang and R. Wang, Theranostics, 2019, 9, 633.
17. J. Tian, Z.-Y. Xu, D.-W. Zhang, H. Wang, S.-H. Xie, D.-W. Xu, Y.-H. Ren, H. Wang, Y. Liu and Z.-T. Li, Nat. Commun., 2016, 7, 11580.
18. L. Grimm, S. Spicher, B. Tkachenko, P. R. Schreiner, S. Grimme and F. Biedermann, Chem. – Eur. J., 2022, 28, e2022200529.
19. (a) L. Cao, M. Šekutor, P. Y. Zavalij, K. Mlinarić-Majerski, R. Glaser and L. Isaacs, Angew. Chem., Int. Ed., 2014, 53, 988–993; (b) L. Cao, D. Škalamera, P. Y. Zavalij, J. Hostaš, P. Hobza, K. Mlinarić-Majerski, R. Glaser and L. Isaacs, Org. Biomol. Chem., 2015, 13, 6249–6254; (c) J. Hostaš, D. Sigwalt, M. Šekutor, H. Ajani, M. Dubecky, J. Řezáč, P. Y. Zavalij, L. Cao, C. Wohlschlager, K. Mlinarić-Majerski, L. Isaacs, R. Glaser and P. Hobza, Chem. – Eur. J., 2016, 22, 17226–17238.
20. (a) A. A. Fokin, A. Merz, N. A. Fokina, H. Schwertfeger, S. L. Liu, J. E. Dahl, R. K. Carlson and P. R. Schreiner, Synthesis, 2009, 909–912; (b) H. Schwertfeger, C. Wuertele and P. R. Schreiner, Synthesis, 2010, 493–495.
21. (a) S. Grimme, J. Chem. Theory Comput., 2019, 15, 2847–2862; (b) P. Pracht, F. Bohle and S. Grimme, Phys. Chem. Chem. Phys., 2020, 22, 7169–7192.
22. D. Škalamera, L. Cao, L. Isaacs, R. Glaser and K. Mlinarić-Majerski, Tetrahedron, 2016, 72, 1541–1546.
23. L. Cao and L. Isaacs, Supramol. Chem., 2014, 26, 251–258.
24. (a) T. Wiseman, S. Williston, J. F. Brandts and L.-N. Lin, Anal. Biochem., 1989, 179, 131–137; (b) A. Velazquez-Campoy and E. Freire, Nat. Protoc., 2006, 1, 186–191; (c) J. Broecker, C. Vargas and S. Keller, Anal. Biochem., 2011, 418, 307–309.
25. S. Sinn, E. Spuling, S. Brase and F. Biedermann, Chem. Sci., 2019, 10, 6584–6593.
26. P. Montes-Navajas, A. Corma and H. Garcia, ChemPhysChem., 2008, 9, 713–720.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3nj00156c

---